Optimal Configuration of Energy Storage Systems in High PV Penetrating Distribution Network
Abstract
:1. Introduction
- Proposed a method for optimal allocation of energy storage capacity of a distribution network based on a two-layer programming model and verified its feasibility.
- Used the K-means method to complete an analysis of the uncertain photovoltaic output into the deterministic scenario.
- The multi-objective particle swarm optimization algorithm was improved to solve the optimal configuration, and the advantages of the improved algorithm were compared.
- By constructing different scenarios, it was verified that energy storage can still improve the power quality in the distribution network with high-light voltage and permeability.
- Through analysis of the optimal configuration of energy storage in the distribution network with different photovoltaic permeabilities, the optimal economic photovoltaic permeability was concluded.
2. Analysis of Photovoltaic Output Characteristic
2.1. K-Means Cluster Analysis Method
- ①
- target scenes with random data are set as the cluster center, and the set of these scenes is .
- ②
- Excluding the cluster center set, the other scene set is set as , and the distance from the other scene set to the cluster center scene set is calculated:
- ③
- The other scene sets excluding the cluster center set are divided into the nearest cluster center according to the distance calculated in ②. We obtain the cluster set , where is a set of similar scenarios.
- ④
- Set the same cluster including scenarios. Add the distances from each scenarios to the others: , and scene in is selected as the clustering center of the next iteration. This is used to calculate the next iteration cluster center set.
- ⑤
- At this point, stable cluster centers and clustering results can be obtained by repeating steps ②–④. The probability number of each type of scenario is the probability number of a single scenario in that type of scenario.
2.2. Selection of Typical Output Scenarios
3. BESS Bi-Level Decision-Making Model Configuration
3.1. Upper-Level Model Objective Function
3.2. Lower Objective Function
- (1)
- The voltage fluctuation of distribution network nodes caused by energy storage access can be expressed as:where indicates the number of system nodes, and indicates the voltage value of node at time .
- (2)
- The load fluctuation of the distribution network caused by access to energy storage can be expressed as:where represents the average load in a period of time when energy storage is connected.
3.3. Constraints
- (1)
- Constraints at the BESS access nodewhere are nodes invested in energy storage, and is the maximum number of nodes expressed as energy storage input.
- (2)
- The constraints of power rating and capacity energy storage devices can be expressed aswhere and is the maximum and minimum value of the rated output of the energy storage, and and are the maximum and minimum values of the energy storage input capacity.
- (3)
- Power balance constraintswhere is the power value received by the grid, is the PV output power, is the output power, is the network loss, and is the BESS input power.
- (5)
- BESS charge and discharge power constraints
- (6)
- Voltage constraints in distribution network nodeswhere and are the minimum and maximum voltages of node at time .Energy storage system constraintswhere is the initial state of the energy storage system, including power and capacity. is the rated capacity of the energy storage battery.
- (7)
- Supplementary constraints
- ①
- Due to the limitation of the range of the BESS, there will be a large number of infeasible solutions during the recovery of its all-day charging and discharging power. If its charge and discharge power is processed, this will greatly improve the convergence rate in the solution process and reduce the amount of calculation.where is the energy storage charge and discharge power value that has been processed at time . In this way, the infeasible solution is transformed into an effective feasible solution, and the charging and discharging power that is not within the SOC range of the energy storage is changed to 0.
- ②
- Using the penalty function method to deal with the constraints that are not within the valid range:where is the penalty coefficient. indicates the negative inequality constraint. indicates the positive inequality constraints. indicates the equality constraint at zero. are the number of constraints.
4. Solution of Model
- ①
- Input the demand parameters of the distribution network into the system.
- ②
- Initialize the decision variables for the upper level (including BESS installation location, power rating, and capacity). Under the constraint, the population and other parameters of the GA algorithm are initialized.
- ③
- Initialize the decision variables of the lower level, including the BESS charge–discharge method. Under its constraints, the IMOPSO algorithm population and other related parameters are initialized to solve the initial fitness of each optimization objective.
- ④
- After the optimization of the lower layer is completed, the TOPSIS multi-attribute decision-making method is used to select the upper Pareto solution set obtained, and the best scheme is selected and fed back to the upper layer to solve the fitness of the upper layer target.
- ⑤
- The upper-level GA algorithm population is updated, and the third and fourth steps are continuously executed until the upper-level optimization is completed.
- ⑥
- The optimal BESS configuration scheme of the upper layer, the corresponding optimal charge-discharge method of the lower layer, and the optimal Pareto solution set are obtained.
4.1. Improved PSO Algorithm
4.2. Multi-Attribute Decision-Making Based on TOPSIS Method
5. Analysis and Discussion
5.1. Case Description
5.2. Energy Storage Optimization Scenario Division
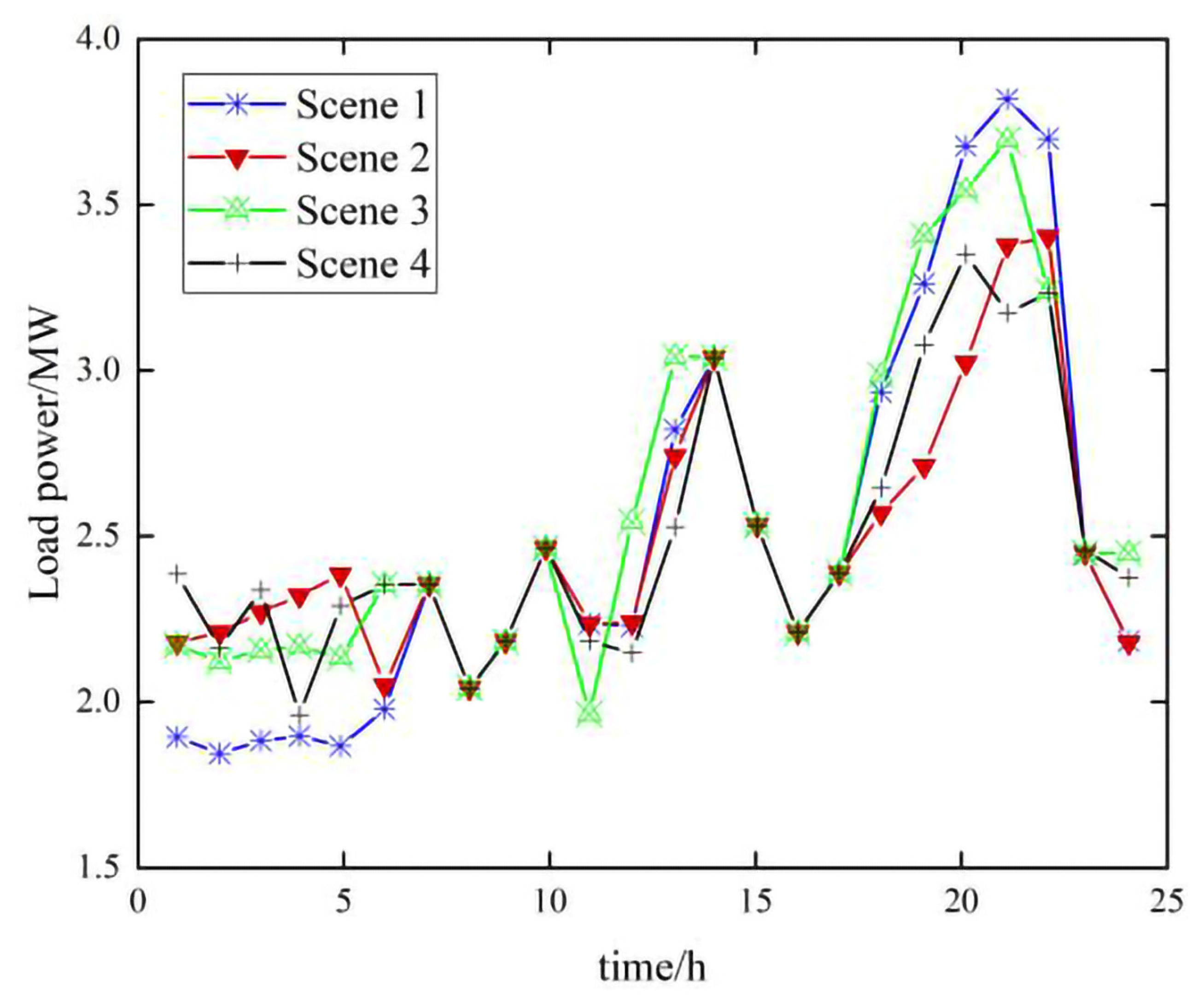
- Scenario 1:
- No energy storage.
- Scenario 2:
- With access to energy storage, use the IMOPSO algorithm in this paper to solve the optimization objective of lower-level model in the bi-level decision-making model; introduce the charging and discharging strategy of the energy storage system to simulate and analyze it.
- Scenario 3:
- When solving its single-level model, ignore the charging and discharging management strategy of energy storage in the lower model, and only the energy storage system and distribution network are considered to have the lowest total cost. At the same time, in the time-of-use electricity price model, the energy storage system is charged and discharged at a constant power regardless of the high or low electricity price.
- Scenario 4:
- The optimal configuration result of energy storage in Scenario 2 is used as the constraint condition of this scenario, and the traditional multi-objective PSO algorithm is used to simulate and analyze the lower model in the optimal configuration model of the energy storage double-level. Node voltage curves and load curves in different scenarios are shown in Figure 10 and Figure 11 below, and Table 5 shows the optimization results of different scenarios.
5.3. Energy Storage Benefit Analysis under Different Photovoltaic Permeability
6. Conclusions
- ①
- Access to energy storage can effectively smooth the load fluctuation and voltage fluctuation of system nodes in a photovoltaic distribution network. In a distribution network with high-light volt permeability, energy storage can effectively improve the off-peak load of the distribution network and reduce the peak load, thus increasing the scheduling flexibility of the distribution network.
- ②
- The bi-level programming model proposed in this paper has a good optimization ability for the rational allocation of energy storage.
- ③
- The improved IMOPSO in this paper has good convergence performance and robustness and has good applicability in application optimization
- ④
- When the optimal energy storage capacity under different photovoltaic permeability is configured, the total cost of the system is optimal when the photovoltaic permeability is 45%, and when the permeability increases again, the total cost of the system will keep rising and seriously affect the operation economy of the system.The analysis of this paper provides a theoretical basis for the optimal configuration of the energy storage system and an important reference for the safe, stable, and economic operation of a high permeability photovoltaic distribution network.
7. Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yao, M.; Cai, X. An Overview of the Photovoltaic Industry Status and Perspective in China. IEEE Access 2019, 7, 181051–181060. [Google Scholar] [CrossRef]
- Jothibasu, S.; Dubey, A.; Santoso, S. Two-Stage Distribution Circuit Design Framework for High Levels of Photovoltaic Generation. IEEE Trans. Power Syst. 2019, 34, 5217–5226. [Google Scholar] [CrossRef]
- Pan, W.; Mao, M.; Zhou, Y.; Quan, X.; Li, Y. The impact of extreme weather condition on the voltage regulation in distribution systems with high penetration of roof-top photovoltaic. Energy Rep. 2021, 7, 320–331. [Google Scholar] [CrossRef]
- Chidurala, A.; Saha, T.K.; Mithulananthan, N. Harmonic impact of high penetration photovoltaic system on unbalanced distribution networks—Learning from an urban photovoltaic network. IET Renew. Power Gener. 2016, 10, 485–494. [Google Scholar] [CrossRef]
- Karimi, M.; Mokhlis, H.; Naidu, K.; Uddin, S.; Bakar, A. Photovoltaic penetration issues and impacts in distribution network – A review. Renew. Sustain. Energy Rev. 2016, 53, 594–605. [Google Scholar] [CrossRef]
- Gandhi, O.; Rodríguez-Gallegos, C.D.; Zhang, W.; Reindl, T.; Srinivasan, D. Levelised cost of PV integration for distribution networks. Renew. Sustain. Energy Rev. 2022, 169, 112922. [Google Scholar] [CrossRef]
- Dhivya, S.K.; Anurag, S.; Dipti, S.; Reindl, T. Stability implications of bulk power networks with large scale PVs. Energy 2019, 187, 115927. [Google Scholar]
- Maharjan, S.; Dhivya, S.K.; Khambadkone, A.M. Enhancing the voltage stability of distribution network during PV ramping conditions with variable speed drive loads. Appl. Energy 2020, 264, 114733. [Google Scholar] [CrossRef]
- Garmabdari, R.; Moghimi, M.; Yang, F.; Lu, J. Multi-objective energy storage capacity optimisation considering Microgrid generation uncertainties. Int. J. Electr. Power Energy Syst. 2020, 199, 105908. [Google Scholar] [CrossRef]
- Kamaruzzaman, Z.A.; Mohamed, A. Dynamic voltage stability of a distribution system with high penetration of grid-connected photovoltaic type solar generators. J. Electr. Syst. 2016, 12, 239–248. [Google Scholar]
- Xu, Z.; Yuan, B.; Liu, J.; Zheng, K.; Xu, S. Energy storage configuration for smoothing the output volatility of PV power generation. IOP Conf. Ser. Earth Environ. Sci. 2019, 295, 052045. [Google Scholar] [CrossRef]
- Rana, M.M.; Uddin, M.; Sarkar, M.R.; Shafiullah, G.M.; Huadong, M.; Atef, M. A review on hybrid photovoltaic—Battery energy storage system: Current status, challenges, and future directions. J. Energy Storage 2022, 51, 104597. [Google Scholar] [CrossRef]
- Haytham, M.A.A.; Ahmed, S.A.A.; Mohamed, H.A.; Salama, M.M.A. Mitigating voltage-sag and voltage-deviation problems in distribution networks using battery energy storage systems. Electr. Power Syst. Res. 2020, 184, 106294. [Google Scholar]
- Amini, M.; Khorsandi, A.; Vahidi, B.; Hosseinian, S.H.; Malakmahmoudi, A. Optimal sizing of battery energy storage in a microgrid considering capacity degradation and replacement year. Electr. Power Syst. Res. 2021, 195, 107170. [Google Scholar] [CrossRef]
- Hossain, S.J.; Biswas, B.D.; Bhattarai, R.; Ahmed, M.; Abdelrazek, S.; Kamalasadan, S. Operational Value Based Energy Storage Management for Photo-Voltaic(PV) Integrated Active Power DistributionSystems. IEEE Trans. Ind. Appl. 2019, 99, 5320–5330. [Google Scholar] [CrossRef]
- Koohi-Fayegh, S.; Rosen, M.A. A review of energy storage types, applications and recent developments. J. Energy Storage 2020, 2, 101047. [Google Scholar] [CrossRef]
- Chang, L.; Zhuo, J.; Zhao, D.; Li, S.; Chen, J.; Wang, J.; Yao, Q. A review on Flexible and safe operation of renewable energy microgrid using energy storage system. Proc. CSEE 2020, 1, 1–18+369. [Google Scholar]
- Rajamand, S.; Miadreza, S.-K.; Catalão, J.P.S. Energy storage systems implementation and photovoltaic output prediction for cost minimization of a Microgrid. Electr. Power Syst. Res. 2022, 202, 107596. [Google Scholar] [CrossRef]
- Rahman, S.; Saha, S.; Haque, M.E.; Islam, S.N.; Arif, M.T.; Mosadeghy, M.; Oo, A.M.T. A framework to assess voltage stability of power grids with high penetration of solar PV systems. Int. J. Electr. Power Energy Syst. 2022, 139, 107815. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, T.; Peng, X.; Zhang, X. A novel long-term power forecasting based smart grid hybrid energy storage system optimal sizing method considering uncertainties. Inf. Sci. 2022, 610, 326–344. [Google Scholar] [CrossRef]
- Liang, J.; Lan, F.; Li, J. A grid scenario evaluation method for energy storage capacity demand of photovoltaic-based distribution network. Autom. Electr. Power Syst. 2018, 42, 40–47+85. [Google Scholar]
- Shoaib, B.; Muhammad, A.; Muqeet Hafiz, A.; Muhammad, S.; Harun, J.; Monia, H.; Sattar, M.A.; Habib, H. Optimal Scheduling of Demand Side Load Management of Smart Grid Considering Energy Efficiency. Front. Energy Res. 2022, 10, 861571. [Google Scholar]
- Waseem, M.; Lin, Z.; Liu, S.; Sajjad, I.A.; Aziz, T. Optimal GWCSO-based home appliances scheduling for demand response considering end-users comfort. Electr. Power Syst. Res. 2020, 187, 106477. [Google Scholar] [CrossRef]
- Rezaeimozafar, M.; Eskandari, M.; Hadi Amini, M.; Moradi, M.H.; Siano, P. A Bi-Layer Multi-Objective Techno-Economical Optimization Model for Optimal Integration of Distributed Energy Resources into Smart/Micro Grids. Energies 2020, 13, 1706. [Google Scholar] [CrossRef] [Green Version]
- Waseem, M.; Lin, Z.; Liu, S.; Zhang, Z.; Aziz, T.; Khan, D. Fuzzy compromised solution-based novel home appliances scheduling and demand response with optimal dispatch of distributed energy resources. Appl. Energy 2021, 290, 116761. [Google Scholar] [CrossRef]
- Li, D.; Cai, W. Optimal configuration of photovoltaic energy storage capacity for large power users. Energy Rep. 2021, 7 (Suppl. S7), 468–478. [Google Scholar] [CrossRef]
- Yang, P.; Nehorai, A. Joint Optimization of Hybrid Energy Storage and Generation Capacity with Renewable Energy. IEEE Trans. Smart Grid 2014, 5, 1566–1574. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Wen, C.; Li, S.; Shi, Q. Capacity optimization allocation of photovoltaic energy storage system based on TOU. Adv. Technol. Electr. Eng. Energy 2018, 37, 23–30. [Google Scholar]
- Lima, D.A.; Feijão, V.R. Stochastic approach for economic viability of photovoltaic systems with battery storage for big electricity consumers in the regulated marketin Brazil. Electr. Power Syst. Res. 2022, 205, 107744. [Google Scholar] [CrossRef]
- Guo, Y.; Xiang, Y. Cost–benefit analysis of photovoltaic-storage investment in integrated energy systems. Energy Rep. 2022, 8 (Suppl. S5), 66–71. [Google Scholar] [CrossRef]
- Lu, S.; Wang, X.; Wu, J. Location and Size Planning of Distributed Photovoltaic Generation in Distribution network System Based on K-means Clustering Analysis. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 052022. [Google Scholar] [CrossRef]
- Home-Ortiz, J.M.; Pourakbari-Kasmaei, M.; Lehtonen, M.; Sanches Mantovani, J.R. Optimal location-allocation of storage devices and renewable-based DG in distribution systems. Electr. Power Syst. Res. 2019, 172, 11–21. [Google Scholar] [CrossRef]
- Wang, W.; Dou, F.; Yu, X.; Liu, G. Scenario analysis of wind power output based on improved k-means algorithm. IOP Conf. Ser. Earth Environ. Sci. 2021, 675, 012092. [Google Scholar] [CrossRef]
- Liang, G.; Sun, B.; Zeng, Y.; Ge, L.; Li, Y.; Wang, Y. An Optimal Allocation Method of Distributed PV and Energy Storage Considering Moderate Curtailment Measure. Energies 2022, 15, 7690. [Google Scholar] [CrossRef]
- Feng, J.; Zhou, H. Bi-Level Optimal Capacity Planning of Load-Side Electric Energy Storage Using an Emission-Considered Carbon Incentive Mechanism. Energies 2022, 15, 4592. [Google Scholar] [CrossRef]
- Feng, H.; Ma, W.; Yin, C.; Cao, D. Trajectory control of electro-hydraulic position servo system using improved PSO-PID controller. Autom. Constr. 2021, 127, 103722. [Google Scholar] [CrossRef]
- Wang, G.; Wan, Z.; Wang, X. Review of two (double) level planning. Adv. Math. 2007, 5, 513–529. [Google Scholar]
- Gong, Z. Study on Two-Stage Optimal Scheduling Strategy and Time-of-Use Price Optimization of Optical Storage System. Master’s Thesis, Hefei University of Technology, Hefei, China, 2021. [Google Scholar]

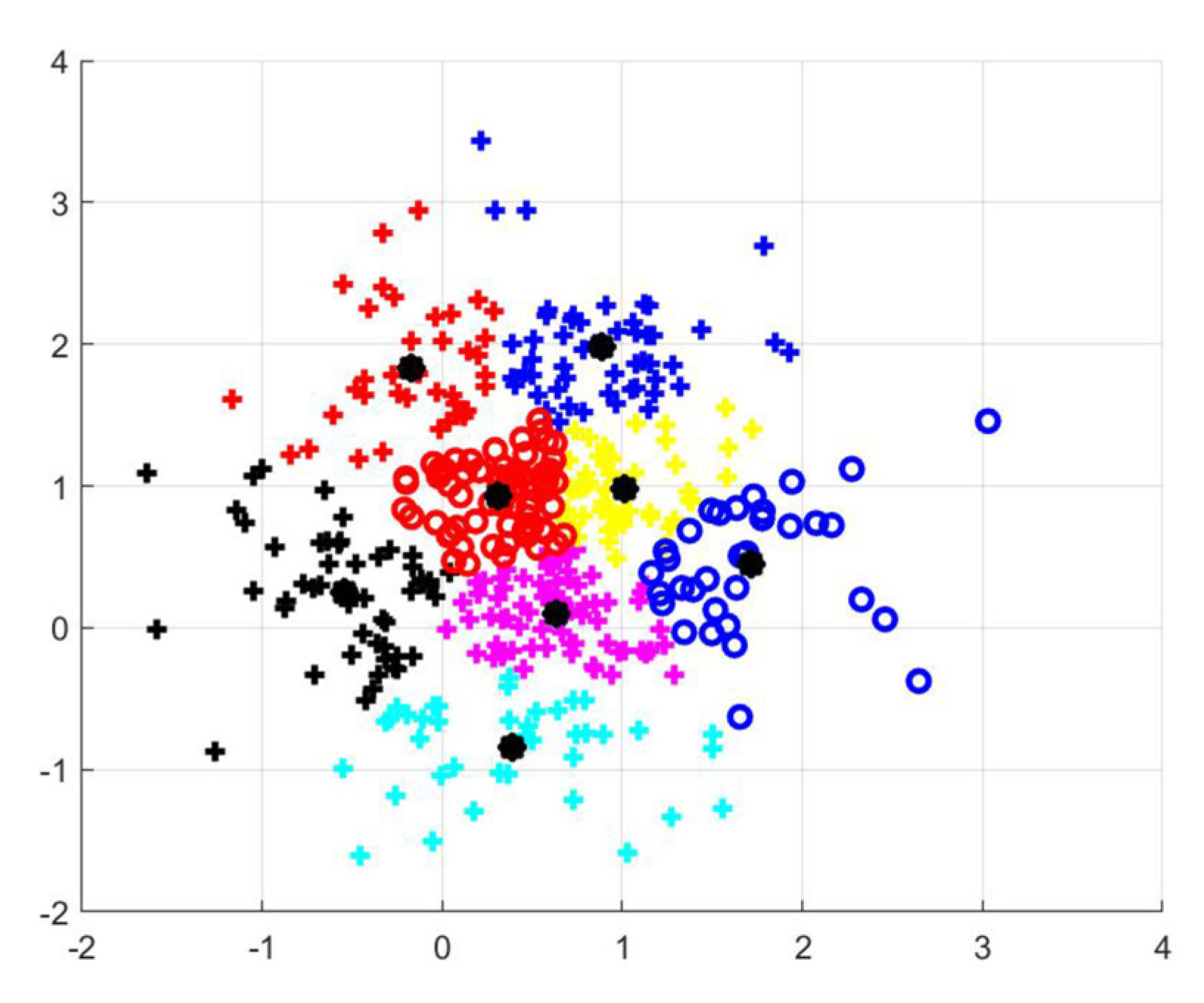














| Scenario | Number of Curves | Probability | Scenario | Number of Curves | Probability |
|---|---|---|---|---|---|
| 1 | 35 | 0.0959 | 4 | 24 | 0.0658 |
| 2 | 7 | 0.0192 | 5 | 127 | 0.3479 |
| 3 | 75 | 0.2055 | 6 | 97 | 0.2658 |
| Type | Period | Electricity Price (yuan/kWh) |
|---|---|---|
| Peak time | 17:00–22:00 | 0.9796 |
| Normal time | 8:00–17:00 22:00–00:00 | 0.6570 |
| Trough time | 00:00–8:00 | 0.35 |
| Energy Storage Control Parameters | Data |
|---|---|
| Service life (year) | 11 |
| Discount Rate | 0.02 |
| Rated power cost (yuan/kW) | 1000 |
| Installation cost (yuan/kW) | 2500 |
| Operation and maintenance cost (yuan/kW) | 0.05 |
| State of charge SOC range | 20–90% |
| Rated power upper limit (MW) | 1 |
| Maximum installed capacity (MWh) | 5 |
| Parameter | Data |
|---|---|
| Power purchase cost of grid | 0.35 |
| Expansion cost | 1000 |
| Expansion annual profit margin | 8% |
| Load annual growth rate | 1.5% |
| Genetic algorithm population size/number of iterations | 60/200 |
| IMOPSO algorithm population size/number of iterations | 100/200 |
| Crossover/variation rate | 0.1/0.05 |
| Inertia weight range | 0.4–0.9 |
| Threshold for difference X | 0.1 |
| The size of the Pareto solution set | 100 |
| Scenario | Node/Power (kw)/Capacity (kwh) | Cost of Investment | Distribution Network Operating Costs (Yuan) | Voltage Fluctuation Value | Load Variance | Total Cost (Yuan) | Degrees of Savings |
|---|---|---|---|---|---|---|---|
| 1 | - | 0 | 16,703.6 | 70.21 | 36,5721.76 | 16,703.6 | 1.77% |
| 2 | 14,650,3392 | 1879.32 | 14,532.67 | 63.52 | 15,3971.12 | 16,411.99 | 0% |
| 3 | 20,273,2733 | 1497.62 | 15,717.64 | 64.98 | 24,9754.21 | 17,215.26 | 4.89% |
| 4 | 14,650,3392 | 1879.32 | 14,767.71 | 64.85 | 15,9894.09 | 16,647.03 | 1.43% |
| Algorithm | External Solution | Distance ‘S’ | |
|---|---|---|---|
| Node Voltage Fluctuation | Load Fluctuation | ||
| MOPSO | 0.8869 | 0.2103 | 0.0485 |
| IMOPSO | 0.7154 | 0.1226 | 0.0317 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Zhu, L.; Zhao, S.; Yan, J.; Lv, L. Optimal Configuration of Energy Storage Systems in High PV Penetrating Distribution Network. Energies 2023, 16, 2168. https://doi.org/10.3390/en16052168
Zhang J, Zhu L, Zhao S, Yan J, Lv L. Optimal Configuration of Energy Storage Systems in High PV Penetrating Distribution Network. Energies. 2023; 16(5):2168. https://doi.org/10.3390/en16052168
Chicago/Turabian StyleZhang, Jinhua, Liding Zhu, Shengchao Zhao, Jie Yan, and Lingling Lv. 2023. "Optimal Configuration of Energy Storage Systems in High PV Penetrating Distribution Network" Energies 16, no. 5: 2168. https://doi.org/10.3390/en16052168
APA StyleZhang, J., Zhu, L., Zhao, S., Yan, J., & Lv, L. (2023). Optimal Configuration of Energy Storage Systems in High PV Penetrating Distribution Network. Energies, 16(5), 2168. https://doi.org/10.3390/en16052168








