d-q Small-Signal Model for Grid-Forming MMC and Its Application in Electromagnetic-Transient Simulations
Abstract
:1. Introduction
- A small-signal model for a grid-forming MMC with dual-loop control. This model includes not only the equivalent impedance, but also the open-circuit voltage-to-reference transfer matrix of the converter;
- A framework for simulation and analyzing inverter-based power grids using impedance models and voltage-to-reference and current-to-reference transfer matrices.
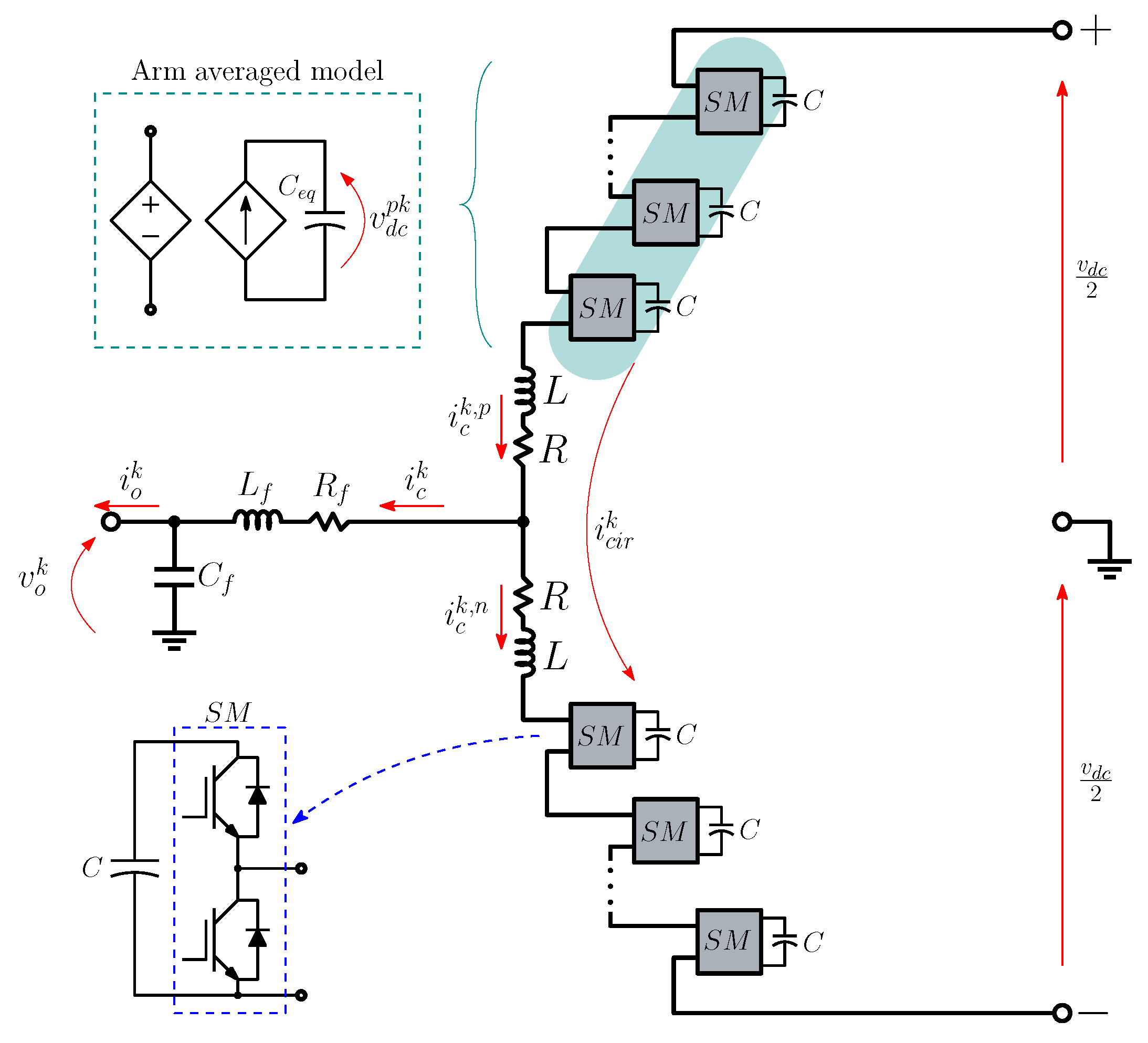
2. Modular Multilevel Converter
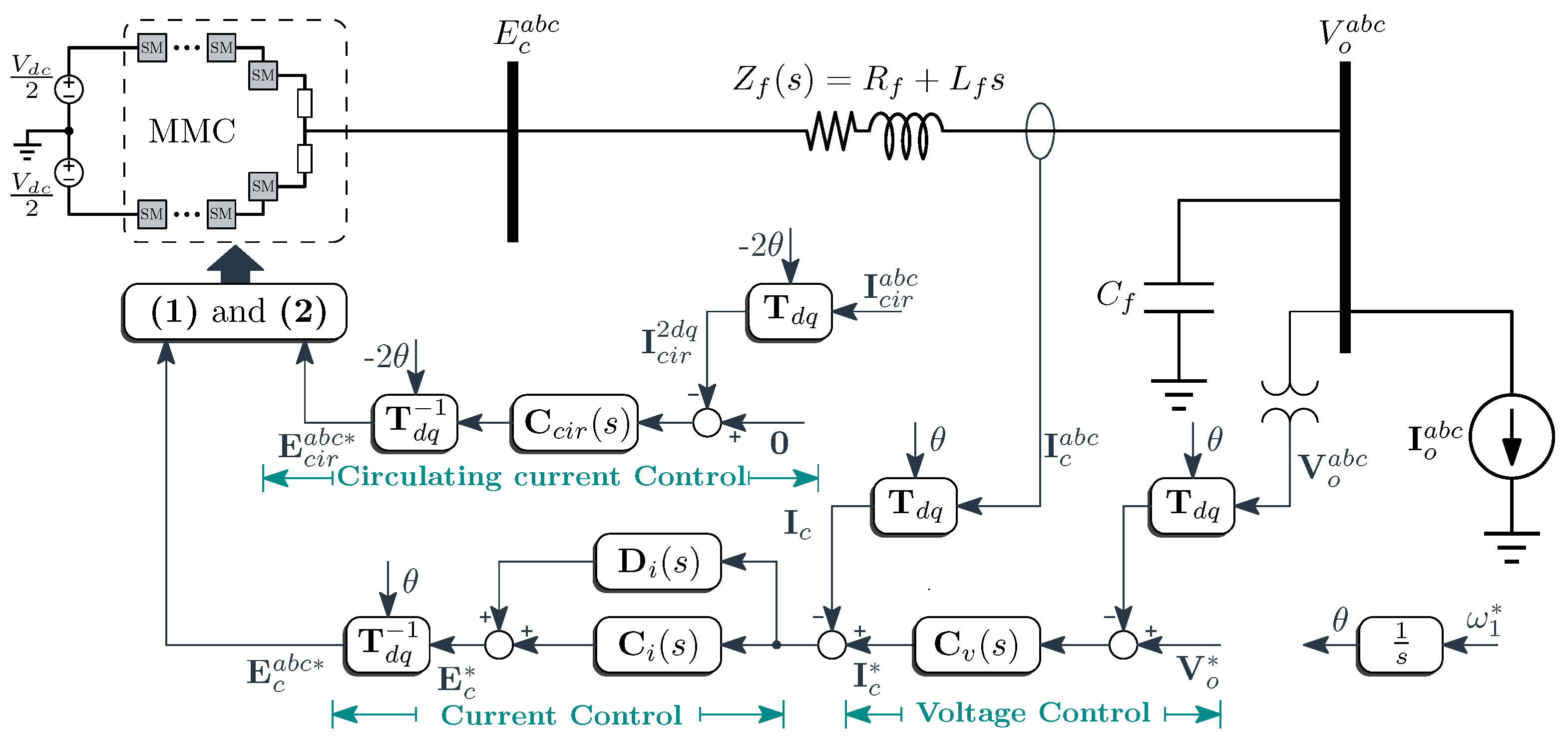
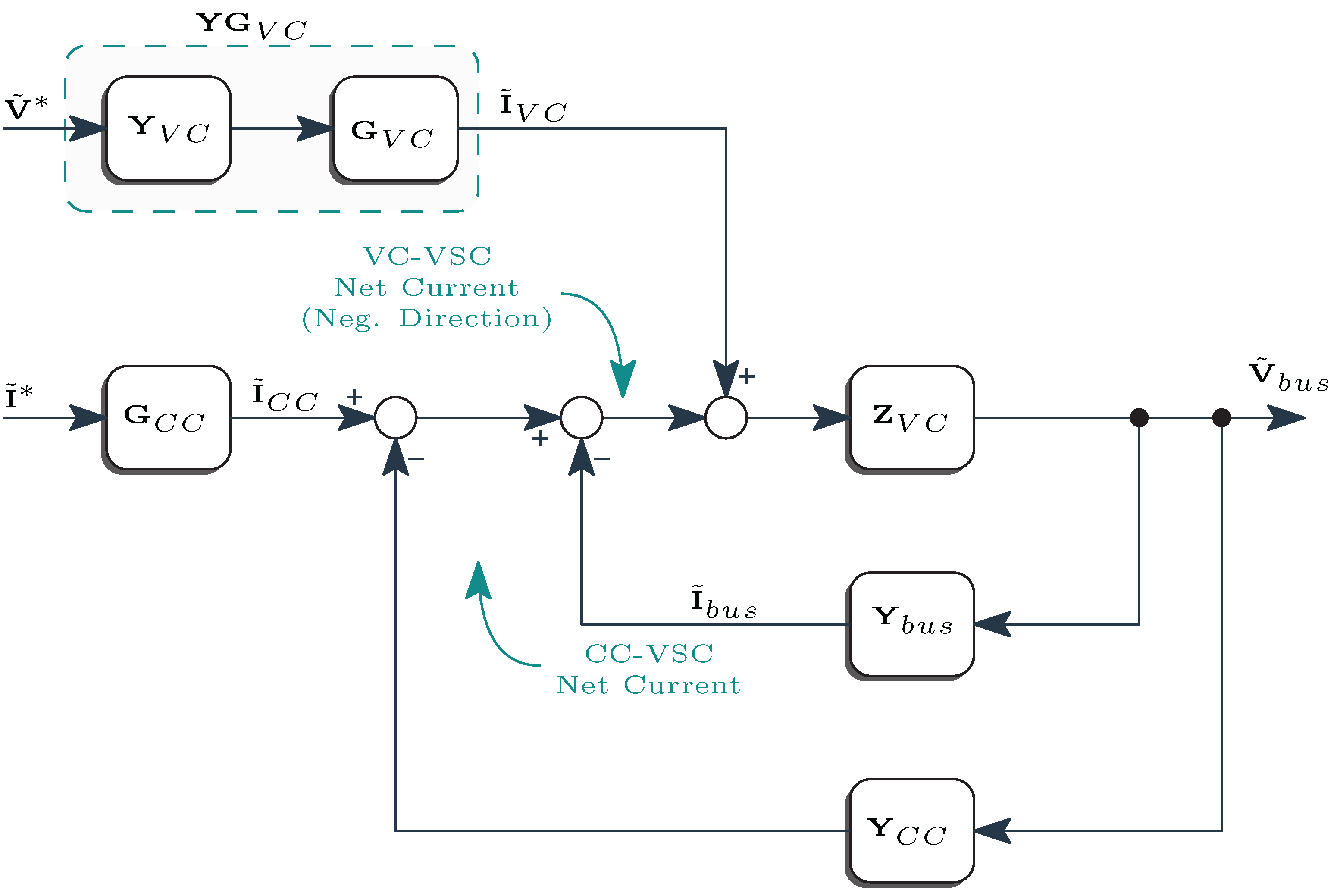
3. Control and Modeling of the MMC
3.1. Output-Current Loop
3.2. Main-Bus Voltage Loop
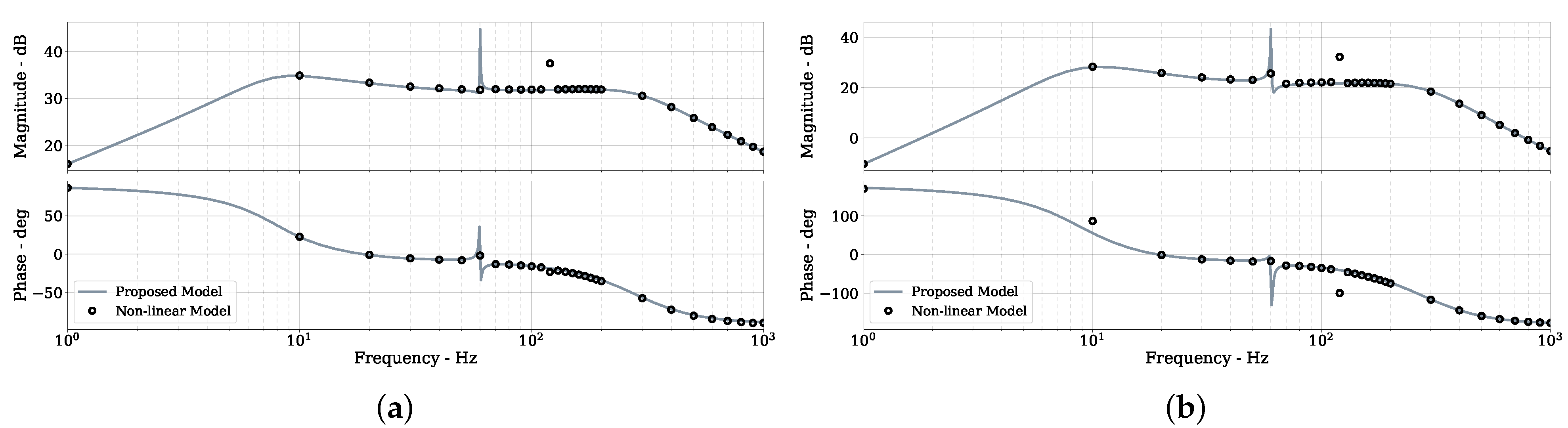
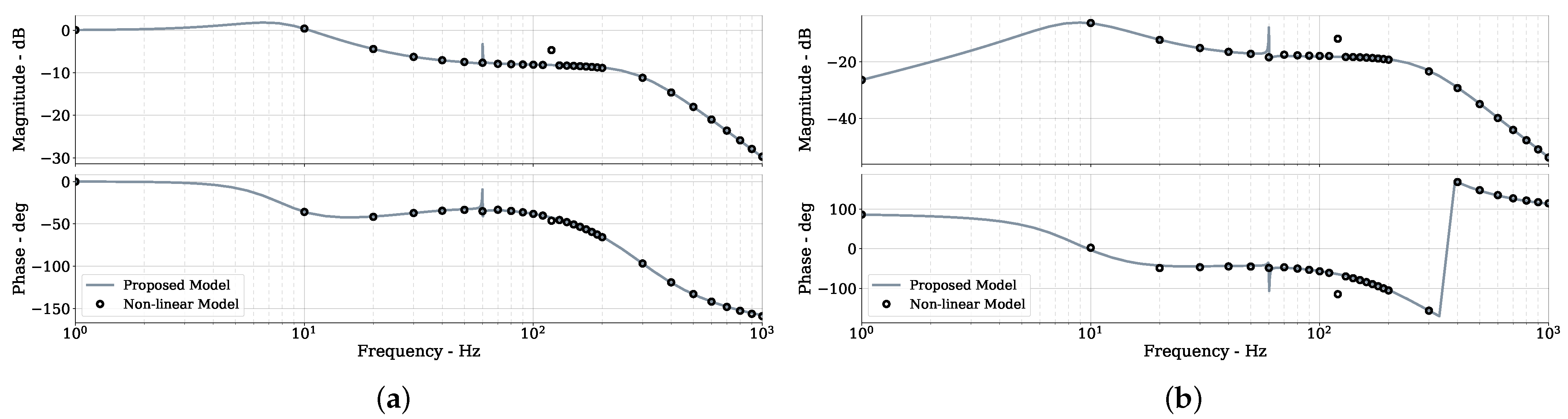
4. Frequency Responses of the MMC
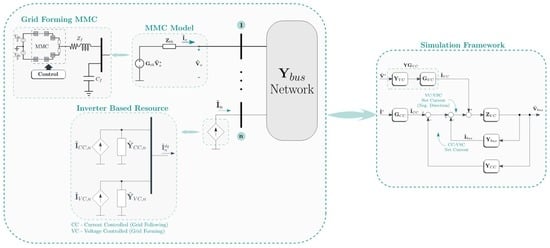
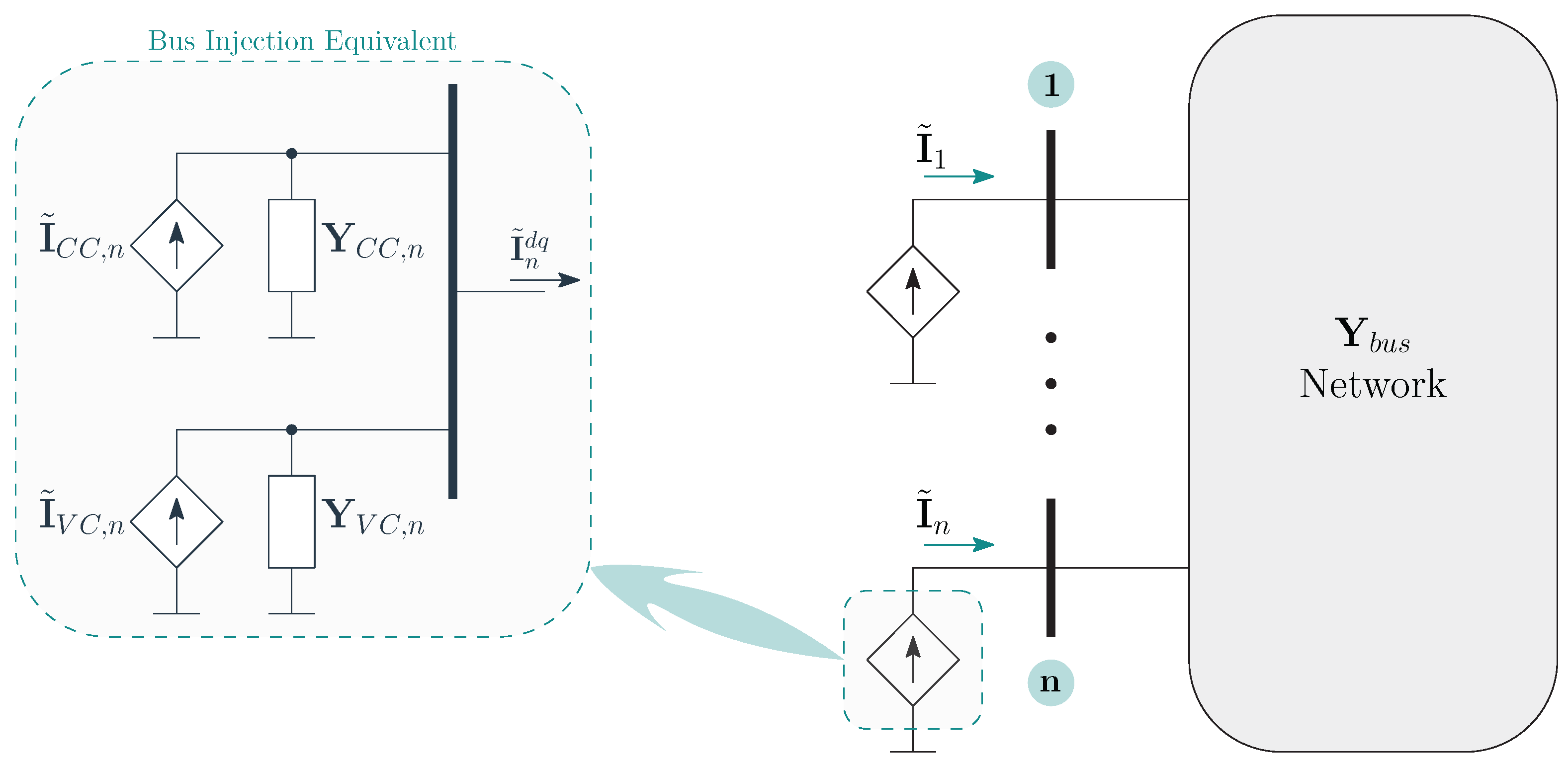
5. Impedance-Based Simulation Framework for Converter-Populated Power Systems
5.1. Simulation Framework
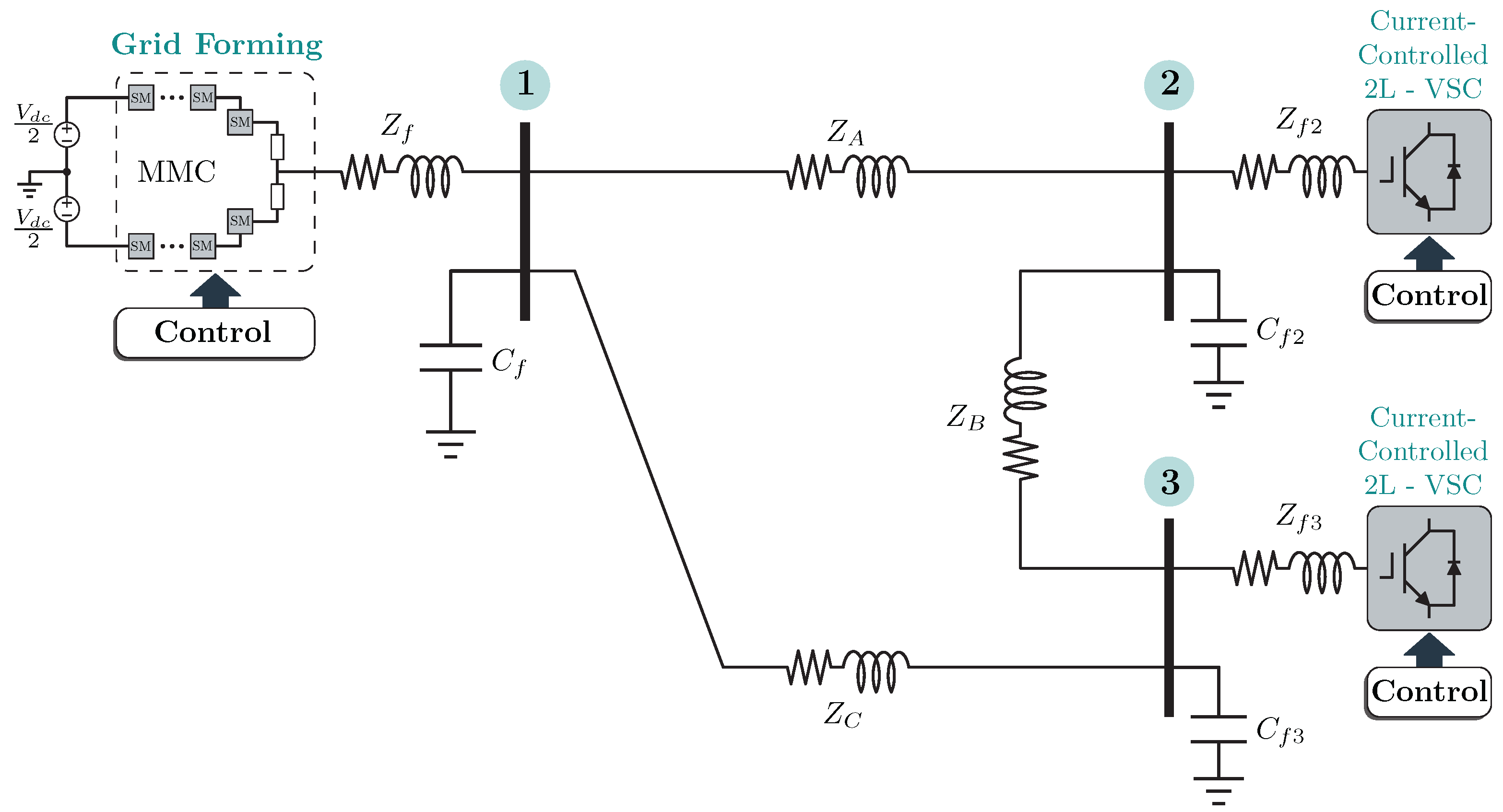
5.2. Three-Bus Test Case
5.2.1. Current-Controlled Two-Level Converter Model
5.2.2. Implementation of the Simulation Framework
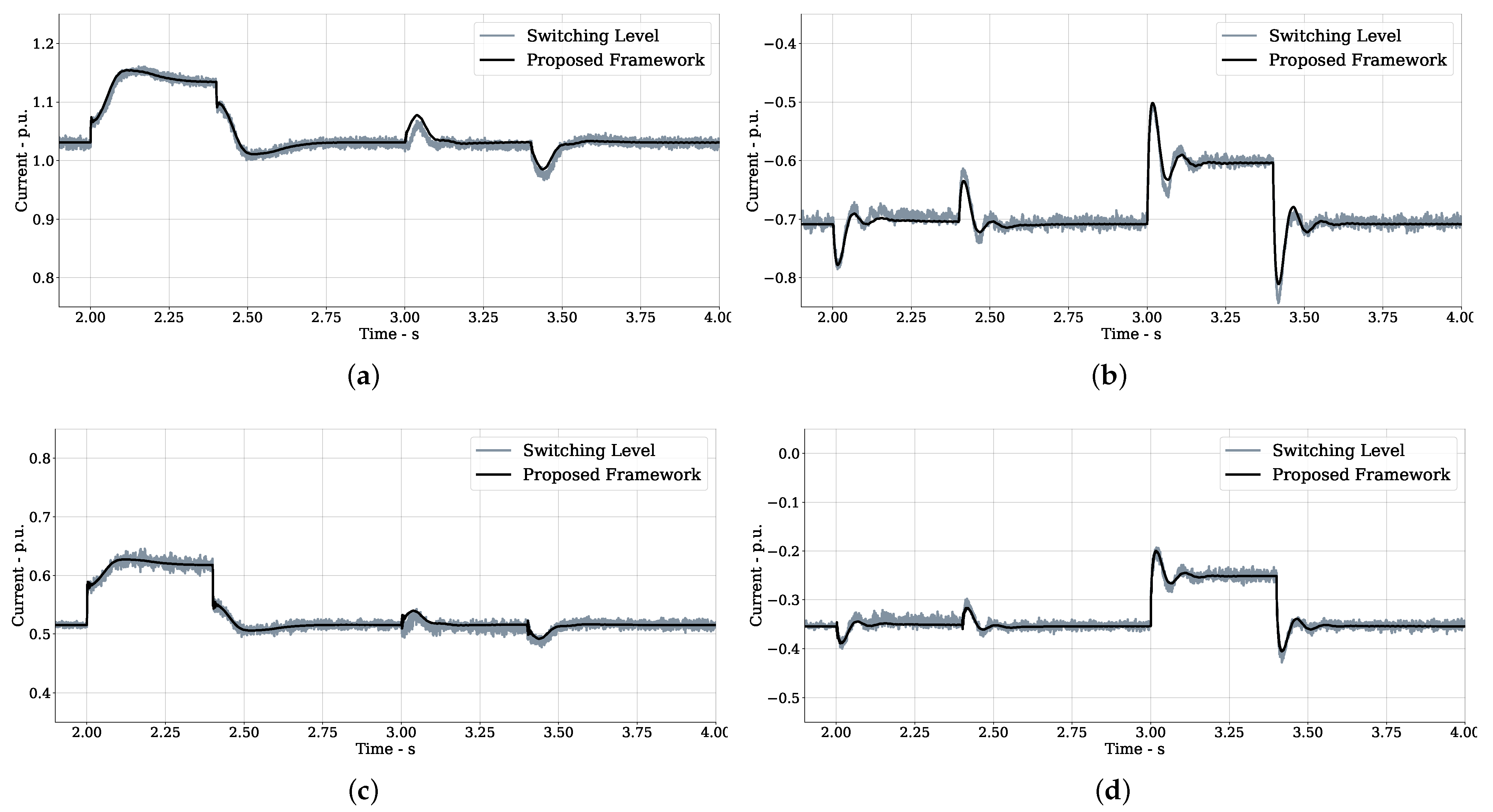
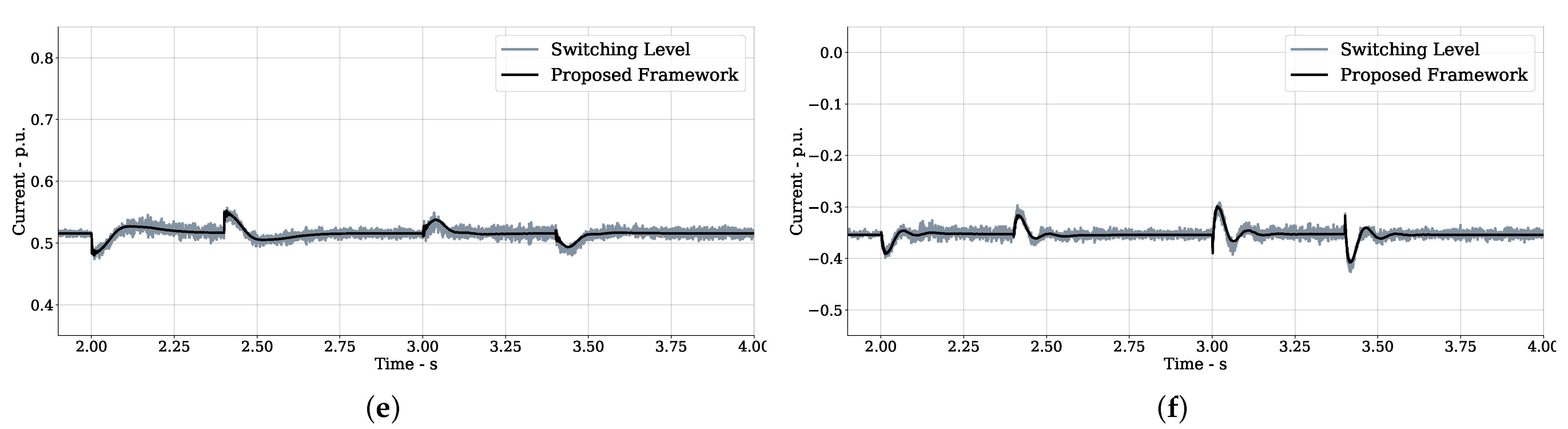
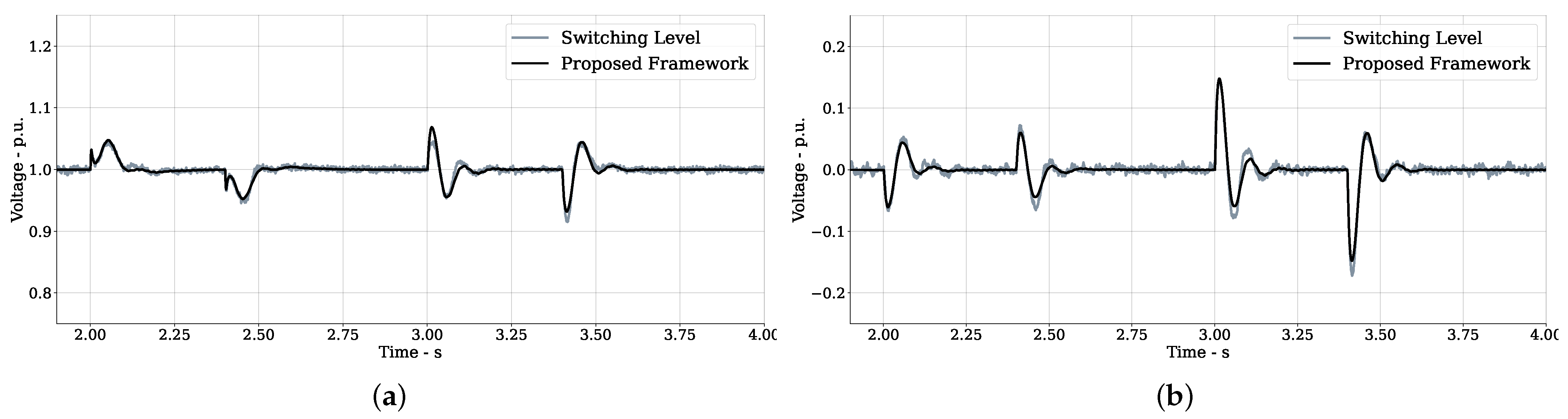
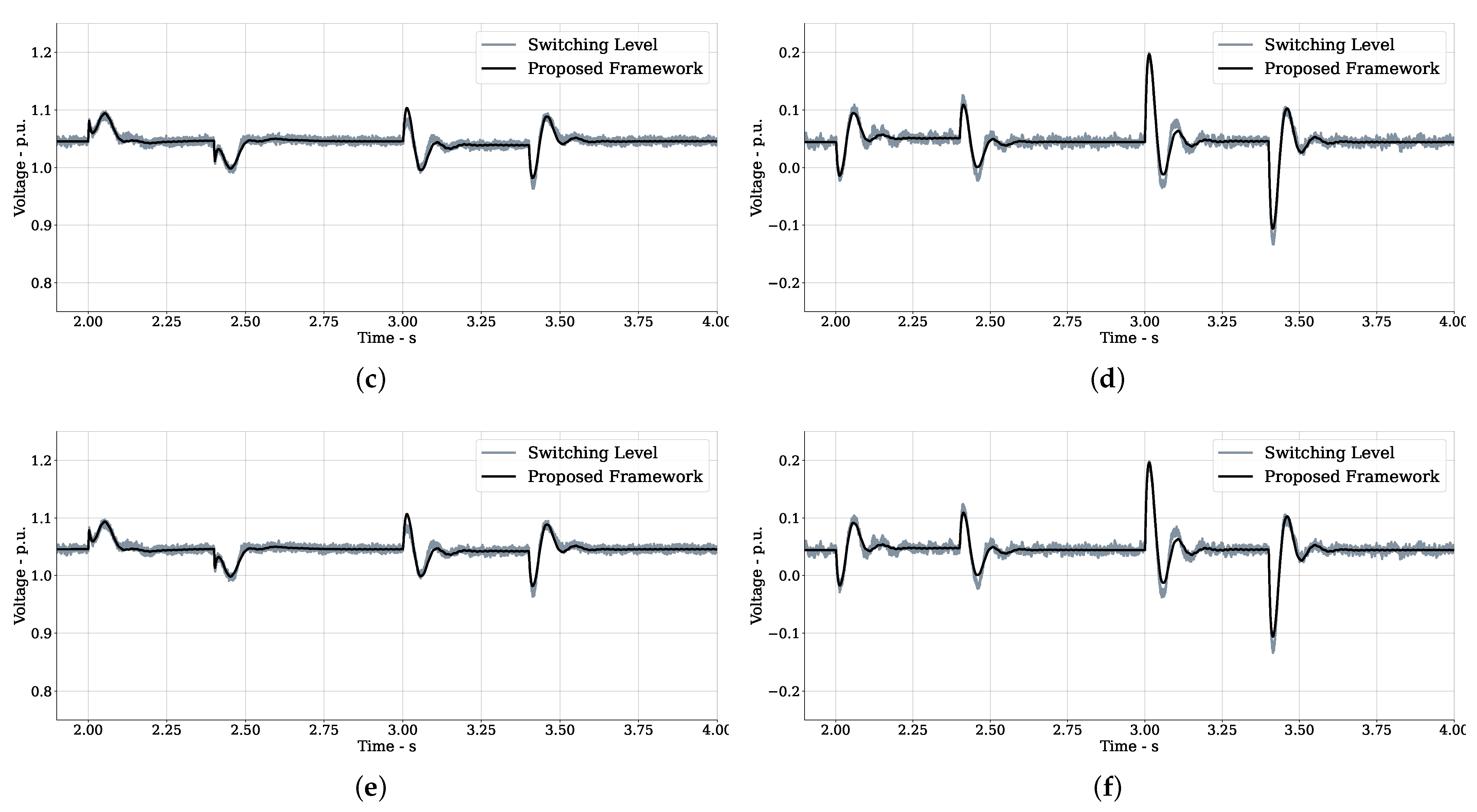
5.3. Results and Comparison
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Parameter-Settings Tables
| MMC | ||
|---|---|---|
| Current-loop Control | / | 0.001 /0.01 s |
| Voltage-loop Control | / | 0.01 /0.01 s |
| Circ-Current-loop Control | / | 0.001 /0.01 s |
| MMC | ||
|---|---|---|
| Rated Power | - | 100 MVA |
| Rated AC Voltage | - | 69 kV |
| Rated DC Voltage | - | 150 kV |
| Number of SMs | N | 20 |
| SM Capacitor | C | 9000 F |
| Arm Impedance | R/L | 1 /19 mH |
| Output Impedance | / | 1 /20 mH |
| AC capacitor bank | 20 F | |
| Two-Level VSCs (Reflected to the High-Voltage Side) and Power Grid | ||
|---|---|---|
| Rated Power | - | 50 MVA |
| Rated AC Voltage | - | 69 kV |
| Rated DC Voltage | - | 125 kV |
| Switching Frequency | - | 2 kHz |
| Output Impedance | / | 1 /20 mH |
| Capacitor bank | / | 20 F |
| Current-loop Control | / | 0.001 A−1/ 0.1 s |
| PLL Control | / | 0.1 rad s−1 V−1/0.001 s |
| Series Impedance A | / | 0.94 /12.5 mH |
| Series Impedance B | / | 0.94 /12.5 mH |
| Series Impedance C | / | 0.94 /12.5 mH |
| Rated Frequency | 60 Hz | |
Appendix B. Some Mathematical Results
Appendix B.1. Entries of the Ybus Matrix
Appendix B.2. Admittances and Other Matrices in Section 5.2.2
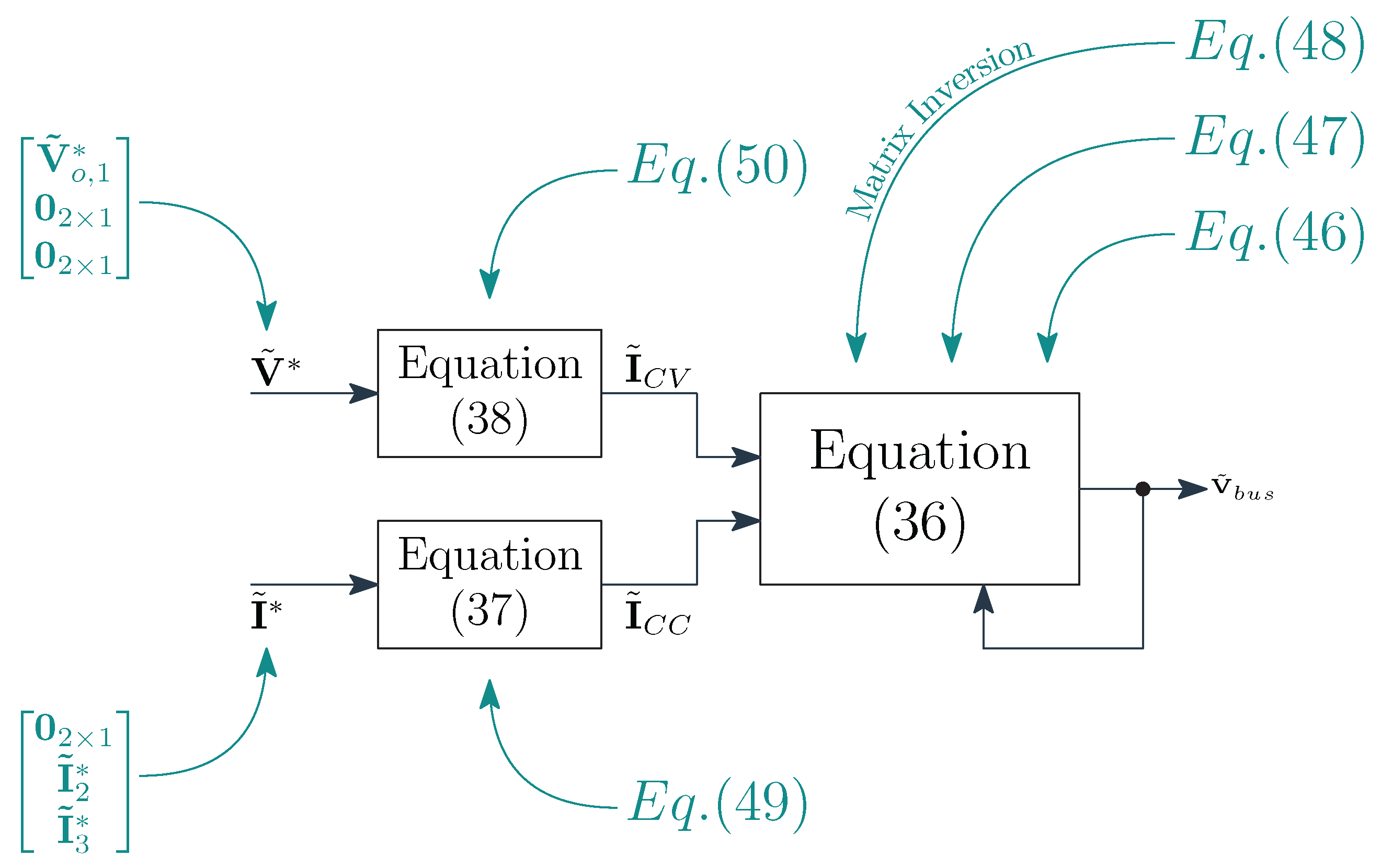
| Expression | Equation | Belongs to | Description |
|---|---|---|---|
| Equation (11) | MMC | equivalent admittance of the current loop of the MMC. | |
| = | Equation (12) | MMC | closed-loop transfer function of the current loop of the MMC. It encompasses the current controller matrix and other passive parameters of the circuit. |
| Equation (13) | MMC | matrix with a parameter-dependent expression of the MMC model. | |
| Equation (16) | MMC | Inner impedance matrix of the MMC located in bus 1. It encompasses the voltage controller matrix and other transfer matrix associated to the current loop. | |
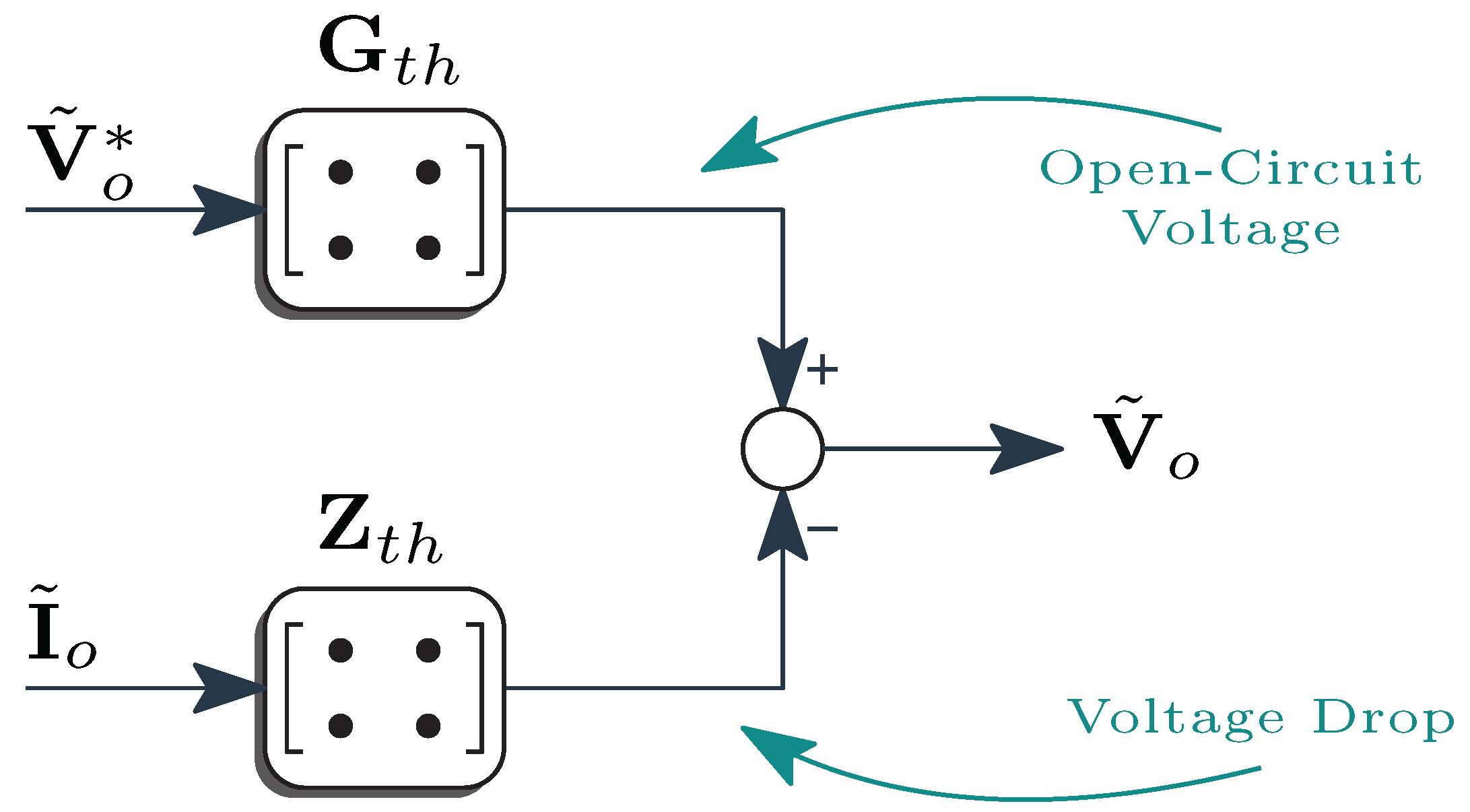
| Equation (20) | MMC | Thévenin-equivalent impedance matrix of the MMC connected to the bus 1. | |
| Equation (21) | MMC | Thévenin-equivalent voltage matrix gain of the MMC connected to the bus 1. | |
| - | - | used in the buses that do not contain a grid-forming converter. A value at least 1000 times bigger than the nominal impedance of the bus should be assigned to it. In a nutshell, this represents an “open-circuit” impedance. | |
| Equation (47) | Framework | This is a matrix in which the entries are also matrices representing the equivalent admittance of the grid-forming converters. | |
| - | Framework | This is a matrix, in which the entries are also matrices representing the closed-loop voltage gain of the grid-forming converters. | |
| Equation (50) | Framework | This is a matrix which represents the product . | |
| Equation (41) | 2L-VSC | This is a representing the equivalent admittance of the current-controlled 2L-VSCs. | |
| Equation (42) | 2L-VSC | This is a matrix representing the equivalent admittance of the current-control loop of the 2L-VSCs. In this case, is the current controller. | |
| Equation (43) | 2L-VSC | This is a matrix representing the admittance created by the PLL of the 2L-VSCs. | |
| Equation (44) | 2L-VSC | This is a matrix representing the influence of the PLL of the 2L-VSCs. and are the interaction of the PLL with the converter itself and with its current loop, respectively. | |
| Equation (48) | Framework | This is a matrix in which the entries are also matrices representing the equivalent admittance of the current-controlled 2L-VSCs. | |
| Equation (45) | 2L-VSC | This is a representing the closed-loop transfer matrix of the current-controlled 2L-VSCs. | |
| Equation (49) | Framework | This is a matrix in which the entries are also matrices representing the closed-loop transfer matrix of the current-controlled 2L-VSCs. |
Appendix B.3. Summary of Equations Used in the Framework
References
- Singh, M.; Lopes, L.A.; Ninad, N.A. Grid-forming Battery Energy Storage System (BESS) for a highly unbalanced hybrid mini-grid. Electr. Power Syst. Res. 2015, 127, 126–133. [Google Scholar] [CrossRef]
- Antonio de Souza Ribeiro, L.; Freijedo, F.D.; de Bosio, F.; Soares Lima, M.; Guerrero, J.M.; Pastorelli, M. Full Discrete Modeling, Controller Design, and Sensitivity Analysis for High-Performance Grid-Forming Converters in Islanded Microgrids. IEEE Trans. Ind. Appl. 2018, 54, 6267–6278. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, S.; Restrepo, C.; Kontos, E.; Pinto, R.T.; Bauer, P. Trends of offshore wind projects. Renew. Sustain. Energy Rev. 2015, 49, 1114–1135. [Google Scholar] [CrossRef]
- Ryndzionek, R.; Sienkiewicz, L. Evolution of the HVDC Link Connecting Offshore Wind Farms to Onshore Power Systems. Energies 2020, 13, 1914. [Google Scholar] [CrossRef] [Green Version]
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters. A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- Lima, L.A.M.; Watanabe, E.H. Hybrid Control Scheme for VSC Presenting Both Grid-Forming and Grid-Following Capabilities. IEEE Trans. Power Deliv. 2022, 37, 4570–4581. [Google Scholar] [CrossRef]
- Mehrasa, M.; Pouresmaeil, E.; Zabihi, S.; Catalão, J.P.S. Dynamic Model, Control and Stability Analysis of MMC in HVDC Transmission Systems. IEEE Trans. Power Deliv. 2017, 32, 1471–1482. [Google Scholar] [CrossRef]
- Leon, A.E.; Amodeo, S.J. Modeling, control, and reduced-order representation of modular multilevel converters. Electr. Power Syst. Res. 2018, 163, 196–210. [Google Scholar] [CrossRef]
- Hao, Q.; Li, Z.; Gao, F.; Zhang, J. Reduced-Order Small-Signal Models of Modular Multilevel Converter and MMC-Based HVdc Grid. IEEE Trans. Ind. Electr. 2019, 66, 2257–2268. [Google Scholar] [CrossRef]
- Wang, G.; Xiao, H.; Xiao, L.; Zhang, Z.; Xu, Z. Electromechanical Transient Modeling and Control Strategy of Decentralized Hybrid HVDC Systems. Energies 2019, 12, 2856. [Google Scholar] [CrossRef] [Green Version]
- Stepanov, A.; Mahseredjian, J.; Karaagac, U.; Saad, H. Adaptive Modular Multilevel Converter Model for Electromagnetic Transient Simulations. IEEE Trans. Power Deliv. 2021, 36, 803–813. [Google Scholar] [CrossRef]
- Hao, Q.; Li, Z.; Yue, C.; Gao, F.; Wang, S. Small-signal Model and Dynamics of MMC- HVDC Grid under Unbalanced Grid Conditions. IEEE Trans. Power Deliv. 2020, 36, 3172–3184. [Google Scholar] [CrossRef]
- Liu, Z.; Miao, S.; Fan, Z.; Kang, Y.; Tu, Q. Analysis of the performance characteristics and arm current control for modular multilevel converter with asymmetric arm parameters. Int. J. Electr. Power Energy Syst. 2019, 110, 258–270. [Google Scholar] [CrossRef]
- Wang, J.; Gao, S.; Ji, Z.; Sun, Y.; Hong, L.; Luo, F.; Gu, W. Time/frequency domain modelling for grid-connected MMC sub-synchronous/super-synchronous oscillation in PV MVDC power collection and integration system. IET Renew. Power Gener. 2019, 13, 57–66. [Google Scholar] [CrossRef]
- Ma, Y.; Lin, H.; Wang, Z. Equivalent Model of Modular Multilevel Converter Considering Capacitor Voltage Ripples. IEEE Trans. Power Deliv. 2019, 34, 2182–2193. [Google Scholar] [CrossRef]
- Bessegato, L.; Ilves, K.; Harnefors, L.; Norrga, S. Effects of Control on the AC-Side Admittance of a Modular Multilevel Converter. IEEE Trans. Power Electr. 2019, 34, 7206–7220. [Google Scholar] [CrossRef] [Green Version]
- Man, J.; Xie, X.; Xu, S.; Zou, C.; Yin, C. Frequency-Coupling Impedance Model Based Analysis of a High-Frequency Resonance Incident in an Actual MMC-HVDC System. IEEE Trans. Power Deliv. 2020, 35, 2963–2971. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, K.; Liao, X.; Qin, L.; Huai, Q.; Xu, Y.; Li, Y.; Wang, F. D-Q Frame Impedance Modeling of Modular Multilevel Converter and Its Application in High-Frequency Resonance Analysis. IEEE Trans. Power Deliv. 2021, 36, 1517–1530. [Google Scholar] [CrossRef]
- Lyu, J.; Cai, X.; Molinas, M. Frequency Domain Stability Analysis of MMC-Based HVdc for Wind Farm Integration. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Sánchez-Sánchez, E.; Prieto-Araujo, E.; Gomis-Bellmunt, O. The Role of the Internal Energy in MMCs Operating in Grid-Forming Mode. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 949–962. [Google Scholar] [CrossRef]
- Freitas, C.M.; Watanabe, E.H.; Monteiro, L.F.C. A linearized small-signal Thévenin-equivalent model of a voltage-controlled modular multilevel converter. Electr. Power Syst. Res. 2020, 182, 106231. [Google Scholar] [CrossRef]
- Sun, J.; Liu, H. Sequence Impedance Modeling of Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 1427–1443. [Google Scholar] [CrossRef]
- Beza, M.; Bongiorno, M.; Stamatiou, G. Analytical Derivation of the AC-Side Input Admittance of a Modular Multilevel Converter With Open- and Closed-Loop Control Strategies. IEEE Trans. Power Deliv. 2018, 33, 248–256. [Google Scholar] [CrossRef]
- Lekić, A.; Beerten, J. Generalized multiport representation of power systems using ABCD parameters for harmonic stability analysis. Electr. Power Syst. Res. 2020, 189, 106658. [Google Scholar] [CrossRef]
- Li, Y.; Shuai, Z.; Liu, X.; Chen, Y.; Li, Z.; Hong, Y.; Shen, Z.J. Stability Analysis and Location Optimization Method for Multiconverter Power Systems Based on Nodal Admittance Matrix. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 529–538. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Liu, W. An Oscillatory Stability Criterion Based on the Unified dq-Frame Impedance Network Model for Power Systems With High-Penetration Renewables. IEEE Trans. Power Syst. 2018, 33, 3472–3485. [Google Scholar] [CrossRef]
- Orellana, L.; Sainz, L.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability Assessment for Multi-Infeed Grid-Connected VSCs Modeled in the Admittance Matrix Form. IEEE Trans. Circuits Syst. Regul. Pap. 2021, 68, 3758–3771. [Google Scholar] [CrossRef]
- Xu, W.; Huang, Z.; Cui, Y.; Wang, H. Harmonic resonance mode analysis. IEEE Trans. Power Deliv. 2005, 20, 1182–1190. [Google Scholar] [CrossRef]
- Angquist, L.; Antonopoulos, A.; Siemaszko, D.; Ilves, K.; Vasiladiotis, M.; Nee, H. Open-Loop Control of Modular Multilevel Converters Using Estimation of Stored Energy. IEEE Trans. Ind. Appl. 2011, 47, 2516–2524. [Google Scholar] [CrossRef]
- Ludois, D.C.; Venkataramanan, G. Simplified Terminal Behavioral Model for a Modular Multilevel Converter. IEEE Trans. Power Electron. 2014, 29, 1622–1631. [Google Scholar] [CrossRef]
- Harnefors, L.; Antonopoulos, A.; Norrga, S.; Angquist, L.; Nee, H. Dynamic Analysis of Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2013, 60, 2526–2537. [Google Scholar] [CrossRef]
- Freitas, C.M.; Watanabe, E.H.; Monteiro, L.F.C. Grid-Forming MMC: A Comparison Between Single—and Dual-Loop Control Approaches. In Proceedings of the 2021 Brazilian Power Electronics Conference (COBEP), Joao Pessoa, Brazil, 7–10 November 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2018, 33, 1775–1787. [Google Scholar] [CrossRef] [Green Version]
- Freitas, C.M. Equivalent Linearized Analytical Models For The Modular Multilevel Converter. Ph.D. Thesis, Federal University of Rio de Janeiro/COPPE, Rio de Janeiro, Brazil, 2020. [Google Scholar]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Sasso, E.; Sotelo, G.; Ferreira, A.; Watanabe, E.; Aredes, M.; Gomes Barbosa, P. Investigação dos modelos de circuitos de sincronismo trifásicos baseados na teoria das potências real e imaginária instantâneas (p-PLL E q-PLL). In Proceedings of the XIV—Congresso Brasileiro de Automática, Natal, Brazil, 2–5 September 2002; (In Portuguese) [Google Scholar] [CrossRef]
- Fritzson, P.; Pop, A.; Abdelhak, K.; Asghar, A.; Bachmann, B.; Braun, W.; Bouskela, D.; Braun, R.; Buffoni, L.; Casella, F.; et al. The OpenModelica Integrated Environment for Modeling, Simulation, and Model-Based Development. Model. Identif. Control Nor. Res. Bull. 2020, 41, 241–295. [Google Scholar] [CrossRef]
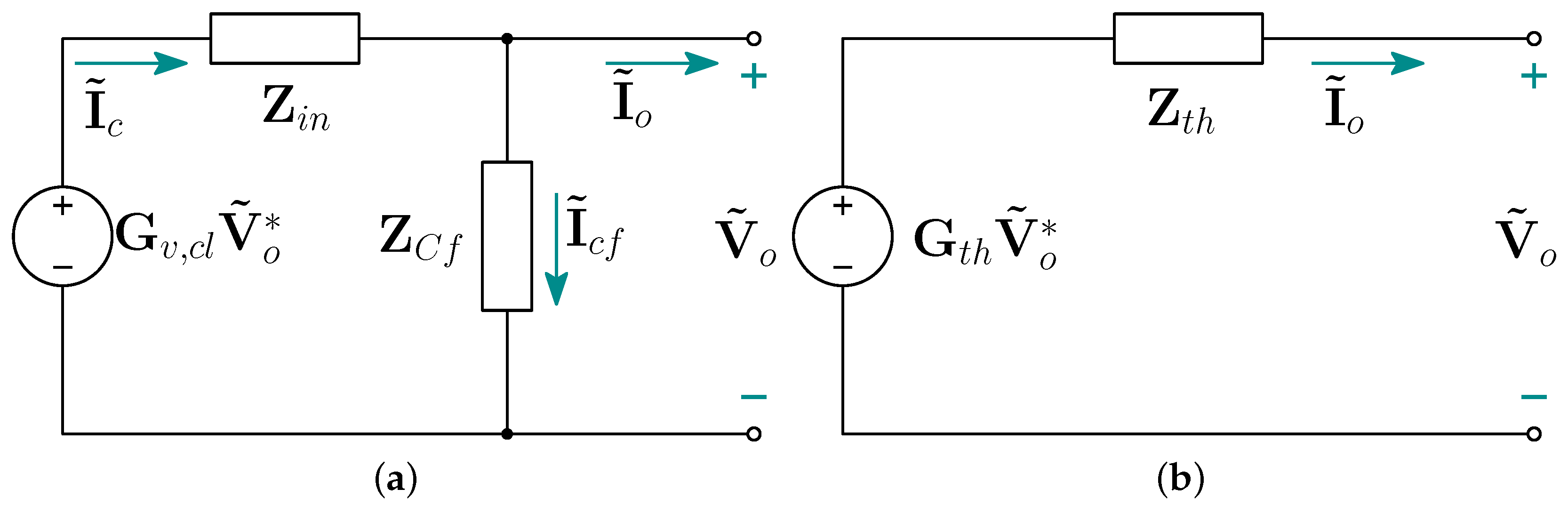
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freitas, C.M.; Watanabe, E.H.; Monteiro, L.F.C. d-q Small-Signal Model for Grid-Forming MMC and Its Application in Electromagnetic-Transient Simulations. Energies 2023, 16, 2195. https://doi.org/10.3390/en16052195
Freitas CM, Watanabe EH, Monteiro LFC. d-q Small-Signal Model for Grid-Forming MMC and Its Application in Electromagnetic-Transient Simulations. Energies. 2023; 16(5):2195. https://doi.org/10.3390/en16052195
Chicago/Turabian StyleFreitas, Cleiton M., Edson H. Watanabe, and Luís F. C. Monteiro. 2023. "d-q Small-Signal Model for Grid-Forming MMC and Its Application in Electromagnetic-Transient Simulations" Energies 16, no. 5: 2195. https://doi.org/10.3390/en16052195