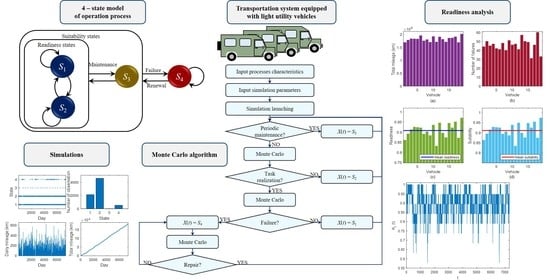
Modelling the Operation Process of Light Utility Vehicles in Transport Systems Using Monte Carlo Simulation and Semi-Markov Approach
Abstract
:1. Introduction
- Development of a simulation model based on Monte Carlo methods;
- Implementation of the Monte Carlo model in the MATLAB environment;
- Validation of simulation models based on the analytical approach of a four-state semi-Markov process;
- Evaluation of the operation and maintenance processes of light utility vehicles using the proposed indicators and sensitivity analysis resulting from changes in the intensity parameters of the operational process.
2. Literature Review
3. Monte Carlo Approach
3.1. Periodic Maintenance
3.2. Operational Process
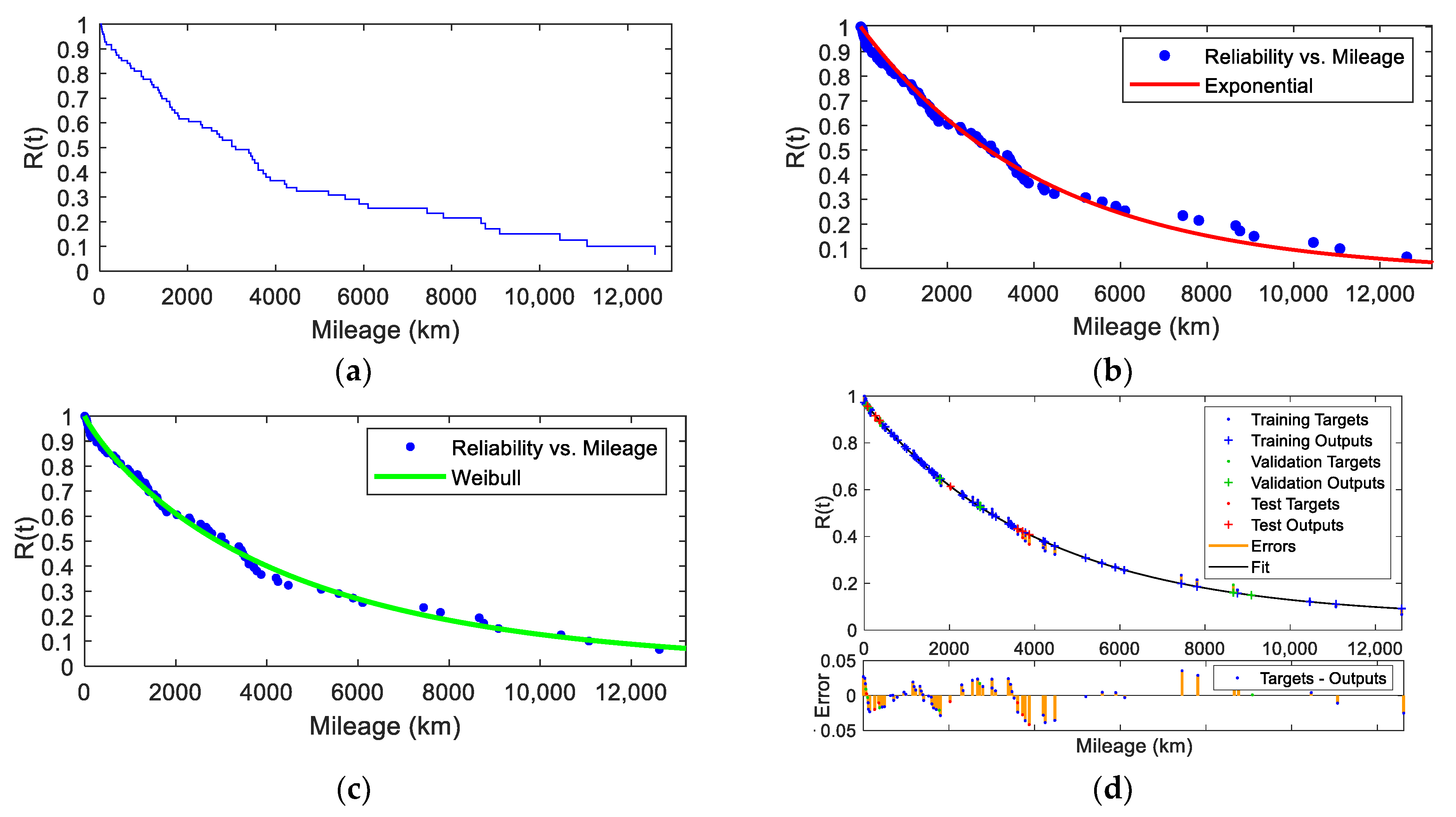
3.3. Reliability
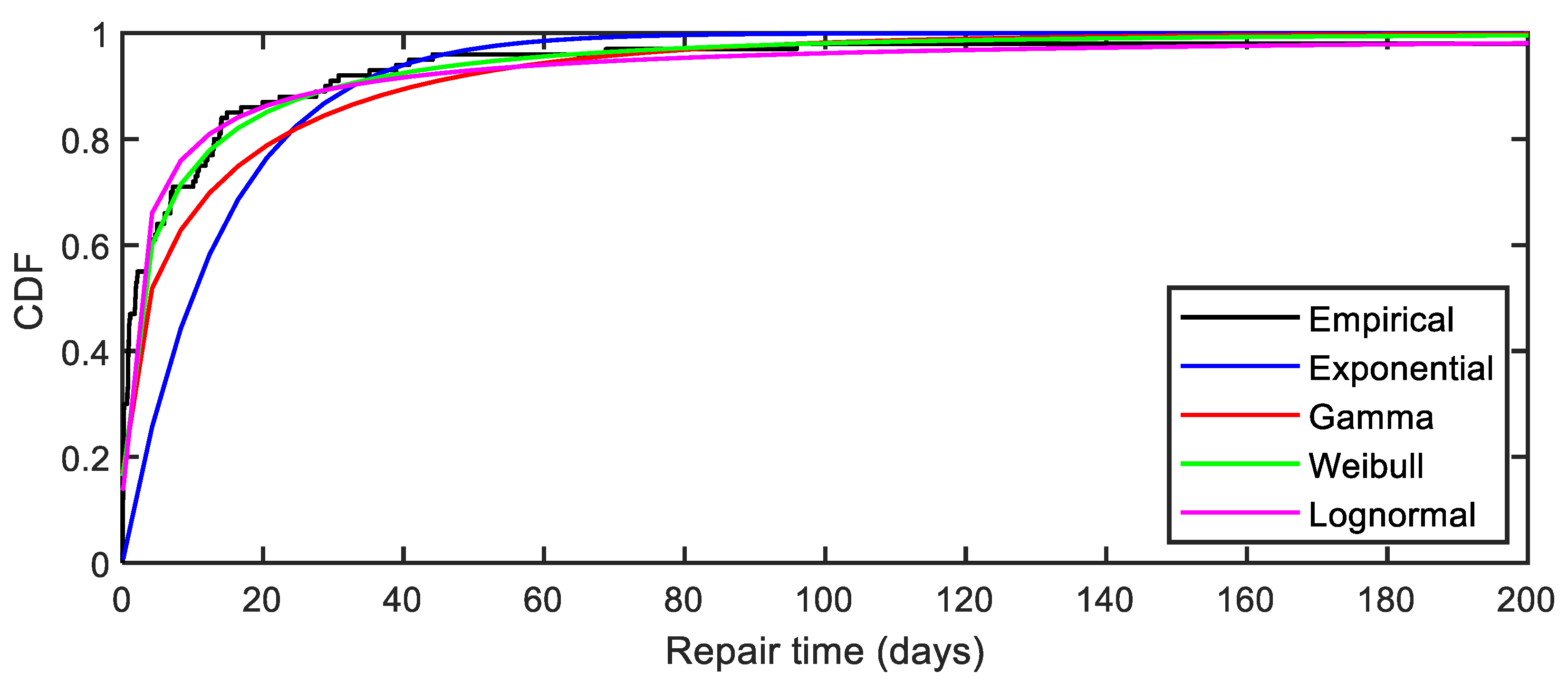
3.4. Failure Diagnostics and Repair
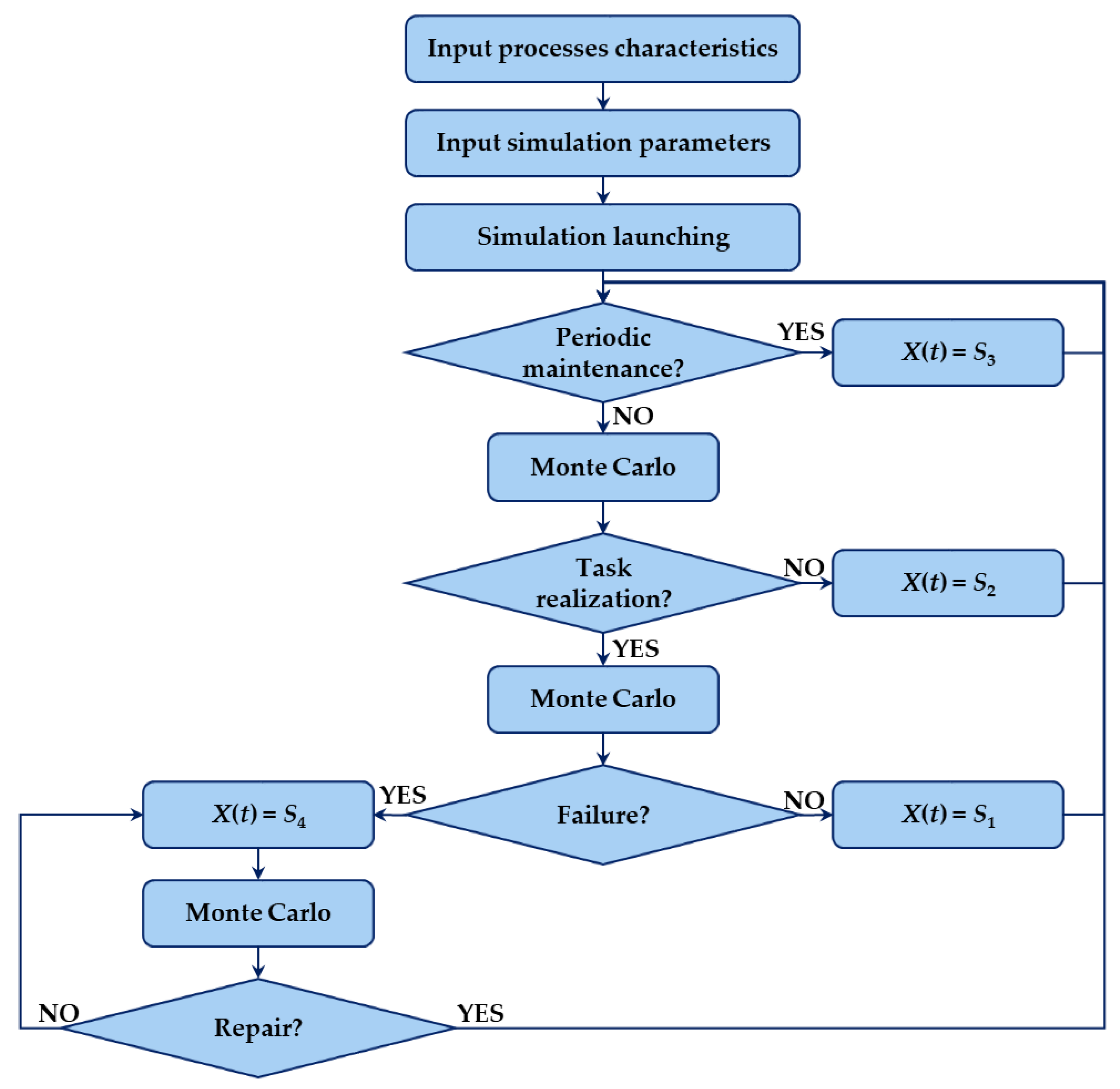
3.5. Monte Carlo Models of Light Utility Vehicle Operation Process
3.6. Software Implementation
| Algorithm 1: Pseudocode of Monte Carlo simulation for the four-state operation process. | |
| Input: Reliability function R(lr), CDF of daily mileage G(ld), probability of assignment task Θ, CDF of repair time H(i), maintenance parameters Lm and Tm, maximum of daily mileage ldmax, number of vehicles Nv, and number of iterations for each vehicle Zi Output: Trajectory X(t), sojourn times T(S1), T(S2), T(S3), T(S4), readiness Kr, and suitability Ks | |
| 1 | for z = 1: Zi do |
| 2 | set t = 1, set random integer values of lm, tm, lr |
| 3 | while t ≤ Zi do |
| 4 | if lm ≥ Lm then |
| 5 | Periodic maintenance X(t) = S3, T(S3) = T(S3) + 1 |
| 6 | lm = 0, tm = 0 |
| 7 | t = t + 1 |
| 8 | elseif tm ≥ Tm then |
| 9 | Periodic maintenance X(t) = S3, T(S3) = T(S3) + 1 |
| 10 | lm = 0, tm = 0 |
| 11 | t = t + 1 |
| 12 | else |
| 13 | q1 = rand |
| 14 | if q1 > Θ then |
| 15 | Awaiting for task X(t) = S2, T(S2) = T(S2) + 1 |
| 16 | t = t + 1 |
| 17 | else |
| 18 | q2 = rand |
| 19 | G(ld) = q2, find ld, |
| 20 | ld (ld > ldmax) = ldmax |
| 21 | q3 = rand |
| 22 | if q3 > probability of failure then |
| 23 | Task realization X(t) = S1, T(S1) = T(S1) + 1 |
| 24 | lr = lr + ld, lm = lm + ld, tm = tm + 1 |
| 25 | t = t + 1 |
| 26 | else |
| 27 | Failure X(t) = S4, T(S4) = T(S4) + 1 |
| 28 | set random value lf → [0.0, ld] |
| 29 | lm = lm + lf, tm = tm + 1 |
| 30 | t = t + 1 |
| 31 | q4 = rand |
| 32 | i = 1 |
| 33 | while q4 > probability of repair in i-th iteration do |
| 34 | if t < Zi then |
| 35 | Repair of vehicle in progress X(t) = S4, T(S4) = T(S4) + 1 |
| 36 | tm = tm + 1 |
| 37 | i = i +1 |
| 38 | q4 = rand |
| 39 | t = t + 1 |
| 40 | else |
| 41 | End of simulation; vehicle inoperable |
| 42 | end if |
| 43 | end while |
| 44 | Vehicle repaired in i-th iteration |
| 45 | lr = 0 |
| 46 | t = t + 1 |
| 47 | end if |
| 48 | end if |
| 49 | end if |
| 50 | end while |
| 51 | end for |
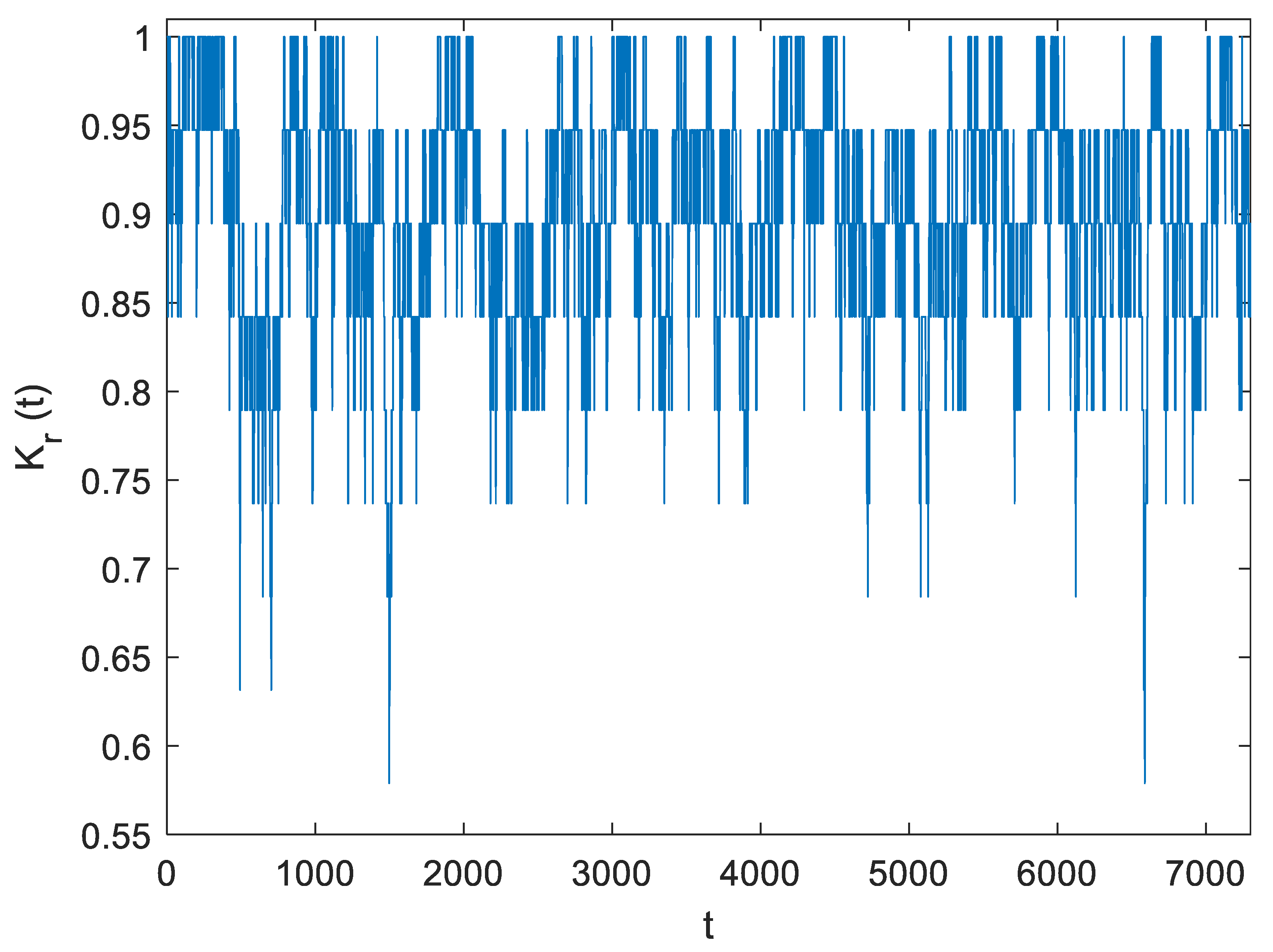
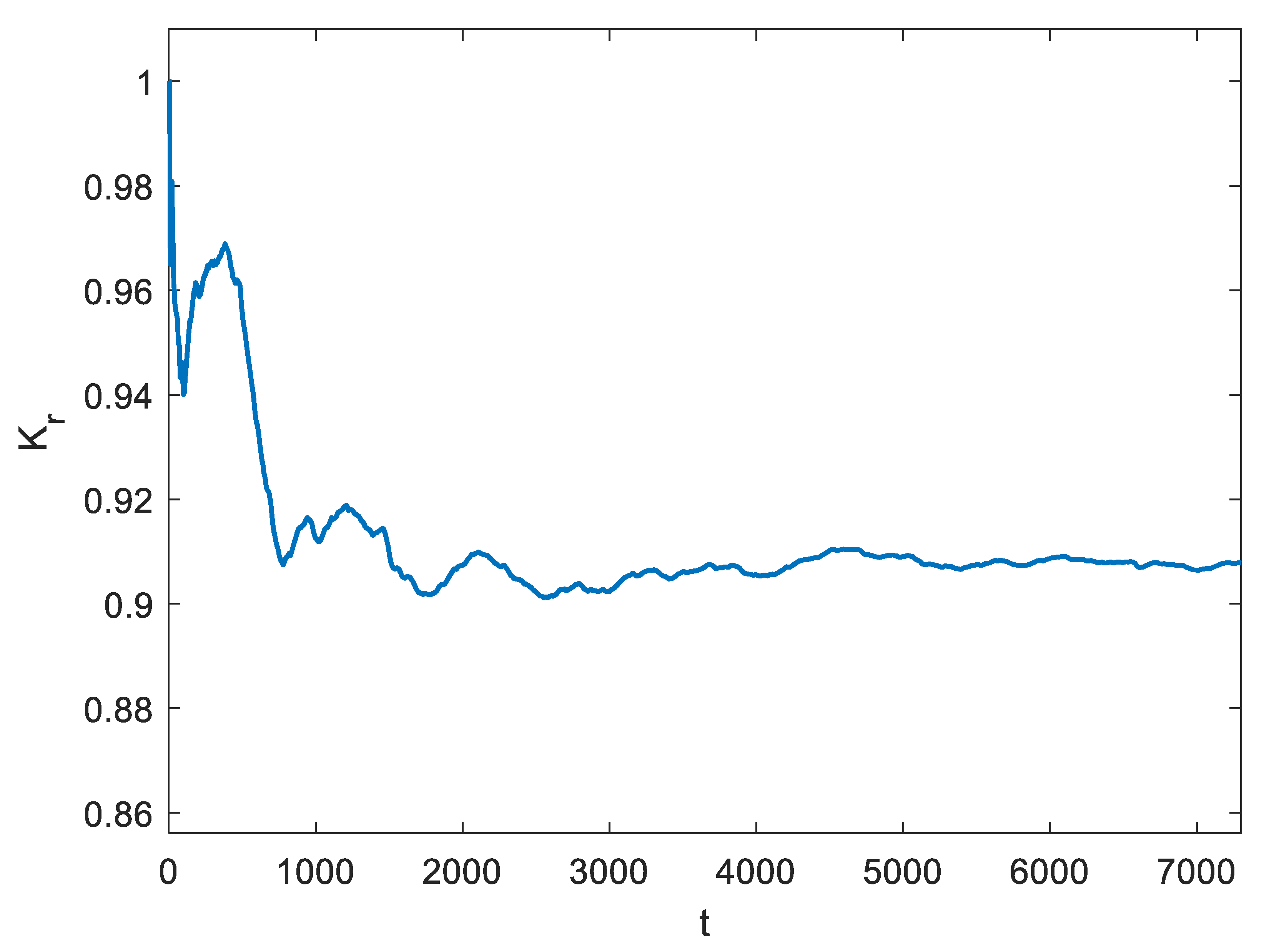
| 52 | Calculate readiness Kr = [T(S1) + T(S2)]/[T(S1) + T(S2) + T(S3) + T(S4)] |
| 53 | Calculate suitability Ks = [T(S1) + T(S2) + T(S3)]/[T(S1) + T(S2) + T(S3) + T(S4)] |
| 54 | returnX(t), T(S1), T(S2), T(S3), T(S4), Kr, Ks |
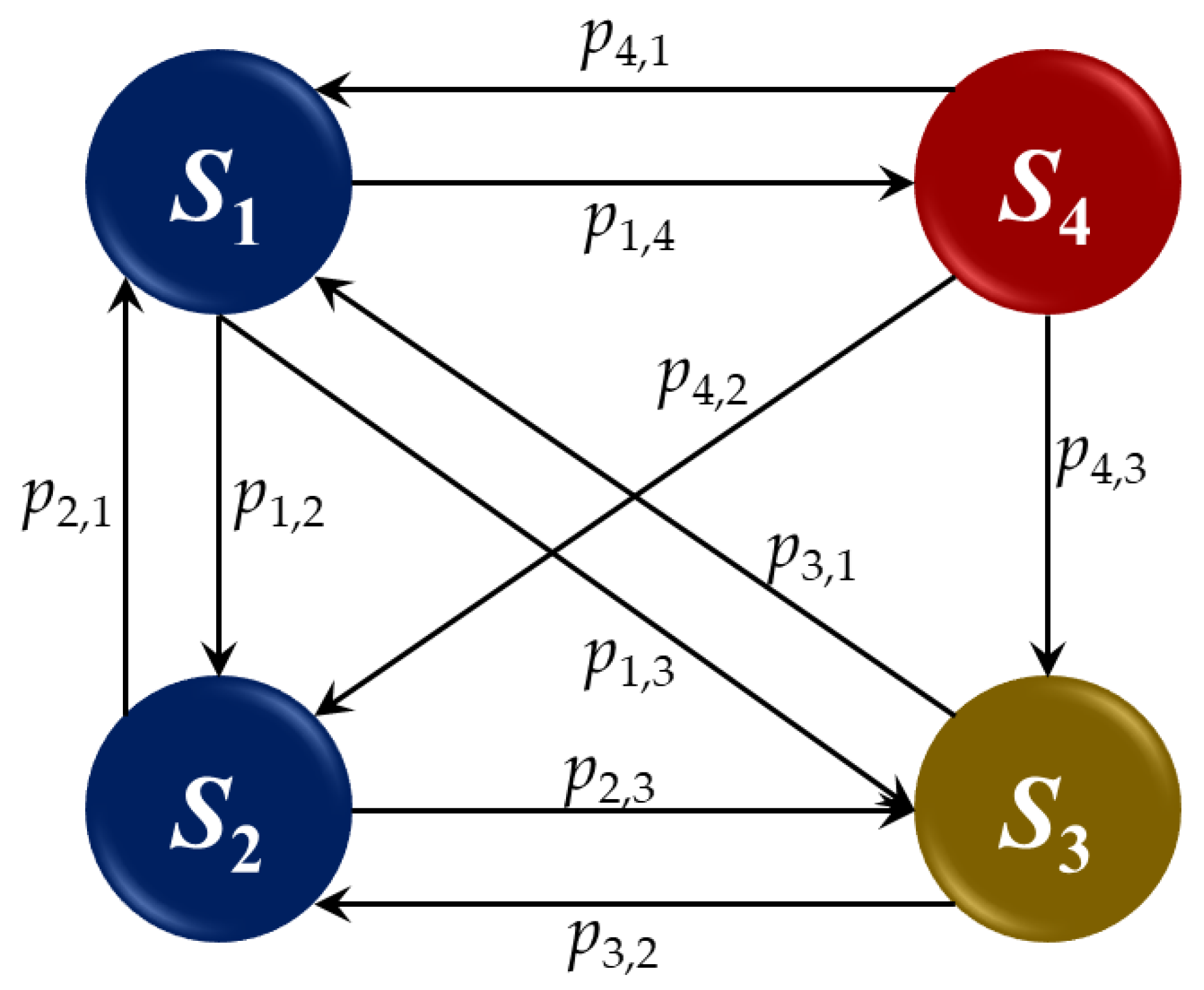
4. Semi-Markov Approach
5. Results and Discussion
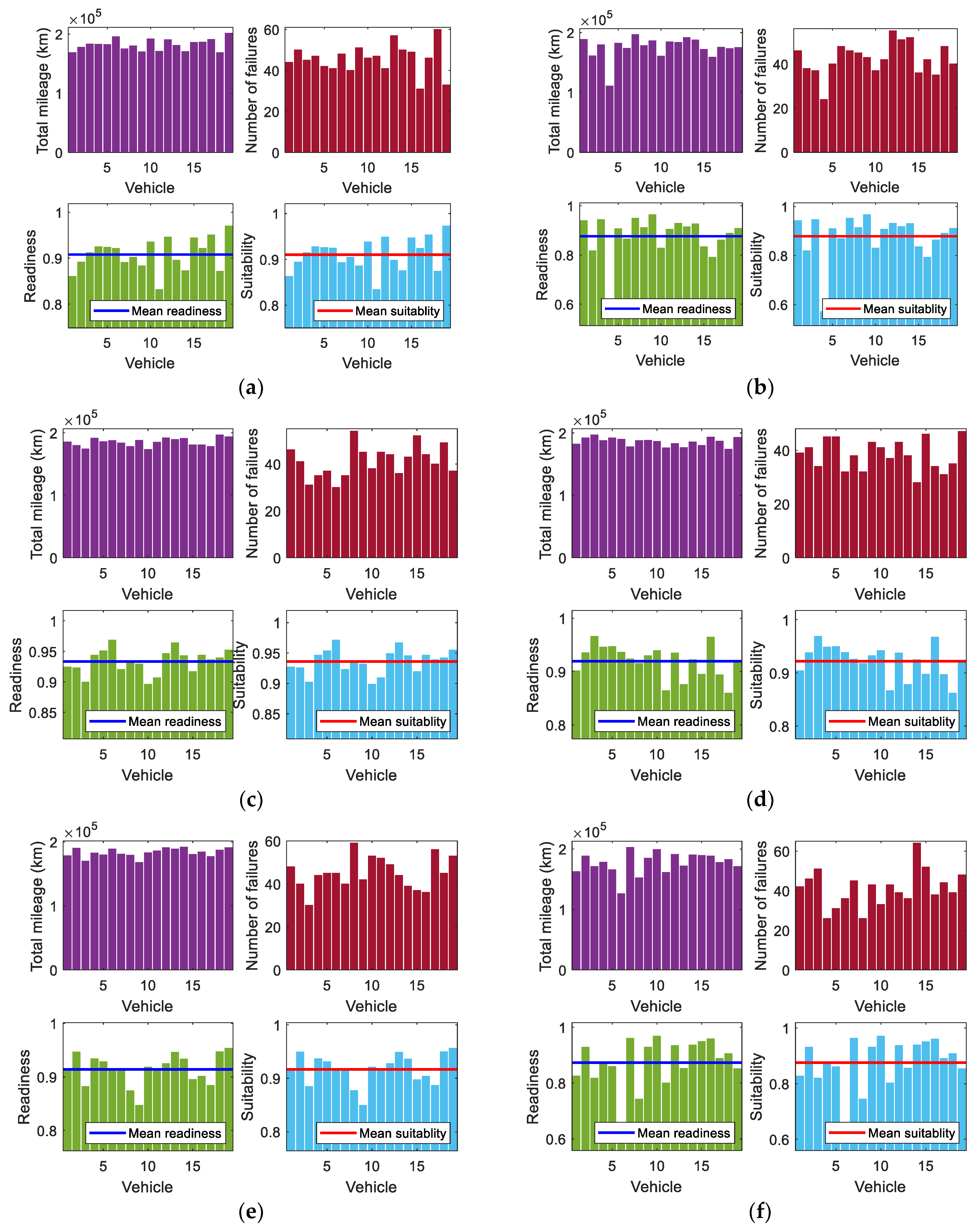
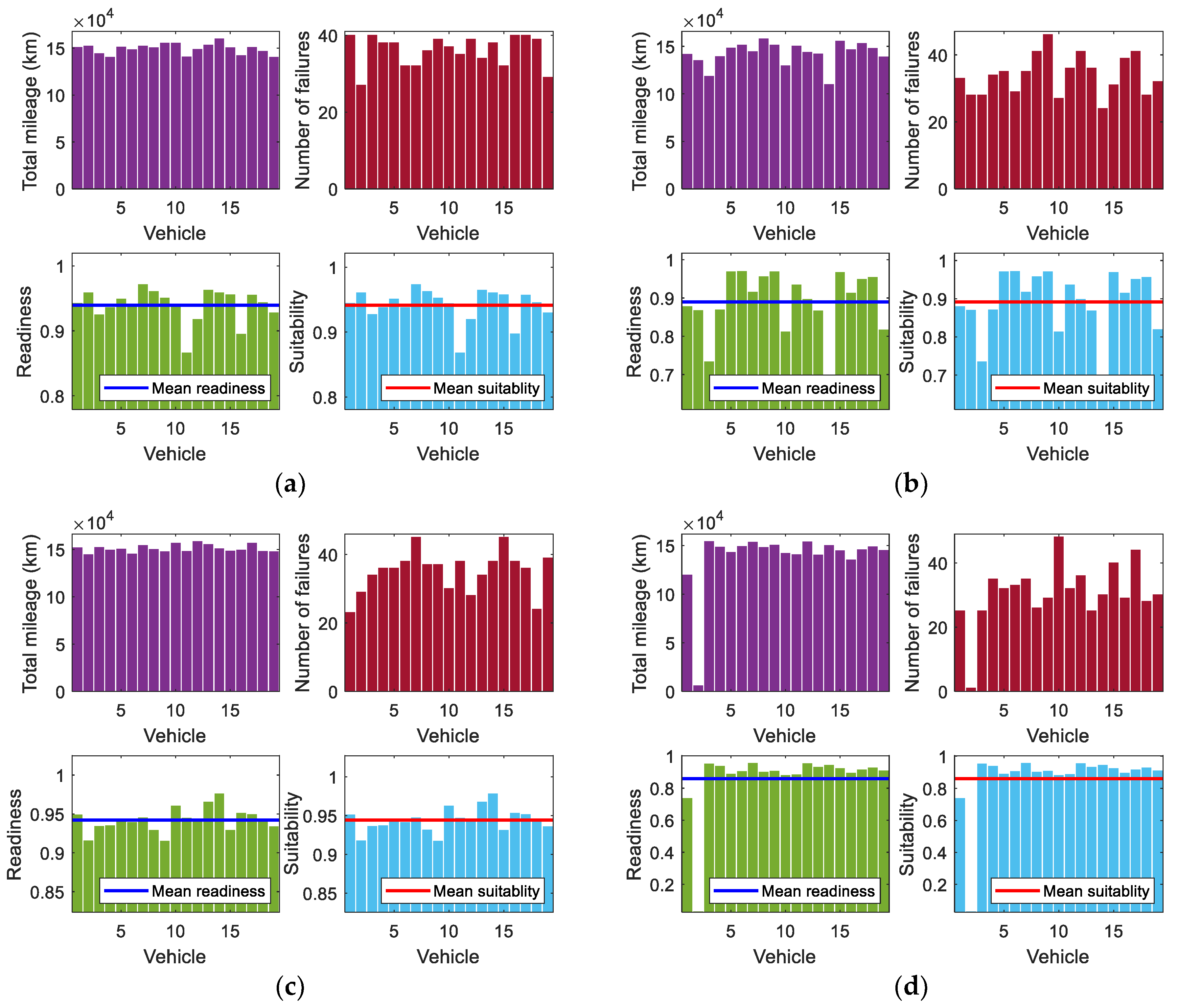
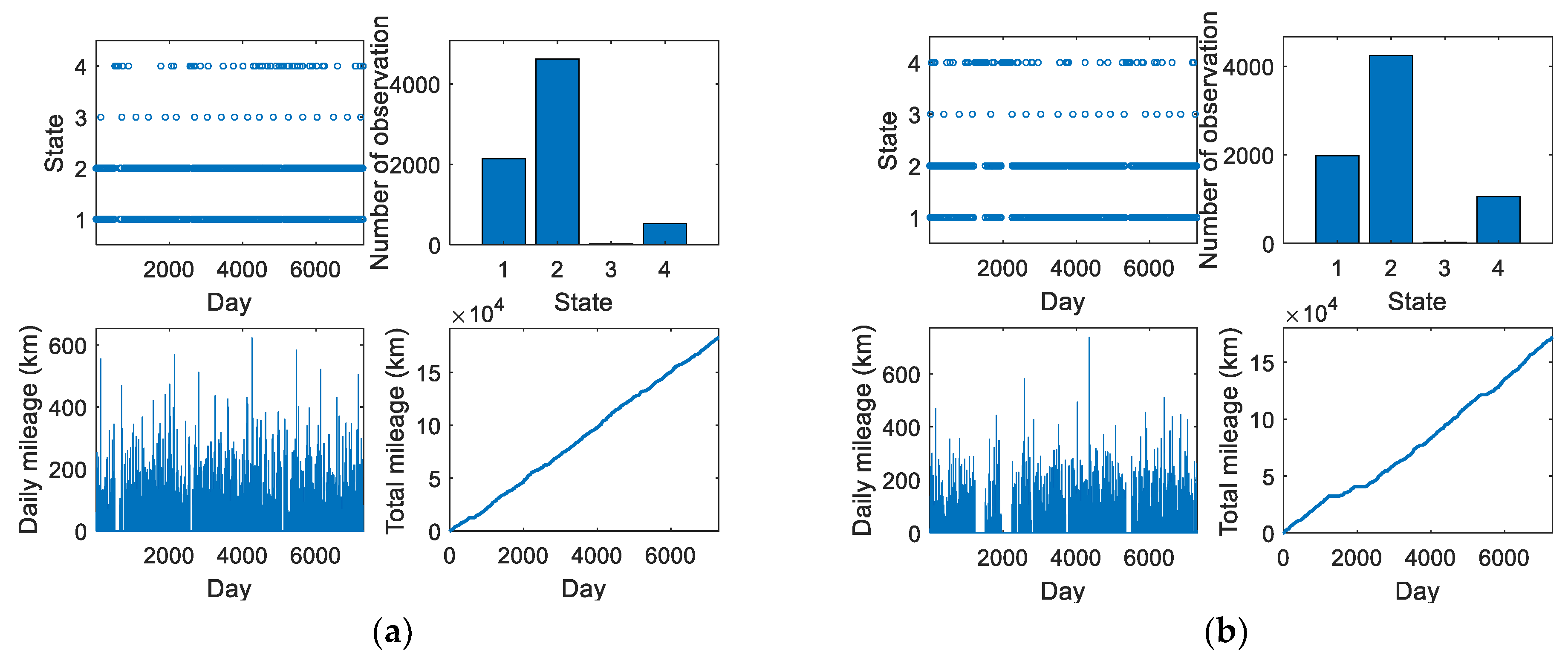
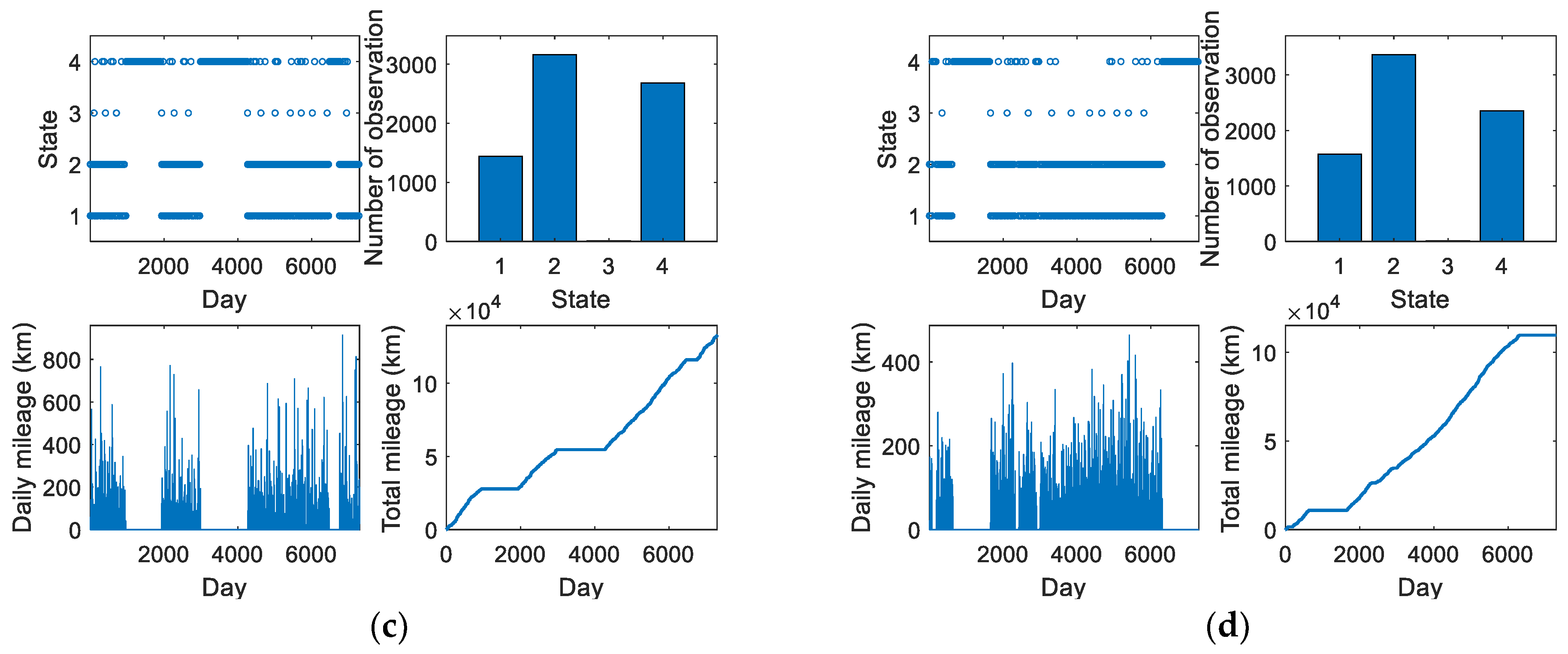
5.1. Monte Carlo Simulations
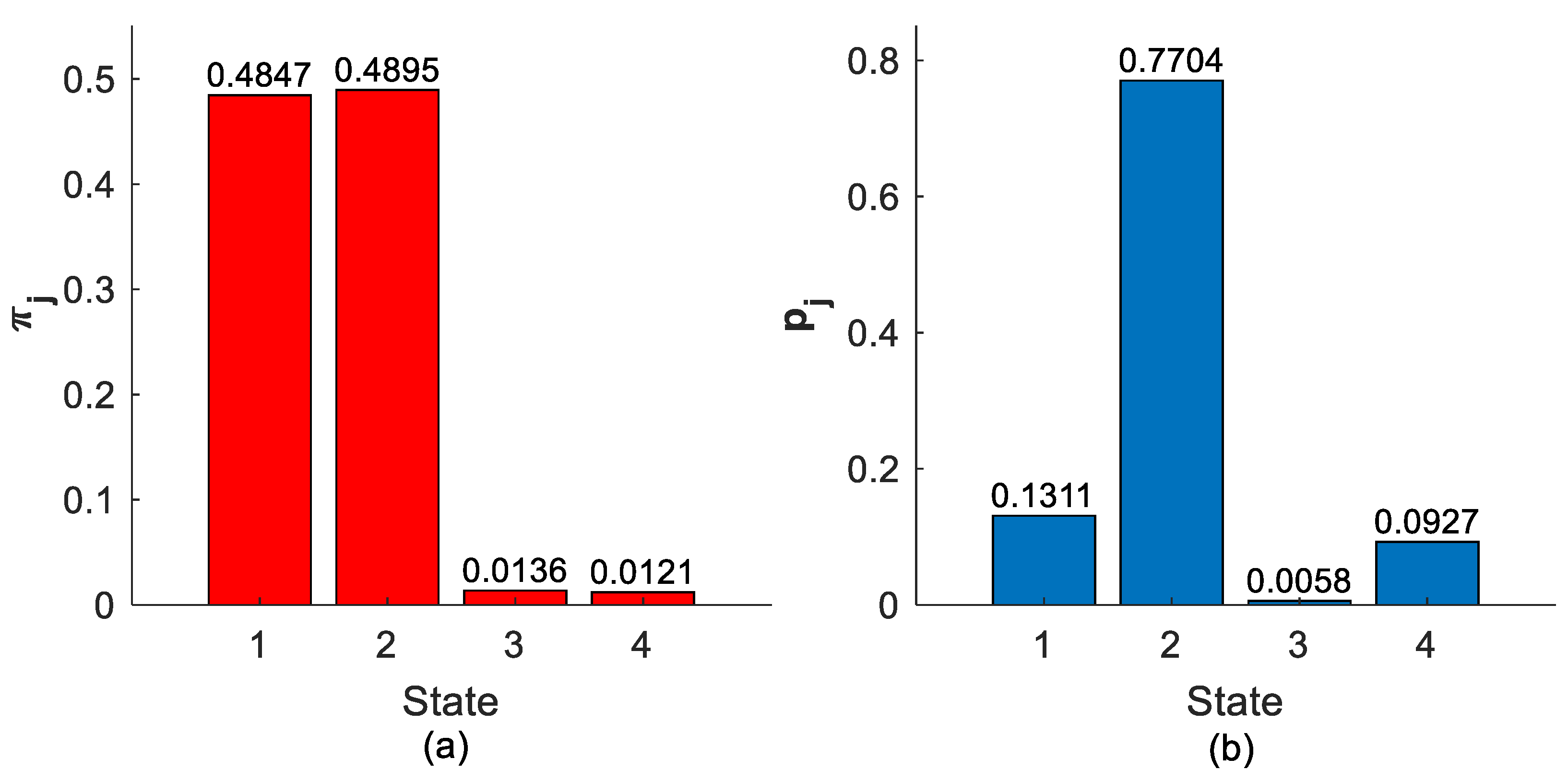
5.2. Semi-Markov Model
5.3. Comparison of the Results
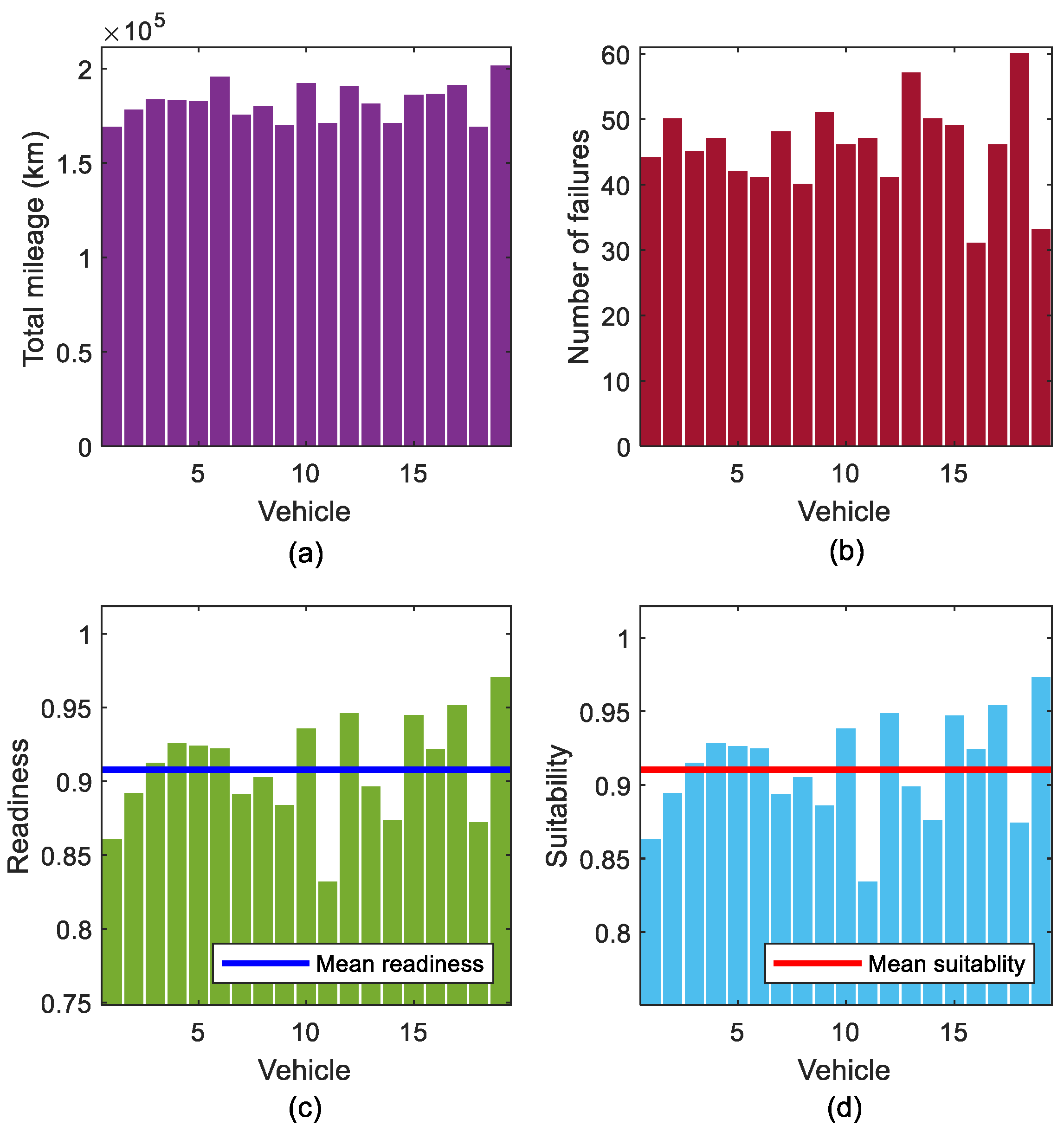
5.4. Functional Readiness
5.5. Sensitivity Analysis of Monte Carlo Model
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Benson, R.; Kellner, D. Monte Carlo Simulation for Reliability. In Proceedings of the 2020 Annual Reliability and Maintainability Symposium (RAMS), Palm Springs, CA, USA, 27–30 January 2020; pp. 1–6. [Google Scholar]
- Acebes, F.; Poza, D.; González-Varona, J.M.; López-Paredes, A. Stochastic Earned Duration Analysis for Project Schedule Management. Engineering 2022, 9, 148–161. [Google Scholar] [CrossRef]
- Dąbrowska, E. Monte Carlo Simulation Approach to Reliability Analysis of Complex Systems. J. Konbin 2020, 50, 155–170. [Google Scholar] [CrossRef]
- Ren, W.; Ma, L.; Wang, Y. Monte Carlo Analysis for Safety and Reliability of Rail Transit Signal System Based on Cloud Computing. J. Phys. Conf. Ser. 2020, 1654, 012065. [Google Scholar] [CrossRef]
- Liu, C.; Kramer, A.; Neumann, S. Reliability Assessment of Repairable Phased-Mission System by Monte Carlo Simulation Based on Modular Sequence-Enforcing Fault Tree Model. Eksploat. I Niezawodn. Maint. Reliab. 2020, 22, 272–281. [Google Scholar] [CrossRef]
- Amjad, M.; Ahmad, I.; Ahmad, M.; Wróblewski, P.; Kamiński, P.; Amjad, U. Prediction of Pile Bearing Capacity Using XGBoost Algorithm: Modeling and Performance Evaluation. Appl. Sci. 2022, 12, 2126. [Google Scholar] [CrossRef]
- Janekova, J.; Fabianova, J.; Kadarova, J. Selection of Optimal Investment Variant Based on Monte Carlo Simulations. Int. J. Simul. Model. 2021, 20, 279–290. [Google Scholar] [CrossRef]
- Żurek, J.; Zieja, M.; Ziółkowski, J.; Borucka, A. Vehicle Operation Process Analysis Using the Markov Processes. In Proceedings of the 29th European Safety and Reliability Conference, Hannover, Germany, 22–26 September 2019; pp. 2598–2605. [Google Scholar]
- Ziółkowski, J.; Borucka, A. Markov Model in Logistic Management of Enterprise. J. Konbin 2016, 38, 271–290. [Google Scholar] [CrossRef] [Green Version]
- Borucka, A.; Niewczas, A.; Hasilova, K. Forecasting the Readiness of Special Vehicles Using the Semi-Markov Model. Eksploat. Niezawodn. Maint. Reliab. 2019, 21, 662–669. [Google Scholar] [CrossRef]
- Świderski, A.; Borucka, A.; Grzelak, M.; Gil, L. Evaluation of Machinery Readiness Using Semi-Markov Processes. Appl. Sci. 2020, 10, 1541. [Google Scholar] [CrossRef] [Green Version]
- Oszczypała, M.; Ziółkowski, J.; Małachowski, J. Reliability Analysis of Military Vehicles Based on Censored Failures Data. Appl. Sci. 2022, 12, 2622. [Google Scholar] [CrossRef]
- Dziubak, T.; Wysocki, T.; Dziubak, S. Selection of Vehicles for Fleet of Transport Company on the Basis of Observation of Their Operational Reliability. Eksploat. Niezawodn. Maint. Reliab. 2021, 23, 184–194. [Google Scholar] [CrossRef]
- Żurek, J.; Ziółkowski, J.; Borucka, A. Application of Markov Processes to the Method for Analysis of Combat Vehicle Operation in the Aspect of Their Availability and Readiness. In Proceedings of the 2nd International Conference on Engineering Sciences and Technologies, Kerbala, Iraq, 26–28 March 2018; pp. 2343–2352. [Google Scholar]
- Oszczypała, M.; Ziółkowski, J.; Małachowski, J. Analysis of Light Utility Vehicle Readiness in Military Transportation Systems Using Markov and Semi-Markov Processes. Energies 2022, 15, 5062. [Google Scholar] [CrossRef]
- Liu, K.; Wu, J.; Liu, H.; Sun, M.; Wang, Y. Reliability Analysis of Thermal Error Model Based on DBN and Monte Carlo Method. Mech. Syst. Signal Process. 2021, 146, 107020. [Google Scholar] [CrossRef]
- Jensen, H.A.; Jerez, D.J.; Valdebenito, M. An Adaptive Scheme for Reliability-Based Global Design Optimization: A Markov Chain Monte Carlo Approach. Mech. Syst. Signal Process. 2020, 143, 106836. [Google Scholar] [CrossRef]
- Zhang, L.; Dong, L.; Cheng, S.; Li, W.; Wang, B.; Liu, H.; Chen, K. Efficient Reliability Assessment Method for Bridges Based on Markov Chain Monte Carlo (MCMC) with Metropolis-Hasting Algorithm (MHA). IOP Conf. Ser. Earth Environ. Sci. 2020, 580, 012030. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, X.; Xiao, M.; Yang, Z.; Tang, X.; Wen, B. Reliability Modeling for Intermittent Working System Based on Wiener Process. Comput. Ind. Eng. 2021, 160, 107599. [Google Scholar] [CrossRef]
- Shahtaheri, Y.; Flint, M.M.; De la Garza, J.M. A Multi-Objective Reliability-Based Decision Support System for Incorporating Decision Maker Utilities in the Design of Infrastructure. Adv. Eng. Inform. 2019, 42, 100939. [Google Scholar] [CrossRef]
- Zhang, K.; Tang, B.; Deng, L.; Yu, X.; Wei, J. Fault Source Location of Wind Turbine Based on Heterogeneous Nodes Complex Network. Eng. Appl. Artif. Intell. 2021, 103, 104300. [Google Scholar] [CrossRef]
- Kallen, M.J. Modelling Imperfect Maintenance and the Reliability of Complex Systems Using Superposed Renewal Processes. Reliab. Eng. Syst. Saf. 2011, 96, 636–641. [Google Scholar] [CrossRef]
- Durczak, K.; Rybacki, P.; Sujak, A. Application of a Selected Pseudorandom Number Generator for the Reliability of Farm Tractors. Appl. Sci. 2022, 12, 12452. [Google Scholar] [CrossRef]
- Singh, C.; Mitra, J. Monte Carlo Simulation for Reliability Analysis of Emergency and Standby Power Systems. In Proceedings of the IAS ’95. Conference Record of the 1995 IEEE Industry Applications Conference Thirtieth IAS Annual Meeting, Orlando, FL, USA, 8–12 October 1995; Volume 3, pp. 2290–2295. [Google Scholar]
- Souza-Franco, R.L.; Clavijo, V.; Schleder, M.; Martins, R. Monte Carlo Simulation to Consider Uncertainty in the Reliability Analysis of Dynamic Positioning Systems. In Proceedings of the 29th European Safety and Reliability Conference (ESREL), Hannover, Germany, 22–26 September 2019; Research Publishing Services: Hannover, Germany, 2019; pp. 2446–2453. [Google Scholar]
- Novak, M.; Sangwongwanich, A.; Blaabjerg, F. Monte Carlo Based Reliability Estimation Methods in Power Electronics. In Proceedings of the 2020 IEEE 21st Workshop on Control and Modeling for Power Electronics (COMPEL), Aalborg, Denmark, 9–12 November 2020; pp. 1–7. [Google Scholar]
- Green, R.C.; Wang, L.; Alam, M.; Singh, C. Intelligent State Space Pruning for Monte Carlo Simulation with Applications in Composite Power System Reliability. Eng. Appl. Artif. Intell. 2013, 26, 1707–1724. [Google Scholar] [CrossRef]
- Roslan, N.N.R.B.; Fauzi, N.F.B.M.; Ridzuan, M.I.M. Sequential and Nonsequential Monte Carlo in Assessing Reliability Performance of Distribution Network. In Proceedings of the 2020 Emerging Technology in Computing, Communication and Electronics (ETCCE), Dhaka, Bangladesh, 21–22 December 2020; pp. 1–6. [Google Scholar]
- Ugurlu, O.F.; Kumral, M. Reliability-Based Performance Analysis of Mining Drilling Operations through Markov Chain Monte Carlo and Mean Reverting Process Simulations. Simulation 2020, 96, 593–604. [Google Scholar] [CrossRef]
- Hu, Y.-W.; Zhang, H.-C.; Liu, S.-J.; Lu, H.-T. Sequential Monte Carlo Method Toward Online RUL Assessment with Applications. Chin. J. Mech. Eng. 2018, 31, 5. [Google Scholar] [CrossRef]
- Sharma, S.; Cui, Y.; He, Q.; Mohammadi, R.; Li, Z. Data-Driven Optimization of Railway Maintenance for Track Geometry. Transp. Res. Part C Emerg. Technol. 2018, 90, 34–58. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, Z.; Cheng, K.; Wang, Y. A Novel Reliability Sensitivity Analysis Method Based on Directional Sampling and Monte Carlo Simulation. Proc. Inst. Mech. Eng. Part O J. Risk Reliab. 2020, 234, 622–635. [Google Scholar] [CrossRef]
- Zhang, K.; Du, Z.; Xiao, F.; Wang, T.; Zhang, L. Improved Sequential Monte Carlo Method Approach to Substation Connection Reliability Assessment. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2357–2362. [Google Scholar]
- Macheret, Y.; Koehn, P.; Sparrow, D. Improving Reliability and Operational Availability of Military Systems. In Proceedings of the 2005 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2003; IEEE Operations Center: Big Sky, MT, USA, 2005; pp. 3948–3957. [Google Scholar]
- Andrade-Michel, A.; Ríos-Solís, Y.A.; Boyer, V. Vehicle and Reliable Driver Scheduling for Public Bus Transportation Systems. Transp. Res. Part B Methodol. 2021, 145, 290–301. [Google Scholar] [CrossRef]
- Wang, Y.; Infield, D. Markov Chain Monte Carlo Simulation of Electric Vehicle Use for Network Integration Studies. Int. J. Electr. Power Energy Syst. 2018, 99, 85–94. [Google Scholar] [CrossRef]
- Ricard, L.; Desaulniers, G.; Lodi, A.; Rousseau, L.-M. Predicting the Probability Distribution of Bus Travel Time to Measure the Reliability of Public Transport Services. Transp. Res. Part C Emerg. Technol. 2022, 138, 103619. [Google Scholar] [CrossRef]
- Salgado Duarte, Y.; Szpytko, J.; Del Castillo Serpa, A.M. Monte Carlo Simulation Model to Coordinate the Preventive Maintenance Scheduling of Generating Units in Isolated Distributed Power Systems. Electr. Power Syst. Res. 2020, 182, 106237. [Google Scholar] [CrossRef]
- Lojowska, A.; Kurowicka, D.; Papaefthymiou, G.; van der Sluis, L. Stochastic Modeling of Power Demand Due to EVs Using Copula. IEEE Trans. Power Syst. 2012, 27, 1960–1968. [Google Scholar] [CrossRef]
- Paś, J.; Klimczak, T.; Rosiński, A.; Stawowy, M. The Analysis of the Operational Process of a Complex Fire Alarm System Used in Transport Facilities. Build. Simul. 2022, 15, 615–629. [Google Scholar] [CrossRef]
- Stawowy, M.; Rosiński, A.; Siergiejczyk, M.; Perlicki, K. Quality and Reliability-Exploitation Modeling of Power Supply Systems. Energies 2021, 14, 2727. [Google Scholar] [CrossRef]
- Borowski, S.; Szubartowski, M.; Migawa, K.; Sołtysiak, A.; Neubauer, A.; Hujo, L.; Nosian, J. Mathematical Model for Determining the Time of Preventive Replacements in the Agricultural Machinery Service System with Minimal Repair. Appl. Sci. 2023, 13, 640. [Google Scholar] [CrossRef]
- Migawa, K.; Borowski, S.; Neubauer, A.; Sołtysiak, A. Semi-Markov Model of the System of Repairs and Preventive Replacements by Age of City Buses. Appl. Sci. 2021, 11, 10411. [Google Scholar] [CrossRef]
- Liu, P.; Wang, G. Optimal Periodic Preventive Maintenance Policies for Systems Subject to Shocks. Appl. Math. Model. 2021, 93, 101–114. [Google Scholar] [CrossRef]
- Park, M.; Jung, K.M.; Park, D.H. Optimization of Periodic Preventive Maintenance Policy Following the Expiration of Two-Dimensional Warranty. Reliab. Eng. Syst. Saf. 2018, 170, 1–9. [Google Scholar] [CrossRef]
- Hu, J.; Shen, J.; Shen, L. Periodic Preventive Maintenance Planning for Systems Working under a Markovian Operating Condition. Comput. Ind. Eng. 2020, 142, 106291. [Google Scholar] [CrossRef]
- Wang, W.; Wu, Z.; Xiong, J.; Xu, Y. Redundancy Optimization of Cold-Standby Systems under Periodic Inspection and Maintenance. Reliab. Eng. Syst. Saf. 2018, 180, 394–402. [Google Scholar] [CrossRef]
- Adekitan, A.I.; Bukola, A.; Kennedy, O. A Data-Based Investigation of Vehicle Maintenance Cost Components Using ANN. IOP Conf. Ser. Mater. Sci. Eng. 2018, 413, 012009. [Google Scholar] [CrossRef]
- Chen, C.; Liu, Y.; Wang, S.; Sun, X.; Di Cairano-Gilfedder, C.; Titmus, S.; Syntetos, A.A. Predictive Maintenance Using Cox Proportional Hazard Deep Learning. Adv. Eng. Inform. 2020, 44, 101054. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Pang, Y.; Liu, Y. Optimal Maintenance Scheduling under Uncertainties Using Linear Programming-Enhanced Reinforcement Learning. Eng. Appl. Artif. Intell. 2022, 109, 104655. [Google Scholar] [CrossRef]
- Sbihi, M.; Varnier, C. Single-Machine Scheduling with Periodic and Flexible Periodic Maintenance to Minimize Maximum Tardiness. Comput. Ind. Eng. 2008, 55, 830–840. [Google Scholar] [CrossRef] [Green Version]
- Ministry of Defense of Poland. DTU-4.22.13.1(A). Catalog of Operating Norms for Land Machinery; Ministry of Defense of Poland; Armed Forces Support Inspectorate: Bydgoszcz, Poland, 2019.
- Redmer, A. Optimisation of the Exploitation Period of Individual Vehicles in Freight Transportation Companies. Transp. Res. Part E Logist. Transp. Rev. 2009, 45, 978–987. [Google Scholar] [CrossRef]
- Betkier, I.; Macioszek, E. Characteristics of Parking Lots Located along Main Roads in Terms of Cargo Truck Requirements: A Case Study of Poland. Sustainability 2022, 14, 15720. [Google Scholar] [CrossRef]
- Soltanali, H.; Rohani, A.; Abbaspour-Fard, M.H.; Farinha, J.T. A Comparative Study of Statistical and Soft Computing Techniques for Reliability Prediction of Automotive Manufacturing. Appl. Soft Comput. 2021, 98, 106738. [Google Scholar] [CrossRef]
- Gołda, P.; Zawisza, T.; Izdebski, M. Evaluation of Efficiency and Reliability of Airport Processes Using Simulation Tools. Eksploat. Niezawodn. 2021, 23, 659–669. [Google Scholar] [CrossRef]
- Wang, J.; Gao, X.; Sun, Z. An Importance Sampling Framework for Time-Variant Reliability Analysis Involving Stochastic Processes. Sustainability 2021, 13, 7776. [Google Scholar] [CrossRef]
- Alkaff, A.; Qomarudin, M.N.; Purwantini, E.; Wiratno, S.E. Dynamic Reliability Modeling for General Standby Systems. Comput. Ind. Eng. 2021, 161, 107615. [Google Scholar] [CrossRef]
- Hao, S.; Yang, J.; Ma, X.; Zhao, Y. Reliability Modeling for Mutually Dependent Competing Failure Processes Due to Degradation and Random Shocks. Appl. Math. Model. 2017, 51, 232–249. [Google Scholar] [CrossRef]
- Hong, L.; Zhai, Q.; Wang, X.; Ye, Z.-S. System Reliability Evaluation Under Dynamic Operating Conditions. IEEE Trans. Reliab. 2019, 68, 800–809. [Google Scholar] [CrossRef]
- Torii, A.J.; Novotny, A.A. A Priori Error Estimates for Local Reliability-Based Sensitivity Analysis with Monte Carlo Simulation. Reliab. Eng. Syst. Saf. 2021, 213, 107749. [Google Scholar] [CrossRef]
- Angus, J.; Ding, Y. On the Ratio of Current Age to Total Life for Null Recurrent Renewal Processes. Stat. Probab. Lett. 2020, 162, 399. [Google Scholar] [CrossRef]
- Vassiliou, P.-C.G. Non-Homogeneous Semi-Markov and Markov Renewal Processes and Change of Measure in Credit Risk. Mathematics 2020, 9, 55. [Google Scholar] [CrossRef]
- Ziółkowski, J.; Małachowski, J.; Oszczypała, M.; Szkutnik-Rogoż, J.; Lęgas, A. Modelling of the Military Helicopter Operation Process in Terms of Readiness. Def. Sci. J. 2021, 71, 602–611. [Google Scholar] [CrossRef]
- Grabski, F. Semi-Markov Failure Rates Processes. Appl. Math. Comput. 2011, 217, 9956–9965. [Google Scholar] [CrossRef]
- Migawa, K. Availability Control for Means of Transport in Decisive Semi-Markov Models of Exploitation Process. Arch. Transp. 2012, 24, 497–508. [Google Scholar] [CrossRef] [Green Version]
- Ivanchenko, O.; Kharchenko, V.; Moroz, B.; Kabak, L.; Smoktii, K. Semi-Markov Availability Model Considering Deliberate Malicious Impacts on an Infrastructure-as-a-Service Cloud. In Proceedings of the 2018 14th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET), Lviv-Slavske, Ukraine, 20–24 February 2018; pp. 570–573. [Google Scholar]
- Karakaya, E.; Vinel, A.; Smith, A.E. Relocations in Container Depots for Different Handling Equipment Types: Markov Models. Comput. Ind. Eng. 2021, 157, 107311. [Google Scholar] [CrossRef]
- Oniszczuk, W. Loss Tandem Networks with Blocking—A Semi-Markov Approach. Bull. Pol. Acad. Sci. Tech. Sci. 2010, 58, 673–681. [Google Scholar] [CrossRef]
- Shepero, M.; Munkhammar, J. Spatial Markov Chain Model for Electric Vehicle Charging in Cities Using Geographical Information System (GIS) Data. Appl. Energy 2018, 231, 1089–1099. [Google Scholar] [CrossRef]
- Iversen, E.B.; Morales, J.M.; Madsen, H. Optimal Charging of an Electric Vehicle Using a Markov Decision Process. Appl. Energy 2014, 123, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Li, K.; Zhao, W.; Ke, H.-C.; Wang, Z. A Sticky Sampling and Markov State Transition Matrix Based Driving Cycle Construction Method for EV. Energies 2022, 15, 1057. [Google Scholar] [CrossRef]
- Brayer, E.F. Calculating the Standard Error of a Proportion. Appl. Stat. 1957, 6, 67–68. [Google Scholar] [CrossRef]
- Gurland, J.; Tripathi, R.C. A Simple Approximation for Unbiased Estimation of the Standard Deviation. Am. Stat. 1971, 25, 30–32. [Google Scholar] [CrossRef]
- Roy, V.; Tan, A.; Flegal, J.M. Estimating Standard Errors for Importance Sampling Estimators with Multiple Markov Chains. Stat. Sin. 2018, 28, 1079–1101. [Google Scholar] [CrossRef] [Green Version]
- Rosychuk, R.J.; Sheng, X.; Stuber, J.L. Comparison of Variance Estimation Approaches in a Two-State Markov Model for Longitudinal Data with Misclassification. Stat. Med. 2006, 25, 1906–1921. [Google Scholar] [CrossRef]


| Methods | Purposes of Research | Case Studies | Simulations | Papers |
|---|---|---|---|---|
| Monte Carlo | Reliability analysis | Coated surface | Sampling of inter-repair time (500 samples) | [22] |
| Monte Carlo, Latin hypercube sampling (LHS) and Iman-Conover methods | Reliability analysis | Agricultural tractors | Sampling of time-to-failure data | [23] |
| Markov Chain Monte Carlo | Reliability and availability analysis | Rotary drilling machines | Simulation of Markov Chain transitions | [29] |
| Markov Chain Monte Carlo | Global minimization of the system failure probability | Structural dynamic systems under stochastic excitation: linear single-degree of freedom system, linear eight-story two dimensional frame structure and a nonlinear three dimensional bridge structural | Random sampling of many variables | [17] |
| Markov Chain Monte Carlo | Modelling of vehicle use patterns | Electric vehicles | Random sampling of daily driving time (105 trials) | [36] |
| Markov Chain Monte Carlo and Sequential Monte Carlo | Assessment of remaining useful life | Milling machine | Sampling from posteriori distribution of states | [30] |
| Markov Chain Monte Carlo with the Metropolis–Hasting Algorithm | Reliability assessment | Bridge health monitoring | Sampling of points to estimate failure probability | [18] |
| Sequential Markov Chain Monte Carlo | Optimisation of preventive maintenance schedule | Isolated Distributed Cuban Power System (wind turbines) | Simulation of wind speed | [38] |
| Sequential and Non-sequential Monte Carlo | Reliability assessment | Distribution network | Simulation by sampling of time-to-failure and time-to-repair | [28] |
| Monte Carlo and Copula | Power demand prediction | Electric vehicles | Simulation by sampling start time, end time, and distance travelled | [39] |
| Monte Carlo and directional sampling | Reliability sensitivity analysis | Headless rivet and wing box structure | Random sampling data (1 × 106 and 2 × 106) | [32] |
| Deep Belief Network and Monte Carlo | Calculate the reliability of the model | Physically-based thermal error model of the servo axis in machine tool | Random sampling data (107 trials) of the thermal characteristic parameters | [16] |
| Iterative Monte Carlo and semi-Markov approach | Assessing readiness and forecasting in various operational scenarios | Transportation system equipped with light utility vehicles | Sampling of task assignments, daily mileages, failures, and repairs based on CDFs and reliability function | This paper |
| Notations | Definitions |
|---|---|
| X(t) | Stochastic process |
| Tm | Normative period between maintenance |
| Lm | Normative mileage between maintenance |
| tm(t) | Time since last periodic maintenance |
| lm(t) | Mileage since last periodic maintenance |
| Θ | Probability of assignment task |
| κ | Redundancy |
| ld | Daily mileage |
| ldmax | Maximum daily mileage |
| lr | Mileage since last failure |
| lf | Mileage on the day of failure |
| G(ld) | Cumulative distribution function (CDF) of daily mileage |
| R(lr) | Reliability function |
| F(lr) | Cumulative distribution function (CDF) of failures |
| f(lr) | Probability density function (PDF) of failures |
| H(i) | Cumulative distribution function (CDF) of repair time |
| q1, q2, q3, q4 | Random values of the uniform distribution on the interval (0, 1) |
| T(S1), T(S2), T(S3), T(S4) | Sojourn times of state S1, S2, S3, S4 |
| Kr | Readiness indicator |
| Ks | Suitability indicator |
| Nv | Number of vehicles |
| Zi | Number of iterations |
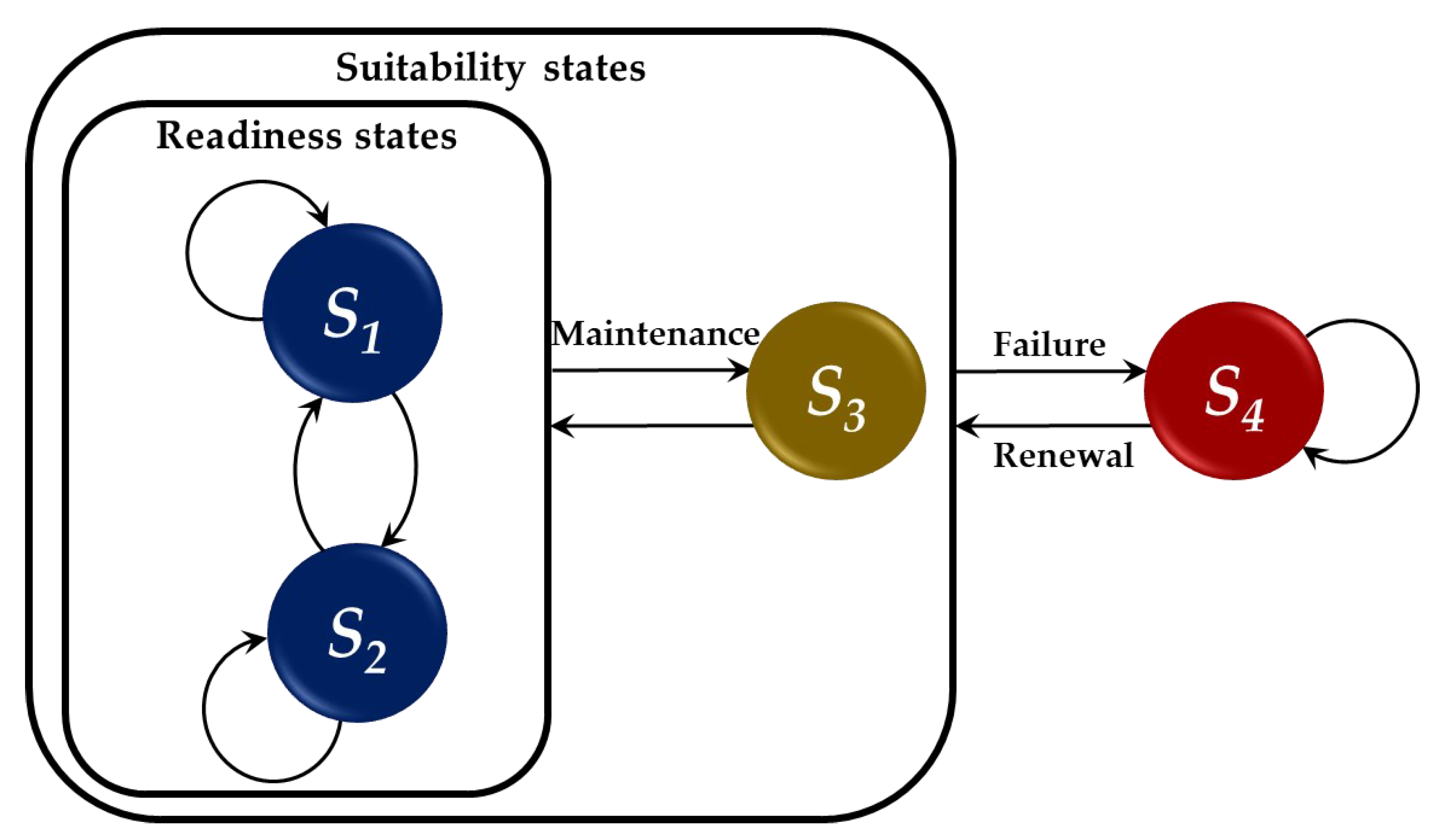
| State | Meaning | Description |
|---|---|---|
| S1 | Task execution | Vehicle is assigned to perform transportation tasks. |
| S2 | Awaiting a transport task | Vehicle in reserve is waiting for a task. |
| S3 | Periodic maintenance | Periodic maintenance is required. Vehicle is being serviced. |
| S4 | Repair | Vehicle has failed. Repair is completed or vehicle is pending repair. |
| Model | CDF | Parameters | Estimation | R |
|---|---|---|---|---|
| Exponential | λ—scale | λ = 0.0113 | 0.9976 | |
| Weibull | α—scale β—shape | α = 91.9967 β = 1.0984 | 0.9970 | |
| Gamma | k—shape θ—scale | k = 1.2618 θ = 70.1488 | 0.9975 | |
| Lognormal | μ—log location σ—log scale | μ = 4.0373 σ = 1.0131 | 0.9994 |
| Model | Reliability Function | R |
|---|---|---|
| Exponential | 0.9945 | |
| Weibull | 0.9971 | |
| Neural | 0.9975 |
| Model | CDF | Parameters | Estimation | R |
|---|---|---|---|---|
| Exponential | λ—scale | λ = 0.0704 | 0.9207 | |
| Weibull | α—scale β—shape | α = 5.0784 β = 0.4612 | 0.9924 | |
| Gamma | k—shape θ—scale | k = 0.3144 θ = 45.1562 | 0.9846 | |
| Lognormal | μ—log location σ—log scale | μ = 0.4768 σ = 2.3254 | 0.9907 |
| Monte Carlo Model | Maintenance | Assignment of Tasks | Operational Process | Reliability | Repair |
|---|---|---|---|---|---|
| MC1 | Deterministic | Binomial | Exponential | Exponential | Weibull |
| MC2 | Deterministic | Binomial | Exponential | Exponential | Lognormal |
| MC3 | Deterministic | Binomial | Exponential | Weibull | Weibull |
| MC4 | Deterministic | Binomial | Exponential | Weibull | Lognormal |
| MC5 | Deterministic | Binomial | Weibull | Exponential | Weibull |
| MC6 | Deterministic | Binomial | Weibull | Exponential | Lognormal |
| MC7 | Deterministic | Binomial | Weibull | Weibull | Weibull |
| MC8 | Deterministic | Binomial | Weibull | Weibull | Lognormal |
| MC9 | Deterministic | Binomial | Lognormal | Exponential | Weibull |
| MC10 | Deterministic | Binomial | Lognormal | Exponential | Lognormal |
| MC11 | Deterministic | Binomial | Lognormal | Weibull | Weibull |
| MC12 | Deterministic | Binomial | Lognormal | Weibull | Lognormal |
| MC13 | Deterministic | Binomial | Gamma | Exponential | Weibull |
| MC14 | Deterministic | Binomial | Gamma | Exponential | Lognormal |
| MC15 | Deterministic | Binomial | Gamma | Weibull | Weibull |
| MC16 | Deterministic | Binomial | Gamma | Weibull | Lognormal |
| Simulation | Readiness Kr | Suitability Ks | ||||
|---|---|---|---|---|---|---|
| Monte Carlo | Semi-Markov | Percentage Error (%) | Monte Carlo | Semi-Markov | Percentage Error (%) | |
| MC1 | 0.9078 | 0.9015 | 0.70 | 0.9104 | 0.9073 | 0.34 |
| MC2 | 0.8766 | 0.9015 | −2.76 | 0.8790 | 0.9073 | −3.12 |
| MC3 | 0.9337 | 0.9015 | 3.57 | 0.9363 | 0.9073 | 3.20 |
| MC4 | 0.9195 | 0.9015 | 2.00 | 0.9221 | 0.9073 | 1.63 |
| MC5 | 0.9142 | 0.9015 | 1.41 | 0.9167 | 0.9073 | 1.04 |
| MC6 | 0.8735 | 0.9015 | −3.11 | 0.8760 | 0.9073 | −3.45 |
| MC7 | 0.9329 | 0.9015 | 3.48 | 0.9355 | 0.9073 | 3.11 |
| MC8 | 0.8791 | 0.9015 | −2.48 | 0.8816 | 0.9073 | −2.83 |
| MC9 | 0.9163 | 0.9015 | 1.64 | 0.9189 | 0.9073 | 1.28 |
| MC10 | 0.8545 | 0.9015 | −5.21 | 0.8571 | 0.9073 | −5.53 |
| MC11 | 0.9257 | 0.9015 | 2.68 | 0.9284 | 0.9073 | 2.33 |
| MC12 | 0.8727 | 0.9015 | −3.19 | 0.8753 | 0.9073 | −3.53 |
| MC13 | 0.9393 | 0.9015 | 4.19 | 0.9414 | 0.9073 | 3.76 |
| MC14 | 0.8895 | 0.9015 | −1.33 | 0.8916 | 0.9073 | −1.73 |
| MC15 | 0.9419 | 0.9015 | 4.48 | 0.9440 | 0.9073 | 4.04 |
| MC16 | 0.8597 | 0.9015 | −4.64 | 0.8617 | 0.9073 | −5.03 |
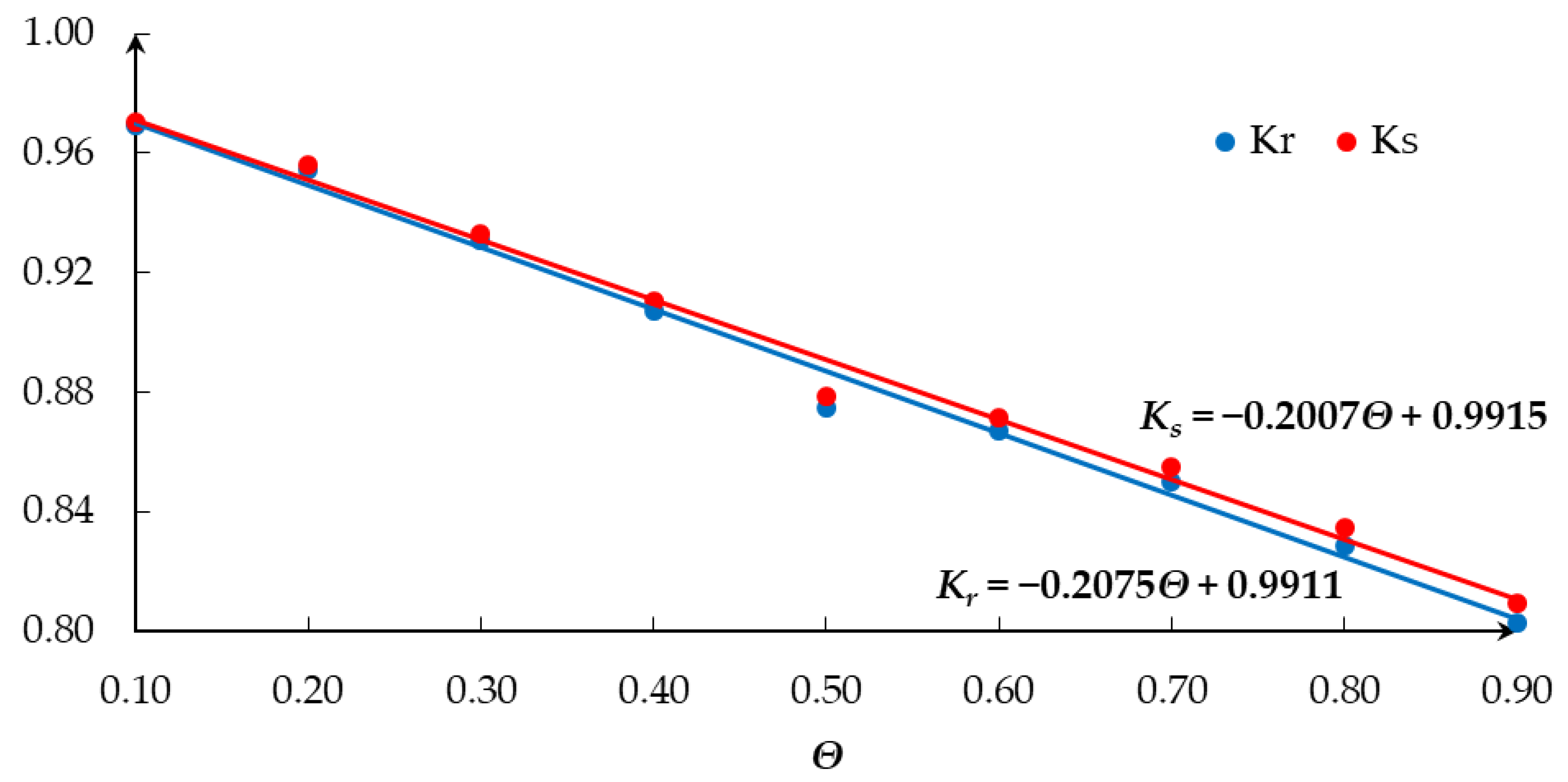
| Θ | Kr | Ks |
|---|---|---|
| 0.10 | 0.9695 | 0.9704 |
| 0.20 | 0.9547 | 0.9564 |
| 0.30 | 0.9309 | 0.9333 |
| 0.40 | 0.9073 | 0.9104 |
| 0.50 | 0.8750 | 0.8788 |
| 0.60 | 0.8670 | 0.8715 |
| 0.70 | 0.8501 | 0.8553 |
| 0.80 | 0.8289 | 0.8347 |
| 0.90 | 0.8031 | 0.8094 |
| 0.10 | 0.9695 | 0.9704 |
| Expected Daily Mileage (km) | Kr | Ks |
|---|---|---|
| 50 | 0.9445 | 0.9461 |
| 60 | 0.9476 | 0.9495 |
| 70 | 0.9431 | 0.9452 |
| 80 | 0.9348 | 0.9371 |
| 90 | 0.9097 | 0.9123 |
| 100 | 0.9094 | 0.9122 |
| 110 | 0.9049 | 0.9080 |
| 120 | 0.8993 | 0.9027 |
| 130 | 0.8838 | 0.8873 |
| 140 | 0.8768 | 0.8806 |
| 150 | 0.8735 | 0.8775 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oszczypała, M.; Ziółkowski, J.; Małachowski, J. Modelling the Operation Process of Light Utility Vehicles in Transport Systems Using Monte Carlo Simulation and Semi-Markov Approach. Energies 2023, 16, 2210. https://doi.org/10.3390/en16052210
Oszczypała M, Ziółkowski J, Małachowski J. Modelling the Operation Process of Light Utility Vehicles in Transport Systems Using Monte Carlo Simulation and Semi-Markov Approach. Energies. 2023; 16(5):2210. https://doi.org/10.3390/en16052210
Chicago/Turabian StyleOszczypała, Mateusz, Jarosław Ziółkowski, and Jerzy Małachowski. 2023. "Modelling the Operation Process of Light Utility Vehicles in Transport Systems Using Monte Carlo Simulation and Semi-Markov Approach" Energies 16, no. 5: 2210. https://doi.org/10.3390/en16052210
APA StyleOszczypała, M., Ziółkowski, J., & Małachowski, J. (2023). Modelling the Operation Process of Light Utility Vehicles in Transport Systems Using Monte Carlo Simulation and Semi-Markov Approach. Energies, 16(5), 2210. https://doi.org/10.3390/en16052210