A Computational Scheme for Stochastic Non-Newtonian Mixed Convection Nanofluid Flow over Oscillatory Sheet
Abstract
:1. Introduction
2. Proposed Numerical Scheme
3. Stability Analysis
4. Consistency Analysis
5. Problem Formulation
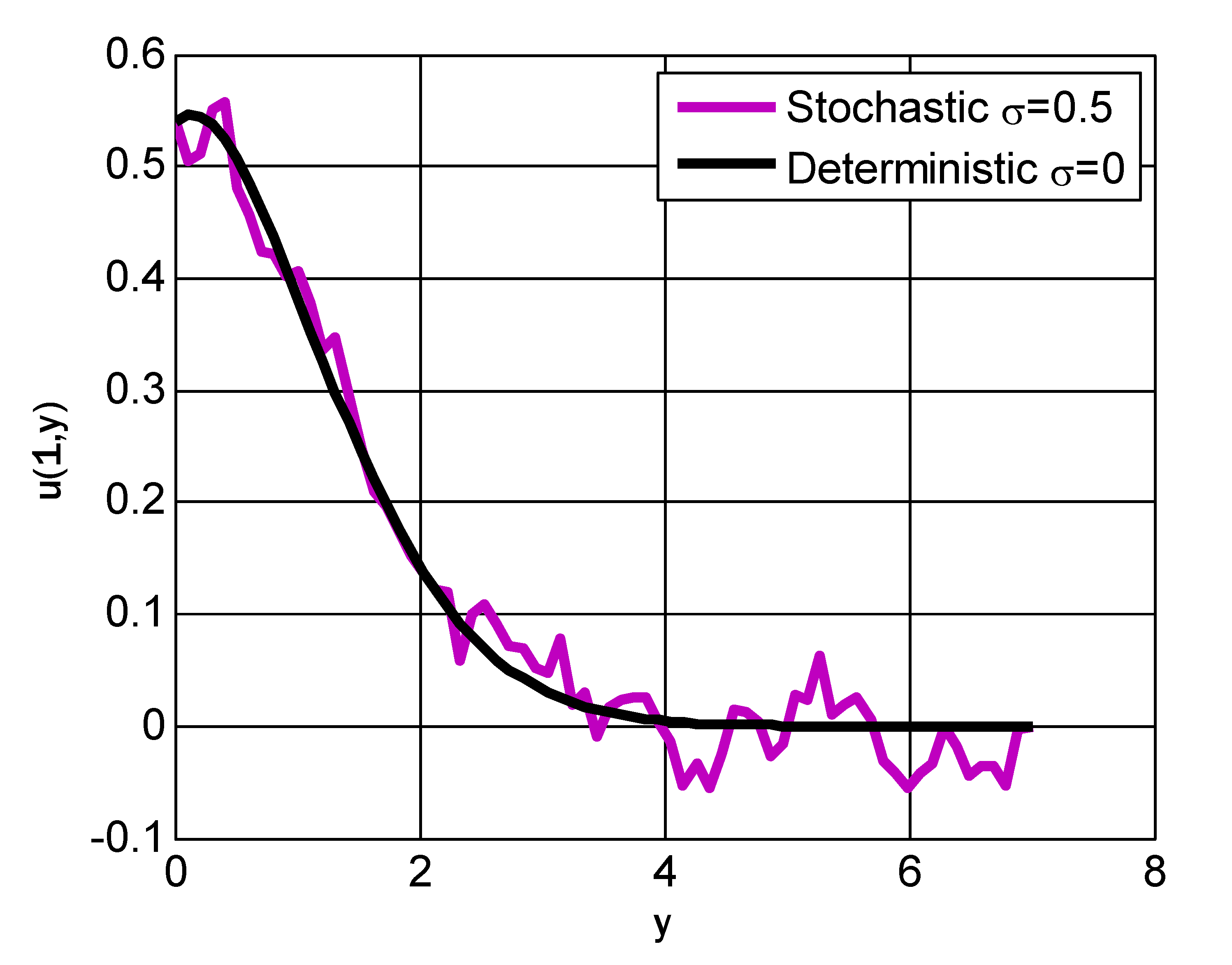
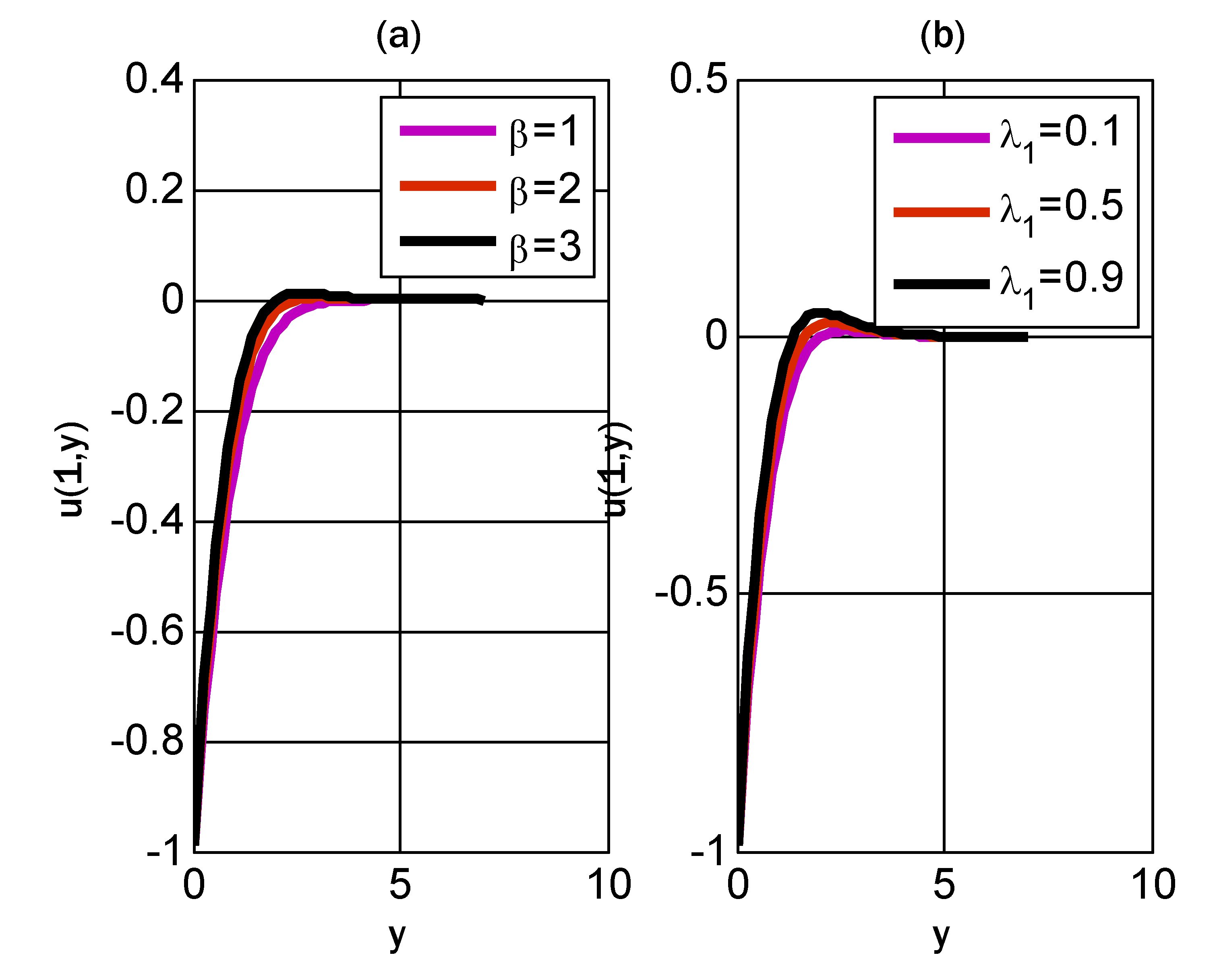
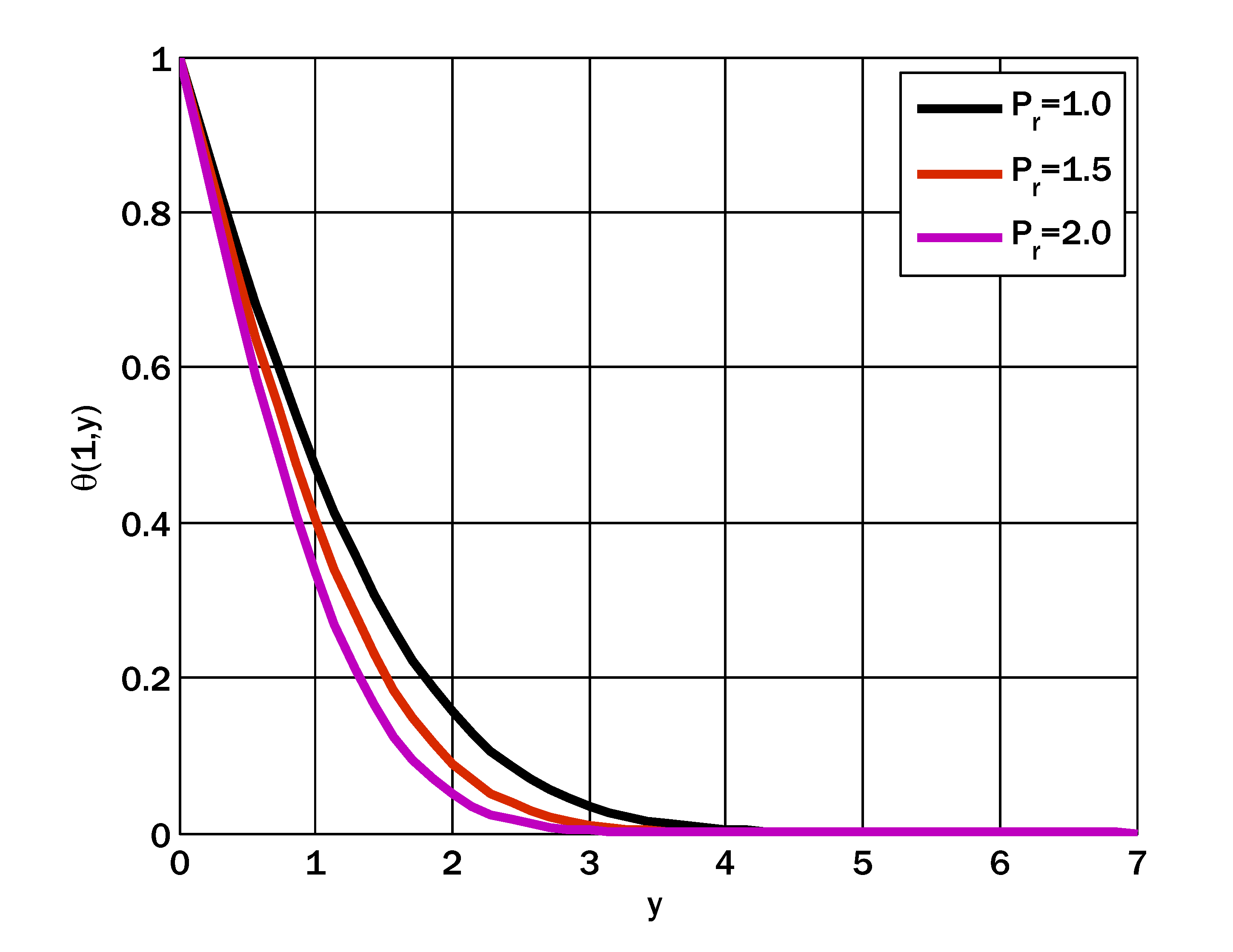
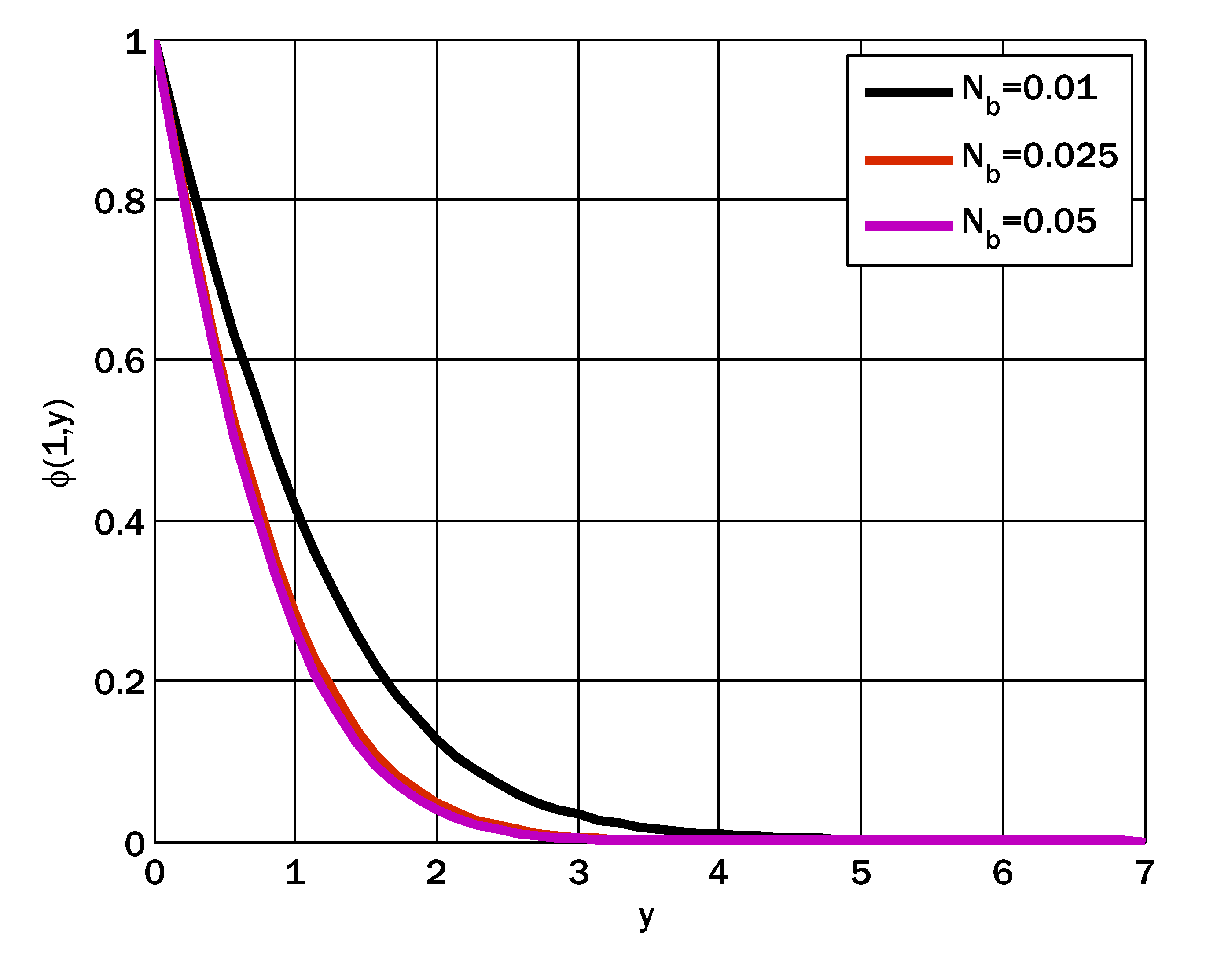
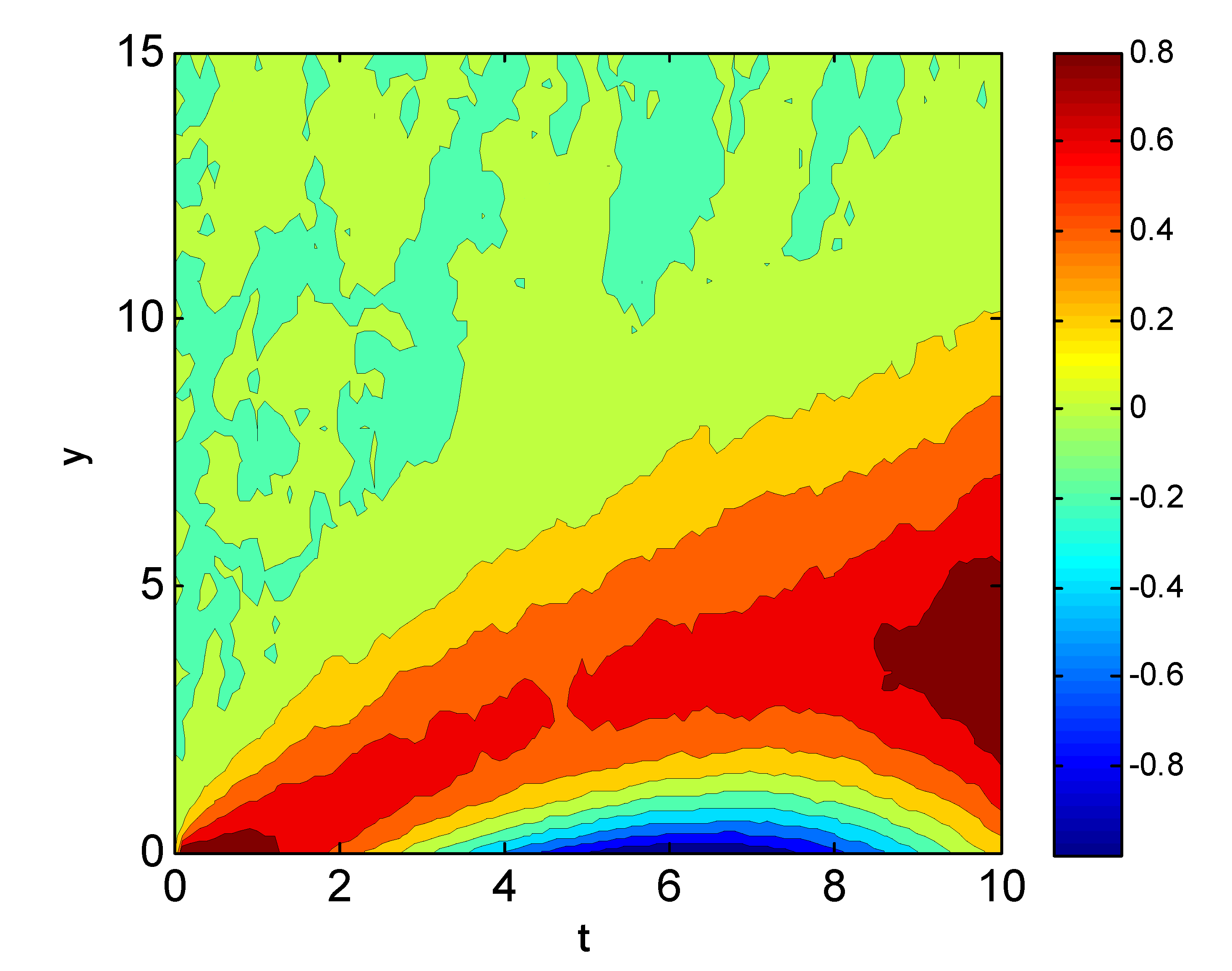
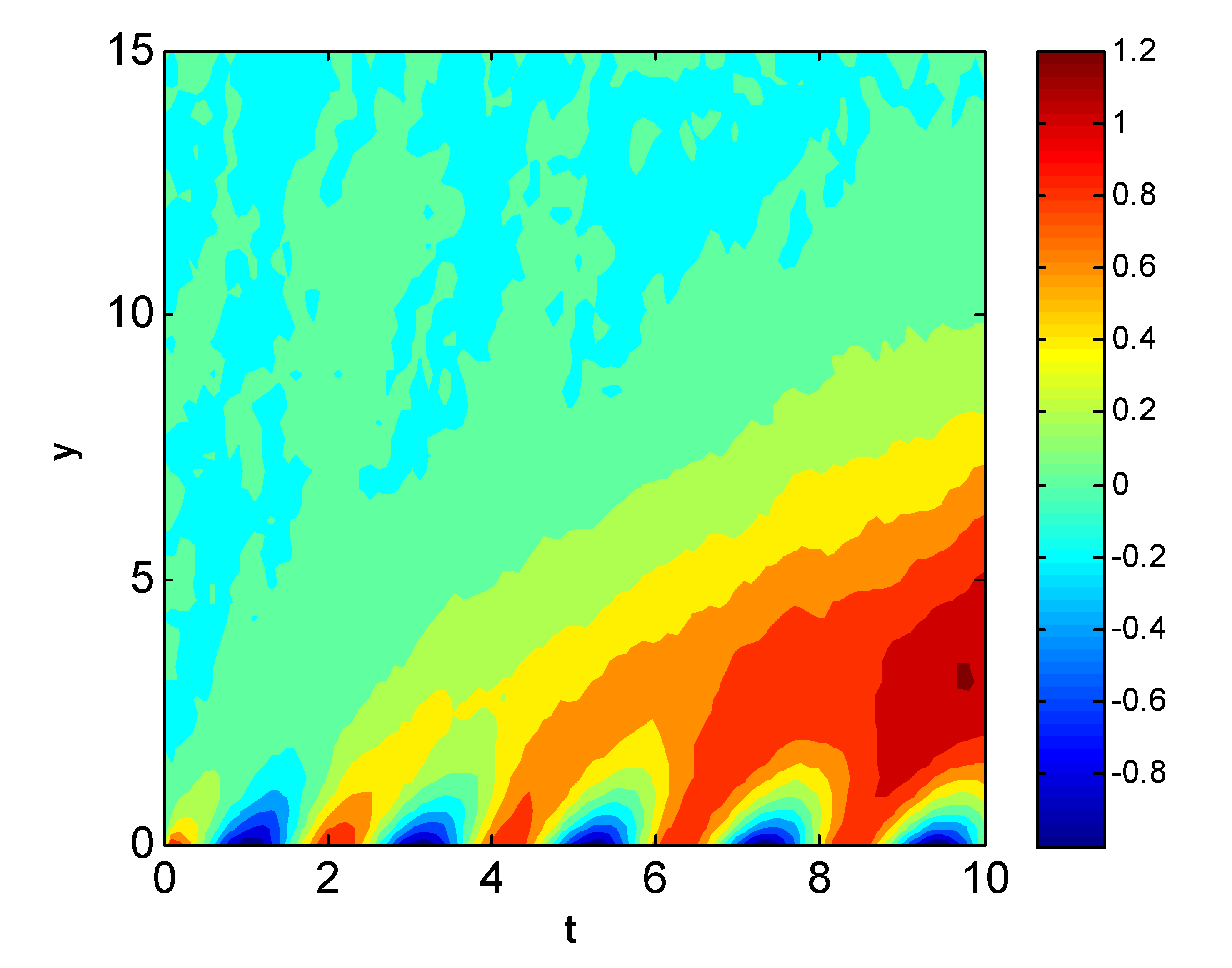
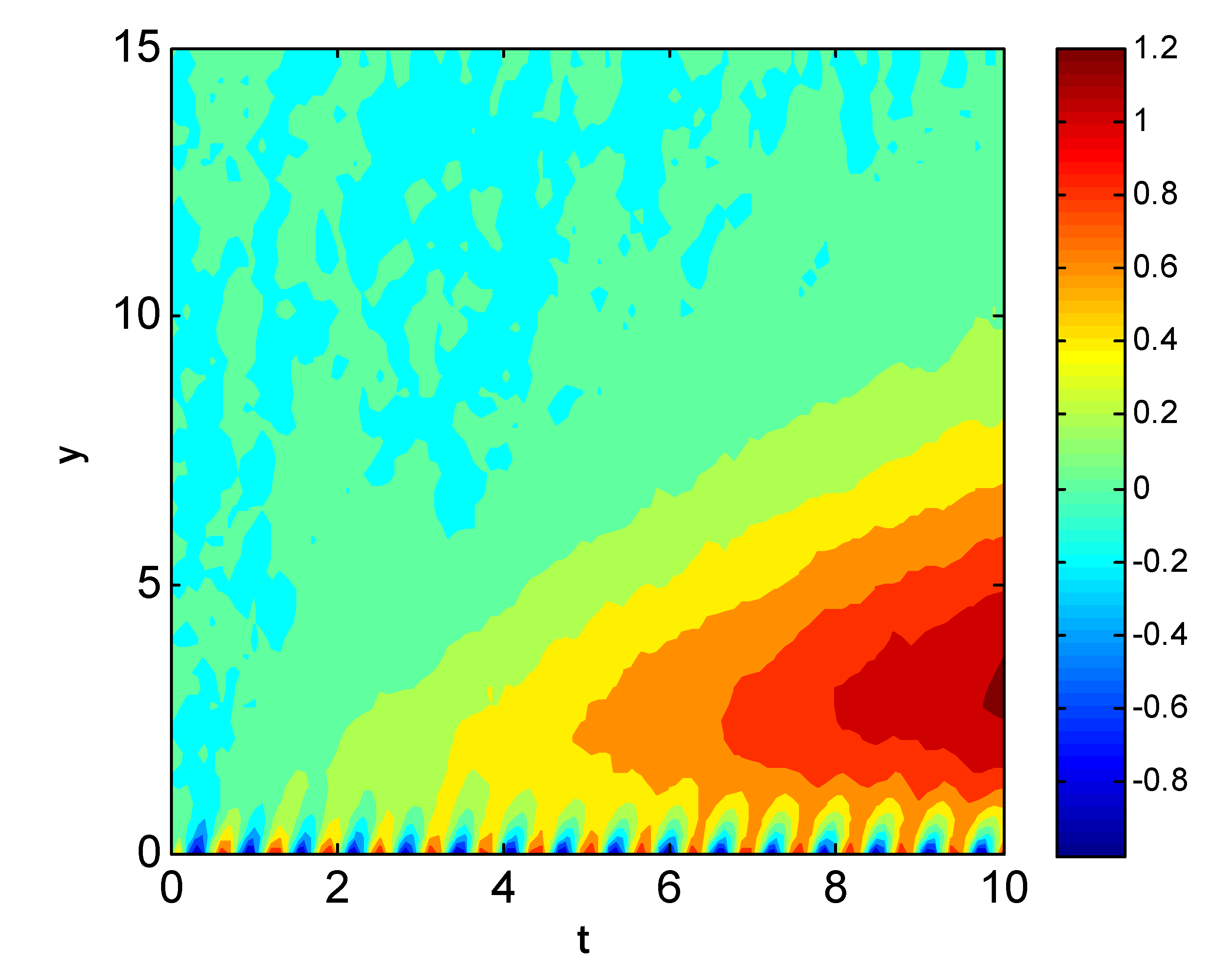
6. Results and Discussion
7. Conclusions
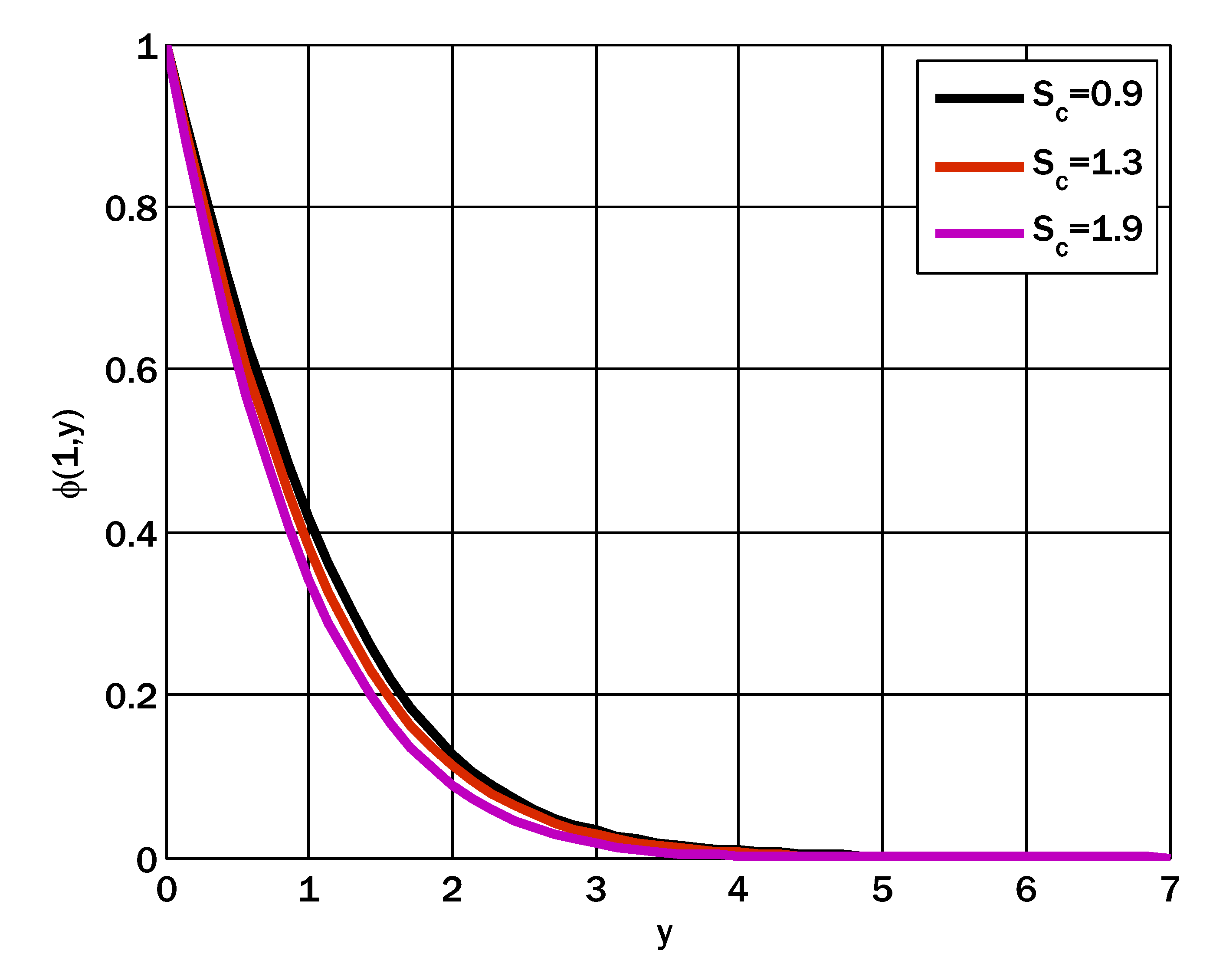
- The velocity profile had dual behavior by incrementing Casson and mixed convection parameters.
- The temperature profile was escalated by enhancing the thermophoresis parameter.
- The concentration profile decayed and grew by increasing the Brownian motion and thermophoresis parameters, respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Simiu, E. Chaotic Transition in Deterministic and Stochastic Systems; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Maciejewski, P.; Moffat, R. Heat Transfer with Very High Free-Stream Turbulence, Part I: Experimental Data. J. Heat Transf. 1992, 114, 827–833. [Google Scholar] [CrossRef]
- Lucor, D.; Karniadakis, G. Noisy Inflows Cause a Shedding Mode Switching in Flow Past an Oscillating Cylinder. Phys. Rev. Lett. 2004, 92, 154501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Espanol, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Lou, Z.; Yang, W.J. A computer simulation of the non-Newtonian blood flow at the aortic bifurcation. J. Biomech. 1993, 26, 37–49. [Google Scholar] [CrossRef] [Green Version]
- Papanastasiou, T.C.; Boudouvis, A.G. Flows of viscoplastic materials: Models and computations. Comput. Struct. 1997, 64, 677–694. [Google Scholar] [CrossRef]
- Li, G.; Chen, B.; Zhou, G. Unsteady non-Newtonian solver on unstructured grid for the simulation of blood flow. Adv. Mech. Eng. 2013, 2013, 596172. [Google Scholar] [CrossRef]
- Venkatesan, J.; Sankar, D.; Hemalatha, K.; Yatim, Y. Mathematical analysis of Casson fluid model for blood rheology in stenosed narrow arteries. J. Appl. Math. 2013, 2013, 583809. [Google Scholar] [CrossRef] [Green Version]
- Amlimohamadi, H.; Akram, M.; Sadeghy, K. Flow of a Casson fluid through a locally constricted porous channel: A numerical study. Korea Aust. Rheol. J. 2016, 28, 129–137. [Google Scholar] [CrossRef]
- Makinde, O.D.; Sandeep, N.; Ajayi, T.; Animasaun, I.L. Numerical Exploration of Heat Transfer and Lorentz Force Effects on the Flow of MHD Casson Fluid over an Upper Horizontal Surface of a Thermally Stratified Melting Surface of a Paraboloid of Revolution. Int. J. Nonlinear Sci. Numer. Simul. 2016, 19, 93–106. [Google Scholar] [CrossRef]
- Thumma, T.; Wakif, A.; Animasaun, I.L. Generalized differential quadrature analysis of unsteady three-dimensional MHD radiating dissipative Casson fluid conveying tiny particles. Heat Transf. 2020, 49, 2595–2626. [Google Scholar] [CrossRef]
- Mahmood, R.; Kousar, N.; Usman, K.; Mehmood, A. Finite element simulations for stationary Bingham fluid flow past a circular cylinder. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 459. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. An Unconditionally Stable Third Order Scheme for Mixed Convection Flow between Parallel Plates with Oscillatory Boundary Conditions; John Wiley and Sons Ltd.: Hoboken, NJ, USA, 2023. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. Predictor–Corrector Scheme for Electrical Magnetohydrodynamic (MHD) Casson Nanofluid Flow: A Computational Study. Appl. Sci. 2023, 13, 1209. [Google Scholar] [CrossRef]
- Arif, M.S.; Abodayeh, K.; Nawaz, Y. The modified finite element method for heat and mass transfer of unsteady reacting flow with mixed convection. Front. Phys. 2022, 10, 802. [Google Scholar] [CrossRef]
- Shatnawi, T.A.M.; Abbas, N.; Shatanawi, W. Mathematical Analysis of Unsteady Stagnation Point Flow of Radiative Casson Hybrid Nanofluid Flow over a Vertical Riga Sheet. Mathematics 2022, 10, 3573. [Google Scholar] [CrossRef]
- Mehmood, A.; Mahmood, R.; Majeed, A.H.; Awan, F.J. Flow of the Bingham Papanastasiou Regularized Material in a Channel in the Presence of Obstacles: Correlation between Hydrodynamic Forces and Spacing of Obstacles. Model. Simul. Eng. 2021, 2021, 5583110. [Google Scholar] [CrossRef]
- Ilyas, H.; Ahmad, I.; Raja, M.A.Z.; Shoaib, M. A novel design of Gaussian wave nets for rotational hybrid nanofluidic flow over a stretching sheet involving thermal radiation. Int. Commun. Heat Mass Transf. 2021, 123, 105196. [Google Scholar] [CrossRef]
- Hamid, A.; Chu, Y.-M.; Khan, M.I.; Kumar, R.N.; Gowd, R.J.P.; Prasannakumara, B.C. Critical values in axisymmetric flow of magneto-cross nanomaterial towards a radially shrinking disk. Int. J. Mod. Phys. B 2021, 35, 2150105. [Google Scholar] [CrossRef]
- Hussain, S.; Tunç, O.; Rahman, G.U.; Khan, H.; Nadia, E. Mathematical analysis of stochastic epidemic model of MERS-corona & application of ergodic theory. Math. Comput. Simul. 2023, 207, 130–150. [Google Scholar] [CrossRef]
- Ahmad, I.; Raja, M.A.Z.; Ramos, H.; Bilal, M.; Shoaib, M. Integrated neuro-evolution-based computing solver for dynamics of non-linear corneal shape model numerically. Neural Comput. Appl. 2021, 33, 5753–5769. [Google Scholar] [CrossRef]
- Shatnawi, T.A.M.; Abbas, N.; Shatanawi, W. Comparative study of Casson hybrid nanofluid models with induced magnetic radiative flow over a vertical permeable exponentially stretching sheet. Am. Inst. Math. Sci. AIMS Math. 2022, 7, 20545–20564. [Google Scholar] [CrossRef]
- Shoaib, M.; Kausar, M.; Khan, M.I.; Zeb, M.; Gowda, R.P.; Prasannakumara, B.; Alzahrani, F.; Raja, M.A.Z. Intelligent backpropagated neural networks application on Darcy-Forchheimer ferrofluid slip flow system. Int. Commun. Heat Mass Transf. 2021, 129, 105730. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.; Khan, M.I.; Alsaedi, A.; Ayub, M. Electromagneto squeezing rotational flow of carbon (C)-water (H2O) kerosene oil nanofluid past a Riga plate: A numerical study. PLoS ONE 2017, 12, e0180976. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wakif, A.; Animasaun, I.; Sehaqui, R. A brief technical note on the onset of convection in a horizontal nanofluid layer of finite depth via Wakif-Galerkin weighted residuals technique (WGWRT). Defect Diffus. Forum 2021, 409, 90–94. [Google Scholar] [CrossRef]
- Shah, Z.; Raja, M.A.Z.; Chu, Y.-M.; Khan, W.A.; Waqas, M.; Shoaib, M.; Abbass, S.Z. Design of neural network based intelligent computing for neumerical treatment of unsteady 3D flow of Eyring-Powell magneto-nanofluidic model. J. Mater. Res. Technol. 2020, 9, 14372–14387. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Unsteady mhd flow with variable viscosity: Applications of spectral scheme. Int. J. Therm. Sci. 2010, 49, 563–570. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Effective Computation of Solutions for Non-linear Heat Transfer Problems in Fins. J. Heat Transfer. 2014, 136, 091901. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Effective computation of exact and analytic approximate solutions to singular non-linear equations of Lane–Emden–Fowler type. Appl. Math. Model. 2013, 37, 7539–7548. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Equivalence of ratio and residual approaches in the homotopy analysis method and some applications in non-linear science and engineering. Comput. Model. Eng. Sci. 2019, 120, 63–81. [Google Scholar]
- Iftikhar, B.; Javed, T.; Siddiqu, M.A. Entropy generation analysis during MHD mixed convection flow of non-Newtonian fluid saturated inside the square cavity. J. Comput. Sci. 2023, 66, 101907. [Google Scholar] [CrossRef]
- Harish, R.; Sivakumar, R. Effects of nanoparticle dispersion on turbulent mixed convection flows in cubical enclosure considering Brownian motion and thermophoresis. Powder Technol. 2021, 378, 303–316. [Google Scholar] [CrossRef]
- Abderrahmane, A.; Alqsair, U.F.; Guedri, K.; Jamshed, W.; Nasir, N.A.A.; Majdi, H.S.; Baghaei, S.; Mourad, A.; Marzouki, R. Analysis of mixed convection of a power-law non-Newtonian nanofluid through a vented enclosure with rotating cylinder under magnetic field. Ann. Nucl. Energy 2022, 178, 109339. [Google Scholar] [CrossRef]
- Hassan, A.; Hussain, A.; Arshad, M.; Awrejcewicz, J.; Pawlowski, W.; Alharbi, F.M.; Karamti, H. Heat and Mass Transport Analysis of MHD Rotating Hybrid Nanofluids Conveying Silver and Molybdenum Di-Sulfide Nano-Particles under Effect of Linear and Non-Linear Radiation. Energies 2022, 15, 6269. [Google Scholar] [CrossRef]
- Arshad, M.; Hussain, A.; Hassan, A.; Karamti, H.; Wróblewski, P.; Khan, I.; Andualem, M.; Galal, A.M. Scrutinization of Slip Due to Lateral Velocity on the Dynamics of Engine Oil Conveying Cupric and Alumina Nanoparticles Subject to Coriolis Force. Math. Probl. Eng. 2022, 2022, 2526951. [Google Scholar] [CrossRef]
- Tessitore, G. Existence, uniqueness and space regularity of the adapted solutions of a backward SPDE. Stoch. Anal. Appl. 1996, 14, 461–486. [Google Scholar] [CrossRef]
- Dozzi, M.; López-Mimbela, J.A. Finite-time blowup and existence of global positive solutions of a semilinear SPDE. Stoch. Process. Appl. 2010, 120, 767–776. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.; Yang, X. Existence and pathwise uniqueness to an SPDE driven by a-stable colored noise. Stoch. Process. Appl. 2019, 129, 2681–2722. [Google Scholar] [CrossRef]
- Altmeyer, R.; Bretschneider, T.; Janák, J.; Reiß, M. Parameter estimation in an SPDE model for cell repolarization SIAM/ASA. J. Uncertain. Quantif. 2022, 10, 179–199. [Google Scholar] [CrossRef]
- Gyöngy, I.; Martínez, T. On numerical solution of stochastic partial differential equations of elliptic type Sto-chastics: An International. J. Probab. Stoch. Process. 2006, 78, 213–231. [Google Scholar] [CrossRef]
- Kamrani, M.; Hosseini, S.M. The role of coefficients of a general SPDE on the stability and convergence of a finite difference method. J. Comput. Appl. Math. 2010, 234, 1426–1434. [Google Scholar] [CrossRef]
- Yasin, M.W.; Iqbal, M.S.; Ahmed, N.; Akgül, A.; Raza, A.; Rafiq, M.; Riaz, M.B. Numerical scheme and stability analysis of stochastic Fitzhugh-Nagumo model. Results Phys. 2022, 32, 105023. [Google Scholar] [CrossRef]
- Yasin, M.W.; Iqbal, M.S.; Seadawy, A.R.; Baber, M.Z.; Younis, M.; Rizvi, S.T. Numerical scheme and analytical solutions to the stochastic nonlinear advection diffusion dynamical model. Int. J. Nonlinear Sci. Numer. Simul. 2021. [Google Scholar] [CrossRef]
- Allen, E.J.; Novosel, S.J.; Zhang, Z. Finite element and difference approximation of some linear stochastic partial differential equations. Stoch. Int. J. Probab. Stoch. Process. 1998, 64, 117–142. [Google Scholar] [CrossRef]
- Kruse, R. Consistency and stability of a Milstein-Galerkin finite element scheme for semilinear SPDE. Stoch. Partial. Differ. Eq. Anal. Comput. 2014, 2, 471–516. [Google Scholar] [CrossRef] [Green Version]
- Roth, C. A combination of finite difference and Wong-Zakai methods for hyperbolic stochastic partial differential equations. Stoch. Anal. Appl. 2006, 24, 221–240. [Google Scholar] [CrossRef]
- Namjoo, M.; Mohebbian, A. Approximation of stochastic partial differential equations with stochastic crank-nicolson method. In Proceedings of the 21st Seminar on Mathematical Analysis and its Applications, Hamedan, Iran, 26–27 November 2014. [Google Scholar]
- Li, Y.; Mao, X.; Song, Q.; Wu, F.; Yin, G. Strong convergence of Euler-Maruyama schemes for McKean-Vlasov stochastic differential equations under local Lipschitz conditions of state variables IMA. J. Numer. Anal. 2022, 2022, 107. [Google Scholar] [CrossRef]
- Hu, L.; Li, X.; Mao, X. Convergence rate and stability of the truncated Euler-Maruyama method forstochastic differential equations. J. Comput. Appl. Math. 2018, 337, 274–289. [Google Scholar] [CrossRef]
- El-Metwally, H.; Sohaly, M.A.; Elbaz, I.M. Mean-square stability of the zero equilibrium of the nonlinear delay differential equation: Nicholson’s blowflies application. Nonlinear Dyn. 2021, 105, 1713–1722. [Google Scholar] [CrossRef]
- Mohammed, M. Well-Posedness for Non-linear Parabolic Stochastic Differential Equations with Non-linear Robin Conditions. Symmetry 2022, 14, 1722. [Google Scholar] [CrossRef]
- Ishfaq, N.; Khan, W.; Khan, Z. The Stokes’ second problem for nanofluids. J. King Saud Univ.-Sci. 2019, 31, 61–65. [Google Scholar] [CrossRef]
- Abodayeh, K.; Raza, A.; Arif, M.S.; Rafiq, M.; Bibi, M.; Fayyaz, R. Numerical analysis of stochastic vector borne plant disease model. Comput. Mater. Contin. 2020, 62, 65–83. [Google Scholar] [CrossRef]
- Arif, M.S.; Raza, A.; Shatanawi, W.; Rafiq, M.; Bibi, M. A stochastic numerical analysis for computer virus model with vertical transmission over the internet. Comput. Mater. Contin. 2019, 61, 1025–1043. [Google Scholar]
- Shatanawi, W.; Raza, A.; Arif, M.S.; Abodayeh, K.; Rafiq, M.; Bibi, M. Design of nonstandard computational method for stochastic susceptible–infected–treated–recovered dynamics of coronavirus model. Adv. Differ. Equ. 2020, 2020, 505. [Google Scholar] [CrossRef] [PubMed]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. The modified homotopy perturbation method with an auxiliary term for the non-linear oscillator with discontinuity. J. Low Freq. Noise Vib. Act. Control. 2019, 38, 1363–1373. [Google Scholar] [CrossRef] [Green Version]
- Bibi, M.; Nawaz, Y.; Arif, M.S.; Abbasi, J.N.; Javed, U.; Nazeer, A. A finite difference method and effective modification of gradient descent optimization algorithm for MHD fluid flow over a linearly stretching surface. Comput. Mater. Contin. 2020, 62, 657–677. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arif, M.S.; Abodayeh, K.; Nawaz, Y. A Computational Scheme for Stochastic Non-Newtonian Mixed Convection Nanofluid Flow over Oscillatory Sheet. Energies 2023, 16, 2298. https://doi.org/10.3390/en16052298
Arif MS, Abodayeh K, Nawaz Y. A Computational Scheme for Stochastic Non-Newtonian Mixed Convection Nanofluid Flow over Oscillatory Sheet. Energies. 2023; 16(5):2298. https://doi.org/10.3390/en16052298
Chicago/Turabian StyleArif, Muhammad Shoaib, Kamaleldin Abodayeh, and Yasir Nawaz. 2023. "A Computational Scheme for Stochastic Non-Newtonian Mixed Convection Nanofluid Flow over Oscillatory Sheet" Energies 16, no. 5: 2298. https://doi.org/10.3390/en16052298





