Simulation for the Effect of Singlet Fission Mechanism of Tetracene on Perovskite Solar Cell
Abstract
:1. Introduction
2. Materials and Methods
2.1. Model Assumptions and Configurations
2.1.1. Model Assumptions
- The sun intensity throughout the testing period was modeled as a constant.
- The only environmental impact from the solar cell’s working conditions considered was temperature. Other effects, such as moisture and dust, were not taken into consideration.
- The perovskite material used in the study was CH3NH3PbI3. The material used to promote singlet fission in this study was tetracene.
- Thermalization loss was considered the only source of energy loss. Other sources, including parasitic loss and optical loss, were neglected due to the lack of generated thermal energy. The loss of non-absorbed photons was included to test the validity of the model.
- The bandgap of the CH3NH3PbI3 layer was modeled as a variable of temperature. However, due to the lack of research regarding the same topic with tetracene, their bandgaps were modeled as constant throughout the simulation.
2.1.2. Configuration
2.2. Incoming Sunlight Model
2.2.1. Solar Spectral Flux Density
2.2.2. Energy of Sunlight
2.2.3. Classification of Photons
- : Photons with not enough energy to excite the CH3NH3PbI3 layer, with photons in total
- : Photons with enough energy to excite the CH3NH3PbI3 layer, but not enough to excite the singlet fission layer, with photons in total
- : Photons with enough energy to excite the tetracene layer, with photons in total
2.3. Modeling of the Pathways of Photons in Solar Cell
2.3.1. Photon Energy Component in Solar Cell
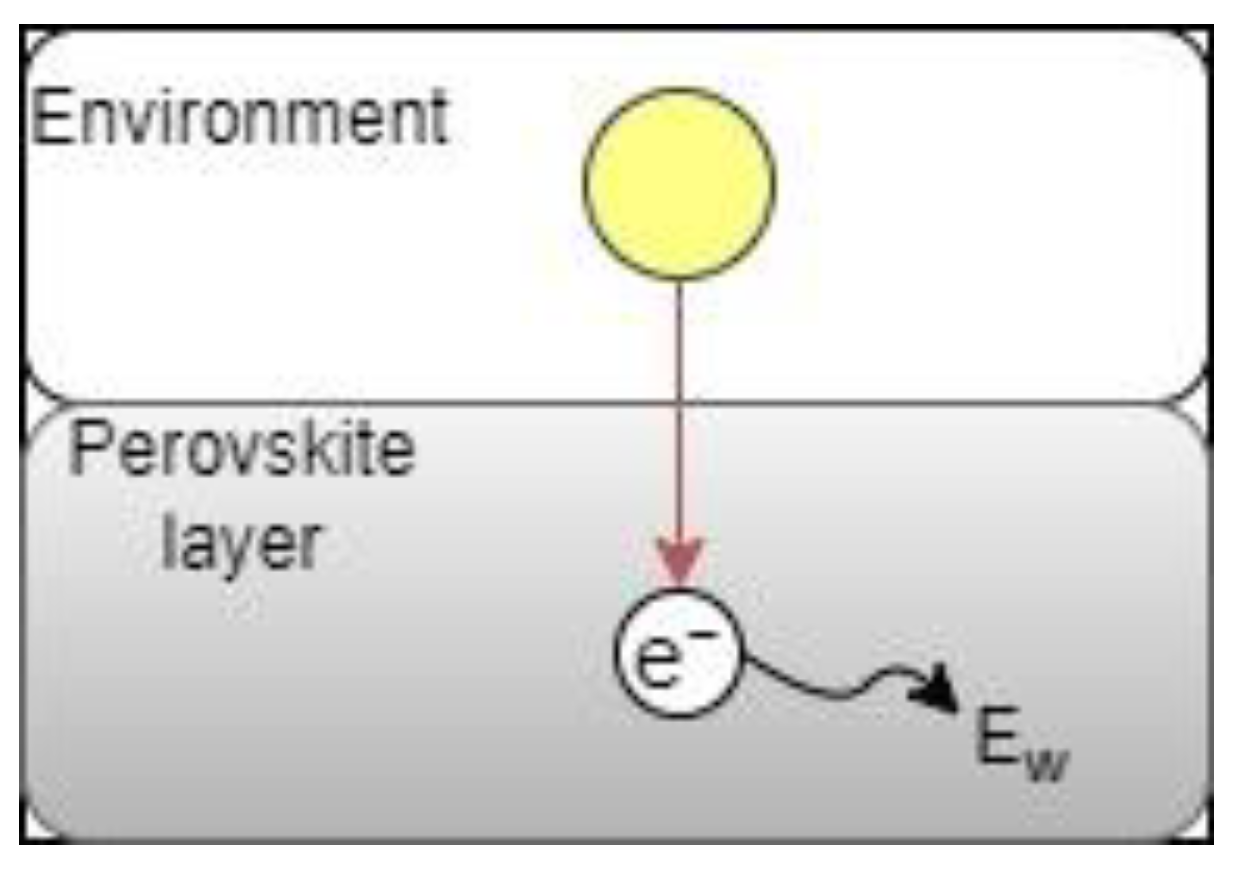
2.3.2. Control Case
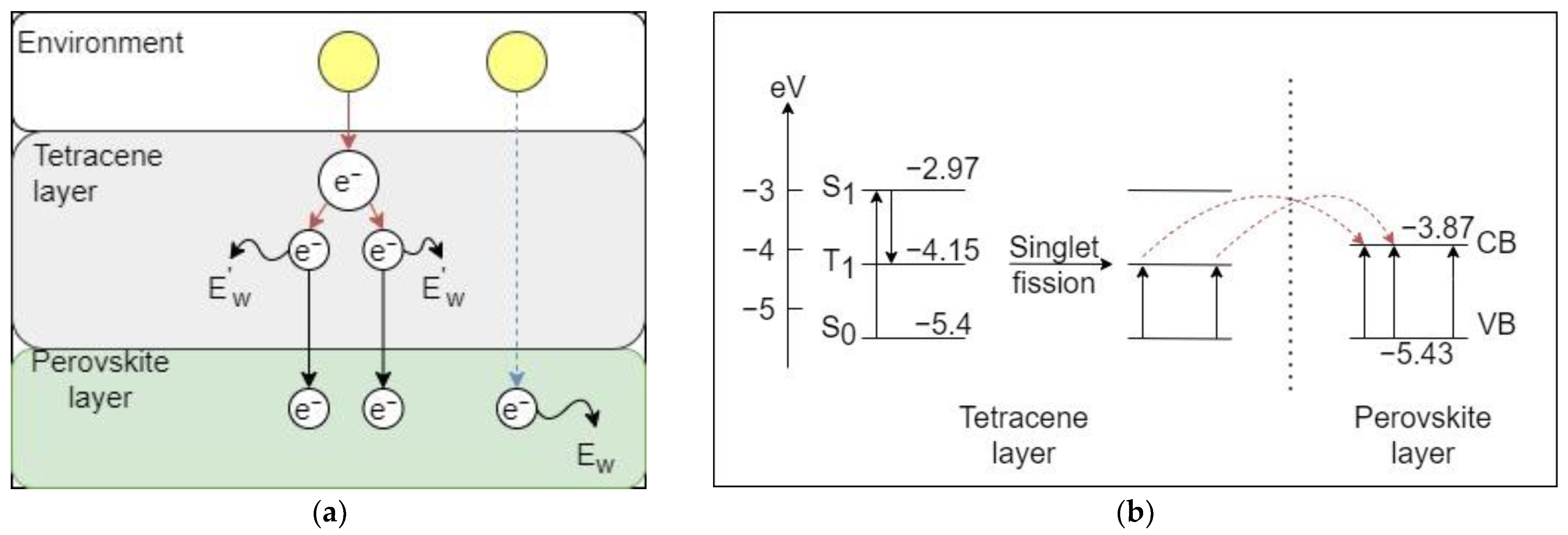
2.3.3. Experimental Case
2.4. Modeling of Heat Transfer
2.4.1. Heating Due to Photon Energy
2.4.2. Heating Due to Conduction Heat Transfer
2.5. Modeling of the Bandgap
2.5.1. Change of Bandgap Due to Thermal Expansion
2.5.2. Change of Bandgap Due to Electron-Phonon Interactions
3. Model Validation and Calibration
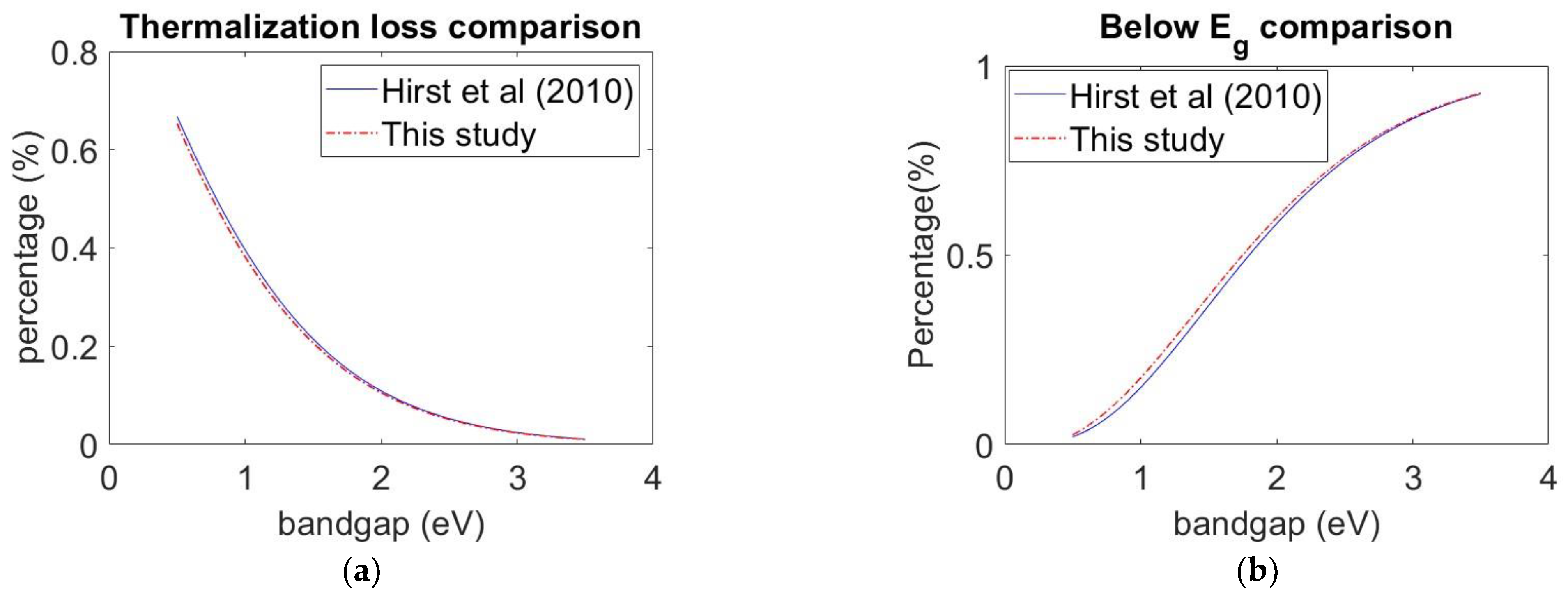
3.1. Model Validation
3.2. Model Validation Result
3.3. Model Calibration
4. Results and Discussion
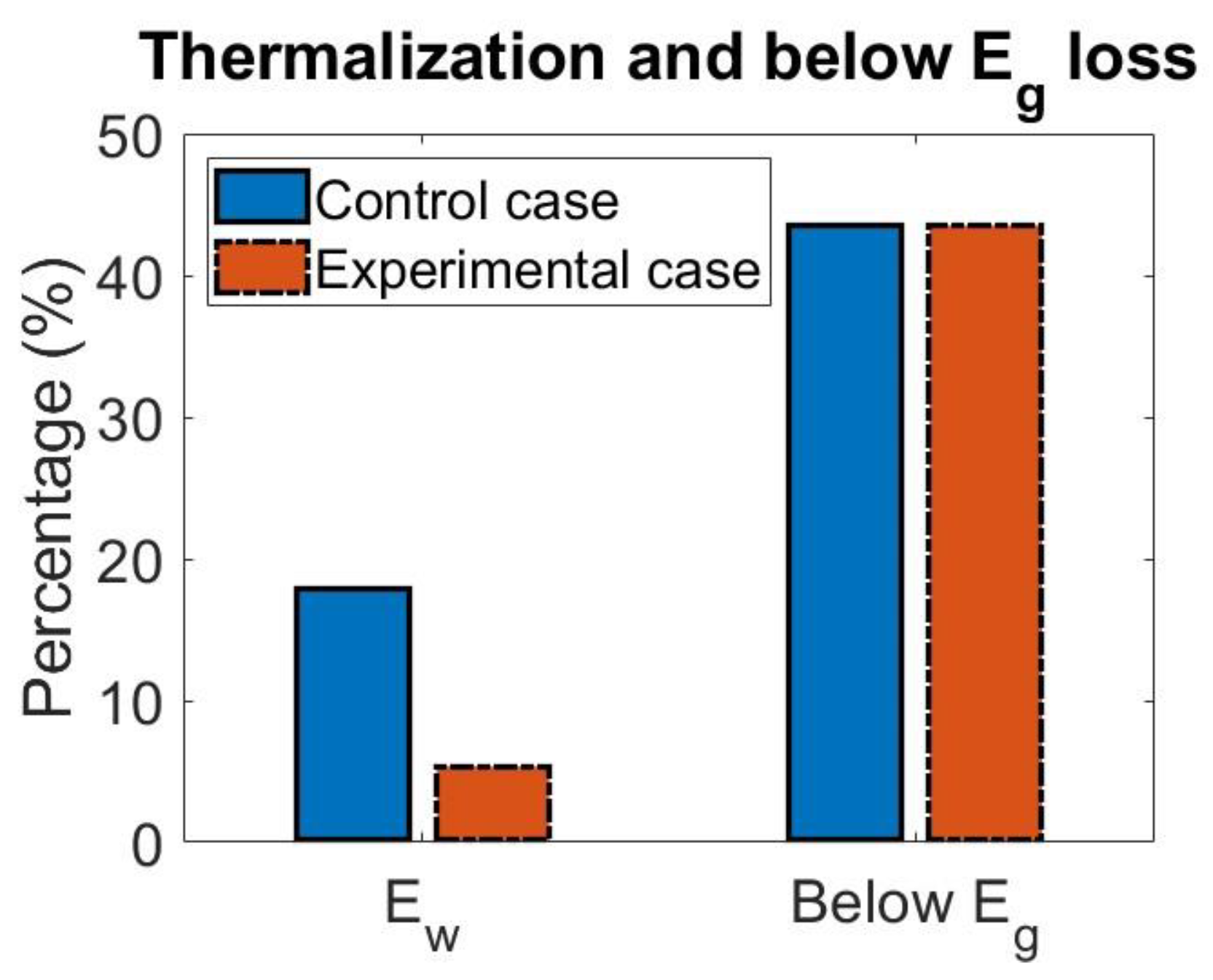
4.1. Effect of Singlet Fission on Losses
4.2. Effect of Singlet Fission on the Heating of the Perovskite Layer
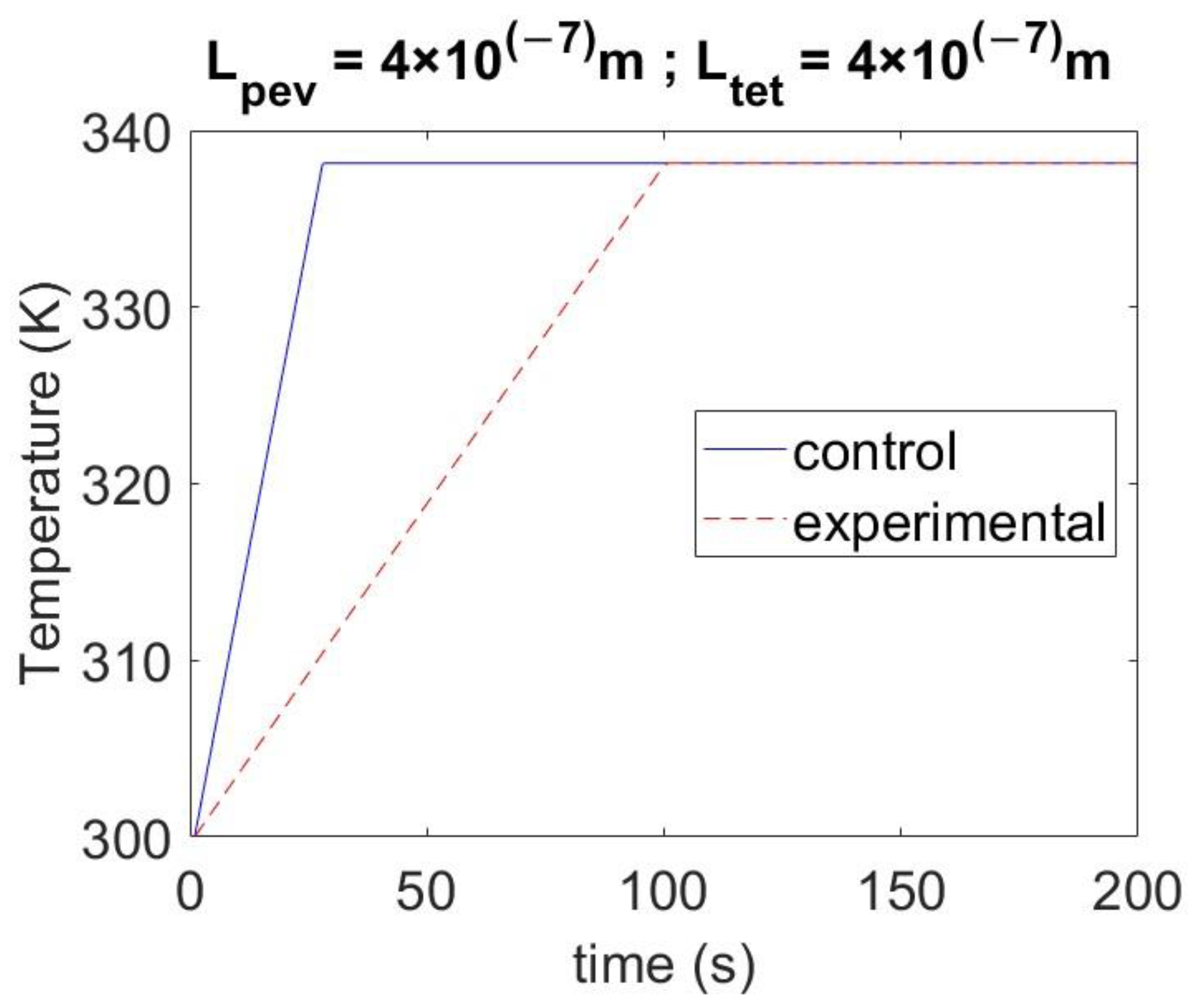
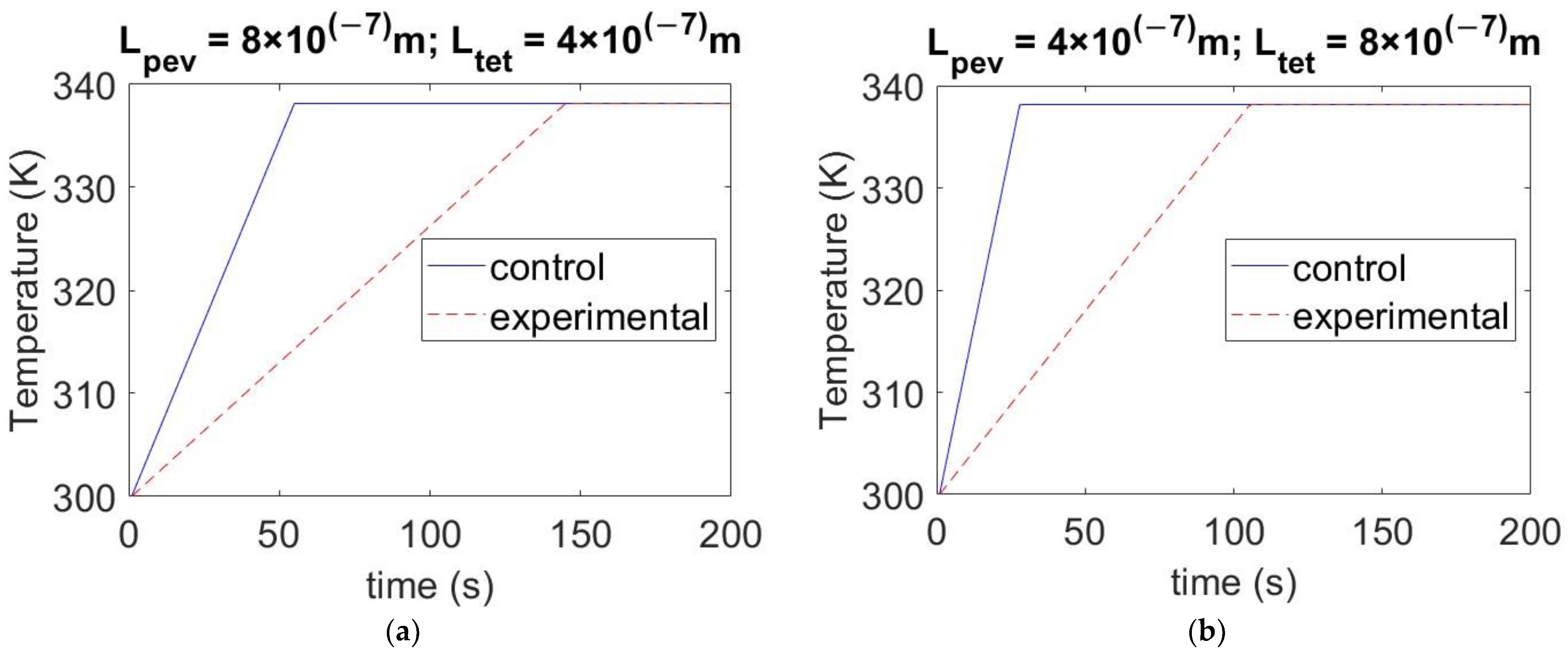
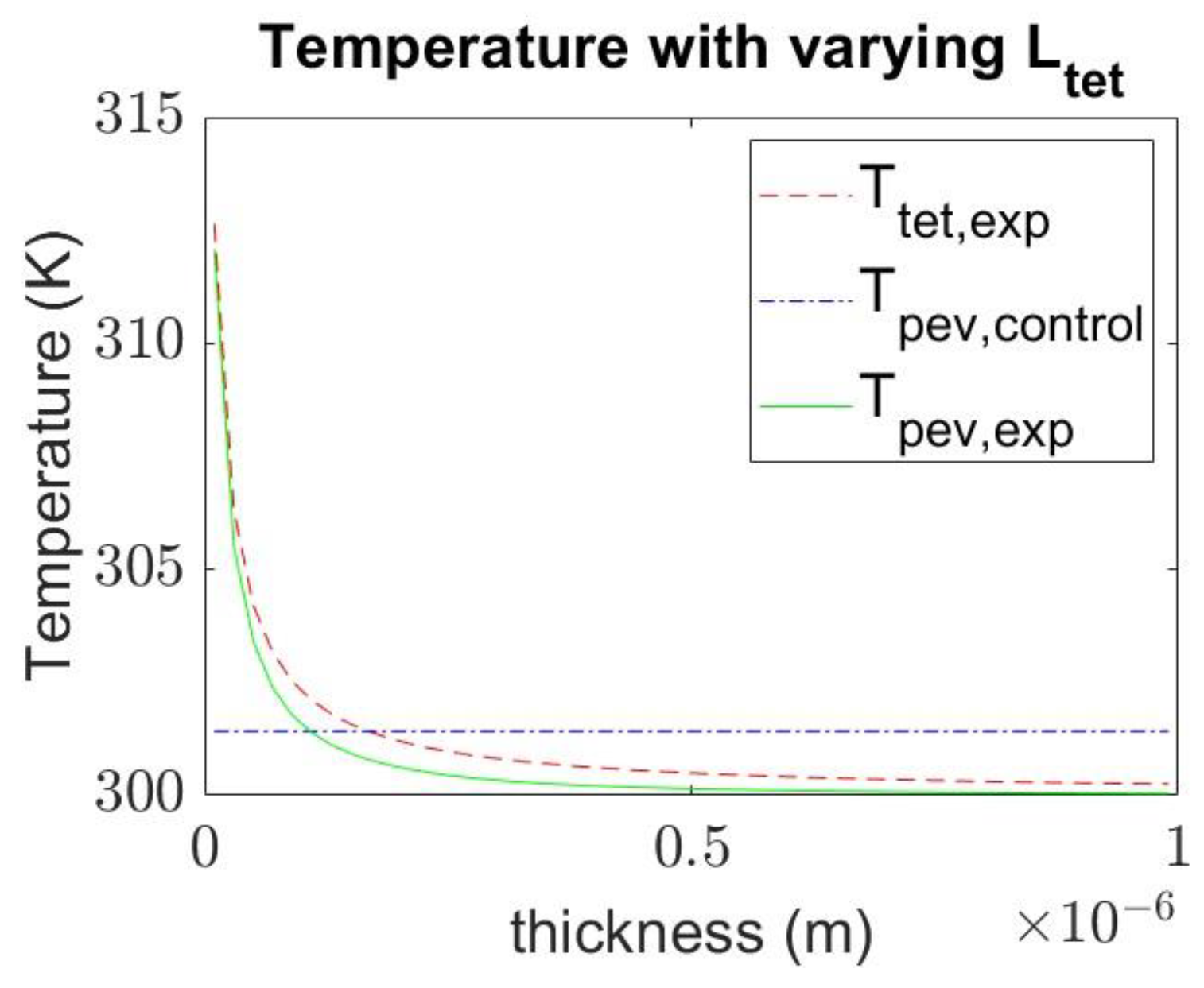
4.3. Effect of Varying the Thickness of Materials on Temperature
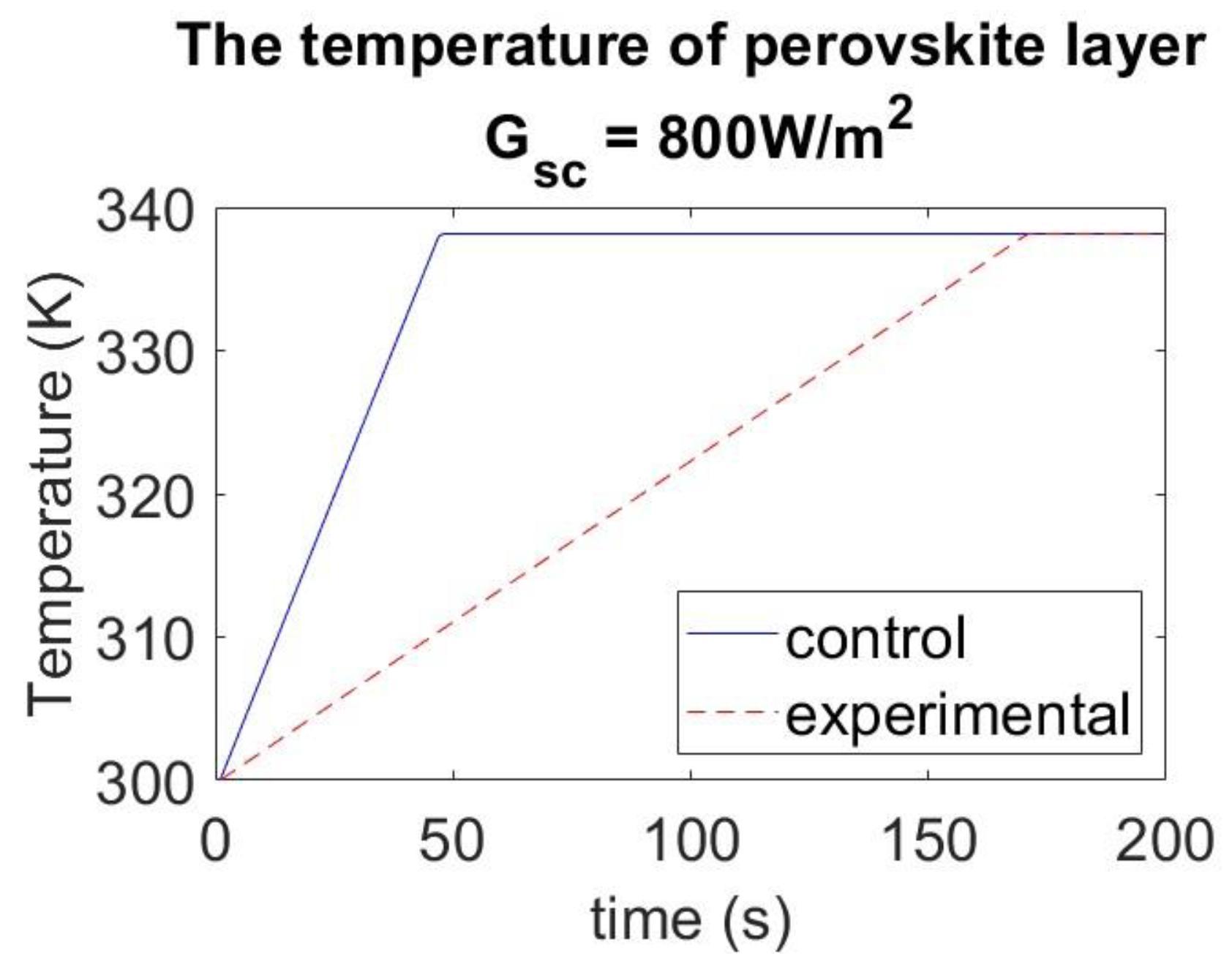
4.4. Effect of Tetracene Layer under Different Solar Radiation Conditions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Definition |
| Solar spectral flux density | |
| Wavelength of light | |
| Solar constant | |
| Modifier parameter | |
| Energy of photons | |
| Planck’s constant | |
| Speed of light | |
| Number of photons | |
| Number of electrons of class P1 | |
| Number of electrons of class P2 | |
| Number of electrons of class P3 | |
| Band gap of the material | |
| The energy level of photon class P2 | |
| The energy level of photon class P3 | |
| Thermalization energy loss | |
| Grounded electron state of perovskite | |
| Excited singlet electron state of perovskite | |
| Wasted energy in the control case | |
| Grounded electron state of tetracene | |
| Triplet electron state of tetracene | |
| Wasted energy in the tetracene layer in the experimental case | |
| Thermalization energy loss of tetracene layer in experimental case | |
| Thermalization energy loss of perovskite layer in experimental case | |
| Change of temperature due to photon energy | |
| Mass of the layer | |
| Specific heat of the material | |
| Heating due to heat transfer | |
| Temperature changes due to heat transfer | |
| Thermal conductivity of the material | |
| Area of contact | |
| Thickness of material | |
| Temperature | |
| Change of bandgap with respect to temperature | |
| Change of bandgap due to thermal expansion | |
| Change of bandgap due to electron-phonon interactions | |
| Volumetric expansion coefficient | |
| Bulk modulus | |
| Change of bandgap with respect to pressure | |
| Electron-phonon coupling constant | |
| Average phonon frequency | |
| Boltzmann constant | |
| Fraction of loss due to below-bandgap photons | |
| Fraction of loss due to thermalization |
References
- Porté-Agel, F.; Bastankhah, M.; Shamsoddin, S. Wind-Turbine and Wind-Farm Flows: A Review. Bound. Layer Meteorol. 2020, 174, 1–59. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.-Z.; Liu, W.-D.; Li, M.; Yin, L.-C.; Gao, H.; Sun, Q.; Wu, H.; Wang, Y.; Shi, X.-L.; Yang, X.; et al. Simultaneously achieving high ZT and mechanical hardness in highly alloyed GeTe with symmetric nanodomains. Chem. Eng. J. 2022, 441, 136131. [Google Scholar] [CrossRef]
- Wang, D.-Z.; Liu, W.-D.; Li, M.; Zheng, K.; Hu, H.; Yin, L.-C.; Wang, Y.; Zhu, H.; Shi, X.-L.; Yang, X.; et al. Hierarchical Architectural Structures Induce High Performance in n-Type GeTe-Based Thermoelectrics. Adv. Funct. Mater. 2023, 2213040. [Google Scholar] [CrossRef]
- Duan, J.; Xu, H.; Sha, W.E.I.; Zhao, Y.; Wang, Y.; Yang, X.; Tang, Q. Inorganic perovskite solar cells: An emerging member of the photovoltaic community. J. Mater. Chem. A 2019, 7, 21036–21068. [Google Scholar] [CrossRef]
- Mutalikdesai, A.; Ramasesha, S.K. Emerging solar technologies: Perovskite solar cell. Resonance 2017, 22, 1061–1083. [Google Scholar] [CrossRef]
- Park, N.-G. Perovskite solar cells: An emerging photovoltaic technology. Mater. Today 2015, 18, 65–72. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Ai, Q.; Gao, G.; Yuan, L.; Fang, Q.; Tian, X.; Zhang, X.; Egap, E.; Ajayan, P.M.; et al. In Situ Synthesis of Lead-Free Halide Perovskite–COF Nanocomposites as Photocatalysts for Photoinduced Polymerization in Both Organic and Aqueous Phases. ACS Mater. Lett. 2022, 4, 464–471. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Miller, K.A.; Zhu, H.; Egap, E. Lead Halide Perovskite Nanocrystals as Photocatalysts for PET-RAFT Polymerization under Visible and Near-Infrared Irradiation. ACS Macro Lett. 2020, 9, 725–730. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.-F.; Yang, M.-Z.; Chen, B.-X.; Wang, X.-D.; Chen, H.-Y.; Kuang, D.-B.; Su, C.-Y. A CsPbBr3 Perovskite Quantum Dot/Graphene Oxide Composite for Photocatalytic CO2 Reduction. J. Am. Chem. Soc. 2017, 139, 5660–5663. [Google Scholar] [CrossRef] [PubMed]
- Wei, K.; Liang, B.; Sun, C.; Jiang, Y.; Yuan, M. Metal Halide Perovskites for Red-Emission Light-Emitting Diodes. Small Struct. 2022, 3, 2200063. [Google Scholar] [CrossRef]
- Yang, W.S.; Noh, J.H.; Jeon, N.J.; Kim, Y.C.; Ryu, S.; Seo, J.; Seok, S.I. High-performance photovoltaic perovskite layers fabricated through intramolecular exchange. Science 2015, 348, 1234–1237. [Google Scholar] [CrossRef] [PubMed]
- Shockley, W.; Queisser, H.J. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Andreani, L.C.; Bozzola, A.; Kowalczewski, P.; Liscidini, M.; Redorici, L. Silicon solar cells: Toward the efficiency limits. Adv. Phys. X 2018, 4, 1548305. [Google Scholar] [CrossRef] [Green Version]
- Perovskite on Silicon Tandem Solar Cell Technology | Oxford PV. Oxfordpv. Retrieved 16 May 16 2021. Available online: https://www.oxfordpv.com/perovskite-silicon-tandem (accessed on 6 February 2023).
- Čulík, P.; Brooks, K.; Momblona, C.; Adams, M.; Kinge, S.; Maréchal, F.; Dyson, P.J.; Nazeeruddin, M.K. Design and Cost Analysis of 100 MW Perovskite Solar Panel Manufacturing Process in Different Locations. ACS Energy Lett. 2022, 7, 3039–3044. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, H.; Yan, K.; Yang, S. Inkjet Printing and Instant Chemical Transformation of a CH3NH3PbI3/Nanocarbon Electrode and Interface for Planar Perovskite Solar Cells. Angew. Chem. Int. Ed. 2014, 53, 13239–13243. [Google Scholar] [CrossRef]
- Kim, Y.Y.; Yang, T.Y.; Suhonen, R.; Kemppainen, A.; Hwang, K.; Jeon, N.J.; Seo, J. Roll-to-roll gravure-printed flexible perovskite solar cells using eco-friendly antisolvent bathing with wide processing window. Nat. Commun. 2020, 11, 5146. [Google Scholar] [CrossRef]
- Ono, L.K.; Qi, Y.; Liu, S. Progress toward Stable Lead Halide Perovskite Solar Cells. Joule 2018, 2, 1961–1990. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, Z.; Najeeb, M.A.; Shakoor, R.A.; Alashraf, A.; Al-Muhtaseb, S.A.; Soliman, A.; Nazeeruddin, M.K. Instability in CH3NH3PbI3 perovskite solar cells due to elemental migration and chemical composition changes. Sci. Rep. 2017, 7, 15406. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Wright, M.; Elumalai, N.K.; Uddin, A. Stability of perovskite solar cells. Sol. Energy Mater. Sol. Cells 2016, 147, 255–275. [Google Scholar] [CrossRef]
- Leijtens, T.; Eperon, G.E.; Pathak, S.; Abate, A.; Lee, M.M.; Snaith, H.J. Overcoming ultraviolet light instability of sensitized TiO2 with meso-superstructured organometal tri-halide perovskite solar cells. Nat. Commun. 2013, 4, 2885. [Google Scholar] [CrossRef] [Green Version]
- Dualeh, A.; Gao, P.; Seok, S.I.; Nazeeruddin, M.K.; Grätzel, M. Thermal Behavior of Methylammonium Lead-Trihalide Perovskite Photovoltaic Light Harvesters. Chem. Mater. 2014, 26, 6160–6164. [Google Scholar] [CrossRef]
- Philippe, B.; Park, B.W.; Lindblad, R.; Oscarsson, J.; Ahmadi, S.; Johansson, E.M.J.; Rensmo, H. Chemical and Electronic Structure Characterization of Lead Halide Perovskites and Stability Behavior under Different Exposures—A Photoelectron Spectroscopy Investigation. Chem. Mater. 2015, 27, 1720–1731. [Google Scholar] [CrossRef]
- Mali, S.S.; Shim, C.S.; Hong, C.K. Highly stable and efficient solid-state solar cells based on methylammonium lead bromide (CH3NH3PbBr3) perovskite quantum dots. NPG Asia Mater. 2015, 7, e208. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Matteocci, F.; Zhu, H.; Rossi, D.; Mejaouri, S.; Cacovich, S.; Auf Der Maur, M.; Sauvage, F.; Gagliardi, A.; Grätzel, M.; et al. Methylamine Gas Treatment Affords Improving Semitransparency, Efficiency, and Stability of CH3NH3PbBr3-Based Perovskite Solar Cells. Sol. RRL 2021, 5, 2100277. [Google Scholar] [CrossRef]
- Wang, L.; Yuan, G.D.; Duan, R.F.; Huang, F.; Wei, T.B.; Liu, Z.Q.; Wang, J.X.; Li, J.M. Tunable bandgap in hybrid perovskite CH3NH3Pb(Br3−yXy) single crystals and photodetector applications. AIP Adv. 2016, 6, 045115. [Google Scholar] [CrossRef] [Green Version]
- Heidarzadeh, H.; Rostami, A.; Dolatyari, M. Management of losses (thermalization-transmission) in the Si-QDs inside 3C–SiC to design an ultra-high-efficiency solar cell. Mater. Sci. Semicond. Process. 2020, 109, 104936. [Google Scholar] [CrossRef]
- Rühle, S. Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Niu, G.; Li, W.; Li, J.; Liang, X.; Wang, L. Enhancement of thermal stability for perovskite solar cells through cesium doping. RSC Adv. 2017, 7, 17473–17479. [Google Scholar] [CrossRef] [Green Version]
- Rolston, N.; Bush, K.A.; Printz, A.D.; Gold-Parker, A.; Ding, Y.; Toney, M.F.; McGehee, M.D.; Dauskardt, R.H. Engineering Stress in Perovskite Solar Cells to Improve Stability. Adv. Energy Mater. 2018, 8, 1802139. [Google Scholar] [CrossRef]
- Choi, K.; Lee, J.; Choi, H.; Kim, G.-W.; Kim, H.I.; Park, T. Heat dissipation effects on the stability of planar perovskite solar cells. Energy Environ. Sci. 2020, 13, 5059–5067. [Google Scholar] [CrossRef]
- Jiang, Y.; Nielsen, M.P.; Baldacchino, A.J.; Green, M.A.; McCamey, D.R.; Tayebjee, M.J.Y.; Schmidt, T.W.; Ekins-Daukes, N.J. Singlet fission and tandem solar cells reduce thermal degradation and enhance lifespan. Prog. Photovolt. Res. Appl. 2021, 29, 899–906. [Google Scholar] [CrossRef]
- Smith, M.B.; Michl, J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. [Google Scholar] [CrossRef]
- Pazos-Outón, L.M.; Lee, J.M.; Futscher, M.H.; Kirch, A.; Tabachnyk, M.; Friend, R.H.; Ehrler, B. A Silicon–Singlet Fission Tandem Solar Cell Exceeding 100% External Quantum Efficiency with High Spectral Stability. ACS Energy Lett. 2017, 2, 476–480. [Google Scholar] [CrossRef] [Green Version]
- United States Department of Energy Basic Energy Sciences Division. Proceedings of the 27th DOE Solar Photochemistry Research Conference, Airlie Conference Center, Warrenton, VA, USA, 6–9 June 2004; United States Department of Energy Basic Energy Sciences Division: Washington, DC, USA, 2004.
- MacQueen, R.W.; Liebhaber, M.; Niederhausen, J.; Mews, M.; Gersmann, C.; Jäckle, S.; Jäger, K.; Tayebjee, M.J.Y.; Schmidt, T.W.; Rech, B.; et al. Crystalline silicon solar cells with tetracene interlayers: The path to silicon-singlet fission heterojunction devices. Mater. Horiz. 2018, 5, 1065–1075. [Google Scholar] [CrossRef] [Green Version]
- Baldacchino, A.J.; Collins, M.I.; Nielsen, M.P.; Schmidt, T.W.; McCamey, D.R.; Tayebjee, M.J.Y. Singlet fission photovoltaics: Progress and promising pathways. Chem. Phys. Rev. 2022, 3, 021304. [Google Scholar] [CrossRef]
- Chan, W.-L.; Ligges, M.; Zhu, X.Y. The energy barrier in singlet fission can be overcome through coherent coupling and entropic gain. Nat. Chem. 2012, 4, 840–845. [Google Scholar] [CrossRef] [PubMed]
- Paci, I.; Johnson, J.C.; Chen, X.; Rana, G.; Popović, D.; David, D.E.; Nozik, A.J.; Ratner, M.A.; Michl, J. Singlet Fission for Dye-Sensitized Solar Cells: Can a Suitable Sensitizer Be Found? J. Am. Chem. Soc. 2006, 128, 16546–16553. [Google Scholar] [CrossRef] [PubMed]
- Thomson, S.A.J.; Niklas, J.; Mardis, K.L.; Mallares, C.; Samuel, I.D.W.; Poluektov, O.G. Charge Separation and Triplet Exciton Formation Pathways in Small-Molecule Solar Cells as Studied by Time-Resolved EPR Spectroscopy. J. Phys. Chem. C 2017, 121, 22707–22719. [Google Scholar] [CrossRef] [Green Version]
- D’Innocenzo, V.; Grancini, G.; Alcocer, M.; Kandada, A.R.S.; Stranks, S.D.; Lee, M.M.; Lanzani, G.; Snaith, H.J.; Petrozza, A. Excitons versus free charges in organo-lead tri-halide perovskites. Nat. Commun. 2014, 5, 3586. [Google Scholar] [CrossRef] [Green Version]
- Asghar, M.I.; Zhang, J.; Wang, H.; Lund, P.D. Device stability of perovskite solar cells—A review. Renew. Sustain. Energy Rev. 2017, 77, 131–146. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Park, N.-G. Stability Issues on Perovskite Solar Cells. Photonics 2015, 2, 1139–1151. [Google Scholar] [CrossRef] [Green Version]
- Xia, J.; Sanders, S.N.; Cheng, W.; Low, J.Z.; Liu, J.; Campos, L.M.; Sun, T. Singlet Fission: Progress and Prospects in Solar Cells. Adv. Mater. 2017, 29, 1601652. [Google Scholar] [CrossRef]
- Wu, T.C.; Thompson, N.J.; Congreve, D.N.; Hontz, E.; Yost, S.R.; Van Voorhis, T.; Baldo, M.A. Singlet fission efficiency in tetracene-based organic solar cells. Appl. Phys. Lett. 2014, 104, 193901. [Google Scholar] [CrossRef] [Green Version]
- Paulescu, M.; Schlett, Z. A simplified but accurate spectral solar irradiance model. Theor. Appl. Climatol. 2003, 75, 203–212. [Google Scholar] [CrossRef]
- Francisco-López, A.; Charles, B.; Weber, O.J.; Alonso, M.I.; Garriga, M.; Campoy-Quiles, M.; Weller, M.T.; Goñi, A.R. Equal Footing of Thermal Expansion and Electron–Phonon Interaction in the Temperature Dependence of Lead Halide Perovskite Band Gaps. J. Phys. Chem. Lett. 2019, 10, 2971–2977. [Google Scholar] [CrossRef]
- Qin, P.; Tanaka, S.; Ito, S.; Tetreault, N.; Manabe, K.; Nishino, H.; Nazeeruddin, M.K.; Grätzel, M. Inorganic hole conductor-based lead halide perovskite solar cells with 12.4% conversion efficiency. Nat. Commun. 2014, 5, 3834. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nakka, L.; Cheng, Y.; Aberle, A.G.; Lin, F. Analytical Review of Spiro-OMeTAD Hole Transport Materials: Paths Toward Stable and Efficient Perovskite Solar Cells. Adv. Energy Sustain. Res. 2022, 3, 2200045. [Google Scholar] [CrossRef]
- de Sabata, C.; Borneas, M.; Rothenstein, B.; Munteanu, A. Bazele Fizice Ale Conversiei Energiei Solare; Facla: Timisoara, Romania, 1982; pp. 28–29. [Google Scholar]
- Şahin, A.D.; Şen, Z. Statistical analysis of the Angström formula coefficients and application for Turkey. Fuel Energy Abstr. 1998, 39, 125. [Google Scholar] [CrossRef]
- Kulkarni, S.A.; Baikie, T.; Boix, P.P.; Yantara, N.; Mathews, N.; Mhaisalkar, S. Band-gap tuning of lead halide perovskites using a sequential deposition process. J. Mater. Chem. A 2014, 2, 9221–9225. [Google Scholar] [CrossRef] [Green Version]
- Lopez-Varo, P.; Amara, M.; Cacovich, S.; Julien, A.; Yaïche, A.; Jouhari, M.; Rousset, J.; Schulz, P.; Guillemoles, J.-F.; Puel, J.-B. Dynamic temperature effects in perovskite solar cells and energy yield. Sustain. Energy Fuels 2021, 5, 5523–5534. [Google Scholar] [CrossRef]
- Starr, D.E.; Sadoughi, G.; Handick, E.; Wilks, R.G.; Alsmeier, J.H.; Köhler, L.; Gorgoi, M.; Snaith, H.J.; Bär, M. Direct observation of an inhomogeneous chlorine distribution in CH3NH3PbI3−xClx layers: Surface depletion and interface enrichment. Energy Environ. Sci. 2015, 8, 1609–1615. [Google Scholar] [CrossRef]
- Tetracene. ChemSpider. Retrieved 11 November 11 2022. Available online: http://www.chemspider.com/Chemical-Structure.6813.html (accessed on 6 February 2023).
- Haeger, T.; Heiderhoff, R.; Riedl, T. Thermal properties of metal-halide perovskites. J. Mater. Chem. C 2020, 8, 14289–14311. [Google Scholar] [CrossRef]
- Tabor, D Mechanical Properties of Energetic Materials. Publication No. ADA039600. Physics & Chemistry of Solids Cavandish Labatory. 1977. Available online: https://apps.dtic.mil/sti/pdfs/ADA039600.pdf (accessed on 6 February 2023).
- Pisoni, A.; Jaćimović, J.; Barišić, O.S.; Spina, M.; Gaál, R.; Forró, L.; Horváth, E. Ultra-Low Thermal Conductivity in Organic–Inorganic Hybrid Perovskite CH3NH3PbI3. J. Phys. Chem. Lett. 2014, 5, 2488–2492. [Google Scholar] [CrossRef] [Green Version]
- Tabor, D.; Field, J.E.; Chaudri, M.M.; Hauser, H.M.; Patel, R.G.; Cambridge Univ (United Kingdom) Cavendish Lab. Mechanical Properties of Energetic Materials. DTIC. Retrieved 31 October 2022. Available online: https://apps.dtic.mil/sti/citations/ADA039600 (accessed on 6 February 2023).
- Hirst, L.C.; Ekins-Daukes, N.J. Fundamental losses in solar cells. Prog. Photovolt. Res. Appl. 2011, 19, 286–293. [Google Scholar] [CrossRef]
- Da, Y.; Xuan, Y.; Li, Q. Quantifying energy losses in planar perovskite solar cells. Sol. Energy Mater. Sol. Cells 2018, 174, 206–213. [Google Scholar] [CrossRef]
- Tanaka, K.; Takahashi, T.; Ban, T.; Kondo, T.; Uchida, K.; Miura, N. Comparative study on the excitons in lead-halide-based perovskite-type crystals CH3NH3PbBr3 CH3NH3PbI3. Solid State Commun. 2003, 127, 619–623. [Google Scholar] [CrossRef]



| Thermalization | ||
|---|---|---|
| Maximum absolute error | 0.0162% | 0.0277% |
| Bandgap value | 1.225 eV | 0.713 eV |
| Perovskite | Tetracene | |
|---|---|---|
| Density (g/cm3) | 4.2864 [54] | 1.2 [55] |
| Specific heat (J·kg−1K−1) | 311 [56] | 1585 [57] |
| Thermal conductivity (W/Km) | 0.3 [58] | 0.16 [59] |
| Surface area (m2) | 1 | 1 |
| Thickness (m) | Varies | Varies |
| Bandgap (eV) | Varies | 2.43 [36] |
| Binding energy (meV) | 50 [62] | - |
| Cutoff temperature (K) | 338.15 | 338.15 |
| Base temperature (K) | 300 | 300 |
| Thermalization | ||
|---|---|---|
| Control | 17.95% | 43.55% |
| Experimental | 5.36% | 43.55% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Le, T.N.; Liu, L. Simulation for the Effect of Singlet Fission Mechanism of Tetracene on Perovskite Solar Cell. Energies 2023, 16, 2428. https://doi.org/10.3390/en16052428
Le TN, Liu L. Simulation for the Effect of Singlet Fission Mechanism of Tetracene on Perovskite Solar Cell. Energies. 2023; 16(5):2428. https://doi.org/10.3390/en16052428
Chicago/Turabian StyleLe, Toan Ngoc, and Lin Liu. 2023. "Simulation for the Effect of Singlet Fission Mechanism of Tetracene on Perovskite Solar Cell" Energies 16, no. 5: 2428. https://doi.org/10.3390/en16052428





