Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification
Abstract
:1. Introduction
- Disclosure of the extent to which actual performance differs from that budgeted.
- Identifying the reasons why actual results differ from those budgeted.
- Defining corrective actions.
- To define the basis for the revision of the current budget.
- Improving the process of preparing future budgets.
2. Theoretical Background
- Calculating the variances of the quantities currently reached or expected to be reached from the budgeted quantities.
- To identify where the variance occurs.
- Variance analysis.
- To identify those responsible for the variance.
- Research into the effects of variances in different areas of company activity.
- Indicating actions to correct variances and postulating remedial actions to eliminate variances in the future.
- To propose changes in the company’s activities.
- To propose improvements in the budgeting process itself.
- Monitoring the changes made.
- Determine the causes of variances (factorial analysis).
- Classify variances (e.g., significant vs. insignificant, favourable vs. unfavourable).
- Examine and evaluate variance levels.
- Examine variance properties (recurrence, trends, configurations).
- Identify causes for variance and determination of actors accountable for variances.
3. Materials and Methods
4. Results
5. Discussion
6. Conclusions
- Assess the degree of budget implementation in the company;
- Compare the quality of budget implementation over time as well as between units.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pandit, A. Budgets and Budgetary Control. J. Bus. Manag. Soc. Sci. Res. 2016, 5, 192–199. [Google Scholar]
- Hansen, D.; Mowen, M. Cost Management; South-Western: Nashville, TN, USA, 2005. [Google Scholar]
- Salman, T. Variance Analysis as a Tool for Management Control; Published Case Study University of Ilorin: Ilorin, Nigeria, 2008. [Google Scholar]
- Armstrong, M. A Handbook of Management Techniques; Kogan Page: London, UK, 2006. [Google Scholar]
- Blocher, E.J.; Stout, D.E.; Juras, P.E.; Smith, S. Cost Management: A Strategic Emphasis; McGraw-Hill: Boston, MA, USA, 2019. [Google Scholar]
- Drury, C. Management and Cost Accounting, Cengage Learning, Hampshire; Cengage Learning: Hampshire, UK, 2012. [Google Scholar]
- Kaplan, R.S. The Significance and Investigation of Cost Variances: Survey and Extensions. J. Account. Res. 1975, 13, 311–337. [Google Scholar] [CrossRef]
- Duncan, A.J. The Economic Design of X Charts Used to Maintain Current Control of a Process. J. Am. Stat. Assoc. 1956, 51, 228–242. [Google Scholar] [CrossRef]
- Taylor, H. The Economic Design of Cumulative Sum Control Charts for Variables. Technometrics 1968, 10, 479–488. [Google Scholar] [CrossRef]
- Goel, A.L.; Wu, S.M. Economically Optimum Design of Cusum Charts. Manag. Sci. 1973, 19, 1271–1282. [Google Scholar] [CrossRef]
- Girshick, M.A.; Rubin, H. A Bayes Approach to a Quality Control Model. Ann. Math. Stat. 1952, 23, 114–125. [Google Scholar] [CrossRef]
- Duvall, R.M. Rules for Investigating Cost Variances. Manag. Sci. 1967, 13, 631–641. [Google Scholar] [CrossRef]
- Kwang, C.W.; Slavin, A. The simple mathematics of variance analysis. Account. Rev. 1962, 37, 415–432. [Google Scholar]
- Zannetos, Z.S. On the mathematics of variance analysis. Account. Rev. 1963, 38, 528–533. [Google Scholar]
- Weber, J.; Schäffer, U. Controlling durch die Nutzung des fruchtbaren Spannungsverhältnisses von Reflexion und Intuitionen. Z. Für Plan. 1999, 10, 205–224. [Google Scholar]
- Bierman, H., Jr.; Fouraker, L.E.; Jaddicke, R.K. A use of probability and statistics in performance evaluation. Account. Rev. 1961, 36, 409. [Google Scholar]
- Plewa, F.; Strozik, G. Wpływ wybranych zachowań indywidualnych konsumentów paliw kopalnych na krajowe zapotrzebowanie na węgiel kamienny i wielkość emisji CO2. Napędy i Sterowanie 2019, 21, 74–80. [Google Scholar]
- Kes, Z.; Kuźmiński, Ł. Application of extreme value analysis in the assessment of budget variance risk. Econometrics 2019, 23, 80–98. [Google Scholar] [CrossRef] [Green Version]
- Gumbel, J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Bortkiewicz, L. Variationsbreite und mittlerer Fehler. Sitz. Berli. Meth. Ges. 1922, 21, 3–11. [Google Scholar]
- Tippett, C. On the Extreme Individuals and the Range of Samples Taken from a normaln population. Biometrika 1925, 17, 364–387. [Google Scholar] [CrossRef]
- Frechet, M. Sur la loi de probabilite de lecart maximum. Ann. Soc. Polon. Math. Cracovie 1927, 6, 93–116. [Google Scholar]
- Fisher, R.; Tippett, L. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Proc. Camb. Phil. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Gumbel, E. La duree extreme de la vie humaine. Actual. Sci. Ind. 1937, 520, 24–29. [Google Scholar]
- Weibull, W. A statistical theory of the strength of materials. Ing. Vet. Akad. Handlingar. 1939, 2, 153. [Google Scholar]
- Gumbel, E. The return period of flood flaws. Ann. Math. Statist. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Gumbel, E. Floods estimated by probability methods. Engrg. News-Rec. 1944, 134, 97–101. [Google Scholar]
- Niewiedział, E.; Niewiedział, R. Krajowe sieci dystrybucyjne a bezpiecze ´nstwo zasilania odbiorców. Wiadomo´sci Elektrotechniczne 2014, 82, 37–41. [Google Scholar]
- Gumbel, E. The Statistical Forecast of Floods. Water Resour. Board Bull. 1949, 2, 1–21. [Google Scholar]
- Rantz, S.; Riggs, H. Magnitude and frequency of floods in the Columbia river basin. Water Supply Pap. 1949, 1080, 317–476. [Google Scholar]
- Nordquist, J. Theory of largest value, applied to earthquake magnitudes. Trans. Amer. Geophys. Union. 1945, 26, 29–31. [Google Scholar] [CrossRef]
- Potter, W. Normalcy Tests of Precipitation and Frequency Studies of Runoff on Small Watersheds; U.S. Department of Agriculture Technical Bulletin: Washington, DC, USA, 1949; No. 985.
- Shen, H.; Bryson, M.; Ochoa, I. Effect of tail behavior assumptions on flood. Water Resour. Res. 1980, 16, 361–364. [Google Scholar] [CrossRef]
- Greis, N.; Wood, E. Regional flood frequency estimation and network design. Water Resour. Res. 1981, 17, 1167–1177. [Google Scholar] [CrossRef]
- Pericchi, L.; Rodriguez-Iturbe, I. On statistical analysis of floods. In A Celebration of Statistics; Atkinson, A.C., Fienberg, S.E., Eds.; The ISI Centenary Volume; Springer: New York, NY, USA, 1985; pp. 511–541. [Google Scholar]
- Beran, M.; Hoskin, J.; Arnell, N. Comment on Two-component extreme value distribution for flood frequency analysis by Fabio Rossi, Mauro Fiorentino, Pasquale Versace. Water Resour. Res. 1986, 22, 263–266. [Google Scholar] [CrossRef]
- Ahmad, M.; Sinclair, C.; Spurr, B. Assessment of flood frequency models using empirical distribution function statistics. Water Resour. Res. 1988, 24, 1323–1328. [Google Scholar] [CrossRef]
- Rossi, F.; Fiorentino, M.; Versace, P. Two-component extreme value distribuition for flood frequency analysis. Water Resour. Res. 1986, 22, 1551–1564. [Google Scholar] [CrossRef]
- Smith, K.; Ward, R. Flood Physical Processes and Human Impacts; John Wiley & Sons: Chichester, UK, 1998. [Google Scholar]
- Jain, D.; Singh, V. Estimating parameters of EV1 distribution for flood frequency analysis. Water Resour. Res. 1987, 23, 59–71. [Google Scholar]
- Wallis, J. Risk and uncertainties in the evaluation of flood events for the design of hydraulic structures. Piene E Siccita 1980, 10, 3–36. [Google Scholar]
- Hipel, K. Extreme Values: Floods and Droughts; Kluwer Dordrecht: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Rasheed, H.; Aldabagh, A.; Ramamoorthy, M. Rainfall analysis by power transformation. J. Clim. Appl. Meteor. 1983, 22, 1411–1415. [Google Scholar] [CrossRef]
- Lettenmaier, D.; Wallis, J.; Wood, E. Effect of regional heterogenity on flood frequency estimation. Water Resour. Res. 1987, 23, 313–323. [Google Scholar] [CrossRef] [Green Version]
- Davenport, A. Wind structure and wind climate. In Seminar on Safety of Structures Under Dynamic Loading; Holand, I., Kavlie R Moe, G., Eds.; Tapir: Trondheim, Norway, 1978. [Google Scholar]
- Simiu, E.; Filliben, J. Probability distributions of extreme wind speeds. J. Structural Div. 1976, 102, 1861–1877. [Google Scholar] [CrossRef]
- Okubo, T.; Narita, N. On the distribution of extreme winds expected in Japan. Natl. Bur. Stand. Spec. Publ. 1980, 560, 1–12. [Google Scholar]
- Wantz, J.; Sinclair, R. Distribution of extreme winds in the Bonneville power adminstration service area. J. Appl. Meteor. 1981, 20, 1400–1411. [Google Scholar] [CrossRef]
- Coles, S.; Wlashaw, D. Directional modelling of extreme wind speeds. Appl. Statist. 1994, 43, 139–157. [Google Scholar] [CrossRef]
- Wallis, J.; Wood, E. Relative accuracy of log Pearson III procedures. J. Hydraul. Eng. 1985, 111, 1043–1056. [Google Scholar] [CrossRef]
- Fałdziński, M. Model warunkowej zmienności wartości ekstremalnej CEVV. Współczesne Trendy W Ekonom. 2008, 8, 201–212. [Google Scholar]
- Fałdziński, M. Zastosowanie zmodyfikowanej metody POT z modelami zmiennosci do oceny ryzyka inwestycji na rynku kapitałowym. Acta Univ. Nicola Copernic. Ekon. 2009, XXXIX, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Fałdziński, M. On the Empirical Importance of the Spectral Risk Measure with Extreme Value Theory Approach. In Financial Markets Principles of Modelling Forecasting and Decision-Making, FindEcon; Nicolaus Copernicus University: Toruń, Poland, 2011; pp. 73–86. [Google Scholar]
- Echaust, K.; Piasecki, K. Porównanie teorii wartości ekstrmelanych i rozkładów bezwarunkowych w pomiarze Value at Risk. Zesz. Nauk. Uniwerstytetu Ekon. W Pozn. 2012, 18–33. [Google Scholar]
- Fałdziński, M.; Osińska, M.; Zdanowicz, T. Detecting Risk Transfer in Financial Markets using Different Risk Measures. Cent. Eur. J. Econ. Model. Econom. 2012, 4, 45–64. [Google Scholar]
- Kuźmiński, Ł.; Szałata, Ł.; Zwoździak, J. Measuring Aquatic Environments az Tool for Flood Risk Management in Terms of Climate Change Dynamics. Pol. J. Environ. Stud. 2018, 27, 1583–1592. [Google Scholar] [CrossRef]
- Kuźmiński, Ł.; Halama, A. Odra River in Lower Silesia: Probabilistic analysis of flood risk dynamics. Manag. Econ. 2018, 19, 205–225. [Google Scholar]
- Fałdziński, M. Teoria Wartości Ekstremlanych w Ekonometrii Finansowej; Wydawnictwo Naukowe Uniwersytetu Mikołaja Kopernika: Toruń, Poland, 2014. [Google Scholar]
- Thomas, M.; Reiss, R. Statistical Analysis of Extreme Value with Applications to Insurance, Finance, Hydrology and Other Fields; Birkhauser: Basel, Switzerland, 2007. [Google Scholar]
- Embrechts, P.; Kluppelberg, C.; Mikosch, T. Modelling Extremal Events for Insurance and Finance; Springer: Berlin, Germany, 2003. [Google Scholar]
- David, H.; Nagaraja, H. Order Statistics; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Balkema, A.; de Haan, L. Residual Life Time at Great Age. Ann. Probab. 1974, 2, 792–804. [Google Scholar] [CrossRef]
- Pickdans, J. Statistical Inference Using Extreme Order Statistics. Ann. Stat. 1975, 3, 119–131. [Google Scholar]
- Kuźmiński, Ł. Modele Probabilistycznego Pomiaru I Oceny Ryzyka Powodziowego Na Przykładzie Dorzecza Śrokowej Odry; Wydawnictwo Uniwersytetu Ekonomicznego we Wrocławiu: Wrocław, Poland, 2018. [Google Scholar]
- Beirlant, J.; Matthys, G. Extreme quantile estimation for heavy-tailed distributions. Rapp. Tech. 2001, 23. [Google Scholar]
- Horngren, C.T.; Foster, G.; Dator, S.M. Cost Accounting: A Managerial Emphasis; Prentice-Hall: London, UK, 1997. [Google Scholar]
- Covaleski, M.A.; Evans, J.H., III; Luft, J.L.; Shields, M.D. Budgeting Research: Three Theoretical Perspectives and Criteria for Selective Integration. J. Manag. Account. Res. 2003, 15, 3–49. [Google Scholar] [CrossRef]
- Norkowaski, M. Zarządzanie Współczesnym Przedsiębiorstwem Według Koncepcji beyond Budgeting; CeDeWu: Warsszawa, Poland, 2015. [Google Scholar]
- Atkinson, A.A. Management Accounting; Prentice Hall: London, UK, 1997. [Google Scholar]
- Fess, P.E.; Warren, C.S. Accounting Principles; South-Western Publishing Co.: Cincinnati, OH, USA, 1987. [Google Scholar]
- Proctor, R. Managerial Accounting for Business Decisions; Prentice Hall: London, UK, 2006. [Google Scholar]
- Rachlin, R.; Sweeny, H.W. Handbook of Budgeting; John Wiley & Sons Inc.: New Yor, NY, USA, 1993. [Google Scholar]
- Pandey, I.M. Fundamentals of Financial Management; Villas Publishing House: New Delhi, India, 2002. [Google Scholar]
- Brown, J.L.; Howard, L.R. Principles and Practice of Management Accountancy; Macdonald and Evans Ltd.: London, UK, 2002. [Google Scholar]
- Davila, A.; Wouters, M. Managing budget emphasis through the explicit design of conditional budgetary slack. Account. Organ. Soc. 2005, 30, 587–608. [Google Scholar] [CrossRef]
- Fisher, J.G.; Fredrickson, J.R.; Peffer, S.A. Budget negotiations in multi-period settings. Account. Organ. Soc. 2006, 31, 511–528. [Google Scholar] [CrossRef]
- King, R.; Clarkson, P.M.; Wallace, S. Budgeting practices and performance in small healthcare businesses. Manag. Account. Res. 2010, 21, 40–55. [Google Scholar] [CrossRef]
- Kes, Z. Metodyka analizy odchyleń w kontroli budżetowej. Pr. Nauk. Uniw. Ekon. We Wrocławiu 2015, 389, 139–149. [Google Scholar] [CrossRef]
- Grimshaw, S.D. Computing Maximum Likelihood Estimates for the Generalized Pareto Distribution. Technometrics 1993, 35, 185–191. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Parameter and Quantile Estimation for the Generalized Pareto Distribution. Technometrics 1987, 29, 339–349. [Google Scholar] [CrossRef]
- Rasmussen, P. Bayesian estimation of change points using the general linear model. Water Resour. Res. 2001, 37, 2723–2731. [Google Scholar] [CrossRef]
- ISO Guide 73:2009; Risk management—Vocabulary: Multiple. American National Standards Institute: Washington, DC, USA, 2009.
- Jedynak, P. Ubezpiecxzenia Gospodarcze. Wybrane Elementy Teorii I Praktyki; Księgarnia Akademicka: Kraków, Poland, 2001. [Google Scholar]
- Kunreuther, H.; Roth, R. Paying the Price; Joseph Henry Press: Washington, DC, USA, 1998. [Google Scholar]
- Yen, B. Stochastic methods and reliability analysis in water resources. Adv. Water Resour. 1988, 11, 115–122. [Google Scholar] [CrossRef]
- Majewski, S.; Mentel, U. Analysis of the properties of weather regressors for econometric modelling: Example of weather stations in Poland. J. Int. Stud. 2022, 15, 122–139. [Google Scholar] [CrossRef]
- Streimikiene, D. Renewable energy technologies in households: Challenges and low carbon energy transition justice. Econ. Sociol. 2022, 15, 108–120. [Google Scholar] [CrossRef]
- Bilan, Y.; Nitsenko, V.; Havrysh, V. Energy aspect of vertical integration in agriculture. Rynek Energii 2017, 132, 98–110. [Google Scholar]
- Dupuis, D. Estimating the probability of obtaining nonfeasible parameter estimates of the generalized Pareto distribution. J. Stat. Comput. Simul. 1996, 54, 197–209. [Google Scholar] [CrossRef]
- Bartosiewicz, J. Wykłady Ze Statystyki Matematycznej; PWN: Warszawa, Poland, 1996. [Google Scholar]
- Štreimikienė, D. Externalities of power generation in Visegrad countries and their integration through support of renewables. Econ. Sociol. 2021, 14, 89–102. [Google Scholar] [CrossRef]
- Ginevičius, R. The efficiency of municipal waste management systems in the environmental context in the countries of the European Union. J. Int. Stud. 2022, 15, 63–79. [Google Scholar] [CrossRef]
- Nagaj, R. Fiscal Policy and Fuel Poverty in Poland. Rynek Energii 2022, 5, 3–10. [Google Scholar]
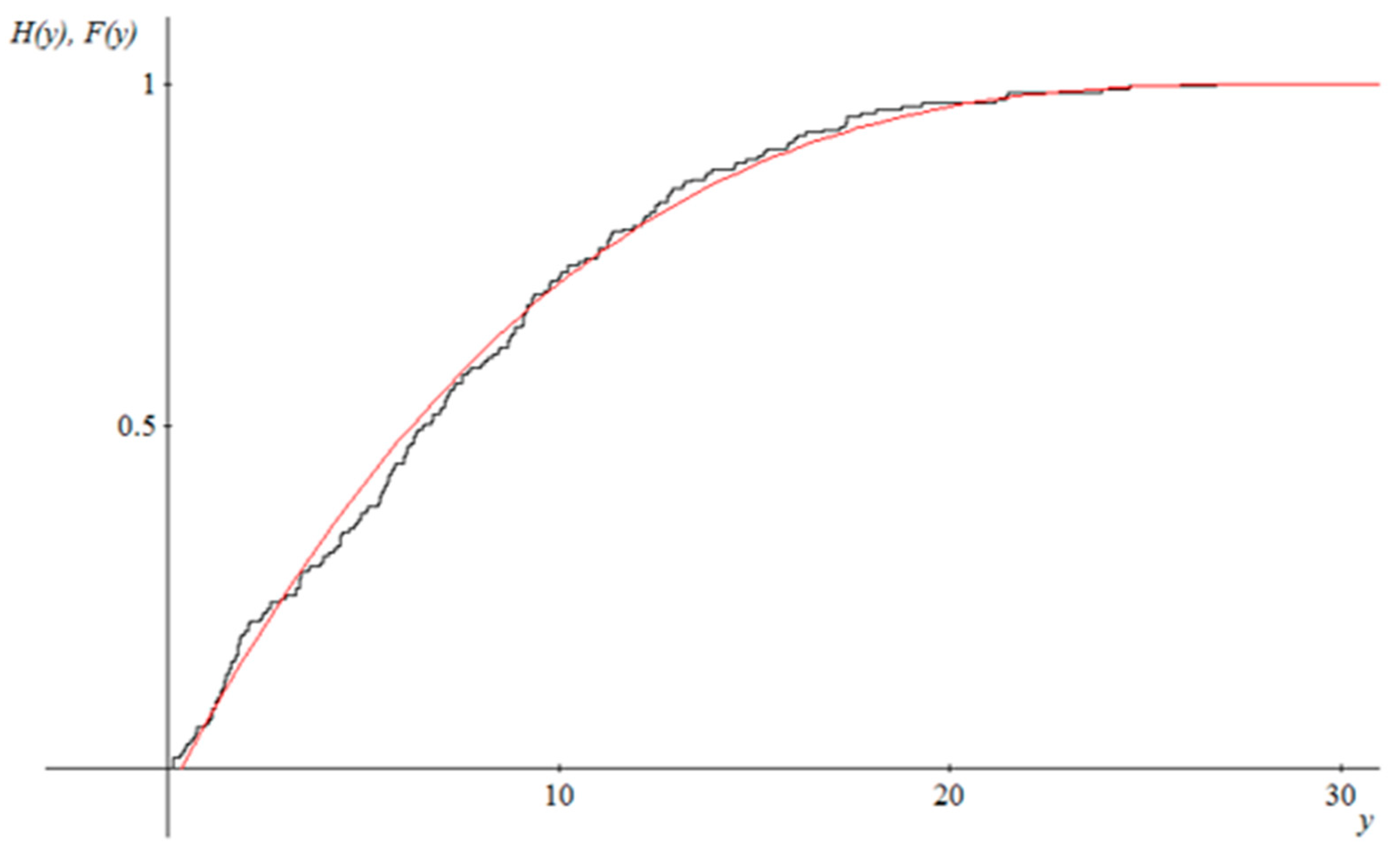
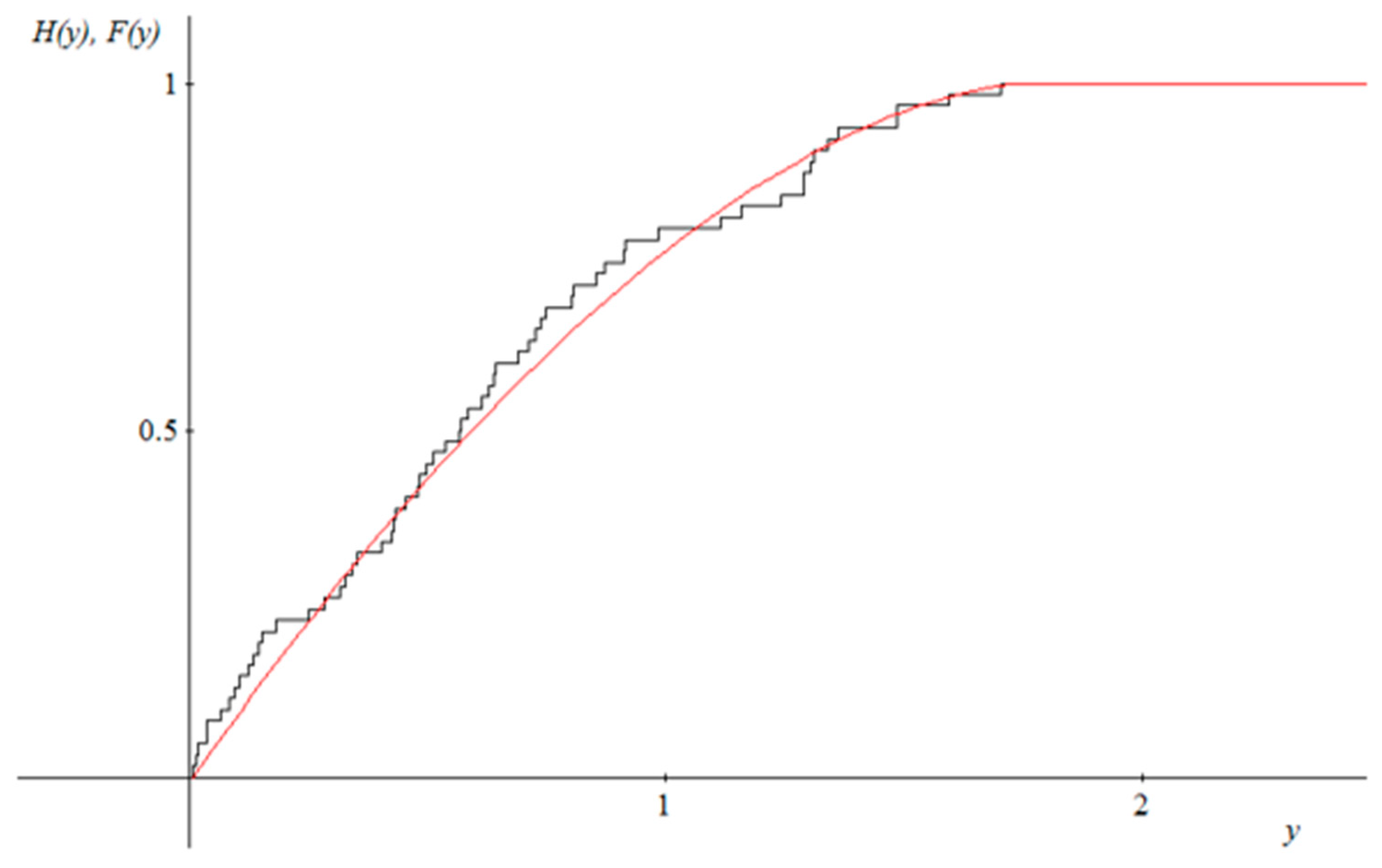
| Variables | A-DPv | K-SPv | |||
|---|---|---|---|---|---|
| Y1 | −0.3147 | 0 | 9.176 | 0.8051 | 0.8456 |
| Y2 | −0.581 | 0 | 1.026 | 0.8417 | 0.937 |
| Variables | Risk Models | Quantile Risk Measures |
|---|---|---|
| Y1 | 9.5122 | |
| 14.1738 | ||
| Y2 | 2.0847 | |
| 2.8575 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuźmiński, Ł.; Kes, Z.; Draskovic, V.; Gawlik, A.; Rabe, M.; Widera, K.; Łopatka, A.; Śniegowski, M. Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification. Energies 2023, 16, 2477. https://doi.org/10.3390/en16052477
Kuźmiński Ł, Kes Z, Draskovic V, Gawlik A, Rabe M, Widera K, Łopatka A, Śniegowski M. Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification. Energies. 2023; 16(5):2477. https://doi.org/10.3390/en16052477
Chicago/Turabian StyleKuźmiński, Łukasz, Zdzisław Kes, Veselin Draskovic, Andrzej Gawlik, Marcin Rabe, Katarzyna Widera, Agnieszka Łopatka, and Maciej Śniegowski. 2023. "Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification" Energies 16, no. 5: 2477. https://doi.org/10.3390/en16052477
APA StyleKuźmiński, Ł., Kes, Z., Draskovic, V., Gawlik, A., Rabe, M., Widera, K., Łopatka, A., & Śniegowski, M. (2023). Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification. Energies, 16(5), 2477. https://doi.org/10.3390/en16052477







