Modelling of the Risk of Budget Variances of Cost Energy Consumption Using Probabilistic Quantification

Abstract

Budgets in organisational units are considered to be traditional management support tools. On the other hand, budgetary control is the essence of control measures, allowing for the increase in the efficiency of an enterprise through appropriate allocation of resources. The methodology used in the analysis of budget variances (obtained as a result of applying budgetary control) undoubtedly influences the management efficiency of almost every organizational unit. The authors indicate a research gap of methodological and application nature in the area of risk measurement in the analysis of budget variances. Therefore, the aim of the article is to create universal and flexible models enabling probabilistic quantification of the risk of budget variance regardless of the nature of the cost, the person budgeting and the budgeting unit. Extreme value theory was used to develop the model. The results of the work are models allowing for the estimation of the limit level of deviation for assumed probabilities and models determining the level of deviation for a given probability level. The application of these models in budgetary control will allow for a synthetic assessment of the degree of budget execution in the company, comparing the quality of budget execution over time as well as between units, defining the limits of materiality of budget variances. For the purpose of model verification, the authors have used budget variances of cost energy consumption, which have been determined on the basis of empirical distributions obtained from data coming from the system of budgetary control implemented at a university located in a larger European city.

1. Introduction

Management of organisations is inseparable from planning and control. The tool that supports these two processes is budgeting. According to the terminology defined by the Chartered Institute of Management Accountants [1], budgeting consists of predicting costs and revenues for the planned course of activities within a certain period of time. Budgetary control, on the other hand, serves to ensure that planned and budgeted activities lead to the desired results. The subject of consideration of the authors of this study are analytical methods used in control. With regard to this part of the Pandit [2] management process, it sees the following possibilities:

• Disclosure of the extent to which actual performance differs from that budgeted.
• Identifying the reasons why actual results differ from those budgeted.
• Defining corrective actions.
• To define the basis for the revision of the current budget.
• Improving the process of preparing future budgets.

D. Hansen and M. Mowen believe that the “budgetary control system” [3] allows for comparison of actual costs with the budgeted ones, by calculating the deviations being the difference between actual and planned costs for the current level of activity. There is a large consensus among authors dealing with topics related to management accounting that budgets are the basis for comparisons with data currently achieved in business activity. According to S. Hansen et al., budgeting (understood as the process of creating budgets) is a pillar of the management control system in almost all organisations [3,4]. Thus, the essence of budgetary control consists of using information about the norms established in the form of budgets to calculate the deviations which, after analysis, constitute the basis for the assessment of activities, as well as for making corrections to the budget or the controlled activities.

The analysed studies did not identify any issues concerning the estimation of the risk of budget variance. It is undoubtedly a research gap of methodological and application nature. The identification of this gap prompted the authors to define the research problem in the form of a question: how to model the risk of budget variance? This research problem determines the following research hypotheses:

H1. 

The Pareto family of generalized distributions is a precise tool, from the point of view of matching them to empirical distributions, to measure the risk of budget variance.

H2. 

Probabilistic risk models for budget variances based on generalised Pareto distributions are, due to their flexibility, universal in nature and can be applied to different budget variances (differing according to the nature of the budget item, budgeting entity or person responsible for budget implementation).

The research hypotheses were verified through the realization of the overarching goal of the work. The authors assumed that the primary goal of the study was to create universal and flexible models that would allow probabilistic quantification of the risk of budget variance regardless of the nature of the cost, person, or budgeting unit.

The tests were carried out using data obtained by means of simulation. The simulations were carried out using decompositions obtained on the basis of calculated deviations for two selected budgeted cost items of an economic university located in a large city of the European Union.

This study is part of the research undertaken, among others, by the authors of this study, to improve the methodology of budget variance analysis with the use of statistical tools. The presented results may supplement the list of analytical tools, enabling the assessment of budget execution and effectiveness of control systems.

2. Theoretical Background

Budgeting derives from management accounting [5]. It should be kept in mind that research shows the rules, stages and effects of budgeting from the perspective of social sciences, such as economics, psychology and sociology [6]. The very concept of budgeting has no one-sided explanation. A comprehensive analysis of the scope of the concept was conducted by Norkowski [7]. The author showed the differences in the understanding of budgeting from the perspective of method, process, system, tools, and procedure. Regardless of the definition of this concept, it should be assumed that the effect of budgeting is, among others, budgets, which are the basis for control. Among many authors there is a consensus that budgets are a quantifiable expression of the organizational unit’s plans, taking into account the consumption of resources or economic benefits (see [8,9,10,11,12]).

Pandey [13] defines budgetary control as the creation of budgets of individual organizational units, as well as the process of comparing actual results with those budgeted to ensure the desired actions. Brown and Howard [14] say the same thing as King, Clarkson and Wallace [15], Davila and Wouters Fisher [16], and Fredrickson and Peffer [17]).

For Pandey [18], the essence of budgetary control lies in the use of information on the norms established in the form of budgets to calculate the deviations which, after analysis, provide a basis for evaluating activities as well as for making corrections to the budget or the audited activities. In the process of budgetary control the following stages can be distinguished [19]:

• Calculating the variances of the quantities currently reached or expected to be reached from the budgeted quantities.
• To identify where the variance occurs.
• Variance analysis.
• To identify those responsible for the variance.
• Research into the effects of variances in different areas of company activity.
• Indicating actions to correct variances and postulating remedial actions to eliminate variances in the future.
• To propose changes in the company’s activities.
• To propose improvements in the budgeting process itself.
• Monitoring the changes made.

In the process of budgetary control, a number of steps can be distinguished, and the analysis of variances should be an integral part of it. Thanks to the analytical activities, it becomes possible, among others, to:

• Determine the causes of variances (factorial analysis).
• Classify variances (e.g., significant vs. insignificant, favourable vs. unfavourable).
• Examine and evaluate variance levels.
• Examine variance properties (recurrence, trends, configurations).
• Identify causes for variance and determination of actors accountable for variances.

Many publications have been devoted to the methodology of variance analysis. The vast majority of them present the methods of division of variances into factors derived from the standard cost account (cf. [20,21,22]). This approach allows us to determine the value of the impact of changes in rates, prices, performance, etc., on variances between standards and performance.

The subject of variance analysis using mathematical and statistical methods has been present in the literature for a long time. The topic of using statistics in research on budget variances is discussed in Kaplan’s [23,24] work, which reviews the models used to set tolerance limits for deviations. For example, these are Duncan [25] using the control chart $\overline{x}$, Taylor [26] and Goel with Wu [27,28,29] develop procedures to design CUSUM charts that minimize long run average cost. In addition, Kaplan cites models that assume different types of variables to determine the state of controlled processes. Girshick and Rubin [30,31,32] proposed a model that defines the states of the process: under control and out of control. Duvall [29,33,34] developed a model with a continuous variable that determines the control status of the process. Kwang and Slavin postulated methods based on the analytical evaluation of two constituents of total variance, i.e., price variance and quantity variance [30]. Further development of these methods placed more emphasis on the examination of intermediary cost (see [31,32,35]). Several authors have explored the potential of statistical methods for variance analyses, cf. ([33,34,36]).

A query on the methods used for analysing budget variances allows us to confirm the thesis that the topic of examining the risk of variance was not addressed. Similarly, analytical methods using extreme value theory were not encountered. In the further part of the article, the scientific achievements related to this theory are presented [37,38,39].

Extreme value theory is an area of statistics that deals with data that are far from the median. It is about determining the probability of an event, consisting of the fact that the set of realizations of a random variable will include extreme observations. Because of this, it is possible to use it in research on natural phenomena, such as floods, precipitation, wind gusts, air pollution, corrosion, etc. The origins of this theory date back to the early 18th century. In 1709, Nicolas Bernoulli considered the greatest average distance between n points distributed randomly over a straight line of a fixed length l [35,40,41].

In the twentieth century there was a dynamic development in the theory of extreme values and it is connected with the publication of Bortkiewicz’s [36,42,43] work, which concerned the range distribution in a random sample from the normal population. In 1925 Tippett [37,44,45] presented in his work a table of maximum values with corresponding probabilities for different samples with normal distributions. Two years later Frechet presented asymptotic distributions of maximum values and identified one of three limit distributions for maximum value distributions [38,46,47,48,49,50]. In the next year, Fisher and Tippett [39] published the results of their considerations on the same issue, showing that extreme limit value distributions can be one of three types of distributions.

At this point it is worth mentioning the contribution of Polish researchers. The works deserve special attention [19,51,52,53,54,55,56,57,58,59,60,61].

3. Materials and Methods

Indirect results of budgetary control are the variances that indicate the degree of implementation of the plan. Deviations can be determined in many ways (Kes calculates 6 forms of calculation formulas). Formula (1) was used to build models for probabilistic quantification of the risk of budget variance:

$$OW=\left|\frac{P_W-P_B}{P_B}\right|·100\%$$

(1)

where:

OW—relative deviation (variance);

$P_B$—value for the budget item (budgeted value);

$P_W$—value for the budget item reached during the budget period.

The description of the conducted studies will be preceded by the characteristics of the data included in the study. For the purpose of achieving the overarching goal of the study, the authors have collected monthly data on budget variances from three years for two cost categories in a selected higher education institution’s costs: electric energy consumption (X₁) and gas consumption (X₂). A university was selected in which cost budgeting for administrative units has been implemented for 3 years. The data were collected from control reports generated in the years 2017–2019. Due to the access to a small number of data, the authors decided to conduct research on simulation data coming from the population with distributions described by F(x₁) and F(x₂).

In order to generate simulation data, it was necessary to select theoretical distributions that would best represent empirical distributions of X₁ and X₂ variables. They say differently, the distributions F(x₁) and F(x₂) should be found.

On the basis of the results of the applied tests for the compatibility of empirical distributions with Anderson–Darling and Kolmogorov–Smirnov theoretical distributions, it turned out that both examined variables best describe mixed distributions as being a mixture of standard distributions. For variable X₁ the mixed distribution describes the cumulative distribution function (cdf):

$$F(x_1)=0.74F_1(x_1)+0.26F_2(x_1),$$

where F₁(x₁) is the normal distribution with parameters μ₁ = 0.655 i σ₁ = 0.422, while F₂(x₁) is the normal distribution with parameters μ₂ = 8.339 i σ₂ = 7.19. The mixed distribution of the X₂ variable is described by the following cdf:

$$F(x_2)=0.92F_1(x_2)+0.08F_2(x_2),$$

where F₁(x₂) is the distribution of normal distribution with parameters μ₁ = 0.517 and σ₁ = 0.283, while F₂(x₂) is the distribution of normal distribution with parameters μ₂ = 3.014 and σ₂ = 0.707. On the basis of matched distributions for each of the variables, random samples with numbers n = 1000 of observations each were generated. The samples obtained as a result of sample simulation were used in further stages of the study.

For the purpose of solving the research problem defined by the authors, the paper uses selected elements of the theory of extreme values, which in general refers to stochastic behaviour of extremes, i.e., maxima and minima of independent random variables with identical distributions. The authors proposed a model of risk of budget variances using a selected family of distributions proposed by the extreme value theory.

Extreme value theory provides tools to model the extremes of cdf F of an unknown distribution of the real X random variable. The only condition that must be met is that there must be a distribution of extreme values for the X random variable. Extreme values are generally defined by Definition 1:

Definition 1.

Extreme values are those which are relatively unlikely to occur and have a large influence on the behaviour of the other values in the series [62].

The study of the behaviour of extreme values of specific random variables comes down to the study of the behaviour of the distribution tails of real random variables. The extreme value index γ is responsible for the behaviour of extreme values. This parameter determines the thickness of the distributing tail. If γ > 0 it means that the random variable x has a distribution with thick (heavy) right tail, if γ = 0 then the distribution of the variable x has a thin (light) right tail, and if γ < 0 then the distribution of the variable x has a short right tail which means that the variable X takes values from a limited set of real numbers. On the basis of the indexed value of extreme values, one can obtain information about the type of distribution of the examined random variable x and information about the distribution of extreme values of this random variable.

The extreme index value can be estimated by commonly used parametric and non-parametric statistical estimation methods. For estimation of parameter γ a sample consisting of appropriate extreme observations of the tested random variable X is needed. The theory of extreme values suggests several approaches to the topic of sample selection for the estimation of extreme index values.

In one random sample approach, extreme implementations of a random variable X are taken from a random sample to a sample which is a sample composed of extreme values (maxima or minima). In this case, the random sample size is not too large, and this approach omits other values In another variant, a very large number of n-elementary samples are taken from the population and from this, sample k of the largest observations is selected and on its basis the parameters of appropriate distribution of maxima are estimated. The methods of data selection also include the method of exceeding the threshold (Peaks over Threshold) or otherwise the method of estimating the tail distribution of a random variable.

In this paper, for the estimation of the extreme value index, a method has been adopted where only those observations that exceed a certain relatively high value assumed by the researchers, called a threshold or threshold, are used. This approach has been applied to the research conducted by the authors in the paper and will therefore be discussed in detail below.

Before discussing in detail the method of transgression in the aspect of its application to solve the research problem defined by the authors, a family of distributions functioning under one name of Generalized Pareto Distribution (GPD) will be presented. GPD distribution is one of the basic distributions in the theory of extreme values and is the foundation of the discussed method of exceedance (POT—Peaks over Threshold). The GPD distribution is defined by Formula (2):

$$H_{\gamma }(x)=\{\begin{array}{l}1-{(1+\gamma x)}^{-1/\gamma }, \mathrm{if} (\gamma >0 \mathrm{and} x\ge 0 ) \mathrm{or} (\gamma <0 \mathrm{and} 0\le x<1/\left|\gamma \right|),\\ 1-e^{-x}, \mathrm{if} \gamma = 0.\end{array}$$

(2)

Using the relationship that, if a random variable X has a distribution of F, then the random variable (μ + σX) has the distribution $F_{\mu ,\sigma }(x)=F((x-\mu )/\sigma )$, and can be extended to the family of generalized GPD distributions Pareto, additionally with position and scale parameters ([63]). This parameterization significantly extends the range of applications of this family to model phenomena from different areas. After adding the position parameter μ (μ ϵ ℝ) and the scale parameter σ (σ > 0) of the general cdf, Pareto $H_{\gamma ,\mu ,\sigma }\left(x\right)=H_{\gamma ,\mu ,\sigma }\left(\frac{x-\mu }{\sigma }\right)$ takes the form from Formula (3) [64,65,66]:

$$H_{\gamma , \mu , \sigma }(x)= \{\begin{array}{l}1-{\left(1+\gamma \left(\frac{x-\mu }{\sigma }\right)\right)}^{-1/\gamma }, \mathrm{if} \gamma \ne 0,\\ 1-\exp \left(-\frac{x-\mu }{\sigma }\right), \mathrm{if} \gamma = 0,\end{array}$$

(3)

while the probability distribution density function after parameterisation is described by Formula (4):

$$g_{\gamma , \mu , \sigma }(x)=\left(\frac{1}{\sigma }\right){\left[1+\gamma \left(\frac{x-\mu }{\sigma }\right)\right]}^{-\left(1+\gamma \right)/\gamma },$$

(4)

For the estimation of GPD distribution parameters, different estimation methods are proposed in the literature. The most common is the most reliable method ([49,67]). Hosking and Walli [68] propose a method of moments. Castill and Hadi describe in their work the percentile method, also known as the xanthine method [69]. Rassmussen [70] in his work proposes a generalised method of probability weighted moments for estimating GPD distribution parameters. A detailed review and comparison of the mentioned methods of estimating the parameters of GPD distribution is included in the paper ([71,72,73]). The authors used the most reliable method of estimation in their research.

Returning to the discussion of the exceedance method, it is assumed at the outset to X₁, …, X_n be a sequence of random variables (i.i.d.) coming from a population with an unknown distribution of F. In the case of the discussed method, the researcher focuses on exceedances above the set (usually relatively high) u threshold value. The top limit of the distribution of F is determined by F, which is recorded as ([74]):

$$x_F=sup\left\{x\in ℝ:F\left(x\right)<1\right\}\le \infty .$$

(5)

It is also necessary to introduce here a definition of conditional distribution of exceedances, which is otherwise referred to as a distribution of above-threshold losses or a distribution of expected value of above-threshold losses. The concept of distribution of above-threshold losses is defined in Definition 2:

Definition 2.

Let X be a random variable with distribution F and u a fixed threshold value. The cdf of the random variable Y = X – u called the excess cdf or the cdf of above-threshold losses is given by Formula (6):

$$F_u(y)=P\left(X-u\le y|X>u\right)$$

(6)

where $0\le y<x_F-u$, a $y=x-u$ to these are transgressions ([74]).

The cdf of the conditional distribution of exceedances can also be presented using the cdf of the tested true random variable F(x) through Equation (7):

$$F_u(y)=\frac{F(u+y)-F(u)}{1-F(u)}=\frac{F(x)-F(u)}{1-F(u)}$$

(7)

For the use of risk assessment models, it is necessary to find the form of conditional distribution of the exceedances and to demonstrate its parameters.

The following statement by Pickands-Balkemy-de Haan ([75,76]), which is alongside that of Fisher and Tippett [39], is considered a fundamental claim in extreme value theory:

Theorem 1.

For a wide family of distributions described by the actual cdf F of the conditional cdf F of exceedances of F_u(y), for a high u, is well approximated by the distribution $F_u(y)\approx H_{\gamma , \sigma }(y), u\to \infty$ where:

$$H_{\gamma , \sigma }(y)=\{\begin{array}{l}1-{\left(1+\frac{\gamma }{\sigma }y\right)}^{-1/\gamma }, if \gamma \ne 0\\ 1-e^{-y/\sigma }, if \gamma =0\end{array}$$

(8)

for if $y\in \left[0, \left(x_F-u\right)\right]$ if $\gamma \ge 0$ I $y\in \left[0, -\frac{\sigma }{\gamma }\right]$, if $\gamma >0$.

It should be noted that if x is defined as x = y + u then the cdf can be $H_{\gamma , \sigma }$ presented as a function of x resulting in a formulae of the formulae $H_{\gamma , \sigma }(x)=1-{\left(1+\gamma \left(x-u\right)/\sigma \right)}^{-1/\gamma }$, which is a distribution of a generalized Pareto distribution described by Formula.

Here they refer to Pickands-Balkemy-de Haan’s claim that it is very important to note the link between Pareto’s generalised decomposition and Poisson’s decomposition. If you assume that the number of exceedances u marked as N_u is a random variable with a Poisson distribution with an intensity parameter λ. The variable N_u is independent from the sequence X_n (i.i.d.). The distribution of the sequence of random variables $Y_1, \dots , Y_{N_u}$ that are above the threshold u is described by the distributed one $H_{\gamma , \sigma }$ and by the $M_{N_u}=\max \left(Y_1, \dots ,Y_{N_u}\right)$ random variable that describes the maximum values of exceedances, then it is true:

$$P\left(M_{N_u}\le y\right)=\exp \left\{-\lambda {\left(1+\gamma \frac{x}{\sigma }\right)}^{-1/\gamma }\right\}=G_{\gamma , \mu , {\sigma }^{\prime }}(y)$$

(9)

where $\mu =\sigma {\gamma }^{-1}({\lambda }^{\gamma }-1)$ is the position parameter and ${\sigma }^{\prime }=\sigma {\lambda }^{\gamma }$ is the scale parameter.

The above property means that the number of exceedances of a given threshold u has a Poisson distribution and the exceedances themselves have a generalized Pareto distribution (GPD), while the maximum values of these exceedances have a generalized extreme value distribution (GEV).

From the point of view of the use of generalized Pareto decomposition, the introduction of the concept of quantile estimator x_p also seems to be important for measuring the risk of budget variances. According to Pickands-Balkemy-de Haan’s claim, tail estimation can be used $x\ge u$:

$$\widehat{F}(x)=\left(1-F_n(u)\right)H_{\gamma , \mu , \sigma }(x)+F_n(u)$$

(10)

To approximate the cdf F. It can be shown that $\widehat{F}(x)$ it is a Pareto cdf, with the same shape parameter γ, but with a changed scale parameter $\tilde{\sigma }=\sigma {\left(1-F_n\left(u\right)\right)}^{\gamma }$ and with a changed position parameter described by the formula:

$$\tilde{\mu }=\mu -\tilde{\sigma }\left({\left(1-F_n\left(u\right)\right)}^{-\gamma }-1\right)/\gamma .$$

(11)

The POT quantile x_p estimator is obtained by reversing the formula $\widehat{F}(x)$. Then, the unknown parameters of GPD decomposition are converted into estimators $\left(\widehat{\gamma }, \widehat{\sigma }\right)$ and obtained:

$${\widehat{x}}_p={\widehat{F}}^{\leftarrow }(p)=H_{\widehat{\gamma }, u, \widehat{\sigma }}^{-1}\left(\frac{p-F_n(u)}{1-F_n(u)}\right)=u+\frac{\widehat{\sigma }}{\widehat{\gamma }}\left({\left(\frac{1-p}{1-F_n(u)}\right)}^{-\widehat{\gamma }}-1\right)$$

(12)

If N_u is the number of exceedances above the threshold value of u and n is the number of all observations in the series, the quantile estimator can be expressed by the formula:

$${\widehat{x}}_p=u+\frac{\widehat{\sigma }}{\widehat{\gamma }}\left({\left(\frac{n}{N_u}(1-p)\right)}^{-\widehat{\gamma }}-1\right)$$

(13)

where p is a probability close to 1.

An important issue is the choice of the u threshold. The theory suggests that this value is optimal, i.e., it reconciles load and variance. When the threshold value is higher, less load is obtained, but fewer exceedances are obtained for analysis and therefore more variance [77].

In order to solve the research problem identified in the paper, the authors proposed their own definition of the risk of budget variance. They described this risk as a risk of budget variance. The definition of this risk was developed on the basis of selected risk definitions available in the literature. Taking into account the guidelines used in all areas of human life, one can refer to the ISO [78] standard which defines risk as the effect of uncertainty on objectives where the effect of that effect may be positive or negative and the risk itself is expressed by a combination of effects and the probability of their occurrence [79,80]. Another definition treats risk as the possibility or probability of loss, e.g., caused by flooding [81]. Another definition of risk is the probability of failure of the system or its element pf, which can be identified in a specific case with flooding, using selected elements of extreme value theory presented in this section. Additionally, for the purposes of probabilistic quantification of the risk of budget variances, the authors proposed a probabilistic measure of risk, which was built using the cdf $H_{\gamma , \mu , \sigma }$ distribution of a random variable Y describing the excess of relative budget variances (X) over the given threshold u. The definitions of risk and its probabilistic measure are described in Definitions 3 and 4, respectively:

Definition 3.

The risk of budget variances is defined as the possibility that a random variable Y may exceed a critical level of d_cr. The random variable Y in this definition defines the level at which the threshold is exceeded by the random variable X which is a relative budget variance (1).

Definition 4.

A probabilistic measure of the risk level of budget variance is defined as the probability that a random variable Y exceeds the critical level of d_cr. The defined measure is determined $D_O\left(u,H_{\gamma , \mu , \sigma }, d_{cr}\right)$ and described by a formula:

$$D_O\left(u,H_{\gamma , \mu , \sigma }, d_{cr} \right)=P\left(Y>d_{cr}\right)=p_{cr}$$

(14)

where u is the excess threshold for the random variable with budget variances and $H_{\gamma , \mu , \sigma }$ means the cdf of the random variable Y matched by the excess sample. Therefore, the Y measure can also be described by a formula:

$$D_O\left(u,H_{\gamma , \mu , \sigma }, d_{cr} \right)=1-H_{\gamma , \mu , \sigma }\left(d_{cr}\right)=p_{cr}$$

(15)

At this point it should also be noted that the critical level of d_cr can be treated as a quantum of the order of 1p_cr of the distribution of a random variable (Y) describing the excesses of the cdf $H_{\gamma , \mu , \sigma }$ and written as: $d_{cr}=y_{(1-p_{cr})}$. It also seems to be useful in the aspect of the research problem defined by the authors to introduce a measure that will allow us to calculate the value of the critical level of d_cr that will be exceeded for a certain probabilistic value of the p_cr measure. Taking advantage of the fact that $d_{cr}=y_{(1-p_{cr})}$ the authors have introduced a definition of a quantum measure of the risk of budget variance:

Definition 5.

A quantifiable measure of the risk of budget variance sets out a quantile, of the order of 1 − p_cr of the distribution of budget variance above the threshold value u being the critical level that will be exceeded with a risk of budget variance at p_cr level and is calculated from the formula:

$$D_{OQ}\left(u,H_{{}_{\gamma , \mu , \sigma }}^{-1}, p_{cr} \right)=h_{cr}=y_{ (1-p_{cr})}$$

(16)

where $H_{\gamma , \mu , \sigma }^{-1}$ it is the inverse cdf of the distribution of budget variance above the u threshold, p_cr is the probabilistic measure of the risk of budget variance described by Formula (1), and $y_{ (1-p_{cr})}$ is defined by Formula (12).

Using the notion of risk of budget variance as defined in Definition 3 and the probabilistic measures of this risk as defined in Definitions 4 and 5, the authors proposed a probabilistic model of risk of budget variance to be used for probabilistic quantification of such risks and is defined in Definition 6.

Definition 6.

A probability risk model for budget variance based on the cdf of $H_{\gamma ,\mu ,\sigma }$ the distribution of the random variable Y, which determines the value of the excess of budget variance described by the random variable X above the threshold u, is described by the following expressions:

$$R_B\left(u, H_{\gamma , \mu , \sigma }, d_{cr}\right)=D_O$$

(17)

and:

$$R_{BQ}\left(u, H_{\gamma , \mu , \sigma }^{-1}, p_{cr}\right)=D_{OQ}$$

(18)

Both risk models of budget variance presented by the authors are two-parametric. This means that two parameters have to be set in order to calculate the measure of appropriate risk. The R_B model at a given threshold value u for budget variances (X) and critical level for overshootings of dcr allows us to estimate a probabilistic measure of risk of budget variance (Y) exceeding d_cr. The second of the proposed models, i.e., the R_BQ model for a given threshold value u and a given probability p_cr, allows us to estimate the level of overshootings $y_{ (1-p_{cr})}$ that will be reached (exceeded) with a given probability p_cr. The following section will present the use of both models to estimate the risk of budget variance for the two types of costs. These are the costs of consumption of materials and external services. The operation of the models will be presented on data from simulations conducted on real theoretical distributions adjusted to the examined cost types.

Economic models and those used in other areas need to be verified in order to assess the quality of their alignment with data describing the phenomena being modelled. In the case of models with a risk of budget variance, the basis for assessing their matching is the assessment of the theoretical cdf of the value of overshootings $H_{\gamma ,\mu ,\sigma }$ to the empirical distribution of the value of overshootings describing the phenomenon under investigation. Therefore, the verification of matching of risk models will be carried out using the measure p-value of relevant tests of compliance of theoretical and empirical distributions. Where p-value in the aspect of compliance tests for distributions in the extreme value theory and proposed risk models is the minimum value of the significance level α, at which the hypothesis that the proposed theoretical cdf of the value of exceedances $H_{\gamma , \mu , \sigma }$ is consistent with the distribution of the empirical distribution of the value of exceedances above the threshold of the modelled random variable X is rejected. In other words, p-value determines the minimum probability of rejection of the above described hypothesis even though it is true.

Verification of hypotheses of conformity of empirical distribution of above-threshold values with the generalised Pareto distribution (GDP) shall be carried out using Anderson–Darling, Cramer von Mises, or Kolmogorov–Smirnov tests, or other known conformity tests. The Anderson–Darling and Cramer von Mises tests and have better properties than, e.g., the chi-quadrant conformity test. Considerations on these tests and their properties together with critical values for selected theoretical distributions can be found in Stephens’ work ([82,83,84,85]) and at work ([86]).

In the further part of the test, the method of exceeding the threshold was applied. In the first step of this method, for the tested two strings of random variables X₁ and X₂ with the number n₁ = n₂ = 1000, threshold values are selected for each of the tested variables. N_u1 and N_u2 will determine the number of observations in the tested samples that exceeds the threshold value in the X₁ and X₂ variables, respectively. For variable X₁, the observations exceeding the threshold value will be determined and calculated from the equality $y_{1i}=x_{1i}-u\ge 0$ and for variable X₂ from the equality of form $y_{2i}=x_{2i}-u\ge 0$. Samples consisting of observations constituting an exceedance for variable X₁ will be realized from a random variable Y₁ and marked as $y_{11}, \dots , y_{1 N_{u1}}$. Similarly, for variable X₂, a sample consisting of transgressions $y_{21}, \dots , y_{2 N_{u2}}$ is the realization of variable Y₂.

In the second step of the exceedance method, on the basis of the determined exceedance samples, the cdf parameters $H_{\gamma , \sigma }(y_1)$ and $H_{\gamma , \sigma }(y_2)$ distributions of the random variables Y₁ and Y₂, respectively, were determined [87]. The highest reliability method was used to estimate the distribution of exceedances.

In the next stage of the study for the selected distribution of theoretical distributions for Y₁ and Y₂ variables, two compliance tests (Anderson–Darling and Kolmogorov–Smirnov) were carried out in order to assess the quality of matching of the proposed theoretical distribution with the empirical distribution of exceedance values. Fitting assessment was carried out on the basis of obtained p-value.

The final stage of the study consisted in estimating the risk level of budget variance using the proposed risk model of budget variance of a given Formula (18). The calculations were made for the established two parameters of the risk model, i.e., the threshold value u and the critical level p_cr. For both variables studied, the authors adopted two levels of p_cr: 0.1 and 0.05.

The choice of the u-threshold value is a very important issue, as the quality of the obtained estimators depends on the choice of the threshold value. Too high threshold value causes the estimators’ variance to be high. It results from the fact that the exceedance attempt is small, but the load of estimators is small. If the threshold value is too low, the situation is the opposite. Therefore, the optimal threshold value should be selected. To choose the optimal value, a quantum–quantile chart can be used. Most often the threshold value at the level of the quantile is assumed to be 0.9–0.95. 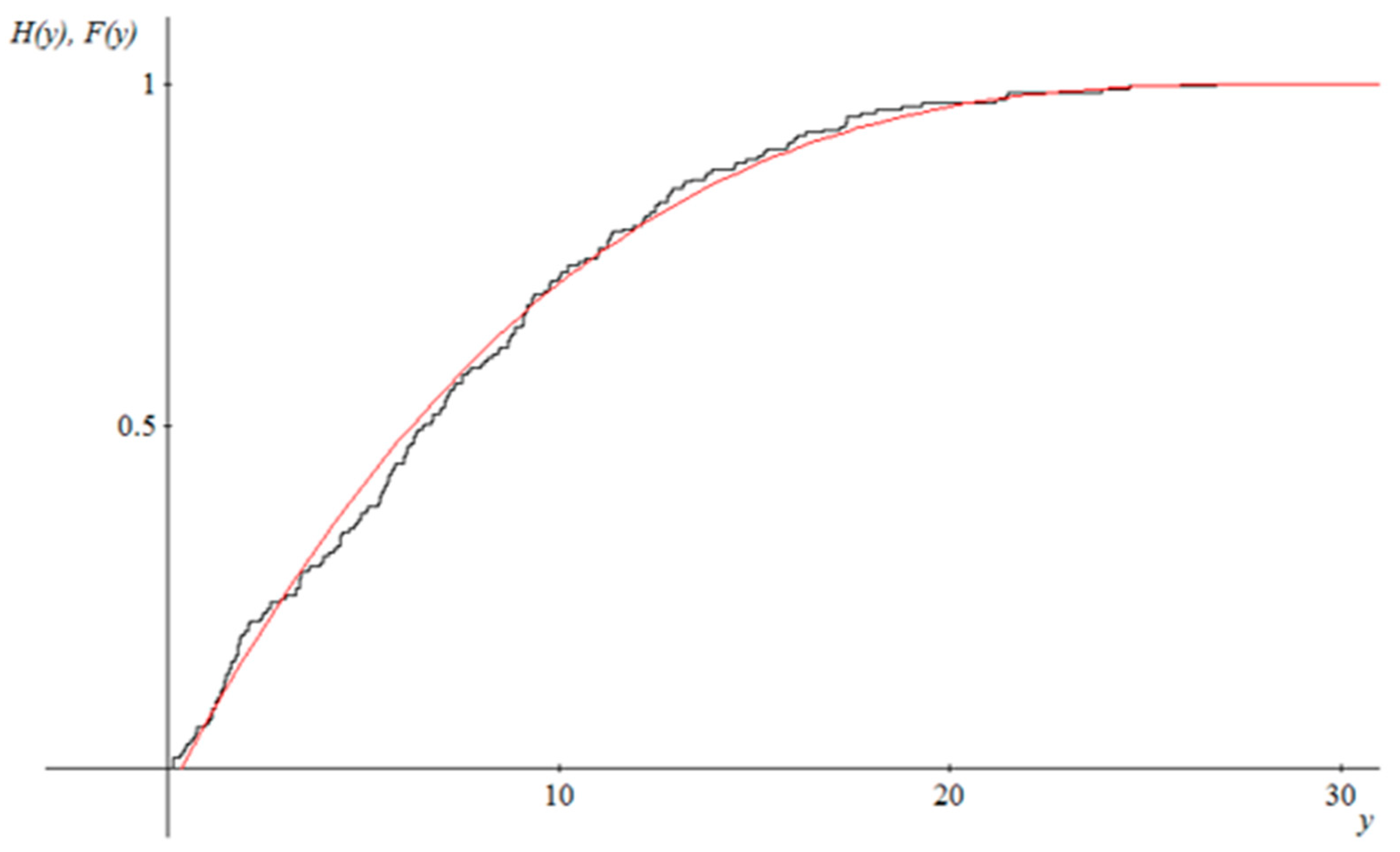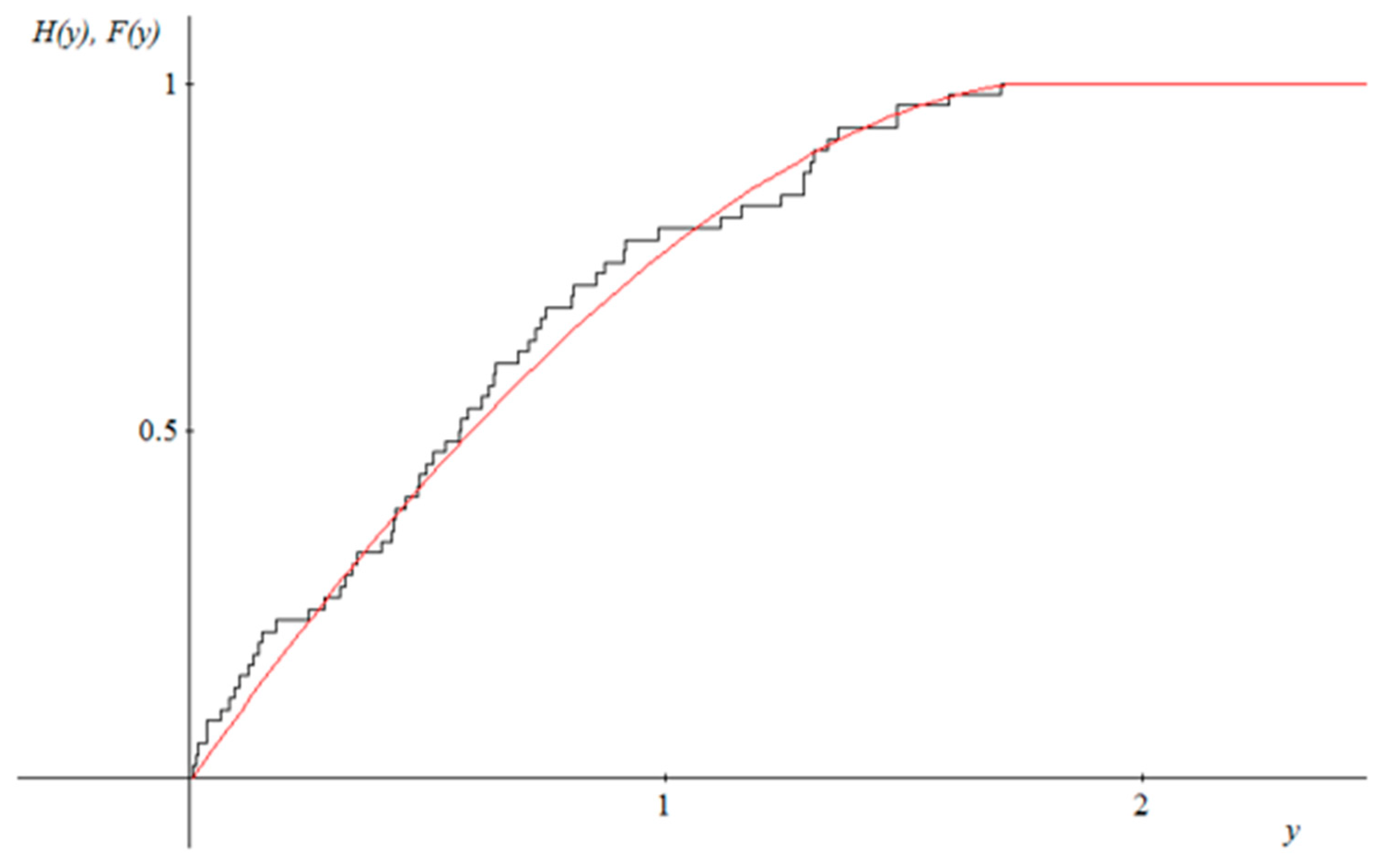The authors of this study have chosen the u-value for variables X₁ and X₂ using the mean excess plot [57]. When the optimum value u is selected, the value from which the points in the graph begin to form a straight line is taken. For the X₁ variable, the optimal threshold value of u₁ = 4.14 and for the X₂ variable, u₂ = 2.65. The threshold value of u₁ generated $N_{u_1}=191$ above-threshold observations from the basic sample, while the value of u2 exceeded only the $N_{u_2}=62$ observations.

4. Results

In the research conducted for the purposes of the research problem defined in this paper, the authors used their own tools for probabilistic quantification of budget variances of costs energy consumption. As already mentioned in the previous section, budget variances within two selected cost categories have been studied. On the basis of monthly observations from three years, the authors adjusted the theoretical distributions of deviations and on their basis simulated data for the study. The research was carried out in accordance with the previous section of the article described in the previous section.

Table 1. Values of the estimators of exceedance $H_{\gamma , \mu , \sigma }$ distribution parameters together with the results of compliance tests.

Variables	$$\widehat{\mathit{\gamma }}$$	$$\widehat{\mathit{\mu }}$$	$$\widehat{\mathit{\sigma }}$$	A-DPv	K-SPv
Y1	−0.3147	0	9.176	0.8051	0.8456
Y2	−0.581	0	1.026	0.8417	0.937

presents the results of the estimation of the distribution parameters of the random variable distributions Y₁ and Y₂ described by Formula (8). The variables illustrate the exceeding of budget variances above the assumed threshold values of u₁ and u₂ for two cost categories. In the last two columns of Table 1 there are results in the form of p-values of two distribution compliance tests carried out (Anderson–Darling and Kolmogorov–Smirnov).

Analysing the obtained test results, it can be seen that both the derived distributions of theoretical distributions for budget variance exceedances are consistent with the corresponding distributions of empirical distributions at any level of significance below the value of 0.8051. Very high (close to unity) p-value values are the basis for the statement that the derived theoretical distributions of the value of budget variance exceedances are very well matched to the empirical distributions of these exceedances. On this basis, the authors conclude that both theoretical distributions of overshootings are a reliable tool for measuring the risk of budget variance using the probabilistic model of risk of budget variance described by Formula (18). The above conclusions are the basis for the first H1 hypothesis put forward by the authors.

The confirmation of high quality of matching the theoretical distributor to the distributor of empirical values of budget variances are the graphs presenting a combination of theoretical and empirical distributor charts (Figure 1 and Figure 2). Empirical cdf charts were made on the basis of commonly used formula for empirical cdf [88,89].

Analysing the values of the estimators of distribution parameters for the two cost categories described by the variables Y₁ and Y₂ (Table 1), it can be clearly stated that the exceedances of budget variances of costs in the first category are characterised by much greater variability than those for the second category [90,91,92]. This is indicated by a large difference between the scale parameters (σ₁ >> σ₂). This result definitely indicates a much higher variability of the exceedances of the deviations above the threshold value for the costs of the second category (material consumption costs) than for the first category (external services) [88,93].

The key parameter estimated in the Pareto generalized distribution used for testing is the shape parameter γ. Its value, from the mathematical point of view, describes the properties of the tails of the distributions of the examined variables [93]. Values above 0 give the distributions with thick tails in which the probability of extreme events is relatively high. The value of zero of the shape parameter occurs in distributions with thin tails which means that extreme values occur with low probability. On the other hand, values below zero for shape parameters are reserved for truncated distributions in which certain maximum values cannot occur. The more the value of the γ parameter deviates to the left of zero, the more the restriction for maximum values that cannot occur moves to the left of zero. In the conducted tests, for both distributions the value of parameter γ below zero was obtained but not significantly. For the Y₁ variable γ₁ = −0.3184 was obtained, and for Y₂ this parameter was γ₂ = −0.581. Both values of the parameters guarantee that the cut-off of the distributions takes place at such values that it does not disqualify them from being used to estimate the risk of budget variances.

Table 2. Risk measures estimated on the basis of a probabilistic risk model for budget variance.

Variables	Risk Models	Quantile Risk Measures
Y1	$R_{BQ}\left(u_1, H_{\gamma , \sigma }^{-1}, 0.1\right)=D_{OQ}$	9.5122
	$R_{BQ}\left(u_1, H_{\gamma , \sigma }^{-1}, 0.05\right)=D_{OQ}$	14.1738
Y2	$R_{BQ}\left(u_2, H_{\gamma , \sigma }^{-1}, 0.1\right)=D_{OQ}$	2.0847
	$R_{BQ}\left(u_2, H_{\gamma , \sigma }^{-1}, 0.05\right)=D_{OQ}$	2.8575

summarises the results of the quantified risk measures of budget variance obtained from the risk model of budget variance described by Formula (18).

The model used allows for a given threshold value u and critical probability p_cr to estimate the level of budget variance that will be exceeded with p_cr probability. In interpreting the results obtained for the first cost category, the level of exceedance above the threshold value u₁ that will be exceeded with a probability of 0.1 is 9.5122 (after conversion into percentages of 951.22 %) and with a probability of 0.05 is 14.1738 (1417.38 %). For the second category costs and the u₂ threshold level, a probability of 0.1 is obtained with 2.0847 (208.47 %) and a probability of 0.05 is obtained with 2.8575 (285.75 %).

5. Discussion

Awareness of the potential effects of budgetary risk, regardless of the nature of the cost, personnel, or budget unit, should be a kind of obligation. It should be emphasized that the effects of this risk are usually passed on to the society as the final recipients of the completed tasks and the addressees of the decisions taken. For this reason, passive acceptance of risks should be excluded, but active prevention of the likelihood of risk occurring and, in particular, its effects.

The aim of the study was to create universal and flexible models that would allow for probabilistic quantification of the risk of budgetary variance regardless of the nature of the cost, personnel or budget unit. The results presented may complement the list of analytical tools to assess the implementation of the budget and the effectiveness of control systems.

The presented models, due to their flexibility, can also support the construction of a strategy of cost units, people, or budgets. Each strategy requires a reliable assessment of budgetary risk in the decisions taken. Taking into account the methodology proposed in this article, it seems possible to determine the limits of the significance of budget deviations, which will be the direction of further research.

6. Conclusions

In the probabilistic models of assessing the risk of budget variance proposed by the authors in this paper, it is necessary at the outset to assign values of two parameters: threshold values u and d_cr for the R_B model and pcr for the R_BQ model. The R_B model has not been used in the study due to the limited publication framework, but it is closely related to the R_BQ model and the authors suggest using one of them. The two-parameters of both presented models makes them a very flexible tool for the probabilistic quantification of the risk of budget variance. As the results of the research have shown, budget variances in one institution for two cost categories have different characteristics. The flexibility of the proposed models allowed us to select a risk model for each cost category, which made it possible to assess the risk of budget variances in spite of different characteristics of the costs studied. The results obtained by the authors additionally confirm the universal character of the proposed probabilistic risk models.

The conclusions presented above give the basis for positive verification of the second research hypothesis H2, as put forward by the authors.

Having models for quantifying the risk of deviation, it is possible to:

• Assess the degree of budget implementation in the company;
• Compare the quality of budget implementation over time as well as between units.

The practical dimension of the application of the models allows for comparison of the level of deviation of the costs examined. If the costs of energy consumption are characterised by the risk of 9.5122 (with the value of the parameter p_cr = 0.1), it means that 90% of the deviations does not exceed 1365% (951% + 414%). Similarly, if the costs of gas consumption are characterized by the risk of 2.0847 (with the value of the parameter pcr = 0.1), it means that 90% of deviations do not exceed 473% (208% + 265%). From this it is easy to conclude that the level of control of material costs was higher than the costs of external services. This is important from the point of view of budgeting evaluation as well as its improvement in subsequent cycles.