Application of Variable-Order Fractional Calculus to the Modeling of Calendar Aging in Lithium-Ion Batteries
Abstract
1. Introduction
2. Fractional-Order Calendar Aging Model under Dynamic Conditions
2.1. Constant-Order Model
2.2. Variable-Order Fractional Calculus
- Case no memory of order
- Case memory of orderor
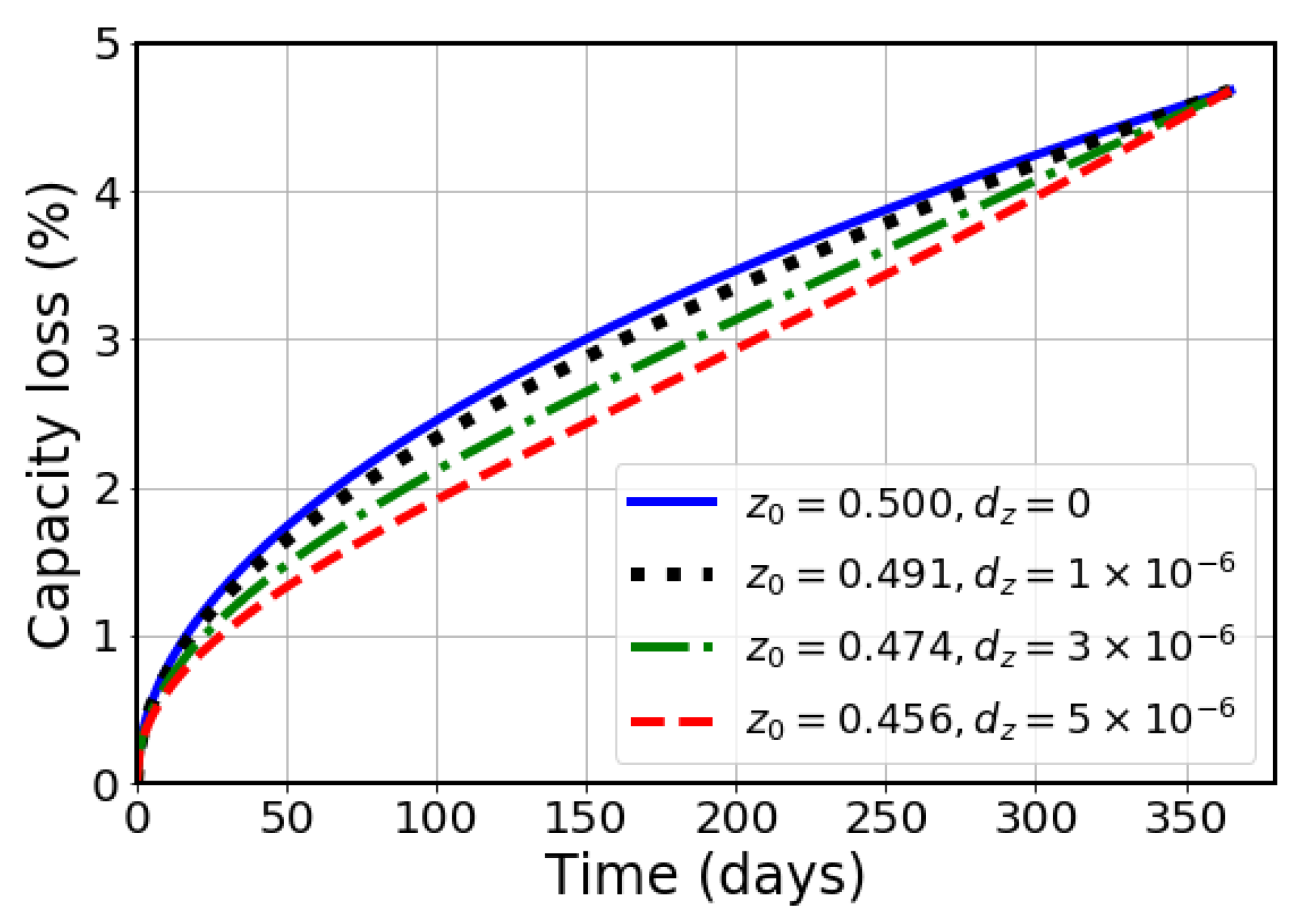
2.3. Variable-Order Model
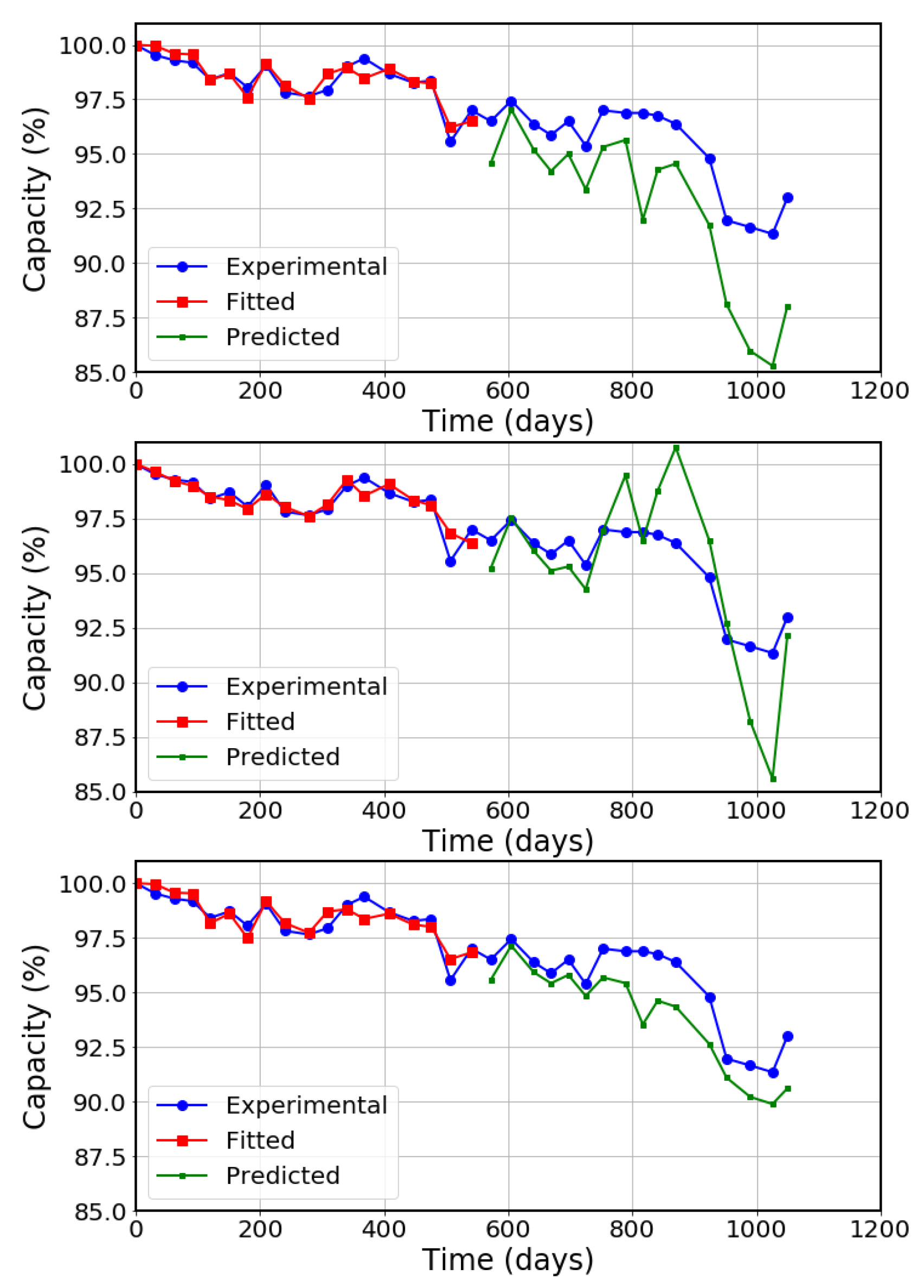
3. Validation Method
4. Comparison with Experimental Results
5. Discussion on Results and Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature | Description |
| Parameter for the SOC dependence in semiempirical model | |
| Slope of order exponent vs. time | |
| Fraction of abandoned nests in Cuckoo search algorithm | |
| Slope of order exponent vs. time with time reference equal to one hour | |
| Slope of order exponent vs. time with time reference equal to one day | |
| Riemann–Liouville integral of order z | |
| Riemann–Liouville integral with variable order | |
| Activation energy | |
| Root-mean-square error | |
| f | General function in integral definitions |
| Fitness in Cuckoo search algorithm | |
| F | Faraday constant |
| Gamma function | |
| Pre-exponential factor in semiempirical model | |
| K | Aging rate, also named stress factor. It is a function of SOC and temperature |
| K function with time unit equal to one day | |
| K function with time unit equal to one hour | |
| Constant K function within subinterval | |
| L | Capacity loss |
| Experimental capacity loss measured at | |
| Capacity loss provided by the model at | |
| n | Number of nests (population size) in Cuckoo search algorithm |
| Q | Battery cell capacity |
| Capacity of a non-aged cell | |
| Universal gas constant | |
| State of charge | |
| t | Time |
| Limits of the time subintervals | |
| Maximum time of measurement | |
| Time reference used as a unit of time for calculation of capacity loss | |
| T | Absolute temperature |
| Reference temperature in semiempirical K model | |
| Dummy variable in Riemann–Liouville integrals | |
| Negative electrode potential as a function of | |
| Reference electrode potential in semiempirical K model | |
| z | Order exponent |
| Time-dependent order exponent | |
| Order exponent dependent on an arbitrary function | |
| Order exponent at time | |
| Order exponent at with time reference equal to one hour | |
| Order exponent at with time reference equal to one day | |
| Fractional-order circuit element |
References
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Stampatori, D.; Raimondi, P.P.; Noussan, M. Li-Ion Batteries: A Review of a Key Technology for Transport Decarbonization. Energies 2020, 13, 2638. [Google Scholar] [CrossRef]
- Berckmans, G.; Messagie, M.; Smekens, J.; Omar, N.; Vanhaverbeke, L.; Van Mierlo, J. Cost Projection of State of the Art Lithium-Ion Batteries for Electric Vehicles Up to 2030. Energies 2017, 10, 1314. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Li, P.; Lin, X.; Bian, X. Data-Driven Battery State of Health Estimation Based on Random Partial Charging Data. IEEE Trans. Power Electron. 2022, 37, 5021–5031. [Google Scholar] [CrossRef]
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Liu, K.; Camblong, H.; Widanage, W.; Marco, J. Data-driven nonparametric Li-ion battery ageing model aiming at learning from real operation data—Part A: Storage operation. J. Energy Storage 2020, 30, 101409. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Liu, K.; Camblong, H.; Widanage, W.; Marco, J. Data-driven nonparametric Li-ion battery ageing model aiming at learning from real operation data—Part B: Cycling operation. J. Energy Storage 2020, 30, 101410. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Sources 2014, 248, 839–851. [Google Scholar] [CrossRef]
- de Hoog, J.; Timmermans, J.M.; Ioan-Stroe, D.; Swierczynski, M.; Jaguemont, J.; Goutam, S.; Omar, N.; Van Mierlo, J.; Van Den Bossche, P. Combined cycling and calendar capacity fade modeling of a Nickel-Manganese-Cobalt Oxide Cell with real-life profile validation. Appl. Energy 2017, 200, 47–61. [Google Scholar] [CrossRef]
- Grolleau, S.; Delaille, A.; Gualous, H.; Gyan, P.; Revel, R.; Bernard, J.; Redondo-Iglesias, E.; Peter, J. Calendar aging of commercial graphite/LiFePO4 cell – Predicting capacity fade under time dependent storage conditions. J. Power Sources 2014, 255, 450–458. [Google Scholar] [CrossRef]
- Bloom, I.; Cole, B.W.; Sohn, J.J.; Jones, S.A.; Polzin, E.G.; Battaglia, V.S.; Henriksen, G.L.; Motloch, C.; Richardson, R.; Unkelhaeuser, T.; et al. An accelerated calendar and cycle life study of Li-ion cells. J. Power Sources 2001, 101, 238–247. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Global Model for Self-Discharge and Capacity Fade in Lithium-Ion Batteries Based on the Generalized Eyring Relationship. IEEE Trans. Veh. Technol. 2018, 67, 104–113. [Google Scholar] [CrossRef]
- Schimpe, M.; von Kuepach, M.E.; Naumann, M.; Hesse, H.C.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A holistic aging model for Li(NiMnCo)O2 based 18650 lithium-ion batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a lifetime prediction model for lithium-ion batteries based on extended accelerated aging test data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Broussely, M.; Herreyre, S.; Biensan, P.; Kasztejna, P.; Nechev, K.; Staniewicz, R. Aging mechanism in Li ion cells and calendar life predictions. J. Power Sources 2001, 97, 13–21. [Google Scholar] [CrossRef]
- Petit, M.; Prada, E.; Sauvant-Moynot, V. Development of an empirical aging model for Li-ion batteries and application to assess the impact of Vehicle-to-Grid strategies on battery lifetime. Appl. Energy 2016, 172, 398–407. [Google Scholar] [CrossRef]
- Naumann, M.; Schimpe, M.; Keil, P.; Hesse, H.C.; Jossen, A. Analysis and modeling of calendar aging of a commercial LiFePO4/graphite cell. J. Energy Storage 2018, 17, 153–169. [Google Scholar] [CrossRef]
- Hahn, S.L.; Storch, M.; Swaminathan, R.; Obry, B.; Bandlow, J.; Birke, K.P. Quantitative validation of calendar aging models for lithium-ion batteries. J. Power Sources 2018, 400, 402–414. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- Sarasketa-Zabala, E.; Gandiaga, I.; Rodriguez-Martinez, L.; Villarreal, I. Calendar ageing analysis of a LiFePO4/graphite cell with dynamic model validations: Towards realistic lifetime predictions. J. Power Sources 2014, 272, 45–57. [Google Scholar] [CrossRef]
- Redondo-Iglesias, E.; Venet, P.; Pelissier, S. Eyring acceleration model for predicting calendar ageing of lithium-ion batteries. J. Energy Storage 2017, 13, 176–183. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, K.; Pan, Y.; Wang, H.; Li, Y.; Zheng, C. Simplified modeling and parameter estimation to predict calendar life of Li-ion batteries. Solid State Ionics 2018, 320, 126–131. [Google Scholar] [CrossRef]
- Shi, N.; Chen, Z.; Niu, M.; He, Z.; Wang, Y.; Cui, J. State-of-charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification. J. Energy Storage 2022, 45, 103518. [Google Scholar] [CrossRef]
- Mathieu, R.; Baghdadi, I.; Briat, O.; Gyan, P.; Vinassa, J.M. D-optimal design of experiments applied to lithium battery for ageing model calibration. Energy 2017, 141, 2108–2119. [Google Scholar] [CrossRef]
- Gasper, P.; Gering, K.; Dufek, E.; Smith, K. Challenging Practices of Algebraic Battery Life Models through Statistical Validation and Model Identification via Machine-Learning. J. Electrochem. Soc. 2021, 168, 020502. [Google Scholar] [CrossRef]
- Khaleghi Rahimian, S.; Forouzan, M.M.; Han, S.; Tang, Y. A generalized physics-based calendar life model for Li-ion cells. Electrochim. Acta 2020, 348, 136343. [Google Scholar] [CrossRef]
- Su, L.; Zhang, J.; Huang, J.; Ge, H.; Li, Z.; Xie, F.; Liaw, B.Y. Path dependence of lithium ion cells aging under storage conditions. J. Power Sources 2016, 315, 35–46. [Google Scholar] [CrossRef]
- Thomas, E.; Bloom, I.; Christophersen, J.; Battaglia, V. Rate-based degradation modeling of lithium-ion cells. J. Power Sources 2012, 206, 378–382. [Google Scholar] [CrossRef]
- Mingant, R.; Petit, M.; Belaïd, S.; Bernard, J. Data-driven model development to predict the aging of a Li-ion battery pack in electric vehicles representative conditions. J. Energy Storage 2021, 39, 102592. [Google Scholar] [CrossRef]
- Lucu, M.; Martinez-Laserna, E.; Gandiaga, I.; Camblong, H. A critical review on self-adaptive Li-ion battery ageing models. J. Power Sources 2018, 401, 85–101. [Google Scholar] [CrossRef]
- López-Villanueva, J.A.; Iturriaga, P.R.; Rodríguez-Bolívar, S. A fractional-order model for calendar aging with dynamic storage conditions. J. Energy Storage 2022, 50, 104537. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Bonfanti, A.; Kaplan, J.L.; Charras, G.; Kabla, A. Fractional viscoelastic models for power-law materials. Soft Matter 2020, 16, 6002–6020. [Google Scholar] [CrossRef]
- Sabatier, J. Fractional Order Models Are Doubly Infinite Dimensional Models and thus of Infinite Memory: Consequences on Initialization and Some Solutions. Symmetry 2021, 13, 1099. [Google Scholar] [CrossRef]
- Wang, M.; Xu, X.; Liu, Q.; Ding, Y.; Shen, F. A nonlinear fractional-order damage model of stress relaxation of net-like red soil. Sci. Rep. 2021, 11, 22917. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, C.; Han, B.; Duan, Z. A creep constitutive model for salt rock based on fractional derivatives. Int. J. Rock Mech. Min. Sci. 2011, 48, 116–121. [Google Scholar] [CrossRef]
- Andre, D.; Meiler, M.; Steiner, K.; Walz, H.; Soczka-Guth, T.; Sauer, D.U. A retrospective on lithium-ion batteries. J. Power Sources 2011, 196, 5349–5356. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Wik, T.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
- Hu, X.; Yuan, H.; Zou, C.; Li, Z.; Zhang, L. Co-Estimation of State of Charge and State of Health for Lithium-Ion Batteries Based on Fractional-Order Calculus. IEEE Trans. Veh. Technol. 2018, 67, 10319–10329. [Google Scholar] [CrossRef]
- Meddings, N.; Heinrich, M.; Overney, F.; Lee, J.S.; Ruiz, V.; Napolitano, E.; Seitz, S.; Hinds, G.; Raccichini, R.; Gaberšček, M.; et al. Application of electrochemical impedance spectroscopy to commercial Li-ion cells: A review. J. Power Sources 2020, 480, 228742. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fraction Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Academic Press: San Diego, CA, USA, 1999; pp. 1–316. [Google Scholar]
- Petras, I. Fractional-Order Nonlinear Systems. Modeling, Analysis and Simulation; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- López-Villanueva, J.A.; Rodríguez Bolívar, S. Constant Phase Element in the Time Domain: The Problem of Initialization. Energies 2022, 15, 792. [Google Scholar] [CrossRef]
- López-Villanueva, J.A.; Rodríguez-Iturriaga, P.; Parrilla, L.; Rodríguez-Bolívar, S. A compact model of the ZARC for circuit simulators in the frequency and time domains. AEU Int. J. Electron. Commun. 2022, 154293. [Google Scholar] [CrossRef]
- Rodríguez-Iturriaga, P.; del Valle, J.A.; Rodríguez-Bolívar, S.; Anseán, D.; Viera, J.C.; López-Villanueva, J.A. A novel Dual Fractional-Order Extended Kalman Filter for the improved estimation of battery state of charge. J. Energy Storage 2022, 56, 105810. [Google Scholar] [CrossRef]
- Patnaik, S.; Hollkamp, J.P.; Semperlotti, F. Applications of variable-order fractional operators: A review. Proc. R. Soc. A-Math. Phys. Eng. Sci. 2020, 476, 20190498. [Google Scholar] [CrossRef]
- Wu, F.; Liu, J.F.; Wang, J. An improved Maxwell creep model for rock based on variable-order fractional derivatives. Environ. Earth Sci. 2015, 73, 6965–6971. [Google Scholar] [CrossRef]
- Patnaik, S.; Semperlotti, F. Variable-order fracture mechanics and its application to dynamic fracture. NPJ Comput. Mater. 2021, 7, 27. [Google Scholar] [CrossRef]
- Samko, S. Fractional integration and differentiation of variable order: An overview. Nonlinear Dyn. 2013, 71, 653–662. [Google Scholar] [CrossRef]
- Lorenzo, C.F.; Hartley, T. Variable order and distributed order fractional operators. Nonlinear Dyn. 2002, 29, 57–98. [Google Scholar] [CrossRef]
- Diethelm, K. A fractional calculus based model for the simulation of an outbreak of dengue fever. Nonlinear Dyn. 2013, 71, 613–619. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Modeling of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A562. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering optimization by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar]
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2013, 39, 315–346. [Google Scholar] [CrossRef]
- AbdelAty, A.; Fouda, M.E.; Elbarawy, M.T.; Radwan, A. Optimal charging of fractional-order circuits with Cuckoo search. J. Adv. Res. 2021, 32, 119–131. [Google Scholar] [CrossRef]
- Yang, X.S. Chapter 9—Cuckoo Search. In Nature-Inspired Optimization Algorithms; Yang, X.S., Ed.; Elsevier: Oxford, UK, 2014; pp. 129–139. [Google Scholar] [CrossRef]
- Liaw, B.Y.; Roth, E.; Jungst, R.G.; Nagasubramanian, G.; Case, H.L.; Doughty, D.H. Correlation of Arrhenius behaviors in power and capacity fades with cell impedance and heat generation in cylindrical lithium-ion cells. J. Power Sources 2003, 119, 874–886. [Google Scholar] [CrossRef]
- Rumberg, B.; Epding, B.; Stradtmann, I.; Schleder, M.; Kwade, A. Holistic calendar aging model parametrization concept for lifetime prediction of graphite/NMC lithium-ion cells. J. Energy Storage 2020, 30, 101510. [Google Scholar] [CrossRef]
- Käbitz, S.; Gerschler, J.B.; Ecker, M.; Yurdagel, Y.; Emmermacher, B.; André, D.; Mitsch, T.; Sauer, D.U. Cycle and calendar life study of a graphite|LiNi1/3Mn1/3Co1/3O2 Li-ion high energy system. Part A: Full cell characterization. J. Power Sources 2013, 239, 572–583. [Google Scholar] [CrossRef]





| Order | [J/mol] | [h ] | ||||
|---|---|---|---|---|---|---|
| Constant | 2.181 | 51,810 | 0.687 | 0 | 5.05% | |
| Variable | 0.701 | 29,025 | 0.300 | 2.94% |
| Case | (J/mol) | (h ) | ||||
|---|---|---|---|---|---|---|
| 0.0983 | 10,543 | 0.658 | ||||
| 0.989 | 26,079 | 0.134 | 3.53% |
| Case | (J/mol) | (h ) | (725 Days) | (1050 Days) | |||
|---|---|---|---|---|---|---|---|
| 0.930 | 17,037 | 0.235 | 8.26% | ||||
| 0.239 | 51,493 | 0.508 | 5.84% | 9.06% | |||
| 0.981 | 21,675 | 0.155 | 4.82% | 6.49% |
| Case | (J/mol) | (h ) | (1050 Days) | |||
|---|---|---|---|---|---|---|
| 15,080 | 3.30% | |||||
| 7328 | 5.15% | |||||
| 17,152 | 3.67% |
| (kJ/mol) | Positive Electrode | Ref. |
|---|---|---|
| 50–55 kJ/mol | NCA | [59] |
| 43.6 kJ/mol | NMC | [61] |
| 47–60 kJ/mol | NMC | [8] |
| 52.1 kJ/mol, 182 kJ/mol | LFP | [10] |
| 35.64 kJ/mol | LFP | [21] |
| 58.0 kJ/mol | NMC | [14] |
| 56.94–73.37 kJ/mol | LFP | [17] |
| 52.86 kJ/mol | NCA | [17] |
| 84.88 kJ/mol | LFP | [12] |
| 27.7–28.7 kJ/mol | NMC | [19] |
| 17.13 kJ/mol | LFP | [18] |
| 79.57 kJ/mol | NMC | [12] |
| 20.59 kJ/mol | LFP | [13] |
| 42.7–44.9 kJ/mol | NMC | [60] |
| 36.36 kJ/mol | NMC | [24] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Villanueva, J.A.; Rodríguez-Iturriaga, P.; Parrilla, L.; Rodríguez-Bolívar, S. Application of Variable-Order Fractional Calculus to the Modeling of Calendar Aging in Lithium-Ion Batteries. Energies 2023, 16, 2484. https://doi.org/10.3390/en16052484
López-Villanueva JA, Rodríguez-Iturriaga P, Parrilla L, Rodríguez-Bolívar S. Application of Variable-Order Fractional Calculus to the Modeling of Calendar Aging in Lithium-Ion Batteries. Energies. 2023; 16(5):2484. https://doi.org/10.3390/en16052484
Chicago/Turabian StyleLópez-Villanueva, Juan Antonio, Pablo Rodríguez-Iturriaga, Luis Parrilla, and Salvador Rodríguez-Bolívar. 2023. "Application of Variable-Order Fractional Calculus to the Modeling of Calendar Aging in Lithium-Ion Batteries" Energies 16, no. 5: 2484. https://doi.org/10.3390/en16052484
APA StyleLópez-Villanueva, J. A., Rodríguez-Iturriaga, P., Parrilla, L., & Rodríguez-Bolívar, S. (2023). Application of Variable-Order Fractional Calculus to the Modeling of Calendar Aging in Lithium-Ion Batteries. Energies, 16(5), 2484. https://doi.org/10.3390/en16052484






