Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids
Abstract
:1. Introduction
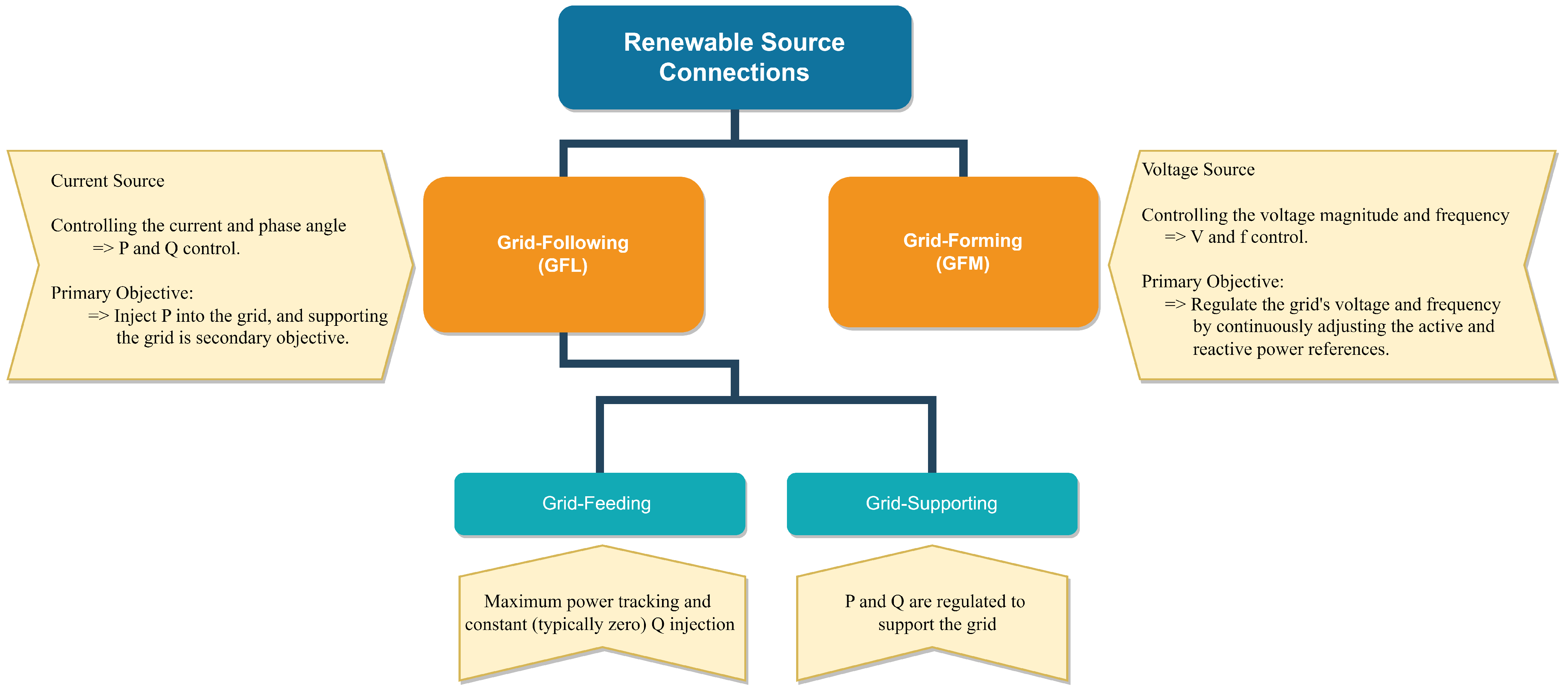
2. Classification of Renewable Source Connections to the Power Systems
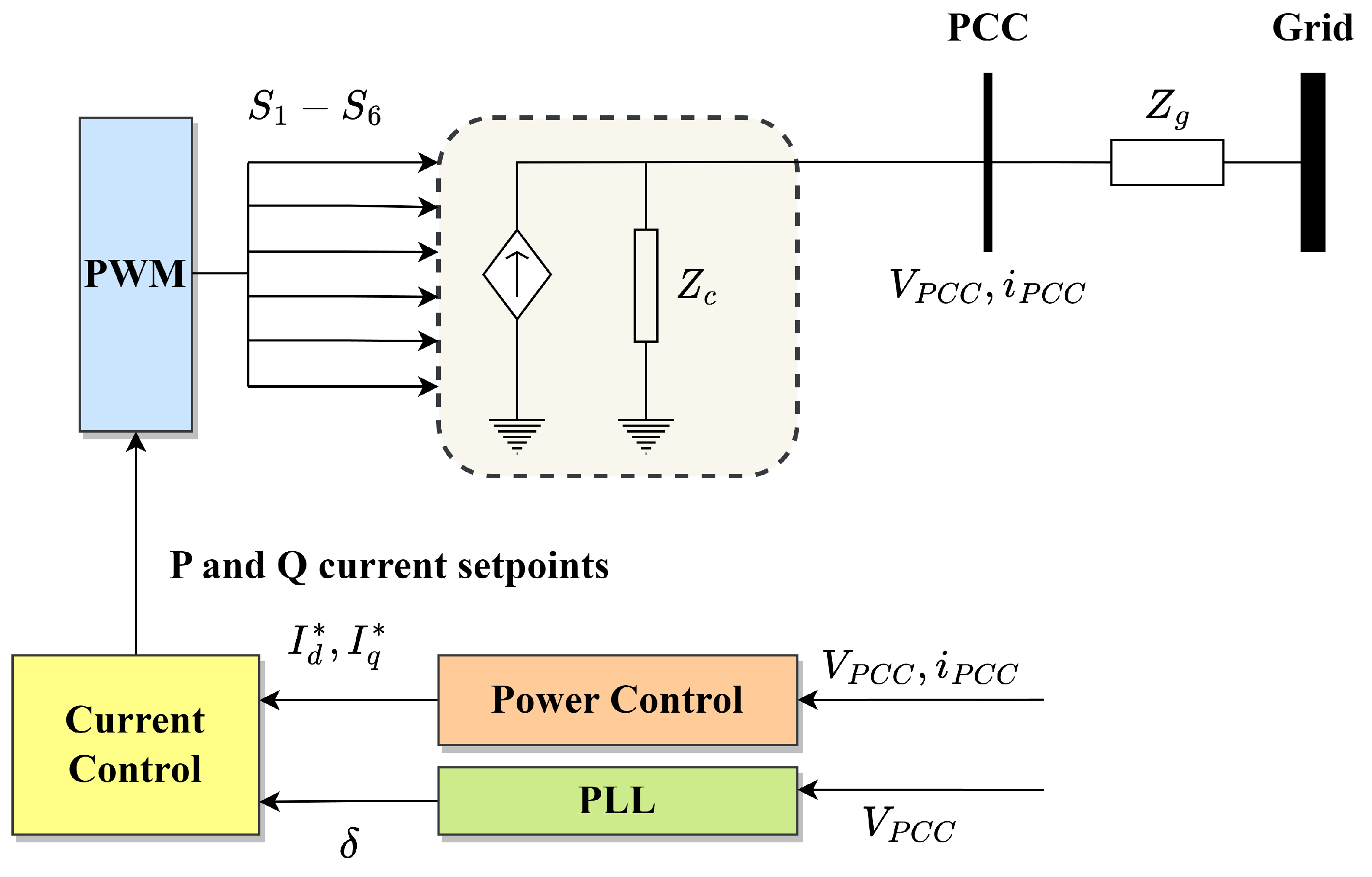
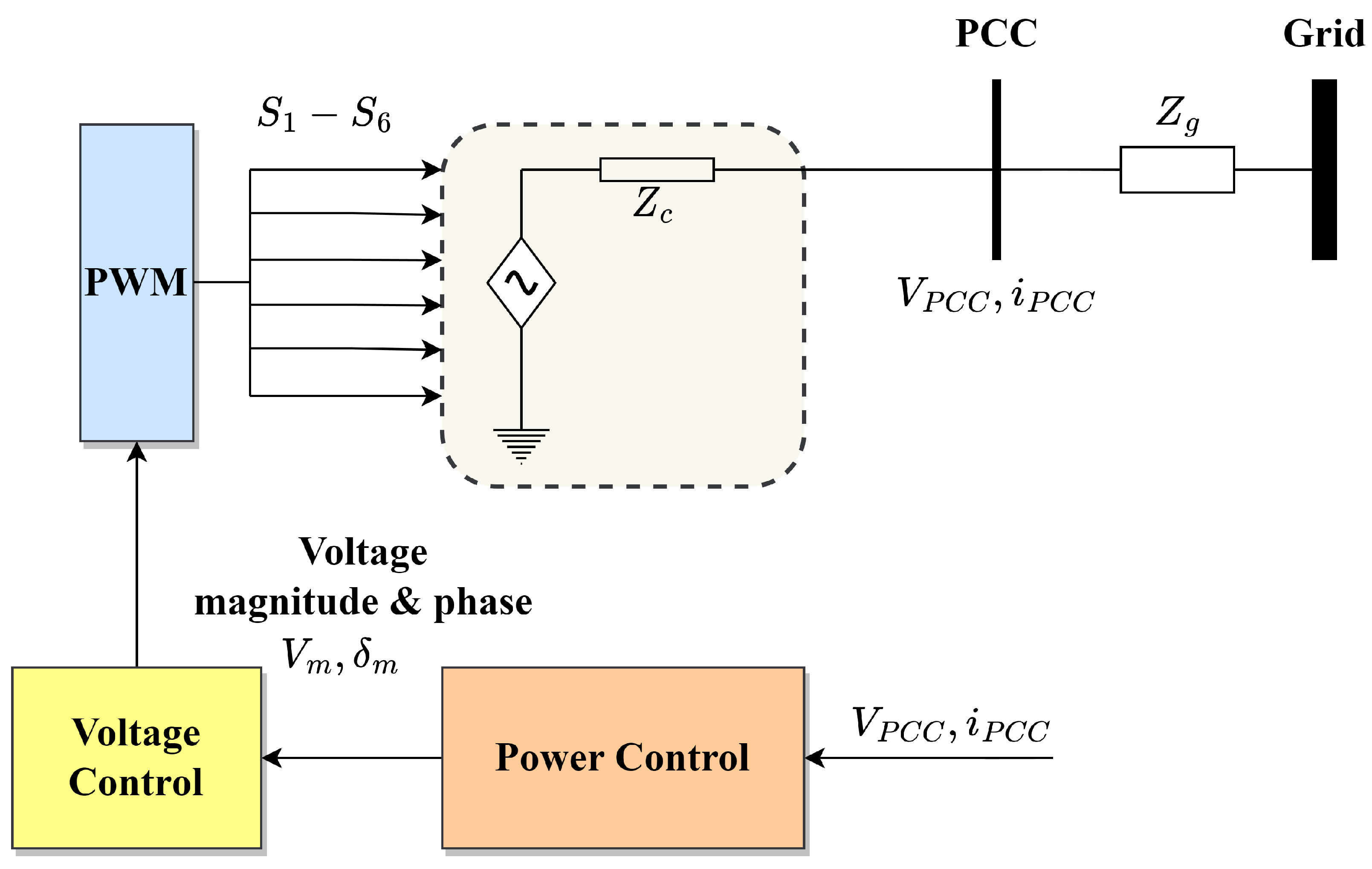
3. Voltage Source Converter/Inverter Topologies
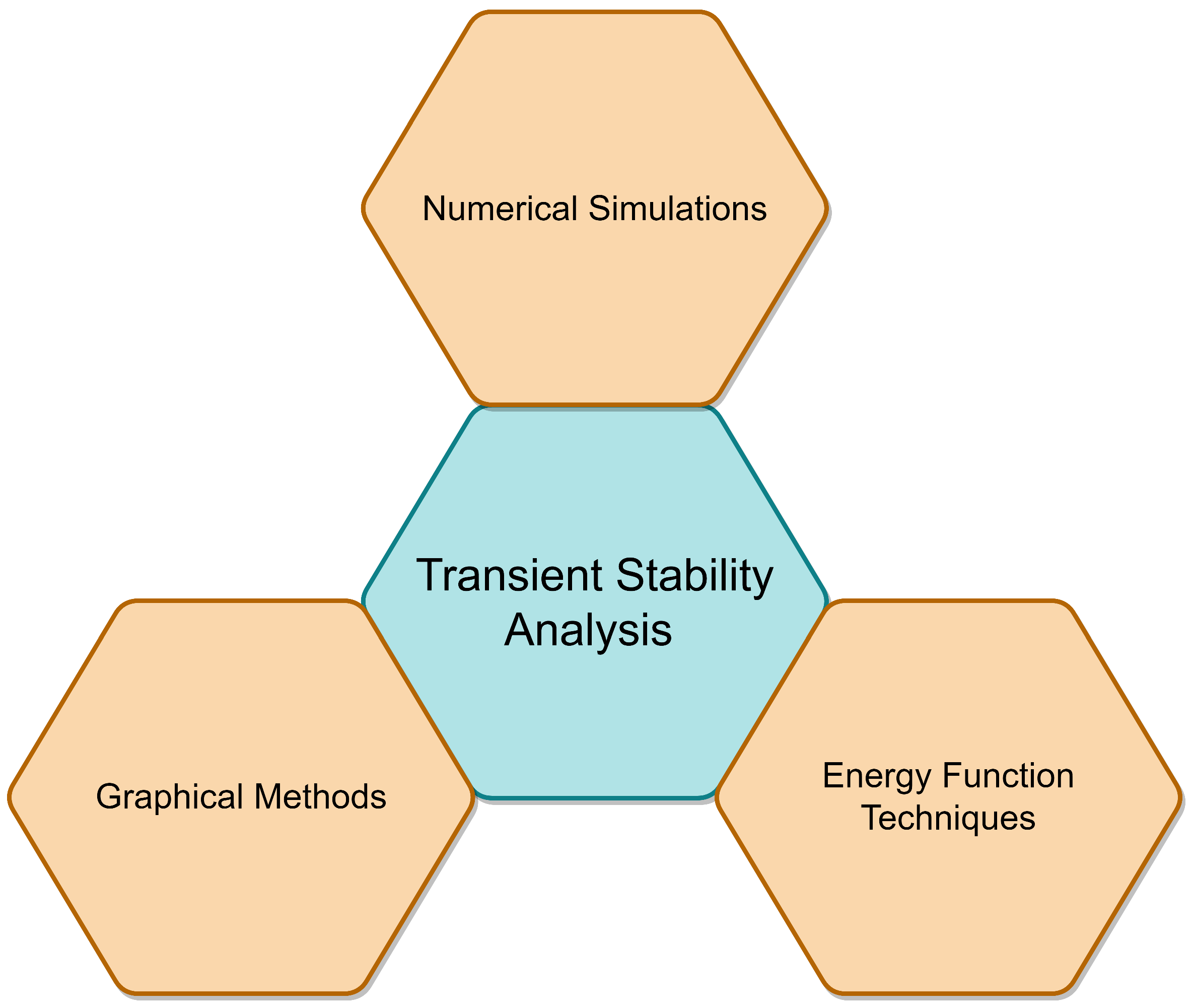
4. Transient Stability Analysis Methods
4.1. Time Domain-Based Numerical Simulation Techniques
4.2. Energy Domain-Based Energy Function Techniques
4.3. Graphical Techniques
5. Transient Stability Enhancement Techniques
5.1. Grid-Following Systems
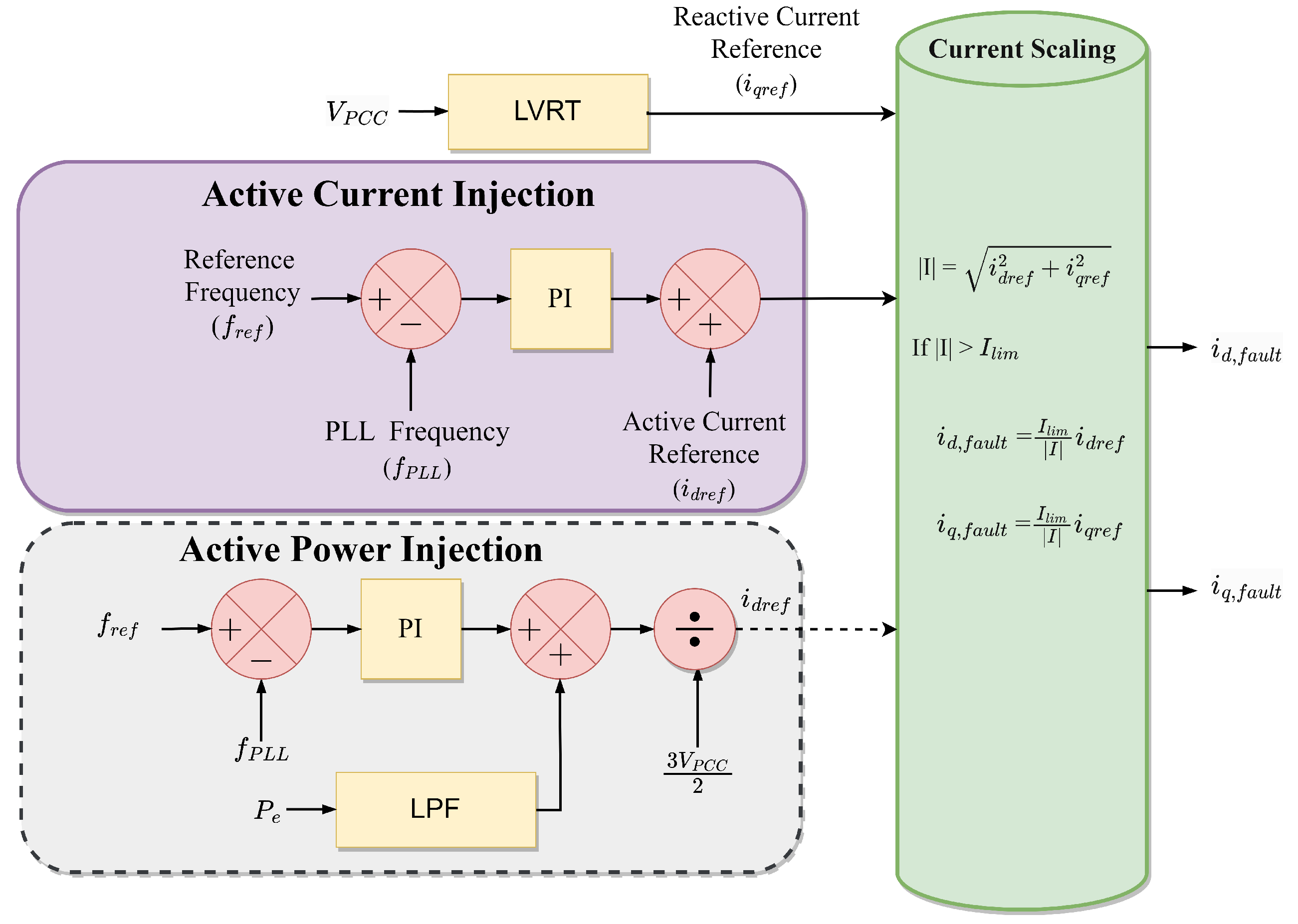
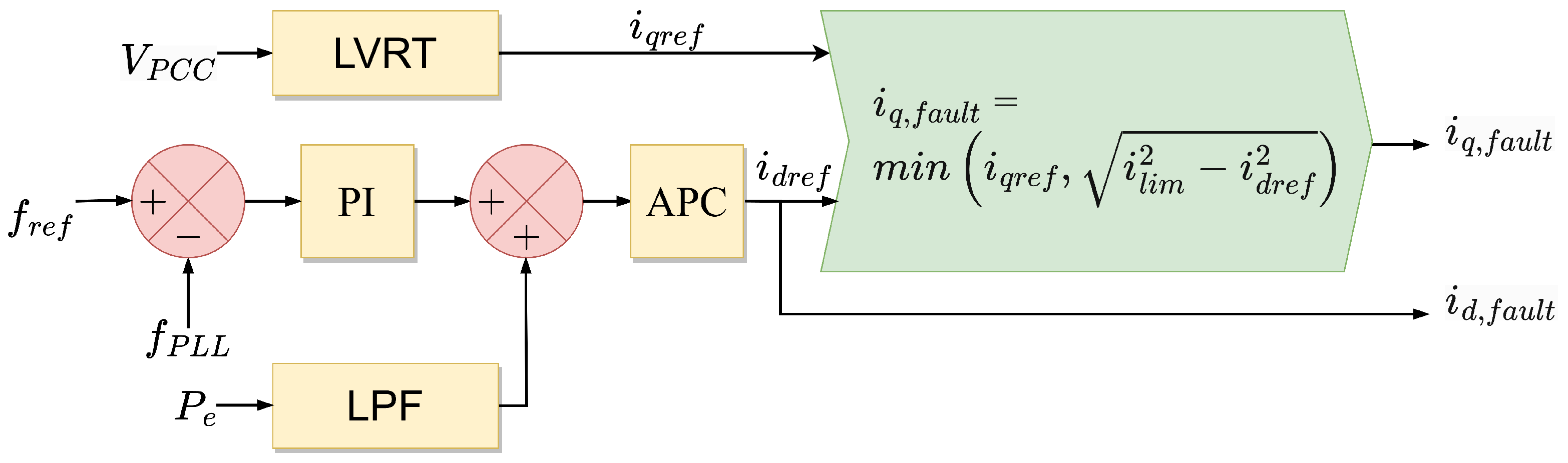
5.1.1. Modify Active Current or Power
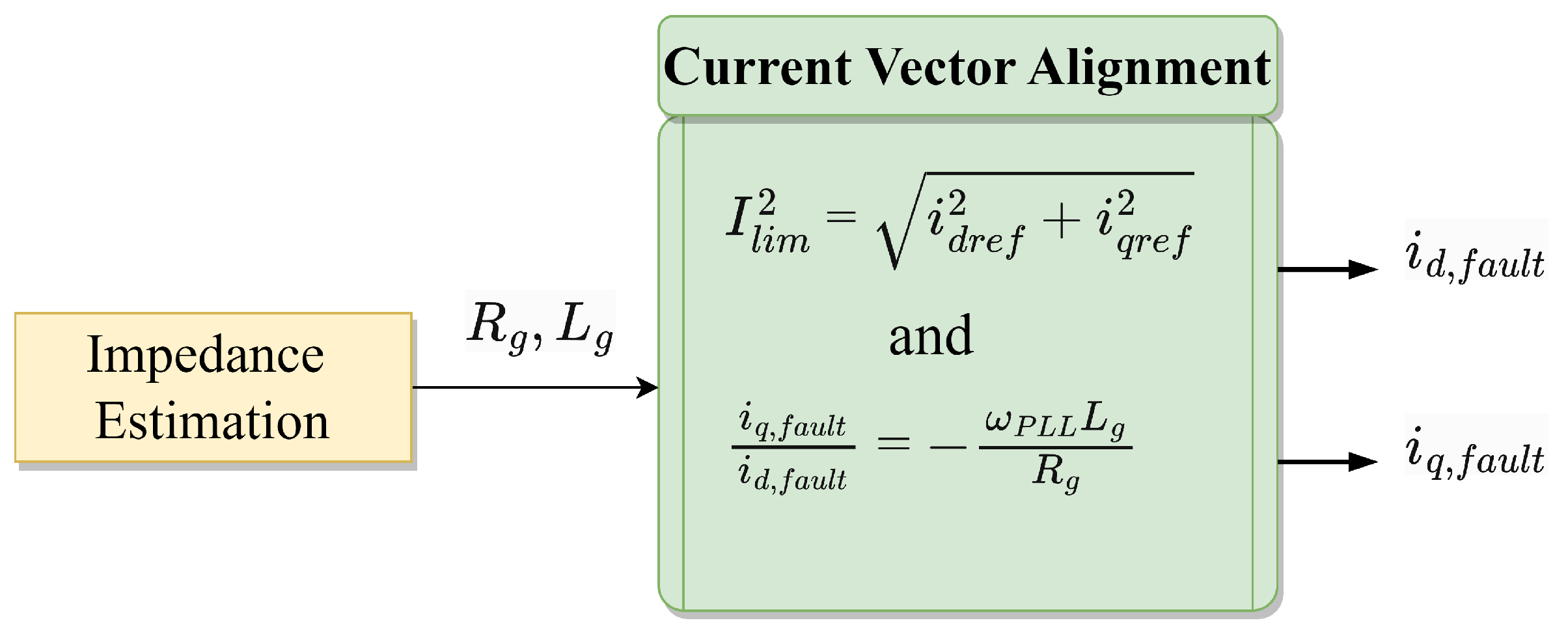
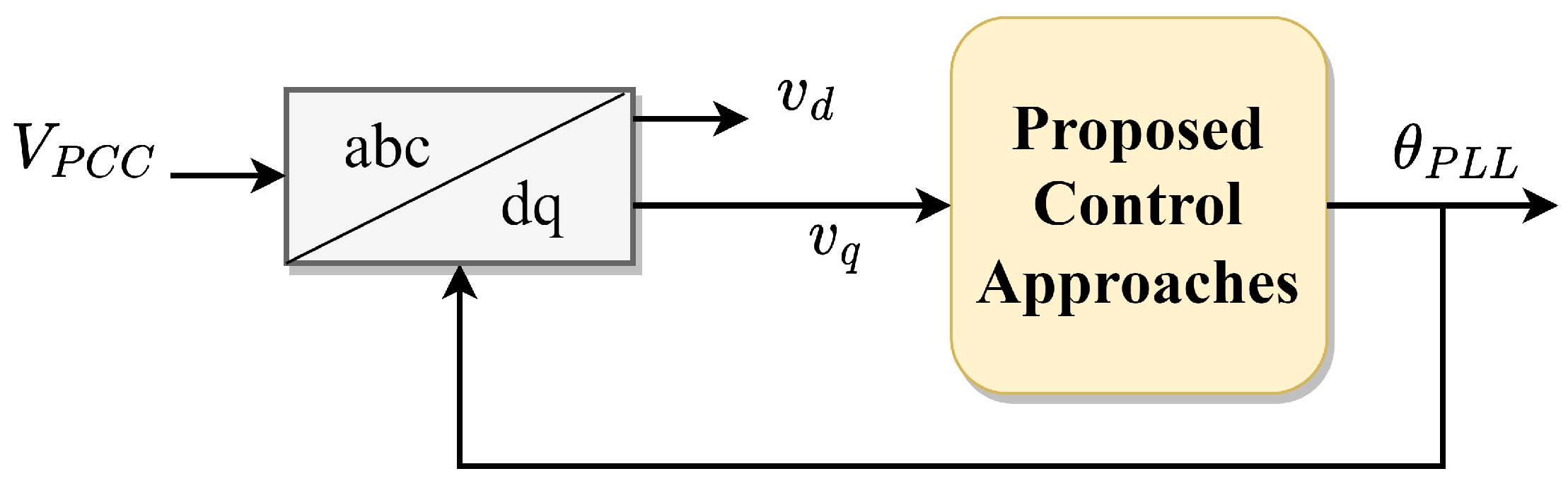
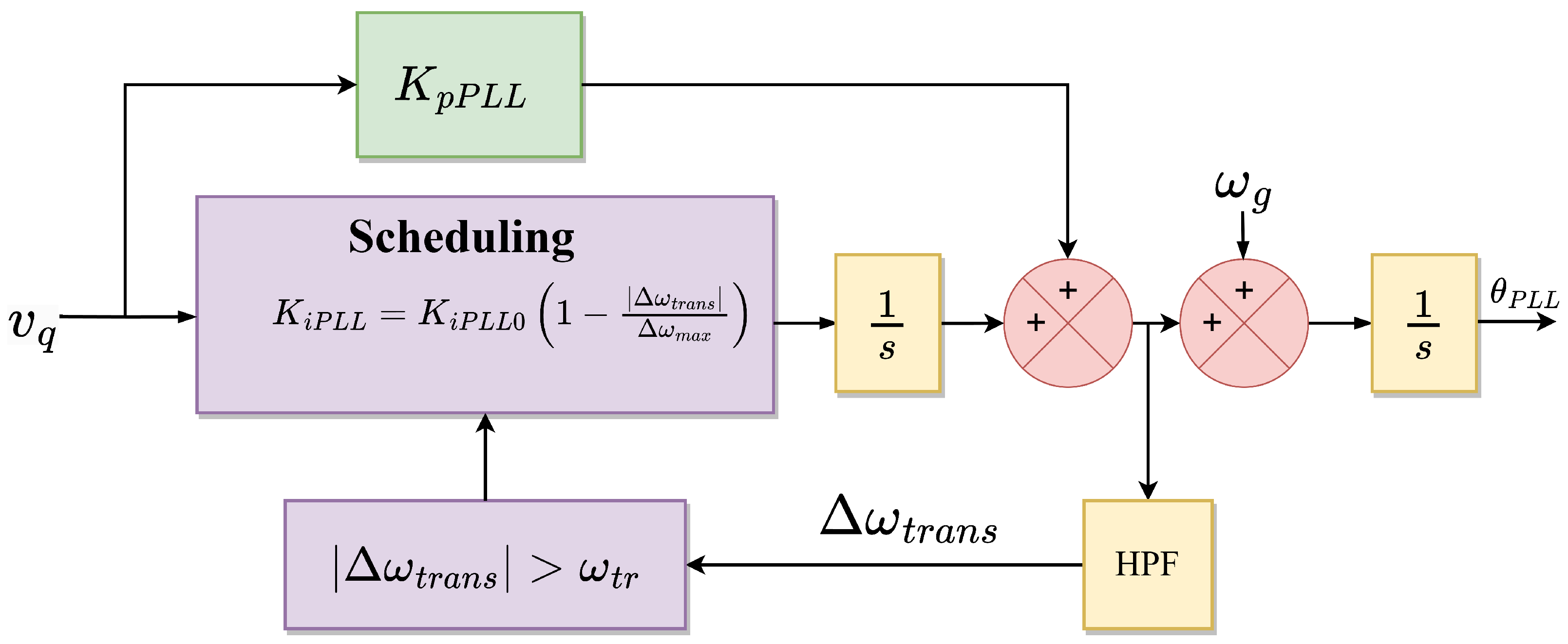
5.1.2. Modify Synchronization Loop
5.2. Grid-Forming Systems
5.2.1. Modify Active and Reactive Power Reference
5.2.2. Modify Control Loops
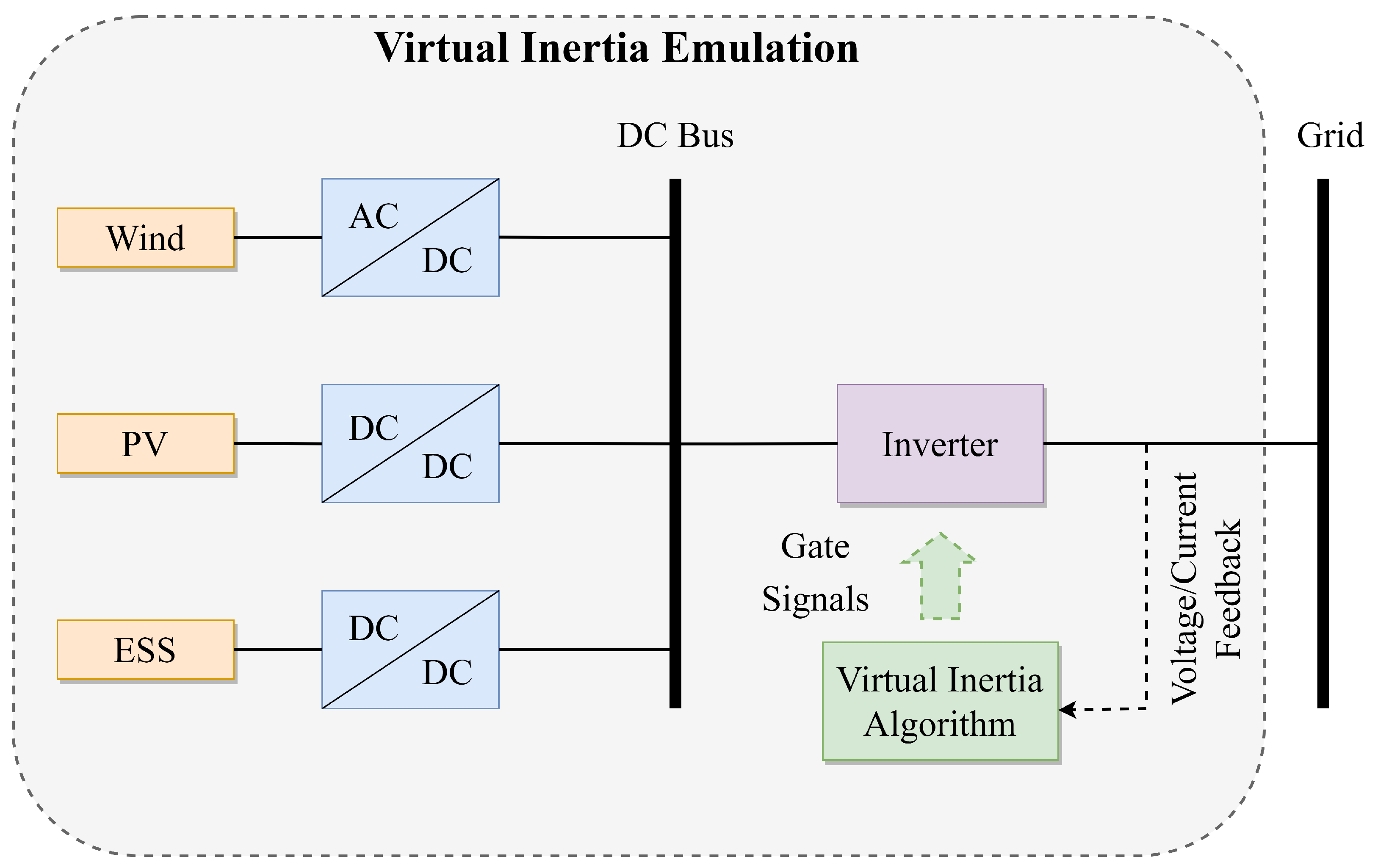
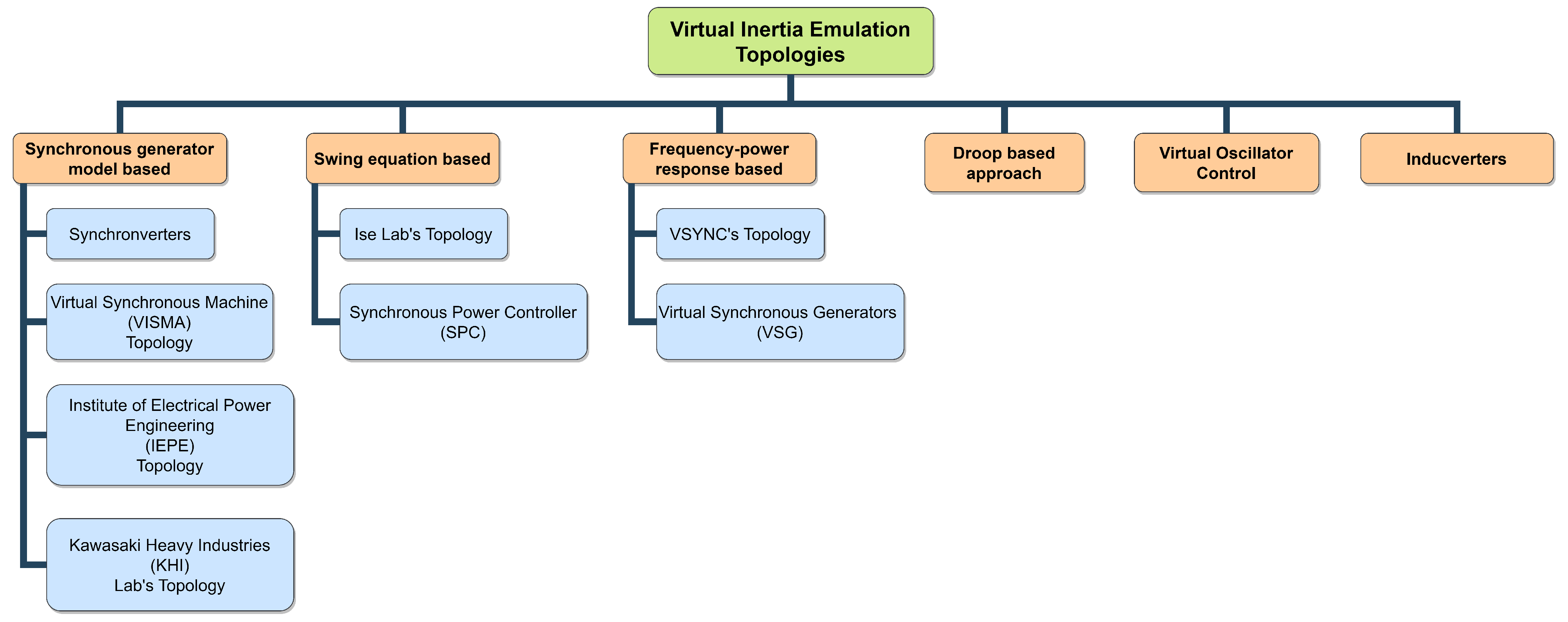
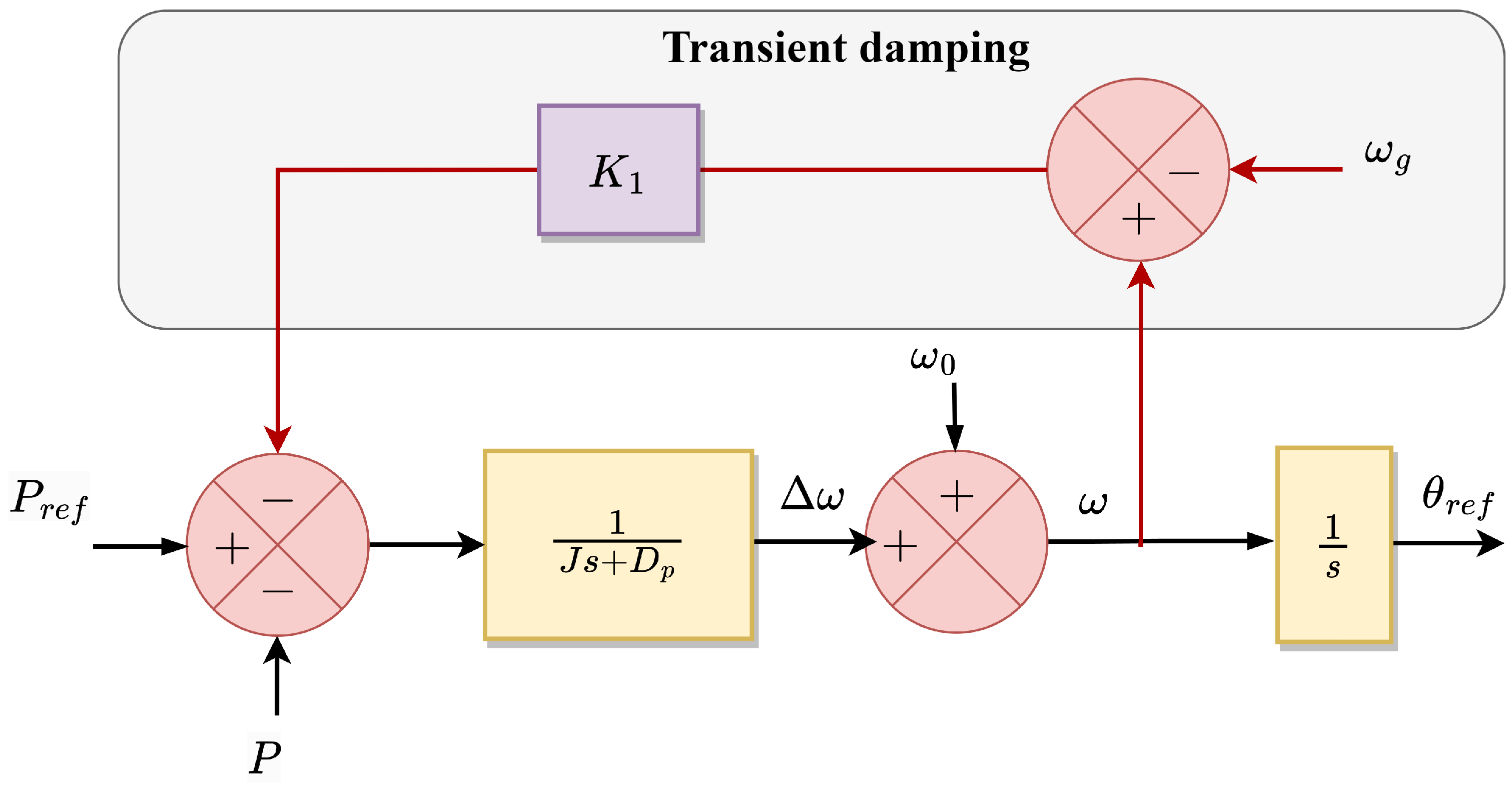
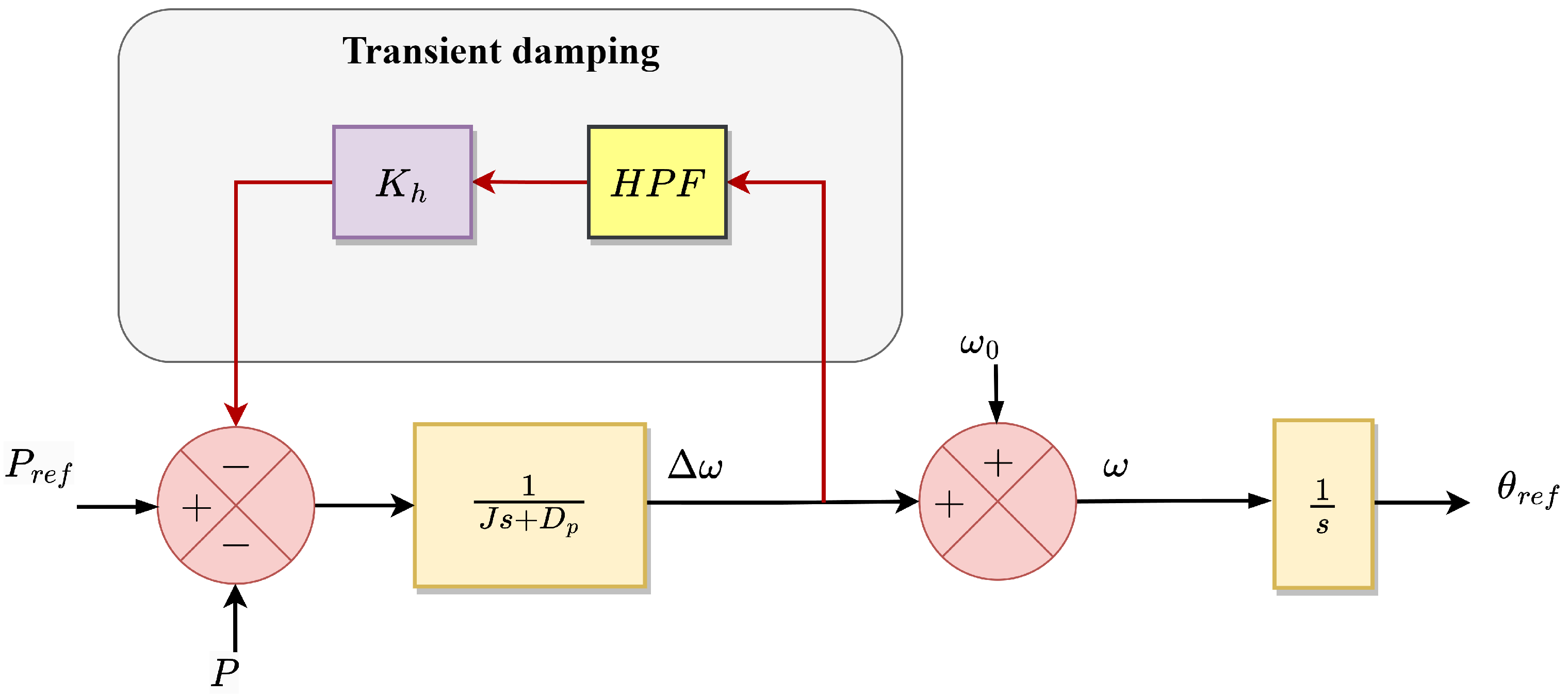
5.2.3. Modify Moment of Inertia and Damping Parameters
5.2.4. Employing Inverter Current Limits
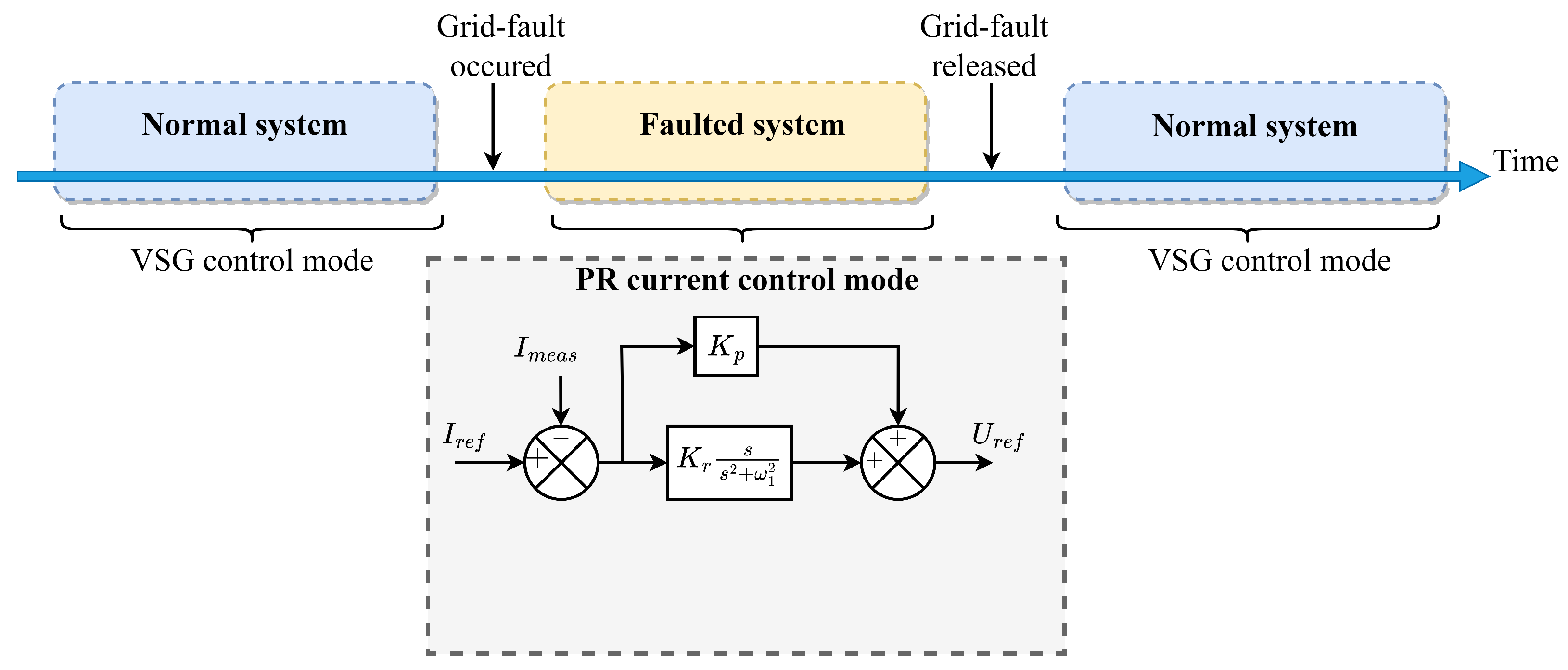
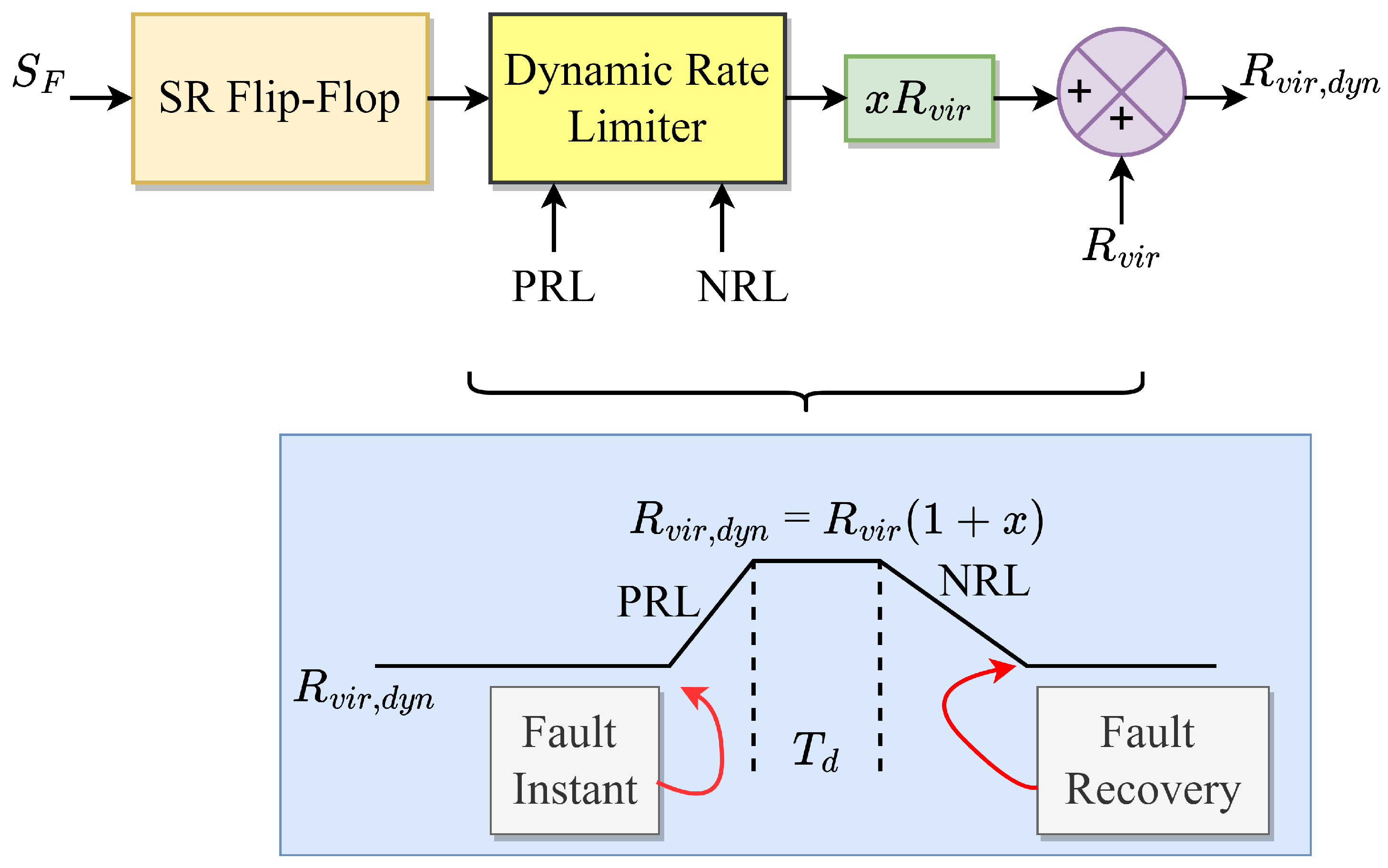
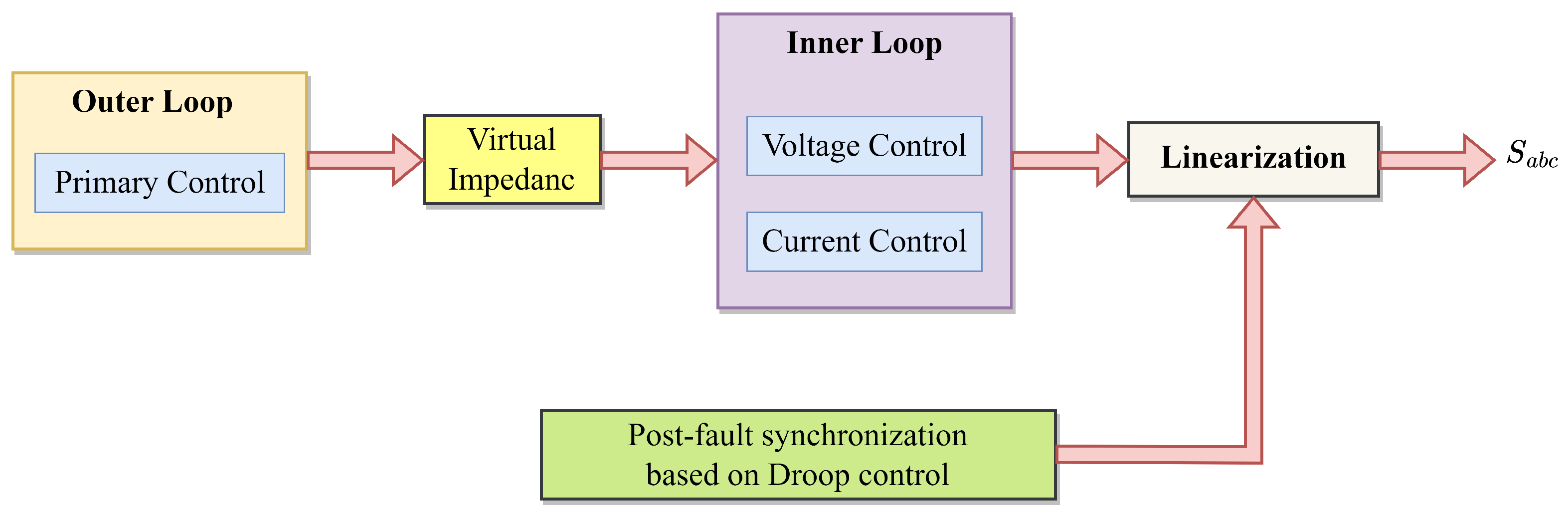
5.2.5. Current Limits along with Post-Fault Enhancement Controls
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Renewable Energy Resources | |
| Grid-Following | |
| Grid-Forming | |
| Synchronous Generator | |
| Power Electronic | |
| Voltage Source Converter | |
| Voltage Source Inverter | |
| Vector Current Control | |
| Direct and Quadrature | |
| Phase Locked Loop | |
| Maximum Power Point Tracking | |
| Point of Common Coupling | |
| Active Power Controller | |
| Reactive Power Controller | |
| Equal Area Criteria | |
| Transient Energy Function | |
| Single Machine Infinite Bus | |
| Loss of Synchronization | |
| Proportional Integral | |
| High Pass Filter | |
| Low Pass Filter | |
| Virtual Synchronous Generator | |
| Automatic Voltage Regulator | |
| Rate of Change of Frequency | |
| Critical Clearing Time | |
| Critical Clearing Angle | |
| Electromagnetic Transient | |
| Differential-Algebraic Equation | |
| Low Voltage Ride Through | |
| Transient Damping Method | |
| Proportional Resonance | |
| Positive Rate Limiter | |
| Negative Rate Limiter | |
| Virtual Resistance |
References
- Lin, Y.; Eto, J.H.; Johnson, B.B.; Flicker, J.D.; Lasseter, R.H.; Villegas Pico, H.N.; Seo, G.S.; Pierre, B.J.; Ellis, A. Research Roadmap on Grid-Forming Inverters; Technical Report; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2020. [Google Scholar]
- Infield, D.; Freris, L. Renewable Energy in Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Peng, Q.; Jiang, Q.; Yang, Y.; Liu, T.; Wang, H.; Blaabjerg, F. On the stability of power electronics-dominated systems: Challenges and potential solutions. IEEE Trans. Ind. Appl. 2019, 55, 7657–7670. [Google Scholar] [CrossRef]
- Kroposki, B.; Johnson, B.; Zhang, Y.; Gevorgian, V.; Denholm, P.; Hodge, B.M.; Hannegan, B. Achieving a 100% renewable grid: Operating electric power systems with extremely high levels of variable renewable energy. IEEE Power Energy Mag. 2017, 15, 61–73. [Google Scholar] [CrossRef]
- Jacobson, M.Z.; Delucchi, M.A.; Bauer, Z.A.; Goodman, S.C.; Chapman, W.E.; Cameron, M.A.; Bozonnat, C.; Chobadi, L.; Clonts, H.A.; Enevoldsen, P.; et al. 100% clean and renewable wind, water, and sunlight all-sector energy roadmaps for 139 countries of the world. Joule 2017, 1, 108–121. [Google Scholar] [CrossRef] [Green Version]
- Busarello, L.; Musca, R. Impact of the high share of converter-interfaced generation on electromechanical oscillations in Continental Europe power system. IET Renew. Power Gener. 2020, 14, 3918–3926. [Google Scholar] [CrossRef]
- Chen, J.; Liu, M.; Milano, F.; O’Donnell, T. 100% Converter-Interfaced generation using virtual synchronous generator control: A case study based on the irish system. Electr. Power Syst. Res. 2020, 187, 106475. [Google Scholar] [CrossRef]
- You, S.; Kou, G.; Liu, Y.; Zhang, X.; Cui, Y.; Till, M.J.; Yao, W.; Liu, Y. Impact of high PV penetration on the inter-area oscillations in the US eastern interconnection. IEEE Access 2017, 5, 4361–4369. [Google Scholar] [CrossRef]
- Musca, R.; Gonzalez-Longatt, F.; Gallego Sánchez, C.A. Power System Oscillations with Different Prevalence of Grid-Following and Grid-Forming Converters. Energies 2022, 15, 4273. [Google Scholar] [CrossRef]
- Tielens, P.; Van Hertem, D. The relevance of inertia in power systems. Renew. Sustain. Energy Rev. 2016, 55, 999–1009. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Yang, Y.; Yang, D.; Wang, X. Distributed power-generation systems and protection. Proc. IEEE 2017, 105, 1311–1331. [Google Scholar] [CrossRef] [Green Version]
- Zhong, Q.C. Power-electronics-enabled autonomous power systems: Architecture and technical routes. IEEE Trans. Ind. Electron. 2017, 64, 5907–5918. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Liserre, M.; Ma, K. Power electronics converters for wind turbine systems. IEEE Trans. Ind. Appl. 2011, 48, 708–719. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power-electronics-based AC systems. IEEE Trans. Power Electron. 2013, 29, 3318–3329. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W.; Blaabjerg, F.; Wang, X. Active harmonic filtering using current-controlled, grid-connected DG units with closed-loop power control. IEEE Trans. Power Electron. 2013, 29, 642–653. [Google Scholar]
- Wang, X.; Li, Y.W.; Blaabjerg, F.; Loh, P.C. Virtual-impedance-based control for voltage-source and current-source converters. IEEE Trans. Power Electron. 2014, 30, 7019–7037. [Google Scholar] [CrossRef]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-based stability assessment of grid-connected VSCs—An overview. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 4, 116–125. [Google Scholar] [CrossRef] [Green Version]
- Kazmierkowski, M.P.; Malesani, L. Current control techniques for three-phase voltage-source PWM converters: A survey. IEEE Trans. Ind. Electron. 1998, 45, 691–703. [Google Scholar] [CrossRef]
- Sang, S.; Gao, N.; Cai, X.; Li, R. A novel power-voltage control strategy for the grid-tied inverter to raise the rated power injection level in a weak grid. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 219–232. [Google Scholar] [CrossRef]
- Li, Z.; Zang, C.; Zeng, P.; Yu, H.; Li, S.; Bian, J. Control of a Grid-Forming Inverter Based on Sliding-Mode and Mixed {H_2}/{H_∖infty} Control. IEEE Trans. Ind. Electron. 2016, 64, 3862–3872. [Google Scholar] [CrossRef]
- Blaabjerg, F.; Teodorescu, R.; Liserre, M.; Timbus, A.V. Overview of control and grid synchronization for distributed power generation systems. IEEE Trans. Ind. Electron. 2006, 53, 1398–1409. [Google Scholar] [CrossRef] [Green Version]
- Ali, Z.; Christofides, N.; Hadjidemetriou, L.; Kyriakides, E.; Yang, Y.; Blaabjerg, F. Three-phase phase-locked loop synchronization algorithms for grid-connected renewable energy systems: A review. Renew. Sustain. Energy Rev. 2018, 90, 434–452. [Google Scholar] [CrossRef] [Green Version]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified impedance model of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2017, 33, 1775–1787. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Nian, H.; Lou, B.; Huang, H. Improved control strategy of grid connected inverter without phase locked loop on PCC voltage disturbance. In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Cincinnati, OH, USA, 1–5 October 2017; pp. 4244–4251. [Google Scholar]
- Davari, M.; Mohamed, Y.A.R.I. Robust vector control of a very weak-grid-connected voltage-source converter considering the phase-locked loop dynamics. IEEE Trans. Power Electron. 2016, 32, 977–994. [Google Scholar] [CrossRef]
- Dong, D.; Wen, B.; Boroyevich, D.; Mattavelli, P.; Xue, Y. Analysis of phase-locked loop low-frequency stability in three-phase grid-connected power converters considering impedance interactions. IEEE Trans. Ind. Electron. 2014, 62, 310–321. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Akrami, M.; Phurailatpam, C.; Me, S.P.; Hadavi, S.; Jayasinghe, G.; Zabihi, S.; Bahrani, B. Grid forming inverter modeling, control, and applications. IEEE Access 2021, 9, 114781–114807. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: An overview of control approaches and future trends. In Proceedings of the 2020 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Detroit, MI, USA, 11–15 October 2020; pp. 4292–4299. [Google Scholar]
- Musca, R.; Vasile, A.; Zizzo, G. Grid-forming converters. A critical review of pilot projects and demonstrators. Renew. Sustain. Energy Rev. 2022, 165, 112551. [Google Scholar] [CrossRef]
- Meegahapola, L.; Mancarella, P.; Flynn, D.; Moreno, R. Power system stability in the transition to a low carbon grid: A techno-economic perspective on challenges and opportunities. Wiley Interdiscip. Rev. Energy Environ. 2021, 10, e399. [Google Scholar] [CrossRef]
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-synchronization stability of converter-based resources—An overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Hu, Q.; Han, R.; Quan, X.; Wu, Z.; Tang, C.; Li, W.; Wang, W. Grid-Forming Inverter Enabled Virtual Power Plants with Inertia Support Capability. IEEE Trans. Smart Grid 2022, 13, 4134–4143. [Google Scholar] [CrossRef]
- Kkuni, K.V.; Mohan, S.; Yang, G.; Xu, W. Comparative assessment of typical controlrealizations of grid forming converters based ontheir voltage source behaviour. arXiv 2021, arXiv:2106.10048. [Google Scholar]
- Roscoe, A.; Brogan, P.; Elliott, D.; Knueppel, T.; Gutierrez, I.; Campion, J.P.; Da Silva, R. Practical experience of operating a grid forming wind park and its response to system events. In Proceedings of the 18th Wind Integration Workshop, Dublin, Ireland, 16–18 October 2019; pp. 16–18. [Google Scholar]
- Peacock, B. World’s Largest Grid-Forming Battery to Begin Constructions in Australia. Available online: https://www.pv-magazine.com/2021/08/10/worlds-largest-grid-forming-battery-to-begin-construction-in-australia/ (accessed on 28 November 2022).
- Nestor, S. Major Grid-Forming Battery Gains Momentum. Available online: https://www.energymagazine.com.au/major-grid-forming-battery-gains-momentum/ (accessed on 28 November 2022).
- Sales. S.A. Grid-Forming Project Setting Worldwide Example. Available online: https://ahlecsolar.com.au/2021/03/12/sa-grid-forming-project-setting-worldwide-example/ (accessed on 28 November 2022).
- Hu, J.; Chi, Y.; Tian, X.; Zhou, Y.; He, W. A coordinated and steadily fault ride through strategy under short-circuit fault of the wind power grid connected system based on the grid-forming control. Energy Rep. 2022, 8, 333–341. [Google Scholar] [CrossRef]
- Aragon, D.; Unamuno, E.; Ceballos, S.; Barrena, J. Comparative small-signal evaluation of advanced grid-forming control techniques. Electr. Power Syst. Res. 2022, 211, 108154. [Google Scholar] [CrossRef]
- Ojo, Y.; Benmiloud, M.; Lestas, I. Frequency and voltage control schemes for three-phase grid-forming inverters. IFAC-PapersOnLine 2020, 53, 13471–13476. [Google Scholar] [CrossRef]
- Tayyebi, A.; Groß, D.; Anta, A.; Kupzog, F.; Dörfler, F. Frequency stability of synchronous machines and grid-forming power converters. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1004–1018. [Google Scholar] [CrossRef] [Green Version]
- Shakerighadi, B.; Johansson, N.; Eriksson, R.; Mitra, P.; Bolzoni, A.; Clark, A.; Nee, H.P. An overview of stability challenges for power-electronic-dominated power systems: The grid-forming approach. IET Gener. Transm. Distrib. 2022, 17, 284–306. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A.; Chow, J.H. Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Xiong, L.; Zhuo, F.; Wang, F.; Liu, X.; Chen, Y.; Zhu, M.; Yi, H. Static synchronous generator model: A new perspective to investigate dynamic characteristics and stability issues of grid-tied PWM inverter. IEEE Trans. Power Electron. 2015, 31, 6264–6280. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An overview of assessment methods for synchronization stability of grid-connected converters under severe symmetrical grid faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef] [Green Version]
- Xiong, L.; Liu, X.; Liu, Y.; Zhuo, F. Modeling and stability issues of voltage-source converter dominated power systems: A review. CSEE J. Power Energy Syst. 2020, 8, 1530–1549. [Google Scholar]
- Shuai, Z.; Shen, C.; Yin, X.; Liu, X.; Shen, Z.J. Fault analysis of inverter-interfaced distributed generators with different control schemes. IEEE Trans. Power Deliv. 2017, 33, 1223–1235. [Google Scholar] [CrossRef]
- He, J.; Li, Y.W. Analysis, design, and implementation of virtual impedance for power electronics interfaced distributed generation. IEEE Trans. Ind. Appl. 2011, 47, 2525–2538. [Google Scholar] [CrossRef]
- Paquette, A.D.; Divan, D.M. Virtual impedance current limiting for inverters in microgrids with synchronous generators. IEEE Trans. Ind. Appl. 2014, 51, 1630–1638. [Google Scholar] [CrossRef]
- Pan, D.; Ruan, X.; Wang, X.; Yu, H.; Xing, Z. Analysis and design of current control schemes for LCL-type grid-connected inverter based on a general mathematical model. IEEE Trans. Power Electron. 2016, 32, 4395–4410. [Google Scholar] [CrossRef]
- Mirafzal, B.; Adib, A. On grid-interactive smart inverters: Features and advancements. IEEE Access 2020, 8, 160526–160536. [Google Scholar] [CrossRef]
- Unruh, P.; Nuschke, M.; Strauß, P.; Welck, F. Overview on grid-forming inverter control methods. Energies 2020, 13, 2589. [Google Scholar] [CrossRef]
- Pattabiraman, D.; Lasseter, R.; Jahns, T. Comparison of grid following and grid forming control for a high inverter penetration power system. In Proceedings of the 2018 IEEE Power & Energy Society General Meeting (PESGM), IEEE, Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Matevosyan, J.; Badrzadeh, B.; Prevost, T.; Quitmann, E.; Ramasubramanian, D.; Urdal, H.; Achilles, S.; MacDowell, J.; Huang, S.H.; Vital, V.; et al. Grid-forming inverters: Are they the key for high renewable penetration? IEEE Power Energy Mag. 2019, 17, 89–98. [Google Scholar] [CrossRef]
- Anttila, S.; Döhler, J.S.; Oliveira, J.G.; Boström, C. Grid Forming Inverters: A Review of the State of the Art of Key Elements for Microgrid Operation. Energies 2022, 15, 5517. [Google Scholar] [CrossRef]
- Khan, S.A.; Wang, M.; Su, W.; Liu, G.; Chaturvedi, S. Grid-Forming Converters for Stability Issues in Future Power Grids. Energies 2022, 15, 4937. [Google Scholar] [CrossRef]
- Rosso, R.; Wang, X.; Liserre, M.; Lu, X.; Engelken, S. Grid-forming converters: Control approaches, grid-synchronization, and future trends—A review. IEEE Open J. Ind. Appl. 2021, 2, 93–109. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Issa, W.; Hossain, M.J. Overview of AC microgrid controls with inverter-interfaced generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Milano, F.; Dörfler, F.; Hug, G.; Hill, D.J.; Verbič, G. Foundations and challenges of low-inertia systems. In Proceedings of the 2018 Power Systems Computation Conference (PSCC), IEEE, Dublin, Ireland, 11–15 June 2018; pp. 1–25. [Google Scholar]
- Bevrani, H.; Ise, T.; Miura, Y. Virtual synchronous generators: A survey and new perspectives. Int. J. Electr. Power Energy Syst. 2014, 54, 244–254. [Google Scholar] [CrossRef]
- Tamrakar, U.; Shrestha, D.; Maharjan, M.; Bhattarai, B.P.; Hansen, T.M.; Tonkoski, R. Virtual inertia: Current trends and future directions. Appl. Sci. 2017, 7, 654. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Liu, K.; Le, J.; Ji, K.; Huai, Q.; Wang, F.; Liao, X. Stability assessment of modular multilevel converters based on linear time-periodic theory: Time-domain vs. frequency-domain. IEEE Trans. Power Deliv. 2022, 37, 3980–3995. [Google Scholar] [CrossRef]
- Tzounas, G.; Dassios, I.; Milano, F. Small-signal stability analysis of numerical integration methods. IEEE Trans. Power Syst. 2022, 37, 4796–4806. [Google Scholar] [CrossRef]
- Chow, J.H.; Sanchez-Gasca, J.J. Power System Modeling, Computation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Poulose, A.; Kim, S. Synchronizing Torque-Based Transient Stability Index of a Multimachine Interconnected Power System. Energies 2022, 15, 3432. [Google Scholar] [CrossRef]
- Chang, Y.; Hu, J.; Yuan, X. Mechanism analysis of DFIG-based wind turbine’s fault current during LVRT with equivalent inductances. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1515–1527. [Google Scholar] [CrossRef]
- Alaboudy, A.K.; Zeineldin, H.H.; Kirtley, J. Microgrid stability characterization subsequent to fault-triggered islanding incidents. IEEE Trans. Power Deliv. 2012, 27, 658–669. [Google Scholar] [CrossRef]
- Weise, B. Impact of K-factor and active current reduction during fault-ride-through of generating units connected via voltage-sourced converters on power system stability. IET Renew. Power Gener. 2015, 9, 25–36. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Stability assessment and optimization methods for microgrid with multiple VSG units. IEEE Trans. Smart Grid 2016, 9, 1462–1471. [Google Scholar] [CrossRef]
- Yang, D.; Wang, X. Unified modular state-space modeling of grid-connected voltage-source converters. IEEE Trans. Power Electron. 2020, 35, 9700–9715. [Google Scholar] [CrossRef]
- Zhang, P.; Martí, J.R.; Dommel, H.W. Shifted-frequency analysis for EMTP simulation of power-system dynamics. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 2564–2574. [Google Scholar] [CrossRef] [Green Version]
- Qi, L.; Woodruff, S. Stability analysis and assessment of integrated power systems using RTDS. In Proceedings of the IEEE Electric Ship Technologies Symposium, 2005, IEEE, Philadelphia, PA, USA, 25–27 July; 2005; pp. 325–332. [Google Scholar]
- Shair, J.; Xie, X.; Liu, W.; Li, X.; Li, H. Modeling and stability analysis methods for investigating subsynchronous control interaction in large-scale wind power systems. Renew. Sustain. Energy Rev. 2021, 135, 110420. [Google Scholar] [CrossRef]
- Li, Y.; Shu, D.; Shi, F.; Yan, Z.; Zhu, Y.; Tai, N. A multi-rate co-simulation of combined phasor-domain and time-domain models for large-scale wind farms. IEEE Trans. Energy Convers. 2019, 35, 324–335. [Google Scholar] [CrossRef]
- Ye, X.; Tang, Y.; Shu, D. Large step size electromagnetic transient simulations by matrix transformation-based shifted-frequency phasor models. IET Gener. Transm. Distrib. 2020, 14, 2890–2900. [Google Scholar] [CrossRef]
- Li, Y.; Shu, D.; Hu, J.; Yan, Z.; Zhou, Y.; Wang, H. A multi-area Thevenin equivalent based multi-rate co-simulation for control design of practical LCC HVDC system. Int. J. Electr. Power Energy Syst. 2020, 115, 105479. [Google Scholar] [CrossRef]
- Jeon, J.H.; Kim, J.Y.; Kim, H.M.; Kim, S.K.; Cho, C.; Kim, J.M.; Ahn, J.B.; Nam, K.Y. Development of hardware in-the-loop simulation system for testing operation and control functions of microgrid. IEEE Trans. Power Electron. 2010, 25, 2919–2929. [Google Scholar] [CrossRef]
- Topcu, U.; Packard, A.; Seiler, P.; Wheeler, T. Stability region analysis using simulations and sum-of-squares programming. In Proceedings of the 2007 American Control Conference, IEEE, New York, NY, USA, 9–13 July 2007; pp. 6009–6014. [Google Scholar]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient angle stability of virtual synchronous generators using Lyapunov’s direct method. IEEE Trans. Smart Grid 2018, 10, 4648–4661. [Google Scholar] [CrossRef]
- Kabalan, M.; Singh, P.; Niebur, D. A design and optimization tool for inverter-based microgrids using large-signal nonlinear analysis. IEEE Trans. Smart Grid 2018, 10, 4566–4576. [Google Scholar] [CrossRef]
- Odun-Ayo, T.; Crow, M.L. Structure-preserved power system transient stability using stochastic energy functions. IEEE Trans. Power Syst. 2012, 27, 1450–1458. [Google Scholar] [CrossRef]
- Demenkov, M. A Matlab tool for regions of attraction estimation via numerical algebraic geometry. In Proceedings of the 2015 International Conference on Mechanics-Seventh Polyakhov’s Reading, IEEE, St. Petersburg, FL, USA, 2–6 February 2015; pp. 1–5. [Google Scholar]
- Fu, X.; Sun, J.; Huang, M.; Tian, Z.; Yan, H.; Iu, H.H.C.; Hu, P.; Zha, X. Large-signal stability of grid-forming and grid-following controls in voltage source converter: A comparative study. IEEE Trans. Power Electron. 2020, 36, 7832–7840. [Google Scholar] [CrossRef]
- Hart, P.; Lesieutre, B. Energy function for a grid-tied, droop-controlled inverter. In Proceedings of the 2014 North American Power Symposium (NAPS), IEEE, Pullman, WA, USA, 7–9 September 2014; pp. 1–6. [Google Scholar]
- Tang, W.; Hu, J.; Chang, Y.; Liu, F. Modeling of DFIG-based wind turbine for power system transient response analysis in rotor speed control timescale. IEEE Trans. Power Syst. 2018, 33, 6795–6805. [Google Scholar] [CrossRef]
- Cheng, H.; Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient angle stability of paralleled synchronous and virtual synchronous generators in islanded microgrids. IEEE Trans. Power Electron. 2020, 35, 8751–8765. [Google Scholar] [CrossRef]
- Yuan, H.; Xin, H.; Huang, L.; Wang, Z.; Wu, D. Stability analysis and enhancement of type-4 wind turbines connected to very weak grids under severe voltage sags. IEEE Trans. Energy Convers. 2018, 34, 838–848. [Google Scholar]
- Bretas, N.G.; Alberto, L.F. Lyapunov function for power systems with transfer conductances: Extension of the invariance principle. IEEE Trans. Power Syst. 2003, 18, 769–777. [Google Scholar] [CrossRef]
- Ma, S.; Geng, H.; Liu, L.; Yang, G.; Pal, B.C. Grid-synchronization stability improvement of large scale wind farm during severe grid fault. IEEE Trans. Power Syst. 2017, 33, 216–226. [Google Scholar] [CrossRef] [Green Version]
- Huang, L.; Xin, H.; Wang, Z.; Zhang, L.; Wu, K.; Hu, J. Transient stability analysis and control design of droop-controlled voltage source converters considering current limitation. IEEE Trans. Smart Grid 2017, 10, 578–591. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters. IEEE Trans. Power Electron. 2019, 35, 3573–3589. [Google Scholar] [CrossRef] [Green Version]
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient stability of voltage-source converters with grid-forming control: A design-oriented study. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1019–1033. [Google Scholar] [CrossRef]
- Naderi, M.; Khayat, Y.; Shafiee, Q.; Dragicevic, T.; Bevrani, H.; Blaabjerg, F. Interconnected autonomous AC microgrids via back-to-back converters—Part I: Small-signal modeling. IEEE Trans. Power Electron. 2019, 35, 4728–4740. [Google Scholar] [CrossRef]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Xin, H.; Huang, L.; Zhang, L.; Wang, Z.; Hu, J. Synchronous instability mechanism of Pf droop-controlled voltage source converter caused by current saturation. IEEE Trans. Power Syst. 2016, 31, 5206–5207. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-oriented transient stability analysis of grid-connected converters with power synchronization control. IEEE Trans. Ind. Electron. 2018, 66, 6473–6482. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-based WTs for small-signal stability analysis in DVC timescale in power electronized power systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Pei, J.; Yao, J.; Liu, R.; Zeng, D.; Sun, P.; Zhang, H.; Liu, Y. Characteristic analysis and risk assessment for voltage–frequency coupled transient instability of large-scale grid-connected renewable energy plants during LVRT. IEEE Trans. Ind. Electron. 2019, 67, 5515–5530. [Google Scholar] [CrossRef]
- Hornik, T.; Zhong, Q.C. Control of Power Inverters in Renewable Energy and Smart Grid Integration; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Kundur, P.S.; Malik, O.P. Power System Stability and Control; McGraw-Hill Education: New York, NY, USA, 2022. [Google Scholar]
- Wang, X.; Blaabjerg, F. Harmonic stability in power electronic-based power systems: Concept, modeling, and analysis. IEEE Trans. Smart Grid 2018, 10, 2858–2870. [Google Scholar] [CrossRef] [Green Version]
- Erlich, I.; Shewarega, F.; Engelhardt, S.; Kretschmann, J.; Fortmann, J.; Koch, F. Effect of wind turbine output current during faults on grid voltage and the transient stability of wind parks. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, IEEE, Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar]
- Shewarega, F.; Erlich, I.; Rueda, J.L. Impact of large offshore wind farms on power system transient stability. In Proceedings of the 2009 IEEE/PES Power Systems Conference and Exposition, IEEE, Seattle, WA, USA, 15–18 March 2009; pp. 1–8. [Google Scholar]
- Göksu, Ö.; Teodorescu, R.; Bak, C.L.; Iov, F.; Kjær, P.C. Instability of wind turbine converters during current injection to low voltage grid faults and PLL frequency based stability solution. IEEE Trans. Power Syst. 2014, 29, 1683–1691. [Google Scholar] [CrossRef]
- Geng, H.; Liu, L.; Li, R. Synchronization and reactive current support of PMSG-based wind farm during severe grid fault. IEEE Trans. Sustain. Energy 2018, 9, 1596–1604. [Google Scholar] [CrossRef]
- Betz, R.E.; Taul, M.G. Identification of grid impedance during severe faults. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 1076–1082. [Google Scholar]
- He, X.; Geng, H.; Li, R.; Pal, B.C. Transient stability analysis and enhancement of renewable energy conversion system during LVRT. IEEE Trans. Sustain. Energy 2019, 11, 1612–1623. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Robust fault ride through of converter-based generation during severe faults with phase jumps. IEEE Trans. Ind. Appl. 2019, 56, 570–583. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Transient stability impact of the phase-locked loop on grid-connected voltage source converters. In Proceedings of the 2018 International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), IEEE, Niigata, Japan, 20–24 May 2018; pp. 2673–2680. [Google Scholar]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Systematic approach for transient stability evaluation of grid-tied converters during power system faults. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 5191–5198. [Google Scholar]
- Wu, H.; Wang, X. An adaptive phase-locked loop for the transient stability enhancement of grid-connected voltage source converters. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Portland, OR, USA, 23–27 September 2018; pp. 5892–5898. [Google Scholar]
- Diedrichs, V.; Beekmann, A.; Adloff, S. Loss of (Angle) Stability of Wind Power Plants. The Underestimated Phenomenon in Case of Very Low Short Circuit Ratio. 2011. Available online: https://www.osti.gov/etdeweb/biblio/21594671 (accessed on 28 November 2022).
- Pan, D.; Wang, X.; Liu, F.; Shi, R. Transient stability impact of reactive power control on grid-connected converters. In Proceedings of the 2019 IEEE Energy Conversion Congress and Exposition (ECCE), IEEE, Baltimore, MD, USA, 29 September–3 October 2019; pp. 4311–4316. [Google Scholar]
- Wu, H.; Wang, X. A mode-adaptive power-angle control method for transient stability enhancement of virtual synchronous generators. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 1034–1049. [Google Scholar] [CrossRef]
- Chen, M.; Zhou, D.; Blaabjerg, F. Enhanced transient angle stability control of grid-forming converter based on virtual synchronous generator. IEEE Trans. Ind. Electron. 2021, 69, 9133–9144. [Google Scholar] [CrossRef]
- Alipoor, J.; Miura, Y.; Ise, T. Power system stabilization using virtual synchronous generator with alternating moment of inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 451–458. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X. A self-adaptive inertia and damping combination control of VSG to support frequency stability. IEEE Trans. Energy Convers. 2016, 32, 397–398. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Khajehoddin, S.A.; Karimi-Ghartemani, M. An improved damping method for virtual synchronous machines. IEEE Trans. Sustain. Energy 2019, 10, 1491–1500. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Hu, B.; Pan, D.; Blaabjerg, F. Transient damping method for improving the synchronization stability of virtual synchronous generators. IEEE Trans. Power Electron. 2020, 36, 7820–7831. [Google Scholar] [CrossRef]
- Xiong, X.; Wu, C.; Cheng, P.; Blaabjerg, F. An optimal damping design of virtual synchronous generators for transient stability enhancement. IEEE Trans. Power Electron. 2021, 36, 11026–11030. [Google Scholar] [CrossRef]
- Shi, K.; Song, W.; Xu, P.; Liu, R.; Fang, Z.; Ji, Y. Low-voltage ride-through control strategy for a virtual synchronous generator based on smooth switching. IEEE Access 2017, 6, 2703–2711. [Google Scholar] [CrossRef]
- Chen, J.; Prystupczuk, F.; O’Donnell, T. Use of voltage limits for current limitations in grid-forming converters. CSEE J. Power Energy Syst. 2020, 6, 259–269. [Google Scholar]
- Awal, M.; Husain, I. Transient Stability Assessment for Current-Constrained and Current-Unconstrained Fault Ride Through in Virtual Oscillator-Controlled Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 6935–6946. [Google Scholar] [CrossRef]
- Rokrok, E.; Qoria, T.; Bruyere, A.; Francois, B.; Guillaud, X. Transient stability assessment and enhancement of grid-forming converters embedding current reference saturation as current limiting strategy. IEEE Trans. Power Syst. 2021, 37, 1519–1531. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. Current limiting control with enhanced dynamics of grid-forming converters during fault conditions. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1062–1073. [Google Scholar] [CrossRef] [Green Version]
- Me, S.P.; Zabihi, S.; Blaabjerg, F.; Bahrani, B. Adaptive Virtual Resistance for Postfault Oscillation Damping in Grid-Forming Inverters. IEEE Trans. Power Electron. 2021, 37, 3813–3824. [Google Scholar] [CrossRef]
- Qoria, T.; Gruson, F.; Colas, F.; Denis, G.; Prevost, T.; Guillaud, X. Critical clearing time determination and enhancement of grid-forming converters embedding virtual impedance as current limitation algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 1050–1061. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.W.; Kao, C.N. An accurate power control strategy for power-electronics-interfaced distributed generation units operating in a low-voltage multibus microgrid. IEEE Trans. Power Electron. 2009, 24, 2977–2988. [Google Scholar]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. Distributed power system virtual inertia implemented by grid-connected power converters. IEEE Trans. Power Electron. 2017, 33, 8488–8499. [Google Scholar] [CrossRef] [Green Version]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the inertia of future more-electronics power systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 7, 2130–2146. [Google Scholar] [CrossRef]
- Denis, G.; Prevost, T.; Debry, M.S.; Xavier, F.; Guillaud, X.; Menze, A. The Migrate project: The challenges of operating a transmission grid with only inverter-based generation. A grid-forming control improvement with transient current-limiting control. IET Renew. Power Gener. 2018, 12, 523–529. [Google Scholar] [CrossRef]
- Sadeghkhani, I.; Golshan, M.E.H.; Guerrero, J.M.; Mehrizi-Sani, A. A current limiting strategy to improve fault ride-through of inverter interfaced autonomous microgrids. IEEE Trans. Smart Grid 2016, 8, 2138–2148. [Google Scholar] [CrossRef] [Green Version]








| Category | Enhancement Technique |
|---|---|
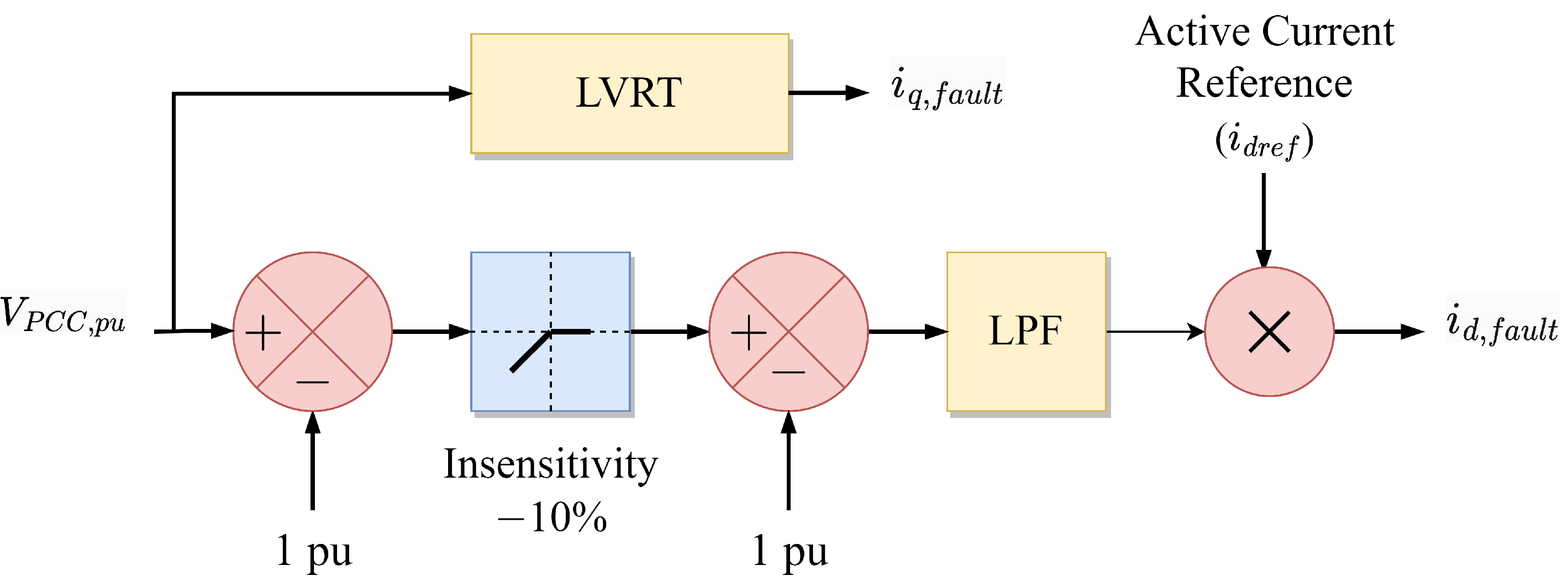
| Modify active current or power | During fault, reduce active current proportional to voltage drop [103,104] |
| Raise active current reference in accordance with frequency error [105] | |
| Raise active power baseline according to [106] | |
| Align vector current angle with vector line impedance angle [107] | |
| Eliminate the accelerating and decelerating areas in by setting reference power equal to actual power [108] | |
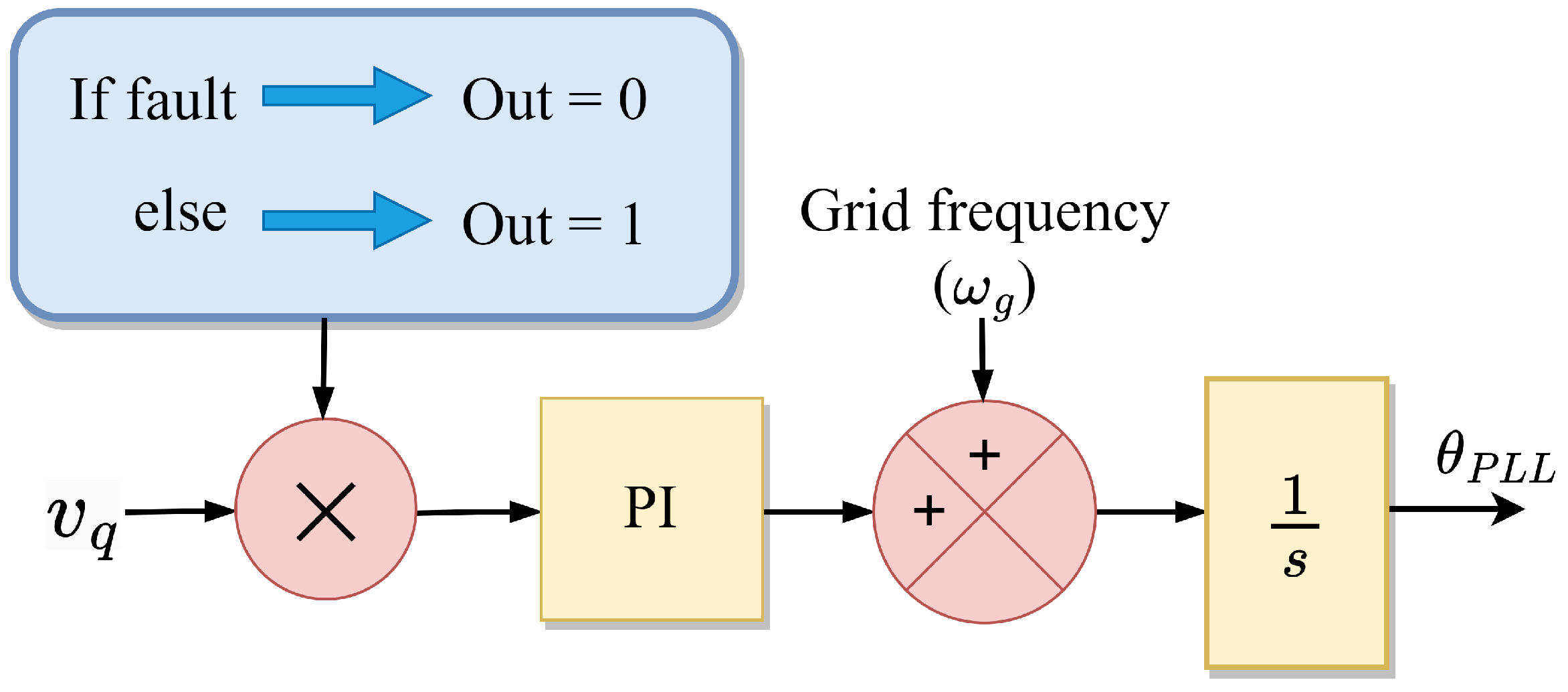
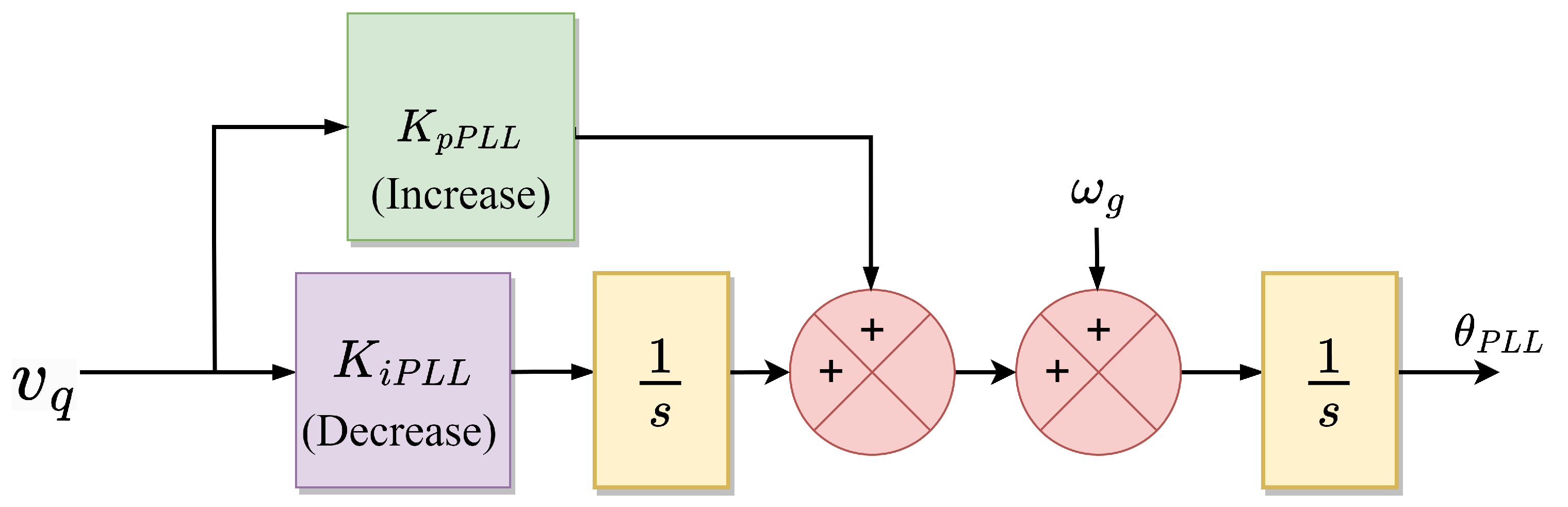
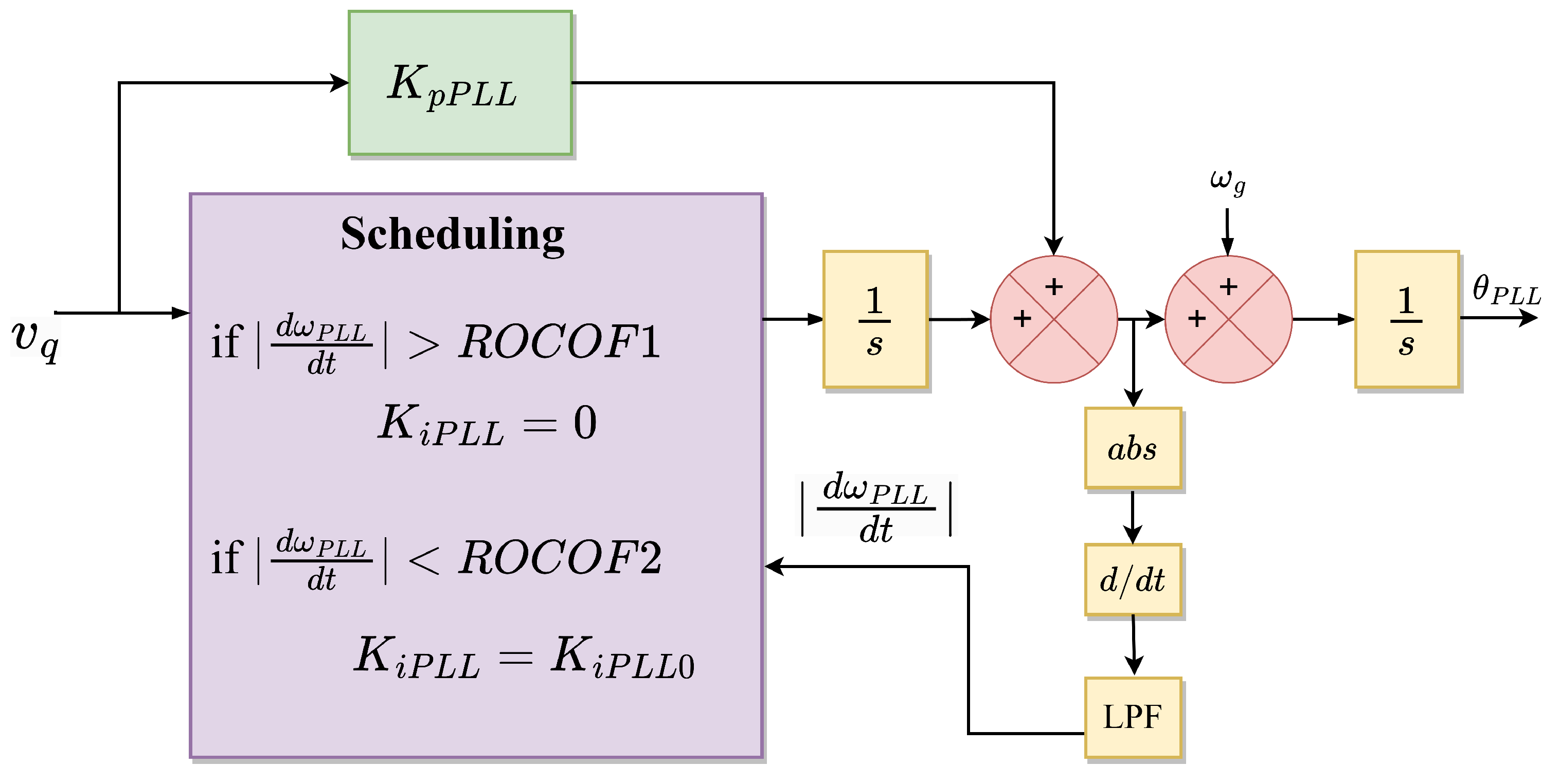
| Modify synchronization loop (means ) | Freeze during fault [69,109] |
| Increase damping ratio of [110,111] | |
| Adaptive decrease integral gain during fault [112] | |
| During fault, transform to a first-order system [92,110] |
| Category | Enhancement Technique |
|---|---|
| Modify active and reactive power reference | Reducing active power reference [80,87] |
| Increase reactive power reference [114] | |
| Modify control loops | Mode-adaptive control [115] |
| Internal voltage regulation control [116] | |
| Modify moment of inertia and damping parameters | Alternating inertia [117] |
| Distinct quantities of virtual inertia [118] | |
| Design guidelines that can enhance the system’s damping and transient stability [93] | |
| Complex damping solutions to avoid steady-state characteristics change [119] | |
| Enhance synchronization stability and frequency stability simultaneously [120] | |
| Adding frequency component to power reference through a [121] | |
| Employing inverter current limits | Switching to a converter [122] |
| Limiting converter output voltage by current limitation [123] | |
| Employing circular current restriction in unified virtual oscillator regulation [124] | |
| Account the effect of current reference angle [125] | |
| Current limits along with post-fault enhancement controls | Modifying power references in accordance with the voltage drop and a virtual resistance [126] |
| Utilizing virtual resistance that is adjustable dependent on the amplitude of post-disturbance fluctuations [127] | |
| Utilize virtual impedance and adjustable controller variables [128] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poulose, A.; Kim, S. Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids. Energies 2023, 16, 2495. https://doi.org/10.3390/en16052495
Poulose A, Kim S. Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids. Energies. 2023; 16(5):2495. https://doi.org/10.3390/en16052495
Chicago/Turabian StylePoulose, Albert, and Soobae Kim. 2023. "Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids" Energies 16, no. 5: 2495. https://doi.org/10.3390/en16052495
APA StylePoulose, A., & Kim, S. (2023). Transient Stability Analysis and Enhancement Techniques of Renewable-Rich Power Grids. Energies, 16(5), 2495. https://doi.org/10.3390/en16052495