Simulation of Series Resistance Increase through Solder Layer Cracking in Si Solar Cells under Thermal Cycling
Abstract
1. Introduction
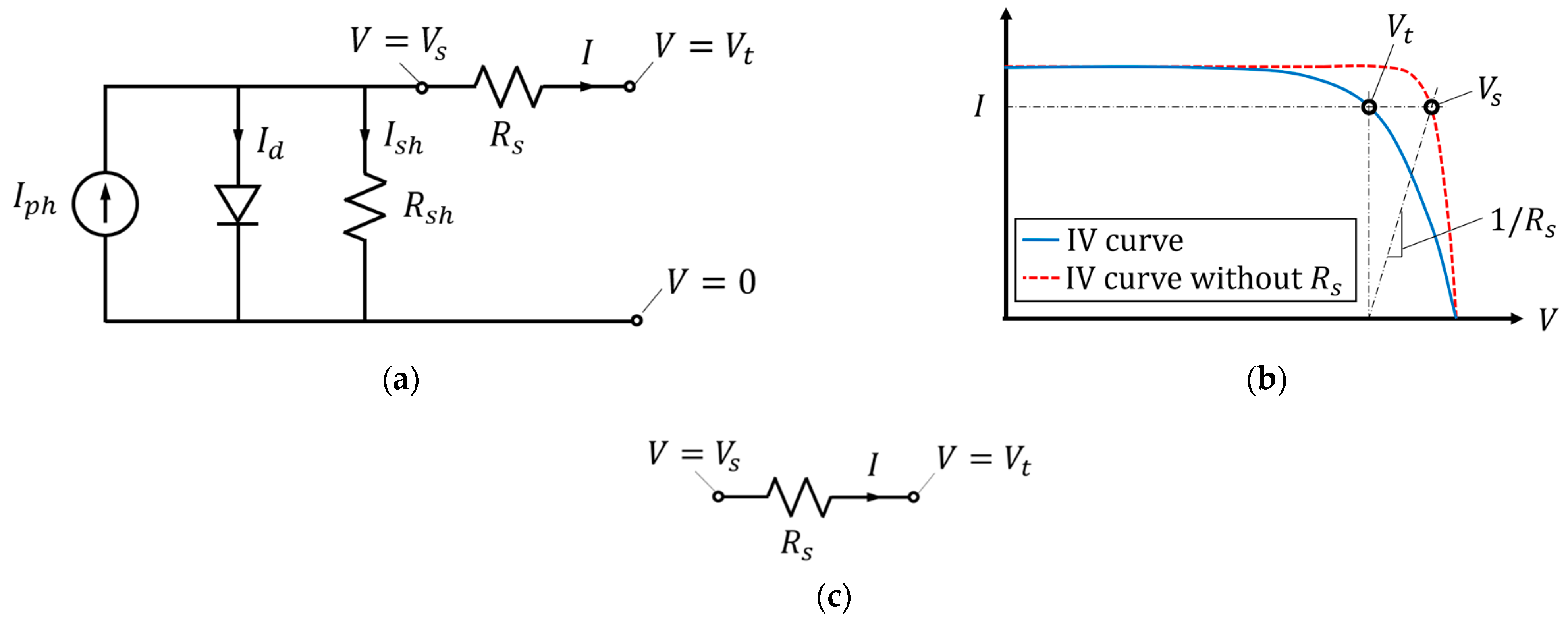
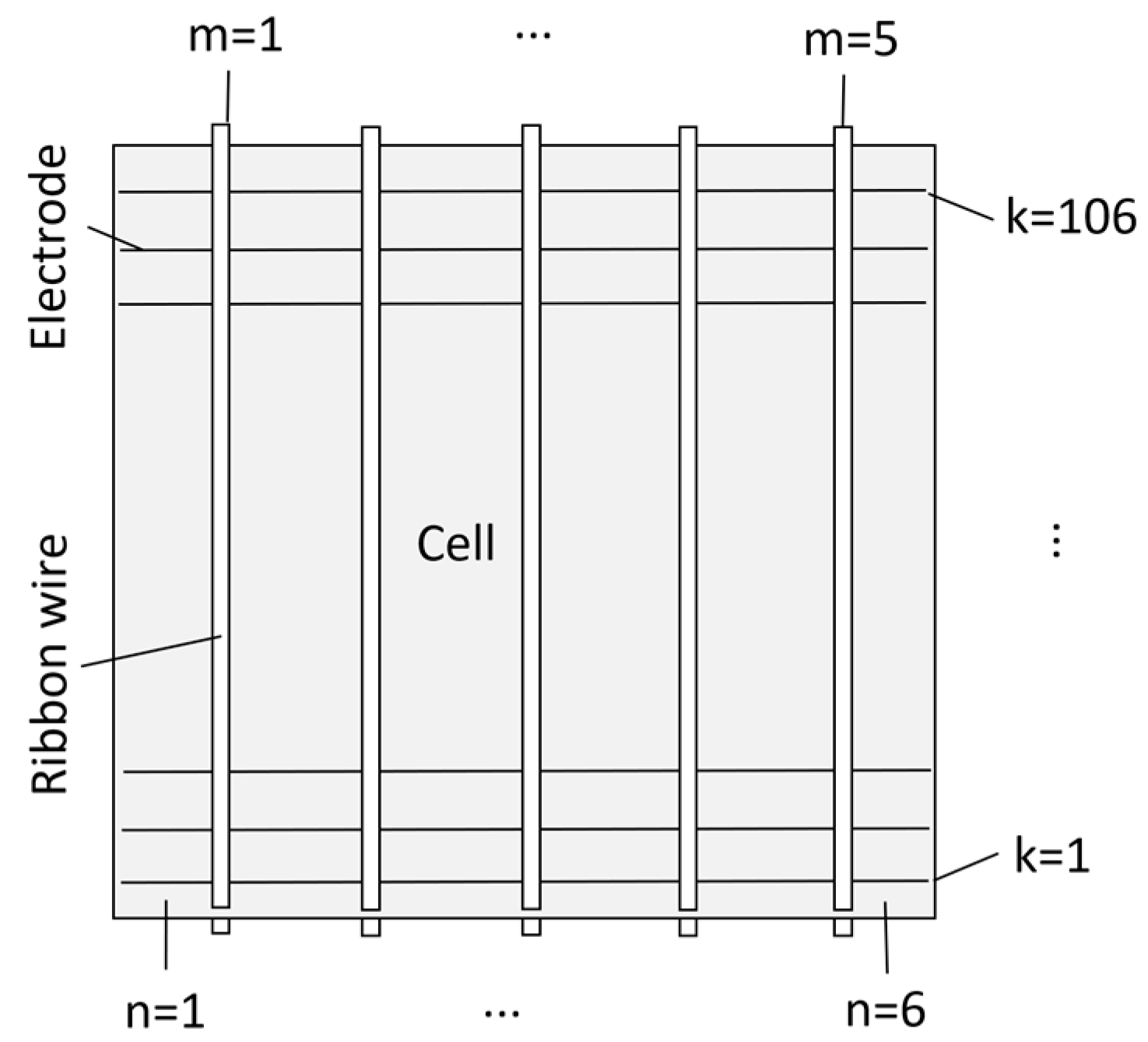
2. Simulation of Series Resistance in Solar Cells
2.1. Electrostatic Modeling Theory in FEM
2.2. Electrostatic Material Properties of Solar Cells
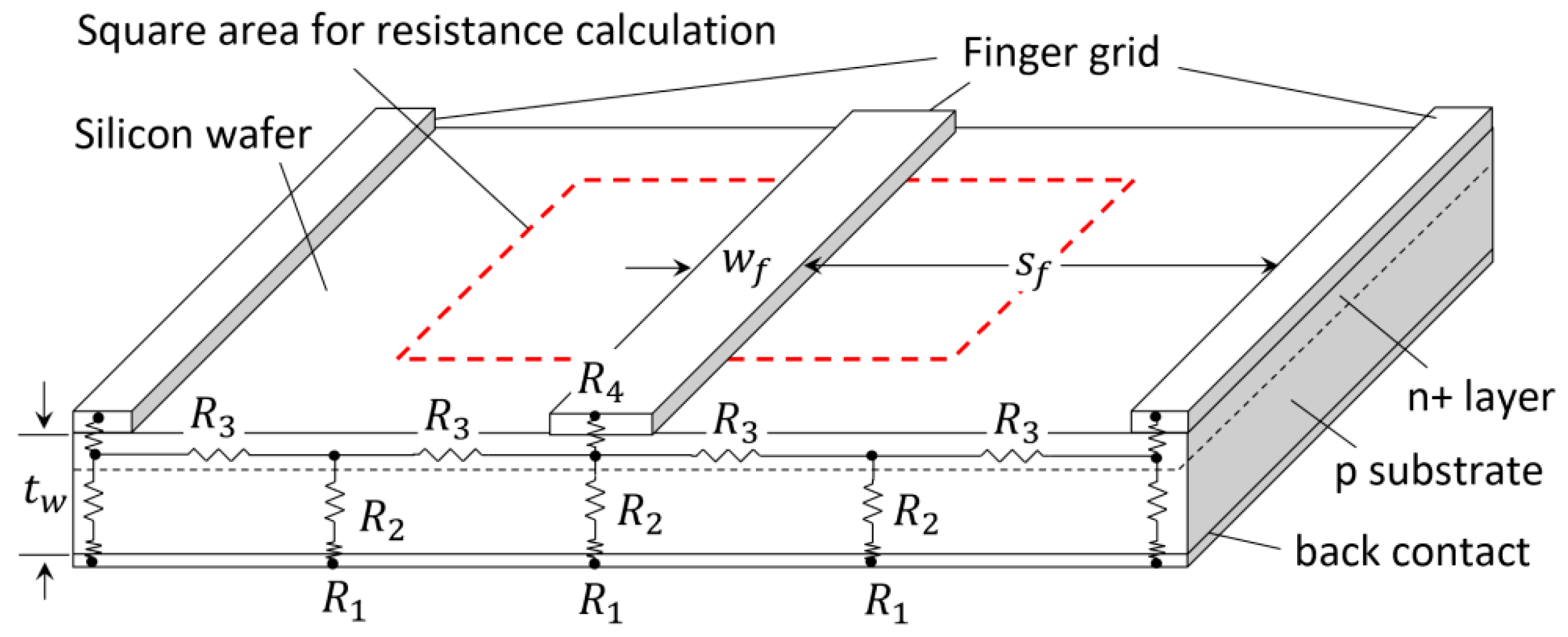
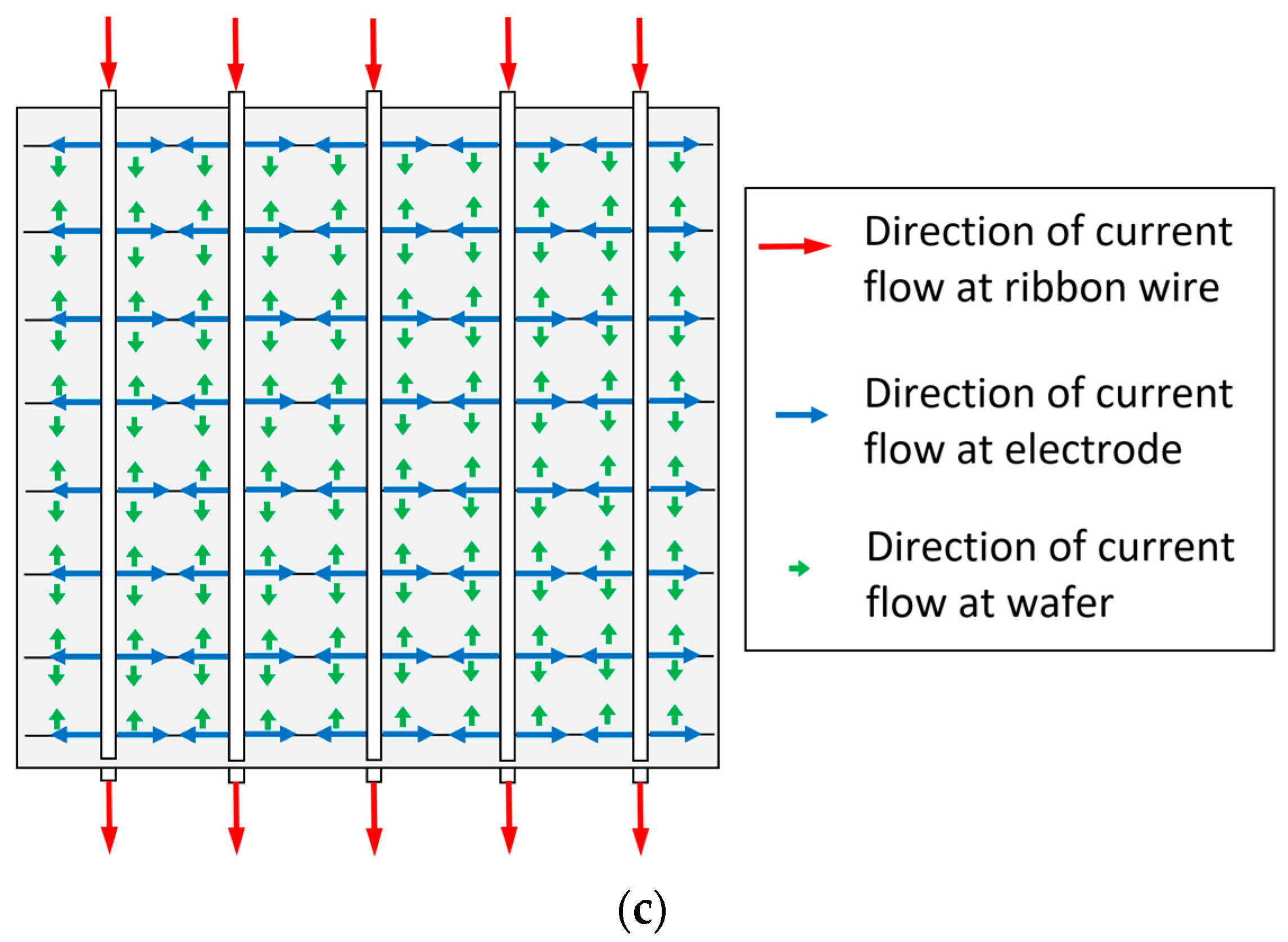
2.3. Series Resistance Calculation
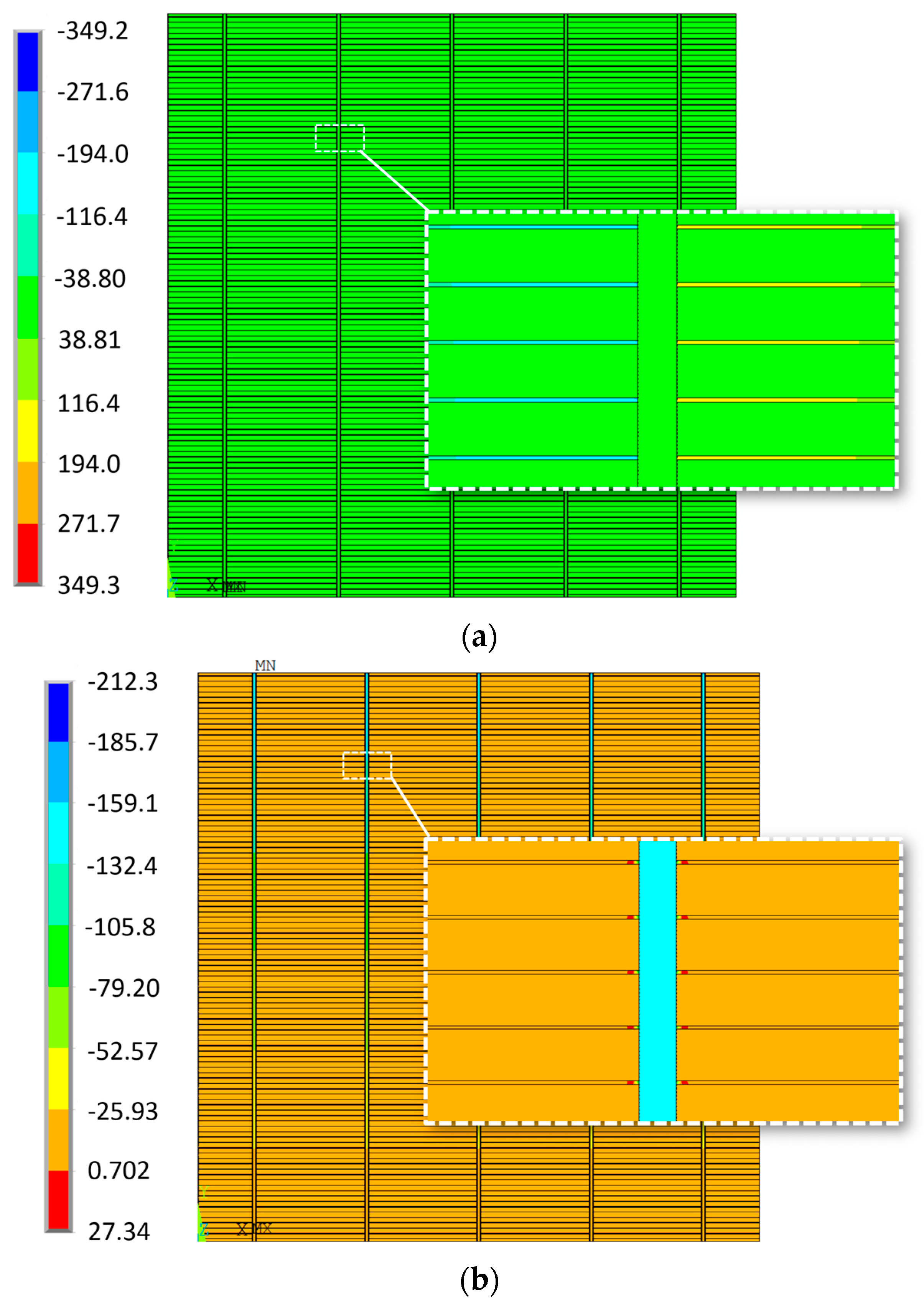
3. Simulation of Series Resistance Increase through Solder Layer Cracking
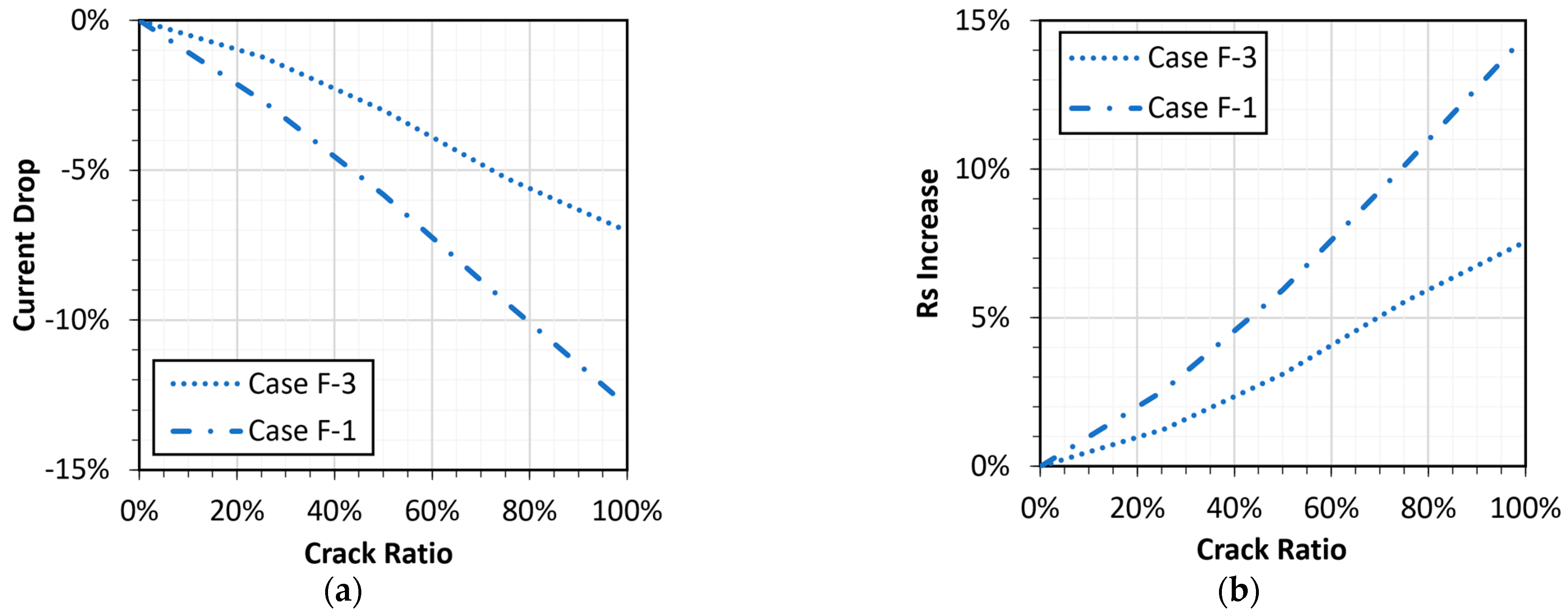
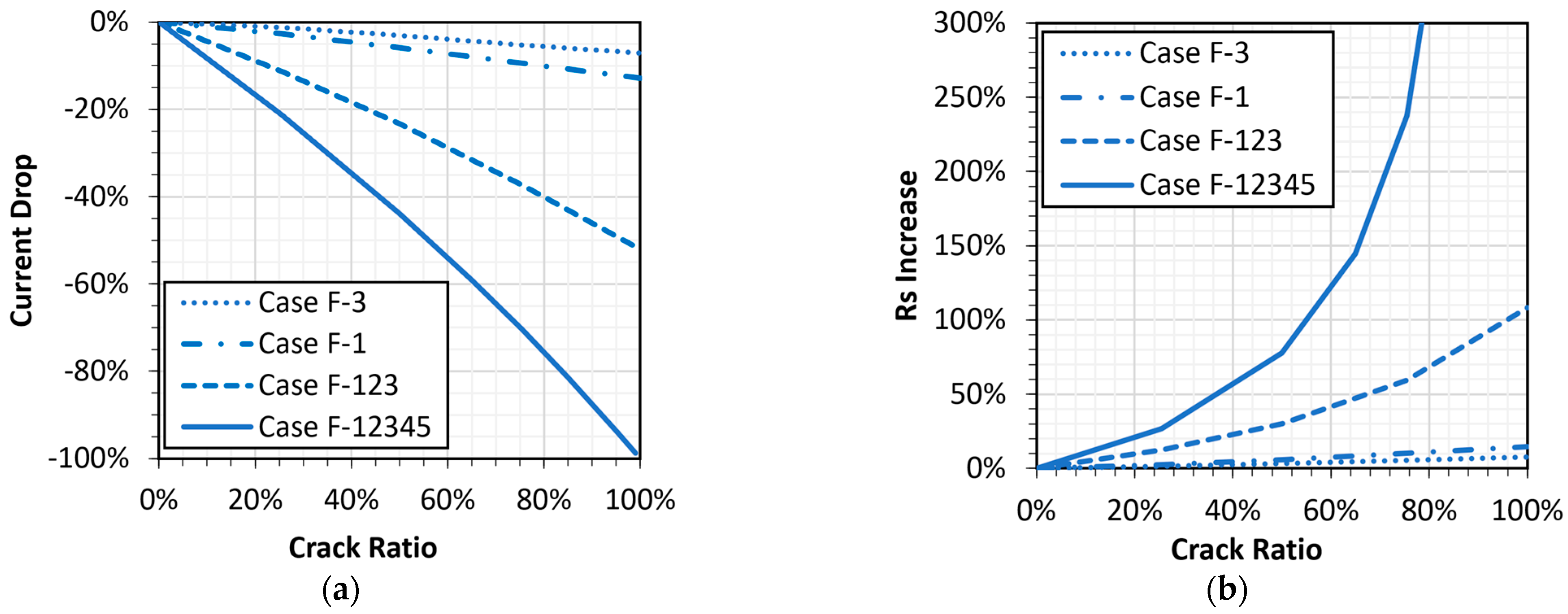
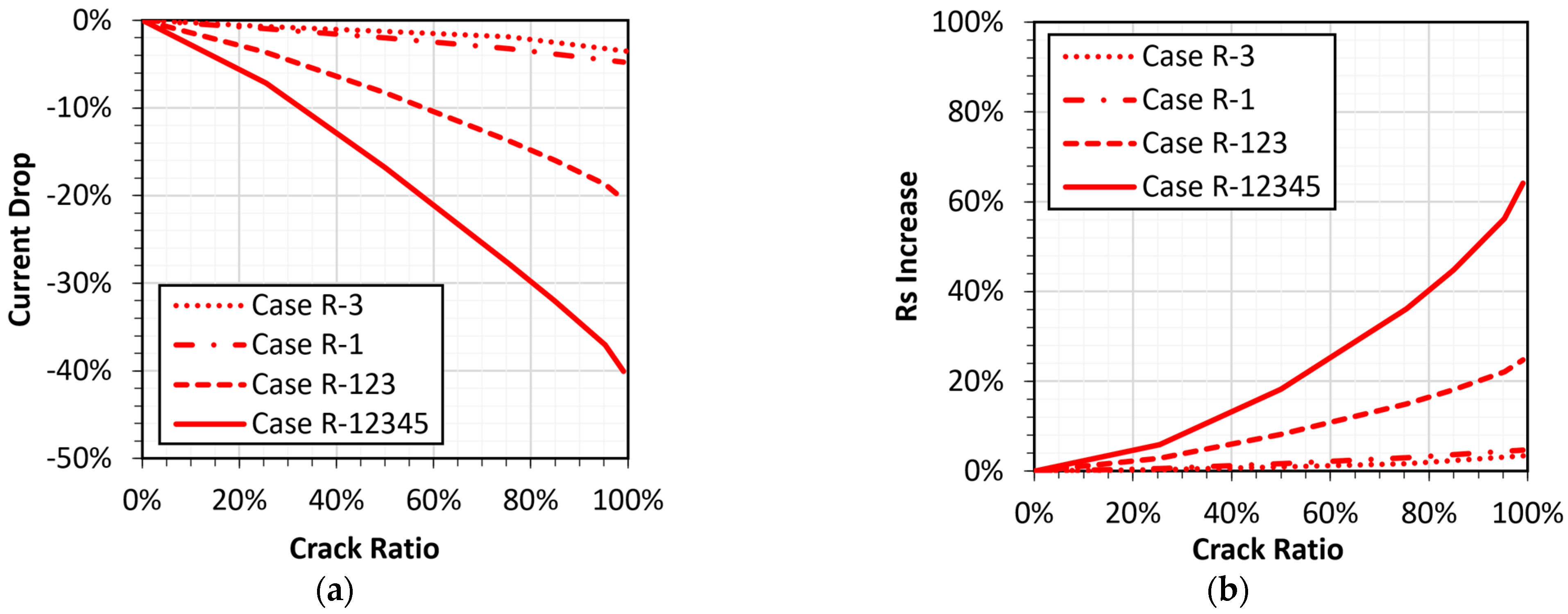
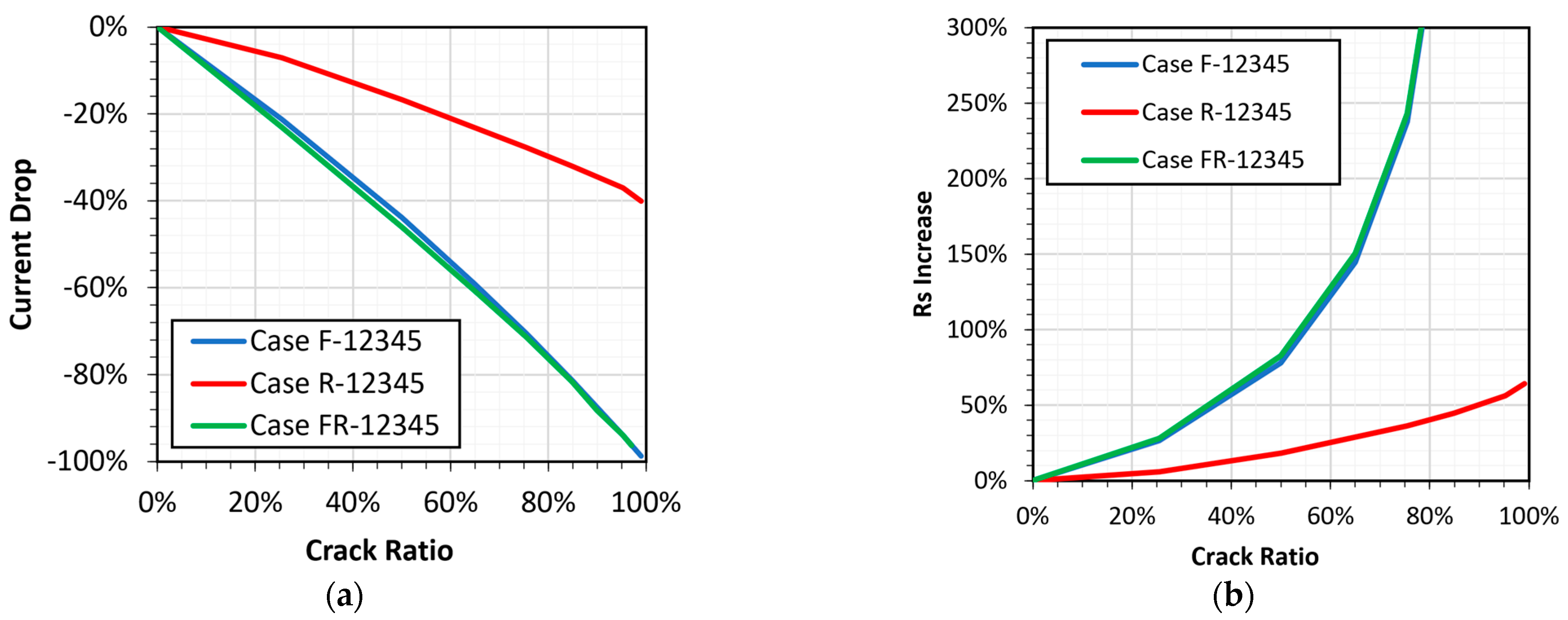
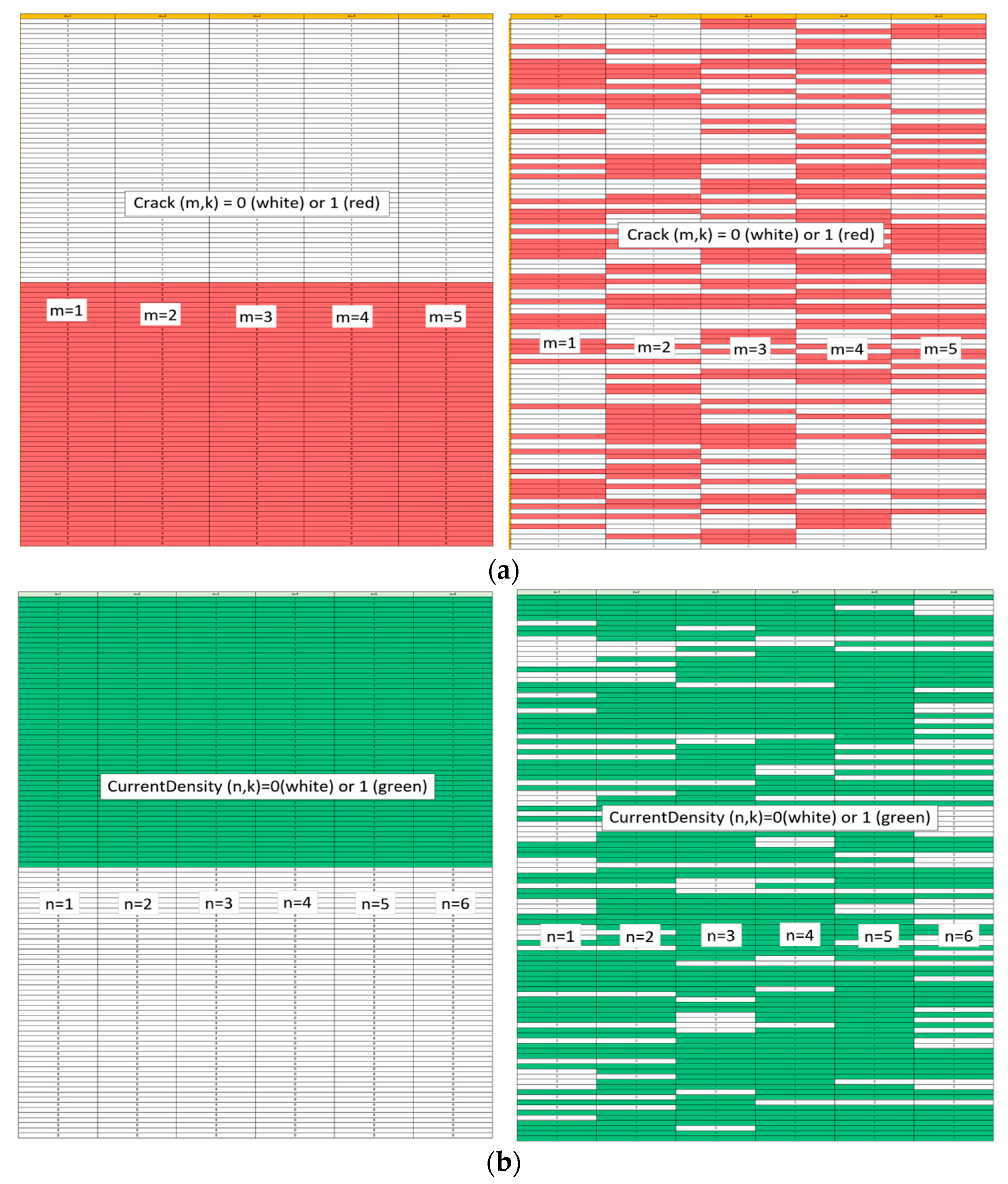
3.1. Cases with Continuous Cracks
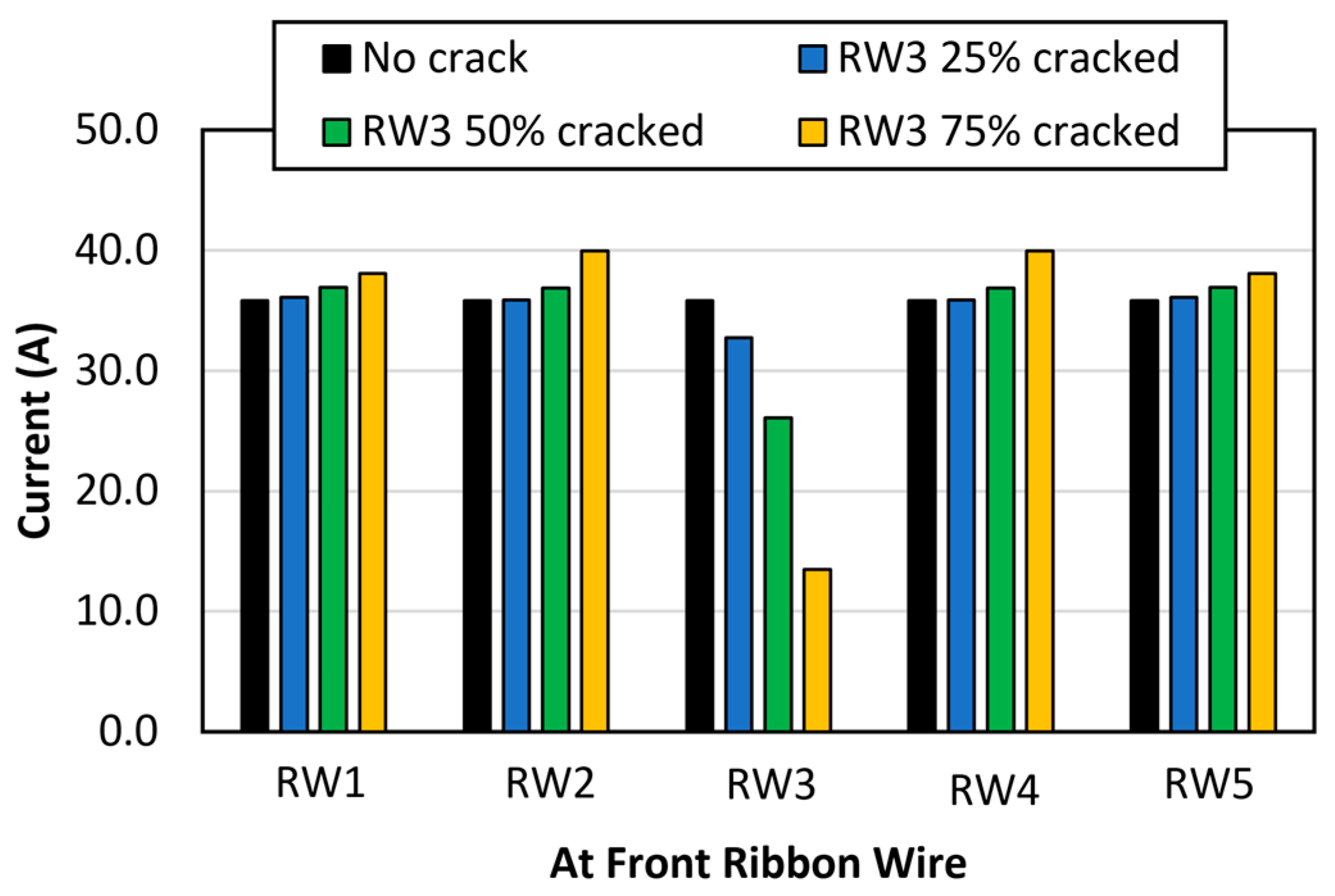
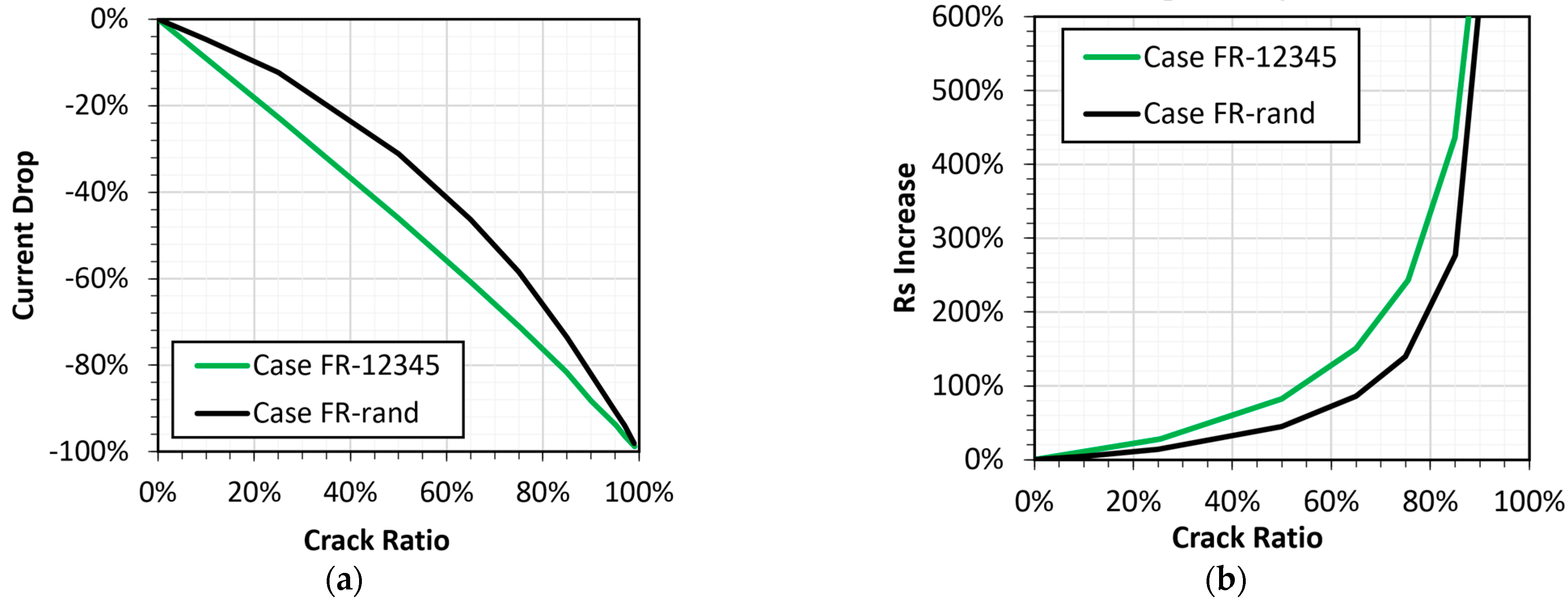
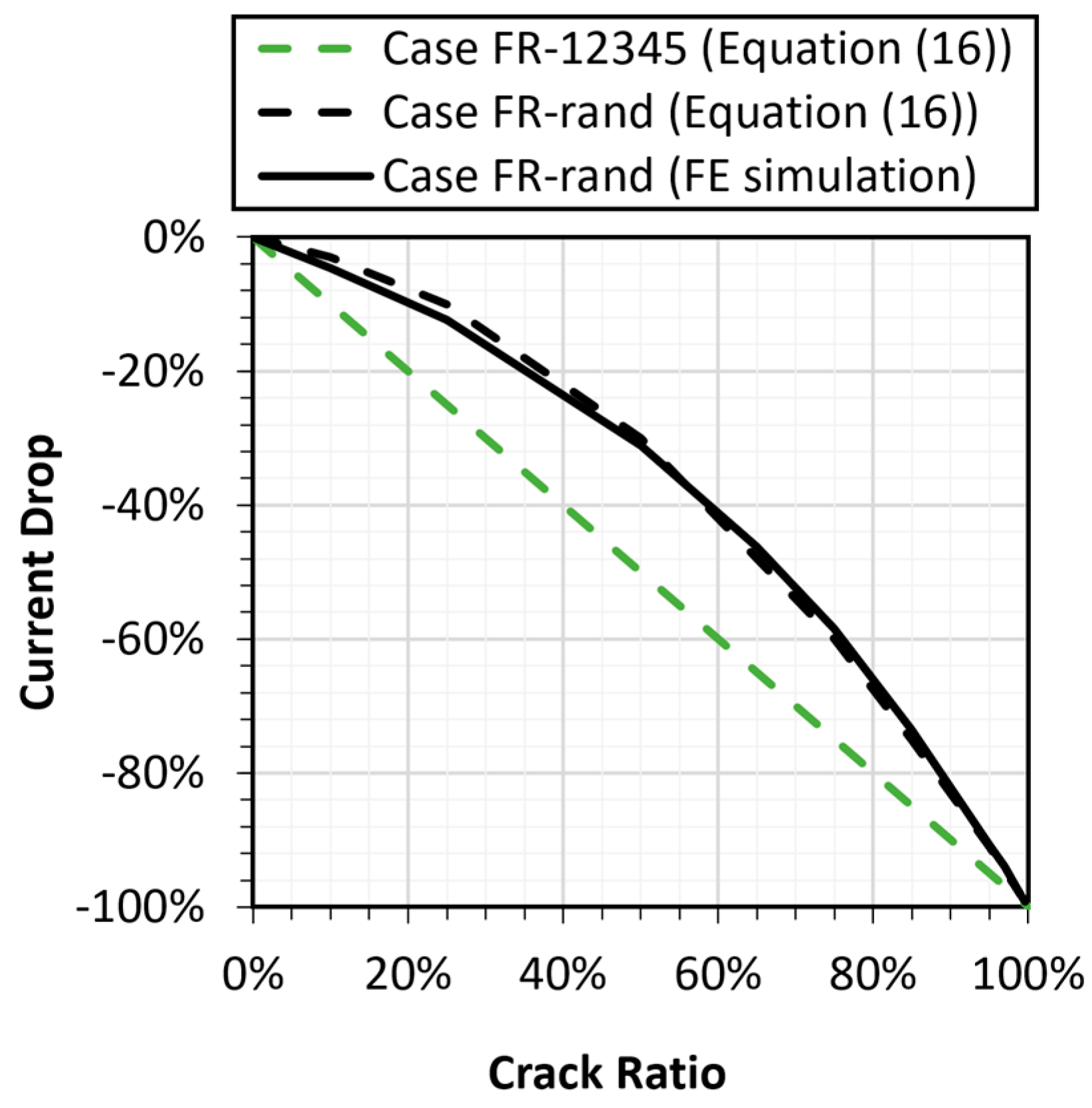
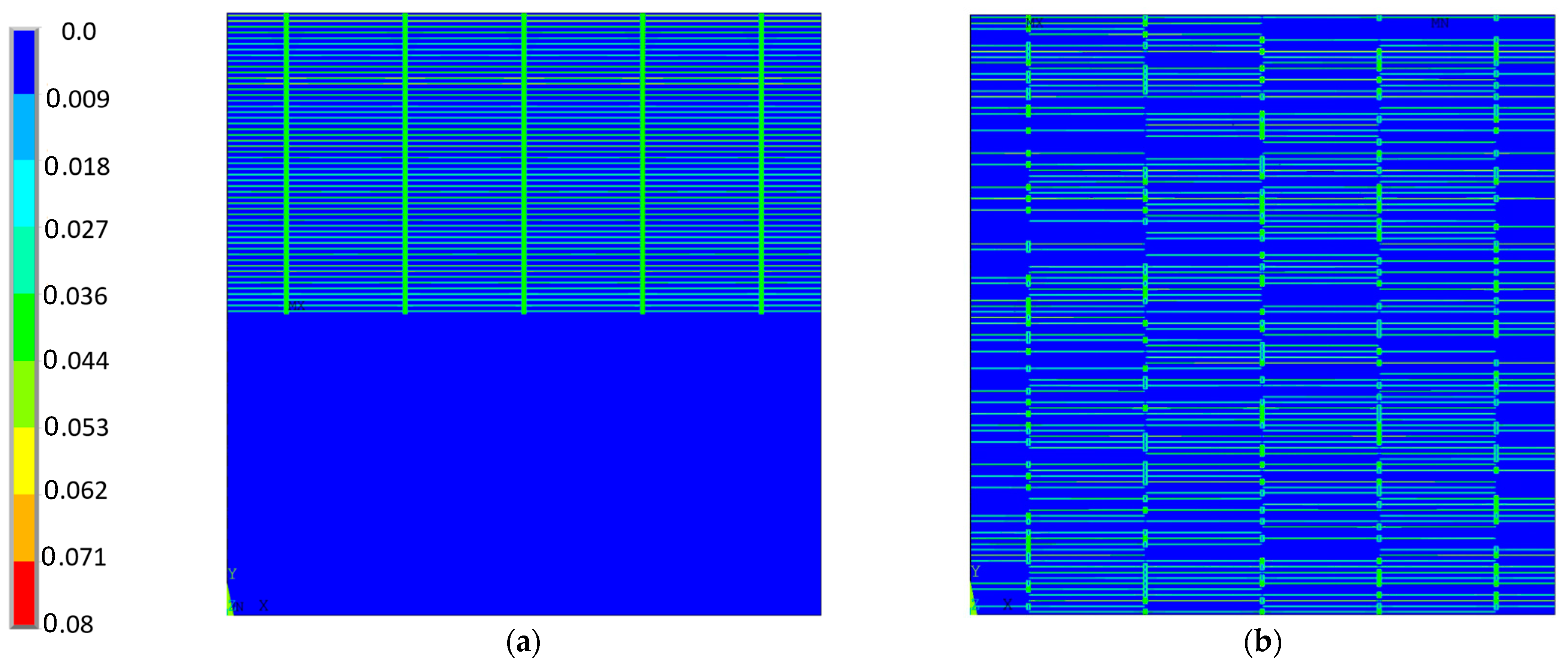
3.2. Case with Random Cracks
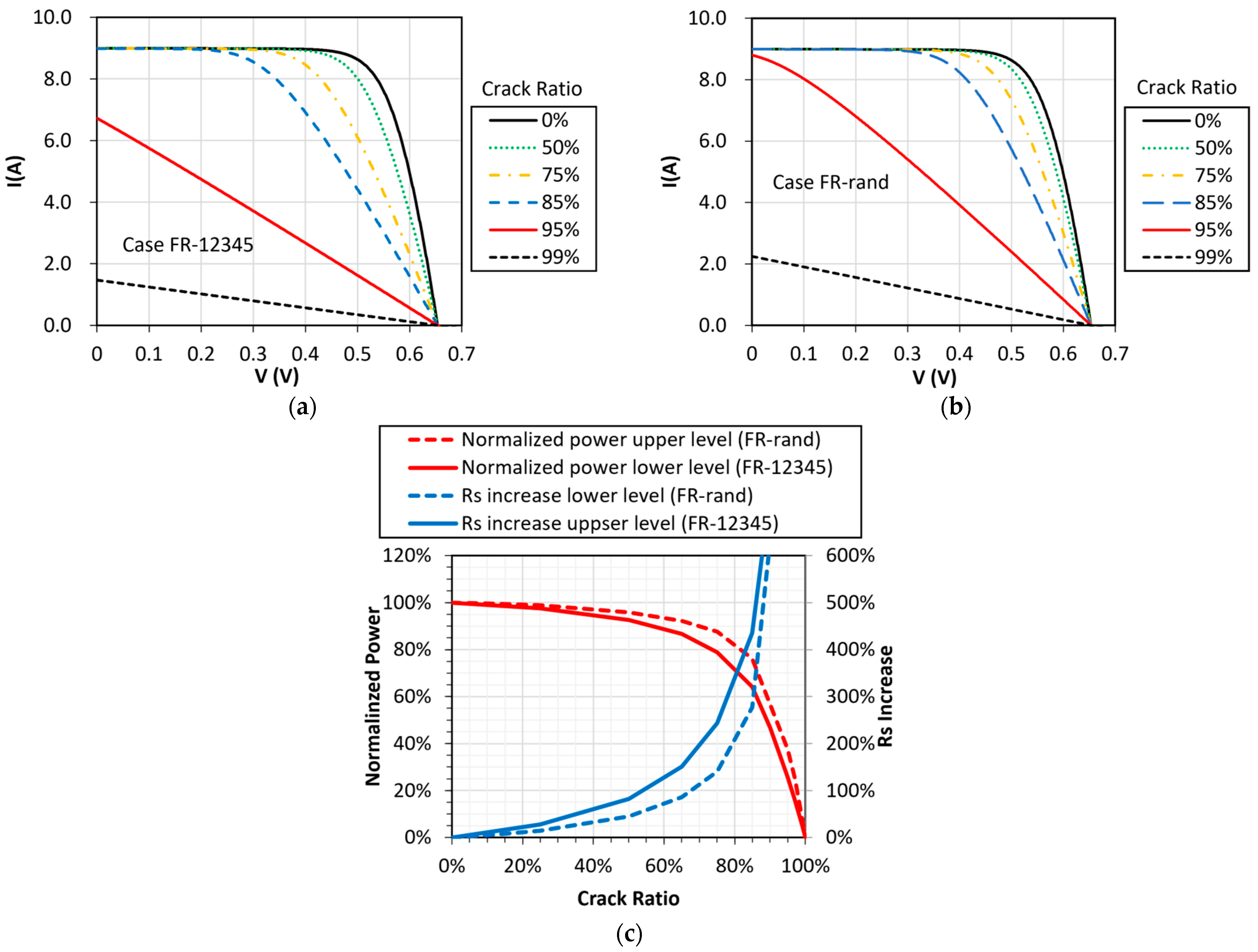
3.3. Power Drop Analysis
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jordan, D.C.; Silverman, T.J.; Wohlgemuth, J.H.; Kurtz, S.R.; VanSant, K.T. Photovoltaic failure and degradation modes. Prog. Photovolt. Res. Appl. 2017, 25, 318–326. [Google Scholar] [CrossRef]
- Skoczek, A.; Sample, T.; Dunlop, E.; Ossenbrink, H. Electrical performance results from physical stress testing of commercial PV modules to the IEC 61215 test sequence. Sol. Energy Mater. Sol. Cells 2008, 92, 1593–1604. [Google Scholar] [CrossRef]
- Jeong, J.; Park, N.; Hong, W.; Han, C. Analysis for the degradation mechanism of photovoltaic ribbon wire under thermal cycling. In Proceedings of the 2011 37th IEEE Photovoltaic Specialists Conference, Seattle, WA, USA, 19–24 June 2011. [Google Scholar]
- Jeong, J.; Park, N.; Han, C. Field failure mechanism study of solder interconnection for crystalline silicon photovoltaic module. Microelectron. Reliab. 2012, 52, 2326–2330. [Google Scholar] [CrossRef]
- Sharma, V.; Chandel, S.S. Performance and degradation analysis for long term reliability of solar photovoltaic systems: A review. Renew. Sustain. Energy Rev. 2013, 27, 753–767. [Google Scholar] [CrossRef]
- Kumar, S.; Gupta, R. Thermo-mechanical degradation at finger-solder interface in a crystalline silicon photovoltaic module under thermal fatigue conditions. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 0118–0121. [Google Scholar]
- Burgelman, M.; Nollet, P.; Degrave, S. Modelling polycrystalline semiconductor solar cells. Thin. Solid Films 2000, 361–362, 527–532. [Google Scholar] [CrossRef]
- Malm, U.; Edoff, M. 2D device modelling and finite element simulations for thin-film solar cells. Sol. Energy Mater. Sol. Cells 2009, 93, 1066–1069. [Google Scholar] [CrossRef]
- Brown, G.F.; Ager, J.W.; Walukiewicz, W.; Wu, J. Finite element simulations of compositionally graded InGaN solar cells. Sol. Energy Mater. Sol. Cells 2010, 94, 478–483. [Google Scholar] [CrossRef]
- Shiradkar, N.; Schneller, E.; Dhere, N.G. Finite element analysis based model to study the electric field distribution and leakage current in PV modules under high voltage bias. In Reliability of Photovoltaic Cells, Modules, Components, and Systems VI; SPIE: Bellingham, WA, USA, 2013; p. 88250G. [Google Scholar]
- Asadpour, R.; Sun, X.; Alam, M.A. Electrical Signatures of Corrosion and Solder Bond Failure in c-Si Solar Cells and Modules. IEEE J. Photovolt. 2019, 9, 759–767. [Google Scholar] [CrossRef]
- Asadpour, R.; Patel, M.T.; Clark, S.; Bosco, N.; Silverman, T.; Alam, M.A. Worldwide Physics-Based Lifetime Prediction of c-Si Modules Due to Solder-Bond Failure. IEEE J. Photovolt. 2022, 12, 533–539. [Google Scholar] [CrossRef]
- Ulaby, F.T.; Michielssen, E.; Ravaioli, U. Fundamentals of Applied Electromagnetics; Pearson: Boston, MA, USA, 2015. [Google Scholar]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- ANSYS. Chapter 5—Electromagnetics. In Mechanical APDL 2019 R2 Theory Reference; ANSYS: Canonsburg, PA, USA, 2019. [Google Scholar]
- ÇadIrlI, E.; Böyük, U.; Kaya, H.; Maraşli, N.; Aksöz, S.; Ocak, Y. Dependence of electrical resistivity on temperature and Sn content in Pb-Sn solders. J. Electron. Mater. 2011, 40, 195–200. [Google Scholar] [CrossRef]
- Giancoli, D. Electric currents and resistance. In Physics for Scientists and Engineers with Modern Physics; Pearson Education: New York, NY, USA, 2009; Volume 4. [Google Scholar]
- Serway, R.A.; Jewett, J.W. Principles of Physics; Saunders College Pub.: Fort Worth, TX, USA, 1998; Volume 1. [Google Scholar]
- López-Escalante, M.C.; Martín, F.; Ramos-Barrado, J. Grouping by bulk resistivity of production-line mono-crystalline silicon wafers and its influence on the manufacturing of solar cells modules. Sol. Energy 2016, 131, 61–70. [Google Scholar] [CrossRef]
- Guo, S.; Aberle, A.G.; Peters, M. Investigating local inhomogeneity effects of silicon wafer solar cells by circuit modelling. Energy Procedia 2013, 33, 110–117. [Google Scholar] [CrossRef]
- Grote, D. Analyses of Silicon Solar Cells and Their Measurement Methods by Distributed Circuit Simulations and by Experiment. Ph.D. Thesis, Universität Konstanz, Konstanz, Germany, 2010. [Google Scholar]
- Schroder, D.K.; Meier, D.L. Solar cell contact resistance—A review. IEEE Trans. Electron Devices 1984, 31, 637–647. [Google Scholar] [CrossRef]
- Honsberg, C.B.; Bowden, S.G. Photovoltaics Education Website. 2019. Available online: www.pveducation.org (accessed on 17 January 2023).
- Park, S.; Han, C. Reliability-driven design optimization of si solar module under thermal cycling. J. Mech. Sci. Technol. 2022, 36, 4099–4114. [Google Scholar] [CrossRef]
- Park, S.; Han, C. Analysis of EL images on Si solar module under thermal cycling. J. Mech. Sci. Technol. 2022, 36, 3429–3436. [Google Scholar] [CrossRef]
- Roy, S.; Kumar, S.; Gupta, R. Investigation and analysis of finger breakages in commercial crystalline silicon photovoltaic modules under standard thermal cycling test. Eng. Fail. Anal. 2019, 101, 309–319. [Google Scholar] [CrossRef]
- Schmauder, J.; Kurz, K.; Schneider, A. Extended Thermal Cycling Lifetime Testing on Crystalline Silicon Solar Modules with Artificially Introduced Defects. In NREL PV Module Reliability Workshop; NREL: Golden, CO, USA, 2016. [Google Scholar]
- IEC 61215-1; Terrestrial Photovoltaic (PV) Modules—Design Qualification and Type Approval—Part 1: Test Requirements. IEC: Geneva, Switzerland, 2016.
- Fuyuki, T.; Kondo, H.; Yamazaki, T.; Takahashi, Y.; Uraoka, Y. Photographic surveying of minority carrier diffusion length in polycrystalline silicon solar cells by electroluminescence. Appl. Phys. Lett. 2005, 86, 262108. [Google Scholar] [CrossRef]
- Analog Devices. LTspice. Available online: https://www.analog.com/en/design-center/design-tools-and-calculators/ltspice-simulator.html (accessed on 26 December 2022).







| Materials | Resistivities | References | |
|---|---|---|---|
| Solder (Pb40Sn60) | 1.50 × 10−4 Ω-mm | [16] | |
| Copper | 1.68 × 10−5 Ω-mm | [17] | |
| Silver | 1.59 × 10−5 Ω-mm | [18] | |
| Aluminum | 2.65 × 10−5 Ω-mm | [18] | |
| Si wafer | 30 Ω-mm | [19] | |
| 55 Ω/sq. | [20,21] | ||
| 0.3 Ω-mm2 | [20,21] | ||
| Notation | Description * | |
|---|---|---|
| Case 0 | No cracking | |
| Case F | Cracking in the RWs at front side: | |
| Case F-1 | continuously from bottom to top at RW1. | |
| Case F-3 | continuously from bottom to top at RW3. | |
| Case F-123 | continuously from bottom to top at RWs 1, 2, and 3. | |
| Case F-12345 | continuously from bottom to top at RWs 1, 2, 3, 4, and 5. | |
| Case R | Cracking in the RWs at rear side: | |
| Case R-1 | continuously from bottom to top at RW1. | |
| Case R-3 | continuously from bottom to top at RW3. | |
| Case R-123 | continuously from bottom to top at RWs 1, 2, and 3. | |
| Case R-12345 | continuously from bottom to top at RWs 1, 2, 3, 4, and 5. | |
| Case FR | Crack in the RWs at both front and rear sides: | |
| Case FR-12345 | continuously from bottom to top at RWs 1, 2, 3, 4, and 5. | |
| Case FR-rand | in random at RWs 1, 2, 3, 4, and 5. | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, C. Simulation of Series Resistance Increase through Solder Layer Cracking in Si Solar Cells under Thermal Cycling. Energies 2023, 16, 2524. https://doi.org/10.3390/en16062524
Han C. Simulation of Series Resistance Increase through Solder Layer Cracking in Si Solar Cells under Thermal Cycling. Energies. 2023; 16(6):2524. https://doi.org/10.3390/en16062524
Chicago/Turabian StyleHan, Changwoon. 2023. "Simulation of Series Resistance Increase through Solder Layer Cracking in Si Solar Cells under Thermal Cycling" Energies 16, no. 6: 2524. https://doi.org/10.3390/en16062524
APA StyleHan, C. (2023). Simulation of Series Resistance Increase through Solder Layer Cracking in Si Solar Cells under Thermal Cycling. Energies, 16(6), 2524. https://doi.org/10.3390/en16062524






