An Overview of Complex Instability Behaviors Induced by Nonlinearity of Power Electronic Systems with Memristive Load
Abstract
:1. Introduction
2. Reviews of Memristors and Memristive Characteristics
2.1. Concept and Characteristics of the Memristor
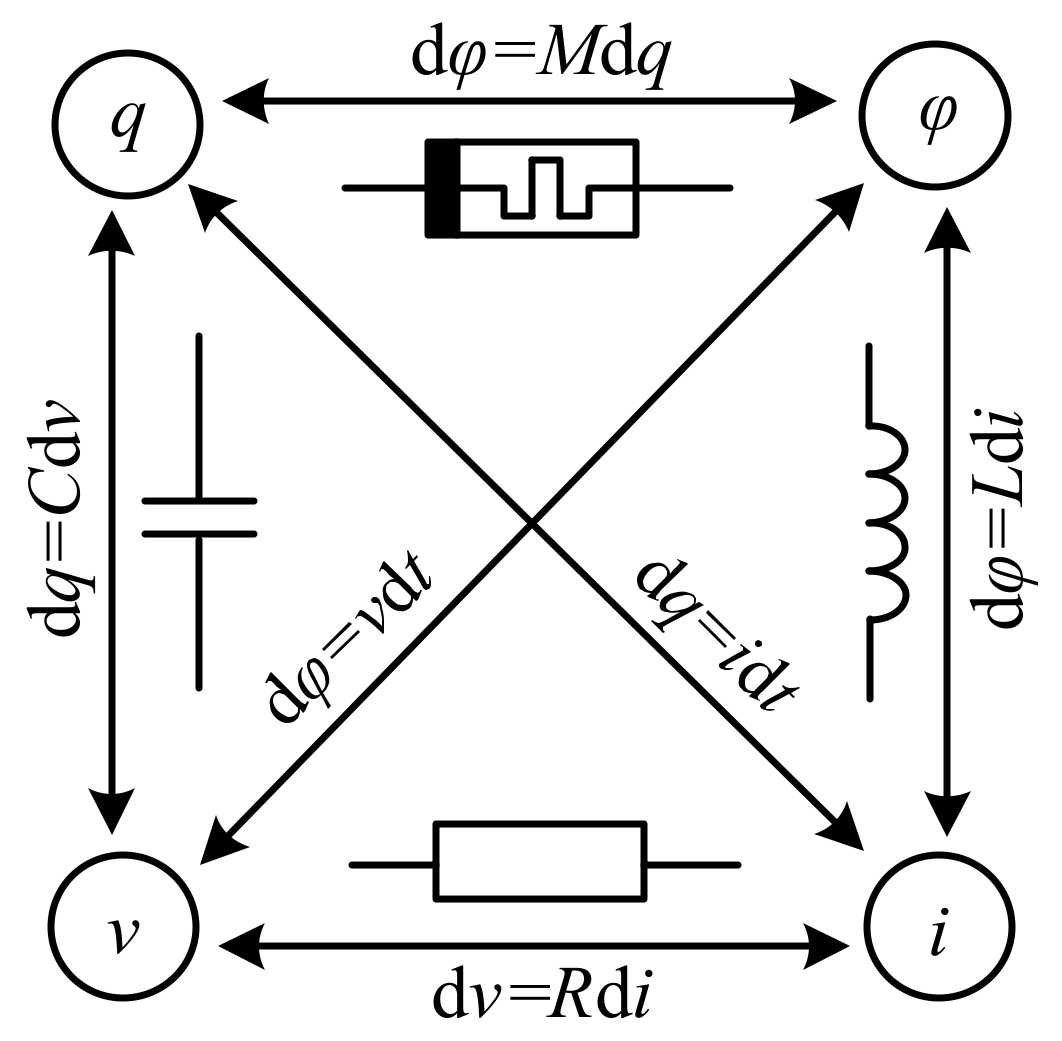
- Concept of the memristor
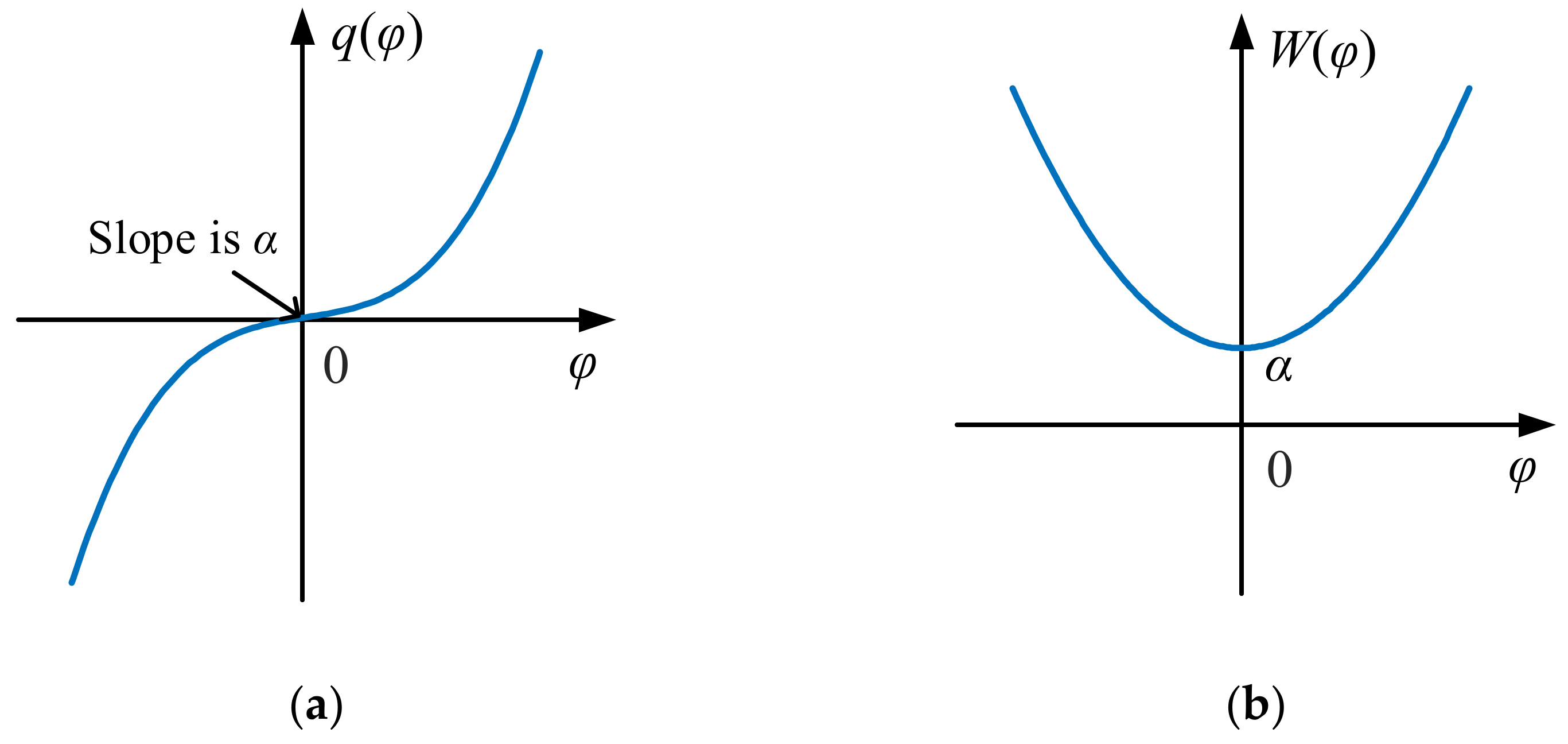
- Volt–ampere characteristic of memristors
| Item | Charge-Controlled Memristor | Flux-Controlled Memristor |
|---|---|---|
| Control variable | i(t) | v(t) |
| Expression | ||
| Characteristic curve | Figure 3a | Figure 3b |

- General definition of a memristor
- Essential characteristics of memristors
2.2. Research Actuality of Memristors
2.2.1. Memristor Model
- Physical model memristors
- Mathematical model memristors
| Item | [48] | [49] | [50] |
|---|---|---|---|
| Memristor | The cubic nonlinear flux-controlled memristor | The piecewise-quadratic flux-controlled memristor | The cubic polynomial flux-controlled memristor |
| Mathematical model | |||
| Memductance | |||
| Characteristic curve | Figure 5 | Figure 6 | Figure 7 |
| Maximum operation frequency | 500 Hz | 1.0 kHz | 15 kHz |

- Memristive equipment and systems
2.2.2. Operation Frequency Range of Memristors
2.2.3. Practical Application of Memristors
2.3. Deficiency in Research Actuality on the Memristor
3. Reviews of Power Electronic Systems and Their Complex Behaviors
3.1. Traditional Inverter and Multilevel Inverter
3.2. Load Types of the Inverter System
3.3. Research of Complex Dynamic Behavior in Power Electronic Systems
3.4. Classification and Control of Complex Dynamic Behavior
3.5. Modeling Methods for Analyzing Complex Dynamic Behaviors
3.6. The Deficiency of Complex Behavior Research in Power Electronic Systems
3.7. Complex Behaviors in the Power Converters with Memristive Loads
4. The Importance and Necessity of Complex Behaviors in Power Electronic Systems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L.O. Memristor-the missing circuit element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Sahin, M.E.; Taskiran, Z.G.C.; Guler, H.; Hamamci, S.E. Simulation and implementation of memristive chaotic system and its application for communication systems. Sens. Actuators A Phys. 2019, 290, 107–118. [Google Scholar] [CrossRef]
- Isah, A.; Nguetcho, A.S.T.; Binczak, S.; Bilbault, J.M. Memristor dynamics involved in cells communication for a 2D non-linear network. IET Signal Process. 2020, 14, 427–434. [Google Scholar] [CrossRef]
- Xiu, C.B.; Zhou, R.X.; Liu, Y.X. New chaotic memristive cellular neural network and its application in secure communication system. Chaos Solitons Fractals 2020, 141, 110316. [Google Scholar] [CrossRef]
- Ji, X.Y.; Dong, Z.K.; Lai, C.S.; Qi, D.L. A brain-inspired in-memory computing system for neuronal communication via memristive circuits. IEEE Commun. Mag. 2022, 60, 100–106. [Google Scholar] [CrossRef]
- Lee, T.H.; Hwang, H.G.; Woo, J.U.; Kim, D.H.; Kim, T.W.; Nahm, S. Synaptic plasticity and metaplasticity of biological synapse realized in a KNbO3 memristor for application to artificial synapse. ACS Appl. Mater. Interfaces 2018, 10, 25673–25682. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Ye, W.B.; Zhou, K.; Chen, H.Y.; Yang, J.Q.; Ding, G.L.; Chen, X.L.; Zhou, Y.; Zhou, L.; Li, F.J.; et al. Bioinspired artificial sensory nerve based on nafion memristor. Adv. Funct. Mater. 2019, 29, 1808783. [Google Scholar] [CrossRef]
- Wu, L.D.; Wang, Z.W.; Wang, B.W.; Chen, Q.Y.; Bao, L.; Yu, Z.Z.; Yang, Y.F.; Ling, Y.T.; Qin, Y.B.; Tang, K.C.; et al. Emulation of biphasic plasticity in retinal electrical synapses for light-adaptive pattern pre-processing. Nanoscale 2021, 13, 3483–3492. [Google Scholar] [CrossRef]
- Dai, Y.H.; Wang, X.Q.; Yang, B. An improved memristor model based on the electrochemical metallization effect as a synapse for biomimetic applications. Phys. Status Solidi B Basic Solid State Phys. 2021, 259, 2100379. [Google Scholar] [CrossRef]
- Liu, S.J.; Wang, Y.Z.; Fardad, M.; Varshney, P.K. A memristor-based optimization framework for artificial intelligence applications. IEEE Circuits Syst. Mag. 2018, 18, 29–44. [Google Scholar] [CrossRef]
- Hajto, D.; Rak, A.; Cserey, G. Robust memristor networks for neuromorphic computation applications. Materials 2019, 12, 3573. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miranda, E.; Sune, J. Memristors for neuromorphic circuits and artificial intelligence applications. Materials 2020, 13, 938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pei, Y.F.; Li, Z.Q.; Li, B.; Zhao, Y.; He, H.; Yan, L.; Li, X.Y.; Wang, J.J.; Zhao, Z.; Sun, Y.; et al. A multifunctional and efficient artificial visual perception nervous system with Sb2Se3/CdS-core/shell (SC) nanorod arrays optoelectronic memristor. Adv. Funct. Mater. 2022, 32, 2203454. [Google Scholar] [CrossRef]
- Duan, S.K.; Hu, X.F.; Wang, L.D.; Li, C.D.; Mazumder, P. Memristor-based RRAM with applications. Sci. China Inf. Sci. 2012, 55, 1446–1460. [Google Scholar] [CrossRef]
- Kim, K.H.; Gaba, S.; Wheeler, D.; Cruz-Albrecht, J.M.; Hussain, T.; Srinivasa, N.; Lu, W. A functional hybrid memristor crossbar-array/CMOS system for data storage and neuromorphic applications. Nano Lett. 2012, 12, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Liu, G.; Wang, C.; Zhang, W.B.; Li, R.W.; Wang, L.X. Polymer memristor for information storage and neuromorphic applications. Mater. Horiz. 2014, 1, 489–506. [Google Scholar] [CrossRef]
- Qian, W.H.; Cheng, X.F.; Zhou, J.; He, J.H.; Li, H.; Xu, Q.F.; Li, N.J.; Chen, D.Y.; Yao, Z.G.; Lu, J.M. Lead-free perovskite MASnBr3-based memristor for quaternary information storage. InfoMat 2020, 2, 743–751. [Google Scholar] [CrossRef] [Green Version]
- Priyanka, M.M.; Ravi, T. Survey on role of memristor in electronics. In Proceedings of the 2015 IEEE International Conference on Control, Instrumentation, Communication and Computational Technologies (ICCICCT), Thuckalay, India, 18–19 December 2015; pp. 722–726. [Google Scholar]
- Chen, Q.Y.; Lin, M.; Wang, Z.W.; Zhao, X.L.; Cai, Y.M.; Liu, Q.; Fang, Y.C.; Yang, Y.C.; He, M.; Huang, R. Low power parylene-based memristors with a graphene barrier layer for flexible electronics applications. Adv. Electron. Mater. 2019, 5, 1800852. [Google Scholar] [CrossRef]
- Yang, Y.; Du, H.Y.; Xue, Q.; Wei, X.H.; Yang, Z.B.; Xu, C.G.; Lin, D.M.; Jie, W.J.; Hao, J.H. Three-terminal memtransistors based on two-dimensional layered gallium selenide nanosheets for potential low-power electronics applications. Nano Energy 2019, 57, 566–573. [Google Scholar] [CrossRef]
- Yang, J.; Lee, H.; Jeong, J.H.; Kim, T.; Lee, S.H.; Song, T. Circuit-level exploration of ternary logic using memristors and MOSFETs. IEEE Trans. Circuits Syst. I Regul. Pap. 2022, 69, 707–720. [Google Scholar] [CrossRef]
- Chua, L.O. The fourth element. Proc. IEEE 2012, 100, 1920–1927. [Google Scholar] [CrossRef]
- Chua, L.O. If it’s pinched it’s a memristor. Semicond. Sci. Technol. 2014, 29, 104001. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive devices and systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Adhikari, S.P.; Sah, M.P.; Kim, H.; Chua, L.O. Three fingerprints of memristor. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 3008–3021. [Google Scholar] [CrossRef]
- Wang, X.B.; Chen, Y.R.; Xi, H.W.; Li, H.; Dimitrov, D. Spintronic memristor through spin-torque-induced magnetization motion. IEEE Electron Device Lett. 2009, 30, 294–297. [Google Scholar] [CrossRef]
- Mostafa, H.; Ismail, Y. Process variation aware design of multi-valued spintronic memristor-based memory arrays. IEEE Trans. Semicond. Manuf. 2016, 29, 145–152. [Google Scholar] [CrossRef]
- Huang, W.C.; Fang, Y.W.; Yin, Y.W.; Tian, B.B.; Zhao, W.B.; Hou, C.M.; Ma, C.; Li, Q.; Tsymbal, E.Y.; Duan, C.G.; et al. Solid-state synapse based on magnetoelectrically coupled memristor. ACS Appl. Mater. Interfaces 2018, 10, 5649–5656. [Google Scholar] [CrossRef]
- Nafea, S.F.; Dessouki, A.A.S.; El-Rabaie, S.; Elnaghi, B.E.; Ismail, Y.; Mostafa, H. An accurate model of domain-wall-based spintronic memristor. Integration 2019, 65, 149–162. [Google Scholar] [CrossRef]
- Zakhidov, A.A.; Jung, B.; Slinker, J.D.; Abruna, H.D.; Malliaras, G.G. A light-emitting memristor. Org. Electron. 2010, 11, 150–153. [Google Scholar] [CrossRef]
- Maier, P.; Hartmann, F.; Dias, M.R.S.; Emmerling, M.; Schneider, C.; Castelano, L.K.; Kamp, M.; Marques, G.E.; Lopez-Richard, V.; Worschech, L.; et al. Light sensitive memristor with bi-directional and wavelength-dependent conductance control. Appl. Phys. Lett. 2016, 109, 023501. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.B.; Wu, C.X.; Xu, Z.W.; Liu, Y.; Hu, H.L.; Guo, T.L.; Kim, T.W.; Chai, Y.; Li, F.S. Light-emitting memristors for optoelectronic artificial efferent nerve. Nano Lett. 2021, 21, 6087–6094. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Zhao, W.S.; Kang, W.; Zhang, Y.; Klein, J.O.; Ravelosona, D.; Zhang, Y.G.; Chappert, C. Nonvolatile boolean logic block based on ferroelectric tunnel memristor. IEEE Trans. Magn. 2014, 50, 9100604. [Google Scholar] [CrossRef]
- Wang, Z.H.; Zhao, W.S.; Kang, W.; Zhang, Y.; Klein, J.O.; Ravelosona, D.; Chappert, C. Compact modelling of ferroelectric tunnel memristor and its use for neuromorphic simulation. Appl. Phys. Lett. 2014, 104, 053505. [Google Scholar] [CrossRef]
- Mikheev, V.; Chouprik, A.; Lebedinskii, Y.; Zarubin, S.; Matveyev, Y.; Kondratyuk, E.; Kozodaev, M.G.; Markeev, A.M.; Zenkevich, A.; Negrov, D. Ferroelectric second-order memristor. ACS Appl. Mater. Interfaces 2019, 11, 32108–32114. [Google Scholar] [CrossRef] [PubMed]
- McConville, J.P.V.; Lu, H.D.; Wang, B.; Tan, Y.Z.; Cochard, C.; Conroy, M.; Moore, K.; Harvey, A.; Bangert, U.; Chen, L.Q.; et al. Ferroelectric domain wall memristor. Adv. Funct. Mater. 2020, 30, 2000109. [Google Scholar] [CrossRef]
- Samardzic, N.; Bajac, B.; Srdic, V.V.; Stojanovic, G.M. Conduction mechanisms in multiferroic multilayer BaTiO3/NiFe2O4/BaTiO3 memristors. J. Electron. Mater. 2017, 46, 5492–5496. [Google Scholar] [CrossRef]
- Samardzic, N.M.; Bajac, B.; Bajic, J.; Durdic, E.; Miljevic, B.; Srdic, V.V.; Stojanovic, G.M. Photoresistive switching of multiferroic thin film memristors. Microelectron. Eng. 2018, 187, 139–143. [Google Scholar] [CrossRef]
- Sun, B.; Zhou, G.D.; Sun, L.F.; Zhao, H.B.; Chen, Y.Z.; Yang, F.; Zhao, Y.; Song, Q.L. ABO3 multiferroic perovskite materials for memristive memory and neuromorphic computing. Nanoscale Horiz. 2021, 6, 939–970. [Google Scholar] [CrossRef]
- Torrezan, A.C.; Strachan, J.P.; Medeiros-Ribeiro, G.; Williams, R.S. Sub-nanosecond switching of a tantalum oxide memristor. Nanotechnology 2011, 22, 485203. [Google Scholar] [CrossRef]
- Leon, J.J.D.; Norris, K.J.; Yang, J.J.; Sevic, J.F.; Kobayashi, N.P. A niobium oxide-tantalum oxide selector-memristor self-aligned nanostack. Appl. Phys. Lett. 2017, 110, 103102. [Google Scholar]
- Mladenov, V.; Kirilov, S. A simplified tantalum oxide memristor model, parameters estimation and application in memory crossbars. Technologies 2022, 10, 6. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H.; Hwang, S.; Kim, M.H.; Chang, Y.F.; Park, B.G. Analog synaptic behavior of a silicon nitride memristor. ACS Appl. Mater. Interfaces 2017, 9, 40420–40427. [Google Scholar] [CrossRef]
- Gismatulin, A.A.; Gritsenko, V.A.; Yen, T.J.; Chin, A. Charge transport mechanism in SiNx-based memristor. Appl. Phys. Lett. 2019, 115, 253502. [Google Scholar] [CrossRef]
- Gismatulin, A.A.; Kamaev, G.N.; Kruchinin, V.N.; Gritsenko, V.A.; Orlov, O.M.; Chin, A. Charge transport mechanism in the forming-free memristor based on silicon nitride. Sci. Rep. 2021, 11, 2417. [Google Scholar] [CrossRef] [PubMed]
- Kochergin, V.S.; Yakimov, A.V.; Klyuev, A.V.; Filatov, D.O.; Gorshkov, O.N.; Antonov, D.A.; Mikhaylov, A.N.; Sunyaikin, D.V.; Shtraub, N.I.; Vasileiadis, N.; et al. Effect of SiO2 sublayer on the retention characteristics of nanometer-sized Si3N4 memristive devices investigated by low-frequency noise spectroscopy. Jpn. J. Appl. Phys. 2022, 61, SM1013. [Google Scholar] [CrossRef]
- Muthuswamy, B. Implementing memristor based chaotic circuits. Int. J. Bifurc. Chaos 2010, 20, 1335–1350. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Zhou, G.H.; Ma, Z.H.; Zou, L. Chaotic memristive circuit: Equivalent circuit realization and dynamical analysis. Chin. Phys. B 2011, 20, 120502. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.Q.; Ma, X.K. A unified cubic flux-controlled memristor: Theoretical analysis, simulation and circuit experiment. Int. J. Numer. Model. Electron. Netw. Devices Fields 2015, 28, 335–345. [Google Scholar] [CrossRef]
- Wu, R.P.; Wang, C.H. A new simple chaotic circuit based on memristor. Int. J. Bifurc. Chaos 2016, 26, 1650145. [Google Scholar] [CrossRef]
- Dong, Y.J.; Wang, G.Y.; Chen, G.R.; Shen, Y.R.; Ying, J.J. A bistable nonvolatile locally-active memristor and its complex dynamics. Commun. Nonlinear Sci. Numer. Simul. 2020, 84, 105203. [Google Scholar] [CrossRef]
- Lin, D.; Chua, L.O.; Hui, S.Y. The first man-made memristor: Circa 1801 [Scanning Our Past]. Proc. IEEE 2015, 103, 131–136. [Google Scholar] [CrossRef]
- Gandhi, G.; Aggarwal, V.; Chua, L.O. The detectors used in the first radios were memristors. In Memristor Networks; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 53–66. [Google Scholar]
- Prodromakis, T.; Toumazou, C.; Chua, L.O. Two centuries of memristors. Nat. Mater. 2012, 11, 478–481. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, G.; Aggarwal, V.; Chua, L.O. The first radios were made using memristors. IEEE Circuits Syst. Mag. 2013, 13, 8–16. [Google Scholar] [CrossRef]
- Lin, D.Y.; Hui, S.Y.R.; Chua, L.O. Gas discharge lamps are volatile memristors. IEEE Trans. Circuits Syst. I Regul. Pap. 2014, 61, 2066–2073. [Google Scholar] [CrossRef] [Green Version]
- Corinto, F.; Ascoli, A. Memristive diode bridge with LCR filter. Electron. Lett. 2012, 48, 824–825. [Google Scholar] [CrossRef]
- Wu, H.G.; Bao, B.C.; Xu, Q. First order generalized memrsitor emulator based on diode bridge and series RL filter. Acta Electron. Sin. 2015, 43, 2129–2132. [Google Scholar]
- Bao, B.C.; Xu, L.; Wu, Z.M.; Chen, M.; Wu, H.G. Coexistence of multiple bifurcation modes in memristive diode-bridge based canonical Chua’s circuit. Int. J. Electron. 2018, 105, 1159–1169. [Google Scholar] [CrossRef]
- Pershin, Y.V.; Di Ventra, M. Practical approach to programmable analog circuits with memristors. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 1857–1864. [Google Scholar] [CrossRef] [Green Version]
- Abuelma’atti, M.T.; Khalifa, Z.J. A new memristor emulator and its application in digital modulation. Analog. Integr. Circuits Signal Process. 2014, 80, 577–584. [Google Scholar] [CrossRef]
- Abuelma’atti, M.T.; Khalifa, Z.J. A continuous-level memristor emulator and its application in a multivibrator circuit. AEU-Int. J. Electron. Commun. 2015, 69, 771–775. [Google Scholar] [CrossRef]
- Sánchez-López, C.; Carrasco-Aguilar, M.A.; Muñiz-Montero, C. A 16Hz–160kHz memristor emulator circuit. AEU-Int. J. Electron. Commun. 2015, 69, 1208–1219. [Google Scholar] [CrossRef]
- Alharbi, A.G.; Fouda, M.E.; Khalifa, Z.J.; Chowdhury, M.H. Electrical nonlinearity emulation technique for current-controlled memristive devices. IEEE Access 2017, 5, 5399–5409. [Google Scholar] [CrossRef]
- Ayten, U.E.; Minaei, S.; Sagbas, M. Memristor emulator circuits using single CBTA. AEU-Int. J. Electron. Commun. 2017, 82, 109–118. [Google Scholar] [CrossRef]
- Sanchez-Lopez, C.; Aguila-Cuapio, L.E. A 860 kHz grounded memristor emulator circuit. AEU-Int. J. Electron. Commun. 2017, 73, 23–33. [Google Scholar] [CrossRef]
- Yesil, A.; Babacan, Y.; Kacar, F. A new DDCC based memristor emulator circuit and its applications. Microelectron. J. 2014, 45, 282–287. [Google Scholar] [CrossRef]
- Yesil, A. A new grounded memristor emulator based on MOSFET-C. AEU-Int. J. Electron. Commun. 2018, 91, 143–149. [Google Scholar] [CrossRef]
- Ranjan, R.K.; Sagar, S.; Roushan, S.; Kumari, B.; Rani, N.; Khateb, F. High-frequency floating memristor emulator and its experimental results. IET Circuits Devices Syst. 2019, 13, 292–302. [Google Scholar] [CrossRef]
- Raj, N.; Ranjan, R.K.; Khateb, F. Flux-controlled memristor emulator and its experimental results. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 1050–1061. [Google Scholar] [CrossRef]
- Prasad, S.S.; Kumar, P.; Ranjan, R.K. Resistorless memristor emulator using CFTA and its experimental verification. IEEE Access 2021, 9, 64065–64075. [Google Scholar] [CrossRef]
- Adesina, N.O.; Khan, M.A.U.; Jian, X. CMOS transistor-based memristor emulator circuit design for high frequency applications. In Proceedings of the 2021 IEEE 12th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 27–30 October 2021. [Google Scholar]
- Vista, J.; Ranjan, A. Flux controlled floating memristor employing VDTA: Incremental or decremental operation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 364–372. [Google Scholar] [CrossRef]
- Sagar; Raj, N.; Verma, V.K. Electronically tunable flux-controlled resistorless memristor emulator. IEEE Can. J. Electr. Comput. Eng. 2022, 45, 311–317. [Google Scholar] [CrossRef]
- Prasad, S.S.; Kumar, P.; Raj, N. A compact floating and grounded memristor model using single active element. AEU-Int. J. Electron. Commun. 2022, 157, 154426. [Google Scholar] [CrossRef]
- Guan, W.H.; Long, S.B.; Liu, Q.; Liu, M.; Wang, W. Nonpolar nonvolatile resistive switching in Cu doped ZrO2. IEEE Electron Device Lett. 2008, 29, 434–437. [Google Scholar] [CrossRef]
- Faruque, K.A.; Biswas, B.R.; Rashid, A.B.M.H.U. Memristor-based low-power high-speed nonvolatile hybrid memory array design. Circuits Syst. Signal Process. 2017, 36, 3585–3597. [Google Scholar] [CrossRef]
- Wong, C.W.I.; Ho, P.W.C. Multilevel memristive non-volatile look-up table using two transmission gates one memristor memory cells. Semicond. Sci. Technol. 2020, 35, 105019. [Google Scholar]
- Wu, L.; Liu, H.X.; Lin, J.F.; Wang, S.L. Volatile and nonvolatile memory operations implemented in a Pt/HfO/Ti memristor. IEEE Trans. Electron Devices 2021, 68, 1622–1626. [Google Scholar] [CrossRef]
- Bao, B.C.; Xu, J.P.; Liu, Z. Initial state dependent dynamical behaviors in a memristor based chaotic circuit. Chin. Phys. Lett. 2010, 27, 070504. [Google Scholar]
- Guo, M.; Xue, Y.B.; Gao, Z.H.; Zhang, Y.M.; Dou, G. Dynamic analysis of a physical SBT memristor-based chaotic circuit. Int. J. Bifurc. Chaos 2018, 27, 1730047. [Google Scholar] [CrossRef]
- Sun, J.W.; Zhao, X.T.; Fang, J.; Wang, Y.F. Autonomous memristor chaotic systems of infinite chaotic attractors and circuitry realization. Nonlinear Dyn. 2018, 94, 2879–2887. [Google Scholar] [CrossRef]
- Lai, Q.; Wan, Z.Q.; Kengne, L.K.; Kuate, P.D.K.; Chen, C.Y. Two-memristor-based chaotic system with infinite coexisting attractors. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2197–2201. [Google Scholar] [CrossRef]
- Papandroulidakis, G.; Vourkas, I.; Vasileiadis, N.; Sirakoulis, G.C. Boolean logic operations and computing circuits based on memristors. IEEE Trans. Circuits Syst. II Express Briefs 2014, 61, 972–976. [Google Scholar] [CrossRef]
- Wang, H.P.; Lin, C.C.; Wu, C.C.; Chen, Y.C.; Wang, C.Y. On synthesizing memristor-based logic circuits with minimal operational pulses. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 2842–2852. [Google Scholar] [CrossRef]
- Luo, L.; Dong, Z.K.; Duan, S.K.; Lai, C.S. Memristor-based stateful logic gates for multi-functional logic circuit. IET Circuits Devices Syst. 2020, 14, 811–818. [Google Scholar] [CrossRef]
- Liu, G.Z.; Shen, S.H.; Jin, P.P.; Wang, G.Y.; Liang, Y. Design of memristor-based combinational logic circuits. Circuits Syst. Signal Process. 2021, 40, 5825–5846. [Google Scholar] [CrossRef]
- Sozen, H.; Cam, U. First-order memristor-capacitor filter circuits employing HP memristor. J. Circuits Syst. Comput. 2014, 23, 1450116. [Google Scholar] [CrossRef]
- Bao, B.C.; Wu, P.Y.; Bao, H.; Chen, M.; Xu, Q. Chaotic bursting in memristive diode bridge-coupled Sallen-Key lowpass filter. Electron. Lett. 2017, 53, 1104–1105. [Google Scholar] [CrossRef]
- Yu, Y.B.; Yang, N.J.; Yang, C.Y.; Nyima, T. Memristor bridge-based low pass filter for image processing. J. Syst. Eng. Electron. 2019, 30, 448–455. [Google Scholar] [CrossRef]
- Zhao, G.K.; You, B.; Wen, X.; Luo, G.Q. A reconfigurable dual-band bandpass filter using memristive switches. J. Electromagn. Waves Appl. 2022, 36, 115–130. [Google Scholar] [CrossRef]
- Cai, Z.W.; Huang, L.H. Functional differential inclusions and dynamic behaviors for memristor-based BAM neural networks with time-varying delays. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1279–1300. [Google Scholar] [CrossRef]
- Nourazar, M.; Rashtchi, V.; Azarpeyvand, A.; Merrikh-Bayat, F. Code acceleration using memristor-based approximate matrix multiplier: Application to convolutional neural networks. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 2684–2695. [Google Scholar] [CrossRef]
- Wang, J.M.; Liu, F.Q.; Qin, S.T. Global exponential stability of uncertain memristor-based recurrent neural networks with mixed time delays. Int. J. Mach. Learn. Cybern. 2019, 10, 743–755. [Google Scholar] [CrossRef]
- Huang, L.X.; Yu, H.Q.; Chen, C.L.; Peng, J.; Diao, J.T.; Nie, H.S.; Li, Z.W.; Liu, H.J. A training strategy for improving the robustness of memristor-based binarized convolutional neural networks. Semicond. Sci. Technol. 2022, 37, 015013. [Google Scholar] [CrossRef]
- Yener, S.C.; Uygur, A.; Kuntman, H.H. Ultra low-voltage ultra low-power memristor based band-pass filter design and its application to EEG signal processing. Analog. Integr. Circuits Signal Process. 2016, 89, 719–726. [Google Scholar] [CrossRef]
- Liu, Z.W.; Tang, J.S.; Gao, B.; Li, X.Y.; Yao, P.; Lin, Y.D.; Liu, D.K.; Hong, B.; Qian, H.; Wu, H.Q. Multichannel parallel processing of neural signals in memristor arrays. Sci. Adv. 2020, 6, eabc4797. [Google Scholar] [CrossRef]
- Zhong, Y.A.; Tang, J.S.; Li, X.Y.; Gao, B.; Qian, H.; Wu, H.Q. Dynamic memristor-based reservoir computing for high-efficiency temporal signal processing. Nat. Commun. 2021, 12, 408. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Liu, Z.W.; Tang, J.S.; Gao, B.; Zhang, Y.F.; Qian, H.; Wu, H.Q. Memristor-based signal processing for edge computing. Tsinghua Sci. Technol. 2022, 27, 455–471. [Google Scholar] [CrossRef]
- Lin, T.C.; Huang, F.Y.; Du, Z.B.; Lin, Y.C. Synchronization of fuzzy modeling chaotic time delay memristor-based Chua’s circuits with application to secure communication. Int. J. Fuzzy Syst. 2015, 17, 206–214. [Google Scholar] [CrossRef]
- Li, H.Z.; Hua, Z.Y.; Bao, H.; Zhu, L.; Chen, M.; Bao, B.C. Two-dimensional memristive hyperchaotic maps and application in secure communication. IEEE Trans. Ind. Electron. 2021, 68, 9931–9940. [Google Scholar] [CrossRef]
- Luo, J.; Qu, S.C.; Chen, Y.; Chen, X.; Xiong, Z.L. Synchronization, circuit and secure communication implementation of a memristor-based hyperchaotic system using single input controller. Chin. J. Phys. 2021, 71, 403–417. [Google Scholar] [CrossRef]
- Yan, W.H.; Dong, W.J.; Wang, P.; Wang, Y.; Xing, Y.A.; Ding, Q. Discrete-time memristor model for enhancing chaotic complexity and application in secure communication. Entropy 2022, 24, 864. [Google Scholar] [CrossRef]
- Bao, B.C.; Zhang, X.; Bao, H.; Wu, P.Y.; Wu, Z.M.; Chen, M. Dynamical effects of memristive load on peak current mode buck-boost switching converter. Chaos Solitons Fractals 2019, 122, 69–79. [Google Scholar] [CrossRef]
- Zhang, J.P.; Yang, Y.; Wang, D.Q. Dynamic analysis and chaos control of the switched-inductor boost converter with the memristive load. Int. J. Circuit Theory Appl. 2021, 49, 2007–2020. [Google Scholar] [CrossRef]
- Yang, Y.; Li, D.D.; Wang, D.Q. Dynamic analysis of the switched-inductor buck-boost converter based on the memristor. Electronics 2021, 10, 452. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, H.; Shi, W.J.; Li, Y.L. A novel half-bridge drive circuit for ultrasonic motor based on FPGA. In Proceedings of the 2017 IEEE Asia-Pacific Transportation Electrification Conference and Exposition (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 897–902. [Google Scholar]
- Nabae, A.; Takahashi, I.; Akagi, H. A new neutral-point-clamped PWM inverter. IEEE Trans. Ind. Appl. 1981, 17, 518–523. [Google Scholar] [CrossRef]
- Rodriguez, J.; Lai, J.S.; Peng, F.Z. Multilevel inverters: A survey of topologies, controls, and applications. IEEE Trans. Ind. Electron. 2002, 49, 724–738. [Google Scholar] [CrossRef] [Green Version]
- Knaup, P. Inverter. International Patent Application, WO2007/048420A1, 3 May 2007. [Google Scholar]
- Schweizer, M.; Kolar, J.W. Design and implementation of a highly efficient three-level T-type converter for low-voltage applications. IEEE Trans. Power Electron. 2013, 28, 899–907. [Google Scholar] [CrossRef]
- Lak, M.; Tsai, Y.T.; Chuang, B.R.; Lee, T.L.; Moradi, M.H. A hybrid method to eliminate leakage current and balance neutral point voltage for photovoltaic three-level T-type inverter. IEEE Trans. Power Electron. 2021, 36, 12070–12089. [Google Scholar] [CrossRef]
- Rodriguez, J.; Bernet, S.; Steimer, P.K.; Lizama, I.E. A survey on neutral-point-clamped inverters. IEEE Trans. Ind. Electron. 2010, 57, 2219–2230. [Google Scholar] [CrossRef]
- Liang, Y.Q.; Wang, R.K.; Hu, B.T. Single-switch open-circuit diagnosis method based on average voltage vector for three-level T-type inverter. IEEE Trans. Power Electron. 2021, 36, 911–921. [Google Scholar] [CrossRef]
- Yang, L.H.; Yang, L.; Yang, F.; Ma, X.K. Slow-scale and fast-scale instabilities in parallel-connected single-phase H-bridge inverters: A design-oriented study. Int. J. Bifurc. Chaos 2020, 30, 2050005. [Google Scholar] [CrossRef]
- Yong, J.; Chen, L.A.; Chen, S.Y. Modeling of home appliances for power distribution system harmonic analysis. IEEE Trans. Power Deliv. 2010, 25, 3147–3155. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Xie, X.M.; Wang, Q.Y.; Zhang, L.H.; Li, Y.H.; Jin, Z.S. A bottom-up approach to evaluate the harmonics and power of home appliances in residential areas. Appl. Energy 2020, 259, 114207. [Google Scholar] [CrossRef]
- Chen, Y.H.; Huang, Z.; Duan, Z.F.; Fu, P.W.; Zhou, G.D.; Luo, L.F. A four-winding inductive filtering transformer to enhance power quality in a high-voltage distribution network supplying nonlinear loads. Energies 2019, 12, 2021. [Google Scholar] [CrossRef] [Green Version]
- Fei, J.T.; Chu, Y.D. Double hidden layer output feedback neural adaptive global sliding mode control of active power filter. IEEE Trans. Power Electron. 2020, 35, 3069–3084. [Google Scholar] [CrossRef]
- Babu, P.N.; Guerrero, J.M.; Siano, P.; Peesapati, R.; Panda, G. An improved adaptive control strategy in grid-tied PV system with active power filter for power quality enhancement. IEEE Syst. J. 2021, 15, 2859–2870. [Google Scholar] [CrossRef]
- Wang, Z.A.; Liu, J.J. Power and Electron Technology; China Machine Press: Beijing, China, 2009. [Google Scholar]
- Tse, C.K.; Di Bernardo, M. Complex behavior in switching power converters. Proc. IEEE 2002, 90, 768–781. [Google Scholar] [CrossRef] [Green Version]
- Hamill, D.C.; Jeffries, D.J. Subharmonics and chaos in a controlled switched-mode power converter. IEEE Trans. Circuits Syst. 1988, 35, 1059–1061. [Google Scholar] [CrossRef]
- Deane, J.H.B.; Hamill, D.C. Instability, subharmonics, and chaos in power electronic systems. IEEE Trans. Power Electron. 1990, 5, 260–268. [Google Scholar] [CrossRef]
- Kavitha, A.; Uma, G. Experimental verification of Hopf bifurcation in DC-DC Luo converter. IEEE Trans. Power Electron. 2008, 23, 2878–2883. [Google Scholar] [CrossRef]
- Zhusubaliyev, Z.T.; Mosekilde, E.; Yanochkina, O.O. Torus-bifurcation mechanisms in a DC/DC converter with pulsewidth-modulated control. IEEE Trans. Power Electron. 2011, 26, 1270–1279. [Google Scholar] [CrossRef]
- Iu, H.H.C.; Zhou, Y.F.; Tse, C.K. Fast-scale instability in a PFC boost converter under average current-mode control. Int. J. Circuit Theory Appl. 2003, 31, 611–624. [Google Scholar] [CrossRef]
- Wang, F.Q.; Zhang, H.; Ma, X.K. Analysis of slow-scale instability in boost PFC converter using the method of harmonic balance and Floquet theory. IEEE Trans. Circuits Syst. I Regul. Pap. 2010, 57, 405–414. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, S.; Zhang, Y.; He, B. Intermediate-frequency oscillation behavior of one-cycle controlled SEPIC power factor correction converter via Floquet multiplier sensitivity analysis. Int. J. Bifurc. Chaos 2016, 26, 1650163. [Google Scholar] [CrossRef]
- Robert, B.; Robert, C. Border collision bifurcations in a one-dimensional piecewise smooth map for a PWM current-programmed H-bridge inverter. Int. J. Control 2002, 75, 1356–1367. [Google Scholar] [CrossRef]
- Kousaka, T.; Sakamoto, K.; Ma, Y. Bifurcation and chaos in a PWM current-mode H-bridge inverter. In Proceedings of the National Conference on Nonlinear Systems & Dynamics, Chennai, India, 6–8 February 2006; pp. 1–4. [Google Scholar]
- Li, M.; Dai, D.; Ma, X. Slow-scale and fast-scale instabilities in voltage-mode controlled full-bridge inverter. Circuits Syst. Signal Process. 2008, 27, 811–831. [Google Scholar] [CrossRef]
- Wang, X.M.; Zhang, B. Study of bifurcation and chaos in single-phase SPWM inverter. Trans. China Electrotech. Soc. 2009, 24, 101–107. [Google Scholar]
- El Aroudi, A.; Rodriguez, E.; Orabi, M.; Alarcon, E. Modeling of switching frequency instabilities in buck-based DC-AC H-bridge inverters. Int. J. Circuit Theory Appl. 2011, 39, 175–193. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, F.; Su, Z.X.; Sun, L.S. Symmetrical dynamical characteristic of peak and valley current-mode controlled single-phase H-bridge inverter. Chin. Phys. B 2013, 22, 110501. [Google Scholar] [CrossRef]
- Shankar, D.P.; Govindarajan, U.; Karunakaran, K. Period-bubbling and mode-locking instabilities in a full-bridge DC-AC buck inverter. IET Power Electron. 2013, 6, 1956–1970. [Google Scholar] [CrossRef]
- Avrutin, V.; Zhusubaliyev, Z. Piecewise-linear map for studying border collision phenomena in DC/AC converters. Int. J. Bifurc. Chaos 2020, 30, 2030015. [Google Scholar] [CrossRef]
- El Aroudi, A.; Debbat, M.; Al-Numay, M.; Abouloiafa, A. Fast-scale instability and stabilization by adaptive slope compensation of a PV-Fed differential boost inverter. Appl. Sci. 2021, 11, 2106. [Google Scholar] [CrossRef]
- Ji, H.Y.; Xie, F.; Shen, L.; Yang, R.; Zhang, B. Unstable behavior analysis and stabilization of double-loop proportional-integral control H-bridge inverter with inductive impedance load. Int. J. Circuit Theory Appl. 2022, 50, 904–925. [Google Scholar] [CrossRef]
- Ma, X.K.; Zou, J.L.; Zhang, H.; Wang, F.Q.; Yang, L.H.; Yang, X.P. Nonlinear Dynamic Analysis of Power Electronic Systems; Beijing Science Press: Beijing, China, 2017. [Google Scholar]
- Cao, H.B.; Wang, F.Q. Slow-scale bifurcation in three-level T-type inverter with passive memristive load. IEEE Trans. Ind. Electron. 2022, 69, 7963–7973. [Google Scholar] [CrossRef]
- Cao, H.B.; Wang, F.Q.; Liu, J.J. Analysis of fast-scale instability in three-level T-type single-phase inverter feeding diode-bridge rectifier with inductive load. IEEE Trans. Power Electron. 2022, 37, 15066–15083. [Google Scholar] [CrossRef]
- Liu, W.; Wang, F.Q.; Ma, X.K. Slow-scale instability in voltage-mode controlled H-bridge inverter with memristive load. Int. J. Bifurc. Chaos 2016, 26, 1650200. [Google Scholar] [CrossRef]
- Chen, G.R.; Moiola, J.L.; Wang, H.O. Bifurcation control: Theories, methods, and applications. Int. J. Bifurc. Chaos 2000, 10, 511–548. [Google Scholar] [CrossRef]
- Tesi, A.; Abed, E.H.; Genesio, R.; Wang, H.O. Harmonic balance analysis of period-doubling bifurcations with implications for control of nonlinear dynamics. Automatica 1996, 32, 1255–1271. [Google Scholar] [CrossRef]
- Chen, D.; Wang, H.O.; Chen, G.R. Anti-control of Hopf bifurcations through washout filters. In Proceedings of the 37th IEEE Conference on Decision and Control, Tampa, FL, USA, 18 December 1998; pp. 3040–3045. [Google Scholar]
- Littleboy, D.M.; Smith, P.R. Using bifurcation methods to aid nonlinear dynamic inversion control law design. J. Guid. Control Dyn. 1998, 21, 632–638. [Google Scholar] [CrossRef]
- Basso, M.; Evangelisti, A.; Genesio, R.; Tesi, A. On bifurcation control in time delay feedback systems. Int. J. Bifurc. Chaos 1998, 8, 713–721. [Google Scholar] [CrossRef]
- David, A.; Sinha, S.C. Bifurcation control of nonlinear systems with time-periodic coefficients. J. Dyn. Syst. Meas. Control 2003, 125, 541–548. [Google Scholar] [CrossRef]
- Yu, P.; Chen, G.R. Hopf bifurcation control using nonlinear feedback with polynomial functions. Int. J. Bifurc. Chaos 2004, 14, 1683–1704. [Google Scholar] [CrossRef]
- Guo, Y.L.; Wang, L.; Wu, Q.H. Bifurcation control method for buck-boost converters based on energy balance principle. Int. J. Bifurc. Chaos 2021, 9, 6947–6954. [Google Scholar] [CrossRef]
- Wu, J.K.; Zhou, L.W.; Lu, W.G. A unified bifurcation control strategy for voltage source inverter. Acta Phys. Sin. 2012, 61, 210202. [Google Scholar]
- Xue, T.S.; Wang, L.T. Slope compensation design for SPWM-H inverter in peak current control mode. Autom. Devices Equip. 2022, 44, 1–4. [Google Scholar]
- Yu, P.; Leung, A.Y.T. The simplest normal form and its application to bifurcation control. Chaos Solitons Fractals 2007, 33, 845–863. [Google Scholar] [CrossRef]
- Liu, F.; Wang, H.O.; Guan, Z.H. Hopf bifurcation control in the XCP for the Internet congestion control system. Nonlinear Anal. Real World Appl. 2012, 13, 1466–1479. [Google Scholar] [CrossRef]
- Yuan, C.H.; Wang, J. Hopf bifurcation analysis and control of three-dimensional Prescott neuron model. J. Vibroeng. 2016, 18, 4105–4115. [Google Scholar] [CrossRef] [Green Version]
- Kwon, J.; Wang, X.F.; Bak, C.L.; Blaabjerg, F. Harmonic interaction analysis in a grid-connected converter using harmonic state-space (HSS) modeling. IEEE Trans. Power Electron. 2017, 32, 6823–6835. [Google Scholar] [CrossRef] [Green Version]
- Lyu, J.; Zhang, X.; Cai, X.; Molinas, M. Harmonic state-space based small-signal impedance modeling of a modular multilevel converter with consideration of internal harmonic dynamics. IEEE Trans. Power Electron. 2019, 34, 2134–2148. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.J.; Lin, H.; Wang, Z.; Ze, Z.Y. Stability analysis of modular multilevel converter based on harmonic state-space theory. IET Power Electron. 2019, 12, 3987–3997. [Google Scholar] [CrossRef]
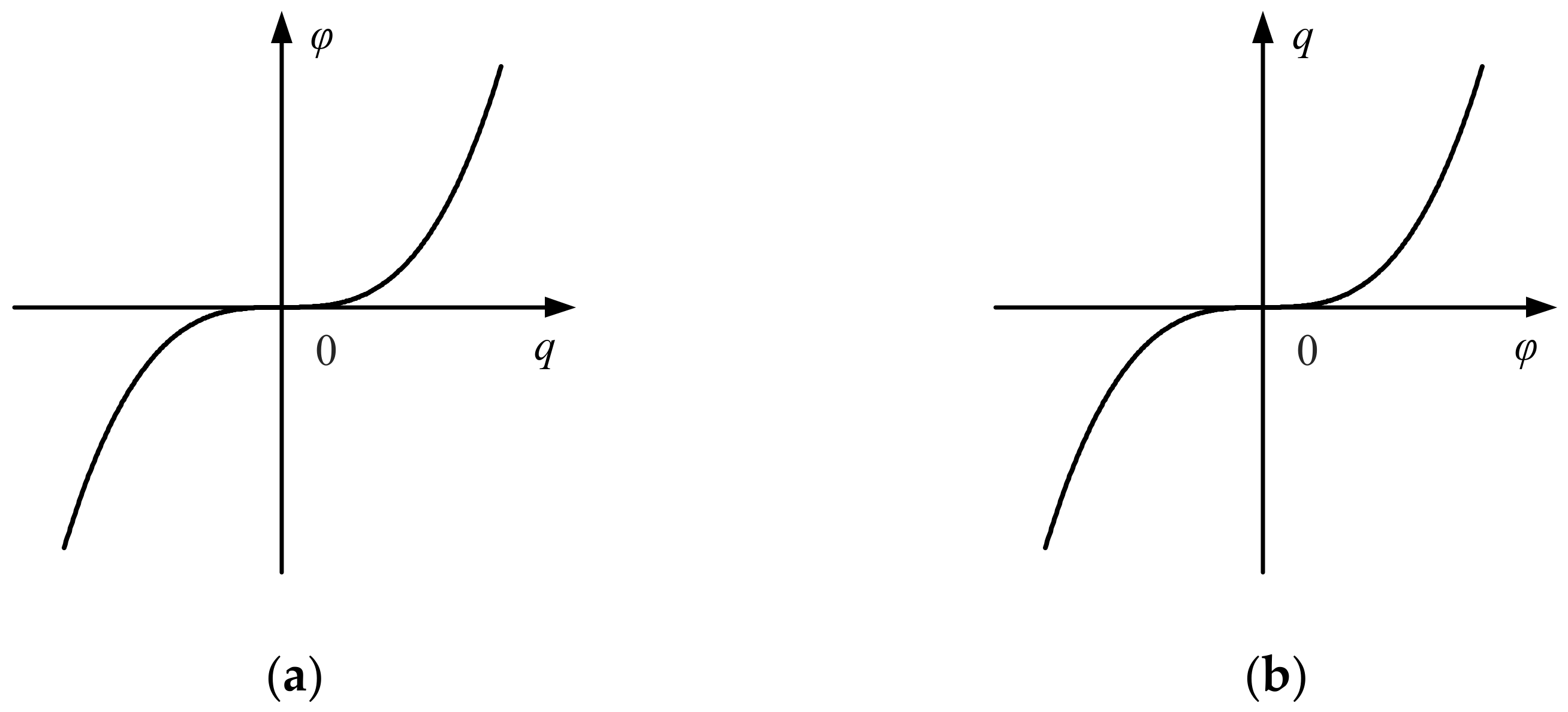
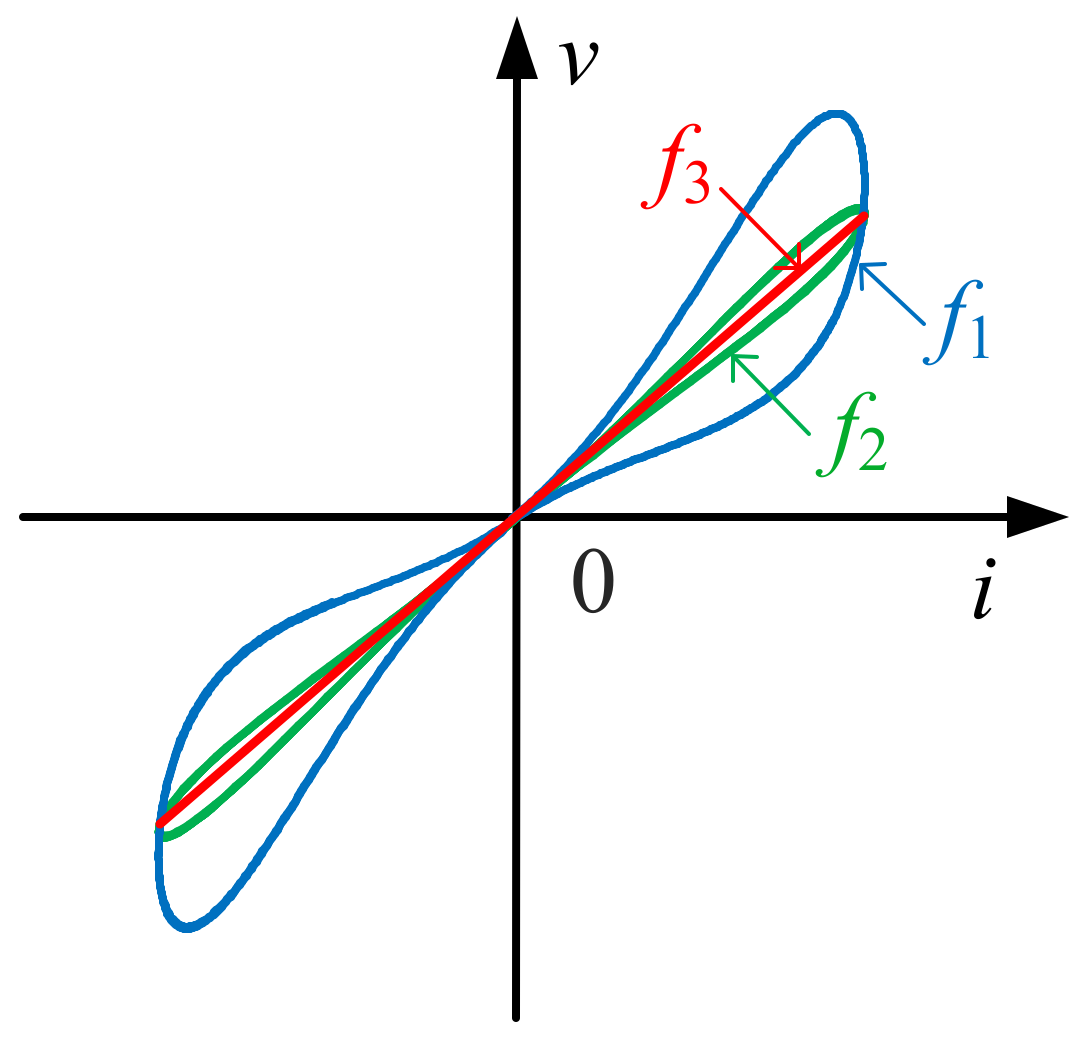




| Item | Charge-Controlled Memristor | Flux-Controlled Memristor |
|---|---|---|
| Internal variable | Charge (q) | Flux (φ) |
| Constitutive relation | ||
| Variable curve | Figure 2a | Figure 2b |
| Item | Current-Controlled Memristor | Voltage-Controlled Memristor |
|---|---|---|
| Control variable | i(t) | v(t) |
| Mathematical model | ||
| Ideal model | ||
| Equivalent model |
| Reference | Component | Structure |
|---|---|---|
| [58] | D1, D2, D3, D4, L, C, R | Figure 8a |
| [59] | D1, D2, D3, D4, L, R | Figure 8b |
| [60] | D1, D2, D3, D4, C, R | Figure 8c |
| Item | I-Type Three-Level Inverter | T-Type Three-Level Inverter |
|---|---|---|
| Quantity of components | Four switches and two diodes | Four switches |
| Switch tube withstand pressure | S1–S4: 0.5 E | S1 and S2: E; S3 and S4: 0.5 E |
| Driving power | 4 | 3 |
| Item | Slow-Scale Instability | Fast-Scale Instability |
|---|---|---|
| Period scales | Far higher than the switching-period scale | On the switching-period scale |
| Oscillation frequency | Low-frequency behavior | High-frequency behavior |
| Curves | Figure 10a | Figure 10b |
| Operation periods | Tens or even thousands of times the switching period | From period-1 to period-2 |
| Characteristics | Global oscillation | Local oscillation |
| Method | Advantages | Deficiencies |
|---|---|---|
| Average-state modeling | Can be used to analyze the low-frequency dynamic behaviors | Ignores the high-frequency dynamic characteristics of the system |
| Discrete-time modeling | Can be used to analyze the low-frequency dynamic behaviors and high-frequency dynamic characteristics | Complicated calculation |
| Harmonic-state-space-modeling | Can be used to analyze the harmonic dynamics of power electronic systems considering harmonic coupling | With the expansion of the model the calculation process will become redundancy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Wang, F. An Overview of Complex Instability Behaviors Induced by Nonlinearity of Power Electronic Systems with Memristive Load. Energies 2023, 16, 2528. https://doi.org/10.3390/en16062528
Cao H, Wang F. An Overview of Complex Instability Behaviors Induced by Nonlinearity of Power Electronic Systems with Memristive Load. Energies. 2023; 16(6):2528. https://doi.org/10.3390/en16062528
Chicago/Turabian StyleCao, Hongbo, and Faqiang Wang. 2023. "An Overview of Complex Instability Behaviors Induced by Nonlinearity of Power Electronic Systems with Memristive Load" Energies 16, no. 6: 2528. https://doi.org/10.3390/en16062528
APA StyleCao, H., & Wang, F. (2023). An Overview of Complex Instability Behaviors Induced by Nonlinearity of Power Electronic Systems with Memristive Load. Energies, 16(6), 2528. https://doi.org/10.3390/en16062528







