1. Introduction
Fission gas nuclides, including the radioisotopes Kr and Xe, are gaseous products of the nuclear fission reaction of fissile material. Fission gas nuclides are important considerations in the design of radiation monitoring systems and the implementation of radiation protection procedures in nuclear reactors as significant source terms in the primary loop [
1,
2,
3,
4], as these are also reflections of the operation conditions of fuel elements in a reactor core [
5,
6]. For example, radioactivity measurements are required for accurate monitoring of the damage of tri-structural isotropic (TRISO)-coated particles in the fuel elements of pebble-bed high-temperature gas-cooled reactors (HTGRs), where the fuel pebbles move in the core [
6,
7]. Fission gas nuclides in the reactor core and primary coolant are also the main sources of radioactive nuclides released into reactor buildings through leakages and the environment via discharges from the stack or relief valve during depressurization accidents [
8,
9]. Hence, inventories are required to evaluate and ensure reactor radiation safety.
Although nuclides such as
129I,
131I and
137Cs exist, the main fission gas nuclides with a dominant contribution to the total activity in the primary coolant consist of
85mKr,
87Kr,
88Kr,
89Kr,
133Xe,
133mXe,
135Xe,
135mXe,
137Xe, and
138Xe regardless of the reactor type [
10,
11,
12]. For instance, the activity fractions in various nuclear reactors such as M310, AP1000, the 10 MW high-temperature gas-cooled experimental reactor (HTR-10), and HTR-PM in normal operation conditions are approximately 81.90, 93.56, 69.77, and 84.06%, respectively [
11], based on numerous online and offline radiation monitoring instruments that have been developed in the past to detect fuel elemental failures [
13,
14].
Inventories of fission gas nuclides are essential for quantifying the radioactive source terms and establishing the relationship between the activity concentration in the primary loop and the status of the fuel elements in the reactor core [
15,
16,
17]. Reliable core inventories are also the basis for source term calculations, radiation protection, and accident analysis. Thus, accurately and efficiently calculating these inventories has been a relevant research area for the past several decades [
18,
19,
20,
21]. In addition, inventory calculations of radionuclides, including fission, fission metallic, and activation nuclides in various reactors are based on point depletion burnup equations, in which full-core calculations are divided into two steps: (1) determination of the point reactor equivalence model for a real reactor and (2) calculation of the solution for point depletion based on numerous inter-coupled ordinary differential equations (ODEs) [
22,
23,
24,
25].
Considering the neutron transport module in the core is necessary to determine the point reactor equivalence model for a real reactor, two approaches are applied for the coupling of neutron transport and depletion modules: the first approach involves solving the neutron transport equation using either deterministic or stochastic methods, in which the coupling is divided into deterministic neutron transport module depletion and stochastic neutron transport module depletion modules; the second approach involves simultaneously solving the neutron transport and point depletion equations using identified parameters, in which the equations can be classified into deep and shallow coupling modes [
26].
Table 1 summarizes the computer codes of the main point depletion burnup for nuclide inventory calculations based on related studies from various countries. This demonstrates that burnup algorithms can be divided into two categories: analytic and numerical methods [
27], which have been verified and validated in several recent studies. For example, Li et al. (2021) [
28] alleviated the testing oracle problem using metamorphic techniques for the NUIT code, while Ilas and Hiscox (2021) [
29] validated ORIGEN-S integrated into SCALE 6.2.4 and ENDF/B-VII.1 data libraries to analyze the nuclide inventory in pressurized water reactors (PWRs). Alves et al. (2020) [
25] calculated the inventories of fission products and source terms to simulate the Argonaut nuclear reactor inside a severe accident using ORIGEN-2. Zwermann et al. (2021) [
30] also provided discussions on the propagation of nuclear data uncertainties to decay heat and nuclide density using DARWIN/PEPIN2, while Castagna and Gilad (2022) [
31] investigated the radionuclide inventory in nuclear fuel under uncertainties in boron concentrations using high-fidelity models. As for HTGRs, Cui et al. [
32] researched uncertainty propagation of fission product yields from uranium and plutonium using pebble-bed burnup calculations. These point depletion burnup computer codes require detailed reactor physics calculations, which are based on the reactor and fuel designs, burnup-dependent fuel composition, locations of specific fuel assemblies in the core, and operational data from the reactor, in which numerous input parameters are normally needed; hence, these often do not meet rapid core diagnosis requirements for radiation monitoring of the primary coolant. To date, only a few studies have focused on the factors that affect inventories of fission gases in the nuclear reactor core.
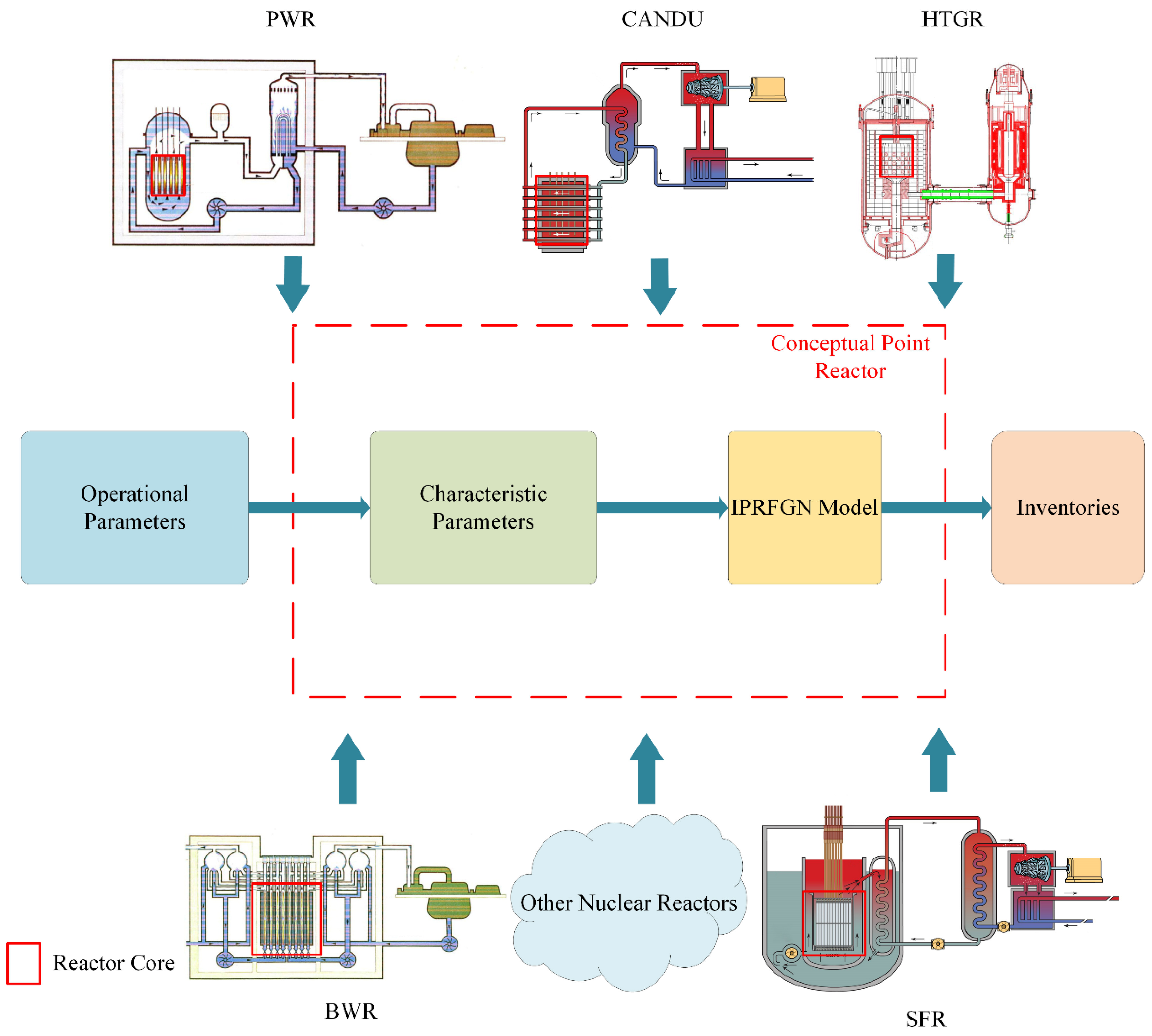
To understand the features of the production chain of short-lived fission gases in the core and establish the relationship between their inventories and reactor parameters, this study aims to investigate the factors affecting the inventories of fission gas nuclides in reactors using a simple, novel, and efficient model called the “Inventories of a Point Reactor for Fission Gas Nuclides” (IPRFGN) to calculate the inventories of short-lived fission gas nuclides based on an analytical approach (
Figure 1). In this study, only two reactor operational parameters (the reduced reactor power in the final stage, or the reactor power, and the average burnup of fuel elements, or the burnup) were used, in which all complex inputs in the point depletion burnup computer codes were reduced to 15 characteristic parameters for various specific reactors.
To grasp the features of the production chain of short-lived fission gases in the core and establish the relationship between their inventories and reactor parameters will be significant for rapid core diagnosis in nuclear safety and nuclear emergency. This study elucidates, in detail, the factors affecting the inventories of fission gas nuclides in reactors. As shown in
Figure 1, the present study proposes a simple, novel, and efficient model called the “Inventories of a Point Reactor for Fission Gas Nuclides” (IPRFGN) to calculate the inventories of short-lived fission gas nuclides for various types of nuclear reactors in an analytic form. Only two reactor operational parameters, which are the reduced reactor power in the final stage (denoted as reactor power) and the average burnup of fuel elements (denoted as burnup), are needed for the calculation of the inventories of short-lived fission gas nuclides for various types of nuclear reactors. All complex inputs in point depletion burnup computer codes are reduced into 15 characteristic parameters for several specific reactors.
To illustrate the model and calculate the inventories of various fission gas nuclides, HTR-10 is considered as an example. HTR-10 was built in Beijing, China, in 2000 and is the only pebble-bed type HTGR that can operate at full power in the world currently. The research on HTR-10 is of great importance for the development of HTGRs [
7]. Further, the model is validated using the HTR-10 reactor as an example. The variations in typical fission gas nuclide inventories concerning reactor power and burnup are explained. The current model provides a clear and intuitive physical understanding of the relationship between the operating conditions of a reactor and the inventories of fission gas nuclides, which is useful for monitoring fuel elements in HTGRs and other nuclear fission reactors [
13,
14,
53].
The remaining sections of the paper are organized as follows: The theoretical model and computational method, including the point depletion burnup equation and IPRFGN model, are presented in
Section 2.
Section 3 and
Section 4 comprise the results and discussion based on the HTR-10 calculation.
2. Method and Model
As previously stated, inventory calculations of radionuclides, including fission, fission metallic, and activation nuclides in various reactors are based on point depletion burnup equations, which can be divided into two steps: (1) determination of the point reactor equivalence model for a real reactor and (2) calculation of the solution for point depletion based on numerous inter-coupled ordinary differential equations (ODEs). This section focuses on Step (2) and introduces general point depletion equations and the IPRFGN model as a simplification of the former due to the properties of fission gas nuclides. Furthermore, computer codes for corresponding methods, KORIGEN and IPRFGN, are presented.
2.1. Point Depletion Burnup Equation
A fundamental procedure in nuclide inventory calculation is numerically solving the point depletion burnup equation, which is approximated using a system of linear first-order differential equations with constant coefficients and has been applied to hundreds of complex burnup chains involving thousands of nuclides. The general point depletion burnup equation is as follows [
44]:
where
Ni represents the atom numbers of radionuclide
i;
Nj is the amount of precursor nuclide
j or fissionable nuclides
j;
nj is the total number of precursor nuclides
i;
N is the number of fissionable nuclides;
λi is the decay constant of radionuclide
i (s
−1);
σa,i is the spectrally averaged neutron absorption cross-section (cm
2);
σj is the spectrally averaged cross-section that yields the nuclide
i (cm
2);
lij is the fraction from radionuclide
j decay into nuclide
i;
fij is the fraction from nuclides
j to radionuclide
i, particularly the fission yields from fissionable nuclides
j to radionuclide
I; and
φ is the neutron flux averaged by space and energy (cm
−2 s
−1) [
44,
45].
Using Equation (1), the inventories of hundreds of radionuclides produced by nuclear fission and other successive reactions, such as decay and neutron absorption, can be calculated. In a simpler form, this equation can also be used to calculate the inventories of fission gas nuclides. The source term of fission gas nuclides, which can be assumed to be constant over a short time for fuel fission, is defined as S2. The value of S2 depends on the neutron flux and amounts of
235U (N
U5),
238U (N
U8),
239Pu (N
Pu9), and
241Pu (N
Pu1) for uranium dioxide fuel elements. Furthermore, because their precursor atom decay constants are much lower than those of fission gas nuclides, the number of precursor atoms achieves equilibrium and remains constant. Thus, the first term on the right side of Equation (1) can serve as a constant value, which is defined as S1. The burnup equation for fission gas nuclide i can be approximated as follows:
where
S is a constant that is equal to
S1 +
S2.
The analytical solution can be easily derived by setting the initial atom
to 0 as follows:
where
Ii is the activity inventory of nuclide
i.
Owing to the large decay constant
λi, fission gas nuclides can easily reach equilibrium, as shown in Equation (4):
Based on Equation (4), the equilibrium activity of the fission gas nuclide i is dependent on the neutron flux, decay constant, neutron absorption cross-section, all precursor nuclide equilibrium activities, and fissionable nuclides amounts, particularly 235U, 238U, 239Pu, and 241Pu.
2.2. IPRFGN Model
The IPRFGN model, which describes the various reactor cores as a point reactor characterized by several key parameters, was used to effectively calculate the inventories of fission gas nuclides in the point reactor. As shown in
Figure 2, the calculation flow illustrates the processes, in which they are connected by dashed lines following the types of reactor, including the different enrichment levels of uranium and plutonium in the fuel elements. Here, the calculated inventories in similar enrichment levels and types of reactor depend on the given operational parameters such as the reactor power and burnup.
Fission gas nuclides normally have two general modes in terms of the number of decay chains: General Modes A and B. In this study, both modes were evaluated. The former is depicted in
Figure 3a [
45,
54], in which the reaction branching ratios were obtained from KORIGEN nuclear data libraries, as these were the most recent data available from the Evaluated Nuclear Structure Data File (ENSDF) of the International Atomic Energy Agency (IAEA) [
45,
55,
56].
Further, General Mode A was derived from the decay chain for
133Xe and
133mXe in
Figure 3b, in which the 100% decay fraction was omitted for simplification. In
Figure 3, Ai refers to the activity of nuclide i, where i can be equal to 1, 21, 22, 3, 01, or 02; and f
i,j refers to the decay fraction from nuclide i to nuclide j.
Equations (5)–(10) are the point depletion burnup equations for General Mode A, where
.
Af,i is defined as the source of nuclide
i obtained directly from fissionable fuel nuclides (atoms):
The following conditions were applied for the above equations:
The (n, γ) neutron absorption reaction was only considered for 135Xe and 133Xe;
235U, 238U, 239Pu, and 241Pu were considered for fissionable nuclides;
All fission gas nuclides were assumed to be in equilibrium, where .
For the second characteristic, A
f,j can be written as follows:
where
σf,U5,
σf,U8,
σf,Pu9, and
σf,Pu1 are the fission cross-sections of
235U,
238U,
239Pu, and
241Pu, respectively (cm
2); and Y
U5,j,
YU8,j,
YPu9,j, and
YPu1,j are fission yields of nuclide
j from fissionable nuclides
235U,
238U,
239Pu, and
241Pu, respectively. All fission yields and cross sections were obtained from the nuclear data libraries of KORIGEN. Three-group pre-generated nuclear data were calculated by Karlsruhe Institute of Technology (KIT) using Evaluated Nuclear Data File (ENDF) in the IAEA database. The characteristic neutron flux spectrum was supplied for four types of nuclear reactors: HTGR, light water reactor (LWR), liquid metal fast breeder reactor (LMFBR), and molten salt breeder reactor (MSBR) [
33,
43]. Further inspection of Equation (11) reveals that
Af,j was proportional to the neutron flux
φ.
The analytical results are listed below:
where
Ii is the inventory of nuclide
i (Bq).
General Mode A includes four sub-modes with the same or simpler forms, and A
0, A
1, A
2, and A
3 were used as their representation, including three other sub-modes, as shown in
Figure 4. Meanwhile, General Mode B was derived from the decay chain of
88Kr, as shown in
Figure 5b.
Hence, the equilibrium inventory of the fission gas nuclide
i (
Ii) can be obtained from the linear combination of the source of nuclide j in the entire decay chain of nuclide
i (
Af,j) and can be expressed as Equation (14). Additional details are provided in
Table 2. All justification of equations is discussed in the
supporting information.
where
αj,i is the linear coefficient of the source of nuclide
i obtained directly from fissionable fuel nuclides
j.
2.3. KORIGEN and IPRFGN
Based on the ORIGEN code created by Oak Ridge National Laboratory (ORNL), the KORIGEN code was developed to calculate isotope generation and depletion and was modified by the Institute for Neutron Physics and Reactor Technology (INR) at the KIT [
45]. The KORIGEN code was used in this study to evaluate the nuclide inventories and depletion and burnup of nuclear fuels loaded into the reactor core, in which the neutron reaction rates of each burnup step were evaluated, and the radioactivity inventories of various reactors were evaluated regardless of the in-pile fuel or spent fuel.
The WrapKORIGEN code, developed by the Institute of Nuclear and New Energy Technology (INET) at Tsinghua University, refers to a series of Python scripts that were used in the pre- and post-processing of the KORIGEN-based inventory calculations for the full-core reactor; it was also used to examine the factors that can affect radionuclide inventories in this study.
Similarly, the IPRFGN code, which was similarly developed by the INET, focuses on the inventories of equilibrium and non-equilibrium conceptual reactors. The IPRFGN model was described above using an analytical approach.
3. Results
3.1. Conceptual Point Reactor for the Equilibrium Core of HTR-10
In this study, the conceptual point reactor was used as an idealized physical model to calculate the inventories of fission gas nuclides, in which a series of parameters were adopted to represent a specific reactor and determine core inventory calculations. Specifically, the neutron flux and atom numbers
235U,
238U,
239Pu, and
241Pu were assigned as the characteristic parameters. However, the effect of
241Pu can be neglected as pure uranium dioxide fuel elements were used in HTR-10. In the current conceptual point reactor, four parameters in the form of a quadratic function were adopted as follows:
where
a,
b, and
c are parameters of the conceptual point reactor,
Pfinal is the reactor power (MW/tU), and B is the burnup (GWd/tU).
The various types of reactors and their corresponding reactor type with various loaded fuels were found to have divergencies. In
Table 3, the conceptual point reactor for HTR-10 at equilibrium is presented. Accordingly, these were fitted with the result of the point depletion burnup computer code KORIGEN. Here, the inventories of short-lived fission gas nuclides for an individual reactor with specific loaded fuel were found to be dependent on two operational parameters: the reactor power and burnup in our conceptual point reactor.
The findings revealed that the obtained full-core reactor values were relatively close to the average conceptual point reactor. In real engineering design and operation, the conceptual point reactor can reliably and effectively substitute the full-core reactor. Hence, the results obtained in this study can similarly be substituted for full-core reactor values, in which the observed physical characteristics were noted in the equilibrium core of HTR-10. The KORIGEN code was used as a reference.
3.2. Neutron Flux
As the reduced reactor power in the final stage refers to the operational power of the reactor per ton of fissionable material (MW/tU) before the experiment duration, the operating history was not relevant. Meanwhile, the average burnup of fuel elements refers to the amount of energy extracted per mass of the initial loaded fuel. In addition, it is given by megawatt-days per metric ton of heavy metal loaded (MWd/MTHM); however, the unit adopted in this study was gigawatt-days per metric ton of uranium (GWd/tU).
In
Figure 6, the neutron flux derived from the KORIGEN code for the equilibrium core of HTR-10 was shown to increase with an increase in the reactor power and burnup. The proportional relationship between the neutron flux and reactor power is due to the proportional relationship between the reactor power and the number of nuclear fission reactions per unit of time, as well as the proportional relationship between the neutron flux and the number of nuclear fission reactions per unit of time. Regarding the increase in neutron flux as burnup increases, the neutron flux rises to compensate for the consumption of total fissile material to maintain constant reactor power as burnup increases.
It also fitted with the quadratic function of burnup with a fixed reactor power, which can be defined as a function of the reactor power and burnup:
where
φref is the reference neutron flux at the reference reactor power (
Pref, 74.6 MW/tU).
φref was fitted as a quadratic function using least-squares fitting:
In
Table 4, the neutron flux values derived from Equation (19) were compared with those calculated using the KORIGEN code with an obtained burnup value and reactor power of 10–150 GWd/tU and 10–150 MW/tU, respectively. It was found that the values were relatively consistent, with relative errors of <1.0%. Hence, this demonstrates that the neutron flux is determined by fitting Equation (19) with the results from the KORIGEN code.
3.3. Fissionable Nuclides
The calculated results for the full-core inventory of the HTR-10 fueled by low-enriched uranium (LEU) indicated that most fission products were obtained from three main fissionable isotopes, namely, 235U, 238U, and 239Pu. The initial fraction of 235U in the uranium was 17%. Based on the calculations in this study, the number of atoms of 235U and 238U decrease from 4.05 × 1026 and 2.10 × 1027 to 9.46 × 1025 and 1.93 × 1027, respectively. In contrast, the number of 239Pu atoms increased from 9.08 × 1024 to 2.05 × 1025.
Mills et al. (2020) [
57] proposed a method for estimating the fractional fission rates of major nuclides in light water and advanced gas-cooled reactors in terms of anti-neutrino emission, particularly when a reactor is at constant power. Here, a series of simplified equations with several key parameters were selected to describe the fractional fission rates of major nuclides by ignoring irrelevant parameters. This series was closely related to the neutron flux and the number of major fissionable atoms in the nuclear reactor. Hence, a similar simplification approach was used in the present study.
Based on the relationship between the fractional fission and the number of fissionable atoms, including the few effects of
241Pu on the inventory calculation of HTR-10, the following equations are proposed to evaluate the number of major atoms (
235U,
238U, and
239Pu) using the least-squares fitting method:
Figure 7 depicts that the number of atoms of
235U and
238U are significantly larger than those of
239Pu. However, the number of
239Pu atoms was only comparable with that of
235U in the same order of magnitude, given that the burnup value exceeded ~100 GWd/tU.
Figure 8 shows that the variations in the number of fissionable atoms were associated with an increase in the burnup value. These variations differed significantly for major nuclides, where relevant atom number variations take the number of fissionable atoms, with a burnup value of 10 GWD/tU used as a reference. These variations were obtained by subtracting the number of fissionable atoms in the initial fuel from those in the fuel with a higher burnup value from the number of fissionable atoms in the initial fuel. Changes in the number of
238U atoms were relatively small, with a maximum value of −7.80%, whereas the relative variations of the number of atoms of
235U and
239Pu were significantly larger with a maximum value of −76.63 and 125.90%, respectively. The linearity of the curve of
238U can also be attributed to the large value and small consumption of the number of atoms. Furthermore, the relative variation of the number of
239Pu was observed to increase with the increase in burnup, until it gradually decreased, which can be attributed to the competition processes between the neutron fission reaction of
239Pu and activation of
238U to
239Pu, which vary with the increase in burnup.
3.4. Inventories of Short-Lived Fission Gas Nuclides
Figure 9 shows the plot of the two inventories at fixed burnup values of 10 and 100 GWd/tU, respectively. All inventories of the fission gas nuclides were distributed within the range of 10
15–10
18 Bq/tU in a descending order as follows:
133Xe,
138Xe,
137Xe,
89Kr,
88Kr,
87Kr,
85mKr,
135mXe, and
133mXe. Particularly,
135Xe exhibited distinct behaviors.
Figure 9 depicts that the inventories of fission gas nuclides excluding
135Xe, i.e.,
85mKr,
87Kr,
88Kr,
89Kr,
133Xe,
133mXe,
135mXe,
137Xe, and
138Xe, were proportional to the reactor power in the final stage. Notably, the inventory of
135Xe increased proportionally to the reactor power, with a gradual decrease toward the equilibrium state (~7.94 × 10
16 Bq/tU).
Based on the general mode analysis and the determined relationship between the proportion of Af,i and the neutron flux (φ), only the 133Xe and 135Xe inventories were relevant to the neutron flux. The equilibrium inventory for the fission gas nuclide i (Ii) was also found to be a linear combination of the source of nuclide j in the entire decay chain of nuclide i (Af,j), in which the reactor power was proportional to the neutron flux at the same fuel burnup value. Hence, the inventories of fission gas nuclides excluding 135Xe, i.e., 85mKr, 87Kr, 88Kr, 89Kr, 133Xe, 133mXe, 135mXe, 137Xe, and 138Xe, were all proportional to the reactor power.
The inventories of
133Xe and
135Xe can be expressed as follows:
where
Af is the whole source from each nuclide in the corresponding decay chains, in which it was proportional to the neutron flux
φ. Given that the value of
σa,01φ was comparable to
λ01, such as those in
135Xe, the inventory of
135Xe increases as the neutron flux increases; however, it was found to progress more gradually compared to other inventories as
λ01 becomes more negligible as the neutron flux increases. A limit value also existed when
φ approached infinity, as shown in Equation (24). For
133Xe,
φ did not approach infinity; thus,
σa,01 was inferred to be inadequate, which makes
σa,01φ incomparable with
λ01. Hence, this resulted in similar exhibited behaviors in the inventory of
133Xe compared to those of other fission gas nuclides.
As shown in
Figure 10, for fixed reactor power, all inventories of fission gas nuclides decreased as the burnup value increased. Several isotopes, such as
133Xe,
133mXe,
137Xe, and
138Xe, were found to be more independent of the burnup in the lower burnup region. In contrast, all the inventories tended to have decreased proportional relationships, particularly in the higher burnup region.
Despite the simultaneous production of
239Pu in the low burnup region, the main inventories of fissionable nuclides, including
238U and
235U, gradually decreased. The neutron flux increased as the burnup value increased for the same reactor power. These findings indicate that the consumption of fissionable nuclides
238U and
235U can be accounted as the main contribution. Therefore, the inventory of fission gas nuclide
i can be recalculated as follows:
where
βk,i is a linear coefficient for radionuclide
i based on the number of fissionable atoms
k, as shown in Equation (26):
For the same nuclide
i (except
135Xe), the variables in
βk,i were constant. The variation in
Ii was derived from the divergences of
φ, N
U5, N
U8, and N
Pu9, in which the sequence was:
NU8 >>
NU5 >
NPu9 >>
φ. Furthermore, with a similar increase in burnup value,
238U showed the least variation, followed by
235U and
239Pu. Hence, it is inferred that a larger value of
βU8,i corresponds to a more constant slope for the nuclide
i (
Figure 10). All nuclides in the decay chain defined as nuclide
j will also be more dependent on the number of
238U atoms.
Ii can be approximated using Equation (27) in the higher burnup region, as follows:
As previously mentioned, NU8 has sufficient linearity and thus explains the proportional decreases in the higher burnup region.
5. Conclusions
The novel, simple, and efficient IPRFGN model can be used to interpret and calculate the inventories of short-lived fission gas nuclides. Regardless of the nuclear fission reactor type, the inventories of short-lived fission gas nuclides can be calculated using two steps: (1) determining the point reactor equivalence of a real reactor and (2) calculating solutions for point depletion based on numerous inter-coupled ordinary differential equations.
The IPRFGN model theoretically simplifies the neutron transport module and depletion module, including their coupling. Using the KORIGEN code, any type of fission reactor, such as the equilibrium HTR-10, can be represented by a few characteristic parameters, namely, the neutron flux and the number of fissionable atoms such as 235U, 238U, and 239Pu. Meanwhile, for an individual reactor with a specific loaded fuel, the inventories of short-lived fission gas nuclides are dependent on two crucial condition parameters, namely, the reactor power and the burnup. The IPRFGN model used in this study highlights the physical relationship between the inventories of short-lived fission gas nuclides and the operational parameters of a reactor, and it successfully provided a scientific basis for designing an effective and responsive online core diagnostic system and implementing radiation protections in the primary loop of nuclear reactors.
Based on the results of the equilibrium core of HTR-10, the following conclusions are made in this study: With the exception of 135Xe, all inventories of fission gas nuclides are distributed between the range of 1015–1018Bq/tU and following descending order of 133Xe, 138Xe, 137Xe, 89Kr, 88Kr, 87Kr, 85mKr, 135mXe, and 133mXe. The inventories of fission gas nuclides excluding 135Xe, i.e., 85mKr, 87Kr, 88Kr, 89Kr, 133Xe, 133mXe, 135mXe, 137Xe, and 138Xe, were proportional to the reactor power. However, the inventory of 135Xe increased with an increase in reactor power and gradually reached equilibrium under a fixed burnup value. All the inventories of fission gas nuclides decreased as the burnup value increased. Several isotopes, such as 133Xe, 133mXe, 137Xe, and 138Xe, were independent of the burnup in the lower burnup region for a fixed reactor power.
Furthermore, the results for the equilibrium core of HTR-10 were relatively close to those of the values obtained from point depletion burnup programs, such as KORIGEN, with a relative error of <1.0%. Thus, this validates the proposed IPRFGN model used in this study. The inventories of fission gas nuclides in the non-equilibrium HTR-10 core throughout the experiment duration were approximately within the range of 1014–1016 Bq. As predicted by the IPRFGN model, their relationship with the reactor power was consistent.
Finally, as all nuclear fission reactors were found to be reduced to a point reactor, the relationships between the short-lived fission gas nuclide inventories and operational reaction parameters were similar, and the proposed IPRFGN model can be applied to both equilibrium and non-equilibrium cores of various fission reactors. In the future, the IPRFGN model will be widely used to calculate inventories of fission gas nuclides using a database of characteristic parameters from various reactors.