External Identification of a Reciprocal Lossy Multiport Circuit under Measurement Uncertainties by Riemannian Gradient Descent
Abstract
:1. Introduction
2. Problem Formulation
2.1. Linear, Time-Invariant Multiport Model
- In principle, the behavior of the multiport system depends on the frequency of the excitation; assuming that the system is linear and time-invariant, it is possible to appeal to the Fourier theory and work with one frequency at a time (in other terms, phasor theory is in force);
- While a two-port network admits one or more of six independent matrix representations (impedance, admittance, scattering, inverse scattering, hybrid, inverse hybrid), a multiport network admits one or more amid a large number of representations, among which only four (impedance, admittance, scattering, inverse scattering) are univocally determined, while the hybrid representations are multiple. The scattering-matrix representations are popular in waveguide theory, while impedance/admittance-matrix representations are common in electrical engineering; in the present paper, we will only consider multiport networks that admit both impedance and admittance representations.
2.2. Model Identification under the Assumption of Perfect Measurements
2.3. Further Assumptions Regarding the Multiport System
- The matrix (termed conductance matrix) is symmetric and positive definite;
- The matrix (termed susceptance matrix) is symmetric.
2.4. Assumptions on the Known Loads
- The matrix is symmetric, positive definite. The block lays at the lower-right corner of the matrix Y. Let us define and , where the symbol denotes a identity matrix. The real part of the matrix possesses the same eigenvalues as the real part of the matrix Y; in fact, their characteristic polynomials in the variable are related by the following:where we used the properties (which may be directly checked) and (by the Lemma 2 in [24]). Therefore, the matrix belongs to the space . By virtue of the Sylvester’s criterion [25], the stated conclusion follows.
- Each matrix is symmetric, positive definite. Since each matrix is symmetric non-negative definite and the matrix is symmetric positive definite, it holds that each is symmetric positive definite. In fact, recall that a matrix is positive definite if, and only if, for any , it holds that . Assume that , where and (namely, A is non-negative definite). Then, . The first term on the right-hand side is non-negative while the second term is positive; hence, . (Notice that, by contrast, each matrix , is generally only symmetric).
- Each matrix-sum is invertible. To prove this assertion, let us take a square complex-valued matrix (that represents the sum ) and write it as , where . Let us make the assumptions that P is symmetric positive-definite and that Q is symmetric. By definition, the matrix M is invertible if, and only if, the equation , with , admits only the trivial solution . Write , with . Therefore,If and , then because , while if and , then because . If both and , then if, and only if, and are both verified. This might only occur for those values of z such that and , namely, only if there exists a non-zero real-valued vector y such that . However, it can immediately be proved that this is never the case, in fact, for every vector , it holds thatWhile the term might be zero, the term is certainly positive; therefore, there is no nonzero vector y (or, hence, any nonzero vector x) such that . We may thus conclude that is invertible as long as . (Alternatively, this result might be proven by invoking the Minkowski determinant theorem [26]).
2.5. Formulation of the Modeling Problem in a Measurement-Error-Prone Setting as a Least-Squares Problem
2.6. De-Embedding of a Device under Test
2.7. Energy Exchange Rate of the Multiport Model
3. Problem Solution: Riemannian Gradient Approach
3.1. Objective Function and Its Gradient
3.2. Geodesic Stepping on the Product Manifold
- Unconditional halting: The iteration proceeds over a predefined number of steps. This criterion has the advantage of guaranteeing to halt in a finite number of steps but cannot ensure convergence.
- Threshold-conditioned halting: The iteration may be stopped when the ratio between the criterion function value at the current step and the initial value falls below a given threshold , namely, whenCare should be taken that the threshold is of the correct value: Too a narrow margin might causes the algorithm to carry on over a large number of steps, which might even result unbounded.
- Unnormalized gradient version: This instance is obtained by setting the stepsize schedules to small constant values, denoted simply by .
- Normalized gradient version: This instance is obtained by choosing the stepsize schedules to be inversely proportional to the gradients norms, namely:with as predefined constants. In order to obtain the final expression in (53), we used the relationship (46). This version of the stepsize schedule ensures a uniform descent speed.
4. Numerical Tests
4.1. Testing the Closed-Form Solution
4.2. Testing the Iterative Algorithm: Dataset and Initial Guess
4.3. Testing the Iterative Algorithm: Definition of Performance Figures
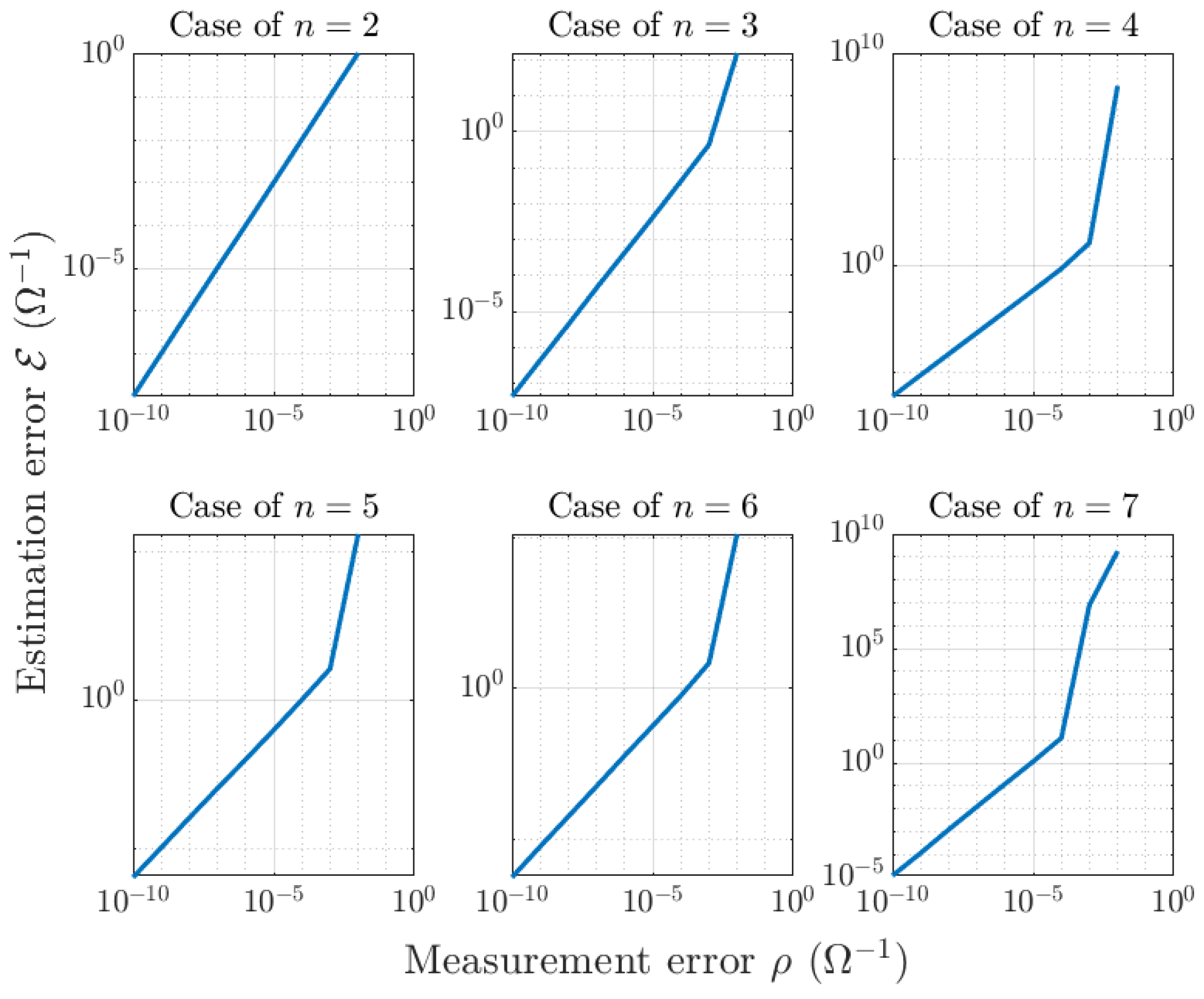
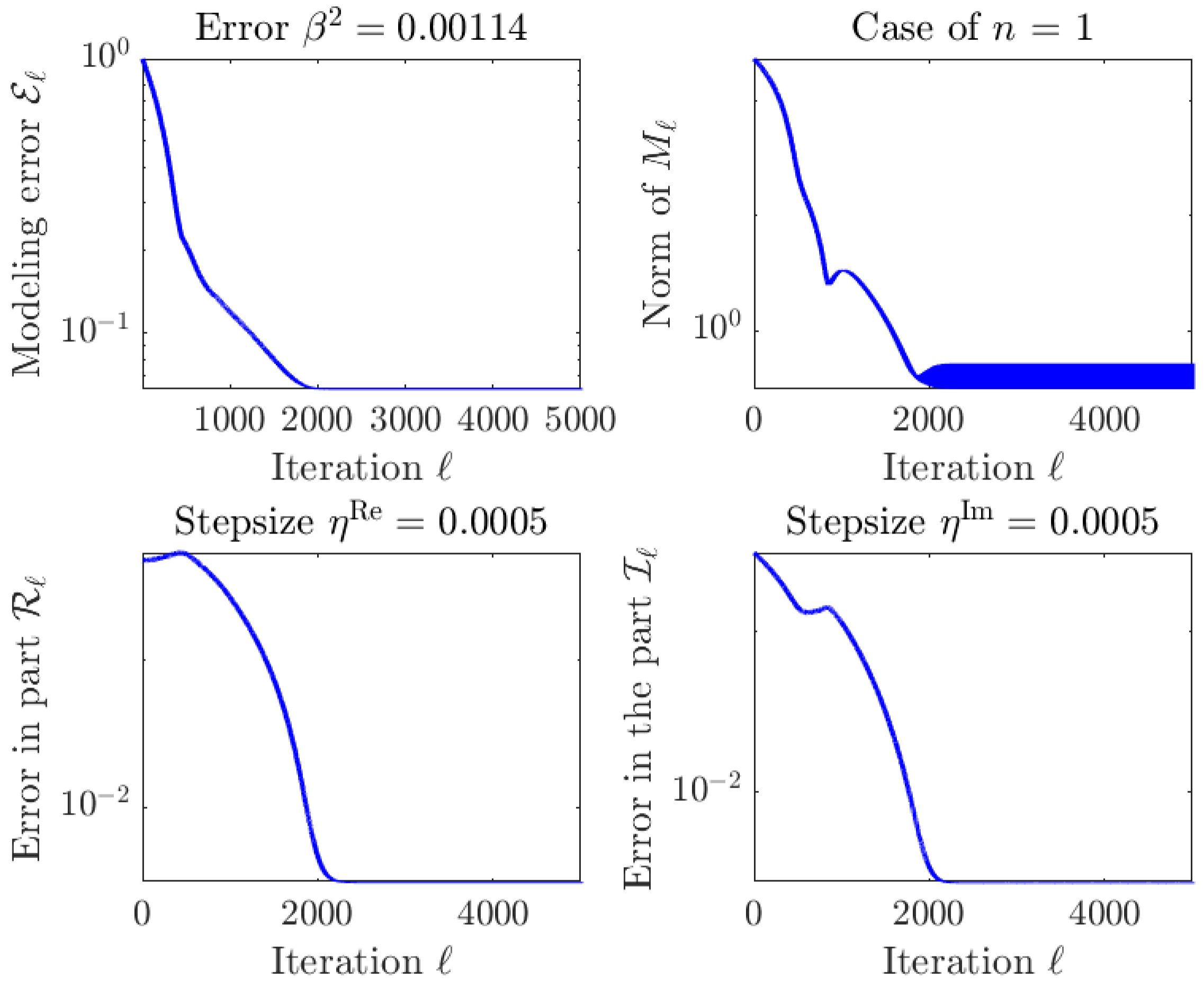
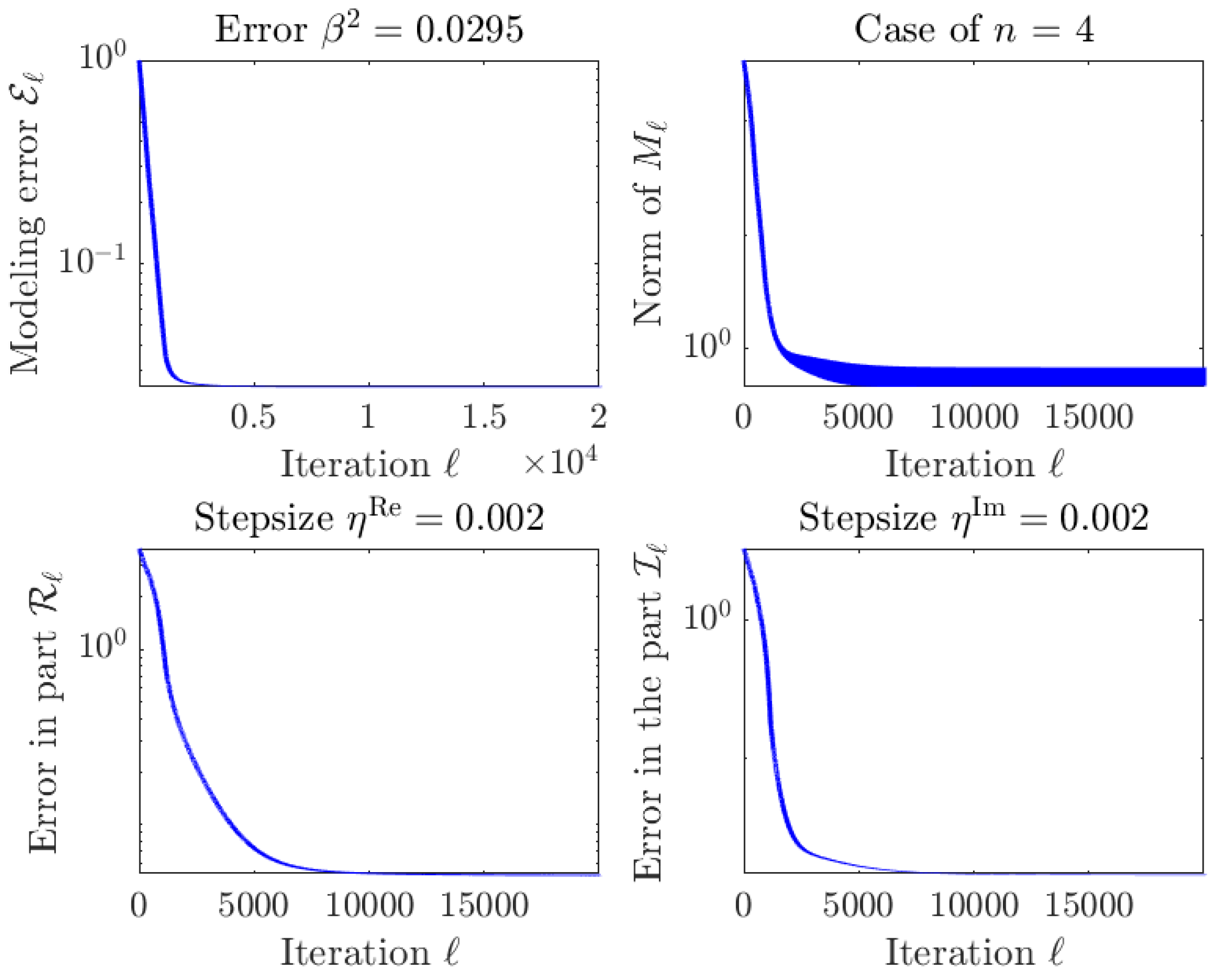
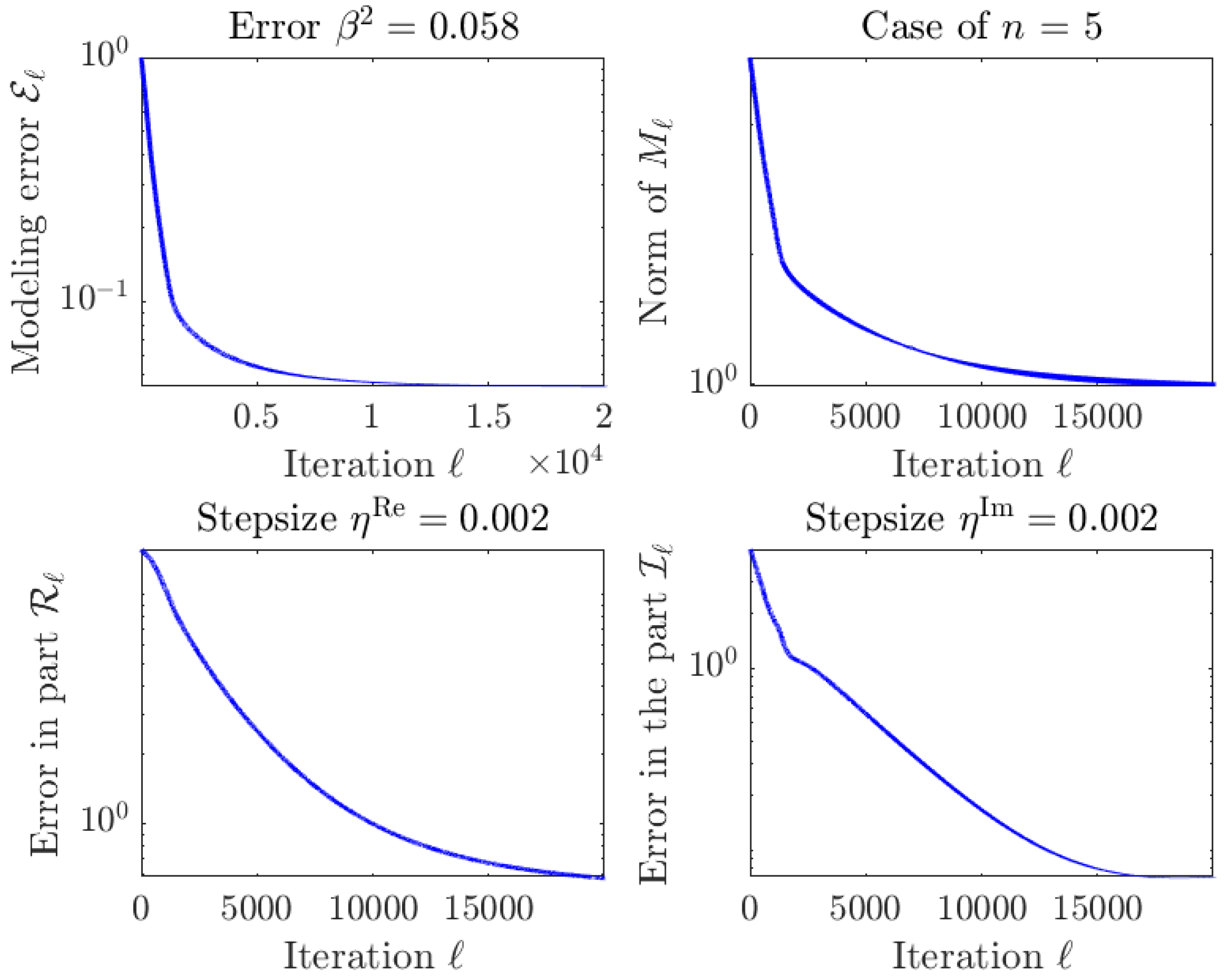
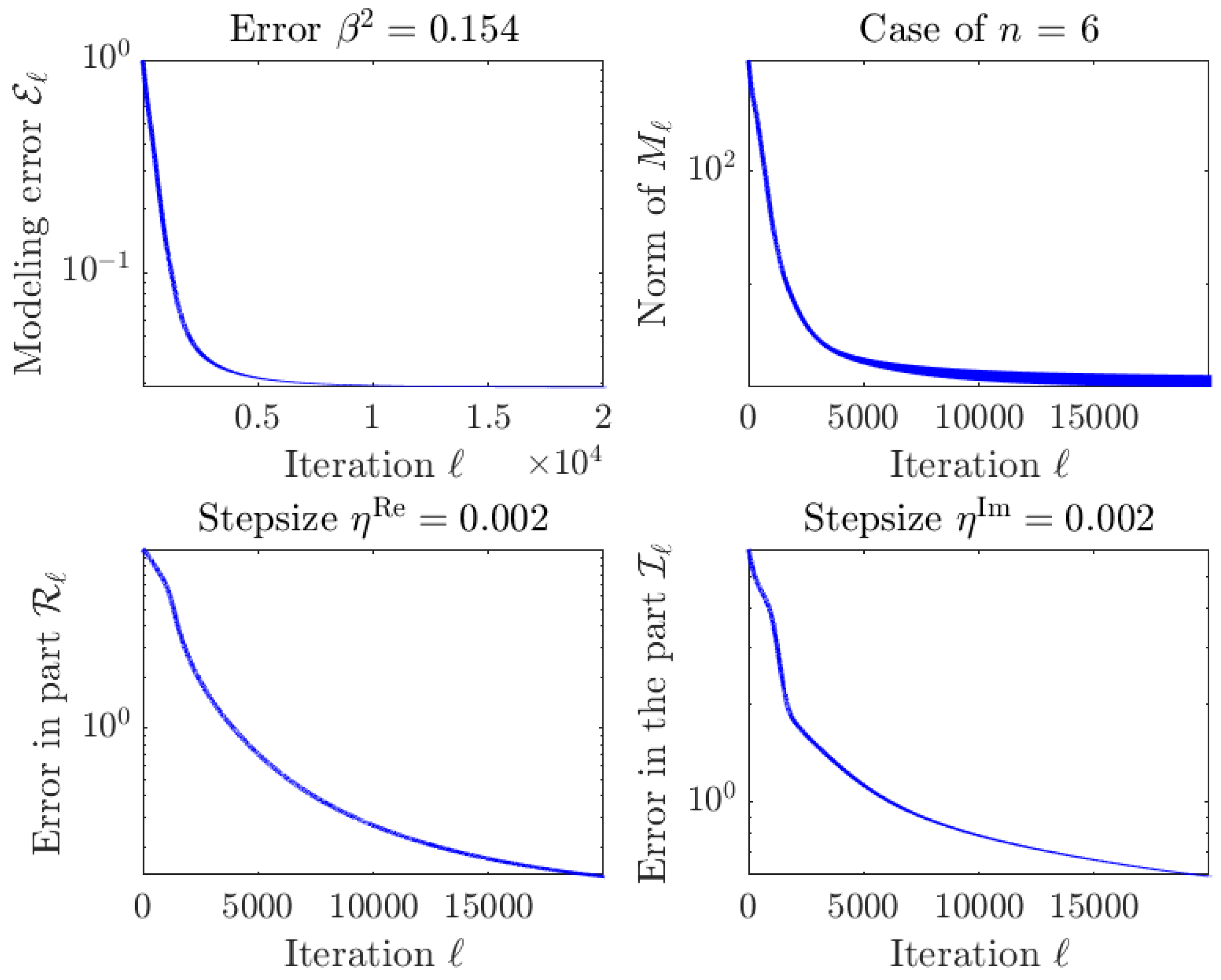
4.4. Numerical Test on the Iterative Algorithm with
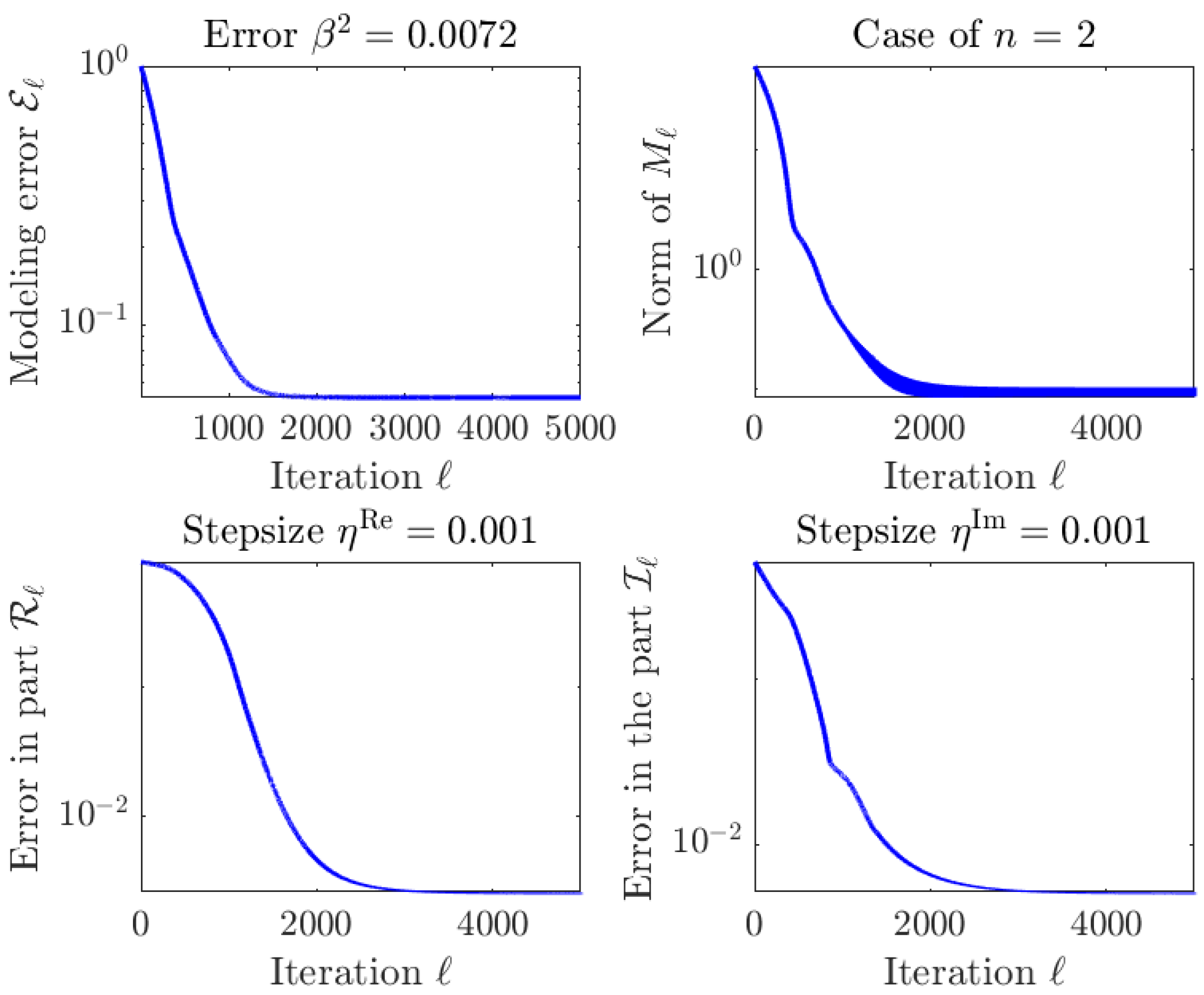
4.5. Numerical Tests on the Iterative Algorithm with
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mimani, A.; Munjal, M.L. Acoustical analysis of a general network of multi-port elements—An impedance matrix approach. Int. J. Acoust. Vib. 2012, 17, 23–46. [Google Scholar]
- Kim, N.; Allen, J.B. Allen Two-port network analysis and modeling of a balanced armature receiver. Hear. Res. 2013, 301, 156–167. [Google Scholar] [CrossRef] [PubMed]
- Snakowska, A.; Jurkiewicz, J. A new approach to the theory of acoustic multi-port networks with multimode wave and its application to muffler analysis. J. Sound Vib. 2021, 490, 115722. [Google Scholar] [CrossRef]
- Lee, H.; Lee, C.; Jang, G.; Kwon, S.-h. Harmonic analysis of the Korean high-speed railway using the eight-port representation model. IEEE Trans. Power Deliv. 2006, 21, 979–986. [Google Scholar] [CrossRef]
- Frasch, H.F.; Kresh, J.Y.; Noordergraaf, A. Two-port analysis of microcirculation: An extension of windkessel. Am. J. Physiol. 1996, 270, 376–385. [Google Scholar] [CrossRef]
- Manhartsgruber, B. Identification of the input-output behavior of hydraulic two-port networks. In Proceedings of the ASME 2009 Dynamic Systems and Control Conference, Hollywood, CA, USA, 12–14 October 2009; Volume 2, pp. 29–35. [Google Scholar]
- Farina, M.; Morini, A.; Rozzi, T. A calibration approach for the segmentation and analysis of microwave circuits. IEEE Trans. Microw. Theory Technol. 2007, 55, 2124–2134. [Google Scholar] [CrossRef]
- Mikulecky, D.C. A network thermodynamic two-port element to represent the coupled flow of salt and current. Improved alternative for the equivalent circuit. Biophys. J. 1979, 25, 323–340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonnin, M.; Traversa, F.L.; Bonani, F. A cascaded two-port network model for the analysis of harmonic chain-based energy harvesters. In Proceedings of the 2021 IEEE International Conference on Environment and Electrical Engineering and 2021 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Bari, Italy, 7–10 September 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Chung, E.; Ha, J.-I.; Bastami, A.A.; Perreault, D.J. Impedance compressing matching network based on two-port network analysis for wireless power transfer system. IEEE J. Emerg. Sel. Top. Ind. Electron. 2022, 3, 432–442. [Google Scholar] [CrossRef]
- Monti, G.; Mongiardo, M.; Minnaert, B.; Costanzo, A.; Tarricone, L. Optimal terminations for a single-input multiple-output resonant inductive WPT link. Energies 2020, 13, 5157. [Google Scholar] [CrossRef]
- Paul, R.J.A. Two-Port Network Representations of D. C. Electro-Mechanical Transducers; Note No. 121; The College of Aeronautics, Cranfield University: Cranfield, UK, 1962; Available online: https://dspace.lib.cranfield.ac.uk/handle/1826/12076 (accessed on 16 September 2022).
- De Gersem, H.; Srinivasan, V.; Muehle, C. Nonlinear three-port magnetic-circuit elements for simulating bending magnets. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2018, 37, 266–279. [Google Scholar] [CrossRef]
- Alazard, D.; Perez-Gonzalez, J.-A.; Loquen, T.; Cumer, C. Two-input two-output port model for mechanical systems. In Proceedings of the Scitech 2015—53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; Available online: http://oatao.univ-toulouse.fr/13642/1/Alazard_13642.pdf (accessed on 25 September 2016).
- Duman, T.; Marti, S.; Moonem, M.A.; Kader, A.A.R.A.; Krishnaswami, H. A modular multilevel converter with power mismatch control for grid-connected photovoltaic systems. Energies 2017, 10, 698. [Google Scholar] [CrossRef] [Green Version]
- Pu, B.; Kim, J.; Nah, W. A de-embedding technique of a three-port network with two ports coupled. J. Electromagn. Eng. Sci. 2015, 15, 258–265. [Google Scholar] [CrossRef] [Green Version]
- Ballicchia, M.; Farina, M.; Morini, A.; Turchetti, C.; Orcioni, S. A methodology for RF modeling of packages with external pin measurements. Int. J. Microw.-Comput.-Aided Eng. 2014, 24, 623–634. [Google Scholar] [CrossRef]
- Schaft, A.v.; Jeltsema, D. Port-Hamiltonian systems: An introductory overview. Found. Trends Syst. Control 2014, 1, 173–378. [Google Scholar] [CrossRef]
- Vlach, J. Linear Circuit Theory: Matrices in Computer Applications; Apple Academic Press: Lansing, MI, USA, 2021. [Google Scholar]
- Kokalari, I.; Karaja, T.; Guerrisi, M. Review on lumped parameter method for modeling the blood flow in systemic arteries. J. Biomed. Sci. Eng. 2013, 6, 92–99. [Google Scholar] [CrossRef] [Green Version]
- Dunsmore, J.P. Handbook of Microwave Component Measurements: With Advanced VNA Techniques; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Boyd, S.; Chua, L.O. On the passivity criterion for LTI n-port. Circuit Theory Appl. 1982, 10, 323–333. [Google Scholar] [CrossRef]
- Silvester, J.R. Determinants of block matrices. Math. Gaz. 2000, 84, 460–467. [Google Scholar] [CrossRef] [Green Version]
- Meyer, C.D. Matrix Analysis and Applied Linear Algebra, Chapter 7.6: Positive Definite Matrices; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2000. [Google Scholar]
- Marcus, M.; Minc, H. A Survey of Matrix Theory and Matrix Inequalities; Dover Publications Inc.: Mineola, NY, USA, 1992. [Google Scholar]
- Nash, S.G.; Sofer, A. Linear and Nonlinear Programming; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1995. [Google Scholar]
- Sun, H.; Zhang, Z.; Peng, L.; Duan, X. An Elementary Introduction to Information Geometry; Science Press: Beijing, China, 2016. (In Chinese) [Google Scholar]
- Fiori, S. Manifold calculus in system theory and control—Fundamentals and first-order systems. Symmetry 2021, 13, 2092. [Google Scholar] [CrossRef]
- Fiori, S. Manifold calculus in system theory and control—Second order structures and systems. Symmetry 2022, 16, 1144. [Google Scholar] [CrossRef]
- Higham, N.J. Functions of Matrices: Theory and Computation; Society for Industrial and Applied Mathematics (SIAM): Philadelphia, PA, USA, 2008; ISBN 978-0-898716-46-7. [Google Scholar]
- Levinger, B.W. The square root of a 2×2 matrix. Math. Mag. 1980, 53, 222–224. [Google Scholar] [CrossRef]
- Bernstein, D.S.; So, W. Some explicit formulas for the matrix exponential. IEEE Trans. Autom. Control 1993, 38, 1228–1232. [Google Scholar] [CrossRef] [Green Version]


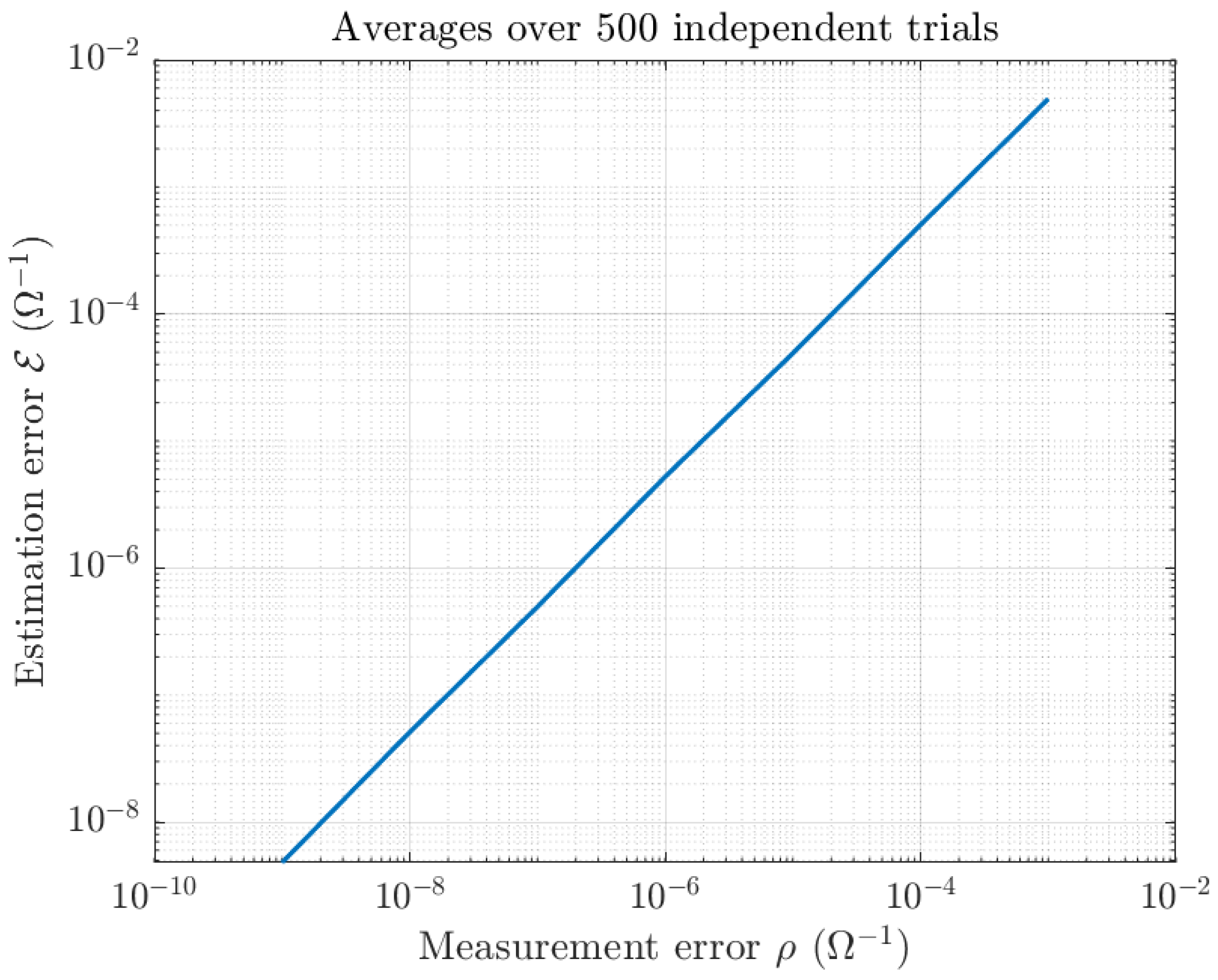

| Admittance () | Admittance () | Error () |
|---|---|---|
| Eigenvalues of () | Eigenvalues of () |
|---|---|
| 0.0679 | 0.0777 |
| 0.1339 | 0.1323 |
| 0.3177 | 0.3189 |
| 0.3632 | 0.3649 |
| 0.9779 | 0.9513 |
| 1.5232 | 1.5382 |
| 3.0090 | 3.0088 |
| 4.7040 | 4.6554 |
| Eigenvalues of () | Eigenvalues of () |
|---|---|
| 0.0133 | 0.0081 |
| 0.1417 | 0.1394 |
| 0.1939 | 0.2003 |
| 0.3158 | 0.3333 |
| 0.8436 | 0.8209 |
| 1.1496 | 1.1470 |
| 2.3292 | 2.3371 |
| 4.0322 | 4.0452 |
| 5.5390 | 5.3469 |
| 20.1115 | 19.9327 |
| Eigenvalues of () | Eigenvalues of () |
|---|---|
| 0.0884 | 0.0884 |
| 0.1349 | 0.1348 |
| 0.2471 | 0.2644 |
| 0.3656 | 0.3906 |
| 0.5338 | 0.5278 |
| 0.5682 | 0.5858 |
| 1.5714 | 1.5986 |
| 2.2601 | 2.2647 |
| 8.4494 | 8.2849 |
| 9.8163 | 10.0289 |
| 18.8331 | 18.7491 |
| 20.8985 | 20.8803 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fiori, S.; Wang, J. External Identification of a Reciprocal Lossy Multiport Circuit under Measurement Uncertainties by Riemannian Gradient Descent. Energies 2023, 16, 2585. https://doi.org/10.3390/en16062585
Fiori S, Wang J. External Identification of a Reciprocal Lossy Multiport Circuit under Measurement Uncertainties by Riemannian Gradient Descent. Energies. 2023; 16(6):2585. https://doi.org/10.3390/en16062585
Chicago/Turabian StyleFiori, Simone, and Jing Wang. 2023. "External Identification of a Reciprocal Lossy Multiport Circuit under Measurement Uncertainties by Riemannian Gradient Descent" Energies 16, no. 6: 2585. https://doi.org/10.3390/en16062585
APA StyleFiori, S., & Wang, J. (2023). External Identification of a Reciprocal Lossy Multiport Circuit under Measurement Uncertainties by Riemannian Gradient Descent. Energies, 16(6), 2585. https://doi.org/10.3390/en16062585







