The Influence of Heat Transfer Coefficient α of Insulating Liquids on Power Transformer Cooling Systems
Abstract
:1. Introduction
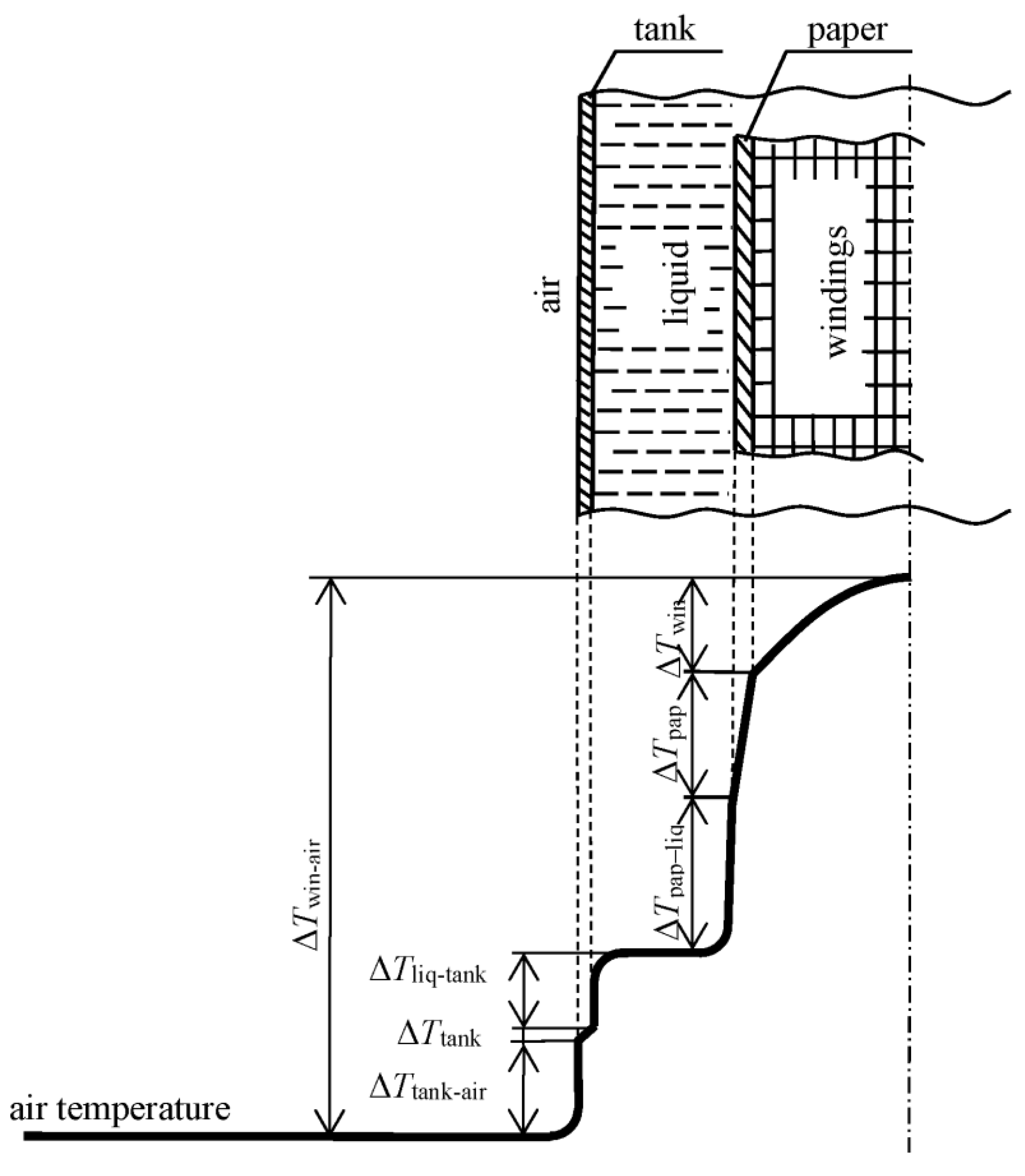
1.1. Heat Sources and Power Transformer Cooling System
- In the windings of the transformer ΔTwin,
- In paper insulation ΔTpap,
- In the insulating liquid from the side of the paper insulation ΔTpap-liq and from the side of the tank ΔTliq-tank,
- In the transformer tank ΔTtank,
- In the air from the side of the tank ΔTtank-air.
1.2. Determination of the Temperature Field Distribution in the Power Transformer
1.3. Determination of the Heat Transfer Coefficient α
2. Test Object
3. Motivation, Thesis and Scope of Research
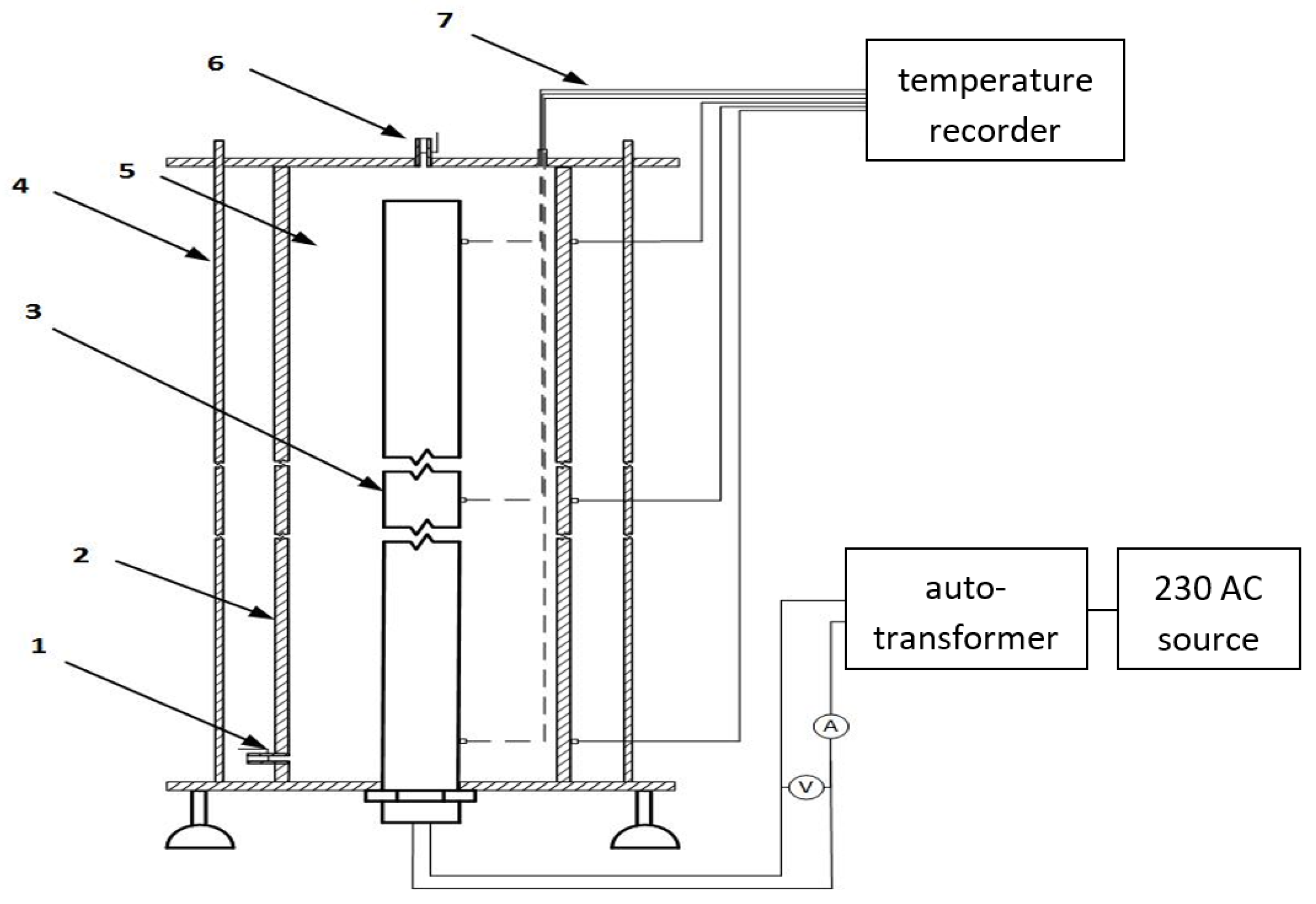
4. Measuring System
5. Measurement Results
5.1. Results of Measurements of the Heat Transfer Coefficient α
- The type of electrical insulating liquid,
- The heat load q of the surface to be cooled on the heating element,
- The length of the heating element δ.
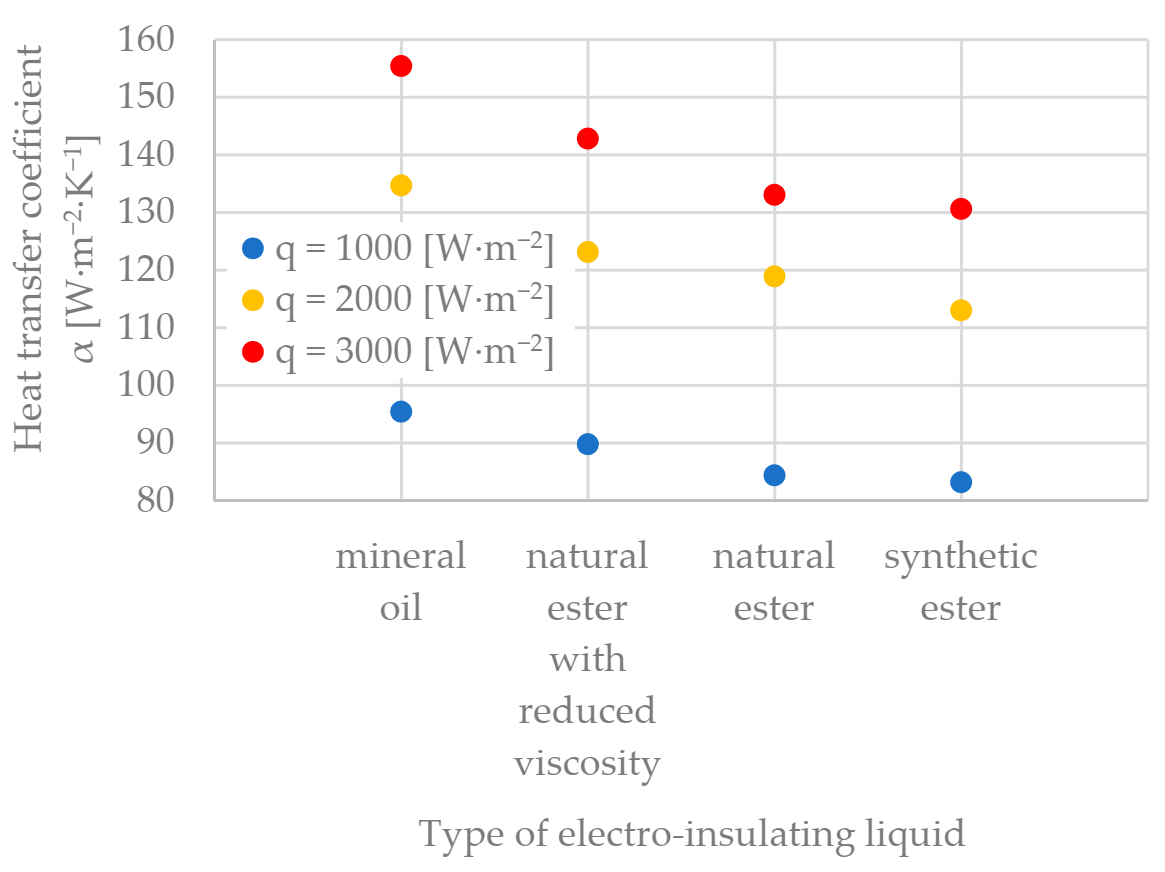
5.2. Heat Transfer Coefficient α Depending on the Type of Electrical Insulating Liquid
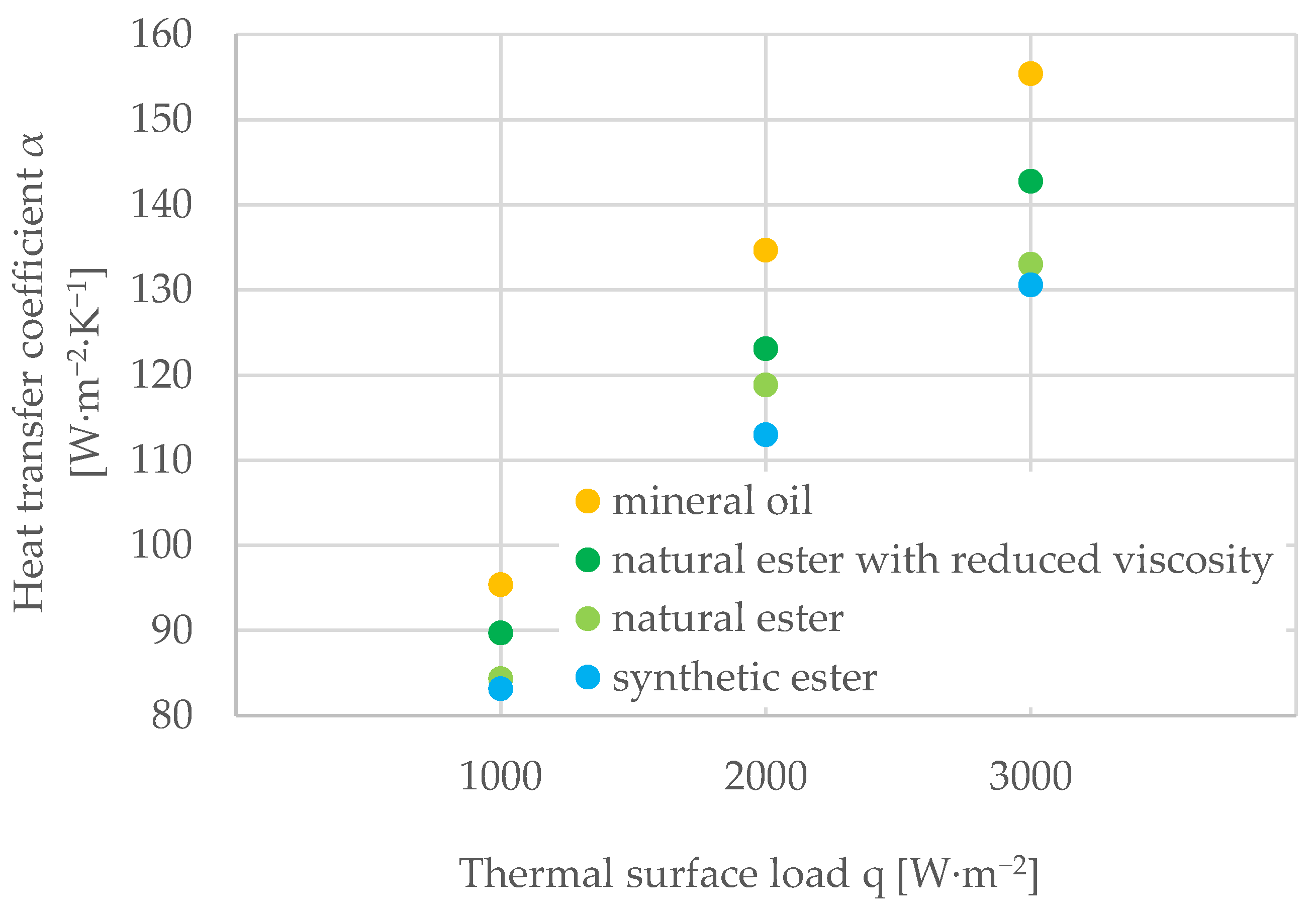
5.3. Heat Transfer Coefficient α Depending on the Value of the Heat Load q
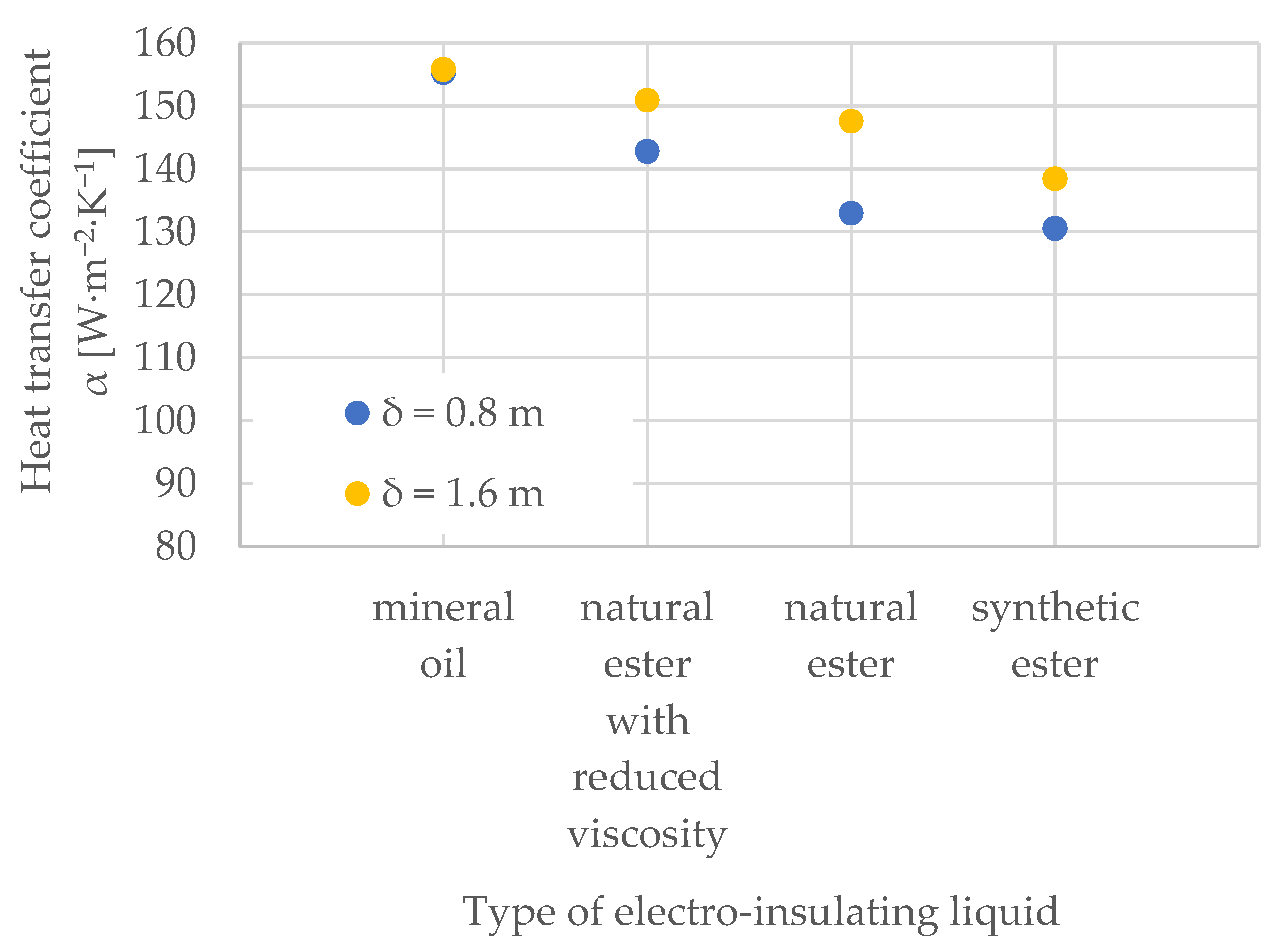
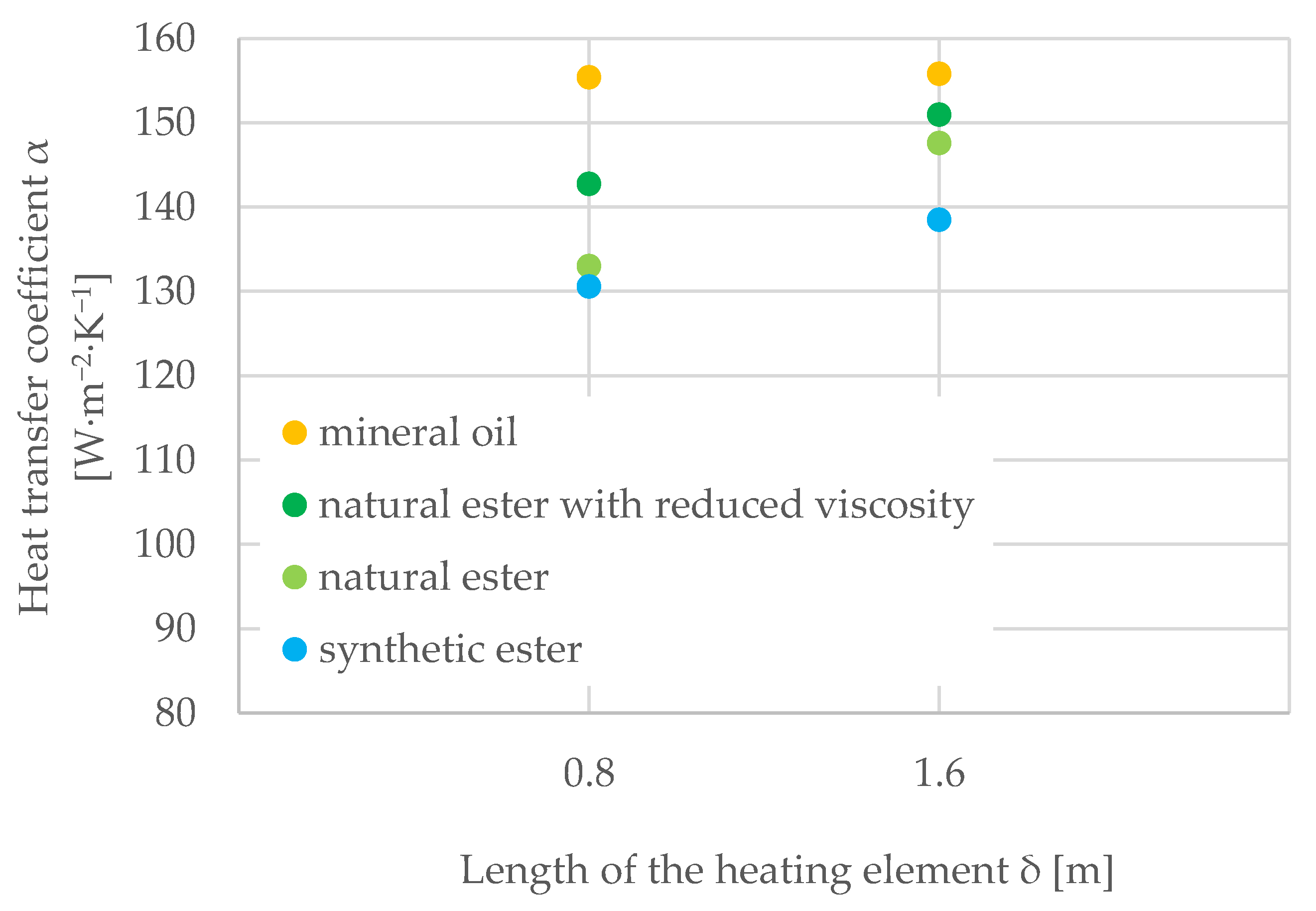
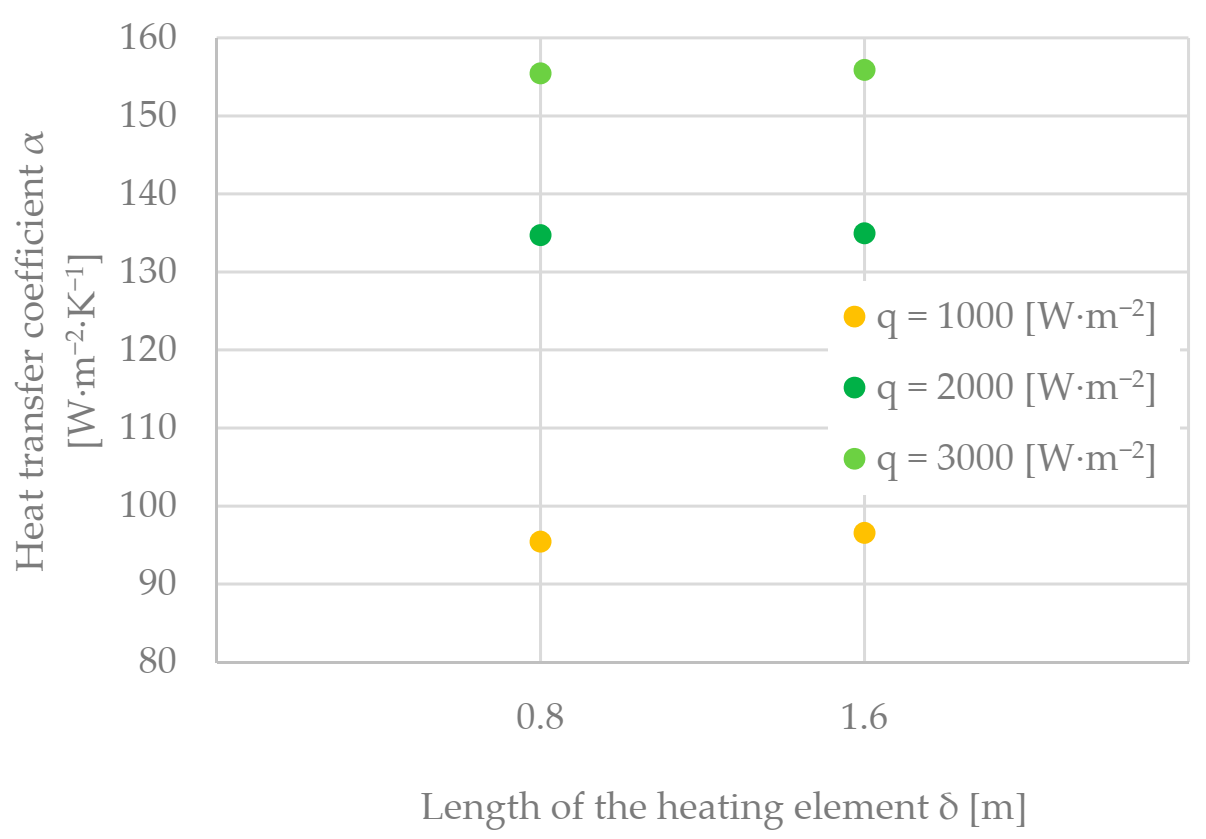
5.4. Heat Transfer Coefficient α Depending on the Length of the Heating Element δ
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, Y.; Li, X.; Li, H.; Wang, J.; Fan, X. Experimental and Numerical Investigation of the Internal Temperature of an Oil-Immersed Power Transformer with DOFS. Appl. Sci. 2020, 10, 5718. [Google Scholar] [CrossRef]
- Kunicki, M.; Borucki, S.; Cichon, A.; Frymus, J. Modeling of the Winding Hot-Spot Temperature in Power Transformers: Case Study of the Low-Loaded Fleet. Energies 2019, 12, 3561. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Guo, Z.; Zhu, T.; Feng, H.; Wang, S. A New Multi-Conductor Transmission Line Model of Transformer Winding for Frequency Response Analysis Considering the Frequency-Dependent Property of the Lamination Core. Energies 2018, 11, 826. [Google Scholar] [CrossRef] [Green Version]
- Paul, A. Practical Study of Mixed-Core High Frequency Power Transformer. Magnetism 2022, 2, 306–327. [Google Scholar] [CrossRef]
- Cheng, L.; Yu, T.; Wang, G.; Yang, B.; Zhou, L. Hot Spot Temperature and Grey Target Theory-Based Dynamic Modelling for Reliability Assessment of Transformer Oil-Paper Insulation Systems: A Practical Case Study. Energies 2018, 11, 249. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Ren, L.; Yu, H.; Xu, Y.; Lei, Q.; Li, X.; Han, B. Dual-Temperature Evaluation of a High-Temperature Insulation System for Liquid-Immersed Transformer. Energies 2018, 11, 1957. [Google Scholar] [CrossRef] [Green Version]
- Souček, J.; Trnka, P.; Hornak, J. Proposal of Physical-Statistical Model of Thermal Aging Respecting Threshold Value. Energies 2017, 10, 1120. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gong, S.; Grzybowski, S. Reliability Evaluation Method for Oil-Paper Insulation in Power Transformers. Energies 2011, 4, 1362–1375. [Google Scholar] [CrossRef]
- Manea, A.; Gorjanu, T.; Lazeanu, A.; Dumitran, L.M. Effect of Electrical Accelerated Aging on DC Resistivity of Mineral Oil Used in Power Transformers. Energies 2023, 16, 294. [Google Scholar] [CrossRef]
- Arsad, S.; Ker, P.; Jamaludin, Z.; Choong, P.; Lee, H.; Thiviyanathan, V.A.; Ghazali, Y. Water Content in Transformer Insulation System: A Review on the Detection and Quantification Methods. Energies 2023, 16, 1920. [Google Scholar] [CrossRef]
- Sikorski, W.; Walczak, K.; Przybylek, P. Moisture Migration in an Oil-Paper Insulation System in Relation to Online Partial Discharge Monitoring of Power Transformers. Energies 2016, 9, 1082. [Google Scholar] [CrossRef] [Green Version]
- Przybylek, P.; Moranda, H.; Moscicka-Grzesiak, H.; Szczesniak, D. Application of Synthetic Ester for Drying Distribution Transformer Insulation—The Influence of Cellulose Thickness on Drying Efficiency. Energies 2019, 12, 3874. [Google Scholar] [CrossRef] [Green Version]
- Nadolny, Z. Determination of Dielectric Losses in a Power Transformer. Energies 2022, 15, 993. [Google Scholar] [CrossRef]
- Fernandez, I. The Need for Experimental and Numerical Analyses of Thermal Ageing in Power Transformers. Energies 2022, 15, 6393. [Google Scholar] [CrossRef]
- Fofana, I.; Hadjadj, Y. Electrical-Based Diagnostic Techniques for Assessing Insulation Condition in Aged Transformers. Energies 2016, 9, 679. [Google Scholar] [CrossRef]
- N’cho, J.S.; Fofana, I.; Hadjadj, Y.; Beroual, A. Review of Physicochemical-Based Diagnostic Techniques for Assessing Insulation Condition in Aged Transformers. Energies 2016, 9, 367. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, K.; Du, Y. Temperature Rise Calculation of Magnetic Core Considering the Temperature Effect of Magnetic Properties in an Electrical Steel Sheet. Symmetry 2022, 14, 2315. [Google Scholar] [CrossRef]
- Gonçalves Mafra, R.; Magalhães, E.; De Campos Salles Anselmo, B.; Belchior, F.; Metrevelle Marcondes Lima e Silva, S. Winding Hottest-Spot Temperature Analysis in Dry-Type Transformer Using Numerical Simulation. Energies 2019, 12, 68. [Google Scholar] [CrossRef] [Green Version]
- Shen, Z.; Xu, B.; Liu, C.; Hu, C.; Liu, B.; Xu, Z.; Jin, L.; Chen, W. The Modeling and Simplification of a Thermal Model of a Planar Transformer Based on Internal Power Loss. Sustainability 2022, 14, 11915. [Google Scholar] [CrossRef]
- Bilal Riaz, M.; Rehman, A.U.; Awrejcewicz, J.; Akgül, A. Power Law Kernel Analysis of MHD Maxwell Fluid with Ramped Boundary Conditions: Transport Phenomena Solutions Based on Special Functions. Fractal Fract. 2021, 5, 248. [Google Scholar] [CrossRef]
- Zdanowski, M. Streaming Electrification of C60 Fullerene Doped Insulating Liquids for Power Transformers Applications. Energies 2022, 15, 2496. [Google Scholar] [CrossRef]
- Cybulski, M.; Przybylek, P. Application of Molecular Sieves for Drying Transformers Insulated with Mineral Oil, Natural Ester, or Synthetic Ester. Energies 2021, 14, 1719. [Google Scholar] [CrossRef]
- Wolny, S. Analysis of High-Frequency Dispersion Characteristics of Capacitance and Loss Factor of Aramid Paper Impregnated with Various Dielectric Liquids. Energies 2019, 12, 1063. [Google Scholar] [CrossRef] [Green Version]
- Beroual, B.; Khaled, U.; Noah, P.; Sitorus, H. Comparative Study of Breakdown Voltage of Mineral, Synthetic and Natural Oils and Based Mineral Oil Mixtures under AC and DC Voltages. Energies 2017, 10, 511. [Google Scholar] [CrossRef]
- Olmo, C.; Méndez, C.; Quintanilla, P.J.; Ortiz, F.; Renedo, C.J.; Ortiz, A. Mineral and Ester Nanofluids as Dielectric Cooling Liquid for Power Transformers. Nanomaterials 2022, 12, 2723. [Google Scholar] [CrossRef]
- Dombek, G.; Nadolny, Z.; Marcinkowska, A. Effects of Nanoparticles Materials on Heat Transfer in Electro-Insulating Liquids. Appl. Sci. 2018, 8, 2538. [Google Scholar] [CrossRef] [Green Version]
- Nadolny, Z.; Dombek, G. Electro-Insulating Nanofluids Based on Synthetic Ester and TiO2 or C60 Nanoparticles in Power Transformer. Energies 2018, 11, 1953. [Google Scholar] [CrossRef] [Green Version]
- Wisniewski, S. Heat Transfer; Scientific and Technical Publishing House: Warsaw, Poland, 2009. [Google Scholar]




| Nature of the Flow | Gr∙Pr | c | n |
|---|---|---|---|
| no flow | <10−3 | 0.45 | 0 |
| laminar flow | 10−3 ÷ 5 × 102 | 1.18 | 0.125 |
| transitional flow | 5 × 10−3 ÷ 2 × 107 | 0.54 | 0.250 |
| turbulent flow | >2 × 107 | 0.14 | 0.333 |
| 25 °C | 40 °C | 60 °C | 80 °C | |
|---|---|---|---|---|
| thermal conductivity λ [W·m−1·K−1] | ||||
| mineral oil | 0.133 | 0.130 | 0.128 | 0.126 |
| synthetic ester | 0.158 | 0.156 | 0.153 | 0.151 |
| natural ester | 0.182 | 0.180 | 0.178 | 0.175 |
| specific heat cp [J·kg−1·K−1] | ||||
| mineral oil | 1902 | 1974 | 2077 | 2187 |
| synthetic ester | 1905 | 1964 | 2052 | 2149 |
| natural ester | 2028 | 2082 | 2166 | 2259 |
| kinematic viscosity ν [mm2·s−1] | ||||
| mineral oil | 17.1 | 9.6 | 5.4 | 3.4 |
| synthetic ester | 55.1 | 28.3 | 14.0 | 8.1 |
| natural ester | 56.3 | 32.7 | 18.3 | 11.5 |
| density ρ [kg·m−3] | ||||
| mineral oil | 867 | 857 | 845 | 832 |
| synthetic ester | 964 | 953 | 940 | 926 |
| natural ester | 917 | 908 | 892 | 880 |
| thermal expansion coefficient β [K−1] | ||||
| mineral oil | 0.00075 | 0.00076 | 0.00078 | 0.00080 |
| synthetic ester | 0.00076 | 0.00077 | 0.00078 | 0.00079 |
| natural ester | 0.00074 | 0.00076 | 0.00078 | 0.00080 |
| Heat Transfer Coefficient α [W∙m−2∙K−1] | ||||
|---|---|---|---|---|
| Mineral Oil | Natural Ester with Reduced Viscosity | Natural Ester | Synthetic Ester | |
| length of heating element δ [m] | 0.8 m | |||
| q = 1000 [W∙m−2∙K−1] | 95.39 | 89.74 | 84.34 | 83.17 |
| q = 2000 [W∙m−2∙K−1] | 134.67 | 123.12 | 118.85 | 112.99 |
| q = 3000 [W∙m−2∙K−1] | 155.40 | 142.79 | 133.01 | 130.59 |
| length of heating element δ [m] | 1.6 m | |||
| q = 1000 [W∙m−2∙K−1] | 96.51 | 90.73 | 84.50 | 86.62 |
| q = 2000 [W∙m−2∙K−1] | 134.92 | 126.04 | 122.76 | 121.48 |
| q = 3000 [W∙m−2∙K−1] | 155.86 | 150.99 | 147.62 | 138.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goscinski, P.; Nadolny, Z.; Tomczewski, A.; Nawrowski, R.; Boczar, T. The Influence of Heat Transfer Coefficient α of Insulating Liquids on Power Transformer Cooling Systems. Energies 2023, 16, 2627. https://doi.org/10.3390/en16062627
Goscinski P, Nadolny Z, Tomczewski A, Nawrowski R, Boczar T. The Influence of Heat Transfer Coefficient α of Insulating Liquids on Power Transformer Cooling Systems. Energies. 2023; 16(6):2627. https://doi.org/10.3390/en16062627
Chicago/Turabian StyleGoscinski, Przemyslaw, Zbigniew Nadolny, Andrzej Tomczewski, Ryszard Nawrowski, and Tomasz Boczar. 2023. "The Influence of Heat Transfer Coefficient α of Insulating Liquids on Power Transformer Cooling Systems" Energies 16, no. 6: 2627. https://doi.org/10.3390/en16062627
APA StyleGoscinski, P., Nadolny, Z., Tomczewski, A., Nawrowski, R., & Boczar, T. (2023). The Influence of Heat Transfer Coefficient α of Insulating Liquids on Power Transformer Cooling Systems. Energies, 16(6), 2627. https://doi.org/10.3390/en16062627







