Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review
Abstract
:1. Introduction
- Comprehensive review of PQDs and their causes and consequences is presented. A review is also provided of PQ measurement (PMU) and summarizes its main points. The requirements of PMU standards for balanced and unbalanced systems are defined.
- Critical and comprehensive review is presented for PQ disturbances characterization with a focus on extraction, selection and classification techniques.
- A state-of-the-art of feature selection (FS) technique that is based on the optimization algorithms features classification applications is provided.
- In-depth and critical analysis of signal processing, optimization algorithms and pattern recognition techniques are done.
- A discussion on the application of parametric and non-parametric methods is performed.
- A critical analysis and future research of relevant issues that are related to the PQ disturbances characterization is performed.
- Section 2 presents the PQDs and their origins and consequences. Then the international standard for PQ characterization is provided. In addition, PQ measurement (PMU) is presented.
- Section 3 deals with feature extraction techniques used for frequency and phasor estimation.
- Section 4 is concerned with the problem of feature selection or parameter optimization for classification purposes.
- Section 5 describes power quality disturbances classification with a focus on classical and pattern recognition techniques.
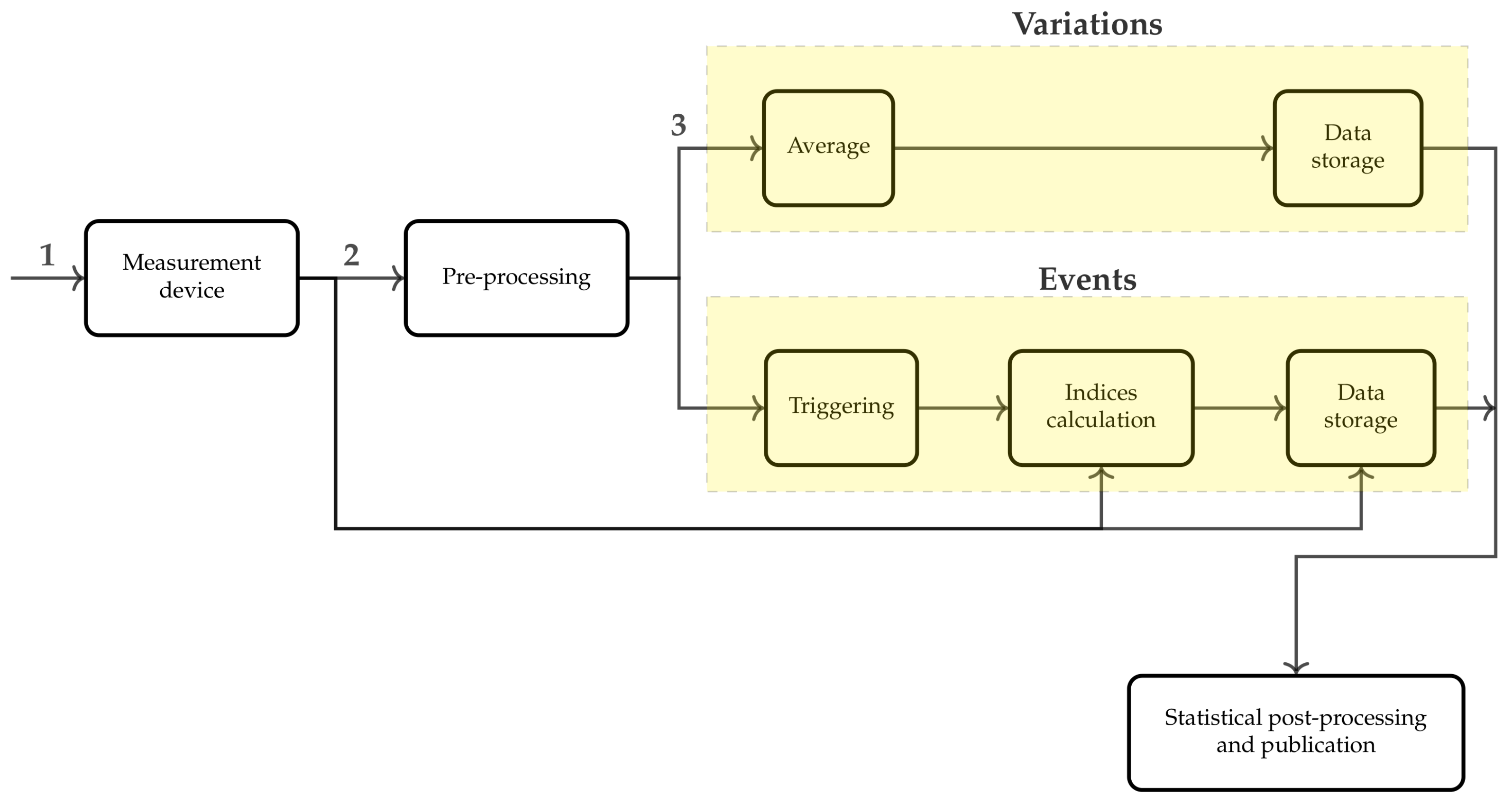
2. PQ Disturbances Monitoring
- Sensors: PQD impacts negatively the performance of measurement devices.
- Protective relays: they can lead to mal-function due to PQDs.
- Equipment’s lifetime: it can be reduced and equipment can be damaged because of these disturbances.
- Electromagnetic compatibility: PQDs are one of the most important sources of electromagnetic noise [36].
- Feature extraction stage: this refers to the voltage estimation (i.e., phasor and frequency) from the acquisition signals that are noise corrupted.
- Feature selection stage.
- Feature detection stage: this presents triggering, i.e., determining the time-points when the event is starting and ending.
- Feature classification stage: this permits the identification of the type of disturbance.
2.1. Disturbances
2.1.1. Disturbance Variations
- Frequency and voltage variations:As mentioned previously, the real-time frequency value has always a small deviation of Hz [16], from the nominal value which is 50 Hz or 60 Hz. Figure 2 presents the measured frequency for several countries. These frequency variations can lead to a variation in motor speed and less power generation in production units.The voltage variation is caused by the variation of the end-user loads and distributed generation [13]. These can affect the performance of equipment. They can also cause overheating and reduce the starting torque of electrical motors (induction motors) [6]. For example, over-voltage is a voltage value that arrives at 110–120% of the nominal value over several periods (one minute). An over-voltage is illustrated by Figure 3.
- Harmonic, inter-harmonic, and non-periodic distortions:These distortions are a deformation of the current or voltage wave-form from its nominal one. These disturbances can lead to over-heating of power electronic equipment, etc. [41,42,43]. The harmonics components are more considered by engineers and researchers since they are more dominant in the electric grid than others disturbances [44]. Total harmonic distortion (THD) is a criterion that is used to analyze the number of harmonic components in the signal. THD is defined by the international standard IEC 61000-4-7 [45] as:where refers to fundamental frequency and corresponds to the amplitude of the th harmonic component. The parameter allows controlling THD.
2.1.2. Events
2.2. Monitoring
2.3. Standards
2.4. Phasor Measurement Units (PMUs)
2.4.1. Definition
2.4.2. Standards
2.4.3. Estimation Evaluation’s Criteria
- Frequency and ROCOF measurement evaluation:The voltage or current of the three-phase power grid can be expressed by the following model:where refers to the phase index, corresponds to the maximum amplitude and is instantaneous phase angle. The frequency expression is given byand the ROCOF is expressed byBoth FE and ROCOF error (RFE) are provided by the standard C37.118 for evaluating the estimation performance of the frequency estimator.The FE is defined asand the RFE is expressed aswhere and correspond to the real and estimated frequency.PMUs must yield high estimation performance in order to meet the requirements specified by the PMU standard. These performances shall meet the requirements of the C37.118 under stationary and non-stationary conditions and for P- and/or M-classes. Table 4 presents the FE and RFE requirements for both classes and under stationary conditions. Under non-stationary conditions, a condition test is also presented that determines the band-width of the synchro-phasor device. In this test, phase modulation and sinusoidal amplitude are used. The model of signals is given bywhere refers to the input signal amplitude, and w are, respectively, the nominal and the modulation angular frequencies in . corresponds to the modulation frequency in Hz, presents the phase index. and correspond, respectively, to the magnitude and the modulation of phase angle. This test must be realized with w, , and over the range of frequency given in Table 5 [21].
- Total vector error evaluation:The C37.118 standard allows for simplifying the compliance specification by combining the angle phase and amplitude in one evaluation criterion which is TVE, which allows for evaluating the estimation performance of the phasor. TVE is then the difference between the real value and the estimated one of the phasor. Let supposing the following synchrophasor representation , the TVE criterion is expressed then aswhere and present, respectively, at the instant n, the real and imaginary values of the fundamental phasor. and refer, respectively, at the instant n, to the real and imaginary estimated values of phasor. Both real and estimated values of the phasor are measured at the same time-point. The PMU standard requires that the TVE does not exceed . Figure 12 presents a circle with a radius of which is the allowed error. This concept is inspired by the international standard IEEE C37.118. The signal’s parameters are considered to be constant under stationary conditions. However, under non-stationary conditions, these parameters can be time-varying. In this case, it is imperative to use a model of signal that takes into consideration the parameter changes.
3. Feature Extraction-Spectral Estimation Techniques for Power Quality Monitoring
3.1. Non-Parametric Methods
3.1.1. Zero-Crossing Transform
3.1.2. Root Mean Square and Peak Voltage Techniques
3.1.3. Fourier Transform and Its Extensions
3.2. Harmonic Decomposition-Based Methods
3.2.1. Pisarenko Method
- Observe N values of the signal .
- Compute the auto-correlation matrix and decompose it into eigenelements.
- Detect variance ( and deduce the number of sinusoids).
- Extract the roots of a complex polynomial of degree .
3.2.2. Prony Method
- Observe values of the signal .
- Solve a complex N-dimensional linear system.
- Extract the roots of a complex polynomial of N degree.
- In order to determine the amplitudes, it is necessary to solve a complex linear system of N dimension.
3.2.3. Least Square Prony Method
3.2.4. Modified Least Square Prony Method
3.3. Parametric Methods
- A good knowledge and hypothesis of generated process.
- Using models that are validated by good experimental results.
3.3.1. Discrete Spectra
3.3.2. Continuous Spectra
3.4. Extension to Non-Stationary Conditions
3.4.1. Hilbert–Huang Transform (HHT)
3.4.2. Kalman Filters
3.4.3. Maximum Likelihood Estimator
- is matrix containing the recorded. This matrix is expressed as
- is a matrix containing the fundamental frequency . This matrix is given by
- is a real-valued matrix containing the amplitudes and initial phases of the three-phase voltage system. This matrix is expressed by
3.5. Discussion
4. Feature Selection Techniques
5. PQ Disturbances Classification Techniques
5.1. Classical Techniques
5.1.1. ABC Classifier
5.1.2. Symmetrical Component Classifier (SCC)
5.2. Techniques-Based on Signal Processing Methods
5.2.1. PQDs Classification Based on Information Theoretic Criteria
5.2.2. PQDs Classification Based on Space Vector Method
5.3. Pattern Recognition (PR) Techniques
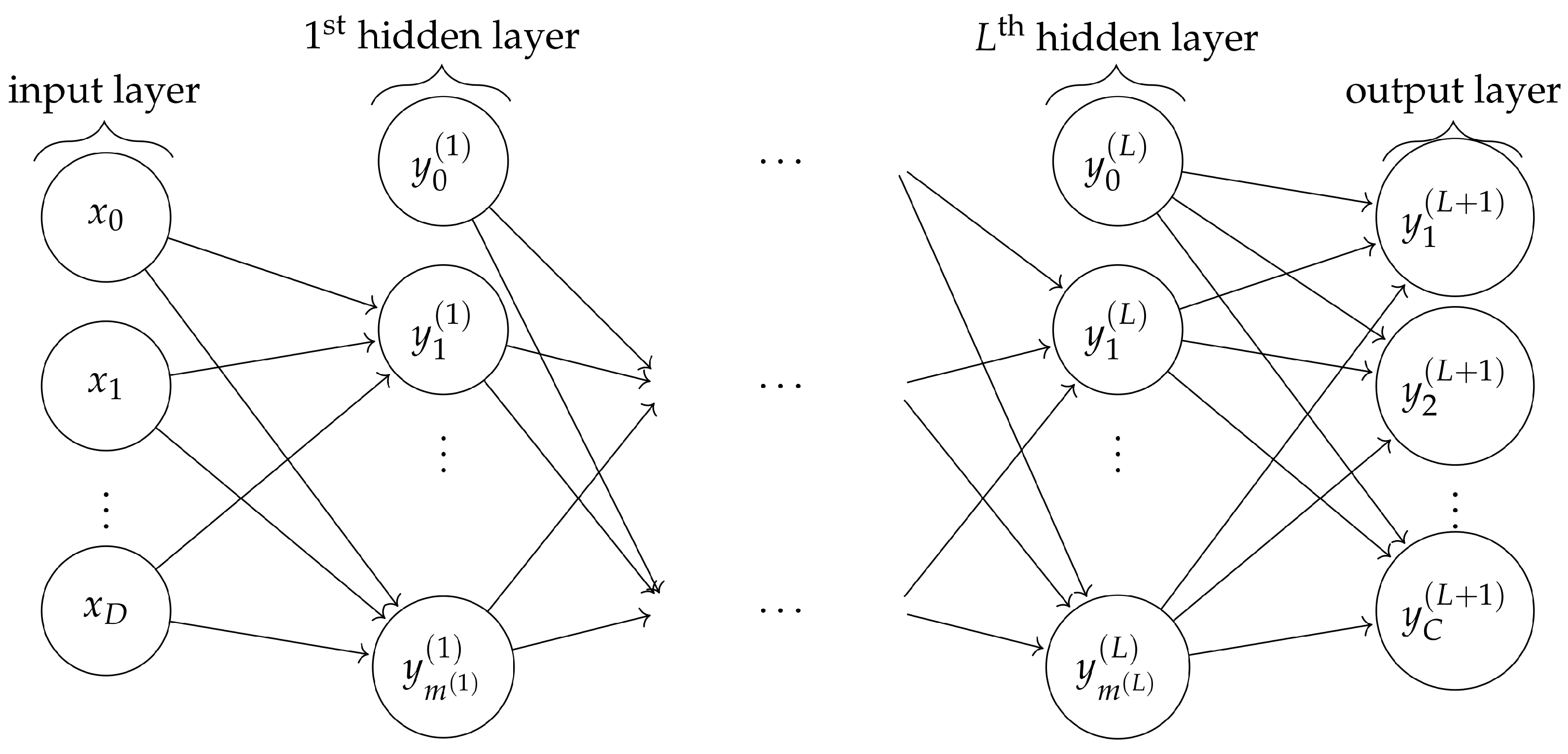
5.3.1. Artificial Neural Networks
5.3.2. Support Vector Machine
5.3.3. Fuzzy Expert Systems
5.3.4. Machine Learning-Based Techniques
6. Comparative Analysis and Discussion
7. Prospects and Challenges
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Farhangi, H. The path of the smart grid. IEEE Power Energy Mag. 2010, 8, 18–28. [Google Scholar] [CrossRef]
- Sauer, P.W.; Pai, M.A.; Chow, J.H. Power System Dynamics and Stability: With Synchrophasor Measurement and Power System Toolbox; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Wasiak, I.; Pawelek, R.; Mienski, R. Energy storage application in low-voltage microgrids for energy management and power quality improvement. IET Gener. Transm. Distrib. 2014, 8, 463–472. [Google Scholar] [CrossRef]
- Bollen, M.H. Understanding power quality problems. In Voltage Sags and Interruptions; IEEE Press: Piscataway, NJ, USA, 2000. [Google Scholar]
- Bollen, M. What is power quality? Electr. Power Syst. Res. 2003, 66, 5–14. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Hassan, F. Integration of Distributed Generation in the Power System; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 80. [Google Scholar]
- Baggini, A. Handbook of Power Quality; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Bollen, M.; Gu, I. Signal Processing of Power-Quality Disturbances; IEEE Press: New York, NY, USA, 2006. [Google Scholar]
- Kusko, A.; Thompson, M.T. Power Quality in Electrical Systems; McGraw-Hill: New York, NY, USA, 2007. [Google Scholar]
- Mohd, A.; Ortjohann, E.; Schmelter, A.; Hamsic, N.; Morton, D. Challenges in integrating distributed energy storage systems into future smart grid. In Proceedings of the IEEE 2008 International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 1627–1632. [Google Scholar]
- Fang, X.; Misra, S.; Xue, G.; Yang, D. Smart grid the new and improved power grid: A survey. IEEE Commun. Surv. Tutor. 2012, 14, 944–980. [Google Scholar] [CrossRef]
- IEEE P2030.2/D9.0; IEEE Approved Draft Guide for the Interoperability of Energy Storage Systems Integrated with the Electric Power Infrastructure. IEEE: New York, NY, USA, 2015; pp. 1–136.
- Bollen, M.H.J. Understanding Power Quality Problems; IEEE Press: New York, NY, USA, 1999; Volume 3. [Google Scholar]
- IEEE Std 1159-2009; IEEE Recommended Practice for Monitoring Electric Power Quality; (Revision of IEEE Std 1159-1995). IEEE: New York, NY, USA, 2009; pp. 1–81.
- IEC 61000-4-30; Testing and Measurement Techniques–Power Quality Measurement Methods. International Electrotechnical Commission Standard: Geneva, Switzerland, 2015.
- EN Std. 50160; Voltage Characteristics of Electricity Supplied by Public Distribution Systems. British Standard: London, UK, 2002.
- Bollen, M.H.; Gu, I.Y.; Santoso, S.; McGranaghan, M.F.; Crossley, P.A.; Ribeiro, M.V.; Ribeiro, P.F. Bridging the gap between signal and power. IEEE Signal Process. Mag. 2009, 26, 12–31. [Google Scholar] [CrossRef]
- Gu, Y.H.; Bollen, M.H.J. Time-frequency and time-scale domain analysis of voltage disturbances. IEEE Trans. Power Deliv. 2000, 15, 1279–1284. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Synchronized Phasor Measurements and Their Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- IEEE Standard C37.118.1-2011; IEEE Standard for Synchrophasor Measurements for Power Systems; Revision of IEEE Standard C37.118-2005. IEEE: New York, NY, USA, 2011.
- IEEE Standard C37.118.1a-2014; IEEE Standard for Synchrophasor Measurements for Power Systems Amendment 1: Modification of Selected Performance Requirements; Amendment to IEEE Standard C37.118.1-2011. IEEE: New York, NY, USA, 2014.
- Liang, X. Emerging power quality challenges due to integration of renewable energy sources. IEEE Trans. Ind. Appl. 2017, 53, 855–866. [Google Scholar] [CrossRef]
- Mishra, M. Power quality disturbance detection and classification using signal processing and soft computing techniques: A comprehensive review. Int. Trans. Electr. Energy Syst. 2019, 29, e12008. [Google Scholar] [CrossRef] [Green Version]
- Chawda, G.S.; Shaik, A.G.; Shaik, M.; Padmanaban, S.; Holm-Nielsen, J.B.; Mahela, O.P.; Kaliannan, P. Comprehensive review on detection and classification of power quality disturbances in utility grid with renewable energy penetration. IEEE Access 2020, 8, 146807–146830. [Google Scholar] [CrossRef]
- Khetarpal, P.; Tripathi, M.M. A critical and comprehensive review on power quality disturbance detection and classification. Sustain. Comput. Inform. Syst. 2020, 28, 100417. [Google Scholar] [CrossRef]
- Alimi, O.A.; Ouahada, K.; Abu-Mahfouz, A.M. A review of machine learning approaches to power system security and stability. IEEE Access 2020, 8, 113512–113531. [Google Scholar] [CrossRef]
- Beniwal, R.K.; Saini, M.K.; Nayyar, A.; Qureshi, B.; Aggarwal, A. A critical analysis of methodologies for detection and classification of power quality events in smart grid. IEEE Access 2021, 9, 83507–83534. [Google Scholar] [CrossRef]
- Martinez, R.; Castro, P.; Arroyo, A.; Manana, M.; Galan, N.; Moreno, F.S.; Laso, A. Techniques to Locate the Origin of Power Quality Disturbances in a Power System: A Review. Sustainability 2022, 14, 7428. [Google Scholar] [CrossRef]
- Bonde, G.N.; Paraskar, S.R.; et Jadhao, S.S. Review on detection and classification of underlying causes of power quality disturbances using signal processing and soft computing technique. Mater. Today Proc. 2022, 58, 509–515. [Google Scholar] [CrossRef]
- Back, T. Evolutionary Algorithms in Theory and Practice: Evolution Strategies, Evolutionary Programming, Genetic Algorithms; Oxford University Press: Oxford, UK, 1996. [Google Scholar]
- Celli, G.; Ghiani, E.; Mocci, S.; Pilo, F. A multiobjective evolutionary algorithm for the sizing and siting of distributed generation. IEEE Trans. Power Syst. 2005, 20, 750–757. [Google Scholar] [CrossRef]
- Gunal, S.; Gerek, O.N.; Ece, D.G.; Edizkan, R. The search for optimal feature set in power quality event classification. Expert Syst. Appl. 2009, 36, 10266–10273. [Google Scholar] [CrossRef]
- Ribeiro, P.F.; Duque, C.A.; Ribeiro, P.M.; Cerqueira, A.S. Power Systems Signal Processing for Smart Grids; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Hu, J.; Zhu, J.; Platt, G. Smart grid the next generation electricity grid with power flow optimization and high power quality. In Proceedings of the 2011 IEEE International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–6. [Google Scholar]
- Dugan, R.C.; McGranaghan, M.F.; Beaty, H.W. Electrical Power Systems Quality; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Chung, H.; Hui, S.; Tse, K. Reduction of power converter emi emission using soft-switching technique. IEEE Trans. Electromagn. Compat. 1998, 40, 282–287. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M. Power quality evaluation in smart grids considering modern distortion in electric power systems. Electr. Power Syst. Res. 2011, 81, 1117–1123. [Google Scholar] [CrossRef]
- Jaramillo, S.H.; Heydt, G.; O’Neill-Carrillo, E. Power quality indices for aperiodic voltages and currents. IEEE Trans. Power Deliv. 2000, 15, 784–790. [Google Scholar] [CrossRef]
- Laughton, M. Analysis of Unbalanced Polyphase Networks by the Method of Phase Co-ordinates. Part 2: Fault Analysis. In Proceedings of the Institution of Electrical Engineers, London, UK, 6–8 May 1969; Volume 116, pp. 857–865. [Google Scholar]
- Kaleybar, H.J.; Brenna, M.; Foiadelli, F.; Fazel, S.S.; Zaninelli, D. Power Quality Phenomena in Electric Railway Power Supply Systems: An Exhaustive Framework and Classification. Energies 2020, 13, 6662. [Google Scholar] [CrossRef]
- Heydt, G.T. Electric Power Quality; Stars in a Circle Publications: Lafayette, IN, USA, 1991. [Google Scholar]
- Arrillaga, J.; Watson, N.R. Power System Harmonics; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Arrillaga, J. Power System Harmonic Analysis; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Wagner, V.; Balda, J.C.; Griffith, D.; McEachern, A.; Barnes, T.; Hartmann, D.; Phileggi, D.; Emannuel, A.; Horton, W.F.; Reid, W.E.; et al. Effects of harmonics on equipment. IEEE Trans. Power Deliv. 1993, 8, 672–680. [Google Scholar] [CrossRef]
- IEC Std. 61000-4-7; Electromagnetic Compatibility (EMC) Part 4–7: Testing and Measurement Techniques—General Guide on Harmonics and Interharmonics Measurements and Instrumentation, for Power Supply Systems and Equipment Connected Thereto. International Electrotechnical Commission: Geneva, Switzerland, 2002.
- DOE EPRI National Database Repository of Power System Events. Available online: http://pqmon.epri.com/disturbance_library (accessed on 1 August 2022).
- Zeng, Z.; Yang, H.; Zhao, R.; Cheng, C. Topologies and control strategies of multi-functional grid-connected inverters for power quality enhancement: A comprehensive review. Renew. Sustain. Energy Rev. 2013, 24, 223–270. [Google Scholar] [CrossRef]
- Ipakchi, A.; Albuyeh, F. Grid of the future. IEEE Power Energy Mag. 2009, 7, 52–62. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Ribeiro, P.; Gu, I.Y.; Duque, C.A. Trends, challenges and opportunities in power quality research. Eur. Trans. Electr. Power 2010, 20, 3–18. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mitra, M.; Sengupta, S. Electric Power Quality; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Bergen, A.R. Power Systems Analysis; Pearson Education: Bengaluru, India, 2000. [Google Scholar]
- McBee, K.D.; Simoes, M.G. Utilizing a smart grid monitoring system to improve voltage quality of customers. IEEE Trans. Smart Grid 2012, 3, 738–743. [Google Scholar] [CrossRef]
- Amin, S.; Wollenberg, B. Toward a smart grid: Power delivery for the 21st century. IEEE Power Energy Mag. 2005, 3, 34–41. [Google Scholar] [CrossRef]
- Granjon, P.; Phua, G.S.L. Estimation of geometric properties of threecomponent signals for system monitoring. Mech. Syst. Signal Process. 2017, 97, 95–111. [Google Scholar] [CrossRef] [Green Version]
- Cablea, G.; Granjon, P.; Bérenguer, C. Three-phase electrical signals analysis for mechanical faults monitoring in rotating machine systems. Mech. Syst. Signal Process. 2017, 92, 278–292. [Google Scholar] [CrossRef]
- IEC Standard 61000-1-1.1; Electromagnetic Compatibility (EMC), Part 1: General, Section 1: Application and Interpretation of Fundamental Definitions and Terms. International Electrotechnical Commission: Geneva, Switzerland, 2011.
- IEEE Standard 519; Recommended Practices and Requirements for Harmonic Control in Electrical Power Systems; ANSI IEEE Std. 519 to 992. IEEE: New York, NY, USA, 1993.
- Narendra, K.; Gurusinghe, D.R.; Rajapakse, A.D. Dynamic performance evaluation and testing of phasor measurement unit (PMU) as per IEEE c37.118.1 standard. In Proceedings of the Doble Client Committee Meetings International Protection Testing Users Group, Chicago, IL, USA, 6–10 August 2012. [Google Scholar]
- Zhang, Q.; Chakhchoukh, Y.; Vittal, V.; Heydt, N.; Logic, G.T.; Sturgill, S. Impact of PMU measurement buffer length on state estimation and its optimization. IEEE Trans. Power Syst. 2013, 28, 1657–1665. [Google Scholar] [CrossRef]
- IEEE Standard C37.118.2005; IEEE Standard for Synchrophasor Measurements for Power Systems; Revision of IEEE Std. 1344–1995. IEEE: New York, NY, USA, 2005.
- Depablos, J.; Centeno, V.; Phadke, A.G.; Ingram, M. Comparative testing of synchronized phasor measurement units. In Proceedings of the Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 948–954. [Google Scholar]
- Papoulis, A.; Maradudin, A. The Fourier Integral and Its Applications; McGraw Hill: New York, NY, USA, 1963. [Google Scholar]
- Brigham, E.O.; Morrow, R. The fast Fourier transform. IEEE Spectr. 1967, 4, 63–70. [Google Scholar]
- Robertson, D.C.; Camps, O.I.; Mayer, J.S.; Gish, W.B. Wavelets and electromagnetic power system transients. IEEE Trans. Power Deliv. 1996, 11, 1050–1058. [Google Scholar] [CrossRef]
- Barchi, G.; Macii, D.; Petri, D. Accuracy of one-cycle dft-based synchrophasor estimators in steady-state and dynamic conditions. In Proceedings of the Instrumentation and Measurement Technology Conference (I2MTC), Ottawa, ON, Canada, 16–19 May 2022; pp. 1529–1534. [Google Scholar]
- Chaitanya, M.N.; Rao, G.S.K. Performance Evaluation of Recursive DFT as Phasor Estimator in PMUs under Power Quality Disturbances. Int. J. Eng. Res. Technol. 2015, 4, 319–325. [Google Scholar]
- Pinto, L.S.; Assunção, M.V.; Ribeiro, D.A.; Ferreira, D.D.; Huallpa, B.N.; Silva, L.R.; Duque, C.A. Compression method of power quality disturbances based on independent component analysis and fast fourier transform. Electr. Power Syst. Res. 2020, 187, 106428. [Google Scholar] [CrossRef]
- Jayasree, D.D. Classification of power quality disturbance signals using FFT, STFT, wavelet transforms and neural networks—A comparative analysis. In Proceedings of the International Conference on Computational Intelligence and Multimedia Applications (ICCIMA 2007), Sivakasi, India, 13–15 December 2007; pp. 335–340. [Google Scholar]
- Barros, J.; Diego, R.I.; Apraiz, M.D. Applications of wavelets in electric power quality: Voltage events. Electr. Power Syst. Res. 2012, 88, 130–136. [Google Scholar] [CrossRef]
- Labos, T.; Rezmer, J.; Janik, P.; Amaris, H.; Alonso, M.; Alvarez, C. Application of wavelets and prony method for disturbance detection in fixed speed wind farms. Int. J. Electr. Power Energy Syst. 2009, 31, 429–436. [Google Scholar] [CrossRef]
- Hauer, J. Initial results in prony analysis of power system response signals. IEEE Trans. Power Syst. 1990, 5, 80–89. [Google Scholar] [CrossRef] [Green Version]
- Pisarenko, V.F. The retrieval of harmonics from a covariance function. Geophys. J. Int. 1973, 33, 347–366. [Google Scholar] [CrossRef] [Green Version]
- Reddy, V.; Egardt, B.; Kailath, T. Least squares type algorithm for adaptive implementation of Pisarenko’s harmonic retrieval method. IEEE Trans. Acoust. Speech Signal Process. 1982, 30, 399–405. [Google Scholar] [CrossRef]
- Bracale, A.; Caramia, P.; Carpinelli, G. Adaptive Prony method for waveform distortion detection in power systems. Int. J. Electr. Power Energy Syst. 2007, 29, 371–379. [Google Scholar] [CrossRef]
- Marple, L. Spectral line analysis by Pisarenko and Prony methods. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’79), Washington, DC, USA, 2–4 April 1979; Volume 4, pp. 159–161. [Google Scholar]
- Lobos, T.; Leonowicz, Z.; Rezmer, J.; Schegner, P. High-resolution spectrum-estimation methods for signal analysis in power systems. IEEE Trans. Instrum. Meas. 2006, 55, 219–225. [Google Scholar] [CrossRef] [Green Version]
- Zygarlicki, J.; Zygarlicka, M.; Mroczka, J.; Latawiec, K. A reduced Prony’s method in power quality analysis – parameters selection. IEEE Trans. Power Deliv. 2010, 25, 979–986. [Google Scholar] [CrossRef]
- Zygarlicki, J.; Mroczka, J. Short time algorithm of power waveforms fundamental harmonic estimations with Prony’s methods use. Metrol. Meas. Syst. 2011, 18, 33–38. [Google Scholar] [CrossRef]
- Zygarlicki, J.; Zygarlicka, M.; Mroczka, J. Prony’s metod in power quality analysis. Energy Spectr. 2009, 4, 26–30. [Google Scholar]
- Zygarlicki, J.; Mroczka, J. Data compression using Prony’s method and wavelet transform in power quality monitoring systems. Metrol. Meas. Syst. 2006, 13, 237–251. [Google Scholar]
- Marple, S.L. Digital Spectral Analysis with Applications; Prentice Hall: Upper Saddle River, NJ, USA, 1987. [Google Scholar]
- Zygarlicki, J.; Mroczka, J. Variable-frequency Prony method in the analysis of electrical power quality. Metrol. Meas. Syst. 2012, 19, 39–48. [Google Scholar] [CrossRef]
- Del Rio, J.E.F.; Sarkar, T.K. Comparison between the Matrix Pencil Method and the Fourier Transform Technique for High-Resolution Spectral Estimation. Digit. Signal Process. 1996, 11, 108–125. [Google Scholar] [CrossRef] [Green Version]
- Markovsky, I.; Van Huffel, S. Overview of total least squares methods. Signal Process. 2007, 87, 2283–2302. [Google Scholar] [CrossRef] [Green Version]
- Robenack, K.; Einschke, K. On generalized inverses of singular matrix pencils. Int. J. Appl. Math. Comput. Sci. 2011, 21, 161–172. [Google Scholar] [CrossRef]
- Stoica, P.; Moses, R.L. Introduction to Spectral Analysis; Prentice Hall: Upper Saddle River, NJ, USA, 1997; Volume 1. [Google Scholar]
- Kay, S.M.; Marple, S.L. Spectrum analysis—A modern perspective. Proc. IEEE 1981, 69, 1380–1419. [Google Scholar] [CrossRef]
- Flandrin, P. Time-Frequency/Time-Scale Analysis; Academic Press: Oxford, UK, 1998; Volume 10. [Google Scholar]
- Duda, K.; Zieliński, T.P. P class and M class compliant PMU based on discrete-time frequency-gain transducer. IEEE Trans. Power Deliv. 2021, 37, 1058–1067. [Google Scholar] [CrossRef]
- Sahu, B.; Dhar, S.; Dash, P.K. Frequency-scaled optimized time-frequency transform for harmonic estimation in photovoltaic-based microgrid. Int. Trans. Electr. Energy Syst. 2020, 30, e12169. [Google Scholar] [CrossRef]
- Reddy, M.V.; Sodhi, R. An open-loop fundamental and harmonic phasor estimator for single-phase voltage signals. IEEE Trans. Ind. Inform. 2019, 16, 4535–4546. [Google Scholar] [CrossRef]
- Hosseini, H.S.; Koochaki, A.; Hosseinian, S.H. A novel scheme for current only directional overcurrent protection based on post-fault current phasor estimation. J. Electr. Eng. Technol. 2019, 14, 1517–1527. [Google Scholar] [CrossRef]
- Rivas, A.E.L.; da Silva, N.; Abrão, T. Adaptive current harmonic estimation under fault conditions for smart grid systems. Electr. Power Syst. Res. 2020, 183, 106276. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P.; Goncalves, P.; Lemoine, O. Time-Frequency Toolbox, for Use with Matlab; Technical Report; CNRS, GDR ISIS: 1995–1996. Available online: http://tftb.nongnu.org/refguide.pdf (accessed on 8 August 2021).
- Jopri, M.; Abdullah, A.; Manap, M.; Yusoff, M.; Sutikno, T.; Habban, M. An improved detection and classification technique of harmonic signals in power distribution by utilizing spectrogram. Int. J. Electr. Comput. Eng. 2017, 7, 12. [Google Scholar] [CrossRef] [Green Version]
- Dehghani, M.; Ghiasi, M.; Niknam, T.; Kavousi-Fard, A.; Padmanaban, S. False data injection attack detection based on Hilbert-huang transform in AC smart islands. IEEE Access 2020, 8, 179002–179017. [Google Scholar] [CrossRef]
- Baayeh, A.G.; Bayati, N. Adaptive overhead transmission lines auto-reclosing based on Hilbert–Huang transform. Energies 2020, 13, 5416. [Google Scholar] [CrossRef]
- Munir, B.S.; Trisetyarso, A.; Reza, M.; Abbas, B.S. Feature Extraction of Low Frequency Oscillation in Power System Using Hilbert–Huang Transform. TEM J. 2019, 8, 12. [Google Scholar]
- Munir, B.S.; Reza, M.; Trisetyarso, A.; Abbas, B.S. Feature extraction using Hilbert–Huang transform for power system oscillation measurements. In Proceedings of the 2017 4th International Conference on Information Technology, Computer, and Electrical Engineering (ICITACEE), Semarang, Indonesia, 18–19 October 2017. [Google Scholar]
- Biswal, B.; Biswal, M.; Mishra, S.; Jalaja, R. Automatic classification of power quality events using balanced neural tree. IEEE Trans. Ind. Electron. 2014, 61, 521–530. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Kumar, R.; Singh, B.; Shahani, D.T. Recognition of single-stage and multiple power quality events using hilbert–huang transform and probabilistic neural network. Electr. Power Compon. Syst. 2015, 43, 607–619. [Google Scholar] [CrossRef]
- Shukla, S.; Mishra, S.; Singh, B. Empirical-mode decomposition with hilbert transform for power-quality assessment. IEEE Trans. Power Deliv. 2009, 24, 2159–2165. [Google Scholar] [CrossRef]
- Manjula, M.; Mishra, S.; Sarma, A. Empirical mode decomposition with hilbert transform for classification of voltage sag causes using probabilistic neural network. Int. J. Electr. Power Energy Syst. 2013, 44, 597–603. [Google Scholar] [CrossRef]
- Saiz, V.M.; Guadalupe, J.B. Application of kalman filtering for continuous real-time tracking of power system harmonics. IEEE Proc.-Gener. Transm. Distrib. 1997, 144, 13–20. [Google Scholar] [CrossRef]
- Kamwa, I.; Grondin, R.; McNabb, D. On-line tracking of changing harmonics in stressed power systems: Application to hydro-quebec network. IEEE Trans. Power Deliv. 1996, 11, 2020–2027. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Dynamic synchrophasor estimation by extended Kalman filter. IEEE Trans. Instrum. Meas. 2019, 69, 4818–4826. [Google Scholar] [CrossRef]
- De Apráiz, M.; Diego, R.I.; Barros, J. An extended Kalman filter approach for accurate instantaneous dynamic phasor estimation. Energies 2018, 11, 2918. [Google Scholar] [CrossRef] [Green Version]
- Girgis, A.A.; Qiu, J. Measurement of the parameters of slowly time varying high frequency transients. IEEE Trans. Instrum. Meas. 1989, 38, 1057–1063. [Google Scholar] [CrossRef]
- Bashian, A.; Macii, D.; Fontanelli, D.; Petri, D. A Tuned Whitening-Based Taylor-Kalman Filter for P Class Phasor Measurement Units. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Mishra, C.; Vanfretti, L.; Jones, K.D. Synchrophasor phase angle data unwrapping using an unscented Kalman filter. IEEE Trans. Power Syst. 2021, 36, 4868–4871. [Google Scholar] [CrossRef]
- Dash, P.K.; Chilukuri, M.V. Hybrid s-transform and kalman filtering approach for detection and measurement of short duration disturbances in power networks. IEEE Trans. Instrum. Meas. 2004, 53, 588–596. [Google Scholar] [CrossRef]
- Reddy, J.; Dash, P.K.; Samantaray, R.; Moharana, A.K. Fast tracking of power quality disturbance signals using an optimized unscented filter. IEEE Trans. Instrum. Meas. 2009, 58, 3943–3952. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Synchrophasor estimation for three-phase systems based on Taylor extended Kalman filtering. IEEE Trans. Instrum. Meas. 2020, 69, 6723–6730. [Google Scholar] [CrossRef]
- Ferrero, R.; Pegoraro, P.A.; Toscani, S. Dynamic fundamental and harmonic synchrophasor estimation by Extended Kalman filter. In Proceedings of the 2016 IEEE International Workshop on Applied Measurements for Power Systems (AMPS), Aachen, Germany, 28–30 September 2016. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice Hall: Upper Saddle River, NJ, USA, 1993; Volume 1. [Google Scholar]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Maximum-likelihood frequency and phasor estimations for electric power grid monitoring. IEEE Trans. Ind. Inform. 2017, 14, 167–177. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M. An improved algorithm for power system fault type classification based on least square phasor estimation. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015. [Google Scholar]
- Kay, S.M. Modern Spectral Estimation; Pearson Education: Bengaluru, India, 1988. [Google Scholar]
- Ibrahim, W.A.; Morcos, M.M. Artificial intelligence and advanced mathematical tools for power quality applications: A survey. IEEE Trans. Power Deliv. 2002, 17, 668–673. [Google Scholar] [CrossRef]
- Nath, S.; Sinha, P.; Goswami, S.K. A wavelet based novel method for the detection of harmonic sources in power systems. Int. J. Electr. Power Energy Syst. 2012, 40, 54–61. [Google Scholar] [CrossRef]
- Ozgonenel, O.; Yalcin, T.; Guney, I.; Kurt, U. A new classification for power quality events in distribution systems. Electr. Power Syst. Res. 2013, 95, 192–199. [Google Scholar] [CrossRef]
- Saxena, D.; Singh, S.; Verma, K.; Singh, S.K. HHT-based classification of composite power quality events. Int. J. Energy Sect. Manag. 2014, 8, 146–159. [Google Scholar] [CrossRef]
- Haykin, S.S. Kalman Filtering and Neural Networks; Wiley Online Library: Hoboken, NJ, USA, 2001. [Google Scholar]
- Moon, T.K.; Stirling, W.C. Mathematical Methods and Algorithms for Signal Processing; Prentice Hall: Hoboken, NJ, USA, 2000. [Google Scholar]
- Abdelsalam, A.A.; Eldesouky, A.A.; Sallam, A.A. Classification of power system disturbances using linear kalman filter and fuzzy-expert system. Int. J. Electr. Power Energy Syst. 2012, 43, 688–695. [Google Scholar] [CrossRef]
- Amirat, Y.; Oubrahim, Z.; Benbouzid, M.E.H. On phasor estimation for voltage sags detection in a smart grid context. In Proceedings of the 2015 IEEE International Symposium on Industrial Electronics, Rio de Janiero, Brazil, 3–5 June 2015; pp. 1351–1356. [Google Scholar]
- Bakirtzis, A.G.; Biskas, P.N.; Zoumas, C.E.; Petridis, V. Optimal power flow by enhanced genetic algorithm. IEEE Trans. Power Syst. 2002, 17, 229–236. [Google Scholar] [CrossRef]
- Sen, O.; Song, Z.; Wang, J.; Chen, D. Application of lvq neural networks combined with genetic algorithm in power quality signals classification. In Proceedings of the 2002 IEEE International Conference on Power System Technology, Kunming, China, 13–17 October 2002; Volume 1, pp. 491–495. [Google Scholar]
- Al-Hasawi, W.M.; El-Naggar, K.M. A genetic based algorithm for voltage flicker measurement. Int. J. Electr. Power Energy Syst. 2004, 26, 593–596. [Google Scholar] [CrossRef]
- Juang, C.-F. A hybrid of genetic algorithm and particle swarm optimization for recurrent network design. IEEE Trans. Syst. Man Cybern. Part (Cybern.) 2004, 34, 997–1006. [Google Scholar] [CrossRef] [PubMed]
- Panigrahi, B.K.; Pandi, V.R. Optimal feature selection for classification of power quality disturbances using wavelet packet-based fuzzy k-nearest neighbour algorithm. IET Gener. Transm. Distrib. 2009, 3, 296–306. [Google Scholar] [CrossRef]
- Priyadarshini, L.; Prasad, E.N.; Dash, P.K. Diagnosis of PQ Disturbances using Local mean decomposition based SVD entropy and modified K-means clustering. In Proceedings of the 2021 International Conference in Advances in Power, Signal, and Information Technology (APSIT), Bhubaneswar, India, 8–10 October 2021. [Google Scholar]
- Krishna, K.; Narasimha Murty, M. Genetic K-means algorithm. IEEE Trans. Syst. Man Cybern. Part (Cybern.) 1999, 29, 433–439. [Google Scholar] [CrossRef] [Green Version]
- Manimala, K.; Selvi, K.; Ahila, R. Hybrid soft computing techniques for feature selection and parameter optimization in power quality data mining. Appl. Soft Comput. 2011, 11, 5485–5497. [Google Scholar] [CrossRef]
- Wang, M.-H.; Tseng, Y.-F. A novel analytic method of power quality using extension genetic algorithm and wavelet transform. Expert Syst. Appl. 2011, 38, 12491–12496. [Google Scholar] [CrossRef]
- Biswal, B.; Dash, P.K.; Panigrahi, B.K. Power quality disturbance classification using fuzzy C-means algorithm and adaptive particle swarm optimization. IEEE Trans Ind Electron. 2009, 56, 212–220. [Google Scholar] [CrossRef]
- Rodriguez-Guerrero, M.A.; Jaen-Cuellar, A.Y.; Carranza-Lopez-Padilla, R.D.; Osornio-Rios, R.A.; Herrera-Ruiz, G.; Romero-Troncoso, R.D.J. Hybrid approach based on GA and PSO for parameter estimation of a full power quality disturbance parameterized model. IEEE Trans. Ind. Inform. 2017, 14, 1016–1028. [Google Scholar] [CrossRef]
- Hajian, M.; Akbari Foroud, A. A new hybrid pattern recognition scheme for automatic discrimination of power quality disturbances. Measurement 2014, 51, 265–280. [Google Scholar] [CrossRef]
- Hajian, M.; Akbari Foroud, A.; Abdoos, A.A. New automated power quality recognition system for online/offline monitoring. Neurocomputing 2014, 128, 389–406. [Google Scholar] [CrossRef]
- Ahila, R.; Sadasivam, V.; Manimala, K. An integrated PSO for parameter determination and feature selection of ELM and its application in classification of power system disturbances. Appl. Soft Comput. 2015, 32, 23–37. [Google Scholar] [CrossRef]
- Chamchuen, S.; Siritaratiwat, A.; Fuangfoo, P.; Suthisopapan, P.; Khunkitti, P. High-Accuracy power quality disturbance classification using the adaptive ABC-PSO as optimal feature selection algorithm. Energies 2021, 14, 1238. [Google Scholar] [CrossRef]
- Chen, J.-F.; Do, Q.H.; Hsieh, H.-N. Training artificial neural networks by a hybrid PSO-CS algorithm. Algorithms 2015, 8, 292–308. [Google Scholar] [CrossRef]
- Huang, N.; Zhang, S.; Cai, G.; Xu, D. Power quality disturbances recognition based on a multiresolution generalized S-transform and a PSO-improved decision tree. Energies 2015, 8, 549–572. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, M.; Birattari, M.; Stitzle, T. Ant Colony Optimization: Arificial Ants as a Computational Intelligence Technique. IEEE Comput. Intell. Mag. 2006, 1, 28–39. [Google Scholar] [CrossRef]
- Singh, U.; Singh, S.N. A new optimal feature selection scheme for classification of power quality disturbances based on ant colony framework. Appl. Soft Comput. 2019, 74, 216–225. [Google Scholar] [CrossRef]
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence properties of the nelder–mead simplex method in low dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Brent, R.P. Algorithms for Minimization without Derivatives; Courier Corporation: Chelmsford, MA, USA, 2013. [Google Scholar]
- Forsythe, G.E.; Moler, C.B.; Malcolm, M.A. Computer Methods for Mathematical Computations; Prentice-Hall: Hoboken, NJ, USA, 1977. [Google Scholar]
- Kay, S.M. Fundamentals of Statistical Signal Processing; PTR Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Khokhar, S.; Zin, A.A.B.M.; Mokhtar, A.S.B.; Pesaran, M. A comprehensive overview on signal processing and artificial intelligence techniques applications in classification of power quality disturbances. Renew. Sustain. Energy Rev. 2015, 51, 1650–1663. [Google Scholar] [CrossRef]
- Saini, M.K.; Kapoor, R. Classification of power quality events—A review. Int. J. Electr. Power Energy Syst. 2012, 43, 11–19. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; Wiley: New York, NY, USA, 1973; Volume 2. [Google Scholar]
- Devroye, L.; Györfi, L.; Lugosi, G. A Probabilistic Theory of Pattern Recognition; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 31. [Google Scholar]
- Huang, J.; Negnevitsky, M.; Nguyen, D.T. A neural-fuzzy classifier for recognition of power quality disturbances. IEEE Trans. Power Deliv. 2002, 17, 609–616. [Google Scholar] [CrossRef]
- Fausett, L.V. Fundamentals of Neural Networks; Prentice-Hall: Hoboken, NJ, USA, 1994. [Google Scholar]
- Jackson, P. Introduction to Expert Systems; Addison-Wesley Publishing Company: Reading, MA, USA, 1986. [Google Scholar]
- Biswal, B.; Dash, P.K.; Panigrahi, B.K. Non-stationary power signal processing for pattern recognition using hs-transform. Appl. Soft Comput. 2009, 9, 107–117. [Google Scholar] [CrossRef]
- Biswal, B.; Dash, P.K.; Panigrahi, B.K.; Reddy, J. Power signal classification using dynamic wavelet network. Appl. Soft Comput. 2009, 9, 118–125. [Google Scholar] [CrossRef]
- Morsi, W.G.; El-Hawary, M. Novel power quality indices based on wavelet packet transform for non-stationary sinusoidal and non-sinusoidal disturbances. Electr. Power Syst. Res. 2010, 80, 753–759. [Google Scholar] [CrossRef]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Classification of three-phase power disturbances based on model order selection in smart grid applications. In Proceedings of the 42nd Annual Conference of the IEEE Industrial Electronics Society (IECON), Florence, Italy, 23–26 October 2016; pp. 5143–5148. [Google Scholar]
- Oubrahim, Z.; Choqueuse, V.; Amirat, Y.; Benbouzid, M.E.H. Disturbances classification based on a model order selection method for power quality monitoring. IEEE Trans. Ind. Electron. 2017, 64, 9421–9432. [Google Scholar] [CrossRef]
- Bollen, M.H.J.; Zhang, L. Different methods for classification of three-phase unbalanced voltage dips due to faults. Electr. Power Syst. Res. 2003, 66, 59–69. [Google Scholar] [CrossRef]
- Bollen, M.H.J. Algorithms for characterizing measured three-phase unbalanced voltage dips. IEEE Trans. Power Deliv. 2003, 18, 937–944. [Google Scholar] [CrossRef]
- Stoica, P.; Selen, Y. Model-order selection: A review of information criterion rules. IEEE Signal Process. Mag. 2004, 21, 36–47. [Google Scholar] [CrossRef]
- Ignatova, V.; Granjon, P.; Bacha, S. Space vector method for voltage dips and swells analysis. IEEE Trans. Power Deliv. 2009, 24, 2054–2061. [Google Scholar] [CrossRef] [Green Version]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Fukunaga, K. Introduction to Statistical Pattern Recognition; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Kamwa, I.; Grondin, R.; Sood, V.; Gagnon, C.; Mereb, J. Recurrent neural networks for phasor detection and adaptive identification in power system control and protection. IEEE Trans. Instrum. Meas. 1996, 45, 657–664. [Google Scholar] [CrossRef]
- Cerqueira, A.S.; Ferreira, D.D.; Ribeiro, M.V.; Duque, C.A. Power quality events recognition using a svm-based method. Electr. Power Syst. Res. 2008, 78, 1546–1552. [Google Scholar] [CrossRef]
- Ma, L.; Lee, K.Y. Fuzzy neural network approach for fault diagnosis of power plant thermal system under different operating points. In Proceedings of the 2008 IEEE Power and Energy Society General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–7. [Google Scholar]
- Haykin, S.S.; Haykin, S.S.; Haykin, S.S.; Haykin, S.S. Neural Networks and Learning Machines; Pearson: Hoboken, NJ, USA, 2009; Volume 3. [Google Scholar]
- Sahani, M.; Dash, P.K. Automatic power quality events recognition based on Hilbert Huang transform and weighted bidirectional extreme learning machine. IEEE Trans. Ind. Inform. 2018, 14, 3849–3858. [Google Scholar] [CrossRef]
- Sahani, M.; Dash, P.; Samal, D. A real-time power quality events recognition using variational mode decomposition and online-sequential extreme learning machine. Measurement 2020, 157, 107597. [Google Scholar] [CrossRef]
- Zhao, C.; Li, K.; Li, Y.; Wang, L.; Luo, Y.; Xu, X.; Ding, X.; Meng, Q. Novel method based on variational mode decomposition and a random discriminative projection extreme learning machine for multiple power quality disturbance recognition. IEEE Trans. Ind. Inform. 2018, 15, 2915–2926. [Google Scholar] [CrossRef]
- Liu, S.; Yang, D. Identification and detection algorithm of electric energy disturbance in microgrid based on wavelet analysis and neural network. EURASIP J. Wirel. Commun. Netw. 2021, 27. [Google Scholar] [CrossRef]
- Lee, C.; Nam, S. Efficient feature vector extraction for automatic classification of power quality disturbances. Electron. Lett. 1998, 34, 1059–1061. [Google Scholar] [CrossRef]
- Monedero, I.; Leon, C.; Ropero, J.; Garcia, A.; Elena, J.M.; Montano, J.C. Classification of electrical disturbances in real time using neural networks. IEEE Trans. Power Deliv. 2007, 22, 1288–1296. [Google Scholar] [CrossRef]
- Valtierra-Rodriguez, M.; de Jesus Romero-Troncoso, R.; Osornio-Rios, R.A.; Garcia-Perez, A. Detection and classification of single and combined power quality disturbances using neural networks. IEEE Trans. Ind. Electron. 2014, 61, 2473–2482. [Google Scholar] [CrossRef]
- Bhende, C.; Mishra, S.; Panigrahi, B. Detection and classification of power quality disturbances using s-transform and modular neural network. Electr. Power Syst. Res. 2008, 78, 122–128. [Google Scholar] [CrossRef]
- Uyar, M.; Yildirim, S.; Gencoglu, M.T. An effective wavelet-based feature extraction method for classification of power quality disturbance signals. Electr. Power Syst. Res. 2008, 78, 1747–1755. [Google Scholar] [CrossRef]
- Negnevitsky, M.; Faybisovich, V.; Santoso, S.; Powers, E.; Grady, W.; Parsons, A. Discussion of “power quality disturbance waveform recognition using waveletbased neural classifier-part 1: Theoretical foundation” [closure to discussion]. IEEE Trans. Power Deliv. 2000, 15, 1347–1348. [Google Scholar] [CrossRef]
- Kanitpanyacharoean, W.; Premrudeepreechacharn, S. Power quality problem classification using wavelet transformation and artificial neural networks. In Proceedings of the 2004 PES General Meeting, New York, NY, USA, 10–13 October 2004; pp. 1496–1501. [Google Scholar]
- Cai, K.; Cao, W.; Aarniovuori, L.; Pang, H.; Lin, Y.; Li, G. Classification of power quality disturbances using Wigner–Ville distribution and deep convolutional neural networks. IEEE Access 2019, 7, 119099–119109. [Google Scholar] [CrossRef]
- Vapnik, V.N.; Kotz, S. Estimation of Dependences Based on Empirical Data; Springer: New York, NY, USA, 1982; Volume 40. [Google Scholar]
- Vapnik, V.N.; Vapnik, V. Statistical Learning Theory; Wiley: New York, NY, USA, 1998; Volume 1. [Google Scholar]
- Choudhary, B. An Advanced Genetic Algorithm with Improved Support Vector Machine for Multi-Class Classification of Real Power Quality Events. Electr. Power Syst. Res. 2021, 191, 106879. [Google Scholar]
- Karasu, S.; Saraç, Z. Investigation of power quality disturbances by using 2D discrete orthonormal S-transform, machine learning and multi-objective evolutionary algorithms. Swarm Evol. Comput. 2019, 44, 1060–1072. [Google Scholar] [CrossRef]
- Motlagh, S.Z.; Foroud, A.A. Power quality disturbances recognition using adaptive chirp mode pursuit and grasshopper optimized support vector machines. Measurement 2021, 168, 108461. [Google Scholar] [CrossRef]
- Nagata, E.A.; Ferreira, D.D.; Bollen, M.H.; Barbosa, B.H.; Ribeiro, E.G.; Duque, C.A.; Ribeiro, P.F. Real-time voltage sag detection and classification for power quality diagnostics. Measurement 2020, 164, 108097. [Google Scholar] [CrossRef]
- Ekici, S. Classification of power system disturbances using support vector machines. Expert Syst. Appl. 2009, 36, 9859–9868. [Google Scholar] [CrossRef]
- Janik, P.; Lobos, T. Automated classification of power-quality disturbances using svm and rbf networks. IEEE Trans. Power Deliv. 2006, 21, 1663–1669. [Google Scholar] [CrossRef] [Green Version]
- Lin, W.-M.; Wu, C.-H.; Lin, C.-H.; Cheng, F.-S. Detection and classification of multiple power-quality disturbances with wavelet multiclass svm. IEEE Trans. Power Deliv. 2008, 23, 2575–2582. [Google Scholar] [CrossRef]
- Liu, Z.; Cui, Y.; Li, W. A classification method for complex power quality disturbances using EEMD and rank wavelet SVM. IEEE Trans. Smart Grid 2015, 6, 1678–1685. [Google Scholar] [CrossRef]
- Axelberg, P.G.; Gu, I.Y.-H.; Bollen, M.H.J. Support vector machine for classification of voltage disturbances. IEEE Trans. Power Deliv. 2007, 22, 1297–1303. [Google Scholar] [CrossRef]
- Eristi, H.; Uçar, A.; Demir, Y. Wavelet-based feature extraction and selection for classification of power system disturbances using support vector machines. Electr. Power Syst. Res. 2010, 80, 743–752. [Google Scholar] [CrossRef]
- Zhan, Y.; Cheng, H.Z.; Ding, Y.F.; Lü, G.Y.; Sun, Y.-B. S-transform-based classification of power quality disturbance signals by support vector machines. Proc. CSEE 2005, 4, 9. [Google Scholar]
- Hu, G.-S.; Xie, J.; Zhu, F.-F. Classification of power quality disturbances using wavelet and fuzzy support vector machines. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; Volume 7, pp. 3981–3984. [Google Scholar]
- Hu, G.-S.; Zhu, F.-F.; Ren, Z. Power quality disturbance identification using wavelet packet energy entropy and weighted support vector machines. Expert Syst. Appl. 2008, 35, 143–149. [Google Scholar] [CrossRef]
- De Yong, D.; Bhowmik, S.; Magnago, F. An effective power quality classifier using wavelet transform and support vector machines. Expert Syst. Appl. 2015, 42, 6075–6081. [Google Scholar] [CrossRef]
- Dash, P.; Mishra, S.; Salama, M.; Liew, A. Classification of power system disturbances using a fuzzy expert system and a fourier linear combiner. IEEE Trans. Power Deliv. 2000, 15, 472–477. [Google Scholar] [CrossRef] [Green Version]
- Rajeshbabu, S.; Manikandan, B.V. Detection and classification of power quality events by expert system using analytic hierarchy method. Cogn. Syst. Res. 2018, 52, 729–740. [Google Scholar] [CrossRef]
- Pires, V.F.; Amaral, T.G.; Martins, J. Power quality disturbances classification using the 3-d space representation and pca based neuro-fuzzy approach. Expert Syst. Appl. 2011, 38, 11911–11917. [Google Scholar] [CrossRef]
- Liao, C.-C.; Yang, H.-T. Recognizing noise-influenced power quality events with integrated feature extraction and neuro-fuzzy network. IEEE Trans. Power Deliv. 2009, 24, 2132–2141. [Google Scholar] [CrossRef]
- Biswal, M.; Dash, P.K. Measurement and classification of simultaneous power signal patterns with an s-transform variant and fuzzy decision tree. IEEE Trans. Ind. Inform. 2013, 9, 1819–1827. [Google Scholar] [CrossRef]
- Saikia, L.; Borah, S.; Pait, S. Detection and classification of power quality disturbances using wavelet transform, fuzzy logic and neural network. In Proceedings of the 2006 IEEE INDICON, Kolkata, India, 15–17 September 2006; pp. 1–5. [Google Scholar]
- Meher, S.K.; Pradhan, A.K. Fuzzy classifiers for power quality events analysis. Electr. Power Syst. Res. 2010, 80, 71–76. [Google Scholar] [CrossRef]
- Decanini, J.G.; Tonelli-Neto, M.S.; Malange, F.C.; Minussi, C.R. Detection and classification of voltage disturbances using a fuzzy-artmap-wavelet network. Electr. Power Syst. Res. 2011, 81, 2057–2065. [Google Scholar] [CrossRef]
- Bizjak, B.; Planinšic, P. Classification of power disturbances using fuzzy logic. In Proceedings of the 2006 IEEE EPE-12th International Power Electronics and Motion Control Conference, Portoroz, Slovenia, 30 August–1 September 2006; pp. 1356–1360. [Google Scholar]
- Eristi, H.; Demir, Y. A new algorithm for automatic classification of power quality events based on wavelet transform and SVM. Expert Syst. Appl. 2010, 37, 4094–4102. [Google Scholar] [CrossRef]
- Chilukuri, M.; Dash, P. Multiresolution s-transform-based fuzzy recognition system for power quality events. IEEE Trans. Power Deliv. 2004, 19, 323–330. [Google Scholar] [CrossRef]
- Wang, S.; Chen, H. A novel deep learning method for the classification of power quality disturbances using deep convolutional neural network. Appl. Energy 2019, 235, 1126–1140. [Google Scholar] [CrossRef]
- Eristi, B.; Eristi, H. A new deep learning method for the classification of power quality disturbances in hybrid power system. Electr. Eng. 2022, 104, 3753–3768. [Google Scholar] [CrossRef]
- Shen, Y.; Abubakar, M.; Liu, H.; Hussain, F. Power quality disturbance monitoring and classification based on improved PCA and convolution neural network for wind-grid distribution systems. Energies 2019, 12, 1280. [Google Scholar] [CrossRef] [Green Version]
- Sindi, H.; Nour, M.; Rawa, M.; Öztürk, Ş.; Polat, K. A novel hybrid deep learning approach including combination of 1D power signals and 2D signal images for power quality disturbance classification. Expert Syst. Appl. 2021, 174, 114785. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Zhou, Y. Ensemble deep learning for automated classification of power quality disturbances signals. Electr. Power Syst. Res. 2022, 213, 108695. [Google Scholar] [CrossRef]
- Sindi, H.; Nour, M.; Rawa, M.; Öztürk, Ş.; Polat, K. An adaptive deep learning framework to classify unknown composite power quality event using known single power quality events. Expert Syst. Appl. 2021, 178, 115023. [Google Scholar] [CrossRef]
- Yılmaz, A.; Küçüker, A.; Bayrak, G. Automated classification of power quality disturbances in a SOFC-PV-based distributed generator using a hybrid machine learning method with high noise immunity. Int. J. Hydrogen Energy 2022, 47, 19797–19809. [Google Scholar] [CrossRef]
- Salles, R.S.; Ribeiro, P.F. The use of deep learning and 2-D wavelet scalograms for power quality disturbances classification. Electr. Power Syst. Res. 2023, 214, 108834. [Google Scholar] [CrossRef]
- Zhong, T.; Zhang, S.; Cai, G.; Huang, N. Power-quality disturbance recognition based on time-frequency analysis and decision tree. IET Gener. Transm. Distrib. 2018, 12, 4153–4162. [Google Scholar] [CrossRef]
- Zhong, T.; Zhang, S.; Cai, G.; Li, Y.; Yang, B.; Chen, Y. Power quality disturbance recognition based on multiresolution S-transform and decision tree. IEEE Access 2019, 7, 88380–88392. [Google Scholar] [CrossRef]
- Minh Khoa, N.; Van Dai, L. Detection and classification of power quality disturbances in power system using modified-combination between the Stockwell transform and decision tree methods. Energies 2020, 13, 3623. [Google Scholar] [CrossRef]
- Shareef, H.; Mohamed, A.; Ibrahim, A.A. An image processing based method for power quality event identification. Int. J. Elect. Power Energy Syst. 2013, 46, 184–197. [Google Scholar] [CrossRef]
- Erişti, H.; Yıldırım, Ö.; Erişti, B.; Demir, Y. Optimal feature selection for classification of the power quality events using wavelet transform and least squares support vector machines. Int. J. Electr. Power Energy Syst. 2013, 49, 95–103. [Google Scholar] [CrossRef]
- Deokar, S.A.; Waghmare, L.M. Integrated DWT–FFT approach for detection and classification of power quality disturbances. Int. J. Electr. Power Energy Syst. 2014, 61, 594–605. [Google Scholar] [CrossRef]
- Manimala, K.; Selvi, K.; Ahila, R. Optimization techniques for improving power quality data mining using wavelet packet based support vector machine. Neurocomputing 2012, 77, 36–47. [Google Scholar] [CrossRef]
- Zhang, M.; Li, K.; Hu, Y. Classification of power quality disturbances using wavelet packet energy and multiclass support vector machine. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 424–442. [Google Scholar] [CrossRef]
- Barik, A.K.; Tripathy, D.; Mohanty, A.K. Detection & mitigation of power quality disturbances using WPT & FACTS technology. Int. J. Sci. Eng. Technol. Res. 2013, 2, 336–343. [Google Scholar]
- He, S.; Li, K.; Zhang, M. A real-time power quality disturbances classification using hybrid method based on S-transform and dynamics. IEEE Trans. Instrum. Meas. 2013, 62, 2465–2475. [Google Scholar] [CrossRef]
- Hasheminejad, S.; Esmaeili, S.; Jazebi, S. Power quality disturbance classification using S-transform and hidden Markov model. Electr. Power Compon. Syst. 2012, 40, 1160–1182. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Recognition of power quality disturbances using S-transform based ruled decision tree and fuzzy C-means clustering classifiers. Appl Soft Comput. 2017, 59, 243–257. [Google Scholar] [CrossRef]
- Mahela, O.P.; Shaik, A.G. Power quality recognition in distribution system with solar energy penetration using S-transform and fuzzy C-means clustering. Renew. Energy 2017, 106, 37–51. [Google Scholar] [CrossRef]
- Reddy, M.V.; Sodhi, R. A modified S-transform and random forests-based power quality assessment framework. IEEE Trans. Instrum. Meas. 2018, 67, 78–89. [Google Scholar] [CrossRef]
- Mahela, O.P.; Khan, B.; Alhelou, H.H.; Siano, P. Power quality assessment and event detection in distribution network with wind energy penetration using stockwell transform and fuzzy clustering. IEEE Trans. Ind. Inform. 2020, 16, 6922–6932. [Google Scholar] [CrossRef]
- Jayasree, T.; Devaraj, D.; Sukanesh, R. Power quality disturbance classification using Hilbert transform and RBF networks. Neurocomputing 2010, 73, 1451–1456. [Google Scholar] [CrossRef]
- Shukla, S.; Mishra, S.; Singh, B. Power quality event classification under noisy conditions using EMD-based de-noising techniques. IEEE Trans. Ind. Inf. 2014, 10, 1044–1054. [Google Scholar] [CrossRef]
- Prakash, S.; Purwar, S.; Mohanty, S.R. Adaptive detection of islanding and power quality disturbances in a grid-integrated photovoltaic system. Arab. J. Sci. Eng. 2020, 45, 6297–6310. [Google Scholar] [CrossRef]
- Singh, H.R.; Mohanty, S.R.; Kishor, N.; Thakur, K.A. Realtime implementation of signal processing techniques for disturbances detection. IEEE Trans. Ind. Electron. 2019, 66, 3550–3560. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Samantaray, S.R.; Manikandan, M.S. Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 2018, 9, 3122–3132. [Google Scholar] [CrossRef]
- Soman, K.P.; Poornachandran, P.; Athira, S.; Harikumar, K. Recursive variational mode decomposition algorithm for real time power signal decomposition. Procedia Technol. 2015, 21, 540–546. [Google Scholar] [CrossRef] [Green Version]
- Muthusamy, T.A.; Ramanathan, N. An expert system based on least mean square and neural network for classification of power system disturbances. Int. J. Future Revolut. Comput. Sci. Commun. 2018, 1, 308–313. [Google Scholar]

















| Disturbance | Causes | Impacts |
|---|---|---|
| Swell | system fault conditions (such as single line-to-ground (SLG) fault), switching off large loads, capacitor banks | Electronic component’s breakdown and damage or other sensitive equipment, insulation failure (induction machine), flicker. |
| Sag | switching of large loads (such as arc furnaces, motors, etc.), disconnecting capacitors, Lightning. | Flicker, decreasing AC motor speed, switching off of control systems. |
| Over-voltage | capacitor banks, lighting, resonances, fault condition and circuit breaker opening | damage of equipment and circuit breaker, flicker. |
| Under-voltage | Low factor of power, overloaded network and transformers, switching off of a large electric generation. | Electromechanical equipment’s life reduction, premature failure. |
| Harmonics | Electronic power converter, non-linear loads, generators and transformers, arc furnaces. | Malfunction of relays and sensitive equipment, degrade of the machine performances, capacitors failures, electromagnetic interference in communication circuits. |
| Interruptions | Human errors, faults, failures of control-command system, natural causes (high winds, ice on the lines, etc.) | Loss of power, equipment failures, shutdown of computer and sensitive equipment. |
| Frequency variation | electric generation loss, an un-synchronous between the power system and generator, overloaded of electric system. | Degrade engine performance, inefficient of motors, power failure. |
| Voltage fluctuation | Electric arc furnaces, start-up of drives, resistance welders, inter-harmonics components in current signal. | Voltages and currents instability of the electronic equipment, flicker. |
| Flicker | Switching of large load, capacitor banks, electric arc furnace, frequent start-up of AC motors. | Flicker. |
| PQ Disturbance | Duration | Voltage Values |
|---|---|---|
| Sag | >0.5 cycles | 0.1 to 0.9 pu |
| Swell | >0.5 cycles | 1.1 to 1.8 pu |
| Outage | >0.5 cycles | <0.1 pu |
| Flicker | >0.5 cycles | 0.9 to 1.1 pu |
| Harmonic | - | THD |
| Inter-harmonic | - | THD |
| Standard | Term | Definition |
|---|---|---|
| IEEE 1159 | Interruption | Voltage below of nominal |
| Sustained interruption | Longer than 3 s | |
| Momentary interruption | cycle to 3 min | |
| Temporary interruption | 3 s to 1 min | |
| IEEE 1250 | Instantaneous interruption | Shorter than 30 cycles |
| Momentary interruption | to 2 s | |
| Temporary interruption | 2 s to 2 min | |
| Sustained interruption | longer than 2 min | |
| EN 50160 | Short interruption | Shorter than 3 min |
| Long interruption | Longer than 3 min | |
| IEEE 1366 | Momentary interruption | Shorter than 5 min |
| Sustained interruption | Longer than 5 min |
| Influence Quantity | Reference Condition | Error Requirements for Compliance | |||
|---|---|---|---|---|---|
| P-Class | M-Class | ||||
| Signal frequency | Frequency () Phase angle constant | Range: | Range: Hz for for Hz for | ||
| Max FE | Max RFE | Max FE | Max RFE | ||
| 0.005 Hz | 0.01 | 0.005 Hz | 0.01 | ||
| Harmonic distortion (same as Table 3 in C37.118-2011) (single harmonic) | <0.2% THD | 1% each harmonic up to 50th | 10% each harmonic up to 50th | ||
| Max Fe | Max RFE | Max Fe | Max RFE | ||
| Fs > 20 | 0.005 Hz | 0.01 | 0.025 Hz | 0.01 | |
| Fs ≤ 20 | 0.005 Hz | 0.01 | 0.025 Hz | 0.01 | |
| Modulation Level, Reference Condition, Range (Use the Same Modulation Levels and Ranges under the Reference Conditions Specified in Table 5 in C37.118-2011 Standard) | Error Requirements for Compliance | |||
|---|---|---|---|---|
| P-Class | M-Class | |||
| Max FE | Max RFE | Max FE | Max RFE | |
| 0.06 Hz | 3 | 0.3 Hz | 30 | |
| 0.01 Hz | 0.2 | 0.06 Hz | 2 | |
| Influence Quantity | Reference Condition | Minimum Range of Influence Quantity over Which PMU Shall Be within Given TVE Limit | |||
|---|---|---|---|---|---|
| P-Class | M-Class | ||||
| Range | Max TVE % | Range | Max TVE % | ||
| Signal frequency range- (test applied nominal +deviation:) | () | Hz | 1 | Hz for for Hz for | 1 |
| The above signal frequency range tests are to be performed over the given ranges and meet the given requirements at three temperatures: nominal (23 C), C, and C | |||||
| Signal voltage magnitude | rated | to rated | 1 | to rated | 1 |
| Signal current magnitude | rated | to rated | 1 | to rated | 1 |
| Phase angle with Hz | Constant or slowly varying angle | 1 | 1 | ||
| Influence Quantity | Reference Condition | Minimum Range of Influence Quantity over Which PMU Shall Be within Given TVE Limit | |||
|---|---|---|---|---|---|
| P Class | M Class | ||||
| Range | Max TVE (%) | Range | Max TVE (%) | ||
| , | rated signal magnitude, | Modulation frequency 0.1 to losser of or 2 Hz | 3 | Modulation frequency 0.1 to losser of or 5 Hz | 3 |
| , | rated signal magnitude, | 3 | 3 | ||
| Method | Ref | Advantages | Drawbacks |
|---|---|---|---|
| Discrete Fourier transform (DFT) | [66] | DFT is the most used computation algorithms for PQDs analysis. In most cases, DFT is used to analysis three-phase signals under stationary conditions. | In real power systems, the three-phase signals are affected by small and large variations (events). In such conditions, the signal parameters are time-varying that affect the performance of DFT. |
| Fast Fourier transform (FFT) | [67] | FFT is commonly used for harmonic analysis and it has lower computation time compared to one DFT. | Due to aliasing and leakage effects, the FFT yields inaccurate results. |
| Short time Fourier transform (STFT) | [68] | STFT is a technique that performs the DFT on the time-dependent length using a “sliding window”. | STFT yields inaccurate results under non-stationary conditions. |
| Wavelet transform (WT) | [69,70,71] | Compared to FT, WT allows obtaining the time and frequency information of the power system signals. | The performance of this technique is affected by the leakage effect and noisy environment. Moreover, using a short sliding window yield to high computation time. |
| Method | Advantages | Drawbacks |
|---|---|---|
| Zero-crossing transform [33] | Low Computationally complexity. | It has low performance under noisy environments and for distorted wave-forms, harmonics, and inter-harmonics. |
| RMS and peak voltage techniques [13] | They are well-proven and simple techniques. | They can not estimate other signal parameters, such as phase angle. Moreover, they achieve low performance in noisy environments. |
| Fourier transform and its extensions [65,119] | They have a simple implementation, low computation complexity, accuracy, and immunity against harmonic components under stationary conditions. | Their estimation performance is limited under off-nominal conditions. |
| Pisarenko [33,72,73] | It has low computation complexity. | Pisarenko method needs exact information on the model order and it gives inaccuracy estimation because of the statistical auto-correlation lag estimation. It suffers also under low noisy environments. |
| Prony method and its extension [69,70,76,77,78,79,80] | They have low computation complexity and high estimation performance compared to those of the Pisarenko method. | These techniques are still sensible to noise and they depend on the system’s parameters. |
| Music approach [8] | It has high resolution than Prony techniques and achieves asymptotically unbiased estimation of signal parameters. | It can not resolve a problem with closely spaced signals under a low SNR environment and its high computational burden. |
| ESPRIT approach [8] | It has a lower computational burden compared to MUSIC. It achieves the highest performance for inter-harmonic estimation. | It needs to know the order of the signal model and it achieves low performance under high noisy environment. |
| Hilbert–Huang transform [96,97,98,99] | It achieves good performance under a non-stationary environment and for non-linear signals. | Its drawbacks are end effects and mode mixing during the process of empirical mode decomposition (EMD). |
| Kalman filters [105,106,107,108,111] | It achieves the highest performance for linear systems. | It leads to poor estimation for non-linear systems. |
| Maximum likelihood [8,116] | It allows achieving the highest performance and it is an asymptotically optimal estimator. | The signal model is required. Moreover, its resolution is near to this of Fourier-based techniques for low SNR. |
| Technique | Advantages | Drawbacks |
|---|---|---|
| GA | It is the heuristic method that can provide multiple solutions for several search and optimization problems. GA design is simple and easy to understand. GA can obtain a solution for difficult problems over traditional methods and it requires less amount of information. | The main drawbacks of GA are the hyper-parameter tuning, time-consuming, and the need for special definitions. Its implementation is still a difficult task. |
| PSA | PSA design is based on particle swarm and it is adapted with mutation computation. PSA requires a few parameters to tune and it can provide fast and multiple solutions. | PSA leads a low performance for complex and large numbers of dimensions and data-sets. IT requires software knowledge and theoretical analysis is still a difficult step. |
| ACO | ACO design is based on ant colony and it may be continuously used and can instantly adjust to changes. It can provide a good solution compared to other methods. | It is complex and the theoretical analysis is still difficult with a random decision. It requires a pre-knowledge of factors and software languages. |
| ABC | Its concept is based on a bee colony and it has the ability to convert to local solutions with good speed. It needs fewer steps for optimization. It adapted to optimization problems that have multi-dimensions. | ABC requires pre-knowledge of factors and software languages. |
| Downhill simplex | This method is a heuristic search that is used for non-linear problems for optimizing 1- or multi-dimensional cost-functions. This method allows for finding the maximum or minimum of the objective function. | However, this technique is highly computationally complex to find the feature with the highest performance. |
| Newtho-Raphson | It is an iterative algorithm and it uses the tangent knowledge of the curve that is close to the root. The main advantage of the Newton–Raphson method is its capability to find the optimum feature in a few iterations. | This technique has two main drawbacks that are: (1) it requires an initial guess that must be close to the searched-for zero in order to obtain a good solution. (2) The computation of the inverse of the derivative is still a difficult task. |
| Type | Class | |||
|---|---|---|---|---|
| Balanced | 0 | E | 0 | |
| A | 0 | V | 0 | |
| C | 0 | |||
| D | 0 | |||
| F | 0 | |||
| G | 0 | |||
| H | E | 0 | ||
| I | E | 0 | ||
| B | ||||
| E |
| Techniques | Benefits | Drawbacks |
|---|---|---|
| ABC | ABC has a simple design to classify the sag voltage. | Nevertheless, The ABC classifier can not select other sag parameters. |
| Symmetrical component classifier | This classifier is used to identify the corresponding sag among sag types C & D [164]. | SCC achieves low-performance classification under noisy environments. |
| Classifier-based on ITC | It yields to highest classification performance with a lower computation time. | It requires a signal model. |
| ANN | It can self-learn the PR of several systems. | It requires sufficient layers and a good knowledge of neurons. Moreover, the learning step results in a high computation time. |
| SVM | has a high ability of learning and it achieves high performance for large dimensional spaces. | SVM has low performance under noisy environments and its training and testing data requires a huge computation time. |
| FES-based classifier | This classifier achieves good accuracy for several PQDs and it can be used to analyze complex systems. | It requires a good knowledge about the disturbances or training database and its performance depends on the learning stage. |
| Machine learning | DL algorithms do not require having specifically coded to automatically learn the best features. | These techniques are highly complex and they rely on the training stage. |
| Ref-Year | Feature Extraction | Feature Selection | Feature Classification | System Employed | Non-Noisy Environment | Noisy Environment |
|---|---|---|---|---|---|---|
| [223], 2012 | DWT | - | - | Synthetic and single data | 98.03 | - |
| [208], 2011 | DWT | - | HHM | Synthetic and multi-phase data | 99.66 | - |
| [224], 2013 | DWT | - | LS-SVM-kMA | Synthetic and multi-phase data | 98.88 | 98.14 |
| [225], 2014 | DWT and FFT | - | Threshold | Synthetic and multi-phase data | 90.04 | - |
| [141], 2015 | DWT | PSO | ELM | Synthetic and multi-phase data | 97.60 | – |
| [226], 2011 | WPT | GA-SA | SVM | Synthetic data | 98.33 | - |
| [227], 2012 | WPT | - | MSVM | Synthetic data | 97.7 | 92.25 |
| [228], 2013 | WPT | - | - | Synthetic and single data in real-time | - | – |
| [27], 2021 | HT-DWT | - | ANN-SVM | Synthetic and single-phase data | 98.11 | - |
| [218], 2022 | un-decimated WT | - | Stochastic Gradient Boosting Trees (SGBT) | Synthetic, simulation and multi-phase data | - | 99.29–99.50 |
| [229], 2013 | ST | - | DT | Real time and multi-phase data | 99.27 | 94.36–97.91 |
| [230], 2012 | ST | - | Hidden Markov model | Synthetic and multi-phase data | 98.14 | 91.86–95.04 |
| [231], 2017 | ST | - | Fuzzy C-means clustering | Synthetic and single-phase data | 99.20 | 98.50 |
| [232], 2017 | ST | - | Fuzzy C-means | Real data | - | <90 |
| [233], 2018 | ST | - | RF | Synthetic and multi-phase data | 99.85 | 99.61 |
| [234], 2020 | ST | - | Fuzzy C-means | Real data | - | <90 |
| [235], 2010 | HT | - | ANN | single-phase data in real-time | 96.75 | - |
| [123], 2014 | HHT | - | PNN–SVM | Synthetic and multi-phase data | 100 | - |
| [236], 2014 | HHT | - | FES | Synthetic and multi-phase data | 98 | 87.22–91.55 |
| [237], 2020 | EMD-HT | - | SVM | Real data | - | <90 |
| [238], 2018 | Orthogonal EMD | - | - | Real data | - | <90 |
| [239], 2018 | VMD | - | DT | Real-time and single-phase data | 98.56 | 96.73 |
| [240], 2015 | VMD | - | DT | Real-time and multi-phase data | 99.50 | 93.80 |
| [241], 2018 | LMS | - | MLP-NN | Synthetic and single-phase data | 96.71 | - |
| [117], 2017 | ML | Newton–Raphson | - | Synthetic and multi-phase data | 100 | - |
| [118], 2015 | ML | Nelder–Mead (fminsearch) | - | Synthetic and multi-phase data | 100 | - |
| [161], 2016 | ML | - | ITC | Synthetic and single data | 100 | 100 |
| [162], 2017 | ML | - | ITC | Synthetic and single data | 100 | 100 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oubrahim, Z.; Amirat, Y.; Benbouzid, M.; Ouassaid, M. Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review. Energies 2023, 16, 2685. https://doi.org/10.3390/en16062685
Oubrahim Z, Amirat Y, Benbouzid M, Ouassaid M. Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review. Energies. 2023; 16(6):2685. https://doi.org/10.3390/en16062685
Chicago/Turabian StyleOubrahim, Zakarya, Yassine Amirat, Mohamed Benbouzid, and Mohammed Ouassaid. 2023. "Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review" Energies 16, no. 6: 2685. https://doi.org/10.3390/en16062685
APA StyleOubrahim, Z., Amirat, Y., Benbouzid, M., & Ouassaid, M. (2023). Power Quality Disturbances Characterization Using Signal Processing and Pattern Recognition Techniques: A Comprehensive Review. Energies, 16(6), 2685. https://doi.org/10.3390/en16062685









