Modelling the Dynamic Linkage Amidst Energy Prices and Twin Deficit in India: Empirical Investigation within Linear and Nonlinear Framework

Abstract

Energy and electricity are critical prerequisites for every nation and critical components of social and economic growth. The monetary policy economist has been debating the issue of relying on core inflation or headline inflation, which includes energy, because the energy price is so volatile that it obscures the trend in inflation and dilutes the objectives of monetary policy. This paper aims at analyzing the impact of the twin deficit on energy inflation within a linear and nonlinear framework in India using time series data covering the period from 1971 to 2021. ARDL and NARDL approaches are employed to investigate the linear/symmetric response of energy inflation due to the twin-deficit in India. Estimates show a negative relationship between the twin-deficit and energy inflation in a symmetric model. The results of the asymmetric model reveal that the response of energy inflation due to expansionary fiscal policy (increment in CFD) and contractionary fiscal policy (decline in CFD) is diverse, in terms of size of the coefficient. Further, estimates of NARDL show the distinct impact of increases and decreases in CAD on energy inflation. The study offers several implications for policymakers and energy economists.

1. Introduction

Energy is among the three main pillars to achieve the Sustainable Development Goal (SDG) 2030; the other two are food and water [1,2,3]. A crisis in anyone may have to create the situation where economies have to compromise to achieve the SDG-2030 [4]. Energy and electricity are critical prerequisites for every nation and important components of social and economic growth [5]. It plays a vital role in economic growth since it directly contributes to manufacturing as a key input for industry and household consumption [6,7]. This significance emerged in the energy sector; the energy business has gained significant attention over the previous few decades. Since energy consumption, pricing, and economic growth have a positive connection, energy efficiency legislation may hurt economic growth [7,8]. The energy industry is critical to increasing wealth and, hence, to the country’s prosperity, as well as to environmental and social sustainability [9,10,11]. Uninterrupted supply of energy is essential for achieving efficiency in agriculture, manufacturing, and other trade and industry, and in case of failure, economies may come across situations of poverty and lag behind in economic development [12,13]. Stable energy supply at a reasonable price is necessary for economic growth and to improve the quality of life [14,15]. In the short run, headline inflation is correlated with energy inflation. Energy inflation refers to the inflation endorsed to the involvement of energy prices [16]. The energy price inflation expectation has been underweighted; however, energy inflation has prolonged implications on the overall price index if proper measures are not taken [17].

According to the Mundell–Flaming model, in an open economy, due to an increase in the budget deficit, interest rates increase. As a result, capital inflows into the country increase, and the domestic currency becomes stronger against the foreign currency. This ultimately led to an upsurge in imports, which further contributes to the current account imbalance. This is basically the traditional Keynesian view about the budget deficit and import relation. Budget and current account deficits are challenges for the majority of countries. The budget deficit is causing inflation in the economy [14]. Both twin deficits have a complex but significant relationship with each other [18,19,20,21,22,23,24]. Various developed and developing economies, including India, are depicting a negative “twin deficit”. The current account and fiscal deficits are together termed the “twin deficit”. Their stability is essential for the growth and development of nations. However, it is not as straightforward as it appears due to the dynamic economic environment. Numerous macroeconomic factors, especially external factors, such as energy prices for oil-importing nations, which are beyond the control of economists. are significantly responsible. Akanbi found that oil is the determining factor in establishing the causal relationship between fiscal policy and the current account [25].

India is the third-largest energy consumer due to rising wages and living standards. Coal, oil, and solid biomass supply 80% of energy demand, which has doubled since 2000. Net dependency on imported oil will rise to almost 90% by 2040 from 75% due to falling domestic oil and gas production [26]. The energy price increase and high inflation have a severe adverse impact on the balance of payments. Imported fuels expose the country to price cycles, volatility, and supply interruptions. If power system operation lacks flexibility, India’s domestic market, particularly the electrical industry, may face energy security issues. Approximately 45 percent of India’s natural gas and 80 percent of its crude oil are imported [27]. Increasing energy prices are a continuous challenge for the Indian economy. The obvious impact of this increasing oil price can be seen in inflation rate in India. In July 2022, a sharp hike of Rs. 25 per liter in fuel prices (diesel and petrol) was recorded.

The issue of whether to rely on core inflation or headline inflation, which includes energy, has been debated by monetary policy economists [28]. Because the oil price is so volatile, it obscures the trend in inflation and dilutes the objectives of monetary policy. The central banks of the countries dismiss energy inflation transmission because they rely on the fact that the volatility is short-term and does not have a long-term impact on the economy [29]. However, earlier studies suggest that energy inflation has a severe impact beyond the short run horizons [30,31]. Energy price inflation is concentrated at frequency ranges 1.5 years to 5.5 years though varies across countries, so it cannot be considered a short-term transitory shock [29]. Very limited literature is available on the relationship between energy inflation and twin deficit which is imperative for policymakers and other stakeholders to stabilize the macroeconomic indicators in this dynamic economic environment using advanced econometric methodology. The main objective of this research is to explore the relationship between energy inflation and the twin deficit with the control variables such as urbanization, carbon emissions, and energy consumption. Considering oil and electricity as two main components of energy, the specific aims of this research paper are as follows:

• To analyse the long run and short run association between twin deficit on energy inflation.
• To examine the impact of twin deficit on energy inflation in under symmetric and asymmetric frameworks.

This research paper makes many contributions to the existing literature on energy inflation and the twin deficit. A great deal of literature has been found on the twin deficit and energy inflation, but there have only been very limited studies that include both variables in a single study, even though it is expected that these two variables are very closely related, particularly in the context of oil importing countries. The present study offers several contributions.

• This study fills this gap by analysing the impact of twin deficit on energy inflation. This is critical for a country like India to design their energy, monetary, and fiscal policies.
• Secondly, the majority of the study considers only oil as a proxy for energy, but since electricity is a significant contribution to energy, this study includes both oil and electricity as proxies for energy and develops two regression models and parameter estimates that are explored using advanced econometric methodology, namely NARDL, so the real impact of the twin deficit on energy inflation will be found out.
• Thirdly, the study presents a research model on twin deficit and energy inflation and transmission channel of twin deficit in other macroeconomic variable, which can be food for thought for future research to improve the understanding of the topic.

This paper is structured in six sections. A review of literature and transmission channels is presented in Section 2. Materials and methodology discussed the data sources, variable descriptions, and econometric approach given in Section 3. Section 4 explains the results of the empirical analysis. A discussion on results of ARDL and NARDL is presented in Section 5. The last section deals with the conclusion, policy implications, and research limitations.

2. Review of Literature and Transmissions Channel

2.1. Review of Literature

A number of studies have discussed the twin deficit and its relationship with other macroeconomic variables, viz., the exchange rate, interest rate, and inflation [32,33,34,35,36]. Macroeconomic stability and instability are the outcomes of fiscal policy and monetary policy, but not only limited to this [20]. In the late 19th century, prolonged fiscal deficit (FD) and escalating current account deficit (CAD) became substantial challenges in both industrialized and emerging nations, including India [37]. Excessive FD not only expands the public debt but also amplifies the inflationary pressure in the economy, while prolonged CAD depreciates the domestic currency, promotes foreign reserve outflow, and escalates the inflation rate [38]. Earlier studies empirically found that a higher fiscal deficit caused a longer-term current account deficit [19,39,40,41]. Interest rates, real production, and exchange rates all affect the twin deficit when the central bank targets inflation. Nautiyal et al. argued that the chronic CAD causes macroeconomic imbalance, which contributed to the economic recession, and that the compensatory cost is very high to adjust the adverse current account deficit in any economy [37].

Oladipo and Akinbobola (2011) pointed out that the continuous budget deficit fuels inflation in the economy and pushes the growth of the current account deficit, which ultimately destabilizes the macroeconomic environment in the economy [42]. Saleh, Nair, and Agalewatte (2005) suggested that budget deficits increase consumers’ disposable income, which increases spending. As a consequence, import will increase, ultimately leading to an increase in the current account deficit [43]. The case of India is not different, and Mallick et al. (2021) found that the current account deficit has a drastic adverse impact on fiscal deficits [18]. Cost–push shocks account for a larger proportion of the volatility in Indian inflation, and cost–push shocks such as oil prices have been identified as major predictors of inflation in India. The budget deficit is the burning problem in India, even though the situation is comparatively adverse as compared to other developing countries [18,37].

Ramakrishnan, Raju, and Gopakumar (2020) and Dhar and Rao (2014) argued that for an open economy like India, the CAD is widely acknowledged as a key measure of economic instability, and India’s current account deficit is widening due to an increasing trade deficit [44,45]. Studies presented that the balance of payment (BoP) crises create potential financial challenges in India, leading to multiple economic crises like inflation, crowding out, higher interest rates, and slow growth [46,47]. According to Okoli et al. (2021), the adverse situation of the current account deficit reduces the tax revenue of government, which leads to fiscal deficit [48]. Further, if the government pursues an expansionary fiscal policy by slashing taxes, the government’s income will decrease, which will also increase the fiscal deficit; the additional spending required to balance the economy will come from foreign economies, which will increase imports and the current account balance [20,49]. The change in taxes, particularly excise taxes, has a considerable association on energy prices in countries like India, where the majority of the energy is imported in the form of crude oil.

Studies show that oil and gas both have explanatory power to measure the variation in inflation [29,50]. According to Bhat et al. (2018), increases in oil prices cause inflation via consumption and cost–push pathways [51]. An increase in oil prices will raise headline inflation because oil-based products make up a sizable percentage of the consumer basket. Researchers concluded that global oil price swings have affected national economies through many methods and categories; these channels can be classified in 6 ways: classical supply-side shock effect, purchasing power effect, inflation effect, real balance effect, sectoral adjustment effect, and psychological effect [52,53,54,55]. Yuan et al. (2008) noted that electricity is among the three specific sources of energy other than oil and coal [56]. On the other hand, Shakeel et al. (2016) and Yasmeen et al. (2019) reported that the price of electricity has been rising steadily, and such price hikes could be attributed to the growth of these economies, which has put demand-induced inflationary pressure on electricity prices. The volatility of oil prices on the global market and severe shortages of primary energy resources have collectively driven up the price of electricity [57,58].

Iqbal et al. (2021) proposed an energy inflation index and found that oil prices and energy imports positively influence the energy inflation index [59]. Talha et al. (2021) and Haider et al. (2013) pointed out that the oil supply has been controlled by a few main countries, and an increase in oil price may impact the energy inflation in oil importing countries, which may have a severe adverse impact on economic activities [60,61]. Acheampong et al. (2021) showed that changes in energy prices have significant implications due to their linkage with other macroeconomic indicators [62]. Rubene (2018) argued that energy prices, particularly crude oil prices, have contributed a significant amount to headline inflation in European countries. However, energy inflation depends on the share of energy in consumption expenditure and on the degree of pass-through of oil price development to consumers energy prices [16]. Andreani and Giri expressed that energy price shock transmit to inflation directly and indirectly [29]. Wong (2015) suggested that in the direct channel, an upsurge in energy prices gives a push to input costs, while the indirect channel is the effect of wage bargaining and price setting that arises from a rise in inflation expectations [63]. Norouzi (2021) studied the worldwide implications and difficulties of the COVID-19 pandemic on the oil and gas industries, as well as potential energy related prospects [64]. The short-term effect is a reduction in petroleum consumption of roughly 25 percent, which gradually recovers and even expands. A 30% to 40% decline in CAPEX and R&D spending throughout the oil and gas sector has led oil extraction projects to decline from over 800 in 2019 to 265 in 2021.

Kousar et al. (2022) attempted to explore the relationship between energy inflation and the twin deficit, but they examined the linear framework only [65]. In a linear framework, El Anshasy and Bradley (2012) examined the relationship between the oil price and fiscal policy [66]. Eregha et al. (2022) expressed that the empirical relationship between the budget-current account deficit with oil price is not get much attention from the researchers, but that it is imperative to understand the relationship [67]. Using SVAR and VECM, Adedokun (2018) suggests that government policies are highly sensitive with respect to oil prices. However, the study could not provide the asymmetric effects of oil price in government policies [68]. Although energy prices are fluctuating in nature, in this case, assessment in asymmetric framework leads to a better conclusion. In addition, the twin deficit is also asymmetric in nature [18]. No previous study has examined the relationship between twin deficits and energy inflation. This study fills this gap by exploring the relationship between these two variables in both linear and non-linear frameworks. In addition, the present study also includes the control variables, such as climate change (CO₂), renewable energy consumption (EC), and urbanization (UB). The present study aims to explore the relationship between energy inflation and the twin deficit with the control variables such as urbanization, carbon emissions, and energy consumption in linear and non-linear framework using the ARDL and NARDL.

2.2. Transmission Channels via Twin Deficit to Energy Inflation

2.2.1. Fiscal Deficit-Energy Inflation Nexus

For financing the fiscal deficit, the government should adopt either borrowings (both domestic and foreign), printing of new money (also known as seigniorage financing), or the combination of both (see Figure 1). The government will seek to issue bonds and securities in order to borrow from markets, and it may facilitate an alluring interest rate to investors. Providing a certain demand for bonds, the rising supply of government bonds and securities may impose a downward influence on their prices and thus upsurge the interest rates. In a resource-scarce country like India, exaggerated borrowing due to expanding fiscal deficit may restrict the availability of loanable funds from the banking system. Due to mismatches between the demand for and supply of loanable funds, this may cause the interest rate to rise. Consequently, higher interest rates dismantle the investment and production, which leads to increases in the prices of various commodities like oil and electricity because of excess energy demand and thus exert upward pressure on inflation. Alternatively, if the government adopts seigniorage financing methods to cover the fiscal deficit, then there will be excessive money supply in the economy. As a result of the increased availability of loanable funds for credit in the banking system, excessive money supply lowers the interest rate. Again, an expansion of money supply would trigger inflationary pressure in the economy.

2.2.2. Current Account Deficit-Energy Inflation Nexus

Theoretically, there are two different transmission channels through which current account deficit (CAD) influences the inflation rate in the economy (see Figure 2). First, an increase in the CAD will culminate in the devaluation of the Indian rupee. Devaluation lowers the value of Indian exports, implying that Indian resources are going to foreign countries at cheap prices which induces the inflation rate in India. Indian investors suffer losses, resulting in a decline in the optimum level of investment and GDP, which reduces the exports and widens CAD. Second, the devaluation of the Indian rupee upsurges the import prices for essential commodities whose demand is inelastic, such as crude oil. Because of inelastic demand for crude oil, as India is an oil-dependent nation, this induces the inflation rate in India. If the economy is experiencing inflation this will have adverse impact on exports and thus expand the CAD.

3. Materials and Methodology

3.1. Data Source

The present study investigates the influence of India’s twin-deficit on energy inflation, utilizing yearly time series data covering the period of 1971 to 2021. This study used two distinct proxies to measure energy inflation viz, oil price (OP), and electricity prices (EP). Moreover, this study deliberated five explanatory variables, including the twin-deficit, i.e., fiscal deficit (CFD), and the current account deficit (CAD), the climate change (CO₂), renewable energy consumption (EC), and urbanization (UB). To reduce the magnitude of the data’s dispersion, we converted all variables except CFD, CAD, and UB into natural logarithms [69,70,71]. This modification also assists in alleviating heteroscedasticity and multicollinearity related concerns [72,73,74].

Table 1. Description of the variables.

Variables	Acronyms	Definition	Source	Sign
Dependent Variables
Oil Prices	OP	Log of oil prices	Energy Information Administration, USA
Electricity Prices	EP	Log of electricity prices	Office of the Economic Adviser, Ministry of Commerce and Industry, India
Independent Variables
Fiscal Deficit	CFD	Central government’s fiscal deficit (as a % of GDP)	RBI	+
Current Account Deficit	CAD	Current account deficit (as a % of GDP)	RBI	+
Control Variables
Energy Consumption	EC	Log of renewable energy consumption	BP Statistical Review of World Energy	-
Carbon Emissions	CO2	Log of carbon dioxide	BP Statistical Review of World Energy	+
Urbanization	UB	Urbanization (annual % of total population)	WDI	+

Source: Authors’ compilation.

comprises a description of each variable, along with its definition, anticipated sign, and sources.

Lastly, Figure 3 depicts the graph of the pertinent variables. Figure 3 clearly demonstrates the trends and variability of the variables.

For robust results, the present study has classified the two functional forms and conferred in the succeeding equations:

Model 1:

OP = f(CFD, CAD, EC, CO₂, Ub)

Model 2:

EP = f(CFD, CAD, EC, CO₂, Ub)

All the variables are defined in Table 1.

3.2. Methodology

There is a myriad of traditional methods for investigating the cointegrating linkage between variables, namely Engle and Granger (1987), Johansen (1988), and Johansen and Juselius (1990) [75,76,77]. The auto-regressive distributed lag (ARDL) technique to cointegration introduced by [78] was implemented to explore the linear/symmetric response of energy inflation to twin-deficit in India. The ARDL model, according to [78], has addressed the major empirical complications inherent with conventional approaches (For a detailed understanding and derivation of ARDL approach, please refer to [67]). [78] postulated some of the most notable properties of the ARDL approach: first, ARDL requires no preceding insights about the variables’ stationarity. Even though the variables’ order of integration is distinct, i.e., I(0) or I(1) or both but not I(2), the ARDL method can be utilized. Second, the ARDL approach yields accurate findings, even when the sample size is minimal. Third, in contrast to the ARDL model, conventional cointegration approaches may be susceptible to endogeneity; fourth, the ARDL model concurrently yields short- and long-run estimates, as well as the error correction term, and overcomes the complications inherent with missing variables and serial-correlation [79].

The study has examined the cointegrating relationship of OP and EP with their covariates individually by implementing the unrestricted error correction model.

Model 1:

$$\begin{gathered} ∆{OP}_t={\alpha }_0+{\sum }_{i=1}^n{\delta }_i∆{OP}_{t-i}+{\sum }_{i=0}^m\left[{\beta }_1∆{CFD}_{t-i}+{\beta }_2∆{CAD}_{t-i}+{\beta }_3∆{EC}_{t-i}+{\beta }_4∆{CO}_{2,t-i}+{\beta }_5∆{Ub}_{t-i}\right]+ \\ {\gamma }_1{OP}_{t-1}+{\gamma }_2{CFD}_{t-1}+{\gamma }_3{CAD}_{t-1}+{\gamma }_4{EC}_{t-1}+{\gamma }_5{CO}_{2,t-1}+{\gamma }_6{Ub}_{t-1}+{\mu }_t \end{gathered}$$

(1)

Model 2:

$$\begin{gathered} \Delta {EP}_t={\alpha }_0+{\sum }_{i=1}^n{\delta }_i\Delta {EP}_{t-i}+{\sum }_{i=0}^m[{\beta }_1\Delta {CFD}_{t-i}+{\beta }_2\Delta {CAD}_{t-i}+{\beta }_3\Delta {EC}_{t-i}+{\beta }_4\Delta {CO}_{2,t-i}+{\beta }_5\Delta {Ub}_{t-i}]+ \\ {\gamma }_1{EP}_{t-1}+{\gamma }_2{CFD}_{t-1}+{\gamma }_3{CAD}_{t-1}+{\gamma }_4{EC}_{t-1}+{\gamma }_5{CO}_{2,t-1}+{\gamma }_6{Ub}_{t-1}+{\mu }_t \end{gathered}$$

(2)

where all the variables are explained in Table 1, and Δ denotes first difference; t represents time period; δ_i and β₁ to β₅ are the coefficients of short-run elasticities; γ₁ to γ₆ are the coefficients of long-run elasticities; and μ_t is the white noise.

F-statistics were employed to test the null hypothesis of no cointegration (i.e., H0: γ₁ = γ₂ = γ₃ = γ₄ = γ₅ = γ₆ = 0) among the variables against the alternative of cointegration (i.e., H1: γ₁ ≠ γ₂ ≠ γ₃ ≠ γ₄ ≠ γ₅ ≠ γ₆ ≠ 0). There are three cases:

(i)

If F-statistic > I(1), we can reject the null hypothesis and conclude the presence of cointegration among the variables.

(ii)

If F-statistic < I(0), we failed to reject the null hypothesis and revealed the absence of cointegration among the variables.

(iii)

If F-statistic > I(0) and F-statistic < I(1), this implies that the outcome is indecisive.

By incorporating the ECM in the analysis, the coefficients of short-run elasticity are ascertained:

Model 1:

$$\begin{gathered} ∆{OP}_t={\alpha }_0+{\sum }_{i=1}^n{\theta }_i∆{OP}_{t-i}+{\sum }_{i=0}^m\left[{\varphi }_1∆{CFD}_{t-i}+{\varphi }_2∆{CAD}_{t-i}+{\varphi }_3∆{EC}_{t-i}+{\varphi }_4∆{CO}_{2,t-i}+{\varphi }_5∆{Ub}_{t-i}\right]+ \\ \psi {ECT}_{t-1}+{\mu }_t \end{gathered}$$

(3)

Model 2:

$$\begin{gathered} ∆{EP}_t={\alpha }_0+{\sum }_{i=1}^n{\theta }_i∆{EP}_{t-i}+{\sum }_{i=0}^m\left[{\varphi }_1∆{CFD}_{t-i}+{\varphi }_2∆{CAD}_{t-i}+{\varphi }_3∆{EC}_{t-i}+{\varphi }_4∆{CO}_{2,t-i}+{\varphi }_5∆{Ub}_{t-i}\right]+ \\ \psi {ECT}_{t-1}+{\mu }_t \end{gathered}$$

(4)

where ${\sum }_{i=1}^n{\theta }_i$ and ${\sum }_{i=0}^m{\varphi }_i$ represent the coefficients of short-run elasticities; ECT reflects error correction term derived from a long-run association; and the coefficient of ECT (ψ) quantifies the rate of correction over time.

The ARDL methodology is centered on the fundamental premise of a symmetric connection between variables, which necessitates linear modification in both the short and long run. Ref. [80] claimed that the NARDL cointegration technique gives superior results if the relationship between exogenous variables and endogenous variable is nonlinear and exogenous variables have an asymmetrical influence on the endogenous variable. NARDL is the expansion of the conventional ARDL framework but in an asymmetric fashion. The NARDL offers several benefits over contemporary econometric methods, including its applicability with small samples and explanatory variables that are not integrated in the same order [81]. This method isolates the positive and negative effects of the endogenous variable on the endogenous variable [82]. This method permits the estimate of short- and long-run asymmetries in the variables, despite the existence of distinct assimilation/integration orders. This attribute of the NARDL methodology offers more trustworthy findings, as it aids in choosing the appropriate lag orders and lessens the risk of multicollinearity [83], further facilitating the formation of pertinent policy. In order to examine the asymmetric influence of twin deficit on energy prices in India, the current study implements the NARDL framework.

The cointegration test is derived from the following version of the NARDL framework:

Model 3:

$${OP}_t={\alpha }_0+{\beta }_1^{+}{CFD}_t^{+}+{\beta }_2^{-}{CFD}_t^{-}+{\beta }_3^{+}{CAD}_t^{+}+{\beta }_4^{-}{CAD}_t^{-}+{\beta }_5{EC}_t+{\beta }_6{CO}_{2,t}+{\beta }_7{Ub}_t+{\mu }_t$$

(5)

Model 4:

$${EP}_t={\alpha }_0+{\beta }_1^{+}{CFD}_t^{+}+{\beta }_2^{-}{CFD}_t^{-}+{\beta }_3^{+}{CAD}_t^{+}+{\beta }_4^{-}{CAD}_t^{-}+{\beta }_5{EC}_t+{\beta }_6{CO}_{2,t}+{\beta }_7{Ub}_t+{\mu }_t$$

(6)

In Equations (5) and (6), the exogenous variables are bifurcated in two distinct partial sums (i.e., positive and negative):

$${CFD}_t^{+}={\sum }_{j=1}^t∆{CFD}_t^{+}={\sum }_{j=1}^t\max \left(∆{CFD}_j,0\right)$$

(7)

$${CFD}_t^{-}={\sum }_{j=1}^t∆{CFD}_t^{-}={\sum }_{j=1}^t\min \left(∆{CFD}_j,0\right)$$

(8)

$${CAD}_t^{+}={\sum }_{j=1}^t∆{CAD}_t^{+}={\sum }_{j=1}^t\max \left(∆{CAD}_j,0\right)$$

(9)

$${CAD}_t^{-}={\sum }_{j=1}^t∆{CAD}_t^{-}={\sum }_{j=1}^t\min \left(∆{CAD}_j,0\right)$$

(10)

Following [78,80], ref. [84] changed Equations (5) and (6), and transposed them in ARDL form:

Model 3:

$$\begin{gathered} ∆{OP}_t=\alpha +\rho {OP}_{t-1}+{\omega }_1^{+}{CFD}_{t-1}^{+}+{\omega }_2^{-}{CFD}_{t-1}^{-}+{\omega }_3^{+}{CAD}_{t-1}^{+}+{\omega }_4^{-}{CAD}_{t-1}^{-}+{\omega }_5{EC}_{t-1}+{\omega }_6{CO}_{2,t-1}+ \\ {\omega }_7{Ub}_{t-1}+{\sum }_{j=1}^p{\delta }_j{∆OP}_{t-j}+{\sum }_{j=0}^q\left[{\theta }_j^{+}{CFD}_{t-j}^{+}+{\theta }_j^{-}{CFD}_{t-j}^{-}+{\pi }_j^{+}{CAD}_{t-j}^{+}+{\pi }_j^{-}{CAD}_{t-j}^{-}+{\varphi }_j{EC}_{t-j}+{\phi }_j{CO}_{2,t-j}+ \\ {\sigma }_j{Ub}_{t-j}\right]+{\mu }_t \end{gathered}$$

(11)

Model 4:

$$\begin{gathered} ∆{EP}_t=\alpha +\rho {EP}_{t-1}+{\omega }_1^{+}{CFD}_{t-1}^{+}+{\omega }_2^{-}{CFD}_{t-1}^{-}+{\omega }_3^{+}{CAD}_{t-1}^{+}+{\omega }_4^{-}{CAD}_{t-1}^{-}+{\omega }_5{EC}_{t-1}+{\omega }_6{CO}_{2,t-1}+ \\ {\omega }_7{Ub}_{t-1}+{\sum }_{j=1}^p{\delta }_j{∆EP}_{t-j}+{\sum }_{j=0}^q\left[{\theta }_j^{+}{CFD}_{t-j}^{+}+{\theta }_j^{-}{CFD}_{t-j}^{-}+{\pi }_j^{+}{CAD}_{t-j}^{+}+{\pi }_j^{-}{CAD}_{t-j}^{-}+{\varphi }_j{EC}_{t-j}+{\phi }_j{CO}_{2,t-j}+ \\ {\sigma }_j{Ub}_{t-j}\right]+{\mu }_t \end{gathered}$$

(12)

In Equations (11) and (12), p and q are the lag orders of endogenous and exogenous variables, respectively. The coefficients (${\omega }_1^{+},{\omega }_2^{-},{\omega }_3^{+},{\omega }_4^{-},{\omega }_5,{\omega }_6,{\omega }_7)$ denote the long-run nexus, whereas coefficients ${\sum }_{j=0}^{q-1}{[\theta }_j^{+},{\theta }_j^{-},{\pi }_j^{+},{\pi }_j^{-},{\varphi }_j,{{\phi }_j,\sigma }_j]$ reflect the short-term nexus among the variables. However, ${\beta }_1^{+}=\left[-\frac{{\omega }_1^{+}}{\rho }\right],{\beta }_2^{-}=\left[-\frac{{\omega }_2^{-}}{\rho }\right],{\beta }_3^{+}=\left[-\frac{{\omega }_3^{+}}{\rho }\right],{\beta }_4^{-}=\left[-\frac{{\omega }_4^{-}}{\rho }\right]$ represents the long-run nonlinear elasticities for CFD⁺, CFD⁻, CAD⁺, and CAD⁻, respectively, on OP and EP. ${\epsilon }_t$ is the white noise.

For assessing cointegration among variables in asymmetric fashion, the concurrent null hypothesis of no cointegration, $\rho ={\omega }_1^{+}={\omega }_2^{-}={\omega }_3^{+}={\omega }_4^{-}={\omega }_5={\omega }_6={\omega }_7=0$, was verified using the F-statistics. Further process is akin to ARDL model (see p. 9) [62].

To determine the short- and long-term asymmetric influences, the WALD statistics were utilized. There are three cases derived from Equations (11) and (12), such as (a) for long-run symmetry, the null hypothesis is ${\beta }_1^{+}={\beta }_2^{-}={\beta }_3^{+}={\beta }_4^{-}$, which means there is symmetry in the long-run. (b) For short-run symmetry, the null hypothesis is ${\sum }_{j=0}^{q-1}{\theta }_j^{+}={\sum }_{j=0}^{q-1}{\theta }_j^{-}={\sum }_{j=0}^{q-1}{\pi }_j^{+}={\sum }_{j=0}^{q-1}{\pi }_j^{-}$, which means that there is symmetry in the short-run (c) if both long-run and short-run symmetry hold good in case Equations (11) and (12) transfigure into standard ARDL model, as advised by [67].

Finally, Equations (11) and (12) can also obtain the dynamic multipliers for both models:

Model 3	Model 4
$m_k^{+}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial OP}_{t+j}}{{\partial CFD}_j^{+}}\right],$	$m_k^{+}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial EP}_{t+j}}{{\partial CFD}_j^{+}}\right],$
$m_k^{-}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial OP}_{t+j}}{{\partial CFD}_j^{-}}\right]$	$m_k^{-}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial EP}_{t+j}}{{\partial CFD}_j^{-}}\right]$
$m_k^{+}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial OP}_{t+j}}{{\partial CAD}_j^{+}}\right],$	$m_k^{+}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial EP}_{t+j}}{{\partial CAD}_j^{+}}\right],$
$m_k^{-}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial OP}_{t+j}}{{\partial CAD}_j^{-}}\right]$	$m_k^{-}={\displaystyle \sum _{j=0}^k}\left[\frac{{\partial EP}_{t+j}}{{\partial CAD}_j^{-}}\right]$

where, k = 0,1,2,3 and $m_k^{+}$ and $m_k^{-}$ tend towards the respective asymmetric long-run coefficients ${\beta }_1^{+}=\left[-\frac{{\omega }_1^{+}}{\rho }\right],{\beta }_2^{-}=\left[-\frac{{\omega }_2^{-}}{\rho }\right],{\beta }_3^{+}=\left[-\frac{{\omega }_3^{+}}{\rho }\right],{\beta }_4^{-}=\left[-\frac{{\omega }_4^{-}}{\rho }\right]$, as k tends to infinity. The complete analytical framework is given in Figure 4.

4. Empirical Results

This section includes the calculation of the models described in the preceding section. It starts with the model’s preliminary estimations.

4.1. Preliminary Analysis

First, the descriptive summary of each underlying variables is compiled in

Table 2. Descriptive statistics.

	OP	EP	CFD	CAD	EC	CO2	UB
Mean	5.155	5.213	5.160	−1.120	12.865	6.626	2.938
Median	5.189	5.190	5.080	−1.200	10.231	6.716	2.749
Maximum	6.554	6.309	9.183	2.317	34.060	7.873	3.955
Minimum	2.645	4.623	2.530	−4.824	2.730	5.258	2.295
Std. Dev.	0.893	0.469	1.505	1.34	9.295	0.825	0.560
Skewness	−0.701	0.438	0.391	0.050	0.819	−0.078	0.699
Kurtosis	3.824	2.257	2.712	4.089	2.492	1.744	2.174
J-B Stats.	5.621	2.807	1.475	2.540	6.134	3.402	5.499
Probability	0.062	0.246	0.478	0.281	0.046	0.182	0.064

Source: Authors’ calculation.

. The OP shows a positive mean value of 5.15, with minimum and maximum values of 2.64 and 6.55, respectively. EP emissions also reflect a positive mean value of 5.21, with minimum and maximum values of 4.62 and 6.30, respectively. Likewise, the mean value for each variable is positive, except for CAD. Further, skewness measures the degree of symmetry in the variable’s distribution, while kurtosis indicates whether the distribution is peaked or flat. Each variable exhibit normality as neither of them exceeds +1 or −1, which suggests that the distribution of the variables has zero skewness. However, except for OP and CAD, kurtosis values of the rest of the variables are less than 3 (platykurtic). Based on Jarque–Bera statistics, all the variables except EC are normally distributed as the p-values are greater than 5% significance level. In the same manner, other statistics can also be interpreted.

Second, we tested the individual integrated characteristics of the series, employing an augmented Dickey–Fuller (ADF) and Phillips–Perron (PP) unit root test by [85] and [86], respectively; the results are summarized in

Table 3. Results of unit root test.

Variables	ADF		PP		Remarks
	I(0)	I(1)	I(0)	I(1)
OP	−2.81 (0.06)	−6.47 *** (0.00)	−2.81 (0.06)	−6.47 *** (0.00)	I(1)
EP	−1.84 (0.35)	−6.76 (0.00)	−1.90 (0.32)	−6.76 *** (0.00)	I(1)
CFD	−3.04 ** (0.03)	-	−3.05 ** (0.03)	-	I(0)
CAD	−3.34 (0.01)	-	−3.32 (0.01)	-	I(0)
EC	10.37 (1.00)	−0.95 (0.76)	10.05 (1.00)	−3.77 ** (0.01)	I(1)
CO2	−1.58 (0.48)	−3.16 ** (0.02)	−1.54 (0.50)	−2.97 ** (0.04)	I(1)
Ub	−1.52 (1.00)	−4.78 *** (0.00)	−1.45 (0.54)	−4.64 (0.00)	I(1)

Note: (a) ** & *** denotes 5 and 1 percent of significance level. (b) Values in the parenthesis represent p-values. (c) I(0) & I(1) denotes integration of order 0 & 1, respectively. Source: Authors’ calculation.

. It is evident from Table 3 that OP, EP, EC, CO₂, and Ub are stationary at first difference i.e., I(1), however, CFD and CAD, as per ADF test and P-P test, are stationary at level; that is, it exhibits I(0). Therefore, unit root testing provides significant rationale for implementing ARDL estimation approaches.

4.2. Symmetric and Asymmetric ARDL Estimates

In order to identify the short-and long-run linkages between the variables, we have estimated the four different models by using ARDL (model 1 and model 2) and NARDL (model 3 and model 4) approaches. The discussion of results is partitioned into two sub-sections based on the motivation for the study.

4.2.1. The Symmetric Nexus between Twin Deficit and Energy Inflation

The study begins with the estimation of the symmetric ARDL. The first phase in estimating the ARDL model is to confirm cointegration among variables using F-test (bound test) and the results are provided in

Table 4. Results of bound test.

Models		Test Statistic	Value	Null Hypothesis: No Levels Relationship
				Sig.	I(0)	I(1)
ARDL	Model 1	F-statistic	7.57	10%	2.49	3.38
		k	5	05%	2.81	3.76
	Model 2	F-statistic	5.51	2.5%	3.11	4.13
		k	5	01%	3.5	4.63
NARDL	Model 3	F-statistic	7.07	10%	2.22	3.17
		k	7	05%	2.5	3.5
	Model 4	F-statistic	4.94	2.5%	2.76	3.81
		k	7	01%	3.07	4.23

Source: Authors’ calculation.

. The calculated F-statistic 7.57 for model 1and 5.51 for model 2 are greater than the upper critical bound value at 5% and 10% significance level. It indicates that there is a cointegration among variables in both the models.

In the long-run, as shown in

Table 5. Outcomes of ARDL and NARDL approach.

Variables	ARDL				NARDL
	Model 1 (1, 0, 0, 0, 0, 0)		Model 2 (1, 0, 0, 0, 0, 0)		Model 3 (1, 0, 0, 1, 0, 0, 0, 0)		Model 4 (1, 2, 0, 0, 0, 1, 2, 1)
	Coef.	p-Value	Coef.	p-Value	Coef.	p-Value	Coef.	p-Value
Panel A: Short-run estimates
ΔCFD	0.08 *	0.00	0.07 ***	0.06	−	−	−	−
ΔCFD+	−	−	−	−	−0.06	0.11	0.11 **	0.04
ΔCFD+−1					−	−	0.02	0.39
ΔCFD−	−	−	−	−	−0.08	0.10	0.09 **	0.05
ΔCAD	0.15 *	0.00	0.19 *	0.00	−	−	−	−
ΔCAD+	−	−	−	−	0.10 **	0.01	0.08 ***	0.08
ΔCAD+−1	−	−	−	−	−0.15 *	0.00	−	−
ΔCAD−	−	−	−	−	−0.23 *	0.00	−0.06	0.18
ΔEC	−0.04 **	0.02	−0.06 **	0.01	−0.05 *	0.00	−0.07 *	0.00
ΔEC−1	−	−	−	−	−	−	0.14	0.27
ΔCO2	1.99 **	0.05	3.42 **	0.01	2.20 *	0.03	1.43	0.12
ΔCO2,−1	−	−	−	−	−	−	5.81 *	0.00
ΔUb	0.61 ***	0.07	0.55	0.24	0.69 **	0.03	0.39	0.09
ΔUb−1	−	−	−	−	−	−	0.83 **	0.05
Trend	0.17 *	0.00	0.27 *	0.00	0.15 *	0.01	−0.13 *	0.00
ECT (−1)	−0.34 *	0.00	−0.54 *	0.00	−0.46 *	0.00	−0.42 **	0.01
Panel B: Long-run estimates
CFD	0.23 **	0.01	0.14 **	0.04	−	−	−	−
CFD+	−	−	−	−	0.14 **	0.04	0.25 **	0.02
CFD−	−	−	−	−	−0.19	0.10	−0.22	0.16
CAD	0.43 *	0.00	0.35 *	0.00	−	−	−	−
CAD+	−	−	−	−	0.33 *	0.00	0.19 ***	0.06
CAD−	−	−	−	−	0.49 *	0.00	0.16 ***	0.09
EC	−0.13 **	0.02	−0.11 *	0.00	−0.12 *	0.00	−0.17 *	0.00
CO2	5.70 *	0.00	6.28 *	0.00	4.69 *	0.00	8.55 *	0.00
Ub	1.78 *	0.00	1.02 *	0.00	1.48 **	0.05	0.19 ***	0.09
Trend	0.48 *	0.00	0.49 *	0.00	0.33 *	0.00	−0.30 **	0.01
Panel C: Diagnostic tests
Adj R2	0.78		0.81		0.81		0.88
χ2SC	2.18	0.11	0.33	0.80	−1.87	0.13	−0.25 **	0.02
χ2HET	1.77	0.11	1.66	0.14	0.79	0.63	0.22	0.06
χ2NOR	0.60	0.73	0.35	0.65	0.93	0.62	−	−
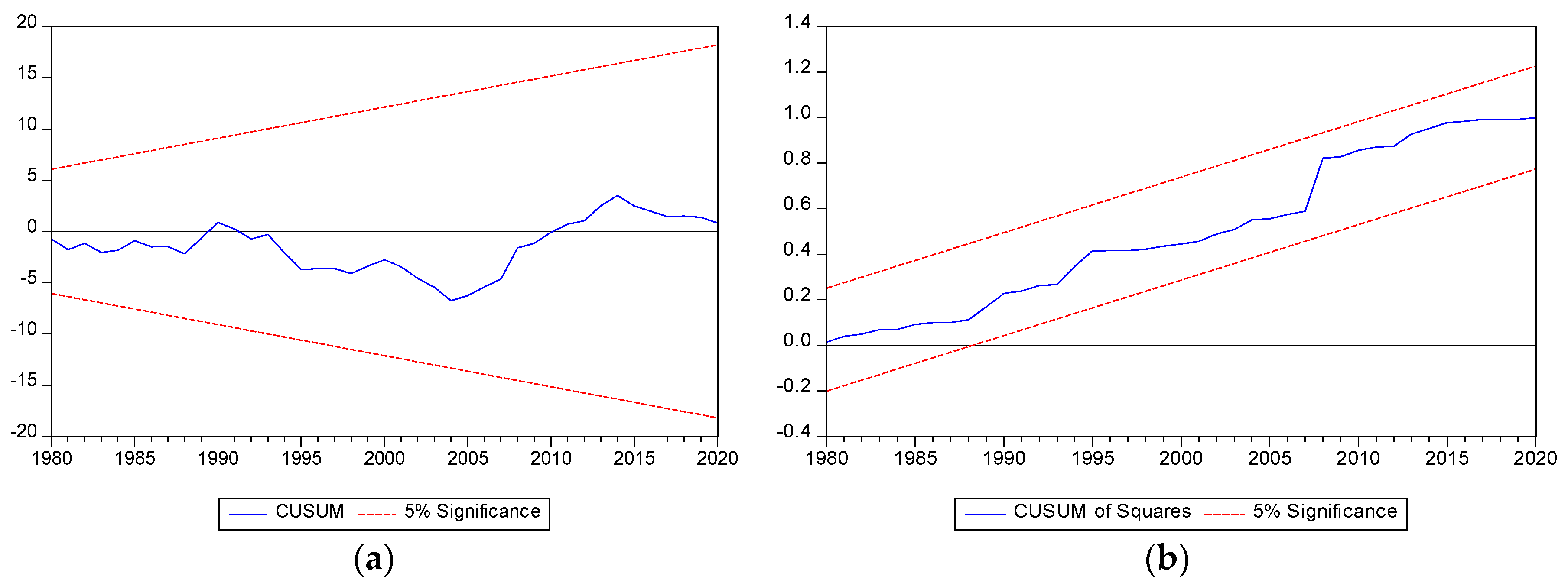
CUSUM	Stable		Stable		Stable		Stable
CUSUMQ	Stable		Stable		Stable		Stable
WLR CFD	−	−	−	−	8.12 *	0.00	20.17 *	0.00
WSR CFD	−	−	−	−	0.69	0.45	1.55	0.76
WLR CAD	−	−	−	−	6.48 **	0.04	5.19 ***	0.08
WSR CAD	−	−	−	−	0.31	0.23	−1.79 ***	0.09

Note: (a) the (+) and (−) superscripts are used for positive and negative components, respectively. (b) χ²_SC; χ²_NOR, and χ²_HET denote Breusch–Godfrey serial correlation LM Test, Jarque–Bera test for normality, and Breusch–Pagan–Godfrey test for heteroscedasticity, respectively. (c) CUSUM and CUSUMQ stand for cumulative sum and cumulative sum of square. (d) *, **, and *** represent 1, 5, and 10% level of significance, respectively. (e) W_LR—WALD Test for Long-run; W_SR—WALD Test for Short-run. (e) ECT denotes Error Correction Term. Source: Authors’ calculation.

(see Panel B), there exists a positive relationship between twin-deficit and energy inflation. More specifically, in model 1, the response of OP due to the change in CFD is positive and significant. It implies that 1% upsurge in CFD leads to rise in OP by 0.23%. Similarly, CAD also exerts a positive and significant impact on OP, i.e., 1% upsurge in CAD leads to rise in OP by 0.43%.

Likewise, in model 2, CFD and CAD have a positive and significant impact on EP. In other words, a 1% rise in CFD and CAD leads to strengthening the EP by 14% and 35%, respectively. It is noteworthy that the impact of CFD and CAD on OP is prominent as compared to EP.

Further, we found that EC has long-run negative elasticity with respect to OP and EP. In specific terms, a 1% increase in EC leads to a reduction in OP by 0.13% and EP by 0.11%. As far as urbanization is concerned, Ub also has long-run positive elasticity with respect to OP and EP. In other words, a 1% increment in Ub strengthens the OP by 1.78% and the EP by 1.02%. Furthermore, we found that CO₂ emissions exert positive influence on both the inflation, i.e., OP and EP. We concluded that 1% upsurge in CO₂ emissions stimulate the OP by 5.70% and EP by 6.28% on an average. The graphical representation of ARDL long-run results of Model 1 and Model 2 are provided in Figure 5.

The outcomes of short-run, as presented in Table 5 (see Panel A), are akin to long-run results for both the models in terms of sign of the coefficients. For instance, except for EC, remaining variables like CFD, CAD, CO₂, and Ub have positive influence on OP and EP. Lastly, the ECT coefficient signifies the rate at which the OP and EP adjust to long-run equilibrium due to variations in their covariates. Following a divergence from the long run in the prior period, convergence to the steady-state is adjusted by 34% for model 1 and 54% in model 2.

In a nutshell, we found that there exists a negative relationship between twin-deficit and energy inflation in symmetric model. However, numerous studies have claimed that CFD and CAD are asymmetric in nature. Therefore, the symmetric (linear ARDL model) relationship may not be appropriate, and a more complex (asymmetric) relationship should be used, as done in the next section.

4.2.2. The Asymmetric Nexus between Twin Deficit and Energy Inflation

To execute the asymmetric ARDL model, the same steps used in the linear ARDL model were followed. The results of Table 4 showed that the F-statistic 7.07 for model 3 and 4.94 for model 4 are above the upper critical values, thus confirming the evidence of nonlinear cointegration for both the models. Having established evidence of nonlinear cointegration in both the models, the study next proceeded to test for symmetry in both the short run and the long run, which is presented in Table 5 (see Panel C). The WALD test was employed to scrutinize the short-run (W_SR) and long-run (W_LR) asymmetries between the positive and negative partial sum of CFD and CAD for validating the NARDL model. For model 3 and 4, the results only found evidence of long-run asymmetries (W_LR) between the positive and negative partial sum of CFD and CAD.

Moreover, we used the general to specific method in a similar fashion to Sharma and Mittal (2019, 2021) [69,71] to estimate the short-run and long-run relationships from the dynamic models. However, the results of Table 5 suggest long-run asymmetries among the variables in both the models, and therefore we have only explained the long-run results of NARDL model. From model 3 and 4 (see Panel B), we inferred that long-run estimated coefficients of CFD⁺ (expansionary fiscal policy) have positive and significant impact on the OP and EP, whereas CFD⁻ (contractionary fiscal policy) fails to influence OP and EP. It implies that if positive shock is given to CFD by 1%, OP and EP will be increased by 0.14% and 0.25%, respectively. Similarly, in model 3 and 4, the long-run estimated coefficients of CAD⁺ (imports over exports) and CAD⁻ (exports over imports) have a positive effect on the OP and EP. It implies that if positive and negative shocks are given to CAD by 1%, OP will be upsurged by 0.33% and 0.49%, respectively, and EP by 0.14% and 0.19%, respectively. These results revealed that twin deficits are asymmetric in nature and have a positive impact on energy inflation in India. The graphical representation of NARDL long-run results of Model 3 and Model 4 is provided in Figure 6.

Moving towards EC, the responses of OP and EP due to change in EC are negative. We infer that 1% rise in EC leads to weakening the OP by 0.12% and EP by 0.17%. Further, the predicted coefficients of CO₂ and Ub have positive and significant impact on OP. More precisely, a 1% rise in CO₂ and Ub lead to boost the OP by 4.69% and 1.48%, respectively. Lastly, the coefficients of ECT are negative and significant which reinforces the cointegrating relationship between the underlying variables. Here, the ECT coefficients demonstrate that the rate of correction toward long-run equilibrium are 46% and 42% per annum.

In a nutshell, the study concluded that the results of asymmetric ARDL model are more or less similar to symmetric ARDL model in terms of signs of the parameters. However, the results of an asymmetric model are more robust and reliable in designing the economic policies in two ways. First, we found that the response of energy inflation due to expansionary fiscal policy (increment in CFD) and contractionary fiscal policy (decline in CFD) is diverse in terms of size of the coefficient. Second, we also found the distinct impact of increase and decrease in CAD on energy inflation.

4.3. Diagnostic Checks/Post Estimation Tests and Parameters Stability

Furthermore, the study performed a few diagnostic tests to evaluate the models’ viability (see Panel-C in Table 5). The values of χ²_SC and χ²_HET show the absence of autocorrelation and heteroscedasticity, respectively, in all the four models. In addition, χ²_NOR shows that the error term is following a white noise process for all the models. Figure 7a,b depict the plots of CUSUM and CUSUMQ tests for model 1, Figure 8a,b for model 2, Figure 9a,b for model 3, and Figure 10a,b for model 4, and all the graphs lie within the conventional critical limit, indicating that all the models are stable. It implies that the predicted models are well-specified and meet the residual normality conditions with no variable omissions.

Cumulative Dynamic Multipliers

The study has analyzed the compelling effects of CFD and CAD on OP and EP separately, using cumulative dynamic multipliers. Figure 11a,b illustrate the sequence of change in OP to its revised equilibrium as a result of positive and negative shocks to the CFD and CAD. In each figure, the continued black line shows positive shocks, the dotted black line exhibits negative shocks, and the dark red dotted line represents the asymmetry plot. In Figure 11a, it can be asserted that the dynamic effects of CFD+ and CFD- on OP are diametrically opposed, indicating the existence of fiscal deficit asymmetries. Figure 11b also shows that the impact of CAD- is much higher than the CAD+ on OP, thus confirming the evidence of current account deficit asymmetries. Further, Figure 12a reveals that the positive inclination of the asymmetric/difference line implies that CFD boosted the EP. At the beginning, the gap between positive and negative change in IR is small but it widens over the horizon. Figure 12b shows that the impact of CAD+ is higher than the CAD- on EP, thus confirming the evidence of current account deficit asymmetries. The dynamic multiplier results are consistent with the Table 5 results of NARDL models.

5. Discussion of the Results

The empirical findings provide some significant evidence about the connection between the twin deficit and energy inflation in India. The response of oil prices and electricity prices due to acceleration in fiscal deficit is positive in the long run. This implies that the fiscal deficit has an antagonistic impact on the Indian economy by reinforcing oil prices and electricity prices. The coherent reason is that the fiscal deficit induces the economy to endure cost–push inflation. Since 1991, the government has discontinued the practice of printing currency notes for financing the fiscal deficit, and therefore the government is a prominent participant in the market for both internal and external borrowing, which drives up interest rates. Consequently, upward pressure on interest rates stimulates the cost of production of some imperative commodities like oil and electricity, which is shifted to the consumers, resulting in a price elevation of the commodities. Another logical justification provided by [65] and [66] is that when the government pursues an expansionary fiscal policy (i.e., spending exceeds revenue), it would elevate oil and electricity prices to cover its expenditures. During COVID-19, the Indian government did not immediately transmit the advantages of declining crude oil prices to consumers. In the second quarter of 2020, Brent crude oil prices plummeted to an all-time low of $16 per barrel, while domestic oil prices and diesel prices remained steady. During and before the COVID-19 outbreak, the Indian government’s fiscal situation was abysmal. The finance ministry intended to lower the fiscal deficit to 3.5% of GDP in accordance with FRBM recommendations. With the economy sliding to a virtual halt as a result of the coronavirus outbreak, this aim was failed by a huge margin and exceeded by 7% of GDP, particularly due to the decline in revenues and the increase in government expenditure on stimulus initiatives. Therefore, the government will endeavor to compensate for the revenue gap by boosting the tariff rate on oil, thus resulting in a higher price level.

In the long run, the growing current account deficit also makes oil and electricity prices go up. These results are akin to the study of [65], which also claimed that external sector imbalance boosts energy prices in the economy. The justification of this outcome is that an increment in the current account deficit spurs the demand for foreign currency, ending in a depreciation of the domestic currency, i.e., Indian rupee. With a depreciation of the Indian rupee, imports become more exorbitant; consequently, for a nation such as India, which imports expensive products and commodities such as crude oil, semiconductors, and electronic goods, the burden on the exchequer is increasing, resulting in an increase in broad-based inflation in India. However, some of the Indian studies [87,88] support the Marshal–Lerner condition in India—that the sum of the price elasticity of demand for exports and imports is greater than one (algebraically). This implies that the devaluation of domestic currency will enhance the balance of payments by making exports cheaper and imports dearer. However, because India is an oil-dependent economy, demand for crude oil imports is highly inelastic, resulting in an increase in import prices and thus exerting upward pressure on the inflation rate.

In contrast, the energy consumption serves as a helping hand for the economy by mitigating the prices of oil and electricity in the long run. The outcome was also found in previous studies that also found evidence of a causal nexus between energy consumption and energy prices [89,90,91]. According to the Reserve Bank of India (RBI), India’s renewable energy (RE) market has played a crucial part in the country’s shift from a power deficiency to a power abundance over the last few years, having substantial influence over the mechanisms that define electricity prices in India. In accordance with the Ministry of Power, the percentage of REs in total capacity installed more than triple between the end of March 2015 and the end of August 2021, from 11.8% to 37.9%. The decline in the cost of REs production has increased its competitive edge over other sources of energy. Albeit without subsidies, RE production has become more economical than that from thermal and traditional sources [92]. As reported by the International Renewable Energy Agency (IRENA), RE generating technologies have emerged as the least expensive choice for the expansion of new capacity in almost all regions of the globe [93]. Therefore, the consumers are substituting oil consumption with renewable sources of energy, which will reduce the demand for crude oil, which in turn reduces the OP in the long run. As the Indian economy is more on RE for generating electricity, this will reduce the EP in the long run.

Similar to [94], which hypothesized that rising UB and rising income levels are to blame for an increase in the demand for electrical equipment, i.e., an increase in the demand for electricity in the residential sector, our findings support the hypothesis. The rising demand for construction materials, logistics, capital goods, and infrastructure is propelling industrial electricity demand. Raised automation and the move to groundwater irrigation throughout the nation are driving the need for pumping equipment and tractors in the agricultural sector, which has increased the demand for oil and electricity, hence enhancing the OP and EP. Lastly, CO₂ also has a long-run positive impact on energy inflation in India. The valid reason is that an increase in urban energy consumption raises demand for oil and electricity, which boosts the OP and EP.

6. Conclusions, Policy Implications, Limitations, and Future Research

The primary contribution of this paper is an examination of linkage amidst twin deficits (fiscal deficit and current account deficit) and energy inflation (oil prices and electricity prices) in the presence of urbanization, climate change, and renewable energy usage in India. Compared to prior research, our model formulation and methodology with unique empirical findings are the most unique aspects. This study employed yearly time series data from 1971 to 2021, and all variable data were gathered from reliable sources. This study estimated two empirical models. In Model 1, electricity prices were used to encapsulate the concept of energy inflation, whereas in Model 2, oil prices were used to gauge energy inflation, with twin deficit (fiscal deficit and current account deficit), urbanization, climate change, and renewable energy consumption serving as independent variables in the empirical models. Using the ARDL and NARDL models, the study explored the nexus between energy inflation and its determinants in a linear and nonlinear paradigm.

The outcomes of the study are summarized as follows. First, as per the ADF test and P-P test, OP, EP, EC, CO₂, and Ub are stationary at first difference i.e., I(1), however, CFD and CAD are stationary at level; that is, it exhibits I(0). Second, F-statistic confirms the cointegration among variables in both the models. Third, the ARDL estimates revealed that the response of OP due to the change in CFD and CAD is positive and significant. Likewise, CFD and CAD have a positive and significant impact on EP. However, the response of OP due to changes in twin deficit is more prominent as compared to EP. Fourth, CO₂ and Ub also strengthen the OP and EP. In contrast to other variables, EC exerts downward pressure on energy inflation by declining the OP and EP. Fifth, the WALD test finds evidence of long-run asymmetries between the positive and negative partial sum of CFD and CAD. Sixth, the NARDL estimates revealed that long-run estimated coefficients of CFD⁺ (expansionary fiscal policy) have a positive and significant impact on the OP and EP, whereas CFD⁻ (contractionary fiscal policy) fails to influence OP and EP. Similarly, long-run estimated coefficients of CAD⁺ (imports over exports) and CAD⁻ (exports over imports) have a positive effect on the OP and EP. Lastly, the dynamic multiplier results are consistent with the results of NARDL models.

6.1. Policy Implications

• According to the findings indicated above, the following policy recommendations are proposed by this study.
• First, in order to curtail the favorable effect of the current account deficit and limit its influence on energy prices, authorities should implement policies to limit import payments and stimulate export revenues.
• Second, authorities should broaden the tax base to raise government revenue and stimulate private sector investment in infrastructure projects to mitigate the effect of fiscal deficit on energy prices.
• Third, India’s energy consumption grew dramatically as a result of climate change, exerting upward pressure on prices; thus, to curb energy inflation, the Indian government should execute various initiatives to augment the green environment and reduce energy demand.
• Fourth, in order to curb energy inflation, the usage of renewable energy sources should be fostered.
• Fifth, India has to pursue alternative avenues to purchase oil and gas from the international market at a lower price. Sixth, India needs to stimulate well-planned urbanization as a means of bringing the nation’s energy demand under control.
• Finally, to regulate energy inflation, the RBI also prevents a significant depreciation of the currency, which might exacerbate core inflation.

6.2. Limitations and Future Research

We employed a single threshold NARDL model to capture asymmetric impact of twin deficit on energy prices. However, the NARDL model fails to examine the impact of minor and major fluctuations in the regressors on the regressand. Therefore, in order to avoid this issue, researchers can employ multiple threshold NARDL models (MTNARDL).

In the present study we have used quantitative variables such as renewable energy consumption, urbanization, and carbon emission to examine the nexus between twin deficit and energy inflation in India. For providing more practical implications, researchers can use some qualitative variables such as political instability, institutional quality, corruption, recession, etc.