First-Order Linear Active Disturbance Rejection Control for Turbofan Engines
Abstract
:1. Introduction
2. Methodology
2.1. Continuous-Time FOLADRC
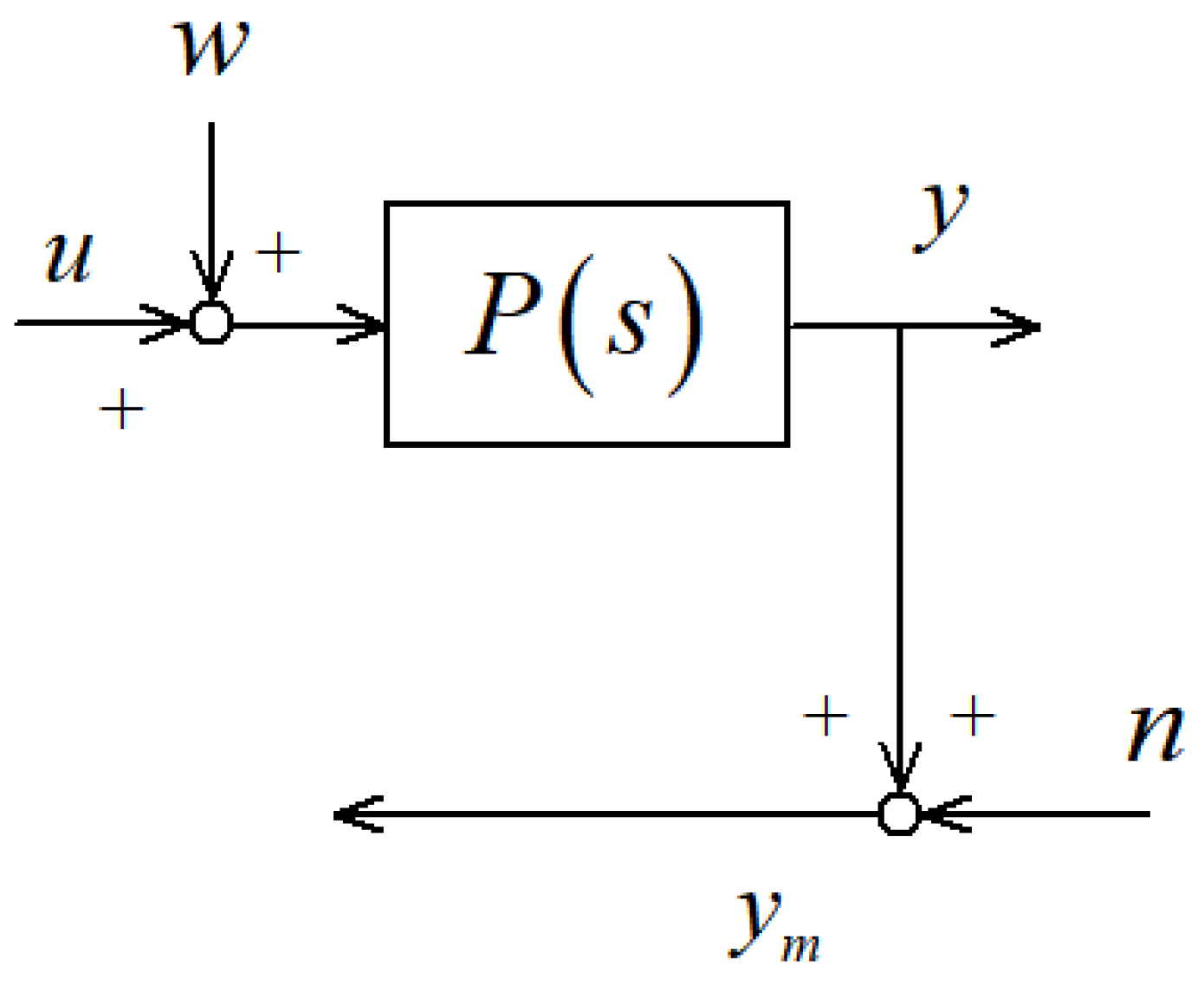
2.2. Transfer Functions and Block Diagram
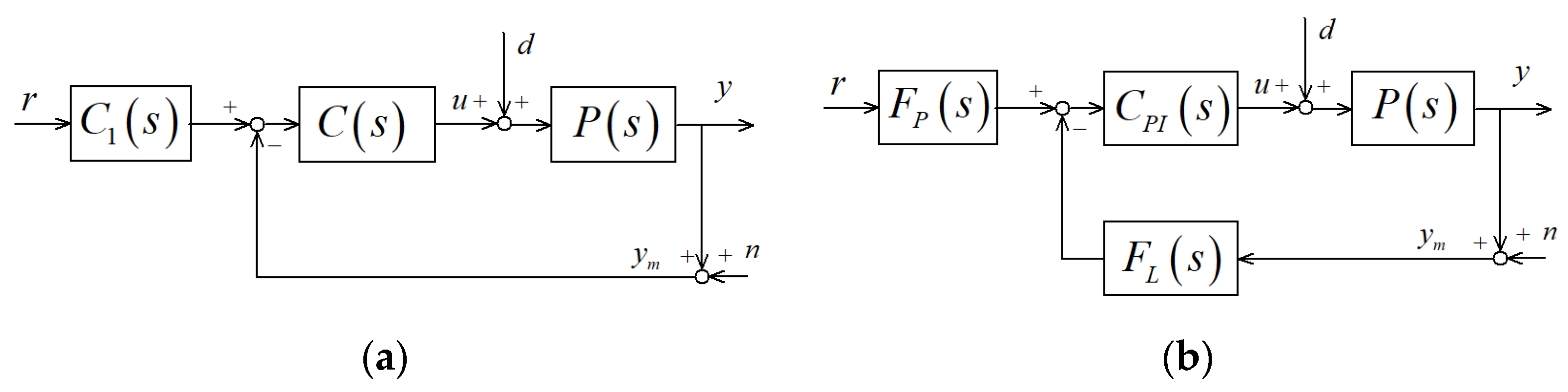
2.3. Comparison between FOLADRC and PI Control
- (C1) FOLADRC can control the plants controlled by the PI controller.
- (C2) Pre-filter can attenuate the overshoot.
- (C3) Low-pass filter is helpful to reject the high-frequency measurement noise.
2.4. Parameters Tuning
3. Fan Speed Control Simulations
3.1. Models and Parameters
3.2. Bode Diagrams, Stability, and Phase Margins
3.3. Transient Performance
4. Discussion
- (1)
- To lessen the number of controllers and simplify the control system. With the knowledge that one FOLADRC controller can replace several PI controllers, it is unnecessary to design a controller for each flight condition. Instead, the flight conditions can be divided into several sets, and one common FOLADRC controller is designed for the flight conditions in each set. In this way, the number of the controllers is lessened, the controller switching/tuning becomes infrequent, and the control system is simplified. Extremely, if one FOLADRC controller can be used for all flight conditions, the controller switching/tuning algorithm becomes unnecessary.
- (2)
- To simplify the stability analysis of the turbofan-engine control system. As discussed in Section 1, when many PI controllers work in the adaptive control framework, stability analysis is a time-consuming work. The more the controllers, the more complicated is the stability analysis. Thus, to replace several PI controllers with one FOLADRC controller can simplify the stability analysis.
- (3)
- To simplify the modeling of a turbofan engine. The number of flight conditions in the entire flight envelope may be lessened because several flight conditions that share a common FOLADRC controller can be merged to one. By lessening the number of flight conditions, the money and time on establishing a mathematical model for the engines can be saved.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Alt | Altitude |
| EPR | Engine Pressure Ratio |
| HPC | High Pressure Compressor |
| HPT | High Pressure Turbine |
| LPC | Low Pressure Compressor |
| PLA | Power Lever Angle |
| PS30 | HPC outlet static pressure |
| T48 | HPT outlet total temperature |
| Nf | Fan speed |
| Nc | Core speed |
| WF | Fuel flow rate |
| ∆Nf | Incremental fan speed |
| ∆Nc | Incremental core speed |
| ∆WF | Incremental fuel flow rate |
| PI | Proportional-integral |
| PID | Proportional-integral-derivative |
| LQR | Linear quadratic regulator |
| ADRC | Active disturbance rejection control |
| LADRC | Linear active disturbance rejection control |
| FOLADRC | First-order linear active disturbance rejection control |
| SOLADRC | Second-order linear active disturbance rejection control |
| ESO | Extended state observer |
| PM | Phase margin |
| MAPSS | Modular aviation propulsion system simulation |
| CMAPSS-1 | Civilian modular aviation propulsion system simulation |
Appendix A
| FC01 | FC05 | FC06 | FC07 | FC08 | FC09 | |
|---|---|---|---|---|---|---|
| Alt (ft) | 0.00 | 10,000.00 | 20,000.00 | 25,000.00 | 35,000.00 | 42,000.00 |
| Mach | 0.00 | 0.25 | 0.70 | 0.62 | 0.84 | 0.84 |
| PLA (°) | 100.00 | 100.00 | 100.00 | 60.00 | 100.00 | 100.00 |
| (pps) | 6.84 | 4.66 | 3.86 | 1.67 | 2.12 | 1.52 |
| (r/min) | 2388.00 | 2319.00 | 2324.00 | 1915.00 | 2223.00 | 2212.00 |
| (r/min) | 9051.00 | 8774.00 | 8719.00 | 8006.00 | 8346.00 | 8317.00 |
| EPR | 1.30 | 1.26 | 1.08 | 0.94 | 1.02 | 1.02 |
| (°R) | 2072.00 | 1947.00 | 1909.00 | 1534.00 | 1750.00 | 1744.00 |
| (psia) | 522.13 | 371.76 | 206.76 | 163.94 | 183.10 | 130.51 |
| LPC R-Line | 1.64 | 1.63 | 2.31 | 1.70 | 1.52 | 1.54 |
| HPC R-Line | 1.95 | 1.96 | 1.98 | 2.03 | 2.00 | 2.03 |
| (lbf) | 86,636.00 | 45,830.00 | 25,774.00 | 11,475.00 | 13,552.00 | 9674.00 |
| Matrices | Transfer Functions | |
|---|---|---|
| FC01 | ||
| FC02 | ||
| FC03 | ||
| FC04 | ||
| FC05 | ||
| FC06 | ||
| FC07 | ||
| FC08 | ||
| FC09 | ||
| FC10 | ||
| FC11 | ||
| FC12 | ||
| FC13 | ||
| FC14 |
References
- Jaw, L.C.; Mattingnly, J.D. Aircraft Engine Controls: Design, System Analysis, and Health Monitoring; AIAA: Reston, VA, USA, 2009. [Google Scholar]
- Richter, H. Advanced Control of Turbofan Engines; Springer: New York, NY, USA, 2011. [Google Scholar]
- Miklosovic, R.; Gao, Z. A dynamic decoupling method for controlling high performance turbofan engines. IFAC Proc. Vol. 2005, 38, 532–537. [Google Scholar] [CrossRef] [Green Version]
- Yao, H. Full Authority Digital Electronic Control System for Aero-Engine; China Aviation Publishing & Media Co., Ltd.: Beijing, China, 2014. (In Chinese) [Google Scholar]
- Han, J. Auto-disturbance-rejection controller and its applications. Control Decis. 1998, 13, 19–23. (In Chinese) [Google Scholar]
- Han, J. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W. Active disturbance rejection control: Methodology and theoretical analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Feng, H.; Guo, B.-Z. Active disturbance rejection control: Old and new results. Annu. Rev. Control 2017, 44, 238–248. [Google Scholar] [CrossRef]
- Zheng, Q.; Gao, Z. Active disturbance rejection control: Some recent experimental and industrial case studies. Control Theory Technol. 2018, 16, 301–312. [Google Scholar] [CrossRef]
- Gao, Z. Scaling and bandwidth parameterization based controller tuning. In Proceedings of the American Control Conference, Denver, CO, USA, 4–6 June 2003; pp. 4989–4996. [Google Scholar]
- Yang, R.; Sun, M.; Chen, Z. Active disturbance rejection control on first-order plant. J. Syst. Eng. Electron. 2009, 22, 95–102. [Google Scholar] [CrossRef]
- Liu, Y.; Nie, L.; Zhang, J.; Yang, X. Research on Pressure Control Algorithm of a Flow Adjustable Gas Generator Based on linear Active Disturbance Rejection Control. J. Propuls. Technol. 2015, 36, 1768–1773. (In Chinese) [Google Scholar]
- Sun, L.; Hua, Q.; Li, D.; Pan, L.; Xue, Y.L.; Lee, K.Y. Direct energy balance based active disturbance rejection control for coal-fired power plant. ISA Trans. 2017, 70, 486–493. [Google Scholar] [PubMed]
- He, T.; Wu, Z.; Shi, R.; Li, D.; Sun, L.; Wang, L.; Zheng, S. Maximum Sensitivity-Constrained Data-Driven Active Disturbance Rejection Control with Application to Airflow Control in Power Plant. Energies 2019, 12, 231. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Xue, Y.; Li, D.; Wu, Z.; He, T. On the Flexible Operation of Supercritical Circulating Fluidized Bed: Burning Carbon Based Decentralized Active Disturbance Rejection Control. Energies 2019, 12, 1132. [Google Scholar] [CrossRef] [Green Version]
- Shi, G.; Wu, Z.; Guo, J.; Li, D.; Ding, Y. Superheated Steam Temperature Control Based on a Hybrid Active Disturbance Rejection Control. Energies 2020, 13, 1757. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Li, D.; Xue, Y.; Sun, L.M.; He, T.; Zheng, S. Modified active disturbance rejection control for fluidized bed combustor. ISA Trans. 2020, 102, 135–153. [Google Scholar] [CrossRef] [PubMed]
- Chiumeo, R.; Raggini, D.; Veroni, A.; Clerici, A. Comparative Analysis of PI and ADRC Control through CHIL Real Time Simulations of a DC-DC DAB into a Multi-Terminal MVDC/LVDC Distribution Network. Energies 2022, 15, 7631. [Google Scholar] [CrossRef]
- Wu, Z.; Gao, Z.; Li, D.; Chen, Y.; Liu, Y. On transitioning from PID to ADRC in thermal power plants. Control Theory Technol. 2021, 19, 3–18. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, J.; Gao, Y. Order and parameter selections for active disturbance rejection controller. Control Theory Appl. 2014, 31, 1480–1485. (In Chinese) [Google Scholar]
- Jin, H.; Chen, Y.; Lan, W. Replacing PI control with first-order linear ADRC. In Proceedings of the IEEE 8th Data Driven Control and Learning Systems Conference (DDCLS), Dali, China, 24–27 May 2019; pp. 1097–1101. [Google Scholar]
- Zhong, S.; Huang, Y.; Guo, L. A parameter formula connecting PID and ADRC. Sci. China Inf. Sci. 2020, 63, 192203. [Google Scholar] [CrossRef]
- Jin, H.; Song, J.; Lan, W.; Gao, Z. On the characteristics of ADRC: A PID interpretation. Sci. China Inf. Sci. 2020, 63, 209201. [Google Scholar]
- Liu, Y.; Frederick, D.K.; DeCastro, J.A.; Litt, J.S.; Chan, W.W. Users Guide for the Commercial Modular Aero-Propulsion System Simulation (C-MAPSS) (Ver. 2.0). NASA Technical Manuscript 2012. Available online: https://ntrs.nasa.gov/api/citations/20120003211/downloads/20120003211.pdf (accessed on 2 February 2023).
- Franklin, G.F.; Powell, J.D.; Emami-Naeini, A. Feedback Control of Dynamic Systems, 8th ed.; Publishing House of Electronics Industry: Beijing, China, 2021. [Google Scholar]

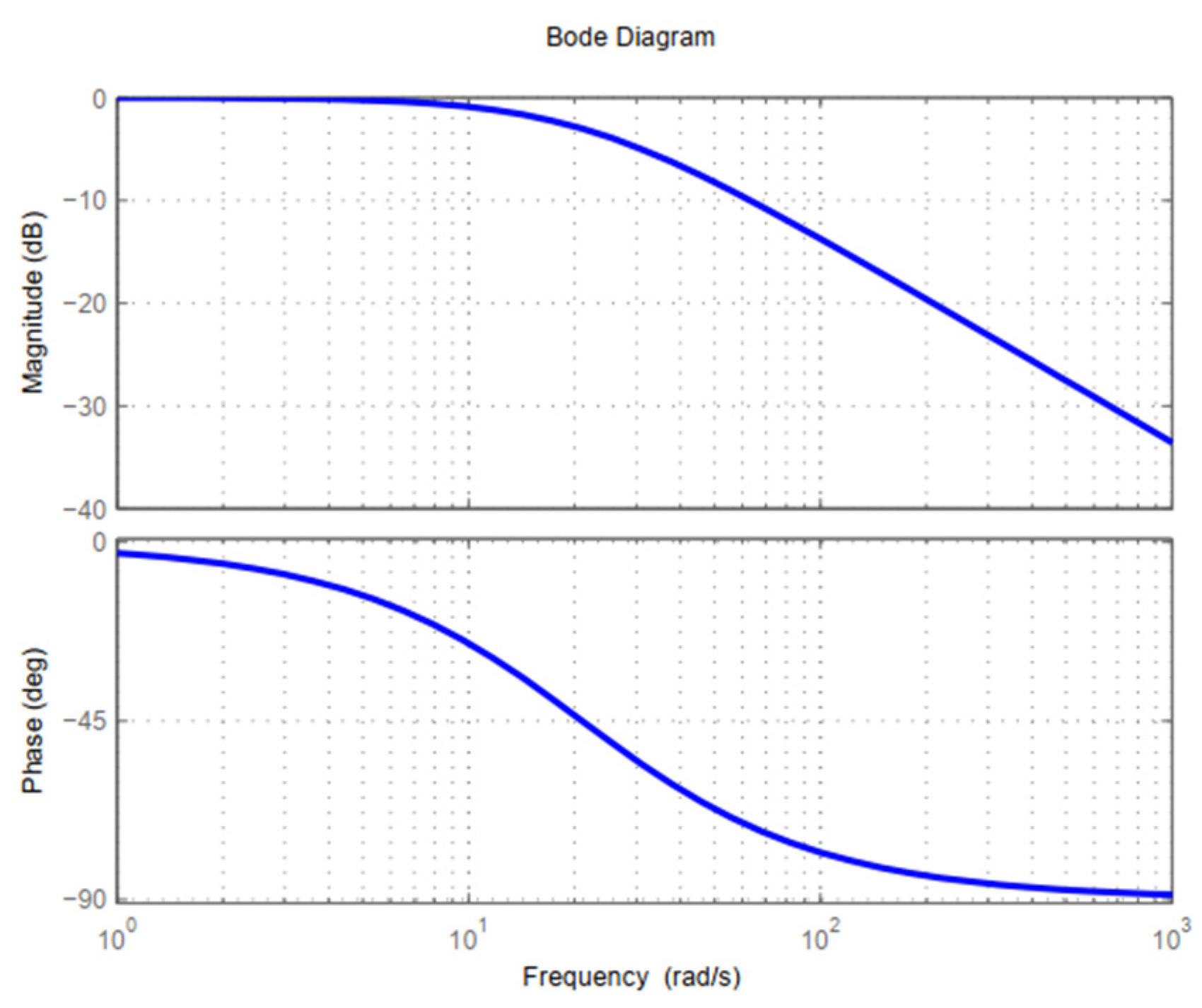
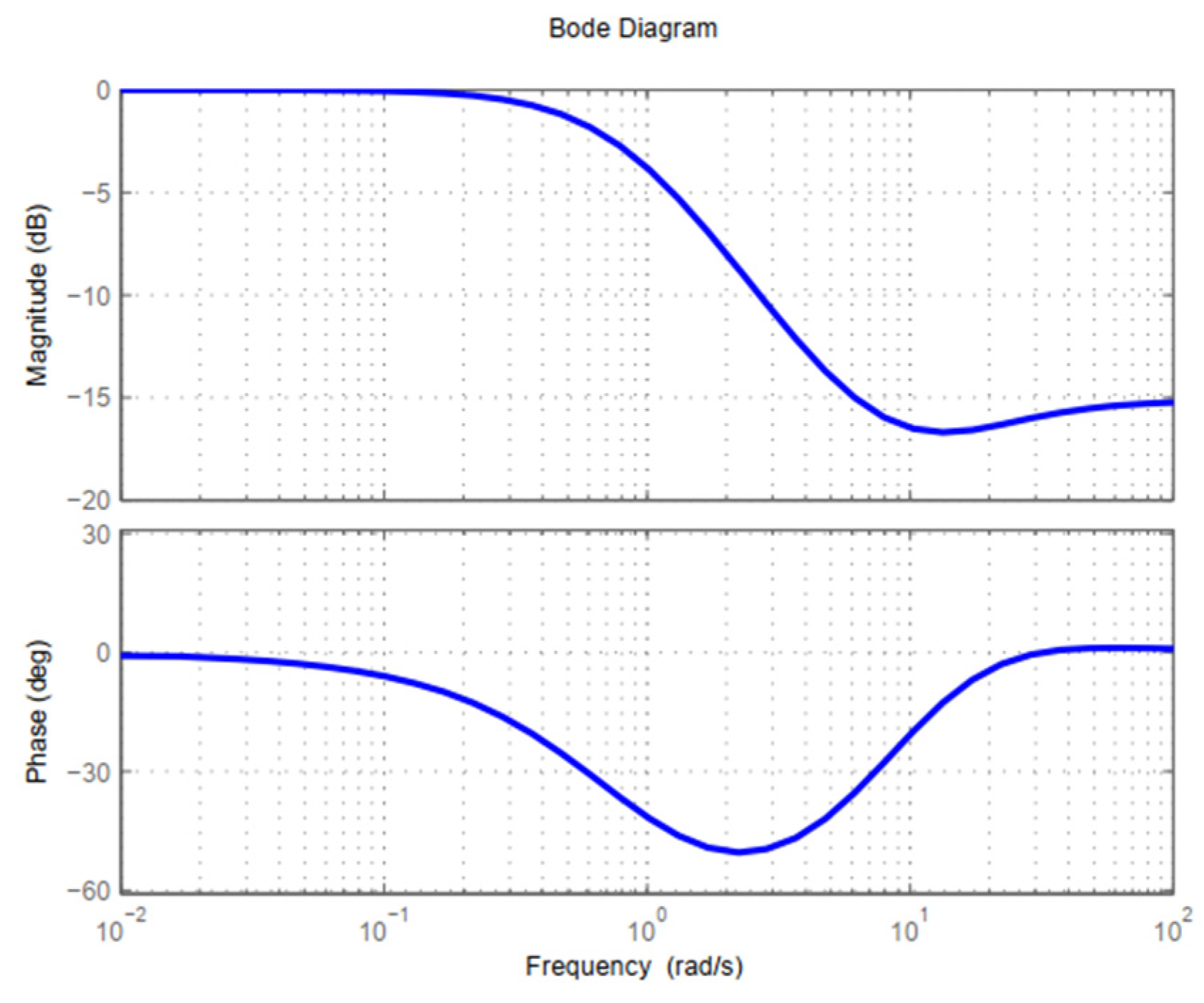
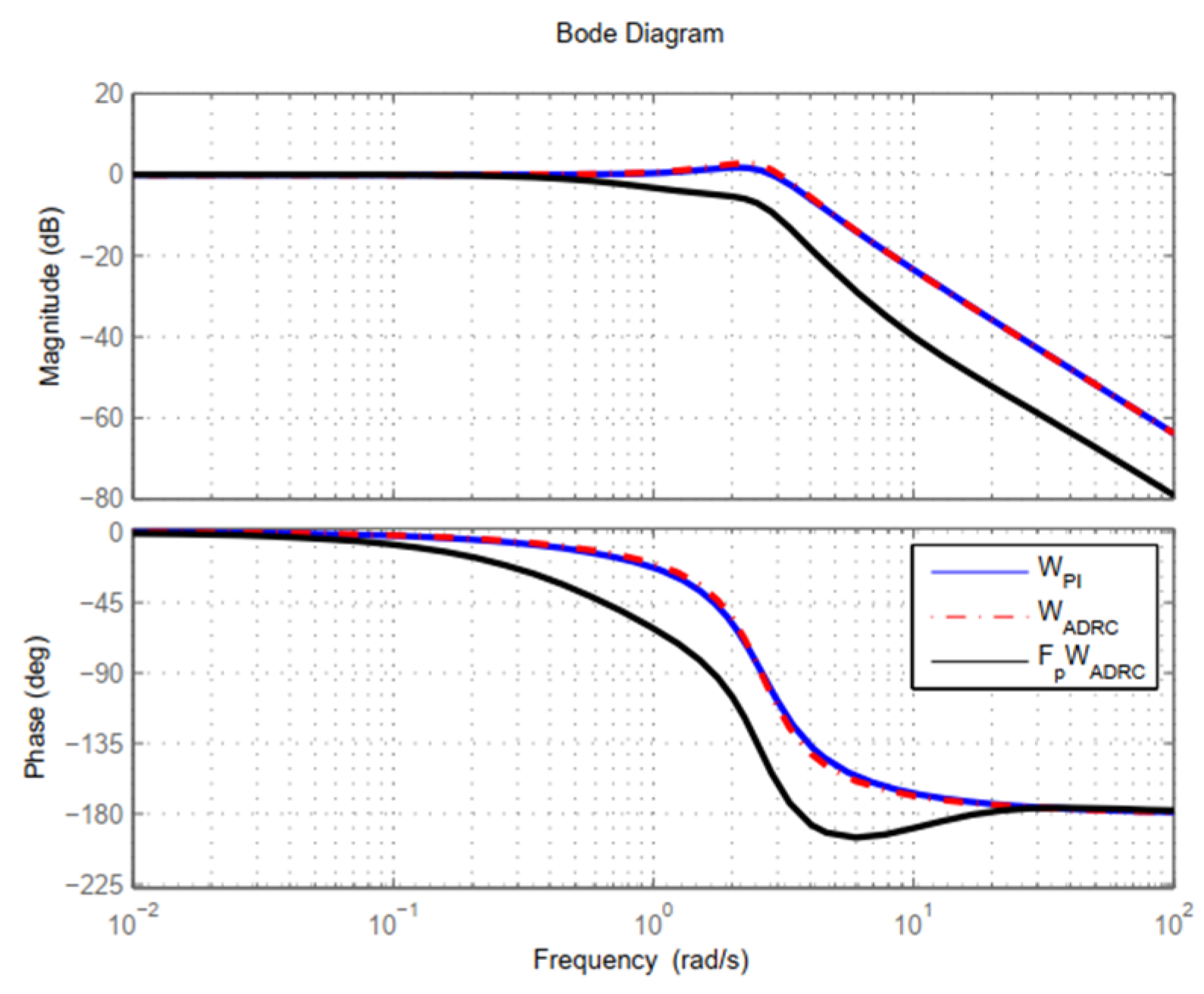
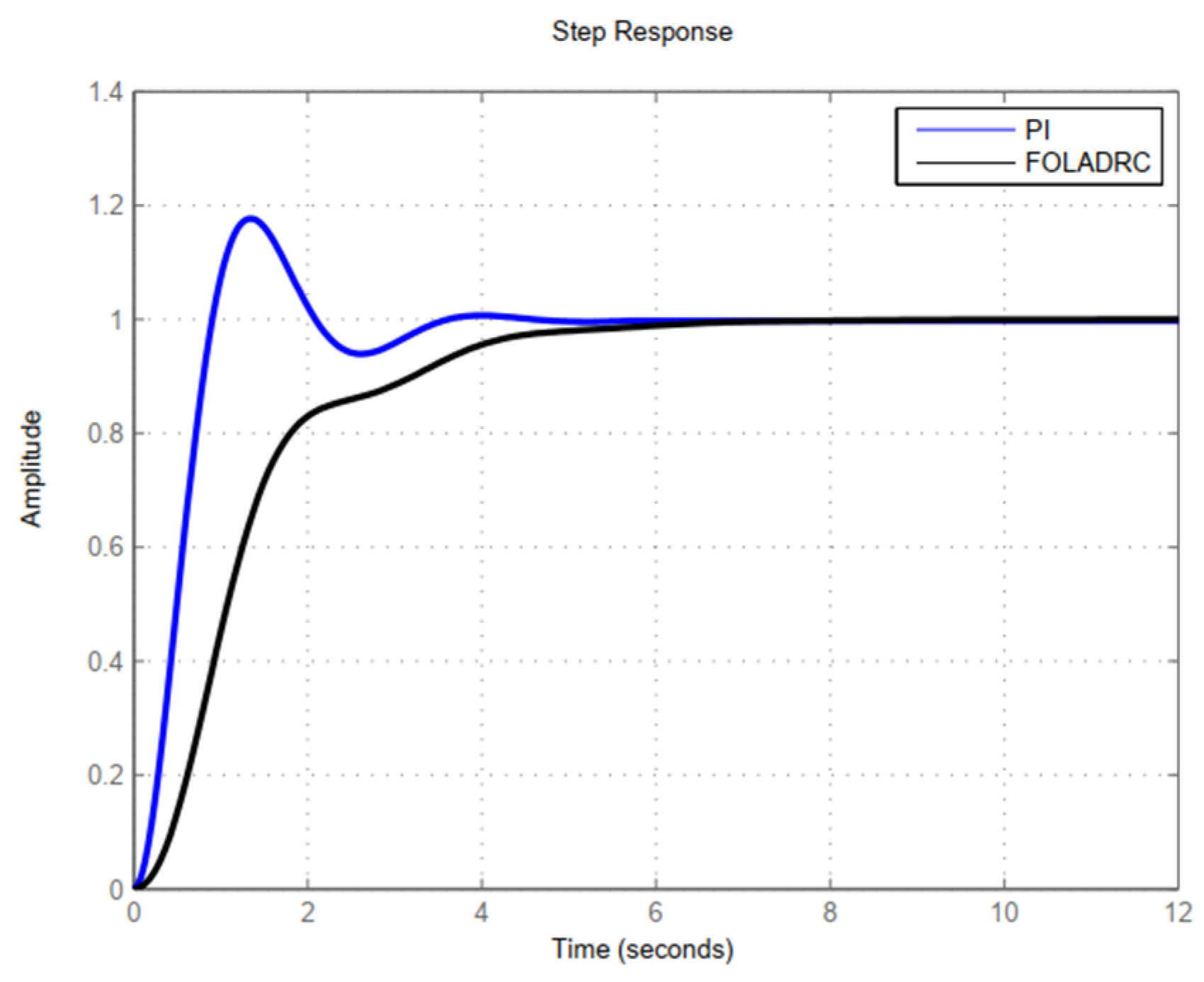

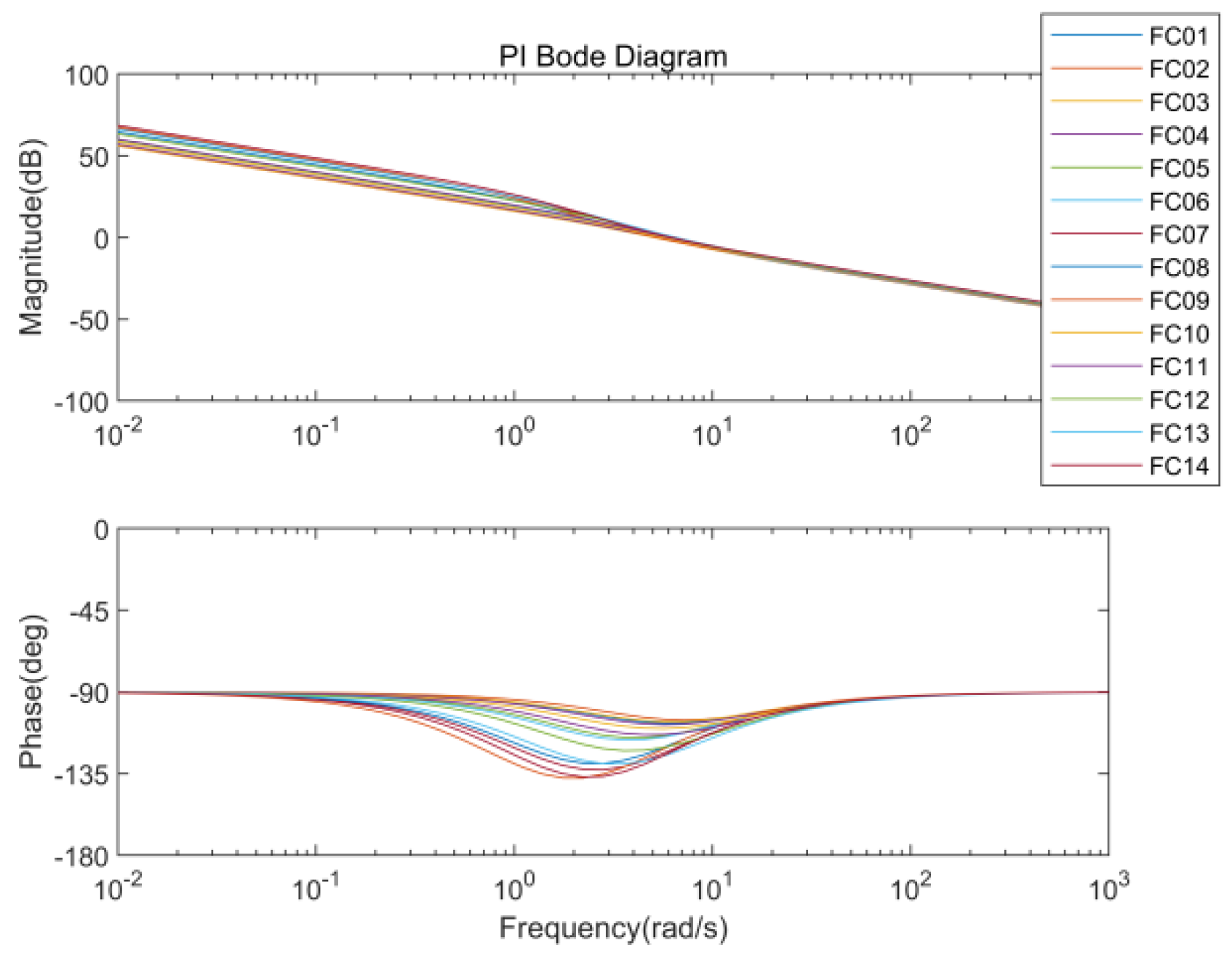
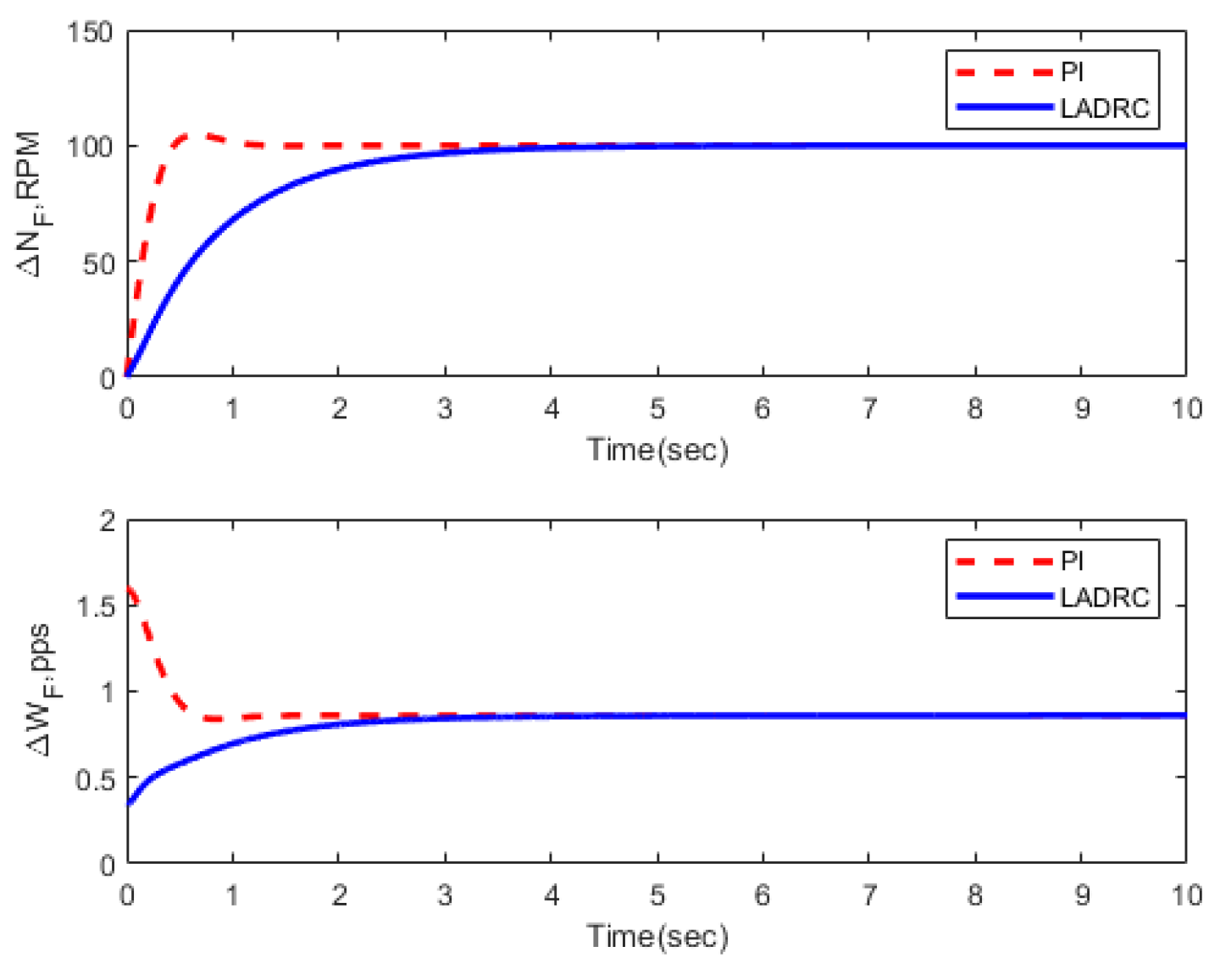

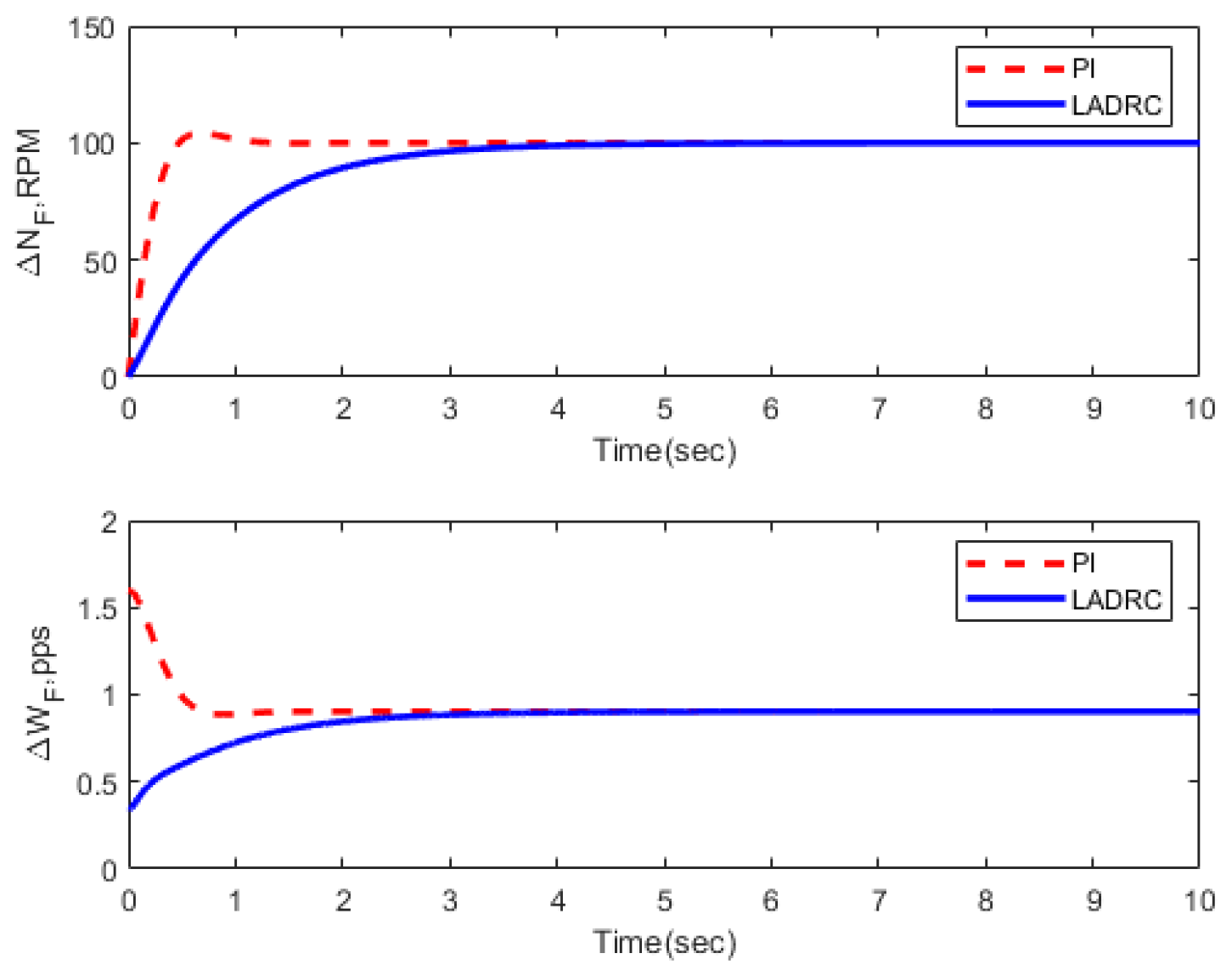

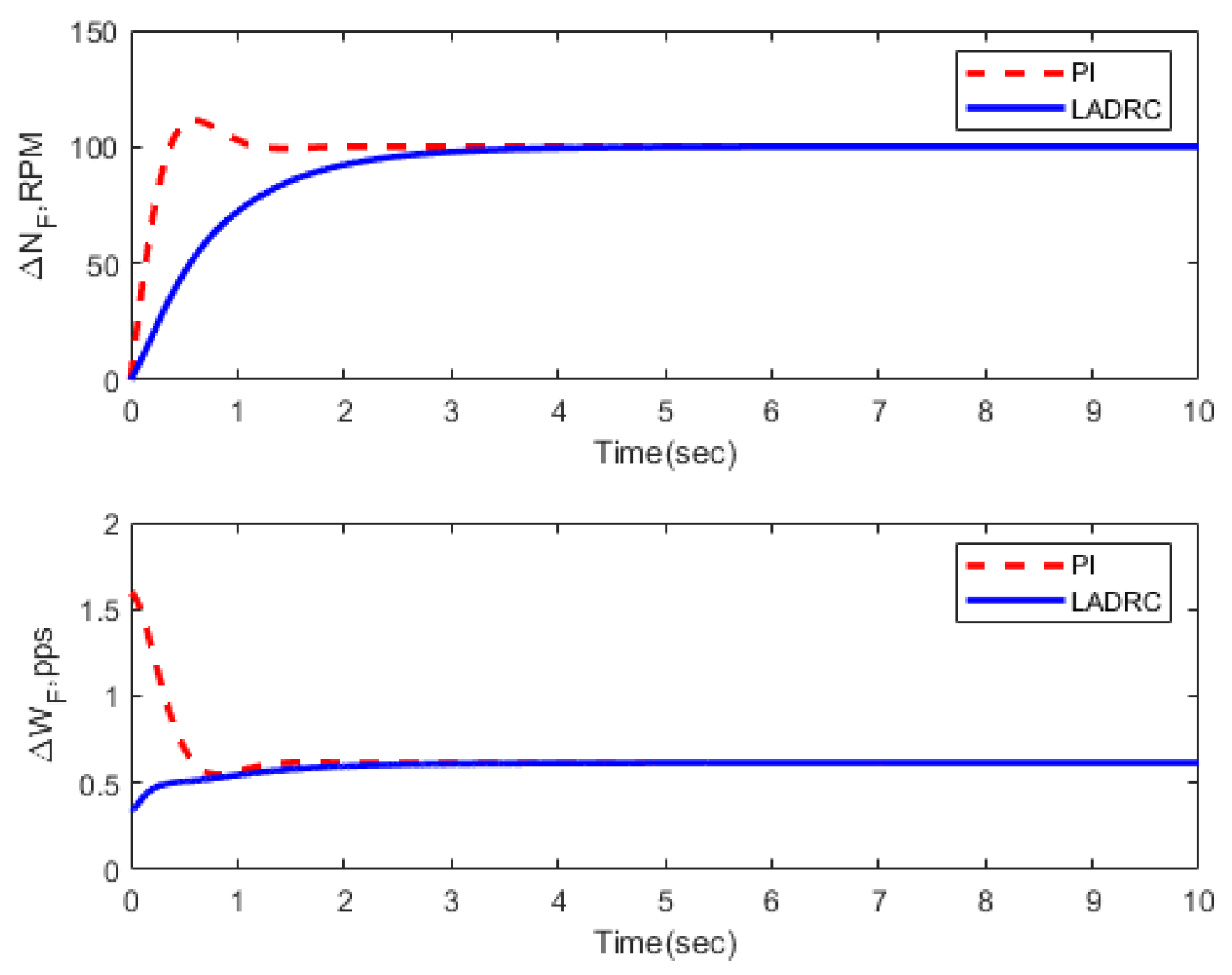

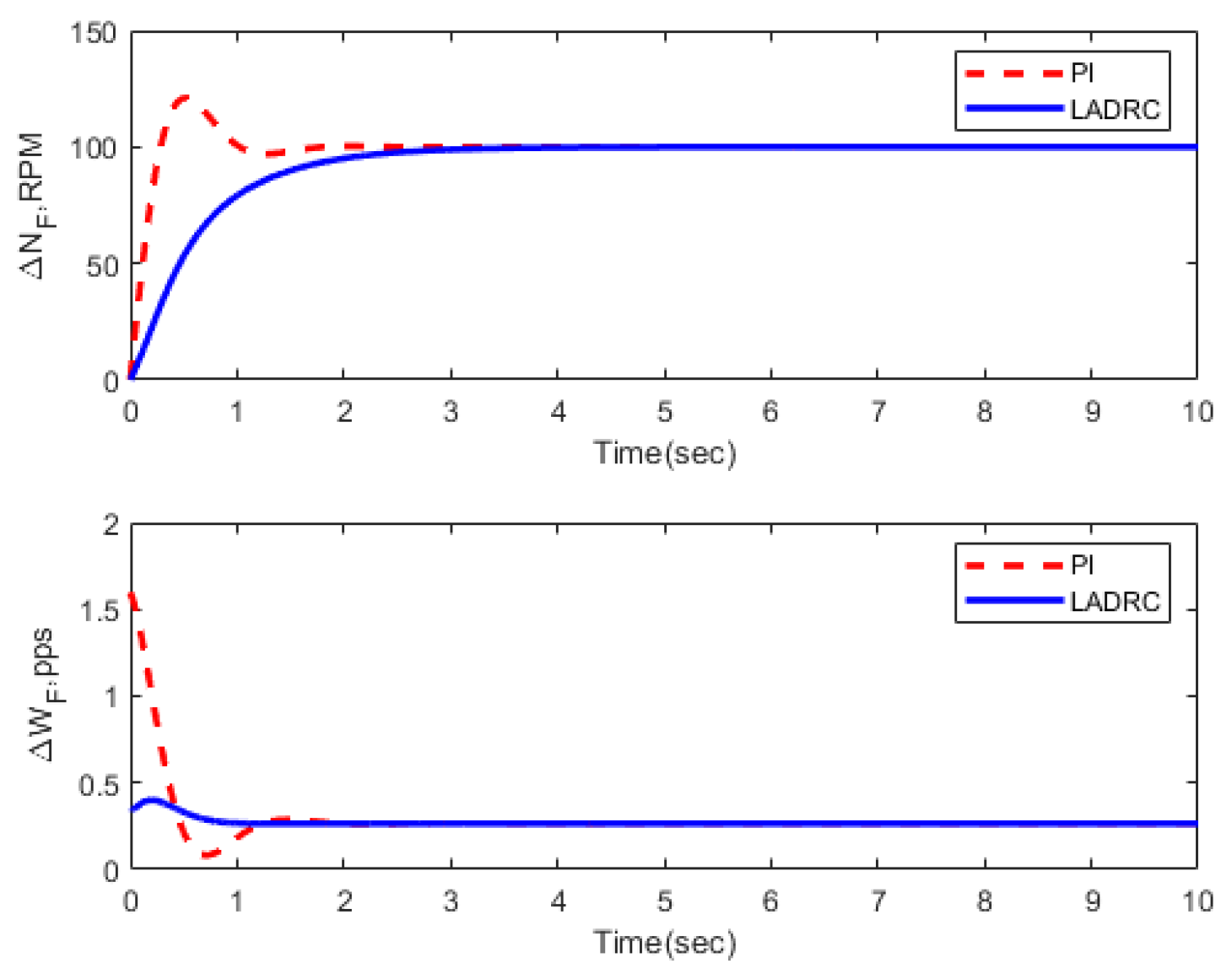

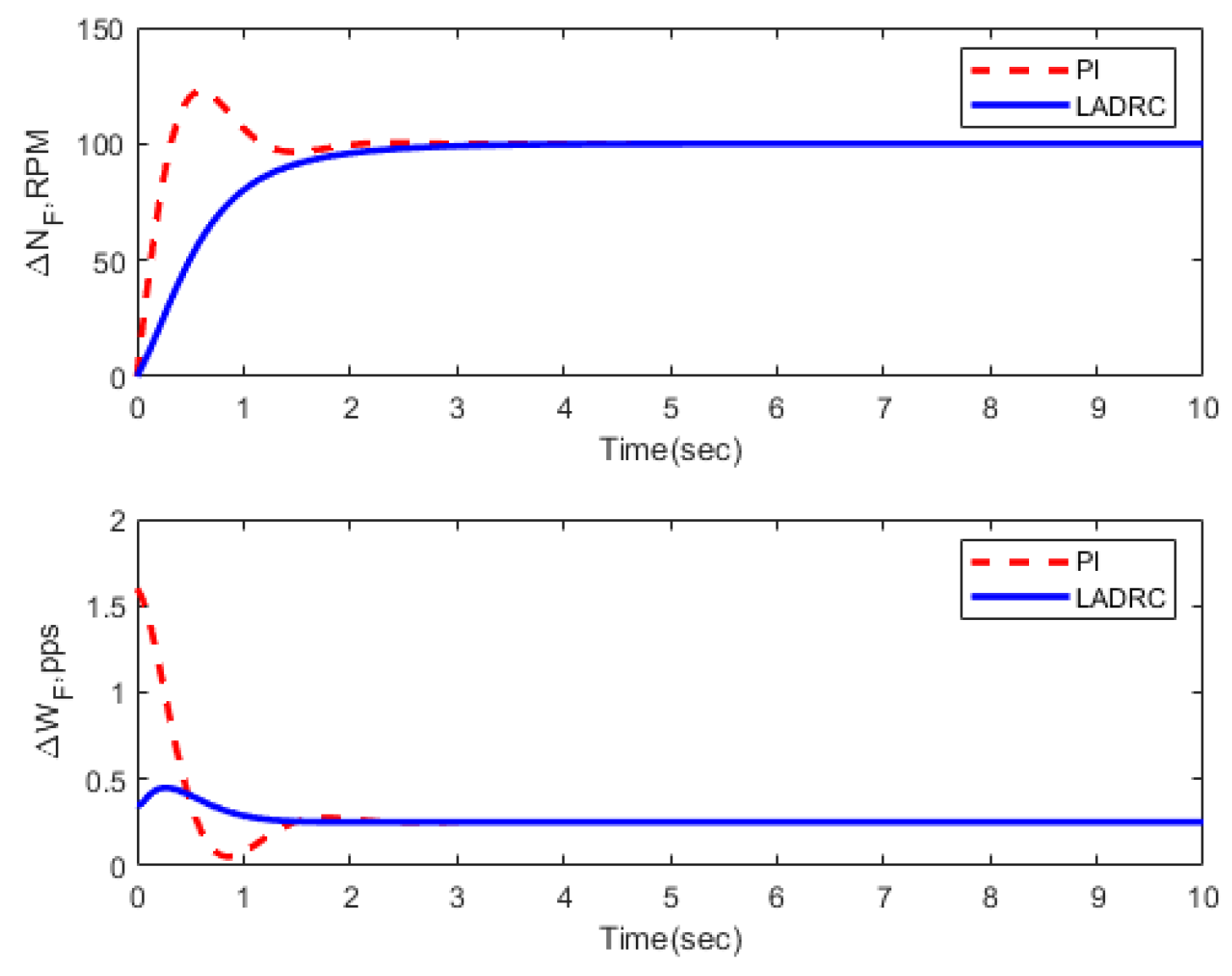
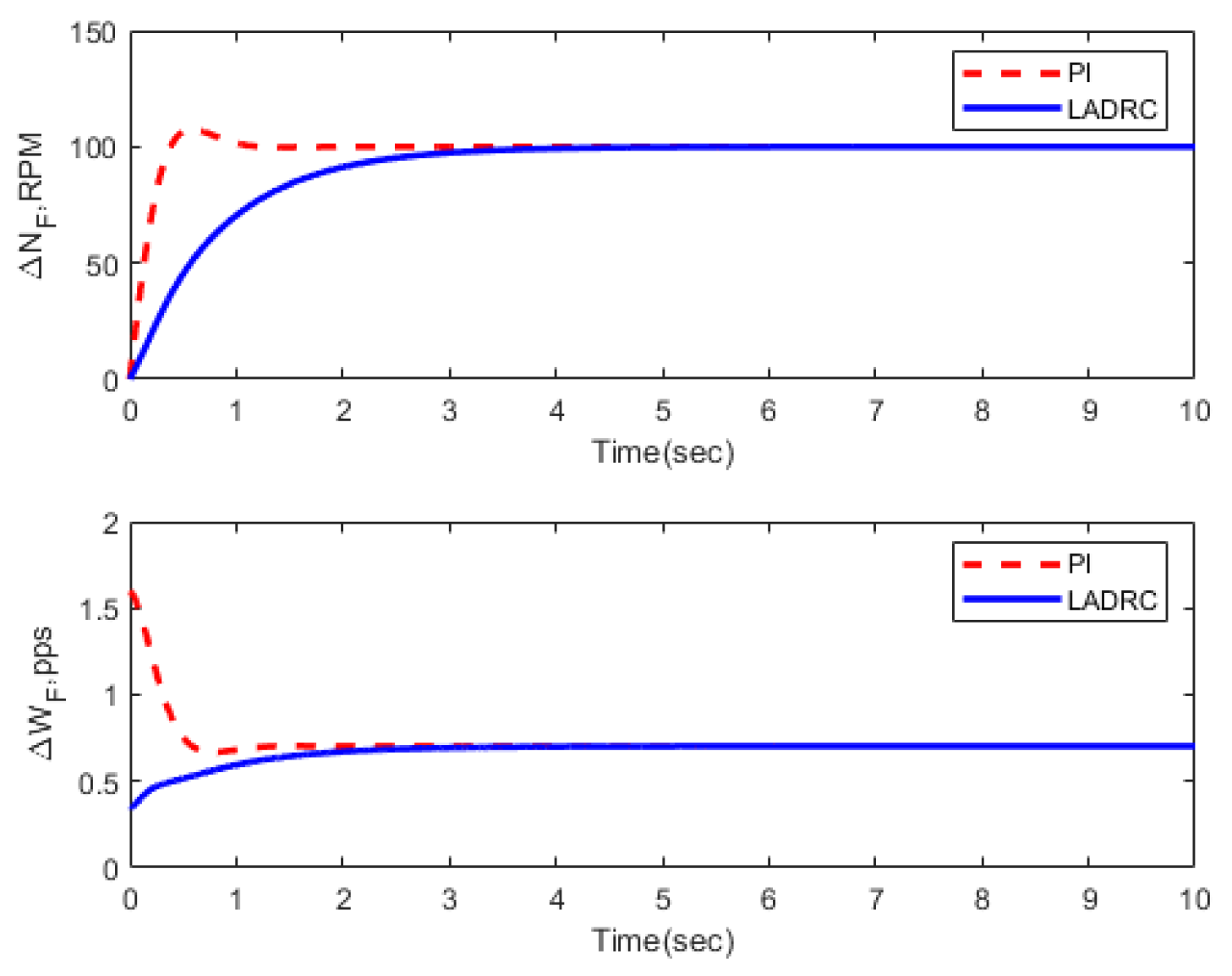

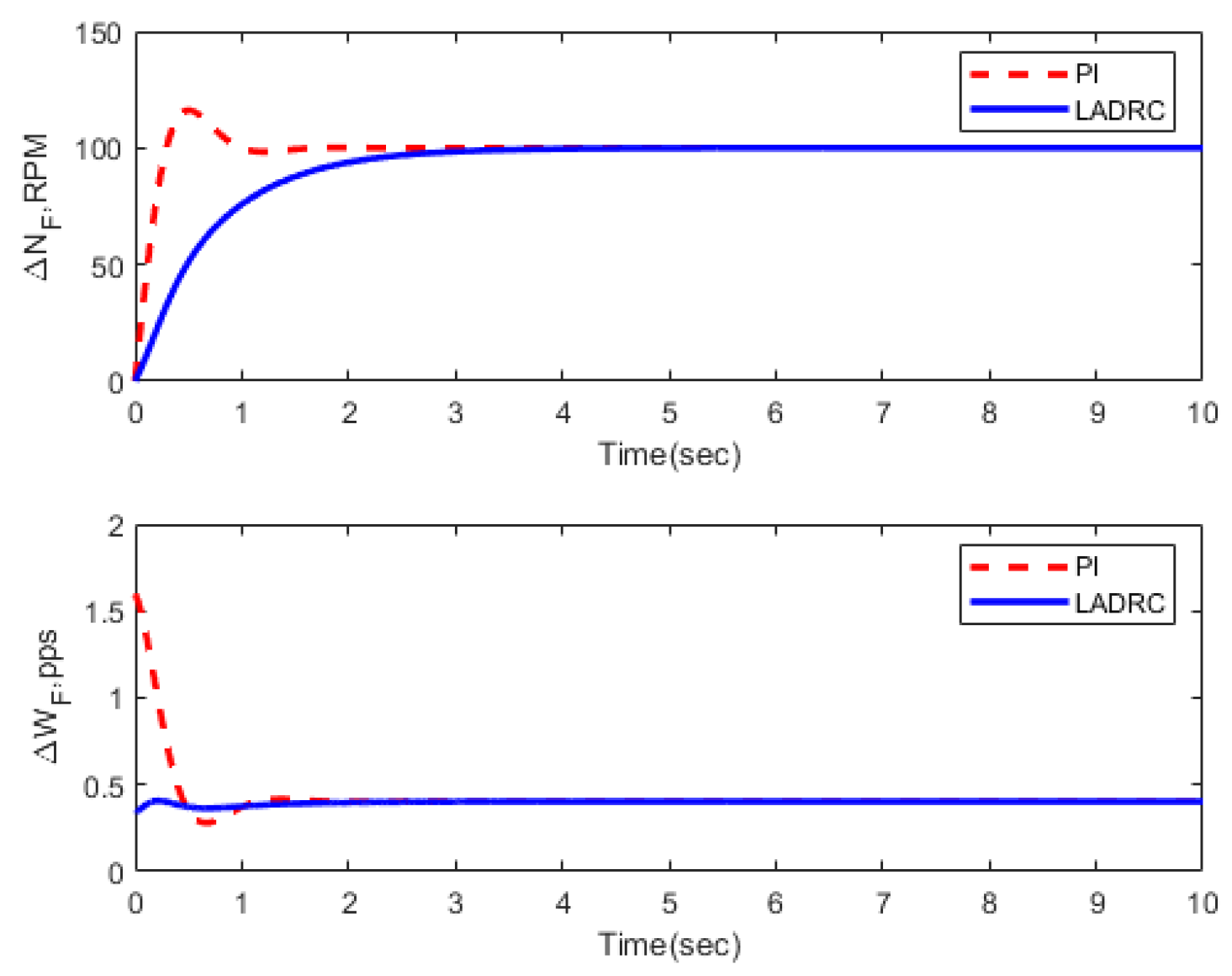
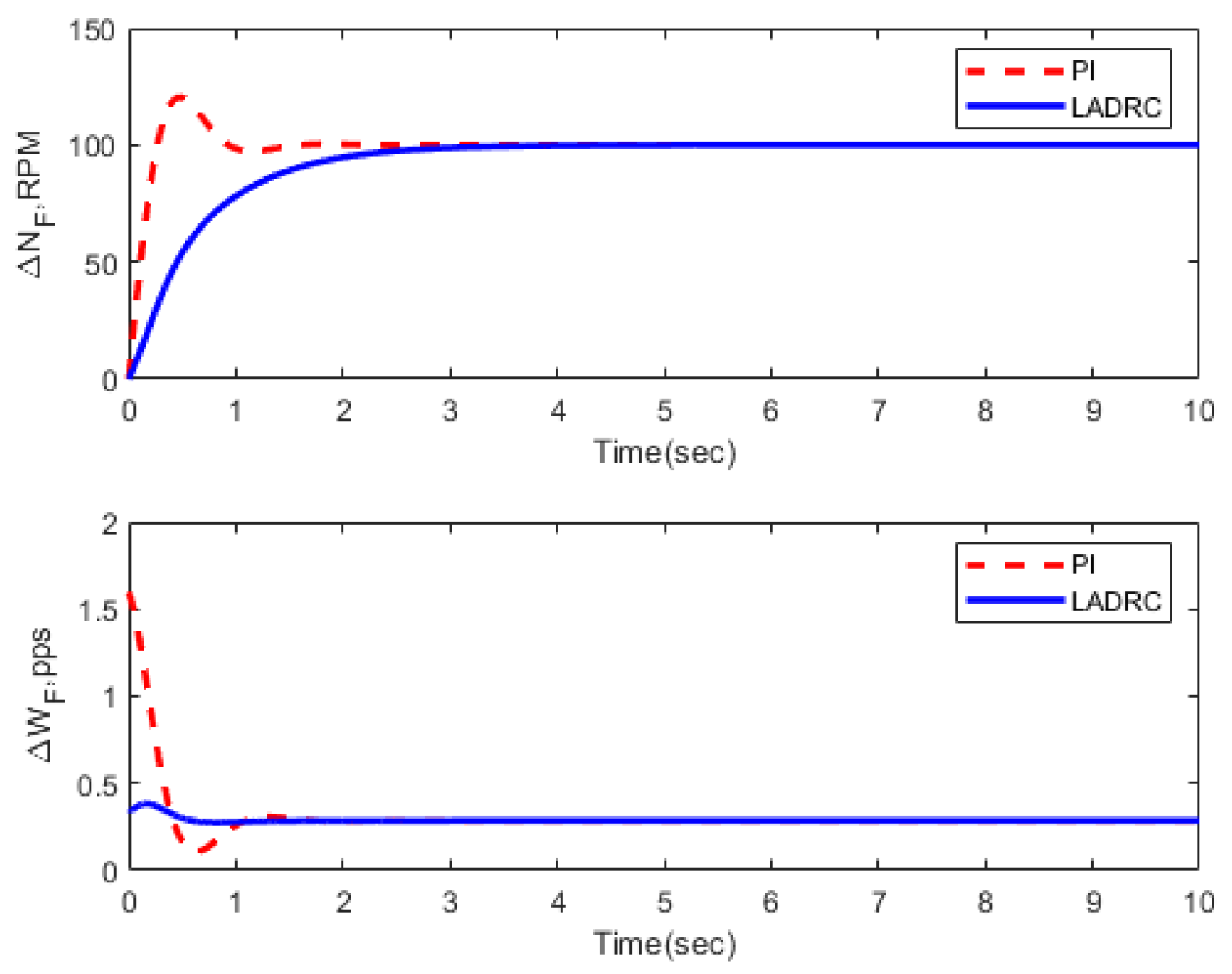
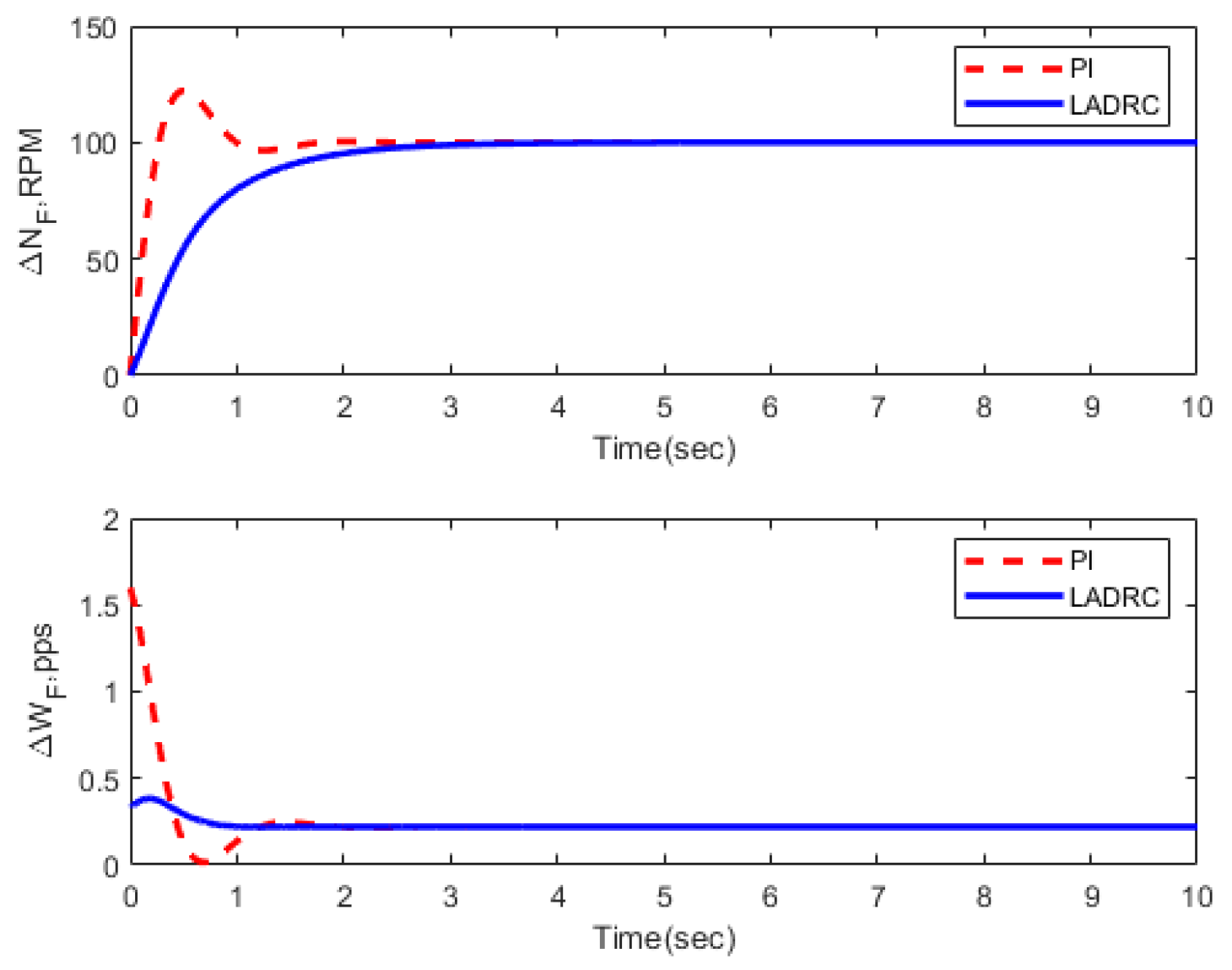
| Condition | FOLADRC | PI Control | ||
|---|---|---|---|---|
| PM (°) | (rad/s) | PM (°) | (rad/s) | |
| FC01 | 84.6 | 5.09 | 73.0° | 5.27 |
| FC02 | 86.8 | 5.10 | 75.2° | 5.28 |
| FC03 | 86.2 | 4.90 | 73.8° | 5.12 |
| FC04 | 83.5 | 5.12 | 72.0° | 5.29 |
| FC05 | 76.3 | 5.26 | 65.6° | 5.40 |
| FC06 | 75.6 | 5.24 | 64.8° | 5.38 |
| FC07 | 65.4 | 6.00 | 57.5° | 6.03 |
| FC08 | 68.9 | 5.22 | 58.4° | 5.36 |
| FC09 | 67.7 | 6.07 | 56.8° | 5.24 |
| FC10 | 79.4 | 5.58 | 69.8° | 5.68 |
| FC11 | 74.7 | 6.00 | 66.7° | 6.03 |
| FC12 | 67.4 | 6.27 | 60.4° | 6.27 |
| FC13 | 63.0 | 6.55 | 57.0° | 6.52 |
| FC14 | 64.3 | 6.21 | 57.1° | 6.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, H.-Y.; Chen, Y. First-Order Linear Active Disturbance Rejection Control for Turbofan Engines. Energies 2023, 16, 2743. https://doi.org/10.3390/en16062743
Jin H-Y, Chen Y. First-Order Linear Active Disturbance Rejection Control for Turbofan Engines. Energies. 2023; 16(6):2743. https://doi.org/10.3390/en16062743
Chicago/Turabian StyleJin, Hui-Yu, and Yang Chen. 2023. "First-Order Linear Active Disturbance Rejection Control for Turbofan Engines" Energies 16, no. 6: 2743. https://doi.org/10.3390/en16062743
APA StyleJin, H.-Y., & Chen, Y. (2023). First-Order Linear Active Disturbance Rejection Control for Turbofan Engines. Energies, 16(6), 2743. https://doi.org/10.3390/en16062743







