Finite Element Study of Electrical MHD Williamson Nanofluid Flow under the Effects of Frictional Heating in the View of Viscous Dissipation
Abstract
:1. Introduction
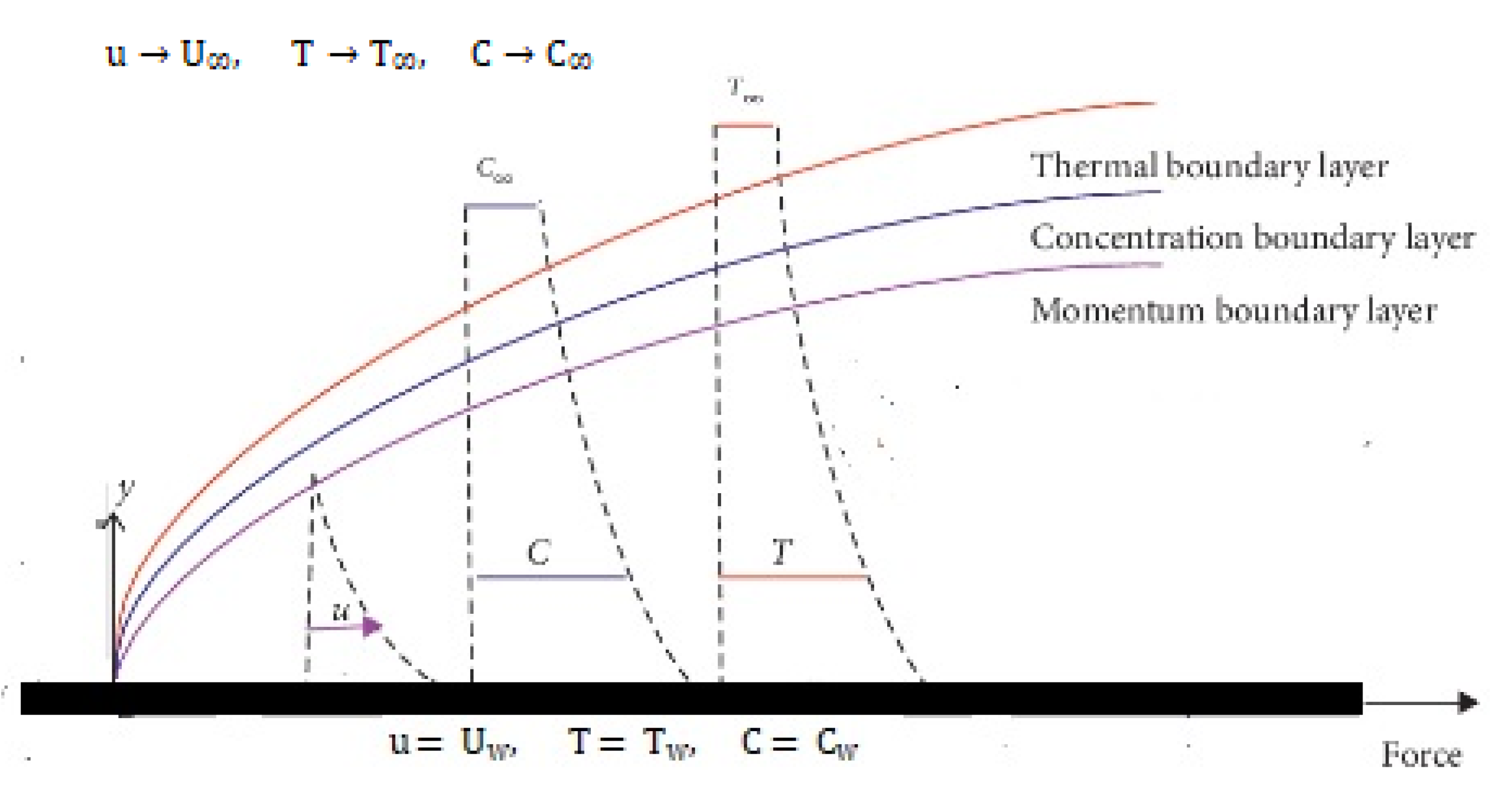
2. Problem Formulation
3. Finite Element Method
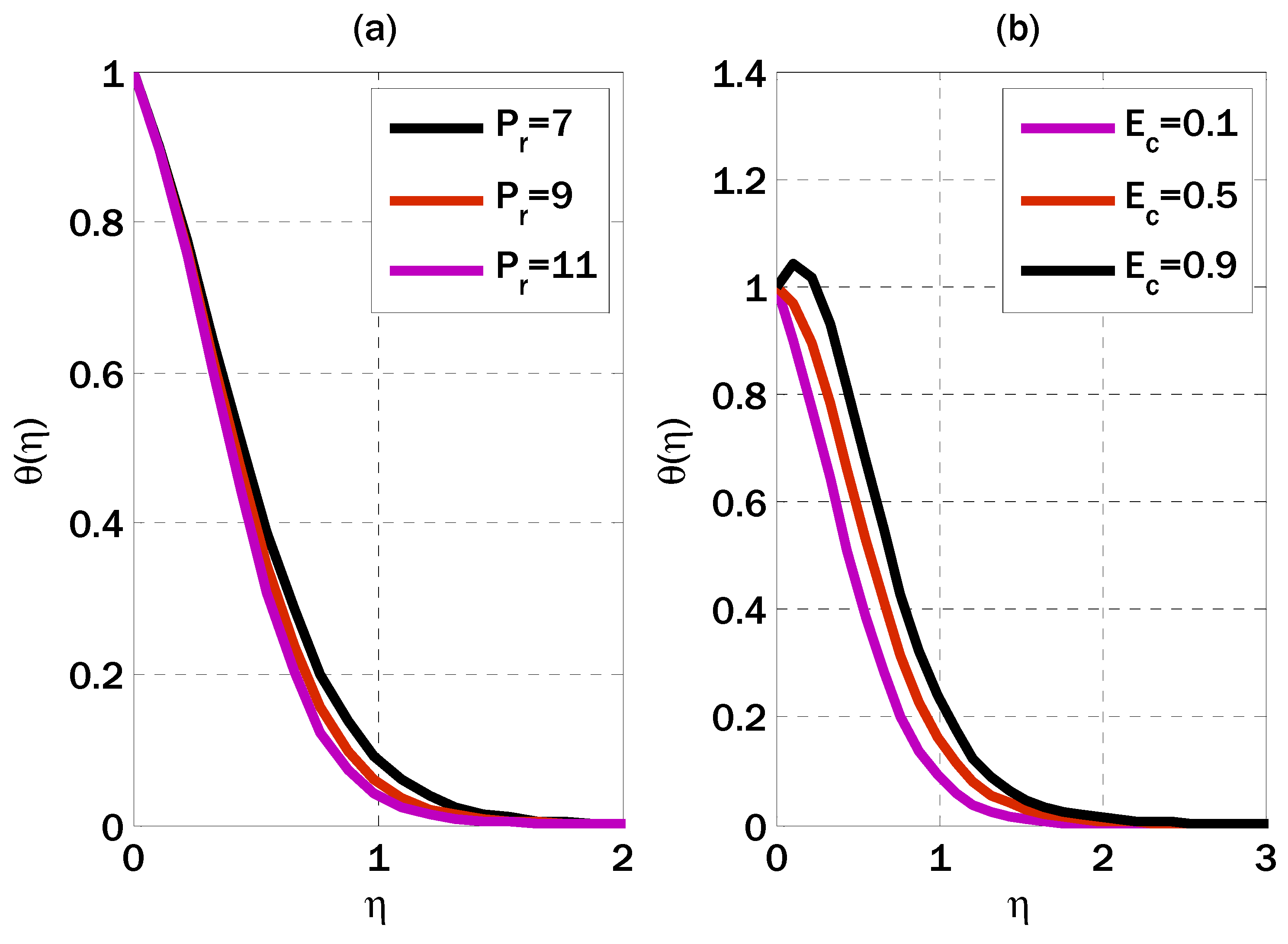
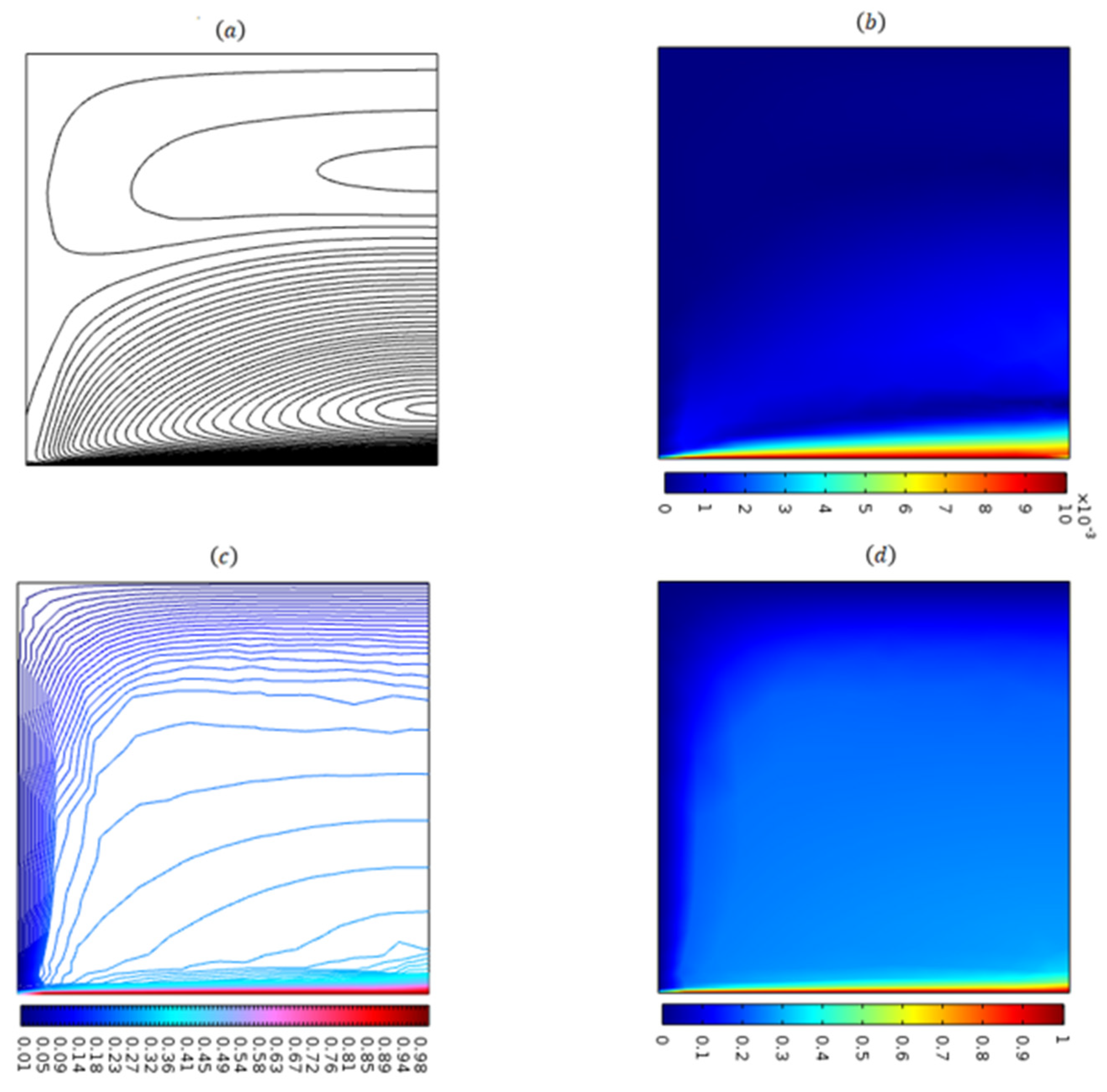
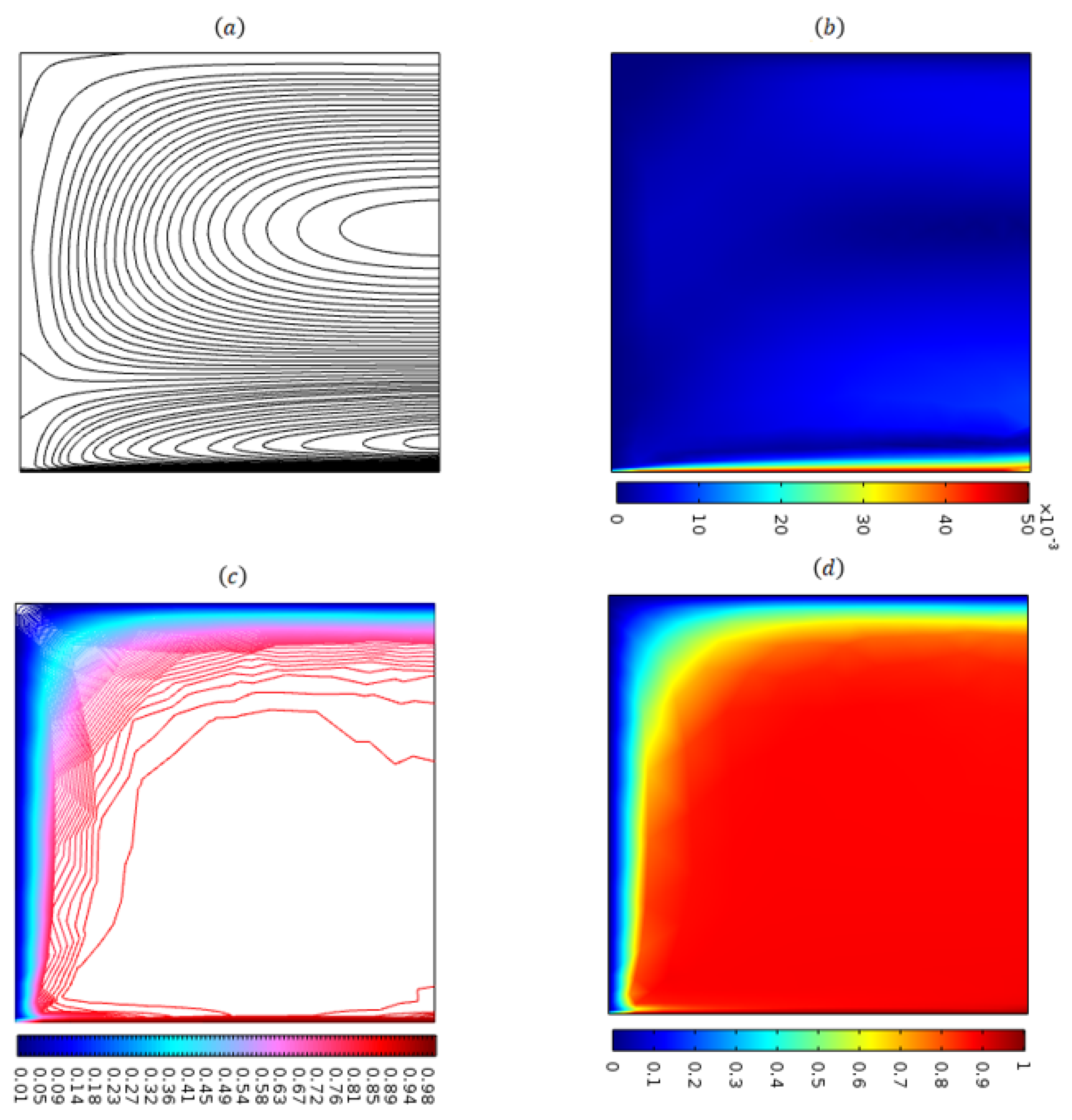
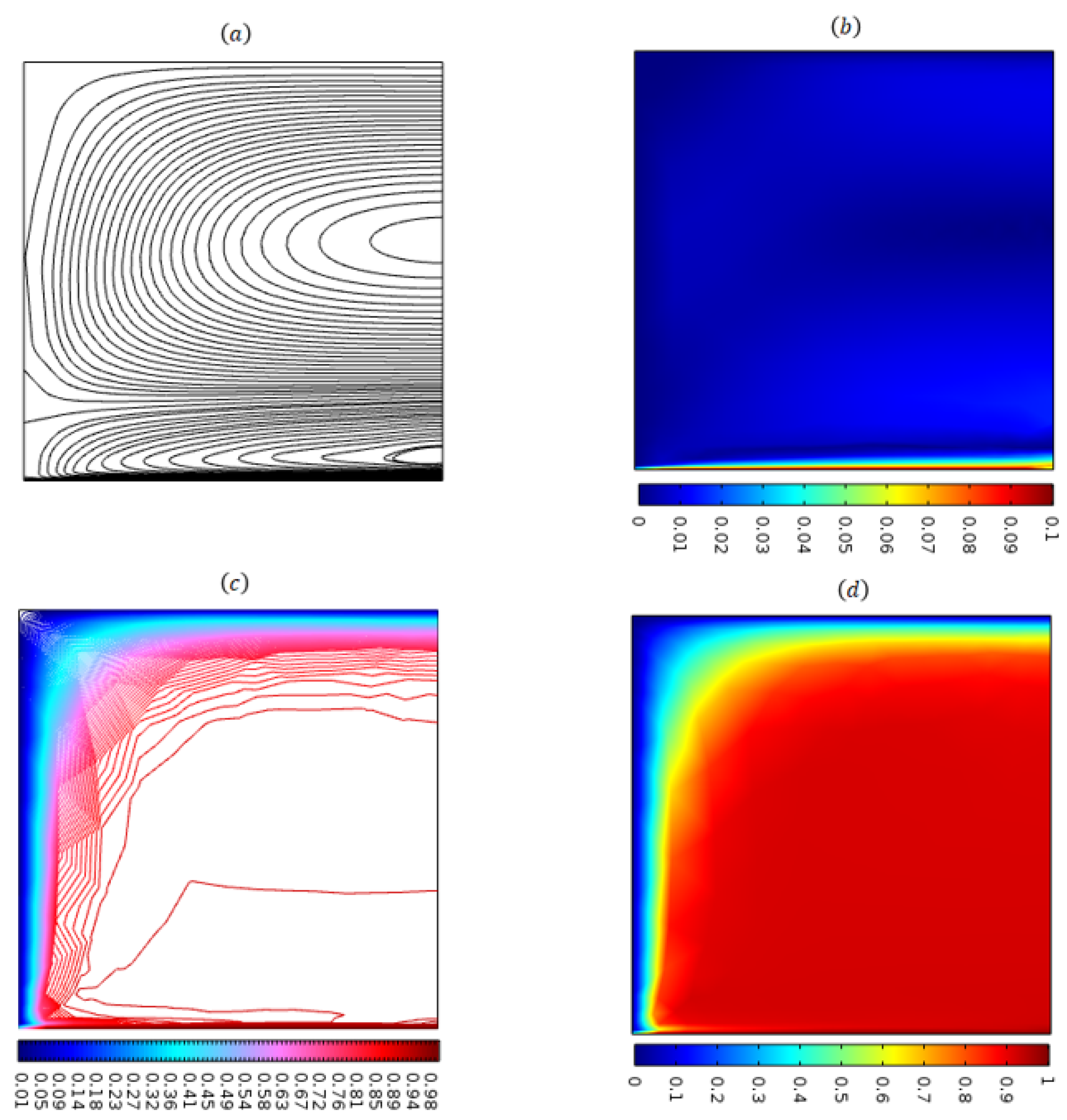
4. Results and Discussions
5. Conclusions
- The decline in the velocity profile was brought about by increasing the electrical parameters.
- As Eckert’s number increased, so did the temperature profile.
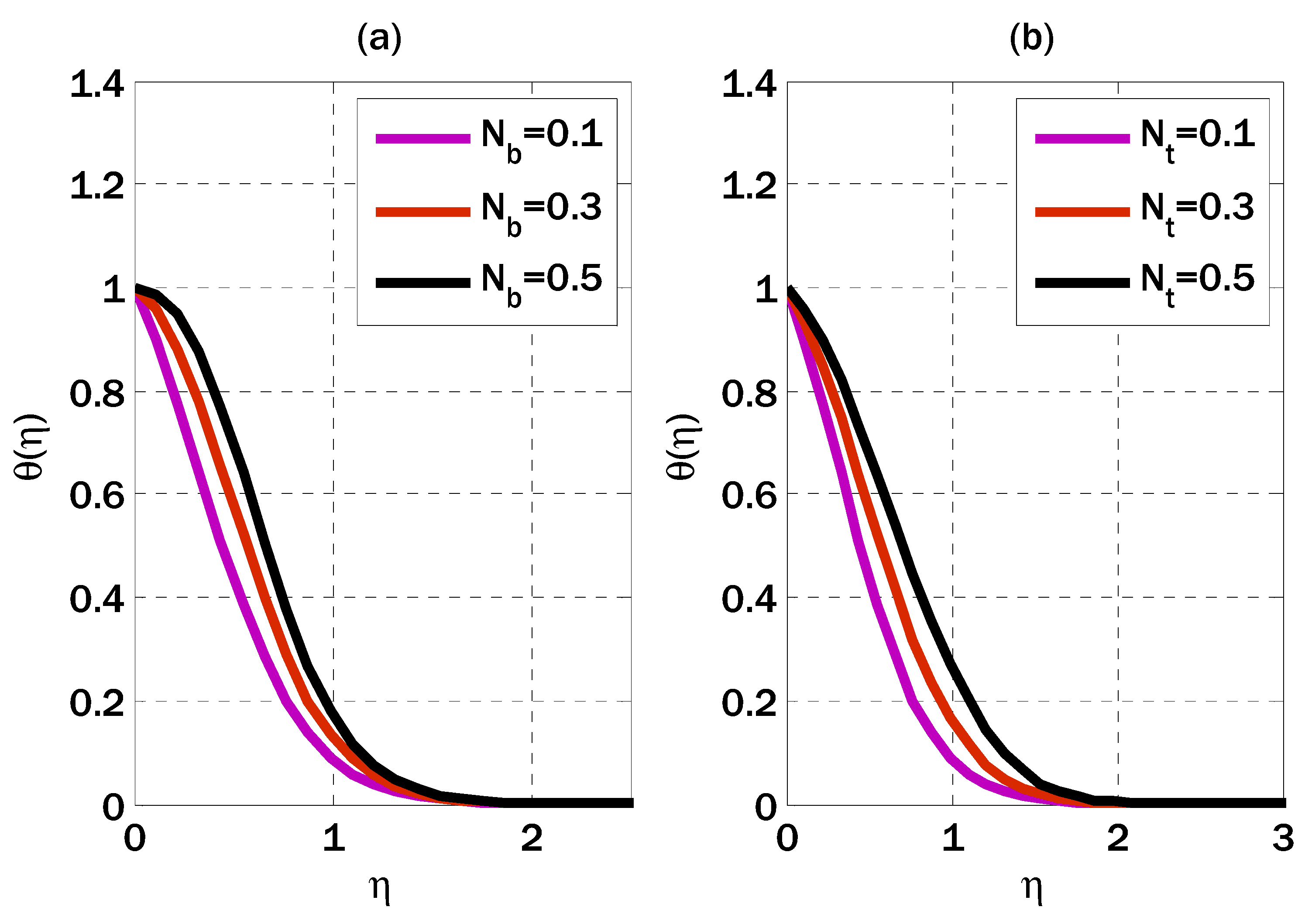
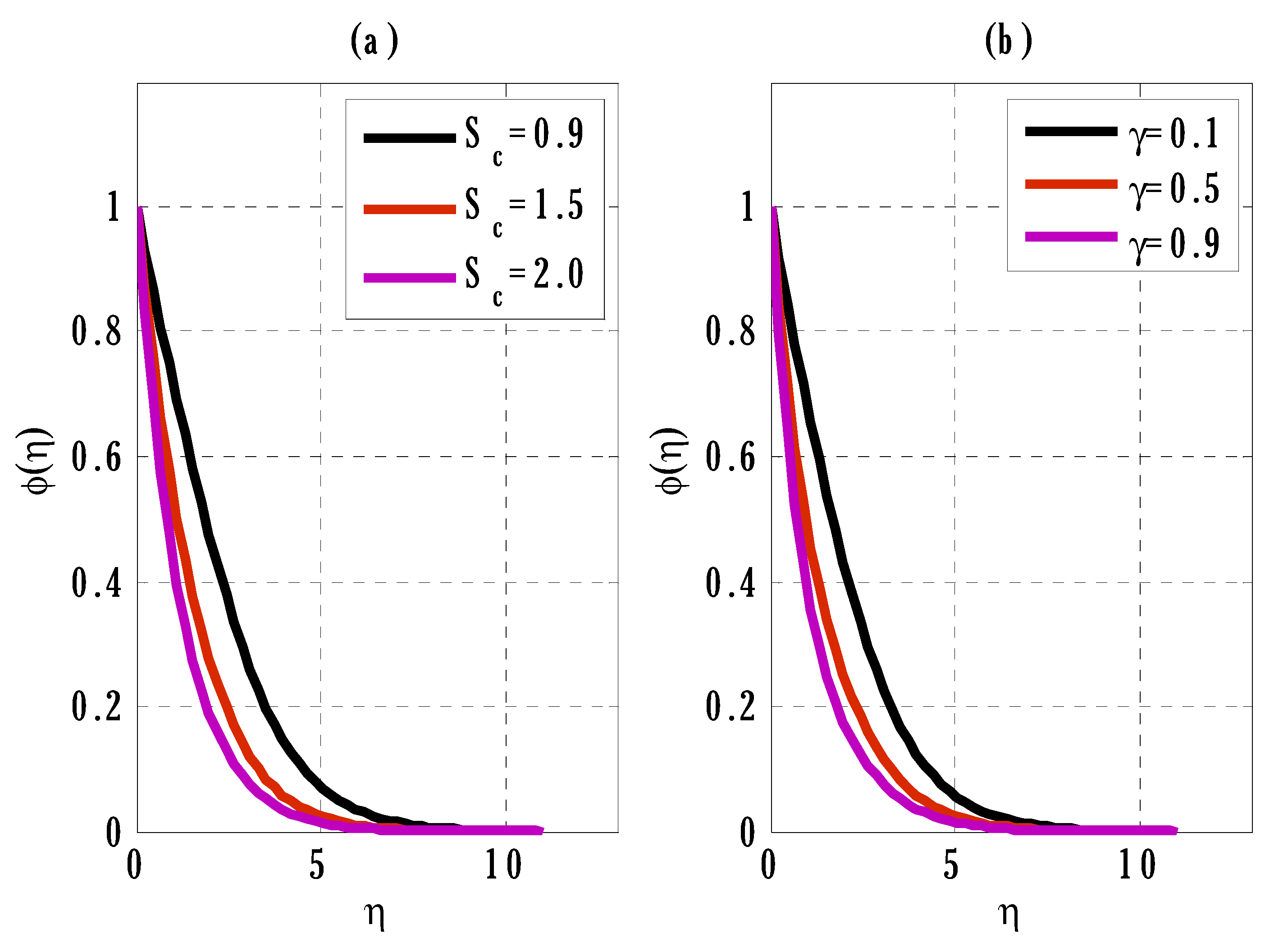
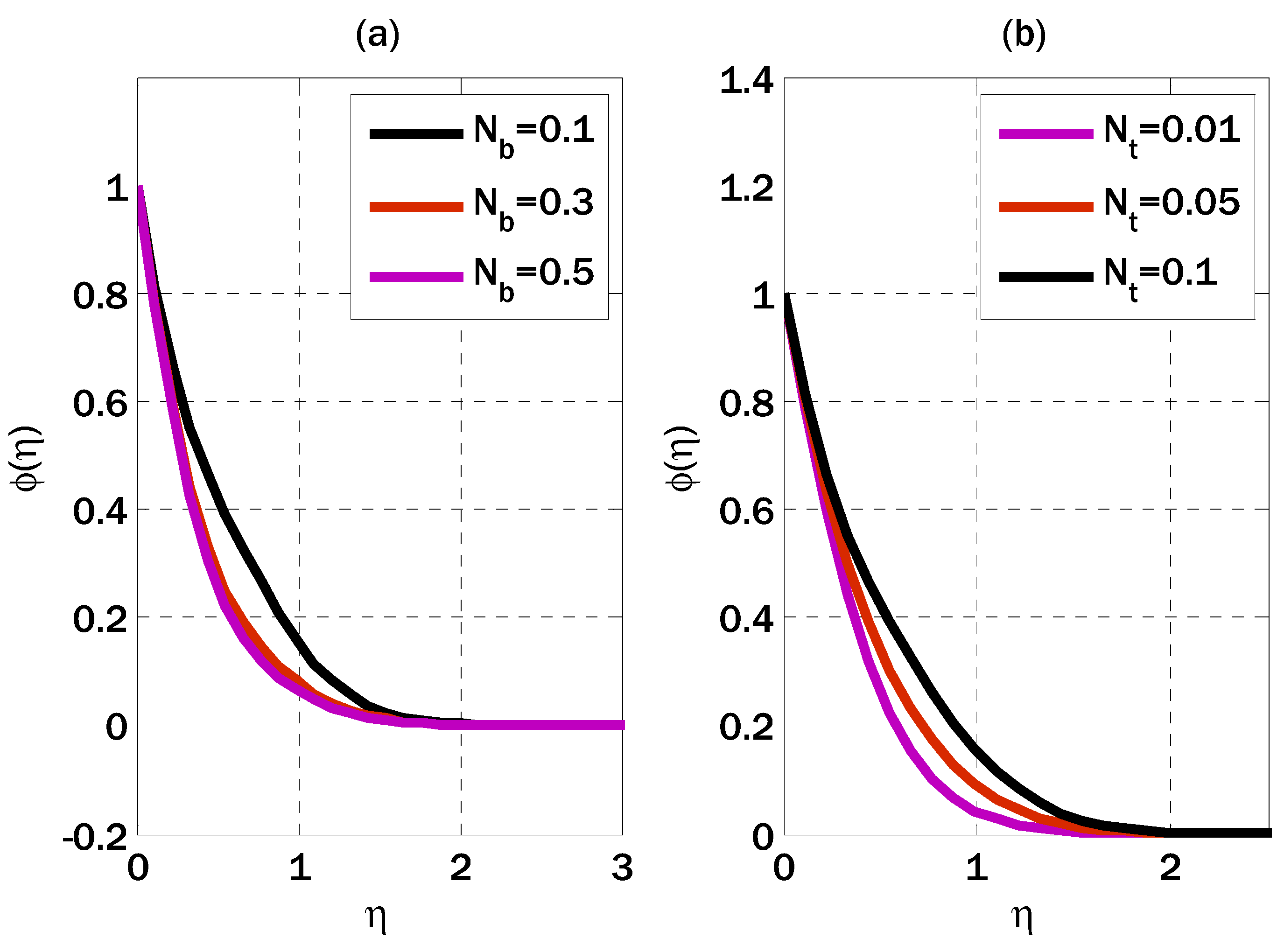
- Growing the thermophoresis parameter decreased the concentration profile.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| horizontal components of velocity | |
| Cartesian co-ordinate | |
| kinematic viscosity | |
| density of fluid | |
| concentration of fluid | |
| Brownian diffusion coefficient | |
| specific heat capacity | |
| strength of electric field | |
| reaction rate | |
| reaction rate parameter | |
| time constant (s) | |
| magnetic parameter | |
| Prandtl number | |
| Brownian motion variable | |
| electrical conductivity of the fluid | |
| temperature of fluid | |
| temperature of fluid at the wall | |
| ambient temperature of the fluid | |
| concentration on the wall | |
| ambient concentration | |
| strength of imposed transverse magnetic field | |
| thermal diffusivity | |
| dynamic viscosity | |
| effective heat capacity of fluid | |
| Eckert number | |
| thermophoresis variable | |
| Schmidt number |
Appendix A
References
- Alfven, H. Existence of electromagnetic-hydrodynamic waves. Nature 1942, 150, 405–406. [Google Scholar] [CrossRef]
- Hartmann, J.; Hg-Dynamics, I. Theory of the laminar flow of an electrically conducting liquid in a homogeneous magnetic field. K. Dan. Vidensk. Selsk. Mat.-Fys. Medd. 1937, 15, 1–27. [Google Scholar]
- Rashidi, M.M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Alsaedi, A.; Hayat, T. Hydromagnetic steady flow of Maxwell fluid over a bidirectional stretching surface with prescribed surface temperature and prescribed surface heat flux. PLoS ONE 2013, 8, e68139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Turkyilmazoglu, M. Exact solutions for the incompressible viscous magnetohydrodynamic fluid of a rotating disk flow. Int. J. Nonlinear Mech. 2011, 46, 306–311. [Google Scholar] [CrossRef]
- Hayat, T.; Shehzad, S.A.; Ashraf, M.B.; Alsaedi, A. Magneto hydrodynamic mixed convection flow of thixotropic fluid with thermophoresis and Joule heating. J. Thermophys. Heat Transf. 2013, 27, 733–740. [Google Scholar] [CrossRef]
- Dandapat, B.S.; Mukhopadhyay, A. Finite amplitude long wave instability of a film of conducting fluid flowing down an inclined plane in presence of electromagnetic field. Int. J. Appl. Mech. Eng. 2003, 8, 379–383. [Google Scholar]
- Sheikholeslami, M.; Gorji-Bandpay, M.; Ganji, D.D. Magnetic field effects on natural convection around a horizontal circular cylinder inside a square enclosure filled with nanofluid. Int. Commun. Heat Mass Transf. 2012, 39, 978–986. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Nawaz, M.; Alsaedi, A. MHD axisymmetric flow of third grade fluid between porous disks with heat transfer. Appl. Math. Mech. 2012, 33, 749–764. [Google Scholar] [CrossRef]
- Ahmad, K.; Nazar, R. Unsteady magnetohydrodynamic mixed convection stagnation point flow of a viscoelastic fluid on a vertical surface. JQMA 2010, 6, 105–117. [Google Scholar]
- Hatami, M.; Sheikholeslami, M.; Hosseini, M.; Ganji, D.D. Analytical investigation of MHD nanofluid flow in non-parallel walls. J. Mol. Liq. 2014, 194, 251–259. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.D.; Gorji-Bandpy, M.; Soleimani, S. Magnetic field effect on nanofluid flow and heat transfer using KKL model. J. Taiwan Inst. Chem. Eng. 2014, 45, 795–807. [Google Scholar] [CrossRef]
- Abolbashari, M.H.; Freidoonimehr, N.; Nazari, F.; Rashidi, M.M. Entropy analysis for and unsteady MHD flow past a stretching permeable surface in nanofluid. Powder Technol. 2014, 267, 256–267. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Erfani, E. Analytical method for solving steady MHD convective and slip flow due to a rotating disk with viscous dissipation and Ohmic heating. Eng. Comput. 2012, 29, 562–579. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Ali, M.; Freidoonimehr, N.; Rostami, B.; Hossain, M.A. Mixed convective heat transfer for MHD viscoelastic fluid flow over a porous wedge with thermal radiation. Adv. Mech. Eng. 2014, 10, 735939. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, K.; Mukhopadhyay, S.; Layek, G.C.; Pop, I. Effects of thermal radiation on micropolar fluid flow and heat transfer over a porous shrinking sheet. Int. J. Heat Mass Transf. 2012, 55, 2945–2952. [Google Scholar] [CrossRef]
- Makinde, O.D.; Ogulu, A. The effect of thermal radiation on the heat and mass transfer flow of a variable viscosity fluid past a vertical porous plate permeated by a transverse magnetic field. Chem. Eng. Commun. 2008, 195, 1575–1584. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Alsaedi, A. Effect of Joule heating and thermal radiation in flow of third-grade fluid over radiative surface. PLoS ONE 2014, 9, e83153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Motsumi, T.G.; Makinde, O.D. Effects of thermal radiation and viscous dissipation on boundary layer flow of nanofluids over a permeable moving flat plate. Phys. Scr. 2012, 86, 045003. [Google Scholar] [CrossRef]
- Makinde, O.D. MHD mixed-convection interaction with thermal radiation and nth order chemical reaction past a vertical porous plate embedded in a porous medium. Chem. Eng. Commun. 2011, 198, 590–608. [Google Scholar] [CrossRef]
- Shehzad, S.A.; Alsaedi, A.; Hayat, T.; Alhuthali, M.S. Thermophoresis particle deposition in mixed convection threedimensional radiative flow of an Oldroyd-B fluid. J. Taiwan Inst. Chem. Eng. 2014, 45, 787–794. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary layer behaviour on continuous moving solid surfaces. I. Boundary layer equations for two-dimensional and axisymmetric flow. II. Boundary layer on a continuous flat surface. iii. boundary layer on a continuous cylindrical surface. Am. Inst. Chem. Eng. J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Crane, L.J. Flow past a stretching sheet. Z. Appl. Math. Phys. 1970, 21, 645–647. [Google Scholar]
- Gupta, P.S.; Gupta, A.S. Heat and mass transfer on a stretching sheet with suction or blowing. Can. J. Chem. Eng. 1977, 55, 744–746. [Google Scholar] [CrossRef]
- Abd El-Aziz, M. Radiation effect on the flow and heat transfer over an unsteady stretching sheet. Int. Commun. Heat Mass Transf. 2009, 36, 521–524. [Google Scholar] [CrossRef]
- Elbashbeshy, E.M.A. Heat transfer over a stretching surface with variable surface a heat flux. J. Phys. D Appl. Phys. 1998, 31, 1951–1954. [Google Scholar] [CrossRef]
- Mukhopadyay, S. Effect of thermal radiation on unsteady mixed convection flow and heat transfer over a porous stretching surface in porous medium. Int. Commun. Heat Mass Transf. 2009, 52, 3261–3265. [Google Scholar] [CrossRef]
- Shateyi, S.; Motsa, S.S. Thermal radiation effects on heat and mass transfer over an unsteady stretching surface. Math. Probl. Eng. 2009, 2009, 965603. [Google Scholar] [CrossRef] [Green Version]
- Abd El-Aziz, M. Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer by hydromagnetic threedimensional free convection over a permeable stretching surface with radiation. Phys. Lett. 2007, 372, 263–272. [Google Scholar] [CrossRef]
- Hady, F.M.; Ibrahim, F.S.; Abdel-Gaied, S.M.; Eid, M.R. Radiation effect on viscous flow of a nanofluid and heat transfer over a nonlinearly stretching sheet. Nanoscale Res. Lett. 2012, 7, 229. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pavlov, K.B. Magnetohydromagnetic flow of an incompressible viscous fluid caused by deformation of a surface. Magn. Gidrodin. 1974, 4, 146–148. [Google Scholar]
- Bianco, V.; Manca, O.; Nardini, S. Second law analysis of Al2O3 water nanofluid turbulent forced convection in a circular cross section tube with constant wall temperature. Adv. Mech. Eng. 2013, 203, 920278. [Google Scholar] [CrossRef]
- Nadeem, S.; Haq, R.U.; Akbar, N.S.; Khan, Z.H. MHD three dimensional Casson fluid flow past a porous linearly stretching sheet. Alex. Eng. J. 2013, 52, 577–582. [Google Scholar] [CrossRef]
- Akbar, N.S.; Haq, R.U.; Nadeem, S. Study of Williamson nanofluid flow in an symmetric channel. Res. Phys. 2013, 3, 161–166. [Google Scholar]
- Elbashbeshy EM, A.; Bazid, M.A. Heat transfer over an unsteady stretching surface with internal heat generation. Appl. Math. Comput. 2003, 138, 239–245. [Google Scholar] [CrossRef]
- Shafiq, A.; Çolak, A.B.; Sindhu, T.N.; Al-Mdallal, Q.M.; Abdeljawad, T. Estimation of unsteady hydromagnetic Williamson fluid flow in a radiative surface through numerical and artificial neural network modeling. Sci. Rep. 2021, 11, 14509. [Google Scholar] [CrossRef]
- Rizk, D.; Ullah, A.; Elattar, S.; Alharbi, K.A.M.; Sohail, M.; Khan, R.; Khan, A.; Mlaiki, N. Impact of the KKL Correlation Model on the Activation of Thermal Energy for the Hybrid Nanofluid (GO+ZnO+Water) Flow through Permeable Vertically Rotating Surface. Energies 2022, 15, 2872. [Google Scholar] [CrossRef]
- Suganya, S.; Muthtamilselvan, M.; Al-Amri, F.; Abdalla, B. An exact solution for unsteady free convection flow of chemically reacting Al2O3–SiO2/water hybrid nanofluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 3749–3763. [Google Scholar] [CrossRef]
- Saeed, A.; Alghamdi, W.; Mukhtar, S.; Shah, S.I.A.; Kumam, P.; Gul, T.; Nasir, S.; Kumam, W. DarcyForchheimer hybrid nanofluid flow over a stretching curved surface with heat and mass transfer. PLoS ONE 2021, 16, e0249434. [Google Scholar] [CrossRef]
- Gul, T.; Noman, W.; Sohail, M.; Khan, M.A. Impact of the Marangoni and thermal radiation convection on the graphene-oxide-water-based and ethylene-glycol-based nanofluids. Adv. Mech. Eng. 2019, 11, 1687814019856773. [Google Scholar] [CrossRef]
- Abbas, A.; Jeelani, M.B.; Alnahdi, A.S.; Ilyas, A. MHD Williamson Nanofluid Fluid Flow and Heat Transfer Past a Nonlinear Stretching Sheet Implanted in a Porous Medium: Effects of Heat Generation and Viscous Dissipation. Processes 2022, 10, 1221. [Google Scholar] [CrossRef]
- Gul, T.; Khan, M.A.; Noman, W.; Khan, I.; Abdullah Alkanhal, T.; Tlili, I. Fractional order forced convection carbon nanotube nanofluid flow passing over a thin needle. Symmetry 2019, 11, 312. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Shafiq, A.; Alsaedi, A. Hydromagnetic boundary layer flow of Williamson fluid in the presence of thermal radiation and Ohmic dissipation. Alex. Eng. J. 2016, 55, 2229–2240. [Google Scholar] [CrossRef] [Green Version]
- Nawaz, Y.; Arif, M.S. An effective modification of finite element method for heat and mass transfer of chemically reactive unsteady flow. Comput. Geosci. 2020, 24, 275–291. [Google Scholar] [CrossRef]
- Khan, W.A.; Pop, I. Boundary layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transfer 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Srinivasulu, T.; Goud, B.S. Effect of inclined magnetic field on flow, heat and mass transfer of Williamson nanofluid over a stretching sheet. Case Stud. Therm. Eng. 2021, 23, 100819. [Google Scholar] [CrossRef]
- Bibi, M.; Nawaz, Y.; Arif, M.S.; Abbasi, J.N.; Javed, U.; Nazeer, A. A finite difference method and effective modification of gradient descent optimization algorithm for MHD fluid flow over a linearly stretching surface. Computers. Mater. Contin. 2020, 62, 657–677. [Google Scholar]
- Arif, M.S.; Bibi, M.; Jhangir, A. Solution of algebraic lyapunov equation on positive-definite hermitian matrices by using extended Hamiltonian algorithm. Comput. Mater. Contin. 2018, 54, 181–195. [Google Scholar]
- Pasha, S.A.; Nawaz, Y.; Arif, M.S. A third-order accurate in time method for boundary layer flow problems. Appl. Numer. Math. 2021, 161, 13–26. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S. Modified class of explicit and enhanced stability region schemes: Application to mixed convection flow in a square cavity with a convective wall. Int. J. Numer. Methods Fluids 2021, 93, 1759–1787. [Google Scholar] [CrossRef]
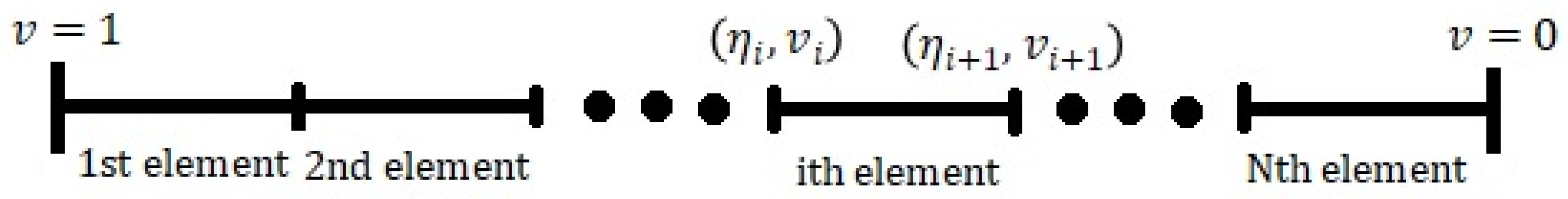
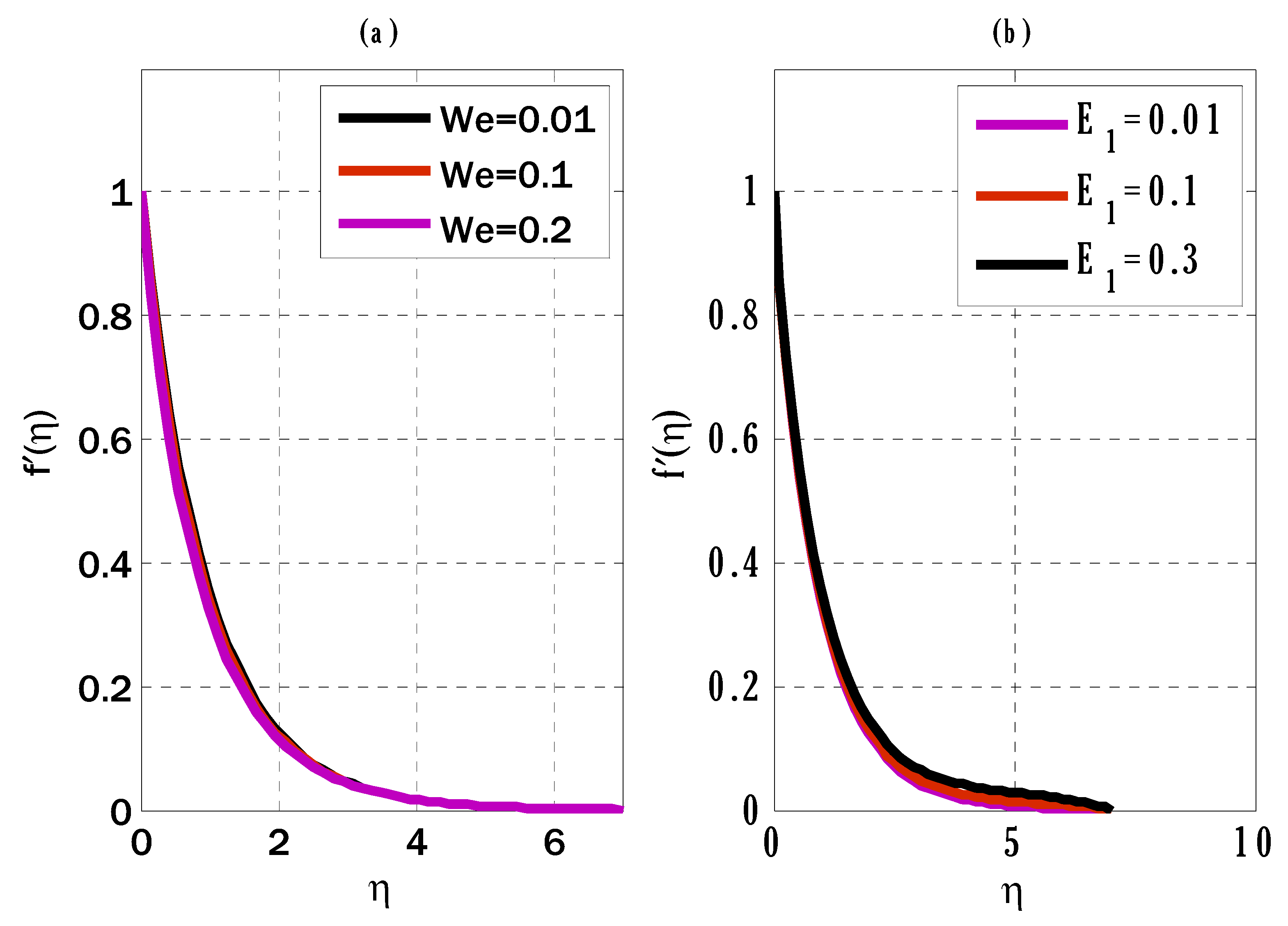
| Number of Elements/Grid Points | ||||||
|---|---|---|---|---|---|---|
| F.E.M | bvp4c | F.E.M | bvp4c | F.E.M | bvp4c | |
| 0.7148 | ||||||
| 0.7148 | ||||||
| Khan & Pop [45] | Srinivasulu & Goud [46] | Present | |
|---|---|---|---|
| 0.01 | ||||
| γ | ||
|---|---|---|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arif, M.S.; Shatanawi, W.; Nawaz, Y. Finite Element Study of Electrical MHD Williamson Nanofluid Flow under the Effects of Frictional Heating in the View of Viscous Dissipation. Energies 2023, 16, 2778. https://doi.org/10.3390/en16062778
Arif MS, Shatanawi W, Nawaz Y. Finite Element Study of Electrical MHD Williamson Nanofluid Flow under the Effects of Frictional Heating in the View of Viscous Dissipation. Energies. 2023; 16(6):2778. https://doi.org/10.3390/en16062778
Chicago/Turabian StyleArif, Muhammad Shoaib, Wasfi Shatanawi, and Yasir Nawaz. 2023. "Finite Element Study of Electrical MHD Williamson Nanofluid Flow under the Effects of Frictional Heating in the View of Viscous Dissipation" Energies 16, no. 6: 2778. https://doi.org/10.3390/en16062778
APA StyleArif, M. S., Shatanawi, W., & Nawaz, Y. (2023). Finite Element Study of Electrical MHD Williamson Nanofluid Flow under the Effects of Frictional Heating in the View of Viscous Dissipation. Energies, 16(6), 2778. https://doi.org/10.3390/en16062778









