Wind Forecast at Medium Voltage Distribution Networks
Abstract
1. Introduction
1.1. Motivation
1.2. State of the Art on Wind Power Forecast Methods
1.3. Contributions
- The development and implementation of a framework to predict wind power generation at the MV level. Performing the forecast at the MV level presents several challenges when compared to the forecast at other scales. At MV, information coming directly from the wind farm is not available, only the power measurements at the substations and the numerical weather predictions in areas of 14 km2 above the wind farm are available, making these data less accurate than if one had the information specifically at a wind farm level. In comparison to the forecast at the regional or national level, the prediction at the MV level is more complicated because wind farms are considered separately, which means that the error in the forecast has a direct impact on the accuracy of the model. At higher levels, several wind farms are considered at the same time, which means that the error in the power generation forecast of a specific wind farm can be minimal or less significant when compared to the overall system. It is important to notice that the secondary substations are normally installed in wind farms but are operated by the DSO. The predictions are used to evaluate the impacts of the wind farms in the distribution system, and, because of that, it is not possible to perform the forecast for more than one wind farm at the same time. One of the requirements of the proposed method is to provide the forecast in a very efficient way in terms of computational time. The main reason for this is that the number of secondary substations operated by a DSO that can arrive at more than 100,000, including the ones used for consumers and for distributed generation.
- The implementation and comparison of several forecasting methods, namely Persistence, Auto-Regressive (AR), Auto-Regressive with Exogenous Variable (ARX), Long Short-Term Memory (LSTM) neural network, XGBOOST, Random Forest (RF), Decision Trees (DTs) and Support Vector Machine (SVM), applied to a case study focused on wind power generation.
- A 20% improvement on the performance of the forecasting model that the Portuguese DSO is currently using, which means that the final XGBOOST model developed in this work could be employed by the DSO for future forecasts, to predict wind power generation more accurately and within a short computation time.
1.4. Paper Organization
2. Wind Forecast at the Secondary Substations Level Framework
2.1. Data
2.2. Pre-Processing
- If the missing data correspond to one hour (four data points) or less, the interpolation approach is used. Since only a small number of values are missing, a straight line between both sides gives a good approximation of the missing values.
- From one hour (four data points) to one day (96 data points) of missing data, an approach based on adjusting the profile of the previous day is used. It considers the time for when the missing data are found and also the previous day’s information for that specific moment, to make a normalization and to adapt it to the current day.
- If the missing data proceeds from one day (96 data points) to one week of 5 days (480 data points), the median approach is used, but in this case, the day of the week and the exact time for when the data are missing is also considered. It is relevant to mention at this point that only real values contribute to the median; values created by the missing data algorithm are not taken into account in the median calculation.
- For more than one week (more than 480 data points) of missing values, the gap is not filled because creating artificial values for long periods of time may have a negative effect on the forecast models, and consequently, on the results. The approach, in this case, is to remove the dates that contain large periods of missing data from the training set, as long as the minimum length defined for the training set is respected.
2.3. Exploratory Data Analysis and Feature Selection
2.4. Forecasting Models
- Training set, the data used by the model to discover and to learn patterns between the features and the forecast variable, power.
- Test set, the data on which the power predictions are generated. It corresponds to unseen data used to evaluate the performance of the model.
2.4.1. Persistence
2.4.2. Auto-Regressive (AR)
2.4.3. Auto-Regressive with Exogenous Variable (ARX)
2.4.4. Long Short-Term Memory (LSTM) Neural Network
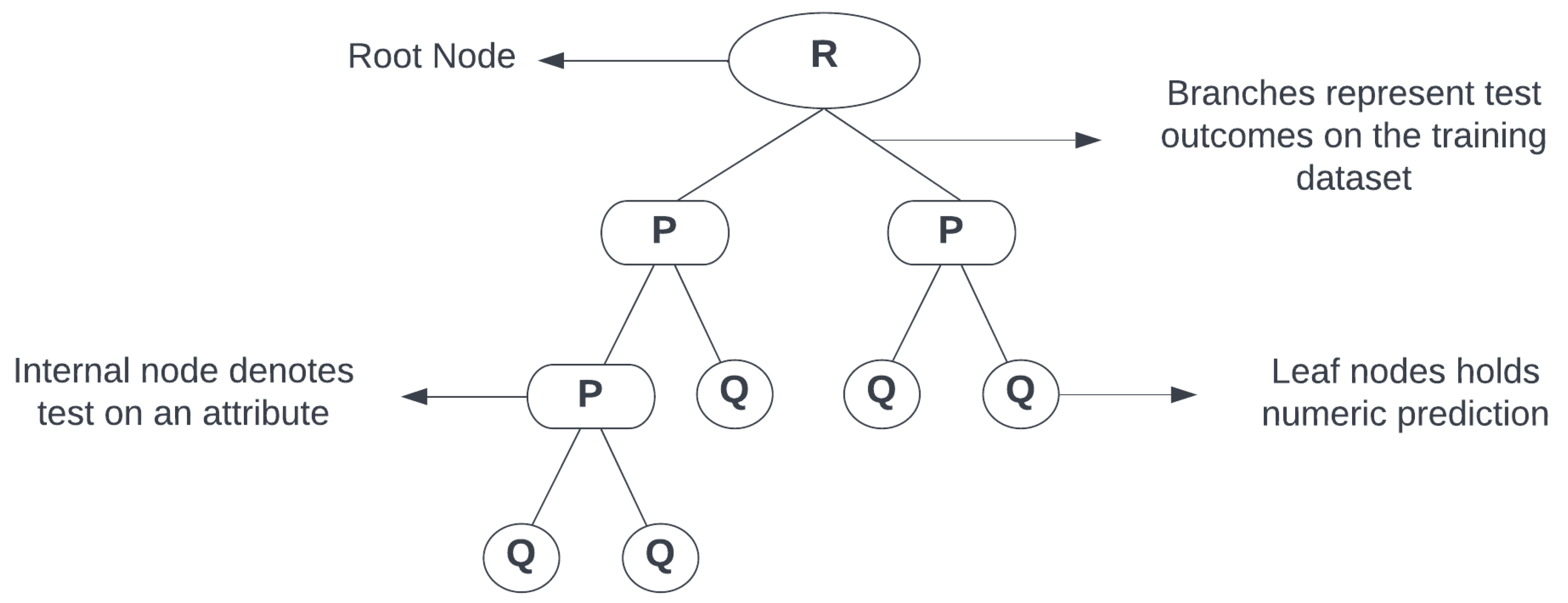
2.4.5. Decision Trees (DTs)
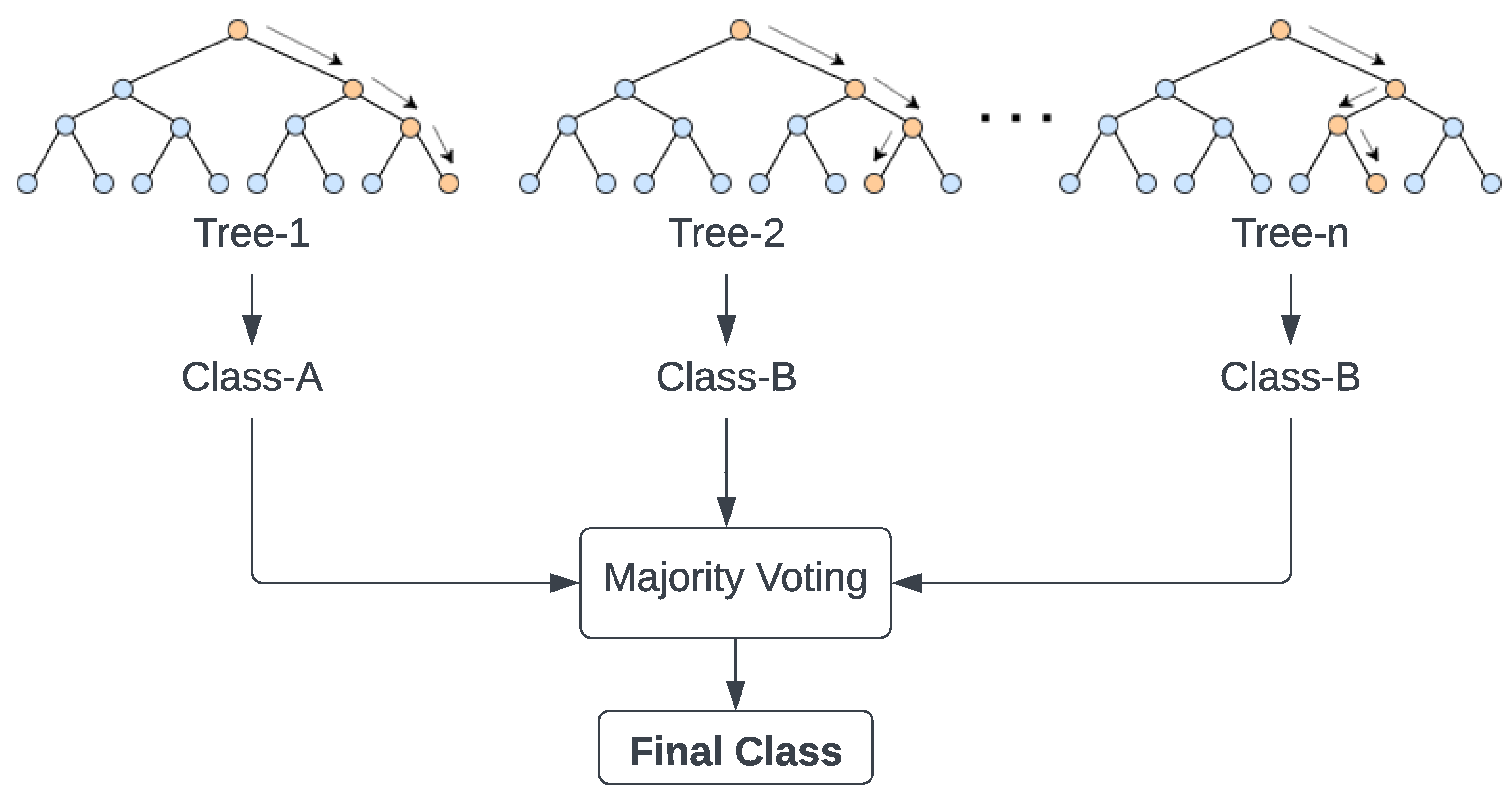
2.4.6. Random Forest (RF)
2.4.7. Extreme Gradient Boosting (XGBOOST)
2.4.8. Support Vector Machine (SVM)
2.5. Post-Processing
- . The predicted power cannot be negative. In the case where there are negative values, they are adjusted to 0.
- . The predicted power cannot be higher than the installed capacity of the wind farm. In this case, the maximum forecast value is limited to the installed capacity.
2.6. Validation
3. Results and Discussion
3.1. WPGF Models
3.2. XGBOOST, Adjusting Training, and Test Periods
- Combination 1: 6 months training (January–June of 2021) and 6 months forecast (July–December of 2021).
- Combination 2: 7 months training (January–July of 2021) and 5 months forecast (August–December of 2021).
- Combination 3: 8 months training (January–August of 2021) and 4 months forecast (September–December of 2021).
- Combination 4: 9 months training (January–September of 2021) and 3 months forecast (October–December of 2021).
- Combination 5: 10 months training (January–October of 2021) and 2 months forecast (November–December of 2021).
- Combination 6: 11 months training (January–November of 2021) and 1 month forecast (December of 2021).
- Combination 7: 1 year training (January–December of 2020) and 6 months forecast (January–June of 2021).
- Combination 8: 1 year training (January–December of 2020) and 1 year forecast (January–December of 2021).
3.3. XGBOOST Hyperparameter Tuning
- max depth: Maximum depth per tree. A deeper tree might increase the performance, but also the complexity and the chances to overfit. The value must be an integer greater than 0. The default is 6.
- learning rate: Determines the step size at each iteration while the model optimizes toward its objective. A low learning rate makes computation slower and requires more rounds to achieve the same reduction in residual error as a model with a high learning rate. The value must be between 0 and 1. The default is 0.3.
- n estimators: The number of trees in our ensemble. Equivalent to the number of boosting rounds. The value must be an integer that is greater than 0. The default is 100.
- colsample bytree: Represents the fraction of columns to be randomly sampled for each tree. It might improve overfitting. The value must be between 0 and 1. The default is 1.
- sub-sample: Represents the fraction of observations to be sampled for each tree. Lower values prevent overfitting but might lead to underfitting. The value must be between 0 and 1. The default is 1.
- min child weight: Defines the minimum sum of weights of all observations required in a child. It is used to control overfitting. The larger it is, the more conservative the algorithm will be. The value must be an integer greater than 0. The default is 1.
3.4. XGBOOST with Backtesting
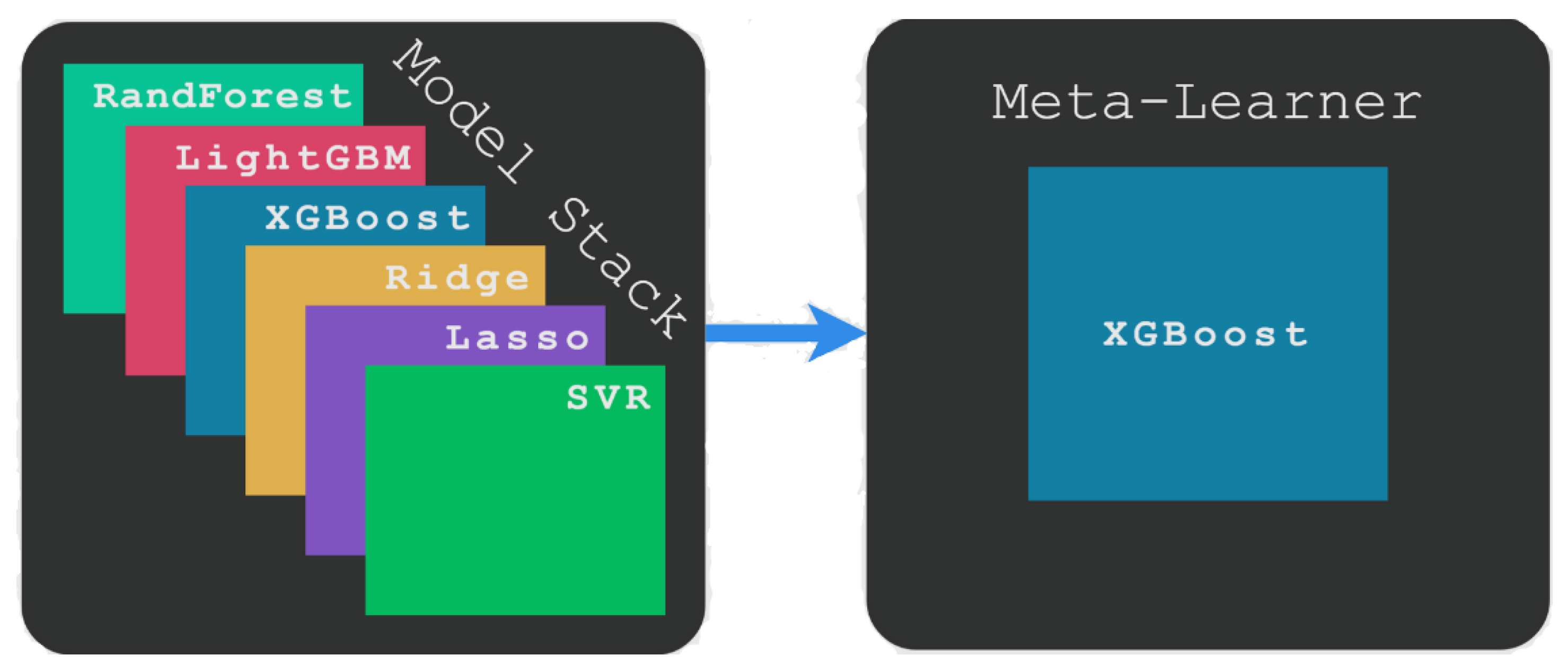
3.5. Stacking
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ANFIS | Adaptative Neural Fuzzy Inference System |
| ANNs | Artificial Neural Networks |
| AR | Auto-Regressive |
| ARX | Auto-Regressive with Exogenous Variable |
| ARIMA | Auto-Regressive Integrated Moving Average |
| ARMA | Auto-Regressive Moving Average |
| BPNN | Back-Propagation Neural Network |
| DSO | Distribution System Operator |
| DTs | Decision Trees |
| EDA | Exploratory Data Analysis |
| EU | European Union |
| FFNN | Feed Forward Neural Network |
| IPMA | Instituto Português do Mar e da Atmosfera |
| LGBM | Light Gradient Boosting Machine |
| LSTM | Long Short-Term Memory |
| MAPE | Mean Absolute Percentage Error |
| ML | Machine Learning |
| MV | Medium Voltage |
| NWP | Numerical Weather Prediction |
| PV | Solar Photovoltaic |
| RESs | Renewable Energy Sources |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| RNN | Recurrent Neural Network |
| RRMSE | Relative Root Mean Square Error |
| SVM | Support Vector Machine |
| TSO | Transmission System Operator |
| WEPs | Weather Ensemble Predictions |
| WPGF | Wind Power Generation Forecast |
| XGBOOST | Extreme Gradient Boosting |
References
- Micheli, S. Policy Strategy Cooperation in the 2030 Climate and Energy Policy Framework. Atl. Econ. J. 2020, 48, 265–267. [Google Scholar] [CrossRef]
- Javed, M.S.; Ma, T.; Jurasz, J.; Amin, M.Y. Solar and wind power generation systems with pumped hydro storage: Review and future perspectives. Renew. Energy 2020, 148, 176–192. [Google Scholar] [CrossRef]
- GWEC Global Wind Energy Council. Available online: https://gwec.net/global-wind-report-2021/ (accessed on 24 April 2022).
- Taylor, J.W.; McSharry, P.E.; Buizza, R. Wind power density forecasting using ensemble predictions and time series models. IEEE Trans. Energy Convers. 2009, 24, 775–782. [Google Scholar] [CrossRef]
- Machado, E.P.; Morais, H.; Pinto, T. Wind Speed Forecasting Using Feed-Forward Artificial Neural Network. In Distributed Computing and Artificial Intelligence, Proceedings of the 18th International Conference, DCAI 2021, Salamanca, Spain, 6–8 October 2021; Lecture Notes in Networks and Systems; Matsui, K., Omatu, S., Yigitcanlar, T., González, S.R., Eds.; Springer: Cham, Stwitzerland, 2022; Volume 327. [Google Scholar] [CrossRef]
- Sijakovic, N.; Terzic, A.; Fotis, G.; Mentis, I.; Zafeiropoulou, M.; Maris, T.I.; Zoulias, E.; Elias, C.; Ristic, V.; Vita, V. Active System Management Approach for Flexibility Services to the Greek Transmission and Distribution System. Energies 2022, 15, 6134. [Google Scholar] [CrossRef]
- Zafeiropoulou, M.; Mentis, I.; Sijakovic, N.; Terzic, A.; Fotis, G.; Maris, T.I.; Vita, V.; Zoulias, E.; Ristic, V.; Ekonomou, L. Forecasting Transmission and Distribution System Flexibility Needs for Severe Weather Condition Resilience and Outage Management. Appl. Sci. 2022, 12, 7334. [Google Scholar] [CrossRef]
- Wilczek, P. Connecting the dots: Distribution grid investments to power the energy transition. In Proceedings of the 11th Solar & Storage Power System Integration Workshop (SIW 2021), Online, 28 September 2021; Volume 2021, pp. 1–18. [Google Scholar] [CrossRef]
- Vargas, S.A.; Esteves, G.R.T.; Maçaira, P.M.; Bastos, B.Q.; Oliveira, F.L.C.; Souza, R.C. Wind power generation: A review and a research agenda. J. Clean. Prod. 2019, 218, 850–870. [Google Scholar] [CrossRef]
- Ernst, B.; Oakleaf, B.; Ahlstrom, M.L.; Lange, M.; Moehrlen, C.; Lange, B.; Focken, U.; Rohrig, K. Predicting the wind. IEEE Power Energy Mag. 2007, 5, 78–89. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the IEEE North American Power Symposium, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Wu, Y.K.; Hong, J.S. A literature review of wind forecasting technology in the world. In Proceedings of the 2007 IEEE Lausanne Powertech, Lausanne, Switzerland, 1–5 July 2007; pp. 504–509. [Google Scholar] [CrossRef]
- Gallego, C.; Pinson, P.; Madsen, H.; Costa, A.; Cuerva, A. Influence of local wind speed and direction on wind power dynamics—Application to offshore very short-term forecasting. Appl. Energy 2011, 88, 4087–4096. [Google Scholar] [CrossRef]
- Duran, M.J.; Cros, D.; Riquelme, J. Short-term wind power forecast based on ARX models. J. Energy Eng. 2007, 133, 172–180. [Google Scholar] [CrossRef]
- Machado, E.; Pinto, T.; Guedes, V.; Morais, H. Electrical Load Demand Forecasting Using Feed-Forward Neural Networks. Energies 2021, 14, 7644. [Google Scholar] [CrossRef]
- Catalão, J.D.S.; Pousinho, H.M.I.; Mendes, V.M.F. Short-term wind power forecasting in Portugal by neural networks and wavelet transform. Renew. Energy 2011, 36, 1245–1251. [Google Scholar] [CrossRef]
- Mabel, M.C.; Fernandez, E. Analysis of wind power generation and prediction using ANN: A case study. Renew. Energy 2008, 33, 986–992. [Google Scholar] [CrossRef]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A critical review of wind power forecasting methods—Past, present and future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Jung, J.; Broadwater, R.P. Current status and future advances for wind speed and power forecasting. Renew. Sustain. Energy Rev. 2014, 31, 762–777. [Google Scholar] [CrossRef]
- Khazaei, S.; Ehsan, M.; Soleymani, S.; Mohammadnezhad-Shourkaei, H. A high-accuracy hybrid method for short-term wind power forecasting. Energy 2022, 238, 122020. [Google Scholar] [CrossRef]
- Zheng, H.; Wu, Y. A xgboost model with weather similarity analysis and feature engineering for short-term wind power forecasting. Appl. Sci. 2019, 9, 3019. [Google Scholar] [CrossRef]
- Kassa, Y.; Zhang, J.H.; Zheng, D.H.; Wei, D. Short term wind power prediction using ANFIS. In Proceedings of the 2016 IEEE International Conference On Power And Renewable Energy (ICPRE), Shanghai, China, 21–23 October 2016; pp. 338–393. [Google Scholar] [CrossRef]
- Fugon, L.; Juban, J.; Kariniotakis, G. Data mining for wind power forecasting. In Proceedings of the 2008 European Wind Energy Conference & Exhibition (EWEC), Brussels, Belgium, 31 March–3 April 2008; 6pAvailable online: https://hal-mines-paristech.archives-ouvertes.fr/hal-00506101 (accessed on 16 February 2023).
- Feature Selection Techniques in Machine Learning. Available online: https://www.javatpoint.com/feature-selection-techniques-in-machine-learning (accessed on 18 May 2022).
- Santamaría-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Akouemo, H.N.; Povinelli, R.J. Data improving in time series using ARX and ANN models. IEEE Trans. Power Syst. 2017, 32, 3352–3359. [Google Scholar] [CrossRef]
- Moghar, A.; Hamiche, M. Stock market prediction using LSTM recurrent neural network. Procedia Comput. Sci. 2020, 170, 1168–1173. [Google Scholar] [CrossRef]
- Decision Trees in Machine Learning Explained. Available online: https://www.seldon.io/decision-trees-in-machine-learning (accessed on 25 May 2022).
- Chaudhary, A.; Sharma, A.; Kumar, A.; Dikshit, K.; Kumar, N. Short term wind power forecasting using machine learning techniques. J. Stat. Manag. Syst. 2020, 23, 145–156. [Google Scholar] [CrossRef]
- Ahmadi, A.; Nabipour, M.; Mohammadi-Ivatloo, B.; Amani, A.M.; Rho, S.; Piran, M.J. Long-term wind power forecasting using tree-based learning algorithms. IEEE Access 2020, 8, 151511–151522. [Google Scholar] [CrossRef]
- Jørgensen, K.L.; Shaker, H.R. Wind power forecasting using machine learning: State of the art, trends and challenges. In Proceedings of the 2020 IEEE 8th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2020; pp. 44–50. [Google Scholar] [CrossRef]
- Dhieb, N.; Ghazzai, H.; Besbes, H.; Massoud, Y. Extreme gradient boosting machine learning algorithm for safe auto insurance operations. In Proceedings of the 2019 IEEE International Conference on Vehicular Electronics and Safety (ICVES), Cairo, Egypt, 4–6 September 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Hyperparameter Tuning in Python: A Complete Guide. Available online: https://neptune.ai/blog/hyperparameter-tuning-in-python-complete-guide (accessed on 5 June 2022).
- XGBoost: A Complete Guide to Fine-Tune and Optimize Your Model. Available online: https://towardsdatascience.com/xgboost-fine-tune-and-optimize-your-model-23d996fab663 (accessed on 7 June 2022).
- Skforecast: Time Series Forecasting with Python and Scikit-Learn. Available online: https://www.cienciadedatos.net/documentos/py27-time-series-forecasting-python-scikitlearn.html (accessed on 3 August 2022).
- Stack Machine Learning Models—Get Better Results. Available online: https://mlfromscratch.com/model-stacking-explained/ (accessed on 20 August 2022).

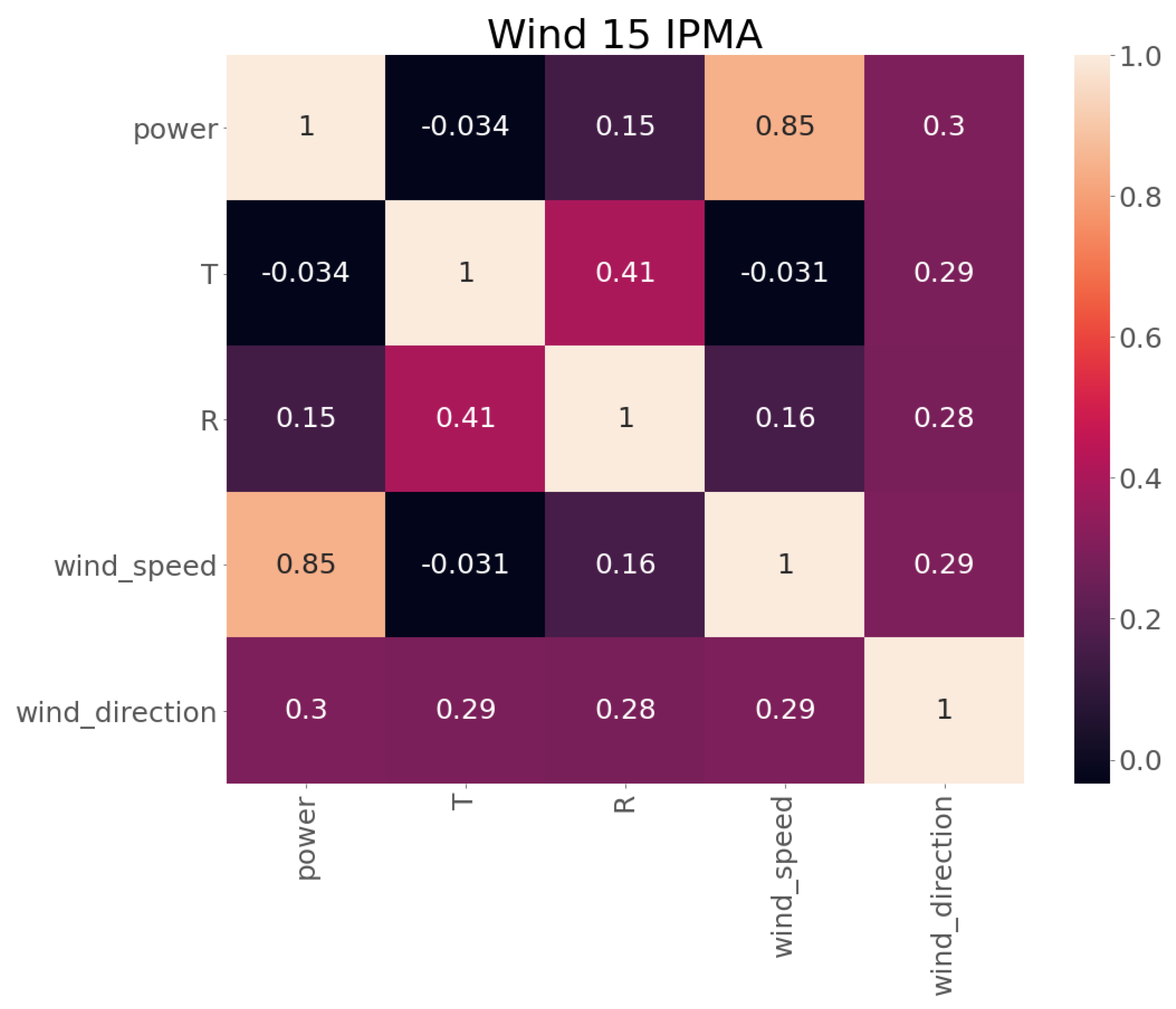




| Measure | Power (kW) | T (K) | R (W/m2) | Wind Speed (m/s) | Wind Direction () |
|---|---|---|---|---|---|
| Mean | 7834.07 | 288.58 | 735.84 | 7.01 | 241.51 |
| Std Dev | 7177.94 | 4.95 | 729.82 | 2.80 | 109.90 |
| Min | 0.00 | 272.94 | 0.00 | 0.14 | 0.02 |
| 25th Perc | 1600.00 | 285.25 | 86.43 | 4.93 | 157.24 |
| 50th Perc | 5610.00 | 288.11 | 524.35 | 6.92 | 284.33 |
| 75th Perc | 13,102.50 | 291.45 | 1193.59 | 9.08 | 338.96 |
| Max | 29,705.29 | 310.58 | 2814.88 | 16.32 | 359.98 |
| Wind Farm | Persistence (%) | AR (%) | ARX (%) | DSO (%) |
|---|---|---|---|---|
| 1 | 24.594 | 16.886 | 15.384 | 13.482 |
| 2 | 37.717 | 35.105 | 19.248 | 16.187 |
| 3 | 14.895 | 12.396 | 12.515 | 41.013 |
| 4 | 35.714 | 32.035 | 28.131 | 19.850 |
| 5 | 30.814 | 26.713 | 20.364 | 14.874 |
| 6 | 32.897 | 27.102 | 21.185 | 18.929 |
| 7 | 35.403 | 28.947 | 19.673 | 50.877 |
| 8 | 38.103 | 32.230 | 27.287 | 21.536 |
| 9 | 30.248 | 26.306 | 20.168 | 14.372 |
| 10 | 34.136 | 30.781 | 20.690 | 45.416 |
| 11 | 31.939 | 29.759 | 23.380 | 29.586 |
| 12 | 24.222 | 19.232 | 17.073 | 15.593 |
| 13 | 33.787 | 29.940 | 18.394 | 17.470 |
| 14 | 38.087 | 30.688 | 25.111 | 21.550 |
| 15 | 26.191 | 20.947 | 13.660 | 11.954 |
| 16 | 37.940 | 26.028 | 36.241 | 21.983 |
| 17 | 34.902 | 23.803 | 29.912 | 19.541 |
| 18 | 34.712 | 28.478 | 33.975 | 26.619 |
| 19 | 31.060 | 19.225 | 24.680 | 18.242 |
| 20 | 29.404 | 21.114 | 26.565 | 18.998 |
| Average | 31.838 | 27.522 | 21.046 | 22.904 |
| Wind Farm | LSTM (%) | DT (%) | RF (%) | XGBOOST (%) | SVM (%) | DSO (%) |
|---|---|---|---|---|---|---|
| 1 | 23.209 | 19.543 | 12.371 | 12.451 | 19.492 | 13.482 |
| 2 | 24.413 | 24.596 | 19.952 | 17.637 | 31.561 | 16.187 |
| 3 | 8.288 | 15.671 | 11.257 | 10.549 | 10.399 | 41.013 |
| 4 | 29.888 | 28.721 | 28.698 | 22.649 | 47.410 | 19.850 |
| 5 | 22.727 | 21.783 | 14.873 | 13.617 | 29.755 | 14.874 |
| 6 | 22.555 | 25.147 | 23.205 | 19.273 | 35.377 | 18.929 |
| 7 | 29.426 | 32.046 | 21.851 | 21.101 | 20.949 | 50.877 |
| 8 | 25.833 | 25.484 | 25.398 | 24.427 | 39.240 | 21.536 |
| 9 | 26.900 | 23.291 | 17.296 | 17.472 | 24.699 | 14.372 |
| 10 | 26.700 | 22.602 | 21.286 | 16.374 | 28.953 | 45.416 |
| 11 | 21.877 | 25.785 | 22.783 | 21.412 | 34.463 | 29.586 |
| 12 | 19.562 | 23.656 | 17.673 | 17.509 | 23.907 | 15.593 |
| 13 | 21.859 | 17.593 | 18.195 | 12.947 | 26.973 | 17.470 |
| 14 | 26.925 | 29.963 | 26.919 | 28.127 | 36.026 | 21.550 |
| 15 | 22.833 | 17.059 | 12.828 | 11.651 | 15.297 | 11.954 |
| 16 | 29.310 | 25.150 | 22.071 | 20.628 | 37.585 | 21.983 |
| 17 | 27.285 | 26.611 | 25.206 | 21.862 | 45.642 | 19.541 |
| 18 | 24.323 | 31.979 | 28.080 | 26.764 | 29.098 | 26.619 |
| 19 | 21.575 | 27.072 | 18.103 | 17.219 | 24.802 | 18.242 |
| 20 | 27.717 | 23.865 | 19.042 | 18.595 | 34.802 | 18.998 |
| Average | 24.160 | 24.381 | 20.354 | 18.613 | 29.822 | 22.904 |
| Wind Farm | Max Depth | Learning Rate | n Estimators | Colsample Bytree | Subsample | Min Child Weight |
|---|---|---|---|---|---|---|
| 1 | 2 | 0.050 | 200 | 0.7 | 0.7 | 10 |
| 2 | 2 | 0.050 | 500 | 1.0 | 0.7 | 10 |
| 3 | 2 | 0.001 | 385 | 1.0 | 1.0 | 5 |
| 4 | 3 | 0.030 | 200 | 1.0 | 0.7 | 5 |
| 5 | 3 | 0.030 | 200 | 1.0 | 1.0 | 10 |
| 6 | 3 | 0.030 | 500 | 1.0 | 0.5 | 10 |
| 7 | 2 | 0.017 | 610 | 0.7 | 1.0 | 5 |
| 8 | 3 | 0.050 | 200 | 1.0 | 0.5 | 5 |
| 9 | 2 | 0.050 | 500 | 1.0 | 0.7 | 10 |
| 10 | 2 | 0.005 | 715 | 1.0 | 1.0 | 3 |
| 11 | 3 | 0.022 | 345 | 1.0 | 0.7 | 10 |
| 12 | 2 | 0.050 | 200 | 1.0 | 0.5 | 3 |
| 13 | 2 | 0.050 | 100 | 1.0 | 1.0 | 10 |
| 14 | 3 | 0.100 | 100 | 0.7 | 1.0 | 10 |
| 15 | 2 | 0.025 | 502 | 1.0 | 1.0 | 5 |
| 16 | 2 | 0.048 | 181 | 1.0 | 0.7 | 5 |
| 17 | 3 | 0.054 | 208 | 1.0 | 1.0 | 5 |
| 18 | 2 | 0.046 | 217 | 0.7 | 0.7 | 3 |
| 19 | 2 | 0.050 | 500 | 1.0 | 0.7 | 10 |
| 20 | 2 | 0.050 | 500 | 1.0 | 0.7 | 10 |
| Average | 2 | 0.04 | 343 | 0.9 | 0.8 | 7 |
| Wind Farm | Best Results until Now (%) | Best Combination (%) | Average Values (%) | DSO (%) |
|---|---|---|---|---|
| 1 | 11.247 | 10.321 | 10.338 | 10.193 |
| 2 | 13.775 | 12.835 | 12.860 | 13.443 |
| 3 | 8.558 | 7.586 | 11.194 | 26.794 |
| 4 | 17.922 | 17.070 | 17.497 | 17.293 |
| 5 | 11.947 | 11.066 | 11.174 | 11.221 |
| 6 | 12.886 | 11.770 | 12.125 | 12.321 |
| 7 | 14.374 | 13.547 | 13.567 | 39.519 |
| 8 | 15.996 | 14.452 | 14.756 | 15.510 |
| 9 | 14.989 | 14.279 | 14.254 | 11.981 |
| 10 | 15.495 | 14.246 | 14.404 | 30.680 |
| 11 | 14.400 | 13.450 | 13.526 | 19.459 |
| 12 | 10.595 | 9.838 | 9.909 | 10.538 |
| 13 | 15.012 | 14.076 | 14.175 | 14.034 |
| 14 | 16.386 | 15.358 | 15.459 | 15.931 |
| 15 | 10.804 | 9.729 | 9.796 | 10.308 |
| 16 | 19.087 | 16.147 | 16.237 | 18.055 |
| 17 | 15.345 | 14.352 | 14.732 | 15.129 |
| 18 | 17.286 | 16.302 | 16.335 | 16.313 |
| 19 | 13.685 | 12.660 | 12.726 | 12.689 |
| 20 | 15.350 | 14.525 | 14.555 | 15.140 |
| Average | 14.257 | 13.180 | 13.481 | 16.827 |
| Wind Farm | Best Results (%) | Backtesting (%) | DSO (%) |
|---|---|---|---|
| 1 | 10.338 | 10.053 | 10.193 |
| 2 | 12.860 | 12.568 | 13.443 |
| 3 | 11.194 | 9.212 | 26.794 |
| 4 | 17.497 | 16.475 | 17.293 |
| 5 | 11.174 | 10.683 | 11.221 |
| 6 | 12.125 | - | 12.321 |
| 7 | 13.567 | 13.247 | 39.519 |
| 8 | 14.756 | 14.109 | 15.510 |
| 9 | 14.254 | 13.740 | 11.981 |
| 10 | 14.404 | 14.031 | 30.680 |
| 11 | 13.526 | 12.901 | 19.459 |
| 12 | 9.909 | 9.355 | 10.538 |
| 13 | 14.175 | 13.983 | 14.034 |
| 14 | 15.459 | 14.809 | 15.931 |
| 15 | 9.796 | 9.575 | 10.308 |
| 16 | 16.237 | 17.668 | 18.055 |
| 17 | 14.732 | 14.153 | 15.129 |
| 18 | 16.335 | 15.899 | 16.313 |
| 19 | 12.726 | 12.547 | 12.689 |
| 20 | 14.555 | 13.832 | 15.140 |
| Average | 13.481 | 13.097 | 16.827 |
| Wind Farm | Best Results (%) | Stacking (%) | DSO (%) |
|---|---|---|---|
| 1 | 10.338 | 10.358 | 10.193 |
| 2 | 12.860 | 12.856 | 13.443 |
| 3 | 11.194 | 8.793 | 26.794 |
| 4 | 17.497 | 17.685 | 17.293 |
| 5 | 11.174 | 11.136 | 11.221 |
| 6 | 12.125 | 12.225 | 12.321 |
| 7 | 13.567 | 13.589 | 39.519 |
| 8 | 14.756 | 14.619 | 15.510 |
| 9 | 14.254 | 14.077 | 11.981 |
| 10 | 14.404 | 14.731 | 30.680 |
| 11 | 13.526 | 13.569 | 19.459 |
| 12 | 9.909 | 9.974 | 10.538 |
| 13 | 14.175 | 14.585 | 14.034 |
| 14 | 15.459 | 15.394 | 15.931 |
| 15 | 9.796 | 9.853 | 10.308 |
| 16 | 16.237 | 16.288 | 18.055 |
| 17 | 14.732 | 14.912 | 15.129 |
| 18 | 16.335 | 16.134 | 16.313 |
| 19 | 12.726 | 12.689 | 12.689 |
| 20 | 14.555 | 14.375 | 15.140 |
| Average | 13.481 | 13.392 | 16.827 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amezquita, H.; Carvalho, P.M.S.; Morais, H. Wind Forecast at Medium Voltage Distribution Networks. Energies 2023, 16, 2887. https://doi.org/10.3390/en16062887
Amezquita H, Carvalho PMS, Morais H. Wind Forecast at Medium Voltage Distribution Networks. Energies. 2023; 16(6):2887. https://doi.org/10.3390/en16062887
Chicago/Turabian StyleAmezquita, Herbert, Pedro M. S. Carvalho, and Hugo Morais. 2023. "Wind Forecast at Medium Voltage Distribution Networks" Energies 16, no. 6: 2887. https://doi.org/10.3390/en16062887
APA StyleAmezquita, H., Carvalho, P. M. S., & Morais, H. (2023). Wind Forecast at Medium Voltage Distribution Networks. Energies, 16(6), 2887. https://doi.org/10.3390/en16062887







