Preferential Concentration of Particles in Forced Turbulent Flows: Effects of Gravity
Abstract
:1. Introduction
2. Numerical Method
2.1. Carrier Phase
2.2. Dispersed Phase
3. Numerical Configuration
4. Effects of Gravity on Preferential Concentration
4.1. Spatial Distribution of Particles
4.2. Particle Preferential Concentration and Vorticity
4.3. Box-Counting Measurement
4.4. Particle Number Density
5. Effects of Gravity on Slip Velocity
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Drag coefficient | |
| Energy spectrum | |
| Froude number | |
| Particle Reynolds number | |
| Turbulent Reynolds number | |
| Taylor Reynolds number | |
| Stokes number | |
| D | Particle diameter |
| I | Box index |
| L | Characteristic size of large eddies |
| Computational domain size in direction i | |
| N | Particle number density |
| Mean velocity of the gas | |
| Particle settling velocity | |
| k | Turbulent kinetic energy |
| Dynamic viscosity of gas | |
| Particle mass | |
| Slip velocity | |
| Gas flow velocity | |
| Gravity | |
| Particle velocity | |
| Drag force | |
| Turbulent dissipation rate | |
| Kolmogorov length scale | |
| wave number magnitude | |
| Fluid viscosity | |
| Gas density | |
| Particle density | |
| Particle relaxation time | |
| Particle volume fraction | |
| Kolmogorov time scale | |
| Vorticity of gas flow | |
| Mean vorticity magnitude | |
| BI | Box index |
| HIT | Homogeneous isotropic turbulence |
| Probability density function | |
| RMS | Root mean square |
References
- Williams, R.; Follows, M. Ocean Dynamics and the Carbon Cycle: Principles and Mechanisms; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Javid, K.; Ali, N.; Asghar, Z. Rheological and magnetic effects on a fluid flow in a curved channel with different peristaltic wave profiles. J. Braz. Soc. Mech. Sci. 2019, 41, 483. [Google Scholar] [CrossRef]
- Gai, G.; Kudriakov, S.; Rogg, B.; Hadjadj, A.; Studer, E.; Thomine, O. Numerical study on laminar flame velocity of hydrogen-air combustion under water spray effects. Int. J. Hydrog. Energy 2019, 44, 17015–17029. [Google Scholar] [CrossRef]
- Asghar, Z.; Javid, K.; Waqas, M.; Ghaffari, A.; Khan, W.A. Cilia-driven fluid flow in a curved channel: Effects of complex wave and porous medium. Fluid Dyn. Res. 2020, 52, 015514. [Google Scholar] [CrossRef]
- Borgnino, M.; Arrieta, J.; Boffetta, G.; Lillo, F.D.; Tuval, I. Turbulence induces clustering and segregation of non-motile, buoyancy-regulating phytoplankton. J. R. Soc. Interface 2019, 16, 20190324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, D.; Luo, K.; Fan, J. Modulation of turbulence by dispersed solid particles in a spatially developing flat-plate boundary layer. J. Fluid Mech. 2016, 802, 359–394. [Google Scholar] [CrossRef]
- Thomine, O. Development of Multi-Scale Methods for the Numerical Simulation of Diphasic Reactive Flows. Ph.D. Thesis, University of Rouen, Rouen, France, 2011. [Google Scholar]
- Thomine, O.; Gai, G.; Hadjadj, A.; Kudriakov, S. Phenomenology of a two-phase laminar flame interacting with a heated cylinder. Int. J. Heat Mass Transf. 2021, 168, 120867. [Google Scholar] [CrossRef]
- Squires, K.; Eaton, J. Particle response and turbulence modification in isotropic turbulence. Phys. Fluids A Fluid Dyn. 1990, 2, 1191–1203. [Google Scholar] [CrossRef]
- Eaton, J.; Fessler, J. Particle response and turbulence modification in isotropic turbulence. Int. J. Multiph. Flow. 1994, 20, 169–209. [Google Scholar] [CrossRef]
- Sigurgeirsson, H.; Stuart, A. A model for preferential concentration. Phys. Fluids 2002, 14, 4352–4361. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.P.; Maxey, M. Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 1993, 256, 27–68. [Google Scholar] [CrossRef] [Green Version]
- Balachandar, S.; Eaton, J. Turbulent Dispersed Multiphase Flow. Annu. Rev. Fluid Mech. 2010, 42, 111–133. [Google Scholar] [CrossRef]
- Sundaram, S.; Collins, L. A numerical study of the modulation of isotropic turbulence by suspended particles. J. Fluid Mech. 1999, 379, 105–143. [Google Scholar] [CrossRef]
- Mallouppas, G.; George, W.; van Wachem, B. Dissipation and inter-scale transfer in fully coupled particle and fluid motions in homogeneous isotropic forced turbulence. Int. J. Heat Fluid Flow 2017, 67, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Ferrante, A.; Elghobashi, S. On the physical mechanisms of two-way coupling in particle-laden isotropic turbulence. Phys. Fluids 2003, 15, 315–329. [Google Scholar] [CrossRef]
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Maxey, M. The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 1987, 174, 441–465. [Google Scholar] [CrossRef]
- Xiao, W.; Jin, T.; Luo, K.; Dai, Q.; Fan, J. Eulerian–Lagrangian direct numerical simulation of preferential accumulation of inertial particles in a compressible turbulent boundary layer. J. Fluid Mech. 2020, 903, A19. [Google Scholar] [CrossRef]
- Reeks, M. On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 1977, 83, 529–546. [Google Scholar] [CrossRef]
- Squires, K.; Eaton, J. Measurements of particle dispersion obtained from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 1991, 226, 1–35. [Google Scholar] [CrossRef]
- Onishi, R.; Takahashi, K.; Komori, S. Influence of gravity on collisions of monodispersed droplets in homogeneous isotropic turbulence. Phys. Fluids 2009, 21, 125108. [Google Scholar] [CrossRef] [Green Version]
- Chaisemartin, S.D. Modèles Eulériens et Simulation Numérique de la Dispersion Turbulente de Brouillards qui S’évaporent. Ph.D. Thesis, Ecole Centrale Paris, Gif-sur-Yvette, France, 2009. [Google Scholar]
- Petersen, A.; Baker, L.; Coletti, F. Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 2019, 864, 925–970. [Google Scholar] [CrossRef] [Green Version]
- Ireland, P.; Bragg, A.; Collins, L. The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 2016, 796, 659–711. [Google Scholar] [CrossRef] [Green Version]
- Berk, T.; Coletti, F. Dynamics of small heavy particles in homogeneous turbulence: A Lagrangian experimental study. J. Fluid Mech. 2021, 917, A47. [Google Scholar] [CrossRef]
- Innocenti, A.; Jaccod, A.; Popinet, S.; Chibbaro, S. Direct numerical simulation of bubble-induced turbulence. J. Fluid Mech. 2021, 918, A23. [Google Scholar] [CrossRef]
- Fréret, L.; Thomine, O.; Reveillon, J.; Chaisemartin, S.D.; Laurent, F.; Massot, M. On the role of preferential segregation in flame dynamics in polydisperse evaporating sprays. In Proceeding of the 2010 Summer Program; Center for Turbulence Research, Stanford University: Stanford, CA, USA, 2011; pp. 383–392. [Google Scholar]
- Pope, S. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar] [CrossRef]
- Reveillon, J.; Guichard, L.; Hauguel, R. Direct Numerical Simulation of Statistically Stationary One- and Two-Phase Turbulent Combustion: A Turbulent Injection Procedure. Flow Turbul. Combust. 2004, 73, 133–167. [Google Scholar] [CrossRef]
- Overholt, M.; Pope, S. A deterministic forcing scheme for direct numerical simulations of turbulence. Comput. Fluids 1998, 27, 11–28. [Google Scholar] [CrossRef]
- Reveillon, J.; Demoulin, F.X. Effects of the preferential segregation of droplets on evaporation and turbulent mixing. J. Fluid Mech. 2007, 583, 273–302. [Google Scholar] [CrossRef] [Green Version]
- Sabot, M. Eulerian Modeling and Numerical Methods for the Description of Turbulent Polydisperse Sprays. Ph.D. Thesis, Université Paris-Saclay, Gif-sur-Yvette, France, 2016. [Google Scholar]
- Mehrabadi, M.; Horwitz, J.; Subramaniam, S.; Mani, A. A direct comparison of particle-resolved and point-particle methods in decaying turbulence. J. Fluid Mech. 2018, 850, 336–369. [Google Scholar] [CrossRef]
- Gai, G.; Thomine, O.; Hadjadj, A.; Kudriakov, S. Modeling of particle cloud dispersion in compressible gas flows with shock waves. Phys. Fluids 2020, 32, 023301. [Google Scholar] [CrossRef]
- Woittiez, E.; Harm, J.; Portela, L. On the Combined Effects of Turbulence and Gravity on Droplet Collisions in Clouds: A Numerical Study. J. Atmos. Sci. 2009, 66, 1926–1943. [Google Scholar] [CrossRef]
- Rouson, D.; Eaton, J. On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 2001, 428, 149–169. [Google Scholar] [CrossRef]
- Monchaux, R.; Bourgoin, M.; Cartellier, A. Analyzing preferential concentration and clustering of inertial particles in turbulence. Int. J. Multiph. Flow 2012, 40, 1–18. [Google Scholar] [CrossRef]
- Letournel, R.; Laurent, F.; Massot, M.; Vié, A. Modulation of homogeneous and isotropic turbulence by sub-Kolmogorov particles: Impact of particle field heterogeneity. Int. J. Multiph. Flow 2020, 125, 103233. [Google Scholar] [CrossRef]
- Hogan, R.; Cuzzi, J. Stokes and Reynolds number dependence of preferential particle concentration in simulated three-dimensional turbulence. Phys. Fluids 2001, 13, 2938–2945. [Google Scholar] [CrossRef]
- Gai, G.; Hadjadj, A.; Kudriakov, S.; Mimouni, S.; Thomine, O. Numerical Study of Spray-Induced Turbulence Using Industrial Fire-Mitigation Nozzles. Energies 2021, 14, 1135. [Google Scholar] [CrossRef]
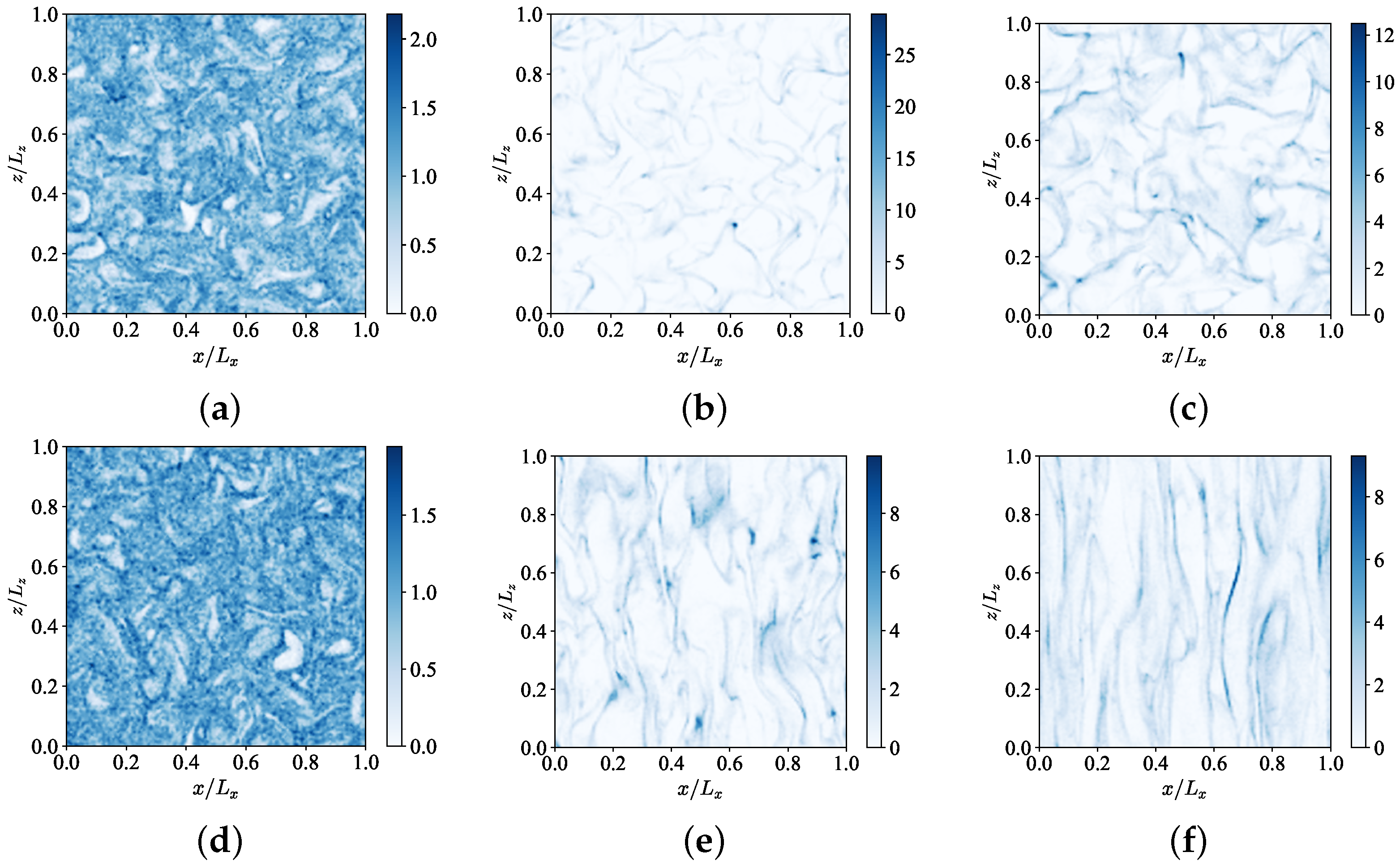

 ) and blue line: without gravity (
) and blue line: without gravity ( ). (a) ; (b) ; (c) ; (d) .
). (a) ; (b) ; (c) ; (d) .
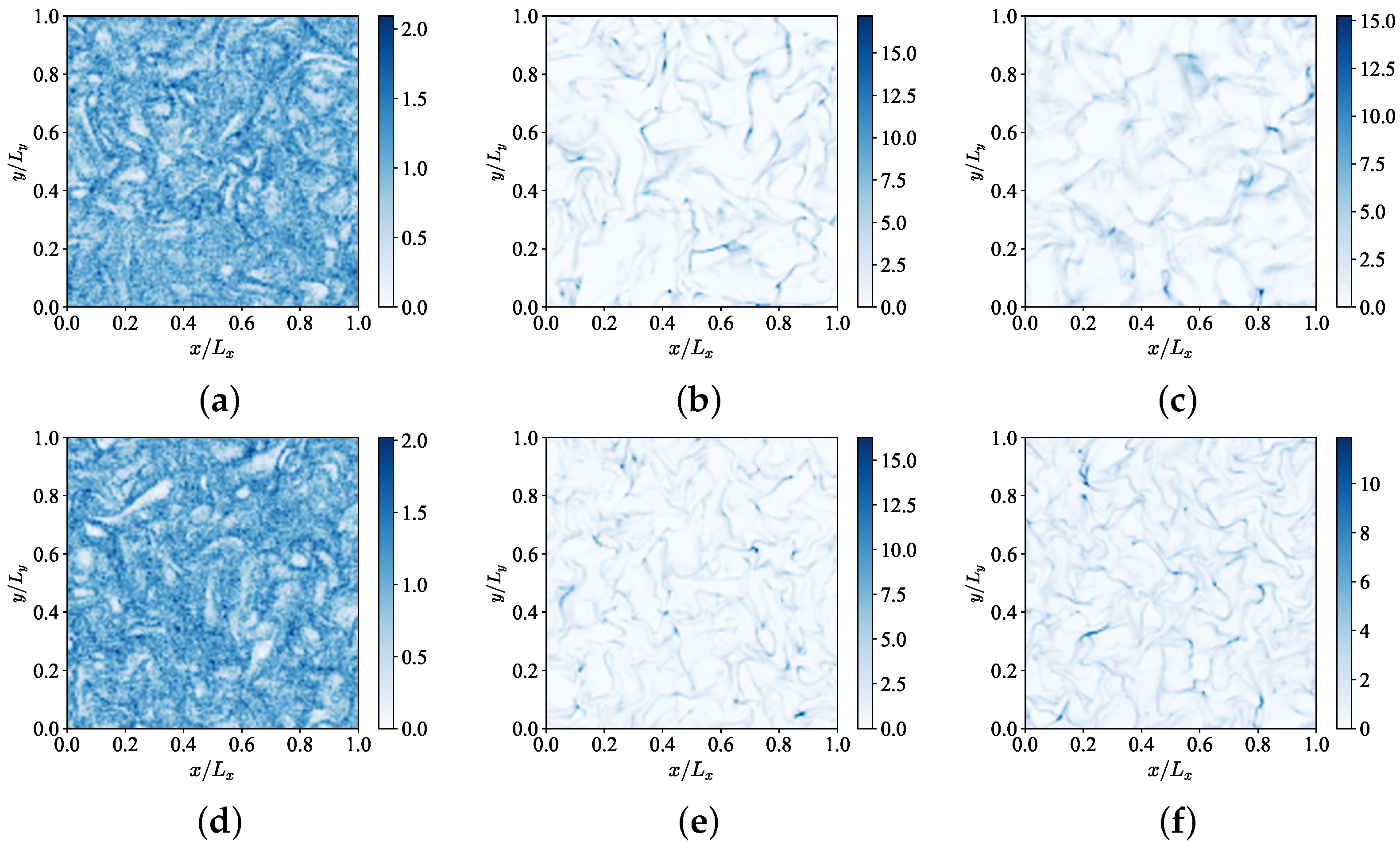
 ) and blue line: without gravity (
) and blue line: without gravity ( ). (a) ; (b) ; (c) ; (d) .
). (a) ; (b) ; (c) ; (d) .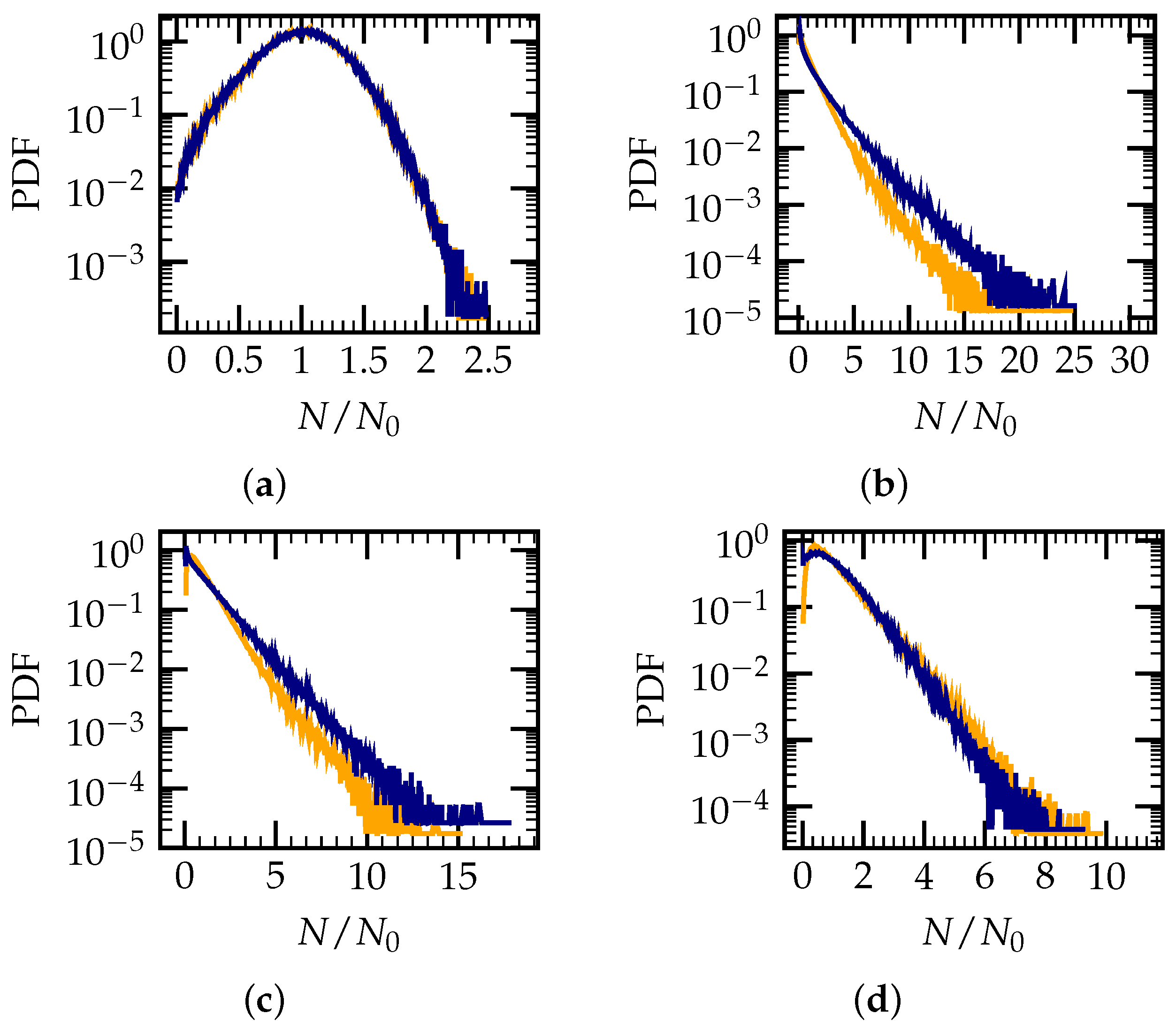
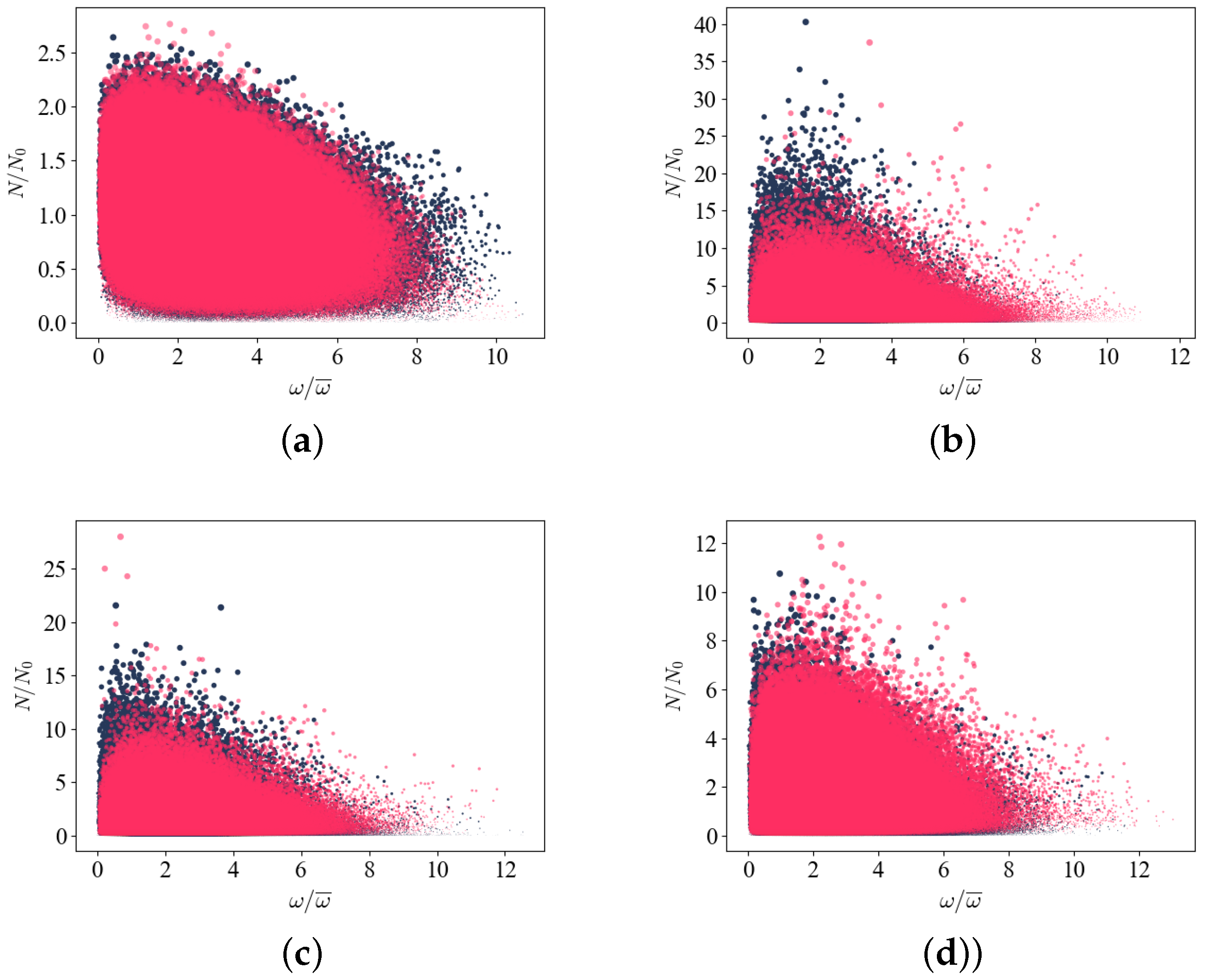
 ), blue curve: without gravity (
), blue curve: without gravity ( ); the normalized particle slip velocity. (a) ; (b) ; (c) ; (d) .
); the normalized particle slip velocity. (a) ; (b) ; (c) ; (d) .
 ), blue curve: without gravity (
), blue curve: without gravity ( ); the normalized particle slip velocity. (a) ; (b) ; (c) ; (d) .
); the normalized particle slip velocity. (a) ; (b) ; (c) ; (d) .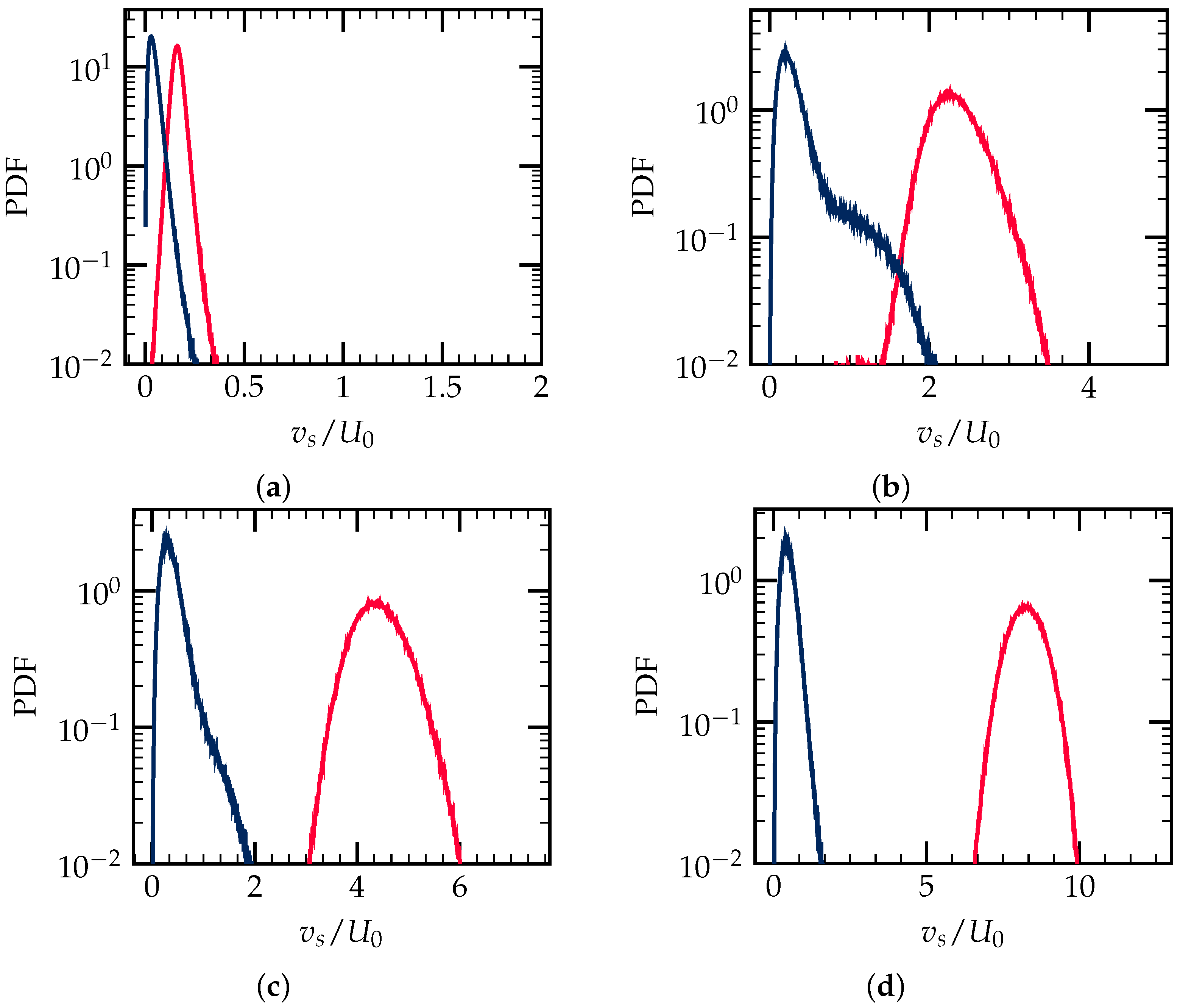
 ), (
), ( ), (
), ( ), (
), ( ), (
), ( ); and (b) comparison between analytical and numerical simulation results with consideration of particle gravity: turbulence forced (
); and (b) comparison between analytical and numerical simulation results with consideration of particle gravity: turbulence forced ( ), free fall (
), free fall ( ). (a) Settling velocity PDF; (b) Forced turbulence (DNS) v.s. free fall.
). (a) Settling velocity PDF; (b) Forced turbulence (DNS) v.s. free fall.
 ), (
), ( ), (
), ( ), (
), ( ), (
), ( ); and (b) comparison between analytical and numerical simulation results with consideration of particle gravity: turbulence forced (
); and (b) comparison between analytical and numerical simulation results with consideration of particle gravity: turbulence forced ( ), free fall (
), free fall ( ). (a) Settling velocity PDF; (b) Forced turbulence (DNS) v.s. free fall.
). (a) Settling velocity PDF; (b) Forced turbulence (DNS) v.s. free fall.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gai, G.; Thomine, O.; Hadjadj, A.; Kudriakov, S.; Wachs, A. Preferential Concentration of Particles in Forced Turbulent Flows: Effects of Gravity. Energies 2023, 16, 2910. https://doi.org/10.3390/en16062910
Gai G, Thomine O, Hadjadj A, Kudriakov S, Wachs A. Preferential Concentration of Particles in Forced Turbulent Flows: Effects of Gravity. Energies. 2023; 16(6):2910. https://doi.org/10.3390/en16062910
Chicago/Turabian StyleGai, Guodong, Olivier Thomine, Abdellah Hadjadj, Sergey Kudriakov, and Anthony Wachs. 2023. "Preferential Concentration of Particles in Forced Turbulent Flows: Effects of Gravity" Energies 16, no. 6: 2910. https://doi.org/10.3390/en16062910
APA StyleGai, G., Thomine, O., Hadjadj, A., Kudriakov, S., & Wachs, A. (2023). Preferential Concentration of Particles in Forced Turbulent Flows: Effects of Gravity. Energies, 16(6), 2910. https://doi.org/10.3390/en16062910







