Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq
Abstract
:1. Introduction
- Short-term forecasting (1–24 h);
- Medium-term forecasting (1 week–1 year);
- Long-term forecasting (up to 1 year).
1.1. Literature Review
1.2. Content and Contributions
2. Determinants in Electrical Load Forecasting
2.1. Factors Affecting Electrical Load Forecasting
2.2. Collection of Input Data
- Loads 1, 2, 3, 7 and 8 are residential feeders;
- Loads 4 and 6 are the government institutions feeder;
- Loads 5 and 9 are industrial feeders;
- Load 10 is the commercial feeder.
3. Methods of Load Forecasting
3.1. Artificial Neural Network (ANN)
- Future-related entries;
- Historical input that includes the max usual loads during a particular prior time;
- Compressible input.
3.2. Adaptive Neuro-Fuzzy Inference System (ANFIS)
3.3. Schematic of ANN Optimized by GA
3.4. Error Validation
4. Methodology
4.1. Utilizing MATLAB to Implement the ANN’s Input Data
- 80% training—20% testing;
- 70% training—30% testing;
- 60% training—40% testing;
- 50% training—50% testing.
- Time in (hours);
- Temperature (°C);
- Humidity (%);
- Previous Day Same Hour Load (MW);
- Previous Week Same Day Same Hour Load (MW).
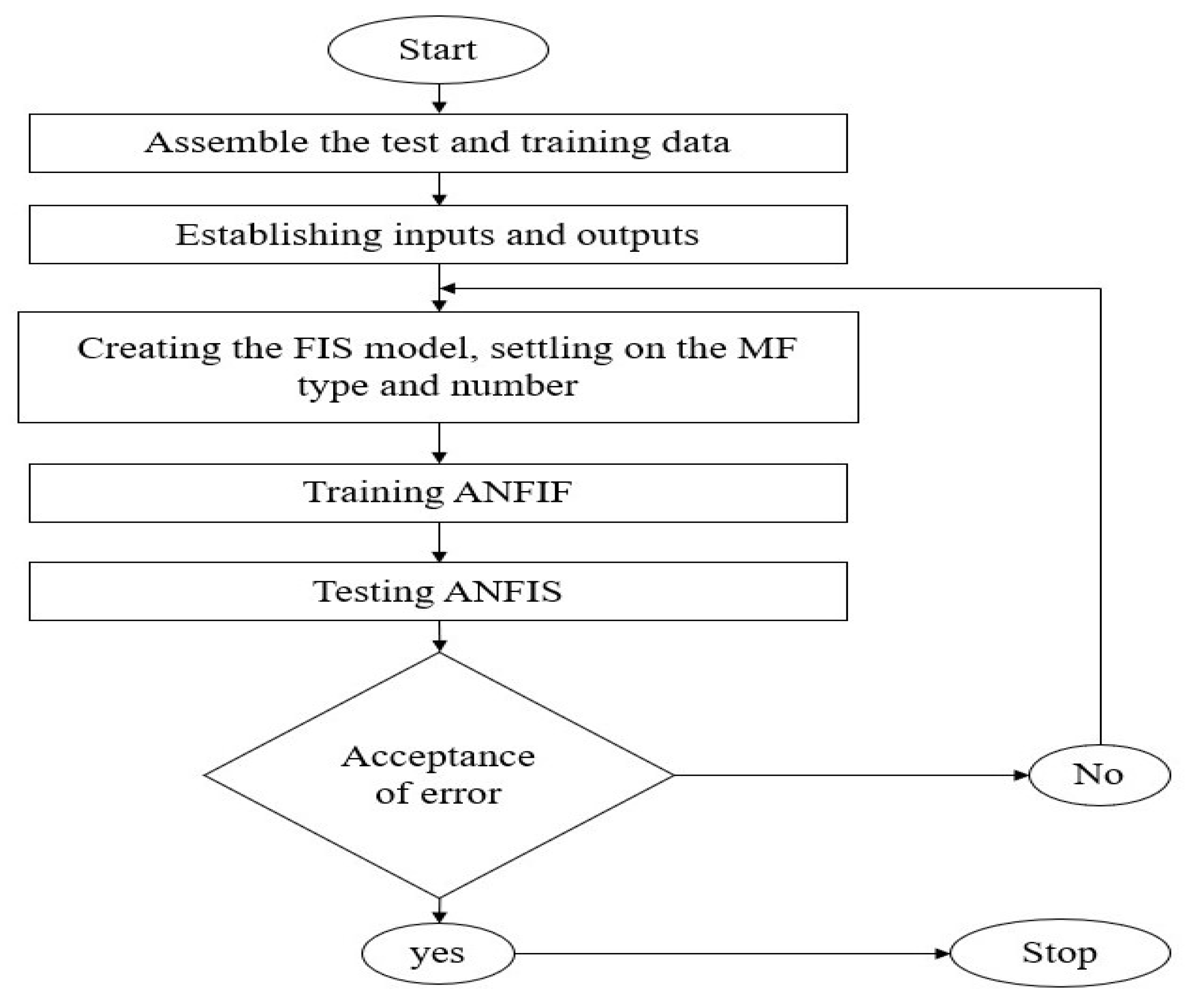
4.2. Implementation of the Adaptive Neuro-Fuzzy Inference System ANFIS Using MATLAB
4.3. Genetic Algorithms (GA) Optimize ANN Predictions
4.4. Results of Tests and Training in Purposed Techniques
5. Conclusions and Suggestions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Matijaš, M. Electric Load Forecasting Using Multivariate Meta-Learning. Ph.D. Thesis, Fakultet elektrotehnike i računarstva, Sveučilište u Zagrebu, Zagreb, Croatia, 2013. [Google Scholar]
- Kotriwala, A.M. Load Forecasting for Temporary Power Installations. Master’s Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2017. [Google Scholar]
- Han, L.; Peng, Y.; Li, Y.; Yong, B.; Zhou, Q.; Shu, L. Enhanced Deep Networks for Short-Term and Medium-Term Load Forecasting. IEEE Access 2018, 7, 4045–4055. [Google Scholar] [CrossRef]
- Nti, I.K.; Teimeh, M.; Nyarko-Boateng, O.; Adekoya, A.F. Electricity load forecasting: A systematic review. J. Electr. Syst. Inf. Technol. 2020, 7, 13. [Google Scholar] [CrossRef]
- Arfoa, A.A. Long-term load forecasting of southern governorates of Jordan distribution electric system. Energy Power Eng. 2015, 7, 242. [Google Scholar] [CrossRef] [Green Version]
- Shareef, H.; Ahmed, M.; Mohamed, A.; Al Hassan, E. Review on home energy management system considering demand responses, smart technologies, and intelligent controllers. IEEE Access 2018, 6, 24498–24509. [Google Scholar] [CrossRef]
- Al Mamun, A.; Sohel, M.; Mohammad, N.; Sunny, M.; Dipta, D.; Hossain, E. A comprehensive review of the load forecasting techniques using single and hybrid predictive models. IEEE Access 2020, 8, 134911–134939. [Google Scholar] [CrossRef]
- Baek, S.-M. Mid-term load pattern forecasting with recurrent artificial neural network. IEEE Access 2019, 7, 172830–172838. [Google Scholar] [CrossRef]
- Ibraheem, I.K.; Ali, M.O. Short term electric load forecasting based on artificial neural networks for weekends of Baghdad power grid. Int. J. Comput. Appl. 2014, 89, 30–37. [Google Scholar]
- Abdullah, A.G.; Suranegara, G.; Hakim, D.L. Hybrid PSO-ANN application for improved accuracy of short term load forecasting. WSEAS Trans. Power Syst. 2014, 9, 51. [Google Scholar]
- Alawode, K.O.; Oyedeji, M.O. Comparison of Neural Network models for Load Forecasting in Nigeria Power Systems. Int. J. Renew. Energy Technol. 2013, 2, 218–222. [Google Scholar]
- Ali, D.; Yohanna, M.; Ijasini, P.; Garkida, M.B. Application of fuzzy–Neuro to model weather parameter variability impacts on electrical load based on long-term forecasting. Alex. Eng. J. 2018, 57, 223–233. [Google Scholar] [CrossRef]
- Ammar, N.; Sulaiman, M.; Nor, A.F.M. Long-term load forecasting of power systems using artificial neural network and ANFIS. ARPN J. Eng. Appl. Sci. 2018, 13, 828–834. [Google Scholar]
- Xu, Y.; Cai, J.; Milanović, J.V. On accuracy of demand forecasting and its extension to demand composition forecasting using artificial intelligence based methods. In Proceedings of the IEEE PES Innovative Smart Grid Technologies, Europe, Istanbul, Turkey, 12–15 October 2014; pp. 1–6. [Google Scholar]
- Panda, S.K.; Mohanty, S.; Jagadev, A.K. Long term electrical load forecasting: An empirical study across techniques and domains. Indian J. Sci. Technol. 2017, 10, 1–16. [Google Scholar] [CrossRef]
- GÖKGÖZ, F.; Filiz, F. Electricity load forecasting via ANN approach in Turkish electricity markets. Bilgi Yönetimi 2020, 3, 170–184. [Google Scholar] [CrossRef]
- Arvanitidis, A.I.; Bargiotas, D.; Daskalopulu, A.; Laitsos, V.; Tsoukalas, L.H. Enhanced Short-Term Load Forecasting Using Artificial Neural Networks. Energies 2021, 14, 7788. [Google Scholar] [CrossRef]
- Pham, M.-H.; Nguyen, M.-N.; Wu, Y.-K. A novel short-term load forecasting method by combining the deep learning with singular spectrum analysis. IEEE Access 2021, 9, 73736–73746. [Google Scholar] [CrossRef]
- Oprea, S.-V.; Bâra, A. Machine learning algorithms for short-term load forecast in residential buildings using smart meters, sensors and big data solutions. IEEE Access 2019, 7, 177874–177889. [Google Scholar] [CrossRef]
- Selvi, M.V.; Mishra, S. Investigation of performance of electric load power forecasting in multiple time horizons with new architecture realized in multivariate linear regression and feed-forward neural network techniques. IEEE Trans. Ind. Appl. 2020, 56, 5603–5612. [Google Scholar] [CrossRef]
- Nespoli, A.; Leva, S.; Mussetta, M.; Ogliari, E.G.C. A Selective Ensemble Approach for Accuracy Improvement and Computational Load Reduction in ANN-Based PV Power Forecasting. IEEE Access 2022, 10, 32900–32911. [Google Scholar] [CrossRef]
- ZulfiqAr, M.; Kamran, M.; Rasheed, M.B.; Alquthami, T.; Milyani, A.H. A Short-Term Load Forecasting Model Based on Self-Adaptive Momentum Factor and Wavelet Neural Network in Smart Grid. IEEE Access 2022, 10, 77587–77602. [Google Scholar] [CrossRef]
- Faraji, J.; Ketabi, A.; Hashemi-Dezaki, H.; Shafie-Khah, M.; Catalão, J.P. Optimal day-ahead self-scheduling and operation of prosumer microgrids using hybrid machine learning-based weather and load forecasting. IEEE Access 2020, 8, 157284–157305. [Google Scholar] [CrossRef]
- Rafi, S.H.; Deeba, S.R.; Hossain, E. A short-term load forecasting method using integrated CNN and LSTM network. IEEE Access 2021, 9, 32436–32448. [Google Scholar] [CrossRef]
- Mahmud, K.; Ravishankar, J.; Hossain, M.J.; Dong, Z.Y. The impact of prediction errors in the domestic peak power demand management. IEEE Trans. Ind. Inform. 2019, 16, 4567–4579. [Google Scholar] [CrossRef]
- Mansoor, H.; Rauf, H.; Mubashar, M.; Khalid, M.; Arshad, N. Past vector similarity for short term electrical load forecasting at the individual household level. IEEE Access 2021, 9, 42771–42785. [Google Scholar] [CrossRef]
- Haq, M.R.; Ni, Z. A new hybrid model for short-term electricity load forecasting. IEEE Access 2019, 7, 125413–125423. [Google Scholar] [CrossRef]
- Song, J.; Xue, G.; Pan, X.; Ma, Y.; Li, H. Hourly heat load prediction model based on temporal convolutional neural network. IEEE Access 2020, 8, 16726–16741. [Google Scholar] [CrossRef]
- Chen, K.; Chen, K.; Wang, Q.; He, Z.; Hu, J.; He, J. Short-term load forecasting with deep residual networks. IEEE Trans. Smart Grid 2018, 10, 3943–3952. [Google Scholar] [CrossRef] [Green Version]
- Kong, W.; Dong, Z.Y.; Jia, Y.; Hill, D.J.; Xu, Y.; Zhang, Y. Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 2017, 10, 841–851. [Google Scholar] [CrossRef]
- Dattatrey, M.; Tiwari, A.K.; Ghoshal, B.; Singh, J. Predicting bone modeling parameters in response to mechanical loading. IEEE Access 2019, 7, 122561–122572. [Google Scholar] [CrossRef]
- Akarslan, E.; Hocaoglu, F.O. Electricity demand forecasting of a micro grid using ANN. In Proceedings of the 2018 9th International Renewable Energy Congress (IREC), Hammamet, Tunisia, 20–22 March 2018; pp. 1–5. [Google Scholar]
- Liu, H.; Wang, Y.; Wei, C.; Li, J.; Lin, Y. Two-stage short-term load forecasting for power transformers under different substation operating conditions. IEEE Access 2019, 7, 161424–161436. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Mohammadi-Ivatloo, B.; Abapour, M.; Anvari-Moghaddam, A.; Roy, S.S. Heating and cooling loads forecasting for residential buildings based on hybrid machine learning applications: A comprehensive review and comparative analysis. IEEE Access 2021, 10, 2196–2215. [Google Scholar] [CrossRef]
- Lin, T.; Pan, Y.; Xue, G.; Song, J.; Qi, C. A novel hybrid spatial-temporal attention-LSTM model for heat load prediction. IEEE Access 2020, 8, 159182–159195. [Google Scholar] [CrossRef]
- Ouyang, T.; He, Y.; Li, H.; Sun, Z.; Baek, S. Modeling and forecasting short-term power load with copula model and deep belief network. IEEE Trans. Emerg. Top. Comput. Intell. 2019, 3, 127–136. [Google Scholar] [CrossRef] [Green Version]















| Splitting Rate | 80% Training—20% Testing | 70% Training—30% Testing | 60% Training—40% Testing | 50% Training—50% Testing | ||||
|---|---|---|---|---|---|---|---|---|
| Training Functions | Levenberg–Marquardt | Levenberg–Marquardt | Levenberg–Marquardt | Levenberg–Marquardt | ||||
| 5 hidden layers | MAPE% | 3.2451 | MAPE% | 5.3756 | MAPE% | 5.4447 | MAPE% | 5.9299 |
| RMSE | 0.4248 | RMSE | 0.6928 | RMSE | 0.7059 | RMSE | 0.7318 | |
| 10 hidden layers | MAPE% | 5.4319 | MAPE% | 7.5222 | MAPE% | 7.6136 | MAPE% | 7.9921 |
| RMSE | 0.7206 | RMSE | 1.0655 | RMSE | 1.1513 | RMSE | 1.2919 | |
| 15 hidden layers | MAPE% | 6.3252 | MAPE% | 8.2533 | MAPE% | 8.5213 | MAPE% | 9.3836 |
| RMSE | 0.8350 | RMSE | 1.0885 | RMSE | 1.2918 | RMSE | 1.3370 | |
| Splitting Rate | 80% Training—20% Testing | 70% Training—30% Testing | 60% Training—40% Testing | 50% Training—50% Testing | ||||
|---|---|---|---|---|---|---|---|---|
| Training Functions | Levenberg–Marquardt | Levenberg–Marquardt | Levenberg–Marquardt | Levenberg–Marquardt | ||||
| 5 hidden layers | MAPE% | 3.7452 | MAPE% | 6.2402 | MAPE% | 6.5315 | MAPE% | 6.8512 |
| RMSE | 0.3177 | RMSE | 0.8452 | RMSE | 0.8997 | RMSE | 0.9682 | |
| 10 hidden layers | MAPE% | 5.4613 | MAPE% | 8.1691 | MAPE% | 8.8338 | MAPE% | 9.2921 |
| RMSE | 1.1954 | RMSE | 1.2181 | RMSE | 1.5890 | RMSE | 1.7019 | |
| 15 hidden layers | MAPE% | 6.9019 | MAPE% | 8.4002 | MAPE% | 9.1607 | MAPE% | 10.2756 |
| RMSE | 1.2876 | RMSE | 1.3403 | RMSE | 1.6893 | RMSE | 1.7601 | |
| Epoch Number | 20 | 30 | 40 | |||
|---|---|---|---|---|---|---|
| Membership Function Type | Triangular Membership Functions | Triangular Membership Functions | Triangular Membership Functions | |||
| 3 membership functions | MAPE% | 3.0165 | MAPE% | 3.0073 | MAPE% | 3.0039 |
| RMSE | 0.3294 | RMSE | 0.3294 | RMSE | 0.3294 | |
| 4 membership functions | MAPE% | 2.9318 | MAPE% | 2.9317 | MAPE% | 2.9330 |
| RMSE | 0.3297 | RMSE | 0.3297 | RMSE | 0.3297 | |
| 5 membership functions | MAPE% | 2.8785 | MAPE% | 2.8761 | MAPE% | 2.8532 |
| RMSE | 0.3301 | RMSE | 0.3302 | RMSE | 0.3301 | |
| Epoch Number | 20 | 30 | 40 | |||
|---|---|---|---|---|---|---|
| Membership Function Type | Triangular Membership Functions | Triangular Membership Functions | Triangular Membership Functions | |||
| 3 membership functions | MAPE% | 2.9065 | MAPE% | 2.9026 | MAPE% | 2.9005 |
| RMSE | 0.3117 | RMSE | 0.3117 | RMSE | 0.3117 | |
| 4 membership functions | MAPE% | 2.8273 | MAPE% | 2.8299 | MAPE% | 2.8303 |
| RMSE | 0.3121 | RMSE | 0.3121 | RMSE | 0.3135 | |
| 5 membership functions | MAPE% | 2.8189 | MAPE% | 2.8118 | MAPE% | 2.8036 |
| RMSE | 0.3125 | RMSE | 0.3125 | RMSE | 0.3125 | |
| Splitting Rate | Error % | |
|---|---|---|
| 5 hidden layers | MAPE% | 1.8663 |
| RMSE | 0.0476 | |
| 10 hidden layers | MAPE% | 4.8722 |
| RMSE | 0.1889 | |
| 15 hidden layers | MAPE% | 5.9395 |
| RMSE | 0.1714 | |
| Splitting Rate | Error % | |
|---|---|---|
| 5 hidden layers | MAPE% | 2.4571 |
| RMSE | 0.0623 | |
| 10 hidden layers | MAPE% | 3.7701 |
| RMSE | 0.0668 | |
| 15 hidden layers | MAPE% | 5.9110 |
| RMSE | 0.1572 | |
| Month | Long-Term Inputs | Target | ANN | ANFIS | ANN–GA | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Temp (°C) | Hum (%) | ACTUAL 2018 (MW) | ACTUAL 2019 (MW) | ACTUAL 2020 (MW) | Predicted 2018 (MW) | Predicted 2019 (MW) | Predicted 2018 (MW) | Predicted 2019 (MW) | Predicted 2018 (MW) | Predicted 2019 (MW) | |
| JAN | 20.40 | 97.44 | 53.856 | 55.85 | 59.35 | 53.88 | 55.84 | 56.44 | 56.43 | 54.27 | 59.96 |
| FEB | 23.42 | 96.81 | 51.012 | 53.01 | 56.51 | 50.96 | 52.94 | 51.53 | 52.98 | 53.97 | 54.45 |
| MAR | 35.73 | 83.12 | 43.665 | 45.66 | 58.92 | 43.69 | 45.67 | 44.83 | 44.91 | 46.20 | 47.49 |
| APR | 33.37 | 95.62 | 39.915 | 41.91 | 45.47 | 39.79 | 41.78 | 41.20 | 43.94 | 40.15 | 44.40 |
| MAY | 39.82 | 80.75 | 41.625 | 43.62 | 47.18 | 41.50 | 43.48 | 49.58 | 44.02 | 42.26 | 44.41 |
| JUN | 41.42 | 61.44 | 43.050 | 45.05 | 48.55 | 42.98 | 44.96 | 43.86 | 47.67 | 45.44 | 47.88 |
| JULY | 42.55 | 60.31 | 42.156 | 44.00 | 47.35 | 42.16 | 43.98 | 41.55 | 44.35 | 44.70 | 45.46 |
| AUG | 49.59 | 60.25 | 40.615 | 42.61 | 46.11 | 40.55 | 42.54 | 42.85 | 43.63 | 42.76 | 43.90 |
| SEP | 42.81 | 55.19 | 37.174 | 39.17 | 42.57 | 37.11 | 39.08 | 39.01 | 40.14 | 40.95 | 40.87 |
| OCT | 38.00 | 86.62 | 34.074 | 36.07 | 39.47 | 34.09 | 36.06 | 38.14 | 39.40 | 34.70 | 37.02 |
| NOV | 26.20 | 91.20 | 31.374 | 33.37 | 37.07 | 31.23 | 33.29 | 33.86 | 35.50 | 33.41 | 36.86 |
| DEC | 20.13 | 97.66 | 37.374 | 39.4 | 54.18 | 37.16 | 39.23 | 37.63 | 40.00 | 37.34 | 40.16 |
| MAPE | 3.245% | 5.017% | 2.853% | 2.807% | 1.866% | 2.457% | |||||
| RMSE | 0.424% | 0.654% | 0.330% | 0.312% | 0.047% | 0.062% | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
AL-Qaysi, A.M.M.; Bozkurt, A.; Ates, Y. Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq. Energies 2023, 16, 2919. https://doi.org/10.3390/en16062919
AL-Qaysi AMM, Bozkurt A, Ates Y. Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq. Energies. 2023; 16(6):2919. https://doi.org/10.3390/en16062919
Chicago/Turabian StyleAL-Qaysi, Ahmed Mazin Majid, Altug Bozkurt, and Yavuz Ates. 2023. "Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq" Energies 16, no. 6: 2919. https://doi.org/10.3390/en16062919
APA StyleAL-Qaysi, A. M. M., Bozkurt, A., & Ates, Y. (2023). Load Forecasting Based on Genetic Algorithm–Artificial Neural Network-Adaptive Neuro-Fuzzy Inference Systems: A Case Study in Iraq. Energies, 16(6), 2919. https://doi.org/10.3390/en16062919






