Biomass Combustion Modeling Using OpenFOAM: Development of a Simple Computational Model and Study of the Combustion Performance of Lippia origanoides Bagasse
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fuel Properties
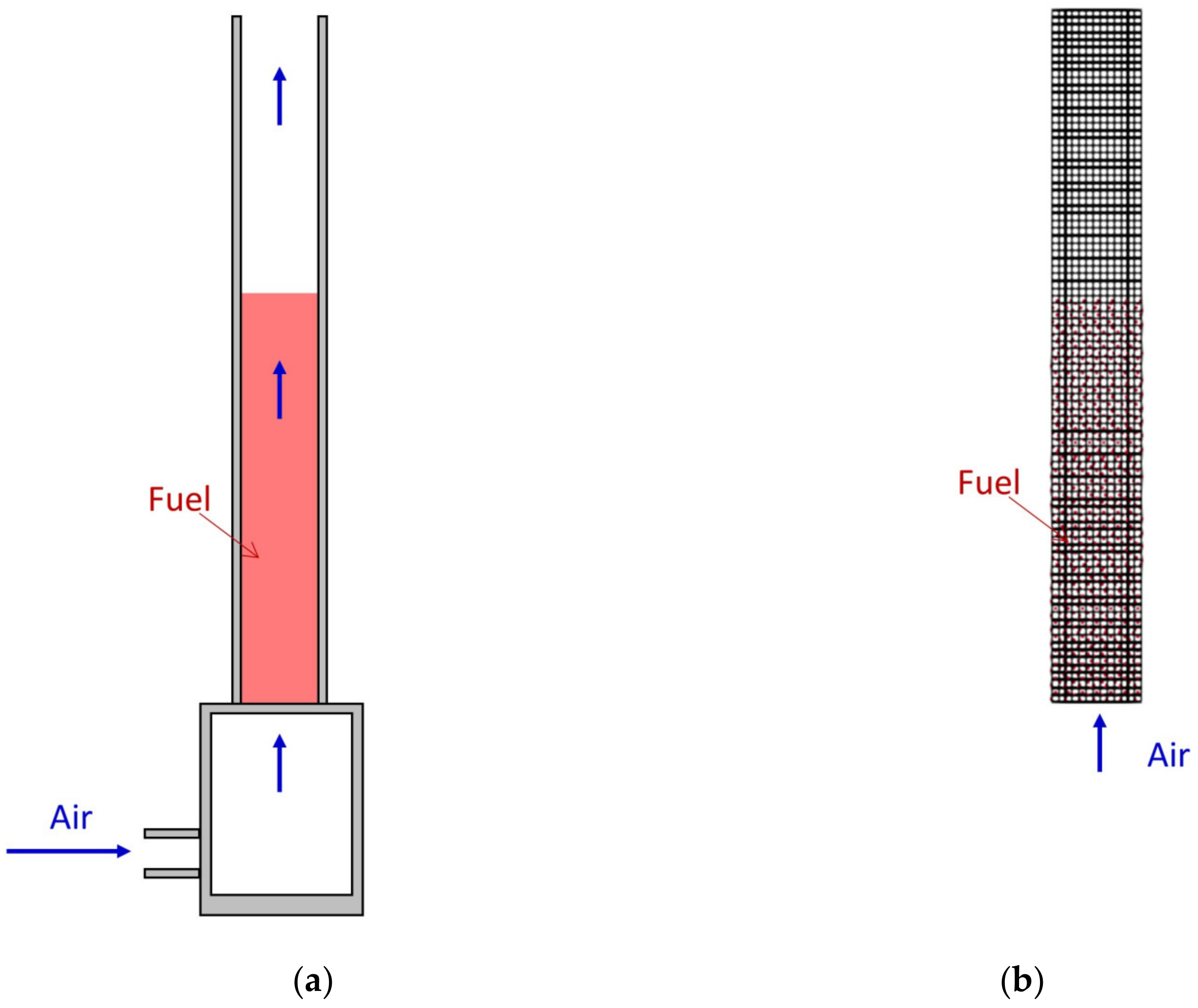
2.2. Experimental Setup and Computational Domain
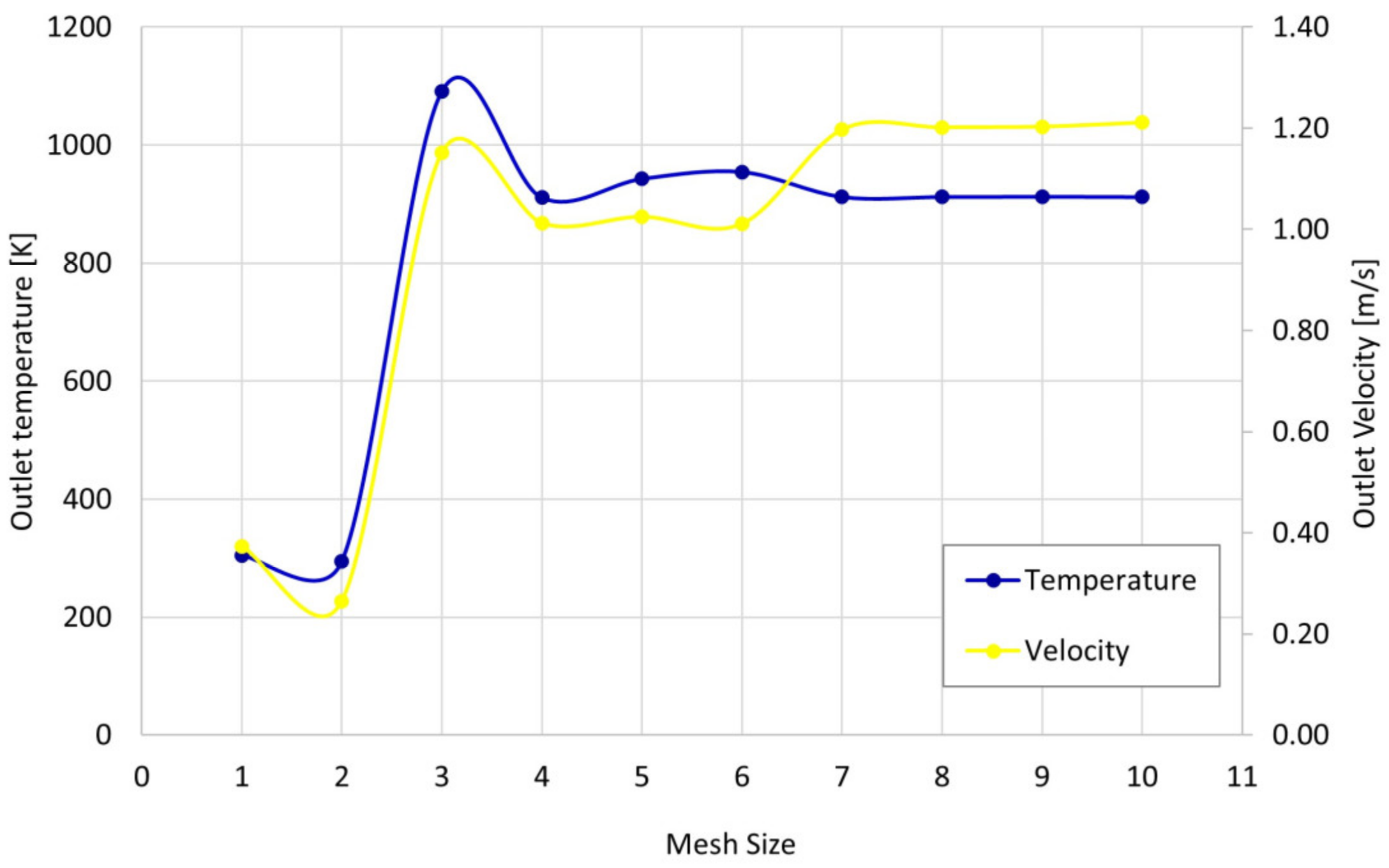
2.3. Mesh Independence Analysis
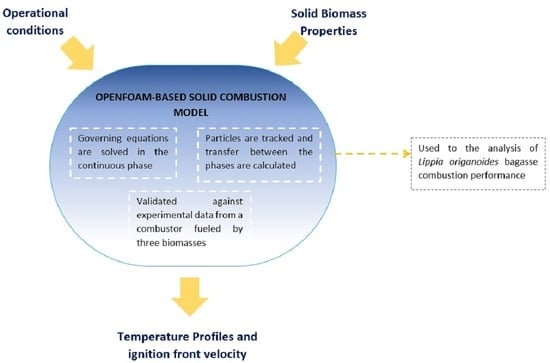
2.4. Model Description
2.5. Submodels
2.5.1. Drying
2.5.2. Devolatilization
2.5.3. Heat Transfer
2.5.4. Combustion
2.5.5. Reaction Mechanism
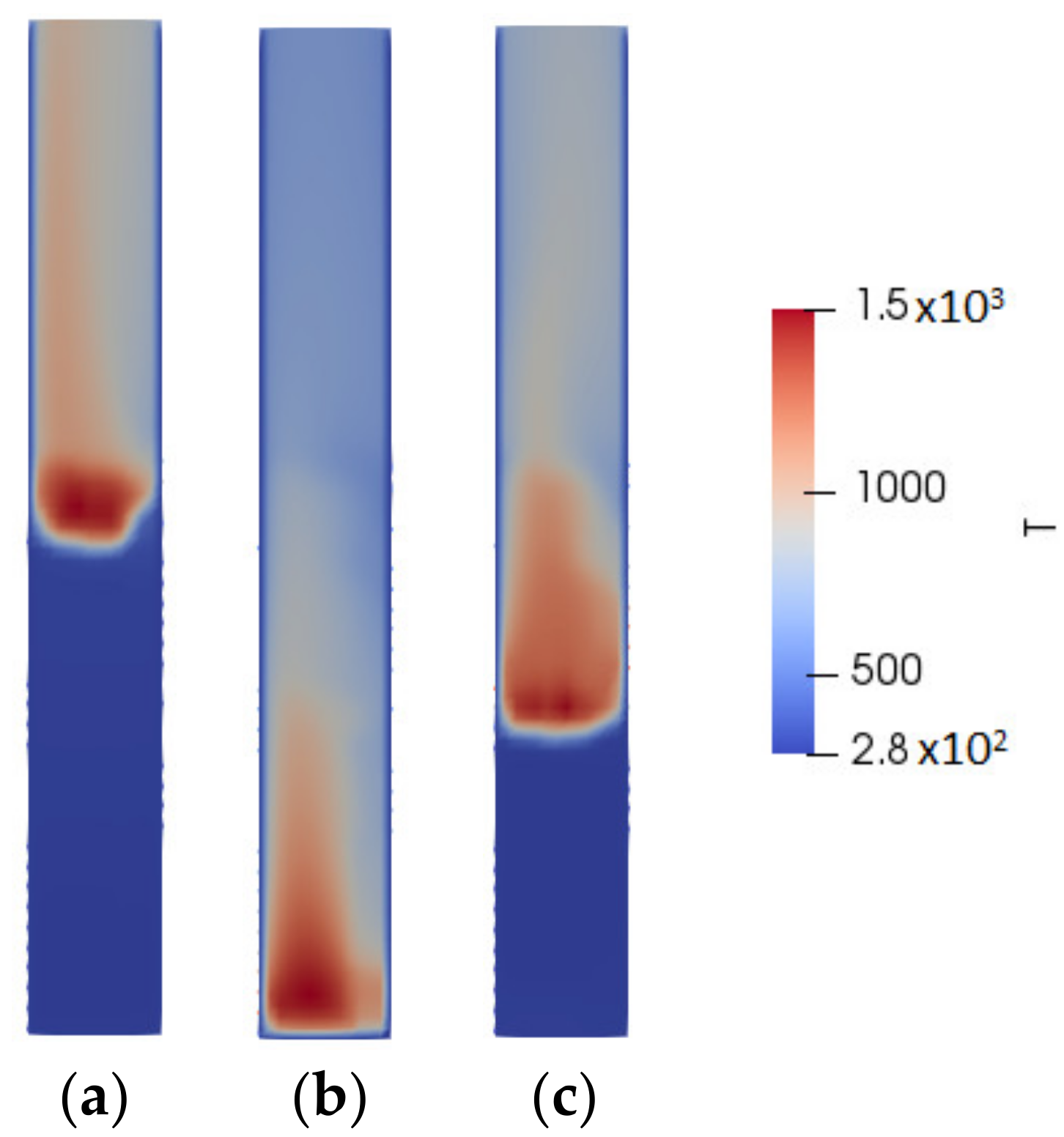
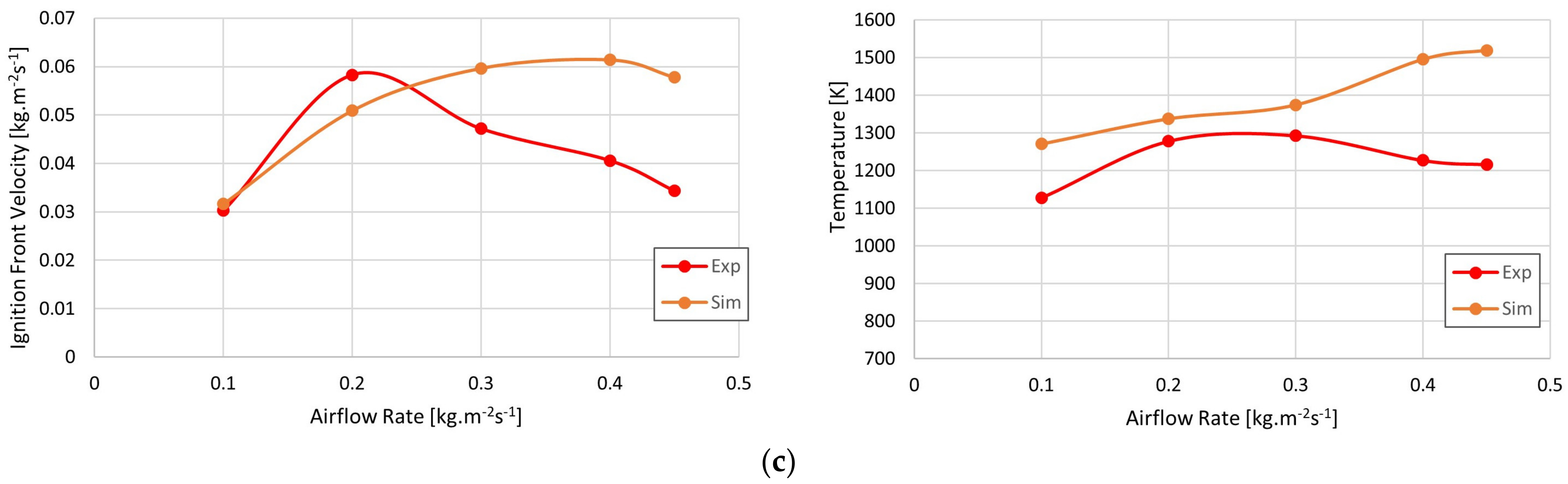
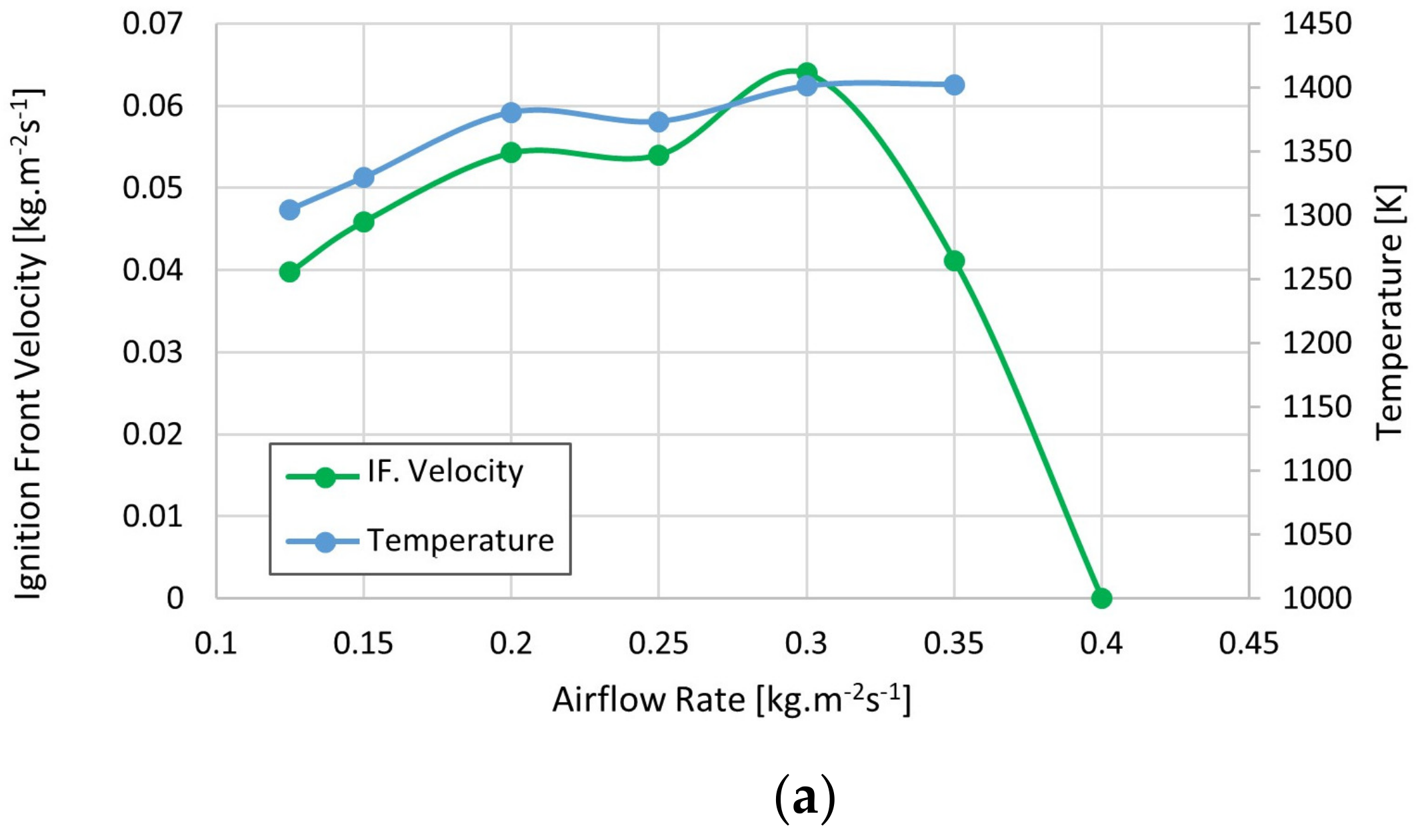
3. Results
4. Discussion
5. Conclusions
- This paper presents a two-dimensional model of solid biomass combustion. The model is useful for studying the performance of a combustion system fueled by different kinds of biomass and under different airflow rates. Unlike other similar studies, this is an efficient numerical model implemented in OpenFOAM, which is a popular computational tool rarely used in this type of application.
- The model was validated by comparing its results with those obtained in a cylindrical combustor fueled with three types of biomass, with relative error values lower than 13% in most cases, which is similar to the errors obtained in recent studies on this subject.
- The stems of Lippia origanoides bagasse show a similar performance to that of other biomass used as solid fuels, while the leaves and mixtures of the same plant present lower performance.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saeed, M.A.; Niedzwiecki, L.; Arshad, M.Y.; Skrinsky, J.; Andrews, G.E.; Phylaktou, H.N. Combustion and Explosion Characteristics of Pulverised Wood, Valorized with Mild Pyrolysis in Pilot Scale Installation, Using the Modified ISO 1 m3 Dust Explosion Vessel. Appl. Sci. 2022, 12, 12928. [Google Scholar] [CrossRef]
- Karim, M.R.; Naser, J. CFD modelling of combustion and associated emission of wet woody biomass in a 4 MW moving grate boiler. Fuel 2018, 222, 656–674. [Google Scholar] [CrossRef]
- Said, Z.; Nguyen, T.H.; Sharma, P.; Li, C.; Ali, H.M.; Nguyen, V.N.; Pham, V.V.; Ahmed, S.F.; Van, D.N.; Truong, T.H. Multi-attribute optimization of sustainable aviation fuel production-process from microalgae source. Fuel 2022, 324, 124759. [Google Scholar] [CrossRef]
- Gobierno de la Republica de Colombia. Estrategia Nacional de Economía Circular. Cierre de Ciclos de Materiales, Innovación Tecnológica, Colaboración y Nuevos Modelos de Negocio; Presidencia de la República; Ministerio de Ambiente y Desarrollo Sostenible; Ministerio de Comercio, Industria y Turismo: Bogotá, Colombia, 2019.
- Unidad de Planeación Minero Energética—UPME. Balance Energético Colombiano—BECO. 2018. Available online: http://www1.upme.gov.co/InformacionCifras/Paginas/BalanceEnergetico.aspx (accessed on 27 July 2021).
- Bhuiyan, A.A.; Karim, M.R.; Naser, J. Chapter 11—Modeling of Solid and Bio-Fuel Combustion Technologies. In Thermofluid Modeling for Energy Efficiency Applications; Khan, M.M.K., Hassan, N.M.S., Eds.; Academic Press: Cambridge, MA, USA, 2016; pp. 259–309. ISBN 978-0-12-802397-6. [Google Scholar]
- Bhuiyan, A.A.; Naser, J. CFD modelling of co-firing of biomass with coal under oxy-fuel combustion in a large scale power plant. Fuel 2015, 159, 150–168. [Google Scholar] [CrossRef]
- Khodaei, H.; Al-Abdeli, Y.M.; Guzzomi, F.; Yeoh, G.H. An overview of processes and considerations in the modelling of fixed-bed biomass combustion. Energy 2015, 88, 946–972. [Google Scholar] [CrossRef]
- Szemmelveisz, K.; Szűcs, I.; Palotás, Á.B.; Winkler, L.; Eddings, E.G. Examination of the combustion conditions of herbaceous biomass. Fuel Process. Technol. 2009, 90, 839–847. [Google Scholar] [CrossRef]
- Yang, Y.B.; Sharifi, V.N.; Swithenbank, J. Effect of air flow rate and fuel moisture on the burning behaviours of biomass and simulated municipal solid wastes in packed beds. Fuel 2004, 83, 1553–1562. [Google Scholar] [CrossRef]
- Dernbecher, A.; Dieguez-Alonso, A.; Ortwein, A.; Tabet, F. Review on modelling approaches based on computational fluid dynamics for biomass combustion systems. Biomass Conv. Bioref. 2019, 9, 129–182. [Google Scholar] [CrossRef]
- Campo, Y.C. Estudio de La Composición Química y Las Actividades Antioxidante y Fotoprotectora de Los Extractos de Damiana y Orégano de Monte, Cultivadas en Santander. Doctorado, Universidad Industrial de Santander, Bucaramanga, Colombia, 2020. [Google Scholar]
- Stashenko, E.E.; Martínez, J.R.; Durán, D.C.; Córdoba, Y.; Caballero, D. Estudio comparativo de la composición química y la actividad antioxidante de los aceites esenciales de algunas plantas del género Lippia (Verbenaceae) cultivadas en Colombia. Rev. Acad. Colomb. Cienc. Exactas Físicas Nat. 2014, 38, 89–105. [Google Scholar] [CrossRef] [Green Version]
- Rajh, B.; Gómez, M.A.; Álvarez-Bermúdez, C.; Cid, N.; Míguez, J.L. Assessment of experimental 1D and analytical 3D steady approaches of packed bed thermal conversion through the simulation of a 60-kW biomass boiler operating at half and full load. Energy Convers. Manag. 2022, 268, 116003. [Google Scholar] [CrossRef]
- Gómez, M.A.; Martín, R.; Chapela, S.; Porteiro, J. Steady CFD combustion modeling for biomass boilers: An application to the study of the exhaust gas recirculation performance. Energy Convers. Manag. 2019, 179, 91–103. [Google Scholar] [CrossRef]
- Karim, M.R.; Naser, J. Numerical study of the ignition front propagation of different pelletised biomass in a packed bed furnace. Appl. Therm. Eng. 2018, 128, 772–784. [Google Scholar] [CrossRef]
- Karim, M.R.; Naser, J. Progress in Numerical Modelling of Packed Bed Biomass Combustion. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- García Sánchez, G.; Chacón Velasco, J.; Fuentes Díaz, D.; Jaramillo Ibarra, J.; Martínez Morales, J. CFD modelling of biomass boilers—A review of the state of the art. Respuestas 2020, 25, 3. [Google Scholar] [CrossRef]
- García Sánchez, G.F.; Chacón Velasco, J.L.; Rueda-Ordoñez, Y.J.; Fuentes Díaz, D.A.; Martínez Morales, J.R. Solid biomass combustion modeling: Bibliometric analysis and literature review of the latest developments in OpenFOAM based simulations. Bioresour. Technol. Rep. 2021, 15, 100781. [Google Scholar] [CrossRef]
- Rodríguez, M.Á.G. Contribuciones al Desarrollo de un Modelo de Simulación de Combustión de Sólidos. Universidade de Vigo, España. 2014. Available online: https://dialnet.unirioja.es/servlet/tesis?codigo=138954 (accessed on 8 June 2019).
- Buchmayr, M.; Gruber, J.; Hargassner, M.; Hochenauer, C. Spatially resolved chemical species concentrations above the fuel bed of a small grate-fired wood-chip boiler. Biomass Bioenergy 2016, 95, 146–156. [Google Scholar] [CrossRef]
- Gómez, M.A.; Porteiro, J.; Patiño, D.; Míguez, J.L. CFD modelling of thermal conversion and packed bed compaction in biomass combustion. Fuel 2014, 117, 716–732. [Google Scholar] [CrossRef]
- Chaney, J.; Hao, L.; Jinxing, L. An overview of CFD modelling of small-scale fixed-bed biomass pellet boilers with preliminary results from a simplified approach—ScienceDirect. Energy Convers. Manag. 2012, 63, 149–156. [Google Scholar] [CrossRef]
- Towara, M.; Schanen, M.; Naumann, U. MPI-Parallel Discrete Adjoint OpenFOAM. Procedia Comput. Sci. 2015, 51, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Patiño Vilas, D. Análisis Experimental de Combustión de Biomasa en un Quemador de Lecho Fijo. Universidade de Vigo. 2009. Available online: https://dialnet.unirioja.es/servlet/tesis?codigo=139004 (accessed on 21 February 2022).
- Rueda-Ordóñez, Y.J.R.; Tannous, K.K. Análisis cinético de la descomposición térmica de biomasas aplicando un esquema de reacciones paralelas independientes. Rev. UIS Ing. 2017, 16, 119–128. [Google Scholar] [CrossRef] [Green Version]
- Sheng, C.; Azevedo, J.L.T. Estimating the higher heating value of biomass fuels from basic analysis data. Biomass Bioenergy 2005, 28, 499–507. [Google Scholar] [CrossRef]
- García Fernández, R. Modelización Cinética y Optimización de Parámetros de Combustión en Calderas de Biomasa. Ph.D. Thesis, Universidad de Oviedo, Oviedo, Spain, 2014. Available online: http://digibuo.uniovi.es/dspace/handle/10651/28947 (accessed on 8 June 2019).
- Dunn, C. Computational Modeling of Coal Devolatilization and Soot Formation in OpenFoam. Master’s Thesis, University of Wyoming, Laramie, WY, USA, 2018. [Google Scholar]
- Van Kuijk, H.A.J.A. Grate Furnace Combustion: A Model for the Solid Fuel Layer. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Haller, J.; Hartmann, I.; König, M.; Ortwein, A. Basic Studies on the Development of Micro Combustion Systems for Biomass. In Proceedings of the European Combustion Meeting, Lund, Sweden, 25–28 June 2013; Available online: https://www.researchgate.net/publication/256715286 (accessed on 13 March 2023).
- Ranz, W.E.; Marshall, W.R. Evaporation from drops: Part I. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Ranz, W.E.; Marshall, W.R. Evaporation from drops: Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Nordin, P.A.N. Complex Chemistry Modeling of Diesel Spray Combustion. 2001. Available online: https://research.chalmers.se/en/publication/724 (accessed on 3 December 2019).
- Cordiner, S.; Mulone, V.; Manni, A.; Rocco, V. Biomass furnace study via 3D numerical modeling. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 515–533. [Google Scholar] [CrossRef]
- Collazo, J.; Porteiro, J.; Patiño, D.; Granada, E. Numerical modeling of the combustion of densified wood under fixed-bed conditions. Fuel 2012, 93, 149–159. [Google Scholar] [CrossRef]


| Fuel | Empirical Formula | Proximate Analysis [wt%] | LHV [MJ/kg] | ρp [kg/m3] | ρa [kg/m3] | |||
|---|---|---|---|---|---|---|---|---|
| Water | Volat. | Char | Ash | |||||
| Wood pellets (wp) | CH1.71O0.70 | 7.3 | 69.0 | 23.0 | 0.7 | 16.6 | 1240 | 690 |
| Olive stone (os) | CH1.50O0.64 | 13 | 61.3 | 25.1 | 0.6 | 15.3 | 1070 | 620 |
| Almond shell (as) | CH1.40O0.68 | 11.9 | 64.1 | 23.4 | 0.6 | 15.6 | 920 | 360 |
| LO leaves (L) | CH1.48O0.92 | 9.5 | 66.4 | 14.8 | 9.4 | 14.5 | 120.9 | 23.1 |
| LO stems (S) | CH1.32O0.75 | 9.3 | 68.7 | 17.1 | 5.0 | 15.6 | 594.2 | 308.8 |
| LO mixture (M) | CH1.39O0.83 | 9.9 | 67.4 | 16.4 | 6.3 | 15.1 | 371.8 | 174.5 |
| Homogeneous Reactions | |
|---|---|
| R1 | |
| R2 | |
| R3 | |
| R4 | |
| R5 | |
| R6 | |
| Airflow [kg/m2s] | wp | os | as | |||
|---|---|---|---|---|---|---|
| F. Velocity | Tmax. | F. Velocity | Tmax. | F. Velocity | Tmax. | |
| 0.1 | 12.69 | 11.77 | 1.16 | - | 4.43 | 12.71 |
| 0.2 | 12.80 | 9.19 | 9.74 | 23.48 | 12.62 | 4.64 |
| 0.3 | 1.29 | 12.62 | 9.21 | 30.97 | 26.46 | 6.32 |
| 0.4 | 5.88 | - | - | - | 51.19 | 21.86 |
| 0.45 | 14.54 | - | - | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
García Sánchez, G.F.; Chacón Velasco, J.L.; Fuentes Díaz, D.A.; Rueda-Ordóñez, Y.J.; Patiño, D.; Rico, J.J.; Martínez Morales, J.R. Biomass Combustion Modeling Using OpenFOAM: Development of a Simple Computational Model and Study of the Combustion Performance of Lippia origanoides Bagasse. Energies 2023, 16, 2932. https://doi.org/10.3390/en16062932
García Sánchez GF, Chacón Velasco JL, Fuentes Díaz DA, Rueda-Ordóñez YJ, Patiño D, Rico JJ, Martínez Morales JR. Biomass Combustion Modeling Using OpenFOAM: Development of a Simple Computational Model and Study of the Combustion Performance of Lippia origanoides Bagasse. Energies. 2023; 16(6):2932. https://doi.org/10.3390/en16062932
Chicago/Turabian StyleGarcía Sánchez, Gabriel Fernando, Jorge Luis Chacón Velasco, David Alfredo Fuentes Díaz, Yesid Javier Rueda-Ordóñez, David Patiño, Juan Jesús Rico, and Jairo René Martínez Morales. 2023. "Biomass Combustion Modeling Using OpenFOAM: Development of a Simple Computational Model and Study of the Combustion Performance of Lippia origanoides Bagasse" Energies 16, no. 6: 2932. https://doi.org/10.3390/en16062932
APA StyleGarcía Sánchez, G. F., Chacón Velasco, J. L., Fuentes Díaz, D. A., Rueda-Ordóñez, Y. J., Patiño, D., Rico, J. J., & Martínez Morales, J. R. (2023). Biomass Combustion Modeling Using OpenFOAM: Development of a Simple Computational Model and Study of the Combustion Performance of Lippia origanoides Bagasse. Energies, 16(6), 2932. https://doi.org/10.3390/en16062932