Rate Decline of Acid Fracturing Stimulated Well in Bi-Zone Composite Carbonate Gas Reservoirs

Abstract

This paper develops a model of the multi-wing finite-conductivity fractures considering stress sensitivity for low-permeability bi-zone composite gas reservoirs. A new semi-analytical solution in the Laplace domain is presented. The main solution includes the theory of source function, Laplace integral transformation, perturbation technique, and Stehfest numerical inversion. Wellbore pressure is obtained by coupling solutions of reservoirs and fractures. The results showed that the pressure and derivative curves generated by this model include a bi-linear flow stage. The model was validated by comparing its results with Wang’s results and the commercial well-test simulator; the results showed excellent agreement. This model illustrated the seepage characteristic of acid fracturing stimulated wells during refracturing treatment and how they are influenced by reservoir and hydraulic fractures parameters (asymmetrical factor and fractures distribution, etc.). The model is suitable to solve the solution of arbitrary-angle hydraulic fracture in refracturing and helpful to understand the transient production rate characteristic of the multi-wing fracturing well.

1. Introduction

Hydraulic fracturing is a common and effective practice in the production of low-permeability gas reservoirs. At present, low gas and gas prices have aroused an interest in enhancing gas and gas production. Compared with drilling a new well, acid fracturing stimulated wells were considered a more budget-friendly way of increasing energy production [1,2]. In refracturing, though the initial hydraulic fracture can have a significant influence on the propagation of a subsequent hydraulic fracture. The new fractures do not route at the same path as the initial fracture, owing to the change in stress anisotropy [3,4].

The pressure dynamic characteristics are widely used in order to evaluate the fracture-characteristic parameters, which is thought as the most effective diagnostic method in gas and gas development. After hydraulic fracturing on the vertical well, there are often many secondary fractures distributing complexly around the wellbore, and there is an angle between the fracture and the fracture, and the length of every hydraulic fracture is not equal. The existence of complex fractures can effectively reduce the resistance that the fluid flows into the hydraulic fractures [5,6].

A large number of simulations and studies have been displayed [7,8] that the change of fracture parameters, especially fracture conductivity, will greatly affect well productivity. Dejam et al. [9] used the combination of the Laplace transform (LT) and finite Fourier Cosine transforms (FFCT) to solve the diffusion coefficient equation and proposed a semi-analytical solution for the transient pressure in vertical Wells in bounded double-pore formations. It showed that compared with the well location and reservoir shape of hydraulic fracturing, the flow coefficient between pores, reservoir ratio, natural fracture permeability anisotropy, and reservoir size play an important role in identifying the flow state.

Zhang et al. [10] proposed a composite model to study the pressure characteristics and production dynamics of a multi-stage fractured vertical well (MFVW) with stimulated reservoir volume (SRV) in coalbed methane reservoirs. The model also considers adsorption–desorption, diffusion, and viscosity flow.

Based on complex geological and engineering factors, Meng et al. [11] proposed a method for fracture evaluation and parameter estimation of well testing in non-uniformly fractured wells. A semi-analytical method and Laplace transform were used to solve the model, and the good relationship between fracturing parameters and the well-test curve was studied.

Xia et al. [12] established a method to evaluate the effect of volumetric fracturing based on well test and production data by dividing the vicinity of the main fracture into different production enhancement zones, which can accurately obtain the fracturing effect, fracture parameters, and fluid nonlinear characteristics, and applying the method to a typical straight well. They concluded that volumetric fracturing could form a complex fracture network. The fracture half-length, equivalent permeability, and reconstruction area dynamically change and gradually decrease with the increase of extraction time, and the fracturing effect gradually decreases until it is destroyed.

Cui et al. [13] established a Blasingame decline semi-analytical analysis model for multi-wing fractured vertical wells using Laplace transform, numerical inversion node analysis, and iterative methods for partial proppant fractures under different stress sensitivity effects. Under the two-zone model with various fracture systems, the impacts of the length of the unsupported portion and various stress-sensitive behaviors are investigated.

Zhao et al. [14] established well-test models of the fully and partially penetrating fractured well for the bi-zonal composite reservoir using point source function theory. A typical characteristic curve is drawn up and analyzed. In order to improve the calculation speed of the finite-conductivity fractured well, Wang et al. [15] resolved the solution of the fractured well and obtained fracture conductivity function, which can solve the wellbore pressure solution of the finite-conductivity fractures quickly and effectively.

However, established models are assumed that the fracture is symmetrical about the wellbore during refracturing. It is possible to create an asymmetrical fracture that propagates along the initial fracture due to the effects of stress anisotropy and different pollution degrees of the initial fracture. In the research on the pressure dynamic of finite-conductivity asymmetric vertical fracture, Rodriguez and Cinco-Ley et al. [16] present a graphical technique, which is based on a new analytical solution for the pressure behavior of a finite-conductivity, asymmetrically fractured well during the pseudolinear and the known bilinear flow solution. The graphical technique can evaluate the asymmetry of hydraulically fractured wells. Berumen et al. [17] obtained an asymmetric constant rate fracture solution by employing numerical simulation methods. Additionally, a series of typical curves are shown to analyze the rate characteristics of asymmetric fracture. Since the solution was solved numerically, the results tend to have some errors. Therefore, the method is not adopted by some authors. Wang et al. [18,19] presented a semi-analytical solution by coupling with the reservoir and hydraulic fracture solutions in a previous paper. A pressure-derivative log–log curve and a complete pressure curve are plotted. They found that when dimensionless fracture conductivity approaches infinity, asymmetric factors have no effect on pressure and pressure-derivative log–log curves.

In order to maximize the well productivity of refractured wells, we always wish that fractures propagate orthogonally to the initial fracture and consider how to create most fractures. Asalkhuzina et al. [20] built a model to measure well production rate and pressure performance before and after refracturing by employing numerical methods. They could check the occurrence of fracture reorientation. Fu et al. [21] conducted mechanics analysis and numerical simulation by employing the boundary element method. They thought that the initial fracture would reopen first and a new fracture would subsequently initiate at some angles along the direction of maximum stress, and various factors could have an effect on the direction and length of fractures. For the study of pressure dynamics on complex fractures formed during refracturing, the new seepage mathematical model of the reservoir and fractures about multi-wing fractures was established. The semi-analytical solution of the models is obtained by using the Laplace transform [22,23,24,25,26,27].

The analytical model of transient flow established by Shan et al. showed that orthogonal fractures generated during the refracturing process will produce orthogonal linear flow in the fractured reservoir volume. The angle between the wellbore and fracture can be estimated by using the pressure transient data analysis technique combined with the double logarithm curve diagnostic diagram [28].

Using the nodal analysis technique, Wu et al. [29] established a set of diffusion coefficient equations describing hydraulically redirected fracture flow. Then, the point source solution is coupled with the discrete fracture solution to obtain the semi-analytical solution. Five typical flow patterns can be observed in the transient response of this model. At the same time, the flux along the redirected fracture is calculated, and the flux distribution at different times is analyzed. On this basis, the influence curves of key parameters such as principal fracture angle, redirected fracture angle, permeability anisotropy, fracture conductivity, and fracture length ratio on transient seepage behavior are established. For rectangular anisotropic reservoirs, the influence of principal fracture angle, permeability anisotropy, and fracture conductivity on the curve type is concentrated in the early and middle stages, and the redirected fracture angle and fracture length ratio mainly affect the linear flow pattern.

Luo et al. [30] proposed a new semi-analytical method in the Laplace domain by coupling the Fredholm integral equation of the fracture with the reservoir equation and studying the unstable pressure characteristics of the “Z” shaped fracture.

Despite the above summary of the literature, the majority of efforts related to complex fractures’ physical modeling or pressure behavior analysis do not take reservoir and fluid properties in different regions into account. Furthermore, the transient production rate per performance for low-permeability bi-zone reservoirs is rarely discussed.

In this research, the physical model of refractured wells with finite-conductivity fractures is derived in Section 2. Then, in Section 3, a mathematical model describing multi-wing fractures (MWFs) with bi-zone reservoirs accounting is derived. In Section 4, the mathematical model is solved through the Stehfest numerical inversion. The pressure and derivative curves are predicted. Results, discussions, and conclusions are provided in Section 5 and Section 6, respectively.

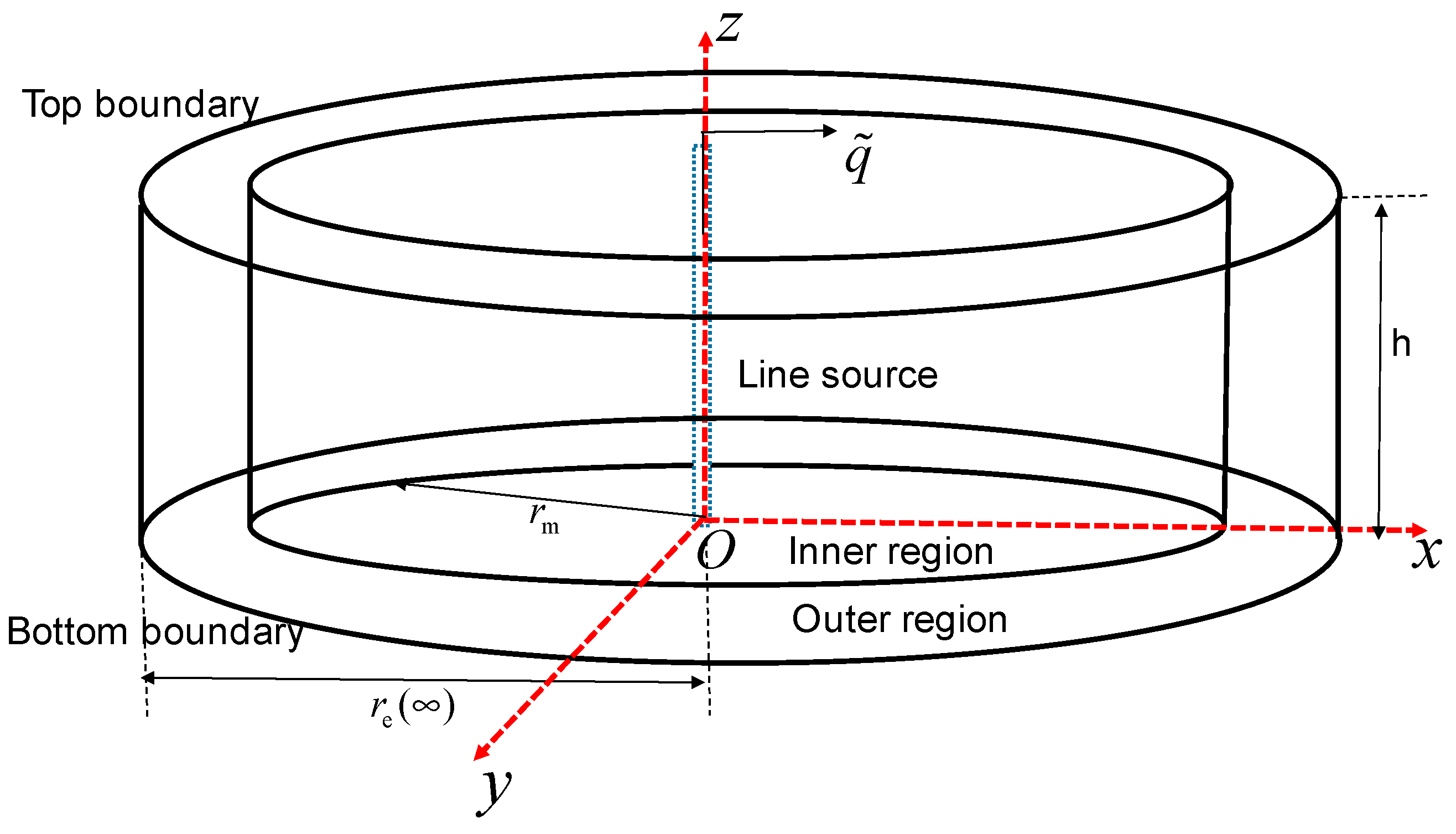
2. Physical Model

In practical refracturing measurement, owing to different stress distributions around the wellbore and initial hydraulic fracture, MWFs with arbitrary angles besides initial hydraulic fracture are formed and produced at a constant rate q_sc in a low-permeability gas reservoir (as shown in Figure 1). However, for convenience of research, it is assumed that width of all hydraulic fractures is equal and each fracture is penetrated fully.

The model presented in this article assumed that MWFs are with M fractures and with arbitrary angle between fracture and fracture. The well is located in center of bi-zone composite reservoirs with inner radius r_m, and all fractures do not penetrate inner region. The infinite lateral boundary closed-upper and closed-bottom boundaries are chosen as the outer boundary in this model.

Other basic assumptions are as follows:

• The length of each hydraulic fracture is not equal, considering existence of angle (θ) between fracture and horizontal direction. The length (L_f), width (W_f), and permeability (k_f) of the different hydraulic fractures are different;
• The fluid in the reservoir conforms to Darcy’s law and law of isothermal percolation;
• The upper and bottom boundaries of the reservoir are closed, and the fluid is incompressible;
• Stress sensitivity of permeability in tight reservoirs is taken into account;
• Negligible gravity and capillary effect are studied.

3. Mathematical Model

3.1. Line-Source Model in Bi-Zone Composite Reservoirs Considering Stress Sensitivity

Bi-zone composite low-permeability reservoirs with impermeable top and bottom boundaries have a line source. It is assumed that the fluid flow in the reservoirs results from an instantaneous pressure drop created at t = 0. The pressure waves propagate outward around the line source, which can make the fluids of inner and outer regions flow into the wellbore (as shown in Figure 2).

The majority of experimental studies demonstrate that during the creation of low-permeability reservoirs, the permeability reduction brought on by stress sensitivity cannot be ignored. The common permeability change with pressure can be calculated with the following expression [31,32,33].

$$k=k_{\mathrm{e}}{e}^{-\gamma ({\psi }_{\mathrm{e}}-\psi )}$$

(1)

It can be seen from Equation (1) that reservoir permeability is a function relating to pressure. Therefore, it presents a strong non-linearity in establishing the differential equation of low-permeability reservoir, which brings great difficulty to solving the solution of this model.

According to corresponding study by Pedrosa [34] and Klkanl and Pedrosa [35], and combining equations of motion, equations of state, and continuous differential equations, the governing differential equations to describe bi-zone composite low-permeability reservoir of the inner and outer regions are established. According to definitions of dimensionless variables in

Table A1. Definitions of Dimensionless Variables.

Variables	Dimensionless Definition	Variables	Dimensionless Definition
Dimensionless pseudo-pressure of inner region	${\psi }_{1D}=\frac{\pi k_{1}h{T}_{\mathrm{sc}}}{p_{\mathrm{sc}}T{q}_{\mathrm{sc}}}({\psi }_{\mathrm{e}}-{\psi }_1)$	Dimensionless z-coordinate	$z_{\mathrm{D}}=\frac{z}{L_{\mathrm{ref}}}$
Dimensionless pseudo-pressure of outer region	${\psi }_{2D}=\frac{\pi k_{1}h{T}_{\mathrm{sc}}}{p_{\mathrm{sc}}T{q}_{\mathrm{sc}}}({\psi }_{\mathrm{e}}-{\psi }_2)$	Dimensionless radius of boundary	$r_{\mathrm{eD}}=\frac{r_{\mathrm{e}}}{L_{\mathrm{ref}}}$
Dimensionless hydraulic fracture pseudo-pressure	${\psi }_{fD}=\frac{\pi k_{1}h{T}_{\mathrm{sc}}}{p_{\mathrm{sc}}T{q}_{\mathrm{sc}}}({\psi }_{\mathrm{e}}-{\psi }_{\mathrm{f}})$	Dimensionless hydraulic fracture conductivity	$C_{\mathrm{fD}}=\frac{k_{\mathrm{f}}{\mathrm{W}}_{\mathrm{f}}}{k_1{L}_{\mathrm{f}}}$
Dimensionless production time	$t_D=\frac{k_{1}t}{\varphi \mu C_{\mathrm{t}1}{L}_{\mathrm{ref}}^2}$	Dimensionless length of wing	$L_{\mathrm{fD}}=\frac{L_{\mathrm{f}}}{L_{\mathrm{ref}}}$
Dimensionless distance	$r_{\mathrm{D}}=\frac{r}{L_{\mathrm{ref}}}$	Dimensionless continuous production	${\tilde{q}}_{\mathrm{fD}}=\frac{L_{\mathrm{ref}}{\tilde{q}}_{\mathrm{f}}}{q_{\mathrm{sc}}}$
Dimensionless radius of inner region	$r_{\mathrm{mD}}=\frac{r_{\mathrm{m}}}{L_{\mathrm{ref}}}$	Permeability ratio	$M_{12}=\frac{k_1/{\mu }_1}{k_2/{\mu }_2}$
Dimensionless x-coordinate	$x_{\mathrm{D}}=\frac{x}{L_{\mathrm{ref}}}$	Diffusivity ratio	${\eta }_{12}=\frac{{\mu }_1{\varphi }_1{C}_{\mathrm{t}1}/k_1}{{\mu }_2{\varphi }_2{C}_{\mathrm{t}2}/k_2}$
Dimensionless y-coordinate	$y_{\mathrm{D}}=\frac{y}{L_{\mathrm{ref}}}$	Dimensionless stress-sensitivity coefficient	${\gamma }_{\mathrm{D}}=\frac{p_{\mathrm{sc}}T{q}_{\mathrm{sc}}}{\pi k_{1}h{T}_{\mathrm{sc}}}\gamma$

, the dimensionless mathematical model of vertical linear source with bi-zone composite low-permeability reservoir. Based on Laplace’s integral transform in Equation (2), the dimensionless mathematical models in Laplace domain are obtained.

$${\overline{\psi }}_{\mathrm{D}}={\displaystyle {\int }_0^{+\infty }{\psi }_{\mathrm{D}}{e}^{-s{t}_{\mathrm{D}}}d{t}_{\mathrm{D}}}$$

(2)

(1)

Governing differential equation of inner region can be written as

$$\begin{array}{c}\frac{1}{r_{\mathrm{D}}}\frac{\partial }{\partial r_{\mathrm{D}}}\left(r_{\mathrm{D}}\frac{\partial {\overline{\psi }}_{\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)-{\gamma }_{\mathrm{D}}{\left(\frac{\partial {\overline{\psi }}_{\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)}^2=e^{{\gamma }_{\mathrm{D}}{p}_{\mathrm{D}1}}s{\overline{\psi }}_{\mathrm{D}1}\\ (1\le r_{\mathrm{D}}\le r_{\mathrm{mD}})\end{array}$$

(3)

(2)

Governing differential equation of outer region can be written as

$$\begin{array}{c}\frac{1}{r_{\mathrm{D}}}\frac{\partial }{\partial r_{\mathrm{D}}}\left(r_{\mathrm{D}}\frac{\partial {\overline{\psi }}_{\mathrm{D}2}}{\partial r_D}\right)-{\gamma }_{\mathrm{D}}{\left(\frac{\partial {\overline{\psi }}_{\mathrm{D}2}}{\partial r_{\mathrm{D}}}\right)}^2=e^{{\gamma }_{\mathrm{D}}{\overline{p}}_{\mathrm{D}2}}{\eta }_{12}s{\overline{\psi }}_{\mathrm{D}2}\\ (r_{\mathrm{mD}}\le r_{\mathrm{D}}\le \infty )\end{array}$$

(4)

(3)

Inner boundary condition can be written as

$$\underset{{\epsilon }_{\mathrm{D}}\to 0}{\lim }{e}^{-{\gamma }_{\mathrm{D}}{\overline{p}}_{\mathrm{D}}}{\left(r_{\mathrm{D}}\frac{\partial {\overline{\psi }}_{\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}={\epsilon }_{\mathrm{D}}}=-{\overline{\tilde{q}}}_{\mathrm{D}}$$

(5)

(4)

Infinite lateral boundary condition can be written as

$${\overline{p}}_{\mathrm{D}2}(r_{\mathrm{D}}\to \infty ,s)=0$$

(6)

(5)

Interface condition between the inner and the outer region can be written as

$$M_{12}{e}^{-{\gamma }_{\mathrm{D}}{\overline{p}}_{\mathrm{D}1}}{\left(\frac{\partial {\overline{\psi }}_{\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}=r_{\mathrm{mD}}}=e^{-{\gamma }_{\mathrm{D}}{\overline{p}}_{\mathrm{D}2}}{\left(\frac{\partial {\overline{\psi }}_{\mathrm{D}2}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}=r_{\mathrm{mD}}}$$

(7)

$${\overline{\psi }}_{\mathrm{D}1}(r_{\mathrm{mD}},s)={\overline{\psi }}_{\mathrm{D}2}(r_{\mathrm{mD}},s)$$

(8)

The line-source model represented by Equations (4)–(8) is strongly nonlinear. To successfully obtain transient pseudo-pressure responses caused by a line source in bi-zone composite low-permeability reservoir, perturbation technique [34] is used widely. When dimensionless permeability modulus is very small, zero-order approximate solution of the perturbation technique can satisfy the requirements of engineering precision. Zero-order approximate perturbation is as follows:

$${\overline{\psi }}_{\mathrm{D}}=-\frac{1}{{\gamma }_{\mathrm{D}}}\ln \left(1-{\gamma }_{\mathrm{D}}{\overline{\xi }}_{\mathrm{D}}\right)$$

(9)

Substitute Equation (10) into Equations (3)–(8), respectively. According to zero-order approximate perturbation given by Equations (9) and (3)–(8) can be written as

$$\left\{\begin{array}{l}\frac{1}{r_{\mathrm{D}}}\frac{\partial }{\partial r_{\mathrm{D}}}\left(r_{\mathrm{D}}\frac{\partial {\overline{\xi }}_{0\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)=s{\overline{\xi }}_{0\mathrm{D}1},1\le r_{\mathrm{D}}\le r_{\mathrm{mD}}\\ \frac{1}{r_{\mathrm{D}}}\frac{\partial }{\partial r_{\mathrm{D}}}\left(r_{\mathrm{D}}\frac{\partial {\overline{\xi }}_{0\mathrm{D}2}}{\partial r_{\mathrm{D}}}\right)={\eta }_{12}s{\overline{\xi }}_{0\mathrm{D}2},r_{\mathrm{mD}}\le r_{\mathrm{D}}\le \infty \\ {\overline{\xi }}_{0\mathrm{D}1}(r_{\mathrm{mD}},s)={\overline{\xi }}_{0\mathrm{D}2}(r_{\mathrm{mD}},s)\\ \underset{{\epsilon }_{\mathrm{D}}\to 0}{\lim }{\left(r_{\mathrm{D}}\frac{\partial {\overline{\xi }}_{0\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}={\epsilon }_{\mathrm{D}}}=-{\overline{\tilde{q}}}_{\mathrm{D}}\\ {\overline{\xi }}_{0\mathrm{D}1}(r_{\mathrm{mD}},s)={\overline{\xi }}_{0\mathrm{D}2}(r_{\mathrm{mD}},s)\\ M_{12}{\left(\frac{\partial {\overline{\xi }}_{0\mathrm{D}1}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}=r_{\mathrm{mD}}}={\left(\frac{\partial {\overline{\xi }}_{0\mathrm{D}2}}{\partial r_{\mathrm{D}}}\right)}_{r_{\mathrm{D}}=r_{\mathrm{mD}}}\\ {\overline{\xi }}_{0\mathrm{D}2}(r_{\mathrm{D}2}\to \infty ,s)=0\end{array}\right.$$

(10)

According to the theory of Bessel’s function, we can get the general solution of governing differential equation of inner and outer region after perturbation as follows:

$${\overline{\xi }}_{0\mathrm{D}1}=a_1{I}_0({\epsilon }_0{r}_{\mathrm{D}})+a_2{K}_0({\epsilon }_0{r}_{\mathrm{D}})$$

(11)

$${\overline{\xi }}_{0\mathrm{D}2}=b_1{I}_0({\epsilon }_1{r}_{\mathrm{D}})+b_2{K}_0({\epsilon }_1{r}_{\mathrm{D}})$$

(12)

where ${\epsilon }_0=\sqrt{s}$; ${\epsilon }_1=\sqrt{{\eta }_{12}s}$.

According to the properties of Bessel’s function,

$$\underset{x\to 0}{\lim }{K}_0(x)=0$$

(13)

$$\underset{x\to 0}{\lim }{I}_0(x)=\infty$$

(14)

$$\underset{x\to 0}{\lim }x{K}_1(x)=1$$

(15)

$$I_0(x)K_0^{\prime }(x)-K_0(x)I_0^{\prime }(x)=-\frac{1}{x}$$

(16)

With Equations (13)–(16) and Equations (11) and (12) inputted into inner and outer boundary conditions and interface condition after perturbation, the coefficient of Equations (11) and (12) are obtained, respectively.

$$a_1=\frac{K_0({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0^{\prime }({\epsilon }_1{r}_{\mathrm{mD}}^{})-M_{12}{K}_0^{\prime }({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0({\epsilon }_1{r}_{\mathrm{mD}}^{})}{M_{12}{I}_0^{\prime }({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0({\epsilon }_1{r}_{\mathrm{mD}}^{})-I_0({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0^{\prime }({\epsilon }_1{r}_{\mathrm{mD}}^{})}{\overline{\tilde{q}}}_{\mathrm{D}}$$

(17)

$$a_2={\overline{\tilde{q}}}_{\mathrm{D}}$$

(18)

$$b_1=0$$

(19)

$$b_2=\frac{{\eta }_{12}{M}_{12}}{r_{\mathrm{mD}}^{}}\frac{{\overline{\tilde{q}}}_{\mathrm{D}}}{M_{12}{I}_0^{\prime }({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0({\epsilon }_1{r}_{\mathrm{mD}}^{})-I_0({\epsilon }_0{r}_{\mathrm{mD}}^{})K_0^{\prime }({\epsilon }_1{r}_{\mathrm{mD}}^{})}$$

(20)

Substituting Equations (17) and (18) into Equation (11), pseudo-pressure is obtained at arbitrary position. However, it is noted that r_D represents the dimensionless distance between the line source and any arbitrary point in low-permeability reservoirs in Equations (11) and (12) when line source is located at the origin.

$$r_{\mathrm{D}}=\sqrt{x_{\mathrm{D}}^2+y_{\mathrm{D}}^2}$$

(21)

If line source is located at (x_w, y_w) instead of the origin, r_D can be written as follows.

$$r_{\mathrm{D}}=\sqrt{{\left(x_{\mathrm{D}}^{}-x_{\mathrm{wD}}^{}\right)}^2+{\left(y_{\mathrm{D}}^{}-y_{\mathrm{wD}}^{}\right)}^2}$$

(22)

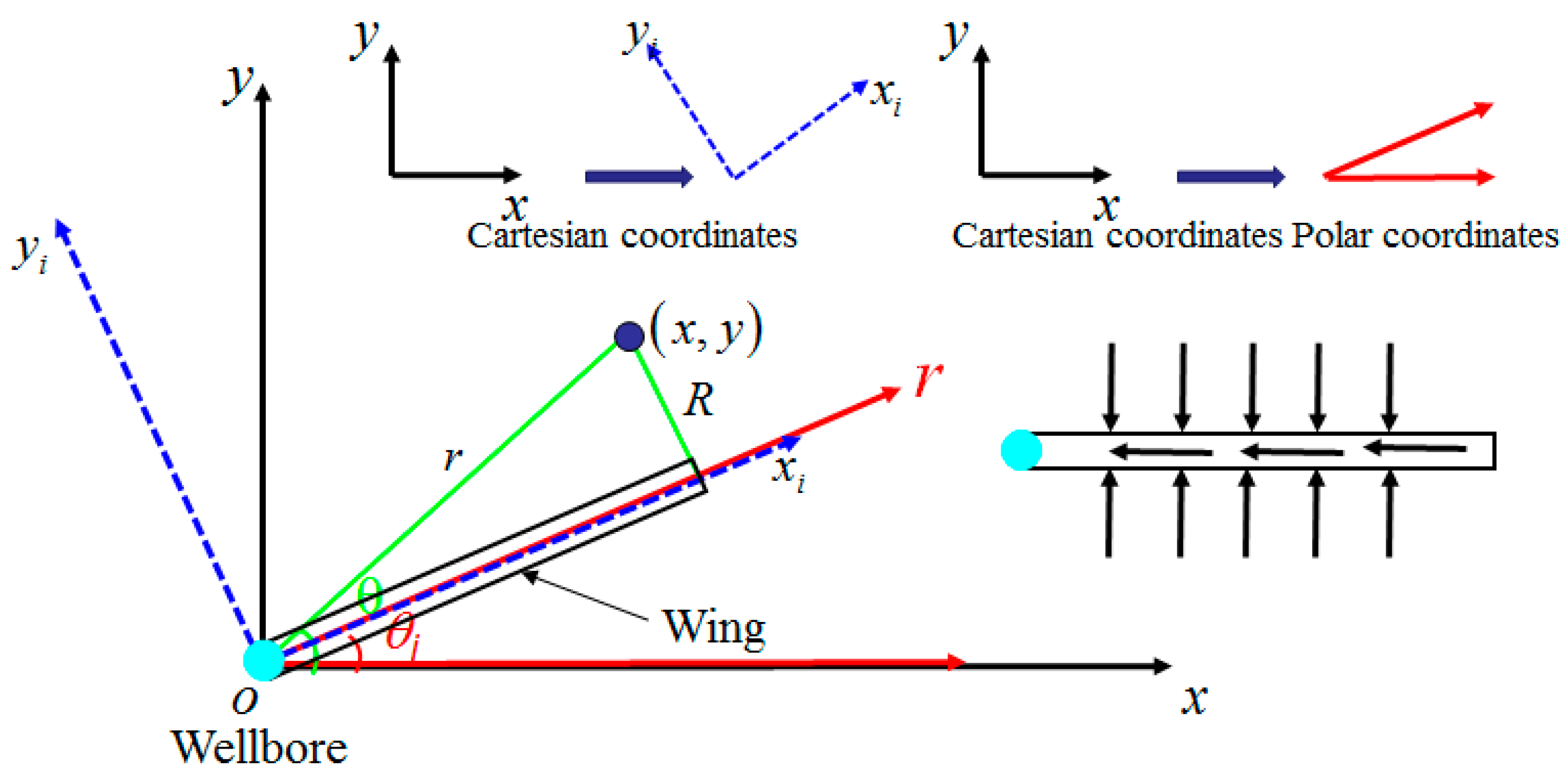
3.2. Surface-Source Model in Bi-Zone Composite Reservoirs Considering Stress Sensitivity

In order to obtain the uniform rate surface solution of the bi-zone composite low-permeability reservoir, we can integrate Equation (13) to obtain the surface-source solution. Based on assumption that hydraulic fracture is symmetric and parallel with the axis, the mathematical model solution is given to a single hydraulic fracture. However, if there is a certain angle between the hydraulic fractures and the coordinate axis or if the lengths of each hydraulic fracture are not equal, we can use the coordinate rotation and transformation method to distribute the hydraulic fractures along the changed coordinates. A schematic diagram of the physical model of the coordinate transformation is shown in Figure 3.

The total pressure drop is obtained by the pressure drop superposition principle. According to previous research [36], the uniform flow surface solution of the ith hydraulic fracture in the polar coordinates for the low-permeability composite reservoir can be written as follows:

$${\overline{\xi }}_{0\mathrm{D}1i}\left(r_{\mathrm{D}}^{},{\theta }_i^{},u\right)={\displaystyle \underset{0}{\overset{L_{\mathrm{fD}i}}{\int }}\left\{\begin{array}{l}{\overline{\tilde{q}}}_{\mathrm{D}i}\left(\alpha ,{\theta }_i,u\right)\times \\ \left[\begin{array}{l}{K}_0\left(\sqrt{u}\sqrt{r_{\mathrm{D}}^2+{\alpha }^2-2r_{\mathrm{D}}^{}\alpha \cos \left(\theta -{\theta }_i^{}\right)}\right)+\\ a_1{I}_0\left(\sqrt{u}\sqrt{r_{\mathrm{D}}^2+{\alpha }^2-2r_{\mathrm{D}}^{}\alpha \cos \left(\theta -{\theta }_i^{}\right)}\right)\end{array}\right]\end{array}\right\}d\alpha }$$

(23)

According to the pressure drop superposition principle, the total pseudo-pressure response of M hydraulic fractures can be expressed as

$${\overline{\xi }}_{0\mathrm{D}1}={\displaystyle \sum _{i=1}^{\mathrm{M}}{\overline{\xi }}_{0\mathrm{D}i}\left(r_{\mathrm{D}}^{},{\theta }_i^{},u\right)}$$

(24)

For a multi-wing well intercepting M hydraulic fractures, the assumption of constant total flow rate can yield the following equation:

$${\displaystyle \sum _{i=1}^{\mathrm{M}}{\displaystyle \underset{0}{\overset{L_{\mathrm{fD}i}}{\int }}{\overline{\tilde{q}}}_{\mathrm{D}i}\left(\alpha ,{\theta }_i,u\right)d\alpha }}=\frac{1}{s}$$

(25)

Based on the study of Cinco-Ley and Meng, we establish the following mathematical model to describe fluid flow in hydraulic fractures. Each hydraulic fracture is assumed as a three-dimensional rectangle with finite conductivity, and the volume of each hydraulic fracture is L_f × W_f × h. End point of each hydraulic fracture is impermeable. Compared with length of hydraulic fracture, width of hydraulic fracture is neglected. After the rotation of the coordinates, we established a mathematical model of low-permeability reservoirs with finite-conductivity hydraulic fracture in the $x^{\prime }-y^{\prime }$ coordinate system.

With consideration of stress-sensitivity, the solution of ith fracture is obtained [25].

$${\overline{\xi }}_{0\mathrm{fD}i}\left(r_{\mathrm{D}i},{\theta }_i,s\right)-{\overline{\xi }}_{0\mathrm{wD}i}=\frac{2\pi }{{\mathrm{C}}_{\mathrm{fD}i}}\left({\displaystyle {\int }_0^{r_{\mathrm{D}}}{\displaystyle {\int }_0^{\alpha }{\overline{\tilde{q}}}_{\mathrm{fD}}}d\alpha d{r}_{\mathrm{D}}}-r_{\mathrm{D}i}{\displaystyle {\int }_0^{L_{\mathrm{fD}i}^{}}{\overline{\tilde{q}}}_{\mathrm{fD}}}d\alpha \right)$$

(26)

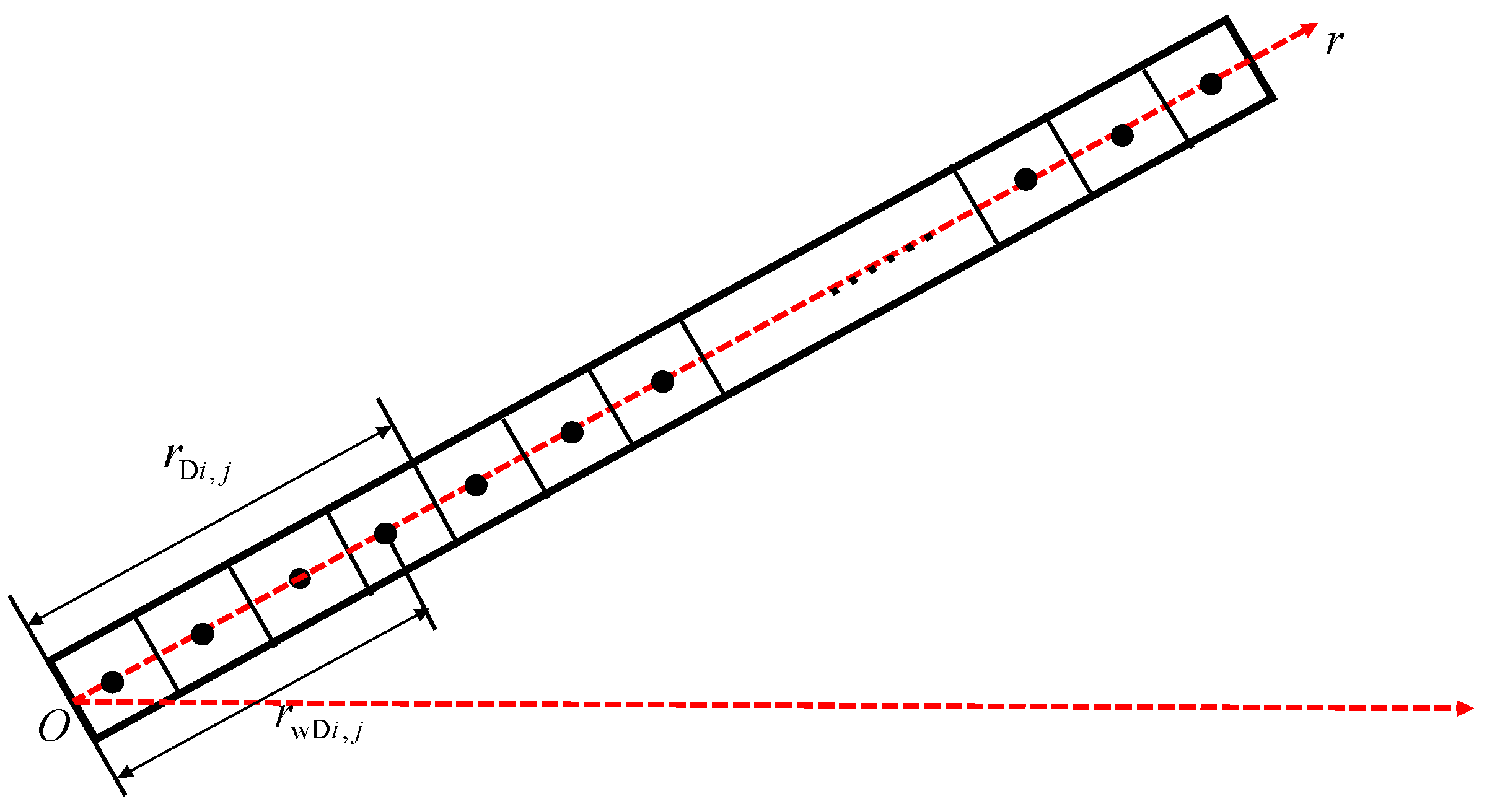
3.3. Coupling of Reservoir Model and Hydraulic Fracture Model

In order to obtain wellbore pseudo-pressure of low-permeability composite reservoir with multi-wing finite-conductivity fracture, combine Equations (23) and (26) to yield the final expression of dimensionless bottom-hole pseudo-pressure.

At the surface of the ith fracture, the reservoir pseudo-pressure and rate should be equal to those of the hydraulic fracture:

$${\overline{\xi }}_{0\mathrm{fD}i}={\overline{\xi }}_{0\mathrm{D}1i}$$

(27)

$${\overline{\tilde{q}}}_{\mathrm{fD}}={\overline{q}}_{\mathrm{D}}$$

(28)

Combining Equations (23) and (26), pseudo-pressure and rate at the surface of the ith fracture satisfy Equations (27) and (28).

$$\begin{array}{l}{\overline{\xi }}_{0\mathrm{wD}}-{\displaystyle \sum _{i=1}^{\mathrm{M}}{\displaystyle \underset{0}{\overset{L_{\mathrm{fD}i}}{\int }}\left\{{\overline{\tilde{q}}}_{\mathrm{D}i}\left(\alpha ,{\theta }_i,u\right)\left[\begin{array}{l}{K}_0\left(\sqrt{u}\sqrt{r_{\mathrm{D}}^2+{\alpha }^2-2r_{\mathrm{D}}^{}\alpha \cos \left(\theta -{\theta }_i^{}\right)}\right)+\\ a_1{I}_0\left(\sqrt{u}\sqrt{r_{\mathrm{D}}^2+{\alpha }^2-2r_{\mathrm{D}}^{}\alpha \cos \left(\theta -{\theta }_i^{}\right)}\right)\end{array}\right]\right\}d\alpha }}=\\ \frac{2\pi }{{\mathrm{C}}_{\mathrm{fD}i}}\left(r_{\mathrm{D}i}{\displaystyle {\int }_0^{L_{\mathrm{fD}i}^{}}{\overline{\tilde{q}}}_{\mathrm{D}}}d\alpha -{\displaystyle {\int }_0^{r_{\mathrm{D}}}{\displaystyle {\int }_0^{\alpha }{\overline{\tilde{q}}}_{\mathrm{D}}}d\alpha d{r}_{\mathrm{D}}}\right)\end{array}$$

(29)

However, the right-side portion of Equation (29) is only Fredholm integral equation. Because the rate of fracture is uneven during constant production, it is more difficult for us to solve wellbore pseudo-pressure of finite-conductivity fractures directly. We can divide fractures into N segments and assume that rate of each segment is equal (as is shown in Figure 4).

According to the study of the Cinco-Ley [10], Equation (29) can be rewritten by discretizing single-wing fracture as follows.

$$\begin{array}{l}{\overline{\xi }}_{0\mathrm{wD}}-{\displaystyle \sum _{i=1}^{\mathrm{M}}{\displaystyle \sum _{j=1}^{\mathrm{N}}{\displaystyle \underset{r_{\mathrm{D}i,j}}{\overset{r_{\mathrm{D}i,j+1}}{\int }}\left\{\begin{array}{l}{\overline{\tilde{q}}}_{\mathrm{D}i,j}\left(\alpha ,{\theta }_i,s\right)\times \\ \left[\begin{array}{l}{K}_0\left({\epsilon }_0\sqrt{r_{\mathrm{wDm},k}^2+{\alpha }^2-2r_{\mathrm{wDm},k}^{}\alpha \cos \left({\theta }_{\mathrm{m}}-{\theta }_i^{}\right)}\right)+\\ a_1\cdot I_0\left({\epsilon }_0\sqrt{r_{\mathrm{wDm},k}^2+{\alpha }^2-2r_{\mathrm{wDm},k}^{}\alpha \cos \left({\theta }_{\mathrm{m}}-{\theta }_i^{}\right)}\right)\end{array}\right]\end{array}\right\}d\alpha }}}\\ =\frac{\mathsf{\pi }}{{\mathrm{C}}_{\mathrm{fD}i}}\left[r_{\mathrm{mD}v,k}{\displaystyle \sum _{k=1}^{\mathrm{N}}{\overline{\tilde{q}}}_{\mathrm{D}v,k}\Delta r_{\mathrm{D}v}}-\frac{\Delta r_{\mathrm{D}v}^2}{8}{\overline{\tilde{q}}}_{\mathrm{D}v,k}-{\displaystyle \sum _{j=1}^{k-1}{\overline{\tilde{q}}}_{\mathrm{D}v,j}\left[\left(k-j\right)\Delta r_{\mathrm{D}v}^2\right]}\right]\\ 1\le v\le M,1\le k\le N\end{array}$$

(30)

Although we can only get M × N linear algebraic equations by Equation (30), M × N + 1 is still unknown. Therefore, if we want to get wellbore of bi-zone composite low-permeability reservoirs, a linear algebraic equation must be given. We can rewrite Equation (25) as following equation:

$${\displaystyle \sum _{i=1}^{\mathrm{M}}{\displaystyle \sum _{j=1}^{\mathrm{N}}{\overline{\tilde{q}}}_{\mathrm{fD}i}\Delta r_{\mathrm{Di}}}}=1/s$$

(31)

Combining Equations (30) and (31), M × N + 1 linear algebraic equations, which can solve wellbore of bi-zone composite low-permeability reservoirs, are gotten.

When M = 2, the asymmetry factor is defined by using the length of the 2 wings.

$$\beta =\frac{\left|L_{\mathrm{f}1}-L_{\mathrm{f}2}\right|}{L_{\mathrm{f}1}+L_{\mathrm{f}2}}$$

(32)

Combining Duhamel’s principle and pseudo-pressure drop superposition principle used in well-test analysis, wellbore pseudo-pressure is obtained considering skin effect and wellbore storage.

$${\overline{\psi }}_{\mathrm{wD}}=\frac{s{\overline{\xi }}_{0\mathrm{wD}}+S}{s+C_{\mathrm{D}}{s}^2(s{\overline{\xi }}_{0\mathrm{wD}}+S)}$$

(33)

Finally, wellbore pseudo-pressure of multi-wing, formed by refracturing old hydraulic fracture, is obtained for bi-zone composite low-permeability reservoirs considering stress sensitivity.

The dimensionless wellbore flow rate equation for the constant pseudo-pressure production in low-permeability gas reservoirs can be determined by the relationship between the dimensionless pseudo-pressure and the rate in the Laplace domain [37]:

$${\overline{q}}_{\mathrm{D}}=\frac{1}{s^2{\overline{p}}_{\mathrm{wD}}}$$

(34)

4. Mathematical Model Solution

Stehfest numerical inversion is used to obtain the pressure and rate of the real-time domain [38]. In this section, our main purpose is to compare the solution obtained in our simple model with the commercial well-test simulator. The model without consideration of stress sensitivity in this article can be simply asymmetry finite-conductivity hydraulic fracture and finite-conductivity symmetry hydraulic fracture with bi-zone composite reservoir separately [39,40]. Martirosyan, A.V. and Ilyushin, Y.V. presented the laboratory installation and mathematical model by changing the temperature field due to the similitude of the mathematical apparatus and the hydrodynamic processes behavior [41]. Ahmadi et al. selected low-permeability carbonate plugs and applied nanoparticles in the porous media [42,43]. If M = 2, L_f1 = L_f2 = 40, θ₁ = 0, θ₂ = 180° in our model, it can be simplified as a conventional finite-conductivity symmetry hydraulic fracture with the bi-zone composite reservoir. To verify the credibility of the model presented in this article, we compared it with the commercial well-test simulator. If M = 2, L_f1 = 20, L_f2 = 60, θ₁ = 0, θ₂ = 180°, and M₁₂ = η₁₂ = 1 in our model, we can again verify the correction of our solution by comparing it with Wang’s model calculated by the asymmetry factor.

If our model can be simplified, it can be used to simulate a conventional finite-conductivity symmetry hydraulic fracture with a bi-zone composite reservoir. We can use a commercial well-test simulator to validate our model. Figure 5 shows that the results of our model are comparable to those of commercial well-test simulators for bi-linear flow, linear flow, and radial flow wells. The comparisons in Figure 5 show that the results calculated from our model are consistent with those obtained from the commercial simulator, confirming the credibility of the model presented in this article.

In addition, we can verify our model and solutions by comparison with Wang’s model mentioned above. Wang studied the pseudo-pressure dynamic characteristics of asymmetric hydraulic fracture by the means that well deviate from the center of the hydraulic fracture. If the angle between the hydraulic fracture and the x-axis is 180° and another angle between the hydraulic fracture and the x-axis is 0°, and the length of 2 hydraulic fractures is not equal in our model, the result of the model presented in this article should be the same as Wang’s model. It is important to confirm the accuracy of our model under conductivity since the conductivity of the hydraulic fracture has a significant impact on the dimensionless pseudo-pressure and pseudo-pressure derivative during the early stages. Figure 6 shows that the results obtained in this article, under conductivity 1 and 10, are consistent with that of Wang’s model, which can verify the accuracy of our model again.

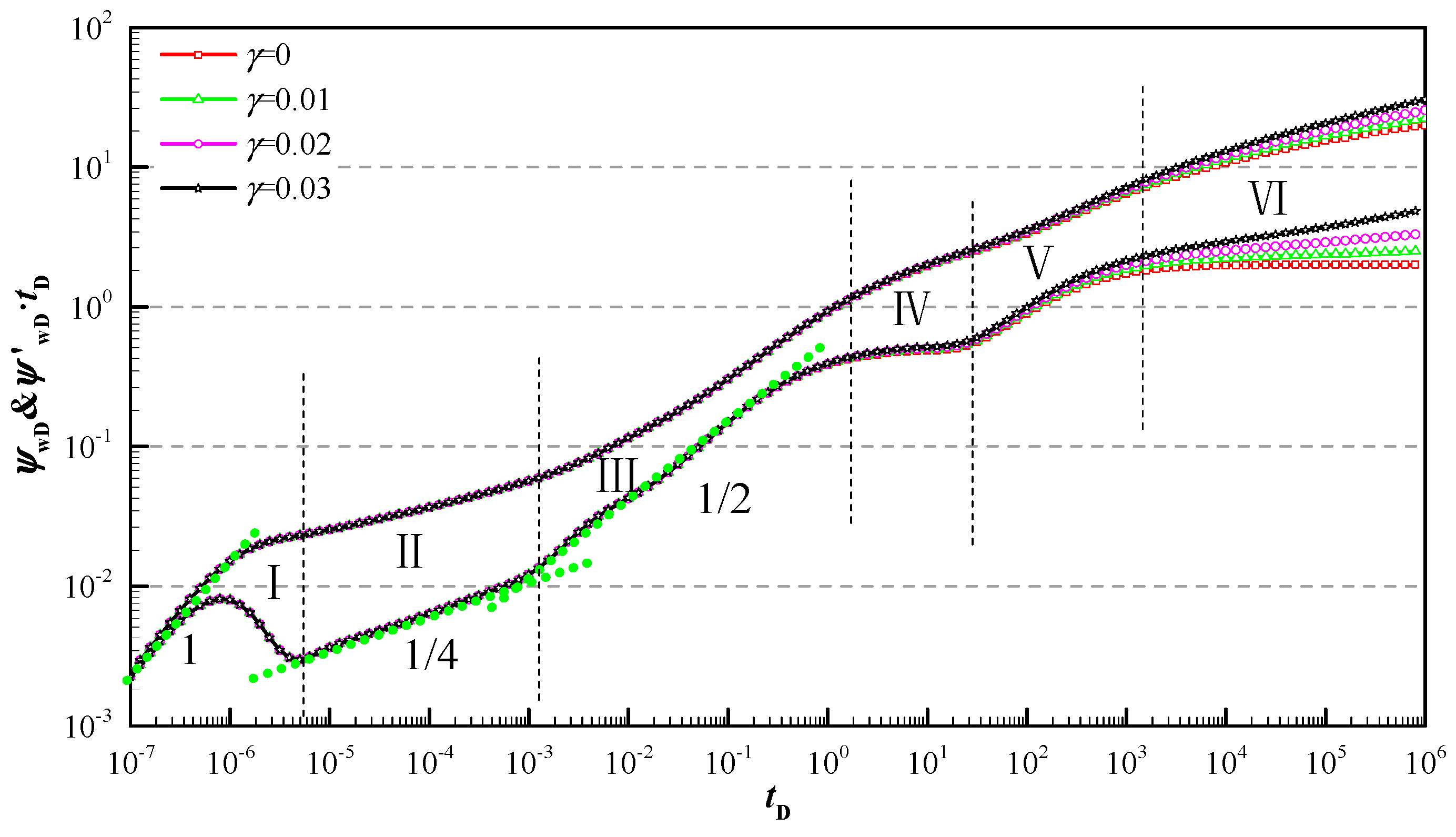
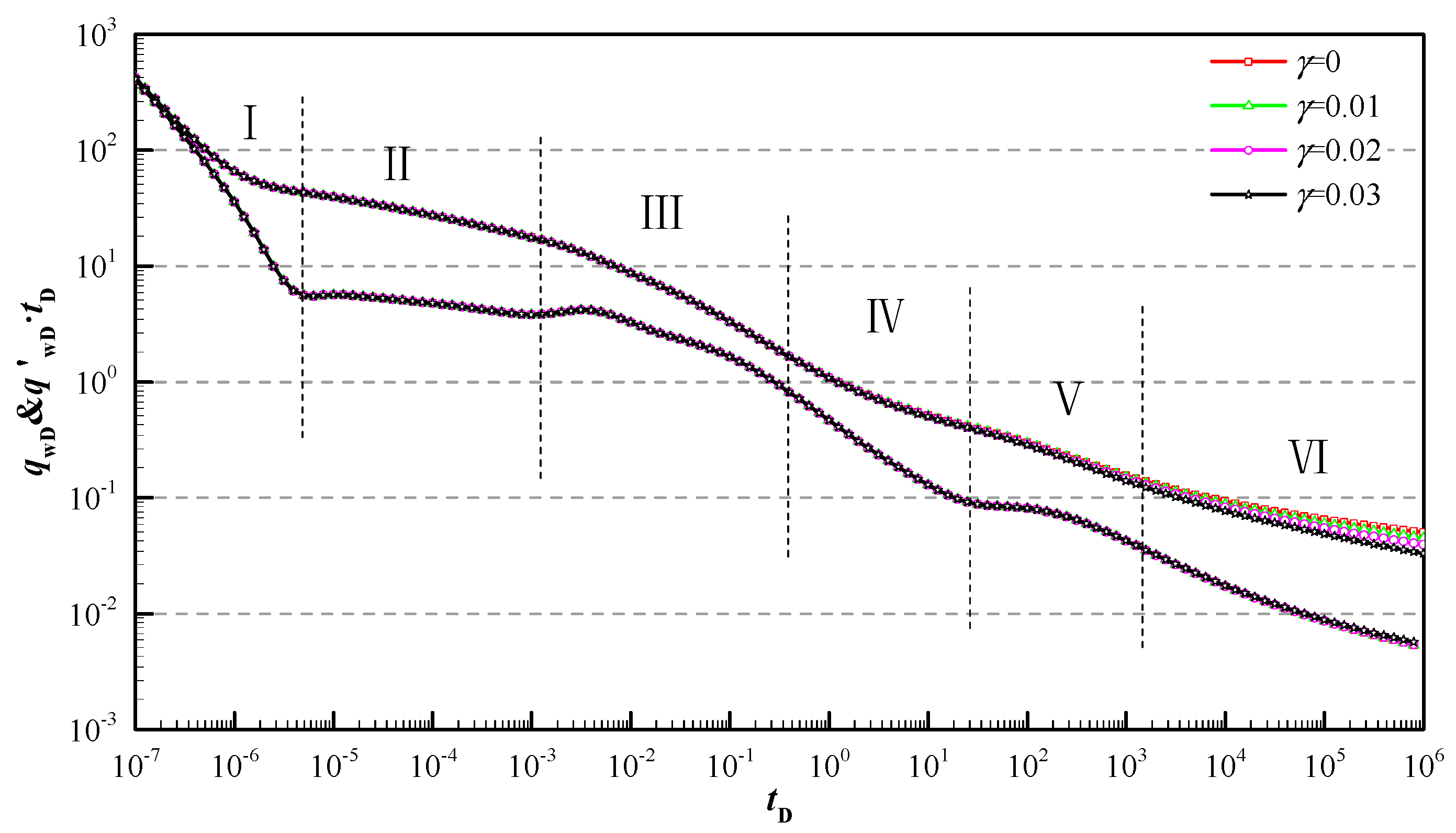
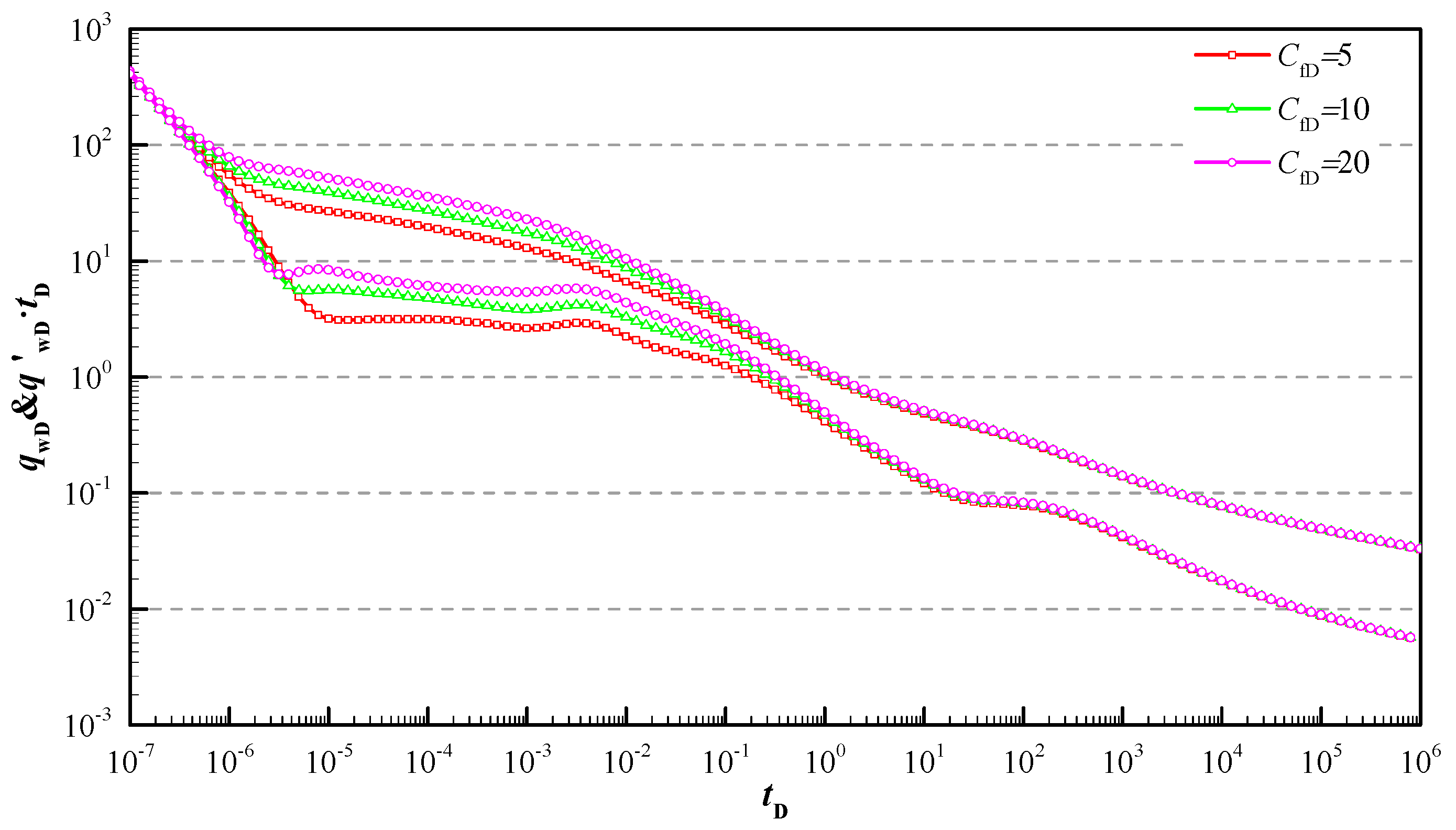
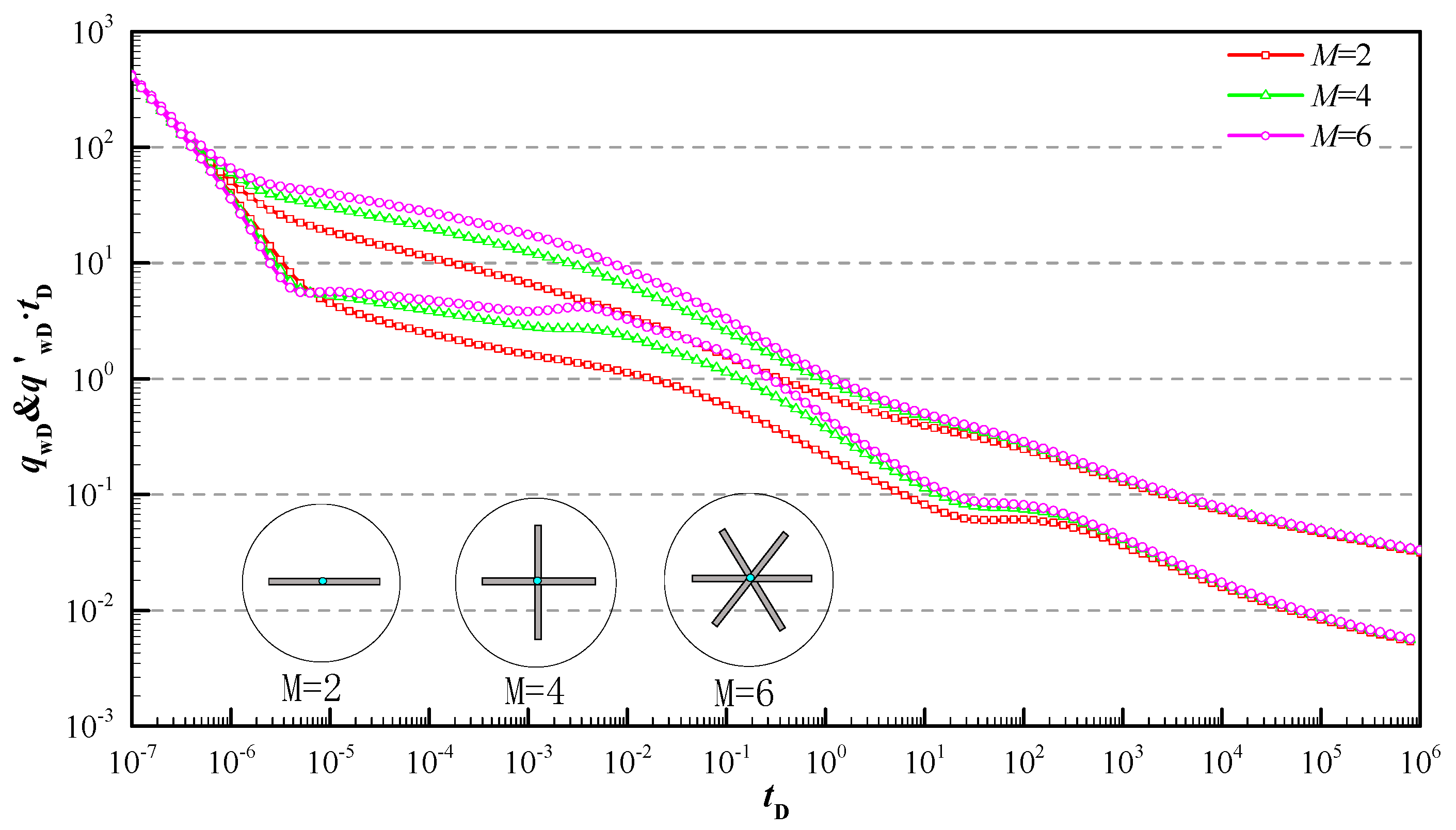
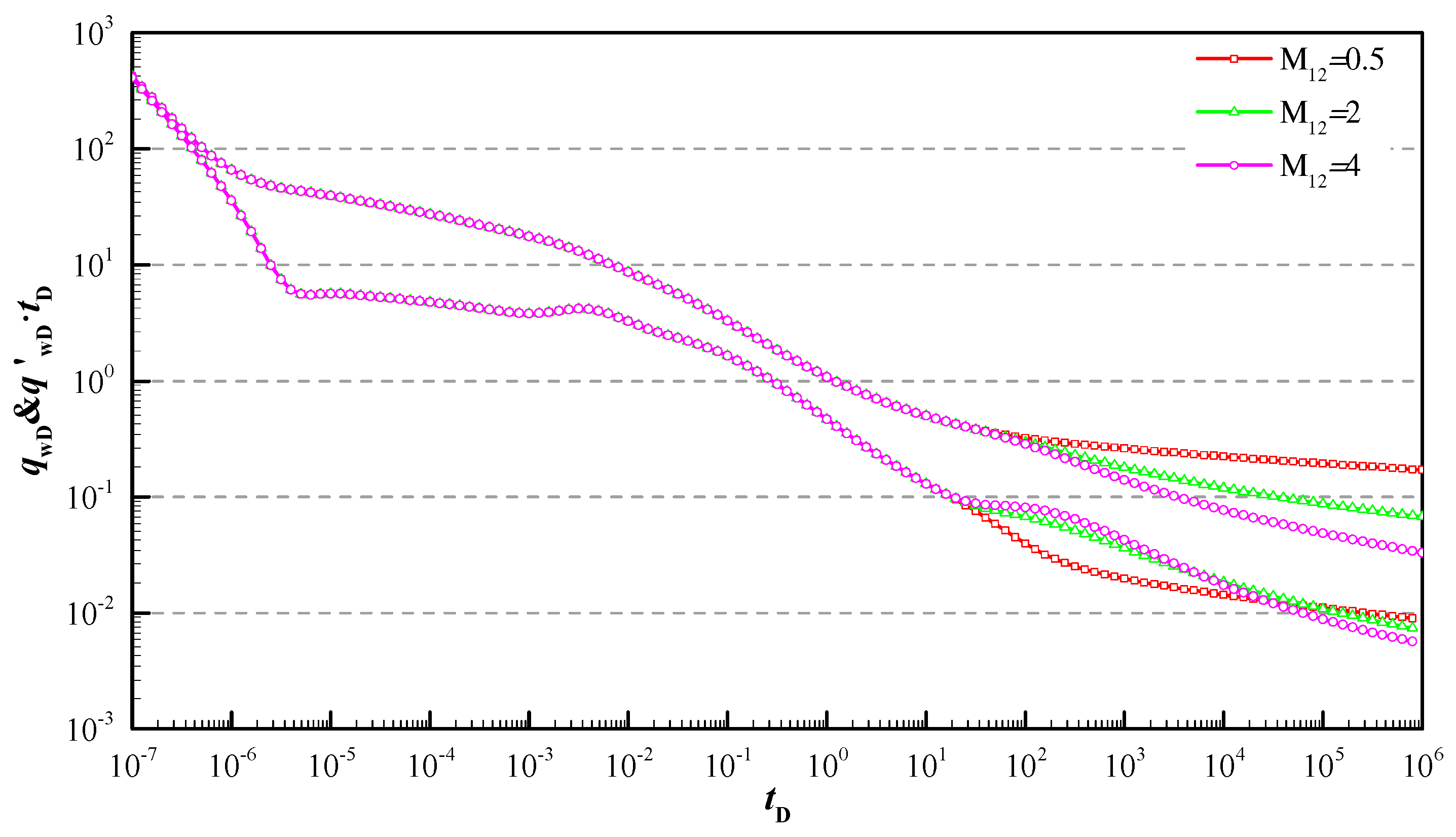
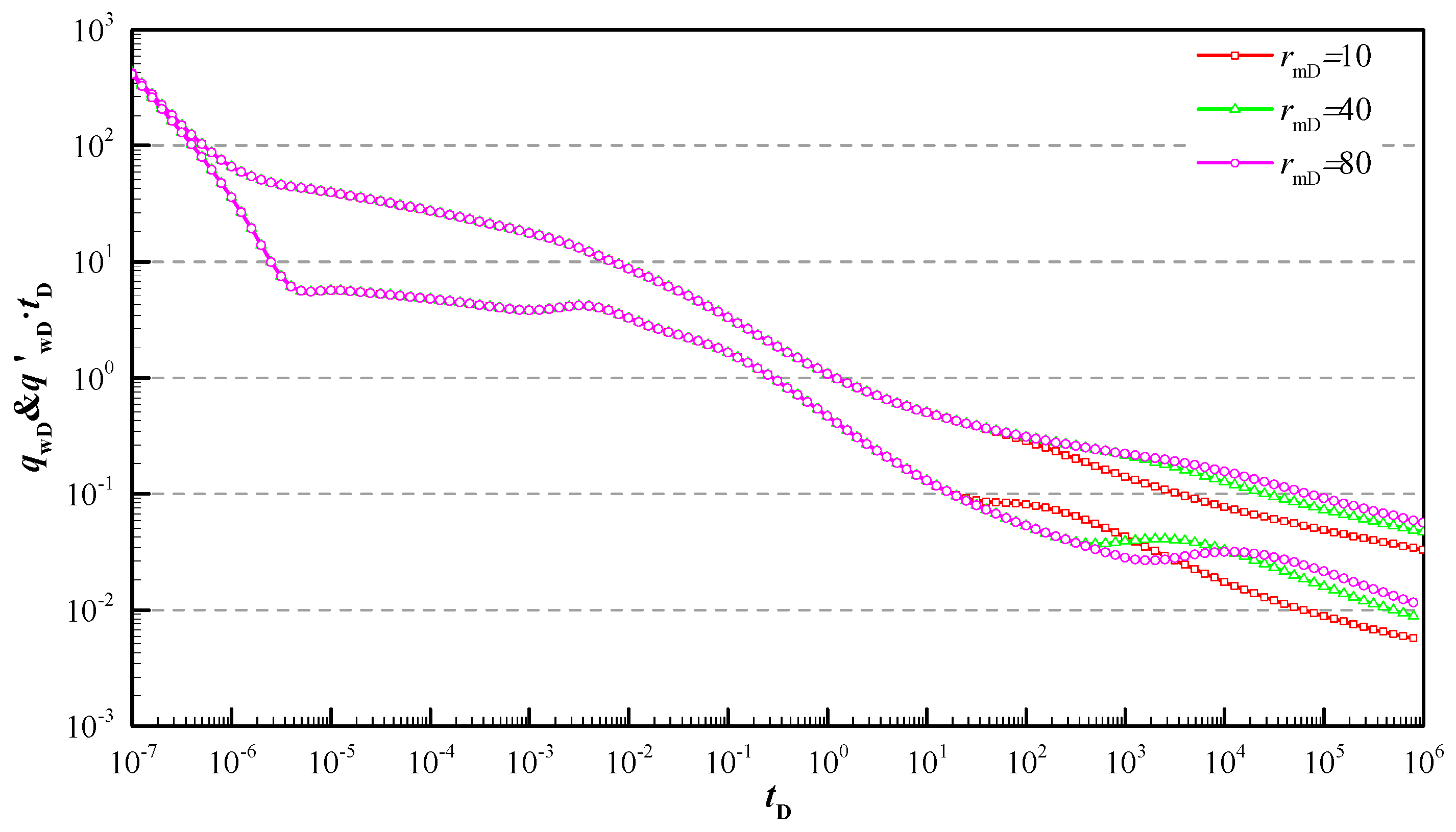
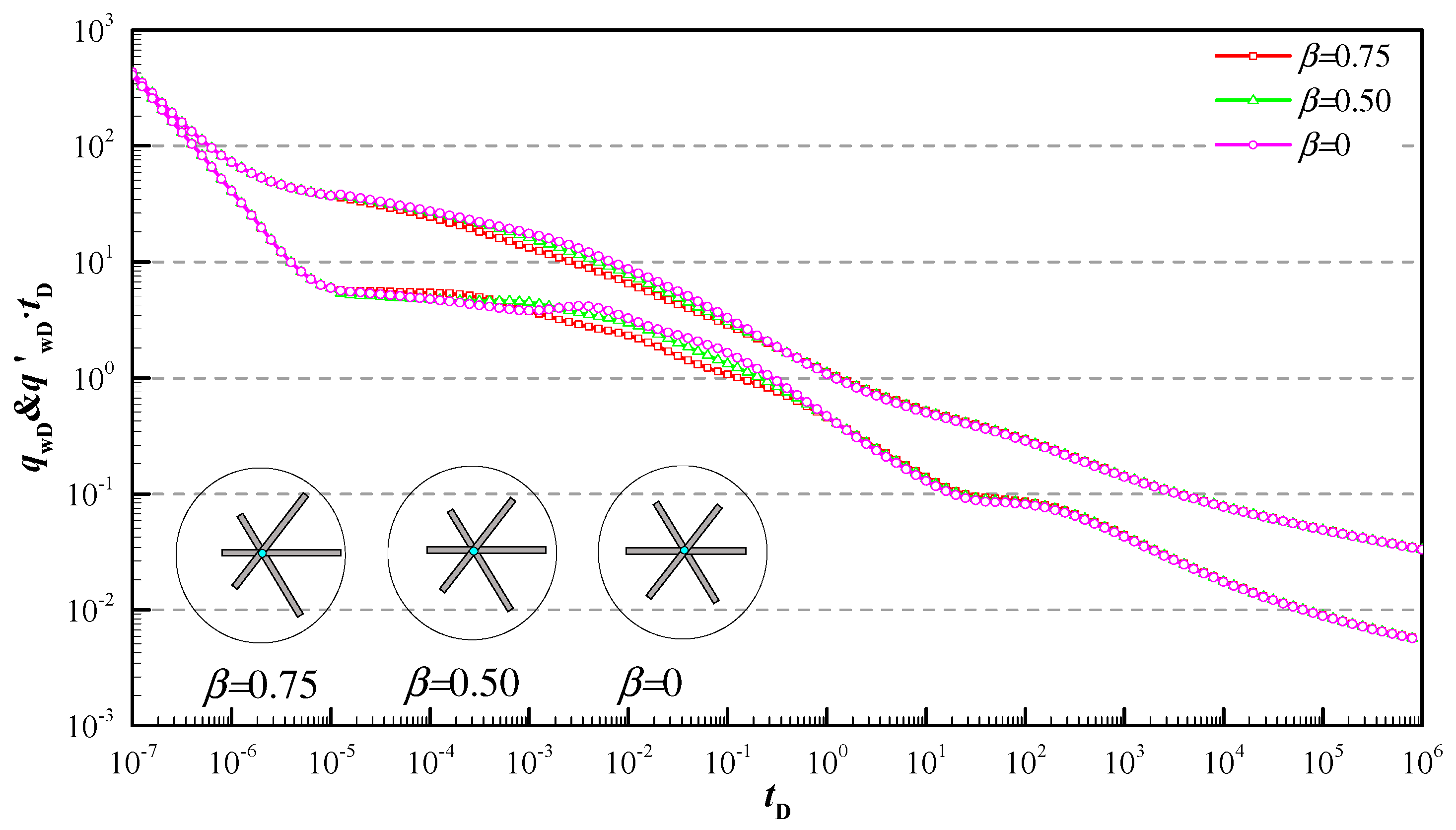
5. Results and Discussion

In order to study the flow regimes of low-permeability bi-zone composite reservoirs more graphically, type curves of pseudo-pressure response and production rate performance are illustrated in Figure 7 and Figure 8. According to the dimensionless pseudo-pressure-derivate characteristic, pseudo-pressure response curves of low-permeability bi-zone composite reservoirs considering stress sensitivity are divided into sex flow periods. It is noted that the red line presents the pseudo-pressure response curve of bi-zone composite reservoirs without considering stress sensitivity.

Period I is the well storage and skin effect stage that occurred during the early period; both dimensionless pseudo-pressure and pseudo-pressure-derivative curves coincide and show as unit-slope straight lines during pure well storage. Curves of production rate and derivative coincide and exhibit a −1-slope line during pure well storage.

Period II is the bi-linear flow stage corresponding to simultaneous linear flow in both hydraulic fractures and reservoirs. The pseudo-pressure-derivative curve exhibits a quarter-slope line in an ideal condition. The production rate curve decreases, and the derivative curve is shown as a level straight line whose value corresponds to conductivity.

Period III is the early linear flow stage, in which the pseudo-pressure derivative curve appears with a half-slope. During this period, the fluid flow mainly appears as a linear flow perpendicular to the hydraulics fracture surfaces. The production rate curve keeps decreasing, and the derivative curve also decreases compared with the bi-linear flow stage.

Period IV is the radial flow stage of the inner region. The pseudo-pressure wave does not propagate to the inner boundary. The fluid flow mainly appears as a radial flow around the whole MWF system during this stage. The pseudo-pressure derivative curve behaves as a 0.5-value horizontal line. Compared with the linear flow stage, the production rate derivative curve drops significantly.

Period V is the transition flow stage between the inner region and outer region.

Period VI is the radial flow stage of the outer region. The pseudo-pressure wave propagates to the inner boundary. The fluid of the outer region flow mainly appears as a radial flow around the whole MWFs system during this stage. Owing to different M₁₂ values of the inner and outer region, the pseudo-pressure derivative curve behaves as a 0.5 M₁₂-value horizontal line without consideration of stress sensitivity. If stress sensitivity is considered, pseudo-pressure and pseudo-pressure derivative curves manifest as a line upward trend. Stress sensitivity has little influence on the production rate derivative curve, but large stress sensitivity can lead to a small production rate curve in the log–log plot.

Transient production rate curves influenced by the fracture number and dimensionless hydraulic fracture conductivity are shown in Figure 9 and Figure 10. Fluid flowing into the wellbore through hydraulic fractures results in a pseudo-pressure loss, which is reflected by hydraulic fracture conductivity. Due to the tiny pseudo-pressure drop loss and short duration of bi-linear flow caused by large conductivity, the transient production rate and derivate curves diminish as the conductivity increases (as shown in Figure 9). More fractures can both boost output when there is constant pseudo-pressure and decrease pseudo-pressure loss when fluid is flowing into the wellbore from the reservoir. Figure 10 shows that fracture number only affects early- and intermediate-time transient production rate and derivate curves. The higher the fracture number is, the larger the transient production rate and derivate curves are during the early and intermediate time (as shown in Figure 10).

Figure 11 and Figure 12 describe transient production rate curves affected by the mobility ratio (inner region to the outer region) and inner radius. The mobility ratio represents the reservoir and fluid’s physical property difference between the inner and outer regions. When the mobility ratio is greater than 1, it indicates that the mobility of the inner is better than that of the outer and vice versa. A smaller mobility ratio can lead to increasing transient production rate curves during the radial flow stage of the outer region (as shown in Figure 11). The inner radius has an influence on not only the duration of the inner radial flow but also the transient production rate curves of the outer radial flow. A small inner radius corresponds to a short duration of inner radial flow and small transient production rate curves (as shown in Figure 12).

Figure 13 and Figure 14 describe transient production rate curves affected by the fracture distribution and asymmetry factor. It is obvious that the effects of fracture distribution appear during the bi-linear and linear stages. When fracture clusters are distributed at an even angle (Model 3 in Figure 13), the contact area between the reservoir and the fracture is fully utilized, which contributes to an increase in production rate while pseudo-pressure is kept constant. Smaller transient production rate curves during the early stage are correlated with a more even fracture distribution (i.e., from Model 1 to Model 3 in Figure 13) (as shown in Figure 13). It is obvious that effects of fracture cluster asymmetry factor appear during the bi-linear and linear stages. The larger the fracture cluster asymmetry factor leads to smaller transient production rate curves during the bi-linear and linear stages (as shown in Figure 14).

6. Conclusions

In this paper, the semi-analytical solution of a finite-conductivity acid fracturing stimulated well formed during refracturing measurement is presented in lateral infinite for bi-zonal reservoirs. This paper considers the influence of stress sensitivity. Dimensionless pseudo-pressure and pseudo-pressure derivative curves under constant production and transient production rate and derivative curves under constant pseudo-pressure are drawn in a log–log plot. Based on the work presented in this paper, the following conclusions are obtained.

(1)

Complicated fractures around the wellbore during refracturing measurement can be modeled using a modified multiple fractures model. Based on the theory of point function, when stress sensitivity is considered, the result of the multiple fractures model describing complicated fractures can be solved analytically in the Laplace domain.

(2)

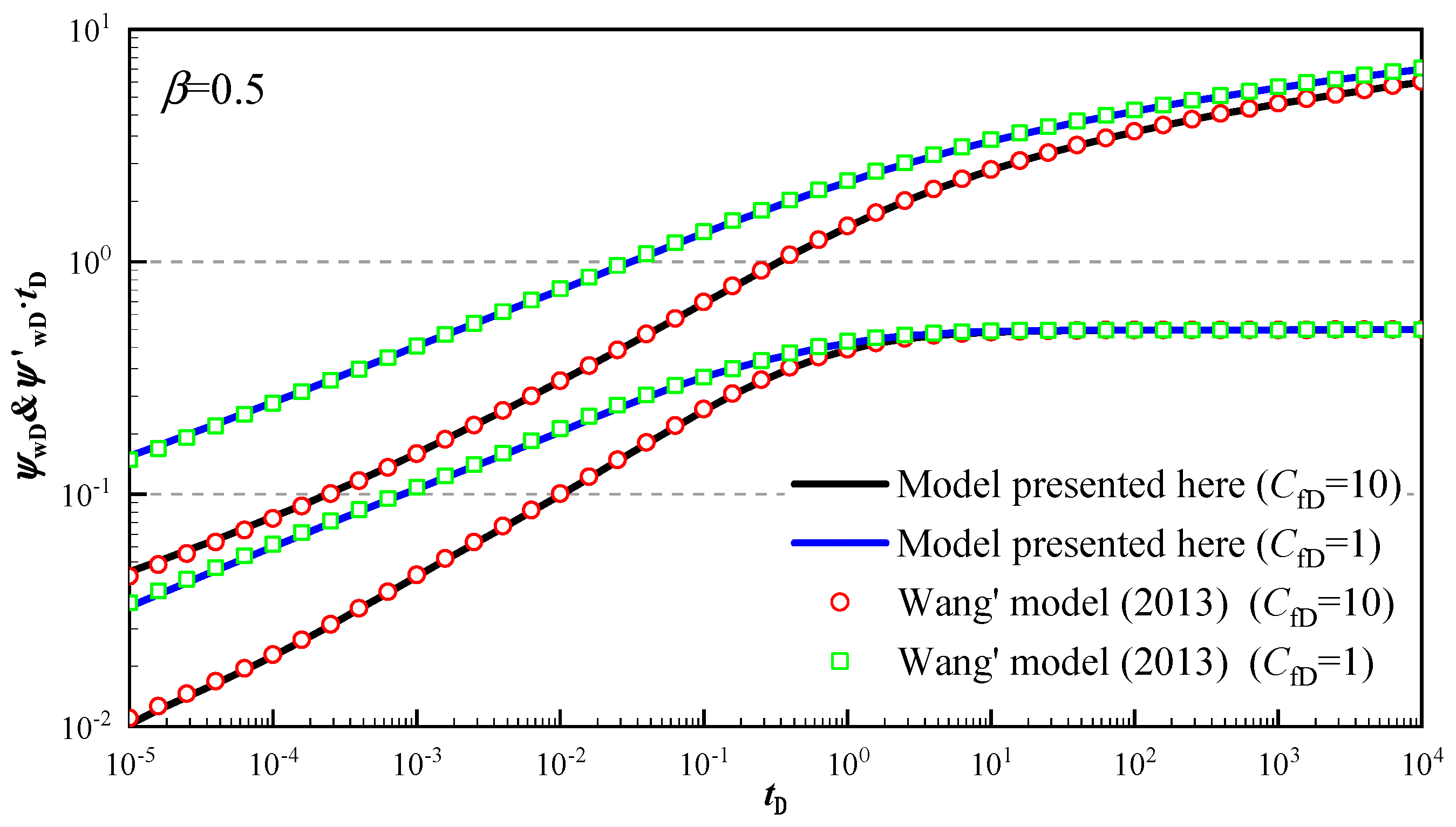
We compared the simplified model obtained from this paper with the result calculated by Wang for asymmetry fracture without stress sensitivity and the result calculated by the commercial well-test simulator for symmetric fracture of bi-zonal composite reservoirs without stress sensitivity, respectively. The results showed excellent agreement.

(3)

The log–log typical curves can be generated using a solution of this model, which mainly includes the bi-linear flow stage (quarter-slope portion), followed by the linear flow stage (quarter-slope portion), then the radial flow stage of the stimulated region (0.5 value) and radial flow stage of the un-stimulated region (0.5 M₁₂ value, without stress sensitivity).

(4)

The model illustrated how the transient production rate curves are influenced by reservoir and hydraulic fracture parameters. Reasonable fracture distribution can effectively decrease the pseudo-pressure loss of the early stage, and the more uneven the fracture distribution along the angle is, the lower the pseudo-pressure curve is; the smaller asymmetric factor leads to larger pseudo-pressure loss and the unobvious bi-linear characteristic.