Energy Management Strategies for Hybrid Loaders: Classification, Comparison and Prospect
Abstract
:1. Introduction
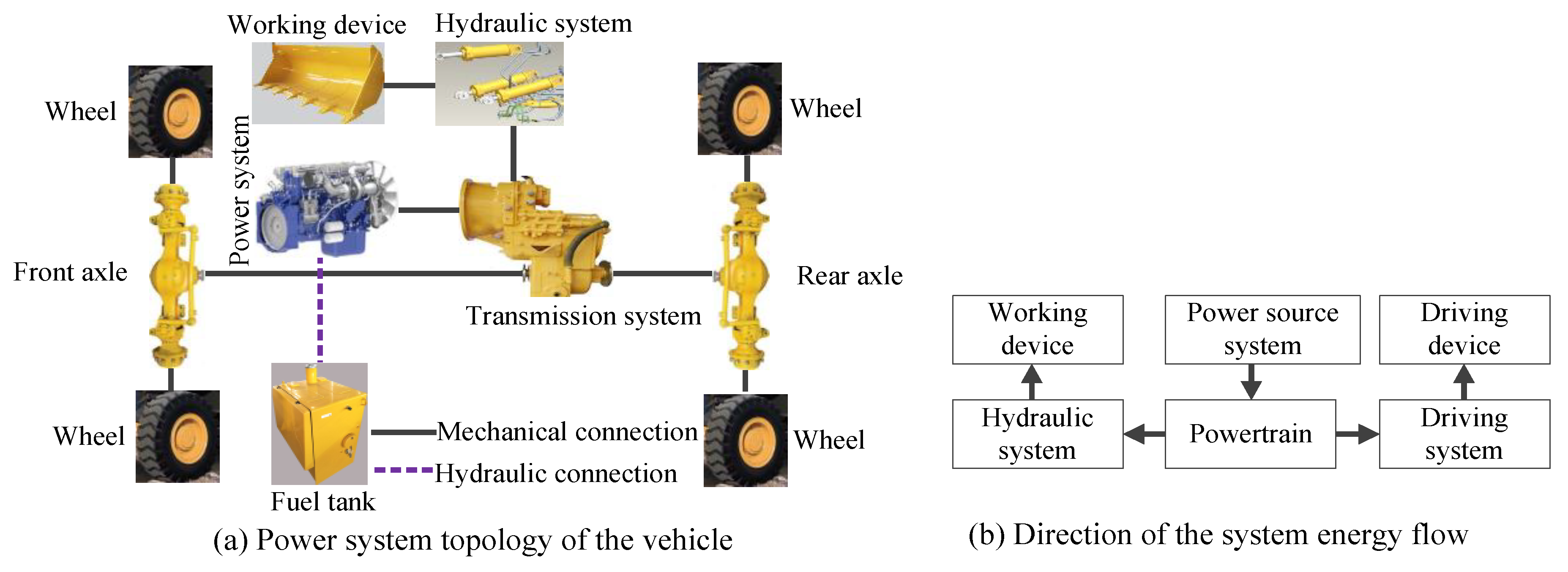
2. Configurations of HLs
2.1. Oil–Hydraulic Hybrid
2.1.1. Series Oil–Hydraulic Hybrid
2.1.2. Parallel Oil–Hydraulic Hybrid
2.2. Oil–Electric Hybrid
2.2.1. Series Oil–Electric Hybrid
- (1)
- The hydraulic pump directly driven by the engine is changed to be driven by the motor, to improve the energy utilization rate of the hydraulic system [39].
- (2)
- For improving the electric energy utilization of the driving system and the vehicle controllability, the centralized driving of the chassis driving motor is replaced by a distributed wheel-driven system [14].
2.2.2. Parallel Oil–Electric Hybrid
2.2.3. Series–Parallel Oil–Electric Hybrid
2.3. Fuel Cell Hybrid
3. Energy Management Strategies of HLs
3.1. RB EMSs
3.1.1. Deterministic RB EMSs
3.1.2. Fuzzy RB EMSs
3.2. OB EMSs
3.2.1. Global Optimization EMSs
3.2.2. Real-Time Optimization EMSs
- Instantaneous optimization EMSs
- 2.
- Local optimal EMSs
3.3. Simulation Analysis of EMSs
4. Discussion and Analysis
- A single strategy not ensuring the optimization effect and real-time performance simultaneously
- 2.
- Dependence on the analytical model weakening the universality of the strategy
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | |
| EMS | energy management strategy |
| HLs | hybrid loaders |
| ERS | energy regeneration system |
| DC | direct current |
| MPC | |
| model predictive control | |
| SoC | state of charge |
| RB | rule-based |
| OB | optimization-based |
| PSOA | particle swarm optimization algorithm |
| GA | genetic algorithm |
| PMP | Pontryagin’s minimum principle |
| DP | dynamic programming |
| ECMS | equivalent consumption minimization strategy |
| RL | reinforcement learning |
| HDP | heuristic dynamic programming |
| Variables and parameters | |
| output power of the power source | |
| output torque of the power source | |
| output speed of the power source | |
| power of wheel | |
| torque of wheel | |
| speed of wheel | |
| driving force of wheel | |
| vehicle speed | |
| power of hydraulic system | |
| torque of hydraulic system | |
| speed of hydraulic system | |
| displacement of hydraulic system | |
| pressure of hydraulic system | |
| energy transmission efficiency between the wheel and power source | |
| energy transmission efficiency between the hydraulic pump and power source | |
| discrete time or distance point | |
| performance index of HLs | |
| cost function | |
| state variables set of HLs | |
| control variables set of the drive system | |
| state space equation of HLs system | |
| constraint conditions of | |
| control variables set of allowable input of | |
| total demand torque of the hydraulic system and drive assembly | |
| minimum value of SoC | |
| maximum value of SoC | |
| lower boundaries of the engine output torque | |
| upper boundaries of the engine output torque | |
| lower boundaries of the motor output torque | |
| upper boundaries of the motor output torque | |
| Hamiltonian function | |
| co-state variable | |
| optimal control law | |
| optimal value of from to time | |
| instantaneous fuel consumption of engine | |
| equivalent fuel of instantaneous power consumption of the battery | |
| engine output torque | |
| engine output speed | |
| engine power | |
| motor output torque | |
| motor output speed | |
| battery power | |
| instantaneous efficiency of the engine | |
| low calorific value of fuel | |
| equivalent factor between electric energy and fuel | |
| penalty factor | |
| prediction window size | |
| probability matrix | |
| demand power | |
| distance | |
| optimal energy consumption approximation of the system | |
| a discount factor |
References
- Tong, Z.; Miao, J.; Li, Y.; Tong, S.; Zhang, Q.; Tan, G. Development of electric construction machinery in China: A review of key technologies and future directions. J. Zhejiang Univ. Sci. A 2021, 22, 245–264. [Google Scholar] [CrossRef]
- Verma, S.; Mishra, S.; Gaur, A.; Chowdhury, S.; Mohapatra, S.; Dwivedi, G. A comprehensive review on energy storage in hybrid electric vehicle. J. Traffic Transp. Eng. Engl. Ed. 2021, 8, 621–637. [Google Scholar] [CrossRef]
- Wang, J.; Yang, Z.; Liu, S.; Zhang, Q.; Han, Y. A Comprehensive overview of hybrid construction machinery. Adv. Mech. Eng. 2016, 8, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, D.; Wang, Z.; Hu, Y. The trend and actuality of hybrid power loaders. Key Eng. Mater. 2014, 621, 649–654. [Google Scholar] [CrossRef]
- He, X.; Jiang, Y. Review of hybrid electric systems for construction machinery. Autom. Constr. 2018, 92, 286–296. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Du, S.; Ma, H.; Zhao, W.; Li, H. Energy management strategies for hybrid construction machinery: Evolution, classification, comparison and future trends. Energies 2019, 12, 2024. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Bian, Y.; Yang, M.; Shao, J.; Liang, A. Parameter Matching of Energy Regeneration System for Parallel Hydraulic Hybrid Loader. Energies 2021, 14, 5014. [Google Scholar] [CrossRef]
- Liu, H.; Li, T. Energy Management strategy development for fuel cell hybrid loaders. IOP Publishing Ltd. In Proceedings of the International Conference on Civil and Hydraulic Engineering, Qingdao, China, 23–25 November 2018; Volume 189, p. 052015. [Google Scholar]
- Zhang, H.; Wang, F.; Xu, B.; Fiebig, W. Extending battery lifetime for electric wheel loaders with electric-hydraulic hybrid powertrain. Energy 2022, 261, 125190. [Google Scholar] [CrossRef]
- K-Series Loaders 644K/724K. Available online: https://www.deere.com/assets/publications/index.html?id=d861a139#1 (accessed on 17 March 2019).
- K-Series 944K Wheel Loader—A Hybrid of Epic Innovations. Available online: http://docplayer.net/77232251-K-series-944k-wheel-loader-a-hybrid-of-epic-innovations.html (accessed on 17 March 2019).
- Ishida, K.; Higurashi, M. Hybrid Wheel Loaders Incorporating Power Electronics. Hitachi Rev. 2015, 64, 398–402. [Google Scholar]
- Tianyu, L.I.; Dingxuan, Z.H.O.; Huailiang, K.A.G.; Zhiwen, Z.H.N.; Zhengfei, Z.H.N.; Chunbo, X.U. Parameter matching of parallel hybrid power loaders. J. Jilin Univ. Eng. Ed. 2013, 43, 916–921. [Google Scholar]
- XC9350 Ultra-Large Tonnage Electric Drive Loader of XCMG. Available online: https://mproduct.cmo2o.com/zhuangzaiji/xcmg/xc9350/ (accessed on 17 March 2019).
- 862H Wheel Loader. Available online: https://www.liugong.com/en/Product/Machines/Wheel-Loaders/862H (accessed on 17 March 2019).
- Kawasaki Launched Hybrid Loader 65Z in Conexpo. Available online: https://www.cehome.com/news/20110326/10612.shtml (accessed on 17 March 2019).
- Lyu, C.; Yanqing, Z.; Meng, L. Loader power-split transmission system based on a planetary gear set. Adv. Mech. Eng. 2018, 10, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zou, N.W.; Dai, Q.L.; Jia, Y.H.; Zhang, W.; Ren, Y.C. Modeling and Simulation Research of Coaxial Parallel Hybrid Loader. Appl. Mech. Mater. 2010, 29–32, 1634–1639. [Google Scholar]
- Zhenbao, W.A.G.; Sicheng, Q.I. Analysis of dynamic characteristics of hydraulic torque converter of loader. J. South China Univ. Technol. Nat. Sci. Ed. 2016, 44, 41–46. [Google Scholar]
- Lin, M.; Yu, Z.; Zhao, L.; Chen, Y. Working cycle identification–based braking control strategy and its application for hydraulic hybrid loader. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Lai, X.; Guan, C. A parameter matching method of the parallel hydraulic hybrid excavator optimized with genetic algorithm. Math. Probl. Eng. 2013, 2013, 765027. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Jing, J. Research on the system configuration and energy control strategy for parallel hydraulic hybrid loader. Autom. Constr. 2010, 19, 213–220. [Google Scholar]
- Du, Z.; Kai, L.C.; Li, P.Y.; Chase, T. Fuel economy comparision of series, parallel and HMT hydraulic hybrid architectures. In Proceedings of the American Control Conference (ACC), Washington, DC, USA, 1 June 2013; IEEE; pp. 5954–5959. [Google Scholar]
- Wen, Q.; Wang, F.; Xu, B. Modeling and design of a series hydraulic hybrid powertrain for compact wheel loaders. American Society of Mechanical Engineers. In Proceedings of the BATH/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018; pp. 1–9. [Google Scholar]
- Wen, Q.; Wang, F.; Xu, B.; Sun, Z. Improving the fuel efficiency of compact wheel loader with a series hydraulic hybrid powertrain. IEEE Trans. Veh. Technol. 2020, 69, 10700–10709. [Google Scholar] [CrossRef]
- Qunya, W.E.; Feng, W.A.G.; Bing, X.U.; Zongxuan, S.U. Power optimization of series hydraulic hybrid powertrain for compact wheel loader. American Society of Mechanical Engineers. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019. [Google Scholar]
- Qunya, W.E.; Feng, W.A.G.; Min, C.H.N.; Bing, X.U.; Zongxuan, S.U. Adaptive Equivalent Consumption Minimization Strategy for Off-Road Hydraulic Hybrid Vehicles: A Cycle-to-Cycle Optimization Approach. IEEE Trans. Veh. Technol. 2022, 71, 2346–2357. [Google Scholar]
- Mikko, H.; Mikko, H.; Jyrki, T.; Matti, L.; Jussi, T. Fuel efficiency optimization of a baseline wheel loader and its hydraulic hybrid variants using dynamic programming. In Proceedings of the BATH/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018. [Google Scholar]
- Pengyu, Z.H.O.; Yinglong, C.H.N.; Hua, Z.H.U. Summary of research on the system and control strategy of hydraulic hybrid engineering machinery. J. Zhejiang Univ. Eng. Ed. 2016, 50, 11. [Google Scholar]
- Yan, L.; Sun, H.; Liu, W.; Jiang, J.; Zhao, Y.; Han, J. Hydraulic hybrid technology of moving construction machinery. J. Jilin Univ. Eng. Ed. 2014, 44, 364–368. [Google Scholar]
- Rongling, S.H.; Hui, S.U. Analysis and optimization of energy saving factors of hydraulic hybrid wheel loader. Agric. Mach. J. 2011, 42, 31–35. [Google Scholar]
- Wang, F.; Zulkefli, M.A.M.; Sun, Z.; Stelson, K.A. Investigation on the energy management strategy for hydraulic hybrid wheel loaders. American Society of Mechanical Engineers. In Proceedings of the ASME Dynamic Systems and Control Conference, virtual, 5–7 October 2013. [Google Scholar]
- Wang, F.; Zulkefli, M.A.M.; Sun, Z.; Stelson, K.A. Energy management strategy for a power-split hydraulic hybrid wheel loader. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2016, 230, 1105–1120. [Google Scholar] [CrossRef]
- Yang, J.; Bian, Y.; Liu, G.; Ji, P.; Chen, Q. Development of a parallel hydraulic hybrid loader through modeling. IOP Publishing Ltd. In Proceedings of the International Conference on Design, Mechanical and Material Engineering (D2ME), Busan, South Korea, 26–28 September 2019; Volume 686, p. 012007. [Google Scholar]
- Hoai-An, T.; Hoai, V.A.T.; Tri, C.D.; Manh, H.N.; Van, D.P.; Kyoung, K.A. Optimization-based energy management strategies for hybrid construction machinery: A review. Energy Rep. 2022, 8, 6035–6057. [Google Scholar]
- Zhao, D.; Zhang, Z.; Li, T.; Lan, H.; Zhang, M.; Dong, Y. Fuzzy logic control strategy of series hybrid power loader. J. Jilin Univ. Eng. Technol. Ed. 2014, 44, 1334–1341. [Google Scholar]
- Stein, G.; Froberg, A.; Martinsson, J.; Brattberg, B.; Filla, R.; Unnebäck, J. Fuel efficiency in construction equipment-optimize the machine as one system. In Proceedings of the AVL International Commercial Powertrain Conference, Graz, Austria, 21–23 May 2013. [Google Scholar]
- Nilsson, T.; Froberg, A.; Aslund, J. Predictive control of a diesel electric wheel loader powertrain. Control. Eng. Pract. 2015, 41, 47–56. [Google Scholar] [CrossRef]
- Lin, Z.; Wang, F.; Xu, B. Improving wheel loader energy efficiency with a series electric hybrid powertrain. In Proceedings of the BATH/ASME 2022 Symposium on Fluid Power and Motion Control, Bath, UK, 14–16 September 2022. [Google Scholar]
- Dingxuan, Z.H.O.; Zhiwen, Z.H.N.; Tianyu, L.I.; Min, Z.H.N.; Yan, D.O.G.; Hao, L.A. Fuzzy logic control strategy of parallel hybrid power loader. J. Jilin Univ. Eng. Technol. Ed. 2014, 44, 1004–1009. [Google Scholar]
- Zhao, D.; Zhang, Z.; LI, M.; Li, T.; Wang, C. Research on control strategy for parallel hybrid loader. In Proceedings of the IEEE 3rd International Conference on Information Science and Technology, Yangzhou, China, 23–25 March 2013; pp. 275–279. [Google Scholar]
- Li, T.; Liu, H.; Zhang, Z.; Ding, D. Shift scheduling strategy development for parallel hybrid construction vehicles. J. Cent. South Univ. 2019, 26, 587–603. [Google Scholar] [CrossRef]
- Zhiwen, Z.H.N.; Dingxuan, Z.H.O.; Tianyu, L.I.; Min, Z.H.N. Control strategy based on automatic transmission for hybrid loader. J. Northeast. Univ. Nat. Sci. 2015, 36, 532–536. [Google Scholar]
- Dingxuan, Z.H.O.; Tianyu, L.I.; Huailiang, K.A.G.; Zhiwen, Z.H.N.; Mufei, L.I. Automatic shift technology of hybrid power engineering vehicle. J. Jilin Univ. Eng. Ed. 2014, 44, 358–363. [Google Scholar]
- Sergio, G.; Andera, B.; Ettore, C. A series-parallel hybrid electric powertrain for industrial vehicles. In Proceedings of the IEEE Vehicle Power and Propulsion Conference, Hanoi, Vietnam, 14–17 October 2010; p. 5729045. [Google Scholar]
- Liu, J.; Peng, H.; Filipi, Z. Modeling and analysis of the Toyota Hybrid System. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Monterey, CA, USA, 27 June–1 July 2005. [Google Scholar]
- Liu, J.; Peng, H. Control optimization for a power-split hybrid vehicle. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14-16 June 2006. [Google Scholar]
- Yin, X.U.; Dong, C.H.N. A new parallel-series hybrid electric car’s driving system. Automot. Eng. 2010, 32, 501–504. [Google Scholar]
- Zhiwen, Z.H.N.; Wenjie, D.U.; Junfei, L.I.N.; Yangang, Z.H.N.; Yawen, W.U. Hierarchical control of composite power loader based on fuel cell. J. Beijing Univ. Aeronaut. Astronaut. 2022, 48, 2165–2176. [Google Scholar]
- Li, T.; Liu, H.; Ding, D. Predictive energy management of fuel cell supercapacitor hybrid construction equipment. Energy 2018, 149, 718–729. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Wang, H.; Yao, Y. Hierarchical predictive control-based economic energy management for fuel cell hybrid construction vehicles. Energy 2020, 198, 117327. [Google Scholar] [CrossRef]
- Li, T.; Liu, H.; Wang, H.; Yao, Y. Multi objective Optimal Predictive Energy Management for Fuel Cell/Battery Hybrid Construction Vehicles. IEEE Access 2020, 8, 25927–25937. [Google Scholar] [CrossRef]
- Hong, Z.; Li, Q.; Chen, W. An energy management strategy based on PMP for the fuel cell hybrid system of locomotive. Proc. CSEE 2019, 39, 3867–3879. [Google Scholar]
- Xiang, M.E.G.; Qi, L.I.; Weirong, C.H.N.; Guorui, Z.H.N. An energy management method based on Pontryagin minimum principle satisfactory optimization for fuel cell hybrid systems. Proc. CSEE 2019, 39, 782–792+957. [Google Scholar]
- Bertini, A.; Ceraolo, M.; Lutzemberger, G. Systematic approach in the hybridization of a hydraulic skid loader. Autom. Constr. 2015, 58, 144–154. [Google Scholar] [CrossRef]
- Luo, P.; Lin, M.; Chen, Y.; Zhao, L.; Ma, B. Energy management strategy for hybrid engineering vehicles with composite energy storage. Lect. Notes Electr. Eng. 2019, 503, 147–156. [Google Scholar]
- Wang, H.; Yang, S.; Lu, T. Mechanical transmission system of loader based on hydraulic hybrid technology. Therm. Sci. 2021, 26, 4233–4240. [Google Scholar] [CrossRef]
- Pontryagin, L.; Boltyanskii, V.; Gamkrelidze, R.; Mishchenko, E. The Mathematical Theory of Optimal Processes; Inderscience Publishers: New York, NY, USA, 1962. [Google Scholar]
- Dimitri, P.; Bertsekas. Dynamic Programming and Optimal Control; Athena Scientific: Belmont, Japan, 1995. [Google Scholar]
- Zhang, Q.; Wang, F.; Xu, B.; Sun, Z. Online optimization of Pontryagin’s minimum principle for a series hydraulic hybrid wheel loader. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 1487–1499. [Google Scholar] [CrossRef]
- Iman, S.; Jan, Å. Energy management of hybrid electric vehicles with battery aging considerations: Wheel loader case study. Control. Eng. Pract. 2021, 110, 104759. [Google Scholar]
- Antti, L. Development of energy management strategies for heavy mobile machinery. American Society of Mechanical Engineers. In Proceedings of the ASME Dynamic Systems and Control Conference, Palo Alto, CA, USA, 21–23 October 2013. [Google Scholar]
- Frank, B. Using optimal control in concept evaluation and system optimization of diesel-electric hybrid construction machines. Institute of Electrical and Electronics Engineers Inc. In Proceedings of the International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles/International Transportation Electrification Conference, Toulouse, France, 2–4 November 2016; p. 7841323. [Google Scholar]
- Uebel, K.; Raduenz, H.; Krus, P.; De Negri, V.J. Design optimisation strategies for a hydraulic hybrid wheel loader. In Proceedings of the BATH/ASME Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018. [Google Scholar]
- Zeng, X.; Bai, G.; Wang, J.; Zhou, Z. The instantaneous optimal control strategy of parallel hybrid loader. Appl. Mech. Mater. 2013, 380–384, 467–471. [Google Scholar] [CrossRef]
- Shafikhani, I.; Åslund, J. Analytical Solution to Equivalent Consumption Minimization Strategy for Series Hybrid Electric Vehicles. IEEE Trans. Veh. Technol. 2021, 70, 2124–2137. [Google Scholar] [CrossRef]
- Zhang, F.; Hu, X.; Xu, K.; Tang, X.; Cui, Y. Current status and prospects for model predictive energy management in hybrid electric vehicles. J. Mech. Eng. 2019, 55, 86–108. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Xue, S.; Zhao, B.; Luo, B.; Wei, Q. Adaptive dynamic programming for control: A survey and recent advances. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 142–160. [Google Scholar] [CrossRef]
- Qi, X.; Wu, G.; Boriboonsomsin, K.; Barth, M.J.; Gonder, J. Data-driven reinforcement learning-based real-time energy management system for plug-in hybrid electric vehicles. Transp. Res. Rec. 2016, 2572, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Wu, Y.K.; Tan, H.C.; Peng, J.K.; Zhang, H.L.; He, H.W. Deep reinforcement learning of energy management with continuous control strategy and traffic information for a series-parallel plug-in hybrid electric bus. Appl. Energy 2019, 247, 454–466. [Google Scholar] [CrossRef]
- Wu, J.; He, H.; Peng, J.; Li, Y.; Li, Z. Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus. Appl. Energy 2018, 222, 799–811. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, J.; Liu, Y.; Gao, G.; Liang, S.; Ma, H. Reinforcement learning-based intelligent energy management architecture for hybrid construction machinery. Appl. Energy 2020, 275, 115401. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, Q. Real-time energy management controller design for a hybrid excavator using reinforcement learning. J. Zhejiang Univ. -SCIENCE A Appl. Phys. Eng. 2017, 18, 855–870. [Google Scholar] [CrossRef]
- Li, G.; Gorges, D. Ecological adaptive cruise control and energy management strategy for hybrid electric vehicles based on heuristic dynamic programming. IEEE Trans. Intell. Transp. Syst. 2019, 20, 3526–3535. [Google Scholar] [CrossRef]
- Liu, J.; Chen, Y.; Zhan, J.; Shang, F. Heuristic dynamic programming based online energy management strategy for plug-in hybrid electric vehicles. IEEE Trans. Veh. Technol. 2019, 68, 4479–4493. [Google Scholar] [CrossRef]









| Configuration Type | Manufacturer | Product Mode | Year | Configuration Characteristics | Oil-Saving Rate | Ref. | |
|---|---|---|---|---|---|---|---|
| Power Chain | Storage Mode | ||||||
| Series oil–electric hybrid | JOHN DEERE | 644k | 2012 | Engine → generator → single assembly driving motor | N/A | 25% | [10] |
| 944k | 2013 | Engine → generator → four wheel motors | N/A | 30% | [11] | ||
| HITACHI | ZW220HYB-5 | 2014 | Engine → generator → front and rear axle assembly driving motor | Super capacitor | 26% | [12,13] | |
| VOLVO | LX1 | 2016 | Engine → generator → four wheel motors | N/A | 50% | [6] | |
| XCMG | XC9350 | 2020 | Engine → generator → four wheel motors | Battery | 20% | [14] | |
| Parallel oil–electric hybrid | VOLVO | L220F | 2008 | Engine + integrated starting/generating motor (coaxial parallel) → driving axle | Super capacitor | 10% | [6] |
| LIUGONG | CLG862 | 2010 | Super capacitor | 10.5% | [15] | ||
| Kawasaki | 65ZV-2 | 2011 | Engine + generator/motor (planetary parallel) → driving axle | Super capacitor | 35% | [16,17] | |
| Parallel oil–hydraulic hybrid | XCMG | ZL50GS | 2010 | Engine + hydraulic driving motor (coupled gear set) → driving axle | Hydraulic accumulator | 10% | [18] |
| EMSs | RB | ECMS | DP | MPC |
|---|---|---|---|---|
| Fuel consumption (L) | 3.92 | 3.15 | 2.42 | 2.73 |
| Simulation time of single step (s) | 0.0037 | 0.0052 | 600 | 0.0065 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Liang, Y.; Chen, Z.; Chen, W. Energy Management Strategies for Hybrid Loaders: Classification, Comparison and Prospect. Energies 2023, 16, 3018. https://doi.org/10.3390/en16073018
Liu J, Liang Y, Chen Z, Chen W. Energy Management Strategies for Hybrid Loaders: Classification, Comparison and Prospect. Energies. 2023; 16(7):3018. https://doi.org/10.3390/en16073018
Chicago/Turabian StyleLiu, Jichao, Yanyan Liang, Zheng Chen, and Wenpeng Chen. 2023. "Energy Management Strategies for Hybrid Loaders: Classification, Comparison and Prospect" Energies 16, no. 7: 3018. https://doi.org/10.3390/en16073018
APA StyleLiu, J., Liang, Y., Chen, Z., & Chen, W. (2023). Energy Management Strategies for Hybrid Loaders: Classification, Comparison and Prospect. Energies, 16(7), 3018. https://doi.org/10.3390/en16073018













