Effect of a Vibrating Blade in a Channel on the Heat Transfer Performance
Abstract
1. Introduction
2. Methodology
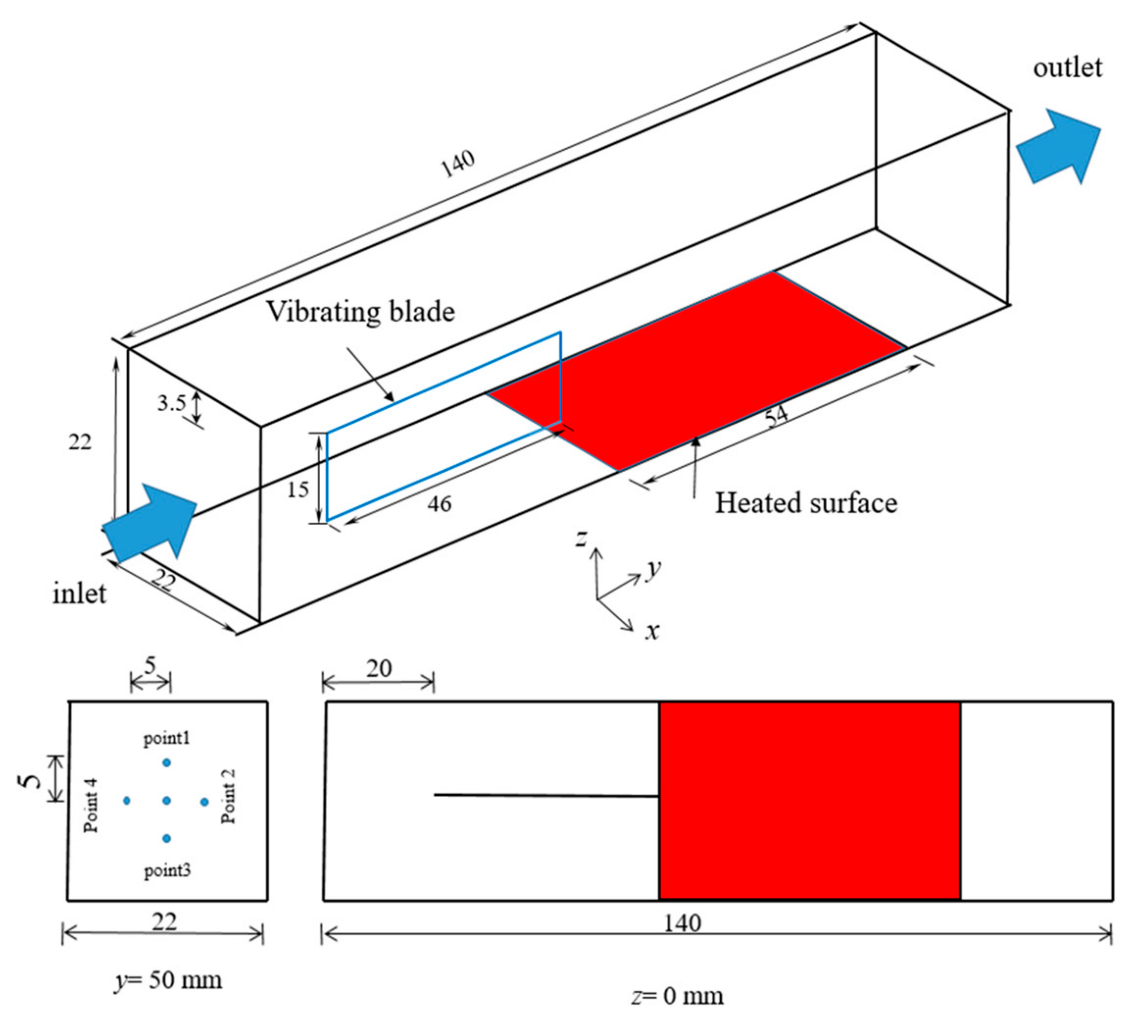
2.1. Computational Domain
2.2. Governing Equations and Boundary Conditions
2.3. Data Reduction
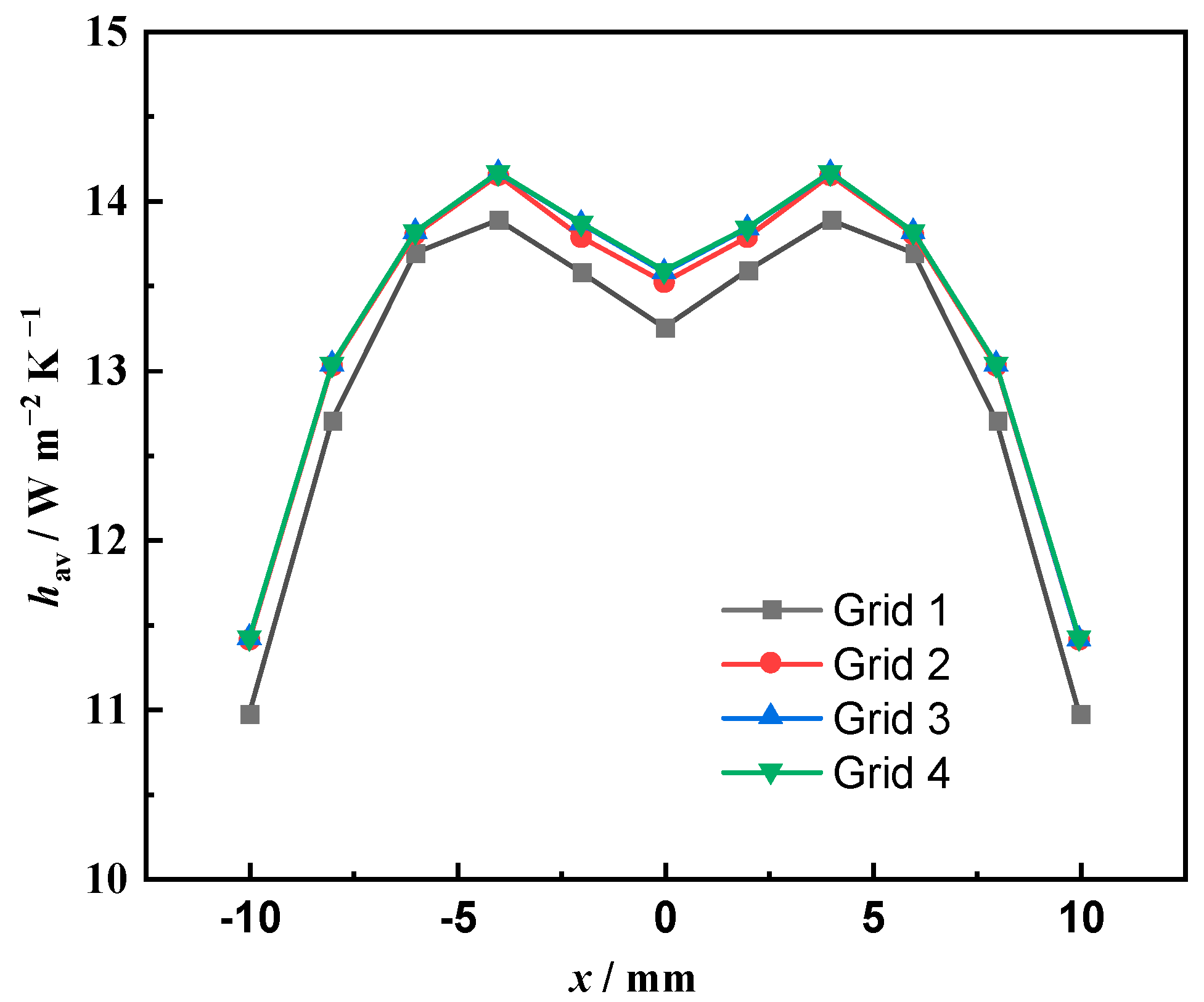
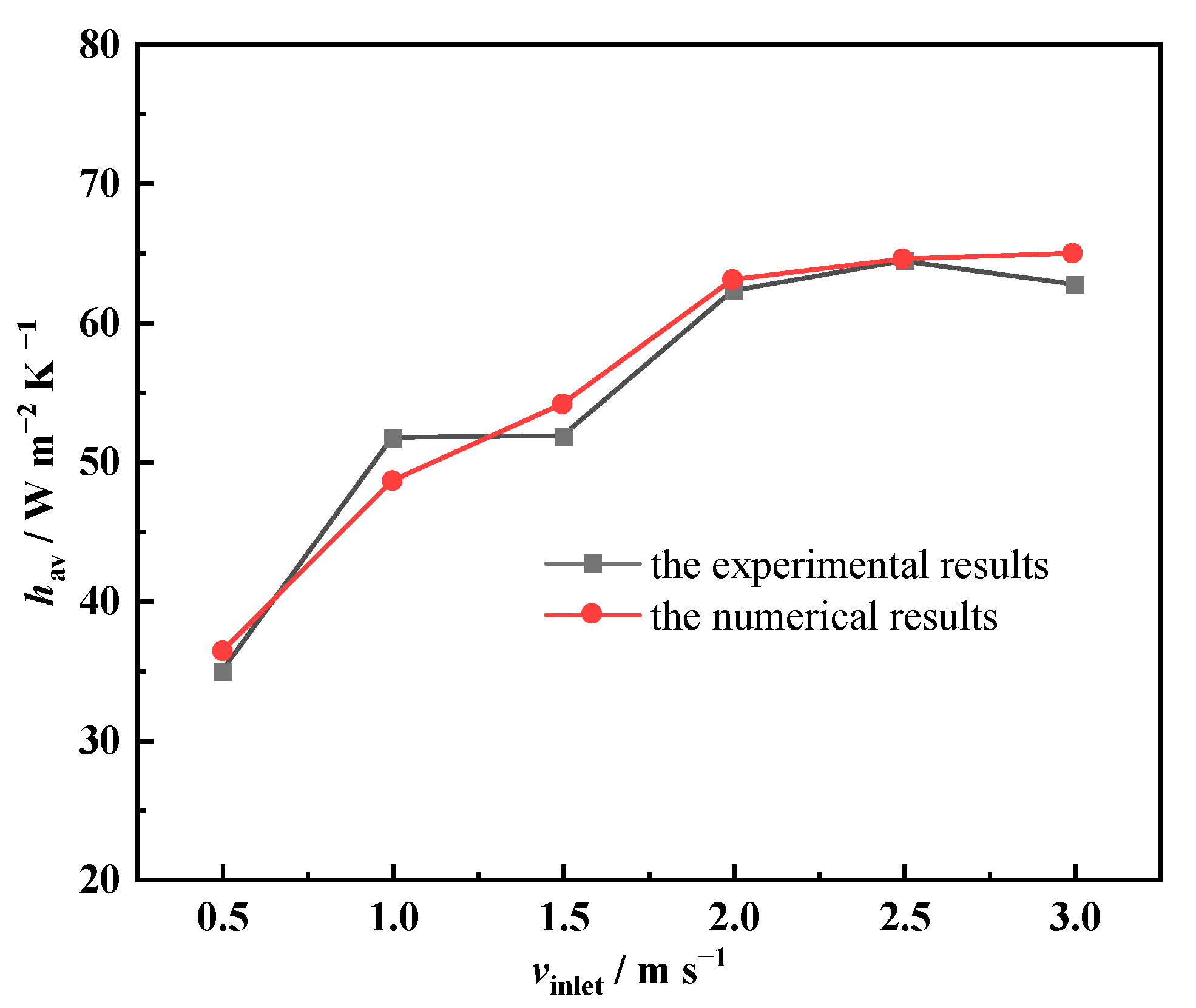
2.4. Grid Independence Validation and Model Validation
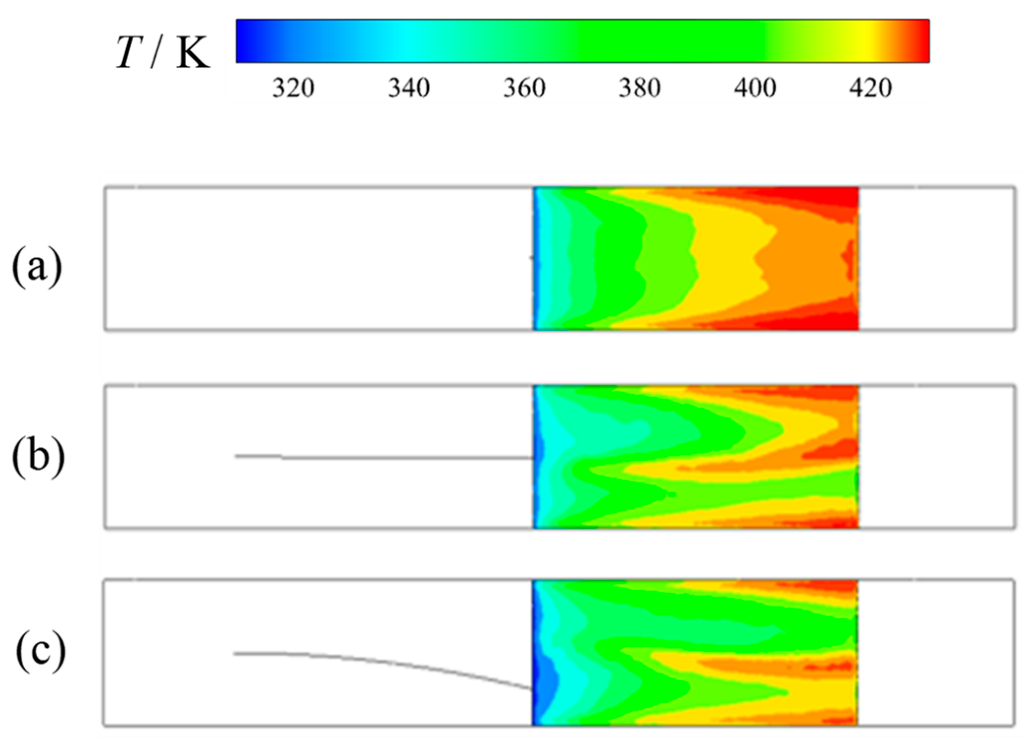
3. Analysis of Heat Transfer Characteristics
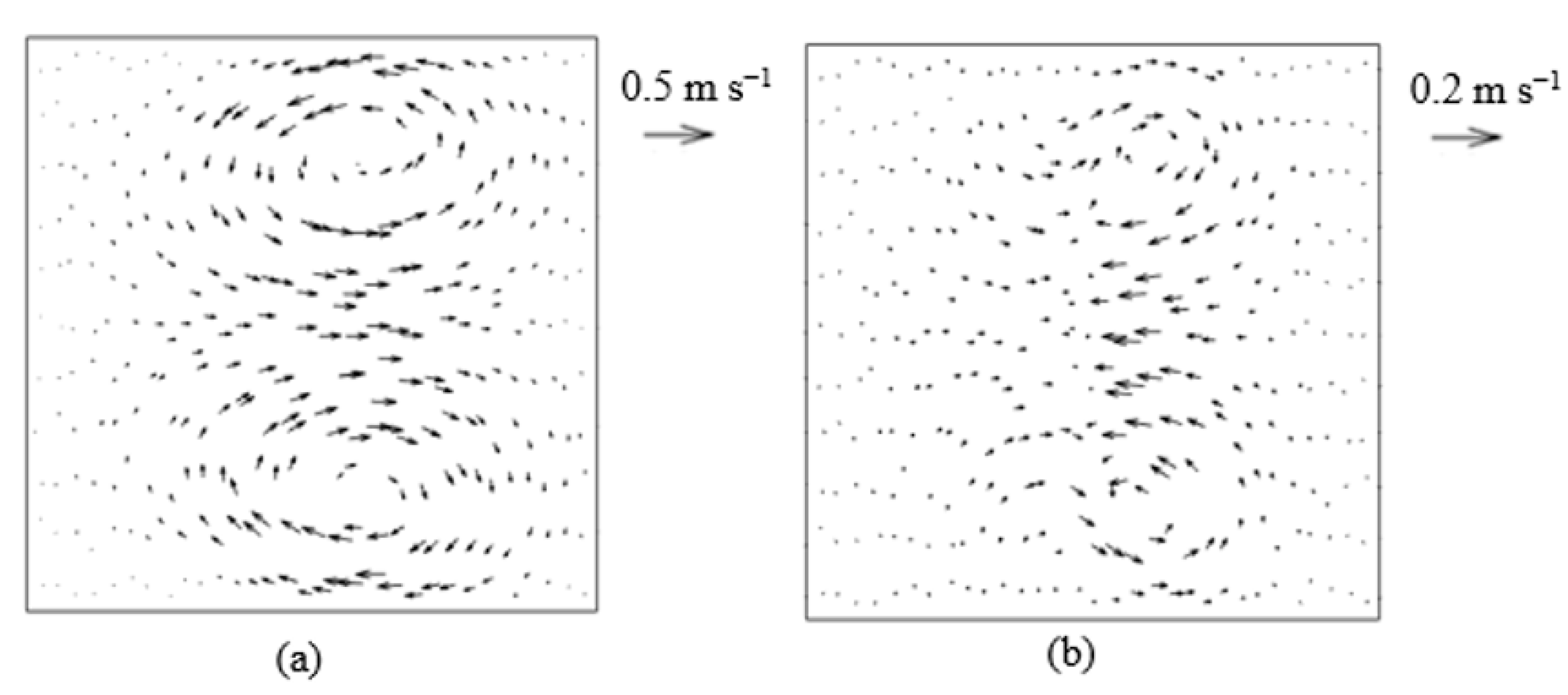
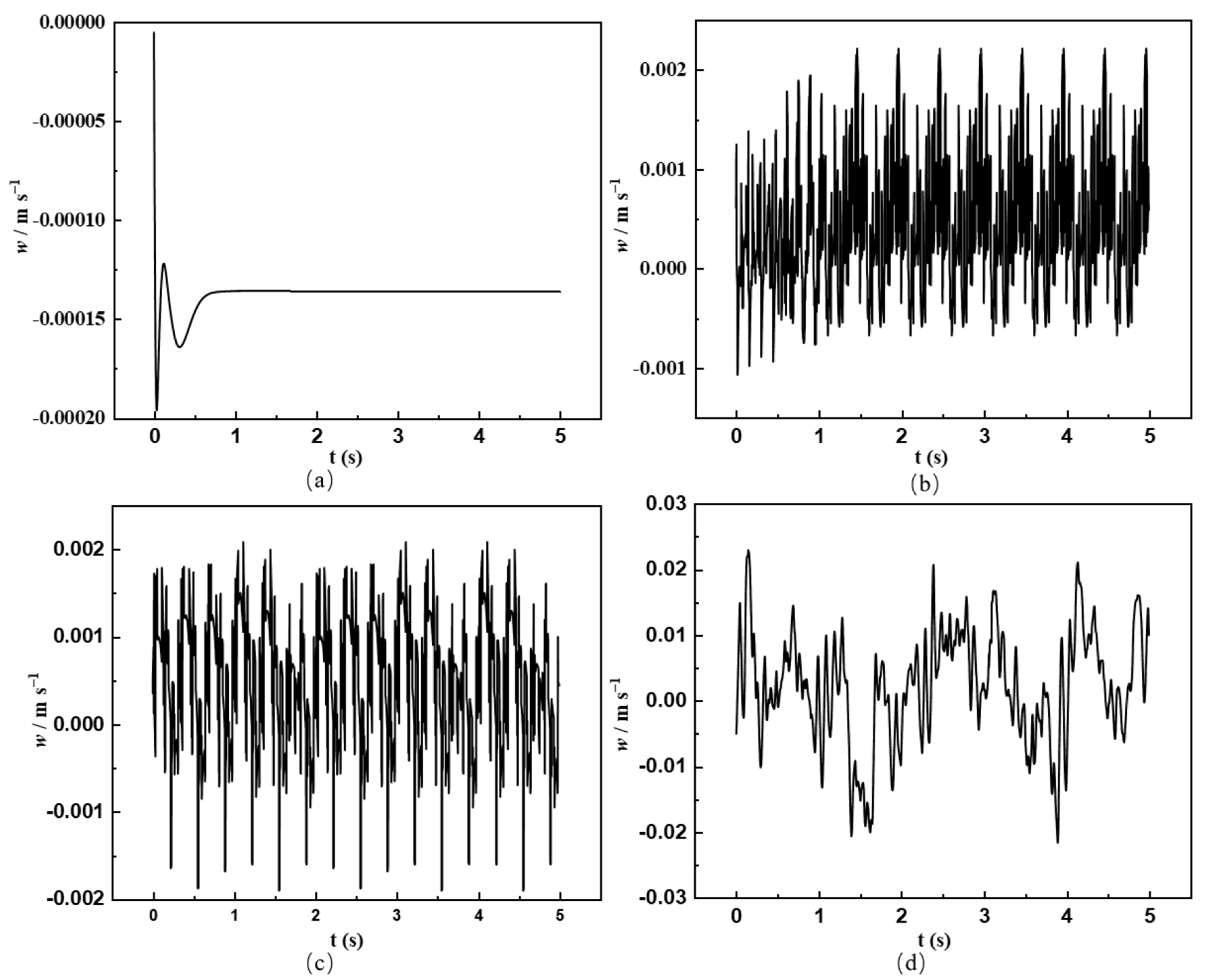
4. Analysis of Chaotic Characteristics
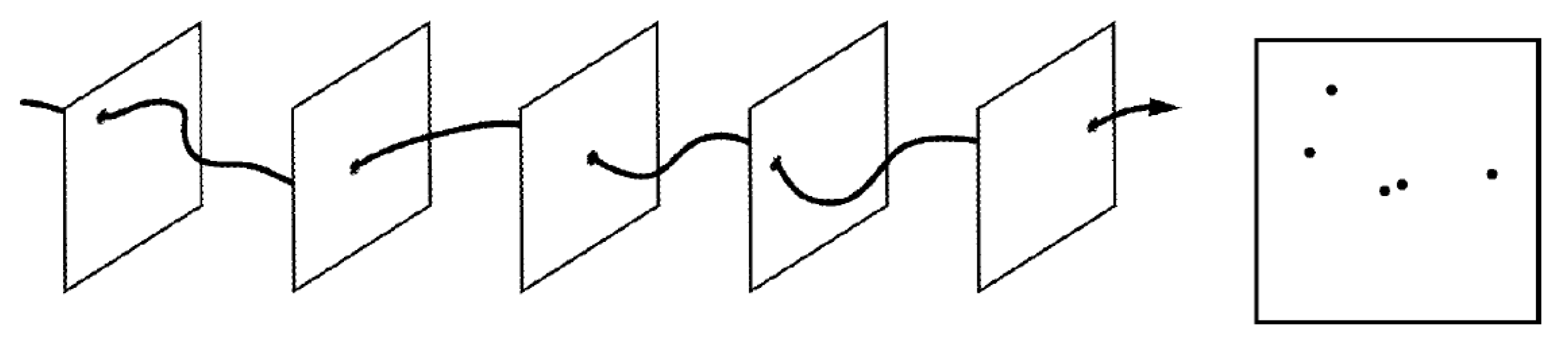
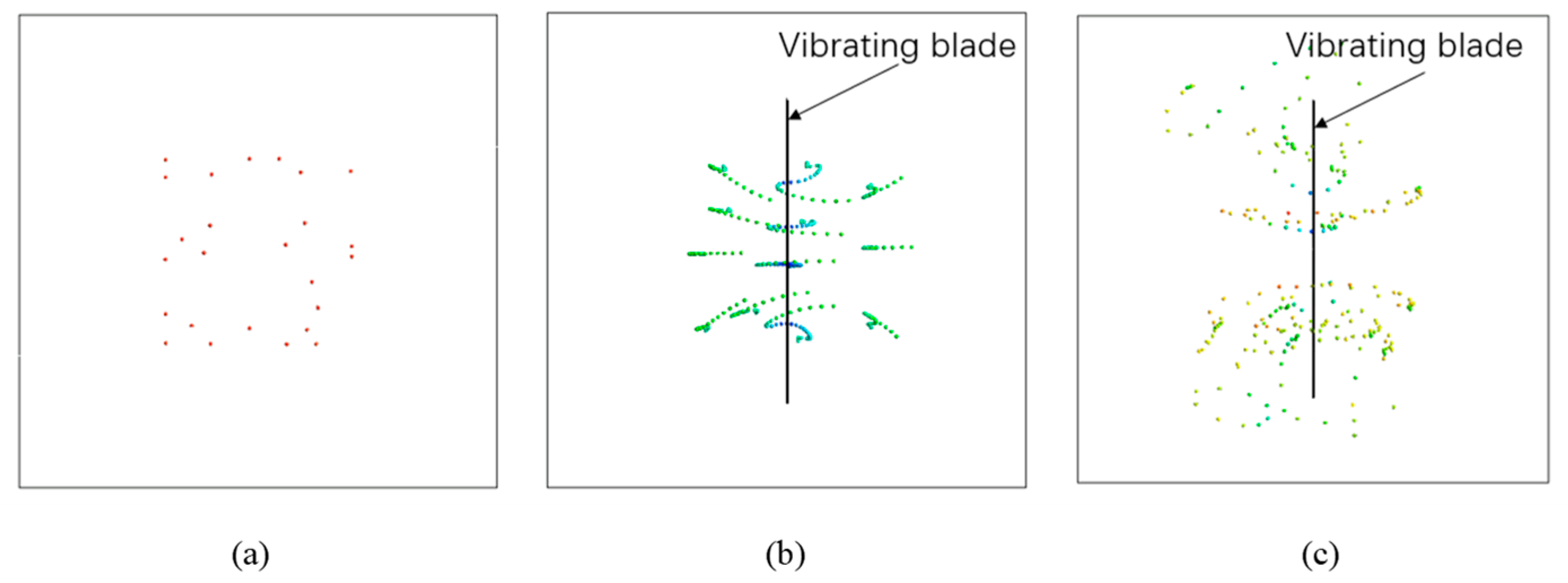
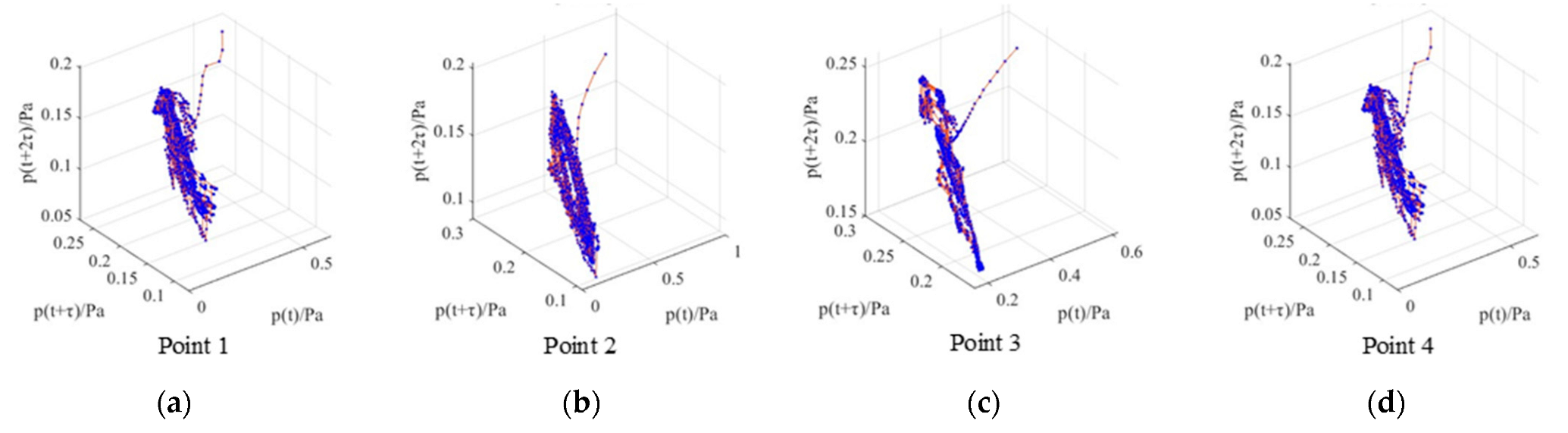
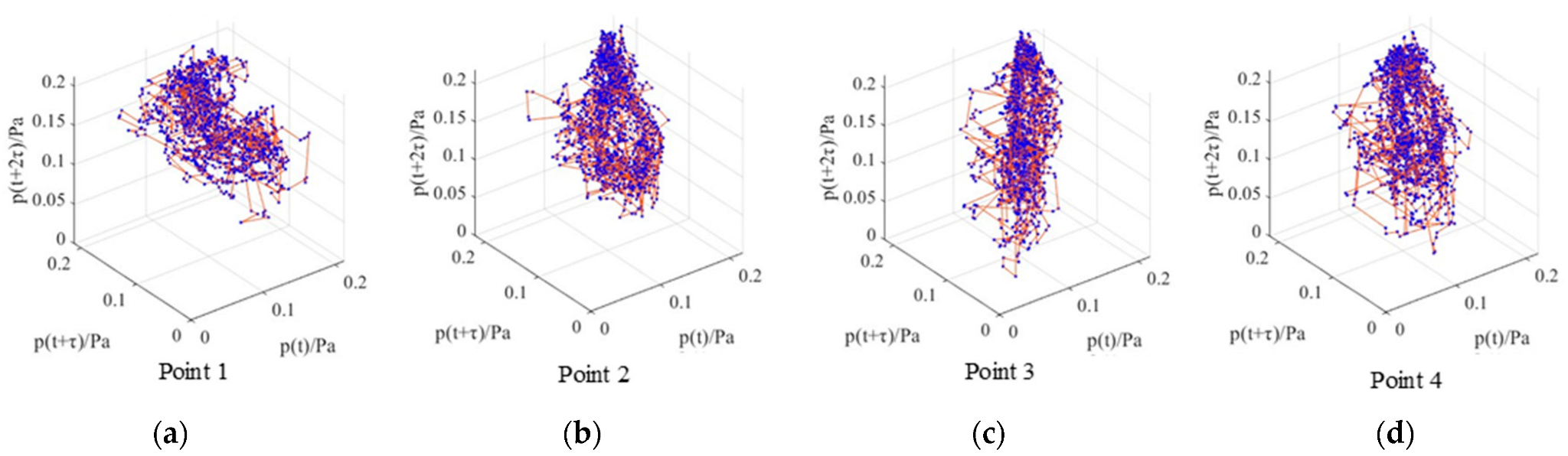
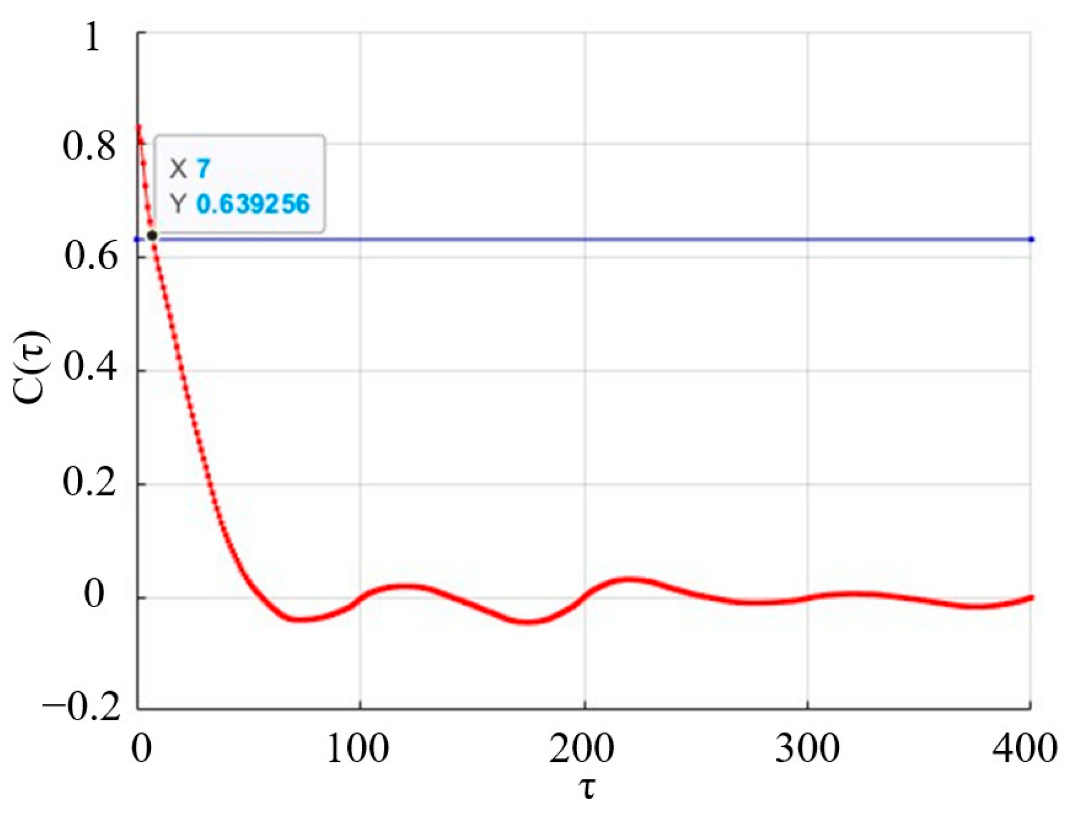
4.1. Poincaré Map
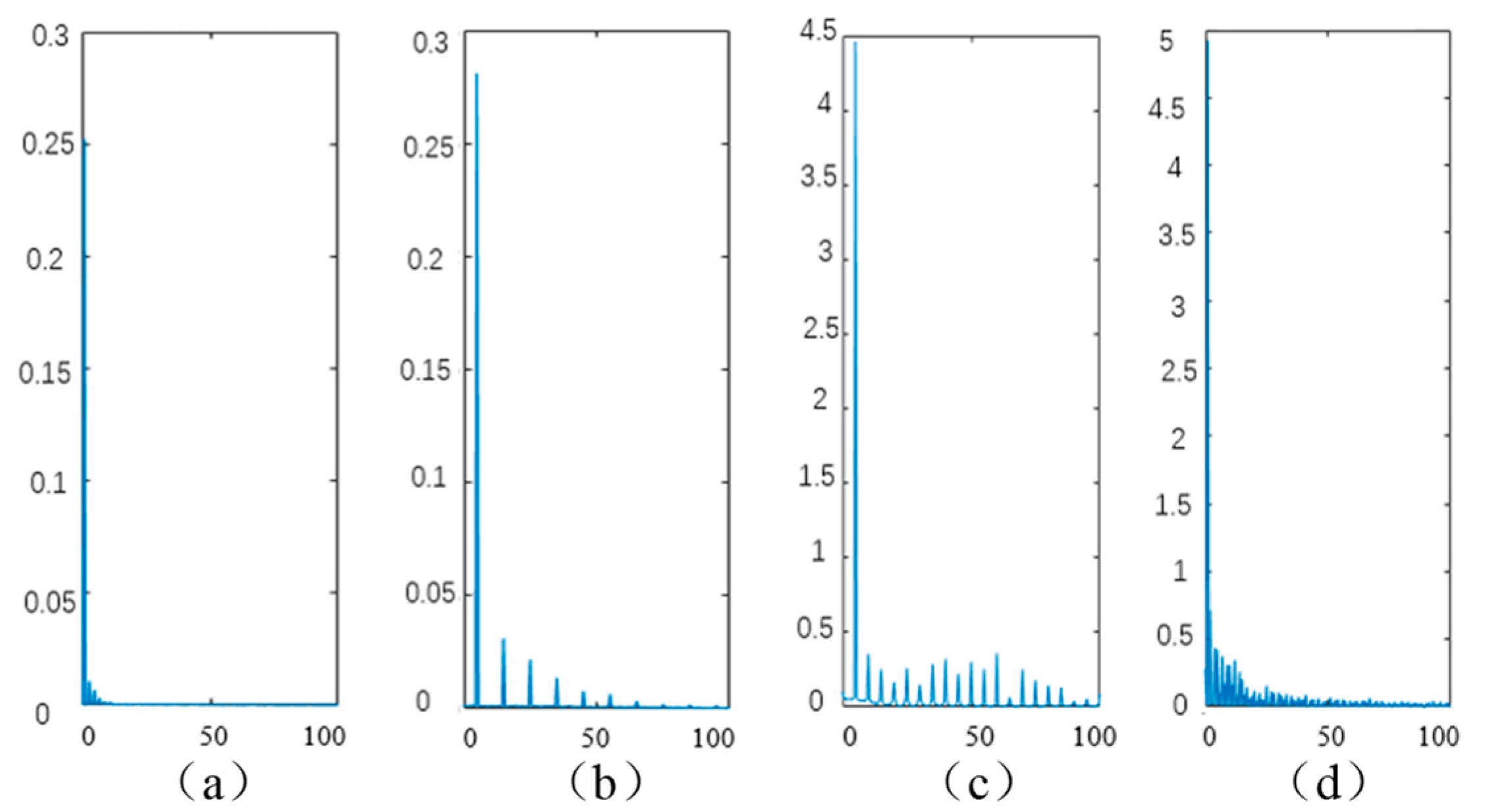
4.2. Power Spectral Density
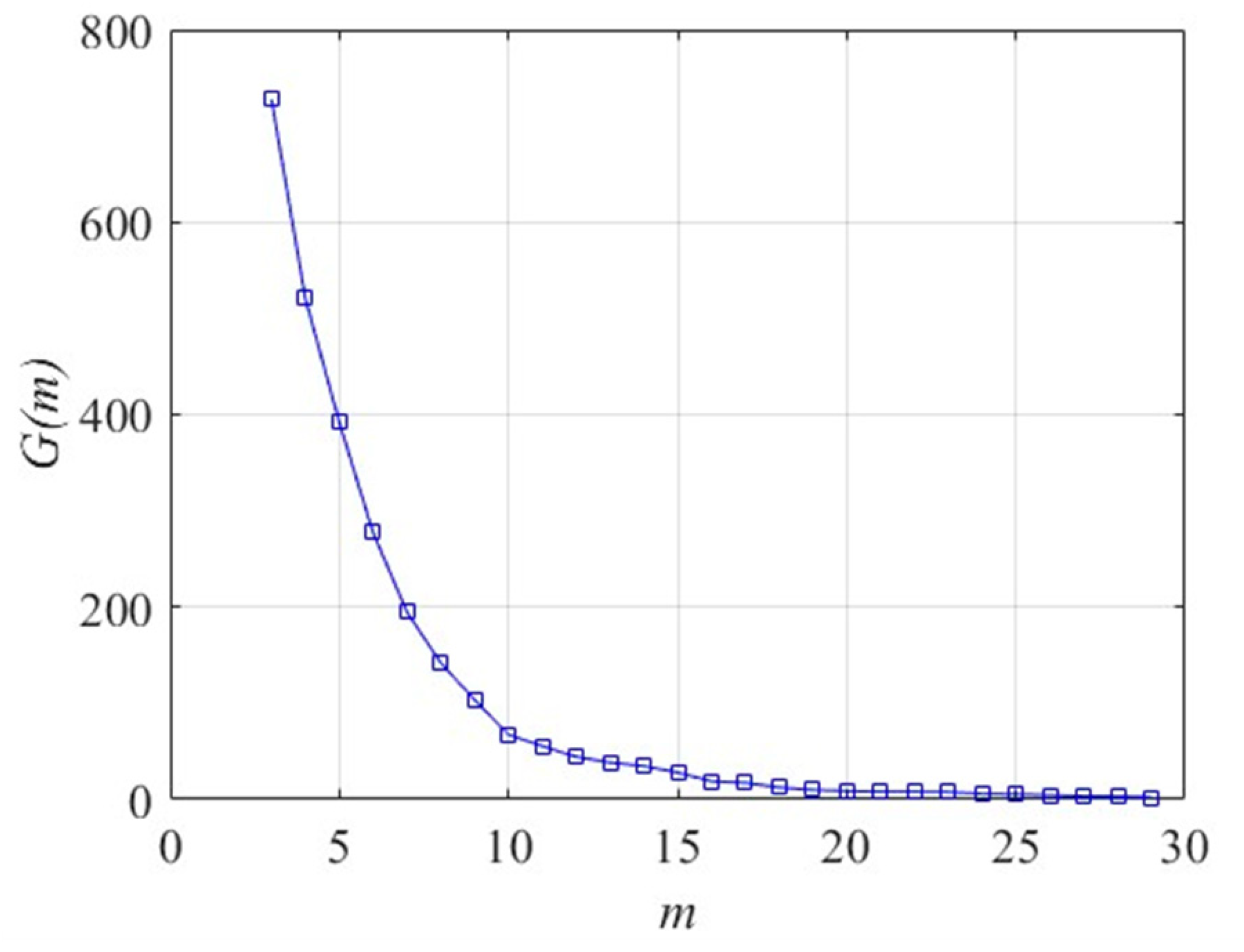
4.3. Phase Space Reconfiguration
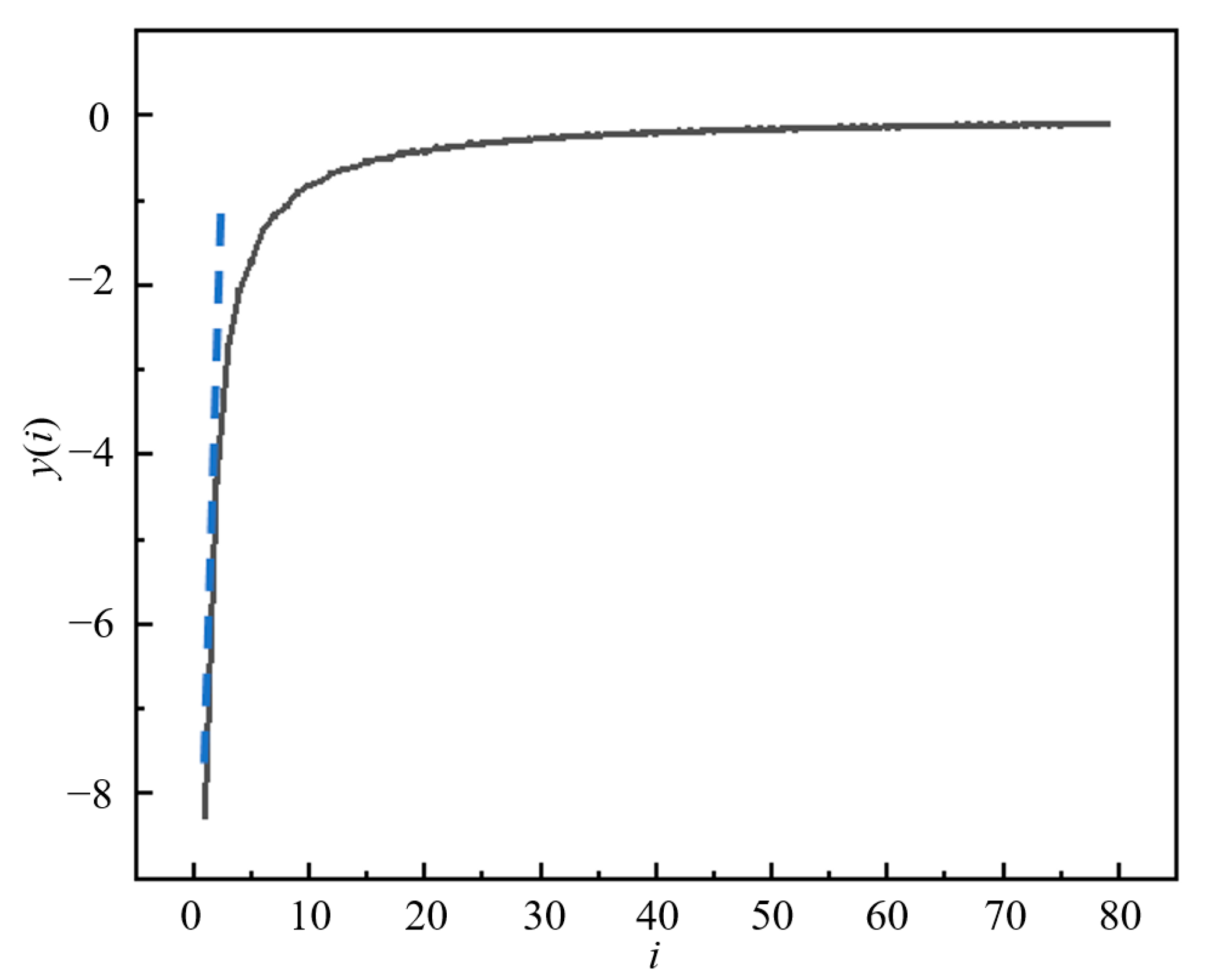
4.4. Maximum Lyapunov Exponent
5. Conclusions
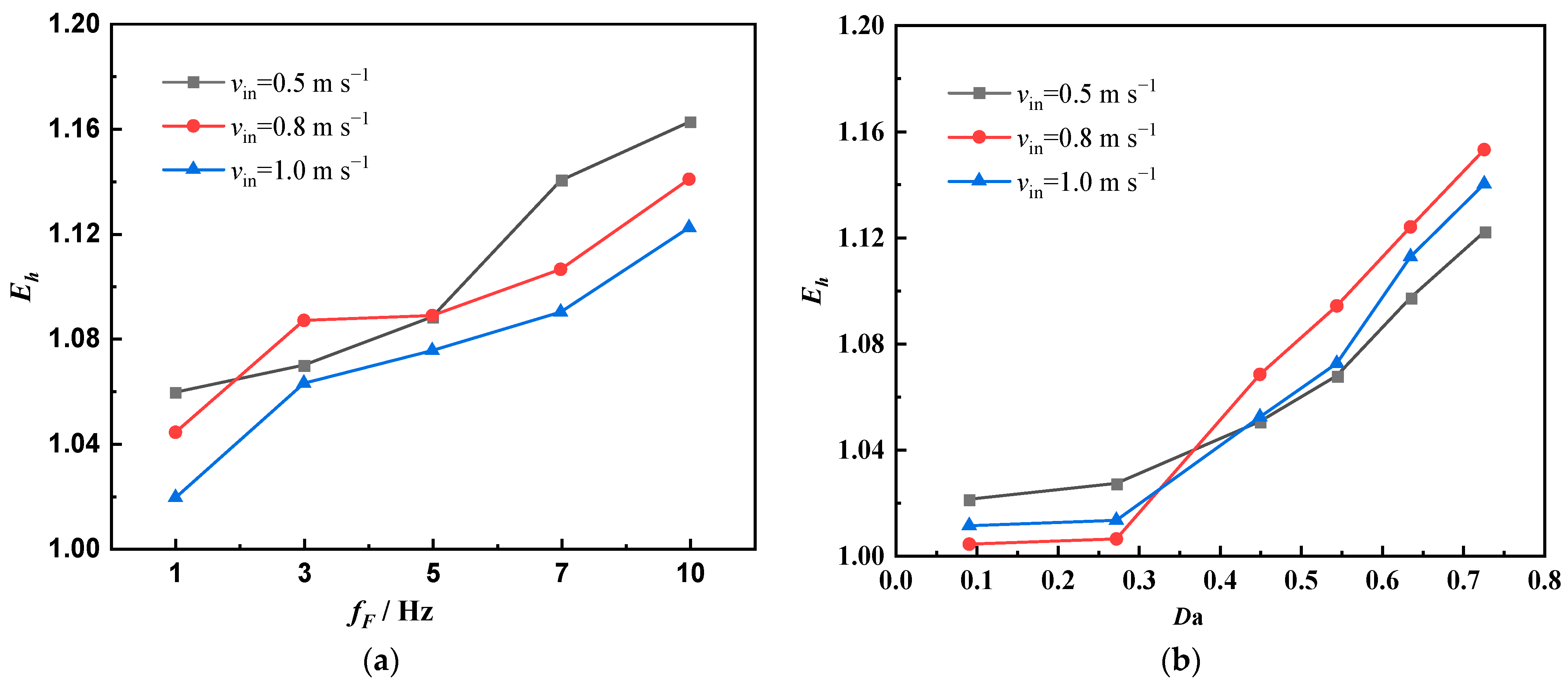
- A larger frequency or amplitude is beneficial to improve heat transfer at the same inlet velocity. When the frequency is 10 Hz, the heat transfer can be increased by 16%. When the maximum amplitude of the blade is 8 mm, the heat transfer can be increased by 15%.
- The vibrating blade forms the longitudinal vortices. Hence, the heat transfer is enhanced.
- More than four incommensurable frequencies are in the power spectrum, indicating that the system has reached a chaotic state. The system reaches a chaotic state when the vibrating frequency is over 5 Hz.
- As the amplitude increases, the system gradually changes from a steady state to a weakly chaotic one. The amplitude increases further to a periodic state and finally to a chaotic state. The degree of chaos becomes more intense when the amplitude is 8 mm.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| Nomenclature | |
| A | amplitude, mm |
| cp | specific heat of air, J kg−1 K−1 |
| Da | dimensionless amplitude |
| Dh | the equivalent diameter, mm |
| f | frequency, Hz |
| k | thermal conductivity, W m−2 K−1 |
| l | length of the blade, mm |
| m | mass, kg |
| h | convective heat transfer coefficient, W m−2 K−1 |
| hav | average convective heat transfer coefficient, W m−2 K−1 |
| p | pressure, Pa |
| q | the heat flow density |
| T | temperature, K |
| vin | inlet velocity, m s −1 |
| u | velocity in x-direction, m s −1 |
| V | volume |
| v | velocity in the y-direction, m s −1 |
| w | velocity in the z-direction, m s −1 |
| Greek symbols | |
| Γ | diffusion coefficient |
| λ | thermal conductivity, Wm−1 K−1 |
| ρ | fluid density, kg m−3 |
| τ | delay time, s |
| μ | the dynamic viscosity, kg m−1 s−1 |
| Dimensionless groups | |
| Nu | Nusselt number |
| Pr | Prandtl number |
| Re | Reynolds number |
| MLE | Maximum Lyapunov exponent |
| Subscript | |
| a | air |
| av | average value |
| blade | vibrating blade |
| max | maximum value |
References
- Aref, H. The development of chaotic advection. Phys. Fluids 2002, 14, 1315–1325. [Google Scholar] [CrossRef]
- Bueghelea, T.; Segre, E. Chaotic flow and efficient mixing in a microchannel with a polymer solution. Phys. Rev. E 2004, 69, 066305. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, E.; Patowari, P.K.; Pati, S. Numerical investigation of mixing performance in spiral micromixers based on Dean flows and chaotic advection. Chem. Eng. Process. 2021, 169, 108609. [Google Scholar] [CrossRef]
- Karami, M.; Shirani, E.; Jarrahi, M.; Peerhossaini, H. Mixing by time-dependent orbits in spatiotemporal chaotic advection. J. Fluids Eng. 2015, 137, 011201. [Google Scholar] [CrossRef]
- Jarrahi, M.; Castelain, C.; Peerhossaini, H. Mixing enhancement by pulsating chaotic advection. Chem. Eng. Process. 2013, 74, 1–13. [Google Scholar] [CrossRef]
- Boyland, P.L.; Aref, H.; Stremler, M.A. Topological fluid mechanics of stirring. J. Fluid Mech. 2000, 403, 277–304. [Google Scholar] [CrossRef]
- Balachandar, S. Chaotic Advection in Stokes Flow. Phys. Fluids 1986, 29, 3515. [Google Scholar]
- Gepner, S.W.; Floryan, J.M. Use of Surface corrugations for Energy-Efficient Chaotic Stirring in Low Reynolds number flows. Sci. Rep. 2020, 10, 9865. [Google Scholar] [CrossRef]
- Yada, N.; Kundu, P.; Paul, S.; Pal, P. Different routes to chaos in low Prandtl-number Rayleigh–Bénard convection. Int. J. Non-Linear Mech. 2016, 81, 261–267. [Google Scholar] [CrossRef]
- Cimarelli, A.; Angeli, D. Routes to chaos of natural convection flows in vertical channels. Int. Commun. Heat Mass Transf. 2017, 81, 201–209. [Google Scholar] [CrossRef]
- Bhowmick, S. Transition to a chaotic flow in a V-shaped triangular cavity heated from below. Int. J. Heat Mass Transf. 2019, 128, 76–86. [Google Scholar] [CrossRef]
- Brett, G.J.; Pratt, L.; Rypina, I. Competition between chaotic advection and diffusion: Stirring and mixing in a 3-D eddy model. Nonlinear Process. Geophys. 2019, 26, 37–60. [Google Scholar] [CrossRef]
- Oteski, L.; Duguet, Y.; Pastur, L.; Quéré, P.L. Quasiperiodic routes to chaos in confined two-dimensional differential convection. Phys. Rev. E 2015, 92, 043020. [Google Scholar] [CrossRef]
- Gao, Z.; Sergent, A.; Podvin, B.; Xin, S.; Quéré, P.L.; Tuckerman, L.S. Transition to chaos of natural convection between two infinite differentially heated vertical plates. Phys. Rev. E 2013, 88, 023010. [Google Scholar] [CrossRef]
- Li, K.; Xun, B.; Hu, W.R. Some bifurcation routes to chaos of thermocapillary convection in two-dimensional liquid layers of finite extent. Phys. Fluids 2016, 28, 130. [Google Scholar] [CrossRef]
- Pouryoussefi, S.M.; Zhang, Y. Analysis of chaotic flow in a 2D multi-turn closed-loop pulsating heat pipe. Appl. Therm. Eng. 2017, 126, 1069–1076. [Google Scholar] [CrossRef]
- Pouryoussefi, S.M. Numerical investigation of chaotic flow in a 2D closed-loop pulsating heat pipe. Appl. Therm. Eng. 2016, 98, 617–627. [Google Scholar] [CrossRef]
- Ghaedamini, H.; Lee, P.S.; Teo, C.J. Enhanced transport phenomenon in small scales using chaotic advection near resonance. Int. J. Heat Mass Transf. 2014, 77, 802–808. [Google Scholar] [CrossRef]
- Cheng, S.; Zhou, T.; Li, J.J. Nonlinear Analysis of Natural Circulation Critical Heat Flux in Narrow Channels. At. Energy Sci. Technol. 2012, 46, 1330–1335. [Google Scholar]
- Bahiraei, M.; Mazaheri, N.; Alighardashi, M. Development of chaotic advection in laminar flow of a non-Newtonian nanofluid: A novel application for efficient use of energy. Appl. Therm. Eng. 2017, 124, 1213–1223. [Google Scholar] [CrossRef]
- Guzman, A.M.; Amon, C.H. Transition to chaos in converging-diverging channel flows: Ruelle-Takens-Newhouse scenario. Phys. Fluids 1994, 6, 1994–2002. [Google Scholar] [CrossRef]
- Cristina, H.; Amon, C.H.; Morel, B. Lagrangian chaos, Eulerian chaos, and mixing enhancement in converging–diverging channel flows. Phys. Fluids 1996, 8, 1192–1206. [Google Scholar]
- Kang, Q.; Jiang, H.; Duan, L.; Zhang, C.; Hu, W. The critical condition and oscillation-transition characteristics of thermocapil-lary convection in the space experiment on SJ-10 satellite. Int. J. Heat Mass Transf. 2019, 135, 479–490. [Google Scholar] [CrossRef]
- Tohidi, A.; Shokrpour, M.; Hosseinalipour, S.M. Heat transfer enhancement utilizing chaotic advection in coiled tube heat exchangers. Appl. Therm. Eng. 2015, 76, 185–195. [Google Scholar] [CrossRef]
- Tohidi, A.; Ghaffari, H.; Nasibi, H.; Mujumdar, A.S. Heat transfer enhancement by combination of chaotic advection and nanofluids flow in helically coiled tube. Appl. Therm. Eng. 2015, 86, 91–105. [Google Scholar] [CrossRef]
- Leonard, A. Large-eddy simulation of chaotic convection and beyond. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1997. [Google Scholar]
- Siddiqa, S.; Naqvi, S.B.; Azam, M.; Aly, A.M.; Molla, M.M. Large-eddy-simulation of turbulent buoyant flow and conjugate heat transfer in a cubic cavity with fin ribbed radiators. Numer. Heat Transf. 2023, 83, 900–918. [Google Scholar] [CrossRef]
- Song, Y.; Xu, J. Chaotic behavior of pulsating heat pipes. Int. J. Heat Mass Transf. 2009, 52, 2932–2941. [Google Scholar] [CrossRef]
- Jian, Q.; Wu, H.; Ping, C. Non-linear analyses of temperature oscillations in a closed-loop pulsating heat pipe. Int. J. Heat Mass Transf. 2009, 52, 3481–3489. [Google Scholar]
- Chen, C.W.; Li, F.; Wang, X.Y.; Zhang, G.M. Improvement of flow and heat transfer performance of manifold microchannel with porous fins. Appl. Therm. Eng. 2022, 206, 118129. [Google Scholar] [CrossRef]
- Jou, R.; Tzeng, S. Numerical research of nature convective heat transfer enhancement filled with nanofluids in rectangular enclosures. Int. Commun. Heat Mass Transf. 2006, 33, 727–736. [Google Scholar] [CrossRef]
- Liu, S.F.; Huang, R.T.; Sheu, W.J. Heat transfer by a piezoelectric fan on a flat surface subject to the influence of horizontal/vertical arrangement. Int. J. Heat Mass Transf. 2009, 52, 2565–2570. [Google Scholar] [CrossRef]
- Lin, C.N. Enhanced heat transfer performance of cylindrical surface by piezoelectric fan under forced convection conditions. Int. J. Heat Mass Transf. 2013, 60, 296–308. [Google Scholar] [CrossRef]
- Shyu, J.C.; Shyu, J.Z. Investigation of heat transfer enhancement of vertical heat sinks by piezoelectric fan. In Proceedings of the 2011 6th International Microsystems, Packaging, Assembly and Circuits Technology Conference (IMPACT), Taipei, Taiwan, 19–21 October 2011; pp. 466–469. [Google Scholar]
- Ding, P.; Liu, Z. Study on the Convective Heat Transfer Characteristic of a Horizontal Piezoelectric Fan. J. Phys. Conf. Ser. 2020, 1670, 012013. [Google Scholar] [CrossRef]
- Lin, C.N. Heat transfer enhancement analysis of a cylindrical surface by a piezoelectric fan. Appl. Therm. Eng. 2013, 50, 693–703. [Google Scholar] [CrossRef]
- Lin, C.N.; Leu, J.S. Analysis of Heat Transfer and Flow Characteristics for the Arrangement of piezoeletric fan on heated cylinder. Heat Tran. Eng. 2015, 36, 1525–1539. [Google Scholar] [CrossRef]
- Lin, C.N.; Leu, J.S. Study of thermal and flow characteristics of a heated cylinder under dual piezoelectric fans actuation. Int. J. Heat Mass Transf. 2014, 78, 1008–1022. [Google Scholar] [CrossRef]
- Tan, L.; Zhang, J.Z.; Tan, X.M. Numerical investigation of convective heat transfer on a vertical surface due to resonating cantilever beam. Int. J. Therm. Sci. 2014, 80, 93–107. [Google Scholar]
- Lin, C.N. Analysis of three-dimensional heat and fluid flow induced by piezoelectric fan. Int. J. Heat Mass Transf. 2012, 55, 3043–3053. [Google Scholar] [CrossRef]
- Kim, K.; Yeom, T. Numerical study on channel-flow convection heat transfer enhancement with piezoelectric fans under various operating conditions. Appl. Therm. Eng. 2023, 219, 119674. [Google Scholar] [CrossRef]
- Choi, M.; Cierpka, C.; Kim, Y.H. Vortex formation by a vibrating cantilever. J. Fluids Struct. 2012, 31, 67–78. [Google Scholar] [CrossRef]
- Sufian, S.F.; Abdullah, M.Z.; Mohamed, J.J. Effect of synchronized piezoelectric fans on microelectronic cooling performance. Int. Commun. Heat Mass Transf. 2013, 43, 1–89. [Google Scholar] [CrossRef]
- Sufian, S.F.; Fairuz, Z.M.; Zubair, M. Thermal analysis of dual piezoelectric fans for cooling multi-LED packages. Microelectron. Reliab. 2014, 54, 1534–1543. [Google Scholar] [CrossRef]
- Hu, J.Q.; Wang, K.; Xie, L.Y.; Min, C.H.; Rao, Z.H. Effects of electromagnetic-vibration fan with folding blades on convective heat transfer. Appl. Therm. Eng. 2022, 213, 118651. [Google Scholar] [CrossRef]
- Soong, C.Y.; Huang, W.T. Triggering and enhancing chaos with a prescribed target Lyapunov exponent using optimized perturbations of minimum power. Phys. Rev. E 2007, 75, 036206. [Google Scholar] [CrossRef] [PubMed]
- Kennel, M.B.; Brown, R.; Abarbanel, H. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef] [PubMed]
- Tiwari, J.; Yeom, T. Enhancement of channel-flow convection heat transfer using piezoelectric fans. Appl. Therm. Eng. 2021, 191, 113917. [Google Scholar] [CrossRef]
- Fallenius, B.; Sattari, A.; Fransson, J. Experimental study on the effect of pulsating inflow to an enclosure for improved mixing. Int. J. Heat Fluid Flow 2013, 44, 108–119. [Google Scholar] [CrossRef]
- Hideshi, I. The second largest Lyapunov exponent and transition to chaos of natural convection in a rectangular cavity. Int. J. Heat Mass Transf. 2006, 49, 5035–5048. [Google Scholar]
- Speetjens, M.; Metcalfe, G.; Rudman, M. Lagrangian transport and chaotic advection in three dimensional laminar flows. Appl. Mech. Rev. 2021, 73, 030801. [Google Scholar] [CrossRef]
- Anxionnaz, Z.; Minvielle, P.T.; Couturier, R. Implementation of ‘chaotic’ advection for viscous fluids in heat exchanger/reactors. Chem. Eng. Process. 2017, 113, 118–127. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, X.; Lan, C.; Hu, J.; Fan, Y.; Min, C. Effect of a Vibrating Blade in a Channel on the Heat Transfer Performance. Energies 2023, 16, 3076. https://doi.org/10.3390/en16073076
Yuan X, Lan C, Hu J, Fan Y, Min C. Effect of a Vibrating Blade in a Channel on the Heat Transfer Performance. Energies. 2023; 16(7):3076. https://doi.org/10.3390/en16073076
Chicago/Turabian StyleYuan, Xinrui, Chenyang Lan, Jinqi Hu, Yuanhong Fan, and Chunhua Min. 2023. "Effect of a Vibrating Blade in a Channel on the Heat Transfer Performance" Energies 16, no. 7: 3076. https://doi.org/10.3390/en16073076
APA StyleYuan, X., Lan, C., Hu, J., Fan, Y., & Min, C. (2023). Effect of a Vibrating Blade in a Channel on the Heat Transfer Performance. Energies, 16(7), 3076. https://doi.org/10.3390/en16073076





