Preliminary Study for the Commercialization of a Electrochemical Hydrogen Compressor
Abstract
:1. Introduction
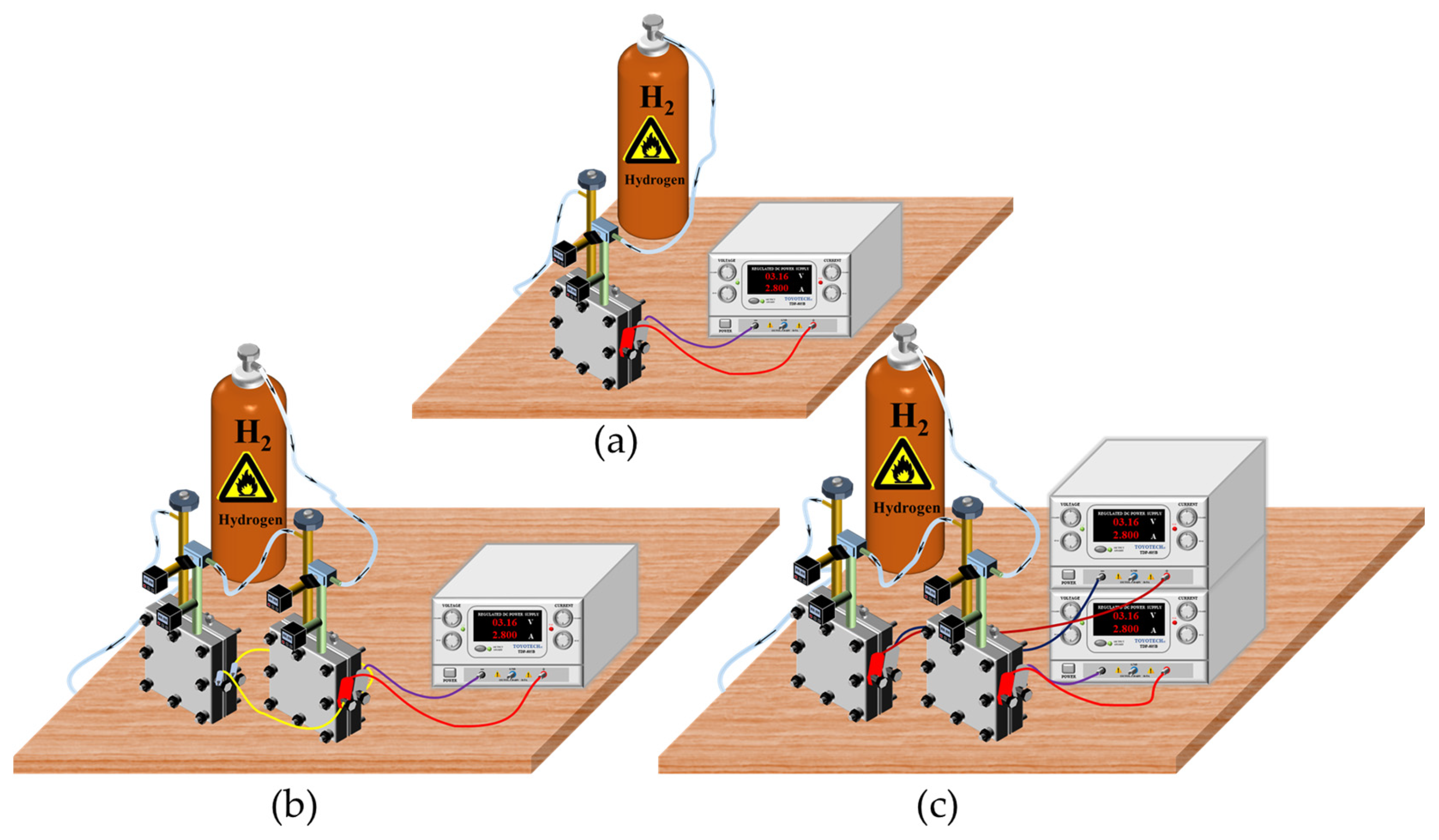
2. Experimental Details
2.1. Experimental Setup
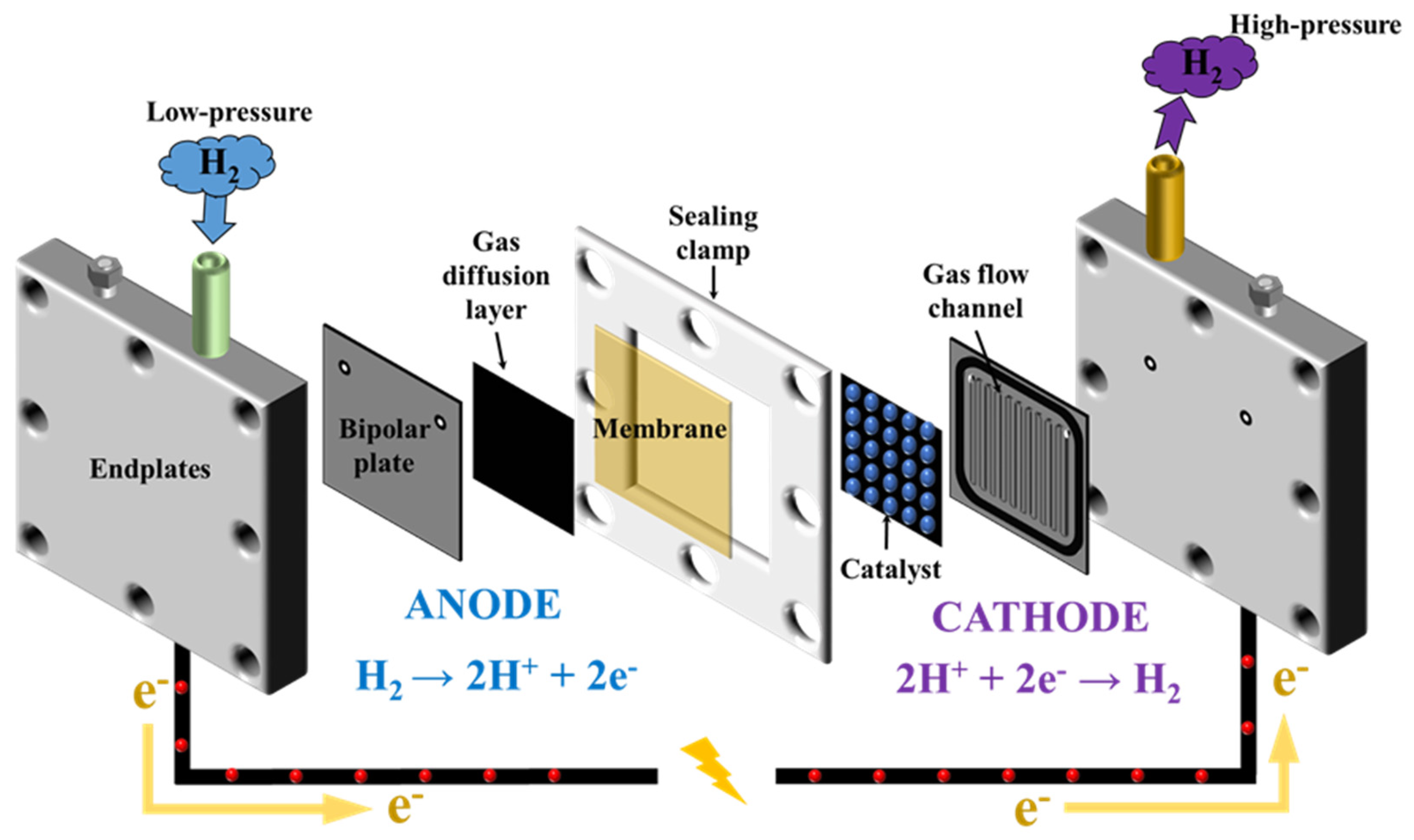
2.2. Electrochemical Cell
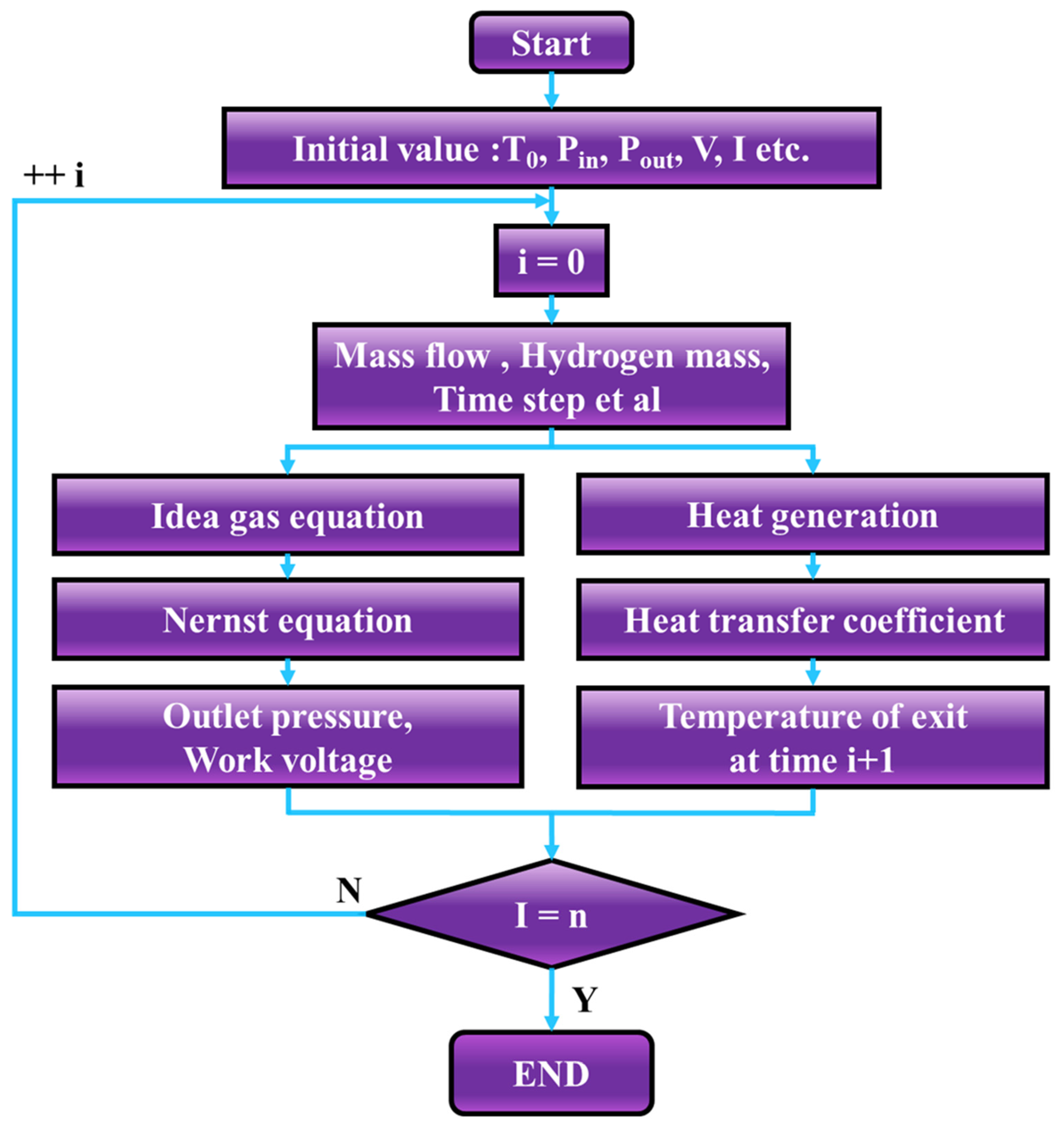
3. Theoretical Calculation
- 1.
- When the current density is infinitely large, the electrons flowing into the electrode from the external circuit are immediately consumed, or the electrons lost to the external circuit are replenished at once. The charge on the electrode surface remains nearly constant;
- 2.
- The external current density is very small, almost equal to zero. Since there is sufficient time for the reactants to combine with or release electrons, there is no excess charge on the electrode, and the electrode remains at an equilibrium potential.
- Constants such as the temperature, initial inlet and outlet pressure, current, and voltage are set;
- The hydrogen supply pressure is selected, and an external voltage is applied.
- The time step, time interval, etc., are set;
- The theoretical voltage is calculated using the Nernst and ideal gas equations;
- The hydrogen mass flow rate is determined using the number of electrons calculated as the theoretical voltage;
- The calorific value and thermal conductivity are calculated using the voltage and current;
- The outlet temperature and pressure are determined using the convective heat transfer coefficient, viscosity coefficient, etc.;
- Thereafter, we return to step 4 and perform the calculation;
- After reaching the set time, the calculation results are output according to the calculated time. The calculation results are the actual working voltage, outlet pressure, outlet temperature, mass flow rate, and other changes in each time period.
4. Results and Discussion
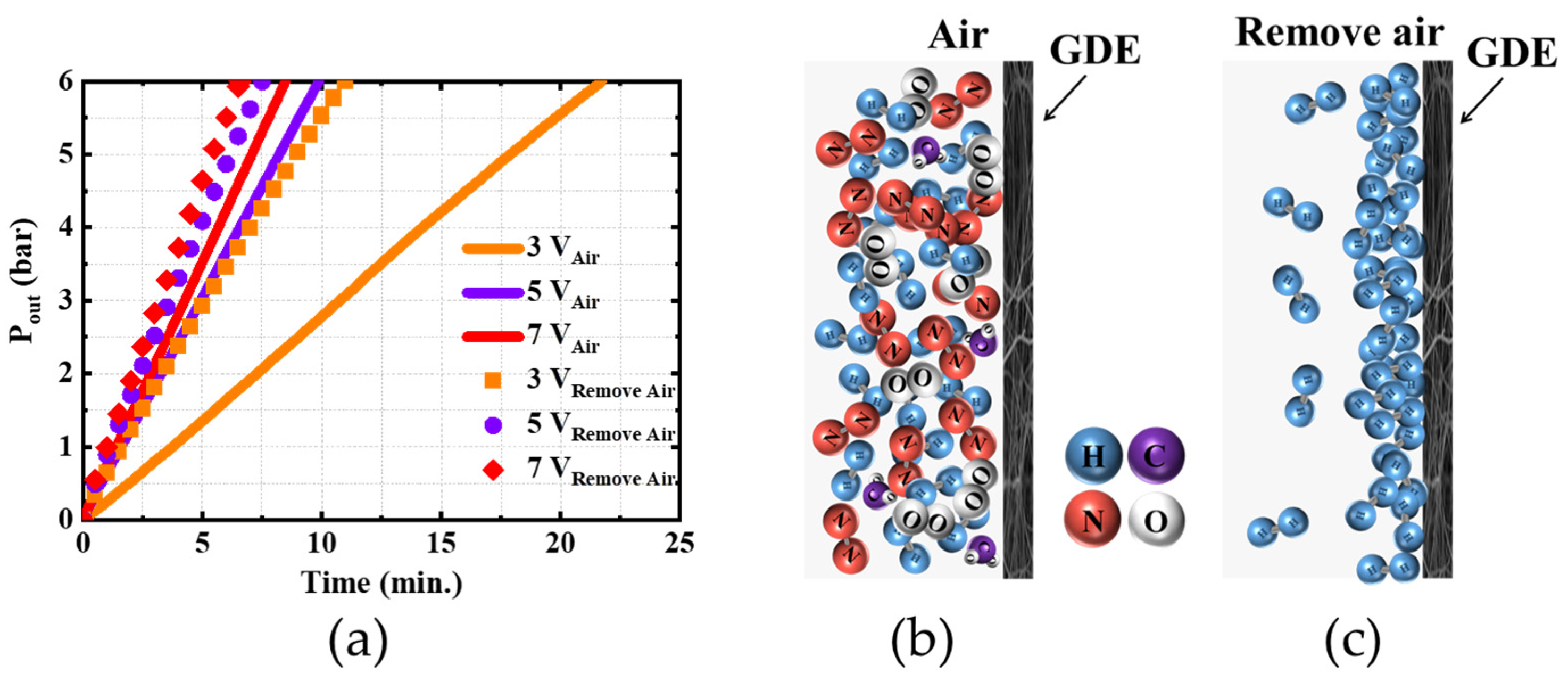
4.1. Effect of Residual Air in the Anode Chamber on the System Performance
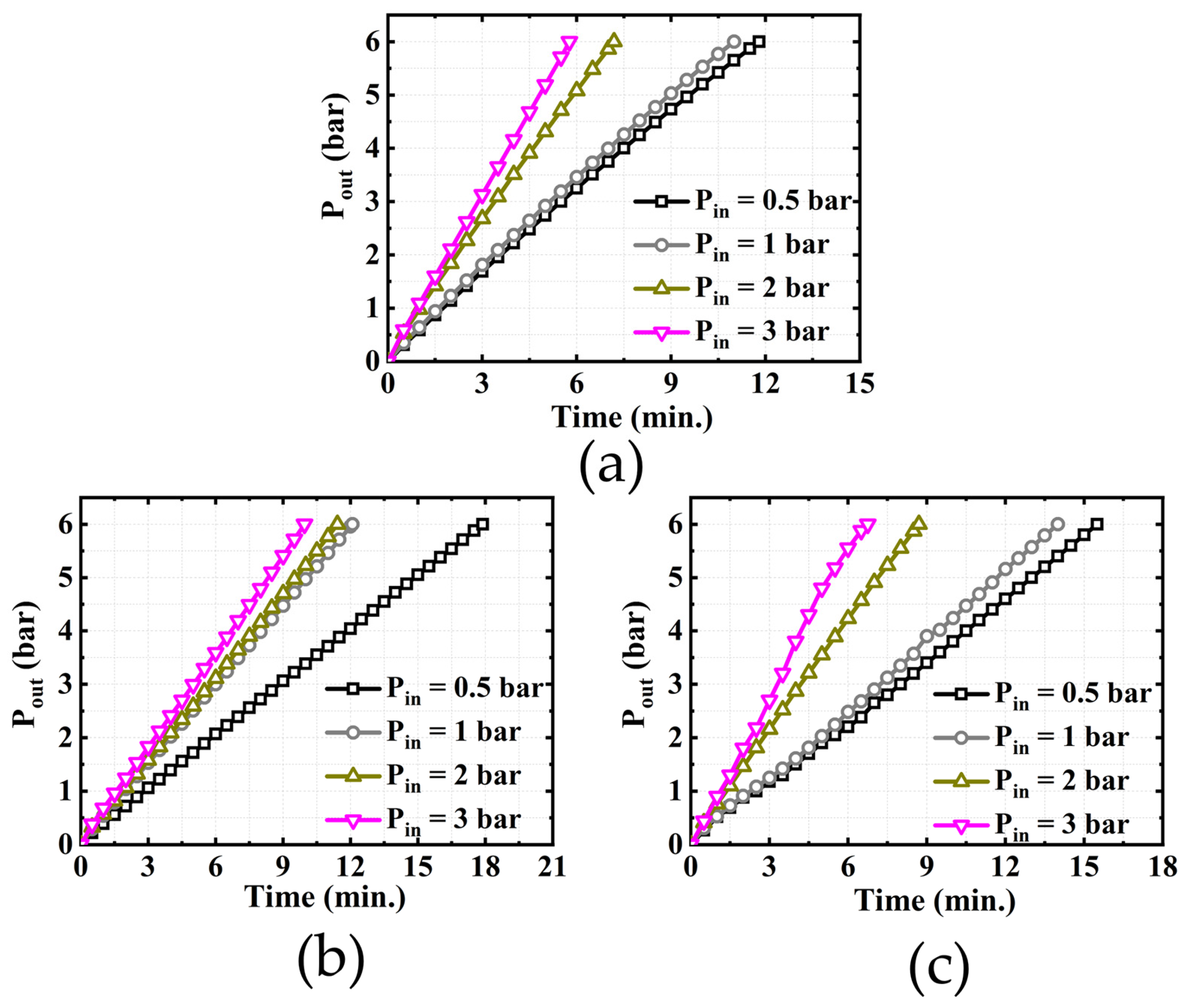
4.2. Effect of Hydrogen Pressure in Anode Chamber on System Performance
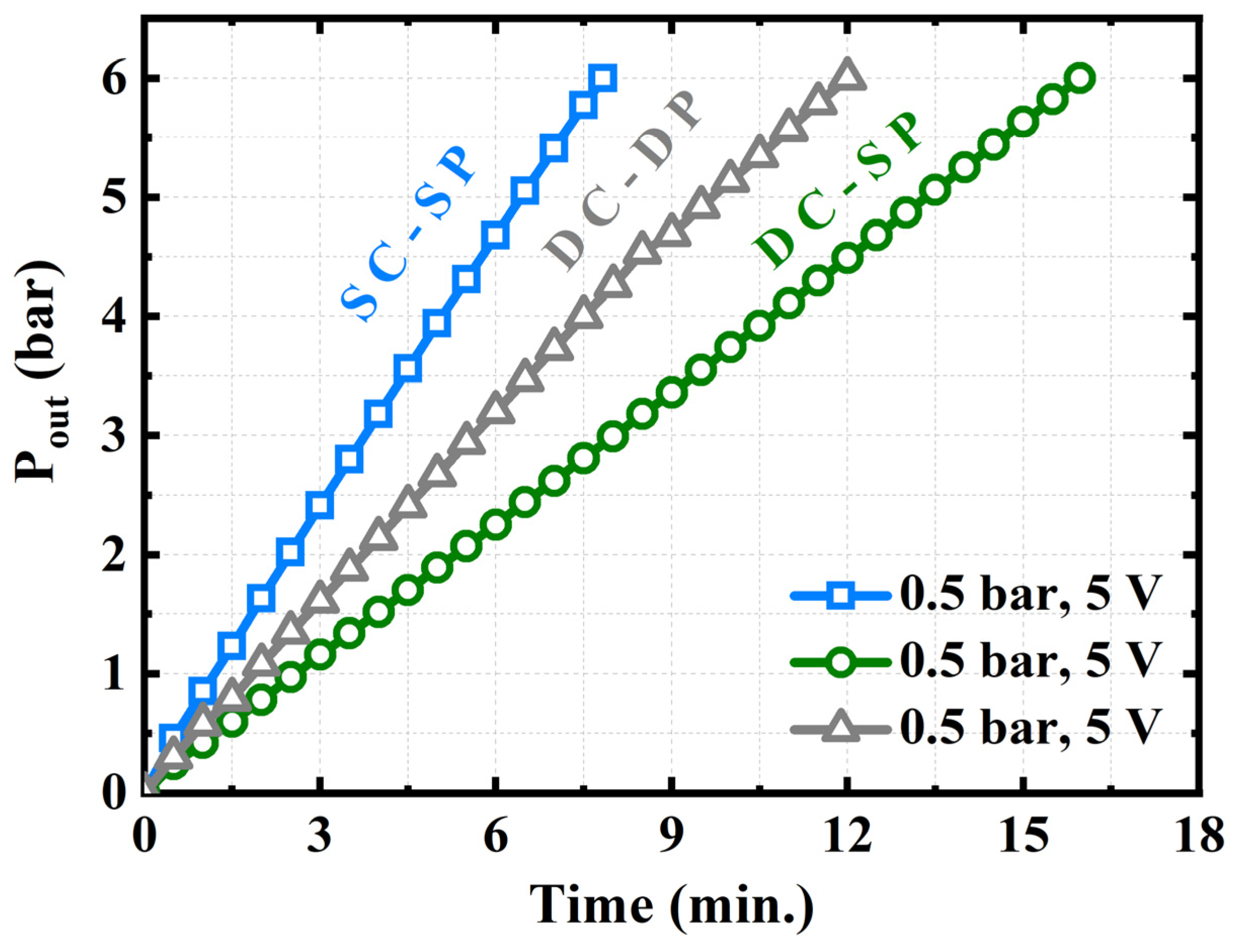
4.3. Comparison between the Three Experimental Setups
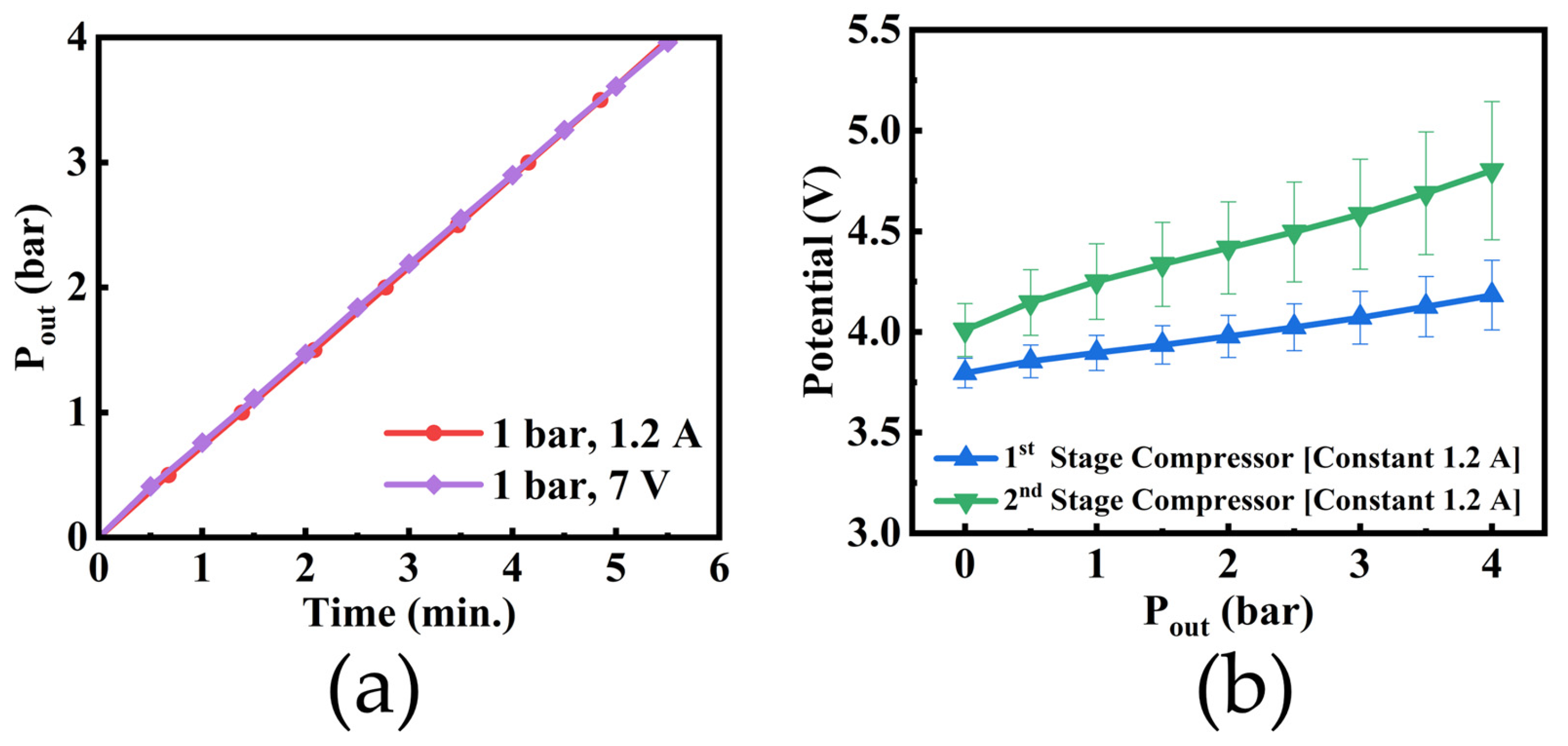
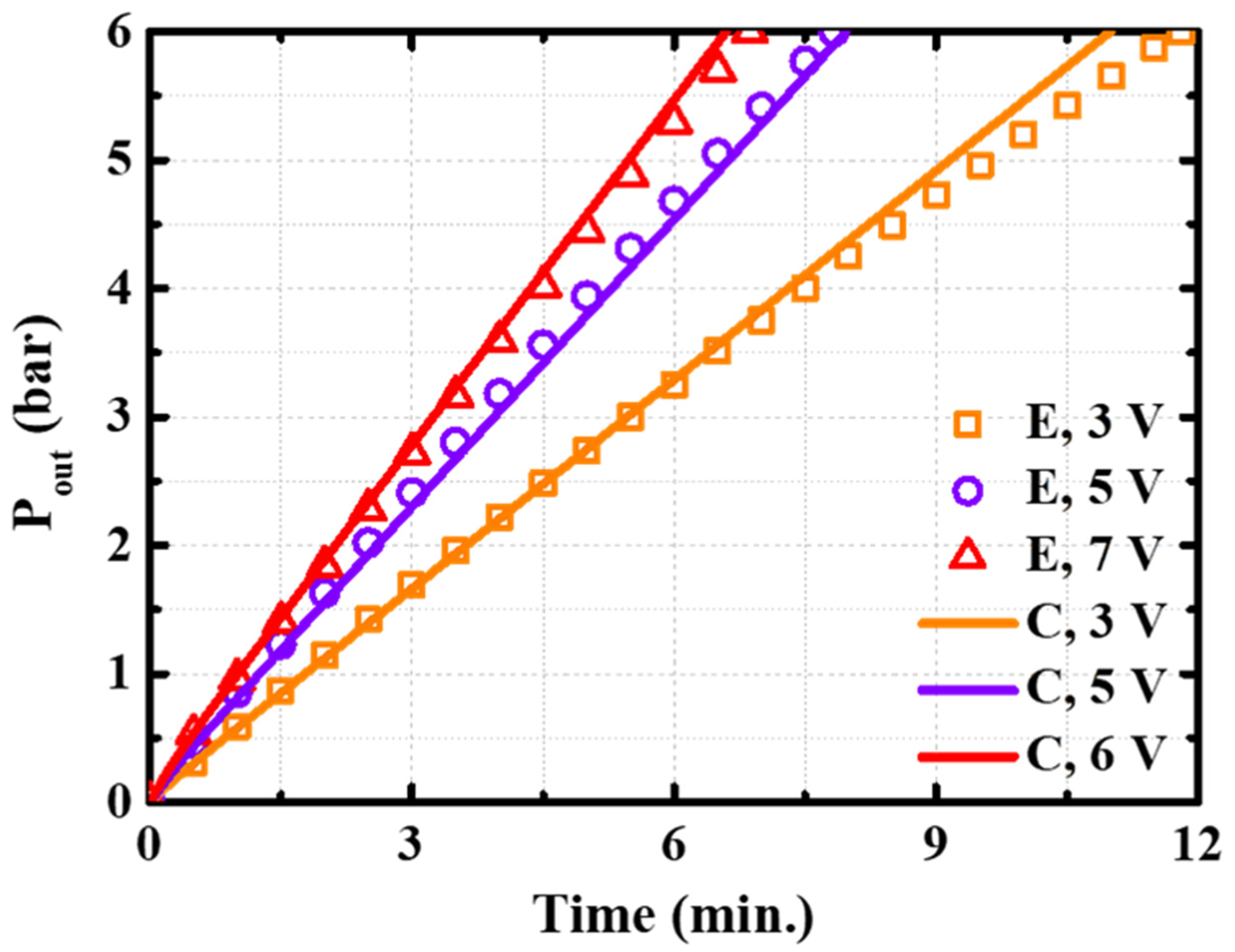
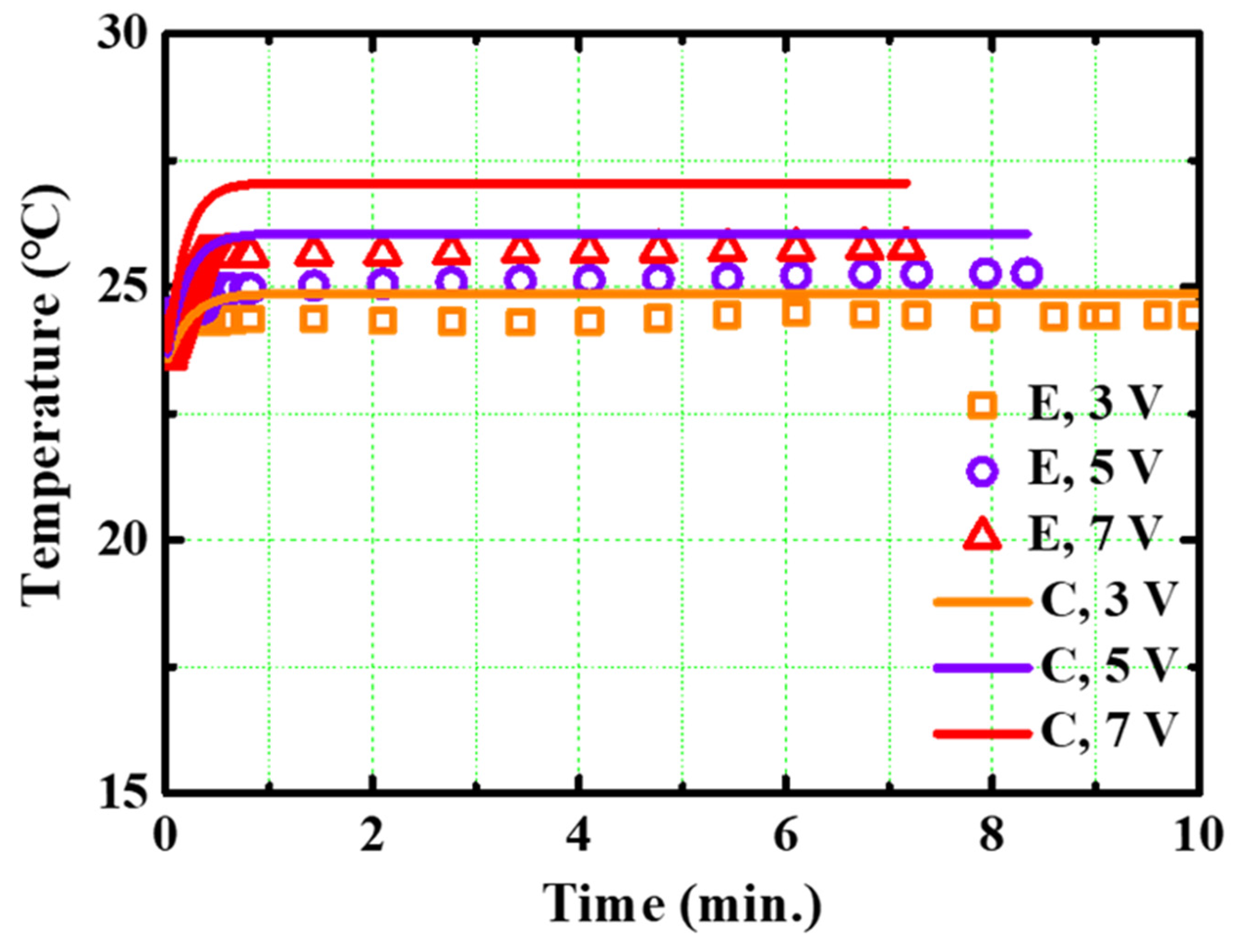
4.4. Calculation Results and Analysis
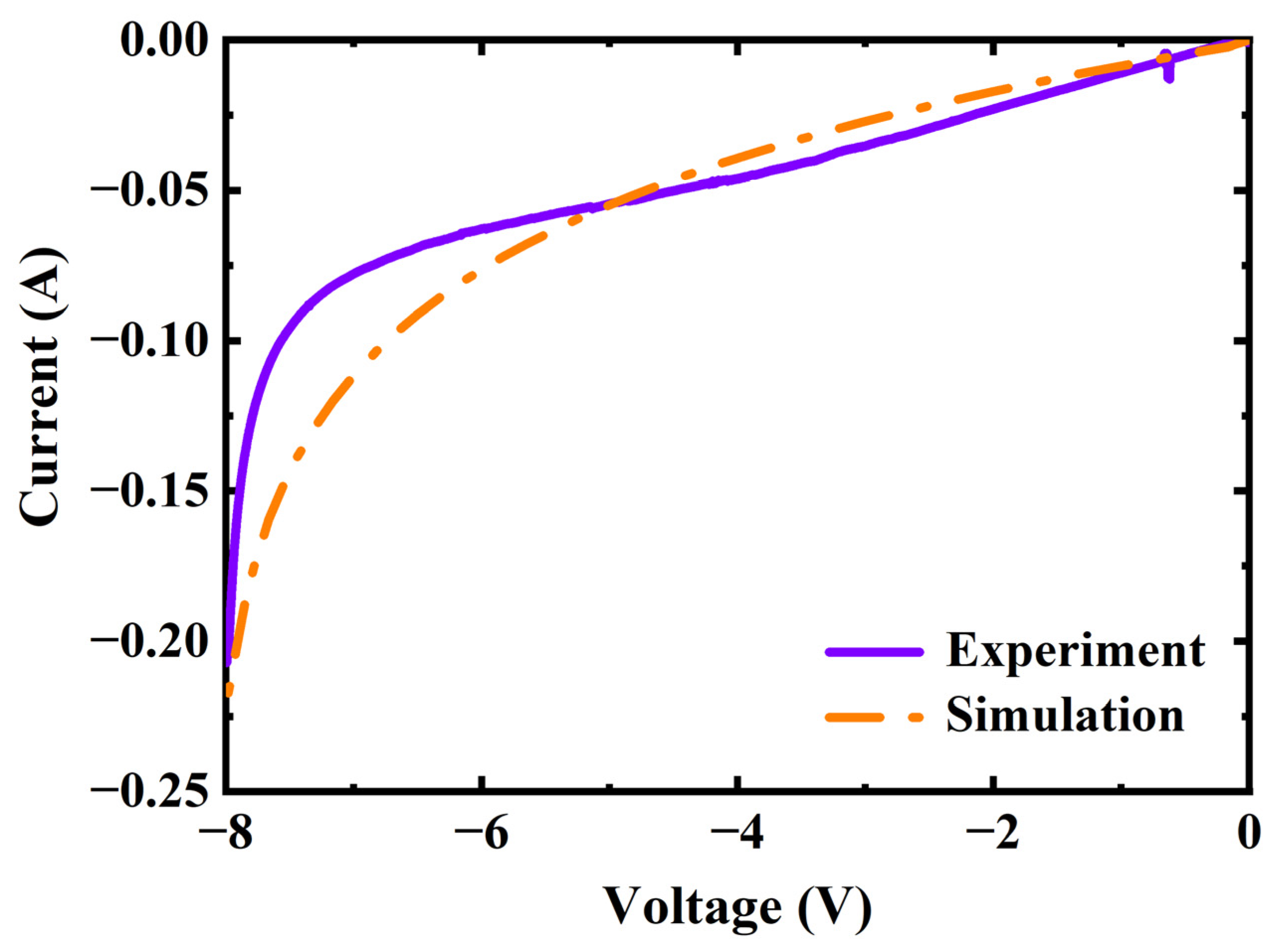
4.5. Variation of Current with Voltage
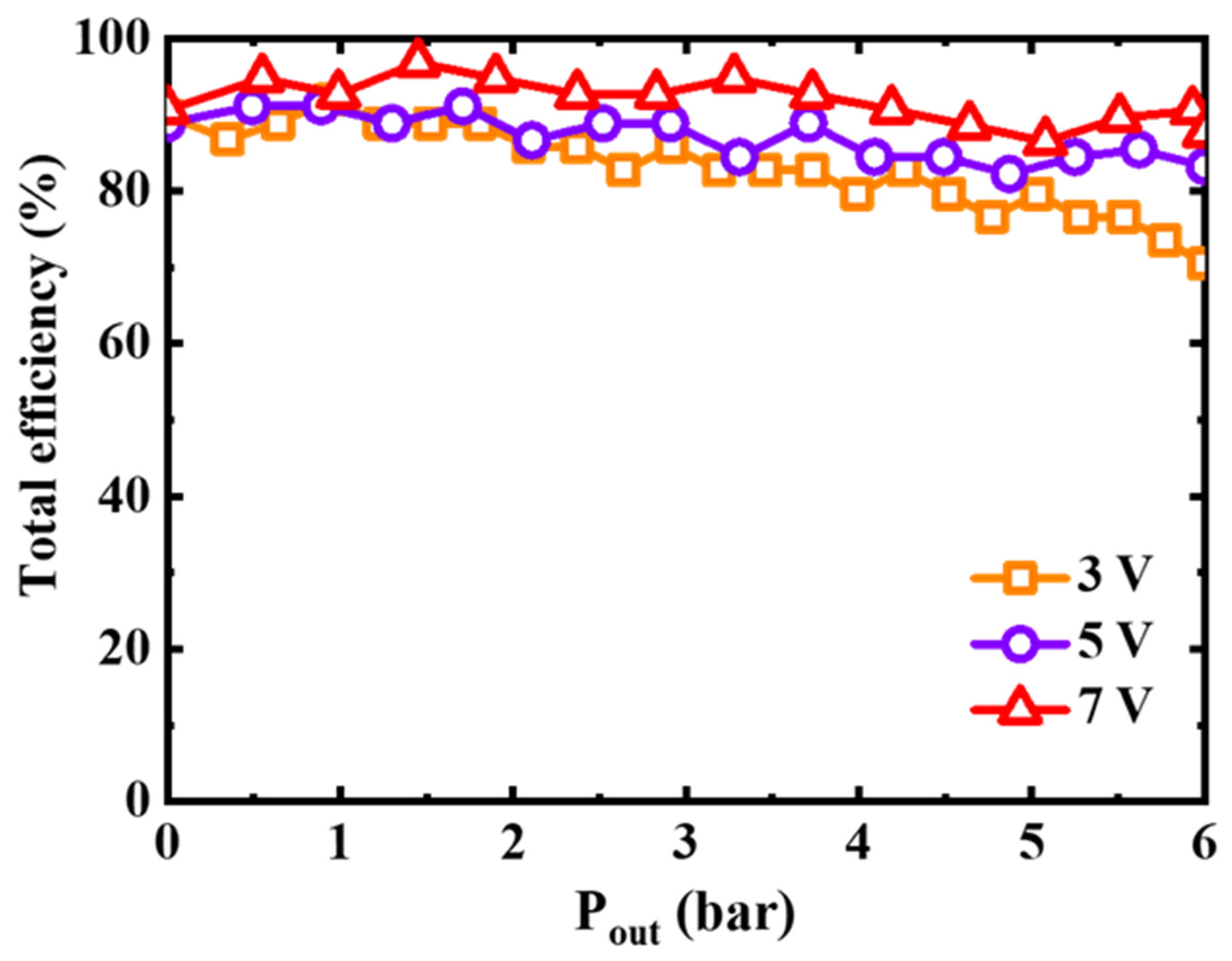
4.6. Theoretical Efficiency
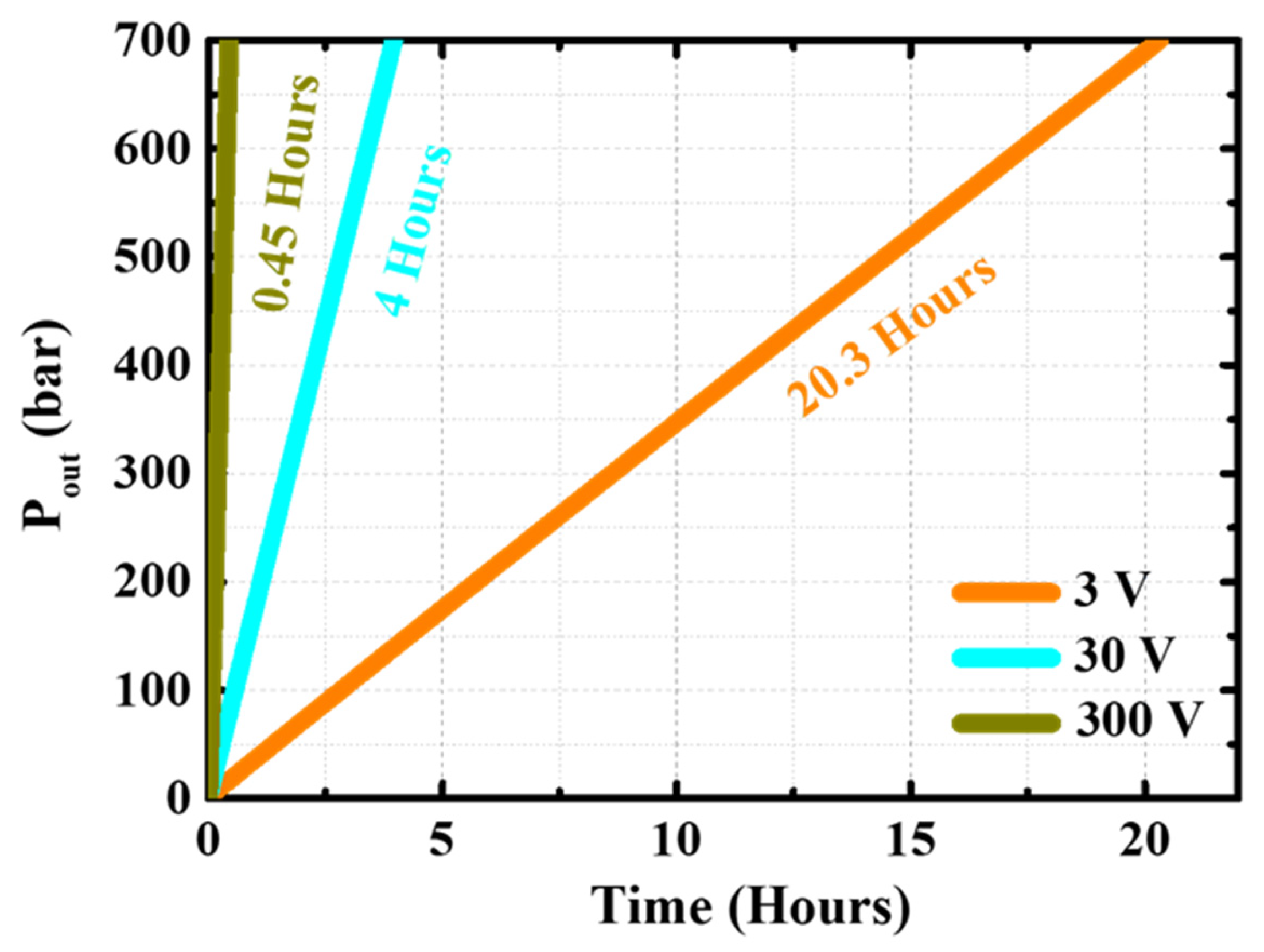
4.7. Commercial Pressure Standard Calculation
5. Conclusions
- The residual air within the EHC hinders contact between electrodes and hydrogen, thereby deteriorating a reaction kinetic;
- As the current increases, the molar flow rate of hydrogen increases, which increases the hydrogen production rate and reduces the time required to reach the desired compression pressure;
- When the applied voltage is constant, the final compression pressure is proportional to the supply pressure at the anode of the EHC. In addition, increasing the supply pressure shortens the time required to reach the final target compression pressure. It also effectively prevents the reverse penetration of hydrogen gas;
- The SC–SP, DC–SP, and DC–DP configurations were analyzed experimentally and compared at the same applied voltage and supply pressure. The SC–SP device exhibited the best performance and efficiency in this study;
- The cathode pressure, temperature, and polarization curves of the SC–SP device were theoretically calculated, and the results were in good agreement with the experimental results;
- The simulation results revealed that industrial hydrogen tanks require at least 20 h, 4 h, and 24 min to reach commercial pressures of 700–800 bar at applied voltages of 3 V, 30 V, and 300 V, respectively, and that commercial EHCs require at least 30 V to reduce the time needed;
- EHCs have a high compression efficiency of 86% or more.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| A | Area, | Pressure at hydrogen outlet, | |
| Specific heat, | Q | Heat rate, W | |
| d | Diameter, m | Heat generated rate, W | |
| e | Electrons | Heat released rate, W | |
| F | Faraday constant, 96,500 C/mol | q | Heat flux rate, W/ |
| g | Acceleration of gravity | R | Universal gas constant, J/mol K |
| h | Heat transfer coefficient, W/ | r | Resistance, Ω |
| i | Current density, A/ | T | Static temperature, K |
| I | Current | Ambient temperature, K | |
| Theoretical amount of compressed hydrogen gas | Outlet temperature, K | ||
| Measured amount of compressed hydrogen gas | t | Time, sec | |
| K | Thermal conductivity, W/m·K | Power supply voltage, | |
| L | Pipe length, m | Initial voltage, | |
| m | Mass, kg | V | Volume |
| M | Relative molecular mass | Operating voltage, | |
| n | Amount of matter | Open-circuit Volume, | |
| NA | Avogadro constant | Activation overpotential, | |
| P | Static pressure, | Concentration overpotential, | |
| Pressure at the hydrogen inlet, | Ohmic overpotential, |
References
- Xu, X.; Zhou, Q.; Yu, D. The Future of Hydrogen Energy: Bio-Hydrogen Production Technology. Int. J. Hydrogen Energy 2022, 47, 33677–33698. [Google Scholar] [CrossRef]
- Arsad, A.Z.; Hannan, M.A.; Al-Shetwi, A.Q.; Mansur, M.; Muttaqi, K.M.; Dong, Z.Y.; Blaabjerg, F. Hydrogen Energy Storage Integrated Hybrid Renewable Energy Systems: A Review Analysis for Future Research Directions. Int. J. Hydrogen Energy 2022, 47, 17285–17312. [Google Scholar] [CrossRef]
- Dutta, S. A Review on Production, Storage of Hydrogen and Its Utilization as an Energy Resource. J. Ind. Eng. Chem. 2014, 20, 1148–1156. [Google Scholar] [CrossRef]
- Nordio, M.; Rizzi, F.; Manzolini, G.; Mulder, M.; Raymakers, L.; Van Sint Annaland, M.; Gallucci, F. Experimental and Modelling Study of an Electrochemical Hydrogen Compressor. Chem. Eng. J. 2019, 369, 432–442. [Google Scholar] [CrossRef]
- Zhou, L. Progress and Problems in Hydrogen Storage Methods. Renew. Sustain. Energy Rev. 2005, 9, 395–408. [Google Scholar] [CrossRef]
- Dale, N.V.; Mann, M.D.; Salehfar, H.; Dhirde, A.M.; Han, T. Modeling and Analysis of Electrochemical Hydrogen Compression. In Proceedings of the NHA Annual Hydrogen Conference, San Antonio, TX, USA, 19–22 March 2007; p. 30. [Google Scholar]
- Tzimas, E.; Filiou, C.; Peteves, S.D.; Veyret, J. Hydrogen Storage: State-of-the-Art and Future Perspective; Office for Official Publications of the European Communities: Luxembourg, 2003; ISBN 9289469501. [Google Scholar]
- Abdin, Z.; Webb, C.J.; Gray, E.M. Modelling and Simulation of a Proton Exchange Membrane (PEM) Electrolyser Cell. Int. J. Hydrogen Energy 2015, 40, 13243–13257. [Google Scholar] [CrossRef]
- Zou, J.; Han, N.; Yan, J.; Feng, Q.; Wang, Y.; Zhao, Z.; Fan, J.; Zeng, L.; Li, H.; Wang, H. Electrochemical Compression Technologies for High-Pressure Hydrogen: Current Status, Challenges and Perspective. Electrochem. Energy Rev. 2020, 3, 690–729. [Google Scholar] [CrossRef]
- Ströbel, R.; Oszcipok, M.; Fasil, M.; Rohland, B.; Jörissen, L.; Garche, J. The Compression of Hydrogen in an Electrochemical Cell Based on a PE Fuel Cell Design. J. Power Sources 2002, 105, 208–215. [Google Scholar] [CrossRef]
- Barbir, F.; Görgün, H. Electrochemical Hydrogen Pump for Recirculation of Hydrogen in a Fuel Cell Stack. J. Appl. Electrochem. 2007, 37, 359–365. [Google Scholar] [CrossRef]
- Lee, H.K.; Choi, H.Y.; Choi, K.H.; Park, J.H.; Lee, T.H. Hydrogen Separation Using Electrochemical Method. J. Power Sources 2004, 132, 92–98. [Google Scholar] [CrossRef]
- Jakobsen, M.T.D.; Jensen, J.O.; Cleemann, L.N.; Li, Q. Durability Issues and Status of PBI-Based Fuel Cells; Springer: Berlin/Heidelberg, Germany, 2016; ISBN 9783319170824. [Google Scholar]
- Yáñez, M.; Relvas, F.; Ortiz, A.; Gorri, D.; Mendes, A.; Ortiz, I. PSA Purification of Waste Hydrogen from Ammonia Plants to Fuel Cell Grade. Sep. Purif. Technol. 2020, 240, 116334. [Google Scholar] [CrossRef]
- Nguyen, M.T.; Grigoriev, S.A.; Kalinnikov, A.A.; Filippov, A.A.; Millet, P.; Fateev, V.N. Characterisation of a Electrochemical Hydrogen Pump Using Electrochemical Impedance Spectroscopy. J. Appl. Electrochem. 2011, 41, 1033–1042. [Google Scholar] [CrossRef]
- Gardner, C.L.; Ternan, M. Electrochemical Separation of Hydrogen from Reformate Using PEM Fuel Cell Technology. J. Power Sources 2007, 171, 835–841. [Google Scholar] [CrossRef]
- Doucet, R.; Gardner, C.L.; Ternan, M. Separation of Hydrogen from Hydrogen/Ethylene Mixtures Using PEM Fuel Cell Technology. Int. J. Hydrogen Energy 2009, 34, 998–1007. [Google Scholar] [CrossRef]
- Onda, K.; Araki, T.; Ichihara, K.; Nagahama, M. Treatment of Low Concentration Hydrogen by Electrochemical Pump or Proton Exchange Membrane Fuel Cell. J. Power Sources 2009, 188, 1–7. [Google Scholar] [CrossRef]
- Sedlak, J.M.; Austin, J.F.; LaConti, A.B. Hydrogen recovery and purification using the solid polymer electrolyte electrolysis cell. Int. J. Hydrogen Energy 1981, 6, 45–51. [Google Scholar] [CrossRef]
- Durmus, G.N.B.; Colpan, C.O.; Devrim, Y. A Review on the Development of the Electrochemical Hydrogen Compressors. J. Power Sources 2021, 494, 229743. [Google Scholar] [CrossRef]
- Marciuš, D.; Kovač, A.; Firak, M. Electrochemical Hydrogen Compressor: Recent Progress and Challenges. Int. J. Hydrogen Energy 2022, 47, 24179–24193. [Google Scholar] [CrossRef]
- Marangio, F.; Santarelli, M.; Calì, M. Theoretical Model and Experimental Analysis of a High Pressure PEM Water Electrolyser for Hydrogen Production. Int. J. Hydrogen Energy 2009, 34, 1143–1158. [Google Scholar] [CrossRef]
- Rohland, B.; Eberle, K.; Ströbel, R.; Scholta, J.; Garche, J. Electrochemical Hydrogen Compressor. Electrochim. Acta 1998, 43, 3841–3846. [Google Scholar] [CrossRef]
- Mantell, C.L. Electrochemical Engineering; McGraw Hill: New York, NY, USA, 1960. [Google Scholar]
- Ball, S.C. 10th Ulm Electrochemical Talks: PGMS Feature in Reliability and Durability Gains and Cost Reduction for Electrochemical Energy Storage and Conversion. Platin. Met. Rev. 2006, 50, 202–204. [Google Scholar] [CrossRef]
- Zawodzinski, T.A.; Derouin, C.; Radzinski, S.; Sherman, R.J.; Smith, V.T.; Springer, T.E.; Gottesfeld, S. Water Uptake by and Transport through Nafion® 117 Membranes. J. Electrochem. Soc. 1993, 140, 1041–1047. [Google Scholar] [CrossRef]
- Marković, N.M.; Grgur, B.N.; Ross, P.N. Temperature-Dependent Hydrogen Electrochemistry on Platinum Low-Index Single-Crystal Surfaces in Acid Solutions. J. Phys. Chem. B 1997, 101, 5405–5413. [Google Scholar] [CrossRef]
- Hao, Y.M.; Nakajima, H.; Yoshizumi, H.; Inada, A.; Sasaki, K.; Ito, K. Characterization of an Electrochemical Hydrogen Pump with Internal Humidifier and Dead-End Anode Channel. Int. J. Hydrogen Energy 2016, 41, 13879–13887. [Google Scholar] [CrossRef]
- Pitts, D.R.; Sissom, L.E. Schaum’s Outline of Theory and Problems of Heat Transfer; McGraw-Hill Companies, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Nordio, M.; Eguaras Barain, M.; Raymakers, L.; Van Sint Annaland, M.; Mulder, M.; Gallucci, F. Effect of CO2 on the Performance of an Electrochemical Hydrogen Compressor. Chem. Eng. J. 2020, 392, 123647. [Google Scholar] [CrossRef]
- Chouhan, A.; Bahar, B.; Prasad, A.K. Effect of Back-Diffusion on the Performance of an Electrochemical Hydrogen Compressor. Int. J. Hydrogen Energy 2020, 45, 10991–10999. [Google Scholar] [CrossRef]
- Dornheim, M.; Baetcke, L.; Akiba, E.; Ares, J.R.; Autrey, T.; Barale, J.; Baricco, M.; Brooks, K.; Chalkiadakis, N.; Charbonnier, V.; et al. Research and Development of Hydrogen Carrier Based Solutions for Hydrogen Compression and Storage. Prog. Energy 2022, 4, 042005. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, R.; Kweon, H.; Kim, K. Preliminary Study for the Commercialization of a Electrochemical Hydrogen Compressor. Energies 2023, 16, 3128. https://doi.org/10.3390/en16073128
Yang R, Kweon H, Kim K. Preliminary Study for the Commercialization of a Electrochemical Hydrogen Compressor. Energies. 2023; 16(7):3128. https://doi.org/10.3390/en16073128
Chicago/Turabian StyleYang, Rui, Hyeokbin Kweon, and Kibum Kim. 2023. "Preliminary Study for the Commercialization of a Electrochemical Hydrogen Compressor" Energies 16, no. 7: 3128. https://doi.org/10.3390/en16073128
APA StyleYang, R., Kweon, H., & Kim, K. (2023). Preliminary Study for the Commercialization of a Electrochemical Hydrogen Compressor. Energies, 16(7), 3128. https://doi.org/10.3390/en16073128






