CFD-Based Analysis of Installed Fuel Consumption and Aerodynamics of Transonic Transport Aircraft during Cruise Flight
Abstract
:1. Introduction
2. Materials and Methods
2.1. Aircraft and Turbofan Model
2.2. CFD Modelling
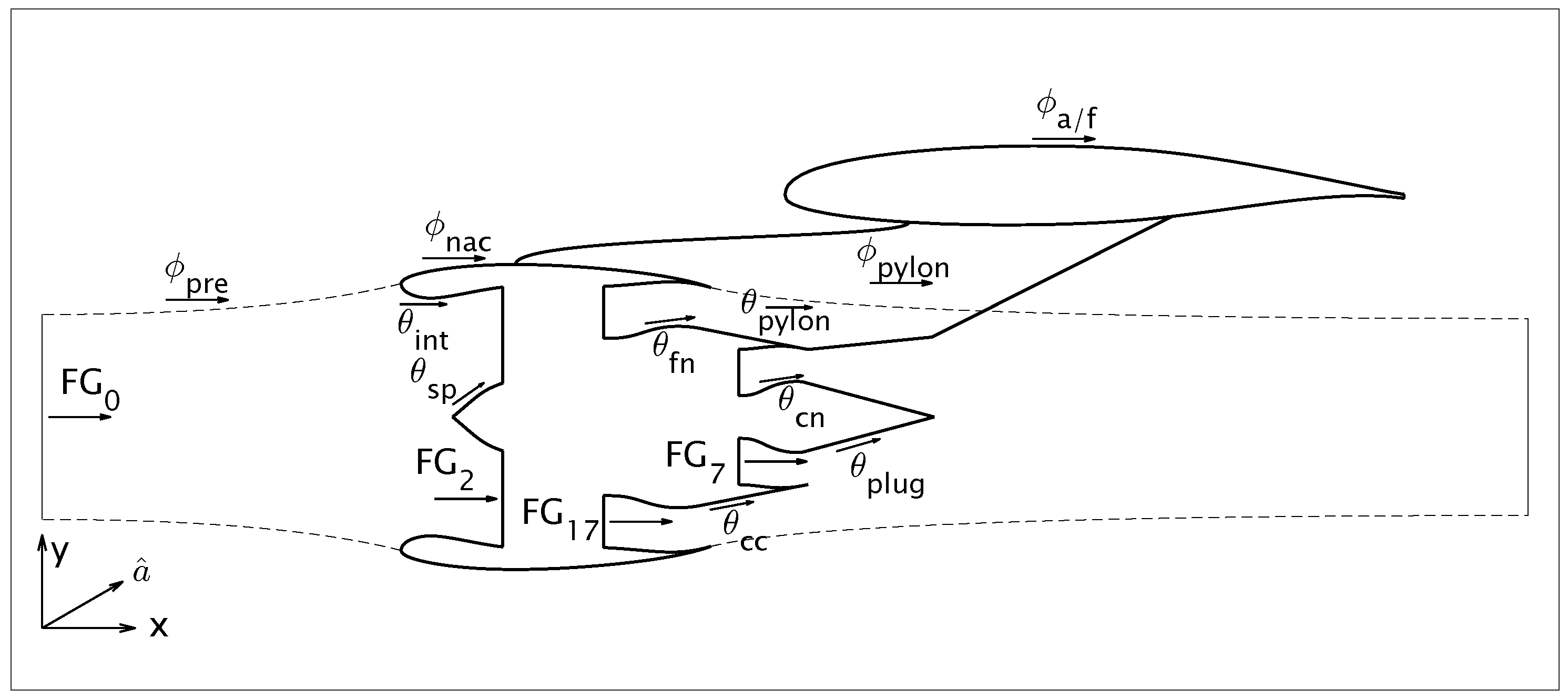
2.3. Thrust–Drag Bookkeeping
2.4. Mission Point Evaluation
3. Results
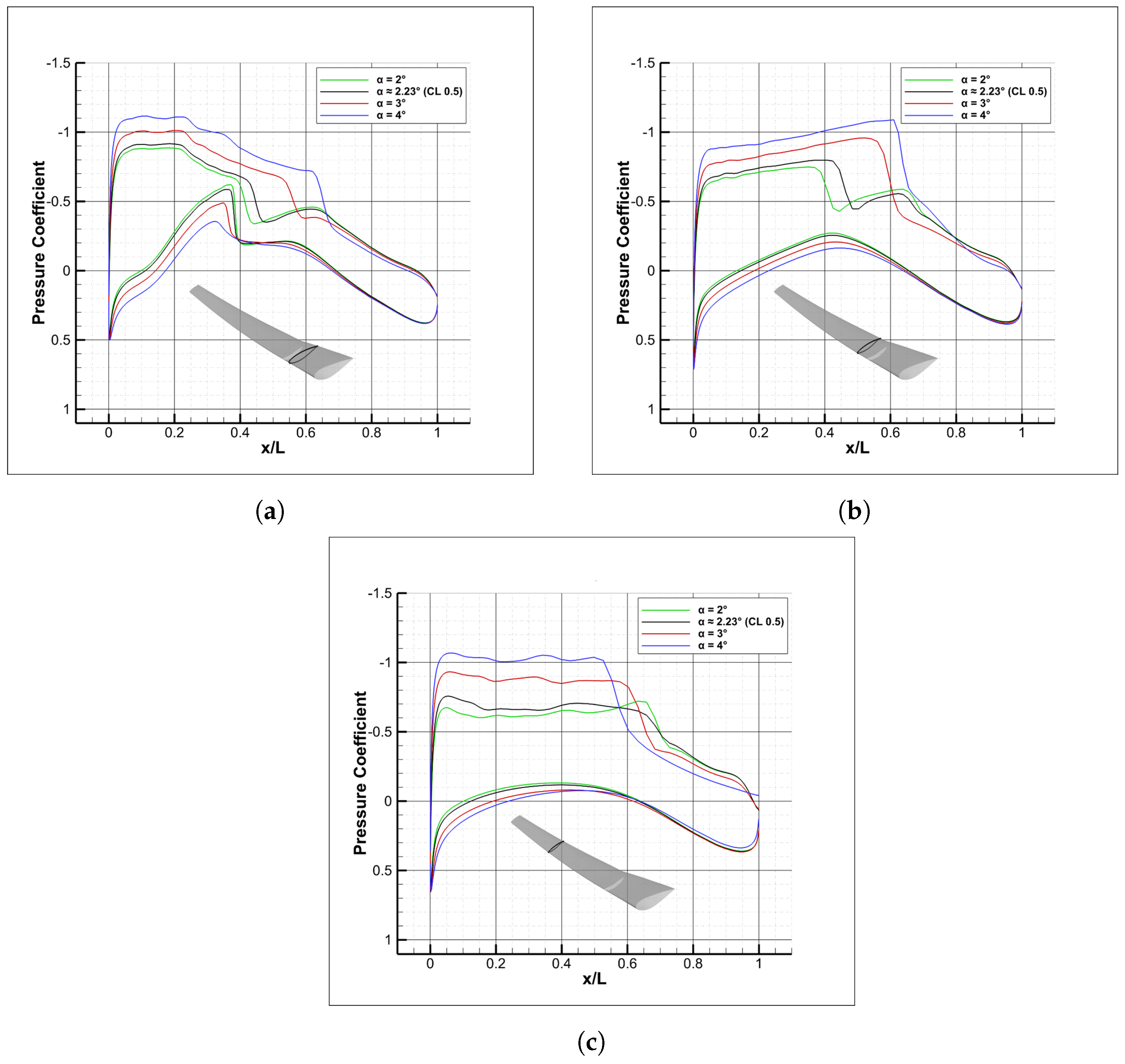
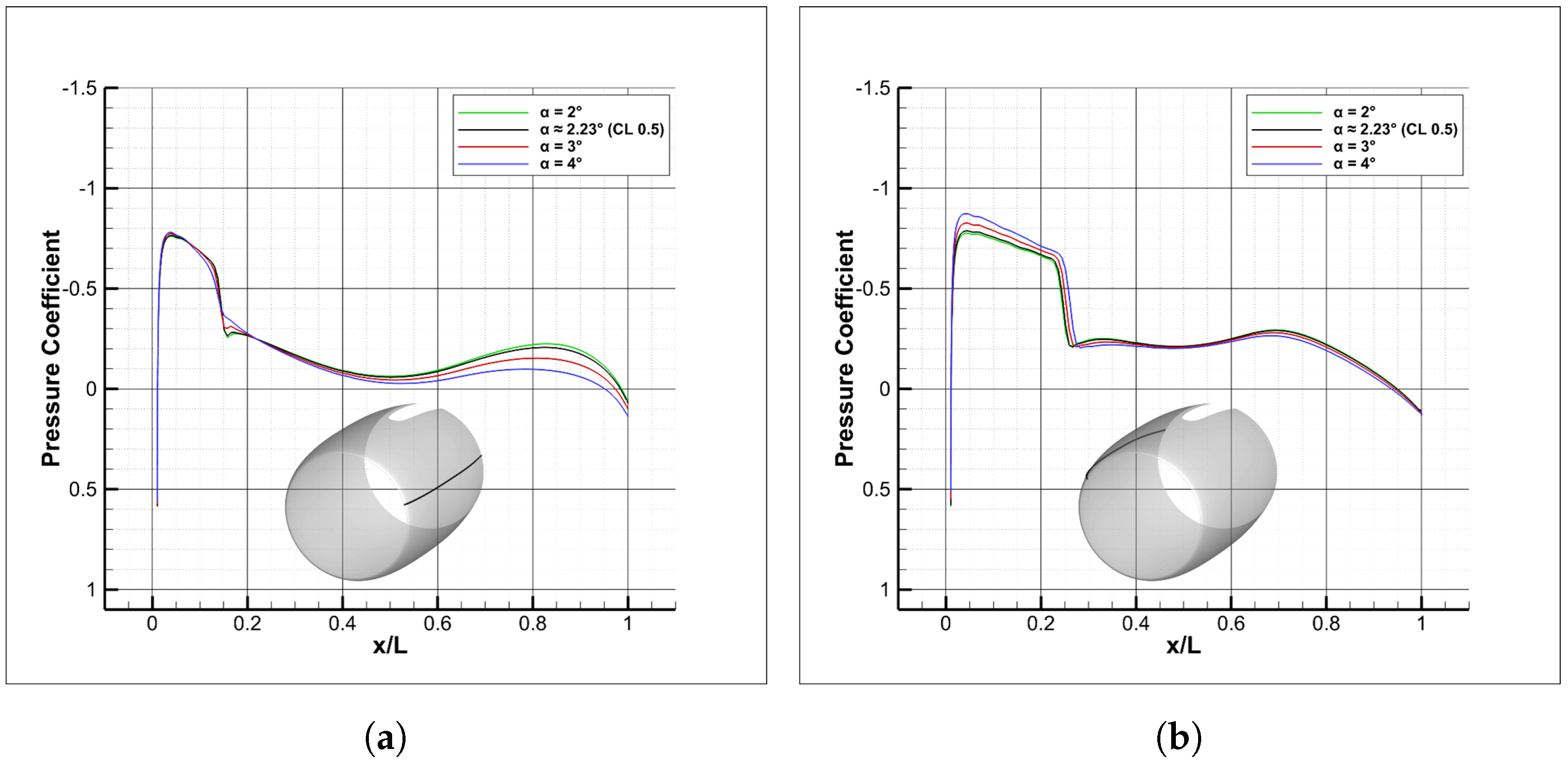
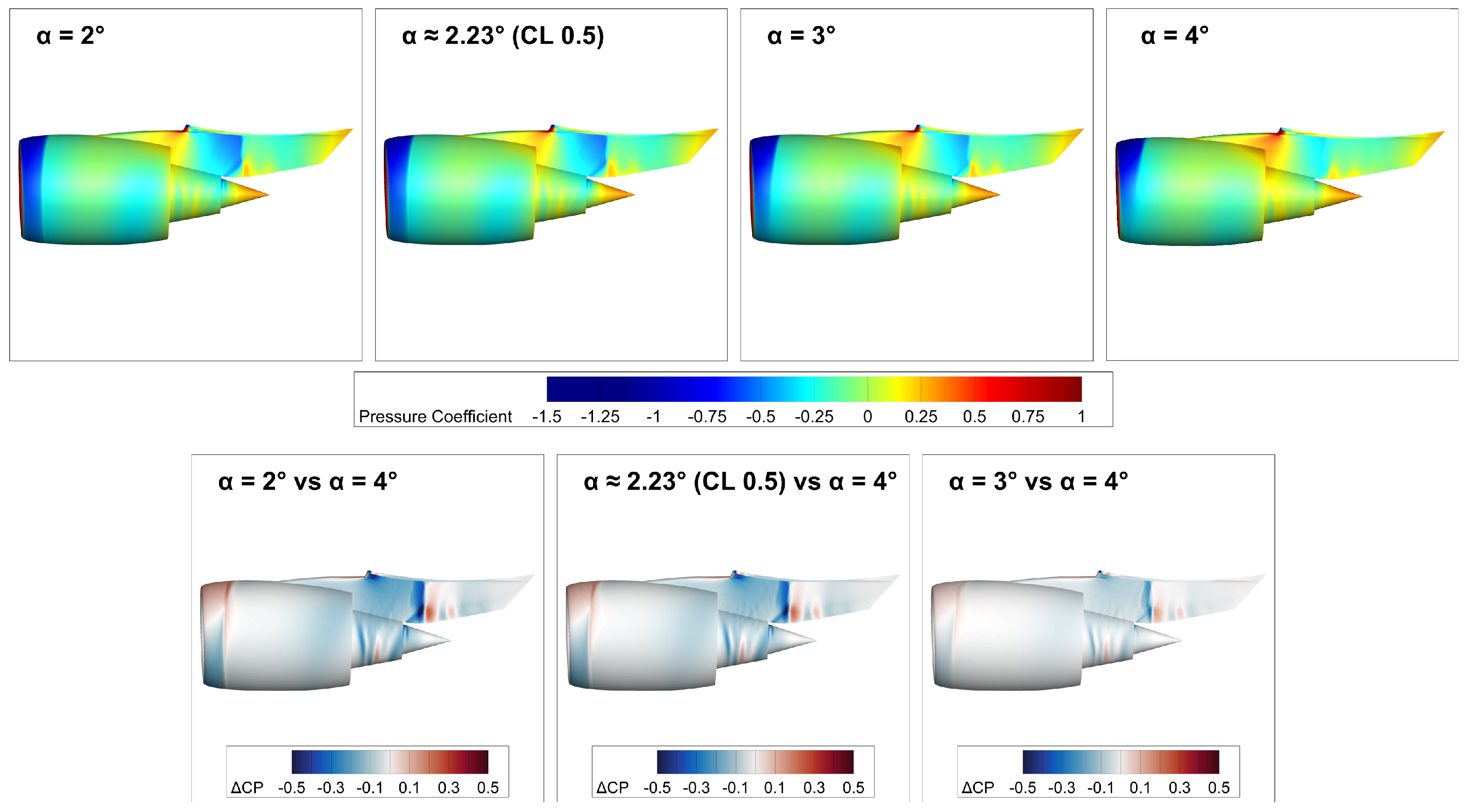
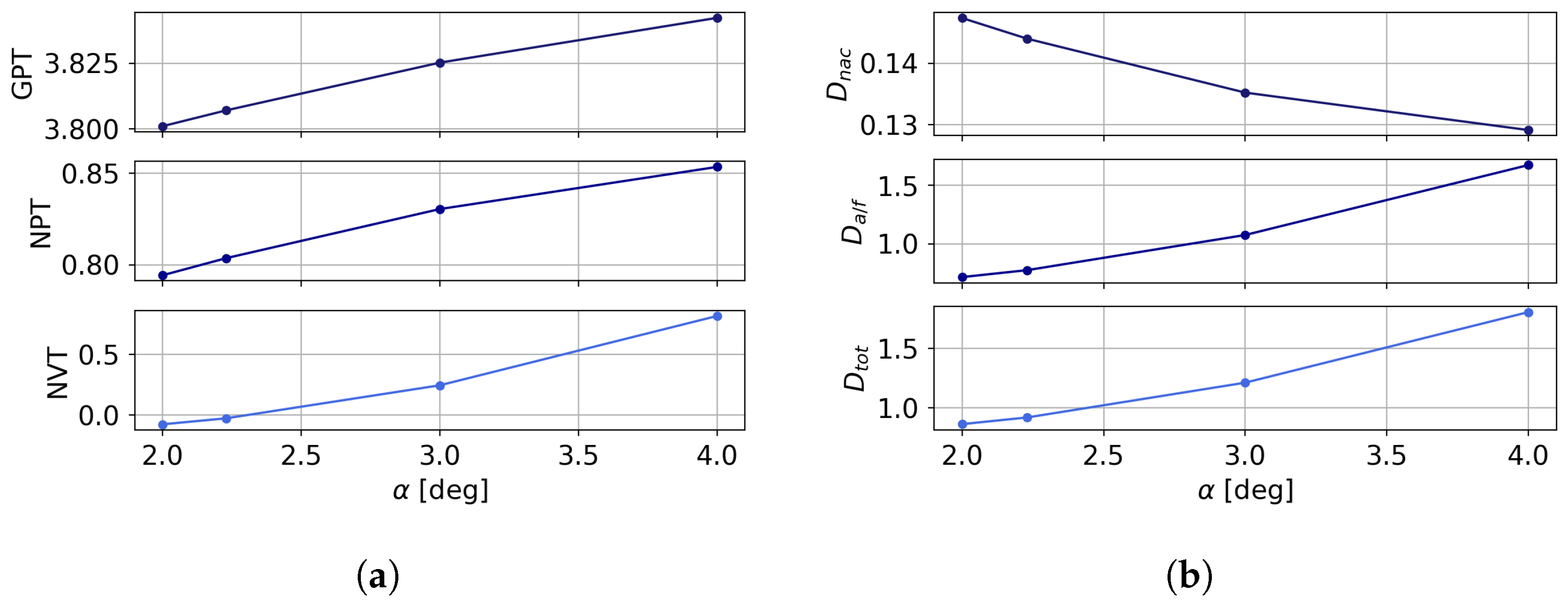
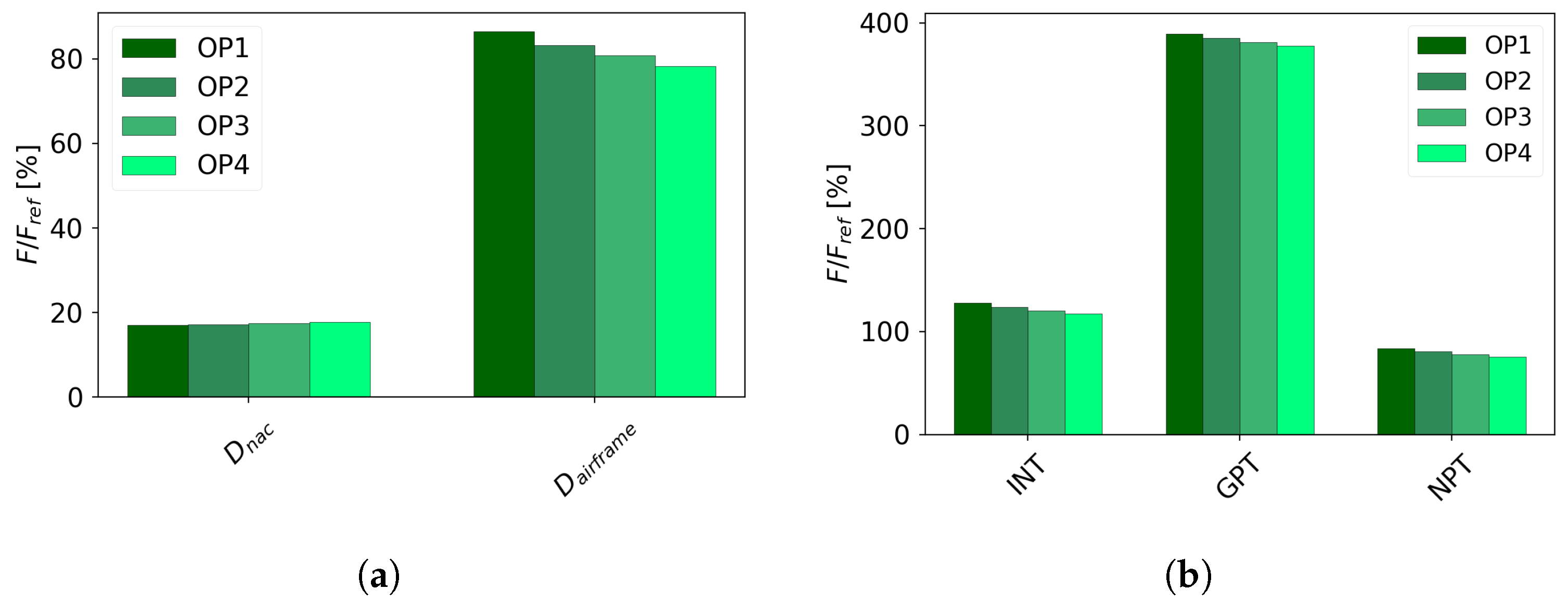
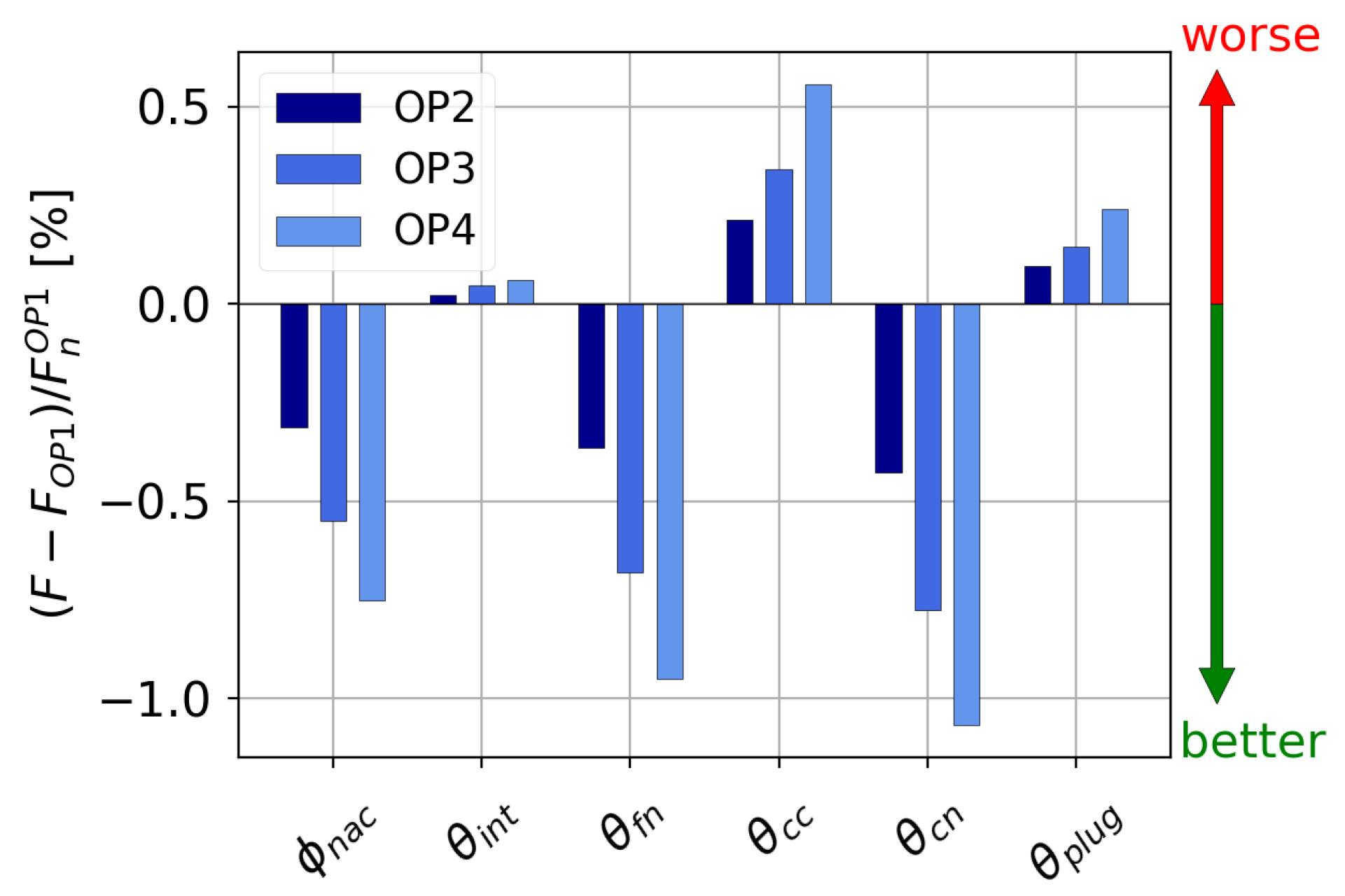
3.1. Flow Characterisation
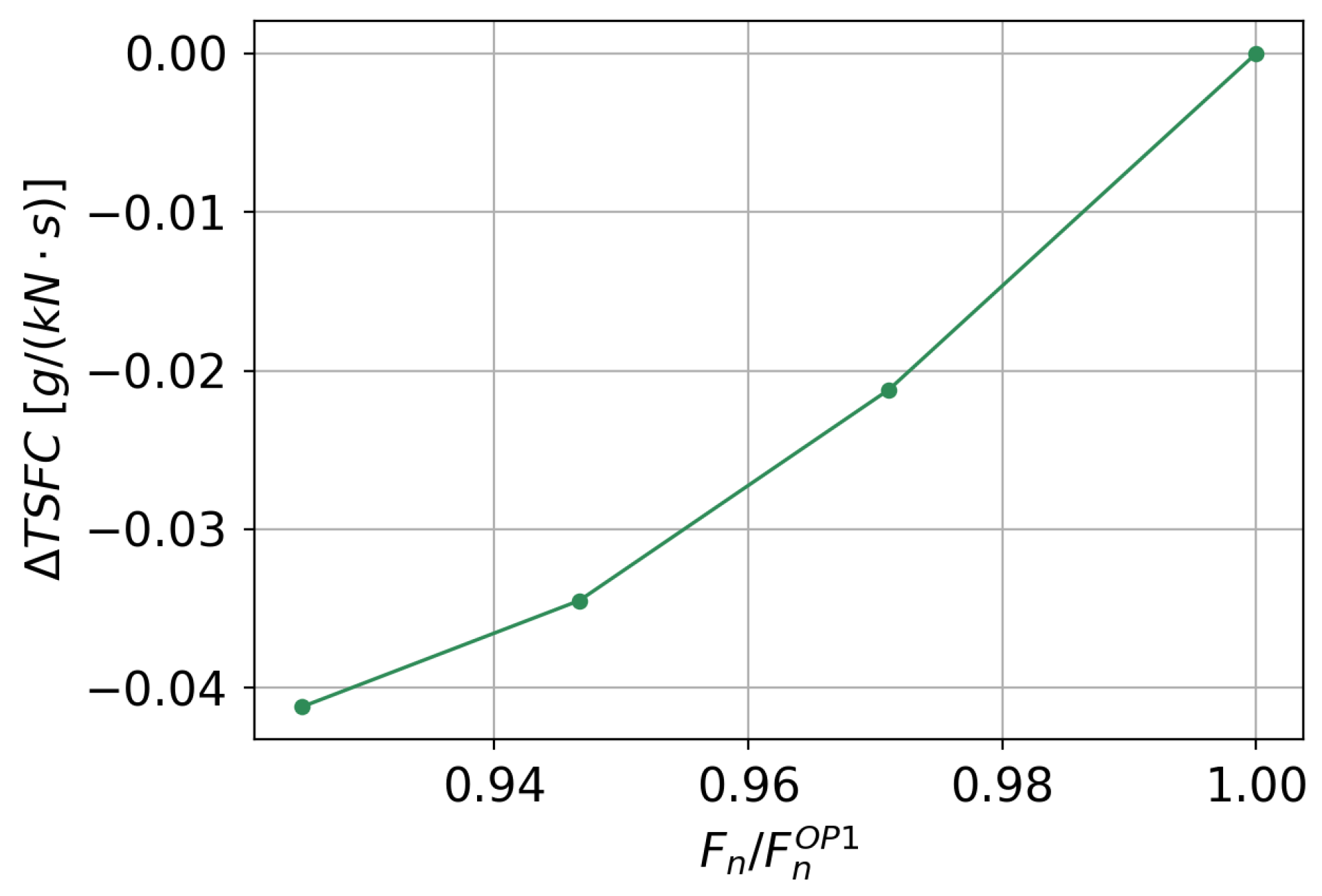
3.2. Integration of the Mission Profile along the Cruise
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| airframe | |
| CFD | Computational Fluid Dynamics |
| Drag coefficient | |
| Lift coefficient | |
| Pressure coefficient | |
| core cowl | |
| core nozzle | |
| Gauge stream force | |
| Net Force | |
| fan nozzle | |
| g | Gravitational acceleration |
| Gross Propulsive Thrust | |
| Intrinsic Net Thrust | |
| intake | |
| Mass flow rate | |
| Fuel mass | |
| M | Mach number |
| Net Propulsive Thrust | |
| Net Vehicle Thrust | |
| nacelle | |
| p | Pressure |
| OP | Operating Point |
| Surface aerodynamic force | |
| pre-entry | |
| Density | |
| RANS | Reynolds-Averaged Navier–Stokes |
| spinner | |
| TSFC | Thrust Specific Fuel Consumption |
| V | Velocity |
| W | Weight |
References
- NLR; SEO Amsterdam Economics. Destination 2050—A Route to Net Zero European Aviation; Report NLR-CR-2020-510; NLR—Royal Netherlands Aerospace Centre: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Epstein, A.H. Aeropropulsion for Commercial Aviation in the Twenty-First Century and Research Directions Needed. AIAA J. 2014, 52, 901–911. [Google Scholar] [CrossRef]
- Borradaile, J. Towards the optimum ducted UHBR engine. In Proceedings of the 24th Joint Propulsion Conference, Boston, MA, USA, 11–13 July 1988. [Google Scholar] [CrossRef]
- Zimbrick, R.A.; Colehour, J.L. Investigation of very high bypass ratio engines for subsonic transports. J. Propuls. Power 1990, 6, 490–496. [Google Scholar] [CrossRef]
- Peacock, N.J.; Sadler, J.H. Advanced propulsion systems for large subsonic transports. J. Propuls. Power 1992, 8, 703–708. [Google Scholar] [CrossRef]
- Hughes, C.E. NASA Collaborative Research on the Ultra High Bypass Engine Cycle and Potential Benefits for Noise, Performance, and Emissions. In Proceedings of the ISABE 2009, Indianapolis, IN, USA, 29 September–1 October 2009. [Google Scholar]
- Daggett, D.L.; Brown, S.T.; Kawai, R.T. Ultra-Efficient Engine Diameter Study; Technical Report NASA/CR-2003-212309; NASA: Washington, DC, USA, 2003. [Google Scholar]
- Guynn, M.; Berton, J.; Fisher, K.; Haller, W.; Tong, M.; Thurman, D. Analysis of Turbofan Design Options for an Advanced Single-Aisle Transport Aircraft. In Proceedings of the 9th AIAA Aviation Technology, Integration, and Operations Conference (ATIO), Hilton Head, SC, USA, 21–23 September 2009. [Google Scholar] [CrossRef] [Green Version]
- Berton, J.J.; Guynn, M.D. Multi-Objective Optimization of a Turbofan for an Advanced, Single-Aisle Transport. J. Aircr. 2011, 48, 1795–1805. [Google Scholar] [CrossRef] [Green Version]
- Guynn, M.D.; Berton, J.J.; Fisher, K.L.; Haller, W.J.; Tong, M.T.; Thurman, D.R. Refined Exploration of Turbofan Design Options for an Advanced Single-Aisle Transport; Technical Report NASA/TM–2011-216883; NASA: Hampton, VA, USA, 2011. [Google Scholar]
- Alexiou, A.; Aretakis, N.; Roumeliotis, I.; Kolias, I.; Mathioudakis, K. Performance modelling of an ultra-high bypass ratio geared turbofan. In Proceedings of the ISABE 2017, Manchester, UK, 3–8 September 2017. [Google Scholar]
- Larsson, L.; Grönstedt, T.; Kyprianidis, K.G. Conceptual Design and Mission Analysis for a Geared Turbofan and an Open Rotor Configuration. In Proceedings of the ASME 2011 Turbo Expo: Turbine Technical Conference and Exposition, Vancouver, BC, USA, 6–10 June 2011. [Google Scholar] [CrossRef]
- Thoma, E.M.; Grönstedt, T.; Zhao, X. Quantifying the Environmental Design Trades for a State-of-the-Art Turbofan Engine. Aerospace 2020, 7, 148. [Google Scholar] [CrossRef]
- ESDU. Drag of Axisymmetric Cowls at Zero Incidence for Subsonic Mach Numbers; Technical Report 81024; ESDU International: London, UK, 1981. [Google Scholar]
- Bijewitz, J.; Seitz, A.; Hornung, M.; Luftfhart Bauhaus, E. Architectural Comparison of Advanced Ultra-High Bypass Ratio Turbofans for Medium to Long Range Application. In Proceedings of the Deutscher Luft-und Raumfhahrtkongress DLR, Augsburg, Germany, 16–18 September 2014; p. 12. [Google Scholar]
- Magrini, A.; Buosi, D.; Benini, E. Analysis of installation aerodynamics and comparison of optimised configuration of an ultra-high bypass ratio turbofan nacelle. Aerosp. Sci. Technol. 2022, 128, 107756. [Google Scholar] [CrossRef]
- Magrini, A.; Benini, E.; Yao, H.D.; Postma, J.; Sheaf, C. A review of installation effects of ultra-high bypass ratio engines. Prog. Aerosp. Sci. 2020, 119, 100680. [Google Scholar] [CrossRef]
- Vassberg, J.; Dehaan, M.; Rivers, M.; Wahls, R. Development of a Common Research Model for Applied CFD Validation Studies. In Proceedings of the 26th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef] [Green Version]
- Vassberg, J.; Tinoco, E.; Mani, M.; Rider, B.; Zickuhr, T.; Levy, D.; Brodersen, O.; Eisfeld, B.; Crippa, S.; Wahls, R.; et al. Summary of the Fourth AIAA CFD Drag Prediction Workshop. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef] [Green Version]
- Levy, D.W.; Laflin, K.R.; Tinoco, E.N.; Vassberg, J.C.; Mani, M.; Rider, B.; Rumsey, C.L.; Wahls, R.A.; Morrison, J.H.; Brodersen, O.P.; et al. Summary of Data from the Fifth Computational Fluid Dynamics Drag Prediction Workshop. J. Aircr. 2014, 51, 1194–1213. [Google Scholar] [CrossRef]
- Tinoco, E.N.; Brodersen, O.P.; Keye, S.; Laflin, K.R.; Feltrop, E.; Vassberg, J.C.; Mani, M.; Rider, B.; Wahls, R.A.; Morrison, J.H.; et al. Summary Data from the Sixth AIAA CFD Drag Prediction Workshop: CRM Cases. J. Aircr. 2018, 55, 1352–1379. [Google Scholar] [CrossRef] [Green Version]
- Kurzke, J.; Halliwell, I. Propulsion and Power; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar] [CrossRef]
- Magrini, A.; Buosi, D.; Benini, E.; Sheaf, C. Ultra-high bypass nacelle geometry design space exploration. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 & 19–21 January 2021. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent 19.2 Theory Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Mavriplis, D.J.; Vassberg, J.C.; Tinoco, E.N.; Mani, M.; Brodersen, O.P.; Eisfeld, B.; Wahls, R.A.; Morrison, J.H.; Zickuhr, T.; Levy, D.; et al. Grid Quality and Resolution Issues from the Drag Prediction Workshop Series. J. Aircr. 2009, 46, 935–950. [Google Scholar] [CrossRef] [Green Version]
- Vassberg, J. A Unified Baseline Grid about the Common Research Model Wing/Body for the Fifth AIAA CFD Drag Prediction Workshop (Invited). In Proceedings of the 29th AIAA Applied Aerodynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef] [Green Version]
- Magrini, A.; Buosi, D.; Benini, E. Maximisation of installed net resulting force through multi-level optimisation of an ultra-high bypass ratio engine nacelle. Aerosp. Sci. Technol. 2021, 119, 107169. [Google Scholar] [CrossRef]
- Ministry-Industry Drag Analysis Panel (MIDAP) Study Group. Guide to In-Flight Thrust Measurement of Turbojets and Fan Engines; AGARD: Neuilly-sur-Seine, France, 1979. [Google Scholar]
- Buosi, D.; Magrini, A.; Benini, E. Installed performance of ultra-high bypass turbofans: Estimation of power saving in optimised configurations at steady flight. In Proceedings of the AIAA Scitech 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Magrini, A.; Benini, E. Aeropropulsive assessment of engine installation at cruise for UHBPR turbofan with body force fan modelling. Aerosp. Sci. Technol. 2023, 132, 108048. [Google Scholar] [CrossRef]
- Balakrishna, S.; Acheson, M. Analysis of NASA Common Research Model Dynamic Data. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef] [Green Version]
- Sebastian, S.; Ralf, R. Experimental assessment of wing lower surface buffet effects induced by the installation of a UHBR nacelle. CEAS Aeronaut. J. 2022. [Google Scholar] [CrossRef]



| Mesh Level | XCoarse | Coarse | Medium | Fine | XFine |
|---|---|---|---|---|---|
| No. of cells [] | 27.0 | 33.8 | 39.1 | 55.2 | 74.8 |
| Grid Factor [] | 1.1111 | 0.9566 | 0.8681 | 0.6898 | 0.5633 |
| Target Wall | 1.15 | 1.09 | 1.03 | 0.98 | 0.93 |
| 0.4999 | 0.4999 | 0.4999 | 0.4998 | 0.4999 | |
| 0.0006 | 0.0005 | 0.0000 | 0.0001 | 0.0000 | |
| 0.6069 | 0.6759 | 1.0138 | 0.9655 | 1.0000 |
| Quantity | OP1 | OP2 | OP3 | OP4 |
|---|---|---|---|---|
| [deg] | 2.260 | 2.146 | 2.025 | 1.962 |
| 0.5008 | 0.4876 | 0.4742 | 0.4627 | |
| [dc] | 0.0 | −35.26 | −41.48 | −47.49 |
| 1.0000 | 0.9711 | 0.9467 | 0.9248 | |
| 3.8947 | 3.8498 | 3.8121 | 3.7783 | |
| 0.8625 | 0.8301 | 0.80258 | 0.7773 | |
| [] | −0.0851 | 0.9432 | −0.6344 | −0.576 |
| [kg] | 3224.05 | 3131.16 | 3052.18 | 2986.68 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magrini, A.; Buosi, D.; Poltronieri, F.; De Leo, E.; Benini, E. CFD-Based Analysis of Installed Fuel Consumption and Aerodynamics of Transonic Transport Aircraft during Cruise Flight. Energies 2023, 16, 3323. https://doi.org/10.3390/en16083323
Magrini A, Buosi D, Poltronieri F, De Leo E, Benini E. CFD-Based Analysis of Installed Fuel Consumption and Aerodynamics of Transonic Transport Aircraft during Cruise Flight. Energies. 2023; 16(8):3323. https://doi.org/10.3390/en16083323
Chicago/Turabian StyleMagrini, Andrea, Denis Buosi, Francesco Poltronieri, Elena De Leo, and Ernesto Benini. 2023. "CFD-Based Analysis of Installed Fuel Consumption and Aerodynamics of Transonic Transport Aircraft during Cruise Flight" Energies 16, no. 8: 3323. https://doi.org/10.3390/en16083323
APA StyleMagrini, A., Buosi, D., Poltronieri, F., De Leo, E., & Benini, E. (2023). CFD-Based Analysis of Installed Fuel Consumption and Aerodynamics of Transonic Transport Aircraft during Cruise Flight. Energies, 16(8), 3323. https://doi.org/10.3390/en16083323










