Integrating Risk Preferences into Game Analysis of Price-Making Retailers in Power Market
Abstract
:1. Introduction
- A game model for price-making retailers is formulated in the electricity retail market while considering the risk caused by uncertain wholesale prices. The MSF of each retailer with risk preference is adopted to describe the elastic and switching behaviors of consumers to the retail prices provided by all retailers.
- The existence and uniqueness of the Nash equilibrium of the proposed model is proved. Then the equilibrium results are derived by the nonlinear complementary approach.
- A theoretical analysis is presented to investigate impacts of wholesale price uncertainty and risk preference on retailer’s bidding strategy. Numerical examples are used to demonstrate the effectiveness of the theoretical analysis.
2. Formulation of Retail Game Model with Risk Preference
2.1. Assumptions
- Considering that the existing electricity markets are all operated as ex ante markets to ensure the security of real-time operation. This paper assumes the proposed retail mechanism to be an hour-ahead market.
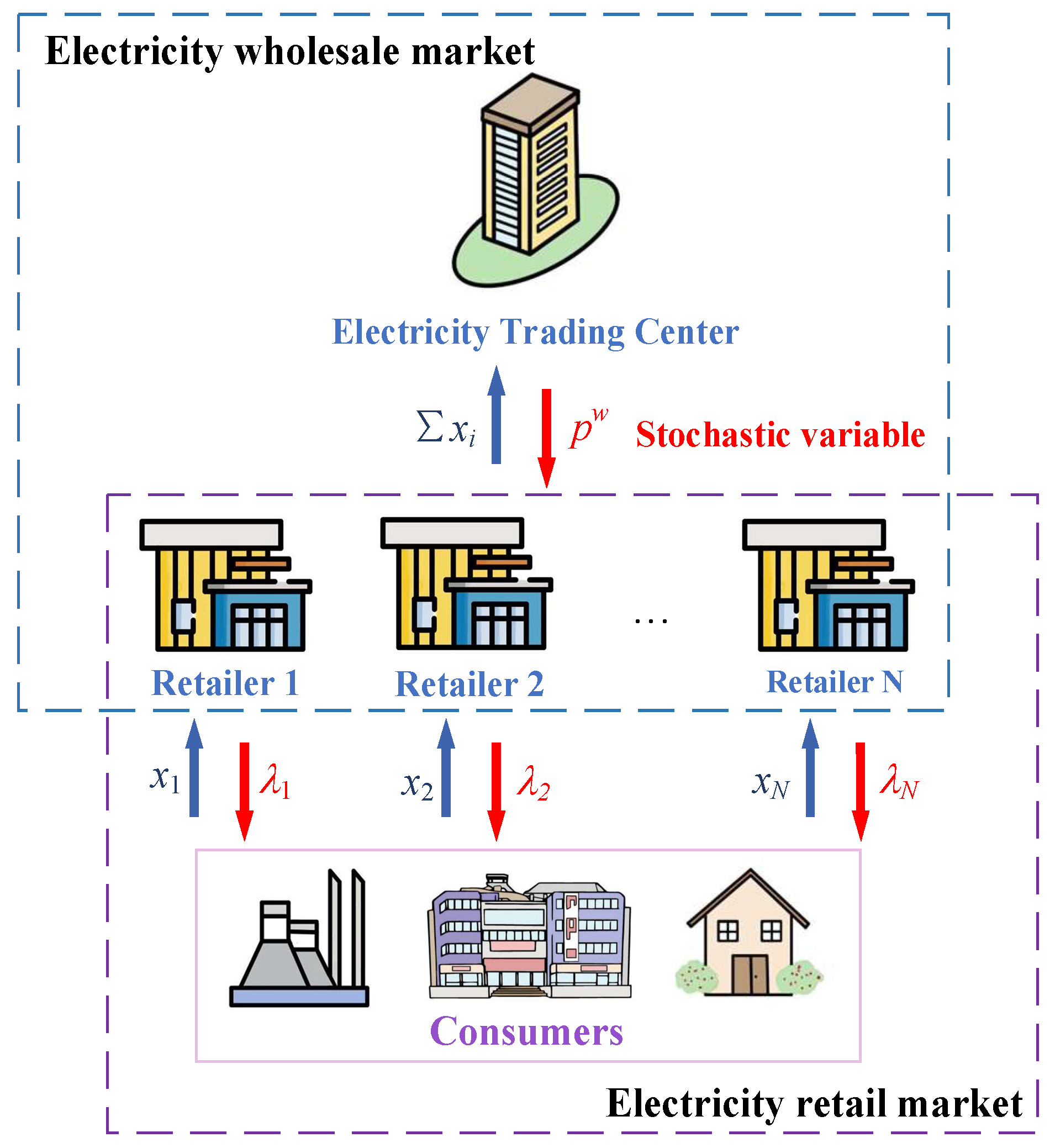
- By utilizing an open information network and smart home technologies in the deregulated electricity market [32], it can be predicted that intelligent consumers will have the ability to switch retailers in real time in the future. Therefore, we consider that multiple price-making retailers participate in the retail market competition, from which consumers will choose and switch their electricity supplies during a single time period (1 h).
- As shown in Figure 1, retailers are intermediaries between the electricity wholesale market and consumers. In the wholesale market, retailers purchase electricity at wholesale price. Because the competition in the wholesale market is unpredictable, the wholesale price is treated as a stochastic variable. In the retail market, retailers sell what they buy to consumers. Through the bidding process, retailers send the retail prices to customers, and the customers should send the load to retailers.
- During the retail bidding process, retailer offers retail bidding price to realize its profit maximization. Once the profile of all retailers’ bidding prices, , is announced, consumers will adjust their demands. Accordingly, the retail load of retailer will change.
- Once retailer retail load is derived, retailer will purchase from the electricity wholesale market at wholesale price, , which is a stochastic parameter, to supply the consumers’ demand.
2.2. Game Model
2.3. Existence and Uniqueness of Nash Equilibrium
- Each retailer’s strategy space is closed, bounded, and convex.
- In regard to the retailer’s strategy of its own, its profit function is continuous and quasi-concave.
2.4. Impacts of the Uncertainty of Wholesale Price Uncertainty and Risk Preference on Retailer’s Bidding Strategy
2.5. Solution Method
3. Numerical Examples
3.1. Impacts of Wholesale Price Uncertainty on Equilibrium Outcomes
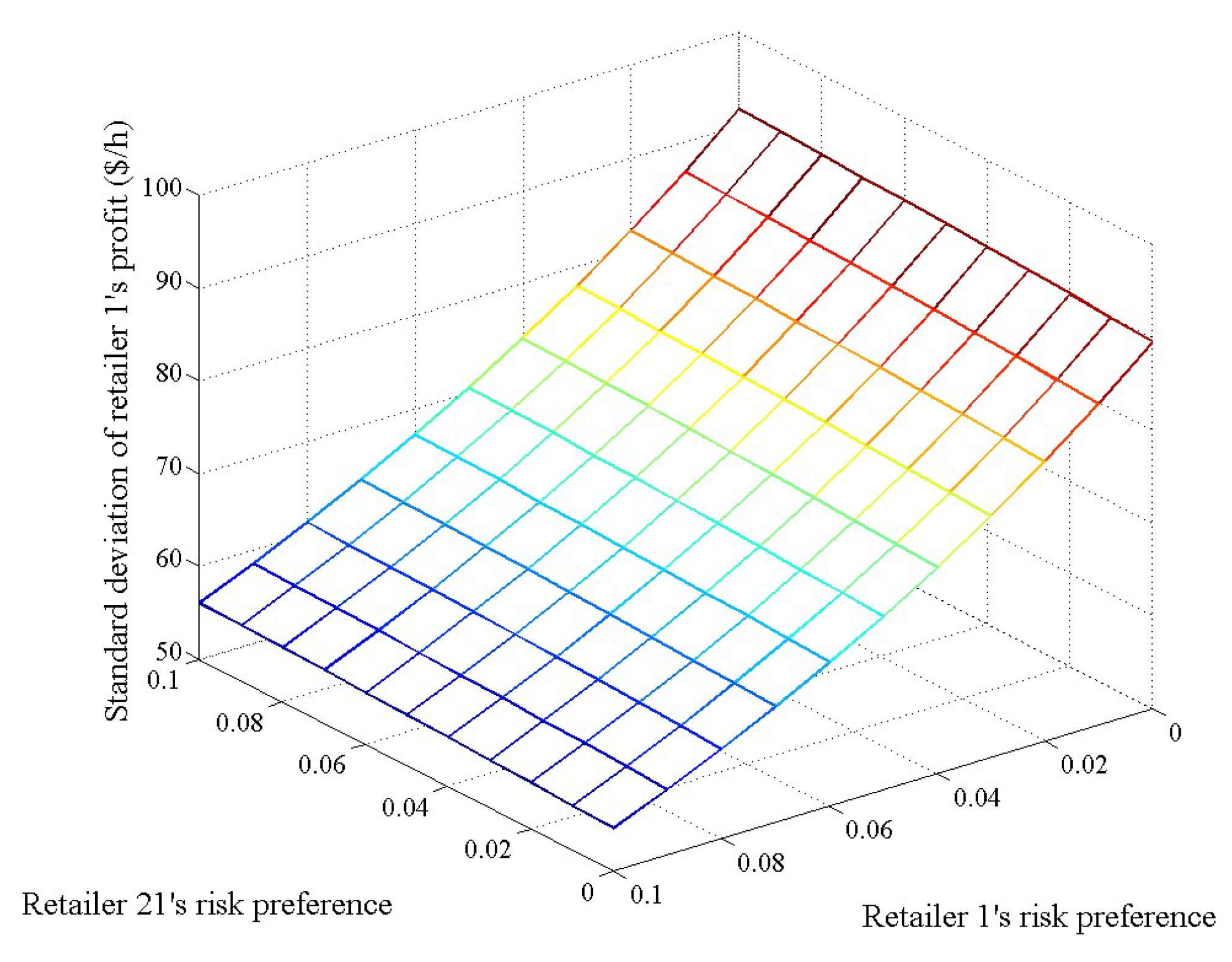
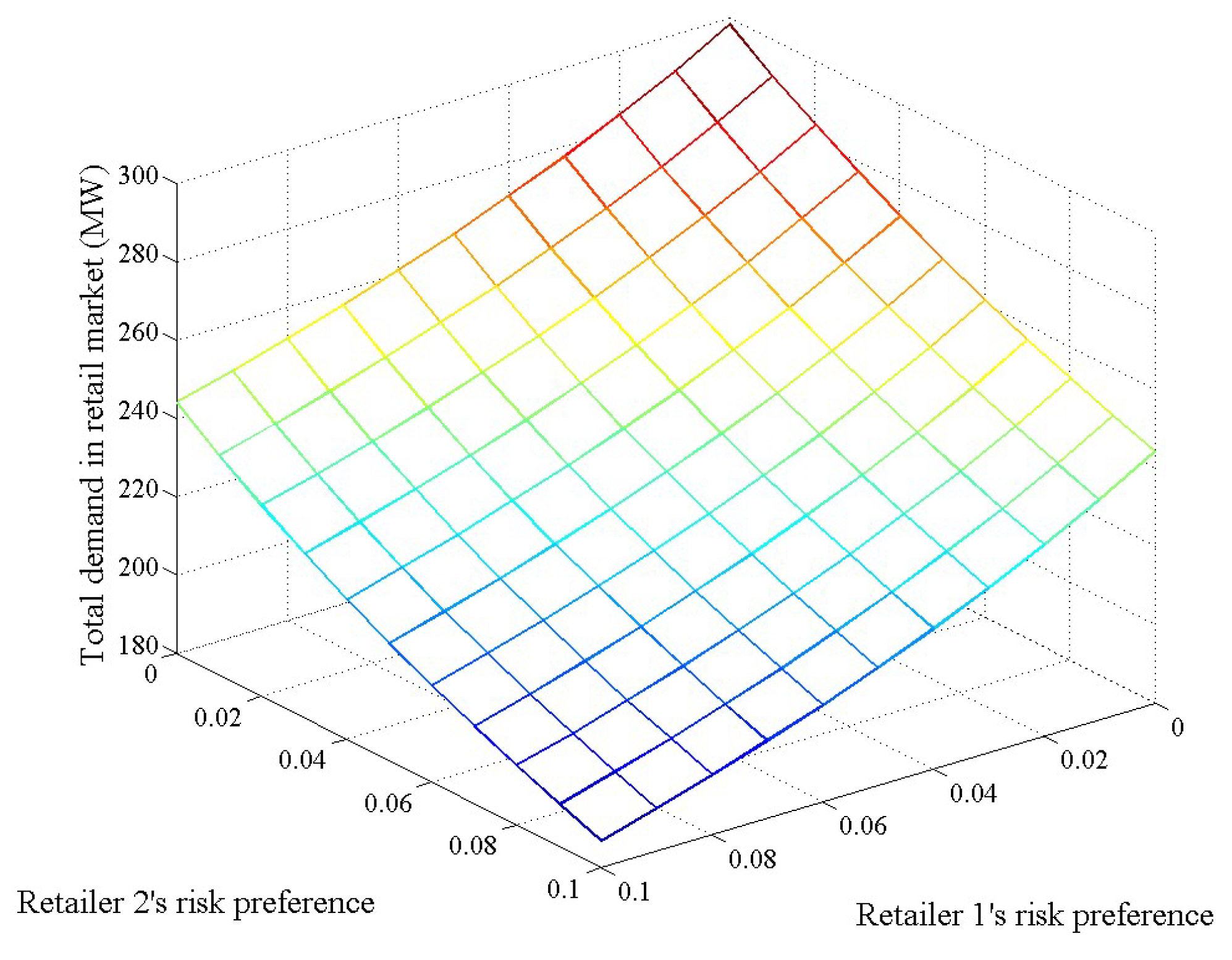
3.2. Impacts of Retailers’ Risk Preferences on Equilibrium Outcomes
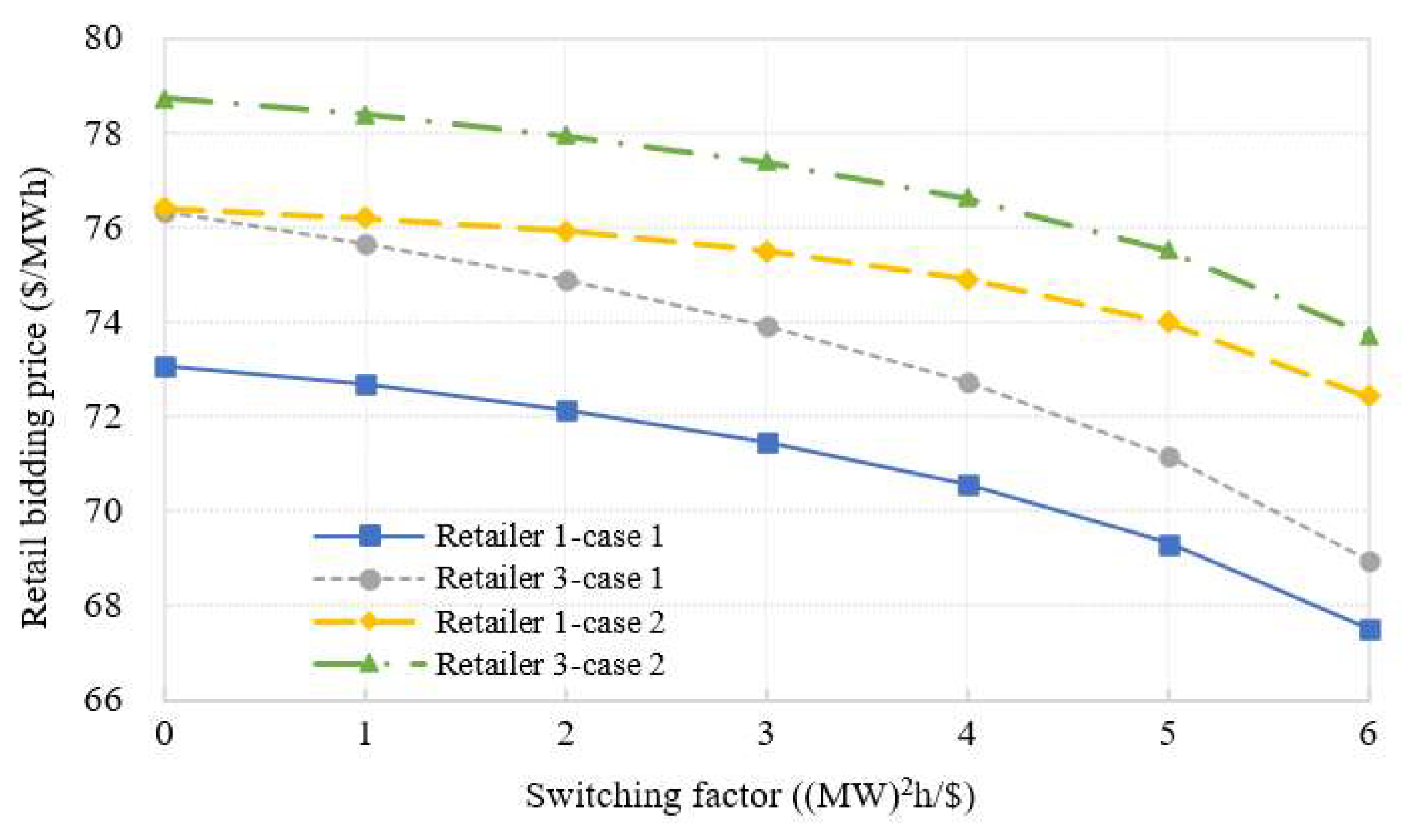
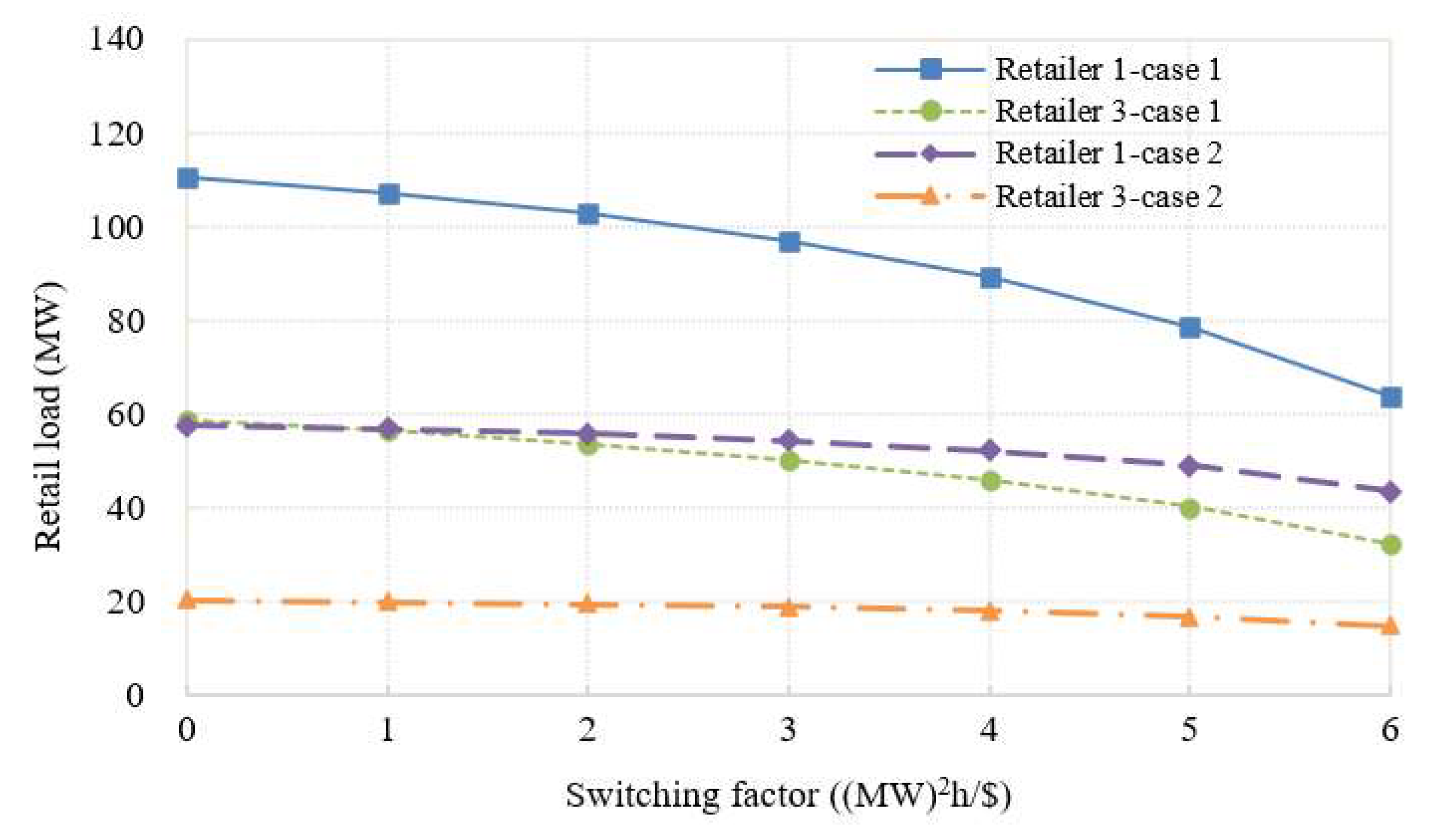
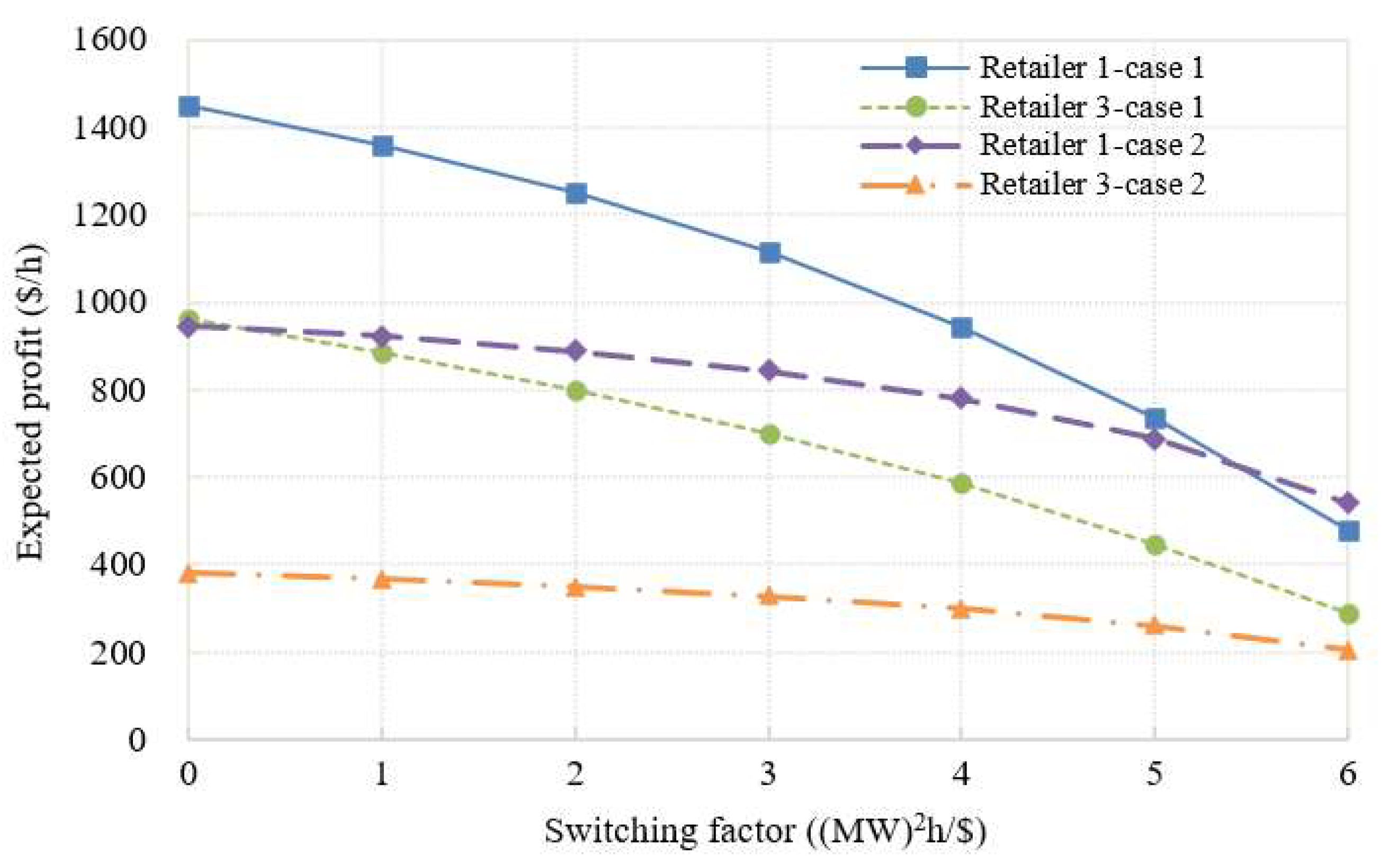
3.3. Impacts of Consumers’ Switching Behavior on Strategic Bidding Behaviors of Retailers with Different Risk-Averse Levels
4. Conclusions
- When risk-averse retailers participate in the retail market competition, every retailer’s bidding price will increase with the increase in the uncertainty of the wholesale price (i.e., a larger standard deviation). The more risk-averse the retailer is, the more obvious this effect will be.
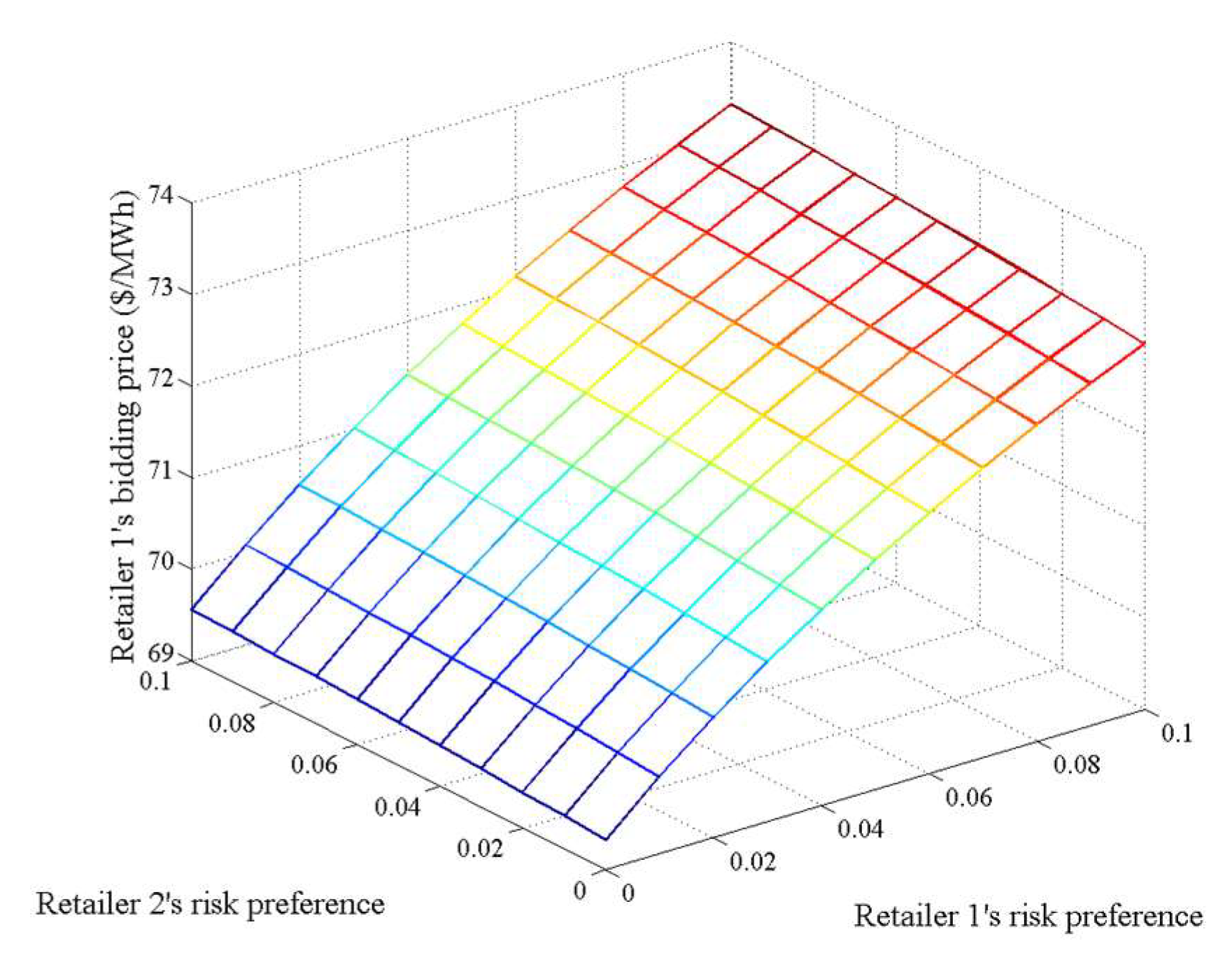
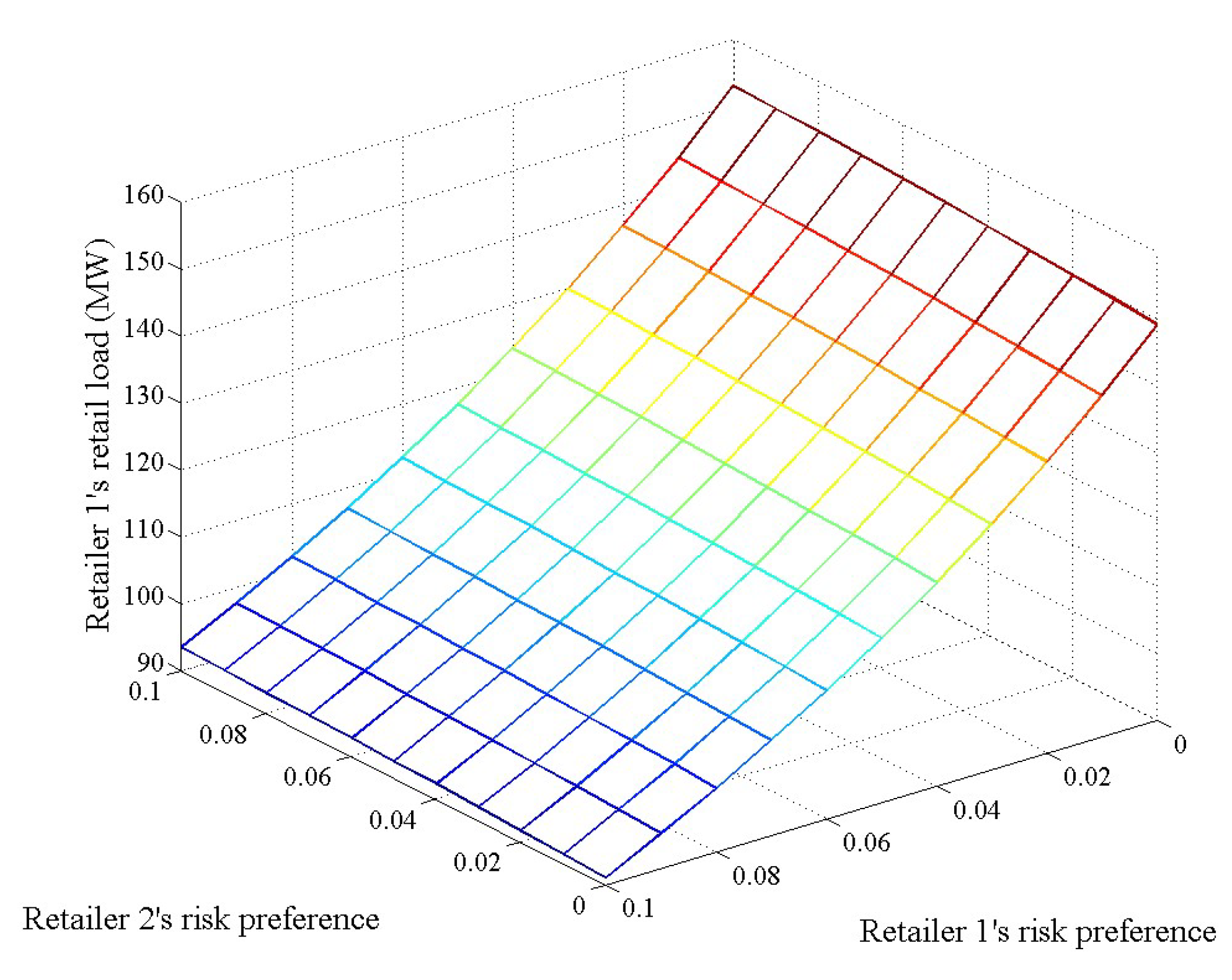
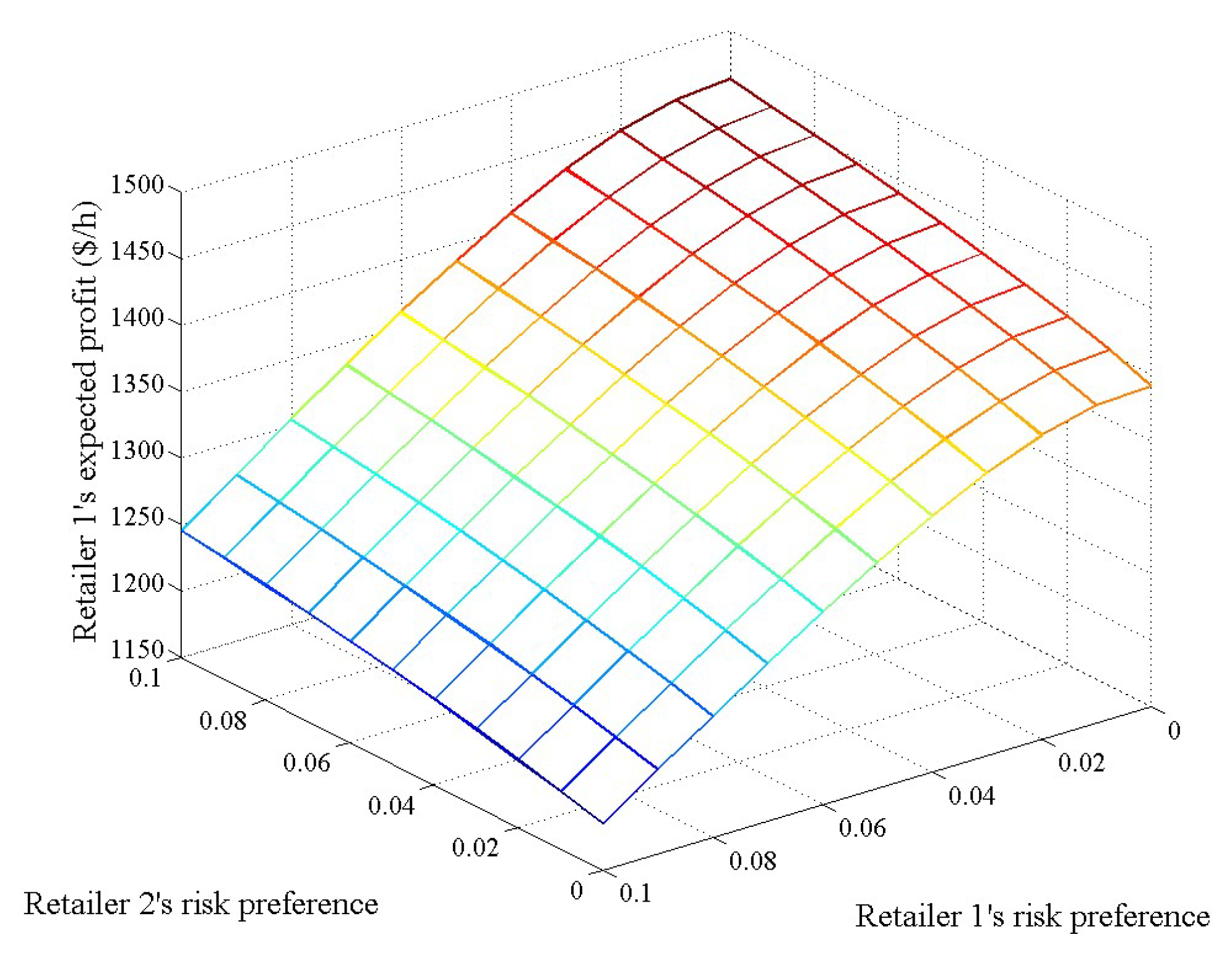
- A retailer will raise its retail bidding price when the risk-averse levels of itself and its rivals increase, and it will be more affected by its own risk-averse level. Meanwhile, a retailer’s expected profit and standard deviation of profit will decrease with the increase in its own risk-averse level and increase with the increase in its rival’s risk-averse level. We also found that a retailer may have a chance to raise its bidding price, occupy a relatively larger market share, and make more profit by exercising market power when the risk-averse level of its rival retailer increases.
- Consumers’ switching behavior can help mitigate the strategic behaviors of retailers and lower the retail prices. Moreover, the more risk-averse the retailers are, the more obvious the mitigative effect of consumers’ switching behavior on their strategic behaviors will be. Moreover, in the case of a relatively lower uncertainty level of the wholesale price, consumers’ switching behavior may have a better mitigative effect on the market power of risk-averse retailers.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Indices and sets | |
| i, j | Index of retailer in the retail market, i, j ∈ I |
| I | Set of retailers |
| λ | Set of retail prices |
| x | Set of retail loads |
| Parameters | |
| N | Number of retailers |
| mw | Mean value of wholesale price |
| sw | Standard deviation |
| b i | Consumers’ demand elasticity to retailer i |
| b i, j | Switching factor |
| ai | Potential market size of retailer i |
| ri | Risk preference of retailer i |
| Lower bound of retailer i’s bidding price | |
| Upper bound of retailer i’s bidding price | |
| Variables | |
| Bidding price of retailer i | |
| Retail load of retailer i | |
| Wholesale price in electricity wholesale market | |
| Utility of retailer i | |
| Dual variable related to lower bounds of retailer i’s bidding price | |
| Dual variable related to upper bounds of retailer i’s bidding price | |
References
- Bao, M.; Ding, Y.; Zhou, X.; Guo, C.; Shao, C. Risk assessment and management of electricity markets: A review with suggestions. CSEE J. Power Energy Syst. 2021, 7, 1322–1333. [Google Scholar]
- Fatras, N.; Ma, Z.; Duan, H.; Jørgensen, B.N. A systematic review of electricity market liberalisation and its alignment with industrial consumer participation: A comparison between the Nordics and China. Renew. Sustain. Energy Rev. 2022, 167, 112793. [Google Scholar] [CrossRef]
- Tsai, C.; Tsai, Y. Competitive retail electricity market under continuous price regulation. Energy Policy 2018, 114, 274–287. [Google Scholar] [CrossRef]
- Zare, K.; Nojavan, S.; Mohammadi-Ivatloo, B. Optimal bidding strategy of electricity retailers using robust optimisation approach considering time-of-use rate demand response programs under market price uncertainties. IET Gener. Transm. Distrib. 2015, 9, 328–338. [Google Scholar]
- He, J.; Cai, L.; Cheng, P.; Fan, J. Optimal investment for retail company in electricity market. IEEE Trans. Ind. Inform. 2015, 11, 1210–1219. [Google Scholar] [CrossRef]
- Mohammad, N.; Mishra, Y. Retailer’s risk-aware trading framework with demand response aggregators in short-term electricity markets. IET Gener. Transm. Distrib. 2019, 13, 2611–2618. [Google Scholar] [CrossRef]
- Woo, C.K.; Zarnikau, J.; Tishler, A.; Cao, K.H. Insuring a small retail electric provider’s procurement cost risk in texas. Energies 2023, 16, 393. [Google Scholar] [CrossRef]
- Boroumand, R.H. Electricity markets and oligopolistic behaviours: The impact of a multimarket structure. Res. Int. Bus. Financ. 2015, 33, 319–333. [Google Scholar] [CrossRef]
- Hampton, H.; Foley, A.; Del Rio, D.F.; Smyth, B.; Laverty, D.; Caulfield, B. Customer engagement strategies in retail electricity markets: A comprehensive and comparative review. Electr. Power Syst. Res. 2022, 90, 102611. [Google Scholar] [CrossRef]
- Yu, C.W.; Zhang, S.H.; Wang, X.; Chung, T.S. Modeling and analysis of strategic forward contracting in transmission constrained power markets. Electr. Power Syst. Res. 2010, 80, 354–361. [Google Scholar] [CrossRef]
- Li, G.; Shi, J.; Qu, X. Modeling methods for GenCo bidding strategy optimization in the liberalized electricity spot market—A state-of-the-art review. Energy 2011, 36, 4686–4700. [Google Scholar] [CrossRef]
- Wang, X.; Li, Y.; Zhang, S. Oligopolistic equilibrium analysis for electricity market: A nonlinear complementary approach. IEEE Trans. Power Syst. 2004, 19, 1348–1355. [Google Scholar]
- Yang, J.; Zhao, J.; Luo, F.; Wen, F.; Dong, Z.Y. Decision-making for electricity retailers: A brief survey. IEEE Trans. Smart Grid 2018, 9, 4140–4153. [Google Scholar] [CrossRef]
- Hao, X.; Kang, M.; Ying, Q.; Li, Y.; Liu, Y.; Hua, Y. Risk optimization of electricity retailer’s revenue considering user utility. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 20–23 September 2020; pp. 1–5. [Google Scholar]
- Hao, Q.; Wang, S.; Zheng, J.; Zhong, X.; Zhang, J.; Xiao, C.; Zhang, C. Research on revenue risk of electricity retailers considering demand response. In Proceedings of the 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27–29 May 2022; pp. 2950–2955. [Google Scholar]
- Jiang, X.; Li, Y.; Yu, S.; Lin, Z.; Ji, C.; Zhang, Z. Power purchasing optimization of electricity retailers considering load uncertainties based on information gap decision theory. Energy Rep. 2022, 8, 693–700. [Google Scholar] [CrossRef]
- Algarvio, H.; Lopes, F. Agent-based retail competition and portfolio optimization in liberalized electricity markets: A study involving real-world consumers. Int. J. Electr. Power Energy Syst. 2022, 137, 107687. [Google Scholar] [CrossRef]
- Iria, J.; Soares, F.; Matos, M. Optimal bidding strategy for an aggregator of prosumers in energy and secondary reserve markets. Appl. Energy 2019, 238, 1361–1372. [Google Scholar] [CrossRef]
- Wang, H.; Riaz, S.; Mancarella, P. Integrated techno-economic modeling, flexibility analysis, and business case assessment of an urban virtual power plant with multi-market co-optimization. Appl. Energy 2020, 259, 114142.1–114142.17. [Google Scholar] [CrossRef]
- Liang, Z.; Su, W. Game theory based bidding strategy for prosumers in a distribution system with a retail electricity market. IET Smart Grid 2018, 1, 104–111. [Google Scholar] [CrossRef]
- Zhao, C.; Zhang, S.; Wang, X.; Li, X.; Wu, L. Game analysis of electricity retail market considering customers’ switching behaviour and retailers’ contract trading. IEEE Access 2018, 6, 75099–75109. [Google Scholar] [CrossRef]
- Kharrati, S.; Kazemi, M.; Ehsan, M. Equilibria in the competitive retail electricity market considering uncertainty and risk management. Energy 2016, 106, 315–328. [Google Scholar] [CrossRef]
- Kang, X.; Wang, X.; Zhang, S. Risk modeling in strategic behaviour and equilibrium of electricity markets with wind power. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 25–28 March 2011; pp. 25–28. [Google Scholar]
- Zou, P.; Chen, Q.; Xia, Q.; He, G.; Kang, C.; Conejo, A.J. Pool equilibria including strategic storage. Appl. Energy 2016, 177, 260–270. [Google Scholar] [CrossRef]
- Dai, T.; Qiao, W. Finding equilibria in the pool-based electricity market with strategic wind power producers and network constraints. IEEE Trans. Power Syst. 2016, 32, 389–399. [Google Scholar] [CrossRef]
- Guo, H.; Chen, Q.; Xia, Q.; Kang, C. Electricity wholesale market equilibrium analysis integrating individual risk-averse features of generation companies. Appl. Energy 2019, 252, 113443. [Google Scholar] [CrossRef]
- Xiao, D.; Chen, H.; Wei, C.; Bai, X. Statistical measure for risk-seeking stochastic wind power offering strategies in electricity markets. J. Mod. Power Syst. Clean Energy 2022, 10, 1437–1442. [Google Scholar] [CrossRef]
- Gazijahani, F.S.; Salehi, J. IGDT-Based complementarity approach for dealing with strategic decision making of price-maker VPP considering demand flexibility. IEEE Trans. Ind. Inform. 2020, 16, 2212–2220. [Google Scholar] [CrossRef]
- Liu, M.; Wu, F.F. Managing price risk in a multimarket environment. IEEE Trans. Power Syst. 2006, 21, 1512–1519. [Google Scholar] [CrossRef]
- Song, M.; Amelin, M. Price-maker bidding in day-ahead electricity market for a retailer with flexible demands. IEEE Trans. Power Syst. 2018, 33, 1948–1958. [Google Scholar] [CrossRef]
- Monfared, H.J.; Ghasemi, A. Retail electricity pricing based on the value of electricity for consumers. Sustain. Energy Grids Netw. 2019, 18, 100205. [Google Scholar] [CrossRef]
- D’hulst, R.; Labeeuw, W.; Beusen, B.; Claessens, S.; Deconinck, G.; Vanthournout, K. Demand response flexibility and flexibility potential of residential smart appliances: Experiences from large pilot test in Belgium. Appl. Energy 2015, 155, 79–90. [Google Scholar] [CrossRef]
- Hatami, A.; Seifi, H.; Sheikheleslami, M.K. A stochastic-based decision-making framework for an electricity retailer: Time-of-use pricing and electricity portfolio optimization. IEEE Trans. Power Syst. 2011, 26, 1808–1816. [Google Scholar] [CrossRef]
- Lus, B.; Muriel, A. Measuring the impact of increased product substitution on pricing and capacity decisions under linear demand models. Prod. Oper. Manag. 2009, 18, 95–113. [Google Scholar] [CrossRef]
- Guan, X.; Wu, J.; Gao, F.; Sun, G. Optimization-based generation asset allocation for forward and spot markets. IEEE Trans. Power Syst. 2008, 23, 1795–1808. [Google Scholar] [CrossRef]
- Cachon, G.P.; Netessine, S. Game theory in supply chain analysis. Int. Ser. Oper. Res. Manag. Sci. 2005, 74, 13–65. [Google Scholar]
- Ye, Y.; Papadaskalopoulos, D.; Moreira, R.; Strbac, G. Investigating the impacts of price-taking and price-making energy storage in electricity markets through an equilibrium programming model. IET Gener. Transm. Distrib. 2019, 13, 305–315. [Google Scholar] [CrossRef]

| Equilibrium Outcomes | = 0.2 | = 0.4 | = 0.6 |
|---|---|---|---|
| ($/MWh) | 69.68 | 70.59 | 71.80 |
| (MW) | 145.09 | 133.51 | 117.55 |
| (103 $/h) | 1.404 | 1.414 | 1.387 |
| ($/h) | 29.02 | 53.40 | 70.53 |
| ($/MWh) | 69.98 | 71.50 | 73.19 |
| (MW) | 139.74 | 117.24 | 92.56 |
| (103 $/h) | 1.394 | 1.348 | 1.221 |
| ($/h) | 27.95 | 46.90 | 55.54 |
| Total demand (MW) | 284.83 | 250.75 | 210.11 |
| Retailer | ($/MWh) | ((MW)2 h/$) |
|---|---|---|
| 1 | 80 | 20 |
| 2 | 90 | 18 |
| 3 | 100 | 17 |
| r3 | Retailer | ($/MWh) | (MW) | (103$/h) | ($/h) |
|---|---|---|---|---|---|
| 0 | 1 | 68.07 | 161.44 | 1.303 | 96.86 |
| 2 | 73.13 | 236.38 | 3.104 | 141.83 | |
| 3 | 78.31 | 311.20 | 5.695 | 186.72 | |
| 0.05 | 1 | 68.31 | 166.20 | 1.381 | 99.72 |
| 2 | 73.40 | 241.11 | 3.230 | 144.67 | |
| 3 | 82.80 | 235.76 | 5.376 | 141.46 | |
| 0.10 | 1 | 68.47 | 169.35 | 1.434 | 101.61 |
| 2 | 73.57 | 244.25 | 3.314 | 146.55 | |
| 3 | 85.78 | 185.78 | 4.789 | 111.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, C.; Sun, J.; He, P.; Zhang, S.; Ji, Y. Integrating Risk Preferences into Game Analysis of Price-Making Retailers in Power Market. Energies 2023, 16, 3339. https://doi.org/10.3390/en16083339
Zhao C, Sun J, He P, Zhang S, Ji Y. Integrating Risk Preferences into Game Analysis of Price-Making Retailers in Power Market. Energies. 2023; 16(8):3339. https://doi.org/10.3390/en16083339
Chicago/Turabian StyleZhao, Chen, Jiaqi Sun, Ping He, Shaohua Zhang, and Yuqi Ji. 2023. "Integrating Risk Preferences into Game Analysis of Price-Making Retailers in Power Market" Energies 16, no. 8: 3339. https://doi.org/10.3390/en16083339
APA StyleZhao, C., Sun, J., He, P., Zhang, S., & Ji, Y. (2023). Integrating Risk Preferences into Game Analysis of Price-Making Retailers in Power Market. Energies, 16(8), 3339. https://doi.org/10.3390/en16083339






