One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation
Abstract
1. Introduction
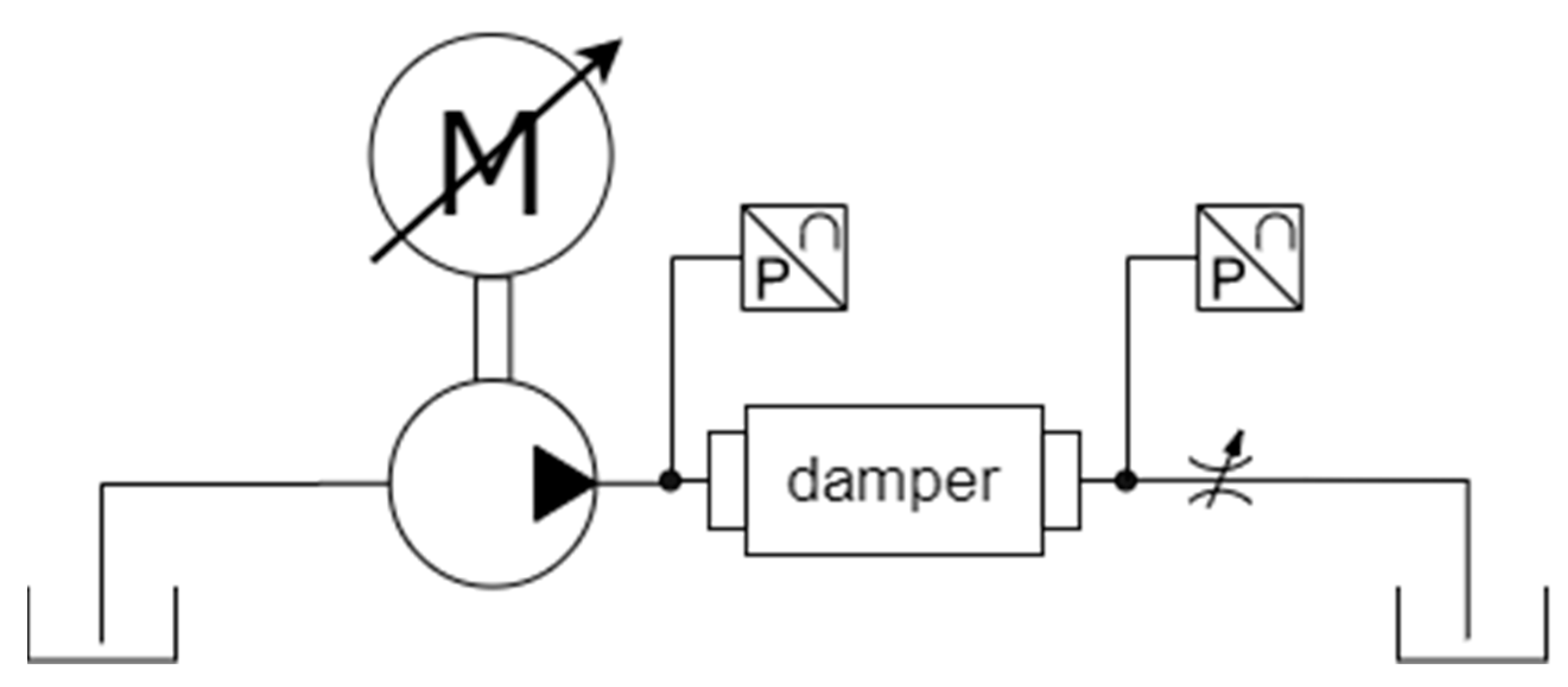
2. Experimental Setup for Damper Testing
2.1. In-Line Bladder Damper Description
2.2. Experimental Activity
3. Mathematical Model
3.1. One-Dimensional Fluid Dynamic Model
3.2. Unsteady Friction Losses
3.3. Numerical Scheme
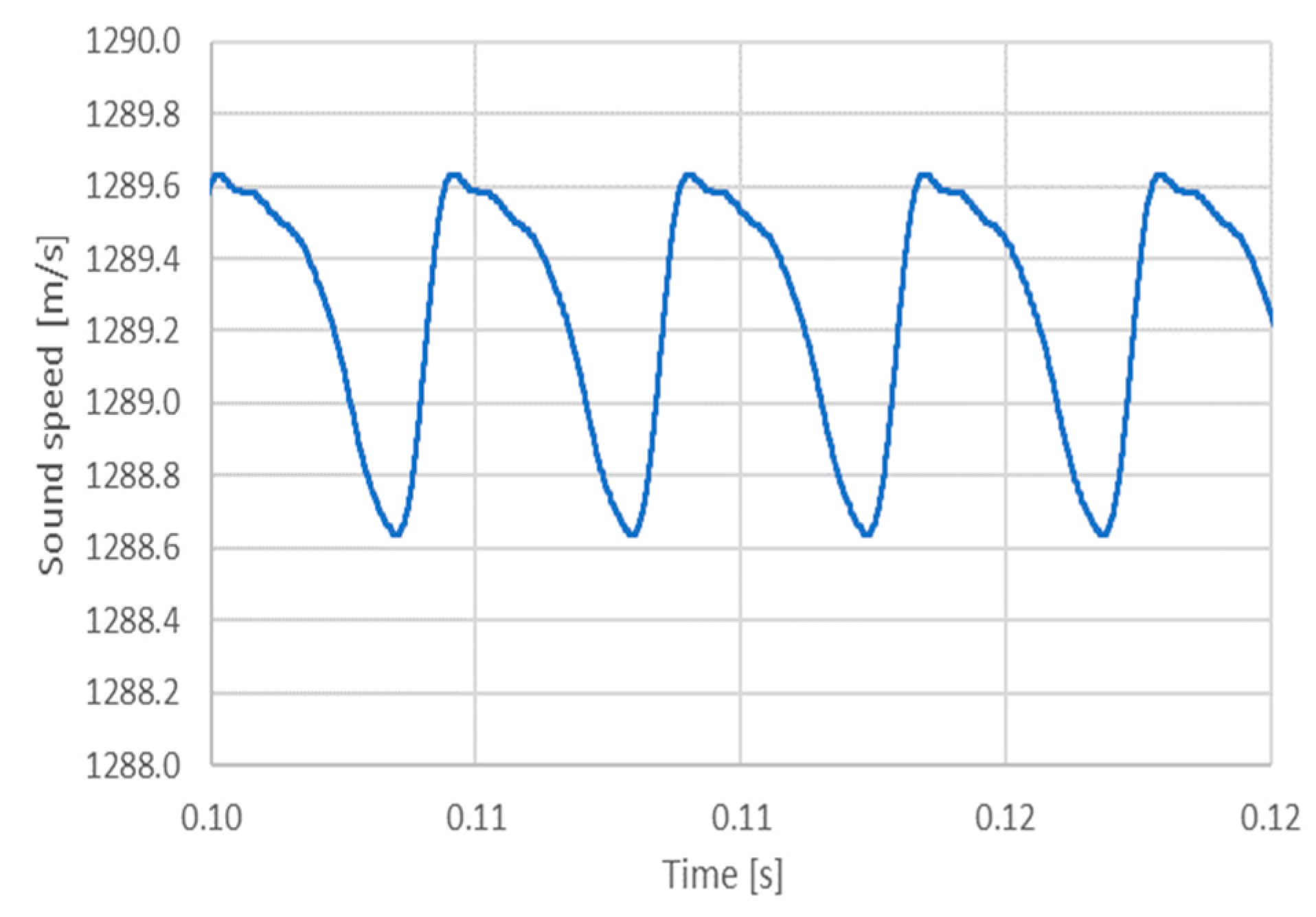
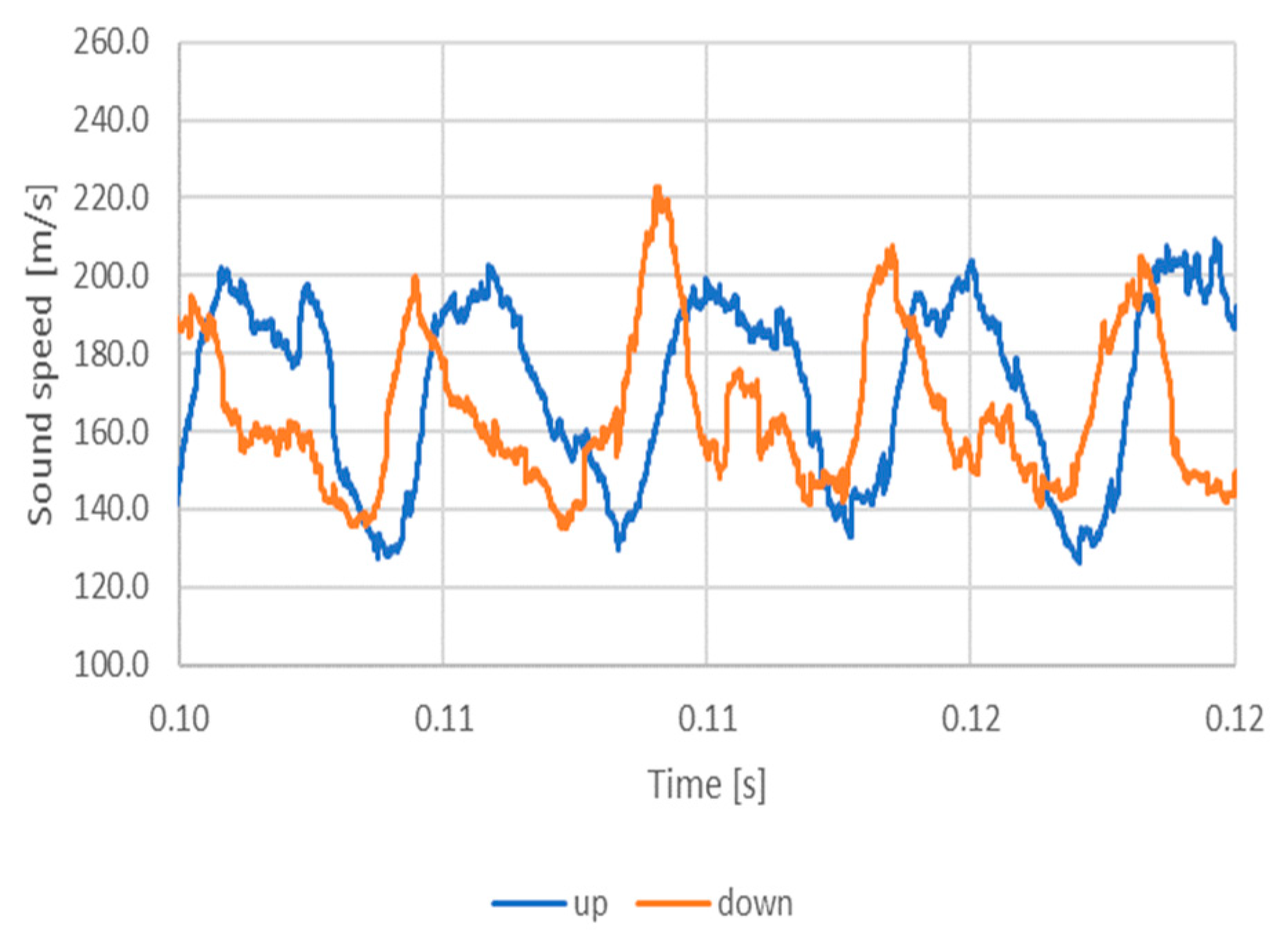
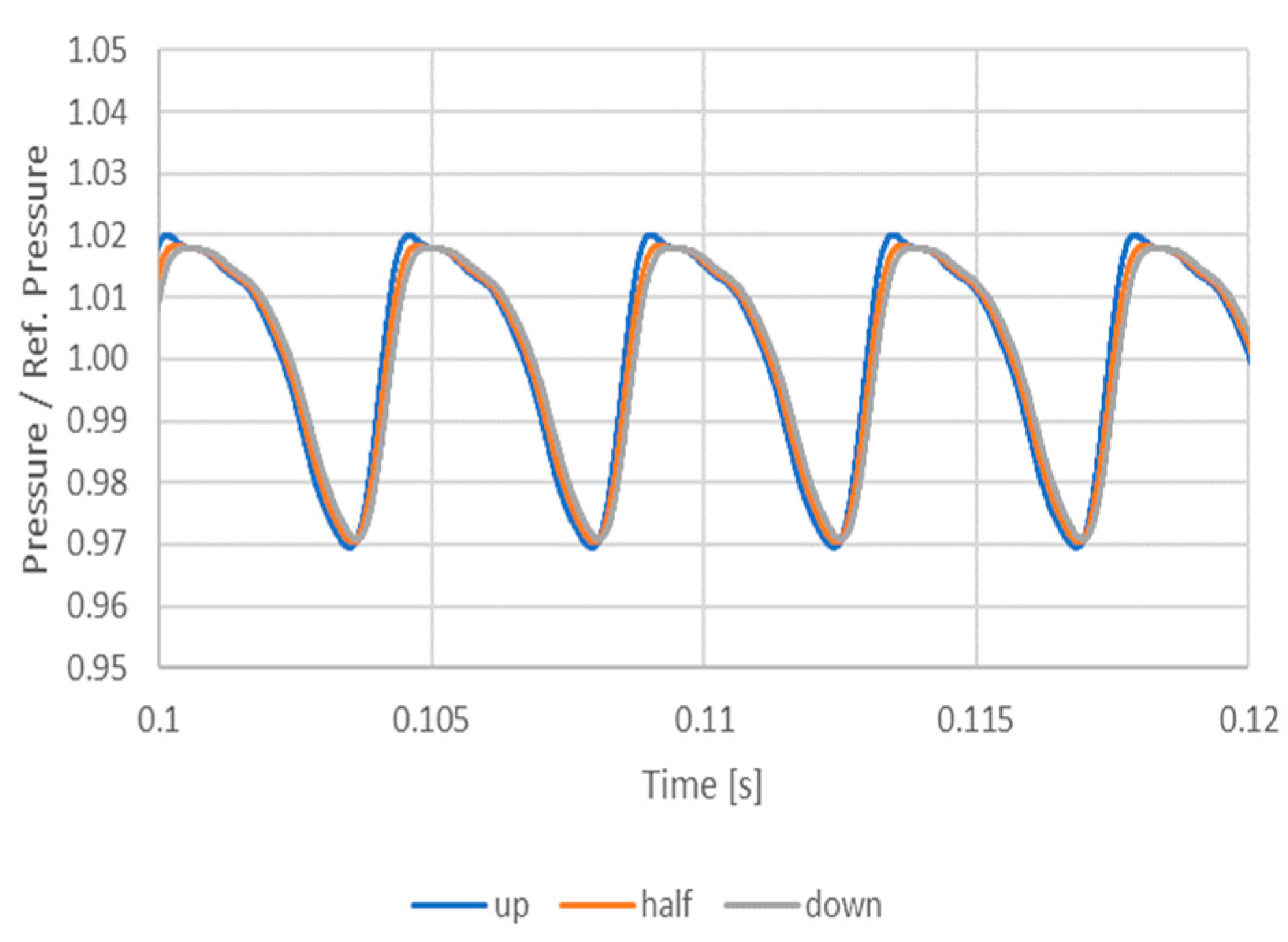
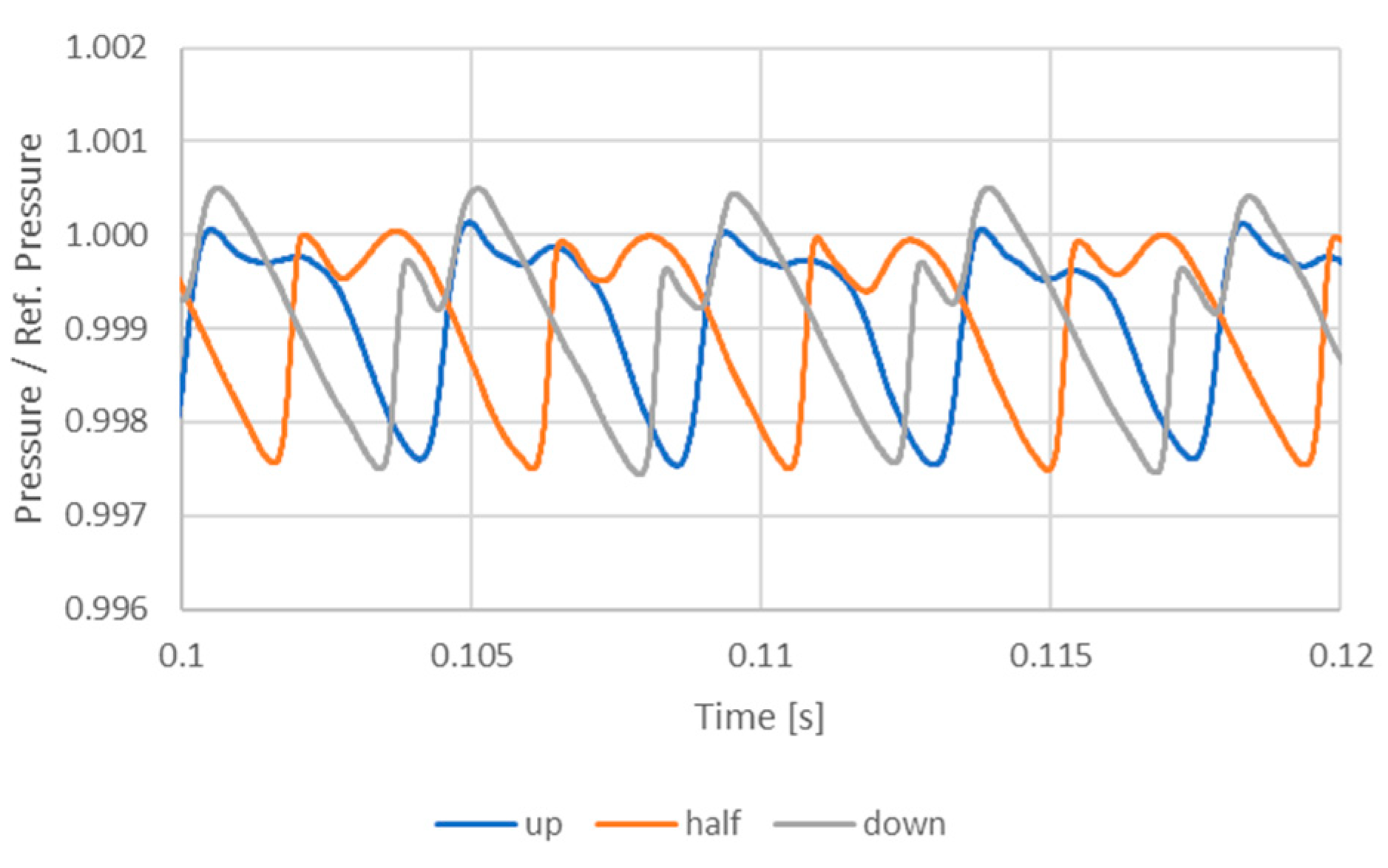
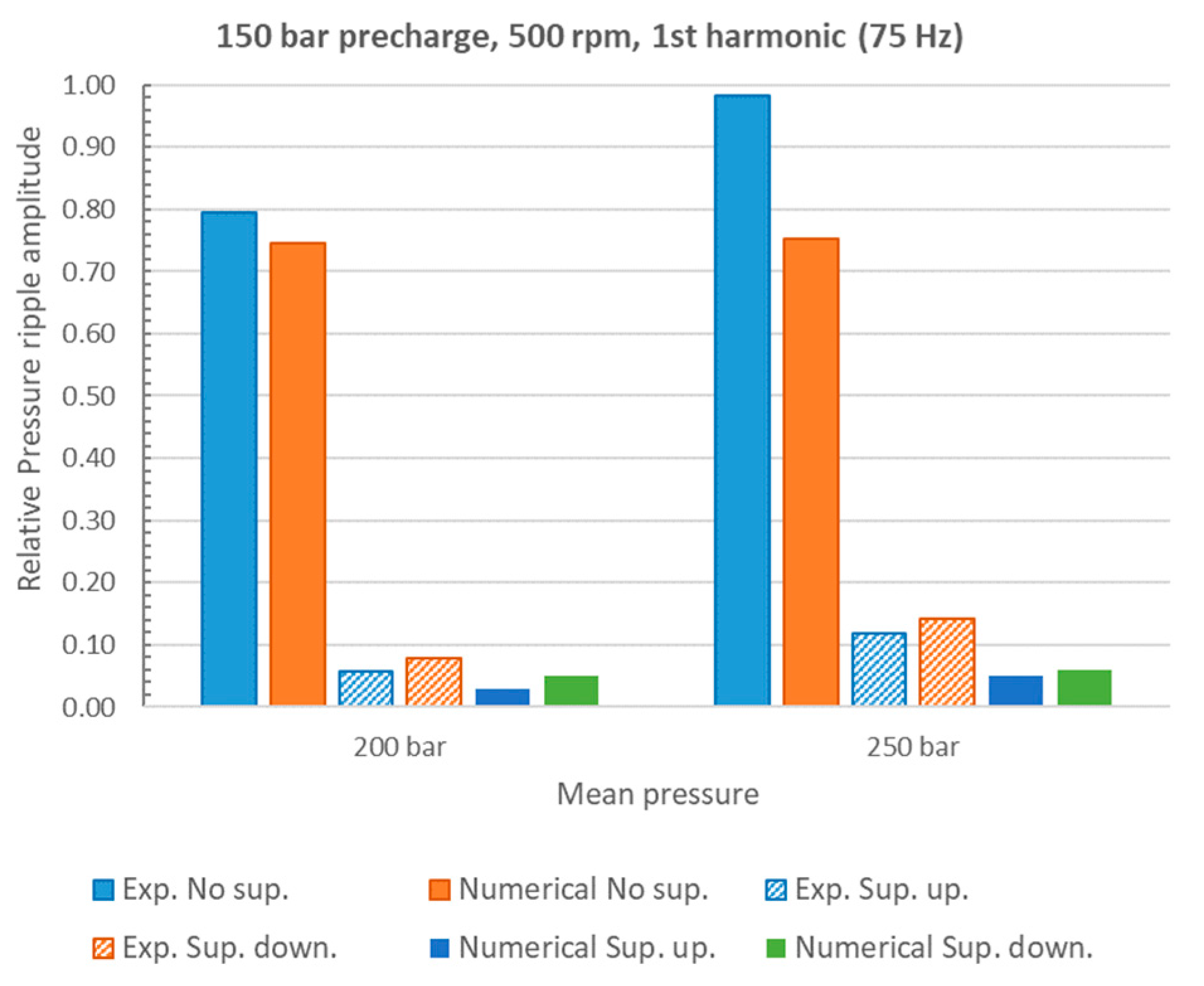
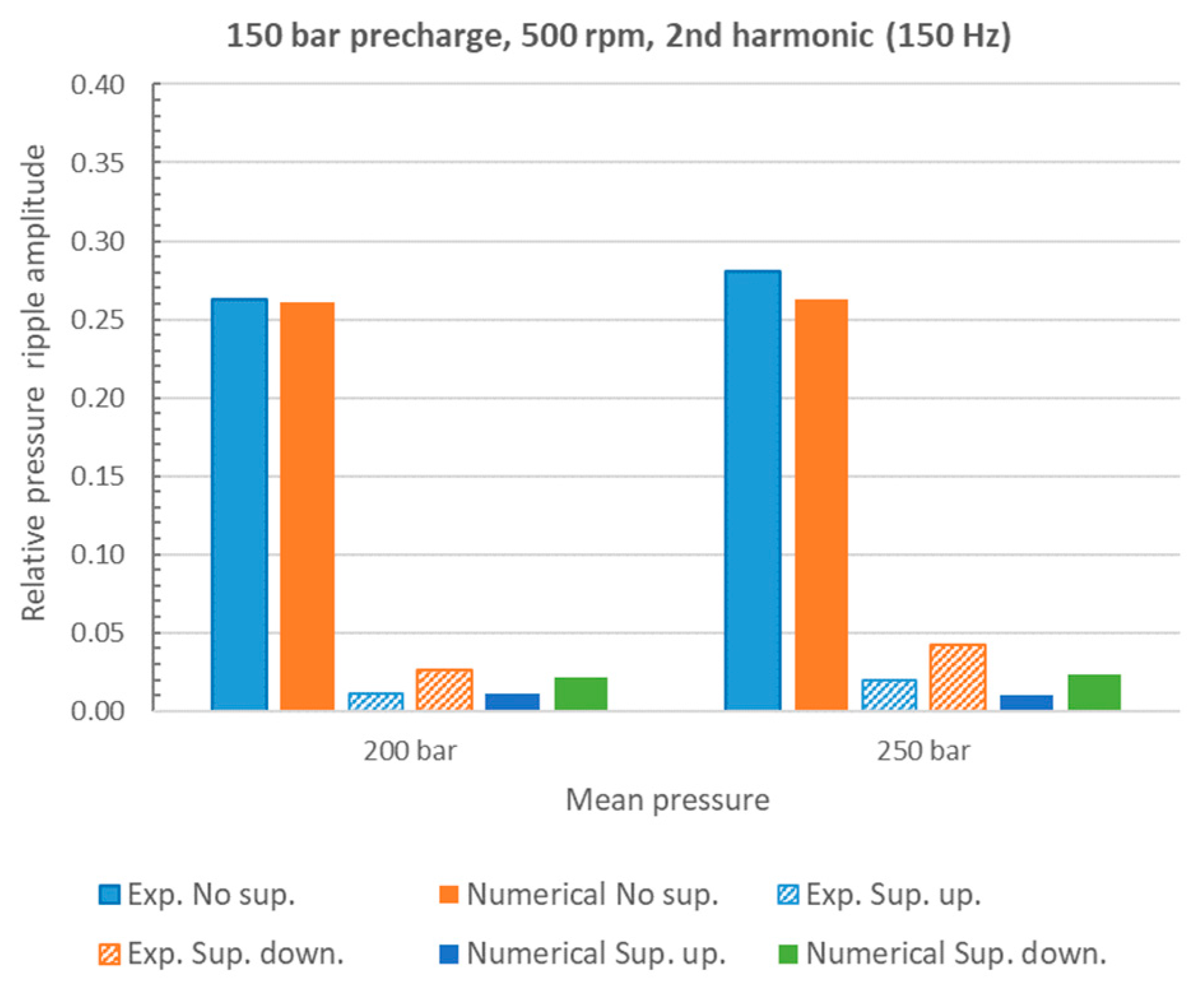
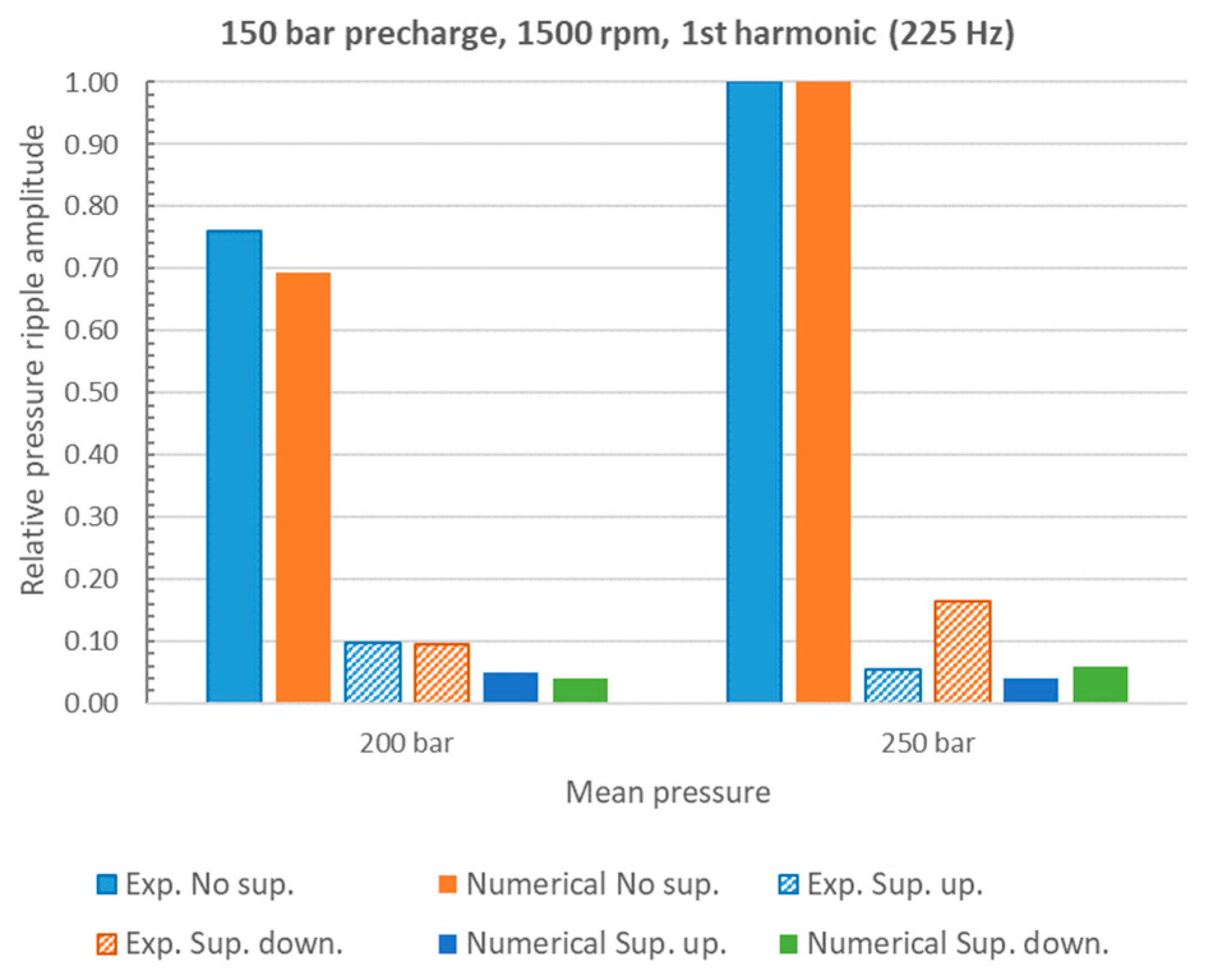
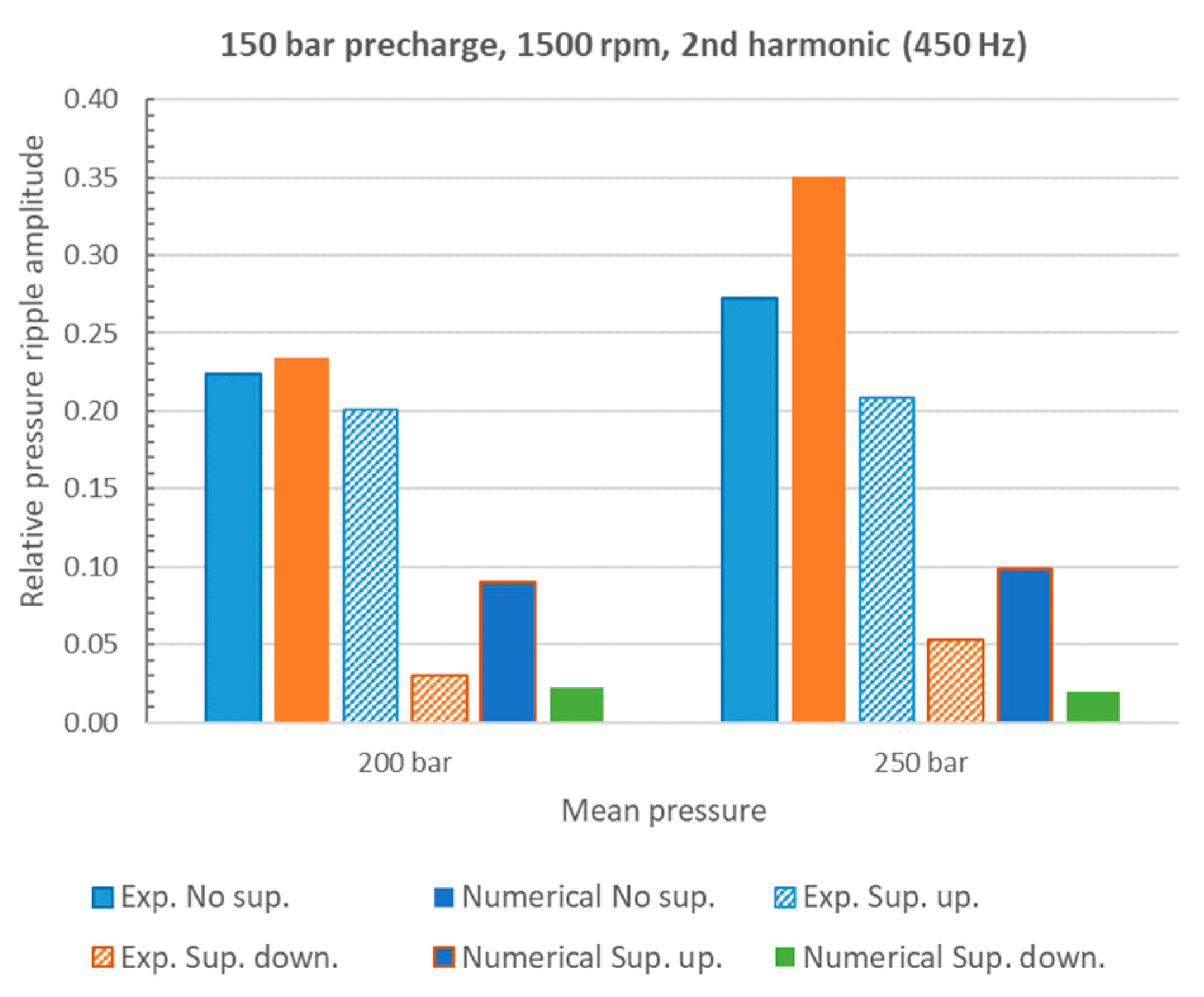
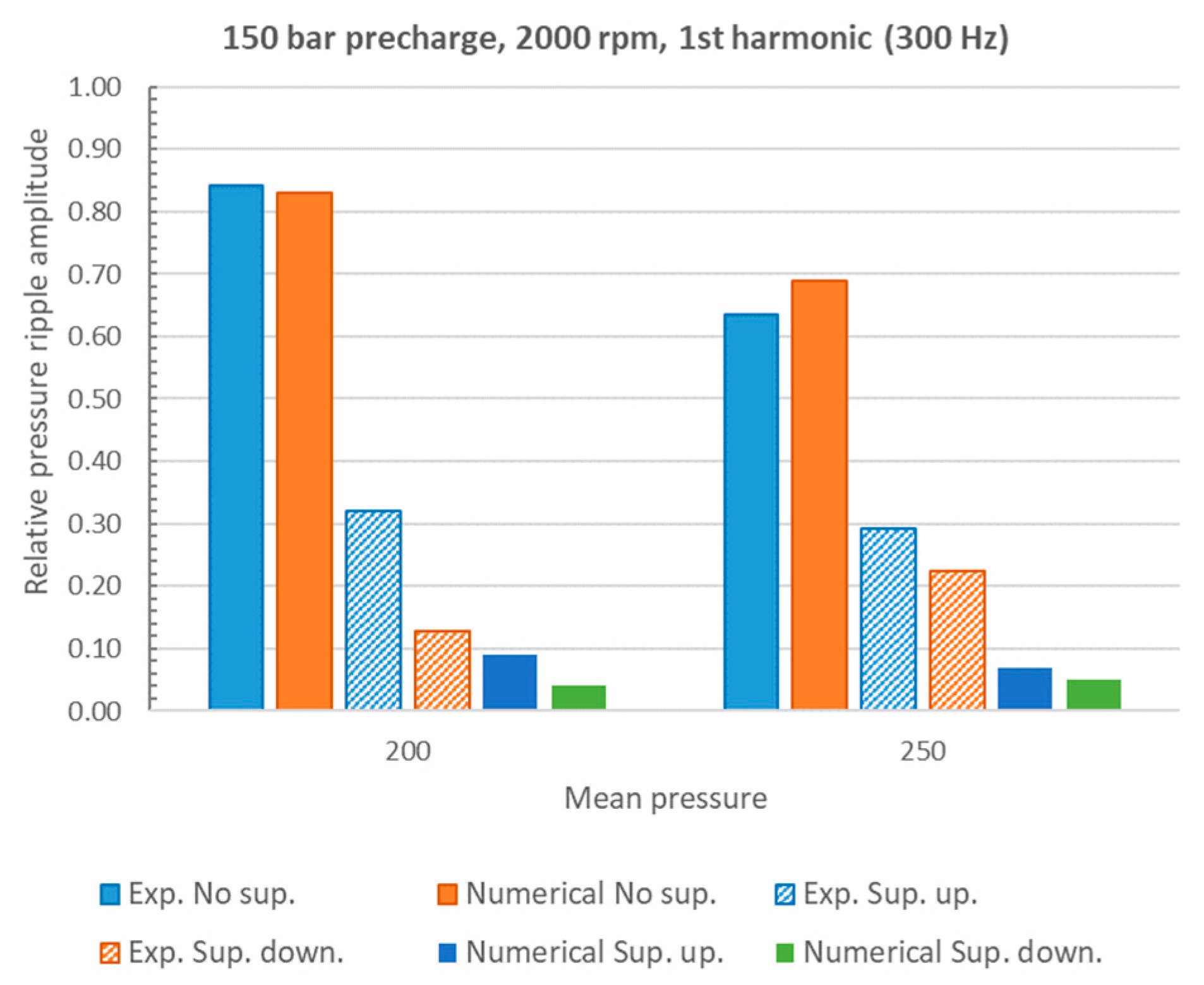
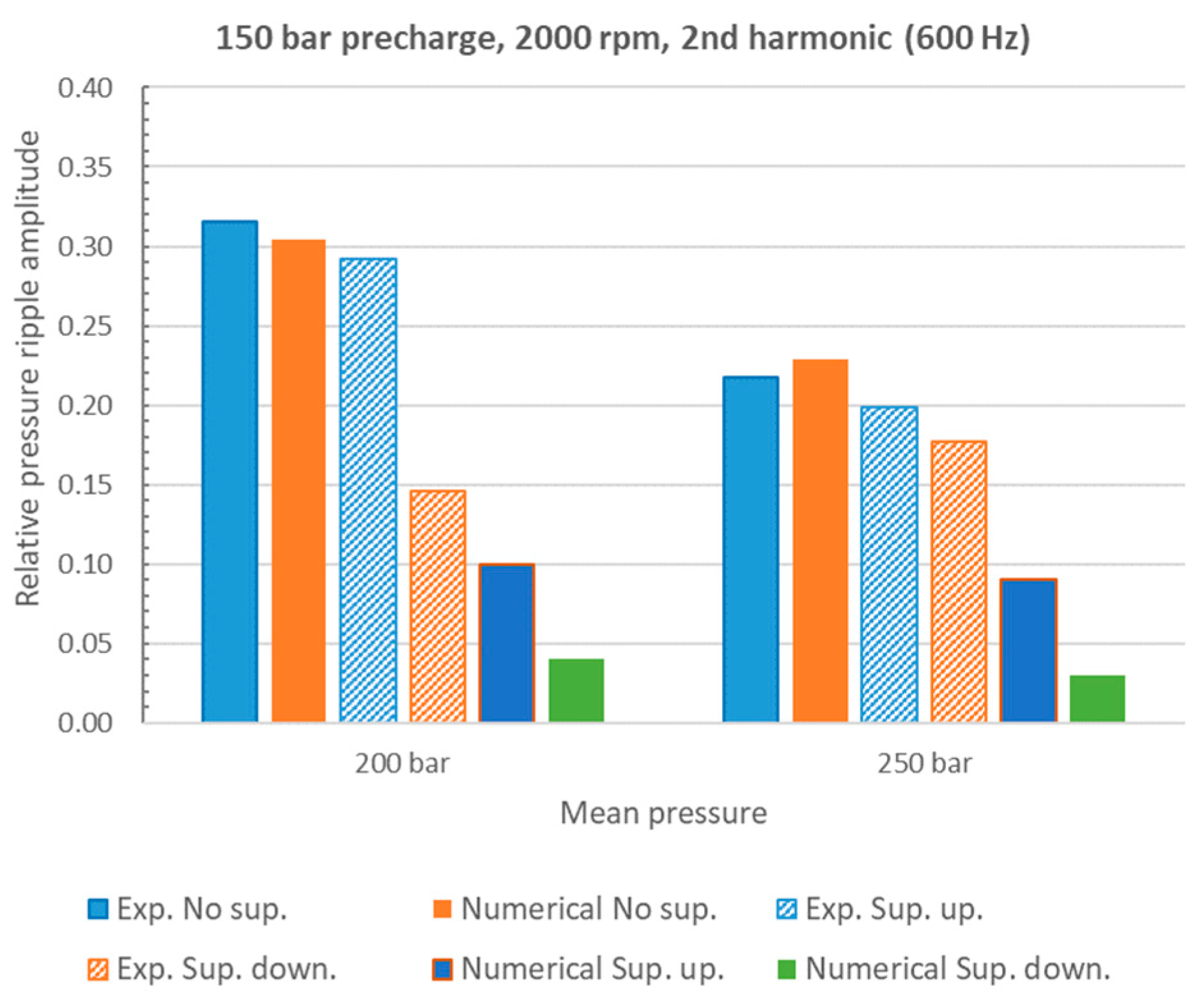
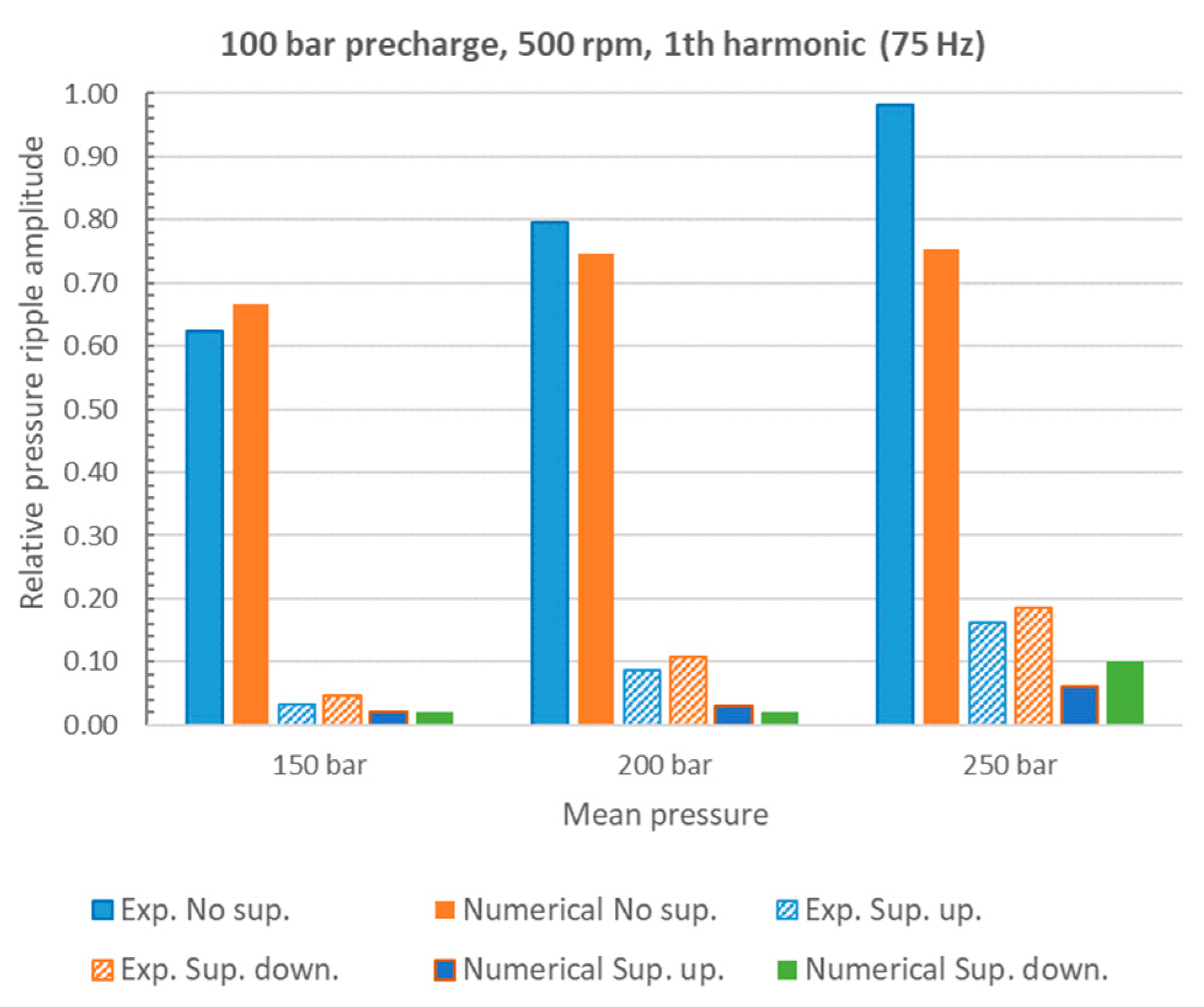
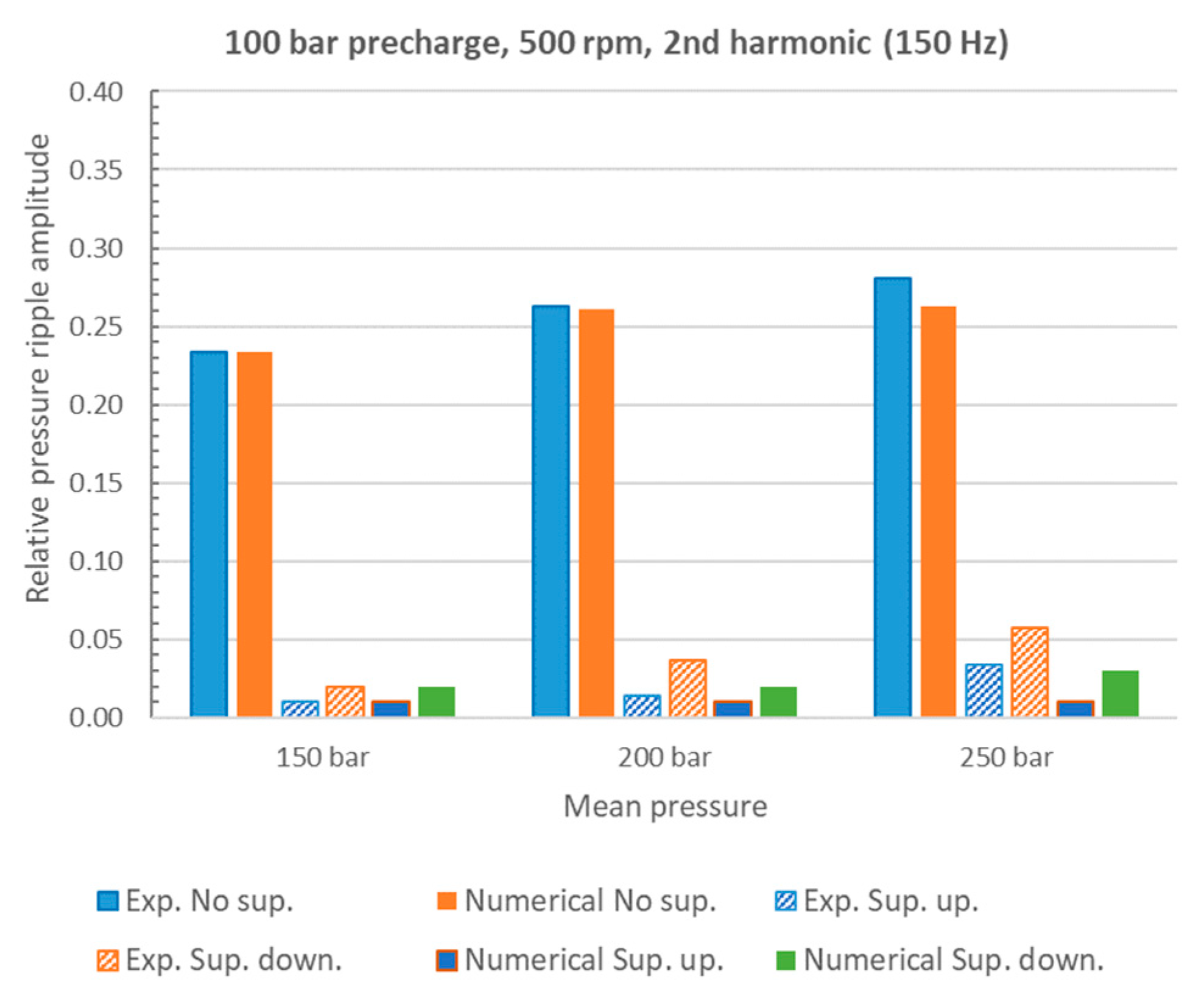
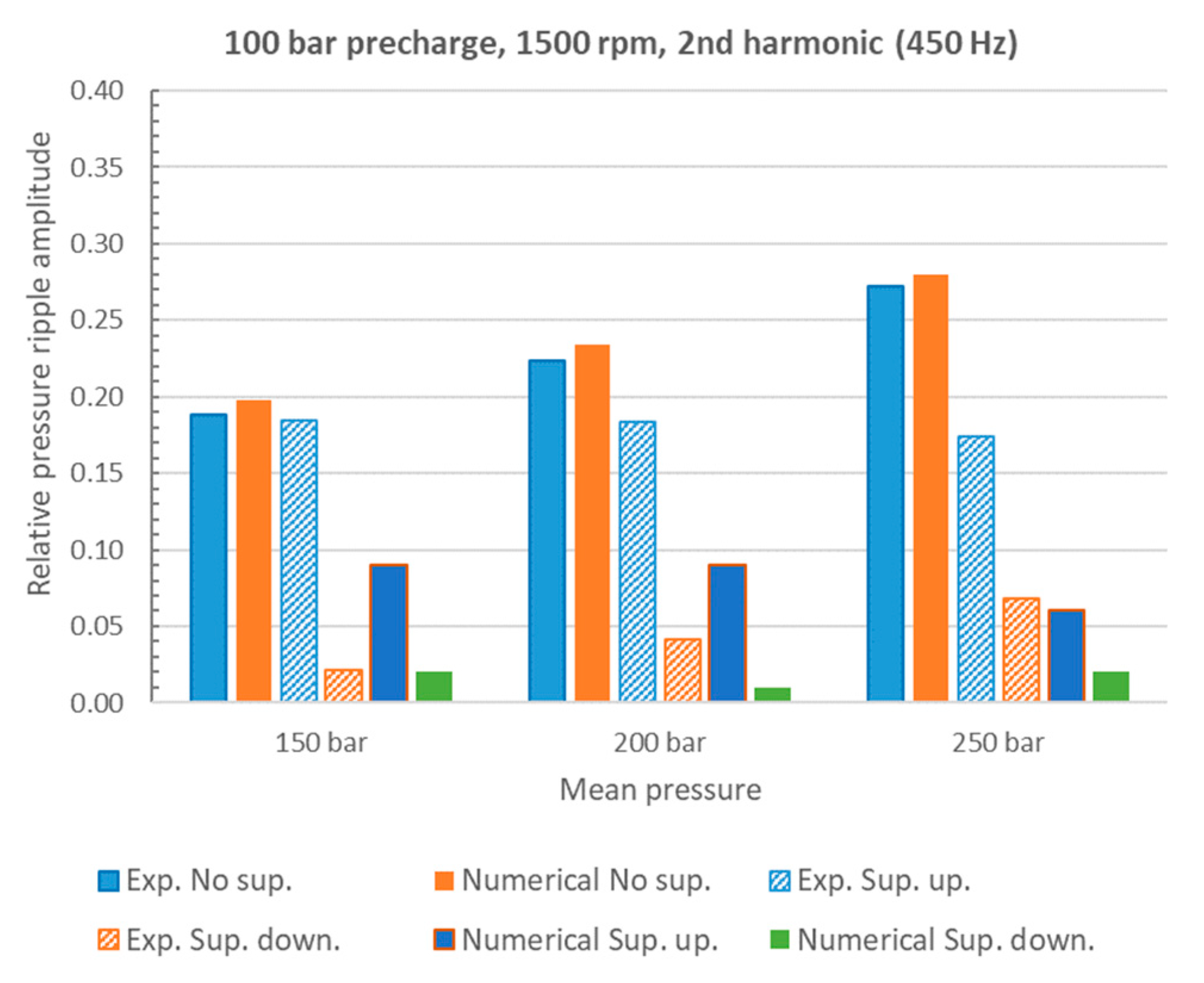
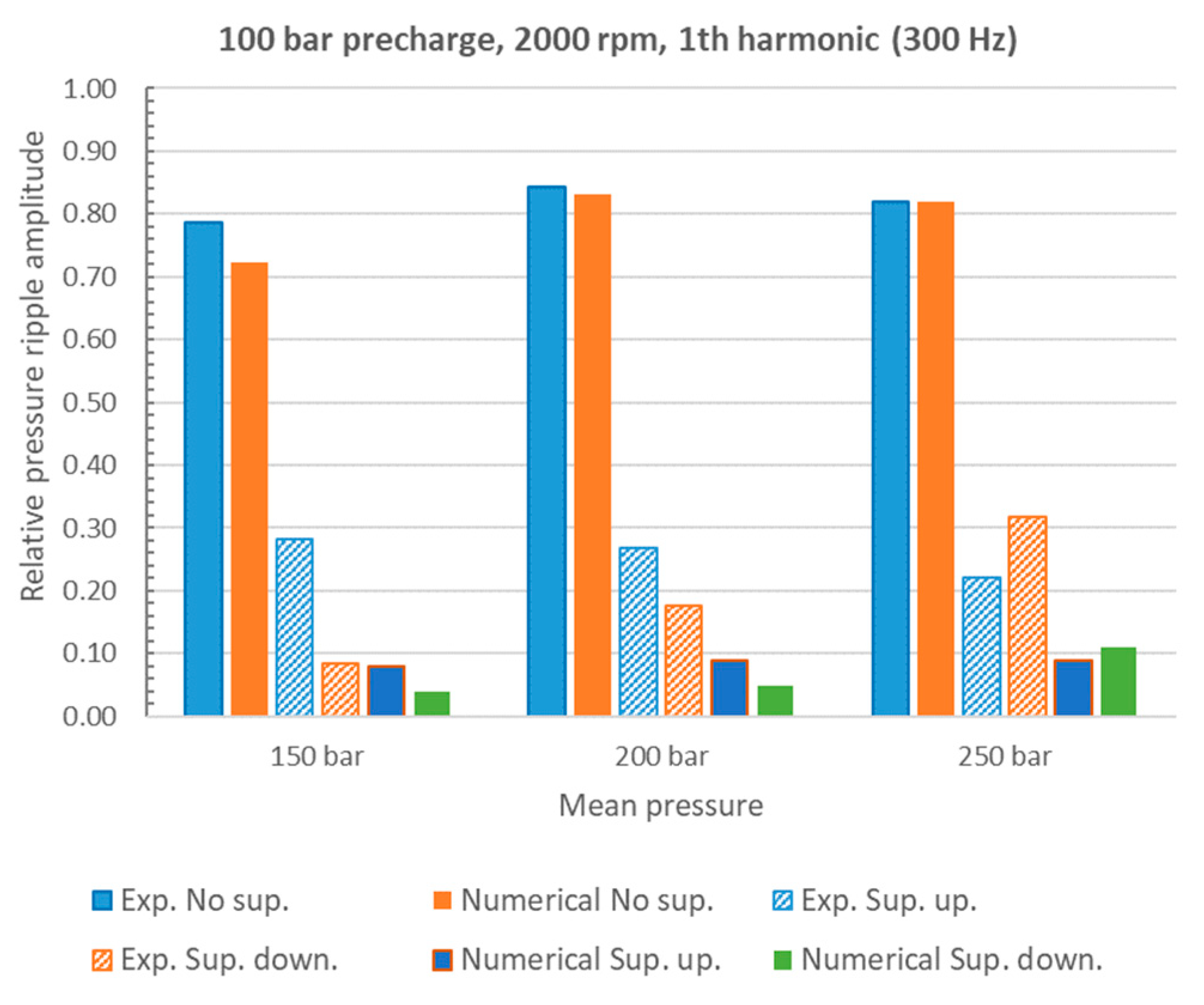
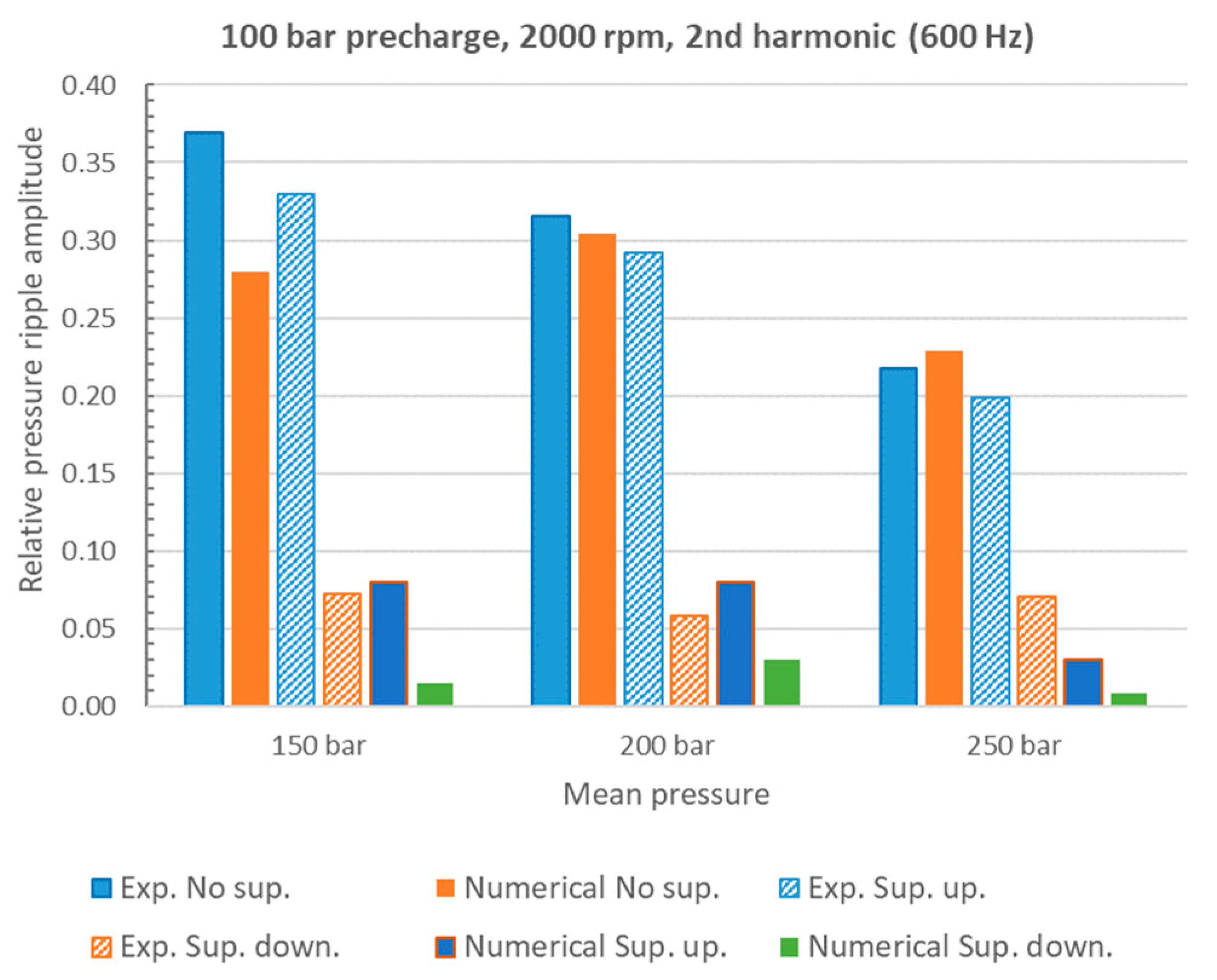
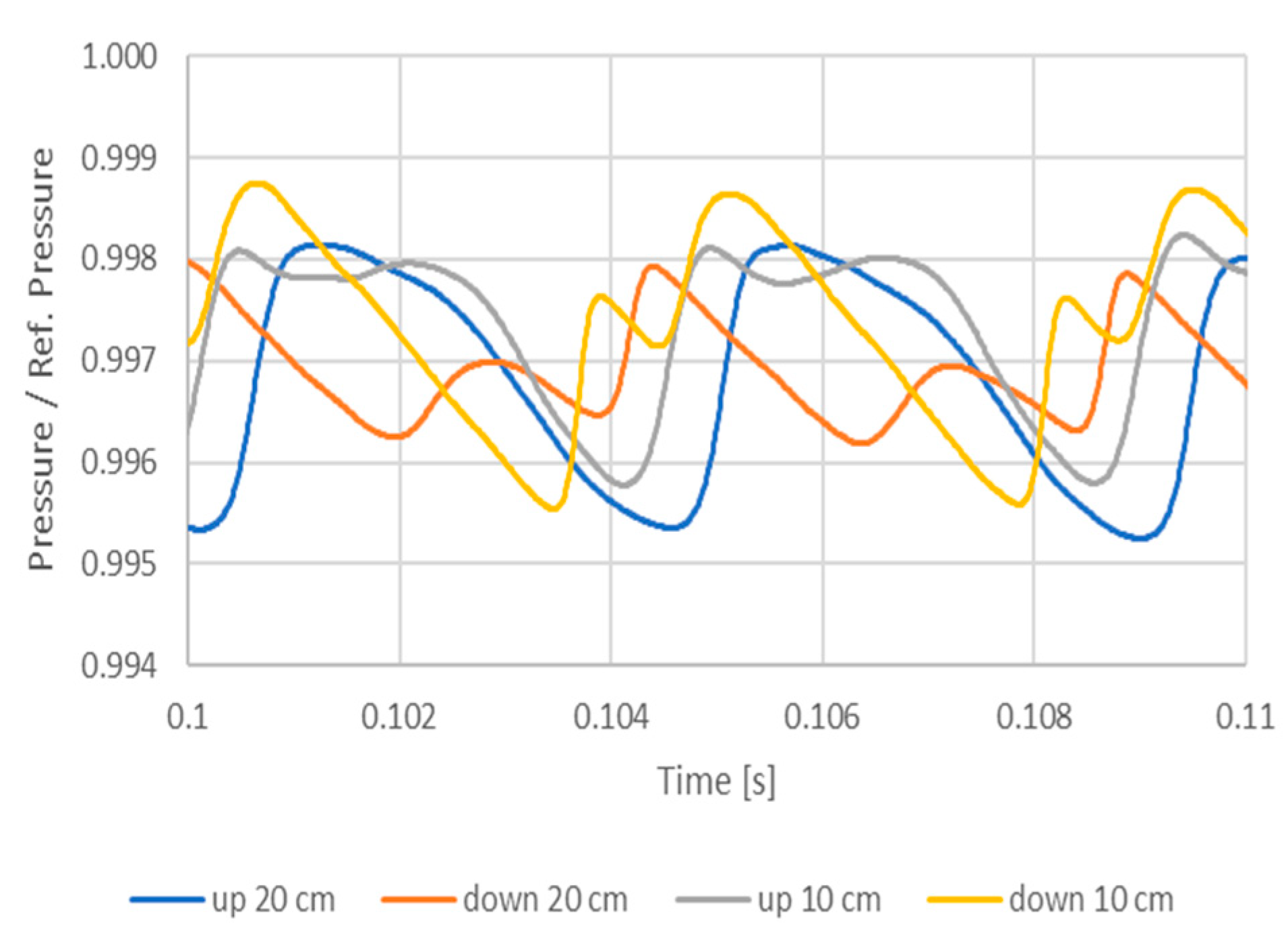
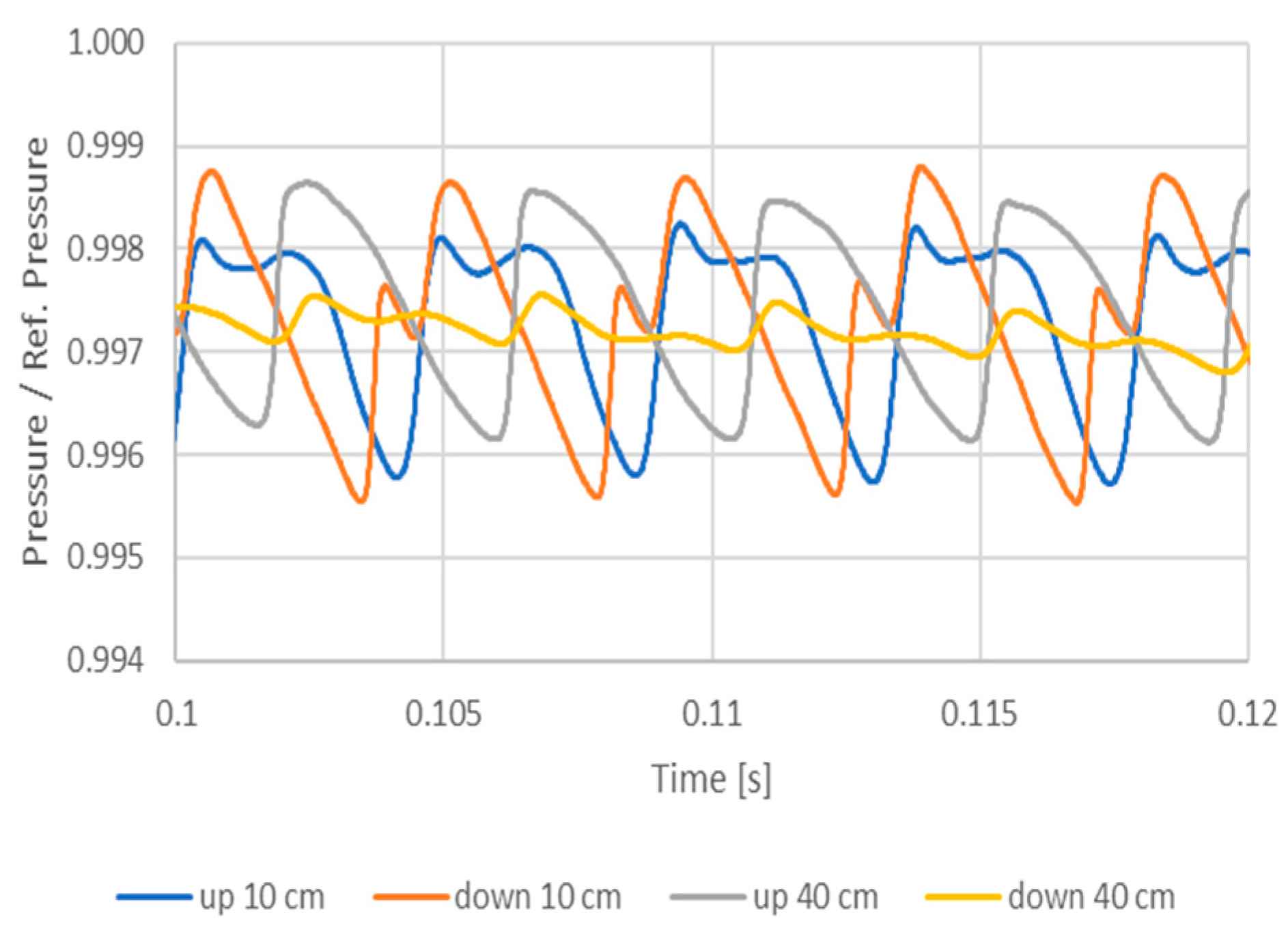
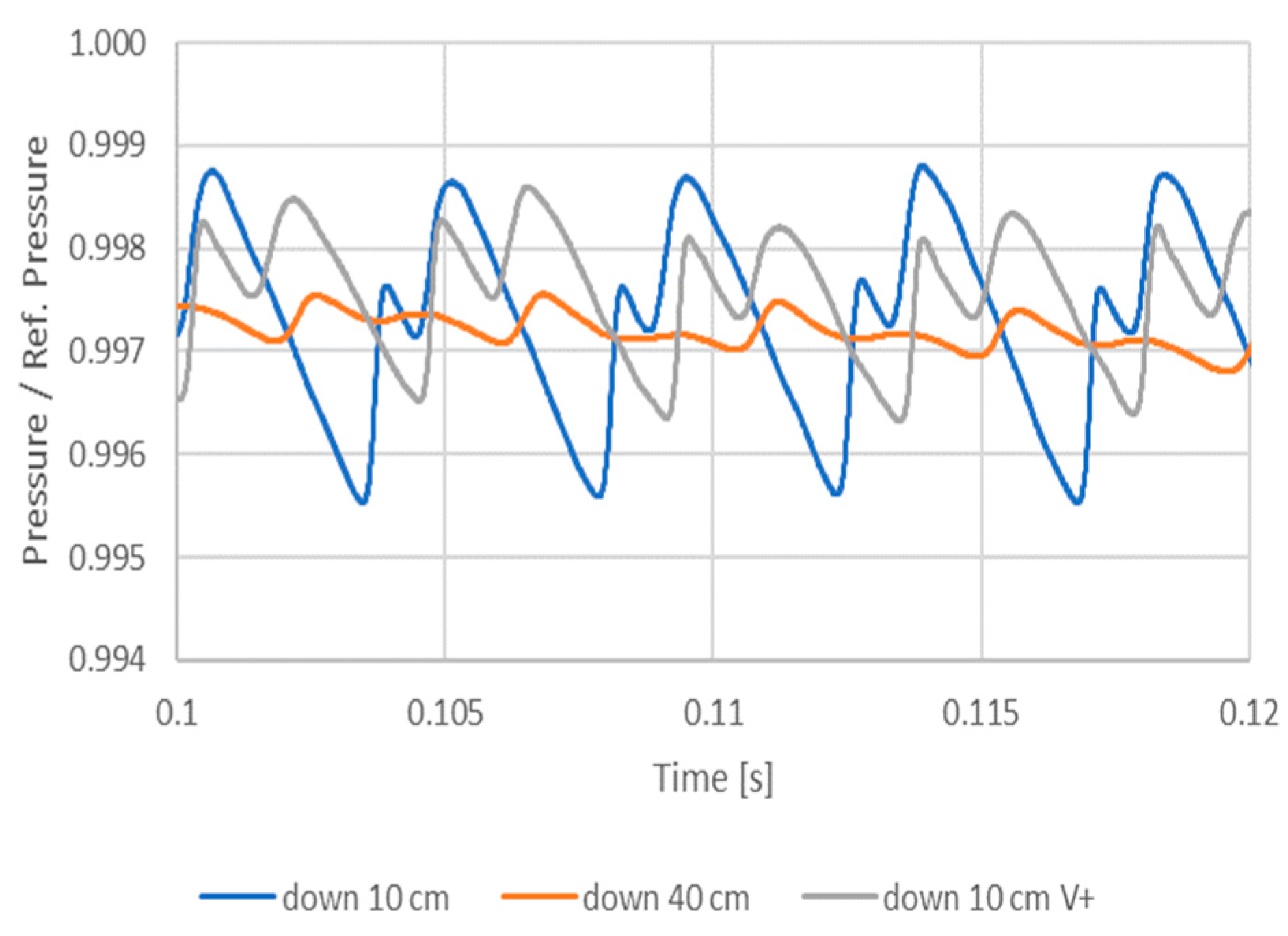
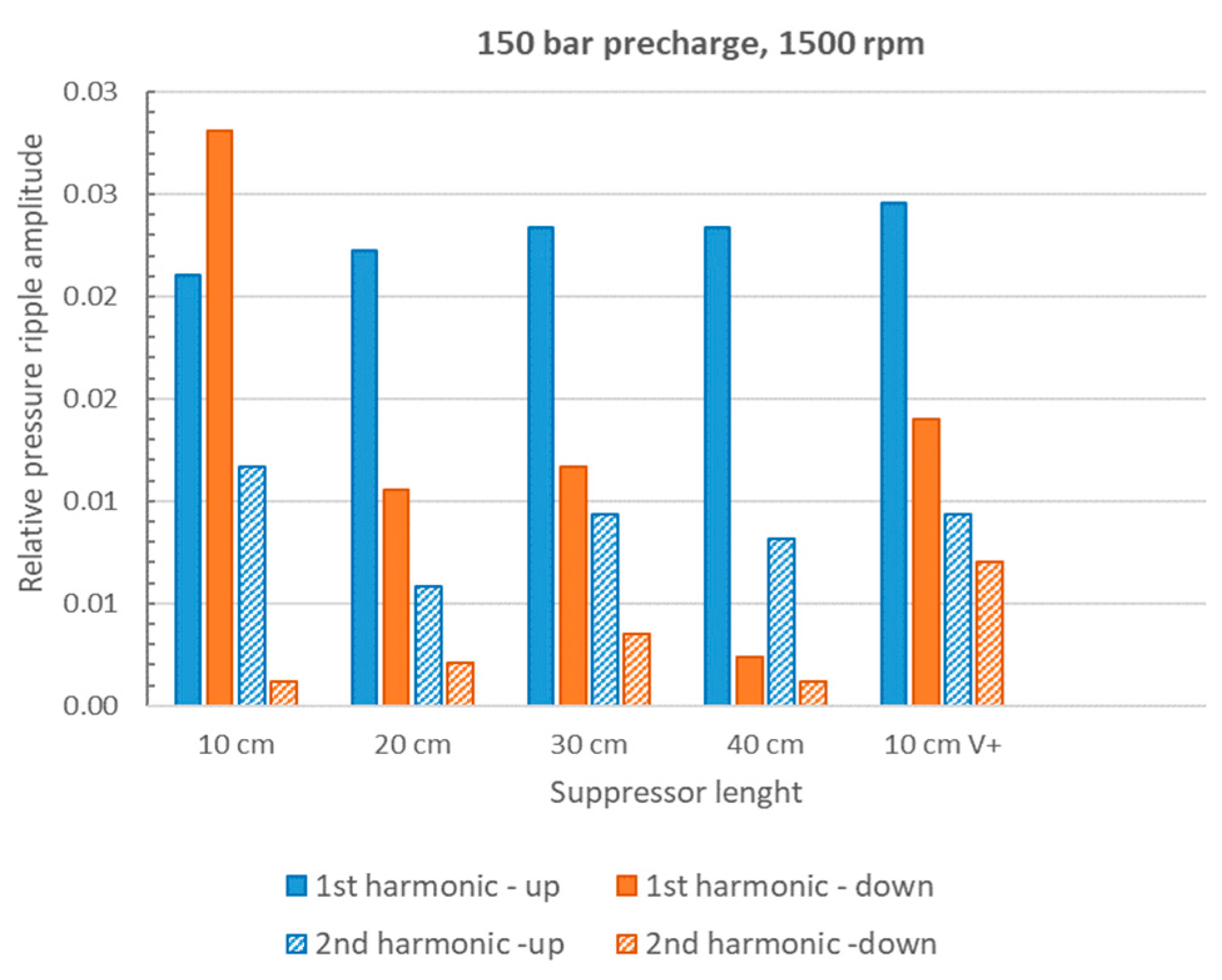
4. Numerical and Experimental Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Cross-sectional area |
| ρ | Density |
| u | Fluid velocity |
| a | Speed of sound |
| Cd | Discharge coefficient |
| p | Fluid pressure |
| m | Mass of the transferred elementary volume |
| K | Bulk modulus |
| Pipe wall holes area | |
| Acceleration of the transferred fluid mass | |
| C | Courant number |
| λ | Fluid friction losses |
| Re | Reynolds number |
| t | Time |
| V | Volume |
| γ | Polytropic coefficient |
| Subscript | |
| n | Temporal step |
| i | Spacial step |
| l | Liquid |
| g | Gas |
| 0 | Reference, initial condition |
| ef | Effective |
| c | Container |
References
- Harrison, A.M.; Edge, K. Reduction of axial piston pump pressure ripple. Proc. Inst. Mech. Eng. 2000, 214, 53–64. [Google Scholar] [CrossRef]
- Manring, N. The Discharge Flow Ripple of an Axial-Piston Swash-Plate Type Hydrostatic Pump. J. Dyn. Syst. Meas. Control 2000, 122, 263–268. [Google Scholar] [CrossRef]
- Johansson, A.; Olvander, J.; Palmberg, J.-O. Experimental verification of cross-angle for noise reduction in hydraulic piston pumps. Proc. Inst. Mech. Eng. Part I J. Syst. Control. Eng. 2007, 221, 321. [Google Scholar] [CrossRef]
- Borghi, M.; Zardin, B. Axial Balance of External Gear Pumps and Motors: Modelling and Discussing the Influence of Elastohydrodynamic Lubrication in the Axial Gap. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Houston, TX, USA, 13–19 November 2015. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Theoretical investigation into the ripple source of external gear pumps. Energies 2019, 12, 535. [Google Scholar] [CrossRef]
- Zhao, X.; Vacca, A. Numerical analysis of theoretical flow in external gear machines. Mech. Mach. Theory 2017, 108, 41–56. [Google Scholar] [CrossRef]
- Zhou, J.; Vacca, A.; Casoli, P. A Novel Approach for Predicting the Operation of External Gear Pumps Under Cavitating Conditions. In Simulation Modelling Practice and Theory; Elsevier: Amsterdam, The Netherlands, 2014; Volume 45, pp. 35–49. [Google Scholar] [CrossRef]
- Corvaglia, A.; Rundo, M.; Casoli, P.; Lettini, A. Evaluation of tooth space pressure and incomplete filling in external gear pumps by means of three-dimensional CFD simulations. Energies 2021, 14, 342. [Google Scholar] [CrossRef]
- Corvaglia, A.; Ferrari, A.; Rundo, M.; Vento, O. Three-dimensional model of an external gear pump with an experimental evaluation of the flow ripple. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 1097–1105. [Google Scholar] [CrossRef]
- Casoli, P.; Pastori, M.; Scolari, F.; Rundo, M. Active pressure ripple control in axial piston pumps through high-frequency swash plate oscillations—A theoretical analysis. Energies 2019, 12, 1377. [Google Scholar] [CrossRef]
- Hagstrom, N.; Harens, M.; Chatterjee, A.; Creswick, M. Piezoelectric actuation to reduce pump flow ripple. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control 2019 FPMC, Sarasota, FL, USA, 7–9 October 2019. [Google Scholar]
- Casoli, P.; Vescovini, C.M.; Scolari, F.; Rundo, M. Theoretical Analysis of Active Flow Ripple Control in Positive Displacement Pumps. Energies 2022, 15, 4703. [Google Scholar] [CrossRef]
- Pan, M.; Ding, B.; Yuan, C.; Zou, J.; Yang, H. Novel Integrated Control of Fluid-Borne Noise in Hydraulic Systems. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control FPMC 2018, Bath, UK, 12–14 September 2018. [Google Scholar]
- Shang, Y.; Tang, H.; Sun, H.; Guan, C.; Wu, S.; Xu, Y.; Jiao, Z. A novel hydraulic pulsation reduction component based on discharge and suction self-oscillation: Principle, design and experiment. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2020, 234, 433–445. [Google Scholar] [CrossRef]
- Rabie, M.G. On the application of oleopneumatic accumulators for the protection of hydraulic transmission lines against water hammer—A theoretical study. Int. J. Fluid Power 2007, 8, 39–49. [Google Scholar] [CrossRef]
- Yokota, S.; Somada, H.; Yamaguchi, H. Study on an active accumulator. JSME Int. J. 1996, 39, 119–124. [Google Scholar] [CrossRef]
- Marek, A.K.; Gruber, E.R.; Cunefare, K.A. Linear multimodal model for a pressurized gas bladder style hydraulic noise suppressor. Int. J. Fluid Power 2013, 14, 5–16. [Google Scholar] [CrossRef]
- Gruber, E.R.; Cunefare, K.A.; Danzl, P.W.; Marek, K.A.; Beyer, M.A. Optimization of Single and Dual Suppressors Under Varying Load and Pressure Conditions. Int. J. Fluid Power 2013, 14, 27–34. [Google Scholar] [CrossRef]
- Yi, X.; Bao-ren, L.; Long-long, G.; Teng-fei, T.; Hui-li, L. Acoustic attenuation performance prediction and analysis of bladder style hydraulic noise suppressors. Appl. Acoust. 2018, 134, 131–137. [Google Scholar]
- Zielke, W. Frequency-dependent friction in transient pipe flow. J. Basic Eng. 1968, 90, 109–115. [Google Scholar] [CrossRef]
- Benjamin, E.W.; Streeter, L. Fluid Transients in Systems; Prentice-Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Hoffman, J.D. Numerical Methods for Engineers and Scientists; Mc Graw Hill: New York, NY, USA, 1992. [Google Scholar]
- Casoli, P.; Pastori, M.; Scolari, F. Swash plate design for pressure ripple reduction—A theoretical analysis. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019. [Google Scholar] [CrossRef]


| Fluid pressure | 150 bar | 200 bar | 250 bar | ||
| Gas pressure precharge | 100 bar | 100 bar | 150 bar | 100 bar | 150 bar |
| 500 r/min | x | x | x | x | x |
| 1500 r/min | x | x | x | x | x |
| 2000 r/min | x | x | x | x | x |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casoli, P.; Vescovini, C.M.; Rundo, M. One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation. Energies 2023, 16, 3368. https://doi.org/10.3390/en16083368
Casoli P, Vescovini CM, Rundo M. One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation. Energies. 2023; 16(8):3368. https://doi.org/10.3390/en16083368
Chicago/Turabian StyleCasoli, Paolo, Carlo Maria Vescovini, and Massimo Rundo. 2023. "One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation" Energies 16, no. 8: 3368. https://doi.org/10.3390/en16083368
APA StyleCasoli, P., Vescovini, C. M., & Rundo, M. (2023). One-Dimensional Fluid Dynamic Modeling of a Gas Bladder Hydraulic Damper for Pump Flow Pulsation. Energies, 16(8), 3368. https://doi.org/10.3390/en16083368








