Abstract
Naturally fractured reservoirs are indescribable systems to characterize and difficult to produce and forecast. For the development of such reservoirs, the role of naturally forming fractures in the different development stages needs to be recognized, especially for the pressure maintenance and enhanced oil recovery stages. Recent development in the field of naturally carbonate fractured aimed at fracture characterization, fracture modeling, and fracture network impact of fracture networks on oil recovery were reviewed. Consequently, fracture identification and characterization played pivotal roles in understanding production mechanisms by integrating multiple geosciences sources and reservoir engineering data. In addition, a realistic fracture modeling approach, such as a hybrid, can provide a more accurate representation of the behavior of the fracture and, hence, a more realistic reservoir model for reservoir production and management. In this respect, the influence of different fracture types present in the reservoir, such as major, medium, minor, and hairline fractures networks, and their orientations were found to have different rules and impacts on oil production in the primary, secondary, and EOR stages. In addition, any simplification or homogenization of the fracture types might end in over or underestimating the oil recovery. Improved fracture network modeling requires numerous considerations, such as data collection, facture characterization, reservoir simulation, model calibration, and model updating based on newly acquired field data are essential for improved fracture network description. Hence, integrating multiple techniques and data sources is recommended for obtaining a reliable reservoir model for optimizing the primary and enhanced oil recovery methods.
1. Introduction
A significant number of reservoirs that contribute to the global petroleum reserves and current production are naturally fractured carbonates. These reservoirs are complex, and their description and production are associated with additional uncertainties about the fracture networks and their impact on production [1,2,3,4,5]. Indistinctness in the distribution of fractures greatly influences fluid flow and displacements, and the challenge of propagating the uncertainty in the fracture distribution patterns into their reservoir flow response needs to be considered [6]. Subsurface rocks and geological formations often exhibit fractures such as joints, faults, and bedding planes. These discontinuities frequently regulate the hydrological behavior of subsurface rocks and form intricate networks [7]. In carbonate and magnesium-bearing carbonate rocks, fractured dissolution channels and cavities are formed during weathering or burial within the sedimentary basin. At the same time, fractures oriented vertically in large portions of the subsurface rocks comprising magnesite, dolomite, silt, and limestone may also be formed due to the tectonic events and increasing overburden stresses, reducing the strength of the rocks [8].
Typically, fractures must form an interconnecting network to be considered as a naturally fractured reservoir. Different fracture characteristics may affect the flow pathways in substantially different ways, e.g., fracture orientation to flow direction or a classification scheme. The assessment of the oil recovery process might be affected by including or excluding these fractures. Therefore, an accurate fracture network characterization is essential for understanding fluid flow behavior [7].
Facture modeling is a complex process that requires a holistic multidisciplinary investigation. Geoscience, reservoir, and production data are pivotal for fracture identification and classification. Different data sources often characterize the fractures on different scales [9]. Alternative to reservoir data, guidelines were proposed for selecting representative outcrops and to prove the correspondence between outcrop and core [10]. Fracture characteristics, such as relative or absolute fracture intensity, structural location, and distributions of height and length, can be quantified through outcrops that are difficult to capture on seismic and core scales. In addition, the results of image logs analysis, such as formation micro-imager (FMI) and electrical micro-imager (EMI), can be used for fracture evaluation, which is more dependable than core data [11]. In the fracture-modeling process, the fractures’ images are used to capture the intersections of the fractures and generate the fracture density logs. The outcrop fracture data with the core observations can improve the fracture modeling for reservoirs with limited or without FMI logs. For example, an improved fracture intensity depiction across a reservoir can be obtained by analyzing the outcrop’s measured properties [12].
In addition to the image logs, modern well and production logs, conventional well logs, cores, and seismic data, production data can be correlated to fracture intensity [12,13,14]. Normally, the high intensity of fractures corresponds to the producing wells. Accordingly, fractured zones with high production rates can be located by integrating fracture data from image logs core and core data. The fracture density logs are used to construct the discrete fracture network (DFN) model. The DFN model is attractive since it can represent fracture characteristics for hydraulically relevant fractures. Fracture network characteristics such as fracture size, orientation, and aperture reflect the rock’s physical properties [15]. Hence, with the DFN model, it is possible to investigate the effect of fracture network features on oil displacement.
Currently, with many naturally fractured reservoirs being in brownfields and most of the light oils being produced, improving their oil production, especially with different EOR methods, is of interest. However, limited EOR projects in naturally fractured reservoirs were implemented, and their analyses still bear many uncertainties [16,17]. This might be due to these reservoirs’ fluid phase and flow behavior, which strongly depends on the matrix and fracture properties. For the practical analysis and development of such reservoirs, the need to recognize the role of natural fractures on production in the different stages of reservoir development is significant. Consequently, fracture characterization through integrating multiple data sources from geosciences and reservoir engineering plays a pivotal role in a deep understanding of reservoir production mechanisms in view of a more realistic dynamic simulation model.
This paper aims to provide a comprehensive review of the fracture characterization of the different types of fracture networks and their impact on the different stages of oil recovery. First, the process of fracture characterization and modeling will be reviewed. Then, an integrated approach for their modeling and their impact on the different stages of production will be discussed.
2. Fracture Characterization
Reservoir characterization of naturally fractured reservoirs needs a complete understanding of the fracture networks and their influence on the fluid flow behavior. Based on this knowledge, representative geo-models can be constructed that provide the field parameters required for dynamic simulation. Modeling fractures presents inherent challenges due to the varying scales at which fracture data and parameters are obtained and characterized. Fracture length varies from cm scale to km scale, whereas fracture apertures and spatial densities are widely spread over various variations. Fracture orientations are complicated and depend on the rocks’ local stress regime. However, all the variations and complexities of the fractures can be covered using specialized software [18].
The DFN modeling can represent fracture characteristics for hydraulically relevant fractures [9]. Fracture distribution, geometry, and fracture orientation are required for creating a DFN model. The DFN is a set of planes representing fractures. Similar and genetically connected fractures are classified into a fracture set, and each fracture network contains at least one or several of such distinct sets [19]. Each fracture network contains at least one fracture set but may have more. Fracture sets are determined deterministically as a group of previously defined fractures due to fault plane interpretation extraction from a seismic cube. Hence, fracture characteristics such as fracture aperture (opening displacement), length, spacing, orientation, and matrix fracture interaction can affect the production behavior of fractured reservoirs. The next sections examine several of the key features of fractures and how they interact with the matrix.
2.1. Fractures Characteristics, Parameters, and Fracture Types
Fracture characterization refers to identifying, measuring, and describing fractures’ physical and geometric properties in a rock formation. The fractures can be characterized using various methods, including; core analysis, well logging, seismic method, and tracer testing. Tracer testing is one of the powerful methods for characterizing fractures and their properties in the subsurface. Tracer tests involve injecting a tracer into a fracture or borehole and monitoring its movement and concentration over time [20,21]. Through the tracer test, one can gain valuable insights into the subsurface flow patterns and better understand the behavior of fractures in the subsurface.
Once a fracture is characterized, its properties can be used to determine its potential for fluid flow or as a pathway for fluid injection. In addition, fracture characterization can be used to identify the type of fracture, such as natural fractures, tectonic fractures, joints, and veins. It can also be used to determine the mechanical properties of fracture, such as fracture aperture, roughness, persistence, and conductivity. The mechanical and morphological characteristics of fractures can significantly impact fluid flow in a reservoir. For example, hydraulic fractures with a branched morphology tend to have higher permeability than those with a non-branched morphology, while tectonic fractures parallel to the direction of fluid flow tend to have higher permeability than those oriented perpendiculars to the flow direction. Understanding fractures’ genetic types and associated characteristics can help develop effective reservoir management strategies.
During the data acquisition, fractures are typically grouped into different discontinuity sets [19]. They can have similar characteristics in the same category, such as the mechanical properties and the origin of occurrence. Fractures in one discontinuity set are parallel, meaning they have a similar dip and dip direction in the case of the systematic fracture sets, making them relatively easy to distinguish [22]. An example of an analyzed Rose diagram showing different fracture sets is illustrated in Figure 1.
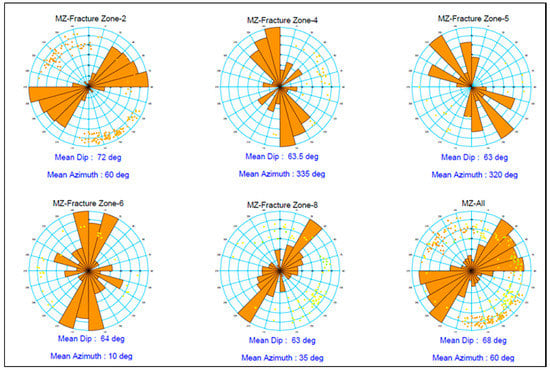
Figure 1.
Rose diagrams showing different fracture sets.
Fracture sets recognition depends on pattern recognition expertise and capabilities. Minor variations in attributes are often disregarded to simplify the modeling process and decrease computational power needs [23].
The fracture length and aperture control the flow behavior of fracture networks. The fracture aperture and porosity are estimated by the fracture length [12]. From the fracture aperture, the permeability of the fracture can be estimated. Simple and complex correlations were proposed for fracture permeability. The basic relation is based on Darcy’s equation which resembles the cubic law [24].
The general technique to differentiate fracture types is separating them into open, partial, and closed fractures. Open fractures can be classified according to their aperture values since they are the main concern for fluid flow in porous media [25]. Based on FMI and EMI logs, fractures can be identified, and their aperture can be estimated using mathematical expression by converting measured logging parameters to aperture. For example, based on the FMI log shown in Figure 2, fractures appear as sinusoidal features with more dip than a structural dip. The blue triangles, circular, and square dips represent the minor, medium, and major open fractures. Based on the aperture size, different fracture types, namely major, medium, minor, and hairline fractures, can be identified if sufficient image logs are available. For example, the four mentioned types were determined in a giant carbonate fractured reservoir with more than 29 image logs [26]. In this classification, the major fractures had the highest continuity and aperture values (600 µm), while the hairline fracture type had the lowest values (10 µm). The medium and minor average apertures were 400 µm and 200 µm, respectively. The hairline fractures can be lumped with a minor fracture if their aperture size is too small.

Figure 2.
FMI image and core of a carbonate formation: major open fractures blue square dips, medium open fractures (blue circular dips), and minor open fractures (blue triangle dips) [11].
2.2. Matrix–Fracture Interaction
Matrix–fracture interaction is a key aspect of subsurface flow and transport in rock formations. The matrix, which is the intact rock surrounding the fractures, and the fractures can possess distinct properties such as permeability and porosity that can influence the flow and movement of fluids. In the fluid transfer between fractures and matrix, non-dimensional numbers such as Capillary, Gravity, and Péclet number control the flow behavior [5]. Hence, the matrix–fracture interaction is governed by matrix and fracture properties. To understand and predict the behavior of subsurface fluids in fractured rocks, it is important to have a detailed understanding of the properties and behavior of the matrix and fractures and their interactions. This can be obtained through laboratory experiments, field measurements, and numerical modeling, such as rock mechanics tests, permeability, and porosity measurements, microscopic imaging, hydraulic tests, geophysical surveys, well logging, DFN modeling, and coupled fluid flow and geomechanical modeling.
In the water-wet rock reservoirs, the effective imbibition of water from the fractures is supported by a counter-current or co-current mechanism to displace oil from the matrix [27]. It is an effective recovery mechanism in water-wet fractured reservoirs, whereas less effective in a mixed-wettability or oil-wet system since a faster increase in the water cut usually happens. The interaction between the matrix blocks highly influences the gravity drainage mechanism, capillary continuity, and the liquid’s reinfiltration. For gas-based EOR methods, it is the main production mechanism, especially in the gas-invaded zone [28,29,30,31]. Due to the height and large density differences (oil and gas phases), pressure contrast between matrix blocks and surrounding fractures occurs, enhancing oil production from the matrix blocks [12,32].
2.3. Modeling and Workflow for Data Integration
Data integration in modeling naturally fractured reservoirs involves combining different data types to create a numerical model accurately representing the reservoir’s geological and hydraulic characteristics. The difficulty of this procedure stems from the intricacy of the fractures and the requirement for validation at every stage of the modeling and scaling process [14]. Usually, production data are used for tuning the model through history matching. This fact necessitates a precise static and dynamic modeling approach for the fracture networks due to their effects on overall reservoir performance. Fractures of the same type generated simultaneously are grouped into a fracture set, and each fracture network contains at least one fracture set or more. Wellbore data in the form of logs, cores, borehole images, or dynamic data provide information on the characteristics of smaller-scale fractures. In contrast, seismic data can provide the distribution parameters of large-scale discontinuities, e.g., major faults. Stochastic methods are used to populate the area between seismic-scale faults, but reliable statistics might result in high extrapolation uncertainties [33].
Statistical methods are commonly recommended for fractured network characterization. Fracture attributes such as the aperture, size distribution, and fracture density are implemented within the rock volume based on experimentally recognized statistical models [7,9]. The Poisson modeling technique was used in commercial software. However, the model tends to have some uncertainty owing to its simplified assumptions, mainly uniform spatial distribution, fracture shape simplification, and neglecting the relationships between geometrical properties and topological relations are the weakness of this approach [9,34,35].
The main techniques utilized for modeling fractured reservoirs, continuum and discrete fracture modeling (DFM), as well as their combination, are explored in the following sections.
2.3.1. Continuum Approach
In this approach, virtual fracture networks are generated as a second, independent continuum dividing the rock matrix, the first continuum in matrix blocks. Both continuums have their own storage, flow properties, and flow equations. A hydraulic coupling between the rock matrix and the fracture network is introduced by a transfer function. A transfer function defined in shape factor interactions with the two continua (fracture and matrix) and determines the fluid transfer between matrix and fractures. This function represents the difference in pressure between matrix blocks and the surrounding fractures [36]. Several transfer functions were proposed to improve the matrix–fracture interaction description and provide accurate modeling [23,37,38].
Two models were used for the continuum approach, namely the dual-porosity (DP) and the dual-permeability (DK) models [39]. The DP model is computationally efficient, but precision might be compromised due to its tendency to underestimate or overestimate the oil recovery during early or late times. The main difference between these two models is that the exchange of fluids is only allowed between the matrix block and the fracture in the dual-porosity model. This corresponds to a situation in which matrix blocks are essentially insulated by the fracture network. The DP model allows for inter blocks flow and directly connects the flow pathway with the wellbore and the inter-porosity flow between matrix and fracture systems. The modeling results might differ for different reservoirs; however, it is not completely proven to be one or the other. The continuum approach’s main benefit is simplifying the fracture networks’ complexity to be suitable for field-scale studies. However, this simplification might provide misleading simulation results [39,40].
2.3.2. Discrete Fractures Approach
The discrete fractures approach explicitly represents fractures as elements or control volumes as an alternative to the dual continuum approach. The approach involves dividing the reservoir into discrete fractures characterized by their geometric properties (length, width, and orientation) and flow properties (permeability and aperture). The fractures are then connected to the surrounding matrix, representing the non-fractured rock. The DFN is used to display the fracture network [41]. When the permeability of the reservoir matrix is low or negligible, fluid flow through the fractures can be modeled using discrete fracture network models. In comparison, other discrete fracture models need to be utilized in the case of fracture matrix interaction [40].
In the DFM models, the need for transfer functions is eliminated, but it could be used to estimate the properties of fractures that are not directly known [42]. The DFM conveniently describes the fractures’ structural features, such as fracture geometry. Fractures aligning with the internal boundaries of the matrix grids is a mandate in the DFM models. Therefore, unstructured grids are necessary for the fractures’ geometrical representation and the matrix domain’s decentralization. However, quality gridding might not be feasible when the distance between the fracture is trivial [43]. It is worth mentioning that DFM models are computationally intensive and fall outside the realm of traditional solution methodologies for field-scale applications [42].
The embedded discrete fracture model (EDFM) is an alternative modeling technique in the discrete fractures approach, with the advantage of using the non-conforming grid to discretize the matrix domain without considering the fracture’s locations. The approach defines the intersection between the fracture polygons and matrix grids after placing the fractures in the matrix grids. The matrix grid boundaries discretize the fractures, so only one fracture segment is created for each infiltrated matrix grid by a fracture [41]. Based on these measures, the model can be compatible with commercial simulators [40].
2.3.3. Hybrid Approach
The hybrid approach combines the continuum and the discrete fracture approaches. To simulate the overall behavior of the rock matrix and fluid flow through it, continuum elements such as finite difference or finite element methods are employed. The discrete elements, such as DFN, are used to model the fractures’ behavior, including their geometry, orientation, and aperture. The construction of the hybrid model has two essential processes: partitioning and lumping. The fracture network is separated into two sets based on a pre-determined cutoff in the partitioning process. The continuum approach implicitly represents the small fracture set, while the discrete fracture approach explicitly represents a large one. It should be noted that the implicitly represented fractures must be subdivided into fracture groups so they can be integrated into a continuum [40]. The hybrid approach is particularly useful for fractured reservoirs because it can accurately capture the complex behavior of the fractures and their interaction with the surrounding rock matrix and fluids, leading to more accurate predictions of fluid flow and production rates.
In summary, different simulation approaches were proposed for fractured reservoirs; however, the simulation outcome might differ depending on the reservoir and fracture properties. For example, water movement and distribution differ between DFN and non-DFN models for water flooding in a low permeability reservoir. The DFN model predicts more water spreading and reaching farther locations than the non-DFN model [44]. Hence, the simulation modeling approach is critical for the secondary oil recovery and EOR stages.
3. Impact of Fractures on Recovery Processes
Fractures can have a considerable effect on oil recovery in various stages of production. They create additional conduits for oil flow, enhancing the permeability of the reservoir, and enhancing the effectiveness of oil recovery techniques. The initial production of fractured reservoirs can reach high levels, and this is due to the oil production from the fracture. However, they might quickly decline [45]. The rapid decline after high initial production flow rates is typical for most fractured reservoirs. At the commencement of the production life cycle, oil mostly fills the fractures and matrix pores. Furthermore, the fracture network’s complexity often results in the injected fluid being channeled or fingered in the displacement process, which results in low oil recovery [46,47]. Therefore, preserving the production is problematic due to the different types and complex structures of fracture networks.
A workflow for quantitatively classifying all types of fractures in fractured shale reservoirs into different categories was presented based on their effects on reservoir performance [48]. The study includes micro-scale and reservoir-scale modeling to investigate the influence of small and large fractures on equivalent permeability, production performance, and pressure propagation speed. The results suggest that an analytical apparent permeability model can be used to describe the effect of isolated and connected fractures on production for certain ranges of fracture aperture and matrix permeability. The study also found that disconnected fractures had a minimal influence on gas production and can be modeled using the matrix–fracture effective permeability method and medium continuum model, while the DFM method should be used for connected fractures. The study provided valuable guidance for optimizing fracture modeling in unconventional fractured reservoirs.
Fractures can also affect the pressure distribution within the reservoir, impacting the effectiveness of primary and secondary recovery methods. Fractures can act as conduits for the injection of water or gas to displace oil and improve recovery. However, if not well understood, they can also cause pressure communication between injectors and producers, leading to early and undesirable water or gas breakthrough.
All fractures might contribute positively to the fluid flow during primary production, but during secondary production, the effect of non-major fractures suddenly diminishes [14,34,35]. Multiple experimental and theoretical studies examined the influence of fractures on oil production [49,50,51,52,53]. However, different observations and conclusions are reported due to the matrix, fracture, and fluid properties used. The categorization of these observations is pending.
3.1. Primary Recovery
Natural fractures have a variety of primary production behaviors and mostly lead to low oil recovery. In the initial primary recovery, oil from the fractures is produced first, resulting in very high recovery peaks, which may decline quickly [45]. Primary fractures mainly contribute to fluid flow in reservoirs with widespread aperture distribution and good fracture network connectivity [34,35,53]. In primary production, fractures provide the path for the oil to flow toward production wells; even small fractures should be considered; hence, all fractures should be included in the primary production stage [14,35,54]. Excluding the medium or minor fractures results in underestimating the oil recovery.
The findings recently published are based on a hypothetical 2D horizontal slice model that assumes the presence of major fractures with a 1.0 mm aperture surrounding a matrix block. Figure 3 illustrates that medium (0.5 mm) and minor (0.1 mm) fractures are present within the matrix block.
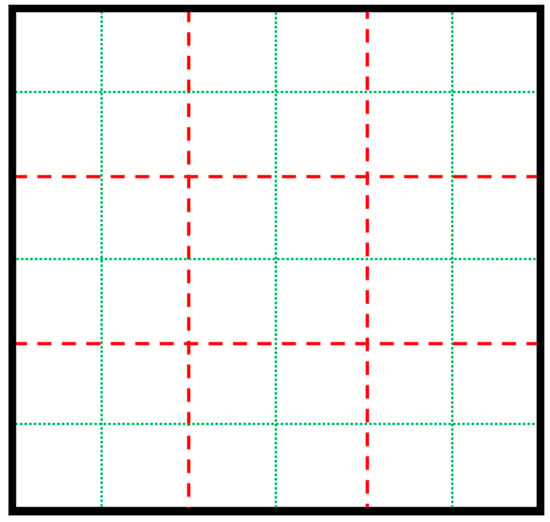
Figure 3.
Scheme of a hypothetical model with the deterministically distributed fractures (black: major; red: medium, green: minor fractures).
The impact of the fracture characteristics was evaluated for a fractured field with 38 years of production history using fracture properties without altering the matrix properties [12]. Most reservoir wells reported excellent matching results with improved fracture modeling. Figure 4 shows the oil production and pressure profile for one of the wells in a studied carbonate fractured reservoir with four different fracture type combinations [14]. Red dots represent the observed production and pressure data, whereas the curves are the simulation results. Realistic predictions are achieved when all effective open fractures are included in the model, although the hairy fractures do not impact the prediction in the study well. Therefore, proper fracture identification and characterization will assist in better history-matching processes for the reservoir under study. Most importantly, fracture properties should not be sadistically modified by local adjustment or multipliers, which might result in a fictitious simulation model without future prediction capability.
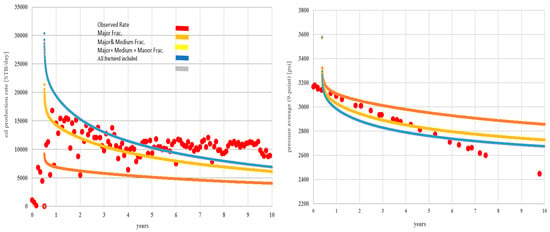
Figure 4.
Oil production rates and pressure under natural depletion [14].
3.2. Secondary Recovery
After the primary production diminishes, the secondary production typically results in gas injection or a waterflood. Oil production depends on the supply of injected water or gas during water or gas floodings. During this stage of recovery, oil production depends on the supply of injected agents. In water-wet reservoirs, the water level rises through fractures, and water injection often starts after increased water saturation. However, due to imbibition, water starts encroaching into the matrix, gradually displacing the oil. Hence, most of the oil is produced from the fracture network before the water breakthrough [55]. The fractures are filled with water upon breakthrough, and then, oil production from the matrix commences [56].
In a model describing a five-spot water flood with major, medium, and minor fractures, minor fractures hardly contributed to the recovery [26]. The results showed that fracture networks performed similarly in the early period, but later major-only fracture networks performed worse when the medium fracture was excluded. Based on the same model with different fracture properties, a relatively small number of fractures carried almost all the injected water to the production well [34]. Yet, fractures might behave as capillary barriers to imbibition and reduce oil recovery, even if they are more permeable than the matrix [35].
In the case of gas injection, faster breakthrough times were observed in fractured reservoirs. The significant permeability difference between fractures and the matrix can cause high injection rates and pressure buildup in the fractures, leading to premature breakthroughs and decreased oil recovery [14]. In addition, the performance is more dependent on fracture permeability changes during gas injection than waterflooding. Horizontal wells performed better than vertical wells, mostly related to enhanced gravity effects [26]. In addition, when the medium fractures are excluded, the recovery is underestimated. The gas/oil ratio behavior led to overestimating the produced gas quantity in the early period. Later, the trend shifted to underestimating the produced gas quantity [53]. It should be noted that the effect of minor fractures was minimum regarding oil recovery. At the same time, it had a noticeable effect on the gas and gas/oil ratio in the different periods of the process. Hence, all fractures should be included in the gas injection process.
The complex nature of fracture properties and their unpredictable geometry pose a challenge in predicting the impact of fractures on secondary recovery. Hence, a discrete fracture model (DFM) approach is advised for simulating and comprehending the behavior of fractured reservoirs.
3.3. Enhanced Oil Recovery
Most known EOR methods can be applied to fractured reservoirs, provided the injection agent rate is optimized [5]. In addition, related mechanisms, such as spontaneous imbibition, gravity drainage, etc., for the fractured reservoir should be boosted. Rock and fluid interactions and molecular diffusion effectively impact recovery; in contrast, an oil-wet rock matrix might hinder the oil recovery in some EOR processes [57,58]. However, spontaneous imbibition in water-wet rock and gravity drainage are important production mechanisms in naturally fractured reservoirs [5,12,31,53,59]. The matrix system is mostly bounded by a fracture system with high conductivity. The oil in the fracture is favorably produced through water injection due to its high conductivity. However, rock wettability can work against the water injection process in some reservoirs. When injected, water tends to ascend and trespasses the oil bank creating fingers and an early breakthrough for the matrix system; the predominant recovery mechanism is spontaneous imbibition, which is driven by capillary pressure [60]. The imbibition rate is related to the mobilities ratio and can be either counter-current or co-current displacement [61,62,63,64]. The spontaneous imbibition mechanism is more efficient in the water-invaded zone, where capillary forces cause water to be absorbed into the rock, resulting in oil production in the fractures. During the imbibition process, co-current production always takes precedence over counter-current production.
Moreover, capillary forces determine fluid exchange between matrix and fracture. The matrix capillary pressure curve differs from the fracture network in a water-wet case. When this happens, the pressure of oil inside the matrix is higher compared to that of the fracture. As a result, water spontaneously imbibes, and oil expels from the matrix to the fracture without difficulty. However, this is not the case in an oil-wet system.
Gas injection has a wide range of applications as an EOR process for fractured reservoirs; due to the good injectivity compared to water or chemical EOR Methods. The gravity drainage mechanism is enhanced due to the high permeable fractures that gas prefers to flow through. Depending on reservoir conditions, the miscible and immiscible gas injection might be feasible as an EOR process [65]. Gravity drainage is the controlling mechanism of oil recovery and acts as the main driving mechanism, where the gas displaces the oil (wetting phase) out of the rock. Because of the significant density difference, gas-assisted gravity drainage (GAGD) is an efficient production mechanism in the gas-invaded zone [31]. Thus, the GAGD mechanism should be reinforced during gas injection processes. The basic principle of gravity drainage mechanism can be described by an oil-filled matrix block surrounded by fractures filled totally or partially with gas. Oil is displaced through gravity drainage and gas diffusion in the matrix, displacing the oil. Fracture and matrix properties can hinder or accelerate the process. Higher recovery can be attained when the permeability of the vertical fracture is higher than the horizontal one [58]. Sufficiently high depth with large reservoir blocks in the direction of gravity provides better oil re-imbibition from matrix to matrix [66].
For thermal processes such as steam and in situ combustion, in the form of steam-assisted gravity drainage (SAGD and in the form of combustion-assisted gravity drainage (COGD)), the orientation of the fractures affects the steam expansion and the combustion propagation from the injection to production wells [67,68,69,70,71]. A simplified two-dimension model fractured system of a matrix surrounded by fractures studied by Kharrat and his co-workers is shown in Figure 5 [70]. One common observation was the overall shape of the front changes compared to the concave shape of the conventional reservoirs for all thermal and non-thermal recovery methods [67,68,69,70,71,72,73,74]. The geometrical fractures properties, such as orientation, density, location, and fracture networks, affected the process performance [67,68,69,70,71,72,73,74].
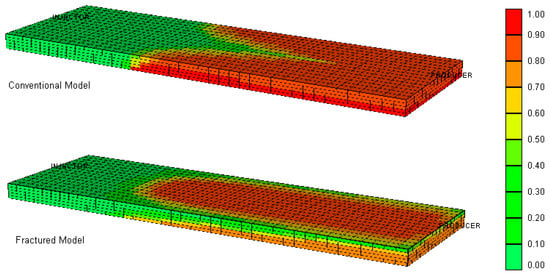
Figure 5.
Oil saturation profile for conventional (top) and fractured (bottom) models. Red refers to oil saturations, whereas green refers to the depleted zoned (So = 0) [70].
For the combustion process, the presence of fractures results in lower combustion front temperature and the formation of the water bank in the fractured zone. The generated water bank prevents oxygen from breaking through fractures into the production well. Water imbibition from the fractures into the matrix can be considered an oil depletion mechanism for the fractured reservoir [70].
For the steam injection, simulation results showed that vertical fractures enhanced SAGD recovery achievable from NFR compared to only horizontal fractures. Higher horizontal fracture density further reduces the ultimate oil recovery since the consequent set of horizontal fractures restricts the steam chamber development more [67].
Fractures can enhance the SAGD and COGD performance by enabling a larger contact area between hot fluid (air and steam) and oil. Vertical fractures increase the performance by spreading the hot chamber shape, whereas horizontal fractures mitigate the effectiveness of the process [67,68,69,70,71]. Hence, a negative impact on oil production results from horizontal fractures, while vertical fractures enhance production. Most reported EOR gravity drainage process studies observed oil production enhancement in the presence of horizontal fractures [67,70,71,72,73,74]. The vapor-assisted gravity drainage (VAGD) process, also known as vapor-assisted petroleum extraction, can similarly gain advantages from fractures in heavy oil reservoirs, just like the SAGD and COGD processes [72,73,74]. Fractures assist in spreading the solvent over a wider area, thereby increasing the duration of interaction between vapor and oil.
Poor sweep efficiency is common in most gas-based enhanced oil recovery (EOR) processes due to gravity override and unfavorable mobility conditions. Hence, mobility control is necessary to enhance sweep efficiency and make the gas-based EOR processes effective.
The water alternating gas method performs better than water or gas injection due to overcoming the underride (water) and overriding (gas) phenomenon. The WAG in naturally fractured reservoirs is feasible if the viscous and capillary forces dominate over gravity [5,75]. In addition, the larger contrast in the fractures and matrix permeabilities is important for a successful application [5].
Foam was used to divert the gas from the fractures into the matrix through gas mobility reduction and wettability alteration. However, harsh fractured reservoir conditions such as high salinity and temperature might hinder the application of foam and other chemicals in fractured reservoirs [31,46,65,76,77]. Foam-assisted gas injection processes’ performance for fractured reservoirs was reported in the literature [76,77]. Fracture properties and foam generation methods might affect the recovery performance [78,79]. The results of in situ foam generation in fractures, as opposed to the injection of pre-generated foam, showed bubble size generation. The in situ generation resulted in larger bubble sizes, four times bigger than pre-generated foam. This difference in bubble size was linked to the number of “snap-off sites” in the fractures compared to the number of snap-off sites in the foam generator [80]. The fracture aperture and the bubble size ratio also impact sweep efficiency. Foam can be used along the WAG process as foam-assisted gravity drainage (FAWAG) to enhance recovery [31]. A recent study showed that fracture networks’ impact is process deepening [53]. The FAWAG process was more sensitive than the WAG and the continuous gas injection process.
The performance of EOR methods was quantified in fractured reservoirs based on acting forces such as viscous, capillary, and gravity [5]. Both gravity number and capillary number can be used to control the behavior of fluids in a fractured reservoir, but it depends on the specific flow mechanism that is being studied. The behavior of viscous fingering is determined by the dimensionless capillary number and gravity segregation by the gravity number [5,74]. These parameters are used to compare fluid behavior and must be considered accordingly. It is important to mention that these numbers do not consider the influence of fracture properties and cannot offer a thorough comprehension of fluid behavior.
Chemicals such as surfactants and polymers were implemented in fractured reservoirs; however, most reported applications are at the pilot scale [80]. The surfactants are mainly used for interfacial tension and wettability alteration of mixed or oil-wet reservoirs, whereas polymers are for mobility control. When surfactants are used, water breakthrough through the fracture is delayed in oil-wet rocks. In water-wet cases, water imbibes in the matrix blocks resulting in the oil displacement from the matrix blocks towards the fractures [81]. The gravity mechanism is more dominated when surfactants are combined with polymers (SP) due to the lower capillary pressure. However, a breakthrough may occur faster for high fracture permeability than the matrix.
Finally, the use of smart water and carbonate water for fractured carbonate reservoirs is worthy of consideration [82,83,84]. These methods offer several advantages over traditional EOR techniques, including improved oil displacement, increased oil recovery, and reduced water production. In carbonate water flooding, carbonate-rich water is injected into the reservoir to mobilize and displace trapped oil. The carbonate in the water reacts with the rock matrix, potentially changing the fracture and matrix permeabilities and leading to enhanced sweep efficiency [82]. Recent studies indicate that these reactions are more active in fractures than in the matrix [84]. Additional studies are necessary to fully understand the influence of carbonated and smart water flooding on the fracture network and the potential production mechanisms that might develop.
4. Summary and Conclusions
It is crucial to comprehend the effects of fractures on production, which can be both positive and negative, to optimize recovery in fractured reservoirs. Accurate modeling is imperative for the success of any secondary or enhanced oil recovery method chosen for implementation in these types of reservoirs. Reservoir models are usually tuned based on the production history in the primary and secondary stages of recovery. However, precise fracture characterization in line with good reservoir characterization is essential in obtaining a reliable reservoir description in the history-matching process. Data, including image logs, faults maps, curvature maps, mud loss maps, productivity indexes, etc., are essential for fracture and reservoir characterizations. The fracture types and density logs can be obtained and classified based on the fractures extracted from the image logs from which a continuous fracture network (CFN) can be constructed. Consequently, a three-dimension DFN model can be generated from the CFN model, providing a basis for a reliable dynamic simulation model and a deep understanding of the production challenges of fractured reservoirs and their impact on oil production in naturally fractured reservoirs.
All conventional EOR methods can be implemented for fractured reservoirs; however, the fracture characteristics and orientation should be considered, and gravity drainage should be enhanced through injection rate optimization and precise well locations. This review indicates that fracture type identification and characterization are vital for providing a more realistic dynamic simulation model by integrating geoscience, reservoir, and production data. The fracture types’ contributions differ in the primary recovery and EOR processes. Almost all fractures contribute to production in the primary recovery, while major fractures mainly contribute to production in the secondary and tertiary stages. In water flooding, the displacement is achieved mostly by the primary (major) fractures, and secondary fractures have a minor effect on the oil displacement from the injection to production wells. Gas-assisted gravity drainage is more beneficial than continued gas injection for the fractured reservoir, especially for reservoirs with high vertical fracture density. For thermal processes where the gravity drainage is assisted, the orientation of the fractures affects the chamber propagation and expansion from the injection to production wells. Vertical fractures and their intensity align with the oil recovery enhancement, while horizontal fracture hinders recovery.
Extensive research was conducted in the last two decades with the objective of more precise identification, characterization, and modeling of fracture networks. The main theme of the published work is related mainly to; integrating data from multiple sources, machine learning, microseismic monitoring, fracture mapping, and integrated reservoir modeling. Data from well logs, core samples, and seismic surveys are used to create a more comprehensive fracture network model, while machine learning techniques are used to analyze large amounts of data and improve fracture prediction.
A comprehensive representation of the reservoir is constructed by combining geological, geomechanical, drilling, reservoir, and production data. Using fracture mapping techniques helps identify fracture patterns in the reservoir and comprehend fluid movement through the fracture network. Optimal characterization and modeling of the fracture network necessitate the integration of multiple techniques and sources of data. Model accuracy and production forecast realism can be improved by aligning the models with field data, such as production and pressure data.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Thuwaini, J.S.; Alwan, A.K.; Ranjan, A. Uncertainty Analysis of a Fractured Carbonate Reservoir. In Proceedings of the SPE Middle East Oil and Gas Show and Conference, Manama, Bahrain, 15–18 March 2009; p. SPE-120722-MS. [Google Scholar]
- Khosravi, M.; Rostami, B.; Fatemi, S. Uncertainty Analysis of a Fractured Reservoir’s Performance: A Case Study. Oil Gas Sci. Technol.-Rev. d’IFP 2012, 67, 423–433. [Google Scholar] [CrossRef]
- Kharrat, R.; Mahdavi, S.; Ghorbani, D. A Comprehensive EOR Study of a Highly Fractured matured field-Case Study, SPE 153311. In Proceedings of the 74th EAGE Conference and Exhibition incorporating EUROPEC 2012, Copenhagen, Denmark, 4–7 June 2012. [Google Scholar]
- Demyanov, V.; Gopa, K.; Arnold, D.; Elfeel, M.A. Production Optimisation under Uncertainty in Fractured Reservoirs. In Proceedings of the ECMOR 2014, 14th European Conference on the Mathematics of Oil Recovery, Catania, Italy, 8–11 September 2014. [Google Scholar]
- Kharrat, R.; Zallaghi, M.; Ott, H. Performance Quantification of Enhanced Oil Recovery Methods in Fractured Reservoirs. Energies 2021, 14, 4739. [Google Scholar] [CrossRef]
- De Hoop, S.; Voskov, D.V.; Bertotti, G.; Barnhoorn, A. An Advanced Discrete Fracture Methodology for Fast, Robust, and Accurate Simulation of Energy Production From Complex Fracture Networks. Water Resour. Res. 2022, 58, e2021WR030743. [Google Scholar] [CrossRef]
- Guerriero, V.; Mazzoli, S.; Iannace, A.; Vitale, S.; Carravetta, A.; Strauss, C. A permeability model for naturally fractured carbonate reservoirs. Mar. Pet. Geol. 2013, 40, 115–134. [Google Scholar] [CrossRef]
- Tiab, D.; Donalson, C. Petrophysics (Fourth Edition) Theory and Practice of Measuring Reservoir Rock and Fluid Transport Properties, Chapter 8—Naturally Fractured Reservoirs; Gulf Professional Publishing: Oxford, UK, 2016; pp. 415–448. [Google Scholar]
- Lei, Q.; Latham, J.-P.; Tsang, C.-F. The use of discrete fracture networks for modeling coupled geomechanical and hydrological behavior of fractured rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Ukar, E.; Laubach, S.E.; Hooker, J.N. Outcrops as guides to subsurface natural fractures: Example from the Nikanassin Formation tight-gas sandstone, Grande Cache, Alberta foothills, Canada. Mar. Pet. Geol. 2019, 103, 255–275. [Google Scholar] [CrossRef]
- Aghli, G.; Mossavi-Harami, R.; Mohammadian, R. Reservoir heterogeneity and fracture parameter determination using electrical image logs and petrophysical data (a case study, carbonate Asmari Formation, Zagros Basin, SW Iran). Pet. Sci. 2020, 17, 51–69. [Google Scholar] [CrossRef]
- Aljuboori, F.A.; Lee, J.H.; Elraies, K.A.; Stephen, K.D. Effect of fracture characteristics on history matching in the Qamchuqa reservoir: A case study from Iraq. Carbonates Evaporites 2020, 35, 87. [Google Scholar] [CrossRef]
- Hosseinzadeh, S.; Kadkhodaie, A.; Reazaee, R.; Kadkhodaie, R. Discrete fracture modeling by integrating image logs, seismic attributes, and production data: A case study from Ilam and Sarvak Formations, Danan Oilfield, southwest of Iran. J. Pet. Explor. Prod. Technol. 2022, 13, 1053–1083. [Google Scholar] [CrossRef]
- Pejic, M.; Kharrat, R.; Kadkhodaaie, A.; Azizmohammadi, S.; Ott, H. Impact of fracture types on the oil recovery in naturally fractured reservoirs. Energies 2022, 15, 7321. [Google Scholar] [CrossRef]
- Kolapo, P.; Ogunsola, N.O.; Munemo, P.; Alewi, D.; Komolafe, K.; Giwa-Bioku, A. DFN: An Emerging Tool for Stochastic Modelling and Geomechanical Design. Eng 2023, 4, 174–205. [Google Scholar] [CrossRef]
- Moreno, M.J.; Gurpinar, O.; Liu, Y. A Holistic Approach to EOR Screening in Dual-Porosity Naturally Fractured Reservoirs. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 11–13 August 2015. SPE-174577-Ms. [Google Scholar]
- Delamaide, E.; Batôt, G.; Alshaqsi, A.; Alkindy, A.; Al-Mejni, R. Enhanced Oil Recovery in Naturally Fractured Reservoirs: State of the Art and Future Perspectives. In Proceedings of the SPE Conference at Oman Petroleum & Energy Show, Muscat, Oman, 21–23 March 2022. SPE-200076-MS. [Google Scholar]
- Zuo, L.; Tan, X.; Yu, W.; Hu, X. Fracture Detection and Numerical Modeling for Fractured Reservoirs. Energies 2019, 386, 15. [Google Scholar] [CrossRef]
- Chesnaux, R.; Allen, D.M.; Jenni, S. Regional fracture network permeability using outcrop scale measurements. Eng. Geol. 2009, 108, 259–271. [Google Scholar] [CrossRef]
- Li, J.; Pei, Y.; Jiang, H.; Zhao, L.; Li, L.; Zhou, H.; Zhao, Y.; Zhang, Z. Tracer Flowback Based Fracture Network Characterization in Hydraulic Fracturing. In Proceedings of the Abu Dhabi International Petroleum Exhibition & Conference, Abu Dhabi, United Arab Emirates, 7–10 November 2016. SPE-183444-MS. [Google Scholar]
- Li, L.; Pinprayong, V.; Meng, F.; Jiang, H.; Li, J. Fracture Network Evaluation Using Tracer Flowback: A Case Study. In Proceedings of the SPE Symposium: Production Enhancement and Cost Optimisation, Kuala Lumpur, Malaysia, 7–8 November 2017. SPE-189273-MS. [Google Scholar]
- Gong, J.; Rossen, W. Shape factor for dual-permeability fractured reservoir simulation: Effect of non-uniform flow in 2D fracture network. Fuel 2016, 184, 81–88. [Google Scholar] [CrossRef]
- Wenli, Y.; Sharifzadeh, M.; Yang, Z.; Xu, G.; Fang, Z. Assessment of fracture characteristics controlling fluid flow performance in discrete fracture networks (DFN). J. Pet. Sci. Eng. 2019, 178, 1104–1111. [Google Scholar] [CrossRef]
- Zimmerman, R.; Bodvarsson, G. Hydraulic Conductivity of Rock Fractures. Transp. Porous Media 1996, 23, 1–30. [Google Scholar] [CrossRef]
- Gilman, J.R.; Kazemi, H. Improvements in Simulation of Naturally Fractured Reservoirs. SPE J. 1983, 23, 695–707. [Google Scholar] [CrossRef]
- Pejic, M. Mechanistic Study of Fracture Types Effect on Oil Production. Master’s Thesis, Montanuniversität Leoben, Leoben, Austria, 2021. [Google Scholar]
- Pooladi-Darvish, M.; Firoozabadi, A. Cocurrent and Counter-current Imbibition in a Water-Wet Matrix Block. SPE J. 2000, 5, 3–11. [Google Scholar] [CrossRef]
- Moghaddam, M.B.; Rasaei, M.R. Experimental Study of the Fracture and Matrix Effects on Free-Fall Gravity Drainage with Micromodels. SPE J. 2014, 20, 324–336. [Google Scholar] [CrossRef]
- Agada, S.; Geiger, S.; Doster, F. Wettability, hysteresis, and fracture–matrix interaction during CO2 EOR and storage in fractured carbonate reservoirs. Int. J. Greenh. Gas Control. 2016, 46, 57–75. [Google Scholar] [CrossRef]
- Zobeidi, K.; Shafie, M.M. Ganjeh-Ghazvini M, The effect of gravity drainage mechanism on oil recovery by reservoir simulation; a case study in an Iranian highly fractured reservoir. J. Pet. Explor. Prod. Technol. 2022, 12, 1633–1647. [Google Scholar] [CrossRef]
- Gugl, R.; Kharrat, R.; Shariat, A.; Ott, H. Evaluation of Gas-based EOR Methods in Gas Invaded Zones of Fractured Carbonate Reservoir. Energies 2022, 15, 4921. [Google Scholar] [CrossRef]
- Harimi, B.; Masihi, M.; Ghazanfari, M.H. An insight into the formation of liquid bridge and its role on fracture capillary pressure during gravity drainage in fractured porous media. Can. J. Chem. Eng. 2021, 99, S212–S231. [Google Scholar] [CrossRef]
- Maerten, L.; Gillespie, P.A.; Daniel, J.M. Three-dimensional geomechanical modeling for constraint of sub seismic fault simulation. AAPG Bull. 2006, 90, 1337–1358. [Google Scholar] [CrossRef]
- Gong, J.; Rossen, W. Modeling flow in naturally fractured reservoirs: Effect of fracture aperture distribution on dominant sub-network for flow. Pet. Sci. 2017, 14, 138–154. [Google Scholar] [CrossRef]
- Gong, J.; Rossen, W. Characteristic fracture spacing in primary and secondary recovery for naturally fractured reservoirs. Fuel 2018, 2213, 470–485. [Google Scholar] [CrossRef]
- Heel, A.P.G.V.; Boerrigter, P.M.; Dorp, J.J.V. Thermal and Hydraulic Matrix-Fracture Interaction in Dual-Permeability Simulation. SPE Res. Eval. Eng. 2008, 11, 735–749. [Google Scholar] [CrossRef]
- Warren, J.E.; Root, P.J. The Behavior of Naturally Fractured Reservoirs. SPE J. 1963, 3, 245–255. [Google Scholar] [CrossRef]
- Quandalle, P.; Sabathier, J.C. Typical features of a multipurpose reservoir simulator. SPE Reserv. Eng. 1989, 4, 475–480. [Google Scholar] [CrossRef]
- Ghaedi, M.; Masihi, M.; Heinemann, Z.E.; Ghazanfari, M.H. History matching of naturally fractured reservoirs based on the recovery curve method. J. Pet. Sci. Eng. 2015, 126, 211–221. [Google Scholar] [CrossRef]
- Wong, D.L.Y.; Doster, F.; Geiger, S.; Francot, E.; Gouth, F. Fluid Flow Characterization Framework for Naturally Fractured Reservoirs Using Small-Scale Fully Explicit Models. Transp. Porous Media 2020, 134, 399–434. [Google Scholar] [CrossRef]
- Xu, Y.; Sepehrnoori, K. Development of an Embedded Discrete Fracture Model for Field-Scale Reservoir Simulation with Complex Corner-Point Grids. SPE J. 2019, 24, 1552–1575. [Google Scholar] [CrossRef]
- Bosma, S.; Hajibeygi, H.; Tene, M.; Tchelepi, H.A. Multiscale finite volume method for discrete fracture modeling on unstructured grids (MS-DFM). J. Comput. Phys. 2017, 351, 145–164. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D. An efficient embedded discrete fracture model based on mimetic finite difference method. J. Pet. Sci. Eng. 2016, 145, 11–21. [Google Scholar] [CrossRef]
- CMG Webinar- Advances in Fractured Reservoir Modelling Using DFN. 2021. Available online: https://www.youtube.com/watch?v=h9h9Ou6BP4E (accessed on 9 February 2023).
- Kleppe, J.; Morse, R. Oil Production from Fractured Reservoirs by Water Displacement. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, Houston, TX, USA, 6–9 October 1974. SPE-5084-MS. [Google Scholar]
- Xu, Z.-X.; Li, S.-Y.; Li, B.-F.; Chen, D.-Q.; Liu, Z.-Y.; Li, Z.-M. A review of development methods and EOR technologies for carbonate reservoirs. Pet. Sci. 2020, 17, 990–1013. [Google Scholar] [CrossRef]
- Khelifa, C.; Zeddouri, A.; Djabes, F. Influence of natural fractures on oil production of unconventional reservoirs. Energy Procedia 2014, 50, 360–367. [Google Scholar] [CrossRef]
- Mi, L.; An, C.; Cao, Y.; Yan, B.; Jiang, H.; Pei, Y.; Killough, J. A Guideline on Optimizing Fracture Modeling for Fractured Reservoir Simulation. In Proceedings of the SPE Asia Pacific Hydraulic Fracturing Conference, Beijing, China, 24–26 August 2016. SPE-181814-MS. [Google Scholar]
- Bahrami, H.; Rezaee, R.; Hossain, M. Characterizing natural fractures in tight gas reservoirs. J. Pet. Explor. Prod. Technol. 2012, 2, 107–115. [Google Scholar] [CrossRef]
- Doe, T.; Lacazette, A.; Dershowitz, W.; Knitter, C. Evaluating the Effect of Natural Fractures on Production from Hydraulically Fractured Wells Using Discrete Fracture Network Models. In Proceedings of the Unconventional Resources Technology Conference URTeC, Denver, CO, USA, 12–14 August 2013; p. 10. [Google Scholar]
- Wei, Y.; Xiaohu, H.; Malin, L.; Weihong, W. Investigation of the Effect of Natural Fractures on Multiple Shale-Gas Well Performance Using Non-Intrusive EDFM Technology. Energies 2019, 12, 16. [Google Scholar]
- Erfani, H.; Malekabadi, A.K.; Ghazanfari, M.H.; Rostami, B. Experimental and Modelling Study of Gravity Drainage in a Three-Block System. Transp. Porous Media 2021, 136, 471–494. [Google Scholar] [CrossRef]
- Nouri, A. Impact of Fractures Networks on Gas-Based EOR Methods. Ph.D. Thesis, University of Leoben, Leoben, Austria, 2022. [Google Scholar]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Res. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Tong, K.; Liu, H.; Zhang, Y. Three-dimensional physical modeling of waterflooding in metamorphic fractured reservoirs. Pet. Explor. Dev. 2015, 42, 538–544. [Google Scholar] [CrossRef]
- Rezaveisi, M.; Ayatollahi, S.; Rostami, B. Experimental Investigation of Matrix Wettability Effects on Water Imbibition in Fractured Artificial Porous Media. J. Pet. Sci. Eng. 2012, 86, 165–171. [Google Scholar] [CrossRef]
- Udoh, F.D.; Igbafe, A.I.; Okon, A.N. Gas-Oil Gravity Drainage and Reinfiltration in Naturally Fractured Reservoirs. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 4–6 August 2015. SPE-178271-MS. [Google Scholar]
- Silva, R.; Maini, B. Evaluation of Gas-Assisted Gravity Drainage GAGD in Naturally Fractured Reservoirs NFR. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 11–13 April 2016; SPE-179585-MS. p. 17. [Google Scholar]
- Saidi, M.A. Simulation of Naturally Fractured Reservoirs. In Proceedings of the 1983 SPE Symposium on Reservoir Simulation, San Francisco, CA, USA, 15–18 November 1983. SPE-12270-MS. [Google Scholar]
- Meng, Q.; Liu, H.; Wang, J. A critical review on fundamental mechanisms of spontaneous imbibition and the impact of boundary condition, fluid viscosity and wettability. Adv. Geo-Energy Res. 2017, 1, 1–17. [Google Scholar] [CrossRef]
- Hamidpour, E.; Mirzaei-Paiaman, A.; Masihi, M. Experimental study of some important factors on non-wetting phase recovery by cocurrent spontaneous imbibition. J. Nat. Gas Sci. Eng. 2015, 27, 1213–1228. [Google Scholar] [CrossRef]
- Hatiboglu, C.U.; Babadagli, T. Experimental and visual analysis of co- and counter-current spontaneous imbibition for different viscosity ratios, interfacial tensions, and wettabilities. J. Pet. Sci. Eng. 2010, 70, 214–228. [Google Scholar] [CrossRef]
- Karpyn, Z.T.; Halleck, P.M.; Grader, A.S. An experimental study of spontaneous imbibition in fractured sandstone with contrasting sedimentary layers. J. Pet. Sci. Eng. 2009, 67, 48–56. [Google Scholar] [CrossRef]
- Mason, G.; Morrow, N.R. Developments in spontaneous imbibition and possibilities for future work. J. Pet. Sci. Eng. 2013, 110, 268–293. [Google Scholar] [CrossRef]
- Mogensen, K.; Masalmeh, S.H. A review of EOR techniques for carbonate reservoirs in challenging geological settings. J. Pet. Sci. Eng. 2020, 195, 107889. [Google Scholar] [CrossRef]
- Aghabarari, A.; Ghaedi, M.; Riazi, M. Prediction of oil recovery in naturally fractured reservoirs subjected to reinfiltration during gravity drainage using a new scaling equation. Pet. Explor. Dev. 2020, 47, 1307–1315. [Google Scholar] [CrossRef]
- Fatemi, S.; Kharrat, R.; Vossoughi, S. Investigation of Steam Assisted Gravity Drainage (SAGD) and Expanding Solvent-SAGD (ES-SAGD) Process in Complex Fractured Models: Effects of Fractures’ Geometrical Properties. In Proceedings of the SPE Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 12–14 December 2011. SPE-150082-MS. [Google Scholar]
- Fatemi, R.; Kharrat, R.; Ghotbi, S. Toe-to-Heel Air Injection (THAI): Investigation of the Effect of Fractures Geometrical Properties on Process Performance. Energy Sources Part A Recovery Util. Environ. Eff. 2012, 33, 2067–2077. [Google Scholar] [CrossRef]
- Fatemi, S.; Kharrat, R.; Vossoughi, S. Investigation of Top-Down In-Situ Combustion Process in Complex Fractured Carbonate Models: Effects of Fractures’ Geometrical Properties. In Proceedings of the Canadian Unconventional Resources Conference, Calgary, AB, Canada, 15–17 November 2014. CSUG/SPE 149314. [Google Scholar]
- Fatemi, S.M.; Kharrat, R.; Vossoughi, S.; Ghotbi, C. Macroscopic Recovery Mechanisms of In-Situ Combustion Process in Heavy Oil Fractured Systems: Effect of Fractures Geometrical Properties and Operational Parameters. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 16–18 April 2012. SPE-154839-MS. [Google Scholar]
- Shojaiepour, A.; Kharrat, R.; Hashemi, A. Experimental and simulation of In situ combustion process in carbonated fractured porous media. J. Jpn. Pet. Inst. 2014, 57, 208–215. [Google Scholar] [CrossRef]
- Fatemi, S.M.; Kharrat, R. Assessment of Vapor Extraction (VAPEX) process performance in naturally fractured reservoirs. J. Pet. Sci. Eng. 2011, 75, 260–273. [Google Scholar] [CrossRef]
- Azin, R.; Kharrat, R.; Vossoughi, S.; Ghotbi, C. Study of The VAPEX Process in Fractured Physical Systems Using Different Solvent Mixtures. Oil Gas Sci. Technol. 2008, 63, 219–227. [Google Scholar] [CrossRef]
- Azin, R.; Kharrat, R.; Rostami, B.; Vossoughi, S. Theoretical Investigation of the VAPEX Process in Fractured Heavy Oil System at Reservoir Conditions. J. Pet. Sci. Eng. 2008, 60, 51–66. [Google Scholar] [CrossRef]
- Heeremans, J.; Esmaiel, T.; Kruijsdijk, C.V. Feasibility Study of WAG Injection in Naturally Fractured Reservoirs. In Proceedings of the SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK, USA, 22–26 April 2006; SPE-100034-MS. p. 10. [Google Scholar]
- Haugen, A.; Fernø, M.A.; Graue, A. Experimental Study of Foam Flow in Fractured Oil-Wet Limestone for Enhanced Oil Recovery. SPE Reserv. Eval. Eng. 2012, 15, 218–228. [Google Scholar] [CrossRef]
- Luo, H.; Mohanty, K.K. Modeling Near-Miscible Gas Foam Injection in Fractured Tight Rocks and Its Challenges. Energies 2021, 14, 1998. [Google Scholar] [CrossRef]
- Ocampo, A.; Restrepo, A.; Clavijo, J.; Mejia, J. Successful Foams EOR Field Pilot in a Naturally Fractured Reservoir by the Injection of the Foaming Agent Dispersed in the Gas Stream. In Proceedings of the SPE Improved Oil Recovery Conference, Virtual, 31 August–4 September 2020; SPE-200377-MS. p. 7. [Google Scholar]
- Ocampo, A.; Restrepo, A.; Lopera, S.; Mejia, J. Creation of Insitu EOR Foams by the Injection of Surfactant in Gas Dispersions-Lab Confirmation and Field Application. In Proceedings of the SPE Improved Oil Recovery Conference, Tulsa, OK, USA, 14–18 April 2018; SPE-190219-MS. p. 8. [Google Scholar]
- Yadali, J. Chemical Flooding in Naturally Fractured Reservoirs: Fundamental Aspects and Field-Scale Practices. Oil Gas Sci. Technol. Rev. d’IFP Energ. Nouv. 2011, 66, 991–1004. [Google Scholar] [CrossRef]
- Cheng, X.; Kleppe, J.; Torsæter, O. Simulation Study of Surfactant Imbibition Mechanisms in Naturally Fractured Reservoirs. In Proceedings of the SPE Norway One Day Seminar, Bergen, Norway, 18 April 2018; SPE-191309-MS. p. 13. [Google Scholar]
- Akbar, M.I.; Agenet, N.; Kamp, A.M.; Gosselin, O.R. Evaluation and Optimisation of Smart Water Injection for Fractured Reservoir. In Proceedings of the SPE Europec featured at 80th EAGE Conference and Exhibition, Copenhagen, Denmark, 11–14 June 2018. SPE-190854-MS. [Google Scholar]
- Bakhshi, P.; Kharrat, R.; Hashemi, A.; Zallaghi, M. Experimental evaluation of carbonated waterflooding: A practical process for enhanced oil recovery and geological CO2 storage. Greenh. Gases Sci. Technol. 2018, 8, 238–256. [Google Scholar] [CrossRef]
- Al Karfy, L.; Kharrat, R.; Ott, H. Mechanistic study of the carbonated smart water in carbonate reservoirs. Greenh. Gases Sci. Technol. 2021, 11, 661–681. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).