Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building
Abstract
1. Introduction
2. Materials and Methods
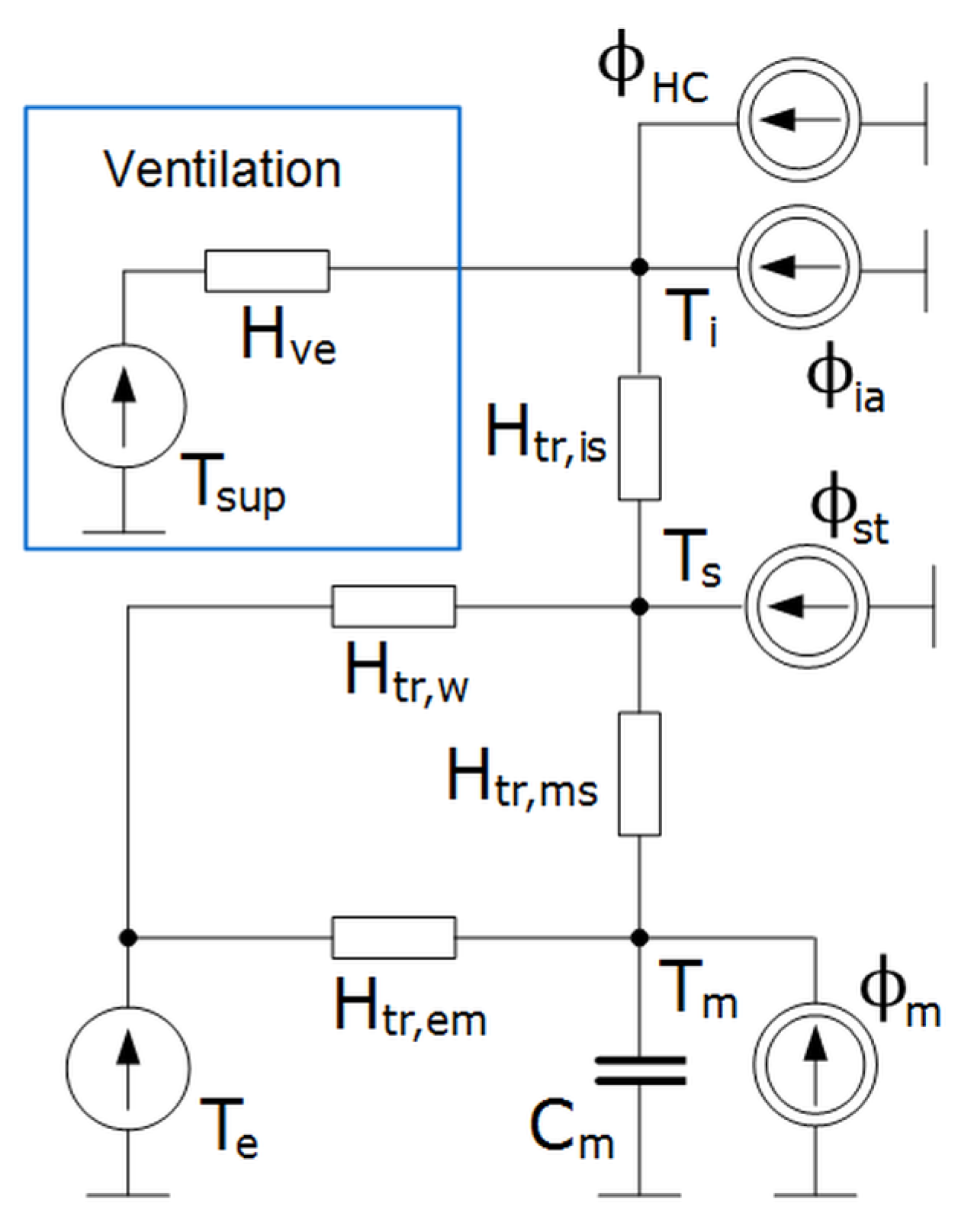
2.1. The 5R1C Model
2.2. Experimental Setup
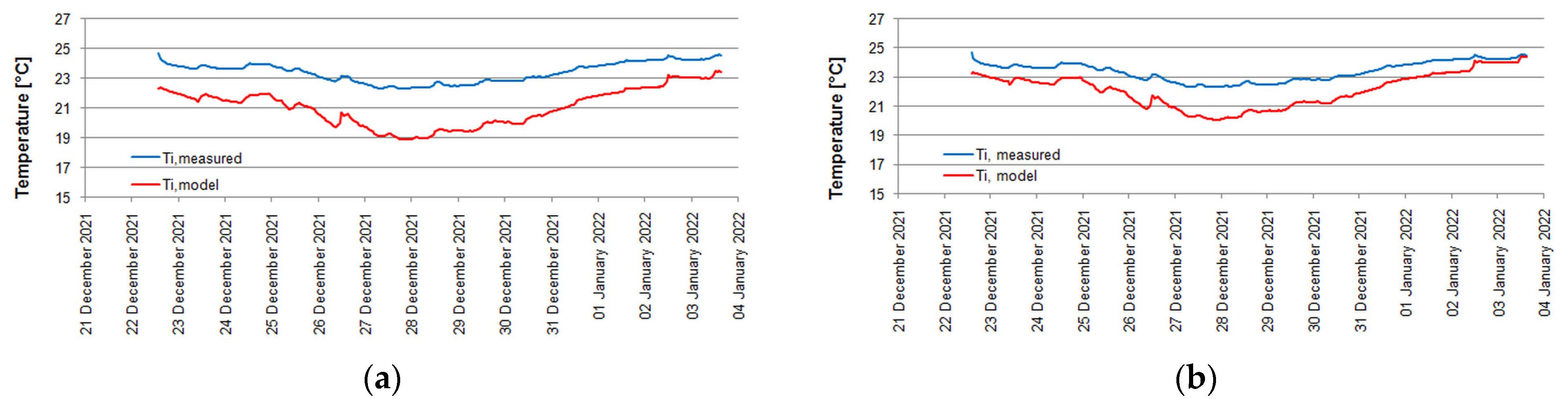
2.3. Evaluation of the Model
3. Results and Discussion
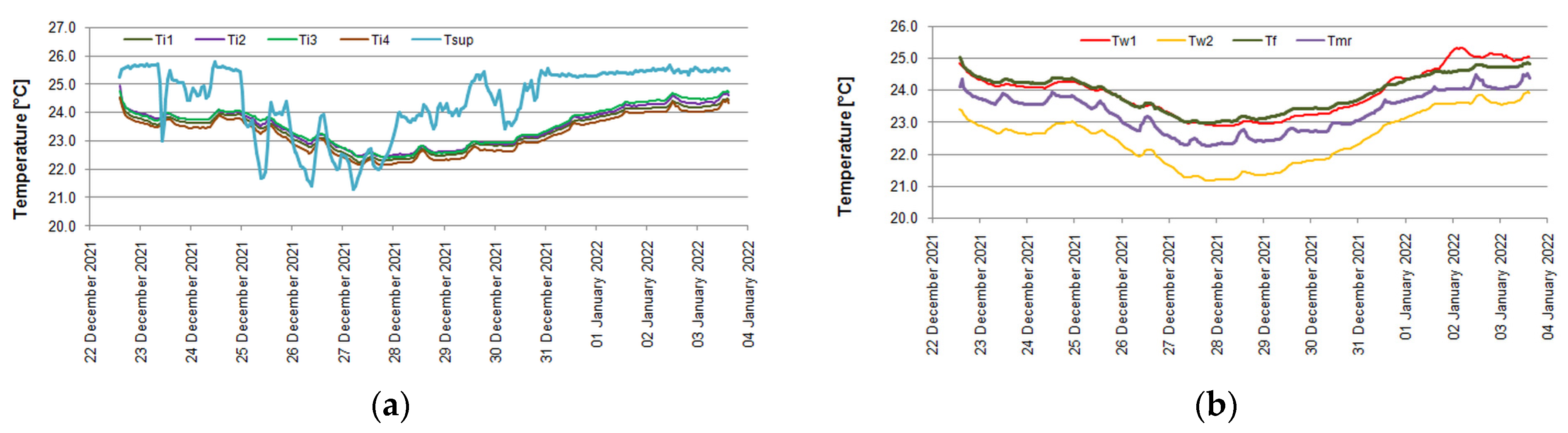
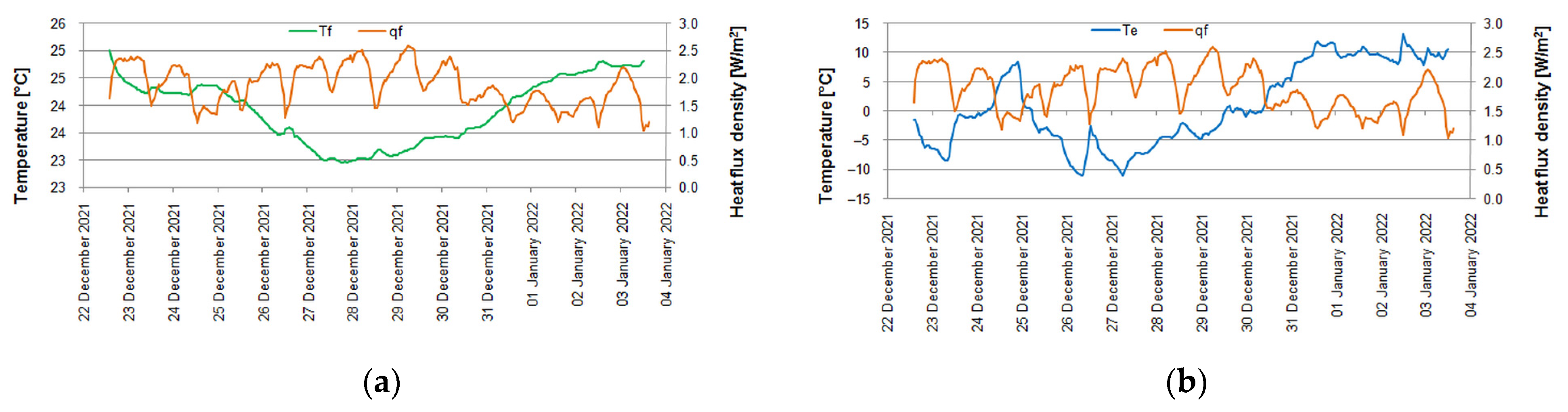
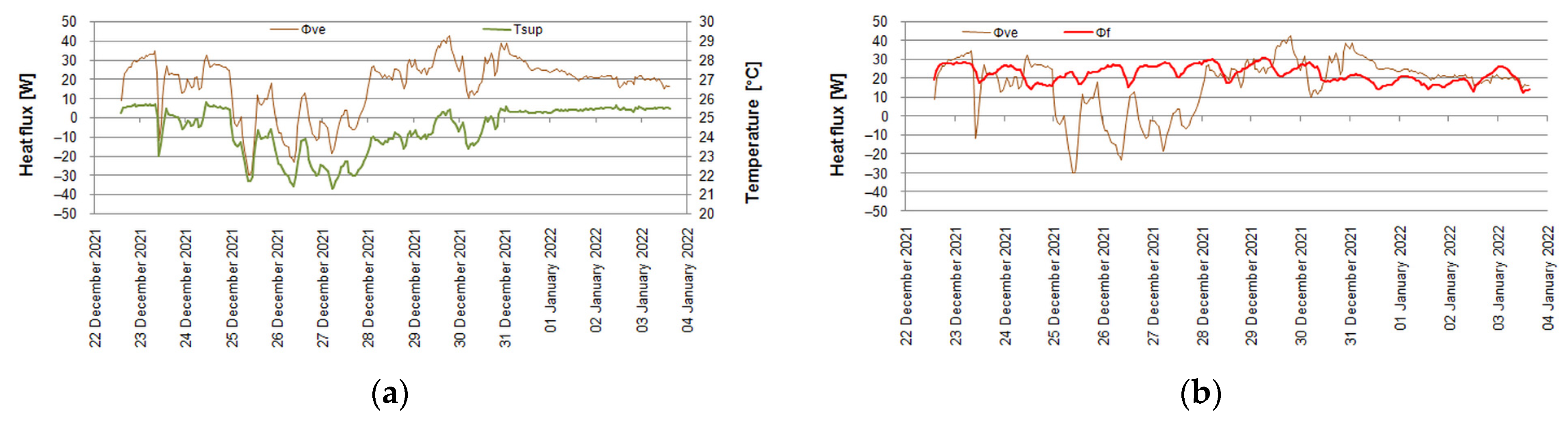
3.1. Measurements
3.2. Simulations
4. Conclusions
Funding
Conflicts of Interest
Symbols
| Af | total conditioned (heated and/or cooled) floor area, m2 |
| Am | effective thermal mass area, m2 |
| Cm | thermal capacity of the building, J/K |
| Htr,em | external part of the Htr,op thermal transmission coefficient, W/K |
| Htr,is | coupling conductance, W/K |
| Htr,ms | internal part of the Htr,op thermal transmission coefficient, W/K |
| Htr,op | thermal transmission coefficient for thermally heavy envelope elements, W/K |
| Htr,w | thermal transmission coefficient for thermally light envelope elements, W/K |
| Hve | thermal transmission coefficient by ventilation air, W/K |
| Te | external (outdoor) air temperature, °C |
| Te;mn;an | mean annual temperature of outdoor air, °C |
| Te;max;m | maximum mean monthly temperature of outdoor air, °C |
| Ti | internal (indoor) air temperature, °C |
| Ti,C,set | set-point indoor air temperature for cooling, °C |
| Ti,H,set | set-point indoor air temperature for heating, °C |
| Tm | average air temperature in the duct, °C |
| Ts | central node temperature, °C |
| Tsup | supply air temperature, °C |
| ca | specific heat capacity of air, J/(kg∙K) |
| ρa | air density, kg/m3 |
| φia | heat flow rate to internal air node, W |
| φint | heat flow rate due to internal heat sources, W |
| φm | heat flow rate to mass node, W |
| φsol | heat flow rate due to solar heat sources, W |
| φst | heat flow rate to central node, W |
| φve | heat flow rate by ventilation, W |
| φHC | heating or cooling power supplied to or extracted from the indoor air node, W |
References
- Jędrzejuk, H.; Dybińnski, O. The influence of a heating system control program and thermal mass of external walls on the internal comfort in the Polish climate. Energy Procedia 2015, 78, 1087–1092. [Google Scholar] [CrossRef]
- Chodkowska-Miszczuk, J.; Szymanska, D. Modernisation of public buildings in Polish towns and the concept of sustainable building. Quaest. Geogr. 2014, 33, 89–99. [Google Scholar] [CrossRef]
- Nowak-Dzieszko, K.; Rojewska-Warchał, M. Thermal comfort of the individual flats of multi–family panel building. Tech. Trans. Civil. Eng. 2014, 5-B/2014, 201–206. [Google Scholar] [CrossRef]
- Sadowska, B. Effects of deep thermal modernization and use of renewable energy in public buildings in north-eastern Poland. In Proceedings of the 20th International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 26–28 May 2018; Malinovska, L., Osadcuks, V., Eds.; Latvia University of Life Sciences and Technologies: Jelgava, Latvia, 2018; pp. 1870–1875. [Google Scholar] [CrossRef]
- Michalak, P.; Szczotka, K.; Szymiczek, J. Energy Effectiveness or Economic Profitability? A Case Study of Thermal Modernization of a School Building. Energies 2021, 14, 1973. [Google Scholar] [CrossRef]
- Ratajczak, K.; Michalak, K.; Narojczyk, M.; Amanowicz, Ł. Real Domestic Hot Water Consumption in Residential Buildings and Its Impact on Buildings’ Energy Performance—Case Study in Poland. Energies 2021, 14, 5010. [Google Scholar] [CrossRef]
- Amanowicz, Ł.; Ratajczak, K.; Dudkiewicz, E. Recent Advancements in Ventilation Systems Used to Decrease Energy Consumption in Buildings—Literature Review. Energies 2023, 16, 1853. [Google Scholar] [CrossRef]
- Xu, Q.; Riffat, S.; Zhang, S. Review of Heat Recovery Technologies for Building Applications. Energies 2019, 12, 1285. [Google Scholar] [CrossRef]
- Zender–Świercz, E. A Review of Heat Recovery in Ventilation. Energies 2021, 14, 1759. [Google Scholar] [CrossRef]
- Attia, S.; Kosiński, P.; Wójcik, R.; Węglarz, A.; Koc, D.; Laurent, O. Energy efficiency in the Polish residential building stock: A literature review. J. Build. Eng. 2022, 45, 103461. [Google Scholar] [CrossRef]
- Firląg, S. Cost-Optimal Plus Energy Building in a Cold Climate. Energies 2019, 12, 3841. [Google Scholar] [CrossRef]
- Sowa, J.; Mijakowski, M. Humidity-Sensitive, Demand-Controlled Ventilation Applied to Multiunit Residential Building—Performance and Energy Consumption in Dfb Continental Climate. Energies 2020, 13, 6669. [Google Scholar] [CrossRef]
- Borowski, M. Hotel Adapted to the Requirements of an nZEB Building—Thermal Energy Performance and Assessment of Energy Retrofit Plan. Energies 2022, 15, 6332. [Google Scholar] [CrossRef]
- Zukowski, M. A Small Modular House as a Response to the Energy Crisis. Energies 2022, 15, 8058. [Google Scholar] [CrossRef]
- EN 12831; Heating Systems in Buildings—Method for Calculation of the Design Heat Load. International Organization for Standardization (ISO): Geneva, Switzerland, 2017.
- Barwińska Małajowicz, A.; Knapková, M.; Szczotka, K.; Martinkovičová, M.; Pyrek, R. Energy Efficiency Policies in Poland and Slovakia in the Context of Individual Well-Being. Energies 2023, 16, 116. [Google Scholar] [CrossRef]
- Rotar, N.; Badescu, V. Considerations on the implementation of the Passive House concept in South-Eastern Europe (Romania). Int. J. Green Energy 2011, 8, 780–794. [Google Scholar] [CrossRef]
- Dall’O’, G.; Sarto, L. Potential and limits to improve energy efficiency in space heating in existing school buildings in northern Italy. Energy Build. 2013, 67, 298–308. [Google Scholar] [CrossRef]
- Szul, T. Assessment of the accuracy of the approximate method used to estimate the heating power demand for single-family houses. J. Res. Appl. Agric. Eng. 2018, 63, 126–129. [Google Scholar]
- Szymiczek, J.; Szczotka, K.; Banaś, M.; Jura, P. Efficiency of a Compressor Heat Pump System in Different Cycle Designs: A Simulation Study for Low-Enthalpy Geothermal Resources. Energies 2022, 15, 5546. [Google Scholar] [CrossRef]
- PLoSkić, A.; Holmberg, S. Low-temperature ventilation pre-heater in combination with conventional room heaters. Energy Build. 2013, 65, 248–259. [Google Scholar] [CrossRef]
- Šimko, M.; Krajčík, M.; Šikula, O.; Šimko, P.; Kalús, D. Insulation panels for active control of heat transfer in walls operated as space heating or as a thermal barrier: Numerical simulations and experiments. Energy Build. 2018, 158, 135–146. [Google Scholar] [CrossRef]
- Krajčík, M.; Šimko, M.; Šikula, O.; Szabó, D.; Petráš, D. Thermal performance of a radiant wall heating and cooling system with pipes attached to thermally insulating bricks. Energy Build. 2021, 246, 111122. [Google Scholar] [CrossRef]
- Krajčík, M.; Arıcı, M.; Šikula, O.; Šimko, M. Review of water-based wall systems: Heating, cooling, and thermal barriers. Energy Build. 2021, 253, 111476. [Google Scholar] [CrossRef]
- Harsem, T.T.; Nourozi, B.; Behzadi, A.; Sadrizadeh, S. Design and Parametric Investigation of an Efficient Heating System, an Effort to Obtain a Higher Seasonal Performance Factor. Energies 2021, 14, 8475. [Google Scholar] [CrossRef]
- Javed, S.; Ørnes, I.R.; Dokka, T.H.; Myrup, M.; Holøs, S.B. Evaluating the Use of Displacement Ventilation for Providing Space Heating in Unoccupied Periods Using Laboratory Experiments, Field Tests and Numerical Simulations. Energies 2021, 14, 952. [Google Scholar] [CrossRef]
- Mao, Y.; Xie, H.; Zhang, X.; Hou, F.; Wang, M. Study on the Applicable Room Size Dimension of Stratum Ventilation for Heating Based on Multi-Criteria Analytic Hierarchy Process-Entropy Weight Model. Buildings 2023, 13, 381. [Google Scholar] [CrossRef]
- Ameen, A.; Choonya, G.; Cehlin, M. Experimental Evaluation of the Ventilation Effectiveness of Corner Stratum Ventilation in an Office Environment. Buildings 2019, 9, 169. [Google Scholar] [CrossRef]
- Ameen, A.; Cehlin, M.; Larsson, U.; Karimipanah, T. Experimental investigation of ventilation performance of different air distribution systems in an office environment—Cooling mode. Energies 2019, 12, 1354. [Google Scholar] [CrossRef]
- Ameen, A.; Cehlin, M.; Larsson, U.; Karimipanah, T. Experimental Investigation of Ventilation Performance of Different Air Distribution Systems in an Office Environment—Heating Mode. Energies 2019, 12, 1835. [Google Scholar] [CrossRef]
- Kong, X.; Xi, C.; Li, H.; Lin, Z. A comparative experimental study on the performance of mixing ventilation and stratum ventilation for space heating. Build. Environ. 2019, 157, 34–46. [Google Scholar] [CrossRef]
- Kowalski, P.; Szałański, P.; Cepiński, W. Waste Heat Recovery by Air-to-Water Heat Pump from Exhausted Ventilating Air for Heating of Multi-Family Residential Buildings. Energies 2021, 14, 7985. [Google Scholar] [CrossRef]
- Lin, Y.; Zhao, L.; Yang, W.; Hao, X.; Li, C.-Q. A review on research and development of passive building in China. J. Build. Eng. 2021, 42, 102509. [Google Scholar] [CrossRef]
- Diaz de Garayo, S.; Martínez, A.; Astrain, D. Optimal combination of an air-to-air thermoelectric heat pump with a heat recovery system to HVAC a passive house dwelling. Appl. Energy 2022, 309, 118443. [Google Scholar] [CrossRef]
- Kang, Y.; Ma, N.; Bunster, V.; Chang, V.W.-C.; Zhou, J. Optimizing the Passive House Planning Package simulation tool: A bottom-up dynamic approach to reduce building performance gap. Energy Build. 2022, 276, 112512. [Google Scholar] [CrossRef]
- Zaniboni, L.; Albatici, R. Natural and Mechanical Ventilation Concepts for Indoor Comfort and Well-Being with a Sustainable Design Perspective: A Systematic Review. Buildings 2022, 12, 1983. [Google Scholar] [CrossRef]
- La Fleur, L.; Moshfegh, B.; Rohdin, P. Measured and predicted energy use and indoor climate before and after a major renovation of an apartment building in Sweden. Energy Build. 2017, 146, 98–110. [Google Scholar] [CrossRef]
- La Fleur, L.; Rohdin, P.; Moshfegh, B. Energy Use and Perceived Indoor Environment in a Swedish Multifamily Building before and after Major Renovation. Sustainability 2018, 10, 766. [Google Scholar] [CrossRef]
- Liu, L.; Rohdin, P.; Moshfegh, B. Evaluating indoor environment of a retrofitted multi-family building with improved energy performance in Sweden. Energy Build. 2015, 102, 32–44. [Google Scholar] [CrossRef]
- Markiewicz-Zahorski, P.; Rucińska, J.; Fedorczak-Cisak, M.; Zielina, M. Building Energy Performance Analysis after Changing Its Form of Use from an Office to a Residential Building. Energies 2021, 14, 564. [Google Scholar] [CrossRef]
- Veršić, Z.; Binički, M.; Nosil Mešić, M. Passive Night Cooling Potential in Office Buildings in Continental and Mediterranean Climate Zone in Croatia. Buildings 2022, 12, 1207. [Google Scholar] [CrossRef]
- EN-ISO 52016-1:2017; Energy Performance of Buildings—Energy Needs for Heating and Cooling, Internal Temperatures and Sensible and Latent Heat Loads—Part 1: Calculation Procedures. ISO: Geneva, Switzerland, 2017.
- Oliveira Panão, M.J.N.; Santos, C.A.P.; Mateus, N.M.; Carrilho Da Graça, G. Validation of a lumped RC model for thermal simulation of a double skin natural and mechanical ventilated test cell. Energy Build. 2016, 121, 92–103. [Google Scholar] [CrossRef]
- EN ISO 13790; Energy Performance of Buildings—Calculation of Energy Use for Space Heating and Cooling. ISO: Geneva, Switzerland, 2008.
- Lundström, L.; Akander, J.; Zambrano, J. Development of a Space Heating Model Suitable for the Automated Model Generation of Existing Multifamily Buildings—A Case Study in Nordic Climate. Energies 2019, 12, 485. [Google Scholar] [CrossRef]
- Zakula, T.; Bagaric, M.; Ferdelji, N.; Milovanovic, B.; Mudrinic, S.; Ritosa, K. Comparison of dynamic simulations and the ISO 52016 standard for the assessment of building energy performance. Appl. Energy 2019, 254, 113553. [Google Scholar] [CrossRef]
- Ballarini, I.; Costantino, A.; Fabrizio, E.; Corrado, V. A Methodology to Investigate the Deviations between Simple and Detailed Dynamic Methods for the Building Energy Performance Assessment. Energies 2020, 13, 6217. [Google Scholar] [CrossRef]
- Gumbarević, S.; Burcar Dunović, I.; Milovanović, B.; Gaši, M. Method for Building Information Modeling Supported Project Control of Nearly Zero-Energy Building Delivery. Energies 2020, 13, 5519. [Google Scholar] [CrossRef]
- Du, L.; Yang, L.; Yang, C.; Hu, C.; Yu, C.; Qiu, M.; Liu, S.; Zhu, S.; Ye, X. Development and Validation of an Energy Consumption Model for Animal Houses Achieving Precision Livestock Farming. Animals 2022, 12, 2580. [Google Scholar] [CrossRef]
- Patrčević, F.; Dović, D.; Horvat, I.; Filipović, P. A Novel Dynamic Approach to Cost-Optimal Energy Performance Calculations of a Solar Hot Water System in an nZEB Multi-Apartment Building. Energies 2022, 15, 509. [Google Scholar] [CrossRef]
- Horvat, I.; Dović, D. Dynamic modeling approach for determining buildings technical system energy performance. Energy Convers. Manag. 2016, 125, 154–165. [Google Scholar] [CrossRef]
- Heidarinejad, M.; Mattise, N.; Dahlhausen, M.; Sharma, K.; Benne, K.; Macumber, D.; Brackney, L.; Srebric, J. Demonstration of reduced-order urban scale building energy models. Energy Build. 2017, 156, 17–28. [Google Scholar] [CrossRef]
- Elci, M.; Delgado, B.M.; Henning, H.M.; Henze, G.P.; Herkel, S. Aggregation of residential buildings for thermal building simulations on an urban district scale. Sustain. Cities Soc. 2018, 39, 537–547. [Google Scholar] [CrossRef]
- Tagliabue, L.C.; Buzzetti, M.; Marenzi, G. Energy performance of greenhouse for energy saving in buildings. Energy Procedia 2012, 30, 1233–1242. [Google Scholar] [CrossRef]
- Fabrizio, E.; Ghiggini, A.; Bariani, M. Energy performance and indoor environmental control of animal houses: A modelling tool. Energy Procedia 2015, 82, 439–444. [Google Scholar] [CrossRef]
- Jayathissa, P.; Luzzatto, M.; Schmidli, J.; Hofer, J.; Nagy, Z.; Schlueter, A. Optimising building net energy demand with dynamic BIPV shading. Appl. Energy 2017, 202, 726–735. [Google Scholar] [CrossRef]
- Klein, K.; Herkel, S.; Henning, H.-M.; Felsmann, C. Load shifting using the heating and cooling system of an office building: Quantitative potential evaluation for different flexibility and storage options. Appl. Energy 2017, 203, 917–937. [Google Scholar] [CrossRef]
- Shen, P.; Braham, W.; Yi, Y. Development of a lightweight building simulation tool using simplified zone thermal coupling for fast parametric study. Appl. Energy 2018, 223, 188–214. [Google Scholar] [CrossRef]
- Michalak, P. Hourly Simulation of an Earth-to-Air Heat Exchanger in a Low-Energy Residential Building. Energies 2022, 15, 1898. [Google Scholar] [CrossRef]
- Fischer, D.; Wolf, T.; Scherer, J.; Wille-Haussmann, B. A stochastic bottom-up model for space heating and domestic hot water load profiles for German households. Energy Build. 2016, 124, 120–128. [Google Scholar] [CrossRef]
- Costantino, A.; Fabrizio, E.; Ghiggini, A.; Bariani, M. Climate control in broiler houses: A thermal model for the calculation of the energy use and indoor environmental conditions. Energy Build. 2018, 169, 110–126. [Google Scholar] [CrossRef]
- Hedegaard, R.E.; Kristensen, M.H.; Pedersen, T.H.; Brun, A.; Petersen, S. Bottom-up modelling methodology for urban-scale analysis of residential space heating demand response. Appl. Energy 2019, 242, 181–204. [Google Scholar] [CrossRef]
- Costantino, A.; Comba, L.; Sicardi, G.; Bariani, M.; Fabrizio, E. Energy performance and climate control in mechanically ventilated greenhouses: A dynamic modelling-based assessment and investigation. Appl. Energy 2021, 288, 116583. [Google Scholar] [CrossRef]
- Buonomano, A.; Forzano, C.; Kalogirou, S.A.; Palombo, A. Building-façade integrated solar thermal collectors: Energy-economic performance and indoor comfort simulation model of a water based prototype for heating, cooling, and DHW production. Renew. Energy 2019, 137, 20–36. [Google Scholar] [CrossRef]
- Dalla Mora, T.; Teso, L.; Carnieletto, L.; Zarrella, A.; Romagnoni, P. Comparative Analysis between Dynamic and Quasi-Steady-State Methods at an Urban Scale on a Social-Housing District in Venice. Energies 2021, 14, 5164. [Google Scholar] [CrossRef]
- Bruno, R.; Pizzuti, G.; Arcuri, N. The Prediction of Thermal Loads in Building by Means of the EN ISO 13790 Dynamic Model: A Comparison with TRNSYS. Energy Procedia 2016, 101, 192–199. [Google Scholar] [CrossRef]
- Michalak, P. Thermal–electrical analogy in dynamic simulations of buildings: Comparison of four numerical solution methods. J. Mech. Energy Eng. 2020, 4, 179–188. [Google Scholar] [CrossRef]
- Michalak, P. Ventilation heat loss in a multifamily building under varying air density. J. Mech. Energy Eng. 2020, 4, 97–102. [Google Scholar] [CrossRef]
- Michalak, P. Impact of Air Density Variation on a Simulated Earth-to-Air Heat Exchanger’s Performance. Energies 2022, 15, 3215. [Google Scholar] [CrossRef]
- Digital Plug & Play Infrared Thermometer in a TO-Can. MLX90614. Available online: https://www.melexis.com/en/product/mlx90614/digital-plug-play-infrared-thermometer-to-can (accessed on 20 February 2023).
- Mobaraki, B.; Komarizadehasl, S.; Castilla Pascual, F.J.; Lozano-Galant, J.A.; Porras Soriano, R. A Novel Data Acquisition System for Obtaining Thermal Parameters of Building Envelopes. Buildings 2022, 12, 670. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, X. High-Precision Measurement of Sea Surface Temperature with Integrated Infrared Thermometer. Sensors 2022, 22, 1872. [Google Scholar] [CrossRef]
- Adeala, A.A.; Huan, Z.; Enweremadu, C.C. Evaluation of global solar radiation using multiple weather parameters as predictors for South Africa Provinces. Therm. Sci. 2015, 19, 495–509. [Google Scholar] [CrossRef]
- Pham, H. A New Criterion for Model Selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef]
- Kadad, I.M.; Ramadan, A.A.; Kandil, K.M.; Ghoneim, A.A. Relationship between Ultraviolet-B Radiation and Broadband Solar Radiation under All Sky Conditions in Kuwait Hot Climate. Energies 2022, 15, 3130. [Google Scholar] [CrossRef]
- Salah, S.; Alsamamra, H.R.; Shoqeir, J.H. Exploring Wind Speed for Energy Considerations in Eastern Jerusalem-Palestine Using Machine-Learning Algorithms. Energies 2022, 15, 2602. [Google Scholar] [CrossRef]
- Varga, Z.; Racz, E. Machine Learning Analysis on the Performance of Dye-Sensitized Solar Cell—Thermoelectric Generator Hybrid System. Energies 2022, 15, 7222. [Google Scholar] [CrossRef]
- Delaforce, S.R.; Hitchin, E.R.; Watson, D.M.T. Convective heat transfer at internal surfaces. Build. Environ. 1993, 28, 211–220. [Google Scholar] [CrossRef]
- Sukamto, D.; Siroux, M.; Gloriant, F. Hot Box Investigations of a Ventilated Bioclimatic Wall for NZEB Building Façade. Energies 2021, 14, 1327. [Google Scholar] [CrossRef]
- Shinoda, J.; Kazanci, O.B.; Tanabe, S.; Olesen, B.W. A review of the surface heat transfer coefficients of radiant heating and cooling systems. Build. Environ. 2019, 159, 106156. [Google Scholar] [CrossRef]
- Do, H.Q.; Luther, M.B.; Amirkhani, M.; Wang, Z.; Martek, I. Radiant Conditioning Retrofitting for Residential Buildings. Energies 2022, 15, 449. [Google Scholar] [CrossRef]
- Hayati, A.; Akander, J.; Eriksson, M. A Case Study of Mapping the Heating Storage Capacity in a Multifamily Building within a District Heating Network in Mid-Sweden. Buildings 2022, 12, 1007. [Google Scholar] [CrossRef]
- ISO 6946:2017; Building Components and Building Elements—Thermal Resistance and Thermal Transmittance—Calculation Methods. International Organization for Standardization: Geneva, Switzerland, 2017.
- EN ISO 10456; Building Materials and Products—Hygrothermal Properties—Tabulated Design Values and Procedures for Determining Declared and Design Thermal Values. International Organization for Standardization: Geneva, Switzerland, 2007.
- ISO 13786:2017; Thermal Performance of Building Components—Dynamic Thermal Characteristics—Calculation Methods. ISO: Geneva, Switzerland, 2017.
- Lomas, K.J. Architectural design of an advanced naturally ventilated building form. Energy Build. 2007, 39, 166–181. [Google Scholar] [CrossRef]
- Skotnicka-Siepsiak, A. An Evaluation of the Performance of a Ground-to-Air Heat Exchanger in Different Ventilation Scenarios in a Single-Family Home in a Climate Characterized by Cold Winters and Hot Summers. Energies 2022, 15, 105. [Google Scholar] [CrossRef]
- Hong, S.H.; Lee, J.M.; Moon, J.W.; Lee, K.H. Thermal Comfort, Energy and Cost Impacts of PMV Control Considering Individual Metabolic Rate Variations in Residential Building. Energies 2018, 11, 1767. [Google Scholar] [CrossRef]
- Cholewa, T.; Siggelsten, S.; Balen, I.; Ficco, G. Heat cost allocation in buildings: Possibilities, problems and solutions. J. Build. Eng. 2020, 31, 101349. [Google Scholar] [CrossRef]
- Bagheri, A.; Genikomsakis, K.N.; Feldheim, V.; Ioakimidis, C.S. Sensitivity Analysis of 4R3C Model Parameters with Respect to Structure and Geometric Characteristics of Buildings. Energies 2021, 14, 657. [Google Scholar] [CrossRef]
- Bagheri, A.; Genikomsakis, K.N.; Ioakimidis, C.S. Implementation of System Identification Techniques and Optimal Control for RC Model Selection by Means of TRNSYS Simulation Results and Experimental Data. Buildings 2022, 12, 1625. [Google Scholar] [CrossRef]
- Boodi, A.; Beddiar, K.; Amirat, Y.; Benbouzid, M. Simplified Building Thermal Model Development and Parameters Evaluation Using a Stochastic Approach. Energies 2020, 13, 2899. [Google Scholar] [CrossRef]
- Michalak, P. Thermal—Airflow Coupling in Hourly Energy Simulation of a Building with Natural Stack Ventilation. Energies 2022, 15, 4175. [Google Scholar] [CrossRef]
- Michalak, P. A thermal-network model for the dynamic simulation of the energy performance of buildings with the time varying ventilation flow. Energy Build. 2019, 202, 109337. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, Y.; Tang, C.Y.; Song, L. Development and validation of a second-order thermal network model for residential buildings. Appl. Energy 2022, 306, 118124. [Google Scholar] [CrossRef]
- Danza, L.; Belussi, L.; Meroni, I.; Salamone, F.; Floreani, F.; Piccinini, A.; Dabusti, A. A Simplified Thermal Model to Control the Energy Fluxes and to Improve the Performance of Buildings. Energy Procedia 2016, 101, 97–104. [Google Scholar] [CrossRef]
- Vivian, J.; Zarrella, A.; Emmi, G.; De Carli, M. An evaluation of the suitability of lumped-capacitance models in calculating energy needs and thermal behaviour of buildings. Energy Build. 2017, 150, 447–465. [Google Scholar] [CrossRef]
- Barone, G.; Buonomano, A.; Forzano, C.; Palombo, A. Building Energy Performance Analysis: An Experimental Validation of an In-House Dynamic Simulation Tool through a Real Test Room. Energies 2019, 12, 4107. [Google Scholar] [CrossRef]
- Ding, Y.; Lyu, Y.; Lu, S.; Wang, R. Load shifting potential assessment of building thermal storage performance for building design. Energy 2022, 243, 123036. [Google Scholar] [CrossRef]
- Zhang, S.; Lin, Z.; Ai, Z.; Wang, F.; Cheng, Y.; Huang, C. Effects of operation parameters on performances of stratum ventilation for heating mode. Build. Environ. 2019, 148, 55–66. [Google Scholar] [CrossRef]
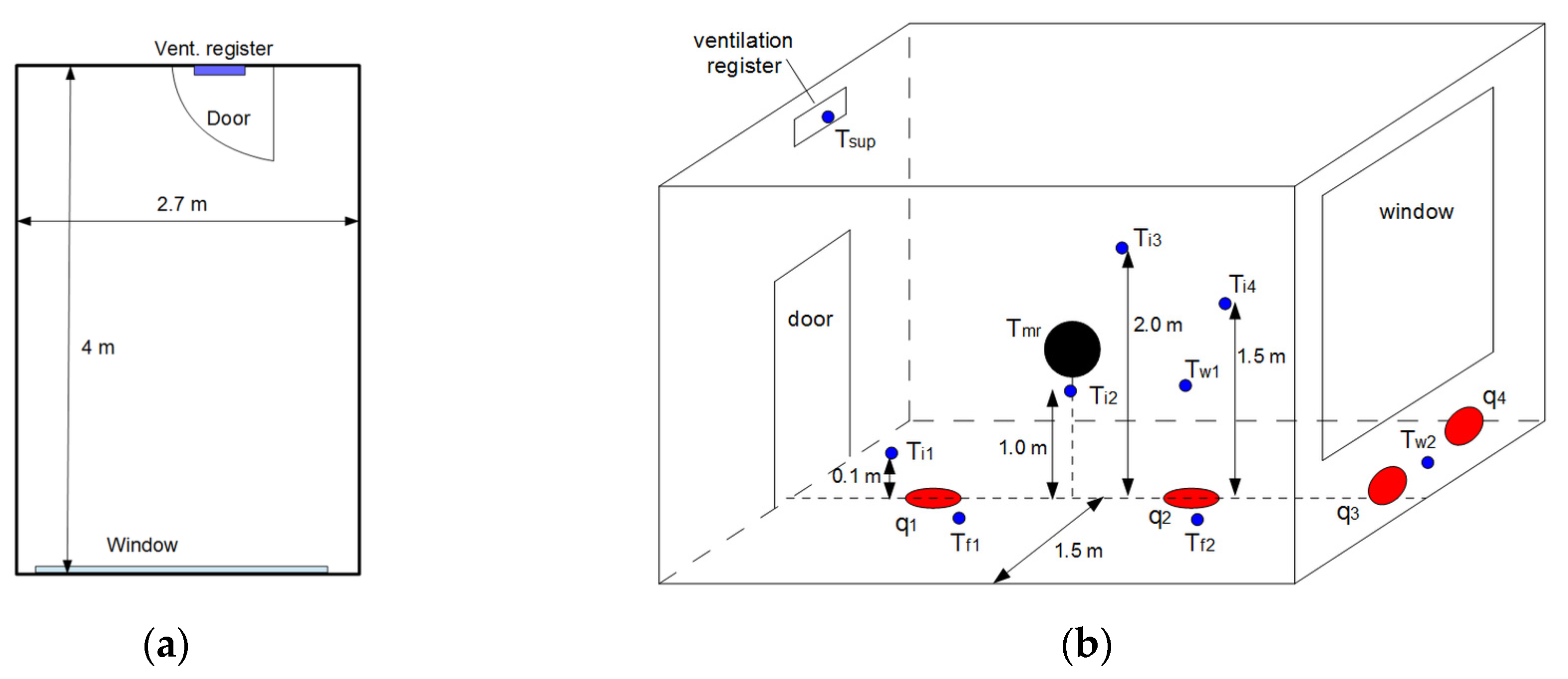


| Sensor | Measured Variable | Measurement Range | Accuracy |
|---|---|---|---|
| Pt100/Pt1000 platinum resistance sensor | Air and floor temperature | −50 °C ÷ +150 °C | Class A (1) |
| TP875.1 with the Pt100 sensor | Radiant temperature | −30 °C ÷ +120 °C | ±0.2 °C |
| CMP11 Kipp&Zonen | Global solar irradiance | 0 ÷ 4000 W/m2 | Spectrally Flat Class A (2) |
| HFP01 Hukseflux | Heat flux | −2000 ÷ 2000 W/m2 | ±3% |
| Testo 417 | Airflow rate | 0 ÷ 200 m3/h | ±0.1 m3/h (3) |
| Element | Value | Unit |
|---|---|---|
| Htr,w | 2.61 | W/K |
| Htr,is | 193.48 | W/K |
| Htr,ms | 264.32 | W/K |
| Htr,em | 0.84 | W/K |
| Hve | 16.67 | W/K |
| Cm | 2.63 | MJ/K |
| Element | Case 1 | Case 2 |
|---|---|---|
| MAE | 2.37 | 1.28 |
| RMSE | 2.45 | 1.38 |
| MSE | 5.98 | 1.91 |
| R2 | 0.71 | 0.77 |
| Reference | Object | Model | Simulation | Measurement | MAE | RMSE | MSE | R2 |
|---|---|---|---|---|---|---|---|---|
| [91] | 9 zones | 2R1C | TRNSYS | N | n.a. | 6.55 °C | 42.51 °C2 | n.a. |
| [91] | 9 zones | 3R1C | TRNSYS | N | n.a. | 8.49 °C | 17.71 °C2 | n.a. |
| [91] | 9 zones | 4R3C | TRNSYS | N | n.a. | 1.06 °C | 0.76 °C2 | n.a. |
| [91] | 9 zones | 5R3C | TRNSYS | N | n.a. | 5.02 °C | 3.37 °C2 | n.a. |
| [91] | 9 zones | 5R4C | TRNSYS | N | n.a. | 0.70 °C | 0.81 °C2 | n.a. |
| [91] | 9 zones | 4R2C | TRNSYS | N | n.a. | 3.08 °C | 6.72 °C2 | n.a. |
| [43] | 1 zone | 5R1C | - | Y | 0.95–1.13 °C | n.a. | n.a. | n.a. |
| [94] | 1 zone | 4R1C | EnergyPlus | N | 0.30–0.48 °C | 0.61–0.93 °C | 0.37–0.86 °C2 | 0.84–0.93 |
| [95] | 1 zone | 3R2C | - | Y | 0.34–0.5 °C | 0.42–0.65 °C | n.a. | n.a. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Michalak, P. Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building. Energies 2023, 16, 3456. https://doi.org/10.3390/en16083456
Michalak P. Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building. Energies. 2023; 16(8):3456. https://doi.org/10.3390/en16083456
Chicago/Turabian StyleMichalak, Piotr. 2023. "Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building" Energies 16, no. 8: 3456. https://doi.org/10.3390/en16083456
APA StyleMichalak, P. (2023). Simulation and Experimental Study on the Use of Ventilation Air for Space Heating of a Room in a Low-Energy Building. Energies, 16(8), 3456. https://doi.org/10.3390/en16083456






