Dual Sagnac Interferometer Distributed Optical Fiber Localization Method Based on Hilbert–Huang Transform
Abstract
:1. Introduction
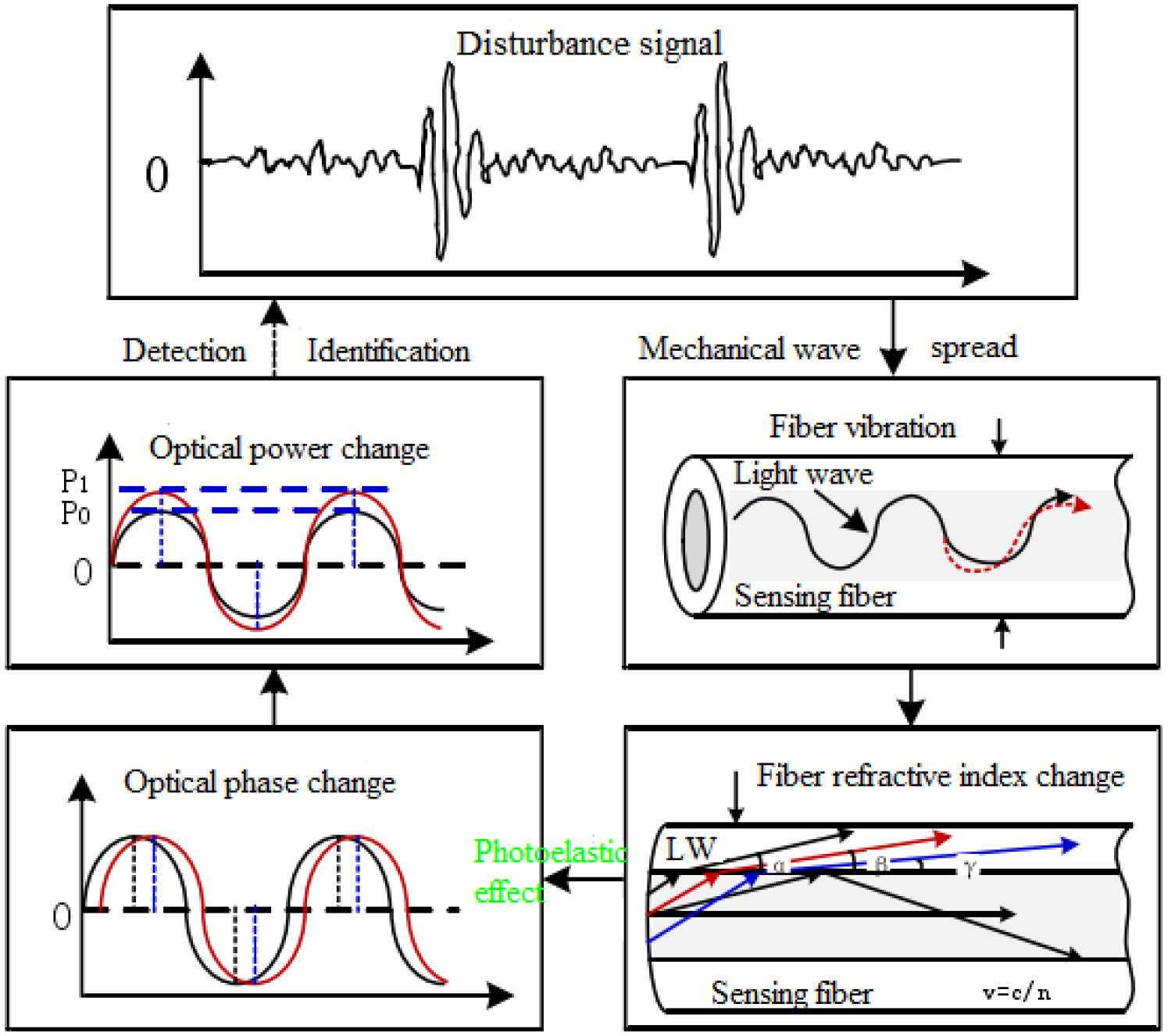
2. Analysis of Optical Fiber Sensing the Interference Signal
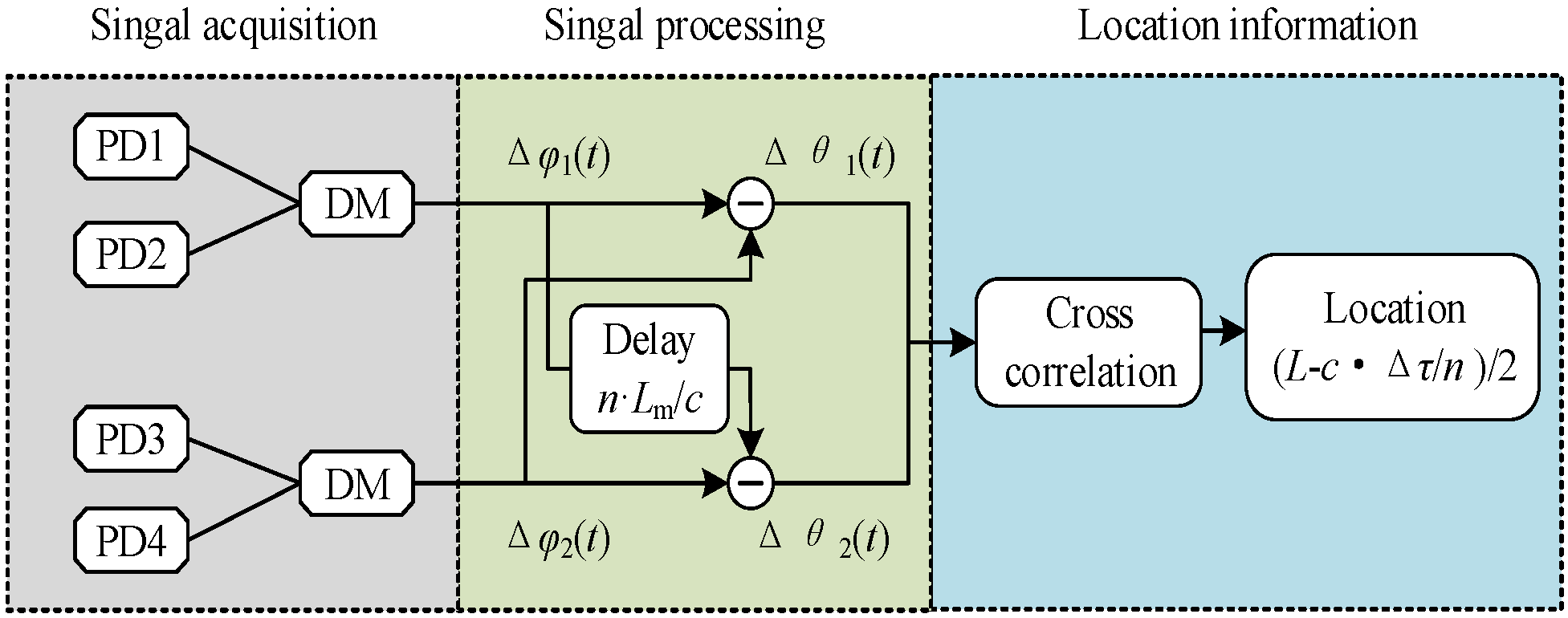
2.1. Optical Fiber Sensor Positioning Detection Analysis
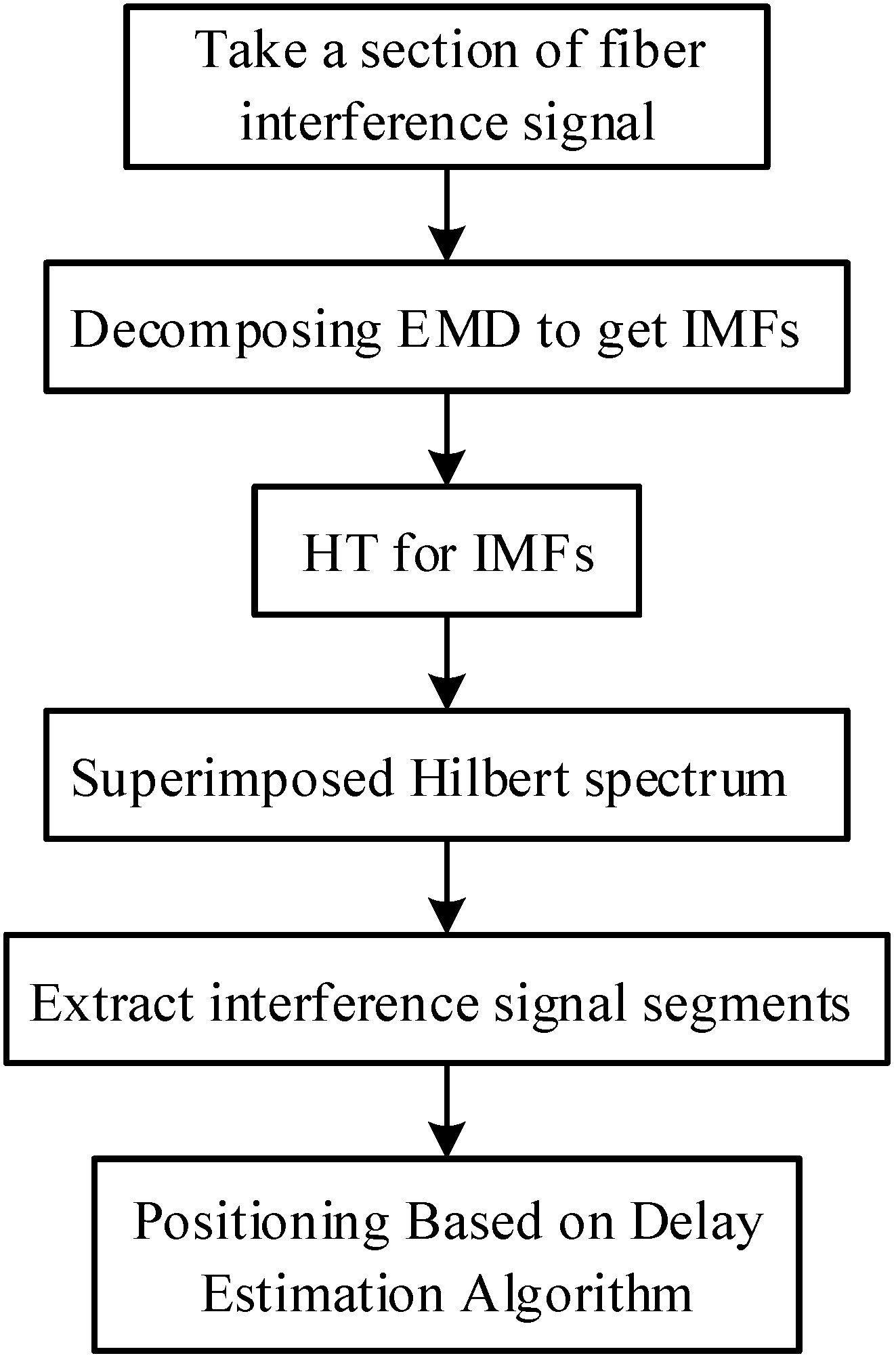
2.2. Hilbert–Huang Transform Algorithm
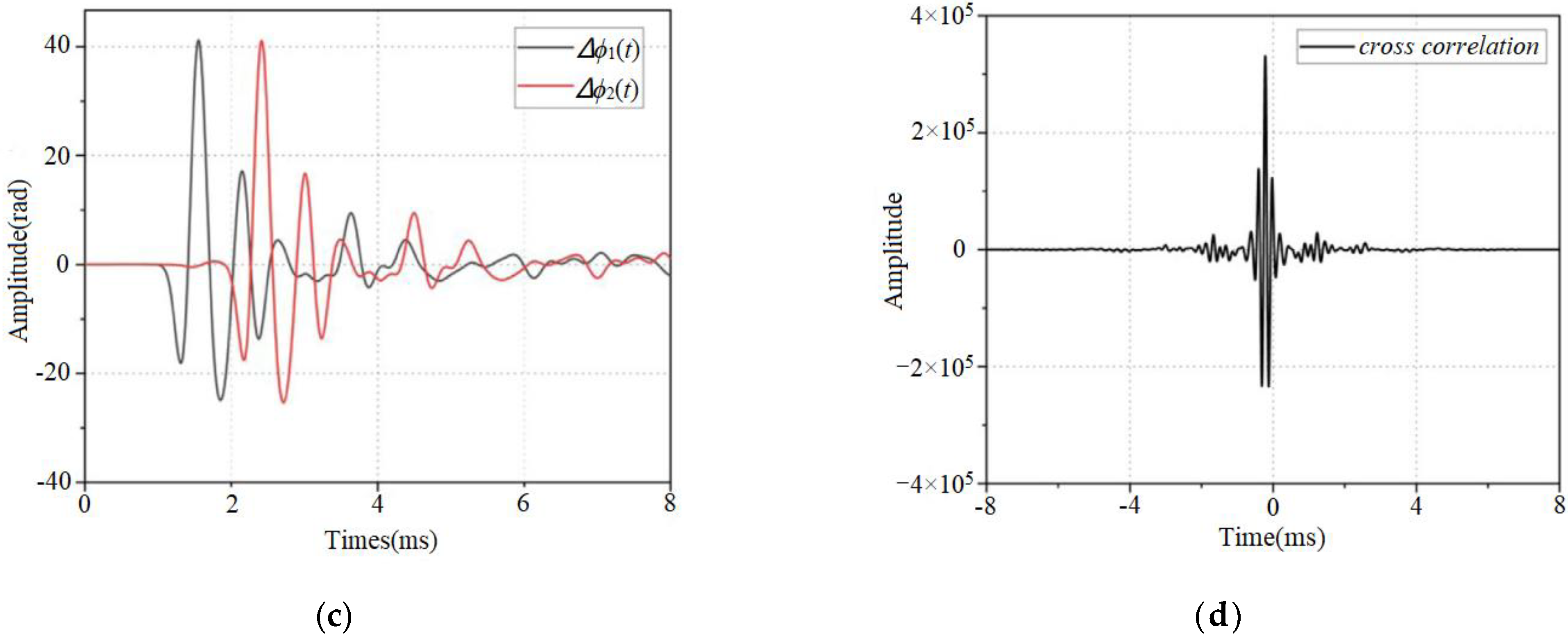
2.3. Delay Estimation Algorithm
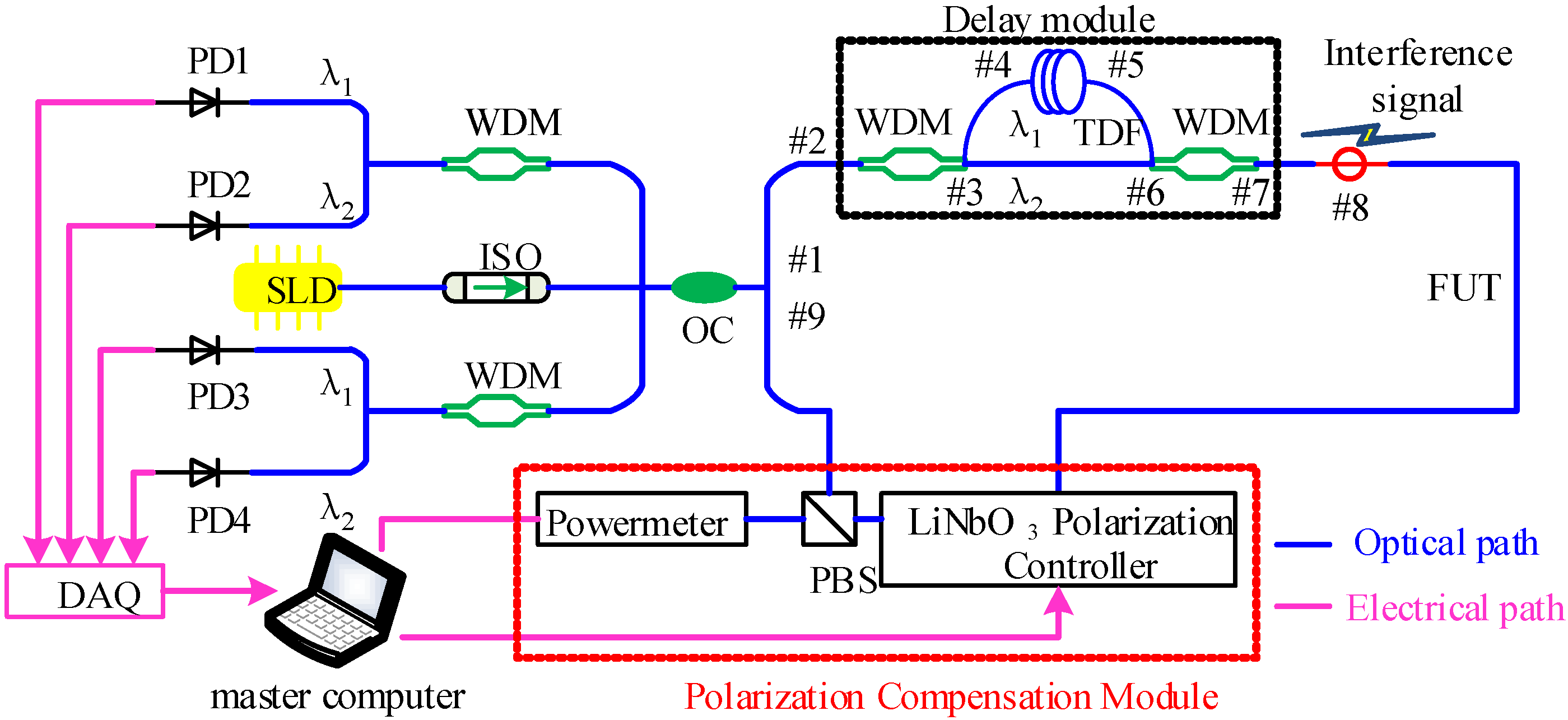
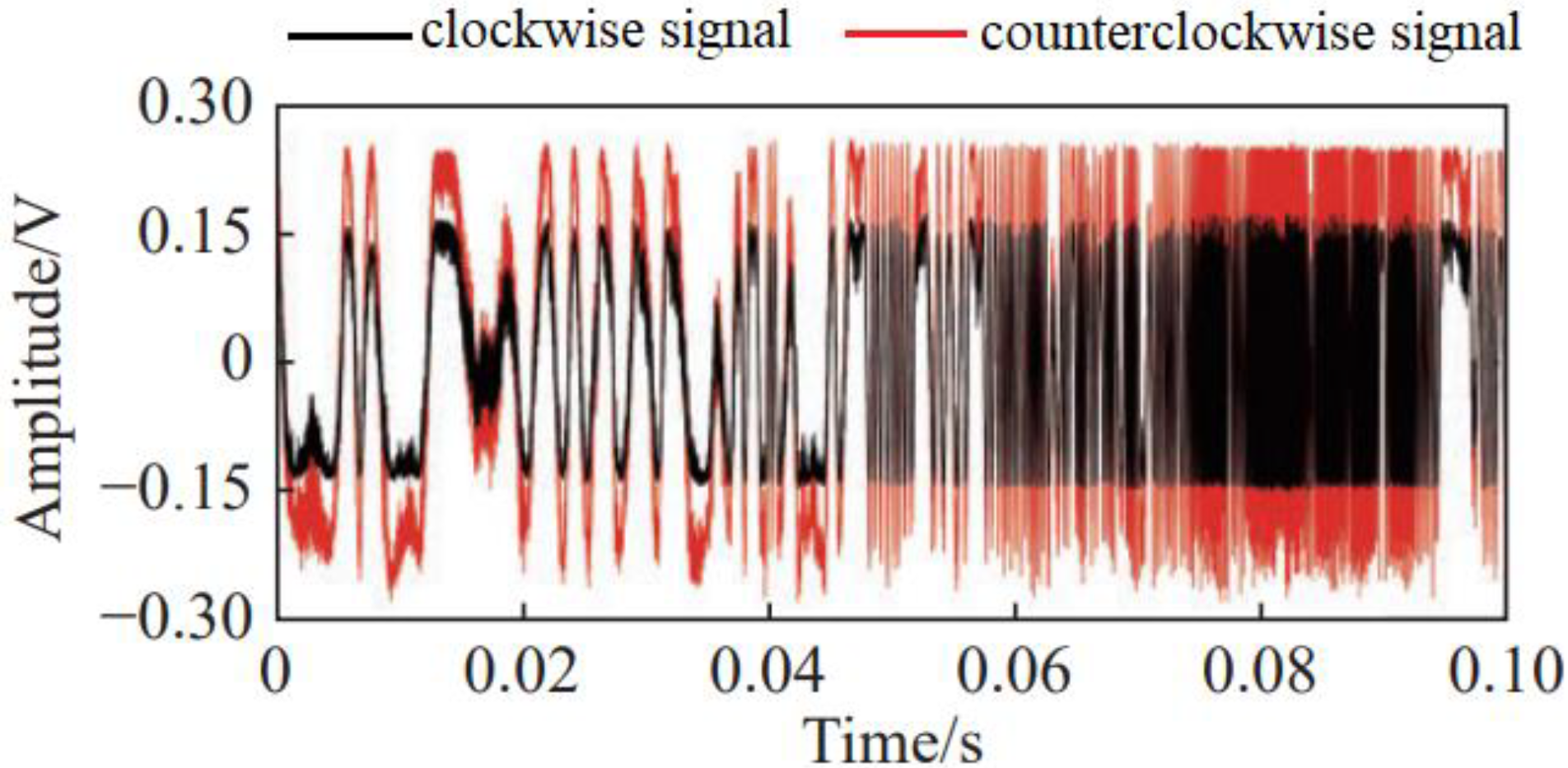
3. Polarization Stability Analysis of Sagnac Interferometer
4. Localization of Distributed Optical Fiber Disturbance for Interference Signal
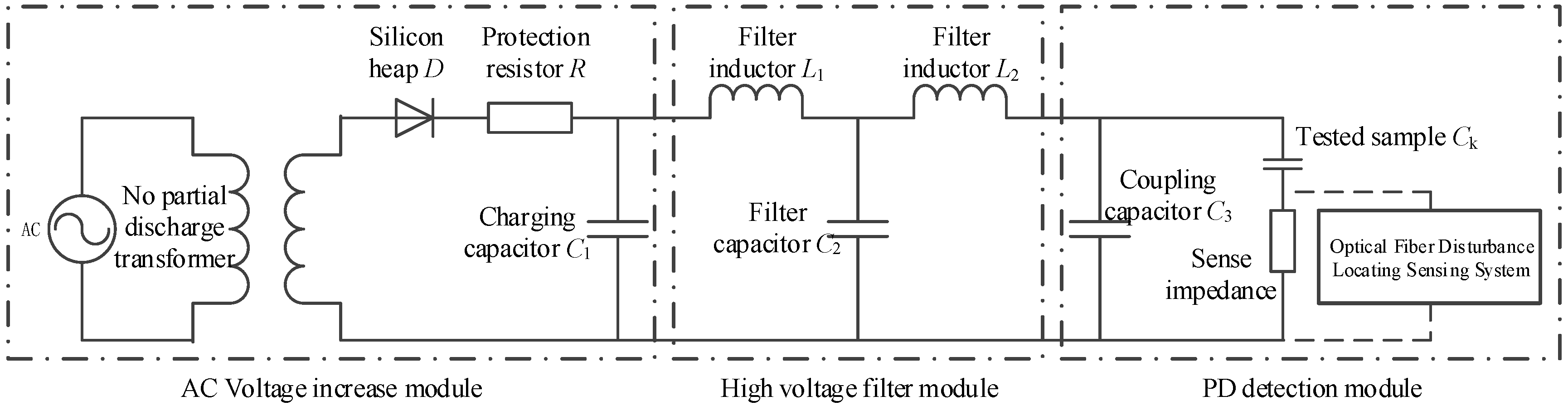
4.1. Partial Discharge Test of Optical Fiber Sensing Cable Joint
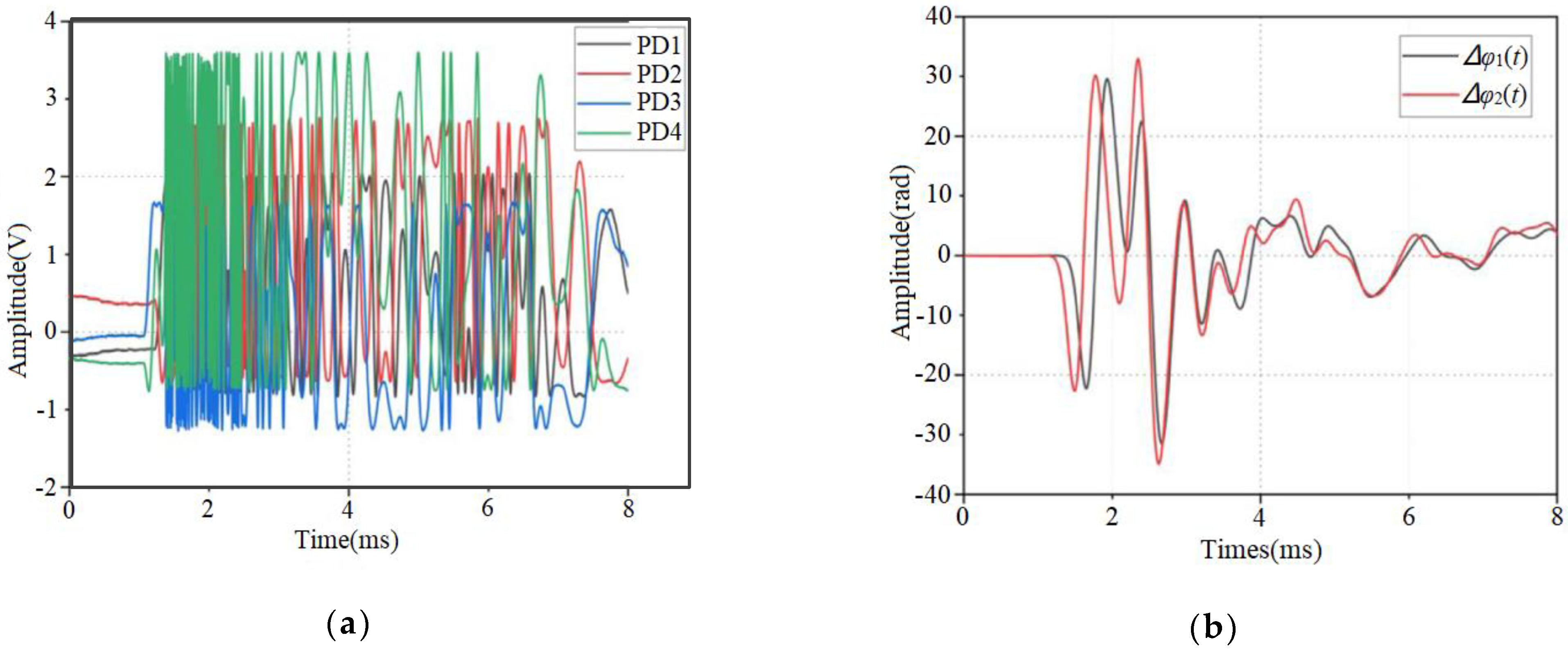
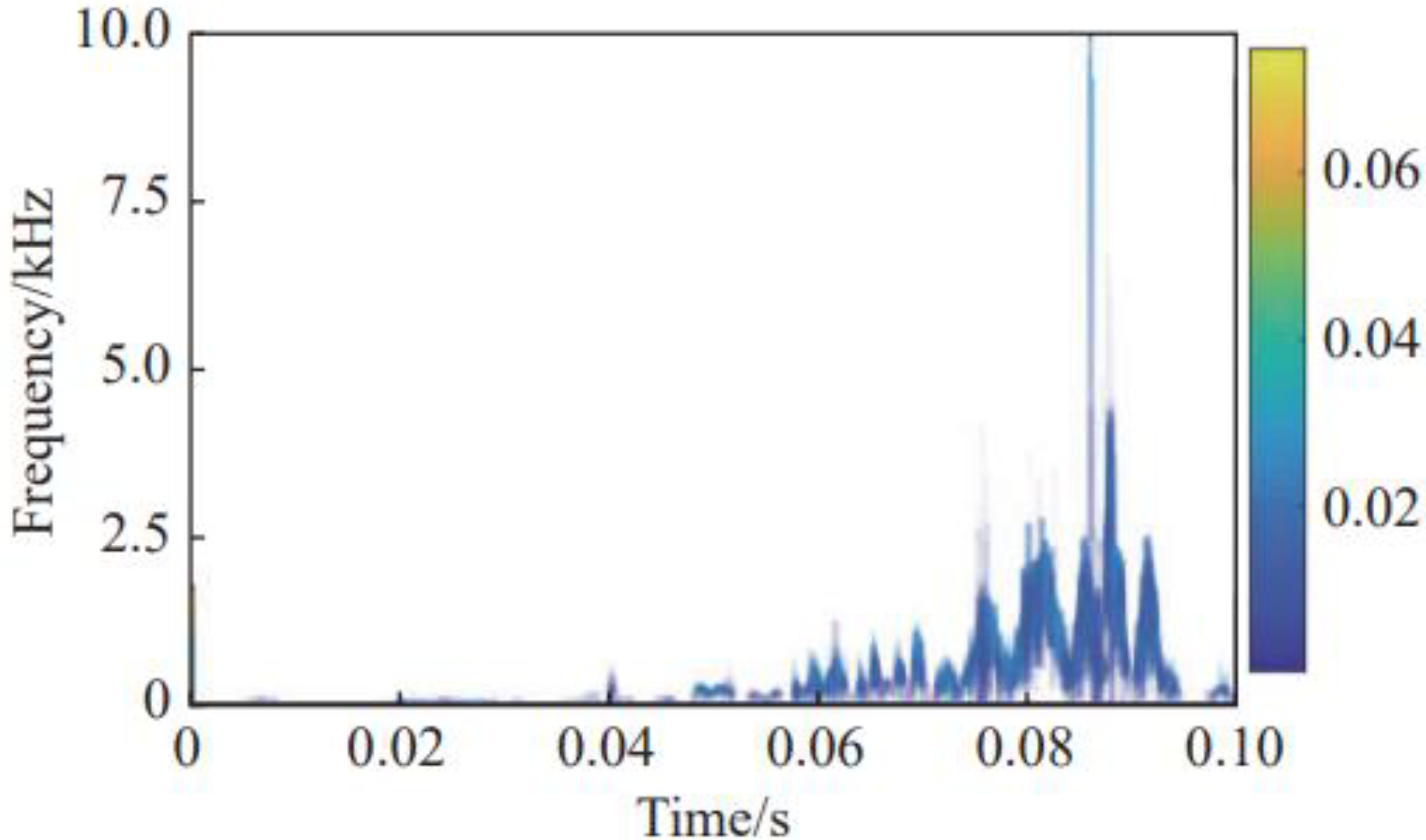
4.2. Signal Acquisition and Processing
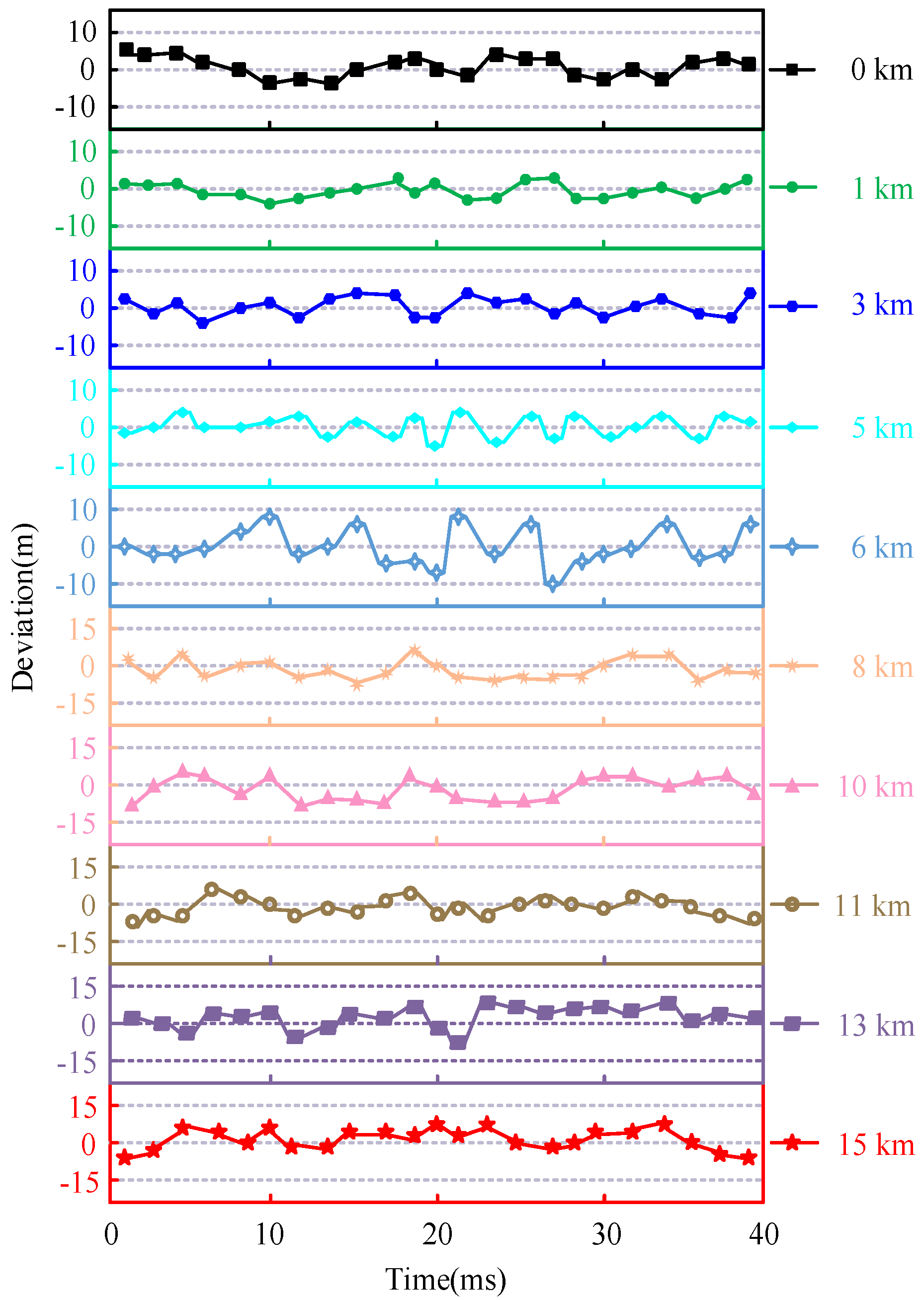
4.3. Optical Fiber Sensing and Localization of Interference Signal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, X.X.; Wang, Y.H.; Zhao, L.; Zhang, Q.; Zhang, M.; Zhang, J.; Qiao, L.; Wang, T.; Gao, S. Research Progress in Brillouin Optical Correlation Domain Analysis Technology. Chin. J. Laser 2021, 48, 0100001. [Google Scholar]
- Long, R. Fast localization mothod for abnormal nodes in distributed optical fiber sensor networks. Laser J. 2021, 42, 85–89. [Google Scholar]
- Ma, Y.; Zhang, Y.; Cheng, Y.; Zhang, Y.; Gao, X.; Shan, K. A Case Study of Field Thermal Response Test and Laboratory Test Based on Distributed Optical Fiber Temperature Sensor. Energies 2022, 15, 8101. [Google Scholar] [CrossRef]
- Liu, Z.L.; Wang, Y.Q.; Chen, X.; Meng, X.K. An optical fiber sensing method for partial discharge in the HVDC cable system. Int. J. Electr. Power Energy Syst. 2021, 128, 106749. [Google Scholar] [CrossRef]
- Bua-Nunez, I.; Posada-Roman, J.E.; Garcia-Souto, J.A. Multichannel Detection of Acoustic Emissions and Localization of the Source with External and Internal Sensors for Partial Discharge Monitoring of Power Transformers. Energies 2021, 14, 7873. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Li, H.; Wang, J.; Fan, X. Experimental and Numerical Investigation of the Internal Temperature of an Oil-Immersed Power Transformer with DOFS. Appl. Sci. 2020, 10, 5718. [Google Scholar] [CrossRef]
- Luo, K.; Wang, B.; Guo, N.; Yu, K.; Yu, C.; Lu, C. Enhancing SNR by Anisotropic Diffusion for Brillouin Distributed Optical Fiber Sensors. J. Lightwave Technol. 2020, 38, 5844–5852. [Google Scholar] [CrossRef]
- Chae, D.H.; Lee, S.J.; Lee, J.-W. Evaluation on the Applicability of Monitoring for Urban Railway Structure Using Brillouin Optical Correlation Domain Analysis Based Distributed Optical Fiber Sensor. J. Korean Geo-Environ. Soc. 2018, 19, 13–19. [Google Scholar]
- Ma, Y.; Song, Y.; Song, Q.; Xiao, Q.; Jia, B. MI-SI Based Distributed Optical Fiber Sensor for No-Blind Zone Location and Pattern Recognition. J. Lightwave Technol. 2022, 40, 3022–3030. [Google Scholar] [CrossRef]
- Chen, K.; Yue, Y.; Tang, Y.J. Research on Temperature Monitoring Method of Cable on 10 kV Railway Power Transmission Lines Based on Distributed Temperature Sensor. Energies 2021, 14, 3705. [Google Scholar] [CrossRef]
- Leal-Junior, A.G.; Ribeiro, D.; Leticia, M.A.; Silveira, M. Wearable and Fully-Portable Smart Garment for Mechanical Perturbation Detection With Nanoparticles Optical Fibers. IEEE Sens. J. 2021, 21, 2995–3003. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.; Ling, Z.W. Experimental Analysis and Leakage Location Detection of Tap Water Pipe Based on Distributed Optical Fiber with Selective Average Threshold. Laser Optoelectron. Prog. 2019, 56, 030602. [Google Scholar] [CrossRef]
- Ren, L.; Jiang, T.; Jia, Z.-G.; Li, D.-S.; Yuan, C.-L.; Li, H.-N. Pipeline corrosion and leakage monitoring based on the distributed optical fiber sensing technology. Measurement 2018, 122, 57–65. [Google Scholar] [CrossRef]
- Zhan, Y.; Song, Z.; Sun, Z.; Yu, M.; Guo, A.; Feng, C.; Zhong, J. A distributed optical fiber sensor system for intrusion detection and location based on the phase-sensitive OTDR with remote pump EDFA. Optik 2021, 225, 165020. [Google Scholar] [CrossRef]
- Mustafa, S.; Sekiya, H.; Morichika, S.; Maeda, I.; Takaba, S.; Hamajima, A. Monitoring internal strains in asphalt pavements under static loads using embedded distributed optical fibers. Opt. Fiber Technol. 2022, 68, 102829. [Google Scholar] [CrossRef]
- Lai, X.; Yu, H.; Ma, Y.; Lin, R.; Song, Q.; Jia, B. Disturbance location and pattern recognition of a distributed optical fiber sensor based on dual-Michelson interferometers. Appl. Opt. 2022, 61, 241–248. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Li, J.; Hu, Y.; Ma, H.; Wang, T.; Zhou, C.; Liu, H. Distributed optical fiber sensor for investigation of normal zone propagation and hot spot location in REBCO cables. Fusion Eng. Des. 2020, 156, 111569. [Google Scholar] [CrossRef]
- Gu, F.; Li, Y.; Song, Y.; Chen, J.; Zhang, J.; Zhang, M. Performance comparison of combining algorithms for polarization-diversity receiving in phase-sensitive OTDR. Opt. Commun. 2019, 435, 140–144. [Google Scholar] [CrossRef]
- Qiao, J.; Yin, X.; Wang, Y.; Xu, W.; Tan, L. A multi-terminal traveling wave fault location method for active distribution network based on residual clustering. Int. J. Electr. Power Energy Syst. 2021, 131, 107070. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Shi, B.; Ding, G.; Dong, F.; Zhang, Z. Intelligent detection technology for leakage bag of baghouse based on distributed optical fiber sensor. Opt. Fiber Technol. 2019, 52, 101947. [Google Scholar] [CrossRef]
- Yang, Y.Y.; Zhang, H.F.; Li, Y. Long-Distance Pipeline Safety Early Warning: A Distributed Optical Fiber Sensing Semi-Supervised Learning Method. IEEE Sens. J. 2021, 21, 19453–19461. [Google Scholar] [CrossRef]
- Zhang, H.; Yuan, Z.X.; Li, X.Y.; Qin, J. Improved Wavelet Threshold De-noising Method for Distributed Optical Fiber Lightning Location. Electr. Power Constr. 2021, 42, 75–82. [Google Scholar]
- Chen, H.; Xu, Y.; Qian, S.; Chen, C.; Guo, J.; Su, L. Distributed Fiber-Optic Ultrasonic Sensor Applied in Detection of Discharging Fault of Power Cable Joint. Acta Opt. Sin. 2021, 41, 22–30. [Google Scholar]
- Zhang, W.; Wu, Q.Y.; Zhang, Z.X.; Tian, Y.J.; Yang, Y.; Xu, X.H.; Ma, J.; Li, J. Application of distributed optical fiber pipeline monitoring technology in long-distance water conveyance project. Water Wastewater Eng. 2022, 58, 124–129. [Google Scholar]
- Yang, F.; Tang, X.L.; Yin, W.K.; Gong, X.; Hu, Y.; Yuan, Q.; Ke, W. Analysis of transmission line wind vibration monitoring based on a multi parameter distributed optical fiber sensor. Power Syst. Prot. Control. 2022, 50, 169–177. [Google Scholar]
- Yang, W.C.; Qin, Z.G.; Liu, Z.J.; Xu, Y.P.; Li, Z.; Qu, S.; Cong, Z.H.; Wang, Z.Q. A Hilbert-Huang transform method for vibration localization based on a dual Mach-Zehnder distributed optical fiber sensor. Chin. Opt. 2021, 14, 1410–1416. [Google Scholar]
- Zazoum, B.; El Hassan, M.; Jendoubi, A. Solar optical fiber daylighting system with an IR filter: Experimental and modeling studies. Energy Rep. 2020, 6, 903–908. [Google Scholar] [CrossRef]
- Al-Amayreh, M.I.; Alahmer, A.; Jendoubi, A. A novel parabolic solar dish design for a hybrid solar lighting-thermal applications. Energy Rep. 2020, 6, 1136–1143. [Google Scholar] [CrossRef]
- Teng, F.; Yi, D.; Hong, X.; Li, X. Distributed fiber optics disturbance sensor using a dual-Sagnac interferometer. Opt. Lett. 2019, 44, 5101–5103. [Google Scholar] [CrossRef]
- Choban, T.V.; Zhirnov, A.A.; Stepanov, K.V.; Koshelev, K.I.; Chernutsky, A.O.; Pnev, A.B.; Karasik, V.E. A Distributed Acoustic Sensor Based on Dual-Sagnac Interferometer with Counter Loops. In Proceedings of the 2021 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 21–25 November 2021; pp. 2922–2928. [Google Scholar]
- Zhirnov, A.A.; Choban, T.V.; Stepanov, K.V.; Koshelev, K.I.; Chernutsky, A.O.; Pnev, A.B.; Karasik, V.E. Distributed Acoustic Sensor Using a Double Sagnac Interferometer Based on Wavelength Division Multiplexing. Sensors 2022, 22, 2772. [Google Scholar] [CrossRef]
- Wu, J.; Zhuo, R.; Wan, S.; Xiong, X.; Xu, X.; Liu, B.; Liu, J.; Shi, J.; Sun, J.; He, X.; et al. Intrusion location technology of Sagnac distributed fiber optical sensing system based on deep learning. IEEE Sens. J. 2021, 21, 13327–13334. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Wang, Y.; Cheng, J.; Han, P.; Liu, Z.; Zhang, Z.; Li, X.; Yao, J. Dual Sagnac Interferometer Distributed Optical Fiber Localization Method Based on Hilbert–Huang Transform. Energies 2023, 16, 3494. https://doi.org/10.3390/en16083494
Liu Z, Wang Y, Cheng J, Han P, Liu Z, Zhang Z, Li X, Yao J. Dual Sagnac Interferometer Distributed Optical Fiber Localization Method Based on Hilbert–Huang Transform. Energies. 2023; 16(8):3494. https://doi.org/10.3390/en16083494
Chicago/Turabian StyleLiu, Zhiheng, Yongqing Wang, Jiuxi Cheng, Peijie Han, Zhibin Liu, Zhaoyan Zhang, Xiaoguang Li, and Jianquan Yao. 2023. "Dual Sagnac Interferometer Distributed Optical Fiber Localization Method Based on Hilbert–Huang Transform" Energies 16, no. 8: 3494. https://doi.org/10.3390/en16083494
APA StyleLiu, Z., Wang, Y., Cheng, J., Han, P., Liu, Z., Zhang, Z., Li, X., & Yao, J. (2023). Dual Sagnac Interferometer Distributed Optical Fiber Localization Method Based on Hilbert–Huang Transform. Energies, 16(8), 3494. https://doi.org/10.3390/en16083494






