Exergy Load Distribution Analysis Applied to the Dehydration of Ethanol by Extractive Distillation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Exergy Analysis
2.2. Analysis by Exergy Load Distribution
3. Results and Discussion
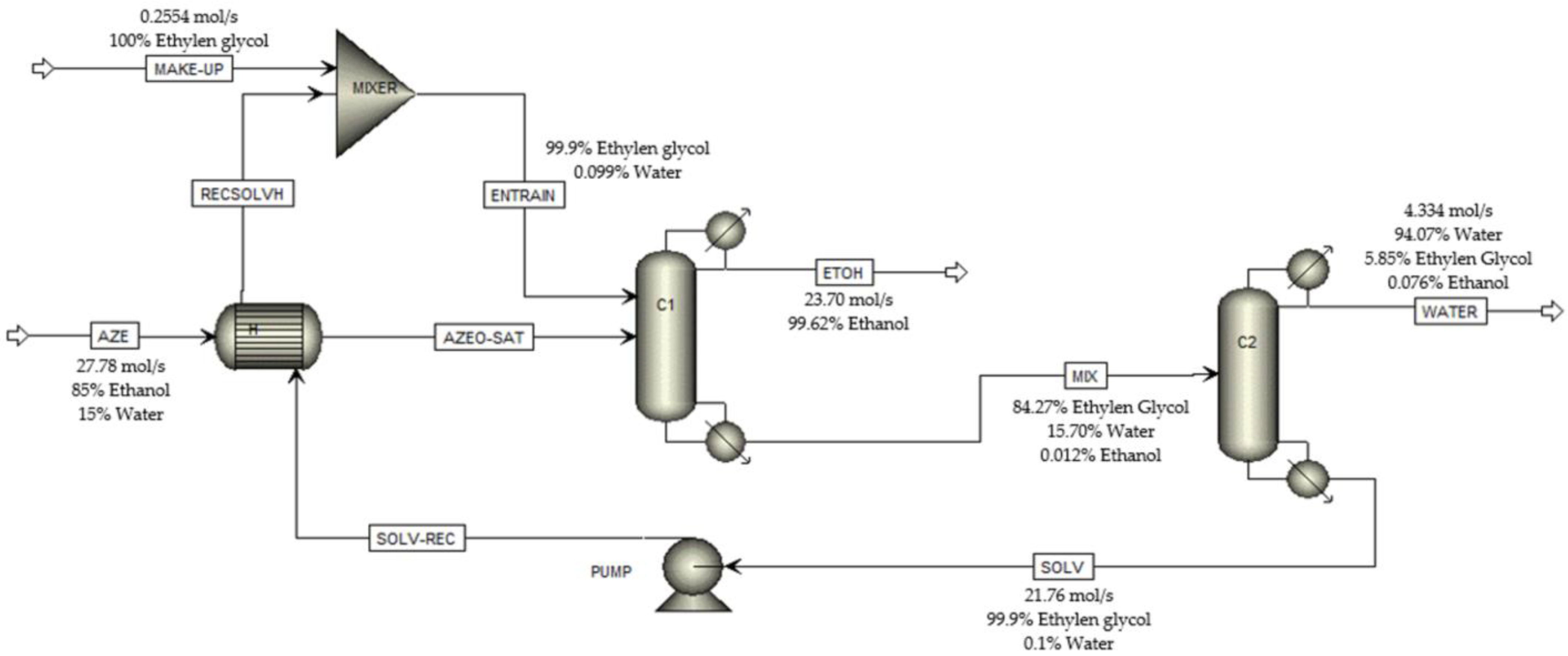
3.1. Extractive Distillation Process Simulation
3.2. Determination of Flow Exergy
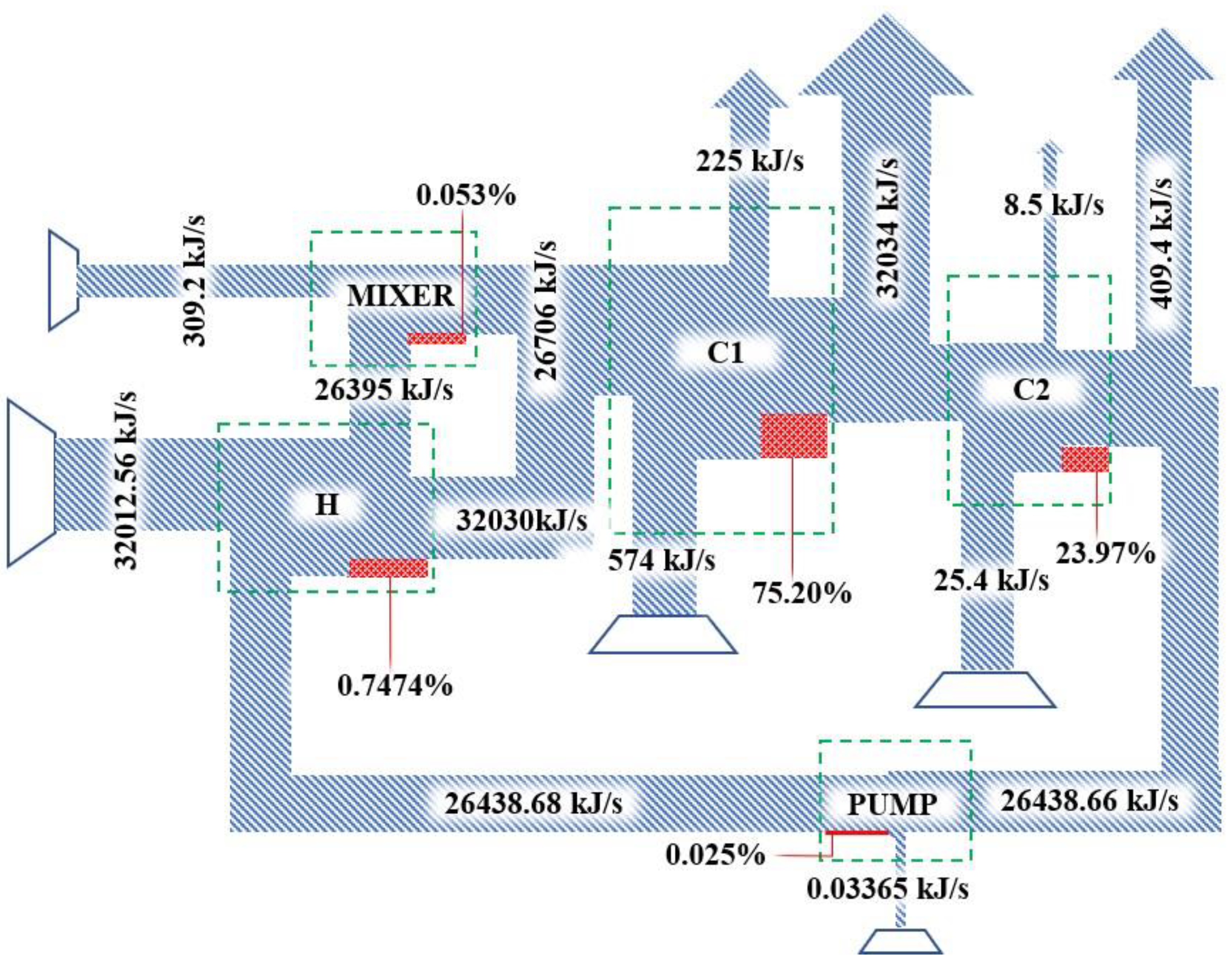
3.3. Destroyed Exergy Determination
3.4. Application of the Exergy Load Distribution Method
3.5. Sensitivity Analysis
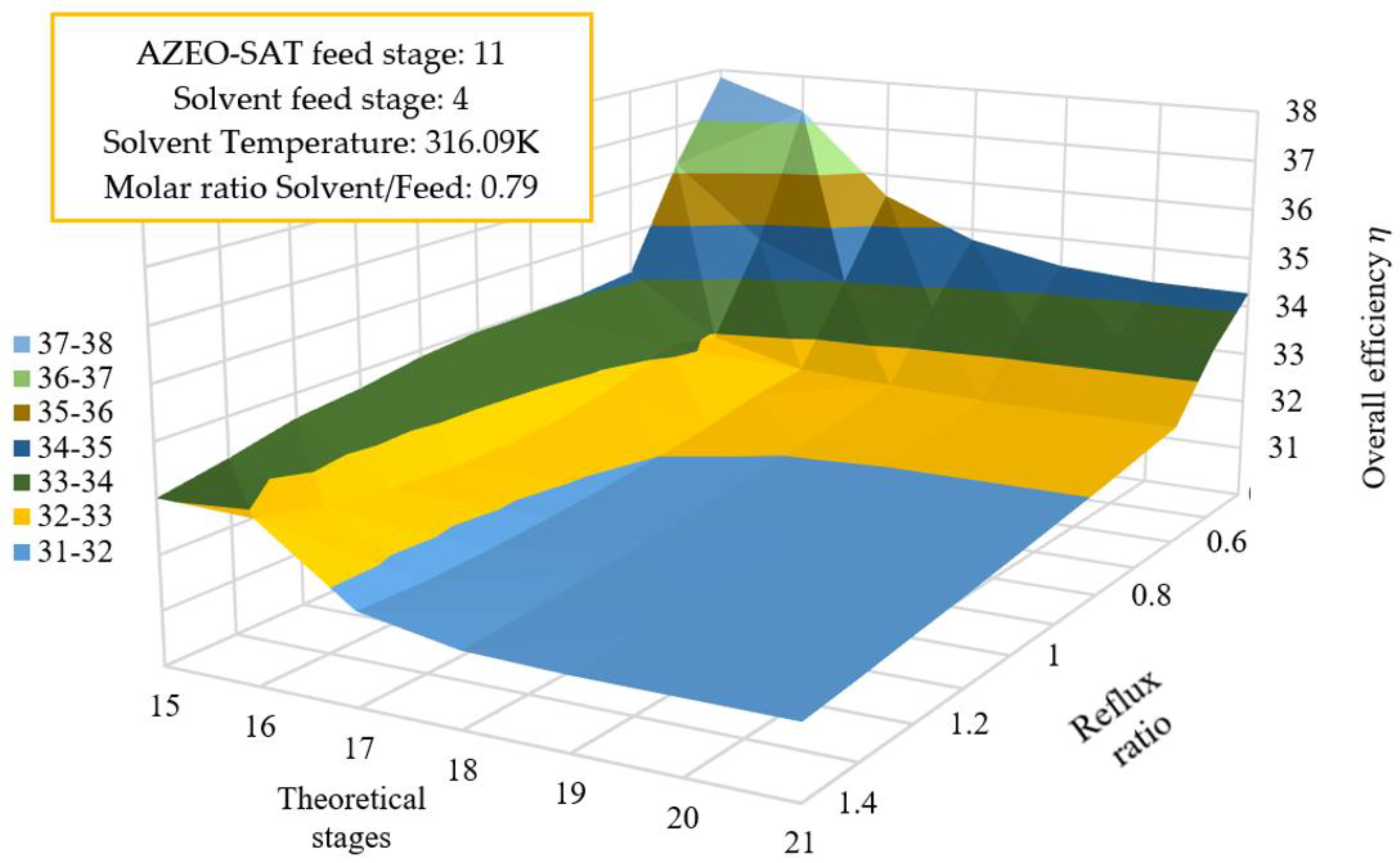
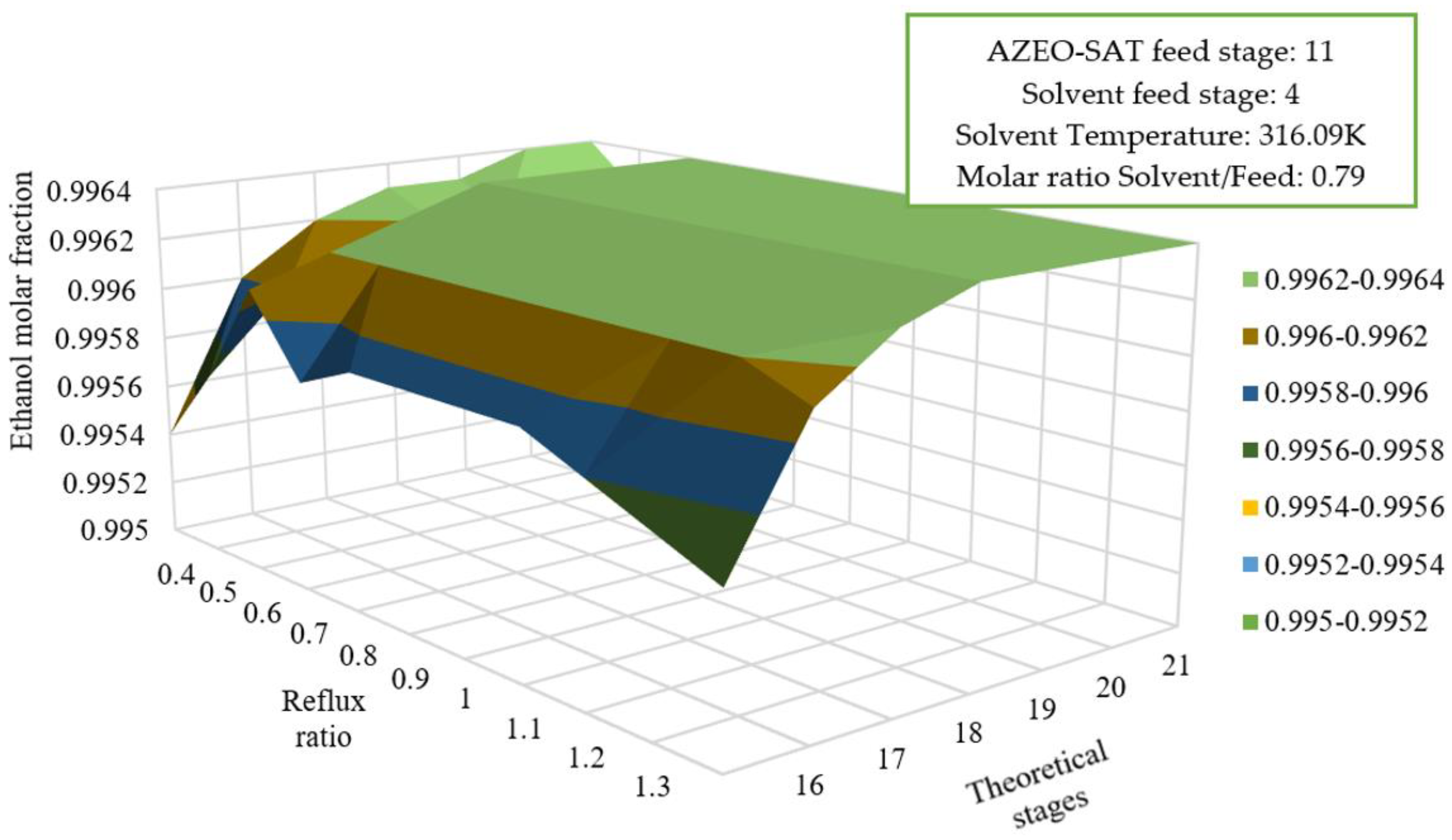
3.5.1. Reflux Ratio Effect, Number of Stages on the Overall Efficiency
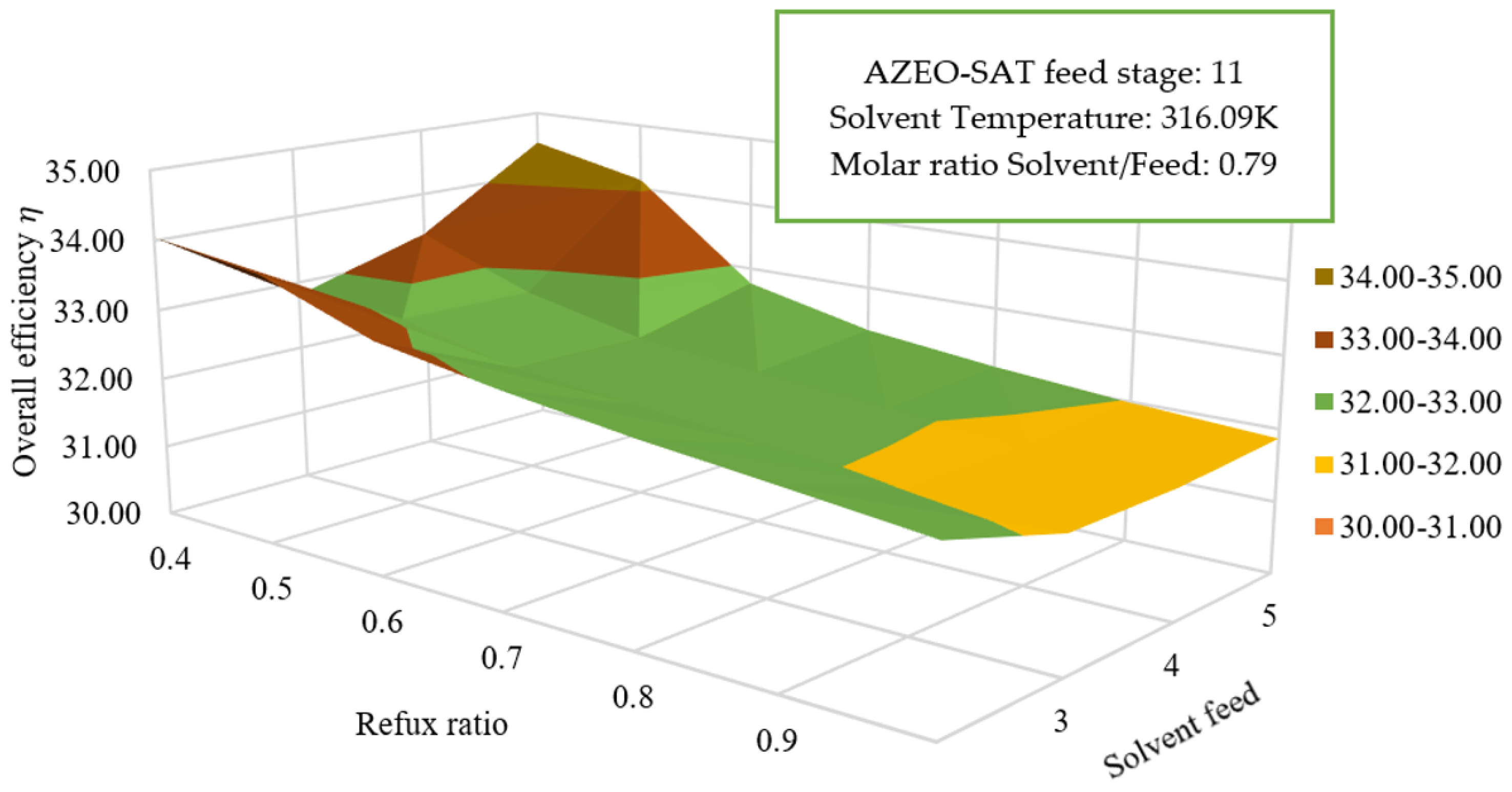
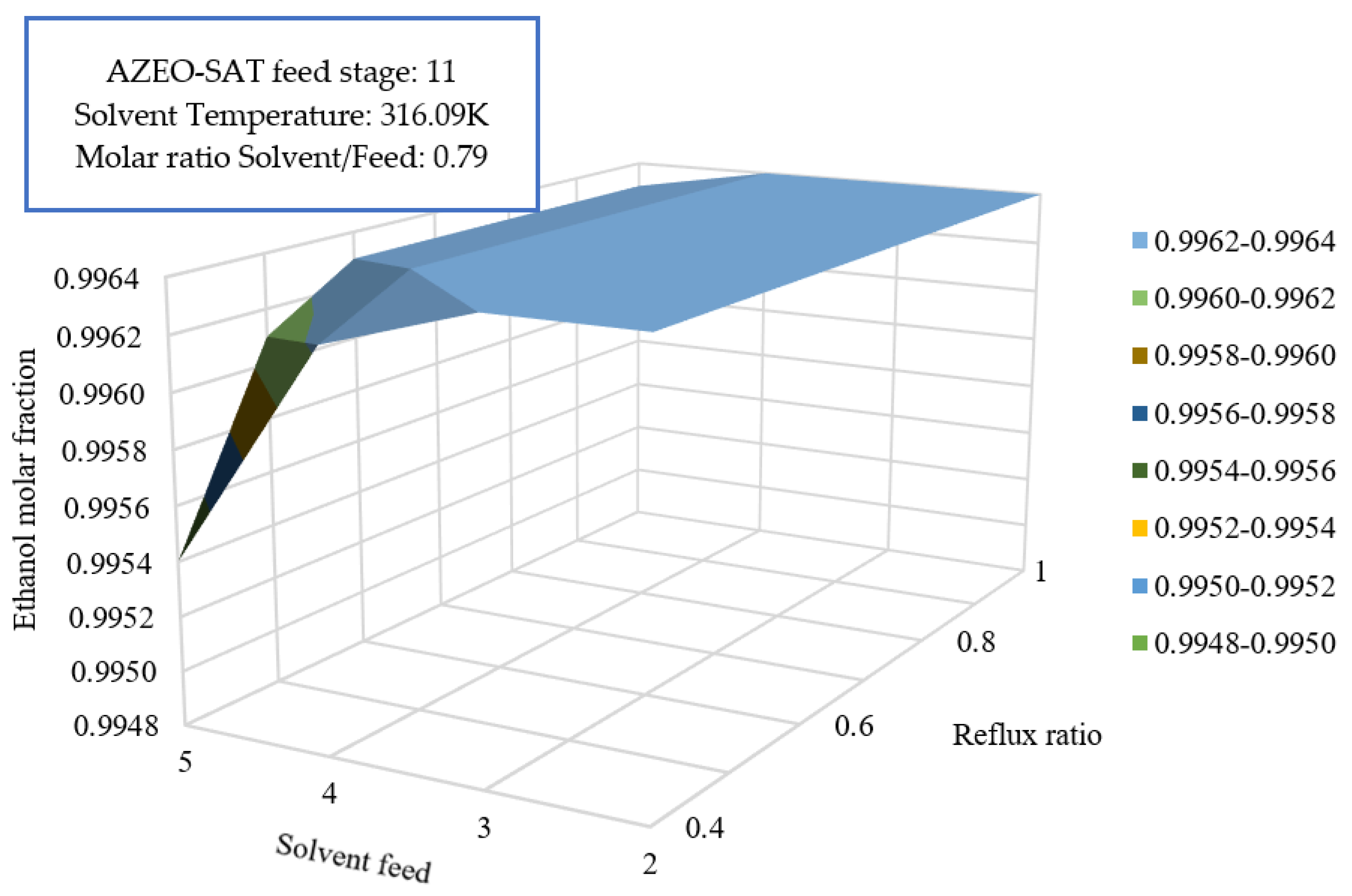
3.5.2. Reflux Ratio Effect and Solvent Feed on Overall Efficiency
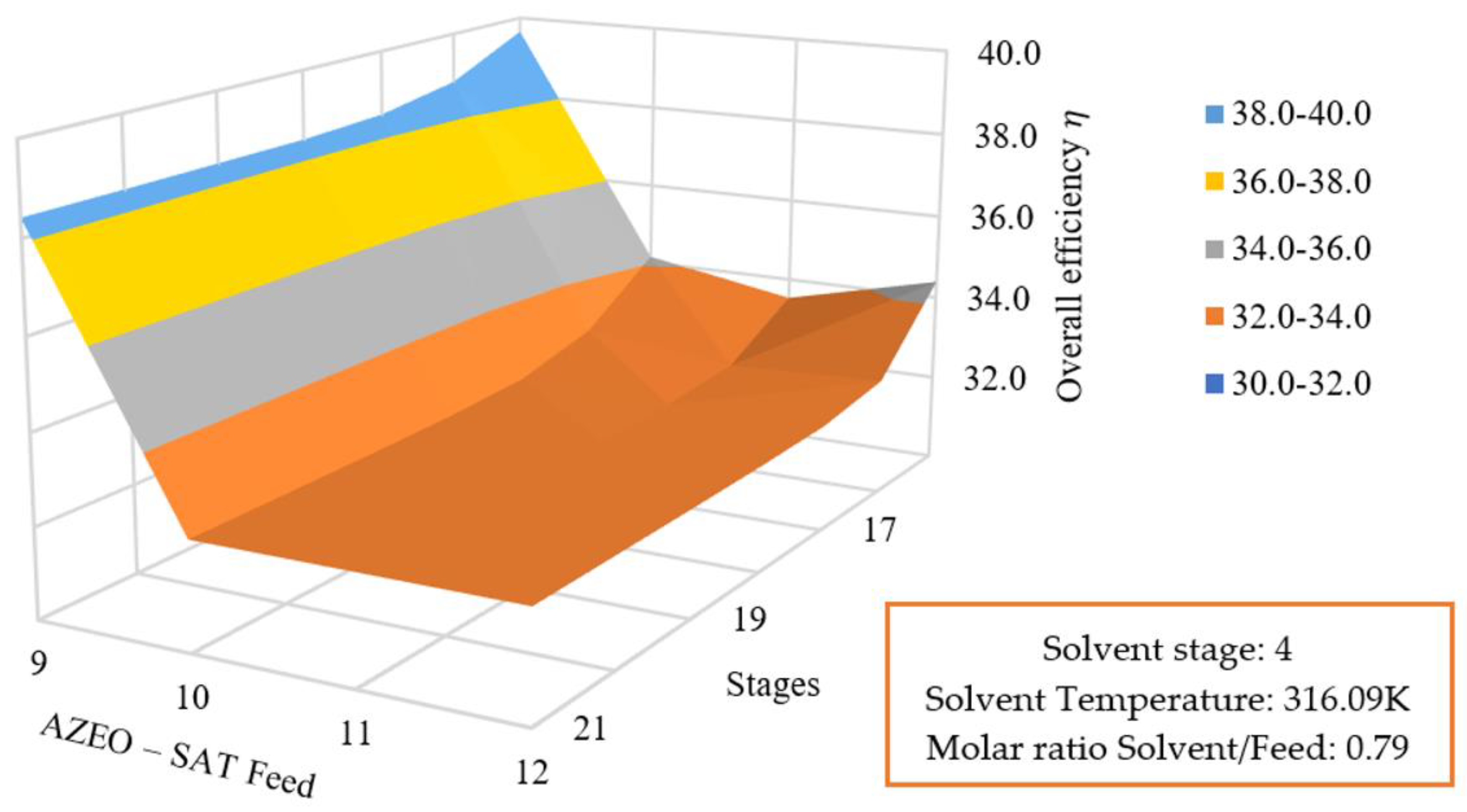
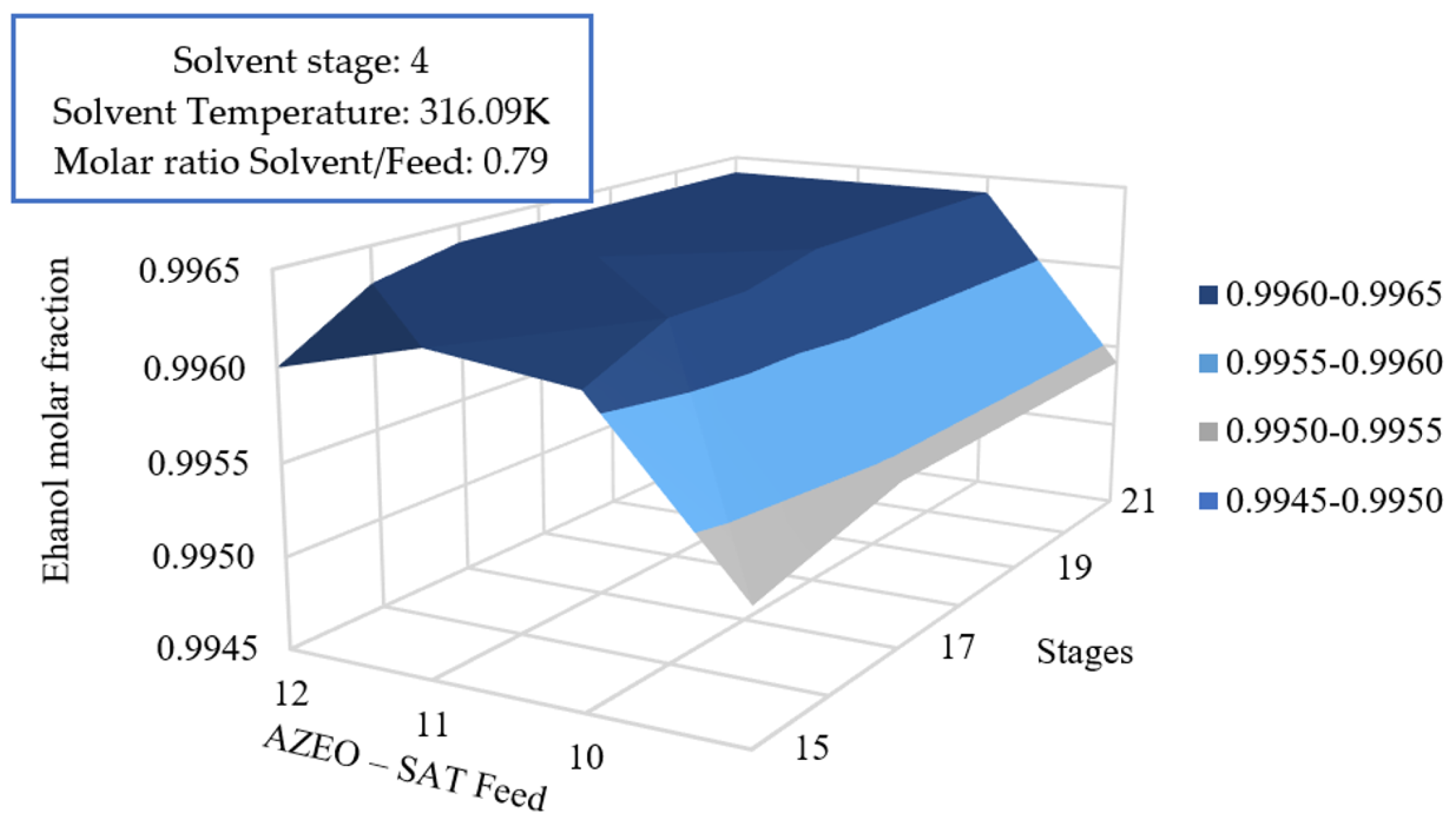
3.5.3. Effect of Azeotrope Feed and Number of Stages on the Global Efficiency
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Altayeb, R.K. Liquid Fuel Production from Pyrolysis of Waste Tires: Process Simulation, Exergetic Analysis, and Life Cycle Assessment; American University of Sharjah: Sharjah, United Arab Emirates, 2015. [Google Scholar]
- Veksha, A.; Giannis, A.; Chang, V.W. Conversion of non-condensable pyrolysis gases from plastics into carbon nanomaterials: Effects of feedstock and temperature. J. Anal. Appl. Pyrolysis 2017, 124, 16–24. [Google Scholar] [CrossRef]
- Chernova, N.I.; Kiseleva, S.V.; Larina, O.M.; Sytchev, G.A. Manufacturing gaseous products by pyrolysis of microalgal biomass. Int. J. Hydrogen Energy 2019, 45, 1569–1577. [Google Scholar] [CrossRef]
- Lestinsky, P.; Palit, A. Wood pyrolysis using aspen plus simulation and industrially applicable model. GeoSci. Eng. 2016, 62, 11. [Google Scholar] [CrossRef]
- Klinger, J.L.; Westover, T.L.; Emerson, R.M.; Williams, C.L.; Hernandez, S.; Monson, G.D.; Ryan, J.C. Effect of biomass type, heating rate, and sample size on microwave-enhanced fast pyrolysis product yields and qualities. Appl. Energy 2018, 228, 535–545. [Google Scholar] [CrossRef]
- Alalwan, H.A.; Alminshid, A.H.; Aljaafari, H.A.S. Promising evolution of biofuel generations. Subject review. Renew. Energy Focus 2019, 28, 13. [Google Scholar] [CrossRef]
- IEA Biofuels. Renewables 2021. Available online: https://www.iea.org/reports/renewables-2021/biofuels?mode=transport®ion=World&publication=2021&flow=Consumption&product=Ethanol (accessed on 2 January 2023).
- IEA Transport Biofuels. Renewable Energy Market Update—May 2022. Available online: https://www.iea.org/reports/renewable-energy-market-update-may-2022/transport-biofuels (accessed on 2 January 2023).
- Joseph, A.; Tulasi, Y.; Shrivastava, D.; Kiran, B. Techno-economic feasibility and exergy analysis of bioethanol production from waste. Energy Convers. Manag. X 2023, 18, 100358. [Google Scholar] [CrossRef]
- Gil, I.; Gómez, J.; Rodríguez, G. Control of an extractive distillation process to dehydrate ethanol using glycerol as entrainer. Comput. Chem. Eng. 2012, 39, 129–142. [Google Scholar] [CrossRef]
- Gil, I.; García, L.; Rodríguez, G. Simulation of ethanol extractive distillation with mixed glycols as separating agent. Braz. J. Chem. Eng. 2014, 31, 259–270. [Google Scholar] [CrossRef]
- Lauzurique, G.; Zumulacáguerri, L.; Pérez, O.; Curbelo, A. Simulación de la destilación extractiva para la obtención de etanol anhidro empleando glicoles. Sci. Teach. Technol. 2016, 53, 362–383. [Google Scholar]
- Batista, E.; Meirelles, A. Simulation and thermal integration SRV in extractive distillation column. J. Chem. Eng. Japan 1997, 30, 45–51. [Google Scholar] [CrossRef]
- Sorin, M.; Brodyansky, V. A method for thermodynamic optimization—I theory and application to an ammonia synthesis plant. Energy 1992, 17, 1019–1031. [Google Scholar] [CrossRef]
- Sorin, M.; Bonhivers, J.; Paris, J. Exergy efficiency and conservation of chemical reactions. Energy Convers. Manag. 1998, 39, 1863–1868. [Google Scholar] [CrossRef]
- Sorin, M.; Bonhivers, J.; Paris, J. Integrated exergy load distribution method and pinch analysis. Comput. Chem. Eng. 1999, 23, 497–507. [Google Scholar] [CrossRef]
- Sorin, M.; Hammache, A.; Diallo, O. Exergy Load Distribution Approach for Multi-step Process Design. Appl. Therm. Eng. 2000, 20, 1365–1380. [Google Scholar] [CrossRef]
- Moran, M.; Shapíro, H.; Boettner, D.; Bailey, M. Fundamentals of Engineering Thermodynamics; John Wiley Sons: New York, NY, USA, 2014. [Google Scholar]
- Luis, P. Exergy as a tool for measurement process intensification in chemical engineering. J. Chem. Technol. Biotechnol. 2013, 88, 1951–1958. [Google Scholar] [CrossRef]
- Cengel, Y.; Boles, M. Termodinámica; Mc Graw Hill Education: México, Mexico, 2011. [Google Scholar]
- Fernández, J. Análisis Termoeconómico de un Proceso de Producción de Biodiesel que Opera de Manera Convencional y oor Destilación Reactiva, Tesis (Grado en Ingeniería Química), Facultad de Ingeniería, Programa de Ingeniería Química; Fundación Universidad de América: Bogotá, Colombia, 2018. [Google Scholar]
- Bylka, J.; Mróz, T. Exergy evaluation of a water distribution system. Energies 2020, 13, 6221. [Google Scholar] [CrossRef]
- Kallio, S.; Siroux, M. Exergy and energy-economic approach to evaluate hybrid renewable energy systems in buildings. Energies 2023, 16, 1029. [Google Scholar] [CrossRef]
- Zhang, L.; Zhai, H.; He, J.; Yang, F.; Wang, S. Application of exergy analysis in flue gas condensation waste heat recovery systems evaluation. Energies 2022, 15, 7525. [Google Scholar] [CrossRef]
- Khoobbakht, G.; Kheiralipour, K.; Rasouli, H.; Rafiee, M.; Hadipour, M.; Karimi, M. Experimental exergy analysis of transesterification in biodiesel production. Energy 2020, 196, 117092. [Google Scholar] [CrossRef]
- Ortiz, P.; Marechal, F.; Oliveira, J. Exergy assessment and techno-economic optimization of bioethanol production routes. Fuel 2020, 279, 118327. [Google Scholar] [CrossRef]
- Meramo-Hurtado, S.; González-Delgado, A.; Rehmann, L.; Quiñones-Bolaños, E.; Mehrvar, M. Comparison of Biobutanol Production Pathways via Acetone–Butanol–Ethanol Fermentation Using a Sustainability Exergy-Based Metric. ACS Omega 2020, 5, 18710–18730. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.; Guo, C.; Jiao, Y.; Liu, X.; He, C.; Awasthi, M.; Liu, L.; Chang, C. Exergy analysis and optimization of bio-methane production from corn stalk pretreated by compound bacteria based on genetic algorithm. Bioresour. Technol. 2022, 346, 126413. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Li, L.; Xu, P.; Liu, B.; Shuai, Y.; Li, B. Hydrogen production through biomass gasification in supercritical water: A review from exergy aspect. Int. J. Hydrogen Energy 2019, 44, 15727–15736. [Google Scholar] [CrossRef]
- Ayala-Ruíz, N.; Malagón-Romero, D.; Milquez-Sanabria, H. Exergoeconomic evaluation of a banana waste pyrolysis plant for biofuel production. J. Clean. Prod. 2022, 359, 132108. [Google Scholar] [CrossRef]
- Vilardi, G.; Verdone, N. Exergy analysis of municipal solid waste incineration processes: The use of O2-enriched air and the oxy-combustion process. Energy 2022, 239, 122147. [Google Scholar] [CrossRef]
- Mehrpooya, M.; Khalili, M.; Sharifzadeh, M. Model development and energy and exergy analysis of the biomass gasification process (Based on the various biomass sources). Renew. Sustain. Energy Rev. 2018, 91, 869–887. [Google Scholar] [CrossRef]
- Singh, R.; Jena, K.; Chakraborty, J.; Sarkar, A. Energy and exergy analysis for torrefaction of pigeon pea stalk (cajanus cajan) and eucalyptus (eucalyptus tereticornis). Int. J. Hydrogen Energy 2020, 45, 18922–18936. [Google Scholar] [CrossRef]
- Balat, M.; Balat, M.; Kırtay, E.; Balat, H. Main routes for the thermo-conversion of biomass into fuels and chemicals. Part 1: Pyrolysis systems. Energy Convers. Manag. 2009, 50, 3147–3157. [Google Scholar] [CrossRef]
- García-García, J.; Marmolejo-Correa, D.; Cárdenas-Guerra, J.; Morales-Rodríguez, R. Exergy analysis of an extractive distillation column for reducing energy consumption in a bioethanol production process. Comput. Aided Process Eng. 2018, 43, 513–518. [Google Scholar] [CrossRef]
- Sato, N. Chemical Energy An Exergy: An Introduction to Chemical Thermodynamics for Engineers; Elsevier Science: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Liang, X.; Liu, Y.; Kang, L. Retrofit and optimization for vacuum gas oil hydrotreating system based on exergy load distribution analysis. Int. J. Exergy 2016, 21, 347–368. [Google Scholar] [CrossRef]
- Uyazán, A.; Gil, I.; Aguilar, J.; Rodríguez, G.; Caicedo, L. Producción de alcohol carburante por destilación extractiva: Simulación del proceso con glicerol. Rev. Ing. Investig. 2006, 26, 45–50. [Google Scholar]
- Meirelles, A.; Weiss, S.; Herfurth, H. Ethanol dehydration by extractive distillation. J. Chem. Technol. Biotechnol. 1992, 53, 181–188. [Google Scholar] [CrossRef]
- Szargut, J. Exergy Method: Technical and Ecological Applications; WIT Press: Southampton, UK, 2005. [Google Scholar]
- Kotas, T. Exergy Method of Thermal Plant Analysis; Butterwoth-Heinemann: Oxford, UK, 1985. [Google Scholar]
- Demirel, Y. Nonequilibrium Thermodynamics Transport and Rate Processes in Physical, Chemical and Biological Systems; Elsevier Science: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Ghannadzadeh, A. Exergetic Balances and Analysis in a Process Simulator: A Way to Enhance Process Energy Integration. Ph.D. Thesis, Departamento de Ingeniería de Procesos y Medio Ambiente, Universidad de Toulouse, Toulouse, France, 2012. Available online: https://oatao.univ-toulouse.fr/9613/1/ghannadzadeh.pdf (accessed on 19 December 2022).
- Kanoglu, M.; Dincer, I.; Rosen, M. Understanding energy and exergy efficiencies for improved energy management in power plants. Energy Policy 2007, 35, 3967–3978. [Google Scholar] [CrossRef]
- Boyaghchi, F.; Molalei, H. Sensitivity analysis of exergy destruction in a real combined cycle power plant based on advanced exergy method. Energy Convers. Manag. 2015, 99, 374–386. [Google Scholar] [CrossRef]
- Demirel, Y. Thermodynamic analysis of separation systems. Sep. Sci. Technol. 2010, 39, 3897–3942. [Google Scholar] [CrossRef]
- Cano, N.A.; Céspedes-Zuluaga, S.; Guerrero-Martin, C.; Gallego, D. Exergy and emergy: Complementary tools for assessing the environmental sustainability use of biosolids generated in wastewater-treatment plant for energy-production. Química Nova 2022, 45, 4–15. [Google Scholar] [CrossRef]
- Ibañez-Gómez, L.F.; Albarracín-Quintero, S.; Céspedes-Zuluaga, S.; Montes-Páez, E.; Ando, O.H., Jr.; Carmo, J.P.; Guerrero-Martin, C.A. Process optimization of the flaring gas for field applications. Energies 2022, 15, 7655. [Google Scholar] [CrossRef]
- Cante Soler, C.A.; Guerrero Martin, C.A.; Malagueta, D.C. Feasibility of the Implementation of Solar Thermal Energy in Steam Assisted Gravity Drainage (Sagd) for Extra Heavy Oil Field in Colombia. Geoenergy Sci. Eng. 2023, 222, 211463. [Google Scholar] [CrossRef]
- Guang, C.; Shi, X.; Zhao, X.; Zhang, Z.; Li, G. Development and intensification of a four-column hybrid process of heteroazeotropic distillation and pressure-swing distillation. Chem. Eng. Process. Process Intensif. 2020, 150, 107875. [Google Scholar] [CrossRef]
| Energy Consumption (kJ/kg ethanol) | |||
|---|---|---|---|
| (C1) | (C2) | Uzayan [38] (C1) | Uzayan [38] (C2) |
| 1277 | 325 | 1249 | 224 |
| Stream | |||
|---|---|---|---|
| AZE | 0 | 32,012.56 | 32,012.56 |
| SOLV-REC | 23.53 | 26,415.16 | 26,438.69 |
| AZEO-SAT | 17.44 | 32,012.56 | 32,030 |
| RECSOLVH | 1.99 | 26,415.16 | 26,417.16 |
| MAKE-UP | 0.174 | 309.03 | 309.27 |
| ENTRAIN | 3.581 | 26,710.74 | 26,714.32 |
| ETOH | 0.3273 | 32,036.59 | 32,036.9 |
| MIX | 86.95 | 26,684.85 | 26,771.81 |
| WATER | 122.3 | 308.6 | 430.9 |
| SOLV | 22.49 | 26,415.56 | 26,438.66 |
| Destroyed Exergy kJ/s | |
|---|---|
| H | 2.8 |
| Pump | 0.3 |
| Mixer | 0.6 |
| Column C1 | 413.7 |
| Column C2 | 118.4 |
| Separation System by Extractive Distillation | |||||
|---|---|---|---|---|---|
| Coefficients (%) | H | Pump | Mixer | C1 | C2 |
| 2.46 | 0.02020 | 0.1743 | 38.66 | 58.68 | |
| 0 | 0.02020 | 0.1743 | 0 | 0 | |
| 80.95 | 19.78 | 99.9 | 13.49 | 42.62 | |
| 30.67 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guerrero-Martin, C.A.; Fernández-Ramírez, J.S.; Arturo-Calvache, J.E.; Milquez-Sanabria, H.A.; da Silva Fernandes, F.A.; Costa Gomes, V.J.; Lima e Silva, W.; Dutra Valente Duarte, E.; Guerrero-Martin, L.E.; Lucas, E.F. Exergy Load Distribution Analysis Applied to the Dehydration of Ethanol by Extractive Distillation. Energies 2023, 16, 3502. https://doi.org/10.3390/en16083502
Guerrero-Martin CA, Fernández-Ramírez JS, Arturo-Calvache JE, Milquez-Sanabria HA, da Silva Fernandes FA, Costa Gomes VJ, Lima e Silva W, Dutra Valente Duarte E, Guerrero-Martin LE, Lucas EF. Exergy Load Distribution Analysis Applied to the Dehydration of Ethanol by Extractive Distillation. Energies. 2023; 16(8):3502. https://doi.org/10.3390/en16083502
Chicago/Turabian StyleGuerrero-Martin, Camilo Andrés, Juan Sebastián Fernández-Ramírez, Jaime Eduardo Arturo-Calvache, Harvey Andrés Milquez-Sanabria, Fernando Antonio da Silva Fernandes, Vando José Costa Gomes, Wanessa Lima e Silva, Emanuele Dutra Valente Duarte, Laura Estefanía Guerrero-Martin, and Elizabete Fernandes Lucas. 2023. "Exergy Load Distribution Analysis Applied to the Dehydration of Ethanol by Extractive Distillation" Energies 16, no. 8: 3502. https://doi.org/10.3390/en16083502
APA StyleGuerrero-Martin, C. A., Fernández-Ramírez, J. S., Arturo-Calvache, J. E., Milquez-Sanabria, H. A., da Silva Fernandes, F. A., Costa Gomes, V. J., Lima e Silva, W., Dutra Valente Duarte, E., Guerrero-Martin, L. E., & Lucas, E. F. (2023). Exergy Load Distribution Analysis Applied to the Dehydration of Ethanol by Extractive Distillation. Energies, 16(8), 3502. https://doi.org/10.3390/en16083502










