Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors
Abstract
1. Introduction
2. Methods
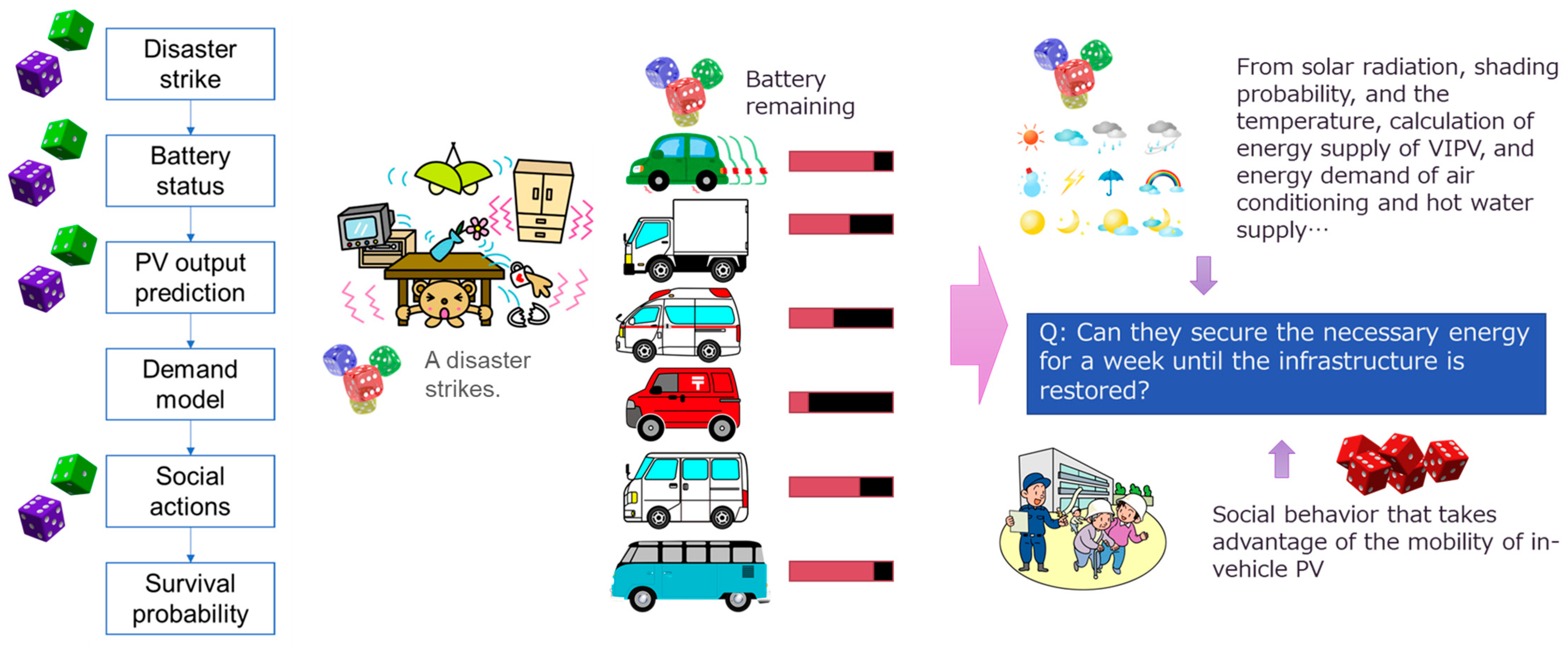
2.1. Resilience Scenario
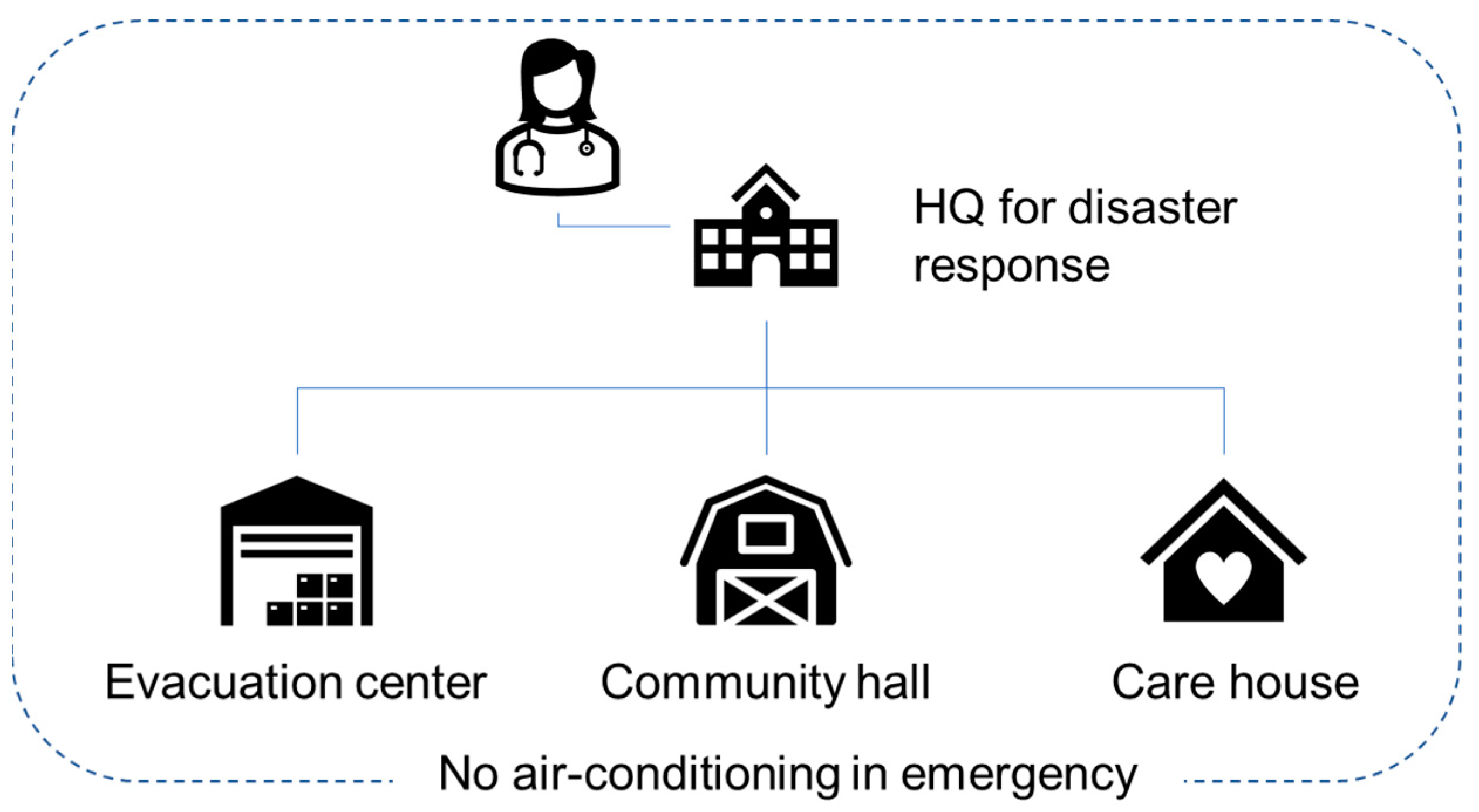
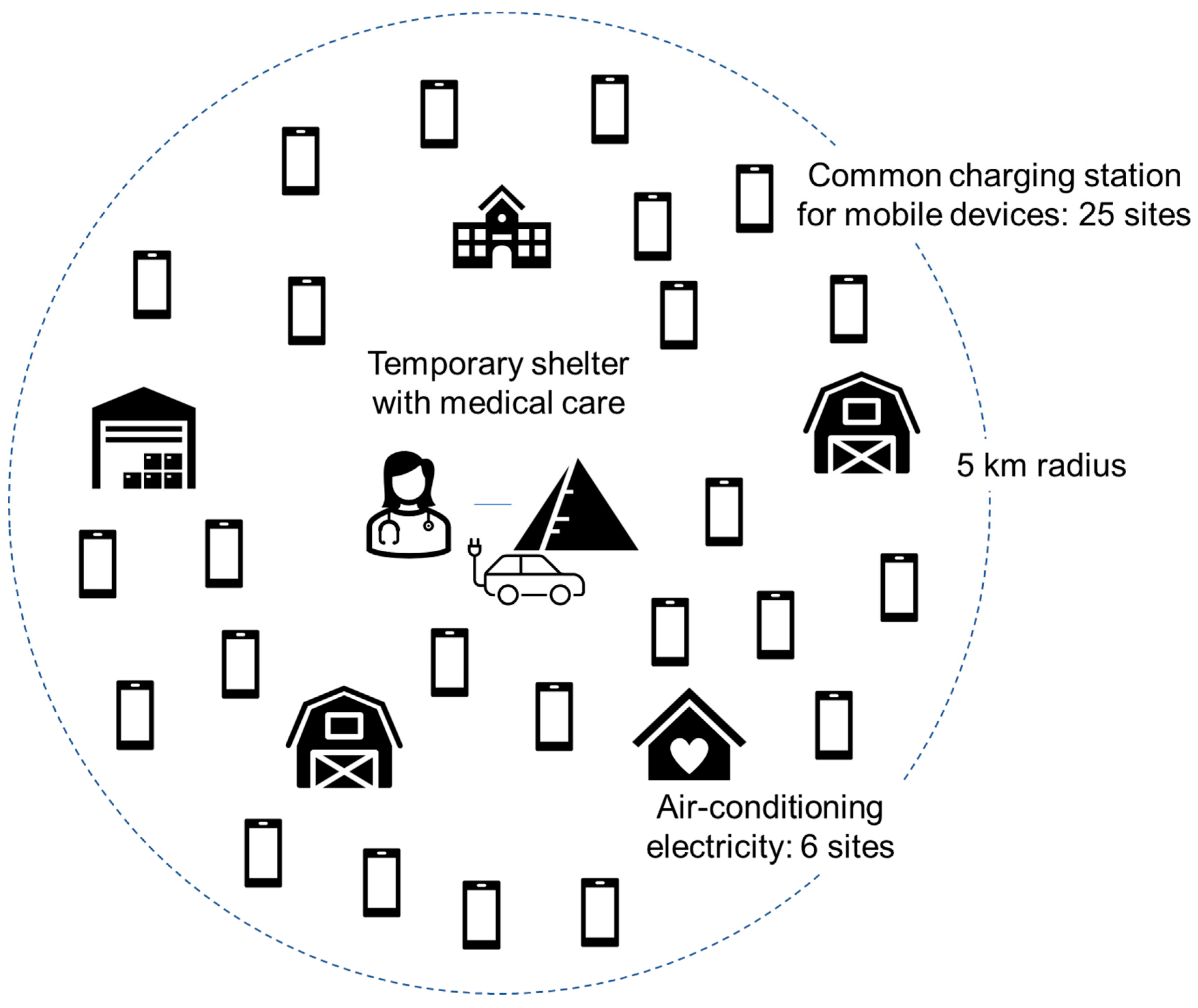
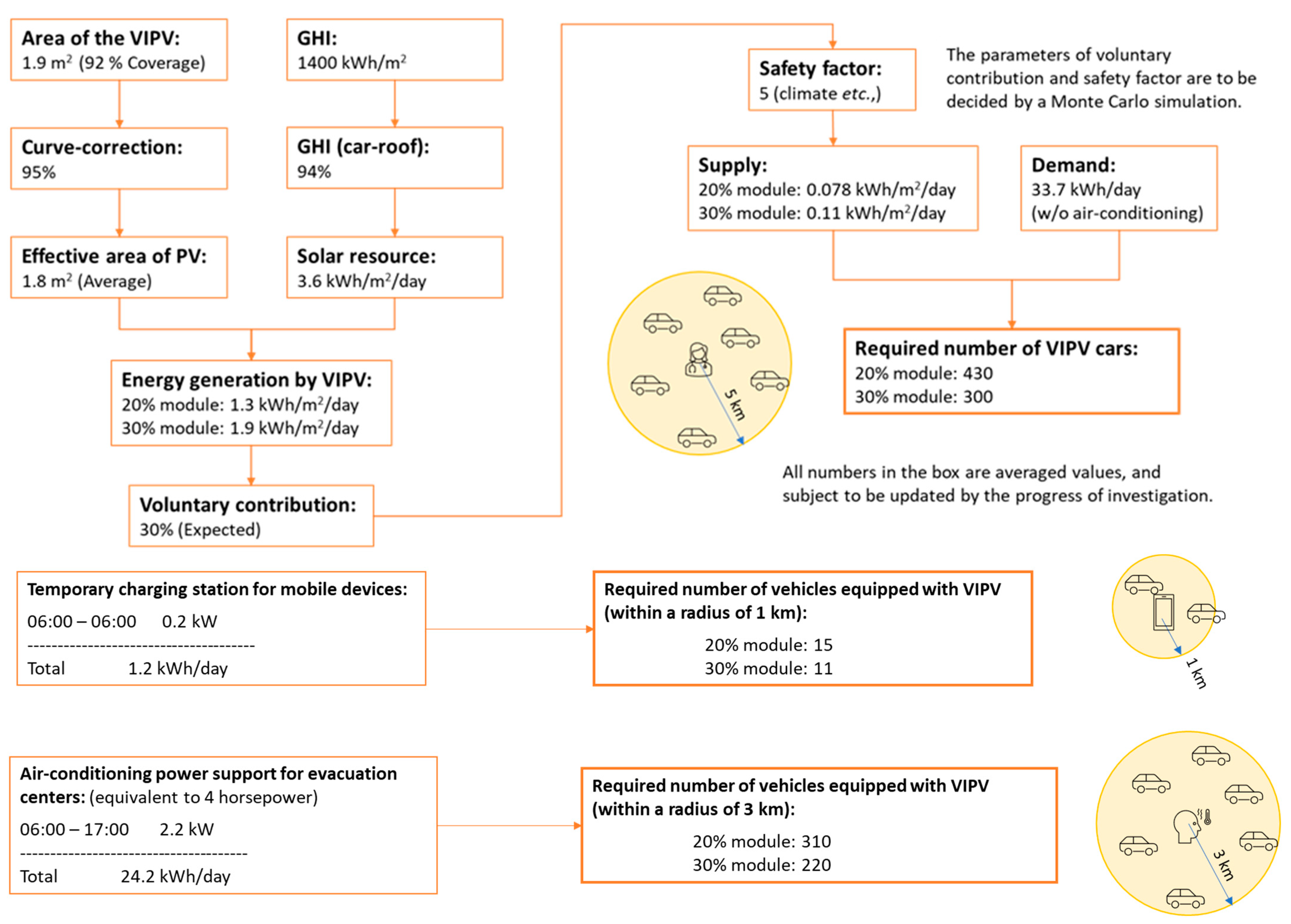
- A significant earthquake occurs in a scenario city (“PV City”) (radius 5 km). In the first few hours, the PV City local government transitions schools, community centers, and care centers to evacuation centers equipped with spot coolers at six locations (4 hp each). In addition, the PV City local government calls for temporary first-aid stations and multiple charging stations for mobile devices for local people to help access disaster information over and above access to conventional disaster infrastructure. The number of temporary charging stations accessible within a 1 km walk is 25. Because such facilities require electricity, the PV City local government calls for a voluntary donation of electricity from PV-equipped vehicles; a certain percentage of drivers check the charging status (SoC) of their vehicles (every hour), and if SoC is over 90%, they decide to go to one of the use points and provide electricity until the charge of the battery falls to 50% (vehicle batteries are recharged by PV on vehicles). Other efforts are in place to help keep disaster prevention equipment and facilities functioning. Seven days later, the PV City local government is notified that regional lifelines have been restored.
2.2. Demand—Supply Balance
- Energy requirements of critical facilities, like headquarters of the disaster response and evacuation centers (based on conventional infrastructure);
- Establishment of temporary evacuation centers essential and suitable for energy supply from VIPV; and
- The need for air conditioning in hot weather (a critical need that is usually ignored in conventional disaster response planning).
- The density and distribution of the SEV;
- Distribution of solar irradiance and climate;
- VIPV-specific losses;
- Energy consumption by SEV to carry the donated energy to the saving points and return; and
- Voluntary donation of VIPV energy to shared facilities (probabilities, conditions, and incentives).
2.3. Demand Model
- Temporary shelter with medical care;
- Mobile device charging station within walking distance; and
- Backup power for air conditioning.
2.4. Supply Model
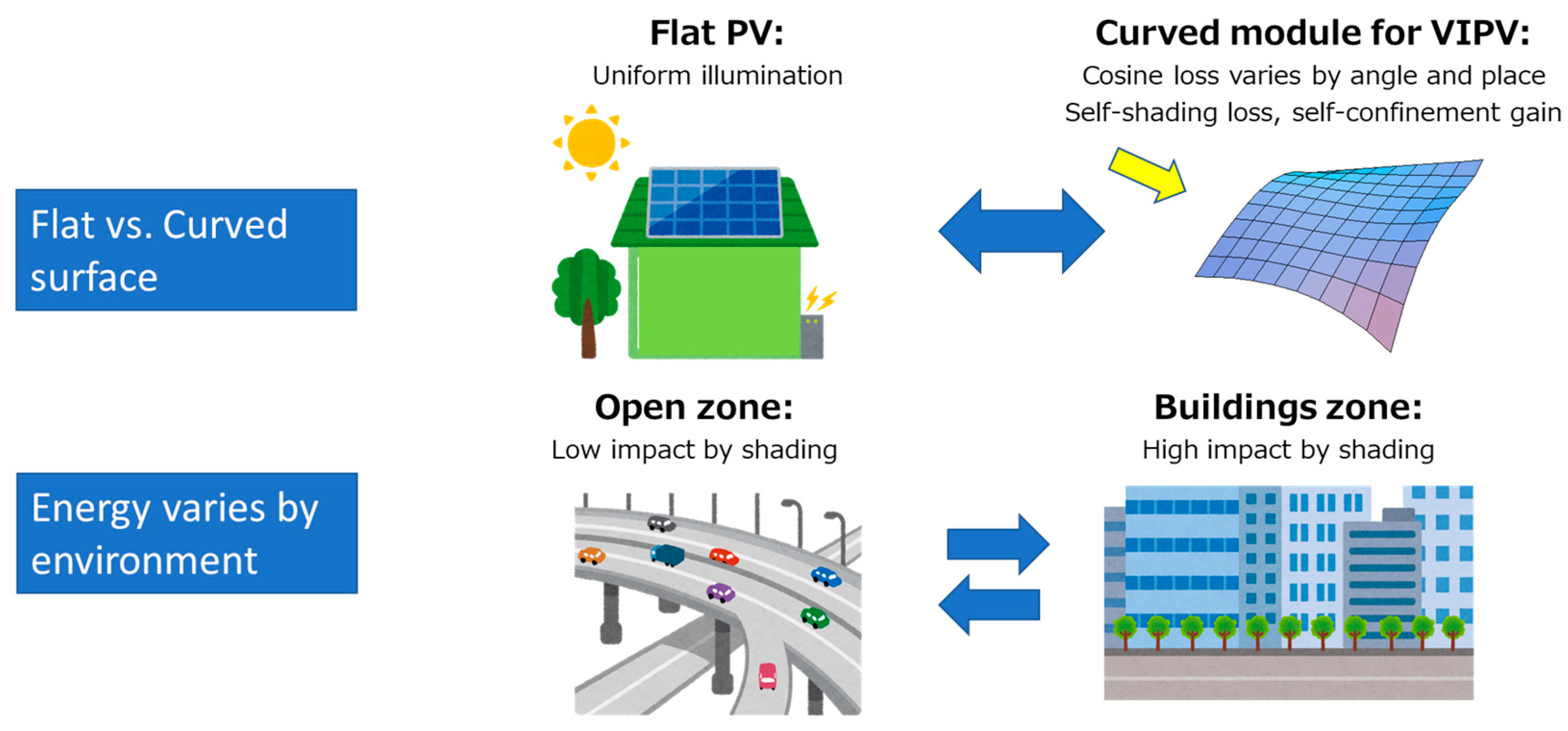
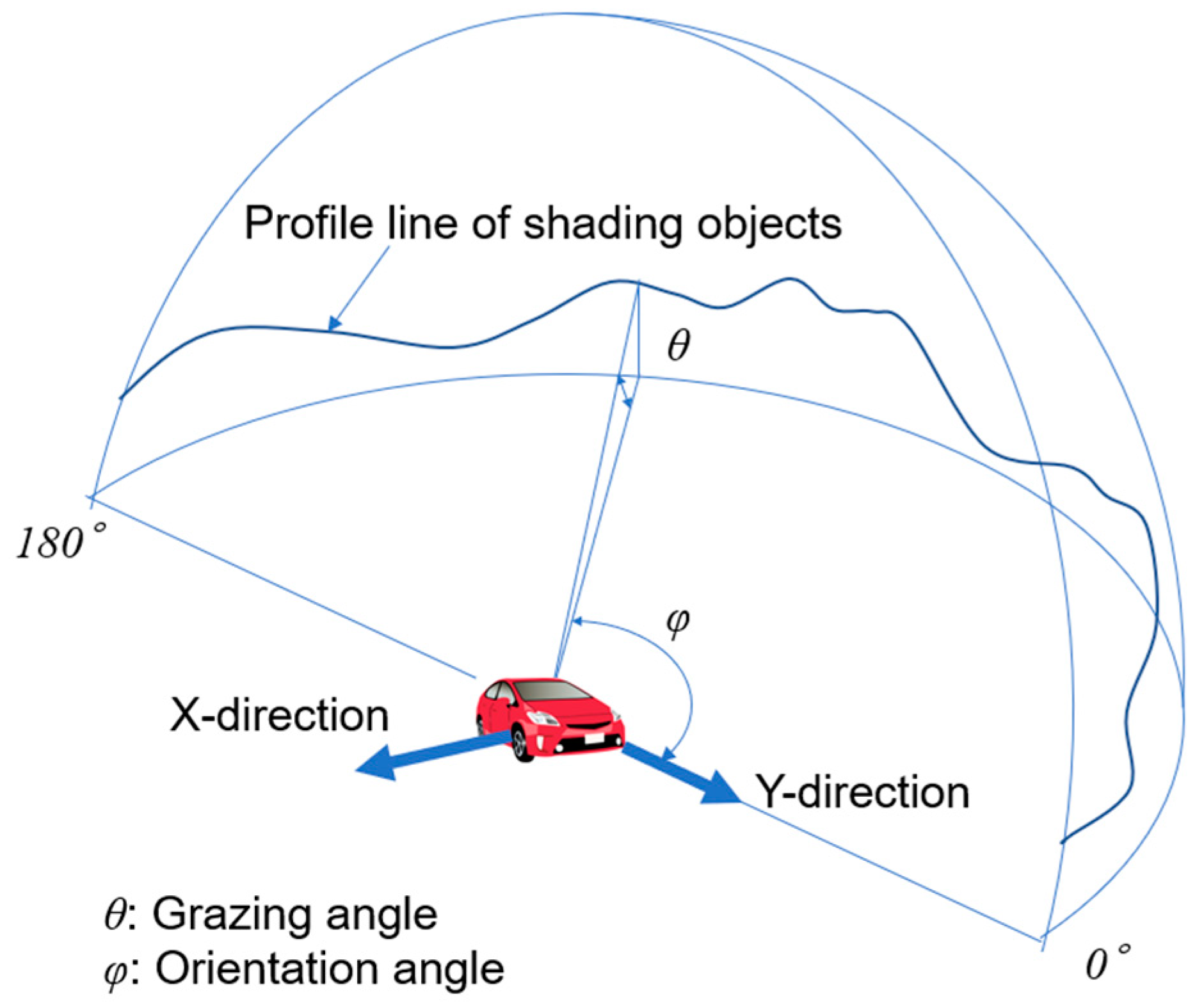
- The orientation angle of the VIPV is not fixed but, rather, frequently changes during driving;
- A moving VIPV has a higher probability of shading than does a fixed-station PV;
- Although the shading objects, such as street trees and traffic signals, are relatively small, they have some effect on VIPV performance;
- Curved surfaces of the vehicle;
- The impacts mentioned above interact and depend on the vehicle’s local coordinates;
- Rapid solar irradiance fluctuation, generally in milliseconds, results from dynamic partial shading;
- Rapid fluctuations in the solar spectrum; and
- Temperature variation between parking and driving.
- Solar irradiance on VIPV (orthogonal 5 axes);
- Distribution of shaded objects used to estimate solar irradiance and irradiation on an arbitrary reference plane tangible to the curved surface of the VIPV;
- Distribution of edges of the shading objects that results in partial shading; and
- Dynamic spectrum fluctuation.
2.5. Curve Correction of VIPV
2.6. Shading Correction of VIPV Performance
2.7. Monte-Carlo Simulation with Social Activities
- SEV drivers check the state of charge (SoC) hourly;
- If the SoC does not exceed 90%, then the SEV driver does not consider energy donation;
- If the SoC exceeds 90%, 5% of drivers in this situation will donate energy, coin toss to randomly determine (5% probability) determine if a driver will donate; and
- The SEV drivers who decide to donate energy to resilient facilities supported by the VIPV, consume energy to move to the facility, donated energy (up to 50% SoC), and return to their original places.
3. Results
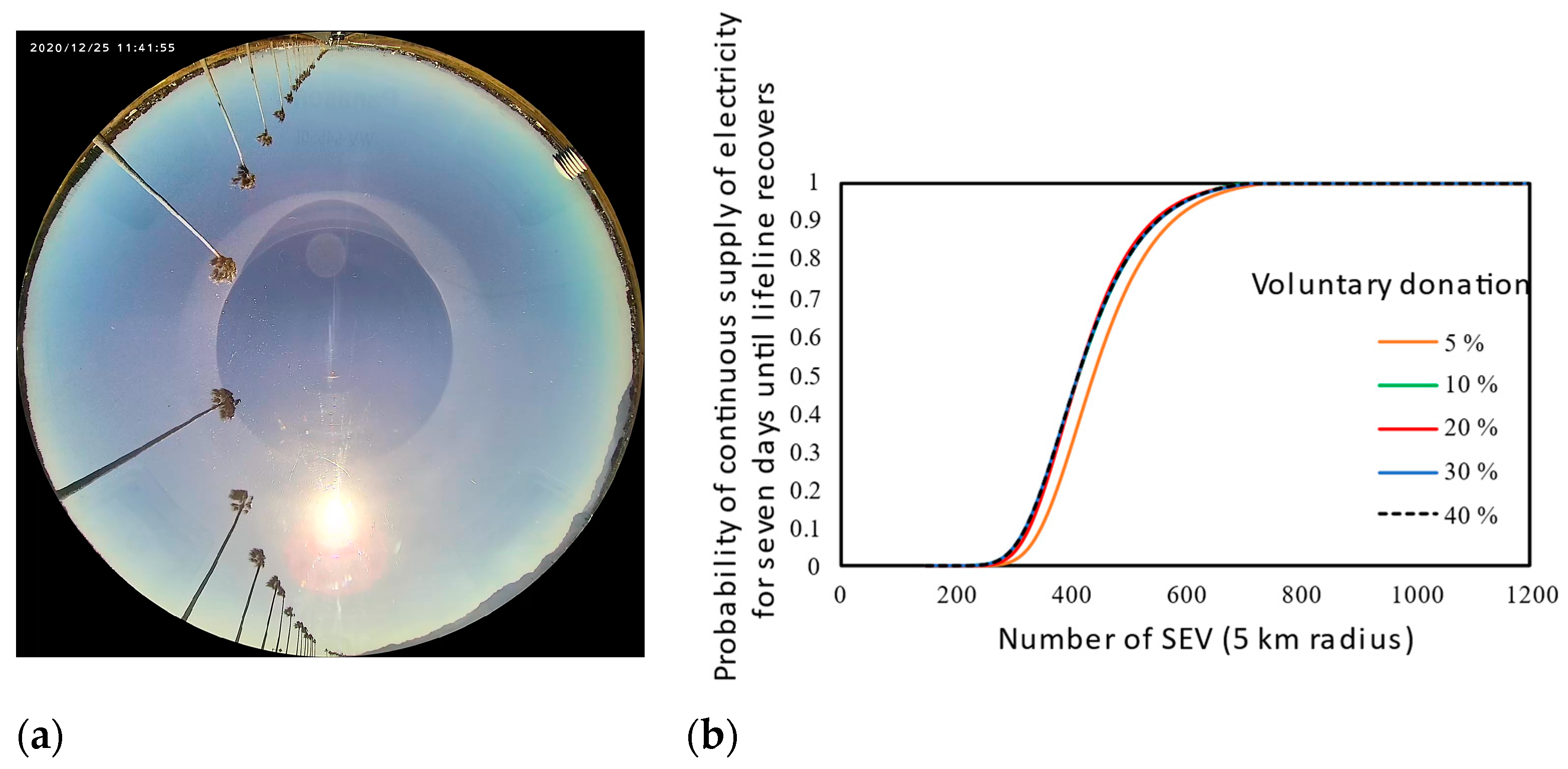
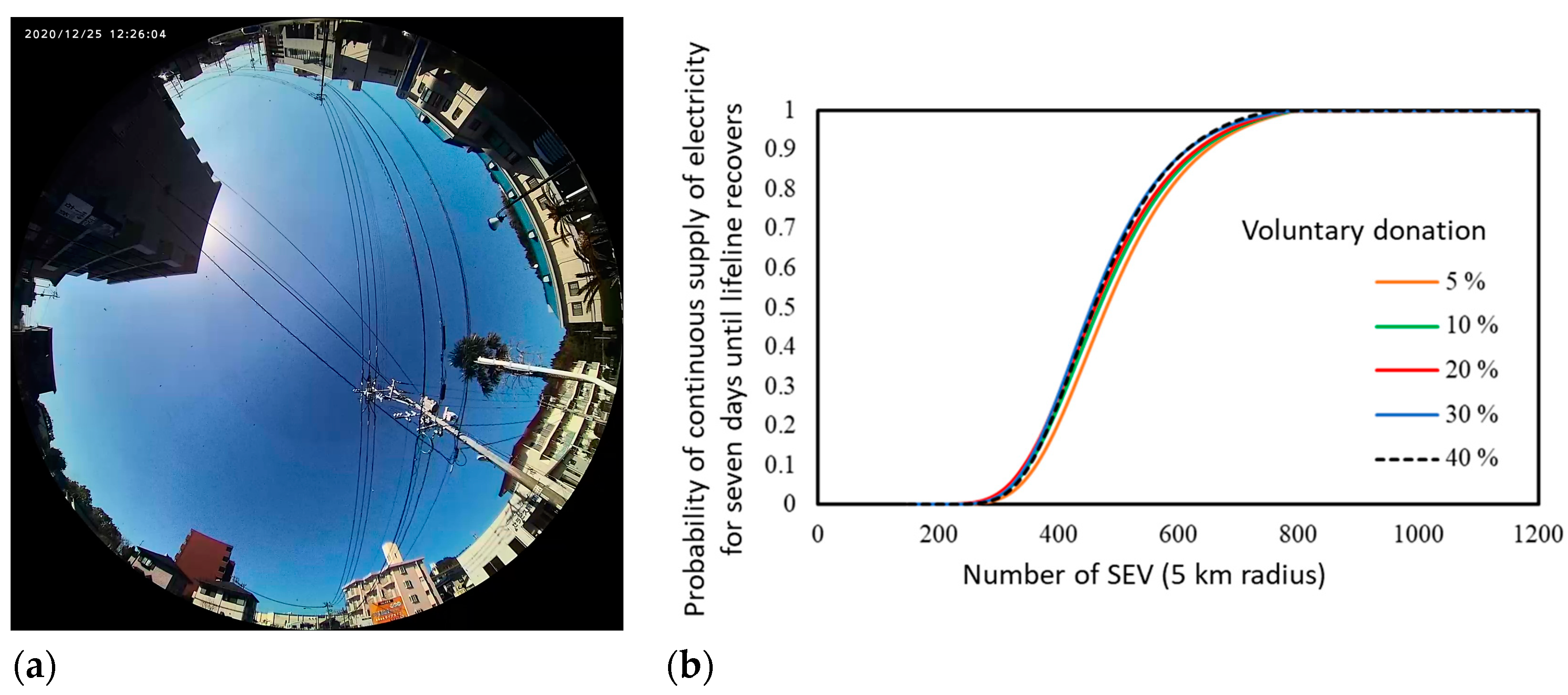
3.1. Measurement and Modeling of the Power of VIPV Affected by Shading Objects
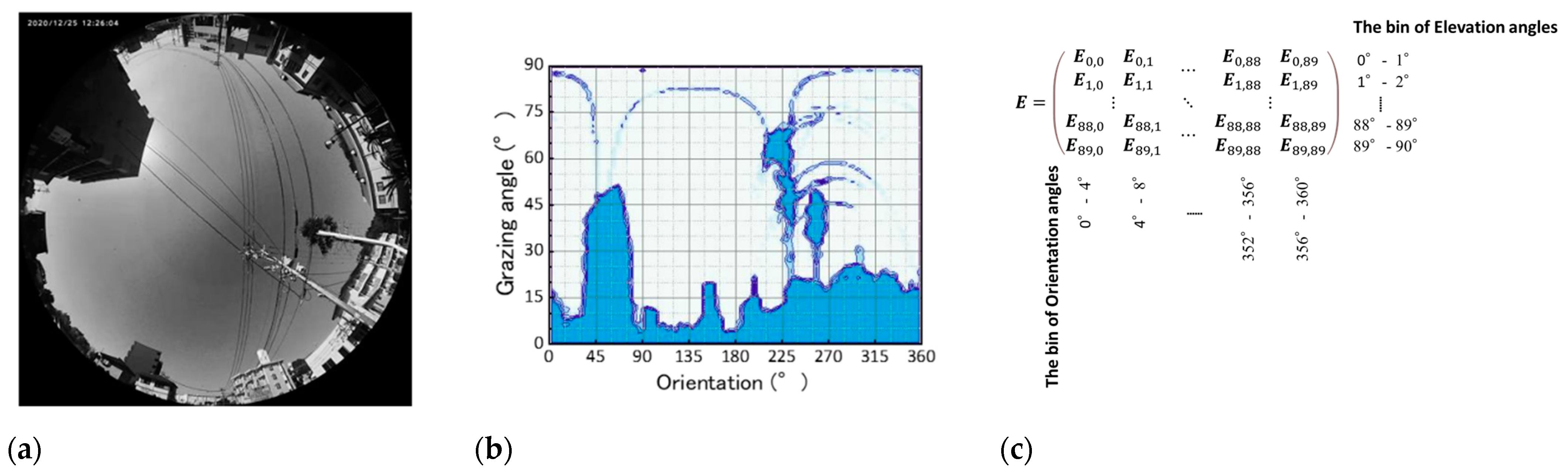
- Area of each surface element of the hemispherical sky;
- The aperture and shading ratio varied according to the grazing and orientation angles, given by the matrix form:
- Cosine of ray from each surface element, cosine of ray relative to unit vector of the surface element of the absorber; and
- Area of the surface element of the absorber.
- Direct normal irradiance (constant value);
- Aperture probability (=0 when shaded and =1 when not shaded);
- Cosine of the ray to the surface element of the absorber; and
- Area of the surface element of the absorber.
- Reflection of the building wall by direct sunlight, the orientation of the normal vector of the wall is within ±90 ° of the direct ray of sunlight;
- Reflection of the building wall by the diffused sunlight; and
- The reflection from the road is given by the product of the reflectivity of the road surface and the horizontal irradiation affected by shading and reflection from the building wall.
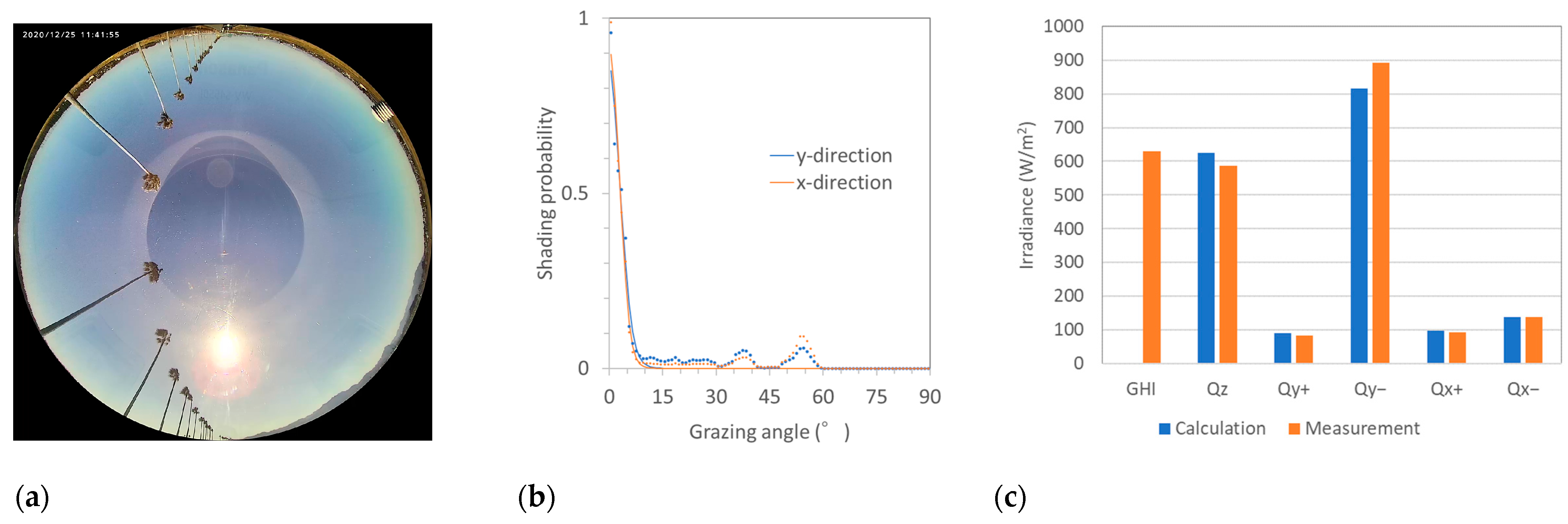
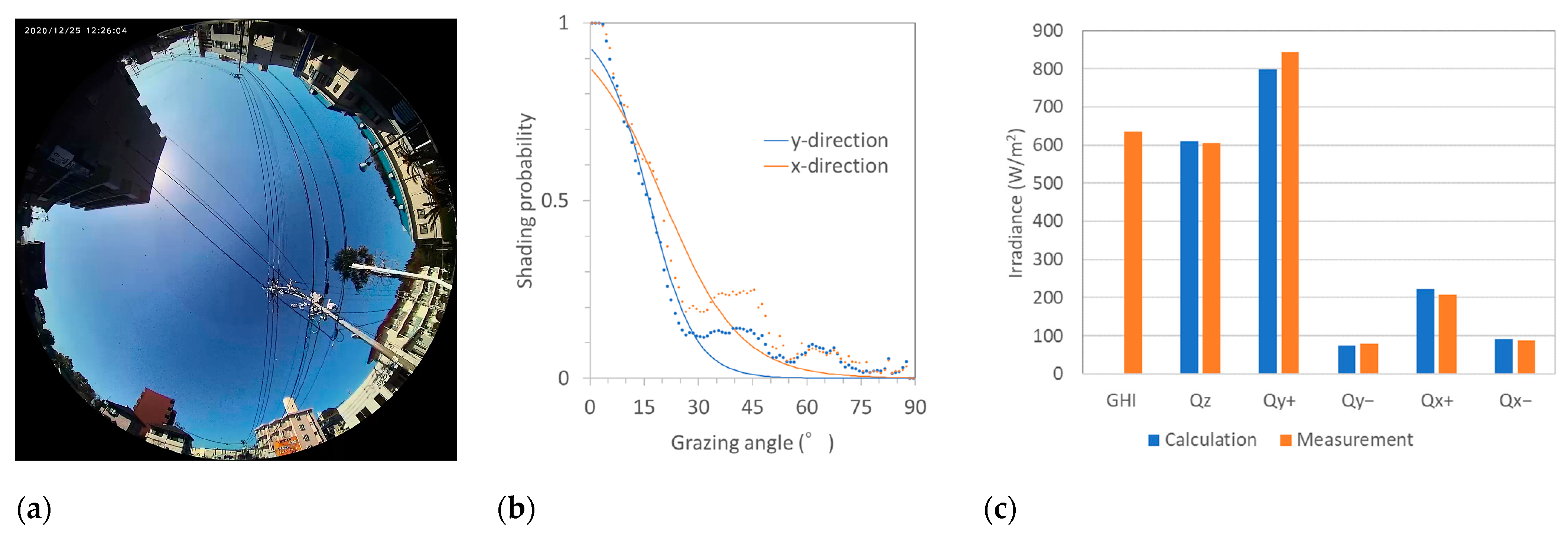
- Direct indication of solar irradiance for PV panels on the roof and side(s) of the vehicle;
- Shading detection was compared with the direction information obtained by comparing four monitored irradiances on the side(s) of the vehicle;
- Three-dimensional solar-resource monitoring, including the angular distribution of solar resources on the roof of a vehicle, is essential for characterizing curved modules; and
- The performance and solar irradiance models for the VIPV were validated by checking more than two orthogonal axes using monitored data in five orthogonal directions.
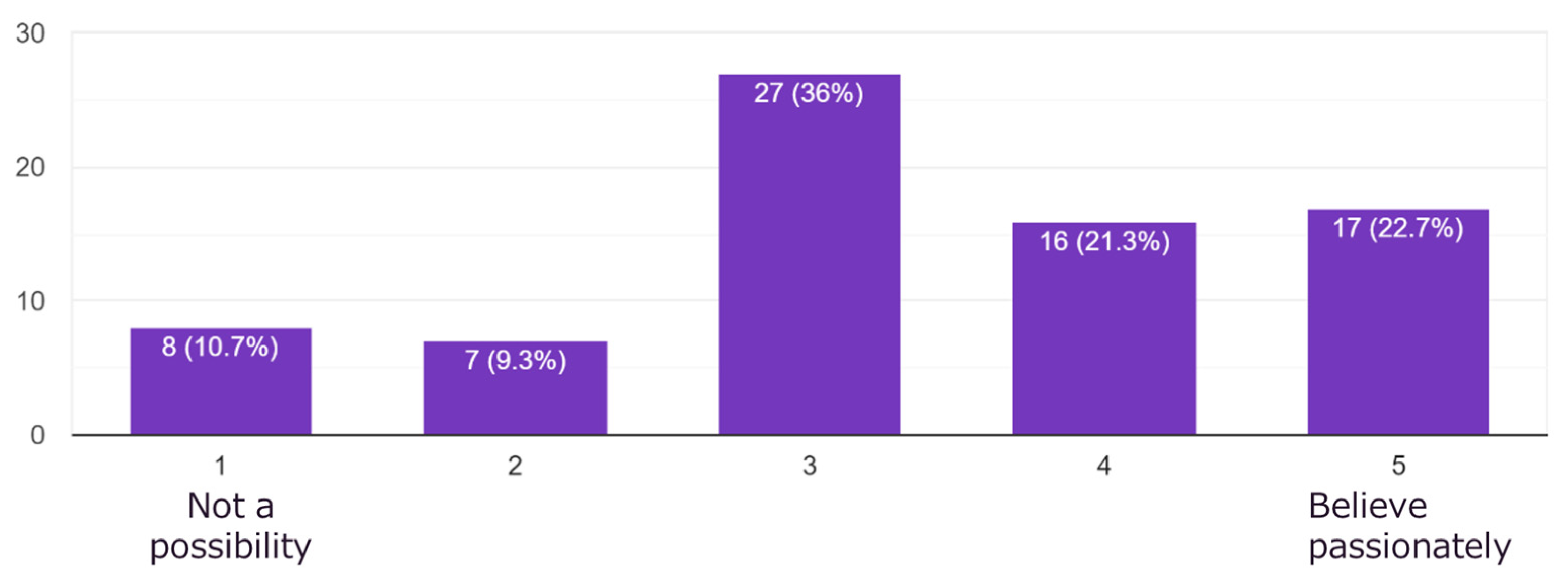
3.2. Survey of the Local Community: Willingness to Donate for Disaster Resilience
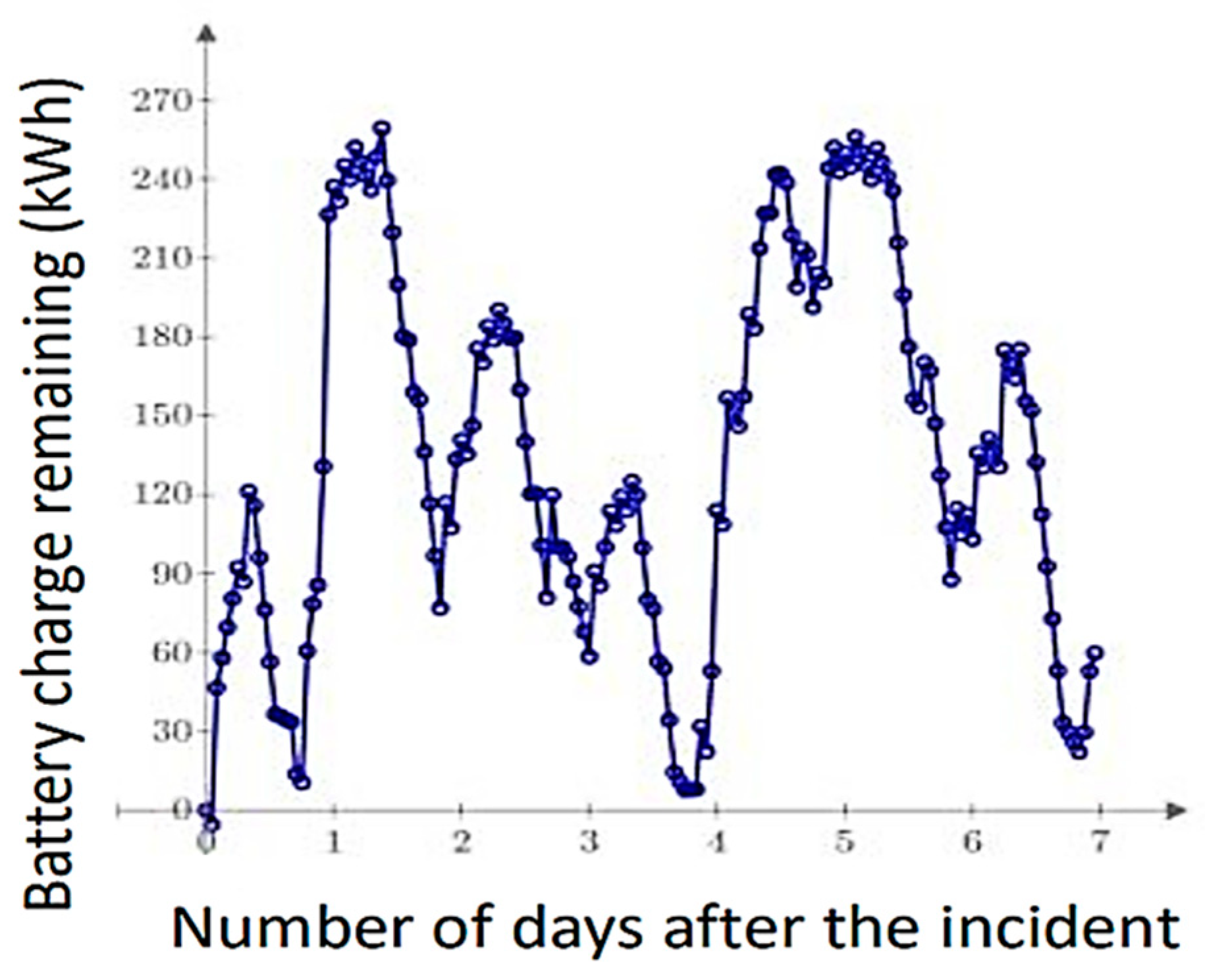
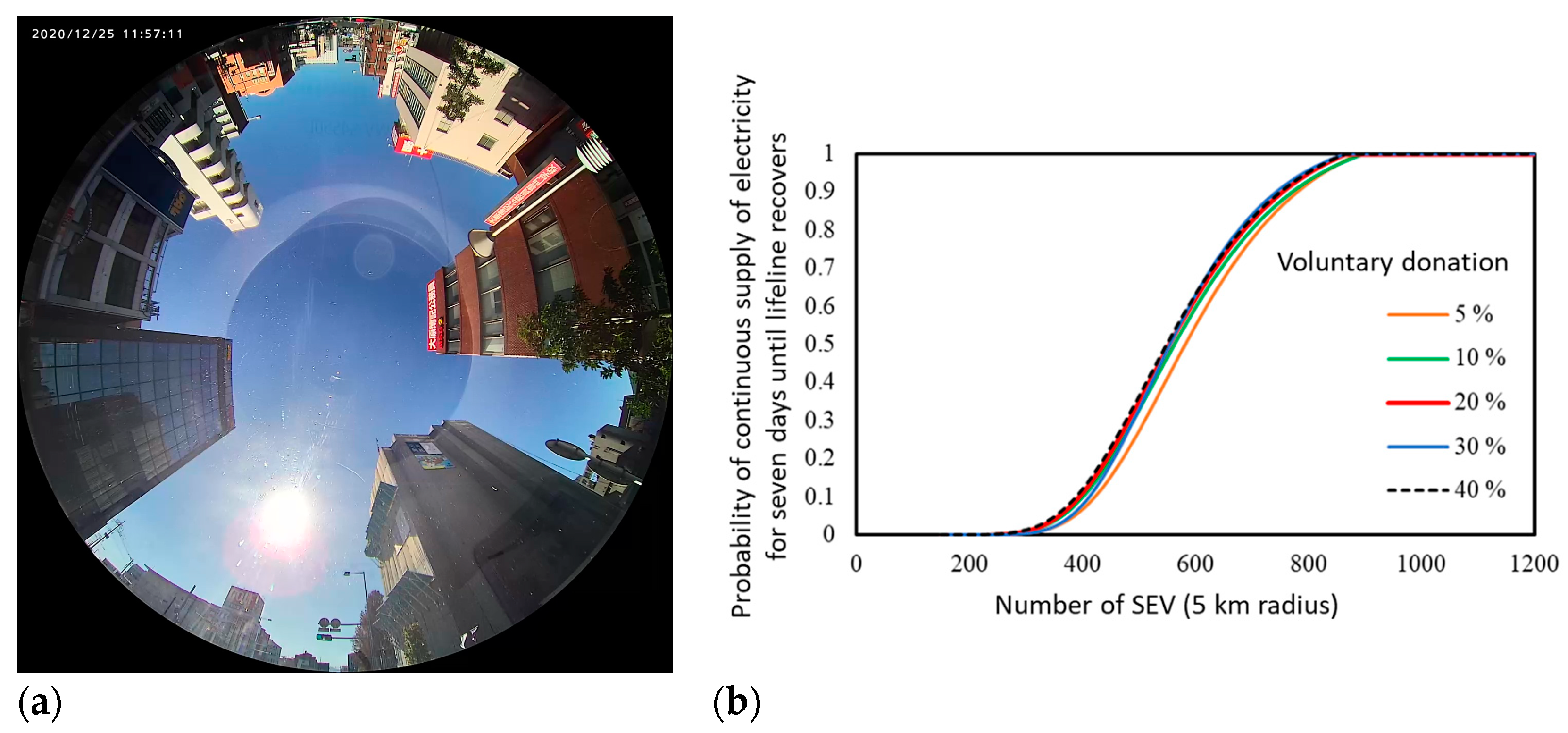
3.3. Monte-Carlo Simulation Results
4. Discussion
5. Conclusions
- Lower risk of an empty battery in VIPV vehicles;
- In BEV vehicles, once the battery is drained, the possibility of energy donation is nil; and
- VIPV makes possible self-generating energy for transportation to the point of relief.
- Lower risk of damage (direct or indirect);
- No trouble with the utility grid or electric cables;
- Avoids reliance on a single centralized PV system (“all or nothing”);
- Units can move to areas of higher irradiance;
- Units can transport both energy and goods; and
- Energy accommodation is possible by carrying energy by vehicles.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, B.; Dehghanian, P.; Kezunovic, M. Optimal allocation of PV generation and battery storage for enhanced resilience. IEEE Trans. Smart Grid 2019, 10, 535–545. [Google Scholar] [CrossRef]
- Laws, N.D.; Anderson, K.; DiOrio, N.A.; Li, X.; McLaren, J. Impacts of valuing resilience on cost-optimal PV and storage systems for commercial buildings. Renew. Energy 2018, 127, 896–909. [Google Scholar] [CrossRef]
- Galvan, E.; Mandal, P.; Sang, Y. Networked microgrids with rooftop solar PV and battery energy storage to improve distribution grids resilience to natural disasters. Int. J. Electr. Power Energy Syst. 2020, 123, 106239. [Google Scholar] [CrossRef]
- Elluru, S.; Gupta, H.; Kaur, H.; Singh, S.P. Proactive and reactive models for disaster resilient supply chain. Ann. Oper. Res. 2019, 283, 199–224. [Google Scholar] [CrossRef]
- Murray-tuite, P.M. A comparison of transportation network resilience under simulated system optimum and user equilibrium conditions. In Proceedings of the 2006 Winter Simulation Conference, Monterey, CA, USA, 3–6 December 2006. [Google Scholar] [CrossRef]
- Ding, T.; Wang, Z.; Jia, W.; Chen, B.; Chen, C.; Shahidehpour, M. Multiperiod distribution system restoration with routing repair crews, mobile electric vehicles, and soft-open-point networked microgrids. IEEE Trans. Smart Grid 2020, 11, 4795–4808. [Google Scholar] [CrossRef]
- Mohammad, A.; Zamora, R.; Lie, T.T. Integration of electric vehicles in the distribution network: A review of PV based electric vehicle modelling. Energies 2020, 13, 4541. [Google Scholar] [CrossRef]
- Esfahani, N.F.; Darwish, A.; Williams, B.W. Power Converter Topologies for Grid-Tied Solar Photovoltaic (PV) Powered Electric Vehicles (EVs)—A Comprehensive Review. Energies 2022, 15, 4648. [Google Scholar] [CrossRef]
- Aziz, M.; Oda, T.; Mitani, T.; Watanabe, Y.; Kashiwagi, T. Utilization of Electric Vehicles and Their Used Batteries for Peak-Load Shifting. Energies 2015, 8, 3720–3738. [Google Scholar] [CrossRef]
- Aleem, S.A.; Hussain, S.M.S.; Ustun, T.S. A Review of Strategies to Increase PV Penetration Level in Smart Grids. Energies 2020, 13, 636. [Google Scholar] [CrossRef]
- Salvatti, G.A.; Carati, E.G.; Cardoso, R.; da Costa, J.P.; Stein, C.M.d.O. Electric Vehicles Energy Management with V2G/G2V Multifactor Optimization of Smart Grids. Energies 2020, 13, 1191. [Google Scholar] [CrossRef]
- Abdalla, M.A.A.; Min, W.; Mohammed, O.A.A. Two-Stage Energy Management Strategy of EV and PV Integrated Smart Home to Minimize Electricity Cost and Flatten Power Load Profile. Energies 2020, 13, 6387. [Google Scholar] [CrossRef]
- Ali, A.I.M.; Sayed, M.A.; Mohamed, A.A.S. Seven-Level Inverter with Reduced Switches for PV System Supporting Home-Grid and EV Charger. Energies 2021, 14, 2718. [Google Scholar] [CrossRef]
- Wang, M.; Abdalla, M.A.A. Optimal Energy Scheduling Based on Jaya Algorithm for Integration of Vehicle-to-Home and Energy Storage System with Photovoltaic Generation in Smart Home. Sensors 2022, 22, 1306. [Google Scholar] [CrossRef]
- Gong, H.; Ionel, D.M. Improving the Power Outage Resilience of Buildings with Solar PV through the Use of Battery Systems and EV Energy Storage. Energies 2021, 14, 5749. [Google Scholar] [CrossRef]
- Sulaeman, I.; Chandra Mouli, G.R.; Shekhar, A.; Bauer, P. Comparison of AC and DC Nanogrid for Office Buildings with EV Charging, PV and Battery Storage. Energies 2021, 14, 5800. [Google Scholar] [CrossRef]
- Vermeer, W.; Chandra Mouli, G.R.; Bauer, P. Real-Time Building Smart Charging System Based on PV Forecast and Li-Ion Battery Degradation. Energies 2020, 13, 3415. [Google Scholar] [CrossRef]
- Nefedov, E.; Sierla, S.; Vyatkin, V. Internet of Energy Approach for Sustainable Use of Electric Vehicles as Energy Storage of Prosumer Buildings. Energies 2018, 11, 2165. [Google Scholar] [CrossRef]
- Cieslik, W.; Szwajca, F.; Golimowski, W.; Berger, A. Experimental Analysis of Residential Photovoltaic (PV) and Electric Vehicle (EV) Systems in Terms of Annual Energy Utilization. Energies 2021, 14, 1085. [Google Scholar] [CrossRef]
- Antić, T.; Capuder, T.; Bolfek, M. A Comprehensive Analysis of the Voltage Unbalance Factor in PV and EV Rich Non-Synthetic Low Voltage Distribution Networks. Energies 2021, 14, 117. [Google Scholar] [CrossRef]
- Strielkowski, W.; Volkova, E.; Pushkareva, L.; Streimikiene, D. Innovative Policies for Energy Efficiency and the Use of Renewables in Households. Energies 2019, 12, 1392. [Google Scholar] [CrossRef]
- Nishimwe, H.; Yoon, S.-G. Combined Optimal Planning and Operation of a Fast EV-Charging Station Integrated with Solar PV and ESS. Energies 2021, 14, 3152. [Google Scholar] [CrossRef]
- Sierra, A.; Gercek, C.; Geurs, K.; Reinders, A. Technical, Financial, and Environmental Feasibility Analysis of Photovoltaic EV Charging Stations With Energy Storage in China and the United States. IEEE J. Photovolt. 2020, 10, 1892–1899. [Google Scholar] [CrossRef]
- Jin, H.; Lee, S.; Nengroo, S.H.; Har, D. Development of Charging/Discharging Scheduling Algorithm for Economical and Energy-Efficient Operation of Multi-EV Charging Station. Appl. Sci. 2022, 12, 4786. [Google Scholar] [CrossRef]
- Mohammed, S.; Titus, F.; Thanikanti, S.B.; Sulaiman, S.M.; Deb, S.; Kumar, N.M. Charge Scheduling Optimization of Plug-In Electric Vehicle in a PV Powered Grid-Connected Charging Station Based on Day-Ahead Solar Energy Forecasting in Australia. Sustainability 2022, 14, 3498. [Google Scholar] [CrossRef]
- Petrusic, A.; Janjic, A. Renewable Energy Tracking and Optimization in a Hybrid Electric Vehicle Charging Station. Appl. Sci. 2021, 11, 245. [Google Scholar] [CrossRef]
- Dai, Q.; Liu, J.; Wei, Q. Optimal Photovoltaic/Battery Energy Storage/Electric Vehicle Charging Station Design Based on Multi-Agent Particle Swarm Optimization Algorithm. Sustainability 2019, 11, 1973. [Google Scholar] [CrossRef]
- Abronzini, U.; Attaianese, C.; D’Arpino, M.; Di Monaco, M.; Tomasso, G. Cost Minimization Energy Control Including Battery Aging for Multi-Source EV Charging Station. Electronics 2019, 8, 31. [Google Scholar] [CrossRef]
- Dukpa, A.; Butrylo, B. MILP-Based Profit Maximization of Electric Vehicle Charging Station Based on Solar and EV Arrival Forecasts. Energies 2022, 15, 5760. [Google Scholar] [CrossRef]
- Zhang, Z.; Gercek, C.; Renner, H.; Reinders, A.; Fickert, L. Resonance Instability of Photovoltaic E-Bike Charging Stations: Control Parameters Analysis, Modeling and Experiment. Appl. Sci. 2019, 9, 252. [Google Scholar] [CrossRef]
- Ghosh, A. Possibilities and Challenges for the Inclusion of the Electric Vehicle (EV) to Reduce the Carbon Footprint in the Transport Sector: A Review. Energies 2020, 13, 2602. [Google Scholar] [CrossRef]
- Muntwyler, U. Towards 100% renewable energy supplies. In Proceedings of the 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 31 March–2 April 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Sierra-Rodriguez, A.; de Santano, T.; MacGill, I.; Ekins-Daukes, N.J.; Reinders, A. A feasibility study of solar PV-powered electric cars using an interdisciplinary modeling approach for the electricity balance, CO2 emissions, and economic aspects: The cases of The Netherlands, Norway, Brazil, and Australia. Prog. Photovolt. Res. Appl. 2020, 28, 517–532. [Google Scholar] [CrossRef]
- The Ford Motor Company. Let the Sun In: Ford C-MAX Solar Energi Concept Goes Off the Grid, Gives Glimpse of Clean Vehicle Future. Available online: https://media.ford.com/content/fordmedia/fna/us/en/news/2014/01/02/let-the-sun-in--ford-c-max-solar-energi-concept-goes-off-the-gri.html (accessed on 3 March 2023).
- Automotive News, Next-Generation Toyota Prius Has Solar Roof for Europe, Japan. Available online: https://www.autonews.com/article/20160616/OEM05/160619900/next-generation-toyota-prius-has-solar-roof-for-europe-japan (accessed on 3 March 2023).
- Automotive News. Available online: https://www.autonews.com/article/20160811/OEM04/308119912/karma-targets-tesla-with-115-000-solar-boosted-hybrid (accessed on 3 March 2023).
- Hanergy Holding Group Ltd. Available online: https://www.autoevolution.com/news/china-s-hanergy-unveils-four-solar-powered-concept-cars-109094.html (accessed on 3 March 2023).
- Nissan Motor Corporation. Nissan Sustainability Report 2014. Available online: https://www.nissan-global.com/EN/SUSTAINABILITY/LIBRARY/SR/2014/ (accessed on 3 March 2023).
- Kronthaler, L.; Maturi, L.; Moser, D.; Alberti, L. Vehicle-integrated Photovoltaic (ViPV) systems: Energy production, Diesel Equivalent, Payback Time; an assessment screening for trucks and busses. In Proceedings of the 2014 Ninth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 25–27 March 2014; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Kutter, C.; Alanis, L.E.; Neuhaus, D.H.; Heinrich, M. Yield potential of vehicle integrated photovoltaics on commercial trucks and vans. In Proceedings of the 38th European PV Solar Energy Conference and Exhibition, Online, 6–10 September 2021; Volume 6, pp. 1412–1420. [Google Scholar] [CrossRef]
- Mallon, K.R.; Assadian, F.; Fu, B. Analysis of On-Board Photovoltaics for a Battery Electric Bus and Their Impact on Battery Lifespan. Energies 2017, 10, 943. [Google Scholar] [CrossRef]
- Masuda, T.; Araki, K.; Okumura, K.; Urabe, S.; Kudo, Y.; Kimura, K.; Nakado, T.; Sato, A.; Yamaguchi, M. Static concentrator photovoltaics for automotive applications. Sol. Energy 2017, 146, 523–531. [Google Scholar] [CrossRef]
- NEDO. Interim Report of the Exploratory Committee on the Automobile Using Photovoltaic System. Available online: http://www.nedo.go.jp/news/press/AA5_100909.html (accessed on 9 May 2018).
- Masuda, T.; Araki, K.; Okumura, K.; Urabe, S.; Kudo, Y.; Kimura, K.; Nakado, T.; Sato, A.; Yamaguchi, M. Next environment-friendly cars: Application of solar power as automobile energy source. In Proceedings of the IEEE 43rd Photovoltaic Specialists Conference (PVSC), Portland, OR, USA, 5–10 June 2016. [Google Scholar] [CrossRef]
- Araki, K.; Sato, D.; Masuda, T.; Lee, K.H.; Yamada, N.; Yamaguchi, M. Why and how does car-roof PV create 50 GW/year of new installations? Also, why is a static CPV suitable to this application? AIP Conf. Proc. 2019, 2149, 050003. [Google Scholar] [CrossRef]
- Sierra, A.; Reinders, A. Designing innovative solutions for solar-powered electric mobility applications. Prog. Photovolt. Res. Appl. 2021, 29, 802–818. [Google Scholar] [CrossRef]
- Kanz, O.; Reinders, A.; May, J.; Ding, K. Environmental Impacts of Integrated Photovoltaic Modules in Light Utility Electric Vehicles. Energies 2020, 13, 5120. [Google Scholar] [CrossRef]
- Kim, S.; Holz, M.; Park, S.; Yoon, Y.; Cho, E.; Yi, J. Future Options for Lightweight Photovoltaic Modules in Electrical Passenger Cars. Sustainability 2021, 13, 2532. [Google Scholar] [CrossRef]
- Macías, J.; Herrero, R.; Núñez, R.; Antón, I. On the effect of cell interconnection in Vehicle Integrated Photovoltaics: Modelling energy under different scenarios. In Proceedings of the 2021 IEEE 48th Photovoltaic Specialists Conference (PVSC), Fort Lauderdale, FL, USA, 20–25 June 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Sagaria, S.; Duarte, G.; Neves, D.; Baptista, P. Photovoltaic integrated electric vehicles: Assessment of synergies between solar energy, vehicle types and usage patterns. J. Clean. Prod. 2022, 348, 131402. [Google Scholar] [CrossRef]
- Sato, D.; Masuda, T.; Araki, K.; Yamaguchi, M.; Okumura, K.; Sato, A.; Tomizawa, R.; Yamada, N. Stretchable Micro-Scale Concentrator Photovoltaic Module with 15.4% Efficiency for Three-Dimensional Curved Surfaces. Commun. Mater. 2021, 2, 7. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Ikeda, K.; Lee, K.-H.; Nishioka, K.; Yamaguchi, M. Possibility of Static Low Concentrator PV Optimized for Vehicle Installation. AIP Conf. Proc. 2016, 1766, 020001. [Google Scholar] [CrossRef]
- Pinto, D.; Lu, Q.; Camocardi, P.; Chatzikomis, C.; Sorniotti, A.; Ragonese, D.; Iuzzolino, G.; Perlo, P.; Lekakou, C. Electric Vehicle Driving Range Extension Using Photovoltaic Panels. In Proceedings of the 2016 IEEE Vehicle Power and Propulsion Conference (VPPC), Hangzhou, China, 17–20 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Conti, S.; Di Mauro, S.; Raciti, A.; Rizzo, S.A.; Susinni, G.; Musumeci, S.; Tenconi, A. Solar electric vehicles: State-of-the-art and perspectives. In Proceedings of the 2018 AEIT International Annual Conference, Bari, Italy, 3–5 October 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Metro News. Available online: https://metro.co.uk/2019/06/26/lightyear-one-solar-powered-electric-car-thatll-450-miles-10072219/ (accessed on 1 March 2023).
- Sono Motors. Available online: https://sonomotors.com/ (accessed on 1 March 2023).
- Araki, K.; Ji, L.; Kelly, G.; Yamaguchi, M. To Do List for Research and Development and International Standardization to Achieve the Goal of Running a Majority of Electric Vehicles on Solar Energy. Coatings 2018, 8, 251. [Google Scholar] [CrossRef]
- Sato, D.; Le., K.-H.; Araki, K.; Masuda, T.; Yamaguchi, M.; Yamada, N. Design of Low-Concentration Static III-V/Si Partial CPV Module with 27.3% Annual Efficiency for Car-Roof Application. Progress in Photovoltaics: Research and Applications 2019, 27, 501–510. [Google Scholar] [CrossRef]
- Abdelhamid, M.; Pilla, S.; Singh, R.; Haque, I.; Filipi, Z. A comprehensive optimized model for on-board solar photovoltaic system for plug-in electric vehicles: Energy and economic impacts: On-board solar photovoltaic system for plug-in electric vehicles. Int. J. Energy Res. 2016, 40, 1489–1508. [Google Scholar] [CrossRef]
- Ota, Y.; Araki, K.; Nagaoka, A.; Nishioka, K. Curve correction of vehicle-integrated photovoltaics using statistics on commercial car bodies. Prog. Photovolt. Res. Appl. 2022, 30, 152–163. [Google Scholar] [CrossRef]
- Araki, K.; Ji, L.; Kelly, G.; Agudo, E.; Anton, I.; Baudrit, M.; Carr, A.; Herrero, R.; Kurtz, S.; Liu, Z.; et al. Modeling and Standardization Researches and Discussions of the Car-roof PV through International Web Meetings. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 2722–2729. [Google Scholar] [CrossRef]
- Araki, K.; Algora, C.; Siefer, G.; Nishioka, K.; Leutz, R.; Carter, S.; Wang, S.; Askins, S.; Ji, L.; Kelly, G. Standardization of the CPV and car-roof PV technology in 2018—Where are we going to go? AIP Conf. Proc. 2018, 2012, 070001. [Google Scholar] [CrossRef]
- Ota, Y.; Masuda, T.; Araki, K.; Yamaguchi, M. Curve-Correction Factor for Characterization of the Output of a Three-Dimensional Curved Photovoltaic Module on a Car Roof. Coatings 2018, 8, 432. [Google Scholar] [CrossRef]
- Tayagaki, T.; Araki, K.; Yamaguchi, M.; Sugaya, T. Impact of Nonplanar Panels on Photovoltaic Power Generation in the Case of Vehicles. IEEE J. Photovolt. 2019, 9, 1721–1726. [Google Scholar] [CrossRef]
- Ota, Y.; Araki, K.; Nagaoka, A.; Nishioka, K. Facilitating vehicle-integrated photovoltaics by considering the radius of curvature of the roof surface for solar cell coverage. Clean. Eng. Technol. 2022, 7, 100446. [Google Scholar] [CrossRef]
- Thiel, C.; Amillo, A.G.; Tansini, A.; Tsakalidis, A.; Fontaras, G.; Dunlop, E.; Taylor, N.; Jäger-Waldau, A.; Araki, K.; Nishioka, K.; et al. Impact of climatic conditions on prospects for integrated photovoltaics in electric vehicle. Renew. Sustain. Energy Rev. 2022, 158, 112109. [Google Scholar] [CrossRef]
- Brito, M.; Santos, T.; Moura, F.; Pera, D.; Rocha, J. Urban solar potential for vehicle integrated photovoltaics. Transp. Res. Part D Transp. Environ. 2021, 94, 102810. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Yamaguchi, M. Measurement and Modeling of 3D Solar Irradiance for Vehicle-Integrated Photovoltaic. Appl. Sci. 2020, 10, 872. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Nishioka, K.; Tobita, H.; Ji, L.; Kelly, G.; Yamaguchi, M. Toward the Standardization of the Car-roof PV–The challenge to the 3-D Sunshine Modeling and Rating of the 3-D Continuously Curved PV Panel. In Proceedings of the 2018 IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 0368–0373. [Google Scholar] [CrossRef]
- Ota, Y.; Masuda, K.; Araki, K.; Yamaguchi, M. A mobile multipyranometer array for the assessment of solar irradiance incident on a photovoltaic-powered vehicle. Sol. Energy 2019, 184, 84–90. [Google Scholar] [CrossRef]
- Araki, K.; Lee, H.; Masuda, T.; Hayakawa, Y.; Yamada, N.; Ota, Y.; Yamaguchi, M. Rough and Straightforward Estimation of the Mismatching Loss by Partial Shading of the PV Modules Installed on an Urban Area or Car-Roof. In Proceedings of the 46th IEEE PVSC, Chicago, IL, USA, 16–21 June 2019. [Google Scholar] [CrossRef]
- Ekins-Daukes, N.J.; Betts, T.R.; Kemmoku, Y.; Araki, K.; Lee, H.S.; Gottschalg, R.; Boreland, M.B.; Infield, D.G.; Yamaguchi, M. Syracuse—A multi-junction concentrator system computer model. In Proceedings of the Conference Record of the Thirty-First IEEE Photovoltaic Specialists Conference, Lake Buena Vista, FL, USA, 3–7 January 2005; IEEE: Piscataway, NJ, USA, 2005; pp. 651–654. [Google Scholar] [CrossRef]
- Araki, K.; Yamaguchi, M.; Kondo, M.; Uozumi, H. Which is the best number of junctions for solar cells under ever-changing terrestrial spectrum? In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003; IEEE: Piscataway, NJ, USA, 2003; Volume 1, pp. 307–310. [Google Scholar]
- Tawa, H.; Saiki, H.; Ota, Y.; Araki, K.; Takamoto, T.; Nishioka, K. Accurate Output Forecasting Method for Various Photovoltaic Modules Considering Incident Angle and Spectral Change Owing to Atmospheric Parameters and Cloud Conditions. Appl. Sci. 2020, 10, 703. [Google Scholar] [CrossRef]
- Araki, K.; Ota, Y.; Lee, K.H.; Nishioka, K.; Yamaguchi, M. Optimization of the Partially Radiative-coupling Multi-junction Solar Cells Considering Fluctuation of Atmospheric Conditions. In Proceedings of the IEEE 7th World Conference on Photovoltaic Energy Conversion (WCPEC) (A Joint Conference of 45th IEEE PVSC, 28th PVSEC & 34th EU PVSEC), Waikoloa Village, HI, USA, 10–15 June 2018; pp. 1661–1666. [Google Scholar] [CrossRef]
- Araki, K.; Tawa, H.; Saiki, H.; Ota, Y.; Nishioka, K.; Yamaguchi, M. The Outdoor Field Test and Energy Yield Model of the Four-Terminal on Si Tandem PV Module. Appl. Sci. 2020, 10, 2529. [Google Scholar] [CrossRef]
- Araki, K.; Yamaguchi, M. Influences of spectrum change to 3-junction concentrator cells. Sol. Energy Mater. Sol. Cells 2003, 75, 707–714. [Google Scholar] [CrossRef]
- Araki, K.; Yamaguchi, M.; Takamoto, T.; Ikeda, E.; Agui, T.; Kurita, H.; Takahashi, K.; Unno, T. Characteristics of GaAs-based concentrator cells. Sol. Energy Mater. Sol. Cells 2001, 66, 559–565. [Google Scholar] [CrossRef]
- Ota, Y.; Araki, K.; Nagaoka, A.; Nishioka, K. Evaluating the Output of a Car-Mounted Photovoltaic Module Under Driving Conditions. IEEE J. Photovolt. 2021, 11, 1299–1304. [Google Scholar] [CrossRef]
- Itagaki, A.; Okumura, H.; Yamada, A. Preparation of meteorological data set throughout Japan for suitable design of PV systems Photovoltaic Energy Conversion. In Proceedings of the 3rd World Conference on Photovoltaic Energy Conversion, Osaka, Japan, 11–18 May 2003. [Google Scholar]
- Shirakawa, K.; Itagaki, A.; Utsunomiya, T. Preparation of hourly solar radiation data on inclined surface (METPV-11) throughout Japan. In Proceedings of the JSES/JWEA Joint Conference, Wakkanai, Japan, 21–22 September 2011. [Google Scholar]





| Type of Facility | HQ, Disaster Response | Evacuation Center | Community Hall | Care House |
|---|---|---|---|---|
| Floor area (m2) | 10,000 | 7000 | 950 | 4200 |
| Capacity (persons) | 250 | 3000 | 200 | 100 |
| Required energy capacity | 294.4 | 262.1 | 54.8 | 363.5 |
| Non-emergency air conditioning capacity (kW) | 200 | 200 | 50 | 300 |
| On-site battery (kWh) | 264 | 133 | 43 | 44 |
| PV (kW) | 165 | 61 | 10 | 32 |
| Co-generator | -- | -- | -- | 0.7 kW |
| Emergency generator (kW) | 200 | 120 | 38.4 | |
| Fuel stock (hr) | 72 | 3 | 5 |
| Type of Facility | Time Period | Average Energy Demand (kW) |
|---|---|---|
| Headquarters of disaster response | 06:00–17:00 | 34.6 |
| 17:00–21:00 | 34.6 | |
| 21:00–06:00 | 32.2 | |
| Evacuation center | 06:00–17:00 | 13.2 |
| 17:00–21:00 | 23.1 | |
| 21:00–06:00 | 13.2 | |
| Community hall | 06:00–17:00 | 0.8 |
| 17:00–21:00 | 1.2 | |
| 21:00–06:00 | 0.7 | |
| Care house | 06:00–17:00 | 23.7 |
| 17:00–21:00 | 25.9 | |
| 21:00–06:00 | 23.1 |
| Type of Facility | Period | Average Power Demand (kW) |
|---|---|---|
| Temporary shelter with medical care | 06:00–17:00 | 34.6 |
| 17:00–21:00 | 34.6 | |
| 21:00–06:00 | 32.2 | |
| Common charging station for mobile devices | 06:00–06:00 | 0.2 kW× 25 |
| Backup power for air conditioning | 06:00–16:00 | 2.2 kW× 6 |
| Parameter | Parameter Description | Variable Type | Distribution |
|---|---|---|---|
| Date/time of the disaster | Step by 1 h starting from 1 January, 00:00–01:00, end on 31 December, 23:00–24:00 | Integer | Ranged uniform (0, 365 × 24 − 1) Once at the beginning |
| SoC at the disaster | Each vehicle | Vector (double-precision float) (Vector size) = (Number of SEV) | Ranged uniform (0%, 100%) Once at the beginning |
| Irradiation deviation | 1: Best year 0: Average year −1: Worst year | Double-precision float | Ranged uniform (−1, 1) Once at the beginning |
| Degree of intention for donation | If (value) < x% and satisfies other conditions, the driver donates the energy. | Vector (double-precision float) (Vector size) = (Number of SEV) × 24 × 7 | Ranged uniform (0, 1) |
| Parameter | Parameter Description | Value |
|---|---|---|
| Site | Miyazaki, Japan (N31.938°, E131.413°) | 87376 (METPV index number) |
| Road reflectance | Reflectance from the road to the vertical plane of vehicles | 0.08 |
| Road reflectance (snow) | (snow cover) > 10 cm, Reflectance from the road to the vertical plane of vehicles | 0.9 |
| The reflectance of the vertical plane of the shading objects | buildings, etc. | 0.25 |
| Number of SEV | Input at the beginning (Integer) | -- |
| Number of mobile charging stations | Distributed by walking distance (1 km) | 25 |
| The required power for a mobile charging station | 24 h (constant) | 0.2 kW each |
| Number of sites demanding energy supply of air conditioning | 6 | |
| The required power for air conditioning | 24 h (constant) | 2.2 kW each (6 horsepower each) |
| Number of temporal shelters with medical care | 1 | |
| The required energy for the temporal shelter with medical care | Required power varies by time zone. | 0.36 kW 00:00–06:00 1.61 kW 06:00–17:00 4.47 kW 17:00–21:00 0.36 kW 21:00–24:00 |
| Drive distance at delivering energy to the public good | 5 km | |
| Electric milage | 8.33 km/kWh | |
| Battery capacity | 40 kWh | |
| Energy management efficiency of EV | 93% | |
| MPPT 1 efficiency for PV power conversion | 95% | |
| VIPV efficiency | 22% | |
| VIPV area | Projected area to a horizontal plane | 1.8 m2 |
| Performance ratio of VIPV | Temperature correction is done separately | 90% |
| Temperature coefficient | Varies by irradiance level | −0.328%/K @ 1 kW/m2 of solar irradiance |
| Type of Facilities | Value |
|---|---|
| Place | Miyazaki, Japan, N |
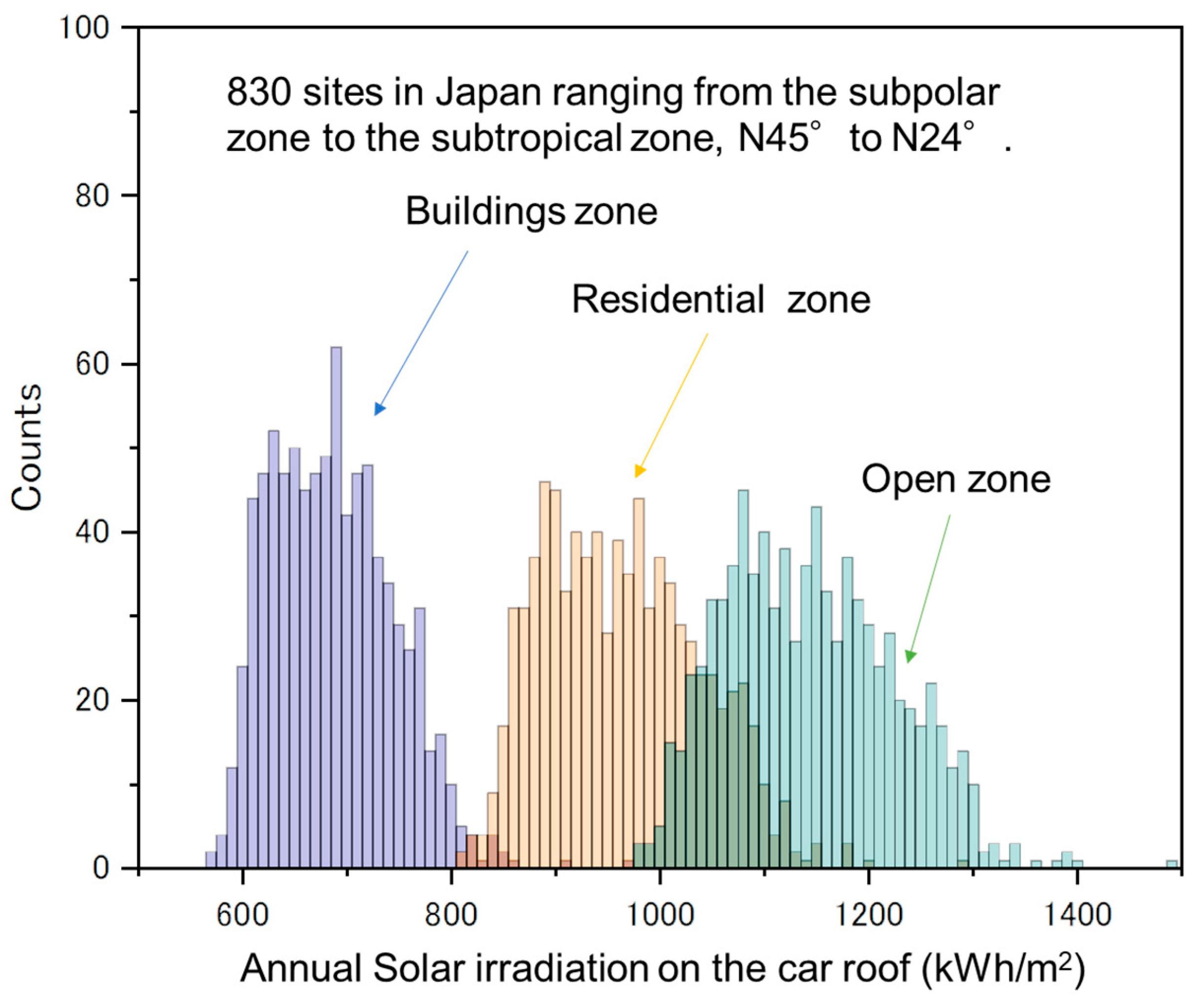
| Climate | Semi-tropical |
| Zone | Residential zone |
| Population density | 624 /km2 |
| Assumed area for calculation | 5 km radius |
| Drive distance at delivering energy to the public good | 5 km |
| Electric mileage (average) | 8.33 km/kWh |
| Battery capacity (average) | 40 kWh |
| Energy management efficiency of EV (average) | 93% |
| MPPT 1 efficiency for PV power conversion (average) | 95% |
| VIPV efficiency (average) | 22% |
| VIPV area (projected area, average) | 1.8 m2 |
| Performance ratio of VIPV (*) | 90% |
| Temperature coefficient (**) | −0.328%/K @ 1 kW/m2 of solar irradiance |
| Calculation result: Number of required SEVs (residential zone) | 720 in a 5 km radius, 9.2 per km2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araki, K.; Ota, Y.; Maeda, A.; Kumano, M.; Nishioka, K. Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors. Energies 2023, 16, 3580. https://doi.org/10.3390/en16083580
Araki K, Ota Y, Maeda A, Kumano M, Nishioka K. Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors. Energies. 2023; 16(8):3580. https://doi.org/10.3390/en16083580
Chicago/Turabian StyleAraki, Kenji, Yasuyuki Ota, Anju Maeda, Minoru Kumano, and Kensuke Nishioka. 2023. "Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors" Energies 16, no. 8: 3580. https://doi.org/10.3390/en16083580
APA StyleAraki, K., Ota, Y., Maeda, A., Kumano, M., & Nishioka, K. (2023). Solar Electric Vehicles as Energy Sources in Disaster Zones: Physical and Social Factors. Energies, 16(8), 3580. https://doi.org/10.3390/en16083580









