Supercritical Heat Transfer and Pyrolysis Characteristics of n-Decane in Circular and Rectangular Channels
Abstract
:1. Introduction
2. Simulation
2.1. Computing Domain and Boundary Conditions
2.2. Reaction Model
2.3. Theoretical Formulation and Numerical Treatment
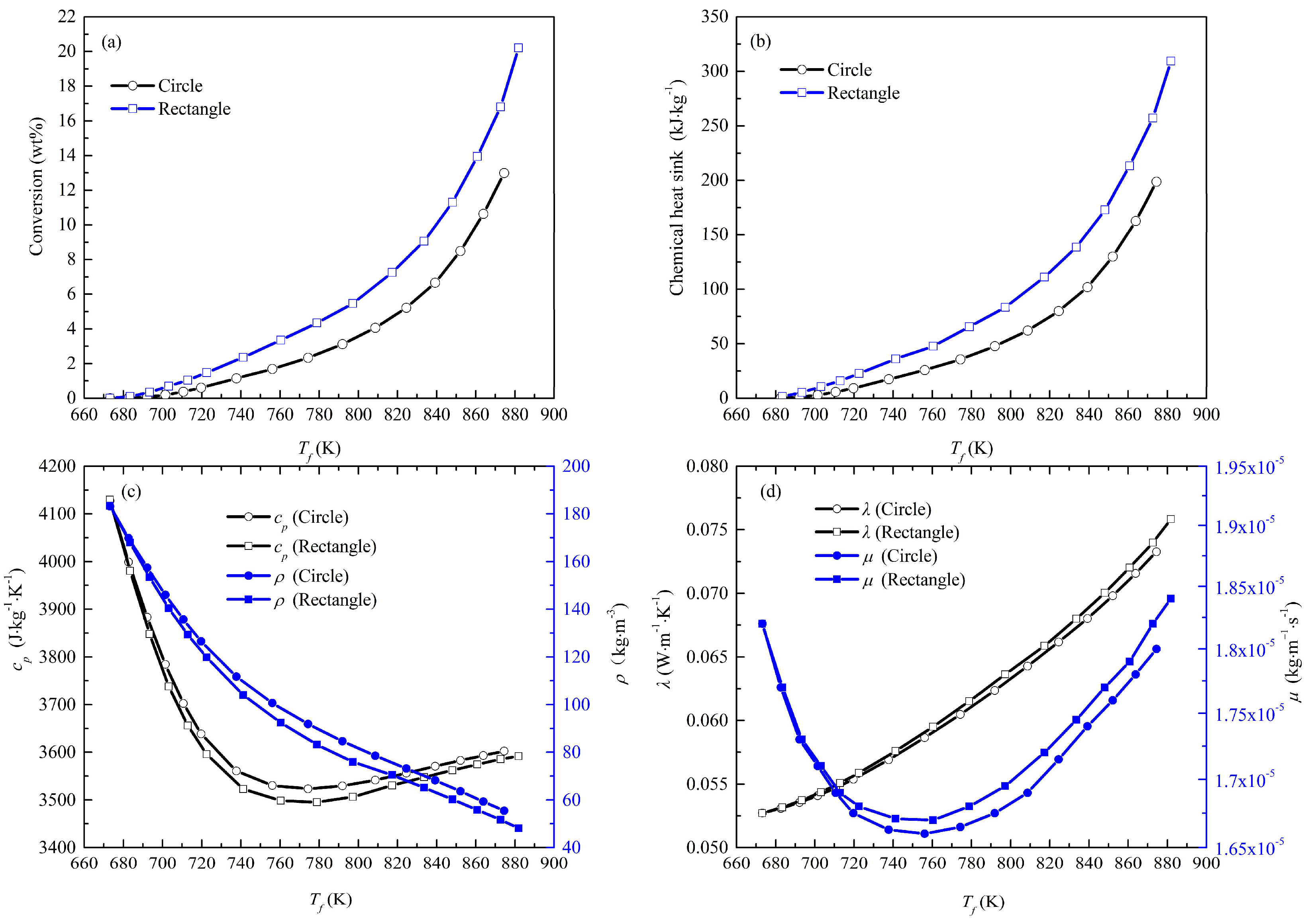
2.4. Property Evaluations and Solution Method
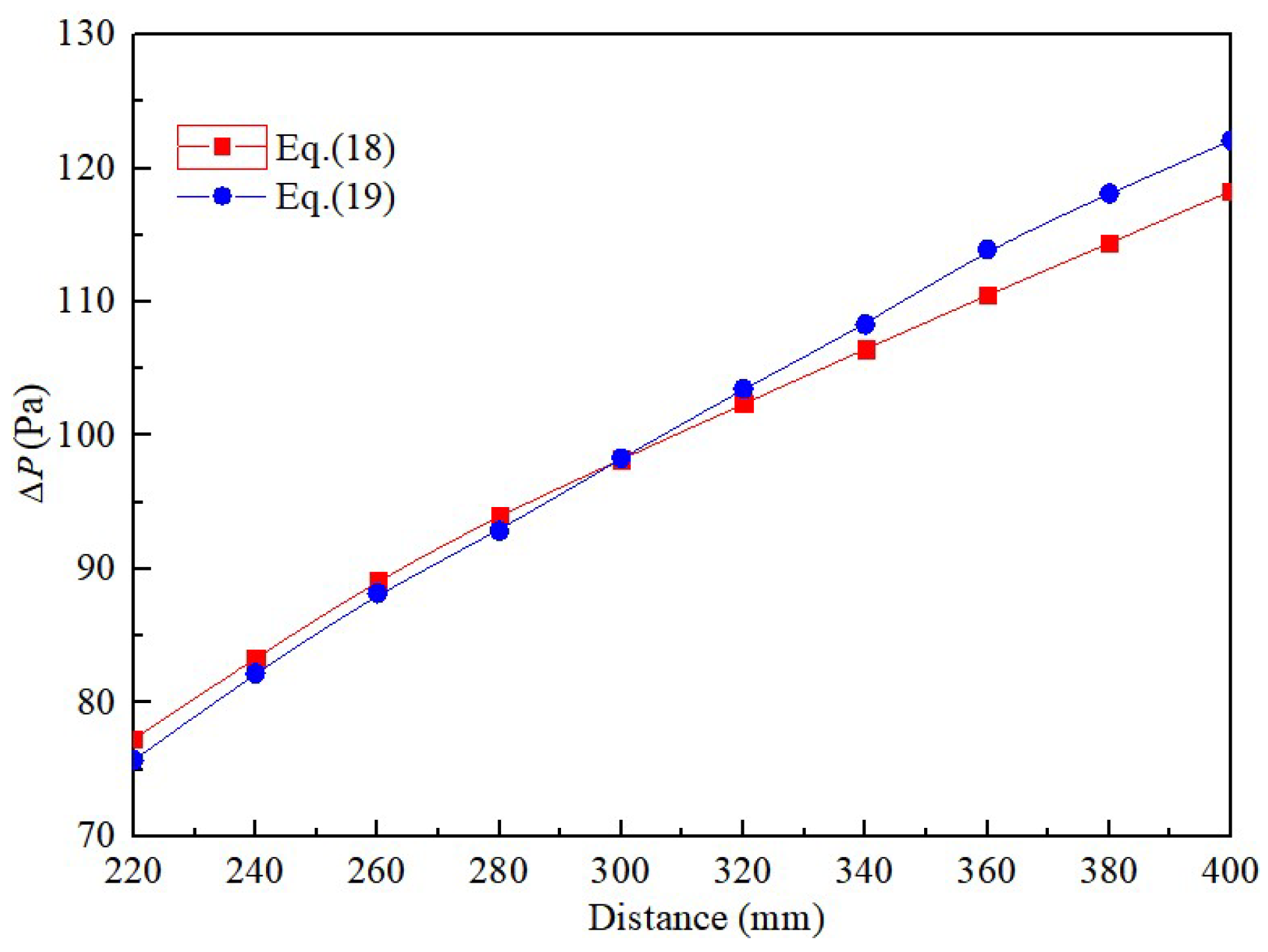
2.5. Parameter Calculation
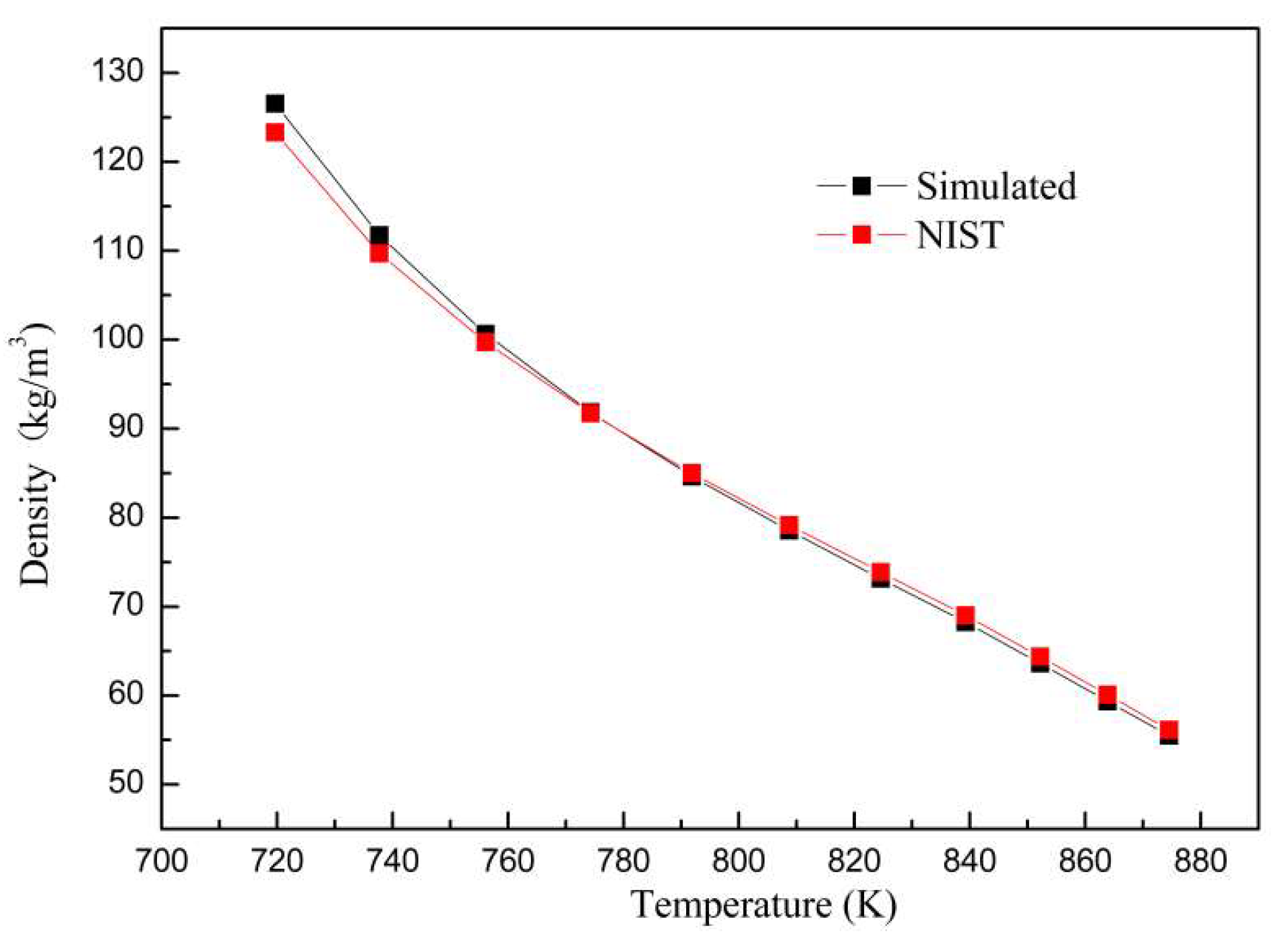
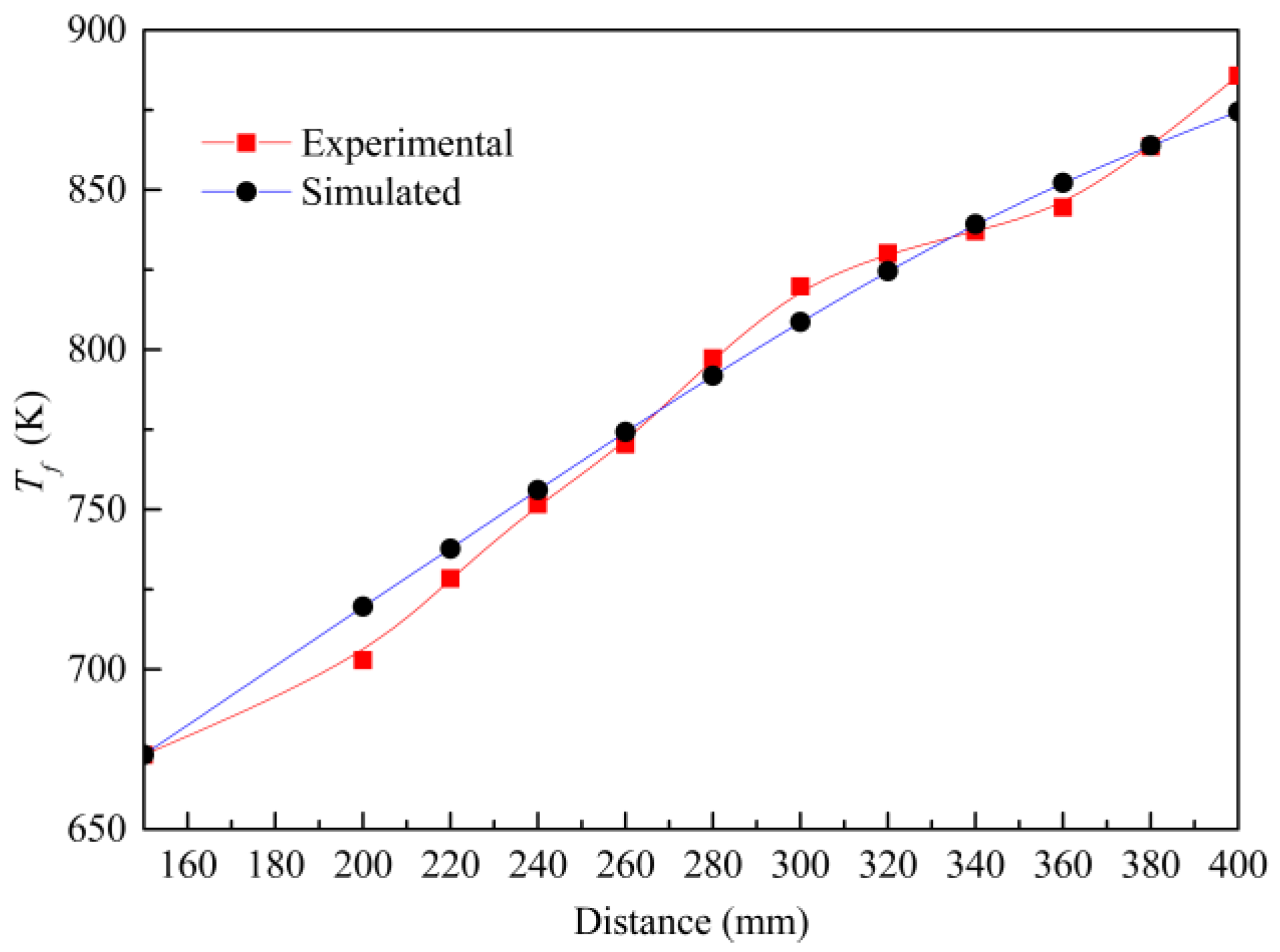
3. Validations
3.1. Grid Independence Study
3.2. Model Validation
4. Results and Analysis
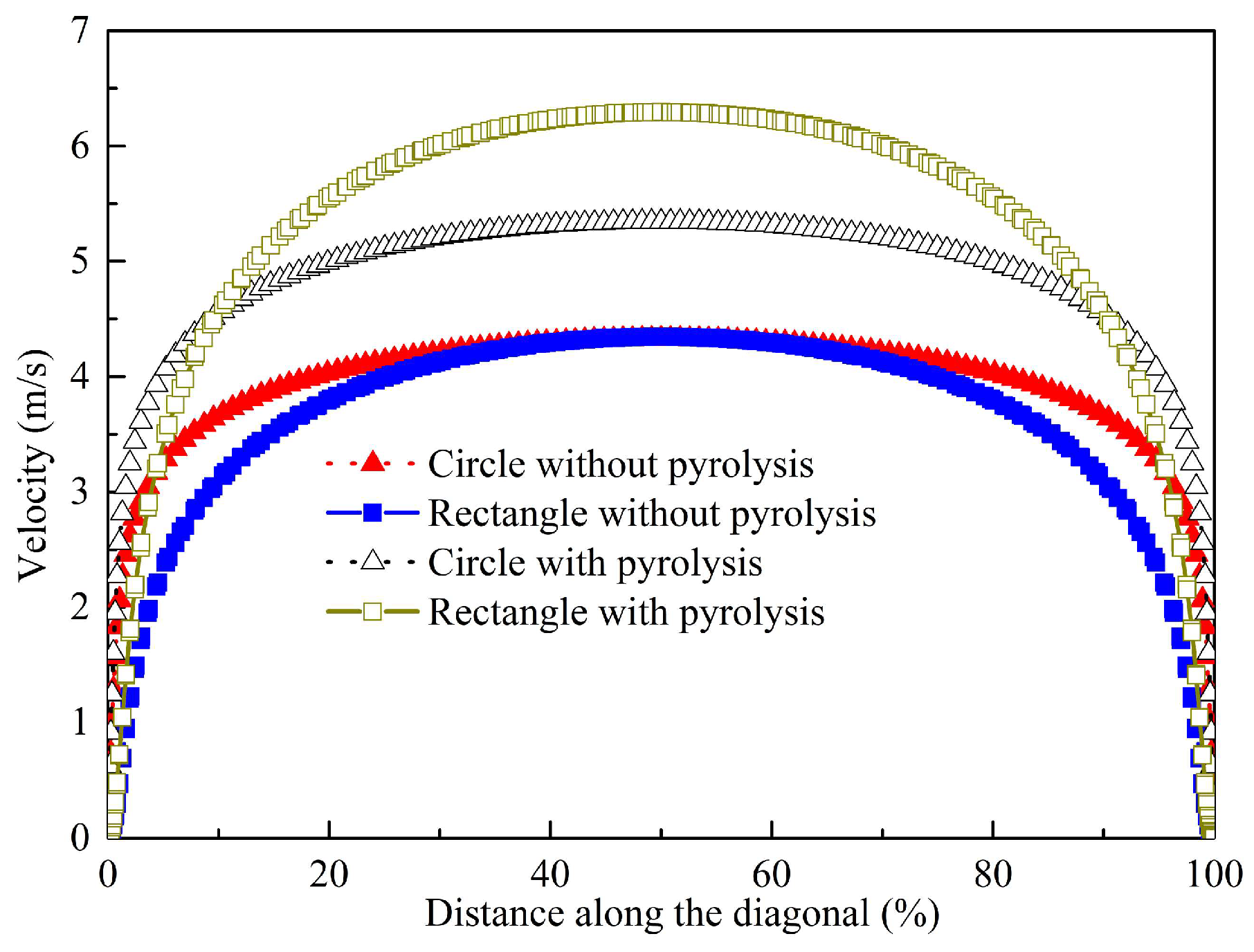
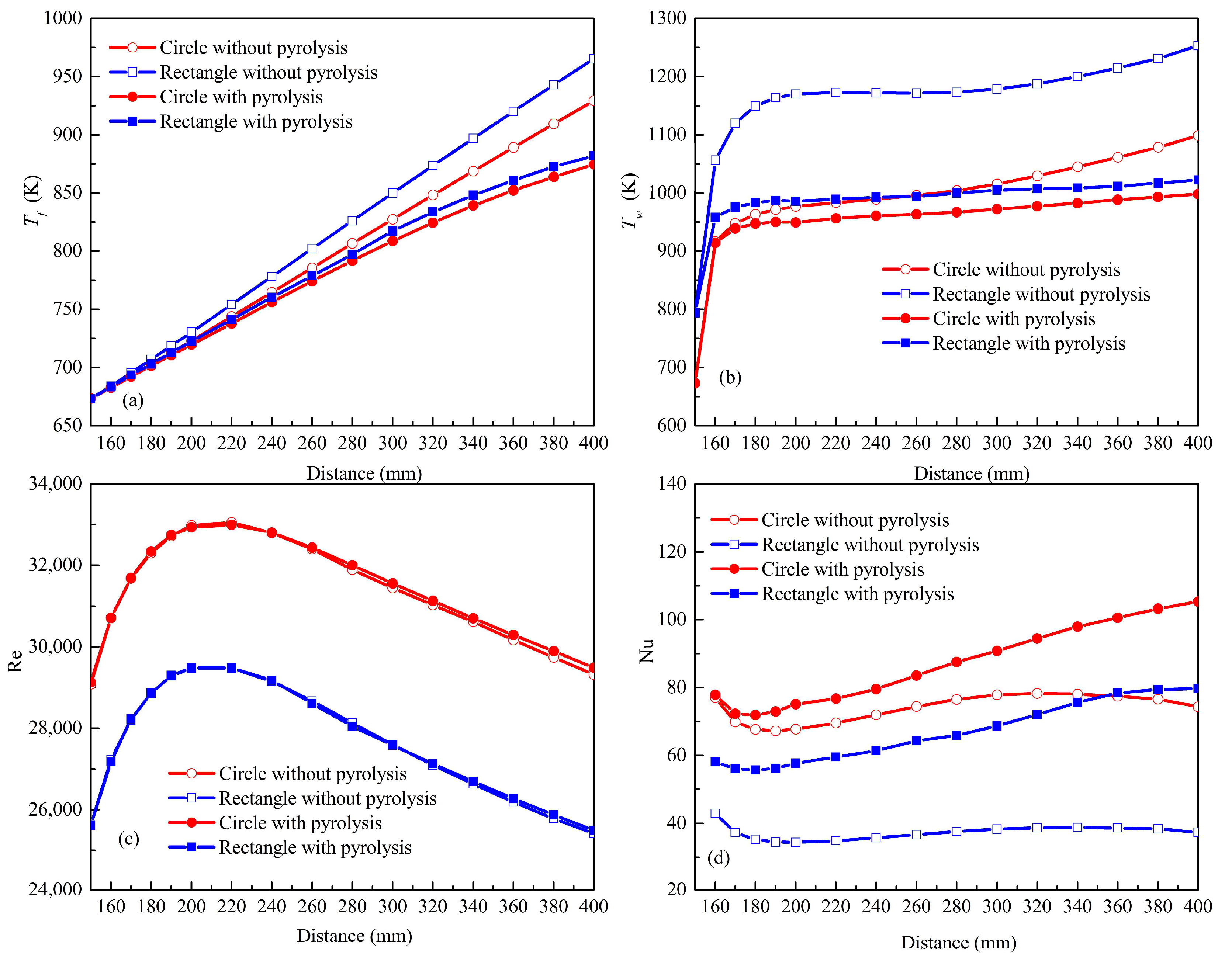
4.1. Influences of Geometry on Flow
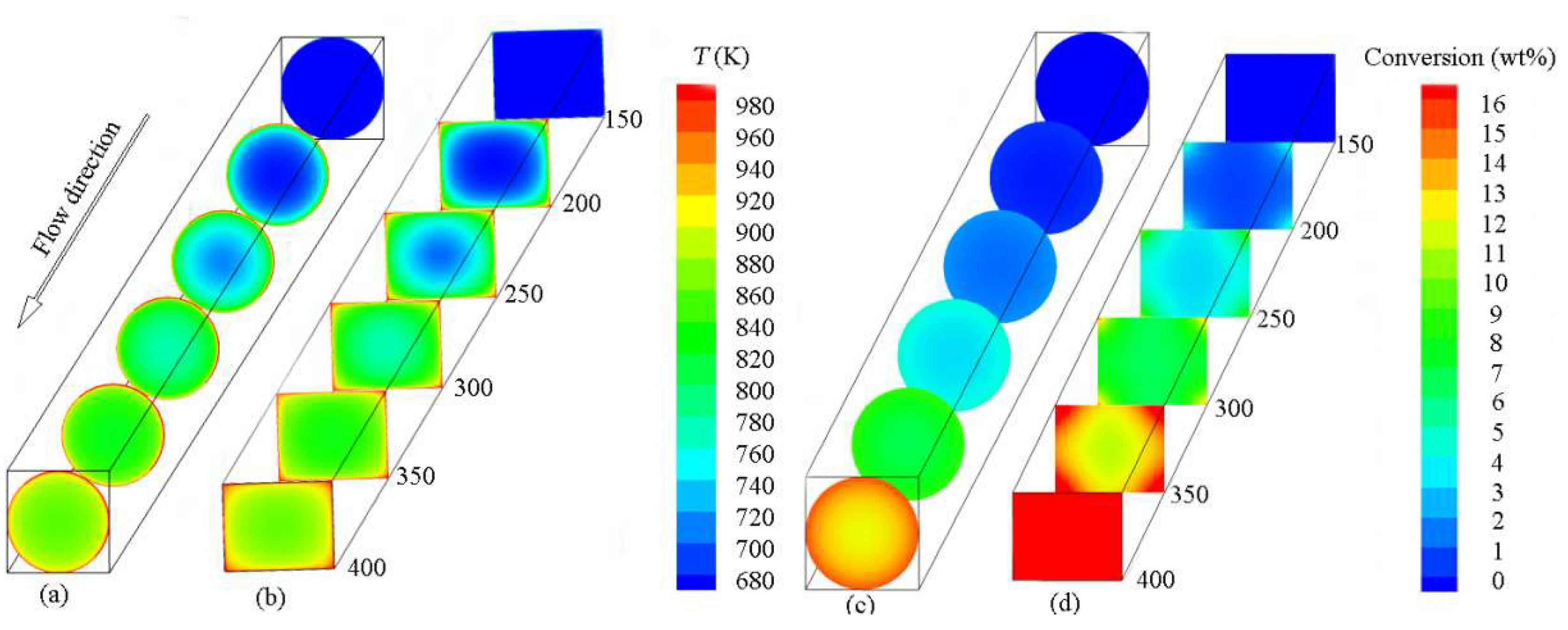
4.2. Effects of Geometry on Pyrolysis
4.3. Effects of Geometry on Heat Transfer
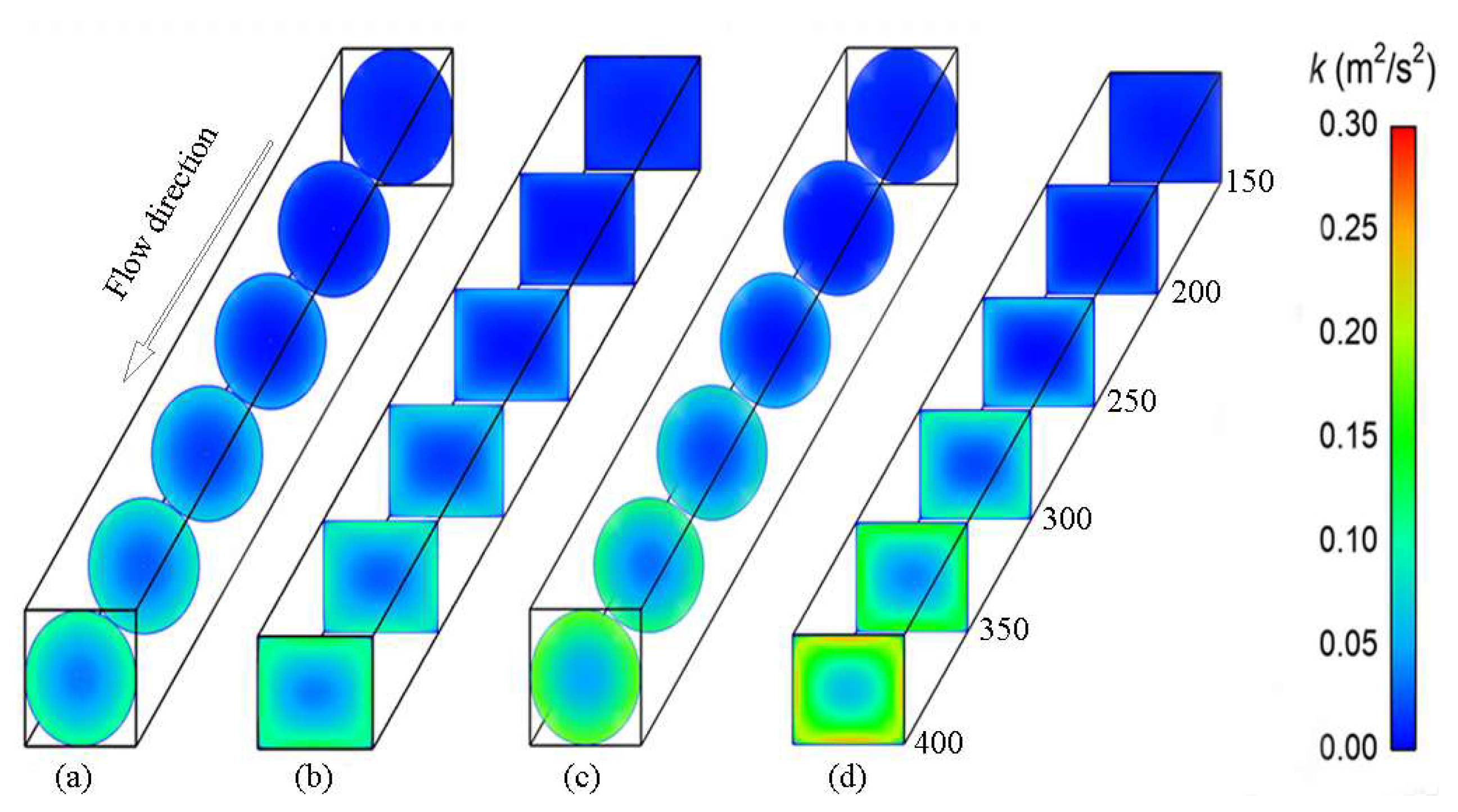
4.4. Mechanisms of Heat Transfer in the Circular and Rectangular Tubes
5. Conclusions
- (1)
- Compared with the flow resistance in the circular channel with pyrolysis, the mean pressure drop in the rectangular channel is 1.18 times as high due to its smaller equivalent diameter. The maximum velocity in the rectangular channel is 1.18 times as high as that in the circular one with pyrolysis due to the higher pyrolysis and lower density.
- (2)
- The area of the high-conversion region in the rectangular tube is much larger than that in the circular tube due to the distribution of the temperature boundary layer in the rectangular tube. The maximum value of the chemical heat sink in the rectangular channel is 1.6 times as high as that in the circular one.
- (3)
- The high-temperature zone of any cross section in the rectangular channel is much larger than that in the circular channel due to the superposition of the boundary layer and lower turbulent kinetic energy in the corners of the rectangular channel. The maximum value of the Nu in the circular channel is 1.3 times as high as that in the rectangular one with pyrolysis due to its larger heat capacity, lower viscosity and higher wall shear stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area (m2) |
| cp | specific heat capacity (J/(kg∙K)) |
| C | circular tube |
| C1ε, C2ε, C3ε | constants in k-ε turbulence models |
| CR | reactant concentration (kmol/m3) |
| dh | equivalent diameter (m) |
| Dω | cross-diffusion term |
| et | total energy (J/kg) |
| Ea | activation energy, 269.2 kJ/mol |
| Gk, Gω | production term |
| h | heat-transfer coefficient (W/(m2∙K)) |
| H | heat sink (kJ/kg) |
| diffusion flux of species j (m2/s) | |
| k | turbulent kinetic energy (m2/s2) |
| k0 | pre-exponential factor, 1.75 × 1015/s |
| K | reaction rate (1/s) |
| l | length of the tube (m) |
| mass flow rate (g/s) | |
| Nu | Nusselt number |
| p | pressure (MPa) |
| Pr | Prandtl number |
| q | heat flux (kW/m2) |
| r | r-axis coordinate (m) |
| R | universal gas constant, 8.314 × 10−3 (kJ/(mol·K)) |
| R | rectangular tube |
| Rj | net rate of production of species j (1/s) |
| ωR | reaction rate of reactant (kmol/(m3·s)) |
| Re | Reynolds number |
| sh | heat of chemical reaction (J) |
| SST | shear stress transport |
| t | time (s) |
| T | temperature (K) |
| velocity vector (m/s) | |
| X | X-axis coordinate (m) |
| y+ | dimensionless distances from the wall |
| Y | Y-axis coordinate (m) |
| Yj | mass fraction of species j (%) |
| Yk, Yω | dissipation term |
| Z | Z-axis coordinate (m) |
| Greek symbols | |
| ε | dissipation rate (m2/s3) |
| ρ | density (kg/m3) |
| μ | viscosity (kg/(m·s)) |
| λ | thermal conductivity (W/(m∙K)) |
| τ | shear stress (N/m2) |
| σk, σω, σε | turbulent Prandtl number |
| ω | specific dissipation rate (1/s) |
| Subscripts | |
| eff | effective value |
| f | bulk fluid |
| in | inlet |
| out | outlet |
| j | species |
| sen | sensible |
| t | turbulent |
| w | wall |
| Superscripts | |
| b, c | index |
References
- Bao, W.; Zhang, S.; Qin, J.; Zhou, W.; Xie, K. Numerical analysis of flowing cracked hydrocarbon fuel inside cooling channels in view of thermal management. Energy 2014, 67, 149–161. [Google Scholar] [CrossRef]
- Chen, M.; Hu, Y.; Han, Z.; Peng, Z.; Zan, H. Study on influence of forced vibration of cooling channel on flow and heat transfer of hydrocarbon fuel at supercritical pressure. Therm. Sci. 2021, 26, 3463–3476. [Google Scholar] [CrossRef]
- Zhang, S.; Feng, Y.; Jiang, Y.; Qin, J.; Bao, W.; Han, J.; Haidn, O.J. Thermal behavior in the cracking reaction zone of scramjet cooling channels at different channel aspect ratios. Acta Astronaut. 2016, 127, 41–56. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, H.; Chen, Y.; Liu, P.; Zhu, Q.; Wang, J.; Li, X. Investigations on the thermal cracking and pyrolysis mechanism of China No.3 aviation kerosene under supercritical conditions. Petrol. Sci. Technol. 2018, 36, 1–9. [Google Scholar] [CrossRef]
- Gongnan, X.; Xiaoxiao, X.; Xianliang, L.; Zhouhang, L.; Yong, L.; Sunden, B. Heat transfer behaviors of some supercritical fluids: A review. Chin. J. Aeronaut. 2022, 35, 290–306. [Google Scholar]
- Mansour, M.K. Numerical study of three-dimensional conjugate heat transfer in liquid mini-scale heat sink. Heat Transf. Res. 2013, 44, 561–588. [Google Scholar] [CrossRef]
- Yu, B.; Zhou, W.; Qin, J.; Bao, W. Dynamic characteristics of hydrocarbon fuel within the channel at supercritical and pyrolysis condition. J. Therm. Sci. 2017, 26, 560–569. [Google Scholar] [CrossRef]
- Ward, T.; Ervin, J.S.; Striebich, R.C.; Zabarnick, S. Simulations of flowing mildly-cracked normal alkanes incorporating proportional product distributions. J. Propul. Power 2004, 20, 394–402. [Google Scholar] [CrossRef]
- Ward, T.A.; Ervin, J.S.; Zabarnick, S.; Shafer, L. Pressure effects on flowing mildly-cracked n-decane. J. Propul. Power 2005, 21, 344–355. [Google Scholar] [CrossRef]
- Jiang, R.; Liu, G.; Zhang, X. Thermal cracking of hydrocarbon aviation fuels in regenerative cooling microchannels. Energy Fuels 2013, 27, 2563–2577. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, B.; Jiang, P. Experimental and numerical investigations on n-decane thermal cracking at supercritical pressures in a vertical tube. Energy Fuels 2013, 28, 466–474. [Google Scholar] [CrossRef]
- Zhao, G.; Song, W.; Zhang, R. Effect of pressure on thermal cracking of china RP-3 aviation kerosene under supercritical conditions. Int. J. Heat Mass Transf. 2015, 84, 625–632. [Google Scholar] [CrossRef]
- Jia, D.; Wang, N.; Pan, Y.; Liu, C.; Wang, S.; Yang, K.; Liu, J. Flow and heat transfer characteristics of supercritical n-decane in adjacent cooling channels with opposite flow directions. Energies 2021, 14, 1071. [Google Scholar] [CrossRef]
- Jiang, Y.; Xu, Y.; Qin, J.; Zhang, S.; Chetehouna, K.; Gascoin, N.; Bao, W. The flow rate distribution of hydrocarbon fuel in parallel channels with different cross section shapes. Appl. Therm. Eng. 2018, 137, 173–183. [Google Scholar] [CrossRef]
- Li, F.; Li, Z.; Jing, K.; Wang, L.; Zhang, X.; Liu, G. Thermal cracking of endothermic hydrocarbon fuel in regenerative cooling channels with different geometric structures. Energy Fuels 2018, 32, 6524–6534. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; Zhang, X.; Liu, G. Coupling of pyrolysis and heat transfer of supercritical hydrocarbon fuel in rectangular minichannels. Chem. Eng. Sci. 2022, 247, 116924. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, X.K.; Liu, P.H.; Zhu, Q.; Wang, J.L.; Li, X.Y. Energy absorption and reaction mechanism for thermal pyrolysis of n-decane under supercritical pressure. Appl. Therm. Eng. 2017, 112, 403–412. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Y.; Liang, C.; Zhang, Q.; Li, X. Heat transfer analysis of n-decane with variable heat flux distributions in a mini-channel. Appl. Therm. Eng. 2018, 144, 695–701. [Google Scholar] [CrossRef]
- Han, C.L.; Zhang, Y.N.; Yu, H.; Lu, Y.P.; Jiao, B. Numerical analysis on non-uniform flow and heat transfer of supercritical cryogenic methane in a heated horizontal circular tube. J. Supercrit. Fluids 2018, 138, 82–91. [Google Scholar] [CrossRef]
- Li, Y.; Xie, G.; Zhang, Y.; Ferla, P.; Sunden, B. Flow characteristics and heat transfer of supercritical n-decane in novel nested channels for scramjet regenerative cooling. Int. J. Heat Mass Tran. 2021, 167, 120836. [Google Scholar] [CrossRef]
- Lei, Z.; He, K.; Huang, Q.; Bao, Z.; Li, X. Numerical study on supercritical heat transfer of n-decane during pyrolysis in rectangular tubes. Appl. Therm. Eng. 2020, 170, 115002. [Google Scholar] [CrossRef]
- Huber, M.L. NIST Standard Reference Database 4-NIST Thermophysical Properties of Hydrocarbon Mixtures Database; Version 3.2; National Institute of Standards and Technology Standard Reference Data Program: Gaithersburg, MD, USA, 2007. [Google Scholar]
- Jia, Z.; Huang, H.; Zhou, W.; Qi, F.; Zeng, M. Experimental and modeling investigation of n-decane pyrolysis at supercritical pressures. Energy Fuels 2014, 28, 6019–6028. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J. On the thermodynamics of solutions. V. An equation of state. Fugacities of gaseous solutions. Chem. Rev. 1949, 44, 233–244. [Google Scholar] [CrossRef]
- Shi, M.Z.; Wang, Z.Z. Principle and Design of Heat Exchangers, 4th ed.; Southeast University Press: Nanjing, China, 2009. [Google Scholar]
- Lei, Z.; Liu, B.; Huang, Q.; He, K.; Bao, Z.; Zhu, Q.; Li, X. Thermal cracking characteristics of n-decane in the rectangular and circular tubes. Chin. J. Chem. Eng. 2019, 27, 2876–2883. [Google Scholar] [CrossRef]



| Mass Fraction of Unreacted n-Decane/% | Error (%) | |
|---|---|---|
| Calculated by SST k–ω | 87.01 | 0.54 |
| Calculated by k–ε | 89.03 | 2.88 |
| Experimental | 86.54 | 0 |
| Algorithms | Mass Fraction of Unreacted n-Decane/% | Temperature/K | Computing Time (min) |
|---|---|---|---|
| SIMPLE | 87.01 | 874.5 | 54 |
| SIMPLEC | 86.93 | 874.2 | 93 |
| PISO | 86.94 | 874.2 | 109 |
| Coupled | 86.95 | 874.3 | 131 |
| Experimental | 86.54 | 885.7 |
| Case No. | Geometry Domain | Mesh Type | Number of Elements (X × Z/r × Y) | Tf (K) | Tw (K) |
|---|---|---|---|---|---|
| 1 | Circular tube (550 × 1) | Quadrilateral | 1326 × 36 | 873 | 994 |
| 2 | 1857 × 50 | 876 | 999 | ||
| 3 | 2600 × 70 | 877 | 1000 | ||
| 4 | 3640 × 98 | 877 | 1000 | ||
| 5 | Rectangular tube (250 × 2 × 1.6) | Hexahedral | 400 × 70 × 50 | 881 | 1016 |
| 6 | 600 × 70 × 50 | 881 | 1018 | ||
| 7 | 800 × 70 × 50 | 881 | 1020 | ||
| 8 | 1250 × 70 × 50 | 881 | 1020 |
| Tube Length/mm | Tube Inner Diameter/mm | Inlet Temperature/K | Mass Flow Rate/g·s−1 | Pressure/ MPa | Heat Flux/MW·m−2 |
|---|---|---|---|---|---|
| 250 | 2 | 673.15 | 0.8 | 3.5 | 0.48 |
| Calculated | Experimental | Error/% | |
|---|---|---|---|
| Mass fraction of unreacted n-decane/% | 87.01 | 86.54 | 0.54 |
| Temperature/K | 874.5 | 885.7 | 1.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lei, Z.; Bao, Z. Supercritical Heat Transfer and Pyrolysis Characteristics of n-Decane in Circular and Rectangular Channels. Energies 2023, 16, 3672. https://doi.org/10.3390/en16093672
Lei Z, Bao Z. Supercritical Heat Transfer and Pyrolysis Characteristics of n-Decane in Circular and Rectangular Channels. Energies. 2023; 16(9):3672. https://doi.org/10.3390/en16093672
Chicago/Turabian StyleLei, Zhiliang, and Zewei Bao. 2023. "Supercritical Heat Transfer and Pyrolysis Characteristics of n-Decane in Circular and Rectangular Channels" Energies 16, no. 9: 3672. https://doi.org/10.3390/en16093672
APA StyleLei, Z., & Bao, Z. (2023). Supercritical Heat Transfer and Pyrolysis Characteristics of n-Decane in Circular and Rectangular Channels. Energies, 16(9), 3672. https://doi.org/10.3390/en16093672






