An Offshore Solar Irradiance Calculator (OSIC) Applied to Photovoltaic Tracking Systems
Abstract
:1. Introduction
2. Materials and Methods
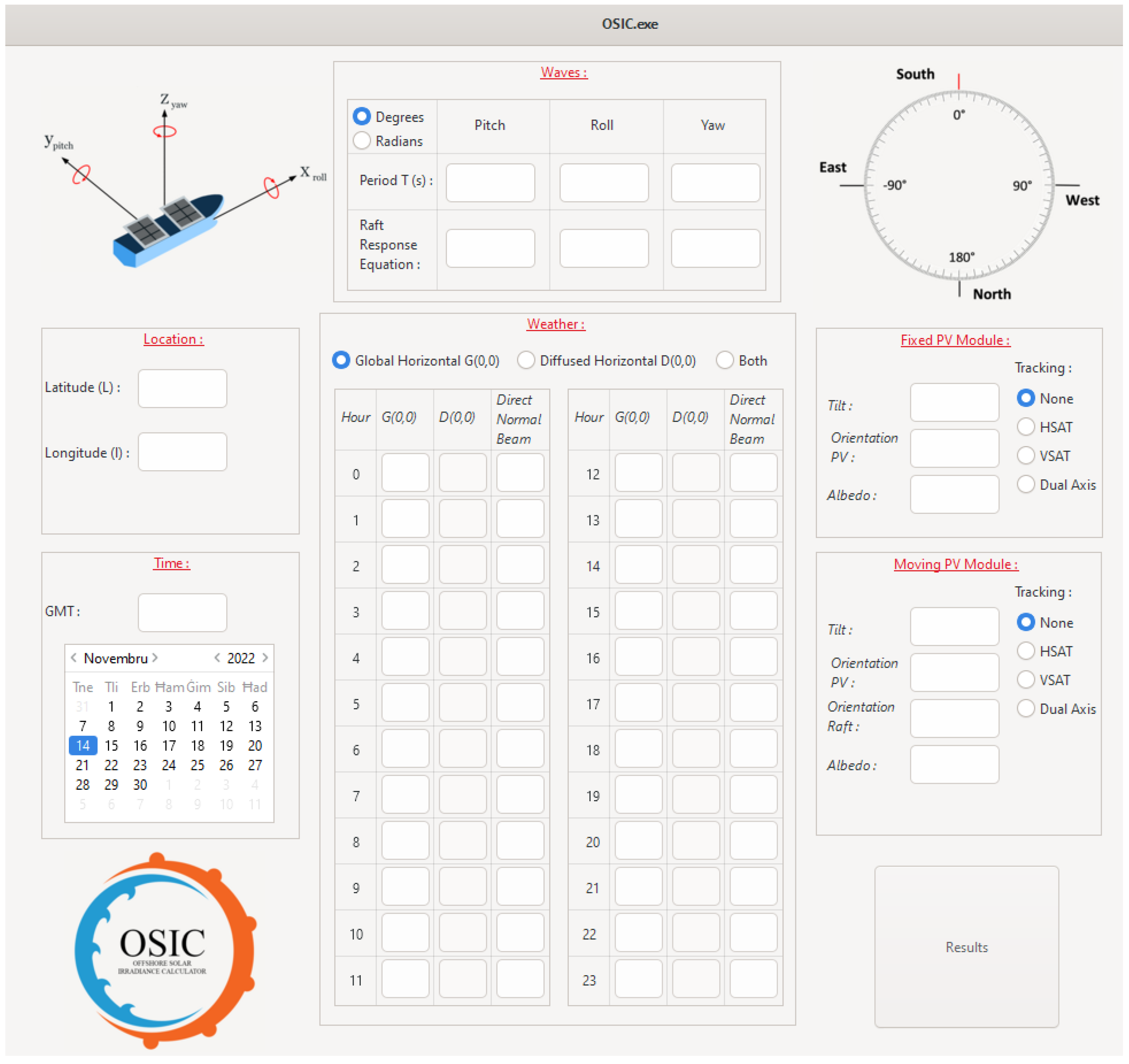
2.1. General Operation of OSIC
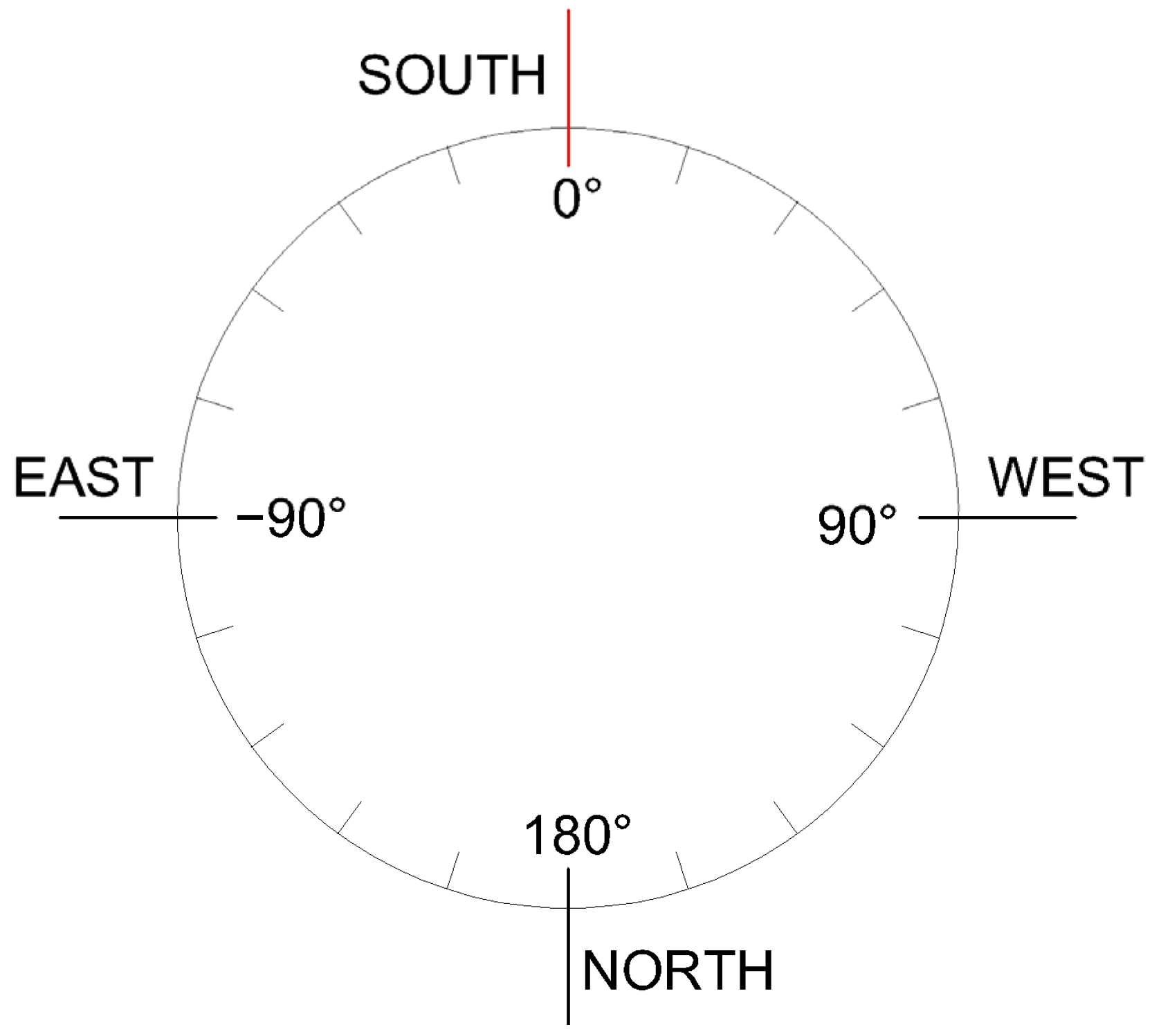
2.2. Calculation of Tilt and Azimuth after Movement
- -
- The vector in front of the raft is oriented south;
- -
- The orientation of the PV module is the same as that of the raft;
- -
- The tilt of the panel is 0°; that is, it is lying horizontally on the raft.
2.3. Calculation of Irradiance on Tracking Surface
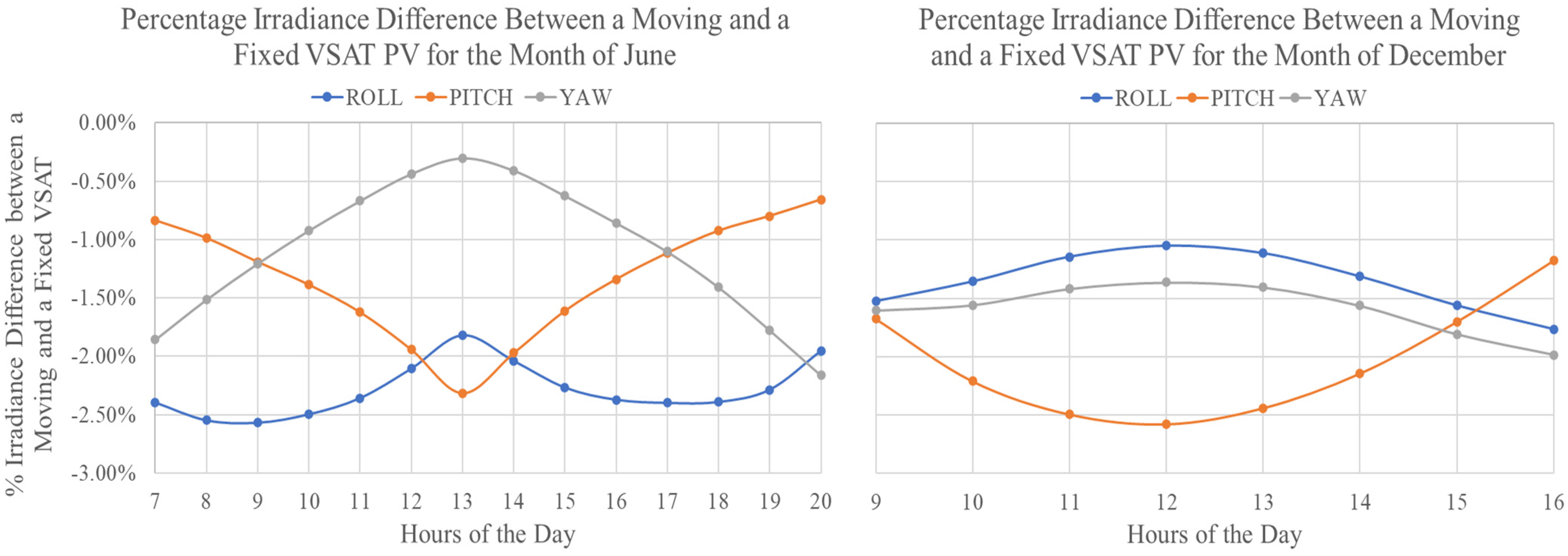
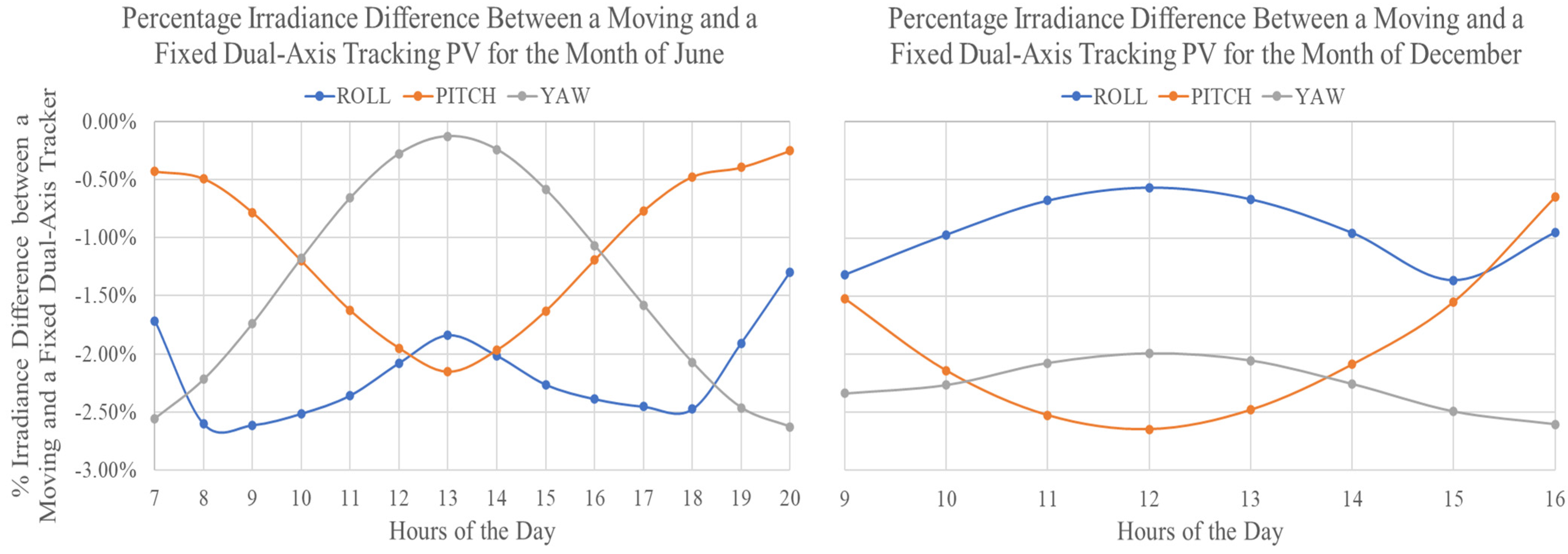
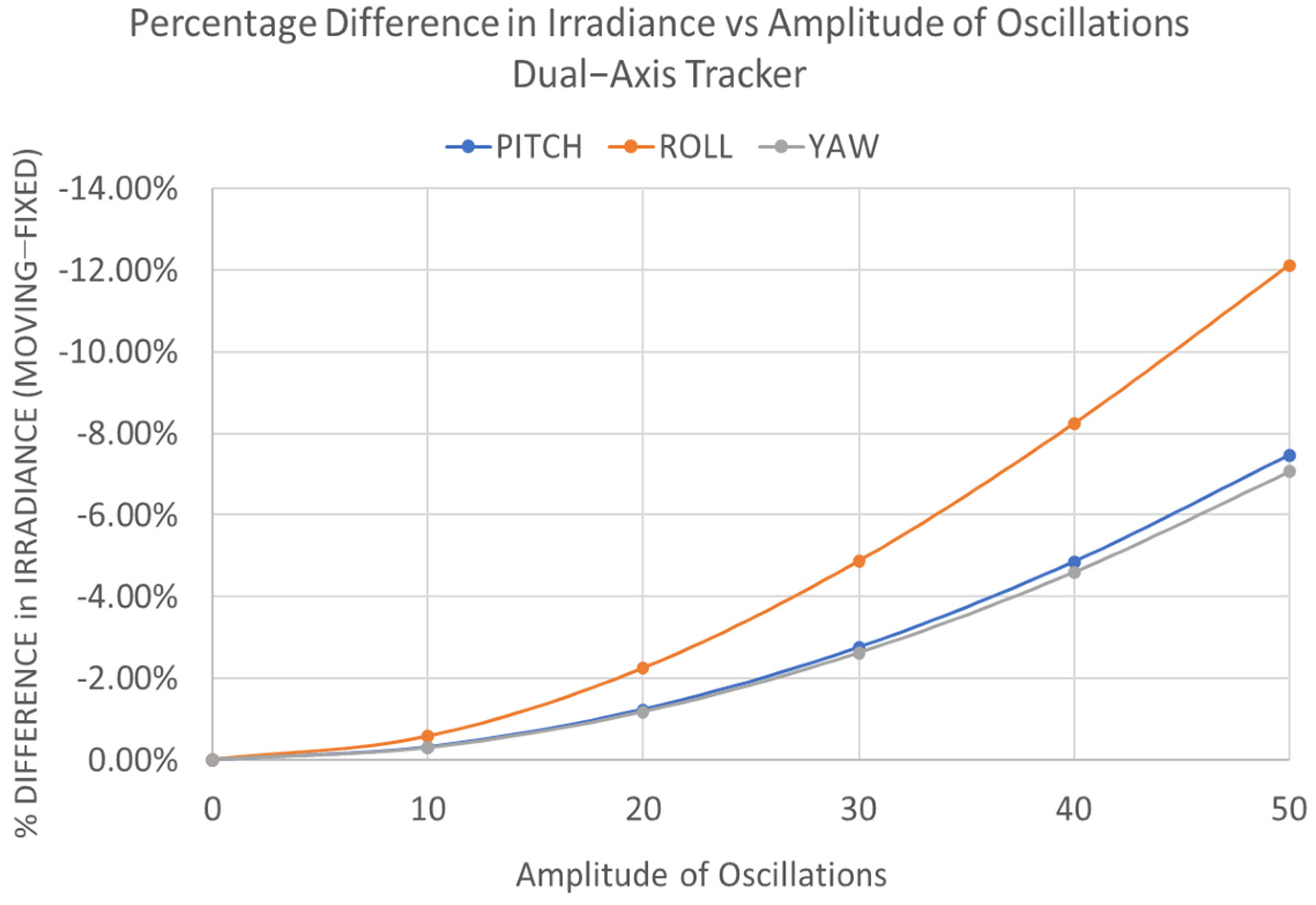
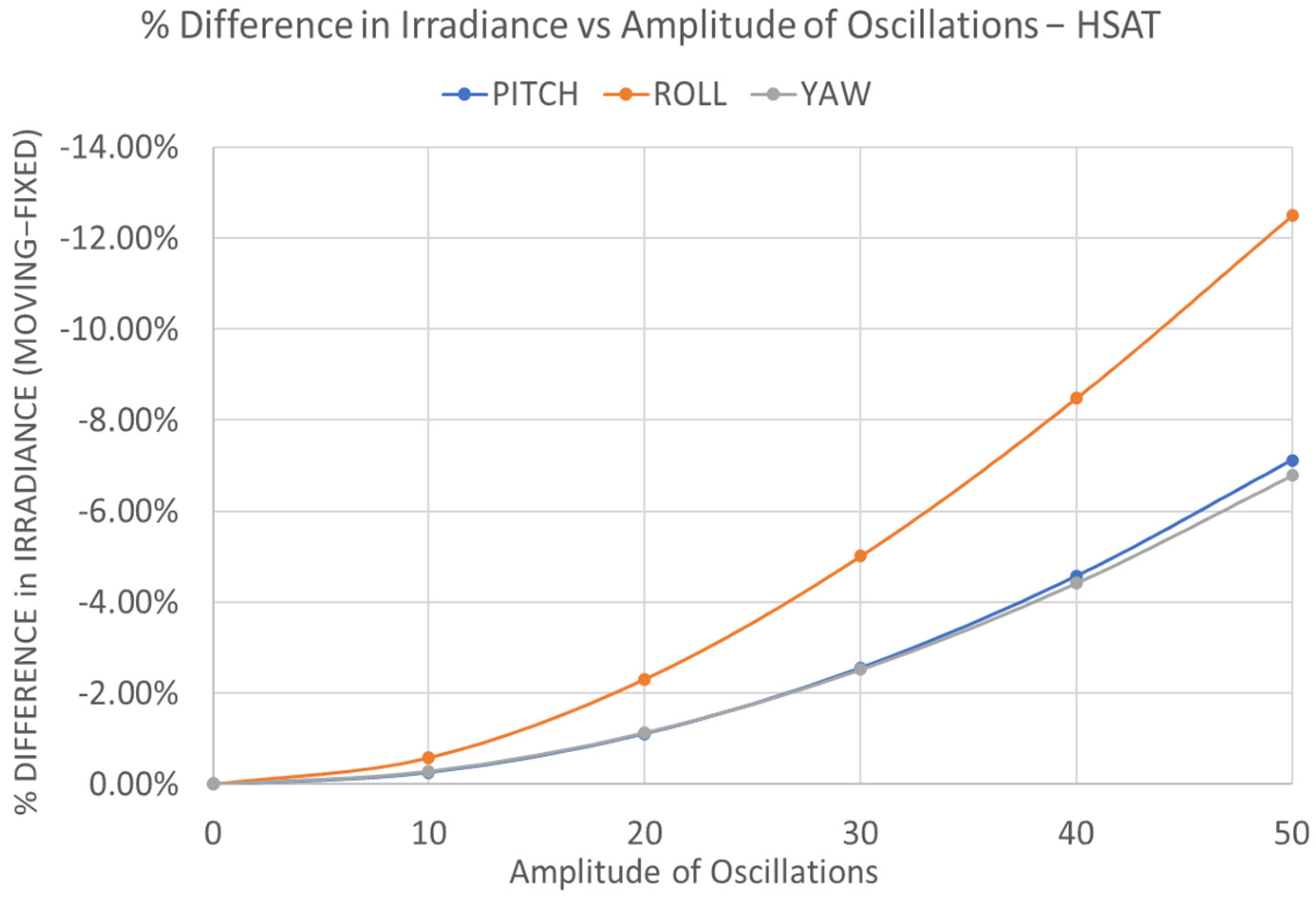
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Description |
| Angle between the orientation of the PV and the orientation of the raft | |
| θ | Angle of rotation around the y-axis of the orthonormal reference frame of the PV panel |
| ϕ | Angle of rotation around the main orthonormal frame |
| βn | New PV tilt angle following a wave response movement |
| PV azimuth following a wave response movement | |
| x, , n | Angular amplitudes of roll, yaw and pitch movements |
| Solar incident angle on tilted surface | |
| Solar declination angle | |
| Hour angle | |
| Solar azimuth angle | |
| Solar altitude | |
| f | Wave response frequency |
| t | Time base |
References
- Gevorkian, P. Alternative Energy Systems in Building Design; McGraw-Hill: New York, NY, USA, 2012; Volume 23. [Google Scholar]
- AL-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Loschi, H.J.; Iano, Y.; León, J.; Moretti, A.; Conte, F.D.; Braga, H. A Review on Photovoltaic Systems: Mechanisms and Methods for Irradiation Tracking and Prediction. Smart Grid Renew. Energy 2015, 6, 187–208. [Google Scholar] [CrossRef]
- Parmar, A.J.N.; Parmar, A.N.; Gautam, V.S. Passive Solar Tracking System. Int. J. Emerg. Technol. Adv. Eng. 2015, 5, 67–88. [Google Scholar]
- Clifford, M.J.; Eastwood, D. Design of a novel passive solar tracker. Solar Energy 2004, 77, 269–280. [Google Scholar] [CrossRef]
- Alexandru, C.; Pozna, C. Different tracking strategies for optimizing the energetic efficiency of a photovoltaic system. In Proceedings of the 2008 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 22–25 May 2008. [Google Scholar] [CrossRef]
- De Melo, K.B.; De Paula, B.H.K.; Da Silva, M.K.; Narváez, D.I.; Moreira, H.S.; Villalva, M.G.; De Siqueira, T.G. A Study on the Influence of Locality in the Viability of Solar Tracker Systems. In Proceedings of the XXII Congresso Brasileiro de Automática, Tambaú, Brazil, 9–12 September 2018. [Google Scholar] [CrossRef]
- Li, G.; Tang, R.; Zhong, H. Optical performance of horizontal single-axis tracked solar panels. Energy Procedia 2012, 16, 1744–1752. [Google Scholar] [CrossRef]
- Li, Z.; Liu, X.; Tang, R. Optical performance of vertical single-axis tracked solar panels. Renew Energy 2011, 36, 64–68. [Google Scholar] [CrossRef]
- Chandel, R.; Chandel, S.S. Performance analysis outcome of a 19-MWp commercial solar photovoltaic plant with fixed-tilt, adjustable-tilt, and solar tracking configurations. Prog. Photovolt. Res. Appl. 2021, 30, 27–48. [Google Scholar] [CrossRef]
- Seme, S.; Srpčič, G.; Kavšek, D.; Božičnik, S.; Letnik, T.; Praunseis, Z.; Štumberger, B.; Hadžiselimović, M. Dual-axis photovoltaic tracking system—Design and experimental investigation. Energy 2017, 139, 1267–1274. [Google Scholar] [CrossRef]
- Rahimi, M.; Banybayat, M.; Tagheie, Y.; Valeh-E-Sheyda, P. An insight on advantage of hybrid sun-wind-tracking over sun-tracking PV system. Energy Convers. Manag. 2015, 105, 294–302. [Google Scholar] [CrossRef]
- Bugeja, R.; Stagno, L.M.; Branche, N. The effect of wave response motion on the insolation on offshore photovoltaic installations. Sol. Energy Adv. 2021, 1, 100008. [Google Scholar] [CrossRef]
- The GTK Team. The GTK Project—A Free and Open-Source Cross-Platform Widget Toolkit. Available online: https://www.gtk.org/ (accessed on 17 January 2023).
- The Glade Project. Glade—A User Interface Designer. 2022. Available online: https://glade.gnome.org/ (accessed on 12 February 2023).
- Johansen, M.F. Inductive Computer Science/pb Plots: A Plotting Library Available in Many Programming Languages. 2023. Available online: https://github.com/InductiveComputerScience/pbPlots (accessed on 12 February 2023).
- U.S. Department of Commerce and NOAA Research. NOAA Earth System Research Laboratory. 2005. Available online: https://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html (accessed on 8 May 2020).
- Perez, R.; Ineichen, P.; Seals, R.; Michalsky, J.; Stewart, R. Modeling daylight availability and irradiance components from direct and global irradiance. Solar Energy 1990, 44, 271–289. [Google Scholar] [CrossRef]
- Perez, R.; Stewart, R.; Arbogast, C.; Seals, R.; Scott, J. An anisotropic hourly diffuse radiation model for sloping surfaces: Description, performance validation, site dependency evaluation. Solar Energy 1986, 36, 481–497. [Google Scholar] [CrossRef]
- Luque, A.; Hegedus, S. Handbook of Photovoltaic Science and Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]

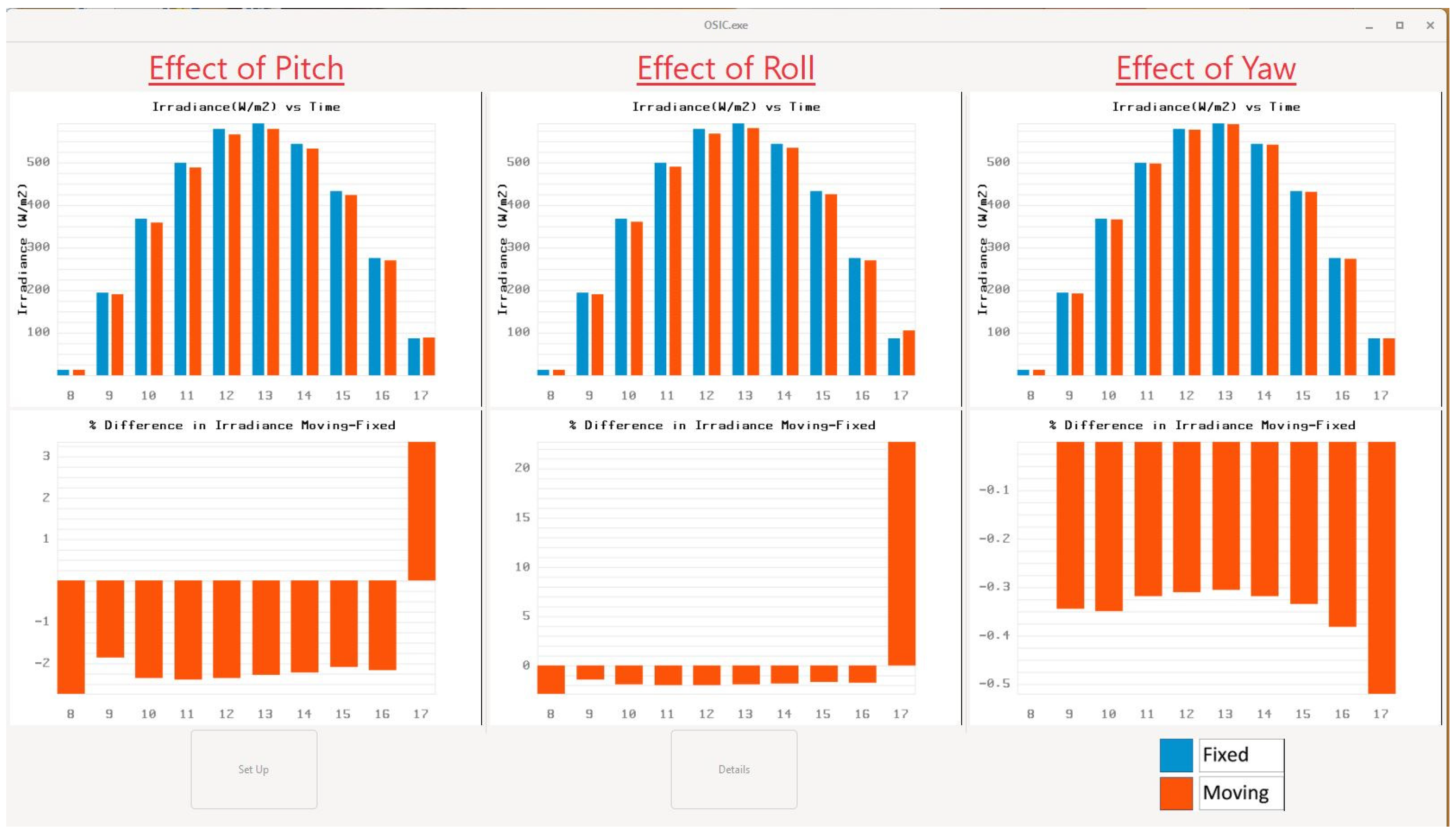

| Insolation Deviation of Offshore Tracking Systems from Land—Horizontal Single-Axis Tracking | |||
| Month | Effect of Pitch | Effect of Roll | Effect of Yaw |
| January | −0.93% | −2.31% | −1.33% |
| February | −0.96% | −2.00% | −1.06% |
| March | −0.98% | −2.16% | −1.14% |
| April | −1.06% | −2.06% | −0.96% |
| May | −1.15% | −2.35% | −1.20% |
| June | −1.11% | −2.31% | −1.13% |
| July | −1.18% | −2.38% | −1.14% |
| August | −1.10% | −2.33% | −1.18% |
| September | −1.00% | −2.28% | −1.24% |
| October | −0.94% | −2.20% | −1.21% |
| November | −0.98% | −2.28% | −1.31% |
| December | −0.88% | −2.21% | −1.34% |
| Insolation deviation of Offshore Tracking Systems from Land—Vertical Single-Axis Tracking Tilt = 30° | |||
| Month | Effect of Pitch | Effect of Roll | Effect of Yaw |
| January | −2.07% | −1.41% | −1.47% |
| February | −1.71% | −1.55% | −1.07% |
| March | −1.66% | −1.83% | −1.04% |
| April | −1.53% | −1.95% | −0.82% |
| May | −1.53% | −2.31% | −0.95% |
| June | −1.48% | −2.28% | −0.89% |
| July | −1.54% | −2.30% | −0.92% |
| August | −1.58% | −2.16% | −0.99% |
| September | −1.70% | −1.93% | −1.12% |
| October | −1.83% | −1.60% | −1.22% |
| November | −2.09% | −1.43% | −1.46% |
| December | −2.15% | −1.30% | −1.55% |
| Insolation Deviation of Offshore Tracking Systems from Land —Dual-Axis Tracking | |||
| Month | Effect of Pitch | Effect of Roll | Effect of Yaw |
| January | −1.95% | −1.08% | −2.13% |
| February | −1.53% | −1.32% | −1.60% |
| March | −1.41% | −1.75% | −1.47% |
| April | −1.30% | −1.94% | −1.10% |
| May | −1.26% | −2.28% | −1.26% |
| June | −1.23% | −2.25% | −1.18% |
| July | −1.29% | −2.30% | −1.20% |
| August | −1.31% | −2.16% | −1.32% |
| September | −1.45% | −1.83% | −1.57% |
| October | −1.65% | −1.40% | −1.79% |
| November | −1.96% | −1.05% | −2.12% |
| December | −2.05% | −0.90% | −2.23% |
| Wave Amplitude = 10° | |||
| VSAT Tilt | Effect of Pitch | Effect of Roll | Effect of Yaw |
| 5° | −0.31% | −0.39% | −0.05% |
| 30° | −0.37% | −0.57% | −0.22% |
| 50° | −0.30% | −0.57% | −0.33% |
| Wave Amplitude = 20° | |||
| 5° | −1.49% | −1.56% | −0.19% |
| 30° | −1.48% | −2.28% | −0.89% |
| 50° | −1.18% | −2.27% | −1.31% |
| Wave Amplitude = 30° | |||
| 5° | −3.63% | −3.49% | −0.42% |
| 30° | −3.31% | −5.06% | −1.99% |
| 50° | −2.64% | −5.07% | −2.93% |
| Wave Amplitude = 40° | |||
| 5° | −6.73% | −5.99% | −0.74% |
| 30° | −5.82% | −8.78% | −3.48% |
| 50° | −4.63% | −8.88% | −5.14% |
| Wave Amplitude = 50° | |||
| 5° | −10.74% | −8.92% | −1.14% |
| 30° | −8.98% | −13.28% | −5.35% |
| 50° | −6.81% | −12.07% | −7.89% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bugeja, R.; Mule’ Stagno, L.; Dexarcis, L. An Offshore Solar Irradiance Calculator (OSIC) Applied to Photovoltaic Tracking Systems. Energies 2023, 16, 3735. https://doi.org/10.3390/en16093735
Bugeja R, Mule’ Stagno L, Dexarcis L. An Offshore Solar Irradiance Calculator (OSIC) Applied to Photovoltaic Tracking Systems. Energies. 2023; 16(9):3735. https://doi.org/10.3390/en16093735
Chicago/Turabian StyleBugeja, Ryan, Luciano Mule’ Stagno, and Lucas Dexarcis. 2023. "An Offshore Solar Irradiance Calculator (OSIC) Applied to Photovoltaic Tracking Systems" Energies 16, no. 9: 3735. https://doi.org/10.3390/en16093735
APA StyleBugeja, R., Mule’ Stagno, L., & Dexarcis, L. (2023). An Offshore Solar Irradiance Calculator (OSIC) Applied to Photovoltaic Tracking Systems. Energies, 16(9), 3735. https://doi.org/10.3390/en16093735






