Mechanistic Exploration of Dendrite Growth and Inhibition for Lithium Metal Batteries
Abstract
1. Introduction
2. Theoretical Framework
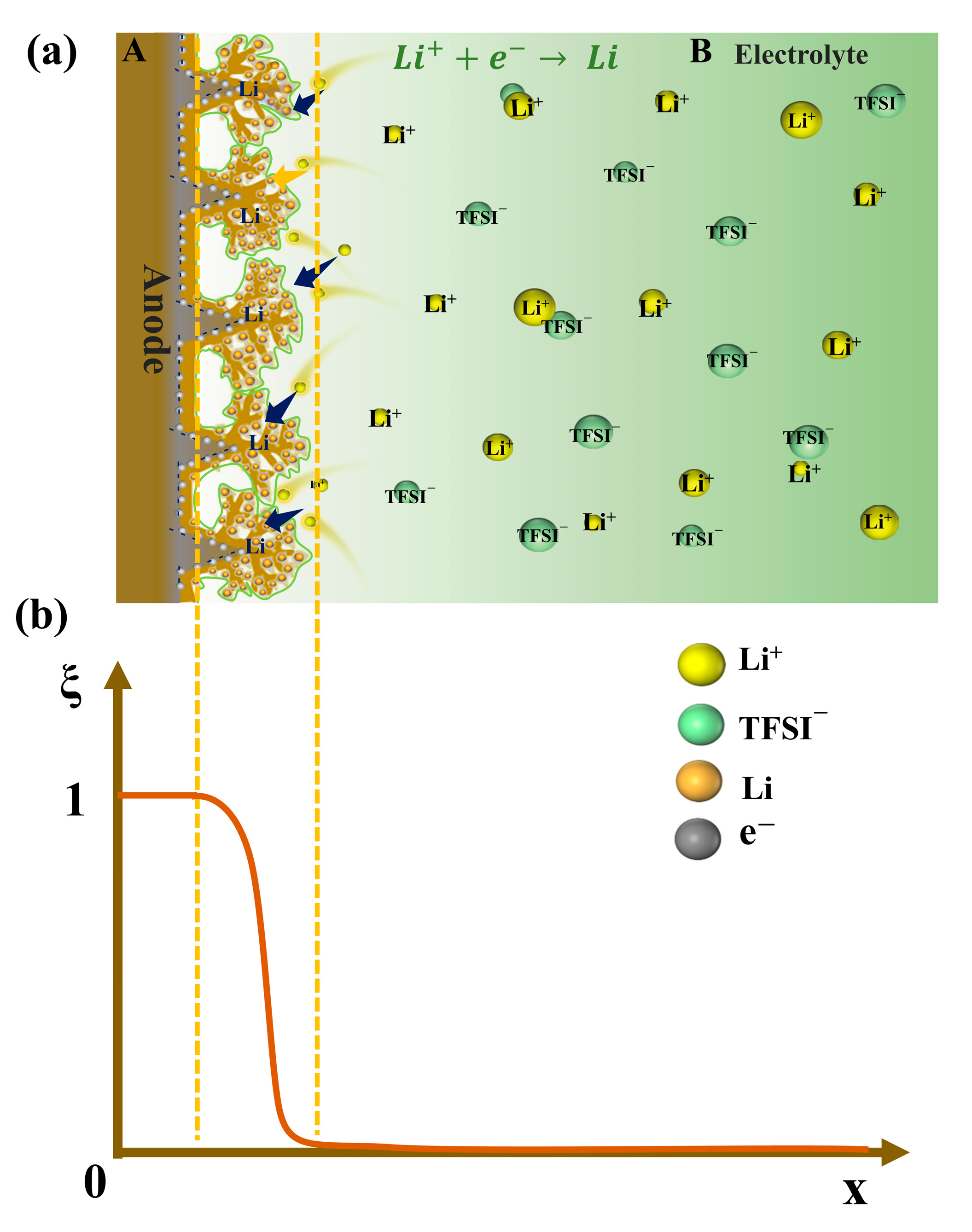
2.1. Phase-Field Equation
- (1)
- (2)
- The electrode surface has enough electrons to participate in the reaction.
2.2. Lithium Ion Diffusion Equation
2.3. The Control Equation for the Electron Transmission Process
2.4. Initial Conditions and Boundary Conditions
3. Experiment
3.1. Material Synthesis
3.2. Coin Cell Assemblage and Electrochemical Testing
3.3. Characterization
4. Results and Discussion
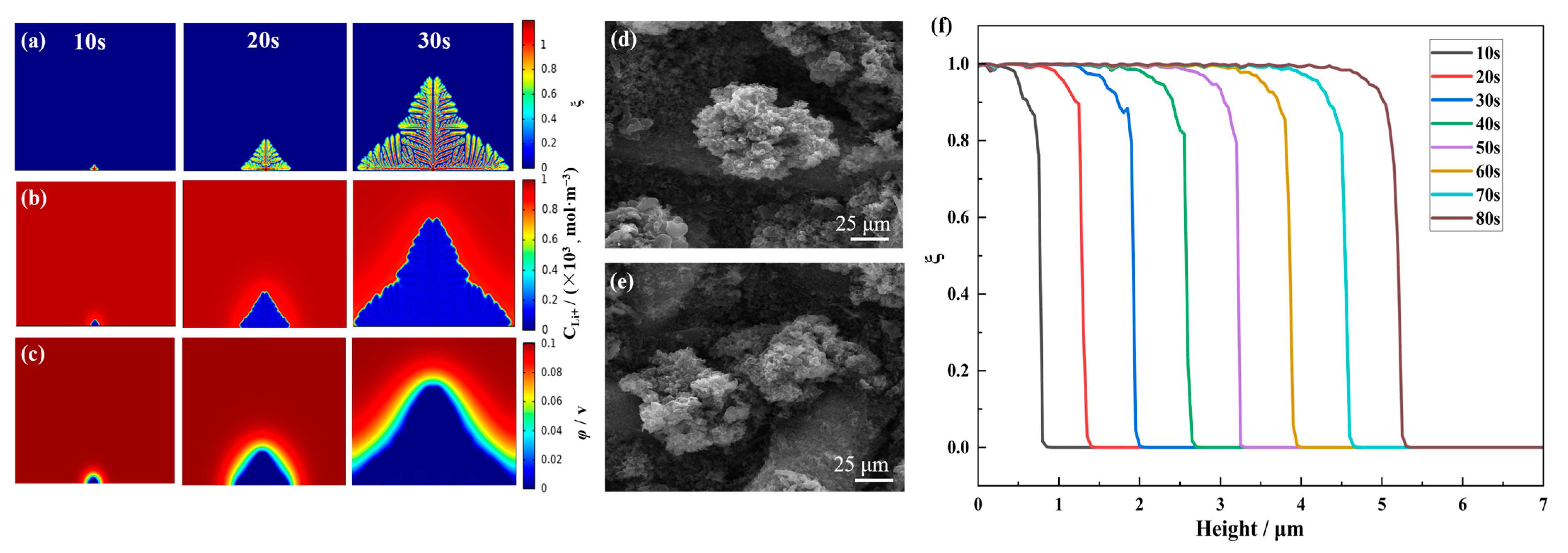
4.1. Morphology and Evolution of the Lithium Dendrites
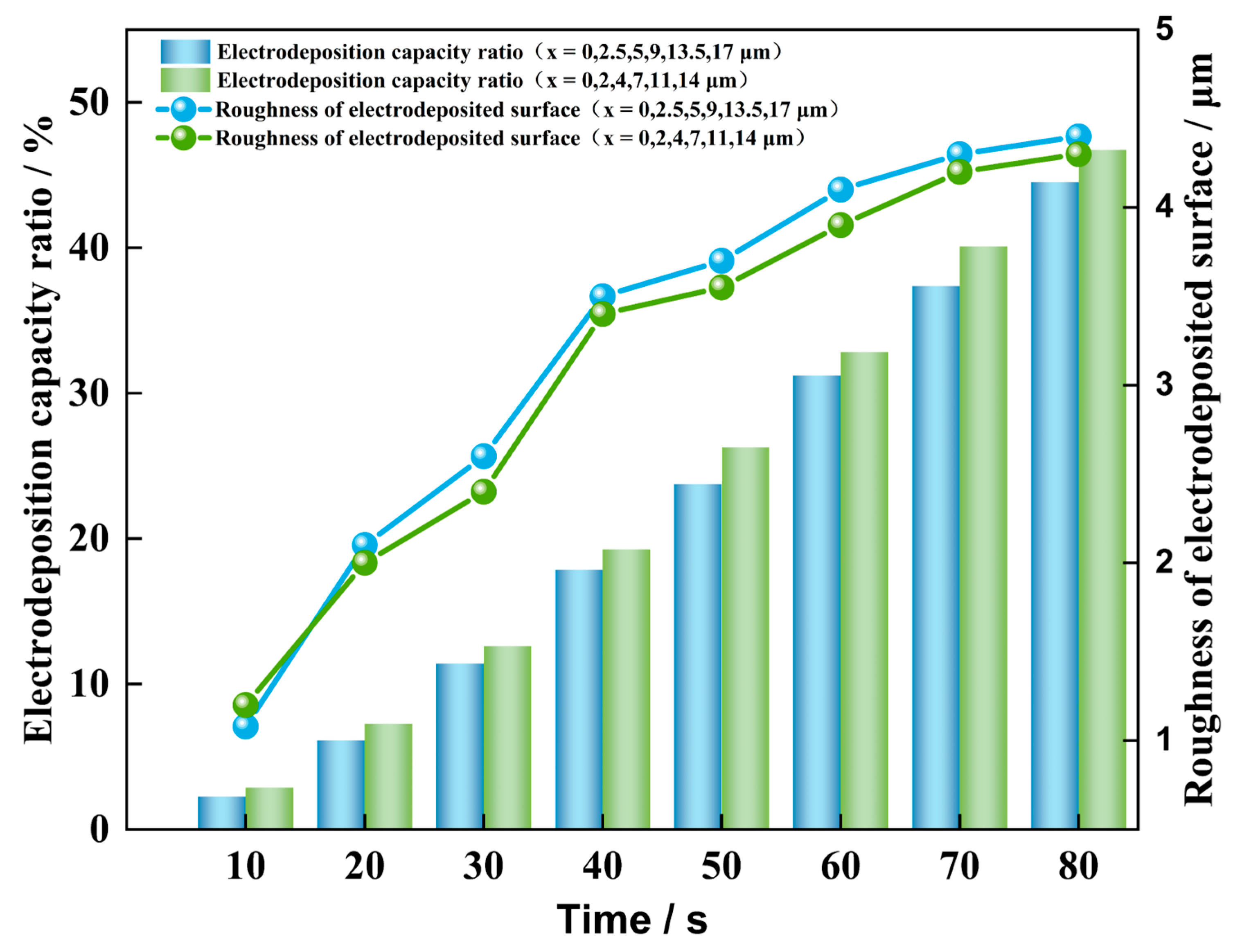
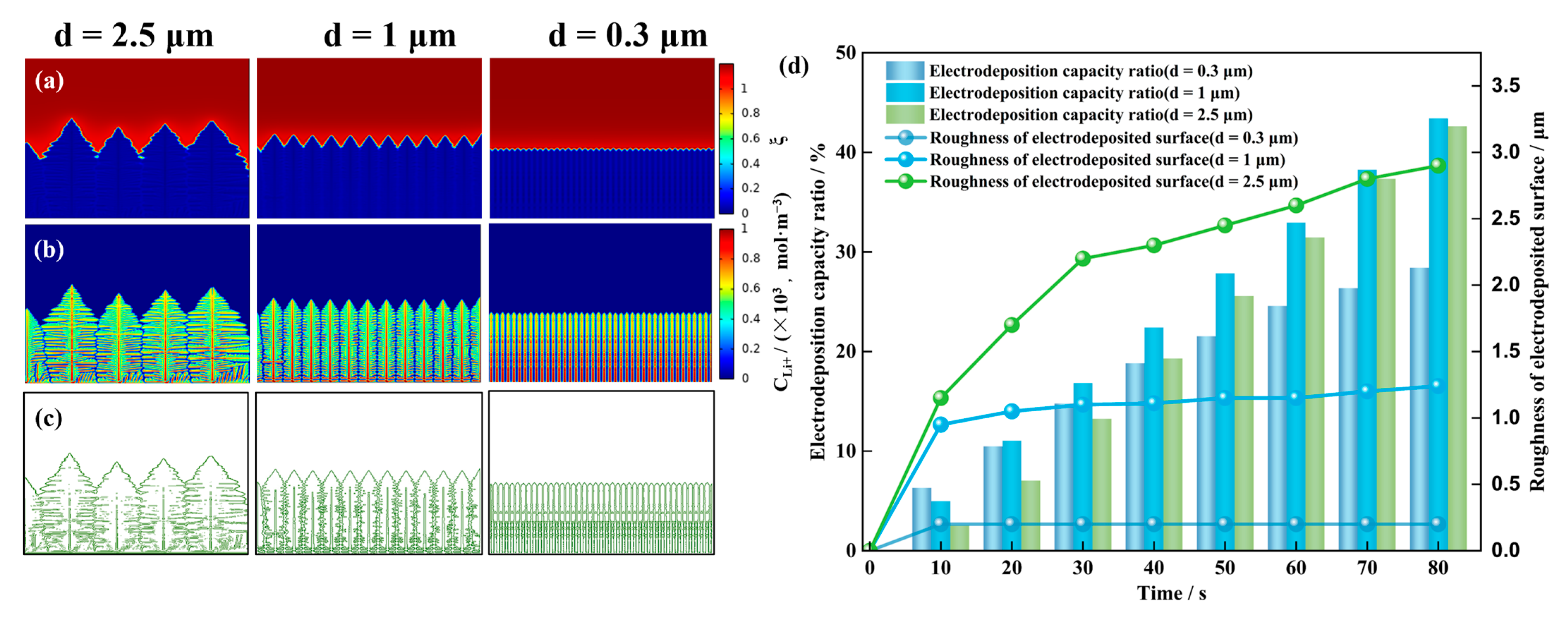
4.2. Influence of Different Initial Nucleation Spacings on the Morphology of the Dendrite Growth
4.3. Influence of the Surface Energy Anisotropy Intensity on the Morphology of the Dendrite Growth
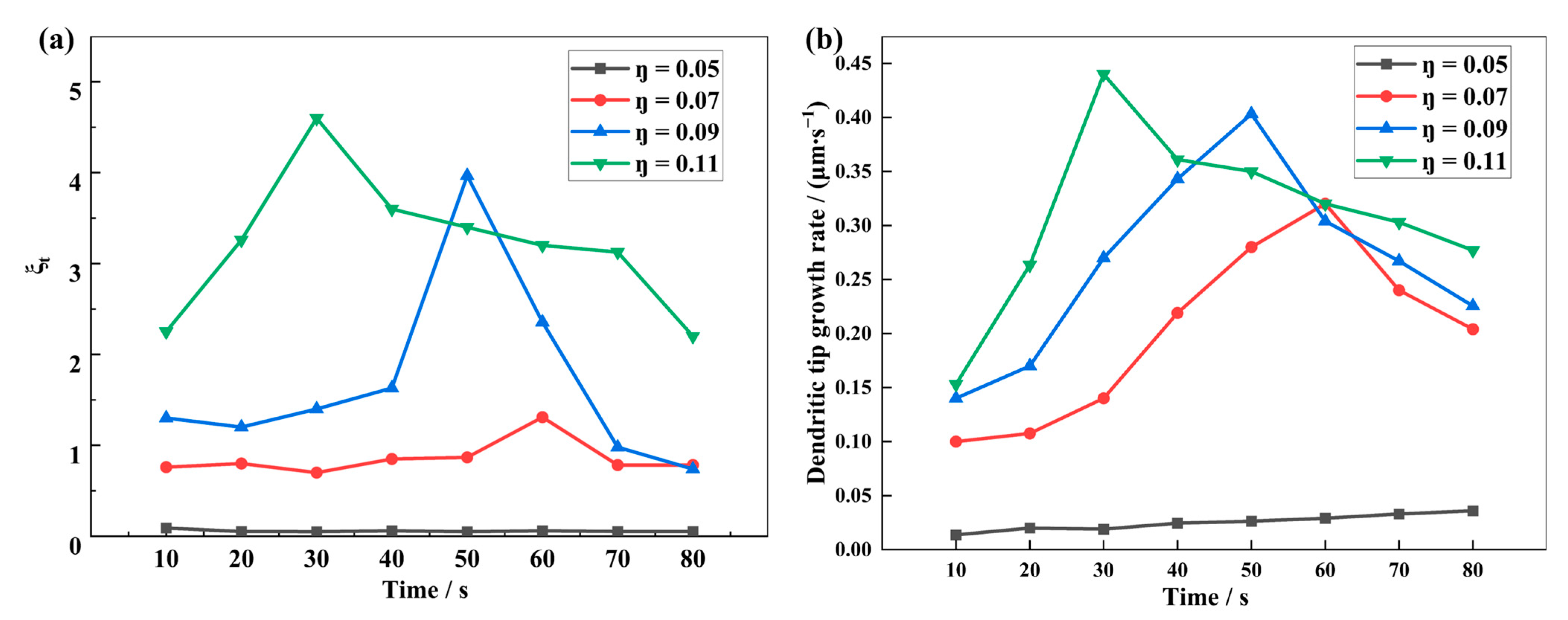
4.4. Influence of the Interfacial Electrochemical Driving Force on the Dendrite Growth
5. Conclusions
- (1)
- A smaller initial nucleation spacing can reduce the surface roughness of the deposited lithium metal and inhibit dendrite growth. When the initial nucleation spacing is small, the lateral branching growth of the dendrites is inhibited. The lithium metal is mainly deposited at the tips of the dendrites, which results in a low surface roughness of the deposited negative electrode, and the shape of dendrite growth is flatter. When the initial nucleation spacing of the dendrites is larger, their lateral branching growth is more pronounced, and the shape of dendrite growth is more shrub-like or dendritic.
- (2)
- A lower interfacial energy anisotropy strength can slow down the growth of dendrite tips. At lower surface energy anisotropy intensity, the dendrites uniformly grow in all the orders with a mossy morphology. When the surface energy anisotropy intensity increases, the dendrites start to have the advantage of main branch growth, the more considerable interfacial energy makes their tips rapidly grow, and their shape appears shrub-like and rod-like. When the interfacial energy anisotropy intensity reaches a specific value, the main branches of rod-like dendrites also split into more slender linear side branches.
- (3)
- Reducing the nucleation overpotential results in a small interfacial electrochemical driving force and a low dendrite growth rate, which effectively suppresses dendrite growth. The dendrite interfacial reaction current and growth rate increase with the increase of the electrochemical driving force. At high nucleation overpotential, the higher the interfacial electrochemical driving force, the greater the apical dominance of dendrite growth and the more likely the formation of shrub-type dendrites. On the contrary, a lower nucleation overpotential and a lower interfacial electrochemical driving force can reduce the growth rate of lithium dendrites and make them more easily grow into thin and long dendrites.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A





References
- Jin, C.; Sheng, O.; Luo, J.; Yuan, H.; Fang, C.; Zhang, W.; Huang, H.; Gan, Y.; Xia, Y.; Liang, C.; et al. 3D lithium metal embedded within lithiophilic porous matrix for stable lithium metal batteries. Nano Energy 2017, 37, 177–186. [Google Scholar] [CrossRef]
- Cheng, X.B.; Hou, T.Z.; Zhang, R.; Peng, H.J.; Zhao, C.Z.; Huang, J.Q.; Zhang, Q. Dendrite-Free Lithium Deposition Induced by Uniformly Distributed Lithium Ions for Efficient Lithium Metal Batteries. Adv. Mater. 2016, 28, 2888–2895. [Google Scholar] [CrossRef] [PubMed]
- Yamada, Y.; Yamada, A. Review—Superconcentrated Electrolytes for Lithium Batteries. J. Electrochem. Soc. 2015, 162, A2406–A2423. [Google Scholar] [CrossRef]
- Jeong, S.-K.; Seo, H.-Y.; Kim, D.-H.; Han, H.-K.; Kim, J.-G.; Lee, Y.B.; Iriyama, Y.; Abe, T.; Ogumi, Z. Suppression of dendritic lithium formation by using concentrated electrolyte solutions. Electrochem. Commun. 2008, 10, 635–638. [Google Scholar] [CrossRef]
- Camacho-Forero, L.E.; Smith, T.W.; Balbuena, P.B. Effects of High and Low Salt Concentration in Electrolytes at Lithium–Metal Anode Surfaces. J. Phys. Chem. C 2016, 121, 182–194. [Google Scholar] [CrossRef]
- Chen, X.; Hou, T.-Z.; Li, B.; Yan, C.; Zhu, L.; Guan, C.; Cheng, X.-B.; Peng, H.-J.; Huang, J.-Q.; Zhang, Q. Towards stable lithium-sulfur batteries: Mechanistic insights into electrolyte decomposition on lithium metal anode. Energy Storage Mater. 2017, 8, 194–201. [Google Scholar] [CrossRef]
- Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 2004, 104, 4303–4417. [Google Scholar] [CrossRef]
- Kuwata, H.; Sonoki, H.; Matsui, M.; Matsuda, Y.; Imanishi, N. Surface Layer and Morphology of Lithium Metal Electrodes. Electrochemistry 2016, 84, 854–860. [Google Scholar] [CrossRef]
- Heine, J.; Hilbig, P.; Qi, X.; Niehoff, P.; Winter, M.; Bieker, P. Fluoroethylene Carbonate as Electrolyte Additive in Tetraethylene Glycol Dimethyl Ether Based Electrolytes for Application in Lithium Ion and Lithium Metal Batteries. J. Electrochem. Soc. 2015, 162, A1094–A1101. [Google Scholar] [CrossRef]
- Ding, F.; Xu, W.; Graff, G.L.; Zhang, J.; Sushko, M.L.; Chen, X.; Shao, Y.; Engelhard, M.H.; Nie, Z.; Xiao, J.; et al. Dendrite-free lithium deposition via self-healing electrostatic shield mechanism. J. Am. Chem. Soc. 2013, 135, 4450–4456. [Google Scholar] [CrossRef]
- Kim, H.J.; Umirov, N.; Park, J.-S.; Lim, J.-H.; Zhu, J.; Kim, S.-S.; Myung, S.-T. Lithium dendritic growth inhibitor enabling high capacity, dendrite-free, and high current operation for rechargeable lithium batteries. Energy Storage Mater. 2022, 46, 76–89. [Google Scholar] [CrossRef]
- Ye, H.; Yin, Y.-X.; Zhang, S.-F.; Shi, Y.; Liu, L.; Zeng, X.-X.; Wen, R.; Guo, Y.-G.; Wan, L.-J. Synergism of Al-containing solid electrolyte interphase layer and Al-based colloidal particles for stable lithium anode. Nano Energy 2017, 36, 411–417. [Google Scholar] [CrossRef]
- Basile, A.; Bhatt, A.I.; O’Mullane, A.P. Stabilizing lithium metal using ionic liquids for long-lived batteries. Nat. Commun. 2016, 7, ncomms11794. [Google Scholar] [CrossRef]
- Xu, X.-Q.; Jiang, F.-N.; Yang, S.-J.; Xiao, Y.; Liu, H.; Liu, F.; Liu, L.; Cheng, X.-B. Dual-layer vermiculite nanosheet based hybrid film to suppress dendrite growth in lithium metal batteries. J. Energy Chem. 2022, 69, 205–210. [Google Scholar] [CrossRef]
- Tu, Z.; Zachman, M.J.; Choudhury, S.; Wei, S.; Ma, L.; Yang, Y.; Kourkoutis, L.F.; Archer, L.A. Nanoporous Hybrid Electrolytes for High-Energy Batteries Based on Reactive Metal Anodes. Adv. Energy Mater. 2017, 7, 1602367. [Google Scholar] [CrossRef]
- Tikekar, M.D.; Archer, L.A.; Koch, D.L. Stabilizing electrodeposition in elastic solid electrolytes containing immobilized anions. Sci. Adv. 2016, 2, e1600320. [Google Scholar] [CrossRef]
- Jia, M.; Zhao, N.; Huo, H.; Guo, X. Comprehensive Investigation into Garnet Electrolytes Toward Application-Oriented Solid Lithium Batteries. Electrochem. Energy Rev. 2020, 3, 656–689. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, Y.; Chi, S.-S.; Woo, H.J.; Yu, K.; Ma, J.; Wang, J.; Wang, C.; Deng, Y. Understanding the lithium dendrites growth in garnet-based solid-state lithium metal batteries. J. Power Sources 2022, 521, 230921. [Google Scholar] [CrossRef]
- Monroe, C.; Newman, J. Dendrite Growth in Lithium/Polymer Systems. J. Electrochem. Soc. 2003, 150, A1377. [Google Scholar] [CrossRef]
- Liang, L.; Qi, Y.; Xue, F.; Bhattacharya, S.; Harris, S.J.; Chen, L.Q. Nonlinear phase-field model for electrode-electrolyte interface evolution. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2012, 86, 051609. [Google Scholar] [CrossRef]
- Ely, D.R.; Jana, A.; García, R.E. Phase field kinetics of lithium electrodeposits. J. Power Sources 2014, 272, 581–594. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, H.W.; Liang, L.Y.; Liu, Z.; Qi, Y.; Lu, P.; Chen, J.; Chen, L.-Q. Modulation of dendritic patterns during electrodeposition: A nonlinear phase-field model. J. Power Sources 2015, 300, 376–385. [Google Scholar] [CrossRef]
- Vu, T.T.; Eom, G.H.; Lee, J.; Park, M.-S.; Moon, J. Electrolyte interface design for regulating Li dendrite growth in rechargeable Li-metal batteries: A theoretical study. J. Power Sources 2021, 496, 229791. [Google Scholar] [CrossRef]
- Lee, H.; Kwak, T.; Lee, W.; Song, J.; Kim, D. Effect of surface topography on dendritic growth in lithium metal batteries. J. Power Sources 2022, 552, 232264. [Google Scholar] [CrossRef]
- Chen, C.-H.; Pao, C.-W. Phase-field study of dendritic morphology in lithium metal batteries. J. Power Sources 2021, 484, 229203. [Google Scholar] [CrossRef]
- Gao, L.; Guo, Z. Phase-field simulation of Li dendrites with multiple parameters influence. Comput. Mater. Sci. 2020, 183, 109919. [Google Scholar] [CrossRef]
- Yan, H.H.; Bie, Y.H.; Cui, X.Y.; Xiong, G.P.; Chen, L. A computational investigation of thermal effect on lithium dendrite growth. Energy Convers. Manag. 2018, 161, 193–204. [Google Scholar] [CrossRef]
- Yurkiv, V.; Foroozan, T.; Ramasubramanian, A.; Shahbazian-Yassar, R.; Mashayek, F. The influence of stress field on Li electrodeposition in Li-metal battery. MRS Commun. 2018, 8, 1285–1291. [Google Scholar] [CrossRef]
- Tan, J.; Tartakovsky, A.M.; Ferris, K.; Ryan, E.M. Investigating the Effects of Anisotropic Mass Transport on Dendrite Growth in High Energy Density Lithium Batteries. J. Electrochem. Soc. 2015, 163, A318–A327. [Google Scholar] [CrossRef]
- Mu, W.; Liu, X.; Wen, Z.; Liu, L. Numerical simulation of the factors affecting the growth of lithium dendrites. J. Energy Storage 2019, 26, 100921. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. Ground state structures in ordered binary alloys with second neighbor interactions. Acta Metall. 1972, 20, 423–433. [Google Scholar] [CrossRef]
- Kodým, R.; Šnita, D.; Bouzek, K. Mathematical Modeling of Electromembrane Processes. In Current Trends and Future Developments on (Bio-) Membranes; Elsevier: Turin, Italy, 2019; pp. 285–326. [Google Scholar]
- Zha, C.X. Introduction to Electrode Process Dynamics, 3rd ed.; Science Press: Beijing, China, 2002; pp. 129–146. [Google Scholar]
- Tu, Z.; Nath, P.; Lu, Y.; Tikekar, M.D.; Archer, L.A. Nanostructured electrolytes for stable lithium electrodeposition in secondary batteries. Acc. Chem. Res. 2015, 48, 2947–2956. [Google Scholar] [CrossRef] [PubMed]
- Stephens, A.W. Texture and Mechanical Anisotropy in the Copper-zinc System; The University of Arizona: Tucson, AZ, USA, 1968. [Google Scholar]
- Yu, F.; Xu, D.; Chen, S.; Chen, K.; Wang, X.; Liu, D.; Ma, Y.; Huang, C.; Yan, D. Effect of Cu Content on Anisotropy of Mechanical Property of Al-Cu-Mn Alloy. Chin. J. Mater. Res. 2018, 32, 853–860. [Google Scholar] [CrossRef]
- Becherer, J.; Kramer, D.; Mönig, R. The growth mechanism of lithium dendrites and its coupling to mechanical stress. J. Mater. Chem. A 2022, 10, 5530–5539. [Google Scholar] [CrossRef]
- Steiger, J.; Kramer, D.; Mönig, R. Microscopic observations of the formation, growth and shrinkage of lithium moss during electrodeposition and dissolution. Electrochim. Acta 2014, 136, 529–536. [Google Scholar] [CrossRef]
- Jackle, M.; Gross, A. Microscopic properties of lithium, sodium, and magnesium battery anode materials related to possible dendrite growth. J. Chem. Phys. 2014, 141, 174710. [Google Scholar] [CrossRef]
- Zhang, H.-W.; Liu, Z.; Liang, L.; Chen, L.; Qi, Y.; Harris, S.J.; Lu, P.; Chen, L.-Q. Understanding and Predicting the Lithium Dendrite Formation in Li-Ion Batteries: Phase Field Model. ECS Trans. 2014, 61, 1. [Google Scholar] [CrossRef]
- Zhang, R.; Shen, X.; Cheng, X.-B.; Zhang, Q. The dendrite growth in 3D structured lithium metal anodes: Electron or ion transfer limitation? Energy Storage Mater. 2019, 23, 556–565. [Google Scholar] [CrossRef]
- Ans, M.; Atif Makhdoom, M.; Faisal Irfan, M.; Al Abir, A. Optimized modelling and kinetic analysis of nickel recovery from waste orthodontic implants using response surface methodology. Miner. Eng. 2022, 175, 107279. [Google Scholar] [CrossRef]
- Yurkiv, V.; Foroozan, T.; Ramasubramanian, A.; Shahbazian-Yassar, R.; Mashayek, F. Phase-field modeling of solid electrolyte interface (SEI) influence on Li dendritic behavior. Electrochim. Acta 2018, 265, 609–619. [Google Scholar] [CrossRef]
- Hadef, F.; Ans, M. X-ray analysis and Rietveld refinement of ball milled Fe50Al35Ni15 powder. Surf. Interfaces 2021, 26, 101303. [Google Scholar] [CrossRef]
- Meng, Q.; Deng, B.; Zhang, H.; Wang, B.; Zhang, W.; Wen, Y.; Ming, H.; Zhu, X.; Guan, Y.; Xiang, Y.; et al. Heterogeneous nucleation and growth of electrodeposited lithium metal on the basal plane of single-layer graphene. Energy Storage Mater. 2019, 16, 419–425. [Google Scholar] [CrossRef]
- Cheng, X.B.; Zhang, R.; Zhao, C.Z.; Zhang, Q. Toward Safe Lithium Metal Anode in Rechargeable Batteries: A Review. Chem. Rev. 2017, 117, 10403–10473. [Google Scholar] [CrossRef]
- Qian, J.; Henderson, W.A.; Xu, W.; Bhattacharya, P.; Engelhard, M.; Borodin, O.; Zhang, J.G. High rate and stable cycling of lithium metal anode. Nat. Commun. 2015, 6, 6362. [Google Scholar] [CrossRef]
- Li, N.W.; Yin, Y.X.; Li, J.Y.; Zhang, C.H.; Guo, Y.G. Passivation of Lithium Metal Anode via Hybrid Ionic Liquid Electrolyte toward Stable Li Plating/Stripping. Adv. Sci. 2017, 4, 1600400. [Google Scholar] [CrossRef]
- Busche, M.R.; Drossel, T.; Leichtweiss, T.; Weber, D.A.; Falk, M.; Schneider, M.; Reich, M.L.; Sommer, H.; Adelhelm, P.; Janek, J. Dynamic formation of a solid-liquid electrolyte interphase and its consequences for hybrid-battery concepts. Nat. Chem. 2016, 8, 426–434. [Google Scholar] [CrossRef]
- Muhammad, A.; Sales, W.F. Iron-graphene based anode material for rechargeable lithium-ion batteries decorated by gold nanoparticles recovered from gold plated waste surgical tools. Surf. Interfaces 2021, 27, 101575. [Google Scholar] [CrossRef]
- Zhang, X.-Q.; Cheng, X.-B.; Chen, X.; Yan, C.; Zhang, Q. Fluoroethylene Carbonate Additives to Render Uniform Li Deposits in Lithium Metal Batteries. Adv. Funct. Mater. 2017, 27, 1605989. [Google Scholar] [CrossRef]
- Liu, F.; Xiao, Q.; Wu, H.B.; Shen, L.; Xu, D.; Cai, M.; Lu, Y. Fabrication of Hybrid Silicate Coatings by a Simple Vapor Deposition Method for Lithium Metal Anodes. Adv. Energy Mater. 2018, 8, 1701744. [Google Scholar] [CrossRef]
- Cao, X.; Ren, X.; Zou, L.; Engelhard, M.H.; Huang, W.; Wang, H.; Matthews, B.E.; Lee, H.; Niu, C.; Arey, B.W.; et al. Monolithic solid–electrolyte interphases formed in fluorinated orthoformate-based electrolytes minimize Li depletion and pulverization. Nat. Energy 2019, 4, 796–805. [Google Scholar] [CrossRef]




| Parameter | Symbol | Value | References |
|---|---|---|---|
| Anisotropic modulus | 4 | [22] | |
| Diffusion coefficient in solution | 0.2 × 10−14 | [33] | |
| Diffusion Coefficient in Electrodes | 1 × 10−14 | [33] | |
| Symmetric factor | 0.5 | [22] | |
| Reaction constant | 1 | [22] | |
| Gradient energy coefficient | 5 × 10−10 | [22,33] | |
| Interfacial mobility | 2.5 × 10−6 | [22] | |
| Faraday constant | 9.65 × 104 | [30,34] | |
| Barrier height | 3.5 × 105 | [22] | |
| Gas constant | 8.314 | [30] | |
| Conductivity in electrode | 1 × 107 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Yuan, X.; He, C.; Gou, Q.; Yang, N.; Xie, G.; Zhang, K.; Yao, Y.; Hou, Y. Mechanistic Exploration of Dendrite Growth and Inhibition for Lithium Metal Batteries. Energies 2023, 16, 3745. https://doi.org/10.3390/en16093745
Chen Y, Yuan X, He C, Gou Q, Yang N, Xie G, Zhang K, Yao Y, Hou Y. Mechanistic Exploration of Dendrite Growth and Inhibition for Lithium Metal Batteries. Energies. 2023; 16(9):3745. https://doi.org/10.3390/en16093745
Chicago/Turabian StyleChen, Yuanliang, Xingping Yuan, Cuiping He, Qingyi Gou, Ni Yang, Gang Xie, Keyu Zhang, Yaochun Yao, and Yanqing Hou. 2023. "Mechanistic Exploration of Dendrite Growth and Inhibition for Lithium Metal Batteries" Energies 16, no. 9: 3745. https://doi.org/10.3390/en16093745
APA StyleChen, Y., Yuan, X., He, C., Gou, Q., Yang, N., Xie, G., Zhang, K., Yao, Y., & Hou, Y. (2023). Mechanistic Exploration of Dendrite Growth and Inhibition for Lithium Metal Batteries. Energies, 16(9), 3745. https://doi.org/10.3390/en16093745





