Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch
Abstract
1. Introduction
1.1. Literature Review
1.2. Contributions of This Work
- A novel reinforcement-learning-based multi-objective differential evolution (RLMODE) algorithm is developed.
- The RLMODE algorithm uses RL to automatically adjust the control parameters, which enhances the search ability and stability.
- The RLMODE algorithm was utilized to solve four CHPEED problems including two large-scale CHPEED problems with more than 100 generating units.
- The superiority of the RLMODE algorithm was verified by comparing with well-established multi-objective optimization algorithms.
2. Mathematical Formulation of CHPEED Problem
2.1. Objective Function
2.1.1. Fuel Cost
2.1.2. Gas Emissions
2.2. Constraints
2.2.1. Power Balance Constraint
2.2.2. Heat Balance Constraint
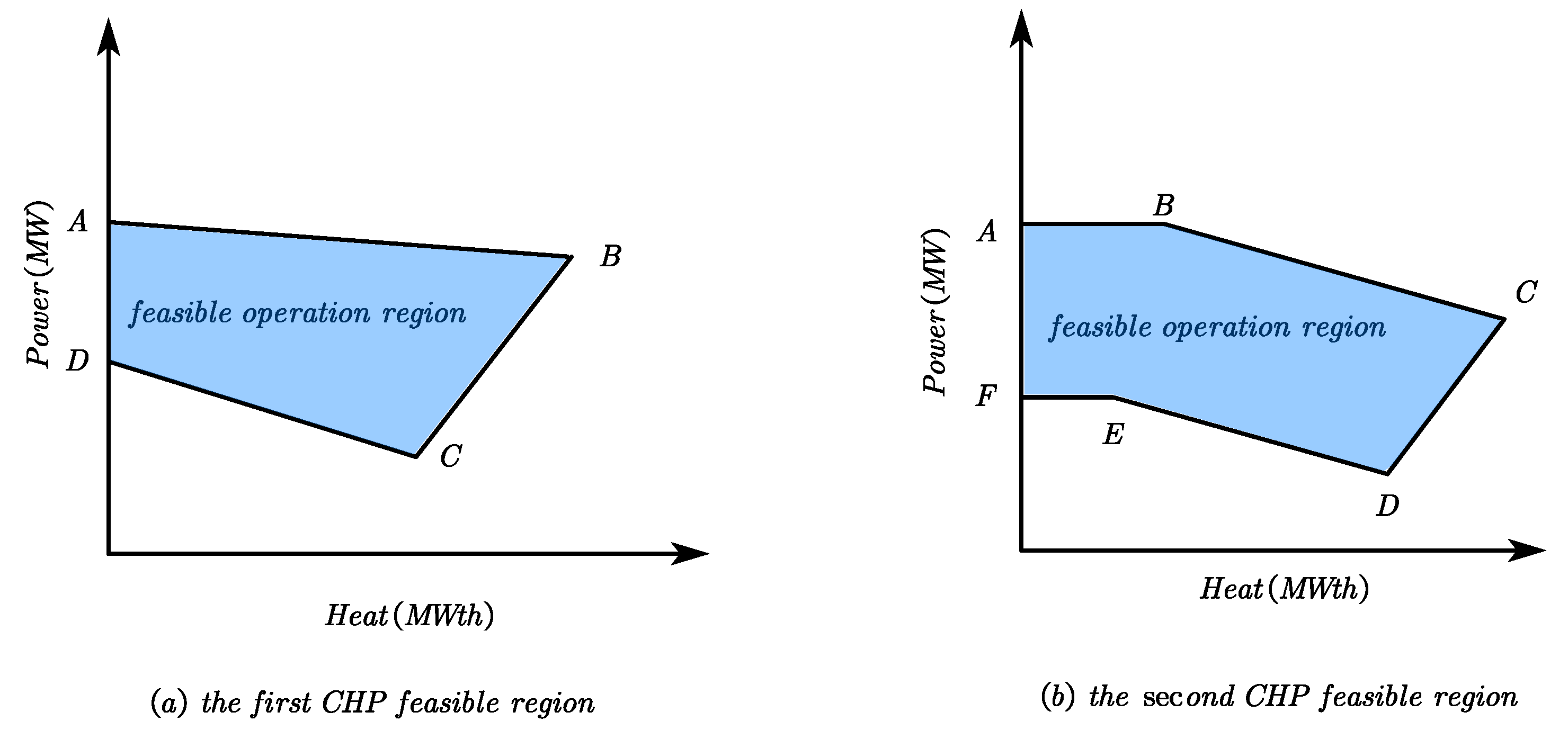
2.2.3. Capacity Constraint of the PO Units
2.2.4. Capacity Constraint of the CHP Units
2.2.5. Capacity Constraint of the HO Units
3. Proposed RLMODE Algorithm
3.1. MODE Algorithm
3.1.1. Initialization
3.1.2. Mutation
3.1.3. Crossover
3.1.4. Selection
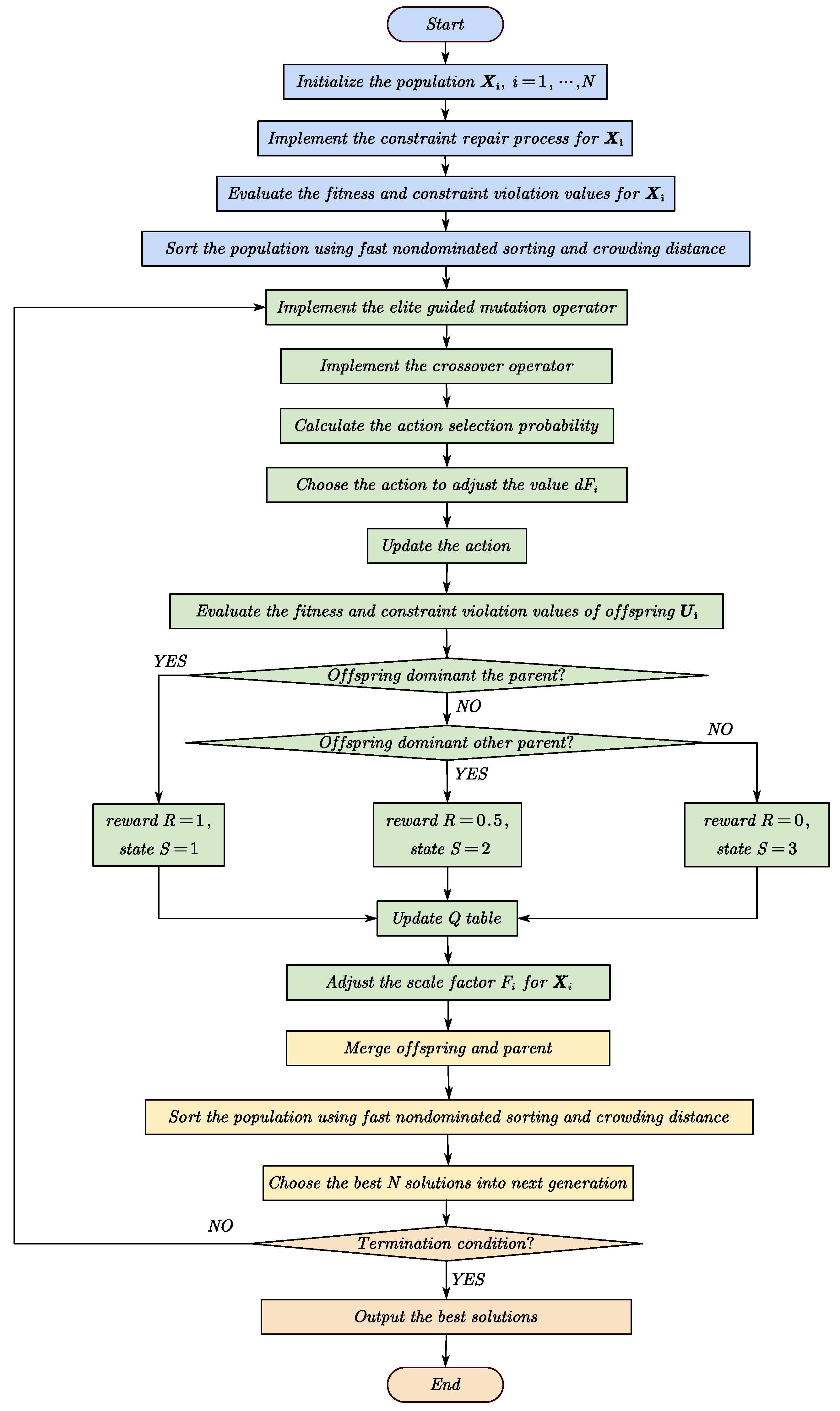
3.2. RLMODE Algorithm
3.2.1. Reinforcement Learning Technique
| Algorithm 1 Pseudocode for Q-learning. |
|
3.2.2. Q-Learning Parameter Adjustment
- State : the offspring solution dominates its own parent solution, indicating that the mutation operator achieves success, and a positive reward value is assigned ;
- State : the offspring solution does not dominate its own parent solution, but dominates one of the other parent solutions, indicating that the mutation operator is relatively successful, and a middle reward value is assigned ;
- State : the offspring solution does not dominate its own parent solution or the other parent solutions, which indicates that the mutation operator fails, and no reward value is assigned .
3.2.3. Elite-Guided Mutation
3.2.4. Pseudocode of RLMODE Algorithm
| Algorithm 2 Pseudocode of the RLMODE algorithm. |
|
4. Implementation of RLMODE for Solving CHPEED
5. Simulation Results
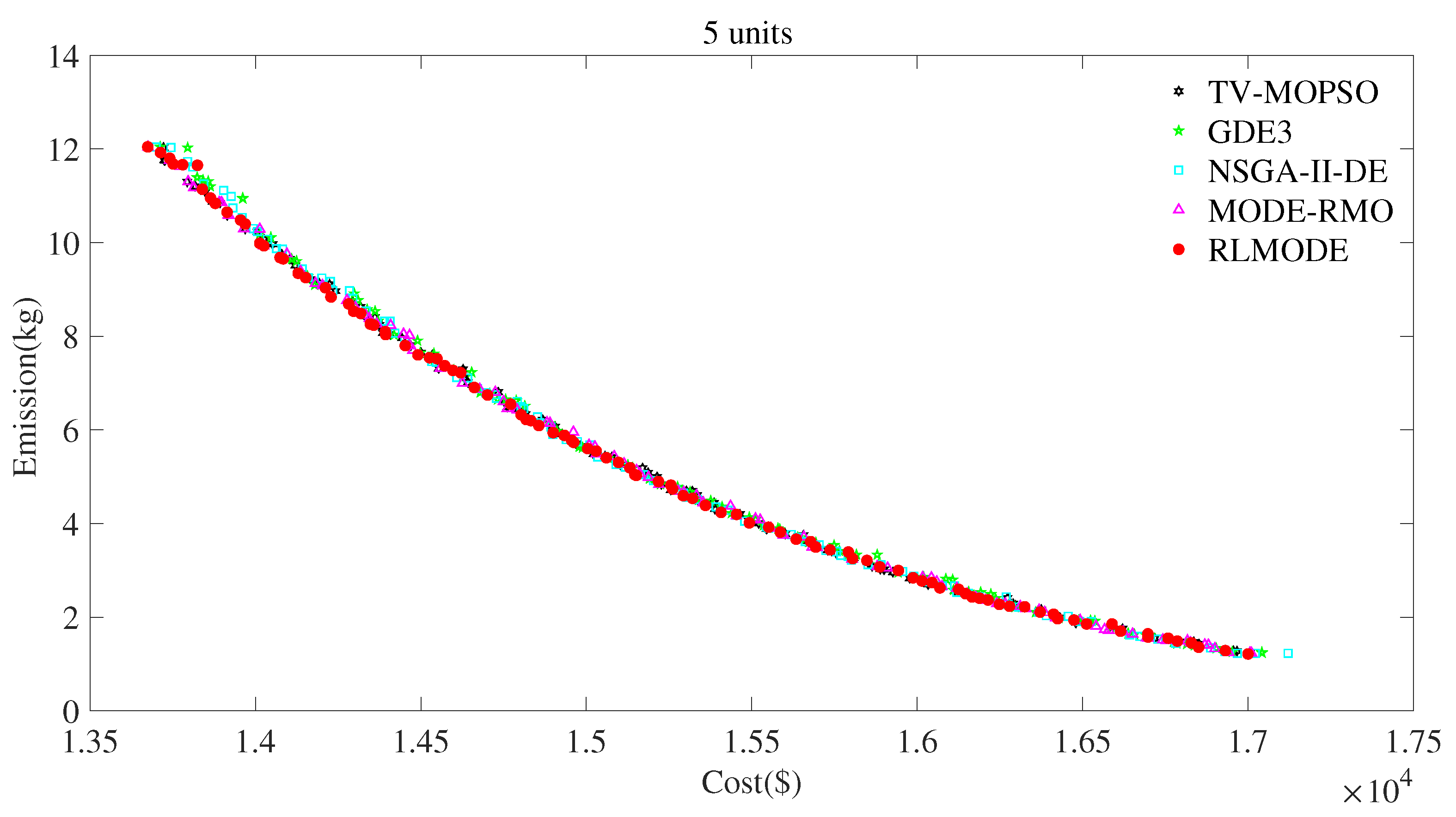
5.1. Case 1: Five-Unit CHPEED Problem
- In the case of EcD, the costs of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were USD 13,686.49, 13,712.33, 13,700.49, 13,675.28, and 13,674.70, respectively. Therefore, RLMDOE achieved the smallest cost among the five algorithms.
- In case of EmD, the emissions of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were 1.21 kg, 1.24 kg, 1.23 kg, 1.23 kg, and 1.21 kg, respectively. Therefore, RLMDOE and TV-MOPSO achieved the smallest emission.
- In the case of EED, the results of the best compromise solutions of the five algorithms were given. The cost and emission of RLMDOE were USD 14,856.36 and 6.09 kg, which were smaller than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. Therefore, RLMODE achieved the best compromise solution. Due to the complexity of the RLMODE algorithm, its simulation time and computational memory were not dominant.
- Concerning DM, the minimum, mean, and maximum values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- Regarding HV, the minimum, mean, and maximum values of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The standard deviation of RLMODE was the second-best after TV-MOPSO.
- Considering IGD, the mean and maximum values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The minimum IGD of RLMODE was the second-best after TV-MOPSO.
- Based on the Wilcoxon test, RLMODE was notably better than GDE3, NSGA-II-DE, and MODE-RMO in terms of DM, HV, and IGD. RLMODE was notably better than TV-MOPSO in terms of HV and similar to TV-MOPSO in terms of DM and IGD.
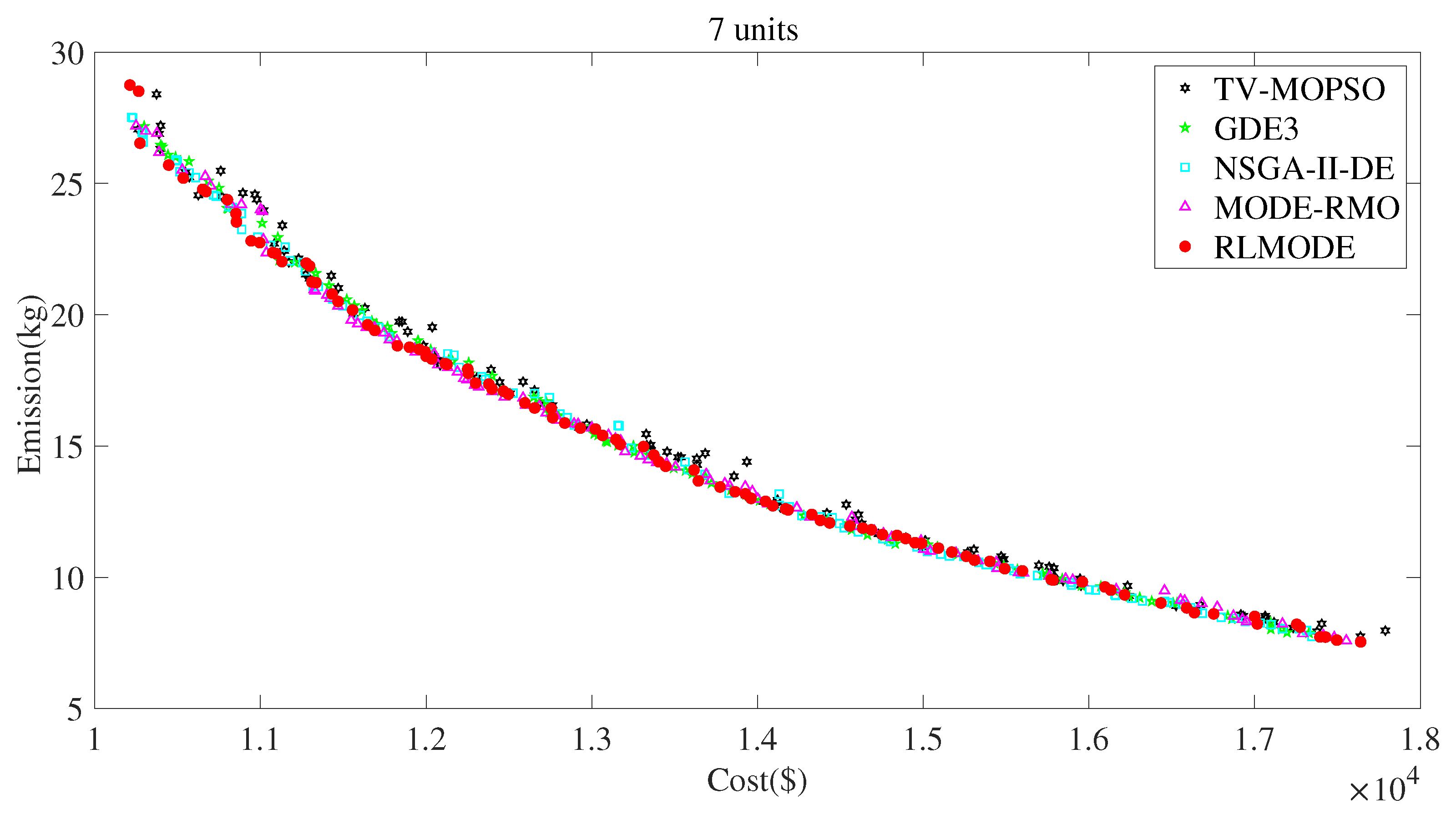
5.2. Case 2: Seven-Unit CHPEED Problem
- In the case of EcD, the costs of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were USD 10,261.88, 10,298.40, 10,222.16, 10,249.37, and 10,212.26. Therefore, RLMDOE achieved the smallest cost among the five algorithms.
- In the case of EmD, the emissions of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were 7.75 kg, 7.88 kg, 7.74 kg, 7.59 kg, and 7.54 kg, respectively. Therefore, RLMDOE achieved the smallest emission among the five algorithms.
- In the case of EED, the cost and emission of RLMDOE were USD 12,000.28 and 18.42 kg, which were smaller than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. Therefore, RLMODE achieved the best compromise solution.
- Concerning DM, the minimum, mean, and maximum values of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- Regarding HV, the minimum, mean, and maximum values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- Considering IGD, the minimum and mean values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The maximum IGD of RLMODE was the second-best after NSGA-II-DE.
- Based on the Wilcoxon test, RLMODE was notably better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO in terms of DM, HV, and IGD.
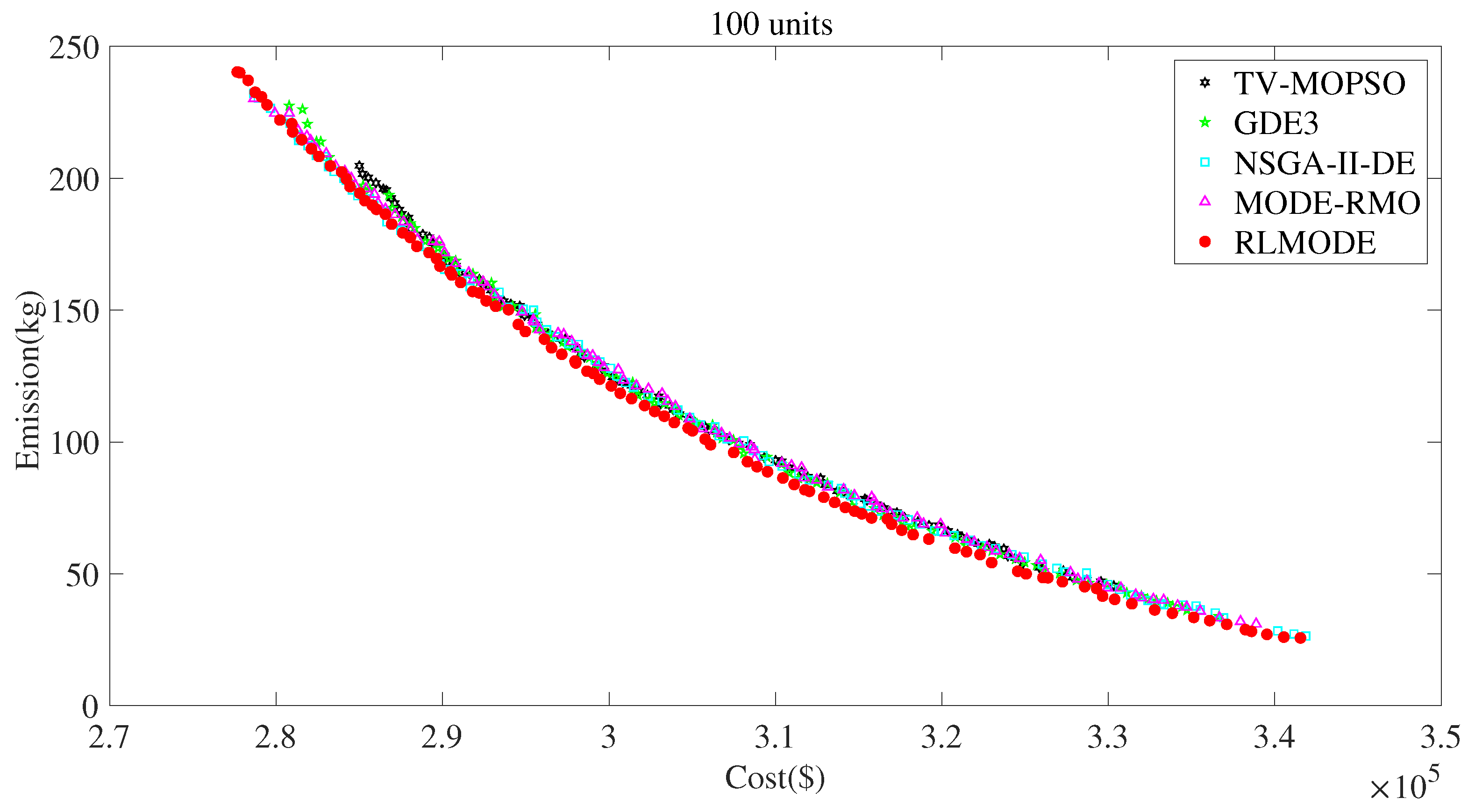
5.3. Case 3: 100-Unit CHPEED Problem
- In the case of EcD, the costs of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were USD 284,998.66, 280,781.47, 278,648.30, 278,670.12, and 278,102.84, respectively. Therefore, RLMDOE achieved the smallest cost.
- In the case of EmD, the emissions of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were 45.49 kg, 33.93 kg, 26.39 kg, 30.99 kg, and 25.56 kg, respectively. Therefore, RLMDOE achieved the smallest emission.
- In the case of EED, the cost and emission of RLMDOE were USD 292,647.89 and 153.57 kg, which were smaller than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. Therefore, RLMODE achieved the best compromise solution.
- Concerning DM, the minimum and mean values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The maximum DM of RLMODE was the second-best after NSGA-II-DE.
- Regarding HV, the minimum, mean, and maximum values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- Considering IGD, the minimum, mean, and maximum values and standard deviation of RLMODE were better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- Based on the Wilcoxon test, RLMODE was notably better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO in terms of DM, HV, and IGD.
5.4. Case 4: 140-Unit CHPEED Problem
- In the case of EcD, the costs of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were USD 237,703.69, 224,936.75, 239,690.11, 225,670.28, and 216,483.24, respectively. Therefore, RLMDOE achieved the smallest cost.
- In the case of EmD, the emissions of TV-MOPSO, GDE3, NSGA-II-DE, MODE-RMO, and RLMDOE were 194.38 kg, 201.67 kg, 180.39 kg, 191.32 kg, and 172.18 kg, respectively. Therefore, RLMDOE achieved the smallest emission.
- In the case of EED, the cost and emission of RLMDOE were USD 239,690.11 and 391.68kg, which were smaller than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. Therefore, RLMODE achieved the best compromise solution.
- Concerning DM, the minimum, mean, and maximum values of RLMODE were better than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The standard deviation of RLMODE was the second-best after NSGA-II-DE.
- Regarding HV, the minimum, mean, and maximum values and standard deviation of RLMODE were better than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The standard deviation of RLMODE was the second-best after NSGA-II-DE.
- Considering IGD, the minimum and mean values of RLMODE were better than those of TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO. The maximum IGD and standard deviation of RLMODE were the second-best after NSGA-II-DE.
- Based on the Wilcoxon test, RLMODE was notably better than TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO in terms of DM, HV, and IGD.
6. Conclusions
- For two small-scale CHPEED problems with 5 and 7 units, the proposed RLMODE achieved better results in the case of economic dispatch (EcD), emission dispatch (EmD), and economic emission dispatch (EED). The costs and emissions of RLMODE were less than the four compared algorithms, TV-MOPSO, GDE3, NSGA-II-DE, and MODE-RMO.
- For two large-scale CHPEED problems with 100 and 140 units, the proposed RLMODE also achieved the best results in the case of EcD, EmD, and EED. The costs and emissions of RLMODE were the smallest among the compared algorithms.
- Considering the performance metrics of the Pareto-optimal Front (i.e., DM, HV, and IGD), the suggested RLMODE obtained better results than the compared algorithms, and the Wilcoxon rank sum test indicated that the superiority was significant.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, W.; Peng, Z.; Yang, Z.; Guo, Y.; Chen, X. An enhanced exploratory whale optimization algorithm for dynamic economic dispatch. J. Abbr. 2021, 7, 7015–7029. [Google Scholar] [CrossRef]
- Nazari-Heris, M.; Mohammadi, I.B.; Asadi, S.; Geem, Z. Large-scale combined heat and power economic dispatch using a novel multi-player harmony search method. Appl. Therm. Eng. 2019, 154, 493–504. [Google Scholar] [CrossRef]
- Chen, X.; Shen, A. Self-adaptive differential evolution with Gaussian–Cauchy mutation for large-scale CHP economic dispatch problem. Neural Comput. Appl. 2022, 34, 11769–11787. [Google Scholar] [CrossRef]
- Rooijers, F.J.; van Amerongen, A.R.A. Static economic dispatch for co-generation systems. IEEE Trans. Power Syst. 1994, 9, 1392–1398. [Google Scholar] [CrossRef]
- Wong, K.P.; Algie, C. Evolutionary programming approach for combined heat and power dispatch. IEEE Trans. Power Syst. 2002, 61, 227–232. [Google Scholar] [CrossRef]
- Rong, A.; Lahdelma, R. An efficient envelope-based Branch and Bound algorithm for non-convex combined heat and power production planning. Eur. J. Oper. Res. 2007, 183, 412–431. [Google Scholar] [CrossRef]
- Zou, D.; Li, S.; Kong, X.; Ouyang, H.; Li, Z. Solving the combined heat and power economic dispatch problems by an improved genetic algorithm and a new constraint handling strategy. Appl. Energy 2019, 237, 646–670. [Google Scholar] [CrossRef]
- Srivastava, A.; Das, D.K. A new Kho-Kho optimization Algorithm: An application to solve combined emission economic dispatch and combined heat and power economic dispatch problem. Eng. Appl. Artif. Intell. 2020, 94, 103763. [Google Scholar] [CrossRef]
- Liu, D.; Hu, Z.; Su, Q.; Liu, M. A niching differential evolution algorithm for the large-scale combined heat and power economic dispatch problem. Appl. Soft Comput. 2021, 113, 108017. [Google Scholar] [CrossRef]
- Zou, D.; Gong, D. Differential evolution based on migrating variables for the combined heat and power dynamic economic dispatch. Energy 2022, 238, 121664. [Google Scholar] [CrossRef]
- Chen, X.; Li, K. Collective information-based particle swarm optimization for multi-fuel CHP economic dispatch problem. Knowl.-Based Syst. 2022, 248, 108902. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Elattar, E.; Ginidi, A.R. An Amalgamated Heap and Jellyfish Optimizer for economic dispatch in Combined heat and power systems including N-1 Unit outages. Energy 2022, 246, 123351. [Google Scholar] [CrossRef]
- Rizk-Allah, R.M.; Hassanien, A.E.; Snášel, V. A hybrid chameleon swarm algorithm with superiority of feasible solutions for optimal combined heat and power economic dispatch problem. Energy 2022, 254, 124340. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Nazari-Heris, M.; Parvathysankar, D.S.; Sundaram, A.; Gnanakkan, C.A.R.C. A hybrid grasshopper optimization algorithm and Harris hawks optimizer for combined heat and power economic dispatch problem. Eng. Appl. Artif. Intell. 2022, 111, 104753. [Google Scholar] [CrossRef]
- Ramachandran, M.; Mirjalili, S.; Ramalingam, M.M.; Gnanakkan, C.A.R.C.; Parvathysankar, D.S.; Sundaram, A. A ranking-based fuzzy adaptive hybrid crow search algorithm for combined heat and power economic dispatch. Expert Syst. Appl. 2022, 197, 116625. [Google Scholar] [CrossRef]
- Yang, Q.; Liu, P.; Zhang, J.; Dong, N. Combined heat and power economic dispatch using an adaptive cuckoo search with differential evolution mutation. Appl. Energy 2022, 307, 118057. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Zhao, D.; Li, G.; Chen, C. A two-stage approach for combined heat and power economic emission dispatch: Combining multi-objective optimization with integrated decision making. Energy 2018, 162, 237–254. [Google Scholar] [CrossRef]
- Elaiw, A.; Xia, X.; Shehata, A. Combined heat and power dynamic economic dispatch with emission limitations using hybrid DE-SQP method. Abstr. Appl. Anal. Hindawi 2013, 2013, 1–10. [Google Scholar] [CrossRef]
- Ahmadi, A.; Moghimi, H.; Nezhad, A.E.; Agelidis, V.G.; Sharaf, A.M. Multi-objective economic emission dispatch considering combined heat and power by normal boundary intersection method. Electr. Power Syst. Res. 2015, 129, 32–43. [Google Scholar] [CrossRef]
- Anand, H.; Narang, N. Civilized swarm optimization for combined heat and power economic emission dispatch. In Proceedings of the 2016 7th India International Conference on Power Electronics (IICPE), Patiala, India, 17–19 November 2016; pp. 1–6. [Google Scholar]
- Sadeghian, H.; Ardehali, M. A novel approach for optimal economic dispatch scheduling of integrated combined heat and power systems for maximum economic profit and minimum environmental emissions based on Benders decomposition. Energy 2016, 102, 10–23. [Google Scholar] [CrossRef]
- Alomoush, M.I. Application of the stochastic fractal search algorithm and compromise programming to combined heat and power economic–emission dispatch. Eng. Optim. 2020, 52, 1992–2010. [Google Scholar] [CrossRef]
- Jadoun, V.K.; Prashanth, G.R.; Joshi, S.S.; Narayanan, K.; Malik, H.; Márquez, F.P.G.A. Optimal fuzzy based economic emission dispatch of combined heat and power units using dynamically controlled Whale Optimization Algorithm. Appl. Energy 2022, 315, 119033. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Roosta, A.; Amiri, B. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch. Energy 2012, 42, 530–545. [Google Scholar] [CrossRef]
- Basu, M. Combined heat and power economic emission dispatch using nondominated sorting genetic algorithm-II. Int. J. Electr. Power Energy Syst. 2013, 53, 135–141. [Google Scholar] [CrossRef]
- Shi, B.; Yan, L.; Wu, W. Multi-objective optimization for combined heat and power economic dispatch with power transmission loss and emission reduction. Energy 2013, 56, 135–143. [Google Scholar] [CrossRef]
- ali Shaabani, Y.; Seifi, A.R.; Kouhanjani, M.J. Stochastic multi-objective optimization of combined heat and power economic/emission dispatch. Energy 2017, 141, 1892–1904. [Google Scholar] [CrossRef]
- Sun, J.; Deng, J.; Li, Y. Indicator & crowding distance-based evolutionary algorithm for combined heat and power economic emission dispatch. Appl. Soft Comput. 2020, 90, 106158. [Google Scholar]
- Sundaram, A. Combined heat and power economic emission dispatch using hybrid NSGA II-MOPSO algorithm incorporating an effective constraint handling mechanism. IEEE Access 2020, 8, 13748–13768. [Google Scholar] [CrossRef]
- Sundaram, A. Multiobjective multi-verse optimization algorithm to solve combined economic, heat and power emission dispatch problems. Appl. Soft Comput. 2020, 91, 106195. [Google Scholar] [CrossRef]
- Xiong, G.; Shuai, M.; Hu, X. Combined heat and power economic emission dispatch using improved bare-bone multi-objective particle swarm optimization. Energy 2022, 244, 123108. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Wang, X.; Dong, Z.; Tang, L. Multiobjective differential evolution with personal archive and biased self-adaptive mutation selection. IEEE Trans. Syst. Man, Cybern. Syst. 2018, 50, 5338–5350. [Google Scholar] [CrossRef]
- Basu, M. Economic environmental dispatch using multi-objective differential evolution. Appl. Soft Comput. 2011, 11, 2845–2853. [Google Scholar] [CrossRef]
- Qiao, B.; Liu, J.; Hao, X. A multi-objective differential evolution algorithm and a constraint handling mechanism based on variables proportion for dynamic economic emission dispatch problems. Appl. Soft Comput. 2021, 108, 107419. [Google Scholar] [CrossRef]
- Hu, Z.; Gong, W.; Li, S. Reinforcement learning-based differential evolution for parameters extraction of photovoltaic models. Energy Rep. 2021, 7, 916–928. [Google Scholar] [CrossRef]
- Chen, X.; Tang, G. Solving static and dynamic multi-area economic dispatch problems using an improved competitive swarm optimization algorithm. Energy 2022, 238, 122035. [Google Scholar] [CrossRef]
- Watkins, C.J.; Dayan, P. Q-learning. Mach. Learn. 1992, 8, 279–292. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Marek, M.; Kadlec, P. Another evolution of generalized differential evolution: Variable number of dimensions. Eng. Optim. 2022, 7, 61–80. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Q. Multiobjective optimization problems with complicated Pareto sets, MOEA/D and NSGA-II. IEEE Trans. Evol. Comput. 2008, 13, 284–302. [Google Scholar] [CrossRef]
- Chen, X.; Du, W.; Qian, F. Multi-objective differential evolution with ranking-based mutation operator and its application in chemical process optimization. Chemom. Intell. Lab. Syst. 2014, 136, 85–96. [Google Scholar] [CrossRef]
- Deb, K.; Jain, S. Running performance metrics for evolutionary multi-objective optimization. In Proceedings of the Fourth Asia-Pacific Conference on Simulated Evolution and Learning (SEAL02), Singapore, 18–22 November 2002; pp. 13–20. [Google Scholar]
- Zitzler, E.; Thiele, L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 1999, 3, 257–271. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Cortés, N.C. Solving multiobjective optimization problems using an artificial immune system. Genet. Program. Evolvable Mach. 2005, 6, 163–190. [Google Scholar] [CrossRef]






| Algorithm | Parameters |
|---|---|
| TV-MOPSO [27] | Population size N = 100, weight coefficient , |
| acceleration coefficient | |
| GDE3 [40] | N = 100, scale factor , crossover rate |
| NSGA-II-DE [41] | , polynomial mutation rate , , |
| MODE-RMO [42] | , , |
| RLMODE |
| Output | TV-MOPSO | GDE3 | NSGA-II-DE | MODE-RMO | RLMODE | |
|---|---|---|---|---|---|---|
| (MW) | 135 | 135 | 135 | 135 | 135 | |
| (MW) | 44.92 | 48.15 | 51.53 | 40.48 | 41.58 | |
| (MW) | 16.52 | 16.30 | 10.30 | 19.52 | 18.43 | |
| (MW) | 103.56 | 100.55 | 103.17 | 105 | 105 | |
| EcD | (MWth) | 68.72 | 69.87 | 74.44 | 75.41 | 76.36 |
| (MWth) | 42.79 | 41.03 | 39.29 | 41.63 | 40.08 | |
| (MWth) | 2.39 | 6.71 | 2.73 | 0 | 0 | |
| (MWth) | 36.10 | 32.39 | 33.54 | 32.96 | 33.56 | |
| Cost (USD) | 13,686.49 | 13,712.33 | 13,700.49 | 13,675.28 | 13,674.70 | |
| Emission (kg) | 12.05 | 12.04 | 12.04 | 12.04 | 12.04 | |
| (MW) | 35 | 35 | 35 | 35 | 35 | |
| (MW) | 116.87 | 118.76 | 115.75 | 118.71 | 114.19 | |
| (MW) | 48.57 | 48.51 | 55.14 | 45.47 | 46.57 | |
| (MW) | 99.56 | 97.73 | 94.11 | 100.83 | 104.24 | |
| EmD | (MWth) | 91.45 | 78.98 | 98.89 | 79.33 | 102.35 |
| (MWth) | 41.92 | 40.98 | 12.57 | 36.08 | 28.83 | |
| (MWth) | 4.22 | 0 | 17.44 | 6.95 | 0 | |
| (MWth) | 12.41 | 30.05 | 21.11 | 27.63 | 18.82 | |
| Cost (USD) | 12.41 | 30.05 | 21.11 | 27.63 | 18.82 | |
| Emission (kg) | 1.21 | 1.24 | 1.23 | 1.23 | 1.21 | |
| (MW) | 94.19 | 94.38 | 95.04 | 94.84 | 94.36 | |
| (MW) | 73.89 | 67.14 | 70.56 | 62.71 | 72.60 | |
| (MW) | 26.92 | 34.55 | 30.82 | 41.62 | 28.78 | |
| (MW) | 105 | 103.93 | 103.58 | 100.83 | 104.26 | |
| EED | (MWth) | 72.64 | 92.75 | 75 | 79.76 | 71.84 |
| (MWth) | 25.71 | 0 | 48.92 | 35.25 | 39.95 | |
| (MWth) | 0 | 0 | 1.20 | 0 | 0 | |
| (MWth) | 51.66 | 57.25 | 24.88 | 34.99 | 38.21 | |
| Cost (USD) | 14,860.23 | 14,889.75 | 14,859.34 | 14,881.14 | 14,856.36 | |
| Emission (kg) | 6.09 | 6.13 | 6.15 | 6.15 | 6.09 | |
| CPU time (s) | 3.0 | 2.3 | 2.4 | 2.2 | 2.5 |
| Metric | Algorithm | Min | Mean | Max | Std | Sig. |
|---|---|---|---|---|---|---|
| DM | TV-MOPSO | 0.7424 | 0.8003 | 0.8457 | 0.0260 | = |
| GDE3 | 0.7183 | 0.7594 | 0.8050 | 0.0273 | + | |
| NSGA-II-DE | 0.6759 | 0.7731 | 0.8096 | 0.0283 | + | |
| MODE-RMO | 0.7060 | 0.7711 | 0.8181 | 0.0224 | + | |
| RLMODE | 0.7863 | 0.8131 | 0.8884 | 0.0229 | ||
| 2HV | TV-MOPSO | 0.1926 | 0.1931 | 0.1934 | 0.0002 | + |
| GDE3 | 0.1914 | 0.1921 | 0.1929 | 0.0004 | + | |
| NSGA-II-DE | 0.1906 | 0.1918 | 0.1926 | 0.0005 | + | |
| MODE-RMO | 0.1914 | 0.1923 | 0.1929 | 0.0004 | + | |
| RLMODE | 0.1927 | 0.1932 | 0.1937 | 0.0003 | ||
| IGD | TV-MOPSO | 9.8452 | 11.6058 | 13.1767 | 0.7173 | = |
| GDE3 | 12.5343 | 14.2121 | 16.4390 | 1.0600 | + | |
| NSGA-II-DE | 11.8049 | 13.8877 | 17.4370 | 1.4504 | + | |
| MODE-RMO | 11.9793 | 13.5678 | 16.6436 | 1.0189 | + | |
| RLMODE | 10.0634 | 11.3487 | 12.6692 | 0.6079 |
| Output | TV-MOPSO | GDE3 | NSGA-II-DE | MODE-RMO | RLMODE | |
|---|---|---|---|---|---|---|
| (MW) | 65.99 | 65.79 | 61.36 | 63.41 | 52.75 | |
| (MW) | 91.23 | 99.49 | 99.91 | 90.82 | 92.99 | |
| (MW) | 109.65 | 100.13 | 102.37 | 109.88 | 112.84 | |
| (MW) | 201.91 | 203.08 | 206.46 | 204.62 | 217.86 | |
| EcD | (MW) | 98.71 | 98.80 | 97.56 | 98.80 | 91.24 |
| (MW) | 40.11 | 40.36 | 40 | 40.07 | 40 | |
| (MWth) | 0.51 | 0 | 7.29 | 0 | 44.54 | |
| (MWth) | 73.41 | 69.63 | 75 | 74.02 | 75 | |
| (MWth) | 76.08 | 80.37 | 67.71 | 75.98 | 30.46 | |
| Cost (USD) | 10,261.88 | 10,298.40 | 10,222.16 | 10,249.37 | 10,212.26 | |
| Emission (kg) | 27.05 | 27.18 | 27.52 | 27.19 | 28.75 | |
| (MW) | 42.55 | 36.59 | 33.85 | 36.48 | 46.41 | |
| (MW) | 31.66 | 38.32 | 53.65 | 44.45 | 52.59 | |
| (MW) | 80.83 | 68.96 | 59.37 | 73.65 | 64.99 | |
| (MW) | 83.10 | 99.71 | 96.54 | 85.49 | 76.57 | |
| EmD | (MW) | 247 | 246.97 | 246.99 | 247 | 245.49 |
| (MW) | 122.60 | 117.15 | 117.36 | 120.68 | 121.79 | |
| (MWth) | 0 | 0 | 0 | 0 | 2.68 | |
| (MWth) | 53.56 | 69.63 | 88.24 | 66.27 | 53.20 | |
| (MWth) | 96.44 | 80.37 | 61.76 | 83.73 | 94.11 | |
| Cost (USD) | 17,638.83 | 17,329.12 | 17,345.52 | 17,553.38 | 17,640.14 | |
| Emission (kg) | 7.75 | 7.88 | 7.74 | 7.59 | 7.54 | |
| (MW) | 61.41 | 73.43 | 75 | 65.39 | 75 | |
| (MW) | 89.41 | 93.62 | 78.87 | 76.39 | 80.07 | |
| (MW) | 102.93 | 114.29 | 99.22 | 121.91 | 105.95 | |
| (MW) | 136.29 | 107.57 | 139.33 | 125.01 | 129.74 | |
| EED | (MW) | 176.91 | 176.97 | 174.48 | 178.74 | 176.19 |
| (MW) | 40.55 | 41.63 | 40.59 | 40 | 40.54 | |
| (MWth) | 0.16 | 0.93 | 24.05 | 0 | 6.87 | |
| (MWth) | 75.47 | 76.41 | 75 | 75 | 75 | |
| (MWth) | 74.36 | 72.66 | 50.95 | 75 | 68.13 | |
| Cost (USD) | 12,047.79 | 12,027.75 | 12,131.14 | 12,049.32 | 12,000.28 | |
| Emission (kg) | 18.42 | 18.67 | 18.52 | 18.51 | 18.42 | |
| CPU time (s) | 5.5 | 4.5 | 4.9 | 4.6 | 5.0 |
| Metric | Algorithm | Min | Mean | Max | Std | Sig. |
|---|---|---|---|---|---|---|
| DM | TV-MOPSO | 0.6859 | 0.7325 | 0.7765 | 0.0225 | + |
| GDE3 | 0.7326 | 0.7657 | 0.8033 | 0.0194 | + | |
| NSGA-II-DE | 0.7032 | 0.7849 | 0.8396 | 0.0339 | + | |
| MODE-RMO | 0.6949 | 0.7624 | 0.8148 | 0.0227 | + | |
| RLMODE | 0.7632 | 0.8048 | 0.8516 | 0.0251 | ||
| HV | TV-MOPSO | 0.2767 | 0.2781 | 0.2796 | 0.0007 | + |
| GDE3 | 0.2785 | 0.2804 | 0.2818 | 0.0009 | + | |
| NSGA-II-DE | 0.2776 | 0.2808 | 0.2827 | 0.0012 | + | |
| MODE-RMO | 0.2779 | 0.2806 | 0.2826 | 0.0010 | + | |
| RLMODE | 0.2805 | 0.2821 | 0.2827 | 0.0005 | ||
| IGD | TV-MOPSO | 31.8580 | 36.3950 | 43.7990 | 2.9514 | + |
| GDE3 | 30.1660 | 37.6670 | 49.0670 | 4.9670 | + | |
| NSGA-II-DE | 25.2580 | 33.6990 | 42.3560 | 4.3386 | + | |
| MODE-RMO | 29.7410 | 36.8890 | 56.5780 | 5.5591 | + | |
| RLMODE | 25.0030 | 29.6970 | 42.9080 | 4.0536 |
| Output | TV-MOPSO | GDE3 | NSGA-II-DE | MODE-RMO | RLMODE | |
|---|---|---|---|---|---|---|
| EcD | Cost (USD) | 284,998.66 | 280,781.47 | 278,648.30 | 278,670.12 | 278,102.84 |
| Emission (kg) | 204.75 | 227.54 | 232.20 | 230.31 | 238.49 | |
| EmD | Cost (USD) | 330,327.51 | 336,643.25 | 341,869.59 | 338,879.12 | 342,104.18 |
| Emission (kg) | 45.49 | 33.93 | 26.39 | 30.99 | 25.56 | |
| EED | Cost (USD) | 292,904.09 | 292,934.82 | 293,398.89 | 293,113.78 | 292,647.89 |
| Emission (kg) | 157.50 | 160.30 | 156.81 | 155.89 | 153.57 | |
| CPU time (s) | 47.4 | 48.0 | 48.0 | 47.9 | 54.9 |
| Metric | Algorithm | Min | Mean | Max | Std | Sig. |
|---|---|---|---|---|---|---|
| DM | TV-MOPSO | 0.6320 | 0.6918 | 0.7543 | 0.0274 | + |
| GDE3 | 0.6956 | 0.7747 | 0.8456 | 0.0371 | + | |
| NSGA-II-DE | 0.7633 | 0.8098 | 0.8764 | 0.0235 | + | |
| MODE-RMO | 0.7633 | 0.8073 | 0.8474 | 0.0206 | + | |
| RLMODE | 0.8168 | 0.8414 | 0.8758 | 0.0144 | ||
| HV | TV-MOPSO | 0.1698 | 0.1733 | 0.1767 | 0.0017 | + |
| GDE3 | 0.1769 | 0.1814 | 0.1836 | 0.0015 | + | |
| NSGA-II-DE | 0.1801 | 0.1836 | 0.1852 | 0.0010 | + | |
| MODE-RMO | 0.1804 | 0.1828 | 0.1845 | 0.0009 | + | |
| RLMODE | 0.1861 | 0.1869 | 0.1879 | 0.0004 | ||
| IGD | TV-MOPSO | 909.1800 | 1234 | 1788.3000 | 206.8600 | + |
| GDE3 | 270.9400 | 487.7000 | 1047.2000 | 166.0400 | + | |
| NSGA-II-DE | 210.3000 | 279.2600 | 442.5800 | 52.9940 | + | |
| MODE-RMO | 252.5700 | 331.1600 | 449.7500 | 55.0550 | + | |
| RLMODE | 169.3400 | 200.3200 | 224.1500 | 11.8440 |
| Output | TV-MOPSO | GDE3 | NSGA-II-DE | MODE-RMO | RLMODE | |
|---|---|---|---|---|---|---|
| EcD | Cost (USD) | 237,703.69 | 224,936.75 | 239,690.11 | 225,670.28 | 216,483.24 |
| Emission (kg) | 466.50 | 526.37 | 391.68 | 554.75 | 544.62 | |
| EmD | Cost (USD) | 330,651.70 | 337,670.10 | 347,284.96 | 340,838.48 | 347,112.22 |
| Emission (kg) | 194.38 | 201.67 | 180.39 | 191.32 | 172.18 | |
| EED | Cost (USD) | 242,778.96 | 243,338.27 | 242,231.62 | 243,210.60 | 239,690.11 |
| Emission (kg) | 423.76 | 428.76 | 418.54 | 425.72 | 391.68 | |
| CPU time (s) | 77.6 | 75.6 | 75.2 | 76.4 | 84.6 |
| Metric | Algorithm | Min | Mean | Max | Std | Sig. |
|---|---|---|---|---|---|---|
| 2DM | TV-MOPSO | 0.6343 | 0.6923 | 0.7416 | 0.0259 | + |
| GDE3 | 0.6008 | 0.6918 | 0.7473 | 0.0343 | + | |
| NSGA-II-DE | 0.7542 | 0.7980 | 0.8465 | 0.0215 | + | |
| MODE-RMO | 0.6396 | 0.7175 | 0.7635 | 0.0360 | + | |
| RLMODE | 0.7660 | 0.8144 | 0.8541 | 0.0228 | ||
| HV | TV-MOPSO | 0.2251 | 0.2278 | 0.2316 | 0.0017 | + |
| GDE3 | 0.2225 | 0.2263 | 0.2297 | 0.0018 | + | |
| NSGA-II-DE | 0.2335 | 0.2361 | 0.2391 | 0.0013 | + | |
| MODE-RMO | 0.2257 | 0.2284 | 0.2318 | 0.0015 | + | |
| RLMODE | 0.2488 | 0.2518 | 0.2553 | 0.0015 | ||
| IGD | TV-MOPSO | 2110.5000 | 3065.3000 | 3751.2000 | 387.1000 | + |
| GDE3 | 795.6700 | 1180.7000 | 1913.3000 | 257.3000 | + | |
| NSGA-II-DE | 445.6000 | 555.7200 | 738.6900 | 62.6100 | + | |
| MODE-RMO | 680.3500 | 1001 | 1611.9000 | 243.1500 | + | |
| RLMODE | 376.3600 | 482.7200 | 783.0600 | 92.9610 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Fang, S.; Li, K. Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch. Energies 2023, 16, 3753. https://doi.org/10.3390/en16093753
Chen X, Fang S, Li K. Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch. Energies. 2023; 16(9):3753. https://doi.org/10.3390/en16093753
Chicago/Turabian StyleChen, Xu, Shuai Fang, and Kangji Li. 2023. "Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch" Energies 16, no. 9: 3753. https://doi.org/10.3390/en16093753
APA StyleChen, X., Fang, S., & Li, K. (2023). Reinforcement-Learning-Based Multi-Objective Differential Evolution Algorithm for Large-Scale Combined Heat and Power Economic Emission Dispatch. Energies, 16(9), 3753. https://doi.org/10.3390/en16093753








