Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications
Abstract
1. Introduction
1.1. Overview
1.2. Motivation
1.3. Related Works on Modeling and Control of Isolated DC–DC Converters
1.4. Contributions
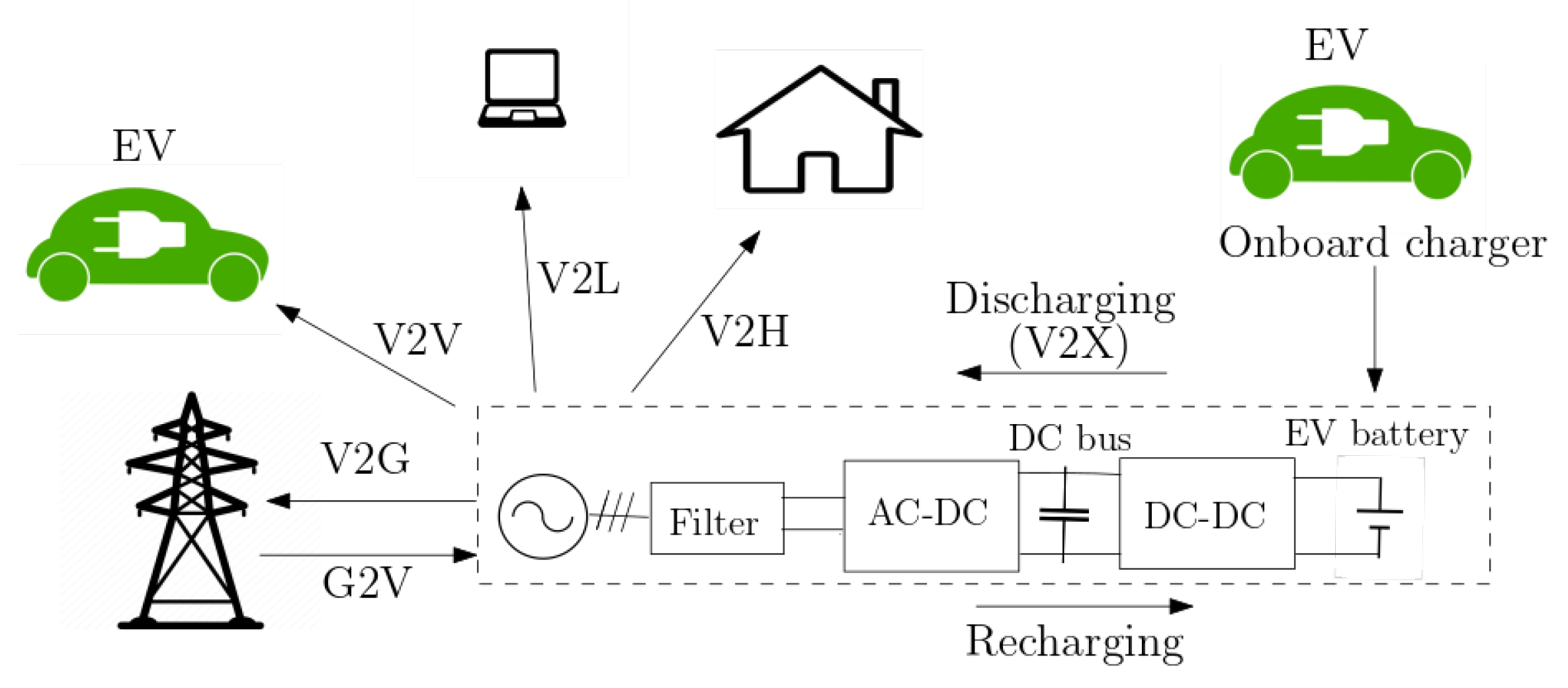
2. Modulation System and Modeling Approaches in V2X Mode
2.1. System Presentation
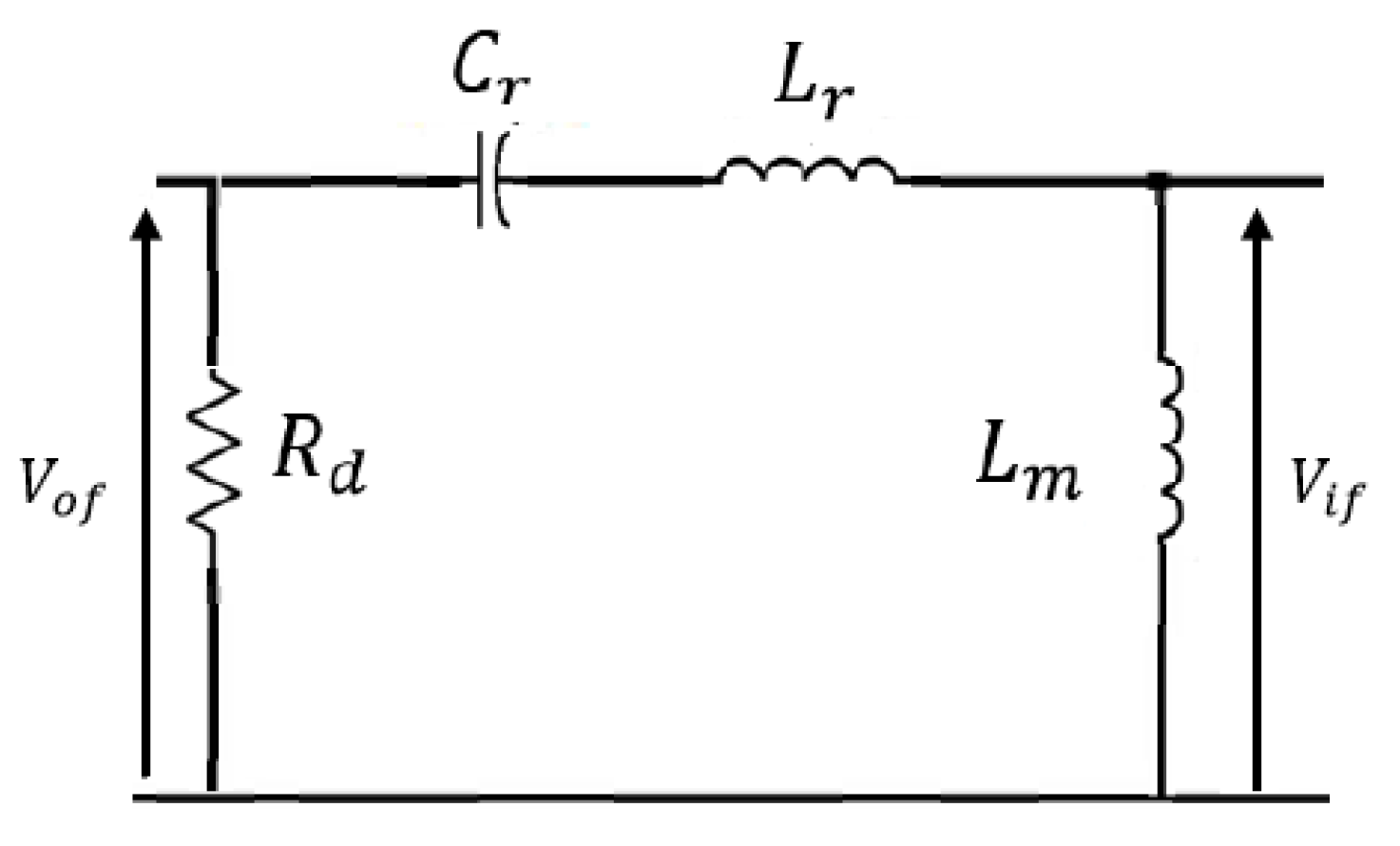
2.2. Modulation System Based Small Signal Modeling
- The input voltage is modeled as an ideal sinusoidal voltage source, in which all higher-order harmonics are ignored and only the fundamental component is reflected;
- The capacitor of the output filter, the leakage inductance of the transformer and the effects of MOSFETs are ignored.
2.2.1. PFM
2.2.2. PWM
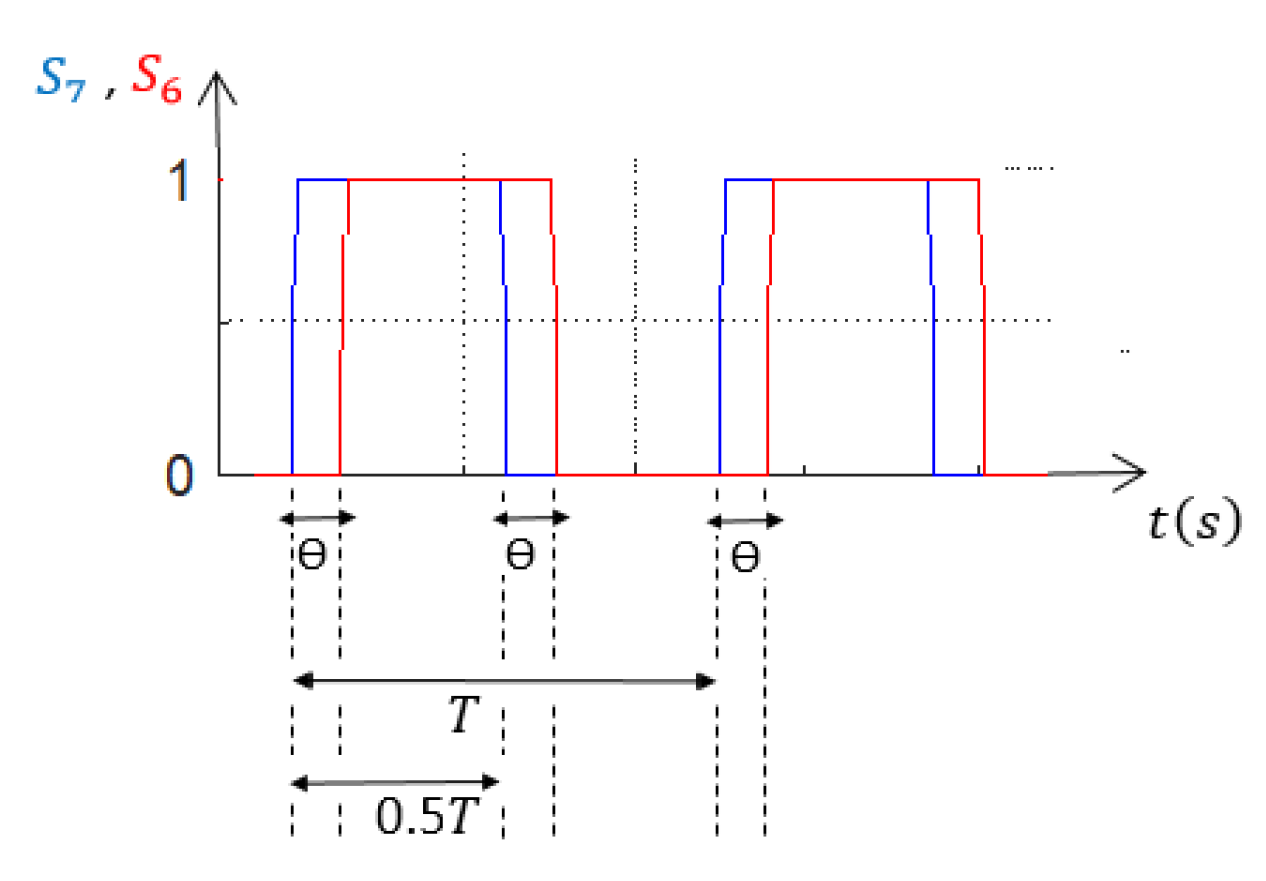
2.2.3. PSM
2.3. Large Signal Modeling
2.3.1. PFM
2.3.2. PSM
3. Control Strategies Based on the LLC Model
3.1. Control Based Small Signal Model
3.1.1. PFM
3.1.2. PWM
3.1.3. PSM
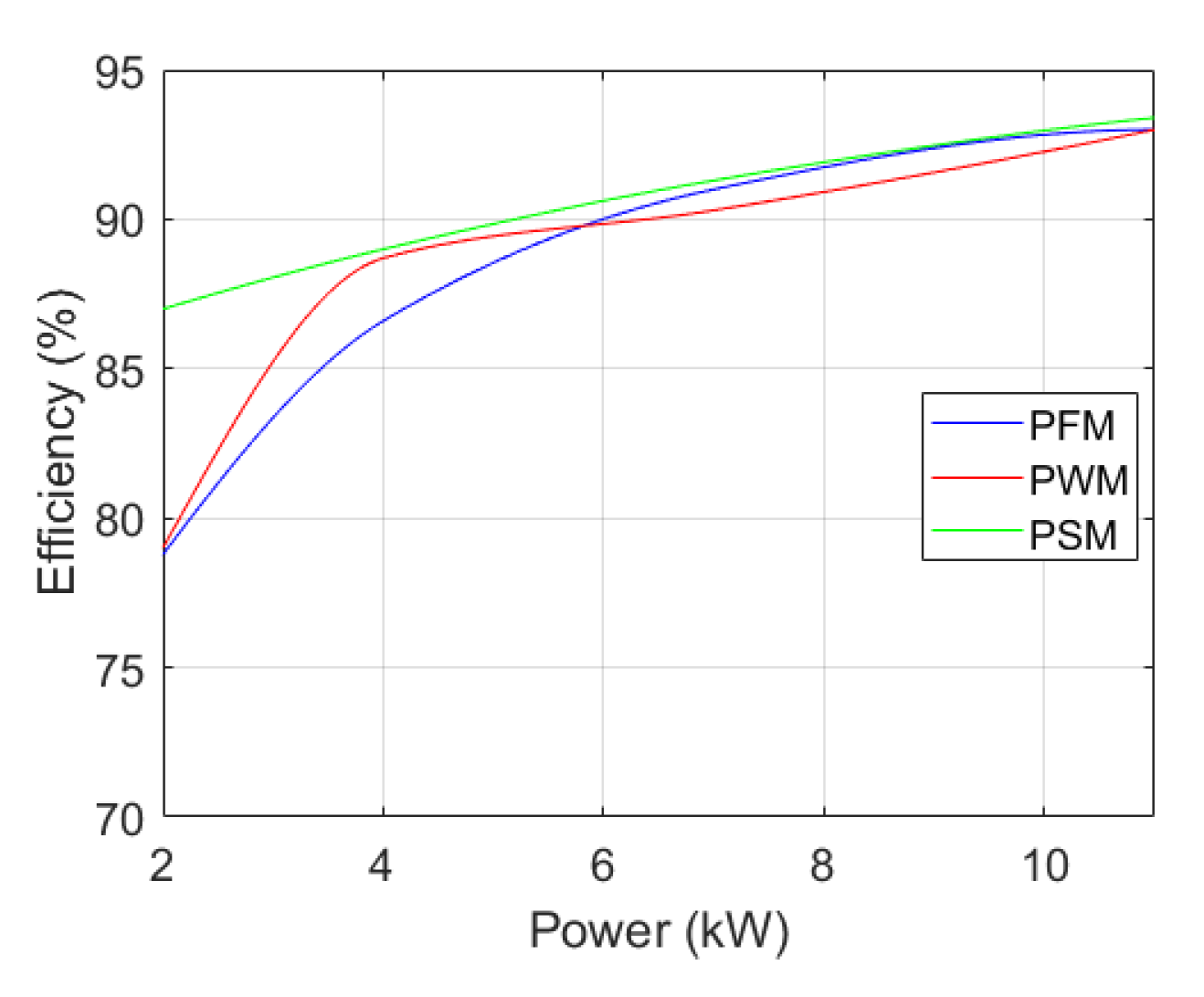
3.1.4. Comparative Study
3.2. Control Based Large Signal Model
3.2.1. Model Predictive Control (MPC)
3.2.2. Model Free Control (MFC)
3.2.3. Adaptive Super Twisting Control (ASTC)
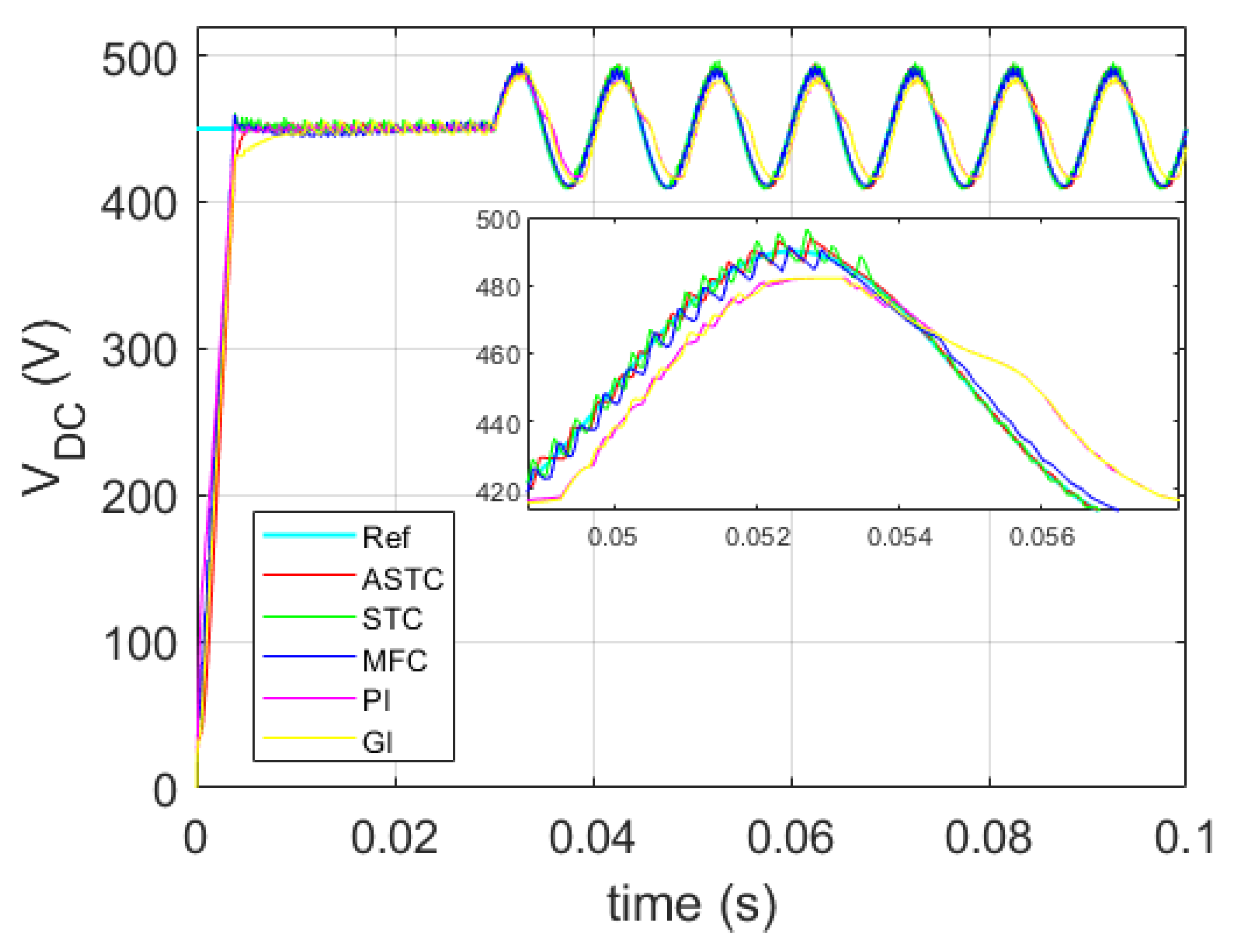
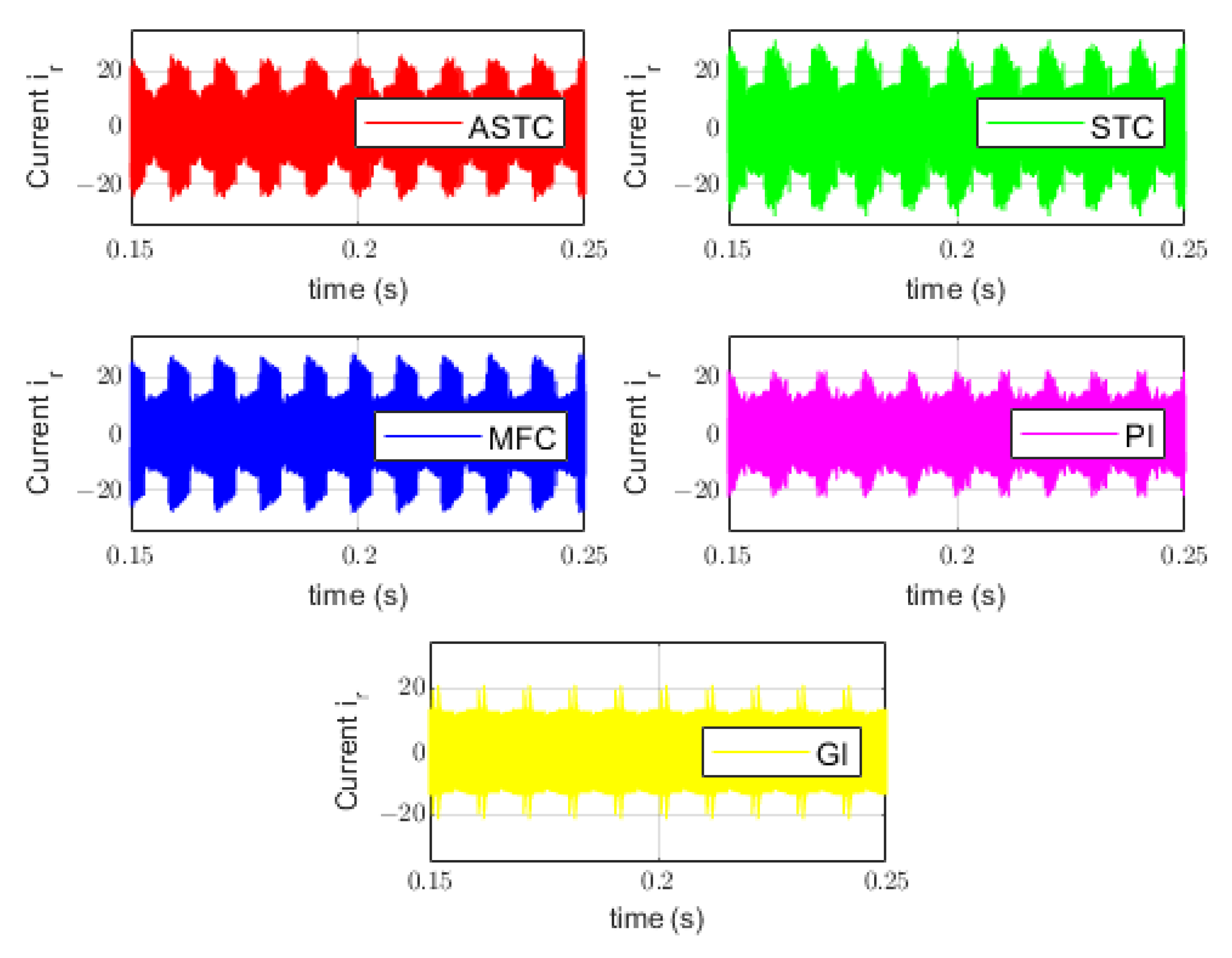
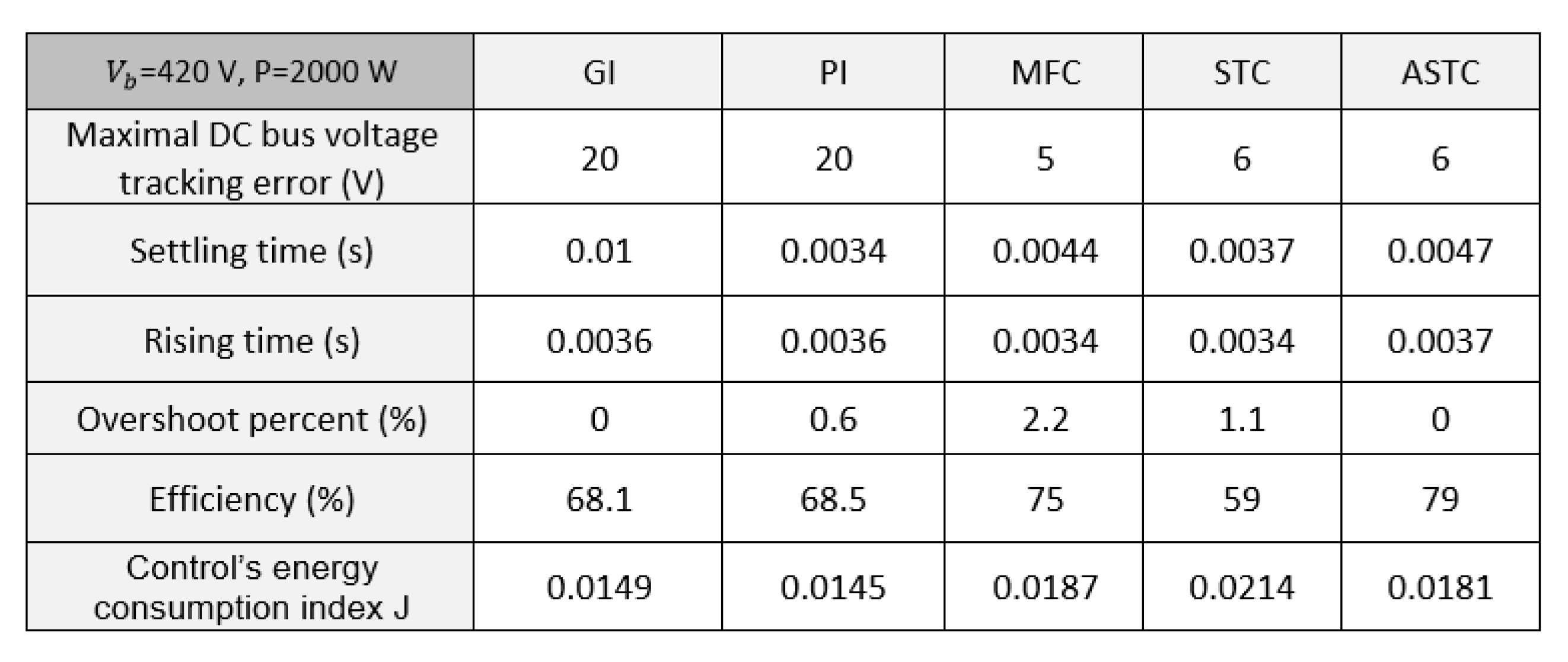
3.2.4. Comparative Study
Comparison with Respect to a DC Bus Current Disturbance
Comparison according to the Trajectory Tracking
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Electric vehicle | |
| Grid to Vehicle | |
| Vehicle to Everything | |
| Series inductor of LLC converter | |
| Series capacitor of LLC converter | |
| Parallel inductor of LLC converter | |
| Zero-Voltage Switching | |
| n | Transformer ratio |
| DC bus voltage | |
| Battery voltage | |
| P | Converter power |
| First Harmonic Approximation | |
| Pulse Frequency Modulation | |
| Pulse Width Modulation | |
| Phase-Shift Modulation | |
| Proportional Integral | |
| Gain Inversion | |
| Model Free Control | |
| Super Twisting Control | |
| Adaptive Super Twisting Control | |
| Feedforward switching frequency in G2V | |
| Feedforward switching frequency in V2X | |
| Minimum authorized switching frequency | |
| Maximum authorized switching frequency |
References
- Garcés Quílez, M.; Abdel-Monem, M.; El Baghdadi, M.; Yang, Y.; Van Mierlo, J.; Hegazy, O. Modelling, Analysis and Performance Evaluation of Power Conversion Unit in G2V/V2G Application—A Review. Energies 2018, 11, 1082. [Google Scholar] [CrossRef]
- Urcan, D.C.; Bica, D. Integrating and modeling the Vehicle to Grid concept in Micro-Grids. In Proceedings of the International Conference on ENERGY and ENVIRONMENT (CIEM), Timisoara, Romania, 17–18 October 2019; pp. 299–303. [Google Scholar]
- Jarraya, F.; Khan, A.; Gastli, A.; Ben-Brahim, L.; Hamila, R. Design considerations, modelling, and control of dual-active full bridge for electric vehicles charging applications. J. Eng. 2019, 2019, 8439–8447. [Google Scholar] [CrossRef]
- Al-Ogaili, A.S.; Aris, I.B.; Verayiah, R.; Ramasamy, A.; Marsadek, M.; Rahmat, N.A.; Hoon, Y.; Aljanad, A.; Al-Masri, A.N. A Three-Level Universal Electric Vehicle Charger Based on Voltage-Oriented Control and Pulse-Width Modulation. Energies 2019, 12, 2375. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Review on Model Based Design of Advanced Control Algorithms for Cogging Torque Reduction in Power Drive Systems. Energies 2022, 15, 8990. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Model-Based Design of an Improved Electric Drive Controller for High-Precision Applications Based on Feedback Linearization Technique. Electronics 2021, 10, 2954. [Google Scholar] [CrossRef]
- Rasool, H.; Verbrugge, B.; Zhaksylyk, A.; Tran, T.M.; Baghdadi, M.E.; Geury, T.; Hegazy, O. Design Optimization and Electro-Thermal Modeling of an Off-Board Charging System for Electric Bus Applications. IEEE Access 2021, 9, 84501–84519. [Google Scholar] [CrossRef]
- Dini, P.; Saponara, S. Electro-Thermal Model-Based Design of Bidirectional On-Board Chargers in Hybrid and Full Electric Vehicles. Electronics 2022, 11, 112. [Google Scholar] [CrossRef]
- Chub, A.; Vinnikov, D.; Kosenko, R.; Liivik, E.; Galkin, I. Bidirectional DC–DC Converter for Modular Residential Battery Energy Storage Systems. IEEE Trans. Ind. Electron. 2020, 67, 1944–1955. [Google Scholar] [CrossRef]
- Wang, F.; Luo, Y. Modelling of a Power Converter with Multiple Operating Modes. World Electr. Veh. J. 2018, 9, 7. [Google Scholar] [CrossRef]
- Krismer, F.; Biela, J.; Kolar, J. A comparative evaluation of isolated bi-directional DC/DC converters with wide input and output voltage range. In Proceedings of the Fourtieth IAS Annual Meeting. Conference Record of the Industry Applications Conference, Hong Kong, China, 2–6 October 2005; Volume 1, pp. 599–606. [Google Scholar] [CrossRef]
- Shah, S.S.; Iyer, V.M.; Bhattacharya, S. Exact Solution of ZVS Boundaries and AC-Port Currents in Dual Active Bridge Type DC–DC Converters. IEEE Trans. Power Electron. 2019, 34, 5043–5047. [Google Scholar] [CrossRef]
- Vieira, A.; Mazza, L.; Antunes, F.; Oliveira, D. Bidirectional dual-active-bridge DC-DC converter for vehicle-to-grid applications in DC microgrids. In Proceedings of the Simposio Brasileiro de Sistemas Eletricos (SBSE), Niteroi, Brazil, 12 May 2018; pp. 1–6. [Google Scholar]
- Li, X.; Bhat, A.K.S. Analysis and Design of High-Frequency Isolated Dual-Bridge Series Resonant DC/DC Converter. IEEE Trans. Power Electron. 2010, 25, 850–862. [Google Scholar] [CrossRef]
- Al Attar, H.; Hamida, M.A.; Ghanes, M.; Taleb, M. LLC DC-DC Converter Performances Improvement for Bidirectional Electric Vehicle Charger Application. World Electr. Veh. J. 2022, 13, 2. [Google Scholar] [CrossRef]
- Yildiran, N. Design Methodology and Implementation of Half-Bridge LLC Resonant Converter. In Proceedings of the International Conference on Electrical, Communication, and Computer Engineering (ICECCE), Istanbul, Turkey, 12–13 June 2020; pp. 1–6. [Google Scholar]
- Liu, C.; Liu, H.; Cai, G.; Cui, S.; Liu, H.; Yao, H. Novel Hybrid LLC Resonant and DAB Linear DC–DC Converter: Average Model and Experimental Verification. IEEE Trans. Ind. Electron. 2017, 64, 6970–6978. [Google Scholar] [CrossRef]
- Zhang, G.; Zeng, J.; Yu, S.S.; Xiao, W.; Zhang, B.; Chen, S.Z.; Zhang, Y. Control Design and Performance Analysis of a Double-Switched LLC Resonant Rectifier for Unity Power Factor and Soft-Switching. IEEE Access 2020, 8, 44511–44521. [Google Scholar] [CrossRef]
- Liu, F.; Ruan, X.; Huang, X.; Qiu, Y. Second Harmonic Current Reduction for Two-Stage Inverter With DCX-LLC Resonant Converter in Front-End DC–DC Converter: Modeling and Control. IEEE Trans. Power Electron. 2021, 36, 4597–4609. [Google Scholar] [CrossRef]
- Ma, H.; Liu, Q.; Guo, J. A sliding-mode control scheme for llc resonant DC/DC converter with fast transient response. In Proceedings of the IECON—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 162–167. [Google Scholar]
- Wang, Y.; Liu, Q.; Ma, H. Discrete pulse frequency modulation control with sliding-mode implementation on LLC resonant DC/DC converter via input?output linearisation. IET Power Electron. 2014, 7, 1033–1043. [Google Scholar] [CrossRef]
- Yao, L.; Li, D.; Liu, L. An improved large signal model of full-bridge LLC converter. PLoS ONE 2018, 13, e0205904. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Duan, S.; Liu, K.; Cai, T. Control of an LLC Resonant Converter Using Load Feedback Linearization. IEEE Trans. Power Electron. 2018, 33, 887–898. [Google Scholar] [CrossRef]
- Al Attar, H.; Ghanes, M.; Hamida, M.; Taleb, M. Control strategies design and comparison of DC-DC LLC converter in V2X mode for electric vehicle charger application. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), San Diego, France, 9–11 August 2021; pp. 1154–1159. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, G.; Zhou, D.; Li, J.; Yin, S. Modeling, Dynamic Analysis and Control Design of Full-Bridge LLC Resonant Converters with Sliding-Mode and PI Control Scheme. J. Power Electron. 2018, 18, 766–777. [Google Scholar]
- Mansour, A.; Hajer, M.; Faouzi, B.; Jamel, G. Analysis and Modeling of LLC Resonant Converter Used in Electric Vehicle. In Proceedings of the International Conference on Advanced Systems and Emergent Technologies (IC_ASET), Hammamet, Tunisia, 19–22 March 2019; pp. 357–362. [Google Scholar]
- Ajmal, F.; Pan, H.; He, C.; Chen, G.; Chen, H. Pulse-width modulation control strategy for high efficiency LLC resonant converter with light load applications. IET Power Electron. 2014, 7, 2887–2894. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, J.; Duan, S.; Shao, J.; Hu, G. Stability Analysis and Trigger Control of LLC Resonant Converter for a Wide Operational Range. Energies 2017, 10, 1448. [Google Scholar] [CrossRef]
- Wei, Y.; Luo, Q.; Wang, Z.; Mantooth, H.A. A Complete Step-by-Step Optimal Design for LLC Resonant Converter. IEEE Trans. Power Electron. 2021, 36, 3674–3691. [Google Scholar] [CrossRef]
- Hillers, A.; Christen, D.; Biela, J. Design of a Highly efficient bidirectional isolated LLC resonant converter. In Proceedings of the 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012. [Google Scholar] [CrossRef]
- Hsieh, G.C.; Tsai, C.Y.; Hsieh, S.H. Design Considerations for LLC Series-Resonant Converter in Two-Resonant Regions. In Proceedings of the IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 731–736. [Google Scholar]
- Wei, Y.; Woldegiorgis, D.; Mantooth, A. Control Strategies Overview for LLC Resonant Converter with Fixed Frequency Operation. In Proceedings of the 2020 IEEE 11th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Dubrovnik, Croatia, 28 September–1 October 2020; pp. 63–68. [Google Scholar] [CrossRef]
- Cao, Q.; Li, Z.; Xue, B.; Wang, H. Fixed Frequency Phase Shift Modulated LLC Resonant Converter Adapted to Ultra Wide Output Voltage Range. In Proceedings of the 2019 IEEE Applied Power Electronics Conference and Exposition (APEC), Anaheim, CA, USA, 17–21 March 2019; pp. 817–822. [Google Scholar] [CrossRef]
- Wei, Y.; Wang, Z.; Luo, Q.; Alan Mantooth, H. MATLAB GUI Based Steady State Open-Loop and Closed-Loop Simulation Tools for Different LLC Converters With all Operation Modes. IEEE Open J. Ind. Appl. 2021, 2, 320–336. [Google Scholar] [CrossRef]
- De Simone, S.; Adragna, C.; Spini, C.; Gattavari, G. Design-oriented steady-state analysis of LLC resonant converters based on FHA. In Proceedings of the International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM, Taormina, Italy, 23–26 May 2006; pp. 200–207. [Google Scholar]
- Shi, Z.; Tang, Y.; Guo, Y.; Li, X.; Sun, H. Optimal Design Method of LLC Half-Bridge Resonant Converter Considering Backflow Power Analysis. IEEE Trans. Ind. Electron. 2022, 69, 3599–3608. [Google Scholar] [CrossRef]
- Liao, Y.; Xu, G.; Sun, Y.; Peng, T.; Su, M.; Guo, B.; Xiong, W. Single-Stage DAB-LLC Hybrid Bidirectional Converter with Tight Voltage Regulation under DCX Operation. IEEE Trans. Ind. Electron. 2021, 68, 293–303. [Google Scholar] [CrossRef]
- Tzafestas, S.; Frangakis, G. Design and implementation of pulse frequency modulation control systems. Trans. Inst. Meas. Control. 1980, 2, 65–78. [Google Scholar] [CrossRef]
- Cheng, B.; Musavi, F.; Dunford, W.G. Novel small signal modeling and control of an LLC resonant converter. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition—APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 2828–2834. [Google Scholar]
- Das, A.; Nademi, H.; Norum, L. A Pulse Width Modulation technique for reducing switching frequency for modular multilevel converter. In Proceedings of the India International Conference on Power Electronics 2010 (IICPE2010), New Delhi, India, 28–30 January 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, X.; Qian, W.; Janabi, A.; Wang, B.; Lu, X.; Zou, K.; Chen, C.; Peng, F.Z. A Simple Phase-Shift Modulation Using Parabolic Carrier for Dual Active Bridge DC–DC Converter. IEEE Trans. Power Electron. 2020, 35, 7729–7734. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y.; Wang, F.; Teng, C. Pulse frequency modulation and unilateral dual-phase-shift hybrid control strategy for bidirectional full-bridge LLC resonant converter. J. Eng. 2019, 2019, 3120–3126. [Google Scholar] [CrossRef]
- Dong, Y.; Wang, Y.; Wang, F.; Wang, S. Zero Input Current Ripple LLC Resonant Converter with Integrated Interleaved Boost Converter. In Proceedings of the 2021 IEEE International Conference on Computer Science, Electronic Information Engineering and Intelligent Control Technology (CEI), Fuzhou, China, 24–26 September 2021; pp. 602–606. [Google Scholar] [CrossRef]
- Ta, L.A.D.; Dao, N.D.; Lee, D.C. High-Efficiency Hybrid LLC Resonant Converter for On-Board Chargers of Plug-In Electric Vehicles. IEEE Trans. Power Electron. 2020, 35, 8324–8334. [Google Scholar] [CrossRef]
- Al Attar, H.; Ghanes, M.; Hamida, M.; Taleb, M. Model Free Control Design of DC-DC LLC Converter with Phase Shift Modulation in V2X Mode for EV Charger Application. In Proceedings of the 2022 IEEE Conference on Control Technology and Applications (CCTA), Trieste, Italy, 23–25 August 2022. [Google Scholar]
- Al Attar, H.; Ghanes, M.; Hamida, M.; Taleb, M. Electric Vehicle Charger Control Design Combining Phase Shift Modulation with an Adaptive Super Twisting Algorithm. In Proceedings of the 2022 IEEE 16th International Workshop on Variable Structure Systems VSS, Rio de Janeiro, Brazil, 11–14 September 2022. [Google Scholar]
- Gerekial, W.G. Bi-Directional Power Converters for Smart Grids; Technical report; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Buccella, C.; Cecati, C.; Latafat, H.; Pepe, P.; Razi, K. Observer-Based Control of LLC DC/DC Resonant Converter Using Extended Describing Functions. IEEE Trans. Power Electron. 2015, 30, 5881–5891. [Google Scholar] [CrossRef]
- Tian, S.; Lee, F.C.; Li, Q. Equivalent Circuit Modeling of LLC Resonant Converter. IEEE Trans. Power Electron. 2020, 35, 8833–8845. [Google Scholar] [CrossRef]
- Salem, M.; Ramachandaramurthy, V.K.; Jusoh, A.; Padmanaban, S.; Kamarol, M.; Teh, J.; Ishak, D. Three-Phase Series Resonant DC-DC Boost Converter With Double LLC Resonant Tanks and Variable Frequency Control. IEEE Access 2020, 8, 22386–22399. [Google Scholar] [CrossRef]
- Li, Z.; Xue, B.; Wang, H. An Interleaved Secondary-Side Modulated LLC Resonant Converter for Wide Output Range Applications. IEEE Trans. Ind. Electron. 2020, 67, 1124–1135. [Google Scholar] [CrossRef]
- Khan, S.; Sha, D.; Jia, X.; Wang, S. Resonant LLC DC–DC Converter Employing Fixed Switching Frequency Based on Dual-Transformer With Wide Input-Voltage Range. IEEE Trans. Power Electron. 2021, 36, 607–616. [Google Scholar] [CrossRef]
- Awasthi, A.; Bagawade, S.; Jain, P.K. Analysis of a Hybrid Variable-Frequency-Duty-Cycle-Modulated Low-Q LLC Resonant Converter for Improving the Light-Load Efficiency for a Wide Input Voltage Range. IEEE Trans. Power Electron. 2021, 36, 8476–8493. [Google Scholar] [CrossRef]
- Mustafa, A.; Mekhilef, S. Dual Phase LLC Resonant Converter With Variable Frequency Zero Circulating Current Phase-Shift Modulation for Wide Input Voltage Range Applications. IEEE Trans. Power Electron. 2021, 36, 2793–2807. [Google Scholar] [CrossRef]
- Ryu, S.H.; Kim, D.H.; Kim, M.J.; Kim, J.S.; Lee, B.K. Adjustable Frequency–Duty-Cycle Hybrid Control Strategy for Full-Bridge Series Resonant Converters in Electric Vehicle Chargers. IEEE Trans. Ind. Electron. 2014, 61, 5354–5362. [Google Scholar]
- Tayebi, S.M.; Hu, H.; Abdel-Rahman, S.; Batarseh, I. Dual-Input Single-Resonant Tank LLC Converter with Phase Shift Control for PV Applications. IEEE Trans. Ind. Appl. 2019, 55, 1729–1739. [Google Scholar] [CrossRef]
- Drazenovic, K.; Peric, A.; Jakopovic, Z.; Sunde, V. Modeling and Predictive Control of LLC Resonant Converter for Solar Powered E-Bicycle Charging Station. In Proceedings of the 2021 International Conference on Electrical Drives and Power Electronics (EDPE), Dubrovnik, Croatia, 22–24 September 2021; pp. 136–143. [Google Scholar] [CrossRef]
- Reyes-Moraga, E.F. Predictive Control of a Direct Series Resonant Converter with Active Output Voltage Compensation. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2015. [Google Scholar]
- Lucia, S.; Navarro, D.; Samago, H.; Lucia, O. Model Predictive Control for Resonant Power Converters Applied to Induction Heating. In Proceedings of the 2018 IEEE 27th International Symposium on Industrial Electronics (ISIE), Cairns, Australia, 12–15 June 2018; pp. 246–251. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C. Intelligent PID controllers. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio, France, 25–27 June 2008; pp. 326–331. [Google Scholar] [CrossRef]
- Fliess, M.; Join, C.; Sira-Ramírez, H. Complex Continuous Nonlinear Systems: Their Black Box Identification and Their Control. IFAC Proc. Vol. 2006, 39, 416–421. [Google Scholar] [CrossRef]
- Shtessel, Y.; Taleb, M.; Plestan, F. A novel adaptive-gain supertwisting sliding mode controller: Methodology and application. Automatica 2012, 48, 759–769. [Google Scholar] [CrossRef]
- Tahoumi, E.; Plestan, F.; Ghanes, M.; Barbot, J.P. Adaptive Exponent Parameter: A Robust Control Solution Balancing Between Linear and Twisting Controllers. In Proceedings of the 2018 15th International Workshop on Variable Structure Systems (VSS), Graz, Austria, 9–11 July 2018; pp. 186–191. [Google Scholar] [CrossRef]






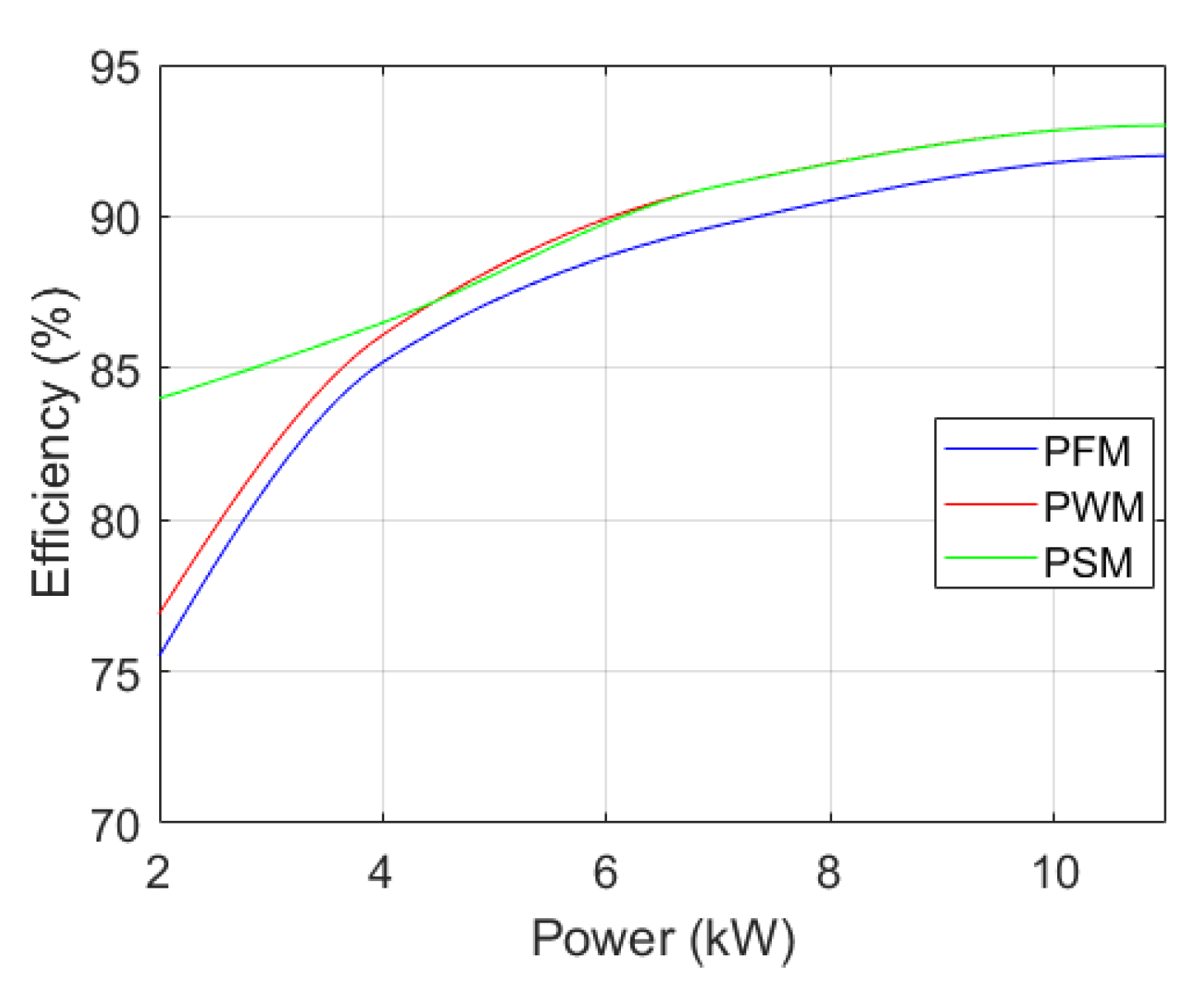


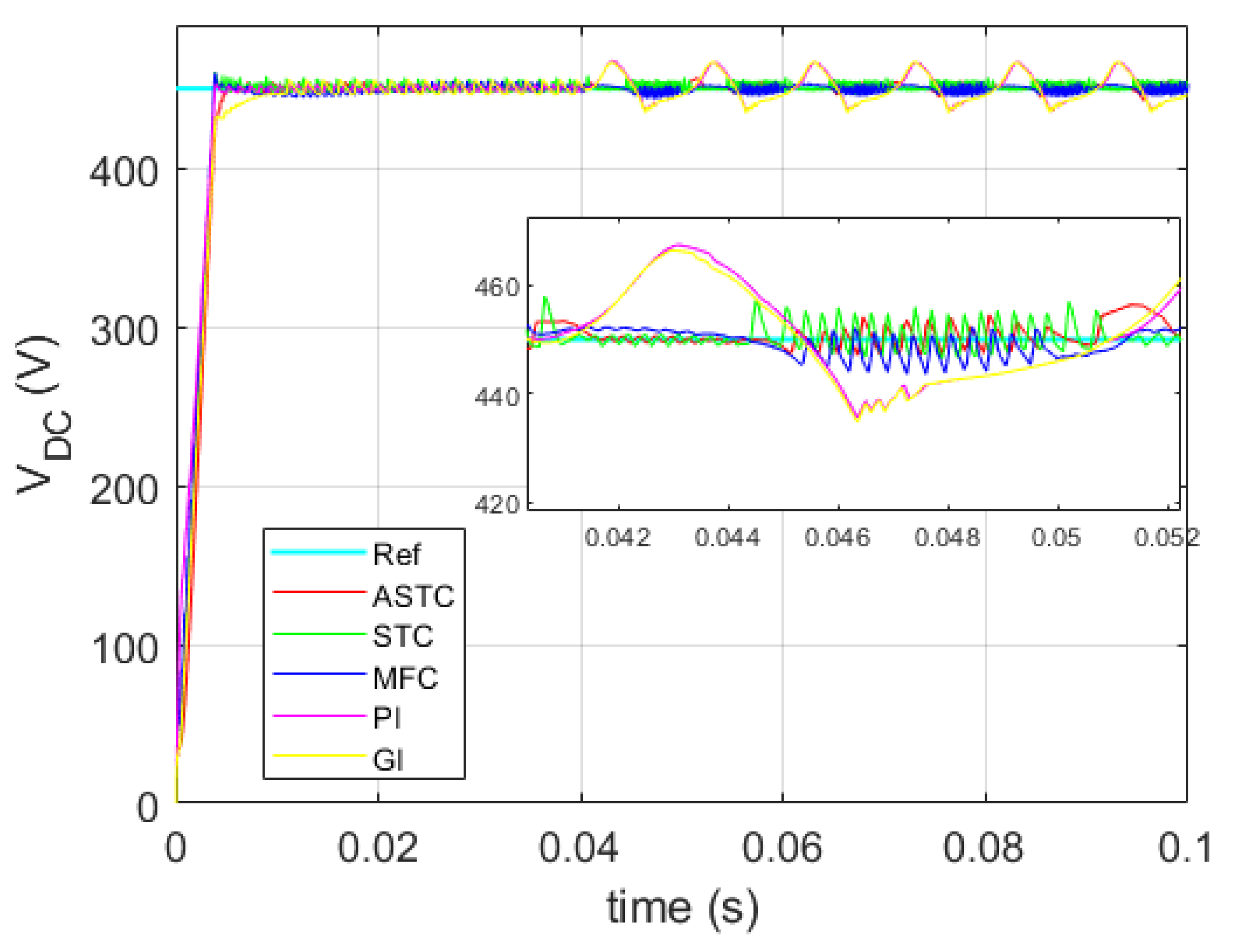
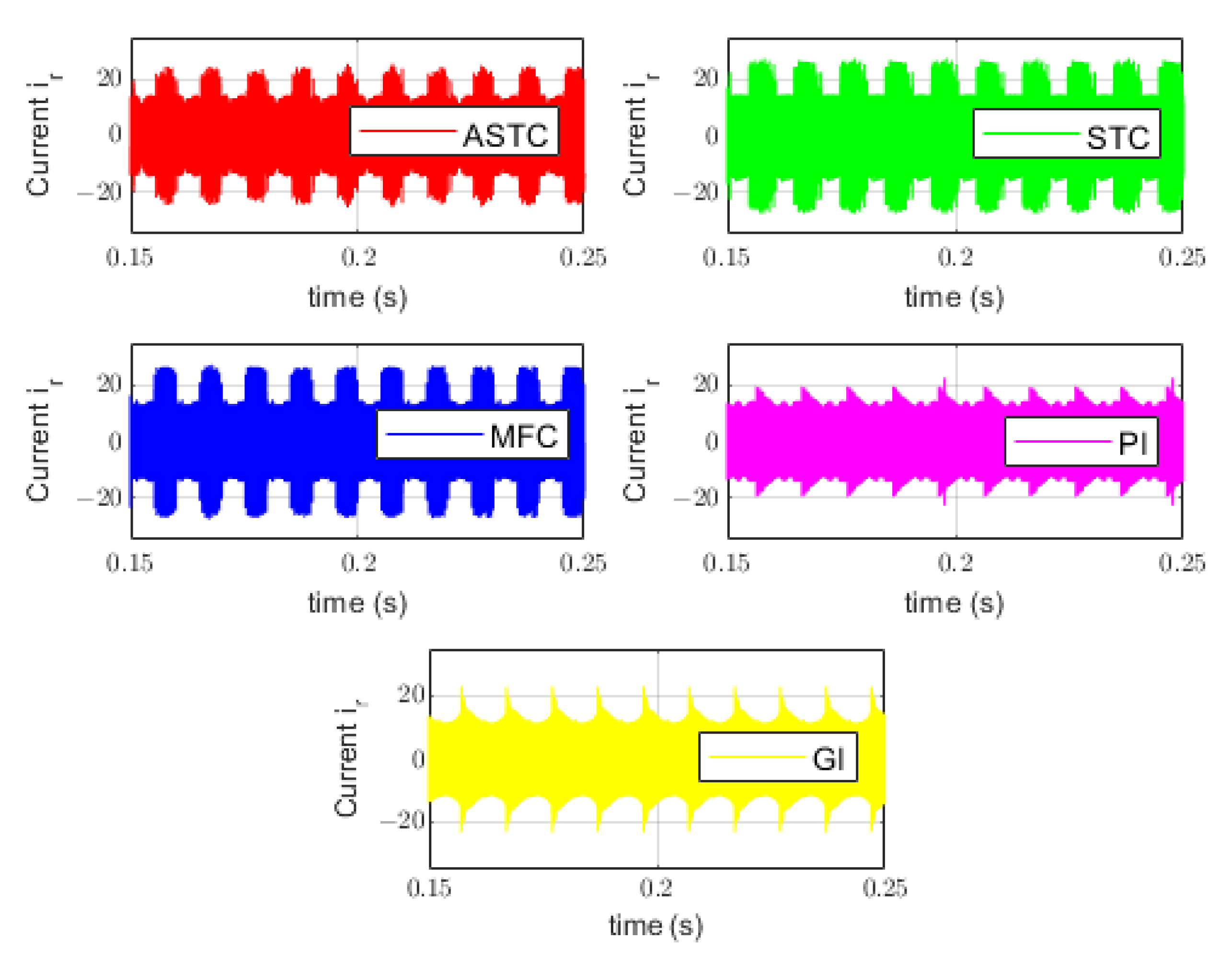
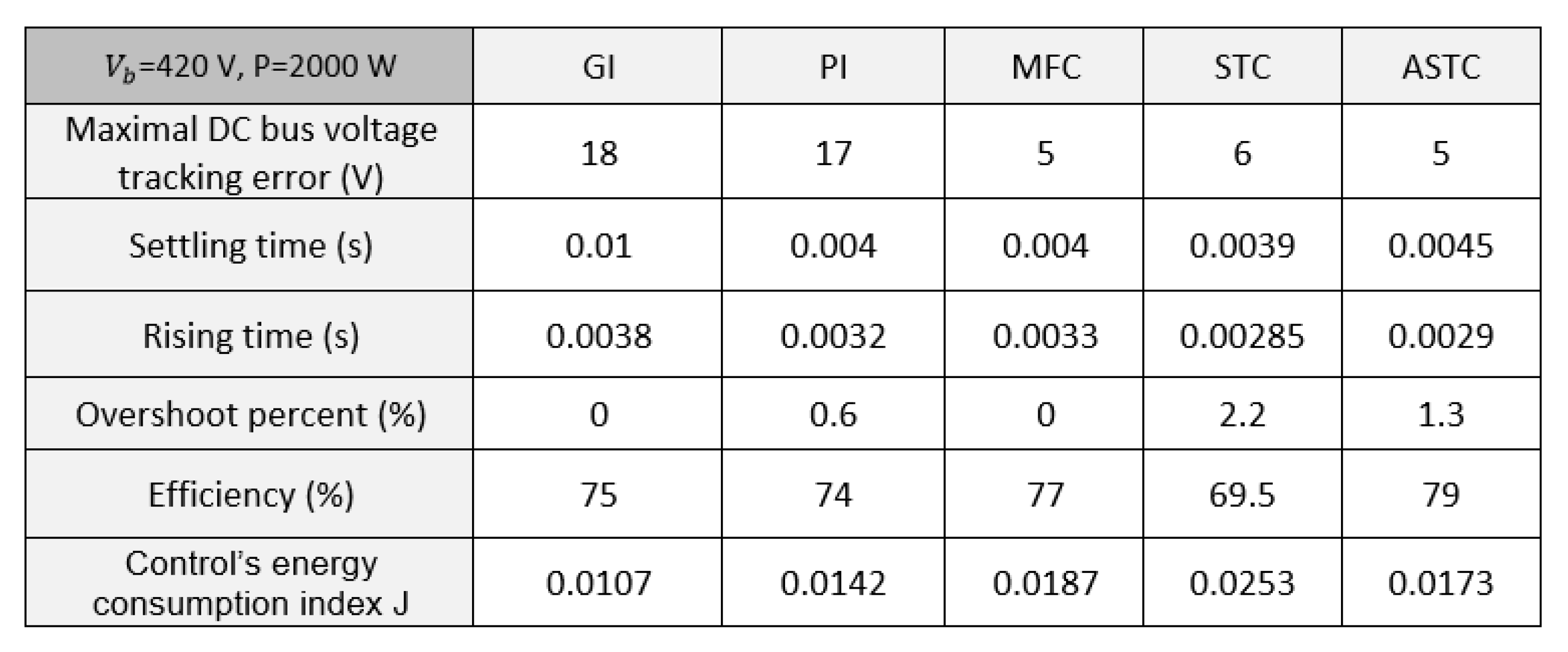
| Characteristics | Limitations | |
|---|---|---|
| Variable switching frequency | Important frequency saturation zone | |
| PFM [24,39,44,45] | Fixed duty cycle at 0.5 | Low efficiency at low power loads |
| ZVS inside the non-saturated zone | Important tracking error in saturation zone | |
| High efficiency at high power loads | ||
| Variable duty cycle | ||
| PWM [27,41] | Fixed switching frequency | No ZVS with duty cycles far from 0.5 |
| Cover more operating points than PFM | Low efficiency at low power loads | |
| High efficiency at high power loads | ||
| Variable phase-shift angle | ||
| Fixed switching frequency | ||
| PSM [31,42,46,47] | Fixed duty cycle at 0.5 | Higher overshoot percent |
| Cover the whole operating zone | Requires soft-start strategy | |
| Improved efficiency at low power loads | ||
| High efficiency at high power loads |
| Characteristics | Limitations | |
|---|---|---|
| Linearized model with transfer function representation | Limited operating zone | |
| Small signal | First harmonic approximation with an averaged model | Lack of realistic model accuracy |
| modeling | Simplified equivalent circuit | Lack of dynamic behavior of state variables |
| [15,17,18,19,24,40] | Simplified control design | Not comfortable with nonlinear controller |
| Ignored effect of harmonics and converter parameters | Lack of robustness | |
| Comfortable with linear controllers | ||
| Nonlinear model with higher order | ||
| Large signal | Dynamic behavior representation | More complex control |
| modeling | Harmonic approximation | More complex design |
| [20,21,22,23,48,49] | Comfortable with nonlinear and robust controllers | Lack of realistic model behavior |
| Closer to the realistic model | Still requires approximation methods | |
| Cover more operating points |
| 75 | 40 | ||
| 80 | 1 | ||
| 30 | 0.00005 | ||
| 120 | 0.00001 | ||
| n | 1.6 | 0.005 | |
| 5 | 0.0001 |
| Characteristics | Limitations | |
|---|---|---|
| Based on small signal model | ||
| Linear controllers (feedback [23], | Simple control design | Less robust versus disturbances |
| control based observer [49], | Less cost in implementation | Lack of precision over the whole operating zone |
| PI [33,37], GI [24]) | Non-complicated gain tuning | Low control performance for many operating points |
| Based on large signal model | ||
| Nonlinear controllers | More robust versus disturbances | More complex control design |
| (Sliding mode [20,21], MFC [46], | Better control performance | Higher cost in implementation |
| ASTC [47], MPC [58]) | Improved efficiency | Complex gain tuning |
| Characteristics | Limitations | |
|---|---|---|
| Simple control design | Requires model knowledge | |
| PI [17,33,34] | Simple gain tuning | Less robust versus disturbances |
| Low implementation cost | ||
| Avoid wide control bandwidth | ||
| Variation around equilibrium point | Requires model knowledge | |
| GI [24] | Simple control design | Less robust versus disturbances |
| Simple gain tuning | Requires equilibrium point | |
| Low implementation cost | ||
| More robust than linear control | More complex control design | |
| MPC [58] | Avoid modulator system | Depends on the system model |
| Optimization of the switching state | Needs integration of all constraints | |
| Simplified model design | Requires the system relative degree | |
| MFC [46] | Based on estimation of a black box model | Requires the output derivative |
| Simple gain tuning | Sensible to noises | |
| More robust control than linear control | High implementation cost | |
| Based on sliding mode control | Chattering phenomenon | |
| STC [47] | More robust control than linear control | Requires model knowledge |
| Non-complicated gain tuning | Higher switching losses | |
| Higher control gains | ||
| More robust control than linear control | ||
| Adaptive control gains | More complex gain tuning | |
| ASTC [47] | Reduced chattering phenomenon | High implementation cost |
| Avoid gain overestimation | Requires a system relative degree equal to 1 | |
| Lower switching losses |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Attar, H.; Hamida, M.A.; Ghanes, M.; Taleb, M. Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications. Energies 2023, 16, 3946. https://doi.org/10.3390/en16093946
Al Attar H, Hamida MA, Ghanes M, Taleb M. Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications. Energies. 2023; 16(9):3946. https://doi.org/10.3390/en16093946
Chicago/Turabian StyleAl Attar, Houssein, Mohamed Assaad Hamida, Malek Ghanes, and Miassa Taleb. 2023. "Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications" Energies 16, no. 9: 3946. https://doi.org/10.3390/en16093946
APA StyleAl Attar, H., Hamida, M. A., Ghanes, M., & Taleb, M. (2023). Review on Modeling and Control Strategies of DC–DC LLC Converters for Bidirectional Electric Vehicle Charger Applications. Energies, 16(9), 3946. https://doi.org/10.3390/en16093946








