An Open-Source Energy Arbitrage Model Involving Price Bands for Risk Hedging with Imperfect Price Signals
Abstract
:1. Introduction
- The MILP scheduling model applies a piece-wise linearisation process to a pumped hydro storage (PHS) system. This allows the non-linear charging behaviour of the PHS to be approximated during scheduling, taking advantage of the speed of MILP optimisation. The piece-wise linearisation process will be a more accurate approximation than assuming the constant linear behaviour of the PHS in all operating conditions.
- Battery degradation has been considered within the piece-wise linearised description of a battery developed by Sakti et al. [14]. This allows for changes to battery voltage efficiency over its lifetime to be included within the MILP scheduling algorithm while maintaining an accurate approximation of the non-linear charging behaviour.
- The rapid optimisation provided by the MILP scheduling algorithm, along with the additional accuracy provided by the non-linear charging model and piece-wise linear approximation of charging behaviour during scheduling, allows the simulation period to cover the entire lifetime of each storage system. This allows for computation of the lifetime-levelised cost of storage metrics (RADP and AADP), enabling a comparison between the arbitrage revenue of storage systems with different lifetimes, cycling behaviour, and degradation rates.
- Charging and discharging efficiencies are considered separately and modelled according to non-linear functions, where appropriate. Some previous studies have assumed the use of a round-trip efficiency during dispatch [19,34], though this may be inappropriate for modelling arbitrage revenue in wholesale energy markets that have a high price ceiling.
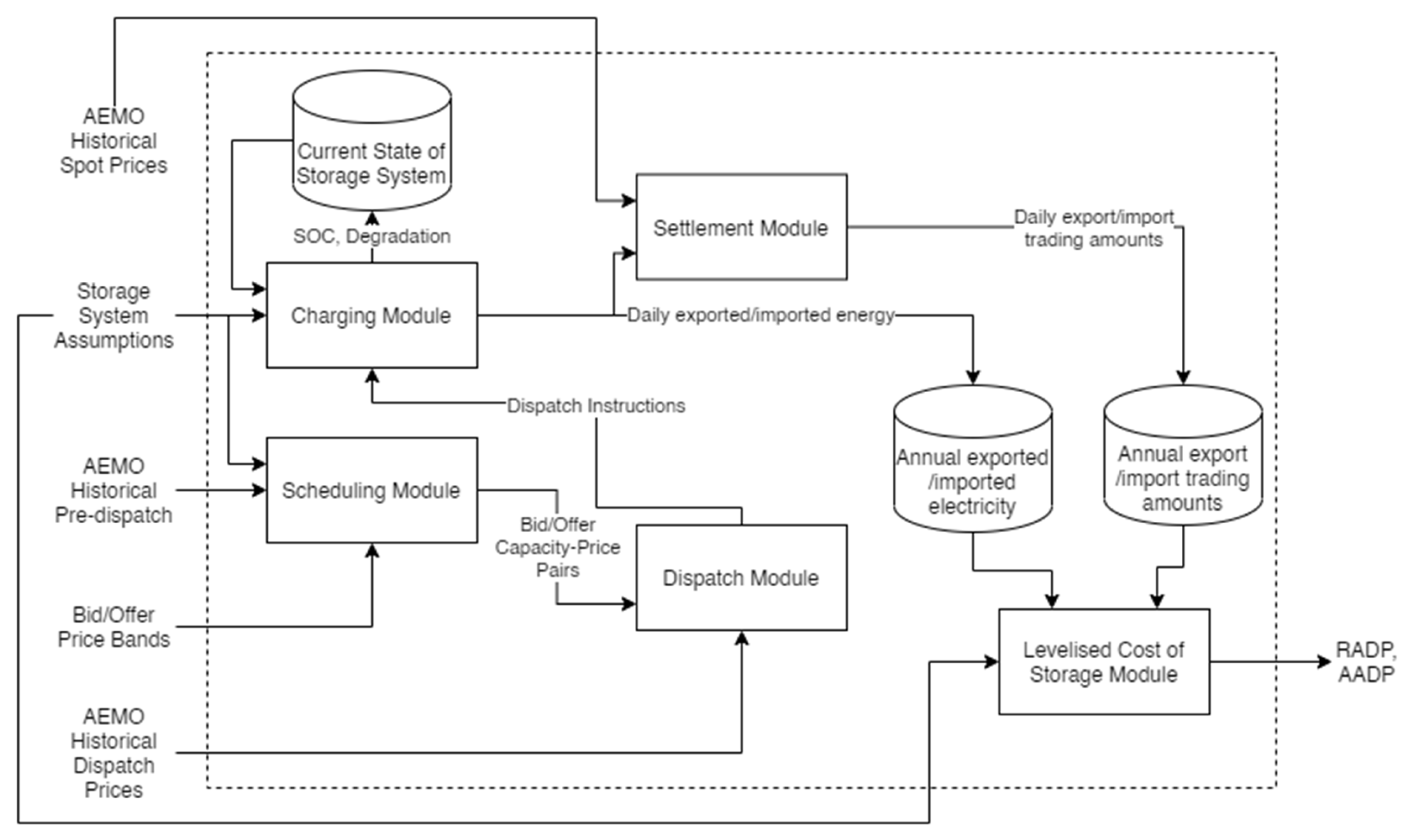
- The code for the model is available open-source on Github. The current version contains a scheduling and charging model for a Li-ion BESS and PHS. The modification of the arbitrage model to analyse alternative storage systems, such as the compressed air energy storage or other battery technologies, would only require the development of bespoke scheduling and charging modules that can be directly integrated with the rest of the system.
2. Model Details
2.1. Arbitrage Model
2.1.1. Charging Module
Pumped Hydro Storage Charging Module
Battery Energy Storage System Charging Module
2.1.2. Scheduling Module
Pumped Hydro Storage Scheduling Module
Battery Energy Storage System Scheduling Module
2.1.3. Price Band Module
2.1.4. Dispatch Module
2.1.5. Settlement Module
2.1.6. Levelised Cost of Storage Module
2.2. Model Assumptions
3. Results and Discussion
3.1. One-at-a-Time Sensitivity Analysis
3.2. Hedging Risk with Price Bands
3.3. Comparison with Other Energy Arbitrage Models
4. Conclusions
- It is possible that the method would provide increased value in a 5 min settlement analysis. Additionally, integrating a capacity-price pair optimisation into the scheduling module, such as a robust or information gap decision theory algorithm, would be expected to maximise the arbitrage revenue while still protecting the system from scheduling during suboptimal events. The impact of such an algorithm on optimisation time would need to be considered to ensure that the model could still generate lifetime levelised cost and revenue metrics.
- The current version of the BESS scheduling module does not account for the long-term impact of battery degradation on arbitrage revenue. Including a degradation cost in the MILP objective function may modify the scheduling behaviour to minimise cycle aging, further increasing the arbitrage revenue.
- A detailed econometric analysis can be performed to determine the influence of variables within the electricity market on RADP and AADP. The econometric analysis could help to tailor risk hedging strategies for BESS and PHS under various market conditions. The charging and scheduling modules will also be expanded to consider other storage systems, such as compressed air energy storage and alternative battery technologies (e.g., nickel, zinc-hybrid or redox-flow batteries). Due to its modular nature, this arbitrage model can be readily extended to analyse alternative energy storage systems by integrating a scheduling and charging module for that storage system.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Abbreviations | |
| AADP | Available average discharge price |
| AEMC | Australian Energy Market Commission |
| AEMO | Australian Energy Market Operator |
| BESS | Battery energy storage system |
| CBC | COIN-OR Branch-and-Cut |
| DLF | Distribution loss factor |
| DUID | Dispatchable unit identifier |
| LCOS | Levelised cost of storage |
| MILP | Mixed-integer linear programming |
| MLF | Marginal loss factor |
| NEM | National Electricity Market |
| NER | National Electricity Rules |
| O&M | Operation and maintenance |
| PHS | Pumped hydro storage |
| RADP | Required average discharge price |
| the Rules | The National Electricity Rules |
| SOC | State of charge |
| VRE | Variable renewable energy |
| WACC | Weighted average cost of capital |
| Nomenclature | |
| Latin symbols | |
| a | Size of a piece along the SOC axis of a maximum power limit piece-wise linear function, % |
| AADP | Available average discharge price, $/MWh |
| AC | Ageing coefficient, Ah/sAEcal (calendar ageing), Ah1−AEcyc (cycle ageing) |
| AE | Ageing exponent, dimensionless |
| AGE | Adjusted gross energy, MWh |
| AhTh | Amp-hour charging throughput, Ah |
| AR | Arbitrage revenue, $ |
| b | Size of a piece along the SOC axis of a maximum power limit piece-wise linear function, % |
| B | Bid price, $/MWh |
| bp | Bid price band, $/MWh |
| BV | Base value, $ |
| c | Size of a piece along the charging loss piece-wise linear function, m3/s (flow rate), MW (power) |
| C | Load bid capacity, MW |
| CalN | Number of calendar loss intervals, dimensionless |
| CAPEX | Capital cost, $/MWh (energy), $/MW (power), $ (fixed) |
| CE | Energy capacity, MWh |
| CLT | Calendar loss time, s |
| CP | Oower capacity, MW |
| d | Size of a piece along the discharging loss piece-wise linear function, m3/s (flow rate), MW (power) |
| D | Generator offer capacity, MW |
| DLF | Distribution loss factor, % |
| DP | Dispatch price, $/MWh |
| dV | Transient adjustment to water volume, m3 |
| E | Optimal energy charged/discharged, MWh |
| Ea | Ageing activation energy, J/mol |
| F | Friction factor, dimensionless |
| FOM | Fixed operation and maintenance cost, $/kW |
| FSL | Full supply level, m |
| g | Acceleration due to gravity, 9.81 m/s2 |
| h | Vertical height, m |
| H | Head, m |
| I | Current, A |
| ii | Value of index i, dimensionless |
| ir | Internal resistance, Ω |
| ITC | Investment tax credit, % |
| jj | Value of index j, dimensionless |
| K | Resistance coefficient |
| L | Penstock pipe length, m |
| ME | Exported energy, MWh |
| MLF | Marginal loss factor, % |
| mm | Value of index m, dimensionless |
| MOL | Minimum operating level, m |
| N | Quantity, dimensionless |
| n | Fraction of piece c used, % |
| nn | Value of open-circuit voltage fitting parameter, dimensionless |
| O | Offer price, $/MWh |
| OCC | Overnight capital cost, $ |
| op | Offer price band. $/MWh |
| p | Fraction of piece d used, % |
| P | Power, MW |
| PD | Penstock pipe diameter, m |
| q | Fraction of piece c used, % |
| Q | Flow rate, m3/s |
| R | Universal gas constant, 8.314 J/K·mol |
| RADP | Required average discharge price, $/MWh |
| RL | Risk level, {1,10} |
| RT | Ramp time, s |
| Re | Reynolds number, dimensionless |
| S | Scheduling forecast horizon |
| sl | Gradient of a piece-wise linear function |
| SOC | State of charge, % |
| SOH | State-of-health, % |
| SP | Spot price, $/MWh |
| ST | Duration of operation, months |
| T | Temperature, K |
| TA | Trading amount, $ |
| U | Open-circuit voltage, V |
| uu | Value of index u, dimensionless |
| V | Volume, m3 |
| VOM | Variable operation and maintenance cost, $/MWh |
| vv | Value of index v, dimensionless |
| w | Charging/discharging decision, {0,1} |
| WV | Water velocity, m/s |
| x | Fraction of piece a used, % |
| y | Fraction of piece b used, % |
| Y | Estimated system lifetime, years |
| z | Piece behaviour, {0,1} |
| Greek symbols | |
| α | Fraction of maximum power that could be used, dimensionless |
| β | Average SOC, % |
| γ | Coefficient for ageing acceleration, Jmol−1A−1 |
| δ | Discount rate, % |
| ε | Absolute roughness, m |
| η | Efficiency, % |
| λ | Effective corporate income tax rate, % |
| Λ | Tax factor, % |
| μ | Dynamic viscosity of water, 8.9 × 10−4 Pa·s |
| ξ | First fitting parameter of empirical function, dimensionless |
| ρ | Water density, 997 kg/m3 |
| σ | Allowable tax depreciation charge, % |
| τ | Dispatch interval length, h |
| ϕ | Second fitting parameter of empirical function, dimensionless |
| χ | Third fitting parameter of empirical function, dimensionless |
| Subscripts | |
| e | Energy parameter |
| effective | Constant approximation of variable |
| fixed | Fixed parameter |
| g | Pump system index |
| gen | Parameter associated with the generator DUID |
| h | Turbine system index |
| i | Piece of the piece-wise linear function for maximum discharge power limit |
| initial | Initial value at the start of the trading day |
| j | Piece of the piece-wise linear function for maximum charge power limit |
| k | Day index |
| l | Year index |
| load | Parameter associated with the load DUID |
| m | Piece of the piece-wise linear function for charge/discharge power loss |
| max | Maximum possible value for a variable |
| min | Minimum possible value for a variable |
| n | Open-circuit voltage fitting parameter |
| nom | Nominal |
| P | Power parameter |
| peak | Value at peak efficiency point |
| s | Trading interval index |
| t | Dispatch interval index |
| u | Bid band index |
| v | Offer band index |
| Supercripts | |
| avg | Average |
| batt | Battery parameter |
| c | Variable or parameter associated with charging battery |
| cal | Calendar ageing parameter |
| cal loss | Loss due to calendar ageing |
| cell | Cell parameter |
| cyc | Cycle ageing parameter |
| cyc loss | Loss due to cycle ageing |
| d | Variable or parameter associated with discharging battery |
| disp | Dispatch instruction |
| fittings | Penstock fittings |
| loss | Variable or parameter associated with the piece-wise function for flow rate/power loss |
| lr | Lower reservoir (internal) |
| lwl | Lower water level relative to bottom of lower reservoir |
| p | Variable or parameter associated with a pump |
| parallel | Cell groups in parallel |
| peak | Parameter when system is at peak flow rate |
| pipe | Penstock pipe |
| pl | Pump loss |
| pre | Previous |
| pd | Predispatch |
| P←TNL | Pump operation to turbine no load |
| r | Bottom of upper reservoir to top of lower reservoir |
| rel | Relative |
| sch | Scheduled |
| series | Cell groups in series |
| sys | Auxiliary system |
| t | Variable or parameter associated with a turbine |
| test | Test variable |
| tl | Turbine loss |
| T←TNL | Turbine operation to turbine no load |
| TNL→P | Turbine no load to pump operation |
| TNL→T | Turbine no load to turbine operation |
| ur | Upper reservoir (internal) |
| uwl | Upper water level relative to bottom of upper reservoir |
| volt | Voltage |
References
- IRENA. Renewable Capacity Statistics 2023; The International Renewable Energy Agency: Abu Dhabi, United Arab Emirates, 2023. [Google Scholar]
- Da Silva, P.P.; Horta, P. The effect of variable renewable energy sources on electricity price volatility: The case of the Iberian market. Int. J. Sustain. Energy 2019, 38, 794–813. [Google Scholar] [CrossRef]
- Rintamäki, T.; Siddiqui, A.S.; Salo, A. Does renewable energy generation decrease the volatility of electricity prices? An analysis of Denmark and Germany. Energy Econ. 2017, 62, 270–282. [Google Scholar] [CrossRef]
- Wozabal, D.; Graf, C.; Hirschmann, D. The effect of intermittent renewables on the electricity price variance. OR Spectr. 2015, 38, 687–709. [Google Scholar] [CrossRef]
- Johnson, E.P.; Oliver, M.E. Renewable Generation Capacity and Wholesale Electricity Price Variance. Energy J. 2019, 40, 143–168. [Google Scholar] [CrossRef]
- Rai, A.; Nunn, O. On the impact of increasing penetration of variable renewables on electricity spot price extremes in Australia. Econ. Anal. Policy 2020, 67, 67–86. [Google Scholar] [CrossRef] [PubMed]
- Maniatis, G.I.; Milonas, N.T. The impact of wind and solar power generation on the level and volatility of wholesale electricity prices in Greece. Energy Policy 2022, 170, 113243. [Google Scholar] [CrossRef]
- Maciejowska, K. Assessing the impact of renewable energy sources on the electricity price level and variability—A quantile regression approach. Energy Econ. 2019, 85, 104532. [Google Scholar] [CrossRef]
- Tselika, K. The impact of variable renewables on the distribution of hourly electricity prices and their variability: A panel approach. Energy Econ. 2022, 113, 106194. [Google Scholar] [CrossRef]
- Denholm, P.; Ela, A.; Kirby, B.; Milligan, M. The Role of Energy Storage with Renewable Electricity Generation; National Renewable Energy Laboratory: Golden, CO, USA, 2010.
- Akhil, A.; Huff, G.; Currier, A.; Kaun, B.; Rastler, D.; Chen, S.; Cotter, A.; Bradshaw, D.; Gauntlett, W. Electricity Storage Handbook in Collaboration with NRECA; Sandi National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2015.
- Wankmüller, F.; Thimmapuram, P.R.; Gallagher, K.G.; Botterud, A. Impact of battery degradation on energy arbitrage revenue of grid-level energy storage. J. Energy Storage 2017, 10, 56–66. [Google Scholar] [CrossRef]
- Arcos-Vargas, A.; Canca, D.; Núñez, F. Impact of Battery Technological Progress on Electricity Arbitrage: An Application to the Iberian market. Appl. Energy 2020, 260, 114273. [Google Scholar] [CrossRef]
- Sakti, A.; Gallagher, K.G.; Sepulveda, N.; Uckun, C.; Vergara, C.; de Sisternes, F.J.; Dees, D.W.; Botterud, A. Enhanced representations of lithium-ion batteries in power systems models and their effect on the valuation of energy arbitrage applications. J. Power Sources 2017, 342, 279–291. [Google Scholar] [CrossRef]
- Fares, R.L.; Webber, M.E. A flexible model for economic operational management of grid battery energy storage. Energy 2014, 78, 768–776. [Google Scholar] [CrossRef]
- Zareipour, H.; Janjani, A.; Leung, H.; Motamedi, A.; Schellenberg, A. Classification of Future Electricity Market Prices. IEEE Trans. Power Syst. 2010, 26, 165–173. [Google Scholar] [CrossRef]
- Antweiler, W. Microeconomic models of electricity storage: Price Forecasting, arbitrage limits, curtailment insurance, and transmission line utilization. Energy Econ. 2021, 101, 105390. [Google Scholar] [CrossRef]
- Sioshansi, R.; Denholm, P.; Jenkin, T.; Weiss, J. Estimating the value of electricity storage in PJM: Arbitrage and some welfare effects. Energy Econ. 2009, 31, 269–277. [Google Scholar] [CrossRef]
- McConnell, D.; Forcey, T.; Sandiford, M. Estimating the value of electricity storage in an energy-only wholesale market. Appl. Energy 2015, 159, 422–432. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Finn, P.; Mathiesen, B.; Leahy, M. Practical operation strategies for pumped hydroelectric energy storage (PHES) utilising electricity price arbitrage. Energy Policy 2011, 39, 4189–4196. [Google Scholar] [CrossRef]
- Thatte, A.A.; Xie, L.; Viassolo, D.E.; Singh, S. Risk Measure Based Robust Bidding Strategy for Arbitrage Using a Wind Farm and Energy Storage. IEEE Trans. Smart Grid 2013, 4, 2191–2199. [Google Scholar] [CrossRef]
- Khani, H.; Dadash Zadeh, M.R. Real-Time Optimal Dispatch and Economic Viability of Cryogenic Energy Storage Exploiting Arbitrage Opportunities in an Electricity Market. IEEE Trans. Smart Grid 2015, 6, 391–401. [Google Scholar] [CrossRef]
- Zamani-Dehkordi, P.; Chitsaz, H.; Rakai, L.; Zareipour, H. A price signal prediction method for energy arbitrage scheduling of energy storage systems. Int. J. Electr. Power Energy Syst. 2020, 122, 106122. [Google Scholar] [CrossRef]
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep Reinforcement Learning-Based Energy Storage Arbitrage With Accurate Lithium-Ion Battery Degradation Model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Cheng, B.; Powell, W. Co-Optimizing Battery Storage for the Frequency Regulation and Energy Arbitrage Using Multi-Scale Dynamic Programming. IEEE Trans. Smart Grid 2018, 9, 1997–2005. [Google Scholar] [CrossRef]
- Díaz, G.; Gómez-Aleixandre, J.; Coto, J.; Conejero, O. Maximum income resulting from energy arbitrage by battery systems subject to cycle aging and price uncertainty from a dynamic programming perspective. Energy 2018, 156, 647–660. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, J.; He, W. Energy arbitrage optimization of lithium-ion battery considering short-term revenue and long-term battery life loss. In Proceedings of the 7th International Conference on Advances on Clean Energy Research (ICACER), Lille, France, 27–29 April 2024; pp. 364–371. [Google Scholar]
- Krishnamurthy, D.; Uckun, C.; Zhou, Z.; Thimmapuram, P.R.; Botterud, A. Energy Storage Arbitrage Under Day-Ahead and Real-Time Price Uncertainty. IEEE Trans. Power Syst. 2017, 33, 84–93. [Google Scholar] [CrossRef]
- Tian, M.-W.; Yan, S.-R.; Tian, X.-X.; Nojavan, S.; Jermsittiparsert, K. Risk and profit-based bidding and offering strategies for pumped hydro storage in the energy market. J. Clean. Prod. 2020, 256, 120715. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, Q.; Guo, Q.; Nojavan, S. RETRACTED: Pumped hydro energy storage arbitrage in the day-ahead market in smart grid using stochastic p-robust optimization method. Sustain. Cities Soc. 2021, 75, 103274. [Google Scholar] [CrossRef]
- Shafiee, S.; Zareipour, H.; Knight, A.M.; Amjady, N.; Mohammadi-Ivatloo, B. Risk-Constrained Bidding and Offering Strategy for a Merchant Compressed Air Energy Storage Plant. IEEE Trans. Power Syst. 2016, 32, 1. [Google Scholar] [CrossRef]
- Shafiee, S.; Zareipour, H.; Knight, A.M. Developing Bidding and Offering Curves of a Price-Maker Energy Storage Facility Based on Robust Optimization. IEEE Trans. Smart Grid 2017, 10, 650–660. [Google Scholar] [CrossRef]
- Belderbos, A.; Delarue, E.; Kessels, K.; D’haeseleer, W. Levelized cost of storage—Introducing novel metrics. Energy Econ. 2017, 67, 287–299. [Google Scholar] [CrossRef]
- Walawalkar, R.; Apt, J.; Mancini, R. Economics of electric energy storage for energy arbitrage and regulation in New York. Energy Policy 2007, 35, 2558–2568. [Google Scholar] [CrossRef]
- Hart, W.E.; Laird, C.D.; Watson, J.-P.; Woodruff, D.L.; Hackebeil, G.A.; Nicholson, B.L.; Siirola, J.D. Pyomo—Optimization Modeling in Python, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Hart, W.E.; Watson, J.-P.; Woodruff, D.L. Pyomo: Modeling and solving mathematical programs in Python. Math. Program. Comput. 2011, 3, 219–260. [Google Scholar] [CrossRef]
- Forrest, J.J.; Vigerske, S.; Santos, H.G.; Ralphs, T.; Hafer, L.; Kristjansson, B.; jpfasano; EdwinStraver; Lubin, M.; rlougee; et al. coin-or/Cbc: Version 2.10.5, COIN-OR. 2020. Available online: https://zenodo.org/badge/latestdoi/173509563 (accessed on 5 September 2021).
- Nag, S.; Lee, K.Y.; Suchitra, D. A Comparison of the Dynamic Performance of Conventional and Ternary Pumped Storage Hydro. Energies 2019, 12, 3513. [Google Scholar] [CrossRef]
- Mousavi, N.; Kothapalli, G.; Habibi, D.; Khiadani, M.; Das, C. An improved mathematical model for a pumped hydro storage system considering electrical, mechanical, and hydraulic losses. Appl. Energy 2019, 247, 228–236. [Google Scholar] [CrossRef]
- Sun, J. Hydraulic Machinery. In Davis’ Handbook of Applied Hydraulics; Zipparro, V., Hasen, H., Eds.; McGraw Hill: New York, NY, USA, 1993; p. 21.23. [Google Scholar]
- Chen, H. Pumped Storage. In Davis’ Handbook of Applied Hydraulics; Zipparro, V., Hasen, H., Eds.; McGraw Hill: New York, NY, USA, 1993; p. 20.23. [Google Scholar]
- Bostan, A.; Dorian, N.; Peris-Bendu, F. The Hill Chart Calculation for Francis Runner Models using the HydroHillChart—Francis Module Software. Analele Univ. Eftimie Murgu Reşiţa 2015, 22, 107–116. [Google Scholar]
- Kent-Johnston, J.; SMEC. Energy Arbitrage Undergraduate Research Interview via Zoom to Timothy Weber. 29 July; 2021.
- Darling, R.M.; Gallagher, K.G.; Kowalski, J.A.; Ha, S.; Brushett, F.R. Pathways to low-cost electrochemical energy storage: A comparison of aqueous and nonaqueous flow batteries. Energy Environ. Sci. 2014, 7, 3459–3477. [Google Scholar] [CrossRef]
- Rancilio, G.; Merlo, M.; Lucas, A.; Kotsakis, E.; Delfanti, M. BESS modeling: Investigating the role of auxiliary system consumption in efficiency derating. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 24–26 June 2020; pp. 189–194. [Google Scholar]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery Under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Ahmadi, L.; Yip, A.; Fowler, M.; Young, S.B.; Fraser, R.A. Environmental feasibility of re-use of electric vehicle batteries. Sustain. Energy Technol. Assess. 2014, 6, 64–74. [Google Scholar] [CrossRef]
- Woody, M.; Arbabzadeh, M.; Lewis, G.M.; Keoleian, G.A.; Stefanopoulou, A. Strategies to limit degradation and maximize Li-ion battery service lifetime—Critical review and guidance for stakeholders. J. Energy Storage 2020, 28, 101231. [Google Scholar] [CrossRef]
- Spotnitz, R. Simulation of capacity fade in lithium-ion batteries. J. Power Sources 2003, 113, 72–80. [Google Scholar] [CrossRef]
- Stroe, D.-I.; Swierczynski, M.; Kar, S.K.; Teodorescu, R. Degradation Behavior of Lithium-Ion Batteries During Calendar Ageing—The Case of the Internal Resistance Increase. In Proceedings of the 8th Annual IEEE Energy Conversion Congress and Exposition (ECCE), Nashville, TN, USA, 29 October–2 November 2023; pp. 517–525. [Google Scholar]
- Petit, M.; Prada, E.; Sauvant-Moynot, V. Development of an empirical aging model for Li-ion batteries and application to assess the impact of Vehicle-to-Grid strategies on battery lifetime. Appl. Energy 2016, 172, 398–407. [Google Scholar] [CrossRef]
- Wang, J.; Liu, P.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Cycle-life model for graphite-LiFePO4 cells. J. Power Sources 2011, 196, 3942–3948. [Google Scholar] [CrossRef]
- National Electricity Rules version 204 (SA). Available online: https://energy-rules.aemc.gov.au/ner/499 (accessed on 18 September 2021).
- AEMC. Interim Report: Transmission Access Reform: Updated Technical Specifications and Cost-Benefit Analysis. 7 September 2020. Available online: https://www.aemc.gov.au/sites/default/files/2020-09/Interim%20report%20-%20transmission%20access%20reform%20-%20Updated%20technical%20specifications%20and%20cost-benefit%20analysis%202020_09_07.PDF (accessed on 11 October 2022).
- Reichelstein, S.; Yorston, M. The prospects for cost competitive solar PV power. Energy Policy 2013, 55, 117–127. [Google Scholar] [CrossRef]
- Income Tax Assessment Act 1997 (Cth). 1997. Available online: https://www.legislation.gov.au/Details/C2023C00472 (accessed on 18 September 2021).
- Grolleau, S.; Molina-Concha, B.; Delaille, A.; Revel, R.; Bernard, J.; Pélissier, S.; Peter, J. The French SIMCAL Research Network For Modelling of Calendar Aging for Energy Storage System in EVs And HEVs—EIS Analysis on LFP/C Cells. ECS Trans. 2013, 45, 73–81. [Google Scholar] [CrossRef]
- AEMO. Current Inputs, Assumptions and Scenarios. 11 December 2020. Available online: https://aemo.com.au/-/media/files/electricity/nem/planning_and_forecasting/inputs-assumptions-methodologies/2020/2020-inputs-and-assumptions-workbook-dec20.xlsx?la=en (accessed on 12 June 2021).
- Graham, P.; Hayward, J.; Foster, J.; Havas, L.; CSIRO. GenCost 2020–21 Consultation Draft. December 2020. Available online: https://www.csiro.au/-/media/News-releases/2020/renewables-cheapest/GenCost2020-21.pdf (accessed on 18 September 2021).
- Moss, S.; AURECON. 2020 Costs and Technical Parameters Review Consultation Report. 10 December 2020. Available online: https://aemo.com.au/-/media/files/electricity/nem/planning_and_forecasting/inputs-assumptions-methodologies/2021/aurecon-cost-and-technical-parameters-review-2020.pdf?la=en (accessed on 18 September 2021).
- AEMO. Pre-Dispatch (SO_OP_3704). 2021. Available online: https://www.aemo.com.au/-/media/files/electricity/nem/5ms/procedures-workstream/stakeholder-consultation/dispatch-procedures/so_op_3704---predispatch---marked-up.pdf (accessed on 16 May 2021).
- Saraiva, J.P.; Lima, B.S.; Gomes, V.M.; Flores, P.H.R.; Gomes, F.A.; Assis, A.O.; Reis, M.R.C.; Araujo, W.R.H.; Abrenhosa, C.; Calixto, W.P. Calculation of sensitivity index using one-at-a-time measures based on graphical analysis. In Proceedings of the 2017 18th International Scientific Conference on Electric Power Engineering (EPE), Kouty nad Desnou, Czech Republic, 17–19 May 2017; pp. 1–6. [Google Scholar]
- Biggins, F.; Ejeh, J.; Brown, S. Going, Going, Gone: Optimising the bidding strategy for an energy storage aggregator and its value in supporting community energy storage. Energy Rep. 2022, 8, 10518–10532. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A. Optimal scheduling of electric vehicle charging and vehicle-to-grid services at household level including battery degradation and price uncertainty. IET Gener. Transm. Distrib. 2014, 8, 1007–1016. [Google Scholar] [CrossRef]
- Biggins, F.; Homan, S.; Ejeh, J.; Brown, S. To trade or not to trade: Simultaneously optimising battery storage for arbitrage and ancillary services. J. Energy Storage 2022, 50, 104234. [Google Scholar] [CrossRef]
- Gundogdu, B.M.; Gladwin, D.T.; Nejad, S.; Stone, D.A. Scheduling of grid-tied battery energy storage system participating in frequency response services and energy arbitrage. IET Gener. Transm. Distrib. 2019, 13, 2930–2941. [Google Scholar] [CrossRef]
- Pusceddu, E.; Zakeri, B.; Gissey, G.C. Synergies between energy arbitrage and fast frequency response for battery energy storage systems. Appl. Energy 2020, 283, 116274. [Google Scholar] [CrossRef]
- SMA. SUNNY TRIPOWER 15000TL/20000TL/25000TL. 2021. Available online: https://files.sma.de/downloads/STP15-25TL-30-DS-en-41.pdf?_ga=2.240538051.1910003011.1633326314-555238174.1633326314 (accessed on 4 October 2021).
- Tesla. Tesla, Inc. Annual Report on Form 10-K for the Year Ended December 31. 2019. Available online: https://www.sec.gov/Archives/edgar/data/1318605/000156459020004475/tsla-10k_20191231.htm (accessed on 19 September 2021).
- Sangal, S.; Garg, A.; Kumar, D. Review of optimal selection of turbines for hydroelectric projects. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 424–430. [Google Scholar]
- Avellan, F. Introduction to cavitation in hydraulic machinery. In Proceedings of the 6th International Conference on Hydraulic Machinery and Hydrodynamics, Timisoara, Romania, 21–22 October 2004; pp. 11–22. [Google Scholar]




| Calendar Aging | ||||||
| SOC | 30% | 65% | 100% | |||
| ACcal | 7.34 × 105 | 6.75 × 105 | 2.18 × 105 | |||
| Eacal [J/mol] | 73,369 | 69,804 | 56,937 | |||
| AEcal | 0.943 | 0.900 | 0.683 | |||
| Cycle Aging | ||||||
| Icell [A] | 1 | 4 | 12 | 20 | ||
| ACcyc | 2.16 × 103 | 2.17 × 104 | 1.29 × 104 | 1.55 × 104 | ||
| Eacyc [J/mol] | 31,700 | |||||
| AEcyc | 0.55 | |||||
| γ [J·mol−1·A−1] | 370.3 | |||||
| Storage System | Metric | Kendall Tau-b for Metric vs. Price Volatility | p-Value |
|---|---|---|---|
| 1 h BESS | RADP | 0.1703 | 6.6260 × 10−2 |
| 12 h PHS | RADP | 0.2593 | 5.1912 × 10−3 |
| 24 h PHS | RADP | 0.2498 | 7.0751 × 10−3 |
| 1 h BESS | AADP | 0.4936 | 1.0306 × 10−7 |
| 12 h PHS | AADP | 0.4182 | 6.5388 × 10−6 |
| 24 h PHS | AADP | 0.4114 | 9.1825 × 10−6 |
| Technology | Variable 1 | Variable 2 | Kendall Tau-b | p-Value |
|---|---|---|---|---|
| BESS | Average Offer Risk Price [$/MWh] | Change in RADP [%] | −0.40 | 1.2 × 10−3 |
| Change in AADP [%] | 0.36 | 4.2 × 10−3 | ||
| Average Bid Risk Price [$/MWh] | Change in RADP [%] | −0.75 | 1.4 × 10−9 | |
| Change in AADP [%] | 0.43 | 5.1 × 10−4 | ||
| 12 h PHS | Average Offer Risk Price [$/MWh] | Change in RADP [%] | −0.33 | 7.7 × 10−8 |
| Change in AADP [%] | 0.39 | 4.0 × 10−10 | ||
| Average Bid Risk Price [$/MWh] | Change in RADP [%] | −0.37 | 2.4 × 10−9 | |
| Change in AADP [%] | 0.44 | 1.3 × 10−12 | ||
| 24 h PHS | Average Offer Risk Price [$/MWh] | Change in RADP [%] | −0.37 | 2.0 × 10−9 |
| Change in AADP [%] | 0.38 | 6.3 × 10−10 | ||
| Average Bid Risk Price [$/MWh] | Change in RADP [%] | −0.43 | 3.0 × 10−12 | |
| Change in AADP [%] | 0.44 | 2.0 × 10−12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weber, T.; Lu, B. An Open-Source Energy Arbitrage Model Involving Price Bands for Risk Hedging with Imperfect Price Signals. Energies 2024, 17, 13. https://doi.org/10.3390/en17010013
Weber T, Lu B. An Open-Source Energy Arbitrage Model Involving Price Bands for Risk Hedging with Imperfect Price Signals. Energies. 2024; 17(1):13. https://doi.org/10.3390/en17010013
Chicago/Turabian StyleWeber, Timothy, and Bin Lu. 2024. "An Open-Source Energy Arbitrage Model Involving Price Bands for Risk Hedging with Imperfect Price Signals" Energies 17, no. 1: 13. https://doi.org/10.3390/en17010013
APA StyleWeber, T., & Lu, B. (2024). An Open-Source Energy Arbitrage Model Involving Price Bands for Risk Hedging with Imperfect Price Signals. Energies, 17(1), 13. https://doi.org/10.3390/en17010013





