Performance Potential of a Concentrated Photovoltaic-Electrochemical Hybrid System
Abstract
:1. Introduction
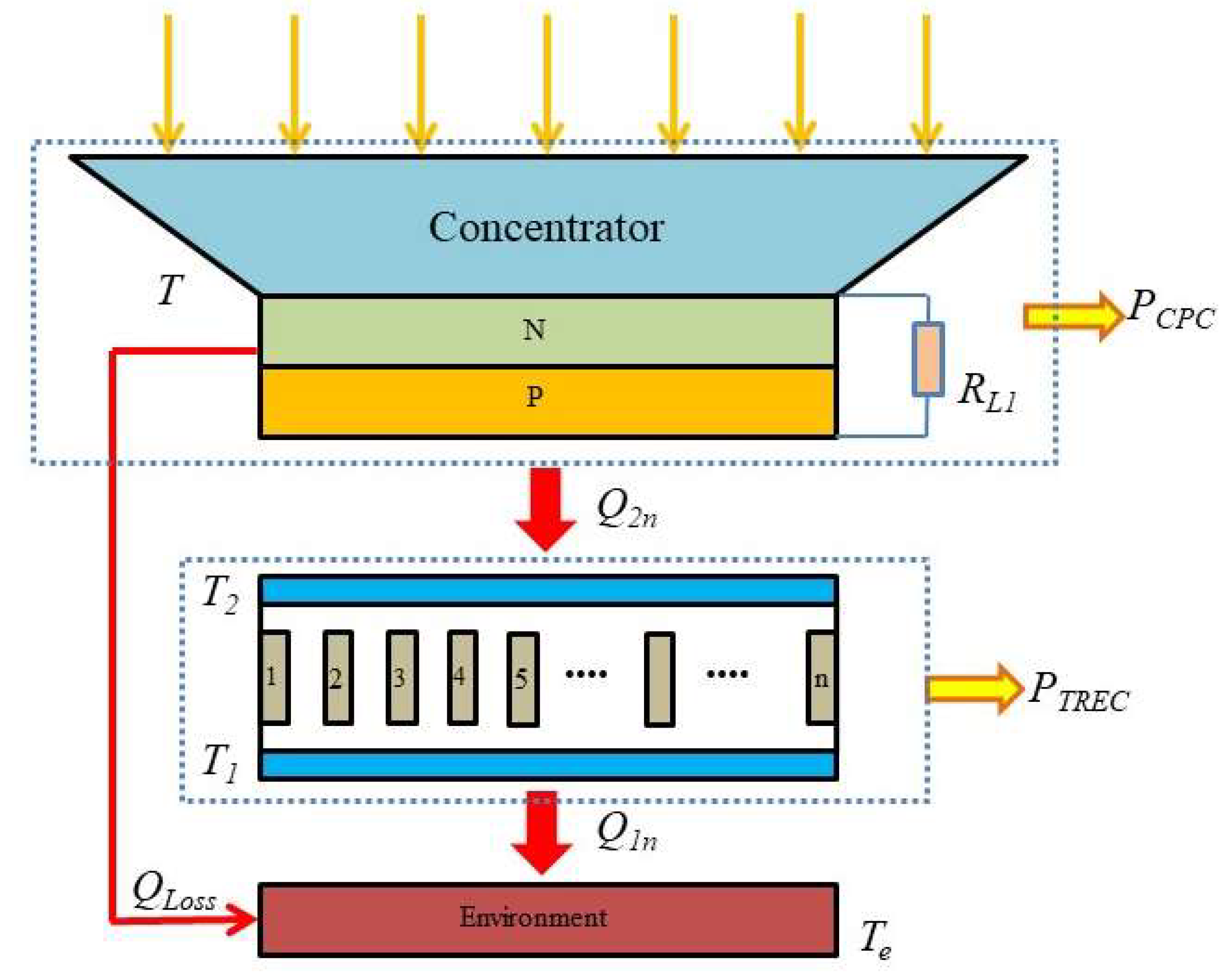
2. System Descriptions
- (1)
- A steady-state heat-transfer model in one dimension (1D) is utilized, focusing solely on heat transfer in the vertical direction without considering lateral heat transfer [15];
- (2)
- The incoming sunlight’s wavelength is converted entirely [16];
- (3)
- The model does not account for irreversible heat transfer between the CPC and the TREC;
- (4)
- As the glass cover is quite thin, any temperature gradient along its thickness can be considered negligible [17];
- (5)
- Operation takes place under steady-state conditions;
- (6)
- The TREC’s heat-sink temperature is equivalent to the surrounding temperature [10];
- (7)
- The TREC’s discharging time equals the charging time, in accordance with reference [18];
- (8)
- The TREC maintains consistent heat capacity, charge capacity, and internal resistance between its charging and discharging phases [19].
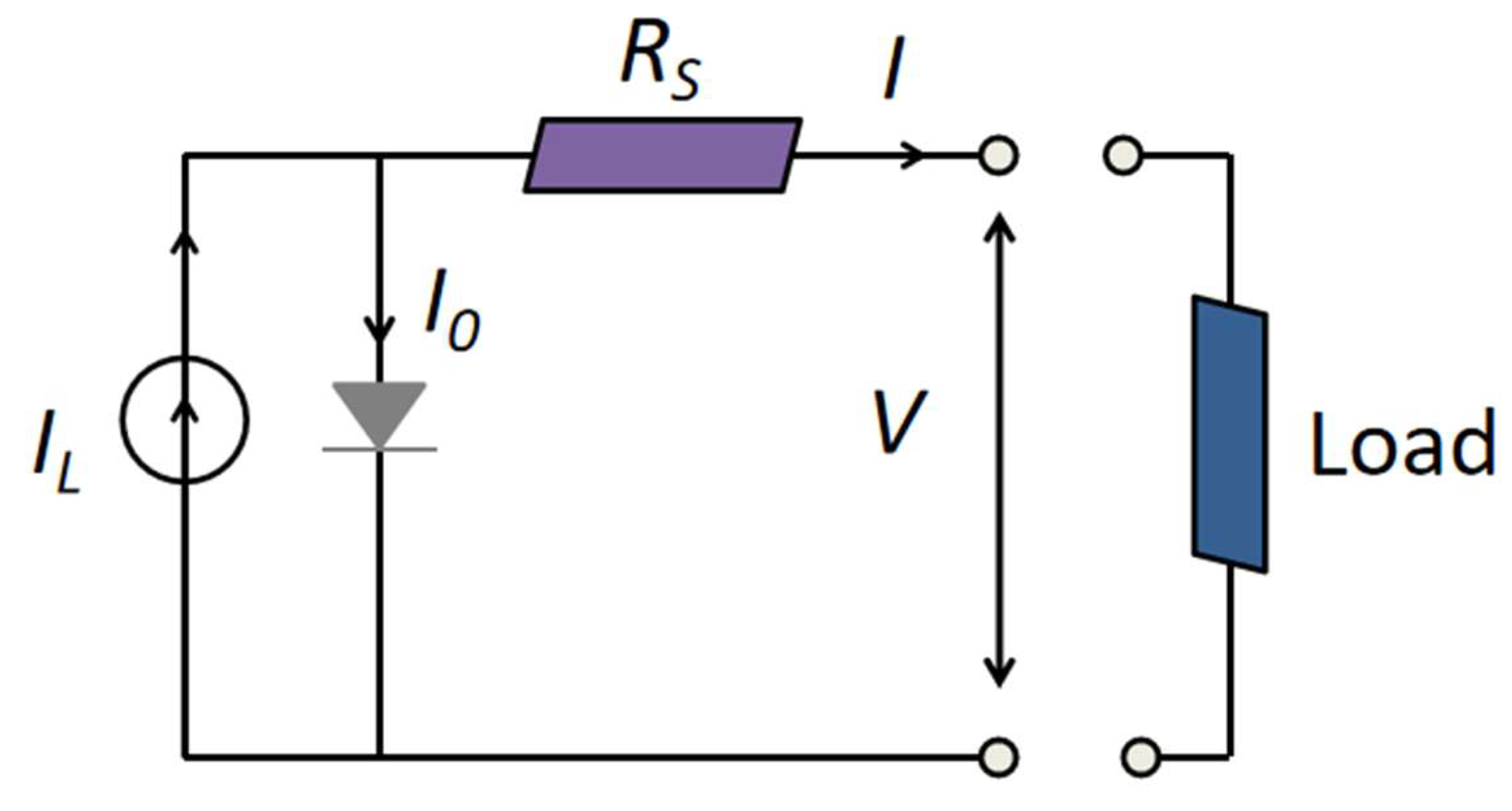
2.1. Concentrated Photovoltaic Cell
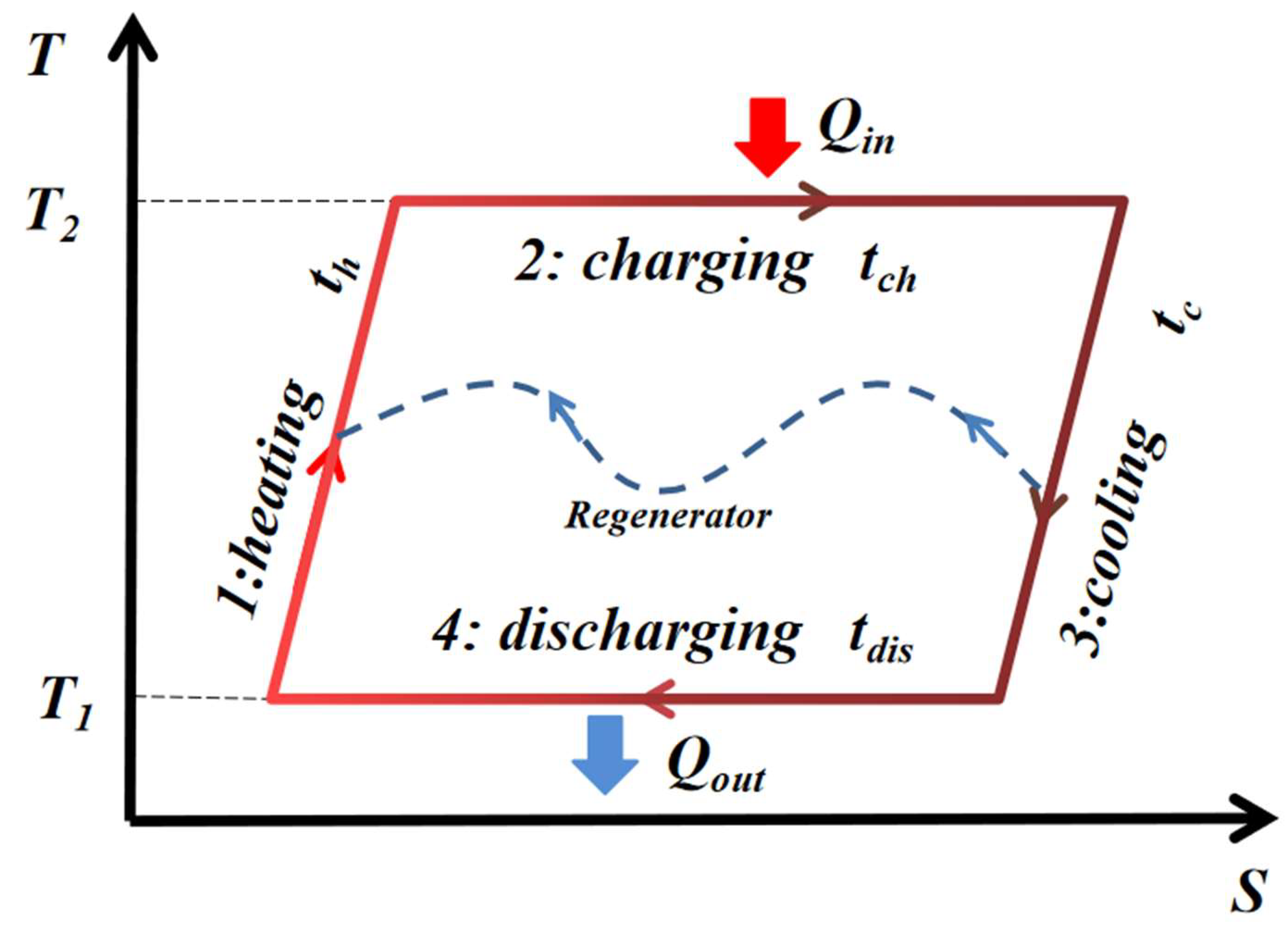
2.2. Thermally Regenerative Electrochemical Cycle
2.3. The Hybrid System
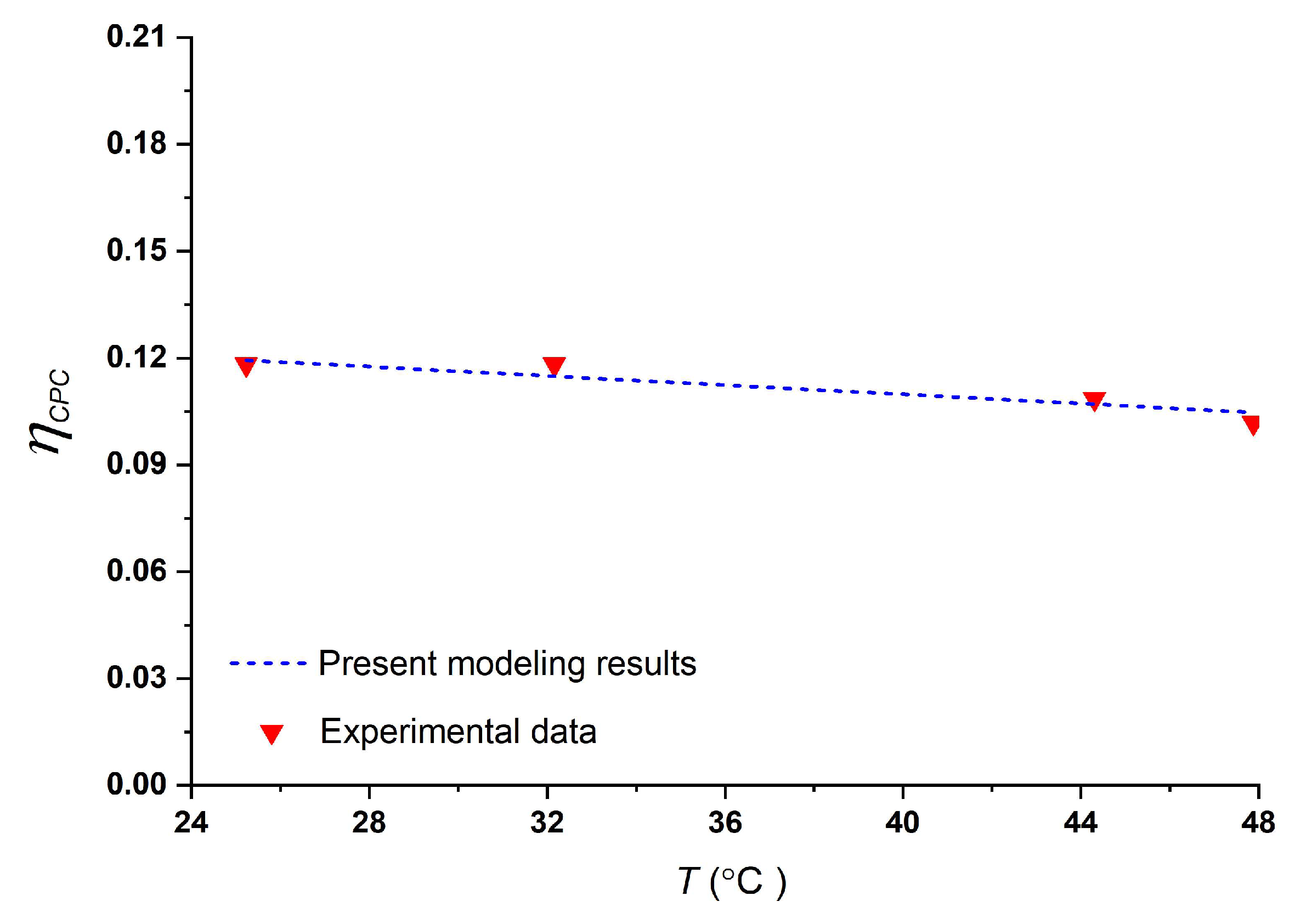
3. Model Validation
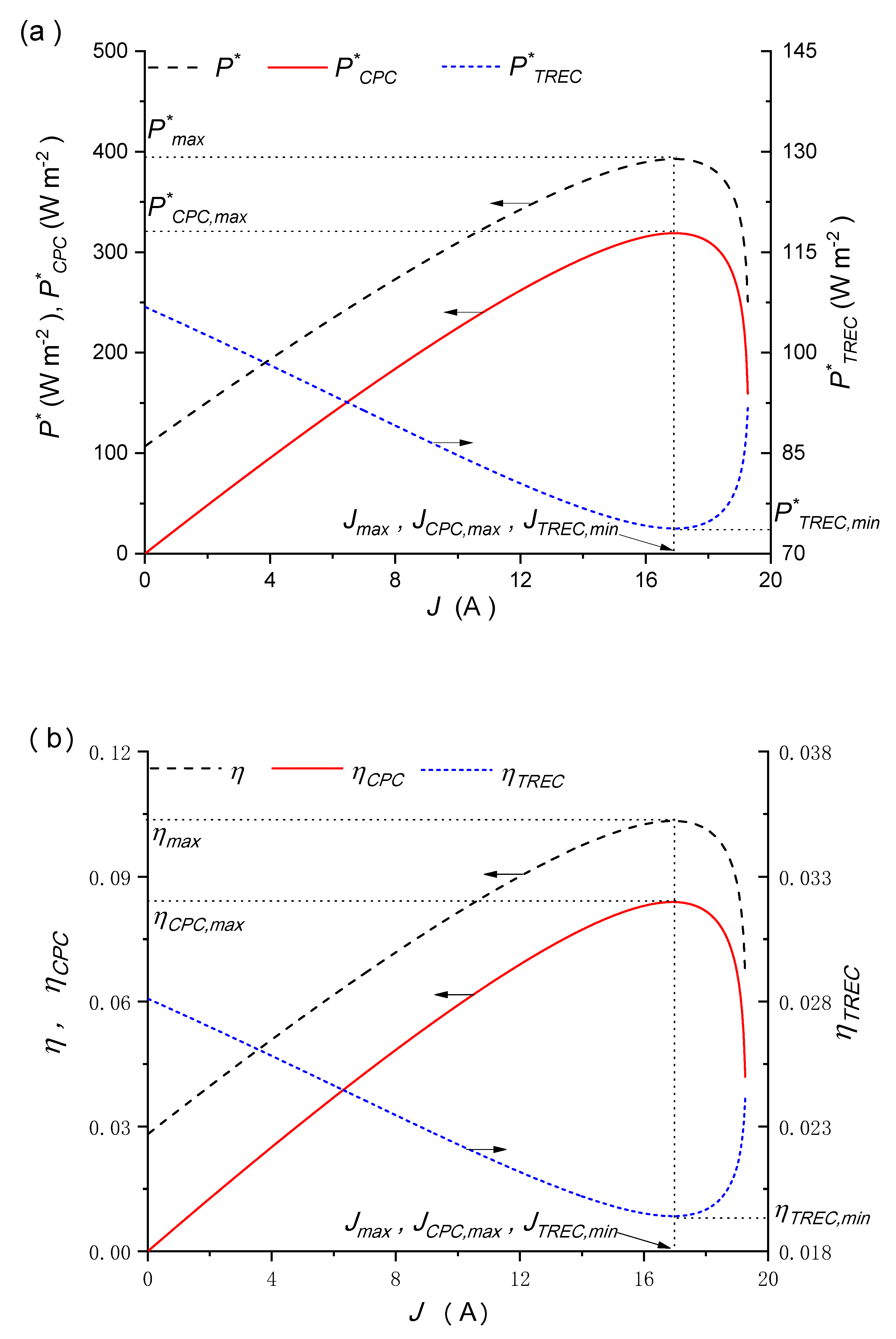
4. Basic Performance Features
5. Results and Discussion
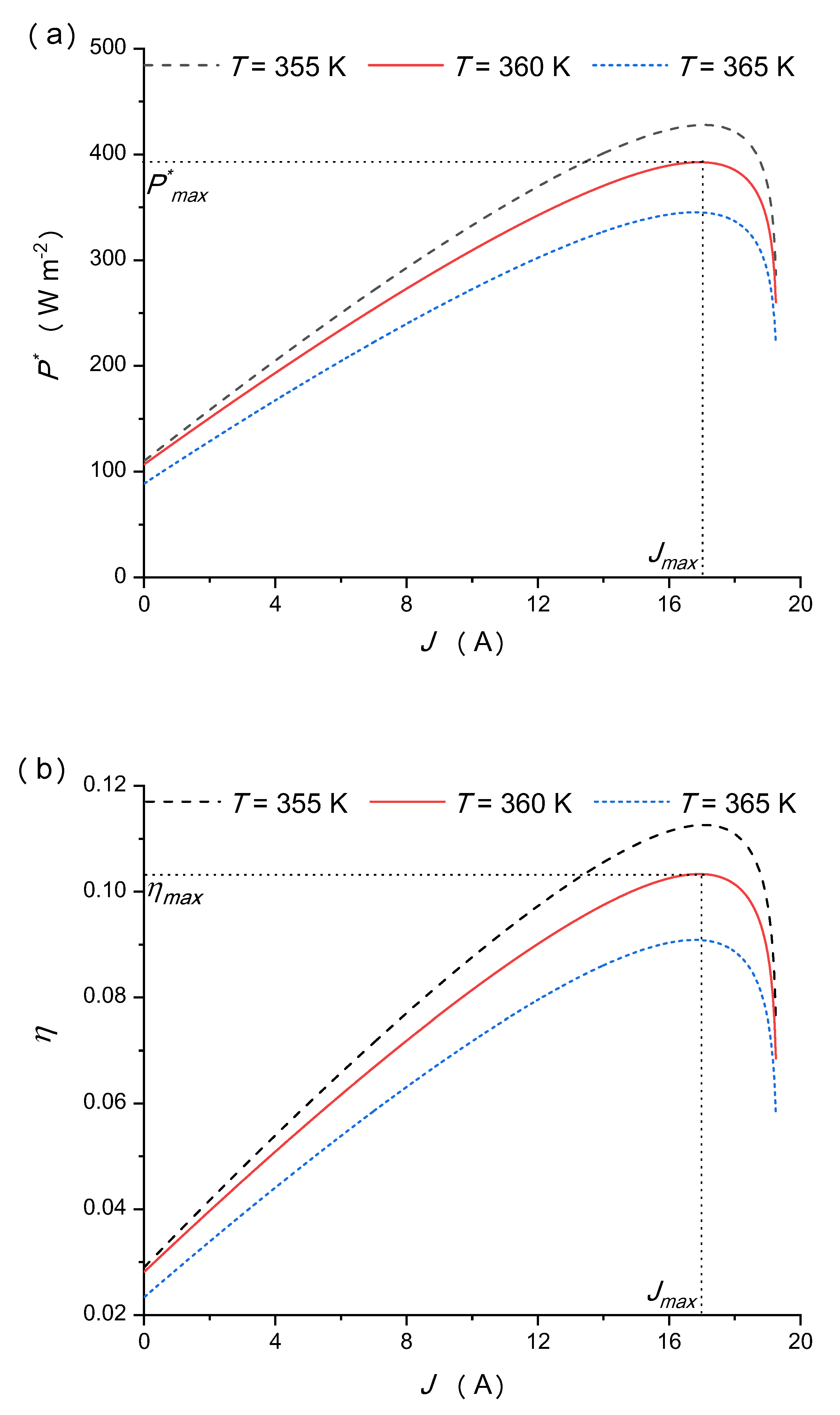
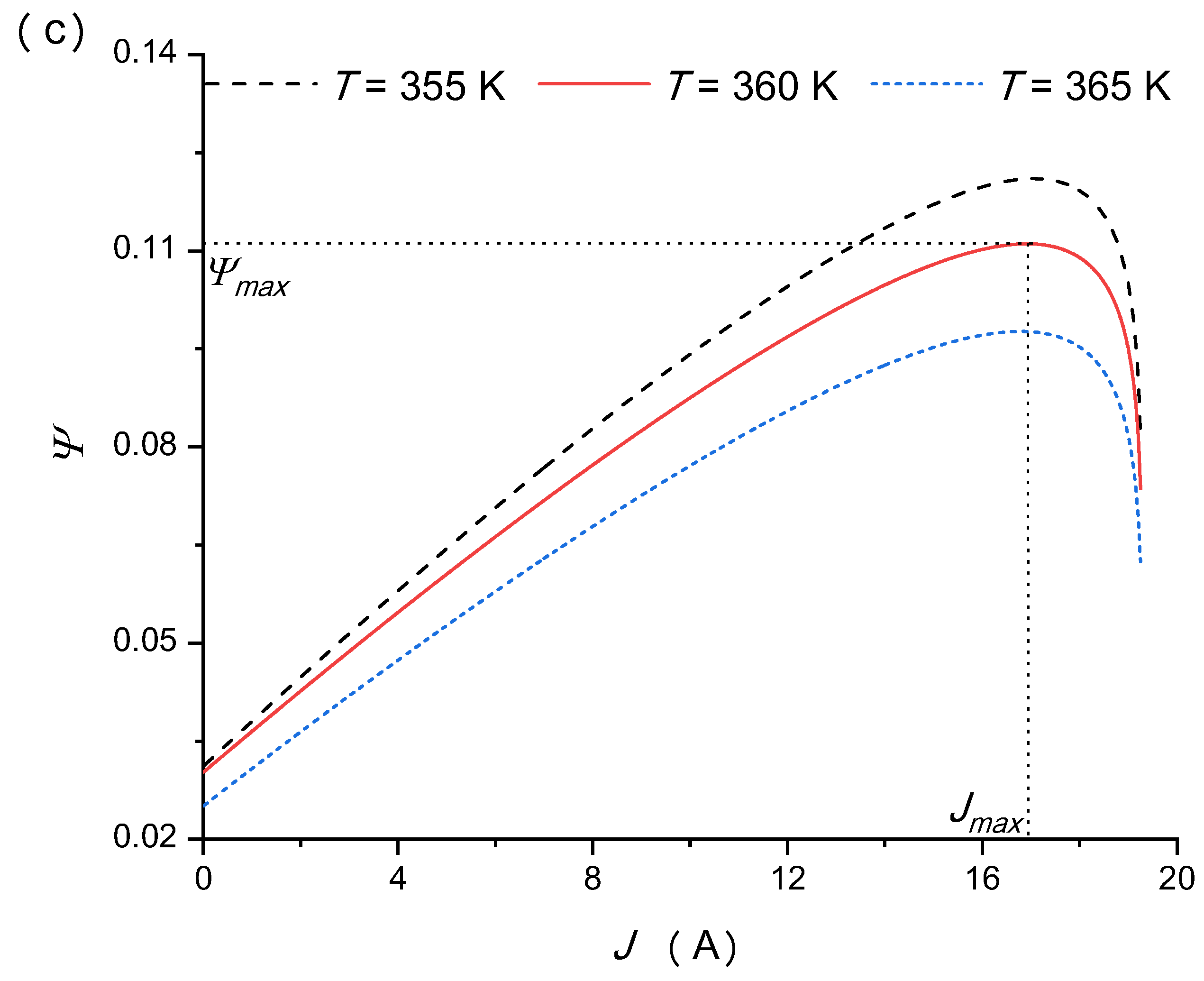
5.1. Effects of the Operating Temperature of the Concentrated Photovoltaic Cell
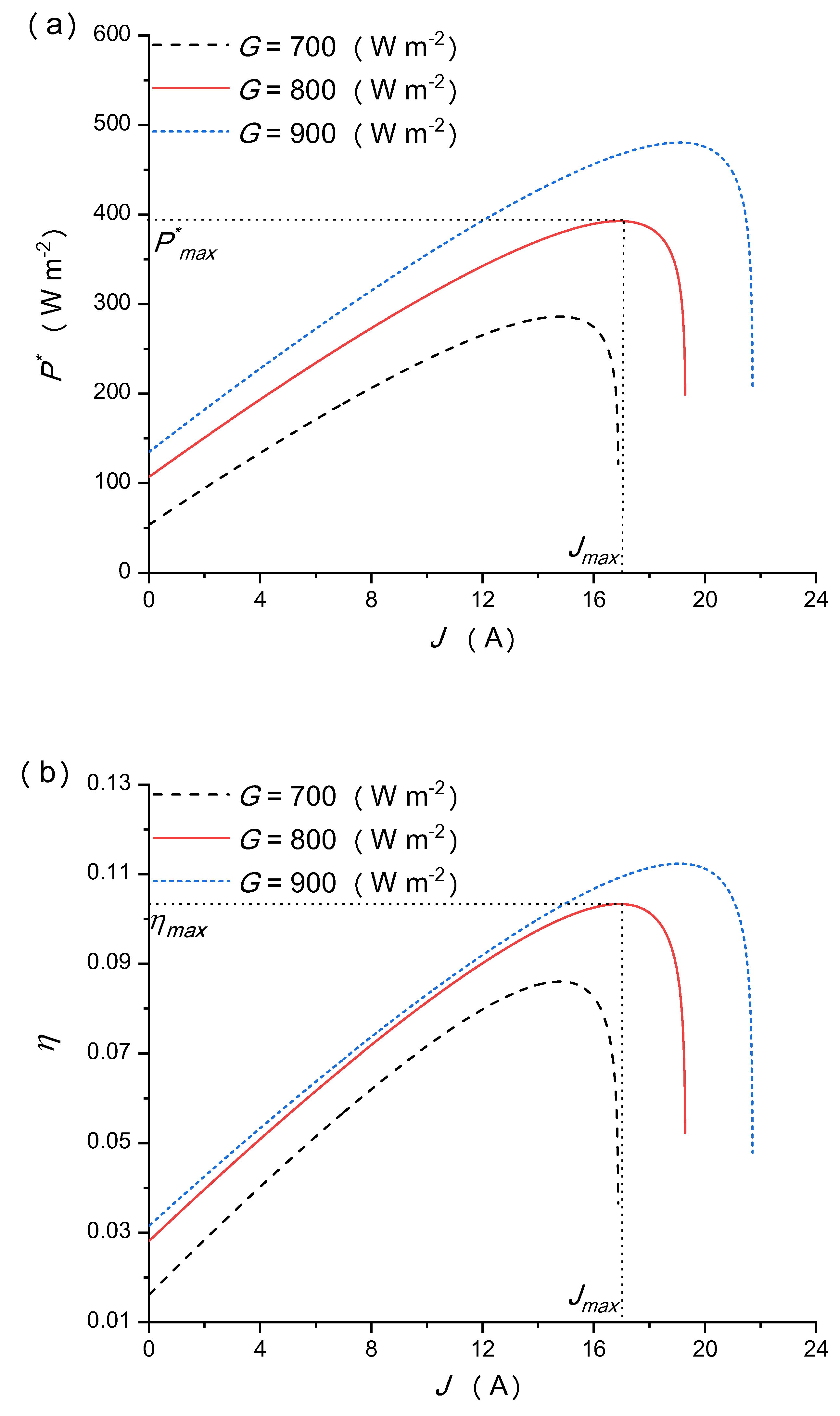
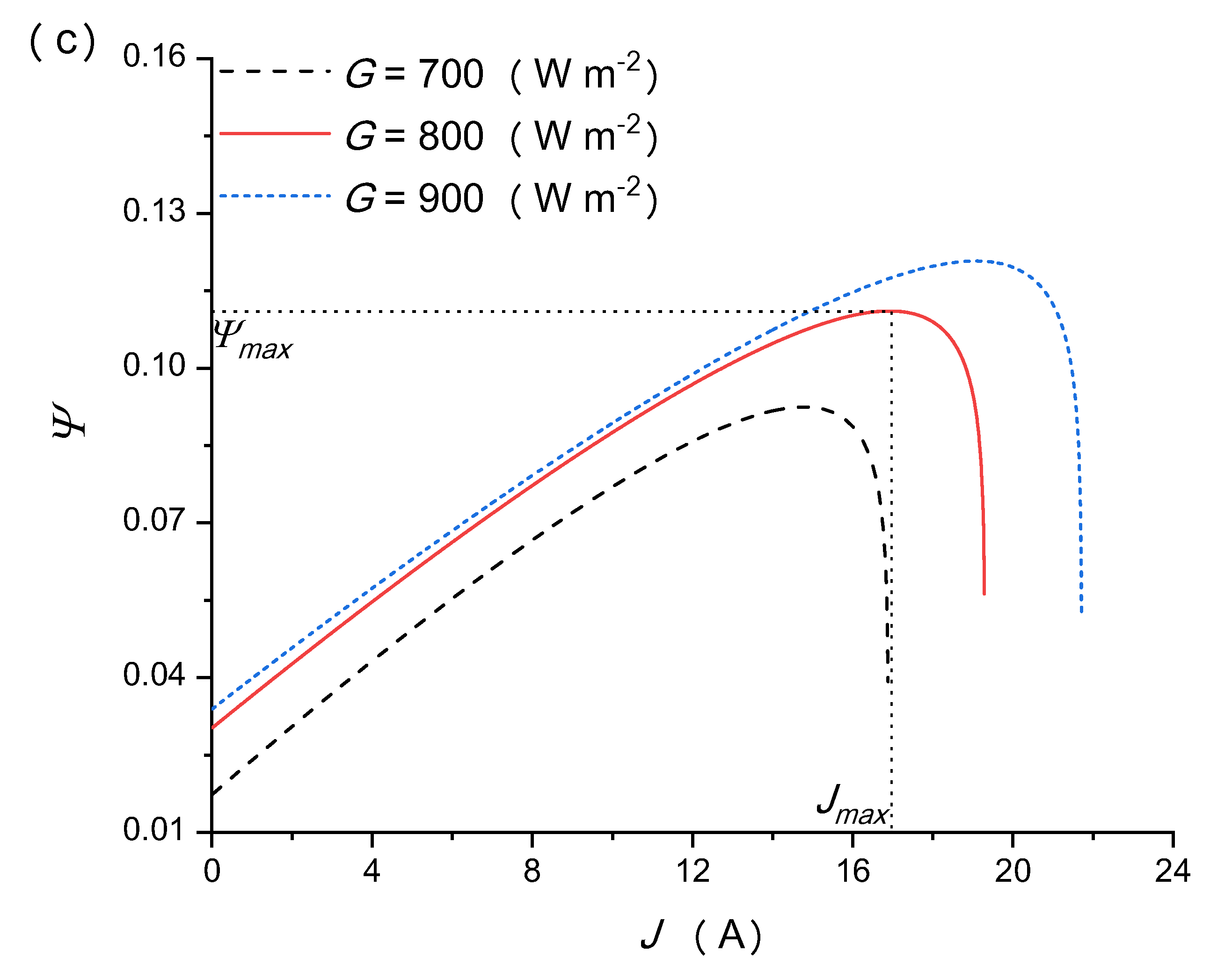
5.2. Effects of the Solar Irradiation
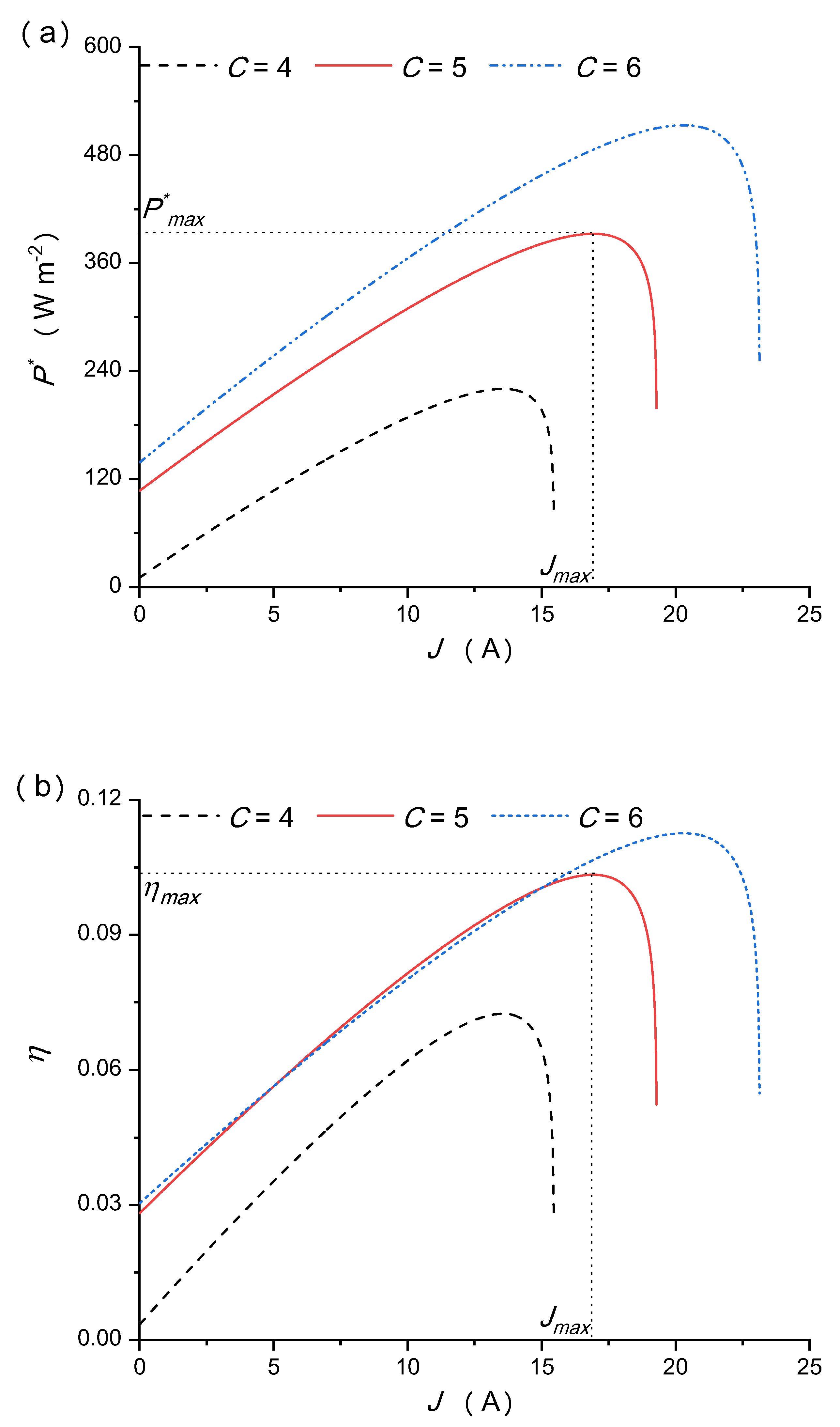
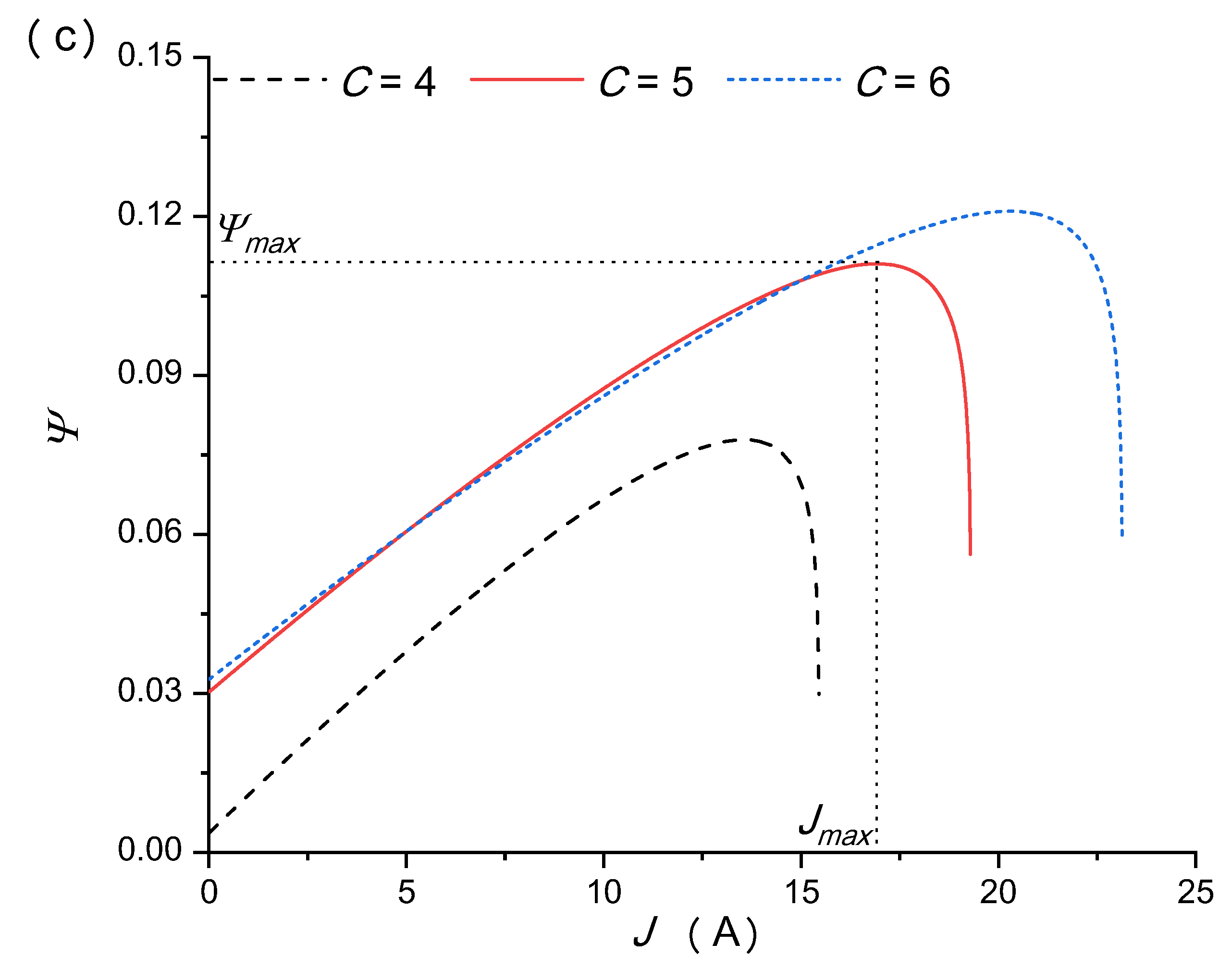
5.3. Effects of the Concentration Ratio
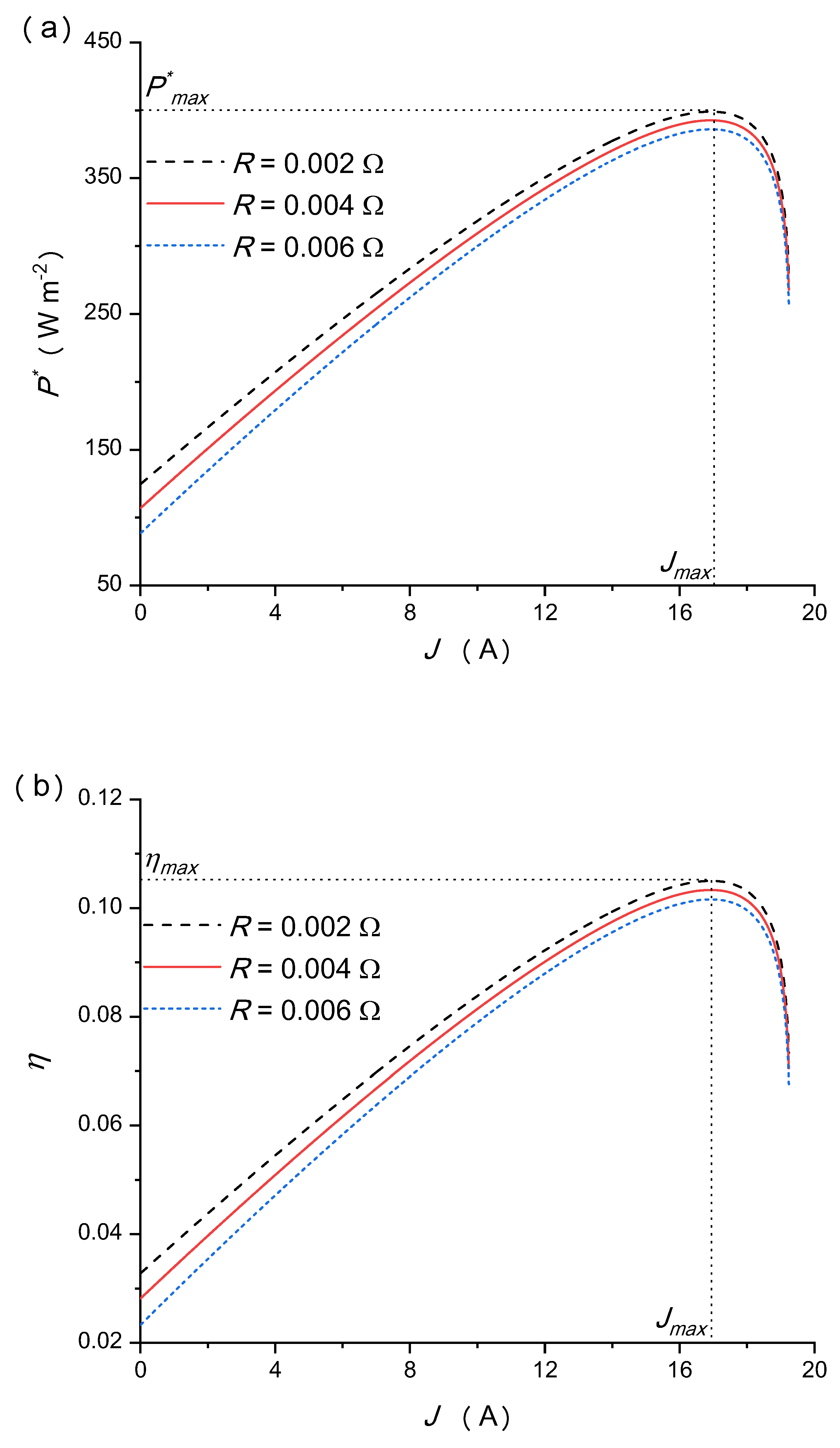
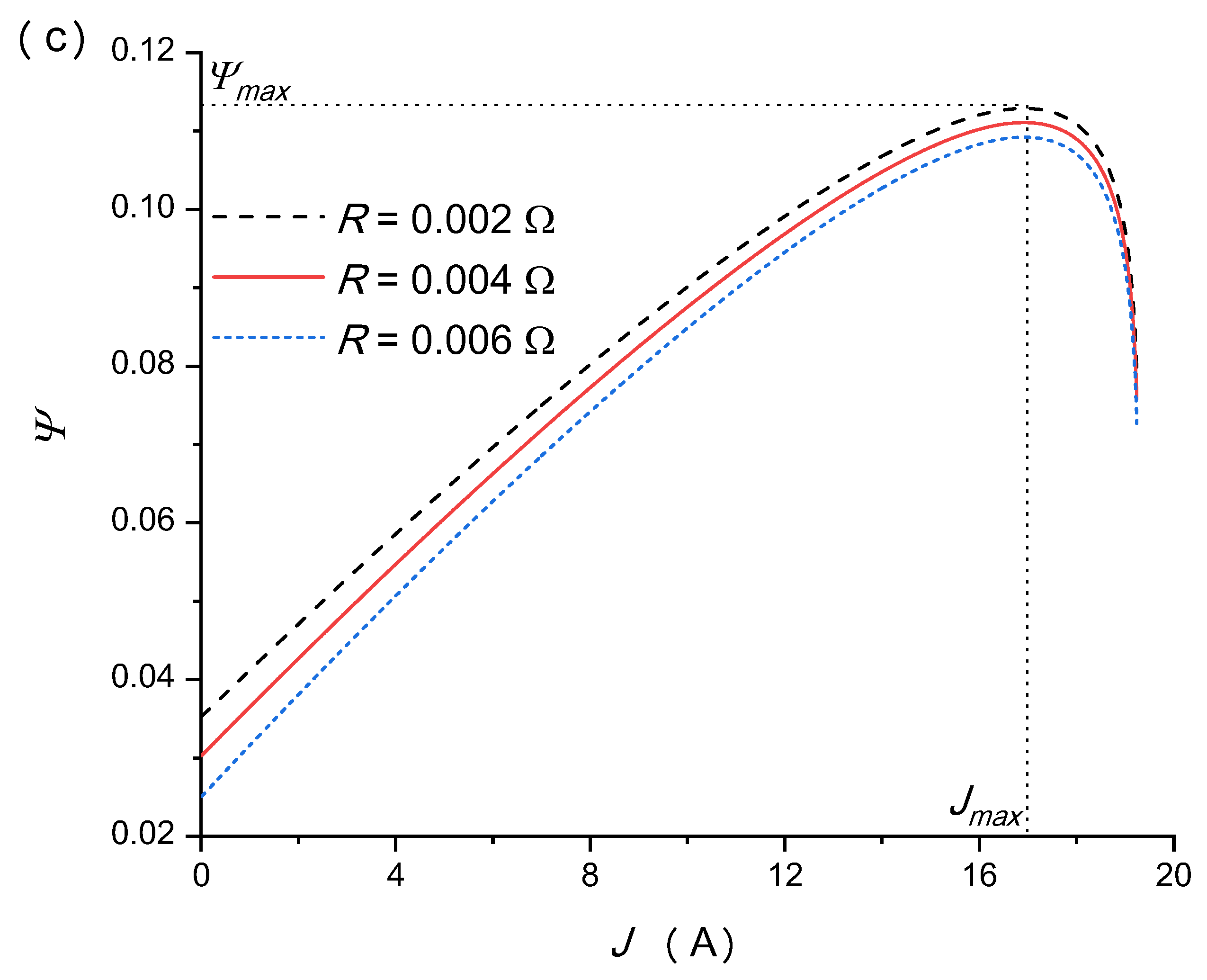
5.4. Effects of the Internal Resistance of Thermally Regenerative Electrochemical Cycle
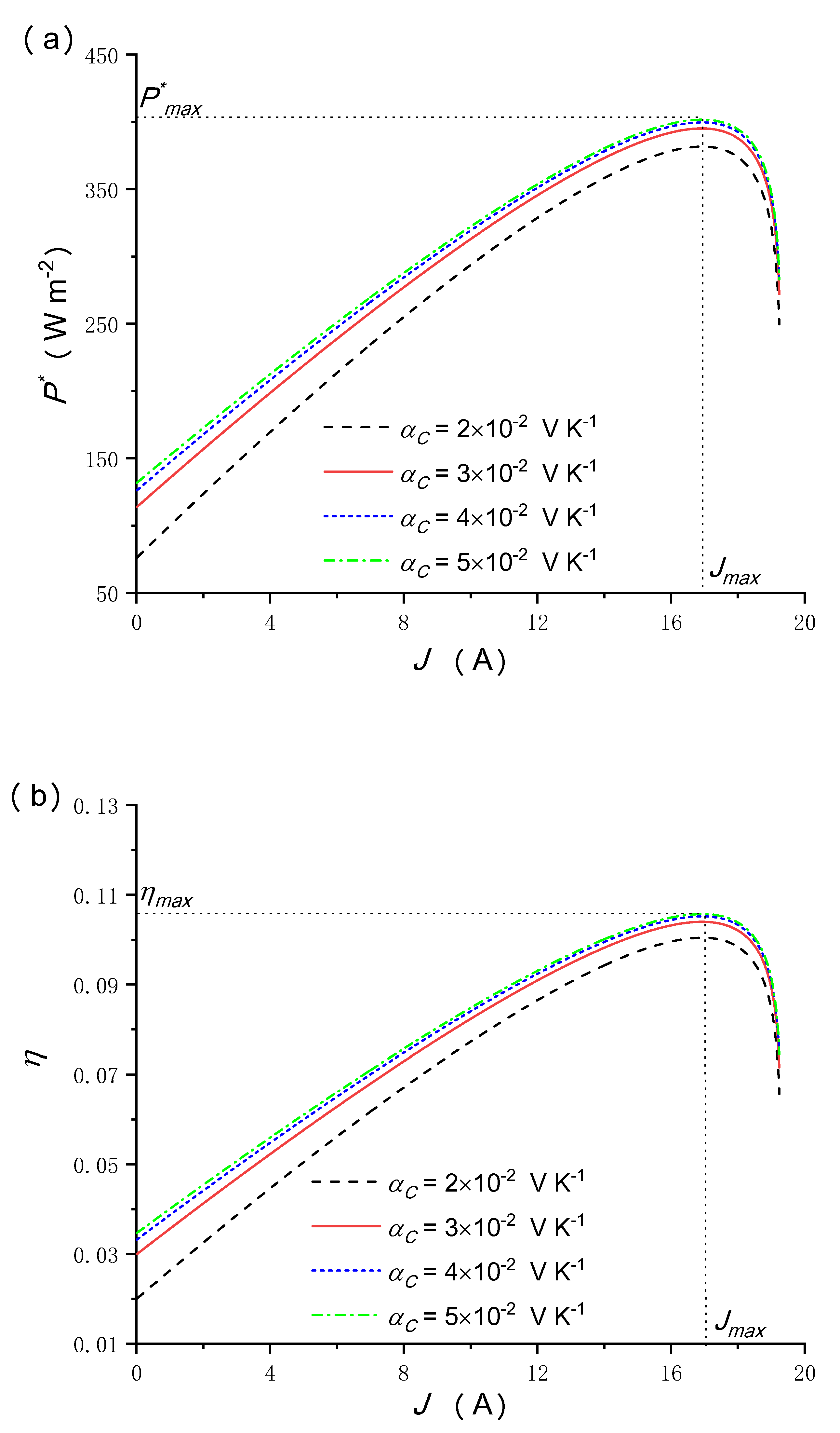
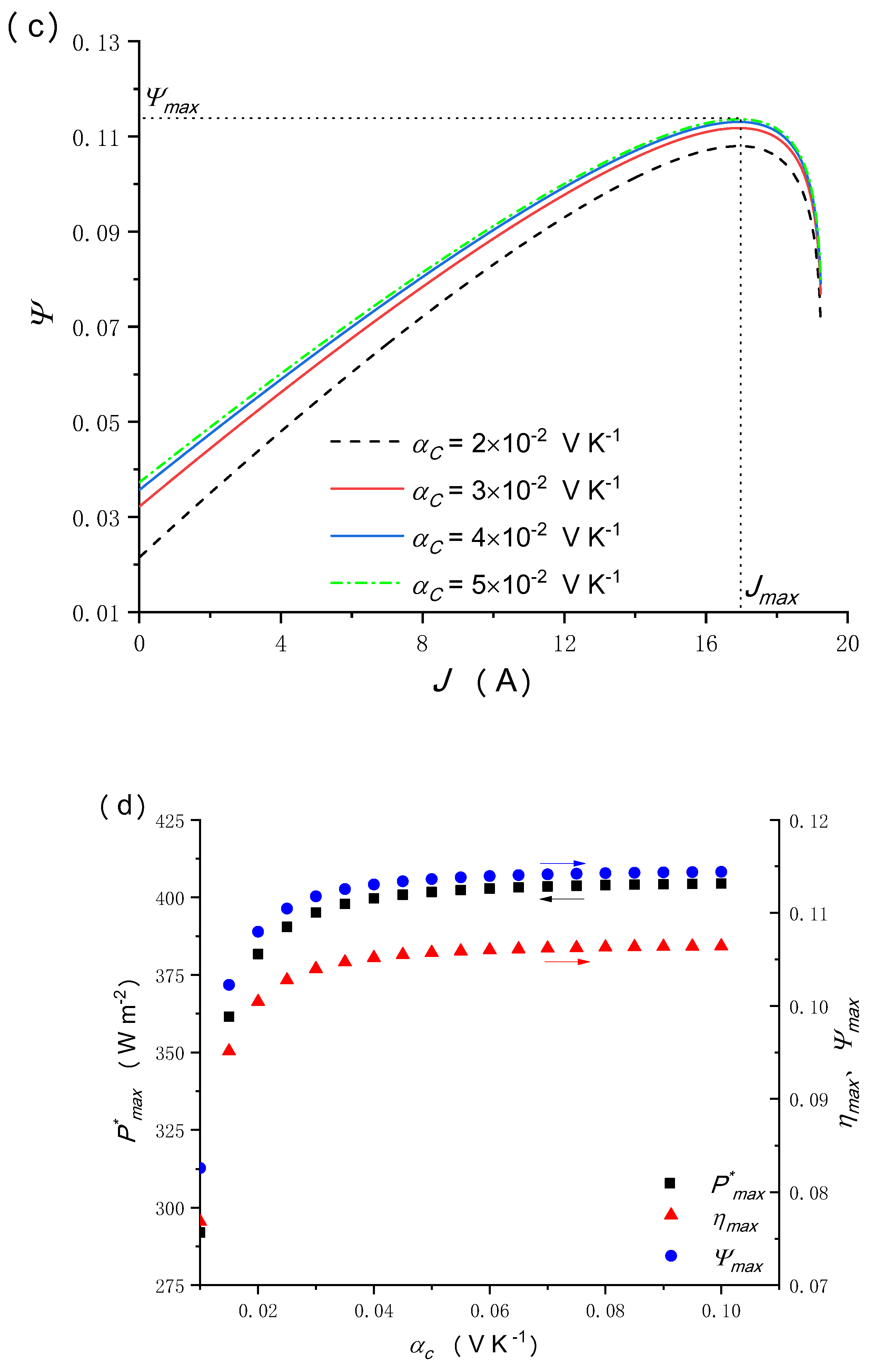
5.5. Effects of the Temperature Coefficient
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Diode ideality factor | |
| Area of PV module (m2) | |
| Optical concentration ratio | |
| Heat capacity (J kg−1 K−1) | |
| Charge capacity (A s−1 kg−1) | |
| Band-gap energy of the semiconductor materials used in the PV (eV) | |
| Total exergy input into the hybrid system per unit time | |
| Exergy output of the hybrid system per unit time | |
| Total exergy input into the TREC | |
| Solar irradiation (W m−2) | |
| Reference solar irradiation (W m−2) | |
| Heat-transfer coefficient of the PV surface | |
| Charge process current (A) | |
| Discharge process current (A) | |
| Losses of the internal irreversibility and external irreversibility in the coupling system | |
| PV array output current (A) | |
| Photocurrent (A) | |
| Diode reverse saturation current (A) | |
| Diode reverse current (A) | |
| Cell short-circuit current at reference temperature and radiation (A) | |
| Overall heat-leak coefficient | |
| Short-circuit current temperature coefficient | |
| Boltzmann constant (J K−1) | |
| Number of cells in parallel | |
| Number of cells in series | |
| Number of the TRECs | |
| Number of cells charging simultaneously | |
| Electric power output of the hybrid system (W) | |
| Electric output power density of the hybrid system (W m−2) | |
| Electric output power density of the CPC (W m−2) | |
| Electric output power density of the TREC (W m−2) | |
| Electric power output of the CPC (W) | |
| Electric power output of the TREC (W) | |
| Charge of an electron (C) | |
| Solar energy transferred to the PV module per unit time (W m−2) | |
| Heat absorbed from the heat released to the cold reservoir during the cycle time (W m−2) | |
| Heat absorbed from the hot reservoir to the cold reservoir during the cycle time (W m−2) | |
| Rate of heat flowing from CPC to TTEG (W m−2) | |
| Rate of heat leaked from the CPC to the environment (W m−2) | |
| Heat absorbed from the hot reservoir to the cold reservoir for a TREC consisting of TREC elements (W m−2) | |
| Heat absorbed from the heat released to the cold reservoir for a TREC consisting of TREC elements (W m−2) | |
| Intrinsic series resistance of the PV cell (Ω) | |
| Load resistances of the CPC module (Ω) | |
| Operating temperature of the CPC (K) | |
| Temperature of cold source (K) | |
| Temperature of heat source (K) | |
| PV cell reference temperature (K) | |
| Environment temperature (K) | |
| Surface temperature of the sun (K) | |
| Time | |
| Time of charge process | |
| Time of discharge process | |
| Time of recombination process | |
| Output voltage of PV module | |
| Wind velocity (m/s) | |
| Greek symbols | |
| Emittance of the selective surface facing the incoming solar radiation | |
| Stefan-Boltzmann constant | |
| Cycle time of the TREC | |
| Efficiency of the hybrid system | |
| Optical energy of the concentrator | |
| Efficiency of regenerative losses | |
| Efficiency of the CPC | |
| Efficiency of the TREC | |
| Temperature coefficient (V K−1) | |
| Exergy efficiencies of the CPC | |
| Exergy efficiencies of the TREC | |
| Exergy efficiencies of the hybrid system | |
| Subscripts | |
| CPC | Concentrated photovoltaic cell |
| max | Maximum |
| min | Minimum |
| Acronyms | |
| MEE | Maximum energy efficiency |
| MPD | Maximum power density |
| MMEE | Maximum exergy |
| PVCs | Photovoltaic cells |
| TREC | Thermally regenerative electrochemical cycle |
| T-S | Temperature-entropy |
References
- Ejaz, A.; Babar, H.; Ali, H.M.; Jamil, F.; Janjua, M.M.; Fattah, I.M.R.; Said, Z.; Li, C. Concentrated photovoltaics as light harvesters: Outlook, recent progress, and challenges. Sustain. Energy Technol. Assess. 2021, 46, 101199. [Google Scholar] [CrossRef]
- Sabry, M.; Lashin, A.; Al Turkestani, M. Experimental and simulation investigations of CPV/TEG hybrid system. J. King Saud Univ. Sci. 2021, 33, 101321. [Google Scholar] [CrossRef]
- Rejeb, O.; Shittu, S.; Ghenai, C.; Li, G.; Zhao, X.; Bettayeb, M. Optimization and performance analysis of a solar concentrated photovoltaic-thermoelectric (CPV-TE) hybrid system. Renew. Energy 2020, 152, 1342–1353. [Google Scholar] [CrossRef]
- Ceylan, İ.; Gürel, A.E.; Ergün, A.; Guma, İ.H.G.; Ağbulut, Ü.; Yıldız, G. A detailed analysis of CPV/T solar air heater system with thermal energy storage: A novel winter season application. J. Build. Eng. 2021, 42, 103097. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Q.; Li, D.; Hong, H. Thermodynamic analysis for a concentrating photovoltaic-photothermochemical hybrid system. Energy 2018, 148, 528–536. [Google Scholar] [CrossRef]
- Long, R.; Li, B.; Liu, Z.; Liu, W. Performance analysis of a thermally regenerative electrochemical cycle for harvesting waste heat. Energy 2015, 87, 463–469. [Google Scholar] [CrossRef]
- Tang, X.; Li, G.; Zhao, X. Performance analysis of a novel hybrid electrical generation system using photovoltaic/thermal and thermally regenerative electrochemical cycle. Energy 2021, 232, 120998. [Google Scholar] [CrossRef]
- Abdollahipour, A.; Sayyaadi, H. Thermal energy recovery of molten carbonate fuel cells by thermally regenerative electrochemical cycles. Energy 2021, 227, 120489. [Google Scholar] [CrossRef]
- Açıkkalp, E.; Ahmadi, M.H. Parametric investigation of phosphoric acid fuel cell—Thermally regenerative electro chemical hybrid system. J. Clean. Prod. 2018, 203, 585–600. [Google Scholar] [CrossRef]
- Zhao, Q.; Guo, X.; Zhang, H.; Ni, M.; Hou, S. Performance evaluation of a novel photovoltaic-electrochemic hybrid system. Energy Convers. Manag. 2019, 195, 1227–1237. [Google Scholar] [CrossRef]
- Zhang, X.; Pan, Y.; Cai, L.; Zhao, Y.; Chen, J. Using electrochemical cycles to efficiently exploit the waste heat from a proton exchange membrane fuel cell. Energy Convers. Manag. 2017, 144, 217–223. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H. Performance analyses of a combined system consisting of high-temperature polymer electrolyte membrane fuel cells and thermally regenerative electrochemical cycles. Energy 2020, 193, 116720. [Google Scholar] [CrossRef]
- Zhang, X.; Cai, L.; Liao, T.; Zhou, Y.; Zhao, Y.; Chen, J. Exploiting the waste heat from an alkaline fuel cell via electrochemical cycles. Energy 2018, 142, 983–990. [Google Scholar] [CrossRef]
- Najafi, H.; Woodbury, K.A. Optimization of a cooling system based on Peltier effect for photovoltaic cells. Sol. Energy 2013, 91, 152–160. [Google Scholar] [CrossRef]
- Lamba, R.; Kaushik, S.C. Solar driven concentrated photovoltaic-thermoelectric hybrid system: Numerical analysis and optimization. Energy Convers. Manag. 2018, 170, 34–49. [Google Scholar] [CrossRef]
- Guo, X.-Z.; Zhang, Y.-D.; Qin, D.; Luo, Y.-H.; Li, D.-M.; Pang, Y.-T.; Meng, Q.-B. Hybrid tandem solar cell for concurrently converting light and heat energy with utilization of full solar spectrum. J. Power Sources 2010, 195, 7684–7690. [Google Scholar] [CrossRef]
- Lamba, R.; Kaushik, S.C. Modeling and performance analysis of a concentrated photovoltaic–thermoelectric hybrid power generation system. Energy Convers. Manag. 2016, 115, 288–298. [Google Scholar] [CrossRef]
- Wang, Y.; Cai, L.; Peng, W.; Zhou, Y.; Chen, J. Maximal continuous power output and parametric optimum design of an electrochemical system driven by low-grade heat. Energy Convers. Manag. 2017, 138, 156–161. [Google Scholar] [CrossRef]
- Long, R.; Li, B.; Liu, Z.; Liu, W. Ecological analysis of a thermally regenerative electrochemical cycle. Energy 2016, 107, 95–102. [Google Scholar] [CrossRef]
- Liao, T.; Lin, B.; Yang, Z. Performance characteristics of a low concentrated photovoltaic–thermoelectric hybrid power generation device. Int. J. Therm. Sci. 2014, 77, 158–164. [Google Scholar] [CrossRef]
- Long, R.; Li, B.; Liu, Z.; Liu, W. Performance analysis of a dual loop thermally regenerative electrochemical cycle for waste heat recovery. Energy 2016, 107, 388–395. [Google Scholar] [CrossRef]
- Ni, M.; Leung, M.K.H.; Leung, D.Y.C.; Sumathy, K. An analytical study of the porosity effect on dye-sensitized solar cell performance. Sol. Energy Mater. Sol. Cells 2006, 90, 1331–1344. [Google Scholar] [CrossRef]
- Lai, C.; Zhao, Q.; Zhang, Z.; Zhang, H.; Hou, S.; Zhao, J. Potential evaluation of flexible annular thermoelectric generator in photovoltaic system performance improvement: Energy and exergy perspectives. Energy Convers. Manag. 2021, 247, 114711. [Google Scholar] [CrossRef]
- Fitra, M.; Daut, I.; Irwanto, M.; Gomesh, N.; Irwan, Y.M. Effect of TiO2 Thickness Dye Solar Cell on Charge Generation. Energy Procedia 2013, 36, 278–286. [Google Scholar] [CrossRef]
- Wu, S.-Y.; Zhong, Z.-H.; Xiao, L.; Chen, Z.-L. Performance analysis on a novel photovoltaic-hydrophilic modified tubular seawater desalination (PV-HMTSD) system. Desalination 2021, 499, 114829. [Google Scholar] [CrossRef]
- Kong, C.; Xu, Z.; Yao, Q. Outdoor performance of a low-concentrated photovoltaic–thermal hybrid system with crystalline silicon solar cells. Appl. Energy 2013, 112, 618–625. [Google Scholar] [CrossRef]

| Parameters | Values |
|---|---|
| 1.0 [20] | |
| (mA K−1) | 2.06 [20] |
| 5.0 [20] | |
| (μA) | 0.118 [20] |
| 1.380 × 10−23 [20] | |
| 1.602 × 10−19 [20] | |
| (W m−2 K−4) | 5.67 × 10−8 [20] |
| 0.85 [20] | |
| (W K−1) | 20 |
| (m2) | 0.632 [20] |
| 1.0 [20] | |
| 36.0 [20] | |
| (W m−2) | 1000.0 [20] |
| (W m−2) | 800.0 [20] |
| (V) | 1.12 [20] |
| (K) | 300.0 [20] |
| (K) | 308.0 [20] |
| (Ω) | 0.004 [10] |
| (V K−1) | 0.027 [10] |
| 1.0 [18] | |
| 2.0 [18] | |
| (K) | 360.0 |
| (K) | 308.0 |
| (J kg−1 K−1) | 2.408 [18] |
| (A h kg−1) | 32.43 [18] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Y.; Xiao, R.; Chen, L.; Zhang, H. Performance Potential of a Concentrated Photovoltaic-Electrochemical Hybrid System. Energies 2024, 17, 163. https://doi.org/10.3390/en17010163
Lin Y, Xiao R, Chen L, Zhang H. Performance Potential of a Concentrated Photovoltaic-Electrochemical Hybrid System. Energies. 2024; 17(1):163. https://doi.org/10.3390/en17010163
Chicago/Turabian StyleLin, Yingyan, Ronghui Xiao, Liwei Chen, and Houcheng Zhang. 2024. "Performance Potential of a Concentrated Photovoltaic-Electrochemical Hybrid System" Energies 17, no. 1: 163. https://doi.org/10.3390/en17010163
APA StyleLin, Y., Xiao, R., Chen, L., & Zhang, H. (2024). Performance Potential of a Concentrated Photovoltaic-Electrochemical Hybrid System. Energies, 17(1), 163. https://doi.org/10.3390/en17010163






