Structural Behavior of a PIP Slip Joint under Pure Bending Considering Nonlinear Buckling

Abstract

This study investigates the structural behavior of a particular mechanical joint subjected to bending and perturbation and the selection of overlapping lengths for this CHS structure arrangement. We began this research by meticulously validating the methodology through a rigorous replication of a prior experimental study, establishing its reliability as a solid foundation. Subsequently, the process was applied to pile-in-pile (PIP) slip joints with varying overlapping lengths. The primary aim was to determine the optimal overlapping length, a critical parameter in this analysis, encompassing the evaluation of stiffness, bending capacities, and joint efficacy. These investigations reveal a clear correlation between increasing overlapping length and heightened joint stiffness. An optimal overlapping length that strikes a harmonious balance between stiffness, bending capacity, and joint efficiency was identified. These findings hold substantial promise for enhancing the joint design of tubular sections, particularly within the context of wind-turbine structures. Using this novel joint can be promising in increasing the efficiency and reliability of CHS structures in future construction and performance.

1. Introduction

Tubular structures are widely used in various engineering applications, such as offshore platforms, bridges, cranes, space frames, and aircraft, due to the ease of their fabrication and maintenance, their good resistance to corrosion and fatigue, and their high strength vs. weight ratios. However, designing tubular structures poses crucial challenges, such as complex stress distribution, local buckling, and joint failure [1]. Therefore, it is necessary to study the structural behavior of tubular joints under different loading conditions and configurations and to develop reliable methods for designing and evaluating their strength and stiffness. By the same token, buckling can reduce load-carrying capacity and joint stiffness; as a result, a progressive collapse could occur in the whole structure. Buckling analysis can also help in optimizing joint design via aiding the selection of appropriate geometrical parameters, material properties, and connection details [2]. Joint analysis considering buckling for tubular structures can optimize the structural performance, reduce the material cost, and ensure the safety and reliability of tubular structures.

The significance of wind energy is increasing day by day due to its immense potential in terms of supplying electricity across the globe. As wind is a native energy source and does not necessitate transportation or mining like other sources, it will be an unparalleled sustainable energy source in the future. The most-used structural sections for support-structure construction are circular hollow sections (CHSs) [3]. When the slenderness of CHSs is relatively low, the interaction of bifurcation and material plasticity often causes them to bend. Coffer et al. (1992) [2] found that tubular members should be designed in consideration of the post-buckled capacity, comprising two factors, as mentioned earlier.

Consequently, some foundational research consisted of analyzing the bending and axial load capacity of CHS structures. Some researchers emphasized the importance of bending loads, as these structures are mainly subject to lateral wind and earthquake loads. It is important to note that the diameter-to-thickness ratio (D/t) is intimately related to CHSs’ bending strength and buckling behavior regardless of axial or bending loads [3]. Some modern codes, like ASME, 2022 [4] (Equation (1) and EN 13480-3, 2012 [5] (Equation (2), accentuate the D/t ratio for calculating the primary design load, represented in Equations (1) and (2).

$$B_1\ast \frac{D\ast p}{2\ast t}+B_2\ast \frac{D\ast M}{2\ast I}\le {\sigma }_{allowable},$$

(1)

Here, allowable stress is represented by σ_allowable; B₁ and B₂ are the primary stress indices for the internal pressure (p); M and I are the moment and the moment of inertia, respectively; D is the outer diameter; and t is the thickness of the CHS structure.

$$\frac{D\ast p}{4\ast t}+i\ast \frac{D\ast M}{2\ast I}\le {\sigma }_{allowable}$$

(2)

These equations emphasize the significance of the D/t ratio in the design of a CHS structure.

Despite the availability of detailed studies regarding the axial load and bending capacities of the CHS system, very few have discussed connecting two CHS members. Research on joint systems and their safety has been a significant area of focus in recent years. Starting with the study by S. Kyriakides et al. (2002) [6], they analyzed the impact of buckling propagation on pipes in a pipe system. Still, the geometric offsets were provided for nonstructural purposes. Following this, a noteworthy probabilistic study was carried out on two-planar local joint flexibility by Ahmadi and Mayeli in (2018) [7]. More recently, Tuan and Lee (2022) [8] conducted significant research on L-type flange joints and found that bolt bending dramatically impacts the safety of flange joints. In parallel, some other studies have tried to identify the characteristics of welded slip joints to predict a system’s capabilities with and without fiber-wrap reinforcement [9]. Additionally, Tüfekci et al., 2020 [10] conducted a significant study on damping and reinforced shell materials and validated the results through analytical and finite-element approaches. This logical arrangement provides a chronological understanding of the research progression in this field.

Several studies have also investigated the behavior and stability of pipelines under various conditions. DelCol et al. (1998) [11] initiated an investigation with experimental testing and finite-element models, studying pipelines with a diameter-to-thickness (D/t) ratio of 92. They found that increased internal pressure lowers the buckling moment but stabilizes post-buckling behavior. Building on this, Ozkan & Mohareb, 2009 [12] conducted a full-scale experimental program on several ‘X65’ pipe specimens with a D/t ratio of 81.2. They aimed to determine the modified plastic moment of the pipes and developed a nonlinear shell finite-element model using ABAQUS to predict moment capacity and local buckling behavior. The research was further expanded through the development of a three-dimensional numerical model. The local buckling failure of high-strength and large-diameter pipelines containing a dent under bending moment was investigated. It was found that the critical buckling moment of the pipeline decreases with the increase in the strain hardening exponent (n) [13]. Zimmerman et al. (2004) [14] contributed to the field by conducting full-scale tests on 30-inch-diameter pipes. They aimed to determine the compressive buckling resistance of spiral-welded pipes and concluded that it matches the buckling capacity of longitudinally welded pipes. Yeter et al. (2019) [15] also conducted numerical and experimental studies on a monopile structure considering geometrical and material nonlinearities. Initial imperfections were also considered in their study. Li and Kim (2022) [16] also considered the initial imperfections and buckling of a stiffened shell structure subjected to axial compressions in their research, which also yielded some substantial numerical predictions of CHS structures. The impact of a local dent on the stability and plastic responses of a mechanically lined pipe system during bending was also studied [17]. It was found that the dent’s orientation affects the pipe’s buckling and collapse. All these studies have significantly contributed to understanding pipeline behavior under various conditions, considering nonlinear material properties. They have used experimental testing, full-scale programs, and finite-element models to investigate and predict the performance and stability of pipelines. The findings from these studies have practical implications for the design and operation of shell structures and pipelines.

In all these studies, some gaps have been identified. Some studies have not explained the structural point of view. Others have not considered nonlinear geometries and material properties together. A few studies have focused on two-planar loadings, but one-planar loading could be more beneficial for installing and upgrading CHS structures. The L-type flange joint is related to making the joints of tubular structures easily installable. However, the PIP slip-joint structure could simplify installation operations. Some research has been conducted on welded joints, but these joints are fixed and cannot be separated like the current PIP slip joint. These gaps in the literature could be filled to improve the understanding and application of these CHS structures. Moreover, structural responses could also be enhanced by using this novel PIP slip joint.

This study aims to develop an easily detachable mechanical joint termed the PIP slip joint. After a careful literature review, we found that this topic has yet to be explored. Some prior experimental studies have used some shell structures similar to these PIP arrangements. A significant study by Guo et al. in 2013 [3], which examined the structural behavior of pipe structures without mechanical joints, served as a reference point. Firstly, the findings of their experiments were validated by using finite-element method (FEM) analysis, and this method was applied to the current novel PIP slip-joint structure. A key concern in this study was the buckling of the shell structure, which can diminish load-carrying capacity and joint stiffness, potentially leading to a progressive collapse of the entire structure. Interestingly, we discovered that the buckling phenomenon in the PIP slip joint was altered due to the frictional surface contact in the overlapping length of the PIP. This finding is elaborated upon in the discussion section of this study. In the case of loadings, the current focus is on pure bending, and frictional contacts were employed to achieve surface-to-surface bonding.

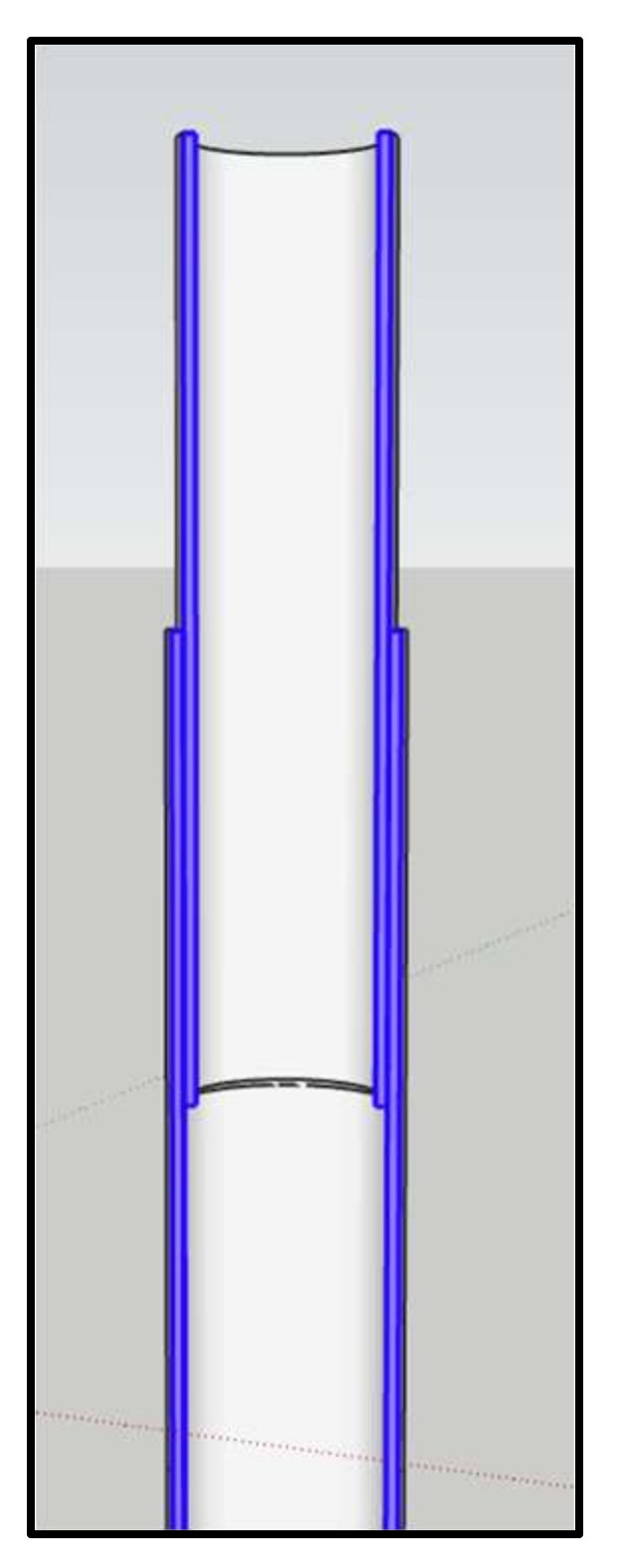
PIP slip joints are unique mechanical joints wherein the contact surfaces of the CHSs can slide apart from each other (as shown in Figure 1). These slip joints can be immensely remunerative in terms of the easy installation of CHS structures, such as monopiles or the legs of various mobile platforms. They are also beneficial for future upgrades, providing cost-effective options for maintenance and retrofitting. In emergencies, separable joints can be highly beneficial, as they can be detached when necessary, making these tubular structures mobile. This feature not only enhances the structural capacity by increasing stiffness but also allows for examining the complex effects of friction. Thus, separable joints could be a critical factor in improving structures’ functionality and safety. Not only are they applicable in the installation and upkeep of wind-turbine structures, but they can also be employed in the industrial sector, where CHS configurations are prevalent. Therefore, it is clear that the importance and significance of this current study cannot be overstated. It holds undeniable value in advancing our interpretation of these arrangements.

2. Materials and Methods

To ensure the accuracy of the simulations and provide a solid foundation for the subsequent analysis of PIP slip joints, this research procedure was designed to ascertain and build upon the previous study’s findings on the behavior of thin-walled CHSs. The first step in this process involved selecting the material strength from prior research. The material properties used in this study were derived from the research conducted by Guo et al. (2013) [3]. This research provided comprehensive data on the behavior of CHSs subjected to pure bending—information that was pertinent to this study. Material strength values (as per

Table 1. Material properties.

fy (MPa)	fu (MPa)	Es (MPa)	υ	δ
190	315	1.88 × 105	0.36	0.51

Here, f_y is the yield stress, f_u is the ultimate tensile strength of steel, E_s is the modulus of elasticity, υ is the Poisson’s ratio, and δ is the elongation ratio of steel.

), in particular, were adopted from this research to ensure the accuracy and relevance of the simulations and analyses.

For this verification, ‘ANSYS Workbench 2023/R2’ [18] was utilized, as it is suitable for investigating CHS tubular sections owing to its robust capabilities in effectively managing intricate geometries and performing comprehensive simulations [19].

The dimensions used in the study of Guo et al. (2013) [3] were also replicated. This replication ensured consistency in the simulations and allowed for a more accurate comparison of results between the previous study and the research on PIP slip joints. In the abovementioned experimental study, there were two different boundary conditions: one was a cantilever beam, and the other was a ‘simply supported beam’. The geometries of the tubes are represented in

Table 2. Geometric properties.

ID	D (mm)	t (mm)	L (mm)	Boundary Condition
DT 100-2	200	2.00	3000	Simply supported
DT 75-1	150	2.00	3000	Simply supported
DT 100-3	200	2.00	1500	Cantilever beam

.

For effective mesh distribution, we followed the ANYS workbench guidelines and the study of Kim et al. (2023) [20]. To allow the adaptive meshwork to adjust the large deformation in the material, a secondary meshing element, HEX20, was applied. The specimen was meshed by side sizing, edge sizing, and face meshing. This element reduced the possibility of distortion in perturbation. Moreover, the utilization of secondary meshing can prove quite advantageous in scenarios characterized by solid localization of deformation [19]. The element and node numbers were 148,432 and 635,628, respectively. For checking mesh quality, the Jacobian Ratio (JR) was utilized. A JR of 1.005 and a standard deviation of 0.00152 constitute a lucid indication of uniform meshing. Four-point bending generates a zone of pure bending between the loading points at the center. A multi-physics constraint (MPC) was used to duplicate the stiffening plate. To validate an experimental investigation, it is essential to employ nonlinear buckling analysis.

2.1. Perturbation or Buckling

This kind of assessment of structural stability is vital for numerous structures and construction systems, such as thin columns, compression members, and vacuum tanks, exemplifying cases in which stability considerations are crucial. Instability may manifest globally, as observed in phenomena like snap-through or local instability, characterized by yielding or buckling at specific points of concentrated load or support. Instability issues often present challenges in achieving convergence, necessitating specialized solution methods. During the initiation of instability, a structure will experience a significant alteration in displacement, denoted as {Δu}, while the load remains relatively unchanged except for a minor perturbation. An idealized fixed-end column will demonstrate the subsequent response (as per Figure 2) when subjected to progressive axial loads (F). For these progressive loads, a bifurcation point will be generated.

A bifurcation point is a point during the load history where two distinct solution branches become plausible. In the scenario of the idealized fixed-end column, it can be seen that upon reaching the critical load $\left(F_{cr}\right)$, the column exhibits the potential to buckle in either the left or right directions, giving rise to two different load trajectories. Geometric flaws influence the load paths of actual structures’ force perturbations (P ≠ 0), as illustrated in Figure 3.

When the value of F is less than F_cr, the column is in a stable equilibrium state. If a minor external force (P ≠ 0) is applied and eliminated, the column will return to its initial position. When the applied force (F) exceeds the critical point $\left(F_{cr}\right)$, the column is in an unstable equilibrium state, meaning that any external force disturbing the column will cause it to collapse. This condition is called the critical load, defined as the point at which a column is in balance. Figure 4 provides a qualitative idealized behavior of the buckled structure.

Nonlinear stabilization can be considered by adding artificial dampers to every degree of freedom (DOF) in the system. Before the critical load is reached, the procedure typically involves small displacements at any given time step. This can be considered a low pseudo-velocity, causing very little resistive force from the artificial dampers. When buckling occurs, larger displacements occur over smaller timesteps, leading to large pseudo-velocities and resistive forces. This has the effect of making the stiffness matrix at the limit point nonsingular. Nonlinear stabilization can be considered by adding artificial dampers to every degree of freedom in the system. The damping force $\left(f_d\right)$of the artificial dashpot element (as per Figure 5) is determined by the solver, which is proportional to the relative pseudo-velocity of the two nodes of the artificial dashpot element. The displacement increment is divided by the sub-step’s time increment to determine the pseudo-velocity.

In this case, the governing equation for this stabilization can be written as shown in Equation (3) (ANSYS mechanical guidelines).

$$\left\{F\left(t\right)\right\}=\left[M\right]\left\{\ddot{u}\right\}+\left[C\right]\left\{\dot{u}\right\}+\left[K\right]\left\{u\right\}+\left[K_d\right]\left\{u\right\}$$

(3)

The terms used above are described below:

[M] = mass matrix;

[C] = damping matrix;

[K] = stiffness matrix;

[K_d] = differential stiffness matrix;

{$\ddot{u}$} = nodal acceleration vector;

{$\dot{u}$} = nodal velocity vector;

{u} = nodal displacement vector;

{F(t)} = load vector.

Generally, there is a sudden energy transfer from the system’s internal energy to its kinetic energy. Furthermore, in most cases, the point of interest is the load at which the buckling occurs rather than how the structure behaves during buckling. That is why the governing equation for a static analysis is generally the starting point. Any degree of freedom (DOF) that tends towards instability is characterized by a notable increase in displacement, resulting in a substantial damping force stabilizing the system. Consequently, this force decreases the displacements at the degrees of freedom (DOFs), leading to stabilization. In the case of stable degrees of freedom (DOFs), the impact of dashpot elements on the outcomes is minimal due to the relatively minor displacements and stabilizing forces compared to the physical forces. The parameter utilized in the computation of the stabilization force is commonly referred to as the damping factor. While having behavior and units similar to those of physical damping, numerical damping lacks a physical counterpart and is solely a numerical concept. Once stabilization has been initiated, it becomes crucial to assess its impact on the correctness of the results. This may be achieved by post-processing the stabilization energy and comparing it to the strain energy. Additionally, it is essential to analyze the force and moment reactions to gain further insights.

2.2. Analysis Procedure

The verification of the FEA model was centered around the force vs. displacement relationship found in the experimental analysis. Both the ‘simply supported beam’ setup and the cantilever beam were modeled using displacement control loading for both cases. The failure modes in the experimental study, along with the force–displacement relationships, were also compared.

Consequently, the PIP slip joint was also modeled in the same way. The dimensions of the PIP arrangements are summarized in

Table 3. Summary of PIP arrangements.

ID	D (mm)		t (mm)		L (mm)	Overlapping Length, Lo (mm)
	Outer Pipe	Inner Pipe	Outer Pipe	Inner Pipe
1.5D	200	196	2.00	2.00	3000	300
2D	200	196	2.00	2.00	3000	400
2.5D	200	196	2.00	2.00	3000	500

.

Figure 6 and Figure 7 illustrate the meshing, replication of boundary conditions, and geometric arrangement of the PIP slip-joint arrangement used in this study.

Three different overlapping lengths were emphasized for an effective and economically optimized joint. In the case of the contact surface between two pipes, frictional faces were considered with a frictional coefficient of 0.4 [21].

2.3. Limitations

This study has three main limitations, which are delineated in this section. However, these limitations in no way invalidate the results of this study.

Initial Geometry in the Experimental Study: The initial geometrical imperfections significantly influence the load-carrying capacity of models with different diameter-to-thickness (D/t) ratios.

Numerous Variables: Moreover, there were multiple variables in this study, such as the PIP joint overlapping length, the strength of the material, and the D/t ratio. In this study, the only D/t ratios considered were 100 and 75.

Ovality Effect in PIP Joint: The ovality of the PIP joint can significantly affect its performance, especially when it experiences bending loads.

Therefore, further research is needed to understand the behavior of the PIP slip joint under these different conditions.

3. Results and Discussion

3.1. Result of Model Validation

One cantilever beam with a D/t ratio of 100 and two simply supported beams with D/t ratios of 100 and 75 were modeled. The boundary conditions of these CHSs were kept the same as those in the prior experimental study. Figure 8 represents the final deformed shapes of the simulation models along with comparisons with those from the experimental research.

Consequently, in Figure 9 and Figure 10, comparisons of the force–displacement relationships for the FEA and the experimental results are presented.

The deviation between the results obtained via the FEA and the experimental study in the case of the cantilever beam was 17%, and the trends were almost the same for both. The deflection shapes and the characteristics of local buckling were also identical, as evident in Figure 8. On the other hand, though the deflection and local buckling characteristics were not precisely the same for the simply supported beam, the variation in force–displacement was smaller. The values of this variation were 12.5% and 11.27% for the 75D/t and 100D/t ratios, respectively. Therefore, the experimental analysis and finite-element analysis (FEA) results are in strong agreement. This concurrence validates the accuracy of the FEA model, demonstrating its reliability for the further analysis of PIP joints and the optimization of development length.

3.2. Results Regarding PIP Slip Joints

The curves for load versus deflection for the PIP slip joint are presented in Figure 11. Here, the joint was evaluated for only the D/t ratio of 100. Three different overlapping lengths were evaluated under pure bending. Also, the only CHS behavior compared here was the performance of the PIP slip joint.

Unlike in the experimental results, the sharp decline of the load vs. displacement curve was not observed here. Moreover, the plateau in the force–displacement relationship extended with the incremental overlapping length. This was due to the interaction of the frictional surfaces between two CHS faces. The ripples that developed in the middle section due to bending also increased the frictional force. It can be seen that the load-carrying capacities also increased significantly with the increment in the overlapping length. In the case of an overlapping length of 1.5D, the load-carrying capacity increased by 8.45%, whereas for the L_o values of 2D and 2.5D, the values were 11.51% and 16.44%, respectively. If the deflection shape and local buckling in Figure 12 are examined, the most stressed area in the PIP slip joint can be observed. Like the normal CHS, it also developed perturbations near the plastic hinge areas. However, the ripple propagated up to the overlapped area. At the edge of the inner pile, the stress distribution was also maximized due to the generation of shear stress in this area. Due to normal stresses, the extreme internal filament along the concave side of the CHS is the most demanding part of the critical transverse section to address. The presence of bending causes the neutral layer to move towards the concave side of the tube, determining the position of the resulting neutral layer in this section. All the PIP slip joints with varying overlapping lengths showed the same stress distribution behavior. Further experimental studies are needed to explain this behavior for different D/t ratios. Moreover, the loading conditions were fixed in this study, and different loading conditions can yield different results. Also, imperfections, the ovality effect, and crack propagation were not considered in this study. These are some of the limitations of this research.

To understand structural designs, it is crucial to determine the failure mechanisms, as they help to identify why structures fail and the consequences of such failure. Using this knowledge, we can improve future designs to prevent these failures from happening again. In Figure 12, the simulation models for an overlapping length of 1.5D have reduced rotation capacities concerning 2D and 2.5D numerically, which were found to constitute 10%. Surprisingly, the overlapping lengths of 2D and 2.5D have almost identical rotational capacities. However, the lengths of the plateau are different for both. Conceptually, an increase in the compactness of the section was observed with an increasing overlapping length when compared to the qualitative diagram for tubular members provided in the NORSOK N-004:2022 code [22]. Evidently, considering the length of the deformation plateau, the ripples in the steel tube were effective in enhancing the specimens’ ductility and preventing brittle failure, as shown in Figure 13. The effects of friction could be the reason for these phenomena. In turn, this can also lead to an increase in rotational capacity.

3.3. Stress Distribution

Another important parameter for designing a tubular structure is section slenderness. To illustrate this, the stress distribution vs. generalized section slenderness ($\lambda =\frac{D}{t}\times \frac{f_y}{250}$, as per Guo et al. 2013 [3]) were plotted and juxtaposed with some widely recognized design codes. The American AISC-LRFD, Australian AS4100, and European Specification codes are only a few of the specifications available with which to design the moment resistance of circular tubes [23]. A routine, representative, conservative design process in estimating ultimate strength is crucial for design purposes. As shown in Figure 14, the stress distribution for overlapping lengths of 2.5D and 2D is better than that for 1.5D. The stress reductions were 3.42% and 3.56% for 2.5D and 2D. As the European Specification is too conservative, the results presented in this study seem to be a bit liberal but remain within the limits of the AISC LRFD guideline. Also, it can be found that bending stresses affect the state of stresses in the critical transverse section prior to the loss of carrying capacity, with the location of the resulting neutral layer being a key factor, as mentioned earlier. However, as per the Engesser–Shanley modified theory [24], the state of stresses in the critical transverse section was highly influenced by both compressive and bending stresses.

3.4. Joint Efficacy (JE)

JE measures the performance of circumferential joints in large-diameter steel pipes under different loadings [25]. It is used to evaluate the ability of joints to withstand stress and to determine whether failure will occur. Factors including the steel’s material properties, the hollow section’s size, and the type and magnitude of applied loads can all have an impact on this efficiency. Here, the JE ($J{E}_{ty}=\frac{\sigma }{{\mathsf{\sigma }}_y}$) was evaluated for fully yielded (plastic) stress distributions. Figure 15 shows that the joint efficacy from 1.5D to 2D increased by almost 25%, whereas for 2D to 2.5D, this increment was only 4%. The JE gradually increased in all cases, although in the case of an overlapping length of 1.5D, the hike was rapid after 74% of maximum rotation. At 0.8 JE, the rotation capacity for a 1.5 D overlapping length rotation capacity decreased and, after that, increased again, indicating the denting of the CHS. From Figure 15, it can be observed that the joint efficacy exhibited a rapid increase over a narrow range of displacement.

Therefore, these results show that the 2D overlapping length yielded the better result in terms of all the aspects that were examined. On this basis, a general equation could also be made for this novel mechanical joint with the help of further experimental analysis. The relationship presented here constitutes the most vital parameters for determining load capacity, rotational ability, and joint efficacy. So, based on these results, general design guidelines can also be proposed after the abovementioned validation process.

4. Conclusions

In this study, an exploration of the behavior of a novel type of slip joint under the influence of bending, considering the impact of nonlinear perturbation, was undertaken. The initial step in this journey involved the establishment of the validity of the FEM analysis method. To achieve this, a duplication of a previous experimental study was conducted. The results obtained from the replication were found to be in good agreement with the original experimental specimen, confirming the reliability of the approach.

Once the methodology had been validated, it was applied to the proposed pile-in-pile (PIP) slip joints. These joints were examined at three overlapping lengths: 1.5D, 2D, and 2.5D. For each of these simulation models, a thorough analysis was conducted on their stiffness, capacities under bending, and joint efficiency.

The findings revealed that, as the overlapping length increased, so did the stiffness of the joints. For 1.5D, the capacity rose by 8.45%, while for 2D and 2.5D, it increased by 11.51% and 16.44%, respectively. Joint efficacy (JE) for plastic stress distributions was also evaluated, showing a 25% increase from 1.5D to 2D and a 4% increment from 2D to 2.5D. Upon considering the optimal values, it was discovered that an overlapping length of 2D delivered superior results compared to the other two overlapping lengths and offered balanced performance in terms of stiffness, bending capacity, and joint efficiency. This insight could have significant implications for designing and applying PIP slip joints in various engineering contexts, especially wind-turbine structures.

An experimental analysis will be a vital step in developing and verifying the viability of this mechanical joint. Moreover, some realistic problems like the ovality effect and complex loading, as well as the combination of axial compression with bending, are also vital topics for studies that could be considered for the future development of this study. Exploration of different values of the D/t ratio and the distance of bending loads and the eccentricity of axial compression could also be vital in the future. In case of axial compression and ring bending, a stopper could also be considered.