An Improved Hybrid Approach for Daily Electricity Peak Demand Forecasting during Disrupted Situations: A Case Study of COVID-19 Impact in Thailand
Abstract
:1. Introduction
2. Methods
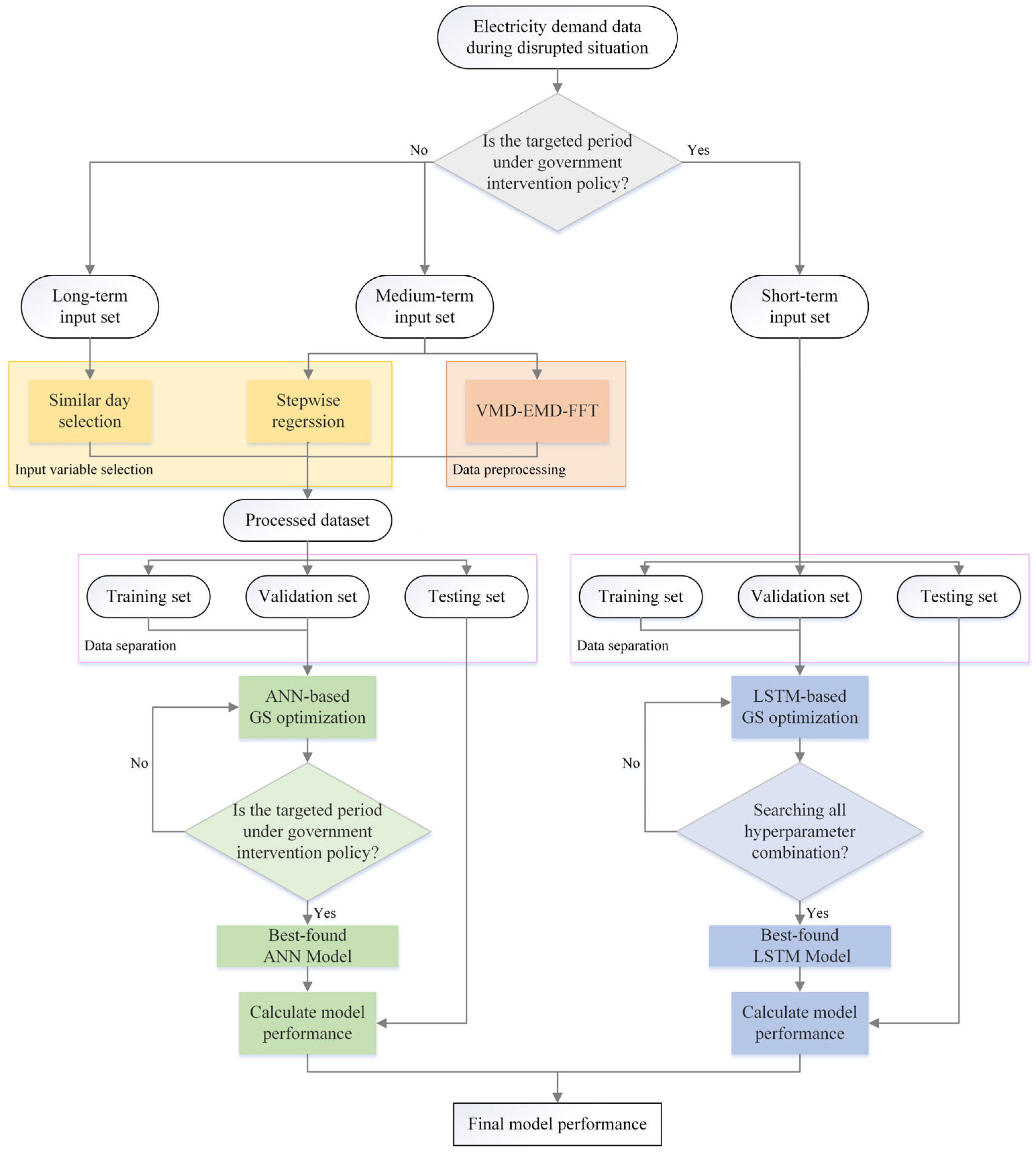
2.1. Overall Procedure of the Proposed Model for the Disrupted Situation
2.2. Input Variable Filtering
2.2.1. Input Variable Description
2.2.2. Stepwise Regression
2.2.3. The Proposed Similar Day Selection for the Disrupted Situation
2.2.4. Example of the Proposed Similar Day Selection for the Disrupted Situation
2.3. Data Preprocessing
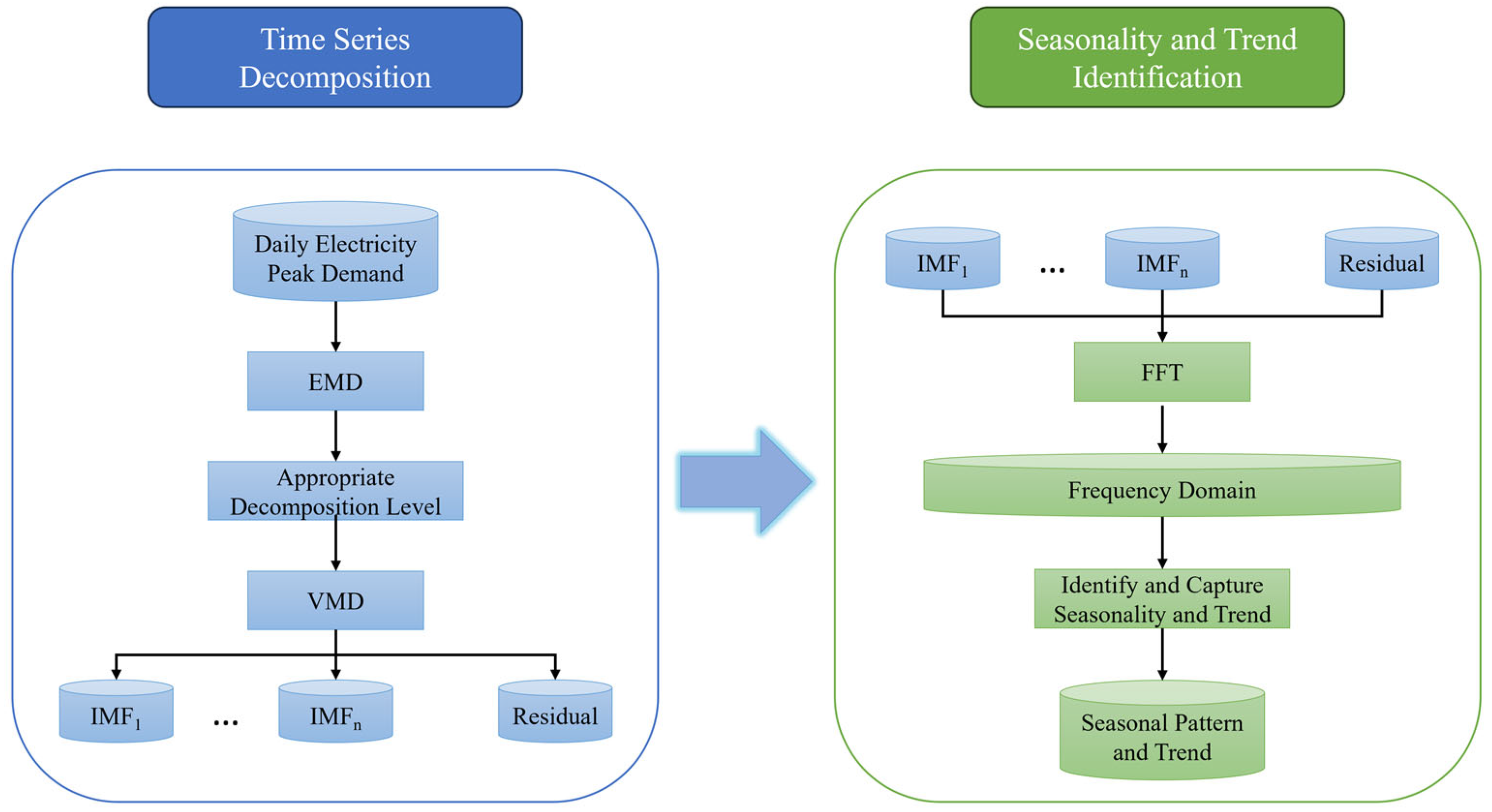
2.3.1. Data Decomposition
2.3.2. Seasonality and Trend Identification
2.4. Prediction and Optimization
2.4.1. Data Separation
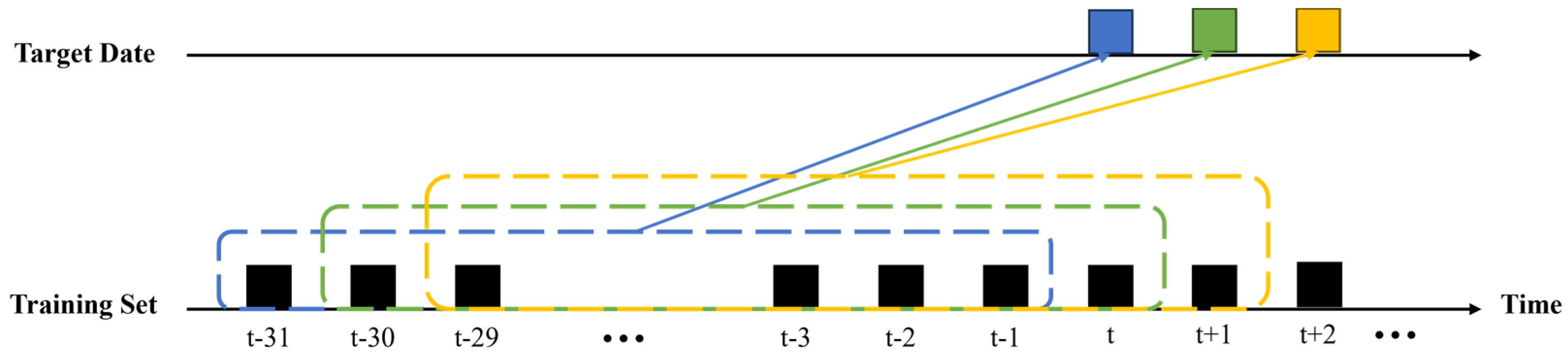
2.4.2. One-Day-Ahead Forecasting with Rolling Datasets
2.4.3. Artificial Neural Network with Grid Search Optimization
2.4.4. Long Short-Term Memory
2.4.5. Grid Search Optimization
3. Case Study: Electricity Peak Demand in Thailand during the COVID-19 Pandemic
3.1. Data Collection and Description
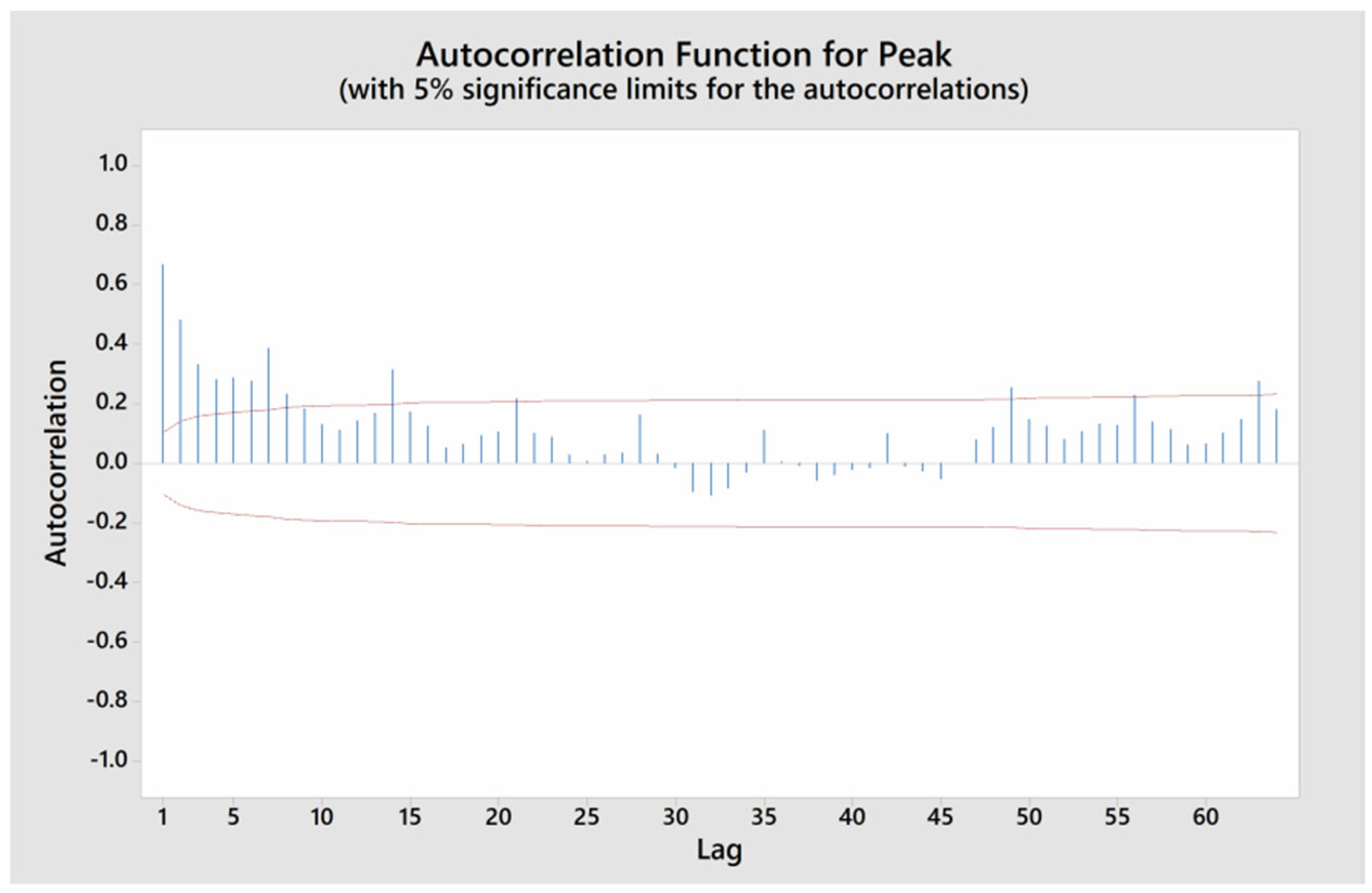
3.2. Data Separation and Sensitivity Factors Identification
3.3. Case 1: Interference with Government Policy
3.4. Case 2: Noninterference with Government Policy
3.4.1. Input Variable Filtering for the Case of the COVID-19 Pandemic
3.4.2. Data Decomposition
3.4.3. Data Splitting and ANN-Based Grid Search Optimization
3.5. Performance Measurement
3.6. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Islam, S.M. Principles of electricity demand forecasting. Power Eng. J. 1997, 10, 139–143. [Google Scholar]
- Xing, X.; Yan, Y.; Zhang, H.; Long, Y.; Wang, Y.; Liang, Y. Optimal design of distributed energy systems for industrial parks under gas shortage based on augmented ε-constraint method. J. Clean. Prod. 2019, 218, 782–795. [Google Scholar] [CrossRef]
- Dong, L.; Lao, L.; Yang, Y.; Luo, J. Probabilistic Load Flow Analysis Considering Power System Random Factors and Their Relevance. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 15–18 March 2011. [Google Scholar]
- Ranaweera, D.K.; Karady, G.G.; Farmer, R.G. Economic Impact Analysis of Load Forecasting. IEEE Trans. Power Syst. 1997, 12, 1388–1392. [Google Scholar] [CrossRef]
- Luo, X.; Wang, J.; Dooner, M.; Clarke, J. Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl. Energy 2015, 137, 511–536. [Google Scholar] [CrossRef]
- Zhang, H.; Song, X.; Xia, T.; Yuan, M.; Fan, Z.; Shibasaki, R.; Liang, Y. Battery electric vehicles in Japan: Human mobile behavior based adoption potential analysis and policy target response. Appl. Energy 2018, 220, 527–535. [Google Scholar] [CrossRef]
- Ramzan, M.; Razi, U.; Quddoos, M.U.; Adebayo, T.S. Do green innovation and financial globalization contribute to the ecological sustainability and energy transition in the United Kingdom? Policy insights from a bootstrap rolling window approach. Sustain. Dev. 2023, 31, 393–414. [Google Scholar] [CrossRef]
- Huterski, R.; Huterska, A.; Zdunek-Rosa, E.; Voss, G. Evaluation of the Level of Electricity Generation from Renewable Energy Sources in European Union Countries. Energies 2021, 14, 8150. [Google Scholar] [CrossRef]
- Piekut, M. The Consumption of Renewable Energy Sources (Res) by the European Union Households between 2004 and 2019. Energies 2021, 14, 5560. [Google Scholar] [CrossRef]
- Igliński, B.; Kiełkowska, U.; Pietrzak, M.B.; Skrzatek, M.; Kumar, G.; Piechota, G. The regional energy transformation in the context of renewable energy sources potential. Renew. Energy 2023, 218, 119246. [Google Scholar] [CrossRef]
- Balcerzak, A.P.; Uddin, G.S.; Igliński, B.; Pietrzak, M.B. Global energy transition: From the main determinants to economic challenges. Equilibrium. Q. J. Econ. Econ. Policy 2023, 18, 597–608. [Google Scholar] [CrossRef]
- Skvarciany, V.; Lapinskaite, I.; Volskyte, G. Circular economy as assistance for sustainable development in OECD countries. Oeconomia Copernicana 2021, 12, 11–34. [Google Scholar] [CrossRef]
- Narajewski, M.; Ziel, F. Change in Electricity Demand Pattern in Europe Due to COVID-19 Shutdowns. arXiv 2020, arXiv:2004.14864. [Google Scholar]
- Chen, Y.; Yang, W.; Zhang, B. Using Mobility for Electrical Load Forecasting During the COVID-19 Pandemic. arXiv 2020, arXiv:2006.08826. [Google Scholar]
- Baek, S.; Mohanty, S.K.; Glambosky, M. COVID-19 and stock market volatility: An industry level analysis. Financ. Res. Lett. 2020, 37, 101748. [Google Scholar] [CrossRef] [PubMed]
- Vitenu-Sackey, P.A.; Barfi, R. The Impact of Covid-19 Pandemic on the Global Economy: Emphasis on Poverty Alleviation and Economic Growth. Econ. Financ. Lett. 2021, 8, 32–43. [Google Scholar] [CrossRef]
- Klemeš, J.J.; Van Fan, Y.; Jiang, P. The energy and environmental footprints of COVID-19 fighting measures—PPE, disinfection, supply chains. Energy 2020, 211, 118701. [Google Scholar] [CrossRef]
- Aktar, M.A.; Alam, M.M.; Al-Amin, A.Q. Global economic crisis, energy use, CO2 emissions, and policy roadmap amid COVID-19. Sustain. Prod. Consum. 2021, 26, 770–781. [Google Scholar] [CrossRef]
- Cheshmehzangi, A. COVID-19 and household energy implications: What are the main impacts on energy use? Heliyon 2020, 6, E05202. [Google Scholar] [CrossRef]
- Abulibdeh, A.; Zaidan, E.; Jabbar, R. The impact of COVID-19 pandemic on electricity consumption and electricity demand forecasting accuracy: Empirical evidence from the state of Qatar. Energy Strateg. Rev. 2022, 44, 100980. [Google Scholar] [CrossRef]
- Yukseltan, E.; Yucekaya, A.; Bilge, A.H. Forecasting electricity demand for Turkey: Modeling periodic variations and demand segregation. Appl. Energy 2017, 193, 287–296. [Google Scholar] [CrossRef]
- Son, H.; Kim, C. Short-term forecasting of electricity demand for the residential sector using weather and social variables. Resour. Conserv. Recycl. 2017, 123, 200–207. [Google Scholar] [CrossRef]
- Pappas, S.S.; Ekonomou, L.; Karamousantas, D.C.; Chatzarakis, G.E.; Katsikas, S.K.; Liatsis, P. Electricity demand loads modeling using AutoRegressive Moving Average (ARMA) models. Energy 2008, 33, 1353–1360. [Google Scholar] [CrossRef]
- Newsham, G.R.; Birt, B.J. Building-Level Occupancy Data to Improve ARIMA-Based Electricity Use Forecasts. In Proceedings of the 2nd ACM Workshop on Embedded Sensing Systems for Energy-Efficiency in Building, Zurich, Switzerland, 2 November 2010. [Google Scholar]
- Hamzacebi, C.; Es, H.A. Forecasting the annual electricity consumption of Turkey using an optimized grey model. Energy 2014, 70, 165–171. [Google Scholar] [CrossRef]
- Alasali, F.; Nusair, K.; Alhmoud, L.; Zarour, E. Impact of the COVID-19 Pandemic on Electricity Demand and Load Forecasting. Sustainability 2021, 13, 1435. [Google Scholar] [CrossRef]
- Huang, L.; Liao, Q.; Qiu, R.; Liang, Y.; Long, Y. Prediction-based analysis on power consumption gap under long-term emergency: A case in China under COVID-19. Appl. Energy 2021, 283, 116339. [Google Scholar] [CrossRef] [PubMed]
- Obst, D.; de Vilmarest, J.; Goude, Y. Adaptive Methods for Short-Term Electricity Load Forecasting during COVID-19 Lockdown in France. IEEE Trans. Power Syst. 2021, 36, 4754–4763. [Google Scholar] [CrossRef] [PubMed]
- Şahin, U.; Ballı, S.; Chen, Y. Forecasting seasonal electricity generation in European countries under Covid-19-induced lockdown using fractional grey prediction models and machine learning methods. Appl. Energy 2021, 302, 117540. [Google Scholar] [CrossRef] [PubMed]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural Networks for Short-Term Load Forecasting: A Review and Evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- L’Heureux, A.; Grolinger, K.; Elyamany, H.F.; Capretz, M.A.M. Machine Learning with Big Data: Challenges and Approaches. IEEE Access 2017, 5, 7776–7797. [Google Scholar] [CrossRef]
- Chen, B.J.; Chang, M.W.; Lin, C.J. Load Forecasting Using Support Vector Machines: A Study on EUNITE Competition 2001. IEEE Trans. Power Syst. 2004, 19, 1821–1830. [Google Scholar] [CrossRef]
- Ekonomou, L. Greek long-term energy consumption prediction using artificial neural networks. Energy 2010, 35, 512–517. [Google Scholar] [CrossRef]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Burnaev, E.V.; Panov, M.E.; Zaytsev, A.A. Regression on the Basis of Nonstationary Gaussian Processes with Bayesian Regularization. J. Commun. Technol. Electron. 2016, 61, 661–671. [Google Scholar] [CrossRef]
- Sözen, A.; İzgeç, M.M.; Kırbaş, İ.; Kazancıoğlu, F.Ş.; Tuncer, A.D. Overview, modeling and forecasting the effects of COVID-19 pandemic on energy market and electricity demand: A case study on Turkey. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–16. [Google Scholar] [CrossRef]
- Li, X.; Wang, Y.; Ma, G.; Chen, X.; Shen, Q.; Yang, B. Electric load forecasting based on Long-Short-Term-Memory network via simplex optimizer during COVID-19. Energy Rep. 2022, 8, 1–12. [Google Scholar] [CrossRef]
- Liu, X.; Lin, Z. Impact of COVID-19 pandemic on electricity demand in the UK based on multivariate time series forecasting with Bidirectional Long Short Term Memory. Energy 2021, 227, 120455. [Google Scholar] [CrossRef] [PubMed]
- Lu, H.; Ma, X.; Ma, M. A hybrid multi-objective optimizer-based model for daily electricity demand prediction considering COVID-19. Energy 2021, 219, 119568. [Google Scholar] [CrossRef]
- Hu, C.; Zhang, J.; Yuan, H.; Gao, T.; Jiang, H.; Yan, J.; Wenzhong Gao, D.; Wang, F.Y. Black swan event small-sample transfer learning (BEST-L) and its case study on electrical power prediction in COVID-19. Appl. Energy 2022, 309, 118458. [Google Scholar] [CrossRef]
- Wang, D.; Luo, H.; Grunder, O.; Lin, Y.; Guo, H. Multi-step ahead electricity price forecasting using a hybrid model based on two-layer decomposition technique and BP neural network optimized by firefly algorithm. Appl. Energy 2017, 190, 390–407. [Google Scholar] [CrossRef]
- AL-Musaylh, M.S.; Deo, R.C.; Li, Y.; Adamowski, J.F. Two-phase particle swarm optimized-support vector regression hybrid model integrated with improved empirical mode decomposition with adaptive noise for multiple-horizon electricity demand forecasting. Appl. Energy 2018, 217, 422–439. [Google Scholar] [CrossRef]
- Wang, G.; Wang, X.; Wang, Z.; Ma, C.; Song, Z. A VMD-CISSA-LSSVM Based Electricity Load Forecasting Model. Mathematics 2022, 10, 28. [Google Scholar] [CrossRef]
- Yu, Y.; Li, W.; Sheng, D.; Chen, J. A novel sensor fault diagnosis method based on Modified Ensemble Empirical Mode Decomposition and Probabilistic Neural Network. Measurement 2015, 68, 328–336. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE international conference on acoustics, speech and signal processing (ICASSP), Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Xiao, Q.; Li, J.; Sun, J.; Feng, H.; Jin, S. Natural-gas pipeline leak location using variational mode decomposition analysis and cross-time–frequency spectrum. Measurement 2018, 124, 163–172. [Google Scholar] [CrossRef]
- Jiang, P.; Li, R.; Liu, N.; Gao, Y. A novel composite electricity demand forecasting framework by data processing and optimized support vector machine. Appl. Energy 2020, 260, 114243. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhu, Z. A hybrid method for noise suppression using variational mode decomposition and singular spectrum analysis. J. Appl. Geophys. 2019, 161, 105–115. [Google Scholar] [CrossRef]
- Zhang, X.; Miao, Q.; Zhang, H.; Wang, L. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery. Mech. Syst. Signal Process. 2018, 108, 58–72. [Google Scholar] [CrossRef]
- Ding, J.; Xiao, D.; Li, X. Gear Fault Diagnosis Based on Genetic Mutation Particle Swarm Optimization VMD and Probabilistic Neural Network Algorithm. IEEE Access 2020, 8, 18456–18474. [Google Scholar] [CrossRef]
- Gai, J.; Shen, J.; Hu, Y.; Wang, H. An integrated method based on hybrid grey wolf optimizer improved variational mode decomposition and deep neural network for fault diagnosis of rolling bearing. Measurement 2020, 162, 107901. [Google Scholar] [CrossRef]
- Venter, G. Review of Optimization Techniques. In Encyclopedia of Aerospace Engineering; John Wiley & Sons Ltd.: Chichester, UK, 2010; pp. 1–10. ISBN 9780470686652. [Google Scholar]
- Aswanuwath, L.; Pannakkong, W.; Buddhakulsomsiri, J.; Karnjana, J.; Huynh, V.-N. A Hybrid Model of VMD-EMD-FFT, Similar Days Selection Method, Stepwise Regression, and Artificial Neural Network for Daily Electricity Peak Load Forecasting. Energies 2023, 16, 1860. [Google Scholar] [CrossRef]
- Galelli, S.; Humphrey, G.B.; Maier, H.R.; Castelletti, A.; Dandy, G.C.; Gibbs, M.S. An evaluation framework for input variable selection algorithms for environmental data-driven models. Environ. Model. Softw. 2014, 62, 33–51. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W. Data-driven input variable selection for rainfall-runoff modeling using binary-coded particle swarm optimization and Extreme Learning Machines. J. Hydrol. 2015, 529, 1617–1632. [Google Scholar] [CrossRef]
- Bonnlander, B.V.; Weigend, A.S. Selecting Input Variables Using Mutual Information and Nonparametric Density Estimation. In Proceedings of the International Symposium on Artificial Neural Networks, Tainan, China, 28 June–2 July 1994. [Google Scholar]
- Bowden, G.J.; Maier, H.R.; Dandy, G.C. Input determination for neural network models in water resources applications. Part 2. Case study: Forecasting salinity in a river. J. Hydrol. 2005, 301, 93–107. [Google Scholar] [CrossRef]
- Niu, D.; Wang, Y.; Wu, D.D. Power load forecasting using support vector machine and ant colony optimization. Expert Syst. Appl. 2010, 37, 2531–2539. [Google Scholar] [CrossRef]
- Gabriels, W.; Goethals, P.L.M.; Dedecker, A.P.; Lek, S.; De Pauw, N. Analysis of macrobenthic communities in Flanders, Belgium, using a stepwise input variable selection procedure with artificial neural networks. Aquat. Ecol. 2007, 41, 427–441. [Google Scholar] [CrossRef]
- Mandal, P.; Senjyu, T.; Funabashi, T. Neural networks approach to forecast several hour ahead electricity prices and loads in deregulated market. Energy Convers. Manag. 2006, 47, 2128–2142. [Google Scholar] [CrossRef]
- Chen, Y.; Luh, P.B.; Guan, C.; Zhao, Y.; Michel, L.D.; Coolbeth, M.A.; Friedland, P.B.; Rourke, S.J. Short-Term Load Forecasting: Similar Day-Based Wavelet Neural Networks. IEEE Trans. Power Syst. 2010, 25, 322–330. [Google Scholar] [CrossRef]
- Fallah, S.N.; Ganjkhani, M.; Shamshirband, S.; Chau, K. wing Computational Intelligence on Short-Term Load Forecasting: A Methodological Overview. Energies 2019, 12, 393. [Google Scholar] [CrossRef]
- Mu, Q.; Wu, Y.; Pan, X.; Huang, L.; Li, X. Short-Term Load Forecasting Using Improved Similar Days Method. In Proceedings of the 2010 Asia-Pacific Power and Energy Engineering Conference (APPEEC), Chengdu, China, 28–31 March 2010. [Google Scholar]
- Zheng, H.; Yuan, J.; Chen, L. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Park, R.-J.; Song, K.-B.; Kwon, B.-S. Short-Term Load Forecasting Algorithm Using a Similar Day Selection Method Based on Reinforcement Learning. Energies 2020, 13, 2640. [Google Scholar] [CrossRef]
- Senjyu, T.; Takara, H.; Uezato, K.; Funabashi, T. One-Hour-Ahead Load Forecasting Using Neural Network. IEEE Trans. Power Syst. 2002, 17, 113–118. [Google Scholar] [CrossRef]
- The Asia Foundation. Available online: https://asiafoundation.org/where-we-work/thailand/ (accessed on 21 February 2022).
- Giordano, F.; La Rocca, M.; Perna, C. Input Variable Selection in Neural Network Models. Commun. Stat. Theory Methods 2014, 43, 735–750. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Humpage, S. An introduction to regression analysis. Sensors 2000, 17, 68–74. [Google Scholar] [CrossRef]
- Lucà, F.; Buttafuoco, G.; Terranova, O. GIS and Soil. Compr. Geogr. Inf. Syst. 2018, 3, 37–50. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- Johnsson, T. A procedure for stepwise regression analysis. Stat. Pap. 1992, 33, 21–29. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hadi, A.S. Regression Analysis by Example, 5th ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2012. [Google Scholar]
- Ramón, J.; Espasa, A.; Grafe, R. Forecasting the electricity load from one day to one week ahead for the Spanish system operator. Int. J. Forecast. 2008, 24, 588–602. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Zhou, F.; Zhou, H.; Li, Z.; Zhao, K. Multi-Step Ahead Short-Term Electricity Load Forecasting Using VMD-TCN and Error Correction Strategy. Energies 2022, 15, 5375. [Google Scholar] [CrossRef]
- Musbah, H. SARIMA Model Forecasting of Short-Term Electrical Load Data Augmented by Fast Fourier Transform Seasonality Detection. In Proceedings of the 2019 IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019. [Google Scholar]
- Aras, S.; Kocakoç, T.D. A new model selection strategy in time series forecasting with artificial neural networks: IHTS. Neurocomputing 2016, 174, 974–987. [Google Scholar] [CrossRef]
- Kaastraa, I.; Boydb, M. Designing a neural network for forecasting financial time series. Neurocomputing 1996, 10, 215–236. [Google Scholar] [CrossRef]
- Negash, B.M.; Yaw, A.D. Artificial neural network based production forecasting for a hydrocarbon reservoir under water injection. Pet. Explor. Dev. 2020, 47, 383–392. [Google Scholar] [CrossRef]
- Svozil, D.; Kvasnička, V.; Pospíchal, J. Introduction to multi-layer feed-forward neural networks. Chemom. Intell. Lab. Syst. 1997, 39, 43–62. [Google Scholar] [CrossRef]
- Lauret, P.; Fock, E.; Randrianarivony, R.N.; Manicom-Ramsamy, J.F. Bayesian neural network approach to short time load forecasting. Energy Convers. Manag. 2008, 49, 1156–1166. [Google Scholar] [CrossRef]
- Dedinec, A.; Filiposka, S.; Dedinec, A.; Kocarev, L. Deep belief network based electricity load forecasting: An analysis of Macedonian case. Energy 2016, 115, 1688–1700. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Urgen Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Graves, A. Supervised Sequence Labelling. In Supervised Sequence Labelling with Recurrent Neural Networks; Springer: Berlin/Heidelberg, Germany, 2012; pp. 5–13. [Google Scholar]
- Erdogan Erten, G.; Bozkurt Keser, S.; Yavuz, M. Grid Search Optimised Artificial Neural Network for Open Stope Stability Prediction. Int. J. Mining Reclam. Environ. 2021, 35, 600–617. [Google Scholar] [CrossRef]
- Marino, D.L.; Amarasinghe, K.; Manic, M. Building Energy Load Forecasting Using Deep Neural Networks. In Proceedings of the IECON 42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 23–26 October 2016. [Google Scholar]
- Madrid, E.A.; Antonio, N. Short-Term Electricity Load Forecasting with Machine Learning. Information 2021, 12, 50. [Google Scholar] [CrossRef]
- Pannakkong, W.; Harncharnchai, T.; Buddhakulsomsiri, J. Forecasting Daily Electricity Consumption in Thailand Using Regression, Artificial Neural Network, Support Vector Machine, and Hybrid Models. Energies 2022, 15, 3105. [Google Scholar] [CrossRef]




| Paper | Forecasting Model | Data Decomposition | Select Input Variable | Hyper Parameter Optimization | Sensitivity Factor | Rolling Dataset | Study Location | Forecasting Period |
|---|---|---|---|---|---|---|---|---|
| [26] | ARIMAX | No | No | No | No | No | Jordan | 30 min, Daily, Monthly |
| [27] | Rolling IMSGM | No | No | No | No | Yes | China | Monthly |
| [28] | Kalman filtering with GAM | No | No | No | No | No | France | 30 min |
| [29] | Fractional grey model | No | No | GA | No | No | European countries | Monthly |
| [36] | LSTM | No | No | No | No | No | Turkey | Daily, Monthly |
| [14] | ANN | No | No | No | Yes | No | European countries, US cities | Daily |
| [37] | LSTM | No | No | Simplex optimizer | Yes | No | China | Daily |
| [38] | Bi-LSTM | No | No | Grid search, Manual search | Yes | No | UK | Daily |
| [39] | SVM | ICEEMDAN | No | MOGWO | Yes | No | US | Daily |
| [40] | Transfer learning with CNN | No | No | No | No | No | China | Monthly |
| Proposed Model | ANN/LSTM | VMD-EMD-FFT | Stepwise regression, SD | Grid search | Yes | Yes | Thailand | Daily |
| Case | Target Date | Type of the Same Special Holiday in the Previous Year | Similar Day Selection | ||||
|---|---|---|---|---|---|---|---|
| Normal Day | Special Holiday | Weekday | Weekend | Weekday | Weekend | ||
| 1 | x | x | N/A | N/A | Pick a similar day from the closest date in the previous year that has the same day of the week (Monday–Sunday) as the target date | ||
| 2 | x | x | |||||
| 3 | x | x | x | Pick a similar day from the same special holiday in the previous year | |||
| 4 | x | x | x | ||||
| 5 | x | x | x | ||||
| 6 | x | x | x | Pick a similar day from the substitute holiday of the special holiday in the previous year | |||
| Target Date | Selected Date |
|---|---|
| 1 April 2020 (Wednesday) | 3 April 2019 (Wednesday) |
| 2 April 2020 (Thursday) | 4 April 2019 (Thursday) |
| 3 April 2020 (Friday) | 5 April 2019 (Friday) |
| 4 April 2020 (Saturday) | 6 April 2019 (Saturday) |
| Target Date | Selected Date |
|---|---|
| I. Target date and the same special holiday in the previous year have the same day type. | |
| Mother’s Day 12 August 2020 (Wednesday) | Mother’s Day 12 August 2019 (Monday) |
| Substitute Asahna Bucha Day 7 July 2020 (Tuesday) | Asahna Bucha Day 16 July 2019 (Tuesday) |
| II. Target date is a weekend, but the same special holiday in the previous year is a weekday. | |
| Asahna Bucha Day 5 July 2020 (Sunday) | Asahna Bucha Day 16 July 2019 (Tuesday) |
| III. Target date is a weekday, but the same special holiday in the previous year is a weekend. | |
| King’s Birthday 28 July 2020 (Tuesday) | Substitute King’s Birthday 29 July 2019 (Monday) |
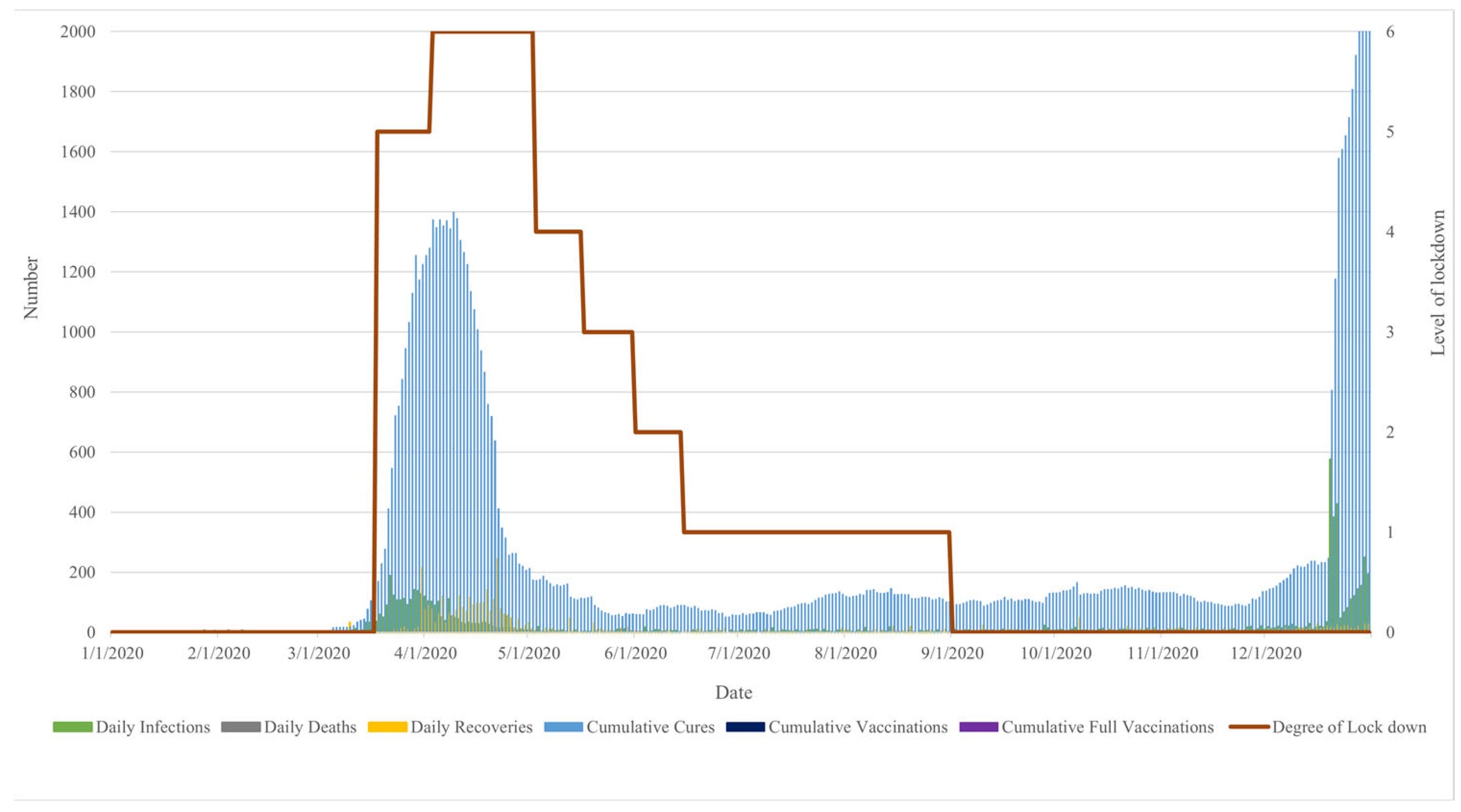
| Date | Lockdown Stage | Event |
|---|---|---|
| 18 March 2020 | 5 | Declaration of lockdown |
| 3 April 2020 | 6 | Declaration of state/national emergency and announcement of a nationwide curfew |
| 3 May 2020 | 4 | Announcement of the loosened COVID-19 restrictions Phase 1 (re-open market, convenient store, restaurant, and outdoor sport) |
| 17 May 2020 | 3 | Announcement of the loosened COVID-19 restrictions Phase 2 (re-open shopping mall, gym, and reduce curfew period) |
| 1 June 2020 | 2 | Announcement of the loosened COVID-19 restrictions Phase 3 (re-open more public spaces, and reduce curfew period) |
| 15 June 2020 | 1 | Announcement of the loosened COVID-19 restrictions Phase 4 and Repeal of a nationwide curfew (re-open school, hotel, theater, and allow transportation across province) |
| 1 September 2020 | 0 | End of lockdown |
| Dataset | No. of Observation | Max | Min | Average | SD |
|---|---|---|---|---|---|
| Electricity Peak Demand | 366 | 28,636.70 | 17,451.90 | 25,481.35 | 1632.73 |
| Daily Infections | 366 | 576 | 0 | 5 | 52.36 |
| Daily Deaths | 366 | 5 | 0 | 0 | 0.62 |
| Daily Recoveries | 366 | 244 | 0 | 3 | 26.93 |
| Current COVID-19 In-Patients | 366 | 2583 | 0 | 108 | 421.00 |
| Cumulative Vaccinations | 366 | 0 | 0 | 0 | 0 |
| Cumulative Full Vaccinations | 366 | 0 | 0 | 0 | 0 |
| Hyperparameter | Definition | GS Range |
|---|---|---|
| Hidden node | The number of hidden nodes on a single hidden layer | 1, 5, 10 |
| Learning rate | The number of magnitudes of the updates made to the weights and biases during the training process | 0.1, 0.01, 0.001 |
| Training cycle | The number of iterations for updating weights and biases | 500, 1000, 1500 |
| Variable Type | Candidate Input Variable |
|---|---|
| Day of the week index | Monday, Tuesday, …, Sunday (7 binary variables) |
| Special holiday index | 0, 1 (1 binary variable) |
| Historical electricity peak demand | T − 1, T − 2, …, T − 7 (7 numerical variables) |
| LMA | Weekly LMA, Monthly LMA (2 numerical variables) |
| MA(P) | MA(2), MA(3), …, MA(7) (6 numerical variables) |
| Hyperparameter | Definition | GS Range |
|---|---|---|
| Hidden node | The number of hidden nodes on a single hidden layer | 1, 5, 10 |
| Learning rate | The number of magnitudes of the updates made to the weights and biases during the training process | 0.1, 0.01, 0.001, 0.0001, 0.00001 |
| Training cycle | The number of iterations for updating weights and biases | 50, 100, 500, 1000, 1500 |
| Month | Benchmark Model | Stepwise | SD Criterion | VMD-EMD-FFT | Forecasting Technique | Test | Degree of Lockdown | ||
|---|---|---|---|---|---|---|---|---|---|
| MAPE | RMSE | MAE | |||||||
| January | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 3.04% | 971 | 754 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 2.34% | 810 | 595 | ||
| 3 | No | No | No | LSTM- based GS | 3.89% | 1303 | 966 | ||
| February | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 3.35% | 956 | 860 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 2.64% | 925 | 680 | ||
| 3 | No | No | No | LSTM- based GS | 2.93% | 975 | 751 | ||
| March | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 3.24% | 1076 | 866 | 0, 5 |
| 2 | Yes | Day type | Yes | ANN- based GS | 3.10% | 1130 | 819 | ||
| 3 | No | No | No | LSTM- based GS | 2.65% | 851 | 714 | ||
| April | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 6.95% | 2368 | 1710 | 6 |
| 2 | Yes | Day type | Yes | ANN- based GS | 5.57% | 2053 | 1343 | ||
| 3 | No | No | No | LSTM- based GS | 3.46% | 1174 | 830 | ||
| May | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.85% | 1543 | 1252 | 6, 4, 3 |
| 2 | Yes | Day type | Yes | ANN- based GS | 4.31% | 1290 | 1108 | ||
| 3 | No | No | No | LSTM- based GS | 3.23% | 1037 | 841 | ||
| June | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 5.95% | 1785 | 1496 | 2, 1 |
| 2 | Yes | Day type | Yes | ANN- based GS | 3.27% | 1163 | 812 | ||
| 3 | No | No | No | LSTM- based GS | 2.52% | 766 | 627 | ||
| July | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.22% | 1337 | 1053 | 1 |
| 2 | Yes | Day type | Yes | ANN- based GS | 3.54% | 1170 | 890 | ||
| 3 | No | No | No | LSTM- based GS | 2.80% | 833 | 701 | ||
| August | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.67% | 1486 | 1166 | 1 |
| 2 | Yes | Day type | Yes | ANN- based GS | 4.21% | 1298 | 1056 | ||
| 3 | No | No | No | LSTM- based GS | 2.43% | 702 | 605 | ||
| September | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.64% | 1413 | 1189 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 2.64% | 845 | 676 | ||
| 3 | No | No | No | LSTM- based GS | 2.73% | 949 | 687 | ||
| October | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 5.56% | 1728 | 1313 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 4.00% | 1200 | 949 | ||
| 3 | No | No | No | LSTM- based GS | 4.48% | 1312 | 1046 | ||
| November | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.51% | 1425 | 1122 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 3.69% | 1255 | 918 | ||
| 3 | No | No | No | LSTM- based GS | 3.95% | 1140 | 977 | ||
| December | 1 | Yes | Euclidean distance | Yes | ANN- based GS | 4.62% | 1300 | 1066 | 0 |
| 2 | Yes | Day type | Yes | ANN- based GS | 4.46% | 1341 | 1015 | ||
| 3 | No | No | No | LSTM- based GS | 4.73% | 1397 | 1070 | ||
| Average 12 Months | Benchmark model 1 | 4.63% | 1501 | 1153 | - | ||||
| Benchmark model 2 | 3.65% | 1244 | 905 | ||||||
| Benchmark model 3 | 3.36% | 1073 | 824 | ||||||
| Proposed model (hybrid) | 3.07% | 999 | 762 | ||||||
| Forecasting Model | Average 12 Months of Test Performance | ||
|---|---|---|---|
| MAPE | RMSE | MAE | |
| Proposed | 3.07% | 999 | 762 |
| Benchmark model 1 [53] | 4.63% | 1501 | 1153 |
| LSTM [88] | 5.15% | 1632 | 1266 |
| XGBoost [89] | 4.12% | 1322 | 1015 |
| SVM [90] | 4.13% | 1305 | 1014 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aswanuwath, L.; Pannakkong, W.; Buddhakulsomsiri, J.; Karnjana, J.; Huynh, V.-N. An Improved Hybrid Approach for Daily Electricity Peak Demand Forecasting during Disrupted Situations: A Case Study of COVID-19 Impact in Thailand. Energies 2024, 17, 78. https://doi.org/10.3390/en17010078
Aswanuwath L, Pannakkong W, Buddhakulsomsiri J, Karnjana J, Huynh V-N. An Improved Hybrid Approach for Daily Electricity Peak Demand Forecasting during Disrupted Situations: A Case Study of COVID-19 Impact in Thailand. Energies. 2024; 17(1):78. https://doi.org/10.3390/en17010078
Chicago/Turabian StyleAswanuwath, Lalitpat, Warut Pannakkong, Jirachai Buddhakulsomsiri, Jessada Karnjana, and Van-Nam Huynh. 2024. "An Improved Hybrid Approach for Daily Electricity Peak Demand Forecasting during Disrupted Situations: A Case Study of COVID-19 Impact in Thailand" Energies 17, no. 1: 78. https://doi.org/10.3390/en17010078
APA StyleAswanuwath, L., Pannakkong, W., Buddhakulsomsiri, J., Karnjana, J., & Huynh, V.-N. (2024). An Improved Hybrid Approach for Daily Electricity Peak Demand Forecasting during Disrupted Situations: A Case Study of COVID-19 Impact in Thailand. Energies, 17(1), 78. https://doi.org/10.3390/en17010078






