A Comprehensive Review on Advanced Control Methods for Floating Offshore Wind Turbine Systems above the Rated Wind Speed

Abstract

This paper presents a comprehensive review of advanced control methods specifically designed for floating offshore wind turbines (FOWTs) above the rated wind speed. Focusing on primary control objectives, including power regulation at rated values, platform pitch mitigation, and structural load reduction, this paper begins by outlining the requirements and challenges inherent in FOWT control systems. It delves into the fundamental aspects of the FOWT system control framework, thereby highlighting challenges, control objectives, and conventional methods derived from bottom-fixed wind turbines. Our review then categorizes advanced control methods above the rated wind speed into three distinct approaches: model-based control, data-driven model-based control, and data-driven model-free control. Each approach is examined in terms of its specific strengths and weaknesses in practical application. The insights provided in this review contribute to a deeper understanding of the dynamic landscape of control strategies for FOWTs, thus offering guidance for researchers and practitioners in the field.

1. Introduction

The release of the 6th assessment report by the Intergovernmental Panel on Climate Change [1] has highlighted the increase in greenhouse gas emissions. One consequence of this rise is the global temperature increase of 1.1 °C compared to the pre-industrial period, and projections suggest a further rise to 1.5 °C by 2030. This warming brings about significant climate and non-climate-related risks for all societies. To mitigate these risks, it is crucial to limit warming by promoting measures aimed at reducing emissions, with the ultimate goal of bringing global net CO₂ emissions to zero. Despite these challenges, global demand for electrical energy continues to grow, with a projected increase of 3.3% in 2024. In this context, enhancing innovation systems for renewable technologies can provide opportunities to curb emission growth while meeting the growing energy needs. Mature clean energy technologies are now more crucial than ever, thus serving as indispensable tools for emerging and developing economies striving to attain their climate targets, including net-zero goals. In 2023, global installed renewable capacity increased to nearly 510 GW, thus marking the fastest growth rate in the past two decades [2]. Among these renewable energies, wind energy is a major resource that has been growing for the past 20 years. The increase in global wind power capacity reached 108 GW in 2023, with a cumulative capacity of 1008 GW [2]. Wind energy technologies are categorized based on location, with distinctions between onshore wind turbines and offshore wind turbines. Offshore turbines are further categorized into bottom-fixed offshore wind turbines and floating offshore wind turbines (FOWTs) based on the specific sub-structure.

Due to limitations faced by onshore wind turbines, such as visual pollution and land requirements for large wind farms, the innovative attention is gradually shifting towards offshore technologies. Indeed, offshore wind turbines offer several advantages compared to their onshore counterparts. Without relief-related obstacles, both bottom-fixed and floating offshore turbines benefit from a superior wind resource in terms of higher average wind speed and lower turbulence rate, thus resulting in increased recoverable power. Furthermore, FOWTs provide a solution to the depth limitation faced by bottom-fixed technology, thereby leading to fewer geo-technical and social constraints. Thus, these turbines can be located in areas with an even more superior wind resource than bottom-fixed, thus enhancing even more electricity production. The FOWT system emerges as a solution for deploying offshore wind turbines in deeper water. Nowadays, the floating wind sector is evolving from 10 single-turbine demonstrators to the current five operational or under-construction wind farms. These include Hywind Scotland & Kincardine (UK), Windfloat Atlantic (Portugal), Hywind Tampen (Norway), and Goto (Japan), thus collectively featuring 32 turbines distributed globally. Among the actors of the floating turbine sector, Europe emerges as a pioneer, as Norway commissioned 60 MW of floating wind capacity in 2022, thus reaching a total installed capacity of 171 MW representing 91% of global installations [3].

The overall FOWT system, illustrated in Figure 1, is composed of a wind turbine to harvest energy from the wind, which is installed on a floating platform attached to the seabed by mooring lines, thereby ensuring support to the wind turbine and the platform. The wind turbine can be classified into two main types: horizontal axis wind turbines (HAWTs) and vertical axis wind turbines. This paper focuses on HAWT systems, given their widespread adoption. The turbine consists typically of a rotor, three blades, a tower, a nacelle housing a low-speed shaft (LSS) and a high-speed shaft (HSS) connected through a gearbox, and a generator. The design of the floating platform is inspired by technologies from the oil and gas platform sector, with the main technologies available being barge, spar–buoy, tension leg, and semi-submersible [4], as illustrated in Figure 2. The barge platform achieves stability through a waterplane area, while the spar–buoy platform is stabilized by a ballast with a lower center of mass. The tension leg platform (TLP) employs tension mooring lines fixed to the seabed for stabilization. The semi-submersible platform combines features of both barge and spar–buoy technologies and is stabilized by a combination of ballast and waterplane area. In all these platform structures, a mooring system is employed to maintain the platform at a specific position and thus prevent drift displacement.

The principle of energy conversion in wind systems relies on transforming the kinetic energy captured by the blades from the wind into electric energy. The blade rotation induces rotor rotation, and within the nacelle, the kinetic energy is converted into mechanical energy as the LSS and HSS rotate with the rotor. This mechanical power is then further converted into electric energy, as the HSS is connected to a generator. The main dynamics acting on the FOWT structure are aerodynamic related to the wind, hydrodynamic and mooring line dynamics associated with waves and currents, structural dynamics exerted on the wind turbine, and servo-dynamics associated with the electrical systems, such as power converters and control systems within the nacelle [5].

In contrast to bottom-fixed offshore wind turbines, floating turbines face more challenges due to the dynamic nature of the floating platform, thus introducing an additional six degrees of freedom in motion (Figure 1). This platform motion renders the system more susceptible to disturbances, which are caused by waves, currents, and a combined effect of wind and waves. Thus, despite being moored to the seabed, the FOWT system is prone to stability issues induced by these environmental loads, thereby directly impacting power generation and increasing operational and maintenance costs. To tackle these challenges, controllers play a crucial role in addressing the dynamic complexities inherent in FOWTs. Considering the significant impact of control systems on the performance, stability, and reliability of these systems during operation, there is a pressing need for substantial advancements in control methodologies. Therefore, this paper aims to fulfill this need by offering a comprehensive exploration of the requirements and challenges associated with FOWT control systems. It delves into the fundamental aspects of FOWT system control technologies above the rated wind speed, thus emphasizing key challenges, control objectives, and conventional methods derived from bottom-fixed wind turbines. The exploration includes a thorough evaluation of the existing advanced control methods primarily utilized for rated power tracking and platform pitch mitigation, thereby covering both model-based control and data-driven control approaches. Following a concise overview of system modeling for control design, model-based methods are categorized into linear and non-linear approaches. The paper also engages in an extensive discussion on data-driven control methods, thus encompassing both model-based data-driven and model-free data-driven approaches applied to FOWT systems above the rated wind speed.

The main contributions of this paper are summarized as follows:

• A comprehensive review of conventional and advanced control methods specific to FOWTs operating above the rated wind speed, which are hereby referred to as Region III;
• A clear distinction between model-based control, data-driven model-based control, and data-driven model-free control methods, which is accompanied by a discussion on their respective limitations;
• By providing an understanding of FOWT control systems and categorizing existing control approaches, this paper provides researchers with valuable guidance for advancing the field.

The paper is structured as follows: In Section 2, the fundamental control framework for FOWTs is provided, thereby introducing conventional control approaches in Region III derived from bottom-fixed technology. Section 3 offers a review of the advanced control methods in Region III, which are categorized as model-based control, data-driven model-based control, and data-driven model-free control, thus addressing limitations and challenges specific to the FOWT system. Finally, the conclusion and the outline perspectives are given in Section 4.

2. Conventional Control Framework for FOWT System

Few viable control solutions currently exist for FOWTs, as their control remains a recent focus within the control systems community. This section introduces conventional control methodologies derived from bottom-fixed onshore and offshore wind turbine systems, and it explores their adaptation to address the complex challenges presented by FOWT systems in Region III, along with their inherent limitations.

2.1. Control Methodologies for Wind Turbine System

To ensure proper operation, as well as the safety and achievement of energy goals, FOWTs are equipped with sensors, actuators, and a control unit. The different sensors capture signal measurements, thus forwarding them to the controller unit, where output signals can then be generated for the actuators. The primary actuators in the system include the blade pitch angle—collective or individual—the generator torque, and the nacelle yaw angle. Before delving into control strategies, the fundamentals of power production for wind turbine systems are briefly revisited.

2.1.1. Power Generation Fundamentals

Wind turbines generate power by harnessing wind energy, which is derived from the recoverable kinetic energy of air passing through a specific surface area. The associated wind power is determined by the following formula:

$$P_{wind}=\frac{1}{2}\rho S{v}^3$$

(1)

where S is the swept air surface area, v is the wind speed, and $\rho$ is the air density under normal temperature and pressure conditions at sea level.

However, not all the wind energy is fully recovered by the wind turbine due to air velocities behind the wind turbine. This phenomenon is characterized by the power coefficient ($C_p$), representing the turbine’s efficiency, and dividing the power of the wind turbine by the power of the wind. This aerodynamic efficiency is a non-linear function of the blade pitch angle ($\beta$) and the tip speed ratio ($\lambda$), which is defined as

$$C_P=f(\beta ,\lambda )\mathrm{with}\lambda =\frac{\omega R}{v}$$

(2)

where R is the rotor radius, and $\omega$ is the rotor speed.

The expression for the recoverable power by the wind turbine can be formulated as

$$P=\frac{1}{2}\rho C_p\pi R^2{v}^3=C_p{P}_{wind}$$

(3)

For each incoming wind value, there exists a rotor speed for which the value of $C_p$ is maximal, thereby corresponding to the optimal tip speed ratio lambda. Therefore, reaching optimal $C_p$ leads to optimal extracted power by the wind turbine. As an energetic system, optimizing power production while maintaining structural integrity to minimize maintenance and operational costs is crucial for the economic viability of the wind turbine. An effective control system is then required to achieve maximum power extraction, as well as to ensure safe turbine operation with reducing loads. The following part discusses the control structure and conventional approaches used to meet these objectives.

2.1.2. Control System and Objectives

Within the FOWT system, primary-level safety control, second-level supervisory control, and third-level closed-loop control collectively ensure the safe operation of the turbine. The third-level closed-loop control is specifically responsible for ensuring that the wind turbine meets power production objectives based on four operating regions, which are determined by incoming wind speed, as depicted in Figure 3.

Regions II and III are primarily focused on power production, thus requiring control strategies to optimize turbine performance. Traditional fixed wind turbine controllers are simple single-input, single-output (SISO) control mechanisms. Control loops for the torque and blade pitch angle run in parallel to achieve control objectives in these two different operating regions, as illustrated in Figure 4.

In Region II, wind speeds range from the cut-in speed ($V_{cut\text{-}in}$) to the rated speed ($V_{rated}$). Here, the objective is to maximize power extraction by operating near the optimal $C_p$. This is achieved through a common control strategy known as maximum power point tracking (MPPT) control [6], which involves fixing the blade pitch angle at an optimal value and utilizing torque control to maintain optimal efficiency at each operating point.

In Region III, where the wind speed is above $V_{rated}$ and below the cut-off speed ($V_{cut\text{-}off}$), the primary control objectives shift from maximizing power extraction to regulating power at its rated value. Several strategies exist, including pitch-to-stall, passive or active, and pitch-to-feather [7]. Pitch-to-stall strategies involve adjusting the blade pitch angle to induce rapid aerodynamic stall, thereby limiting power without additional mechanical or electrical elements. Passive stall control fixes the blade pitch angle, thus relying solely on wind speed to induce stall, but it lacks operating point optimization and requires a high-torque brake system. Active stall allows for blade pitch angle adjustment, thereby providing more precise control over aerodynamics and maintaining the torque at a constant level until total stall occurs. The pitch-to-feather strategy involves aggressive adjustment of the blade pitch angle to reduce the lift and rotor speed, thus offering adaptability to varying conditions while reducing aerodynamic forces on the blade and tower constraints. As a result, pitch-to-feather control is commonly used due to its flexibility and effectiveness in regulating wind turbines across various operating conditions.

Furthermore, the blade pitch control can be collective or individual, depending on whether all the blades are controlled simultaneously or individually. The collective blade pitch (CPB) control is more commonly used than the individual blade pitch (IBP) control, which is a more recent strategy that provides individual signals to each blade actuator. While the IBP approach reduces the loads on the blades, it demands higher requirements for the actuators compared to the CBP control method.

As for the generator torque control in Region III, two common strategies exist: constant power and constant torque. In the constant power strategy, the generator torque is adjusted inversely proportional to the rotor speed, thus aiming to mitigate power fluctuations. However, these torque fluctuations induce torsional forces on the shaft, thereby potentially causing damage to mechanical components.

In the constant torque strategy, the generator torque $T_g$ is maintained fixed at its rated value, while the blade pitch angle regulates the generator speed ${\omega }_g$ to achieve rated power.

$$P_g={\eta }_g{T}_g{\omega }_g$$

(4)

where ${\eta }_g$ is the gearbox ratio, and $P_g$ is the generated power.

The constant torque strategy is commonly used due to its simplicity and reduced load on the drive train, although it may impact the quality of the power generated compared to the constant power strategy.

$$T_g=\frac{P_g}{{\eta }_g{\omega }_g}$$

(5)

Thus, the prevalent control strategy for conventional wind turbines operating in Region III involves maintaining the generator torque at its rated value. Simultaneously, the CBP closed-loop control ensures that the rotor speed matches its rated value by using feedback from the difference between the actual rotor speed and its rated speed, thereby employing a proportional–integral–derivative (PID) control approach [8].

2.2. Conventional Control Methodologies for FOWT System

2.2.1. Negative Damping Phenomenon

In the application of FOWTs, the same operating regions are distinguished, but the control objectives become more challenging due to the additional floating platform system. When traditional wind turbine control strategies with blade pitch angle and torque control loops [9,10] are applied to floating wind turbines, an increased pitching motion of the platform emerges, thereby potentially causing instability in Region III, which is known as negative damping [9]. Indeed, due to the blade pitch angle control being beyond rated speed, the pitching motion of the platform become a critical dynamic.

The negative damping phenomenon in Region III unfolds as depicted in Figure 5: when the wind speed surpasses the rated speed, the traditional control system reduces the aerodynamic torque on the turbine blades to maintain a constant rotor speed or regulate power. However, this reduction in aerodynamic torque also decreases the aerodynamic thrust on the rotor. As a result, the floating platform starts pitching forward more aggressively. This pitching motion is the swinging or tilting of the platform in response to the wind forces. Paradoxically, this intensified pitching motion causes the rotor to experience even higher wind speeds, thus accelerating its rotation.

Consequently, the negative damping phenomenon creates a trade-off between maintaining stable power regulation and limiting the pitching motion of the floating platform. This dynamic interaction between the control system and the natural movements of the floating structure can lead to instability and challenges in maintaining both power output and platform stability in Region III of FOWTs.

Thus, traditional control methods employed for bottom-fixed offshore wind turbine technology reveal their limitations when applied to FOWT technology in Region III. Therefore, control strategies must be adapted to the specificity of the FOWT system to achieve power extraction objectives while ensuring the stability of the floating platform when operating in Region III.

Efforts are directed toward refining control methodologies to address critical platform motion. One control strategy focuses on the mass–spring–damper system for FOWTs, thereby providing stiffness and damping to the platform and adding degrees of freedoms to enhance stability. Another approach involves blade pitch-based FOWT control methods using the blade pitch angle, generator torque, or yaw angle of the turbine to achieve control objectives and platform stability. This paper focuses on the latter approach for achieving control objectives in operating Region III, where the negative damping phenomenon poses more significant challenges.

These methodologies can be further divided into two sub-categories: conventional and advanced control methods for FOWTs operating in Region III. Conventional methods involve the adaptation of traditional wind turbine controllers to perform effectively on FOWTs.

2.2.2. Conventional Controllers for FOWT System

Traditional fixed wind turbine controllers in Region III can be modified to include the platform motion suppression objective. Similar to their bottom-fixed counterparts, conventional controllers for FOWTs are characterized by simple SISO systems. These systems employ independent, parallel control strategies for the torque and blade pitch angle. In Region III, the majority of control algorithms leverage the blade pitch control loop, thereby directing blade actuation to provide the wind turbine with aerodynamic thrust to achieve control objectives.

To mitigate the platform pitching, the gain scheduling proportional integral (GSPI) control initially designed for fixed wind systems has been adapted to suit FOWT control challenges in [10]. In Region III, this adaptation consists of reducing the platform pitch motion by ensuring that the frequency of the blade pitch actuator remains lower than the platform’s resonance frequency. Given the non-linearity of floating turbine systems, a conventional collective pitch implementation may compromise desired performance. To address this, gain scheduling laws are designed, thereby associating each operating point with a linear model and its control. The control system dynamically selects the most appropriate regulation loop based on input variables. This methodology, tested on a spar platform, successfully demonstrated a reduction in platform movements compared to conventional methods. However, it introduced a 30% increase in speed error, thereby highlighting a trade-off between enhanced platform stability and power quality, as well as rotor speed regulation.

Further instances of classic PID controllers, adapted for use in floating wind turbines with programmed gains, are demonstrated in the works of Jonkman et al. [5,11,12]. An alternative GSPI controller, aimed at mitigating negative damping, was employed, thus adjusting the rotor speed based on the blade pitch activity [5]. In the control system of the 5 MW turbine developed by the National Renewable Energy Laboratory of United States mounted on a barge platform [11], the generator torque control loop maintains the power at its rated value in Region III. Simultaneously, a GSPI controller modulates the rotor speed in response to the collective blade pitch activity. To meet the control objectives, three additional control loops were introduced: tower–top feedback control, active pitch-to-stall control, and a controller with detuned gains. The inclusion of the tower movement speed into the control loop did not yield improve performance. While active pitch-to-stall control effectively regulated power, it resulted in increased platform movements. However, the detuned gains controller has proven most suitable by minimizing the blade pitch activity and effectively addressing the negative damping issue. Indeed, by detuning the controller gains so that the natural frequency of the closed-loop system is lower than the platform pitch natural frequency, the platform pitch motion can be significantly reduced. This configuration is now considered the baseline control of FOWT and serves as the benchmark for testing new controller designs. This baseline controller has undergone analysis and modification for different platforms types, as outlined in [13]. A comparative study was conducted on the fatigue loads and stability of the barge, TLP, and spar–buoy floating systems. The findings highlight platform-dependent instabilities, with the barge platform emerging as the most unstable solution. In terms of tower loading resistance, the spar–buoy platform showed superior performance compared to the barge platform. Nevertheless, the deployment of the spar–buoy platform is hindered by its intricate design and assembly, thereby resulting in higher costs. The TLP was identified as the most stable solution with lower mechanical loads. However, the anchoring system of the TLP may contribute to increased costs.

A GSPI-based CBP control incorporated a novel approach in [14] to address platform instability by employing the pitching velocity of the platform as an input to regulate the generator rated speed in Region III. This method uses the generator speed to counteract the thrust, thereby mitigating the platform pitch motion and promoting stability. While this control strategy, tested on a barge platform, successfully reduced the negative damping phenomenon and blade pitch activity, it resulted in increased rotor speed and power fluctuations. In [9], a control strategy based on wind speed estimation was proposed to address negative damping. This approach demonstrated enhancements in tower loading and nacelle oscillations. However, it resulted in degraded rotor speed regulation and reduced power generation when compared to the conventional blade pitch mechanism. The efficacy of this method is mainly influenced by the accuracy of the wind speed estimation. In [15], the control system involved the individual adjustment of the blade pitch angles, which was achieved through two expert proportional–integral (PI) controllers coupled with a traditional PID controller for collective blade pitch angle control. This approach facilitates adaptive gain tuning based on the FOWT’s experience. Another controller, detailed in [16], employed two linked PID correctors for the collective and individual blade pitch angle controls. Gains in this setup were determined online through the optimization of an objective function. However, the computational expense of such optimization makes it impractical for real-world applications.

2.2.3. Limitations and Challenges

These conventional approaches, derived from bottom-fixed wind turbines and employing SISO logic, serve as an easily implementable foundation for FOWT systems operating in Region III. Nevertheless, there are limitations in terms of performance, particularly in managing multiple control loops, which then requires a thorough understanding of the system. These methods remain sensitive to disturbances and lead to more structural fatigue, thereby making them less suitable for complex non-linear FOWT systems, which are subjected to significant combined disturbances. Moreover, the tuning process for different operating points to maintain high performances is fastidious.

To further enhance the performance of the FOWT systems in Region III, advanced control methods employing a multiple-input multiple-output (MIMO) logic can address the cross-coupling of control loops and disturbances. As a result, several studies propose the utilization of advanced control approaches for FOWT in Region III.

3. Review on Advanced Control of FOWT System

This section provides an exhaustive exploration of the advanced control methodologies designed to overcome the limitations inherent in conventional SISO approaches. The intricate dynamics of FOWTs, specifically the pitching motion of floating platforms, emphasize the need for efficient control strategies in Region III. In recent years, a spectrum of advanced MIMO control techniques has emerged, which is dedicated to regulating power while simultaneously mitigating platform motion and fatigue loads in FOWTs. The prevalence of MIMO control methods applied to FOWTs is grounded in analytical models of the FOWT plant, thus categorizing these strategies as model-based control.

Moreover, the advent of cutting-edge sensor technologies and enhanced computational capabilities allows for a reservoir of data, thereby serving not only as support for advanced classical model-based methods but also for the emerging field of data-driven control approaches [17]. In the context of control systems, the term data-driven control methods refers to approaches wherein the design and optimization of control strategies are primarily based on data obtained from the system rather than relying on explicit analytical models [17,18]. These methods leverage artificial intelligence (AI) such as machine learning, statistical analysis, and other data-driven techniques to infer the system’s behavior, identify patterns, and develop control policies directly from observed data. This definition serves as a cornerstone, thereby highlighting two key tenets:

• The direct utilization of measured input/output data;
• The reliance on data modeling rather than mathematical modeling.

Consequently, data-driven control techniques manifest in both model-based and model-free approaches, namely data-driven model-based control and data-driven model-free control. In the former, optimal control actions hinge on a model approximated or modified by data, while in the latter, the controller design relies solely on measured input and output data, thereby relegating the traditional plant model to the background. Therefore, a clear distinction between classical model-based control and data-driven control exists. Classical model-based control involves designing the controller based on the system model, while data-driven control does not consider explicit information from the mathematical model of the controller system.

Based on the distinction between model-based, data-driven model-based and data-driven model-free control approaches, as presented in Figure 6, this section explores their application in the context of FOWTs operating in Region III. Additionally, the inherent limitations and insightful perspectives of these three approaches are investigated.

3.1. Model-Based Control for FOWT System

This sub-section covers classical model-based control methodologies for FOWT systems in Region III, where controllers are developed based on the system dynamics model. Within this framework, a distinction is made between linear and non-linear control approaches. Furthermore, the integration of intelligent control techniques, leveraging data-driven tools, can enhance the performance of these model-based controllers.

3.1.1. Modelling of FOWT System

In recent years, numerous models for FOWTs have emerged, thereby displaying different degrees of fidelity to reality. A classification based on this fidelity can be established, thus distinguishing between models that are highly faithful to reality and reduced models.

Highly faithful models use precise calculation methods thanks to advanced software such as Ansys AQWA v14.5, OpenFOAM v11, ABAQUS v6.6, and Autodesk v14.0. Leveraging computational fluid dynamics or the finite element method, these models enable detailed analyses of phenomena and local loads across the entire structure. While offering a comprehensive understanding of the system, these approaches demand significant computational resources, thus making them ideal for in-depth analysis but less practical for control laws validation due to prolonged resolution times. To address this computational time challenge, highly accurate numerical methods can be synergized with less intensive computing approaches. Integrated software solutions include FAST v8 (and its open-source version OpenFAST), SimPack v6, HAWC2 v13.0, and Bladed Orcaflex v11.4c for the modeling of FOWTs. These combined tools provide a balance between model fidelity and computation time and are particularly suitable for developing linear control laws around operating points.

However, when it comes to developing innovative control laws, reduced models present significant advantages. Despite being based on restrictive assumptions with simplified equations and ignored physics, these simplified models capture the essential dynamics of FOWTs. This results in reduced computation times and a more streamlined approach to control design. Non-linear reduced models are particularly employed for the development of advanced non-linear control laws. In the recent literature, the most accurate non-linear models employed for control design are credited to Betti [19], Lemmer [20], and Homer [21]. These models are commonly referred to as control-oriented models (COMs). The Betti COM is associated with the 5 MW TLP-based FOWT presented in [13]. The second non-linear Lemmer COM is linked to the 5 MW spar–buoy FOWT proposed in [11], with a more condensed version found in [20]. The non-linear Homer COM is tied to the 5 MW semi-submersible-based FOWT introduced in [22].

3.1.2. Classical Model-Based Control Methods

Existing controllers for FOWTs in Region III can be classified into two groups based on the aforementioned modeling approaches: linear controllers and nonlinear controllers. The majority of existing model-based controllers for FOWT in Region III are developed using models linearized around specific operating points extracted from FAST or a derived non-linear COM. However, in recent years, there has been a trend towards designing non-linear controllers directly based on the COM itself, without the need for linearization around operating points [23,24,25,26].

The majority of advanced controllers designed for FOWTs are based on state space control. In this approach, the design process involves linearizing the non-linear system model at an operating point and transforming the state x into the deviation $\Delta x$ around the defined operating point. Subsequently, linear control theory is applied to design a controller that achieves the specified objectives. The state space equations can be expressed as follows:

$$\begin{array}{c}\hfill \Delta \dot{x}=A\Delta x+B\Delta u+B_d\Delta u_d\\ \hfill \Delta \dot{y}=C\Delta x+D\Delta u+D_d\Delta u_d\end{array}$$

(6)

where u corresponds to the control input, $u_d$ is the disturbances, y is the measured output, with $\Delta$ representing the deviation from the operating point, and A, B, $B_d$, C, D, and $D_d$ are matrices describing the system dynamics.

The main advanced controllers proposed in the literature for FOWT systems in Region III, based on linearization around an operating point, include the linear quadratic regulator (LQR), ${\mathrm{H}}_{\infty }$ control, linear parameter-varying control (LPV), and model predictive control (MPC). All of these controllers have been developed based on linearization around one or more operating points. Some studies have also employed MIMO control, thus using IBP as control inputs to achieve control objectives such as power regulation, the reduction of platform motion, and fatigue load mitigation.

LQR controllers have demonstrated effectiveness in reducing platform motion in Region III. Initially applied to a FOWT system in [27], the LQR controller showed a reduction in the rotor speed variation and platform pitch motion compared to [12]. This work used a classic CBP strategy, thus achieving the control objectives through a penalty function optimizing the trade-off between speed regulation and platform pitching. Subsequently, additional LQR controllers were developed to address platform motions for different FOWT platforms in Region III [28,29,30], thus comparing CBP control and IBP control. Specifically, LQR-based CBP (LQR-CBP) controllers and LQR-based IBP (LQR-IBP) controllers were designed and tested for a barge platform [28]. The study found that LQR-IBP controller exhibited better performance in terms of rotor speed and power regulation, although the platform pitching motion remained significant. Indeed, while the LQR-CBP control structure for FOWTs demonstrated improvements in speed regulation, it led to increased tower loads due to overlapping blade pitch commands for rotor speed control and platform pitch mitigation. To address this, the IBP control mechanism was used, thereby creating asymmetric rotor loads by pitching blades separately. The overlapping blade pitch commands for rotor speed regulation and platform motion suppression were effectively resolved. An enhancement to the LQR-IBP control was the addition of disturbance adaptation control (DAC), namely LQR-IBP-DAC, thus ensuring improved speed and power regulation by estimating wind and minimizing its impact on the system [29]. LQR-IBP-DAC was designed for FOWTs on a barge and TLP. However, it was found unsuitable for a barge platform, which is mainly influenced by waves, as LQR-IBP-DAC is designed to address wind disturbances. Yet, improvements related to the power and speed regulation were achieved using LQR-IBP-DAC for the TLP. These controllers, initially designed for the barge and TLP, were later used to investigate the performance of a spar–buoy platform in [30]. While the LQR-IBP control scheme improved the tower loading for the barge platform and enhanced the rotor speed and power regulation for barges and TLPs [28,30], its effectiveness in dealing with platform pitching was limited for spars–buoys due to their low natural frequency. However, LQR-IBP offers improved rotor and power regulation through increased blade pitch actuation for the spar–buoy platform. More recently in [31], an LQR approach combined with a wind estimator and a state observer has been introduced to enhance control performances. In an extended work [32], an additional LQR control loop was integrated into an onshore wind turbine controller, thereby effectively reducing power fluctuations and platform motion. In the paper [33], the authors employed a simplified 6-degree-of-freedom model and incorporated wave disturbances into the state model, thus demonstrating the response of the system under sea conditions with an LQR controller. In comparison to previous studies, this controller acts on two actuators: the blades and the generator torque.

These various studies emphasize that the IBP control has been the subject of extensive research in recent years. Resolving the conflict between the blade angle control for the platform and the rotor regulation can be achieved through an IBP control approach, thus creating an asymmetric aerodynamic load on the rotor. Due to the periodic nature of wind turbines, implementing an IBP controller requires the gains to vary periodically based on the azimuth angle of the rotor. The findings from [28,29,30,34], proposing an IBP control approach to reduce the loads, indicate a reduction in the platform movements, thus consequently improving stability. In [28,29,30], the IBP mechanism was integrated with disturbance accommodating control. The multi-input controller achieved multiple objectives, such as a significant reduction in platform motions and tower fatigue compared to GSPI [5], as well as improvements in the power and rotor speed regulation. However, the IBP control approach increases the number of degrees of freedom, thereby complicating control schemes. Additionally, an extensive use of 4 to 12 times larger than GSPI for the blade pitch actuators is required. As explained in these papers, blade pitch control cannot simultaneously reduce the structural motion and the tower loads.

In order to regulate power and reduce structural loads in Region III, a state feedback linear parameter-varying (LPV) method and an output feedback LQR method, both associated with gain scheduling (GS), were tested on a barge platform in [35]. In the LPV control structure, all states of the system were compared to equilibrium states, while in the LQR controller structure, only the generator speed serving as output in the control loop was considered. It was observed that the GS-LPV and GS-LQR controllers outperformed the baseline controller in terms of power regulation and platform pitch minimization. The state feedback LPV method yielded better results in platform pitch motion reduction, while the output feedback LQR showed better power regulation. Another approach, the switching LPV-based CBP (SLPV-CBP) control, was introduced for a semi-submersible FOWT to effectively manage platform motions and associated power regulation in Region III [36]. Developed based on the linearized Homer COM [21], the SLPV demonstrated satisfactory achievement in generator speed and power regulation, thus surpassing the performance of the baseline controller.

The optimal controller ${\mathrm{H}}_{\infty }$ encompasses a set of effective methods for designing control laws that ensure good performance and robustness to modeling uncertainties. ${\mathrm{H}}_{\infty }$ synthesis involves constructing controllers using frequency-based tools and has been applied to FOWT systems. In [37,38], ${\mathrm{H}}_{\infty }$ controllers were designed based on a family of linear state space models, namely the LPV models. This approach has proven effective in reducing generator speed and torque oscillations under extreme wind and wave conditions, thereby demonstrating better performance compared to controllers based on a single linear model. Similarly, an ${\mathrm{H}}_{\infty }$-based CBP (${\mathrm{H}}_{\infty }$-CBP) control was developed to manage the platform motion, regulate extracted power, and reduce associated loads [39]. It was based on a reduced non-linear COM [21] of a semi-submersible FOWT using linearization around operating points in Region III. This approach achieved a rotor speed regulation of up to 40%, which was accompanied by relatively smaller improvements in platform pitch motion reduction and load mitigation. A controller with a GS output feedback and ${\mathrm{H}}_{\infty }$ strategy demonstrated enhancements in tower load and rotor speed regulation [40]. The design relied on a linearized model generated from FAST [11] model dynamics. Linear models were generated at multiple operating points based on output feedback ${\mathrm{H}}_{\infty }$ control, and a scheduling mechanism was implemented. Significant improvements were observed in terms of tower loading and rotor speed regulation. In [41], an ${\mathrm{H}}_{\infty }$ control law was implemented on a scaled FOWT system, thereby demonstrating effective rotor speed regulation and the platform pitch motion reduction in experimental results.

MPC is an advanced control methodology that optimizes the future behavior of a system within a defined time interval, known as the prediction horizon, by leveraging input variables. Unlike traditional control strategies, MPC actions are not solely determined by the errors between the output and the setpoint. Instead, MPC bases its decisions on the control input and the system’s response to that input. While commonly applied in the context of bottom-fixed wind turbines, this strategy demonstrates great performance outcomes when applied to FOWTs. An MPC-based CPB controller, designed based on a linear model with the goal of maintaining power at its rated value and minimizing structural loads, was implemented for a 10 MW FOWT [42]. This strategy exhibited superior performance compared to a PI controller, especially in terms of power regulation, platform pitch reduction, and successful tower fatigue reduction. In [43], a linear MPC was designed for a 10 MW FOWT. The proposed controller was tested on a simplified linear model and demonstrated a reduction in tower bending and platform pitch motion with less power variation compared to [14].

However, these studies were based on linear representations of FOWTs obtained for a specific operating point dependent on wind conditions and rotor speed. The control design relies on these linearized models, thus presenting a significant drawback when the turbine operates away from the defined operating point; as a result, the controller tends to lose efficiency and desired performance. Consequently, a tedious process of tuning the controller for each operating point becomes necessary to maintain its effectiveness. The main non-linear controllers proposed in the literature for FOWT systems, based on reduced model such as COM, include non-linear MPC (NMPC) and sliding mode control (SMC).

In contrast to MPC based on linear models, NMPC can be designed using non-linear reduced models. For instance, in [44], an NMPC with CBP (NMPC-CBP) approach was developed based on the reduced Lemmer model [20]. Wind and wave estimations were incorporated, where the incoming wind information was obtained using light detection and ranging (LIDAR) remote sensing technology. The control objective aimed to maintain steady generated power and rotor speed steady, thereby relying on an ideal estimation of the wind and wave previews [45]. Simulations were carried out under extreme wind and wave conditions, and a comparison with the baseline controller was made. The results indicate a 90% reduction in speed and generated power errors, along with a decrease in blade loads. Nonetheless, this improvement came at the expense of a significant 228% increase in blade usage and higher computational resource requirements. Subsequently, the same author introduced an extended version of the NMPC [46], but this time with an IBP approach (NMPC-IBP). While this controller achieved an additional reduction in fatigue loads on the blades and rotor, the persistently high computational resources required raise concerns about the practicality of employing these controllers for real-time system control. In a more recent development, the study presented in [47] demonstrated a slight reduction in platform movements, particularly in sway and heave, through the application of the NMPC method coupled with disturbance forecasting. The utilization of forecasting tools is gaining interest, thereby providing the controller with crucial information to effectively guide its actions on the system. In [48], following the identification of the MPC’s internal model using FAST, the controls were tested across diverse wind and wave scenarios. The control method exhibits robustness and adaptability to disturbances, thus leading to significant reductions in mechanical loads, power variations, and platform movements, as indicated by the results.

One of the most robust non-linear control methods is SMC, which is renowned for its effectiveness in handling external disturbances and modeling uncertainties across a wide range of non-linear systems. SMC involves directing the state trajectory of a system onto a sliding surface and regulating its switching behavior around this surface using appropriate switching logic. By employing discontinuous control signals, SMC guarantees finite time convergence of the sliding variable to the origin. The gains in the SMC algorithm are typically designed based on upper-bound information about disturbances and uncertainties. However, the inherent discontinuity in the control input may lead to chattering effects, thus resulting in over-actuation and performance degradation. To address the challenges associated with traditional SMC, super-twisting sliding mode control (ST-SMC) can be employed due to its high-performance characteristics and effectiveness in reducing chattering phenomenon. Moreover, the integration of adaptive algorithms with standard SMC, such as adaptive ST-SMC, enables robust control even with limited information about the system model. Indeed, for challenging FOWT systems, obtaining bounds for uncertainties and perturbations can be difficult. In addressing the control challenges specific to Region III for FOWT systems, prior research has developed a first-order SMC based on a non-linear model [49]. In comparison to the baseline model, the SMC exhibited enhancements in the regulation of generator speed, which were attributed to the consideration of wind speed in the control design. However, the platform pitch motions remained similar to those of the baseline wind turbine, considering that no revisions to the control design specifically addressing platform motions were made. Additionally, the super-twisting algorithm has been successfully implemented in [50,51], thereby leveraging a linear model generated by OpenFAST and incorporating adaptive control laws from [52]. These studies demonstrate that adaptive ST-SMC controllers significantly reduce the tuning process time. However, it is noteworthy that these controllers were developed based on linearized models from OpenFAST, which may not capture all the non-linear dynamics of FOWTs. An adaptive form of the ST-SMC controller has also been employed in [53], thus showcasing superior performance in terms of rotor speed control, power regulation, and reduction of the platform pitch motion when compared to traditional GSPI approaches. Furthermore, in [54,55], a new iteration of the adaptive super-twisting controller has been designed that features adaptive laws with two parameters that have been applied to the FOWT system in Region III. In recent studies [24,25], two SMC strategies were developed based on the modified Betti COM [23] and validated through OpenFAST simulations for a FOWT mounted on a TLP. The modification of the Betti COM enables its use in synthesizing non-linear controllers without the need for model dynamics linearization. The latter work [25] integrated a Barrier function into the adaptive SMC algorithm, thereby enabling gain adaptation to achieve control objectives without requiring knowledge of the upper bound of disturbances and without overestimating the control gain. Simulation results demonstrated the superiority of both controllers over the baseline GSPI controller in regulating rotor speed and mitigating platform motion. Additionally, the Barrier function-based SMC controller exhibited reduced mechanical stress on the blades. A comparative study of three high-order SMCs for the same 5 MW TLP-based FOWT has been conducted in [26], thereby employing the adjusted non-linear COM. The three algorithms compared included a continuous-twisting algorithm, a quasi-continuous homogeneous algorithm, and an SMC algorithm. Validations of these three proposed controllers through OpenFAST simulations demonstrated their effectiveness in tracking the rated generator speed, as well as stabilizing the platform pitch angle.

3.1.3. Model-Based Control Associated with Data-Driven Techniques

The aforementioned model-based control methods can achieve enhanced performance in Region III through the integration of data-driven techniques. In particular, the increased computing and data processing capabilities present an opportunity for implementing controllers that incorporate AI techniques. In the context of control applications, AI techniques primarily rely on regression or optimization methods [56]. For regression, notable approaches include expert systems, fuzzy logic, and machine learning, including deep learning methods. On the optimization front, machine and deep learning, as well as meta-heuristic methods, are preferred. Today, machine learning methods, encompassing deep learning methods with artificial neural networks (ANNs) are becoming more powerful. This sub-section encompasses research focused on model-based control systems that leverage AI tools, with a primary objective of enhancing performance.

The fuzzy logic method has proven to be effective in handling systems with challenging-to-predict disturbances. The design process of a fuzzy logic method typically involves defining input and output variables, fuzzification, rule base design, and defuzzification. Hybridization, combining two control methods, is a strategy to integrate fuzzy logic into model-based control algorithms. While extensively explored for bottom-fixed wind turbines [57,58,59], recent advancements proposed in [58,59] have extended its applicability. Moreover, controllers involving fuzzy-based approaches have shown significant potential for FOWTs as well [60,61,62]. In [60], an IBP control system integrated with DAC and MPC through fuzzy control was developed to alleviate fatigue loads. DAC mitigates the effects of wind disturbances, while MPC counters the effects of waves on the structure. Thus, the hybrid IBP control strategy, combining DAC and MPC through fuzzy control, proves effective in handling both wind and wave disturbances. The proposed hybrid IBP controller was tested on a 5 MW FOWT mounted on a barge platform and a spread mooring system. Simulation results in operating Region III revealed a significant reduction in both tower and blade fatigue loads compared to the baseline control, thus ranging from 20% to 40%. In addition to reducing fatigue loads, the controller ensures stable power output and exhibited excellent robustness. The simulation results confirm the proposed IBP controller’s high effectiveness in reducing fatigue loads. In [61], a hybrid pitch controller was developed integrating a fuzzy logic-based controller with a GS incremental proportional–derivative controller to regulate the power at its rated value. In this proposed hybrid controller, a fuzzy lookup table generates the pitch reference, while a genetic algorithm tunes the gains for various operating conditions. Simulation analysis on a 5 MW FOWT mounted on a barge platform using FAST code demonstrated the controller’s superiority over of the baseline GSPI. It achieved a 23% reduction in tower top displacement and a 33% reduction in platform pitch vibration. Moreover, in [62], an advanced fuzzy logic pitch controller enhanced the performance of a conventional PI controller for tracking rated power, thereby leveraging insights from turbine operators to optimize the system behavior. Outperforming baseline PI controller and previously validated fuzzy logic counterparts, the proposed controller demonstrated superior pitch adjustment for a wind turbine on a semi-submersible platform.

Within the domain of machine learning methods, the family of deep learning methods, particularly ANNs, holds significant promise for advancing the control of FOWTs. Two prominent types of feedforward neural networks in this context are the multi-layer perceptron (MLP) and radial basis function (RBF) neural network. These networks typically comprise three layers: the input layer, the hidden layer, and the output layer. Neurons in the input layer generally have a linear activation function, while non-linear activation functions such as sigmoid, logarithmic, and hyperbolic tangent functions are employed in the hidden and output layers for MLP. Conversely, RBF networks utilize a Gaussian activation function for their hidden layer. An illustrative architectural scheme for an RBF network with a single hidden layer is presented in Figure 7.

An example of the integration of neural networks for FOWT is given in [63], where an IBP controller based on SMC associated with RBF neural network (RBF-SMC-IBP) was developed. The online learning capability of the RBF neural network is harnessed to dynamically adjust the gain of the SMC with variable structure in real time. This adaptation helps the sliding mode function approach the switching surface, thus effectively reducing the chattering associated with SMC. The proposed RBF-SMC-IBP control method was tested through simulations on a 5 MW floating wind turbine mounted on a spar–buoy platform. Simulation results demonstrated the effectiveness of the RBF-SMC-IBP controller in reducing platform motions while ensuring stable power generation.

AI-based techniques applied to control systems show significant promise in enhancing the overall performance and energy generation of FOWT systems. Furthermore, the predictive capabilities of machine learning have proven valuable for environmental conditions forecasting, thereby contributing to the improved performance of control systems (Figure 8). This ability to predict incident wind and waves has the potential to empower advanced controllers with real-time, data-driven insights. Various data-driven forecasting tools have been developed in the literature to achieve these objectives.

Statistical time series models and machine learning techniques, extensively studied for wind and waves forecasts, leverage historical environmental data to extrapolate underlying patterns and provide future predictions. Conventional statistical models, including the autoregressive model (AR) [64,65,66], autoregressive moving average model (ARMA) [66,67,68], autoregressive integral moving average (ARIMA) [69], fractional-ARIMA [70], and Hammerstein autoregressive (HAR) models [71], have been employed. In comparison to statistical models, machine learning techniques exhibit superior performance in handling the non-linear nature of wind and waves. These methods, considering atmospheric variables like humidity, elevation, and atmospheric pressure, include ANNs [72,73], MLP neural networks [74,75,76], recurrent neural networks (RNN) [77,78], convolution neural networks (CNNs) [79], Bayesian networks [80], the support vector machine (SVM) [81,82,83], the least squares support vector machine (LSSVM) [84,85], the Gaussian process (GP) [86], adaptive neuro-fuzzy interference systems (ANFISs) [87], and extreme learning machines (ELMs) [88]. Combining statistical and machine learning data-driven techniques has also been explored for improved performance. For instance, a hybrid model combining the linear ARIMA and non-linear ANNs, as well as a hybrid model combining ELMs and ARIMAs, demonstrated improved wind forecasting [89,90].

The integration of wind and wave previews into advanced controllers may improve the performance of FOWTs by providing the system with sufficient time to deal with the incoming disturbances. However, challenges such as a lack of sufficient site data, poor anomaly detection, and scalability issues arise due to the reliance on historical information. Additionally, considerations about the prediction horizon length and forecast quality are essential when employing these prediction mechanisms. Integrating these data-driven forecasting tools into the framework of model-based controllers represents a significant area of research, thereby offering the potential for substantial improvements in control system performance.

3.1.4. Discussion on Model-Based Control Approaches

Many existing control methodologies for FOWTs operating in Region III heavily rely on model-based approaches, thus leveraging models as essential tools to provide essential information for FOWT controllers. While conventional SISO strategies possess inherent limitations, employing model-based methods with MIMO strategies enable the control of more system variables and the implementation of advanced control systems. Performance improvements are further achieved by incorporating IBP mechanisms or by integrating data-driven methods such as AI, thereby allowing, for instance, the implementation of feedforward control loops based on wind and waves predictions.

However, achieving an accurate representation of the floating wind turbine requires intricate non-linear multi-physics modeling. This modeling process involves a trade-off between fidelity and computational complexity, which is a crucial consideration in the design of model-based control systems. Some models may have high accuracy, but their computational complexity poses challenge for real-time implementation. Conversely, models that simplify dynamics to alleviate computational load may result in degraded control performance. The issues of unmodeled dynamics and robustness are intertwined within the classical model-based theoretical framework, thus making simultaneous resolution difficult. Additionally, stochastic environmental uncertainties such as time-varying wind and wave conditions, along with turbine parameter uncertainties, further compound the complexity of FOWT model-based control. These uncertainties not only pose challenges in building an accurate analytical model but also complicate the development of controllers with strong robustness and adaptability. Furthermore, the accuracy of the model directly influences the effort required for control system design. Developing a control system based on an accurate, high-order model may lead to a controller with impractical complexity, as high-order controllers are unsuitable for practical use. This creates a paradox wherein accurate modeling for high performance is followed by the necessity to simplify the model for practical control.

Therefore, the development of appropriate FOWT models emerges as a crucial consideration in the design of model-based control systems. Despite the potential of model-based non-linear control strategies for FOWTs, their applications remain limited in the literature. Primary non-linear COM [23] appears constrained within the control framework, thus often being reduced and linearized to derive control laws. Consequently, many controllers for floating wind turbines resort to linearization around an operating point, where deviating from this point can lead to a degradation in performance.

To overcome the challenges associated with classical model-based approaches and to enhance the adaptability and robustness of control methods, data-driven control strategies emerge as a promising alternative.

3.2. Data-Driven Model-Based Control for FOWT System

Existing FOWT controllers, which mostly rely on accurate analytical models, encounter challenges in adapting to uncertainties and modeling errors. The classical model-based feedback controller, utilizing precise analytical models, may exhibit sub-optimal performance due to inaccuracies in the plant model. This discrepancy impacts the calculation of the tracking error and subsequently influences the determination of controller parameters through optimization algorithms based on this model.

In contrast to classical model-based control approaches, data-driven model-based control methods leverage learning techniques and system identification tools to approximate plant models or to estimate the unmodeled dynamics of FOWTs. Data modeling establishes relationships among the data without inherent physical meaning. The resulting equivalent data model is integrated into the controller framework, thereby enabling the prediction of plant output for effective controller implementation. Consequently, a data-driven model-based controller, shaped by data-driven modeling of the closed-loop plant, mitigates the influence of unmodeled dynamics, as the controller operates independently of the analytical plant model.

The key distinction between classical model-based control and data-driven model-based control lies in how the controller is designed. While classical model-based control relies on a given analytical plant model, data-driven control methods design the controller independently of the mathematical modeling. This independence necessitates predicting the system’s real one-step-ahead output for controller parameter tuning. Various existing data-driven prediction methods can theoretically be used to achieve system output prediction. These include, for instance, rule-based models, machine learning techniques, and deep learning with neural network techniques. The significance of data-based modeling becomes apparent in the development of data-driven control theories, thus facilitating the emergence of data-driven model-based control for systems that are challenging to model using traditional approaches. Data-driven model-based FOWT control applications in Region III are presented in the following sub-section.

3.2.1. Data-Driven Model-Based Literature Overview

In [91], to fulfill the robustness and tracking requirements of the FOWT control system using terminal SMC with dynamic surface control, an RBF neural network was designed to estimate the unknown dynamics of the model system. The neural network determines the upper bound of uncertainty and noise online, thus leading to reduced conservative high-gain control actions. This adaptation aims to achieve the robustness of classical feedback controllers against structural deviations of the turbine body. The RBF neural network controller, with its adaptive and robust structure, enhances system robustness and stability against uncertainties and stochastic noises. By filtering undesired noises and uncertainties in input actions and providing error dynamics in integral form, it maintains the finite horizon tracking error around zero. Detailed software simulations comparing the LQR and the designed RBF neural network control systems demonstrated the superiority of the neural network-based approach for a turbine with triangular floating cylinders and a central control tower. The authors highlighted the effectiveness of their approach in compensating for uncertainties through radial basis approximation. However, they acknowledged the need for more test data to optimize neural network tuning.

Another study [92] introduced a neural network-based MPC approach to enhance the operational efficiency of a 5 MW FOWT equipped with a permanent magnet synchronous generator (PMSG). Within this closed-loop system, a Hammerstein structure was employed to approximate the dynamic behavior of the FOWT. MLP neural networks were utilized to estimate the aerodynamic characteristics of the non-linear steady state component, while a linear autoregressive with exogenous input (ARX) model identified the linear time-invariant dynamic segment. The algorithm, sidestepping the need for non-linear optimization, employs quadratic programming to derive control actions. The designed control system exhibited rapid and stable responses to grid frequency variations, thereby optimizing the coordination between pitch and torque. The Hammerstein structure effectively captures the dynamics of the wind turbine by integrating a static non-linear mapping with a linear time-invariant (LTI) sub-system. The distinct parts, including the non-linear steady state and linear dynamic aspects, are defined independently. The neural approximation utilizes simulated datasets, thus incorporating inputs like wind speed, tip speed ratio, and pitch angle for the non-linear steady state sub-system. The primary outputs encompass rotor torque and rotor thrust. The structure of the neural network-based MPC, outlined in Figure 9, features the Hammerstein model involving aerodynamic variables as input signals, with wind speed as the measured disturbance. The output signals of consecutive networks are denoted as auxiliary variables in the Hammerstein model. The proposed controller outperformed the baseline GSPI controller in terms of performance and efficiency.

To address the challenges posed by intricate modeling and conflicting control objectives in FOWT systems, a novel multi-objective predictive control strategy was proposed in [93]. This strategy integrates deep learning models, specifically the gated recurrent neural network, with multi-objective optimization to enhance pitch angle control while adhering to constraints. The approach consists of establishing a dynamic prediction model for FOWT based on a gated recurrent neural network. Using this dynamic prediction model, a multi-objective predictive control algorithm for individual pitch control of FOWTs has been developed. A comprehensive coupled block diagram, illustrating the dynamic simulation environment and control scheme, is given in Figure 10. Simulations conducted under various wind conditions using FAST indicated that the proposed method outperformed collective pitch control and gain scheduling PI individual pitch control, thus achieving power output closer to the rated level. Furthermore, the proposed method significantly reduced the mechanical load on the blade root and effectively restrained platform pitching motion when compared to gain scheduling PI individual pitch control.

A novel AI-based method [94], termed SADA (Software-in-the-Loop Combined Artificial Intelligence Method for Dynamic Response Analysis of FOWTs), was introduced for predicting the dynamic responses of FOWTs. The SADA methodology involves selecting key disciplinary parameters (KDPs), and its AI module is integrated into the in-house program DARwind, which encompasses a coupled aero-hydro-servo-elastic system. The reinforcement learning algorithms, specifically deep deterministic policy gradient (DDPG), contribute to the policy decision aspect of SADA. The AI module was trained using experimental results from a basin study of a Hywind spar-type FOWT. SADA dynamically adjusted the values of the KDPs through the DDPG actor network based on the feedback from training, thereby comparing DARwind simulation results with experimental data for 6-degree-of-freedom motions of the Hywind platform. The case study demonstrated that SADA, utilizing the intelligent DARwind, achieved higher accuracy in predicting various dynamic responses, even those unmeasurable in basin experiments. The results showed promising improvements, with a 21% reduction in the maximum error of surge motion.

In-depth exploration of the key technologies related to the KDPs in the SADA method was conducted to develop a novel and accurate analysis approach for predicting the dynamic responses of FOWTs in [95]. The categorization of the KDPs into environmental, disciplinary, and specific groups was introduced. The study further investigated two crucial factors in the SADA method, the number of KDPs and the boundary adjustment of KDPs, thereby utilizing reinforcement learning algorithms. AI training was performed using basin experimental data of a spar-type FOWT. The findings highlight that a more suitable set of KDPs in the SADA method leads to higher prediction accuracy for FOWTs. Additionally, reasonable boundary conditions contribute significantly to efficient algorithm convergence. The study concluded by providing guidance on optimal KDP selection and setting boundary conditions. The application of KDPs in the SADA method not only enhances the understanding of the dynamic response of the entire FOWTs system but also contributes to improved prediction accuracy.

Moreover, a simulated annealing diagnosis algorithm was employed in [96] to optimize the prediction of dynamic response prediction in FOWTs, thereby employing reinforcement learning. Similar to the approach in [95], the reinforcement learning method was used to adjust the key parameters based on feedback from 6-degree-of-freedom motions. The effectiveness of the proposed method was validated through experimentation involving 12 test cases. Nevertheless, challenges persist, particularly concerning the tuning of hyper-parameters within the deep neural network. Further exploration and experience are necessary to effectively address these issues.

In their work [97,98], the researchers explored the utilization of an MLP network for modeling a hybrid floating wave energy–wind turbine platform. Subsequently, they introduced a fuzzy logic control system to implement a structural controller aimed at mitigating undesirable vibrations within the platform. First, Ref. [97] delved into the creation of a control-oriented regressive model for a hybrid FOWT with an oscillating water column wave energy converters platform. The primary objective was to leverage the predictive capabilities and computational simplicity of deep-layered MLP to develop a feasible, lightweight, control-oriented model in contrast to complex dynamical models. The deep-layered MLP model was designed and trained to match the hybrid platform’s structural performance. Validation of the model was conducted against standard Multisurf–Wamit–FAST 5 MW FOWT output data for various challenging scenarios, thus demonstrating the proposed ANN COM’s adequate performance and accuracy. This model provides an alternative to traditionally used complex non-linear models, thereby enabling the implementation of advanced control schemes in a computationally convenient, straightforward manner. Following this, Ref. [98] implemented an ad hoc fuzzy-based control system based on the proposed MLP-based FOWT model for platform stabilization. Fuzzy logic control was developed and applied to establish a structural controller that mitigates undesired vibrations. Both the modeling and control schemes were successfully implemented, thereby showcasing superior performance compared to the standard barge-based FOWT system. Experimental results demonstrated that the proposed fuzzy logic controller improved the platform’s dynamic behavior, thus enhancing its stability under a wide range of wind and wave conditions.

3.2.2. Limitations of Data-Driven Model-Based Control Approaches

Data-driven model-based control methods, although promising for addressing the complexities of non-linear systems that are difficult to model such as FOWTs, exhibit notable limitations. One significant disadvantage lies in their reliance on the quality and quantity of available data. These methods heavily depend on historical data for model learning, thus potentially compromising performance if the training data are insufficient, inaccurate, or not representative of the system’s diverse operating conditions. Another concern is the susceptibility to overfitting, where models capture noise or anomalies in the training set, thus resulting in poor generalization to new scenarios, which is particularly challenging for FOWT dynamic systems that are subject to uncertainties and variations. Moreover, these control methods may struggle when faced with abrupt changes or novel conditions not represented in the training data. The models may fail to adapt appropriately, thus highlighting the challenge of achieving robustness in the face of unforeseen circumstances.

The interpretability of data-driven models poses an additional challenge. Unlike classical analytical models, these approaches often result in complex and opaque models that lack clear physical interpretations. This complexity makes it difficult to gain insights into the underlying mechanisms governing system behavior.

Lastly, the computational demands of training and maintaining complex data-driven models can be significant. Large-scale models, especially those based on deep learning, may require heavy computational resources and time for training. This aspect raises concerns regarding the practical feasibility and efficiency of implementing these methods in real-time control systems.

In conclusion, while data-driven model-based control methods present innovative approaches, their limitations highlight the importance of considering data quality, overfitting risks, adaptability to changes, interpretability, and computational requirements when applying to real-world FOWT systems.

3.3. Data-Driven Model-Free Control for FOWT System

Departing from model-based control, whether reliant on analytical or data modeling, data-driven model-free control emerges as a promising alternative to address the constraints of its model-based counterparts. In this approach, controllers are designed directly using data, thus eliminating the need for explicit system dynamics. Generally, these methods iteratively seek optimal control actions based on user-defined objective functions or rewards. This sub-section delves into the literature on data-driven model-free control strategies for operating Region III of FOWTs, with a particular emphasis on reinforcement learning (RL) and deep RL (DRL) end-to-end algorithms employed for control design.

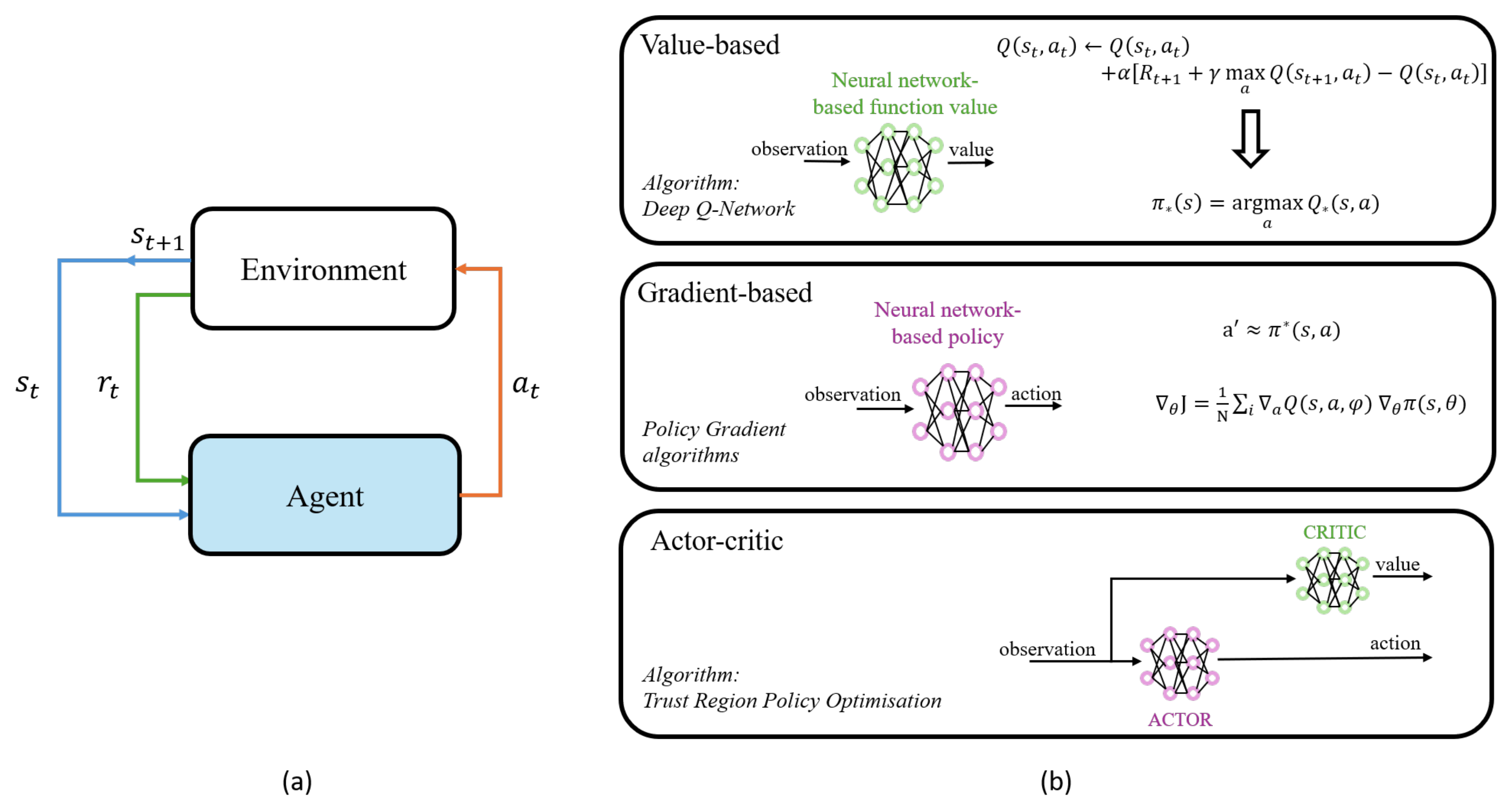
3.3.1. RL and DRL Algorithms

Among data-driven methods, RL stands out as one of the most interesting approaches for model-free control. RL, and particularly DRL, holds a prominent position in the realm of machine learning techniques, thereby representing a dynamic and influential field within AI [99]. Built upon the trial-and-error principle, RL continually refines control performance to optimize long-term rewards. By incorporating neural network structures into the RL framework, DRL demonstrates a remarkable ability to address the high-complexity control challenges inherent in conventional model-based control methods, which often struggle within the context of difficult-to-model systems. Importantly, RL algorithms exhibit a notable advantage by learning system information and optimal control actions directly from data or through interactions with environments, all without the need for explicit system models.

The fundamental principle of RL methods for control applications is grounded in dynamic programming, which was originally introduced by Bellman within the context of optimal control theory [100,101]. The discretized manifestation of this framework corresponds to the Markov decision process (MDP), expressed as (s,a,p,r,$\gamma$), wherein the agent learns a policy ($\pi$) to effectively influences the system’s behavior and achieve control objectives. This learning unfolds through direct interactions with the environment involving observations (s), actions (a), and rewards (r) signals, as illustrated in Figure 11a. Observations represent the system states available to the agent, actions are the commands given to the controlled system, and rewards evaluate the quality of the action taken in pursuit of control objectives. The probabilities of transitioning to the next state $s_{t+1}$ when in the current state $s_t$ and taking action $a_t$ are governed by the transition function (p), which is denoted as $p\left(s_{t+1}\right|s_t,a_t)$. A discount factor ($\gamma$) is introduced to balance immediate and future rewards in a cumulative return function ($G_t$). This return function is obtained through either the state value function $V_{\pi }\left(s\right)$, the expected value of being in the state s given the policy $\pi$, or the action value function $Q_{\pi }(s,a)$ corresponding to the expected value of being in the state s and taking the action a following policy $\pi$. The ultimate aim is to identify a policy $\pi$ that results in optimal actions—thus maximizing the expected return function—which are defined by either V or Q. The cumulative rewards, as determined by these values functions, serve as estimates of the desirability for the agent to be in a given state and execute a given action for this state. In DRL, neural networks play a pivotal role in representing the policy and/or value functions, thereby enabling the agent to generalize and apply the policy to new states based on learned state values. Therefore, the process of learning the optimal policy through the interaction between the agent and the environment is equivalent to learning the optimal control law.

DRL algorithms can be categorized into three primary families: value-based, gradient-based, and actor–critic methods, as illustrated in the Figure 11b. In the value-based framework, a neural network exclusively represents the value function, thus estimating either the value of a given state or a given pair of state–action. The action taken by the policy is then derived from these estimated values to maximize the cumulative reward function. Conversely, in the gradient-based framework, the neural network structure is solely adopted by the policy function. The policy network is updated to maximize the cumulative reward function, thus resulting in optimal actions as output. The actor–critic framework employs neural networks to represent both the value function and policy, namely the critic and the actor, respectively. The critic, responsible for evaluating the complex reward function, collaborates with the actor, which derives optimal control actions based on the estimated reward function. This dual-network approach facilitates a more comprehensive understanding and efficient optimization of the control system, thereby making it one of the most popular choices for control applications.

RL-based methods demonstrated an inherent ability to handle dynamic measurements and achieve closed-loop control under varying environmental conditions. The data-driven and model-free characteristics of these methods have encouraged attempts to apply RL to control tasks in FOWT systems. These applications have showcased enhanced performance in tracking rated power and mitigating platform pitch. However, it is essential to note that FOWT control tasks inherently exhibit partial Markov processes, which is primarily due to the stochastic nature of environmental conditions. To effectively address this challenge, researchers have focused on appropriately designing states, rewards, and actions to transform the partial Markov decision problems into more manageable Markov decision problems.

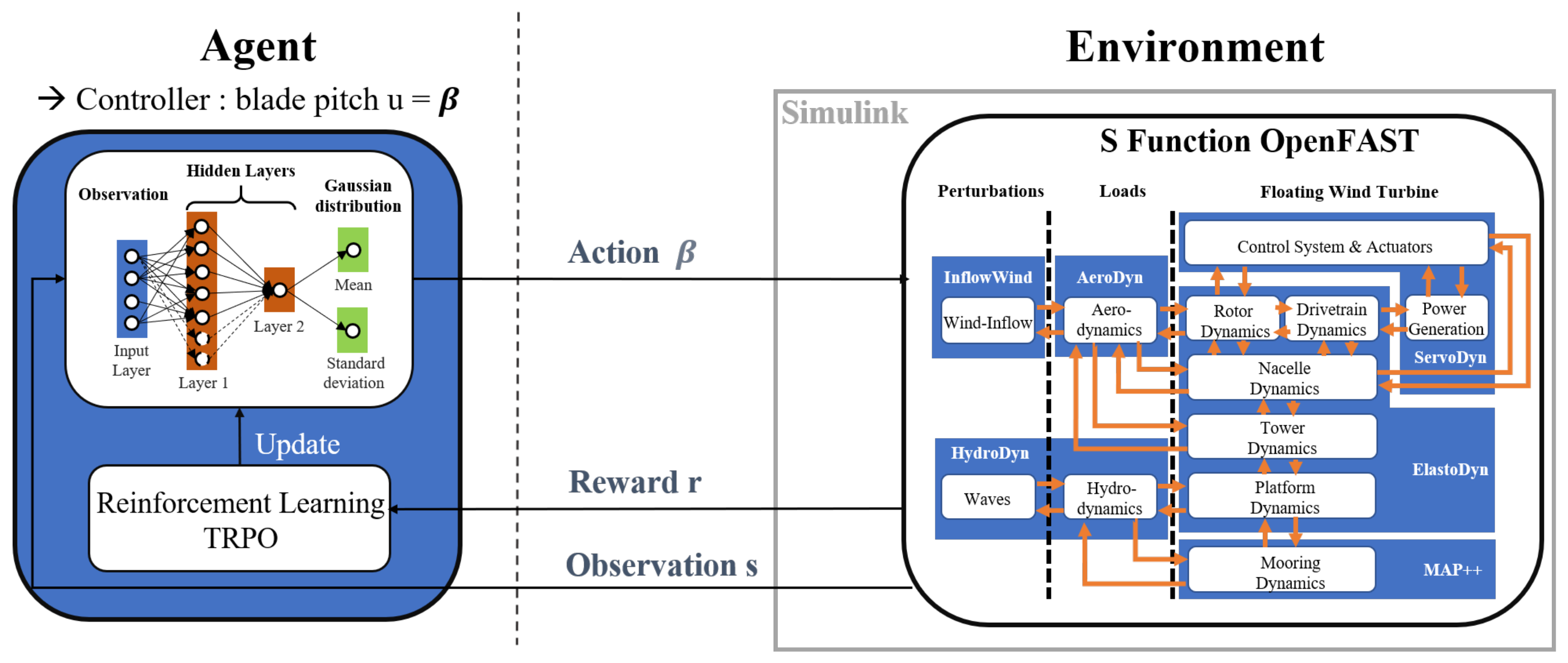
3.3.2. Data-Driven Model-Free Literature Overview

This sub-section introduces the existing data-driven model-free control approaches for FOWTs operating in Region III.

The study conducted in [102] introduced a DRL-based control approach to achieve power regulation and load reduction in FOWTs. The controller combines CBP control and IBP control with an incremental model-based dual heuristic programming (IDHP) strategy, thereby resulting in reducing structural loads. Notably, the controller incorporates the online-learned FOWT dynamics into the dual heuristic programming process, thus making the entire control scheme data-driven and free from dependence on analytical models. An innovative aspect of the proposed method is its departure from conventional IDHP approaches, as only partial system dynamics need to be learned. This design choice simplifies the overall structure and enhances training efficiency. Simulation tests conducted using the high-fidelity FOWT simulator OpenFAST validated the effectiveness of the proposed control method.

Moreover, in [103], a novel control system based on DRL was introduced to mitigate the impact of both disturbance and noise effects in the context of FOWTs. The system leverages the large volume of information generated by significant variations in wind and water waves to facilitate the convergent learning of neural network models for the wind turbine. To address sudden wind variations and disturbances, the approach incorporates an adaptive inverse control mechanism, seamlessly integrated with DRL, specifically employing the DDPG algorithm. In the proposed approach, rewards derived from the DDPG algorithm undergo a new training algorithm, thereby influencing control actions to minimize the loss function. Through software implementation tests, the paper demonstrates the system’s capability to attenuate disturbance and noise, thereby resulting in improved tracking performance of the closed-loop FOWT. The tuning of DRL weights, accomplished through the direct Lyapunov method, plays a pivotal role in extracting the loss function while effectively addressing issues such as getting trapped in local minima and mitigating the vanishing gradient problem. This paper adopts a black box simplification process, thus bypassing the need for intricate dynamical equations.

In another investigation [104], a machine learning-based control strategy was introduced employing a genetic program for the iterative evolution of effective control strategies. These strategies were formulated using sensor data obtained from simulated FOWTs within the OpenFAST simulation environment. The study demonstrated the effectiveness of the method by achieving a notable 41% reduction in both fatigue and ultimate loading. This reduction was realized under the specific conditions outlined by the Aerodynamic Turbines with Load Attenuation Systems (ATLAS) competition, which is organized by the Advanced Research Projects Agency–Rnergy (ARPA-E). Notably, unlike some ML techniques relying on opaque models, the proposed method produced interpretable outcomes. This feature facilitates the identification of crucial design aspects, thereby contributing valuable insights for future controller development.

In [105], an innovative CBP controller was introduced to address hydraulic actuator response delays. Leveraging a deep learning-based algorithm, the controller predicts delay times, thereby enabling the proactive adjustment of blade pitch control angles. Specifically, the long short-term memory (LSTM) algorithm, belonging to the class of RNNs, was employed, as illustrated in Figure 12. Through FAST simulation of a 5 MW semi-submersible FOWT, the LSTM-based CBP controller demonstrated enhanced power generation by approximately 5% and reduced pitch motion standard deviation by roughly 50% compared to a CBP controller in response delay.

Finally, in [106], a DRL approach employing the actor–critic trust region policy optimization (TRPO) algorithm was used to regulate the generator speed to its rated value while mitigating platform pitch motion. The TRPO agent used online data simulated by OpenFAST to update the neural network weights, thereby determining the optimal policy corresponding to the optimal control law. The architecture of the proposed DRL controller is given in Figure 13. The validation results of the trained agent for a 5 MW FOWT mounted on a barge platform demonstrate the capability of the proposed DRL controller to ensure power tracking while preserving the structural integrity of the FOWT. However, further testing is required to validate the DRL controller across a wider range of wind conditions for operating in Region III.

3.3.3. Discussion on Data-Driven Model-Free Control Approaches

While data-driven model-free control methods exhibit the potential for enhanced performance of the FOWT in Region III, thus leveraging the absence of constraints imposed by underlying analytical models, they are not without limitations that impact their applicability and effectiveness.

The inherent black box nature of data-driven model-free approaches, especially those involving deep neural networks, introduces challenges in interpreting the resulting control system and lacks systematic designing procedures and a means of analysis. Understanding why a particular command is chosen by the model may be challenging, thus making it difficult to trust and optimize control strategies. Moreover, model-free algorithms often require the fine-tuning of various hyper-parameters, and their performance can be sensitive to these choices. Identifying the optimal set of hyper-parameters demands additional effort and expertise, with sub-optimal selection potentially leading to poor control performance. Additionally, model-free methods may struggle with changes in the system dynamics or the introduction of new disturbances, thereby posing challenges to ensure robustness and adaptability to evolving conditions. Consequently, these methods may require multiple retraining sessions to maintain optimal performance.

RL and DRL algorithms often require a large number of interactions with the environment to learn effective control policies. The sample inefficiency can be a significant limitation, especially in situations where acquiring real-world data is expensive or impractical. Balancing exploration and exploitation is another fundamental challenge in RL, where the algorithm must explore new actions to learn their effects while exploiting known actions that yield greater rewards. Achieving an optimal balance is intricate, and inefficient exploration can lead to sub-optimal control policies. Furthermore, these methods may struggle to ensure stability and safety during the learning phase, as exploration strategies may result in undesirable system behavior or unsafe actions.

Generally, data-driven model-free methods encounter difficulties in generalizing control laws to conditions not encountered during training. Changes in the environment, system dynamics, or unexpected disturbances can pose challenges, and the learned control law may exhibit sub-optimal performance in scenarios that are inadequately represented in the training data. Addressing these limitations is crucial for advancing the practical implementation of model-free control methods applied to FOWT systems.

4. Conclusions

4.1. Synthesis on Advanced Control Methods

This comprehensive review explored advanced control methods designed for FOWT systems operating in Region III, thus emphasizing key control objectives such as power regulation at rated value, platform pitch mitigation, and structural load reduction. Categorized into model-based control, data-driven model-based control and data-driven model-free control, each approach presents distinct strengths and weaknesses:

Model-based control methods:

Strengths:

• Analytical Precision: Utilizes analytical models for a precise understanding of system dynamics;
• Optimization Capability: Enables the determination of optimal control parameters through analytical model-based optimization algorithms;
• Stability and Predictability: Benefits from well-established mathematical foundations for stability and predictability.

Weaknesses:

• Sensitivity to Modeling Errors: Performance degradation due to inaccuracies in analytical models impacting control robustness;
• Limited Adaptability: Struggles with uncertainties and unmodeled dynamics, thus hindering adaptation to changing conditions;
• Linearization Dependency: Existing model-based control methods often rely on linearization, thus leading to performance degradation.

Data-driven tools, particularly AI with machine and deep learning, offer new perspectives for model-based control of FOWTs, as they can help mitigate the limitations of classical model-based control and enhance their adaptability. Environmental conditions prediction using these tools demonstrates significant potential for optimizing power generation within the control framework:

Data-driven model-based control:

Strengths:

• Adaptability to Uncertainties: Utilizes learning techniques for modeling uncertainties;
• Mitigation of Modeling Errors: Operates independently of analytical plant models, thereby reducing the impact of inaccuracies;
• Effective for Challenging Systems: Suited for systems that are challenging to model analytically.

Weaknesses:

• Dependence on Data Quality: Performance relies heavily on the quality of the training data;
• Complex Controller Design: Designing controllers independently of physical plant models demands accurate system output prediction.

Data-driven model-free control:

Strengths:

• Handling Complexity: Effective for complex systems that are challenging for traditional model-based control methods;
• Adaptation to Dynamic Environments: Manages dynamic measurements and closed-loop control under time-varying conditions;
• Generalization Capability: Learns policies applicable to new, unseen conditions based on generalized state values.

Weaknesses:

• Sample Inefficiency: Requires a large number of interactions, thereby limiting applicability in scenarios with limited data;
• Exploration–Exploitation Challenge: Balancing exploration and exploitation during learning can be challenging;
• Stability and Safety Concerns: Potential issues with stability and safety, particularly in critical applications.

In conclusion, the selection among model-based, data-driven model-based, or data-driven model-free control relies on specific system characteristics, data availability, and the desired trade-offs between precision and adaptability. Model-based control offers analytical precision but lacks adaptability. In contrast, data-driven methods, both model-based and model-free, offer flexibility at the cost of some precision and stability guarantee. Each approach has its strengths and weaknesses, and for FOWTs, data-driven methods show promise but require further research to effectively address their limitations and offer innovative solutions for the challenges in Region III.

Perspectives

The intricate nature of FOWTs poses a persistent challenge for control system design in Region III, which is marked by diverse control objectives and instability phenomena, including negative damping. To advance FOWT technologies, several key areas warrant attention in future research:

• Simplified COM:
  The existing non-linear COMs for FOWTs are still too complex to be directly employed for the derivation of non-linear controllers. Future research endeavors should focus on simplifying these non-linear COMs to facilitate the implementation of non-linear controllers in Region III without the need for linearization around operating points.
• Integration of hybrid approaches:
  There is a growing inclination towards integrating diverse control approaches to leverage their respective strengths. Hybrid approaches, combining the features of model-based, data-driven model-based, and data-driven model-free control, are emerging as promising avenues. For instance, by combining machine learning data-driven insights with analytical models, a more comprehensive understanding of turbine dynamics is achievable. This integration holds potential benefits, including improved adaptability through data-driven techniques while retaining the precision of analytical models. Future research is likely to explore the synergies between these approaches, thereby creating controllers that are both structurally sound and adaptable to evolving conditions.
• Dynamic data incorporation:
  While the literature extensively covers different machine learning methods to improve control strategies, there is a notable gap in addressing the integration of real-time data and dynamic modeling into these control processes. The influence of real-time data, which includes variables like weather conditions, power demand, and turbine health, on FOWT system performance is substantial. Future research should prioritize the development of adaptive control strategies that dynamically adjust based on real-time data, thus potentially leading to more efficient and reliable FOWT operations. Moreover, exploring dynamic modeling techniques that consider changing environmental conditions and equipment degradation over time could significantly improve the accuracy of performance predictions.
• Interpretability and explainability:
  As data-driven methods often operate as ‘black boxes’, future research will likely prioritize developing techniques providing insights into the decision-making process of these controllers. Explainable AI and interpretable machine learning methodologies will be essential for gaining trust in autonomous and safety-critical systems such as FOWTs.
• Advancements in RL techniques:
  For data-driven model-free control, especially those employing RL and DRL, continuous advancements in algorithms are expected. These improvements, such as enhanced sample efficiency and stability in learning processes, will contribute to the wider applicability of DRL in real-world control scenarios. Addressing the challenges related to exploration–exploitation trade-offs and ensuring safety during the learning phase will be focal points for future developments.
• Robustness enhancement and safety assurance:
  To address the limitations of data-driven control methods, there is a growing emphasis on enhancing robustness and ensuring safety. Researchers are actively exploring methodologies to improve the robustness of data-driven controllers against uncertainties and disturbances. Techniques ensuring stability and safety during the learning phase will be crucial for future developments and the real-world implementation of FOWT.
• Real-time implementation and hardware integration:
  The practical deployment of advanced control methods requires a seamless integration with real-time systems and consideration of hardware constraints. Future perspectives include the development of control algorithms optimized for efficient real-time implementation on FOWT embedded systems.
• Grid integration challenges:
  Integrating the power generated by FOWTs into the grid poses significant technical and logistical challenges. The intermittent nature of wind energy production, combined with the variable output from offshore sites, complicates grid stability and reliability. Issues such as voltage and frequency control, grid congestion, and the need for grid reinforcement in remote offshore areas must be addressed. Future research should focus on developing advanced grid integration strategies, including smart grid technologies, energy storage systems, and grid-friendly control algorithms, to ensure seamless integration of FOWT power into the grid while maintaining grid stability. These efforts are crucial for enhancing FOWT technology development and advancing the transition towards renewable energy sources.

In summary, the future of control systems for FOWTs will likely witness a convergence of different methodologies, with a strong focus on improving robustness, safety, and real-time implementation. Interdisciplinary collaboration will play a pivotal role in shaping innovative control solutions that meet the challenging control objectives inherent in FOWTs.