Exploring Motion Stability of a Novel Semi-Submersible Platform for Offshore Wind Turbines
Abstract
:1. Introduction
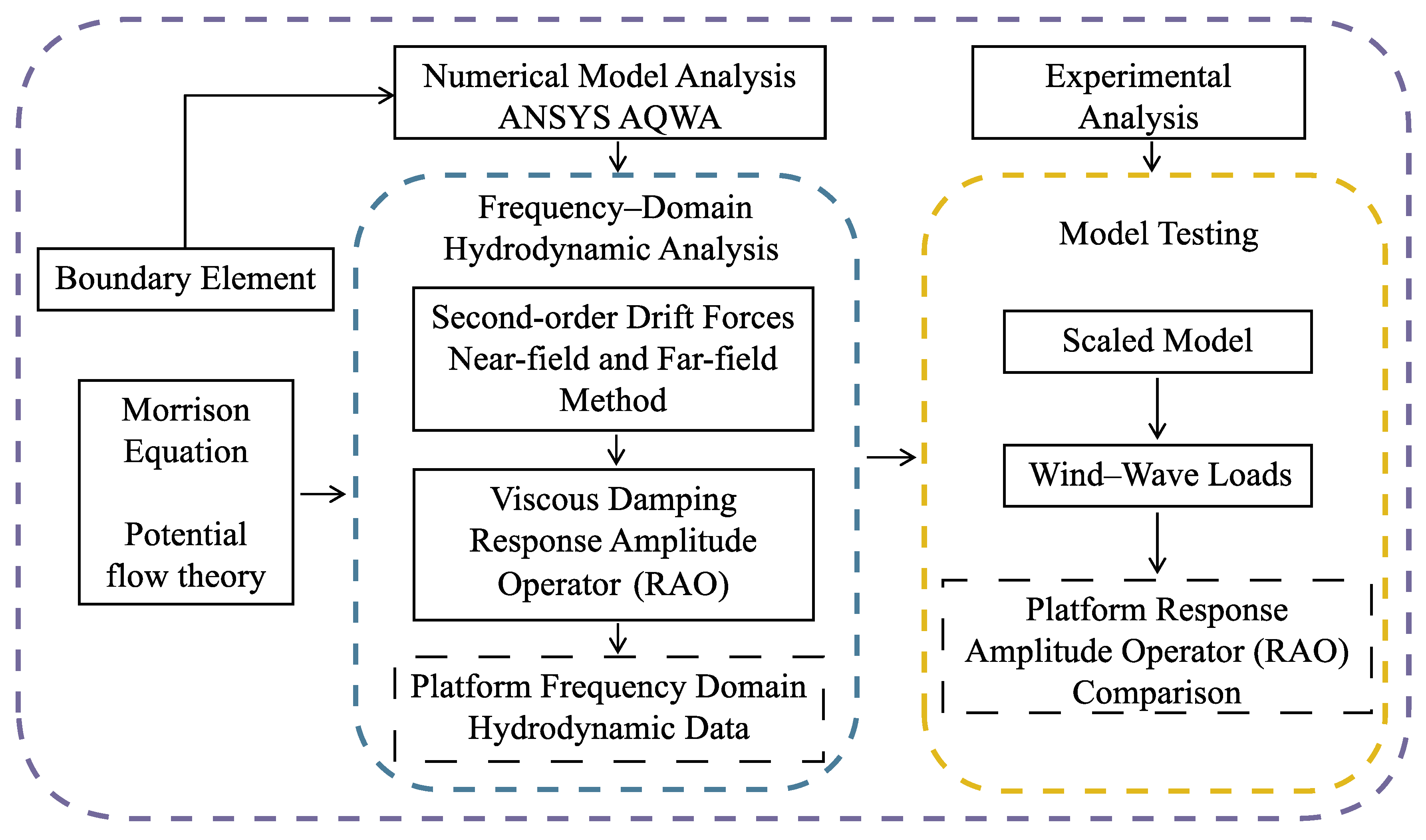
2. Mathematical Theory
2.1. Morrison Equation
2.2. Potential Flow Theory
2.3. Hydrodynamic Theory
3. The Proposed Floating Platform
3.1. Numerical Model
3.2. Mooring System
4. Frequency–Domain Analysis
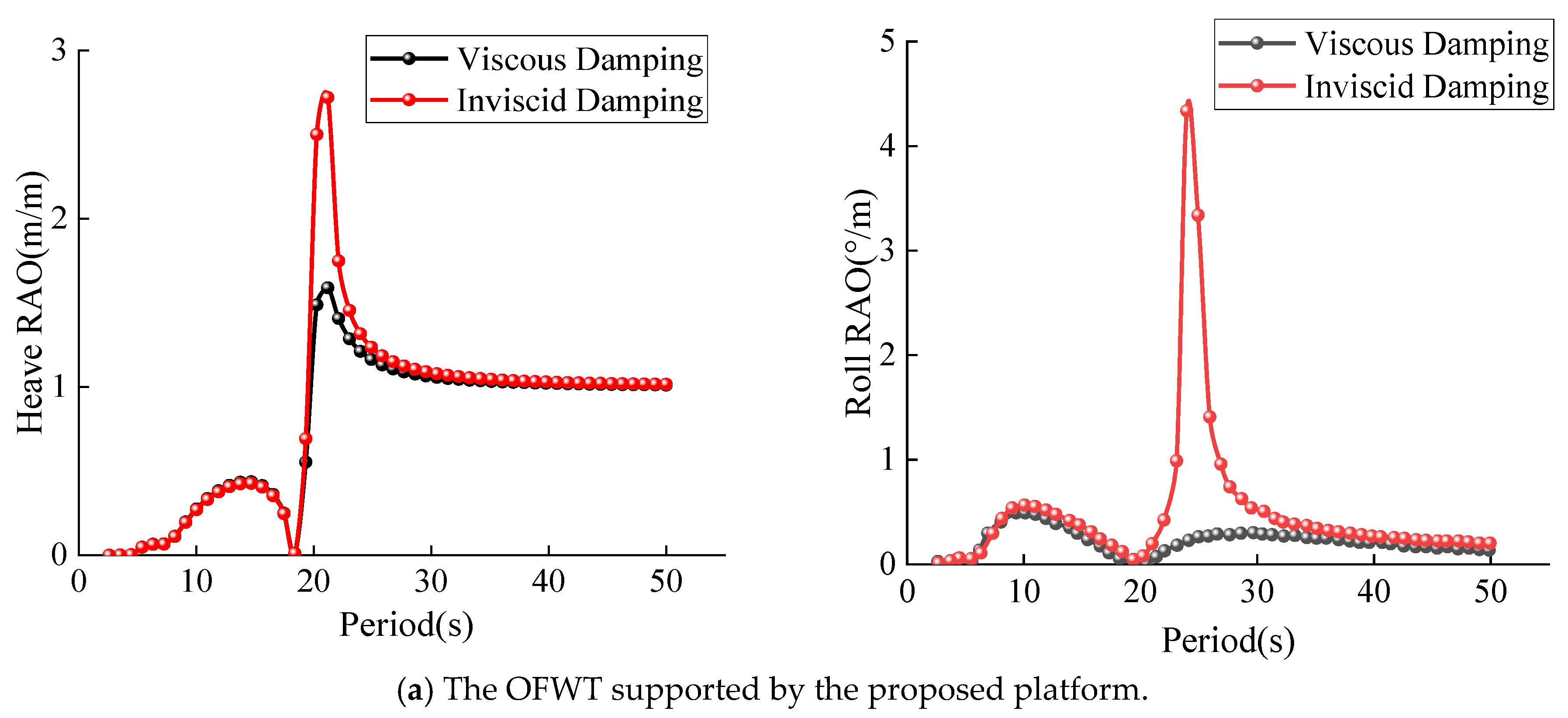
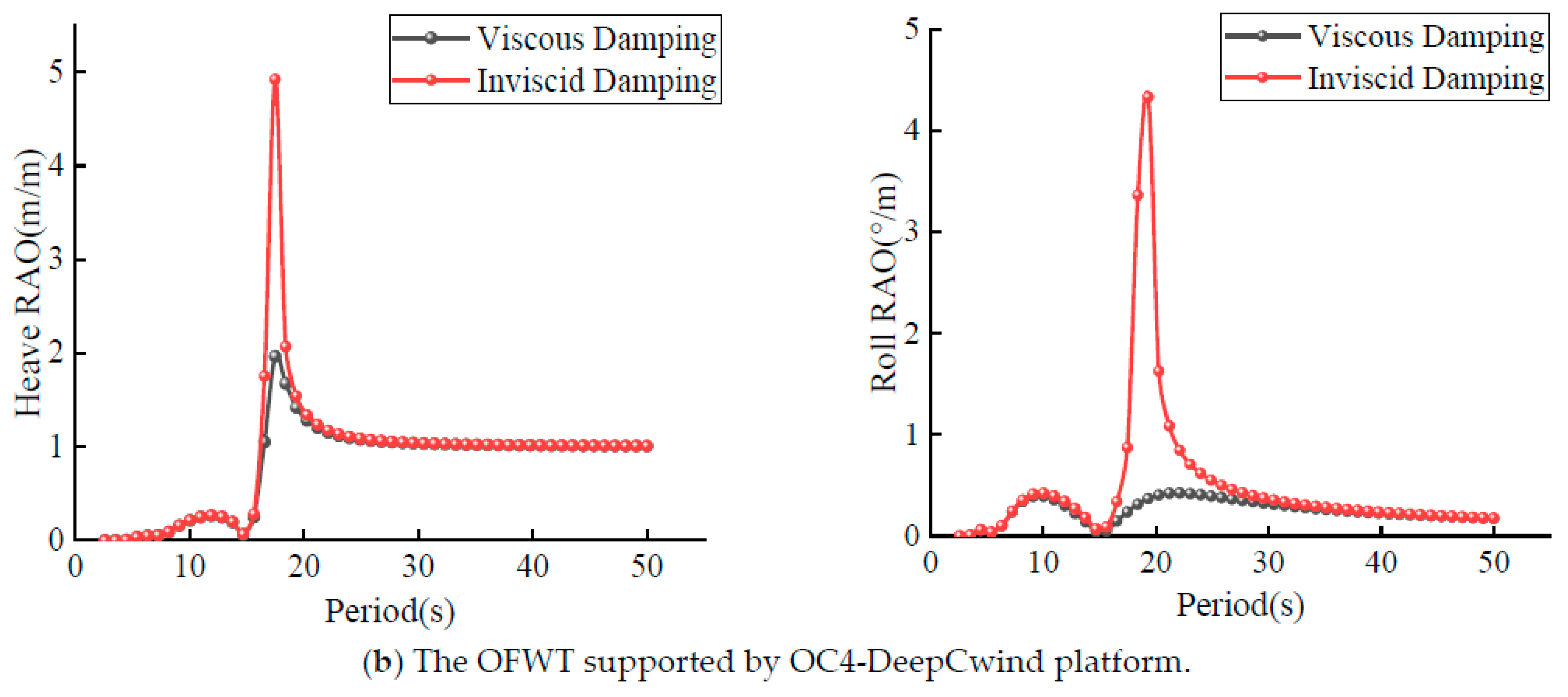
4.1. Hydrodynamic Viscous Damping
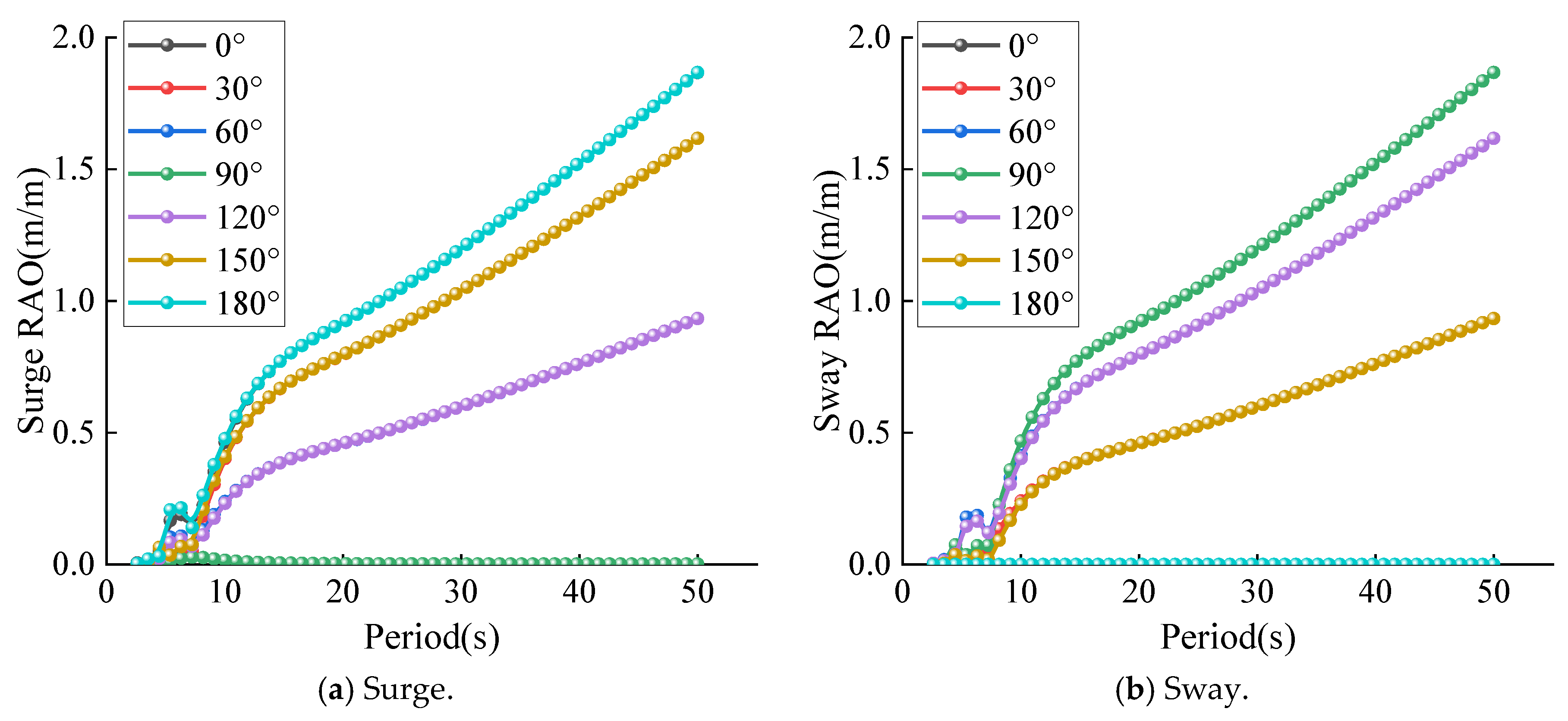
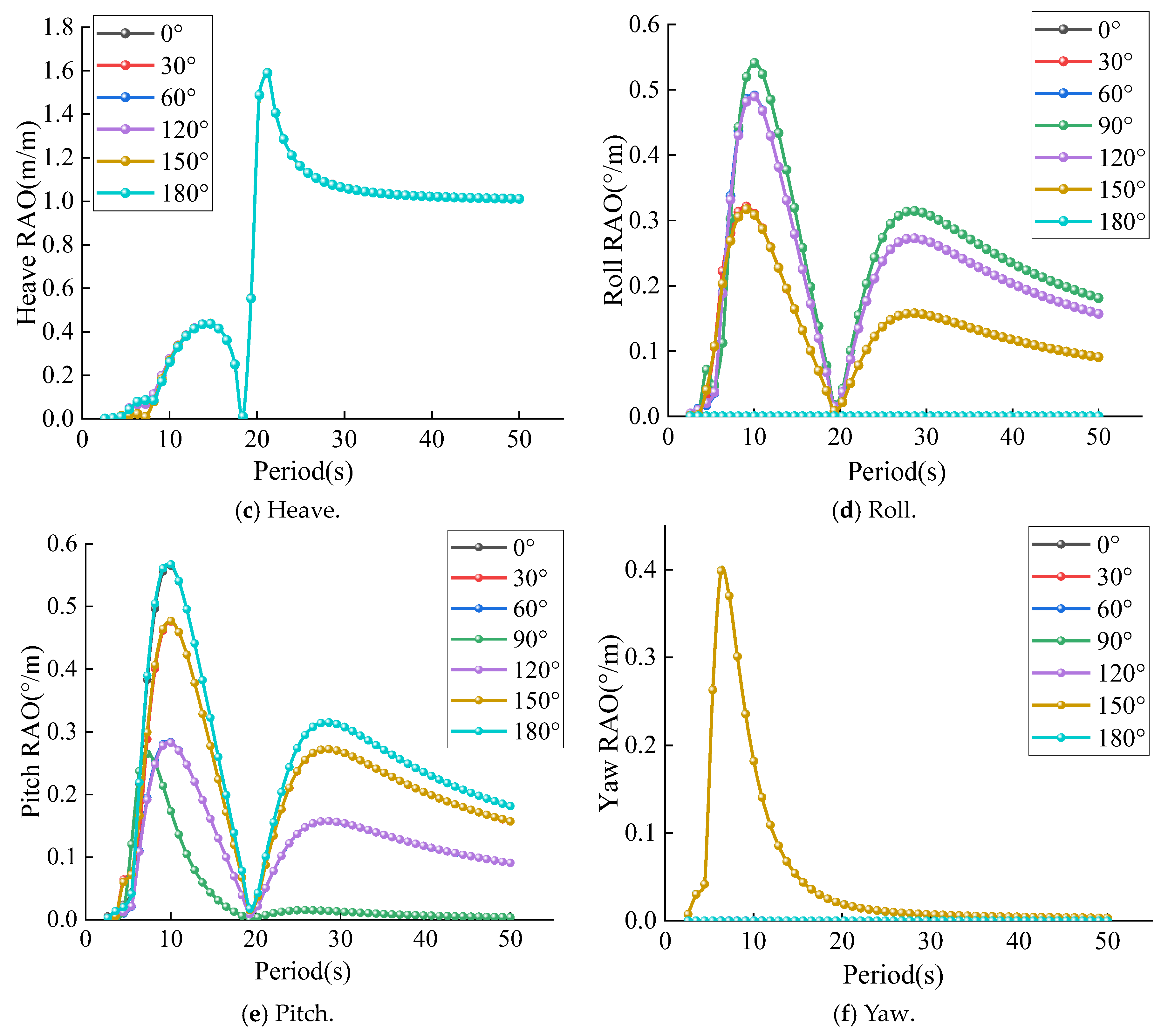
4.2. Hydrodynamic Response
5. Verification Test
5.1. Experimental Setup
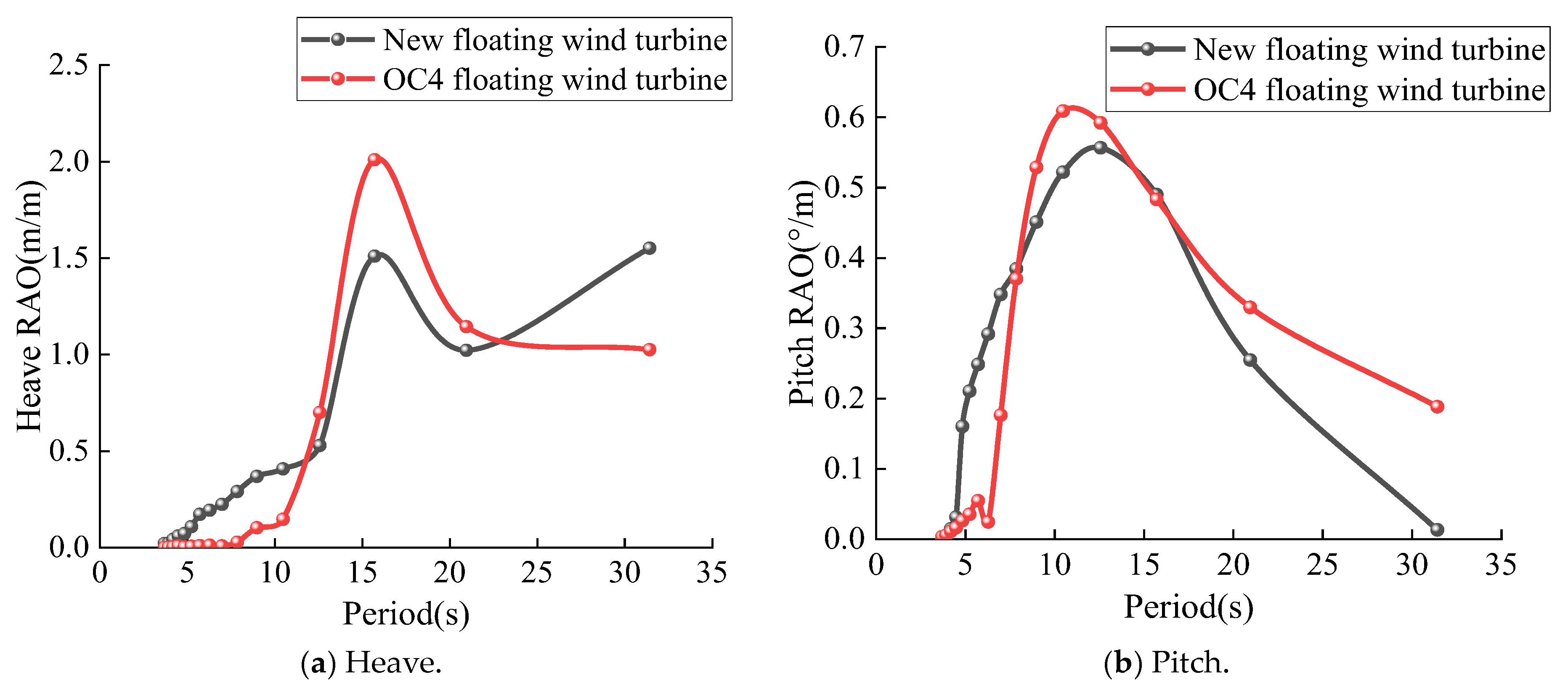
5.2. Results and Discussion
6. Conclusions
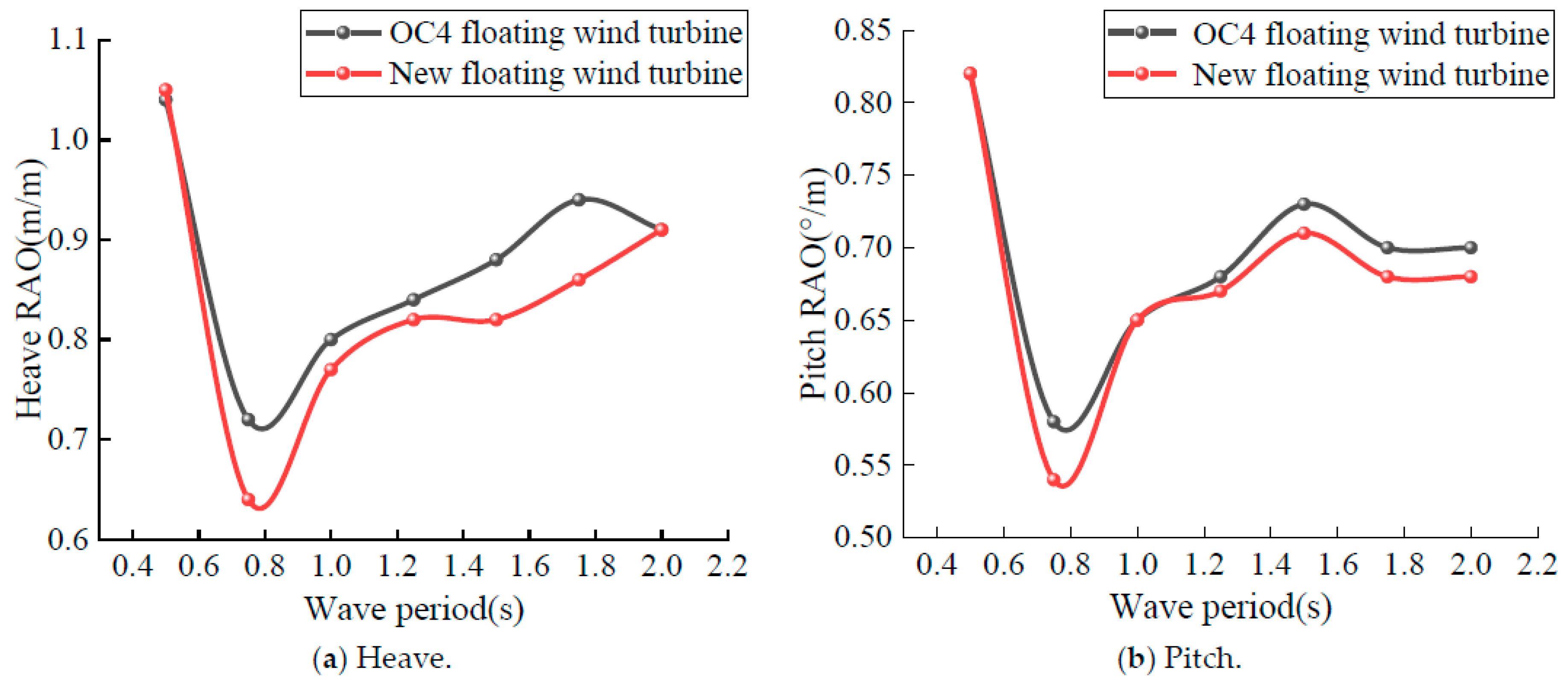
- Introducing viscous damping enables a more accurate determination of the corresponding natural period’s RAO, thus providing a more realistic reflection of the hydrodynamic characteristics of floating wind turbines. This enhances the reliability of the simulation comparisons between the two semi-submersible wind turbine platforms. The results indicate a lower RAO for the new floating wind turbine platform.
- The comparative frequency–domain analysis between the new design of the semi-submersible floating wind turbine and the OC4-DeepCwind platform revealed that a smaller diameter float contacting the water surface resulted in a better motion performance. However, the interaction between the floater and the water surface changes as the platform moves. Therefore, the next step could involve altering the height of the floater’s small waterline area and conducting fully coupled simulation experiments for the better optimization of the new design of the semi-submersible floating platform’s structure and performance.
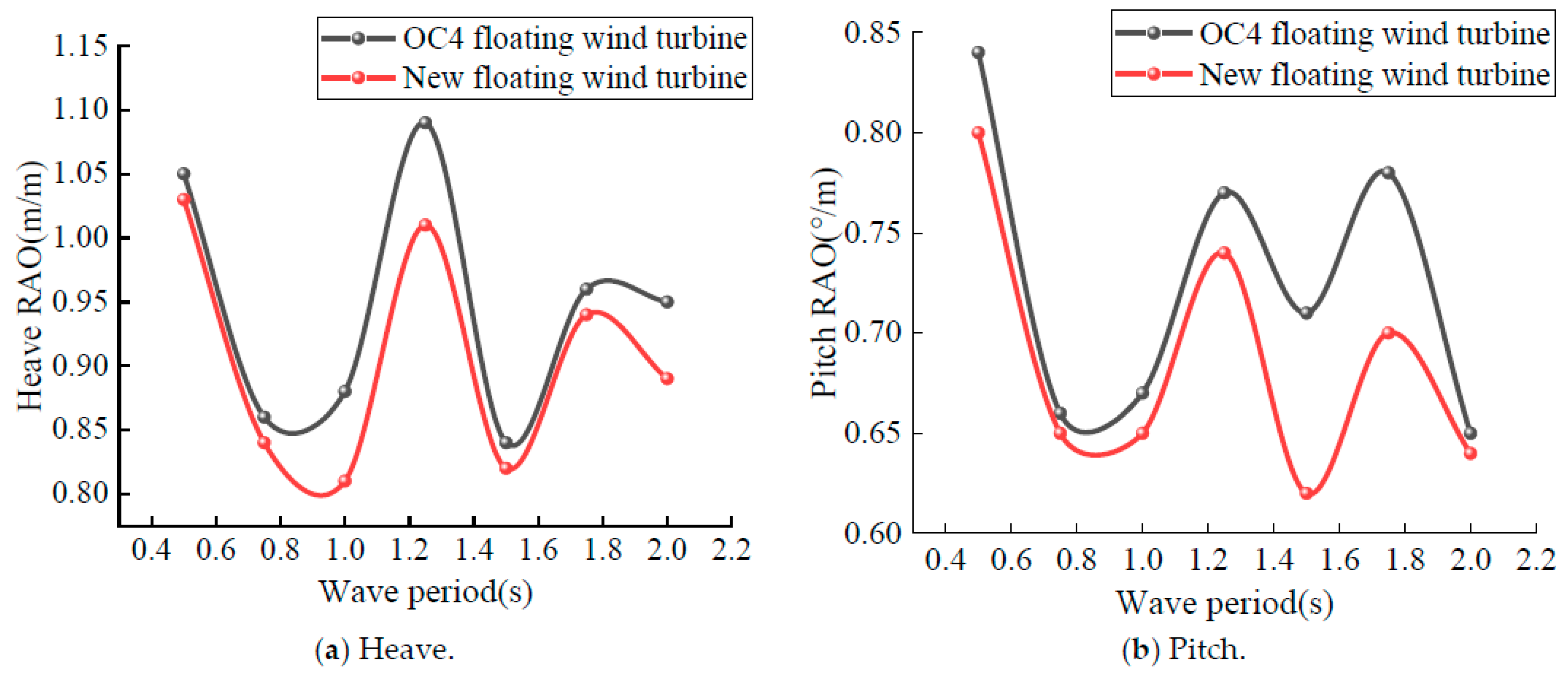
- In scale model experiments under wind–wave conditions, the comparative analysis between the experimental and numerical simulations revealed the significant impact of steady wind waves on OFWTs at different wave periods. Compared to the OC4-DeepCwind platform, the new floating offshore wind turbine could better avoid energy concentration areas and low-frequency wave ranges, thereby preventing platform resonance and improving motion stability.
- The reduced diameter of the float at the waterline in the new design of the semi-submersible floating wind turbine could lower manufacturing costs as compared to the OC4-DeepCwind platform. However, the extent of diameter reduction must be considered in conjunction with overall strength. Future work will involve comprehensive strength testing of the new design of the semi-submersible floating platform.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Edwards, E.C.; Holcombe, A.; Brown, S.; Ransley, E.; Hann, M.; Greaves, D. Trends in floating offshore wind platforms: A review of early-stage devices. Renew. Sustain. Energy Rev. 2024, 193, 114271. [Google Scholar] [CrossRef]
- Zhou, B.; Zhang, Z.; Li, G.; Yang, D.; Santos, M. Review of key technologies for offshore floating wind power generation. Energies 2023, 16, 710. [Google Scholar] [CrossRef]
- Lemmer, F.; Yu, W.; Müller, K.; Cheng, P.W. Semi-submersible wind turbine hull shape design for a favorable system response behavior. Mar. Struct. 2020, 71, 102725. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, H.; Cai, X.; Xie, J.; Wang, Y.; Zhang, N. Novel method for designing and optimising the floating platforms of offshore wind turbines. Ocean Eng. 2022, 266, 112781. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Q.; Tu, Y.; Wang, W.; Hua, X. Proposal of a novel semi-submersible floating wind turbine platform composed of inclined columns and multi-segmented mooring lines. Energies 2019, 12, 1809. [Google Scholar] [CrossRef]
- Scicluna, D.; De Marco Muscat-Fenech, C.; Sant, T.; Vernengo, G.; Tezdogan, T. Preliminary analysis on the hydrostatic stability of a self-aligning floating offshore wind turbine. J. Mar. Sci. Eng. 2022, 10, 2017. [Google Scholar] [CrossRef]
- Rezanejad, K.; Gadelho, J.F.M.; Xu, S.; Soares, C.G. Experimental investigation on the hydrodynamic performance of a new type floating Oscillating Water Column device with dual-chambers. Ocean Eng. 2021, 234, 109307. [Google Scholar] [CrossRef]
- Cheng, P.; Huang, Y.; Wan, D. A numerical model for fully coupled aero-hydrodynamic analysis of floating offshore wind turbine. Ocean Eng. 2019, 173, 183–196. [Google Scholar] [CrossRef]
- Tabeshpour, M.R.; Hajnoruzi, F. Conceptual study on dynamic responses of semi-submersible platforms. In Proceedings of the Institution of Civil Engineers-Maritime Engineering; Thomas Telford Ltd.: London, UK, 2023; Volume 176, pp. 31–43. [Google Scholar]
- Yang, Y.; Bashir, M.; Michailides, C.; Li, C.; Wang, J. Development and application of an aero-hydro-servo-elastic coupling framework for analysis of floating offshore wind turbines. Renew. Energy 2020, 161, 606–625. [Google Scholar] [CrossRef]
- Gao, J.L.; Lyu, J.; Wang, J.H.; Zhang, J.; Liu, Q.; Zang, J.; Zou, T. Study on transient gap resonance with consideration of the motion of floating body. China Ocean Eng. 2022, 36, 994–1006. [Google Scholar] [CrossRef]
- Gao, J.L.; Lyu, J.; Zhang, J.; Zang, J. Influences of floater motion on gap resonance triggered by focused wave groups. China Ocean Eng. 2023, 37, 685–697. [Google Scholar] [CrossRef]
- Gong, S.K.; Gao, J.L.; Mao, H.F. Investigations on fluid resonance within a narrow gap formed by two fixed bodies with varying breadth ratios. China Ocean Eng. 2023, 37, 962–974. [Google Scholar] [CrossRef]
- Zou, Q.; Lu, Z.; Shen, Y. Short-term prediction of hydrodynamic response of a novel semi-submersible FOWT platform under wind, current and wave loads. Ocean Eng. 2023, 27, 114471. [Google Scholar] [CrossRef]
- Bashetty, S.; Ozcelik, S. Review on dynamics of offshore floating wind turbine platforms. Energies 2021, 14, 6026. [Google Scholar] [CrossRef]
- Deng, Y.; Feng, W.; Xu, S.; Chen, X.; Wang, B. A novel approach for motion predictions of a semi-submersible platform with neural network. J. Mar. Sci. Technol. 2020, 26, 883–895. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, H.; Law, Y.; Santo, H.; Magee, A. Hydrodynamic analysis and validation of the floating DeepCwind semi-submersible under 3-h irregular wave with the HOS and CFD coupling method. Ocean Eng. 2023, 287, 115701. [Google Scholar] [CrossRef]
- Falnes, J.; Kurniawan, A. Ocean Waves and Oscillating Systems: Linear Interactions Including Wave-Energy Extraction; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Robertson, A.; Jonkman, J.; Masciola, M.; Song, H.; Goupee, A.; Coulling, A.; Luan, C. Definition of the Semi-Submersible Floating System for Phase II of OC4; National Renewable Energy Lab.(NREL): Golden, CO, USA, 2014.
- Choi, Y.R.; Hong, S.Y.; Choi, H.S. An analysis of second-order wave forces on floating bodies by using a higher-order boundary element method. Ocean Eng. 2001, 28, 117–138. [Google Scholar] [CrossRef]
- Tran, T.T.; Kim, D.H. The coupled dynamic response computation for a semi-submersible platform of floating offshore wind turbine. J. Wind Eng. Ind. Aerodyn. 2015, 147, 104–119. [Google Scholar] [CrossRef]
- Liu, Z.; He, J.; Meng, Y.; Zhang, H.; Zhou, Y.; Tao, L. Numerical and experimental study on the influence of a moonpool on motion performance and stability of a drillship. Ocean Eng. 2022, 262, 112241. [Google Scholar] [CrossRef]
- Lopez-Pavon, C.; Souto-Iglesias, A. Hydrodynamic coefficients and pressure loads on heave plates for semi-submersible floating offshore wind turbines: A comparative analysis using large scale models. Renew. Energy 2015, 81, 864–881. [Google Scholar] [CrossRef]
- Joseph, D.D. Potential flow of viscous fluids: Historical notes. Int. J. Multiph. Flow 2006, 32, 285–310. [Google Scholar] [CrossRef]
- Felder, S.; Chanson, H. Turbulence, dynamic similarity and scale effects in high-velocity free-surface flows above a stepped chute. Exp. Fluids 2009, 47, 1–18. [Google Scholar] [CrossRef]

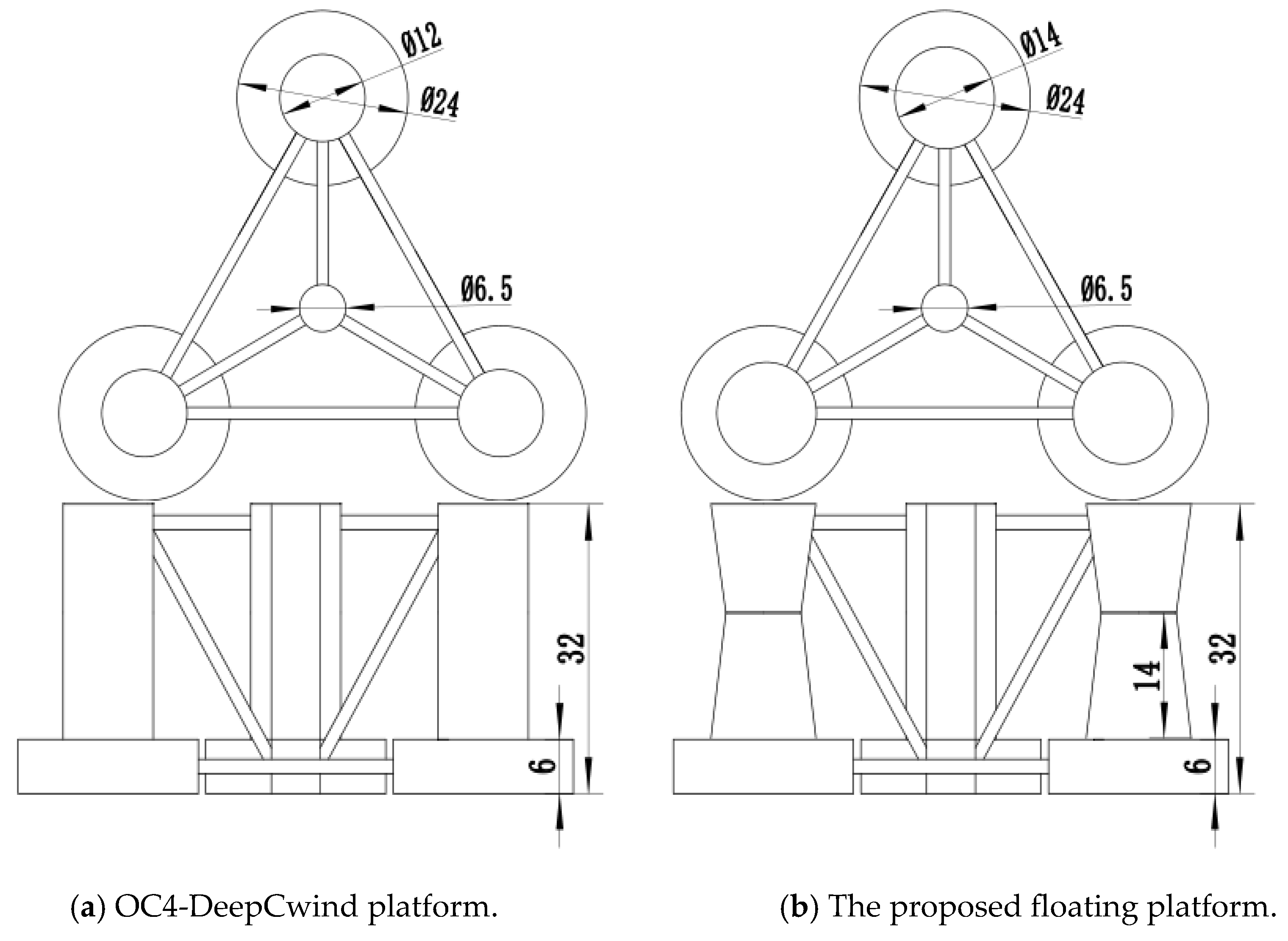

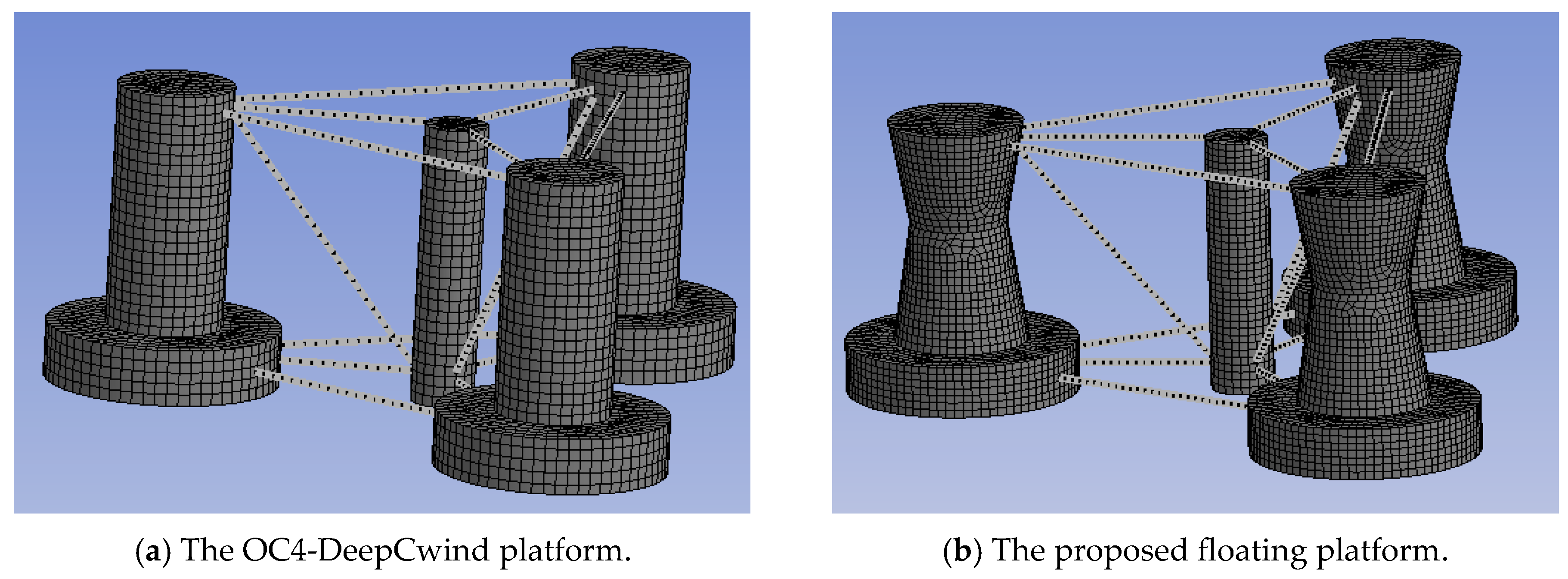





| Parameters | Proposed Floating Platform | OC4-DeepCwind Platform |
|---|---|---|
| Draft (m) | 20 | 20 |
| Height above waterline of floater (m) | 12 | 12 |
| Outer bottom floater diameter (m) | 24 | 24 |
| Diameter at the outer draft line (m) | 10 | 12 |
| Diameter of outer floater (m) | 12 | 12 |
| Diameter of lower conical floater (m) | 12 | 12 |
| Height of lower conical float below Waterline (m) | 14 | 14 |
| Height of upper conical floater above Waterline (m) | 12 | 12 |
| Distance between outer-side pontoons (m) | 50 | 50 |
| Diameter of central pontoon (m) | 6 | 6 |
| Height of central pontoon (m) | 30 | 30 |
| Diameter of support column (m) | 1.6 | 1.6 |
| Total mass (kg) | 1.335 × 107 | 1.347 × 107 |
| Moment of inertia Ixx (kg/m2) | 7.370 × 109 | 6.827 × 109 |
| Moment of inertia Iyy (kg/m2) | 7.371 × 109 | 6.827 × 109 |
| Moment of inertia Izz (kg/m2) | 1.114 × 1010 | 1.226 × 1010 |
| Parameters | Numerical Value |
|---|---|
| Quantity | 3 |
| Length (m) | 507 |
| Mass per unit length (kg/m) | 150 |
| Equivalent interfacial area (m2) | 0.01 |
| Axial stiffness (N/m) | 753,600,000 |
| Breaking force (N) | 6,090,000 |
| Added mass coefficient | 1.1 |
| Drag coefficient | 1.0 |
| Axial drag coefficient | 0.1 |
| Longitudinal damping coefficient | 0.025 |
| Platform | DOFs | Inertial Mass/kg | Added Mass/kg | Restoring Stiffness/N × m−1 | Critical Damping /N × (m/s)−1 or /N × m × (°/s)−1 | Viscous Damping /N × (m/s)−1 or /N × m × (°/s)−1 |
|---|---|---|---|---|---|---|
| Proposed platform | Heave | 1.33 × 107 | 1.44 × 107 | 2.75 × 108 | 1.75 × 106 | 8.74 × 105 |
| Roll | 7.37 × 109 | 1.08 × 108 | 1.67 × 107 | 7.07 × 108 | 3.53 × 107 | |
| Pitch | 7.37 × 109 | 1.08 × 108 | 1.67 × 107 | 7.07 × 108 | 3.53 × 107 | |
| OC4-Deep Cwind | Heave | 1.34 × 107 | 1.42 × 107 | 3.79 × 106 | 2.05 × 107 | 1.02 × 106 |
| Roll | 6.82 × 109 | 1.08 × 108 | 2.55 × 107 | 8.42 × 108 | 4.21 × 107 | |
| Pitch | 6.82 × 109 | 1.08 × 108 | 2.55 × 107 | 8.42 × 108 | 4.21 × 107 |
| Loading Conditions | Wave Period (s) | Wave Height (m) | Wind Speed (m/s) |
|---|---|---|---|
| Pure wave | 0.50 | 0.05 | --- |
| 0.75 | 0.05 | --- | |
| 1.00 | 0.05 | --- | |
| 1.25 | 0.05 | --- | |
| 1.50 | 0.05 | --- | |
| 1.75 | 0.05 | --- | |
| 2.00 | 0.05 | ||
| Wind–wave combined | 0.50 | 0.05 | 6.0 |
| 0.75 | 0.05 | 6.0 | |
| 1.00 | 0.05 | 6.0 | |
| 1.25 | 0.05 | 6.0 | |
| 1.50 | 0.05 | 6.0 | |
| 1.75 | 0.05 | 6.0 | |
| 2.00 | 0.05 | 6.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Wu, X.; Zhou, Z. Exploring Motion Stability of a Novel Semi-Submersible Platform for Offshore Wind Turbines. Energies 2024, 17, 2313. https://doi.org/10.3390/en17102313
Zhao H, Wu X, Zhou Z. Exploring Motion Stability of a Novel Semi-Submersible Platform for Offshore Wind Turbines. Energies. 2024; 17(10):2313. https://doi.org/10.3390/en17102313
Chicago/Turabian StyleZhao, Hongxu, Xiang Wu, and Zhou Zhou. 2024. "Exploring Motion Stability of a Novel Semi-Submersible Platform for Offshore Wind Turbines" Energies 17, no. 10: 2313. https://doi.org/10.3390/en17102313
APA StyleZhao, H., Wu, X., & Zhou, Z. (2024). Exploring Motion Stability of a Novel Semi-Submersible Platform for Offshore Wind Turbines. Energies, 17(10), 2313. https://doi.org/10.3390/en17102313





