The Impact of Replacing Synchronous Generators with Renewable-Energy Technologies on the Transient Stability of the Mangystau Power System: An Introduction to Flexible Automatic Dosage of Exposures
Abstract
:1. Introduction
- (a)
- This is the first attempt to analyze the impact of the replacement of synchronous generation on rotor angle transient stability using a real power system in the Mangystau region, Kazakhstan.
- (b)
- This is the first attempt to consider a more severe emergency mode that is applicable in practice while exploiting the power system.
- (c)
- Based on actions taken to analyze the impact of the replacement, this study proposes a method for identifying the maximum allowable amount of synchronous generation that can be replaced with renewable energy technologies to still have a transiently stable power system.
- (d)
- Increasing the auto-reclose delay time mitigates the exposure of the synchronous generators to the considered emergency mode and increases the transient stability.
- (e)
- The application of special load-shedding automation succeeds in avoiding the loss of synchronism with high renewable energy penetration.
- (f)
- This paper provides an appropriate smart-grid solution by implementing the Flexible Automatic Dosage of Exposures, which enhances the power system’s stability with a high penetration of non-inertial generation.
- (1)
- Modeling a real diagram of the Mangystau power system.
- (2)
- Linking the inertial constant to the nominal parameters of existing synchronous generators of the Mangistau energy system.
- (3)
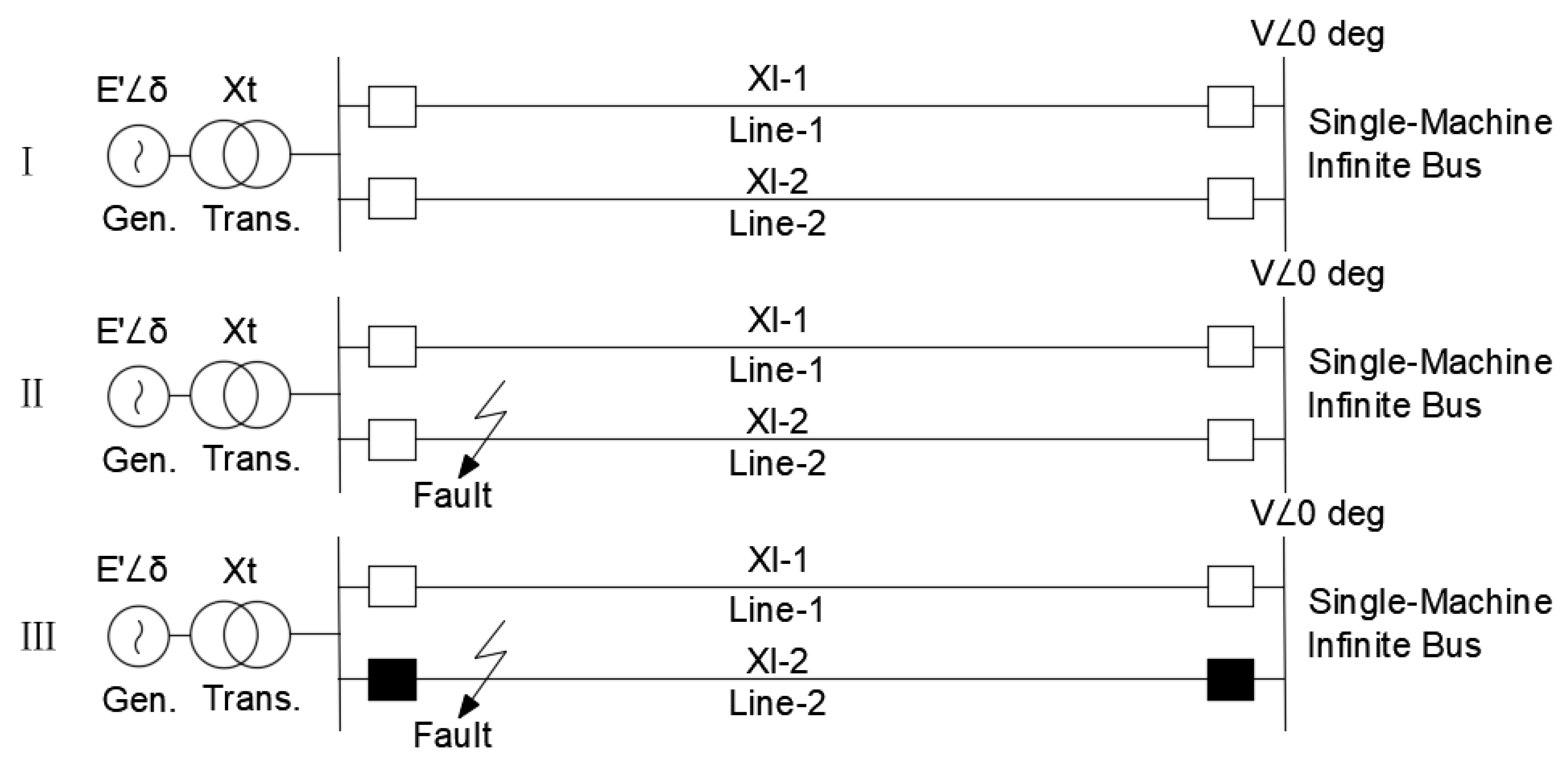
- Setting the fault using a three-phase short circuit on the 220 kV intersystem transmission line with subsequent tripping action via relay protection and automatic reclosure action. In this case, the line is switched on for an unresolved short circuit, and the line is switched off again by the action of the protection.
- (4)
- Identifying the maximum possible share of DFIG generation that can replace synchronous generators.
- (5)
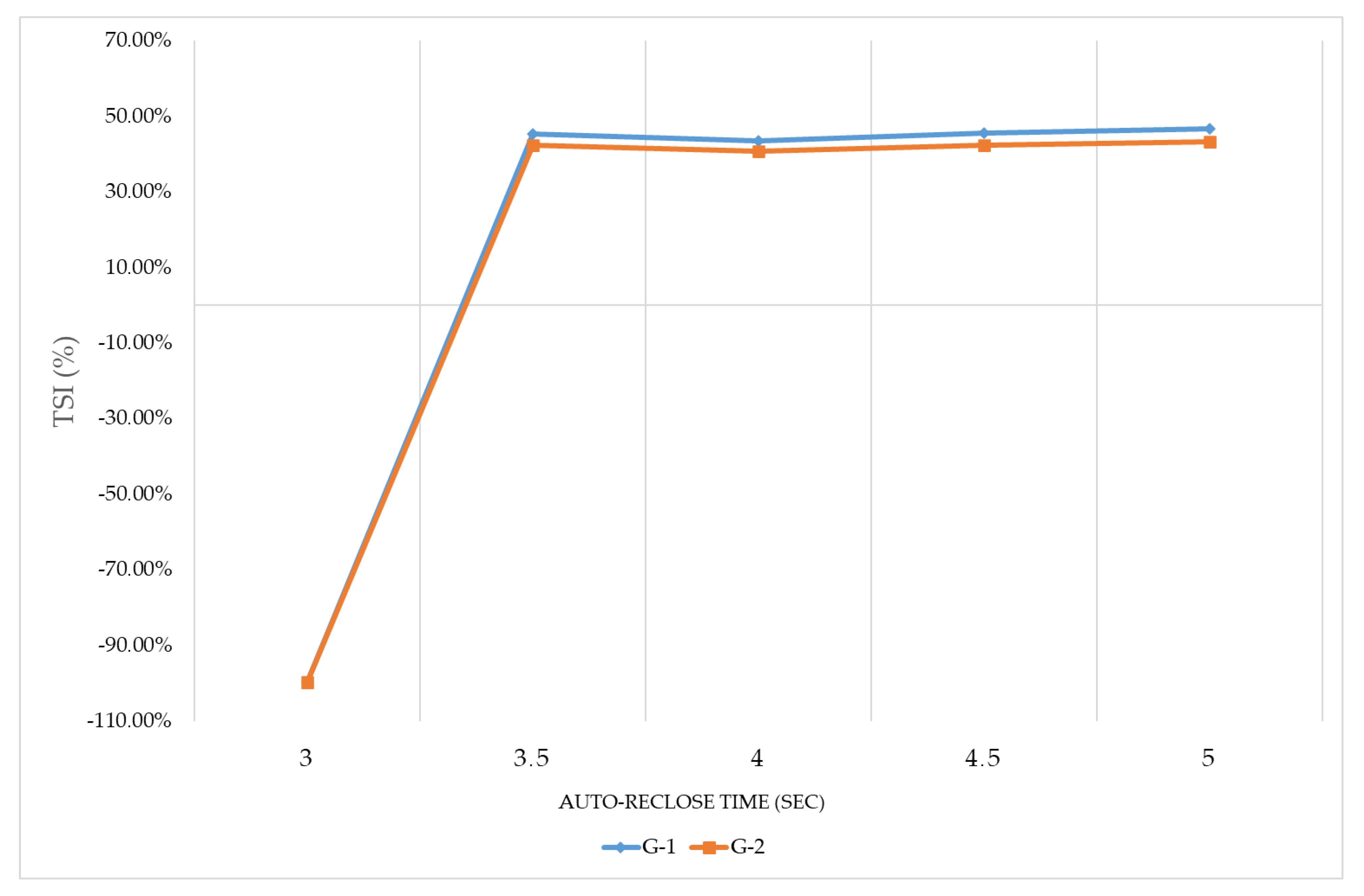
- Identifying the influence of the automatic-reclosure response time delay on a faulted line, as a means of enhancing the transient stability of the power system with high DFIG integration.
- (6)
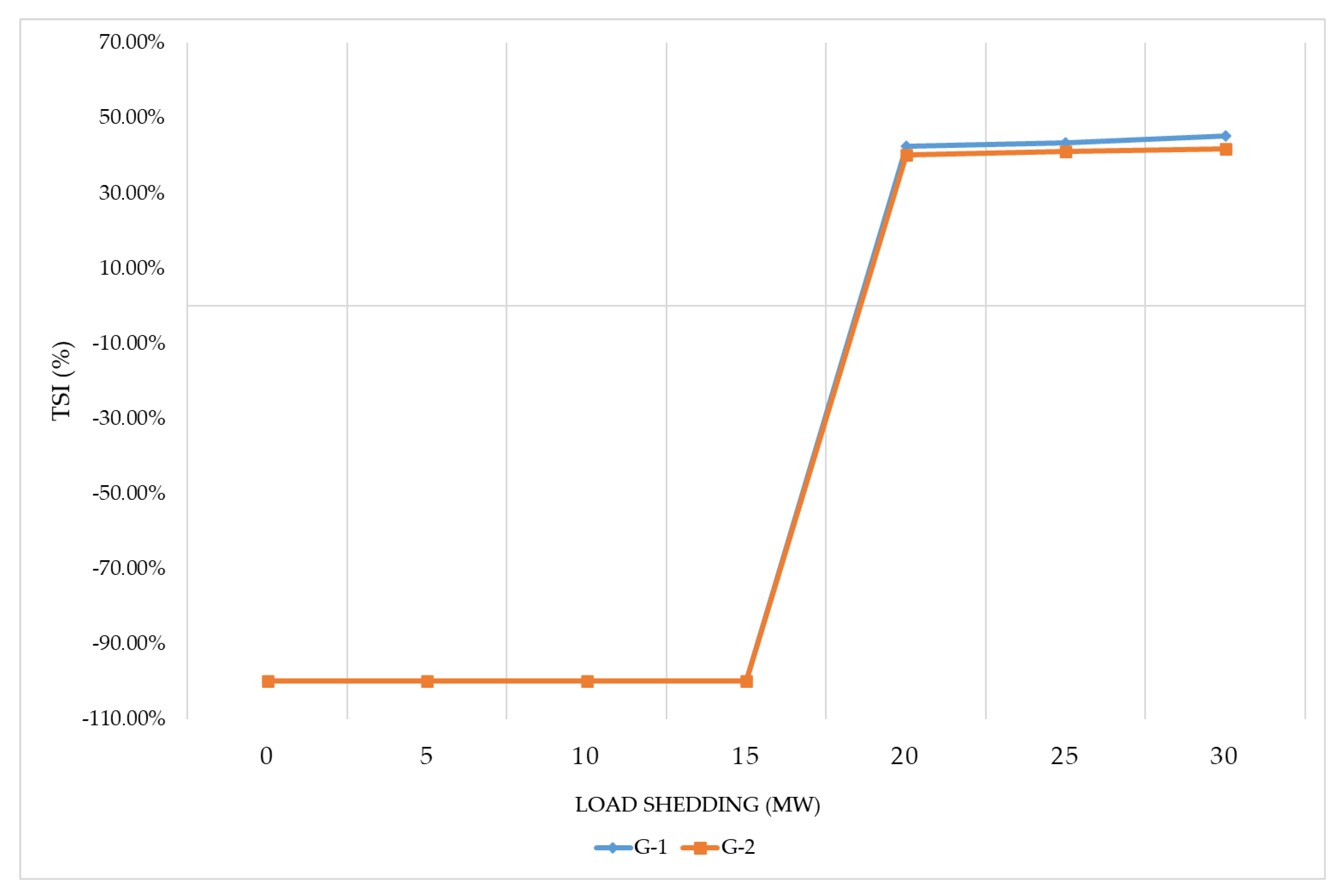
- Identifying the influence of the magnitude of load shedding as a means of improving transient stability under the conditions of high DFIG integration.
- (7)
- Providing an algorithm by which the Flexible Automatic Dosage of Exposures works.
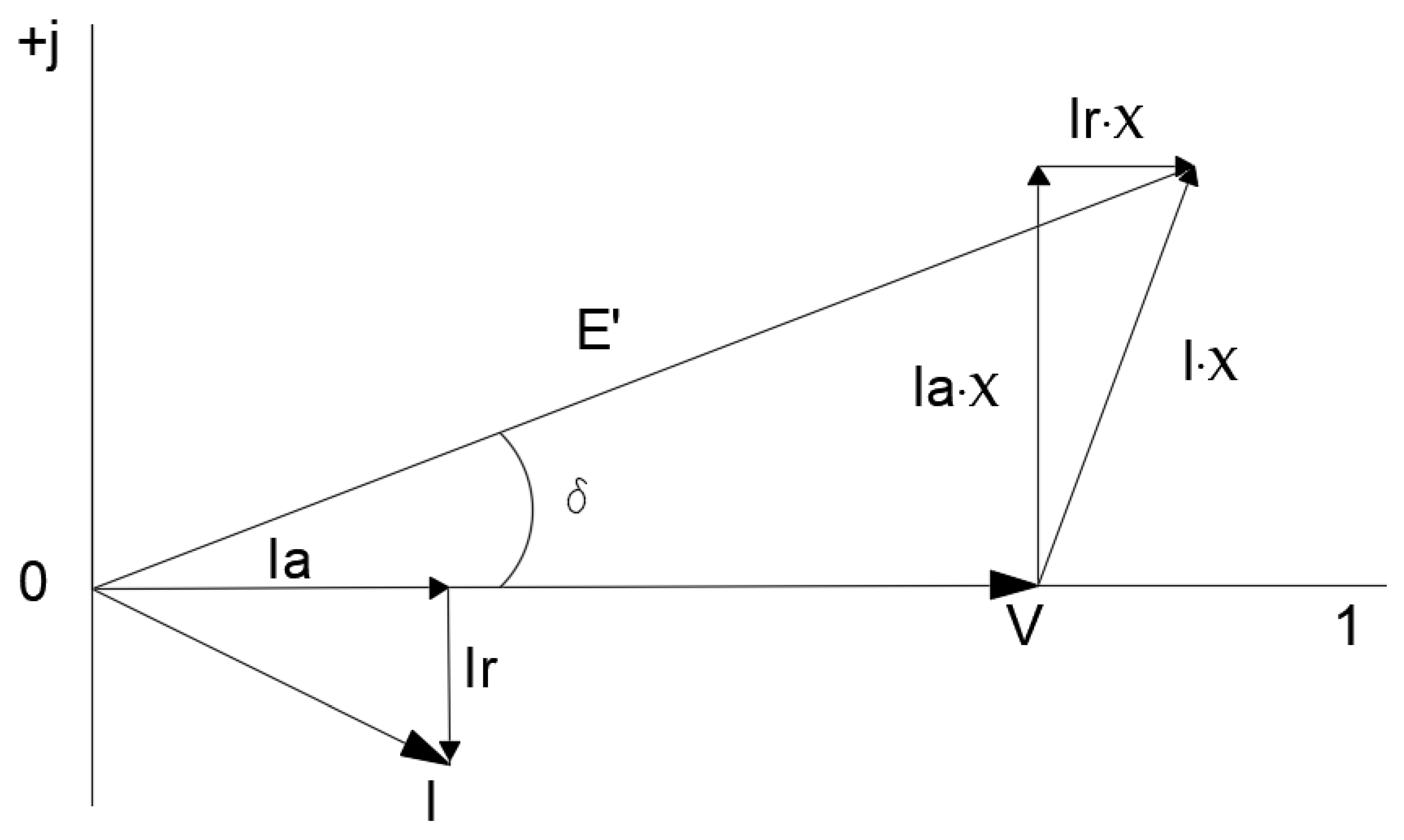
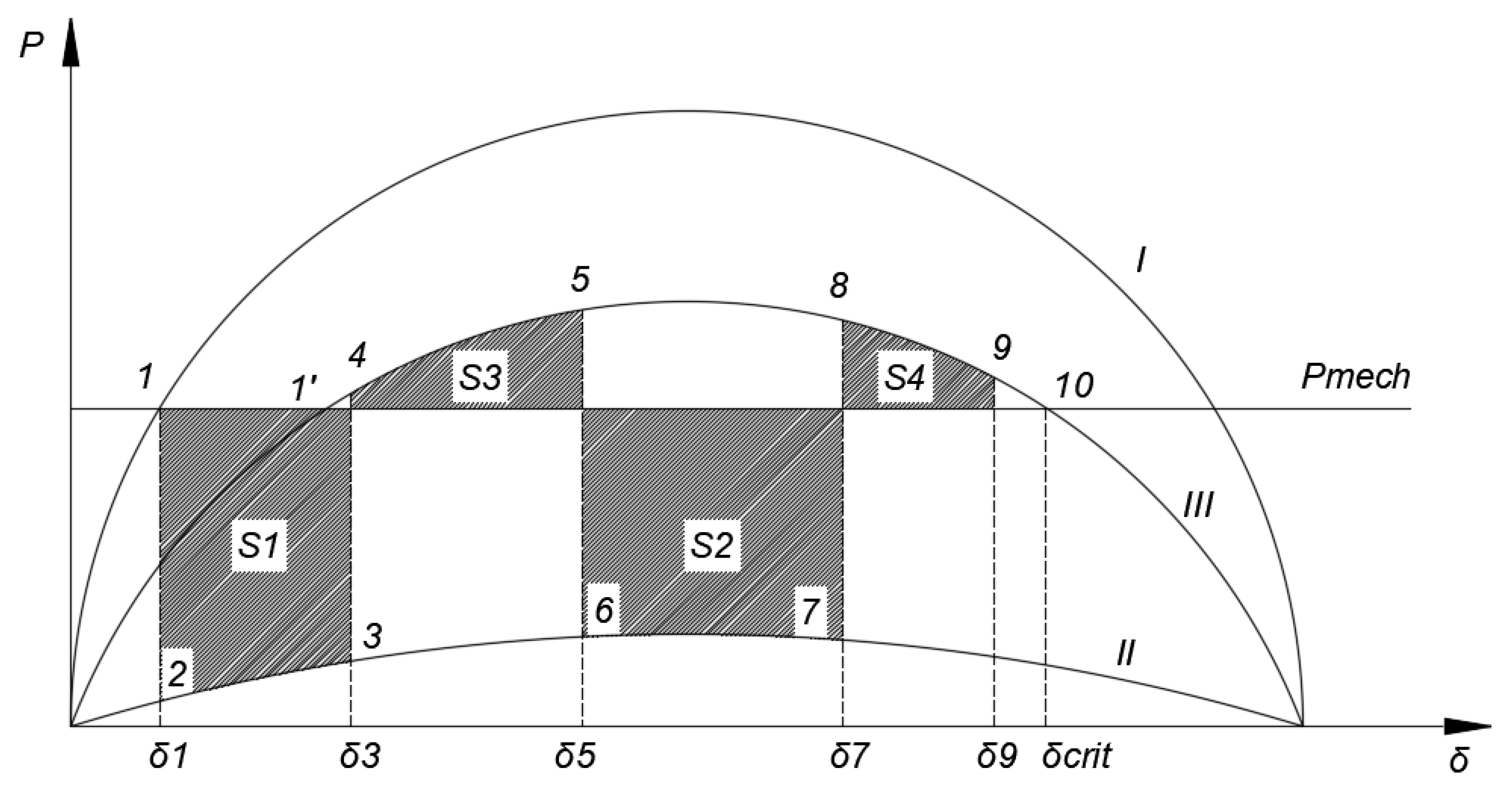
2. Theoretical Philosophy of Transient Stability and Equal Area Criterion
3. Materials and Methods
3.1. Configuration of the Mangystau Energy System
- −
- The electrical power system under study consists of three main coal-fired power plants: Stations 1, 2, and 3.
- −
- There are 110 kV Open Switchgears at Station 1 and 2, while Station 3 has both 110 and 220 kV Open Switchgears.
- −
- The given transmission network is connected to the rest of the Unified Power System of Kazakhstan through two 220 kV lines between Station 3 and Substation 4. All of the generators in Stations 1, 2, and 3 rotate in synchronism with the aggregated Unified Power System. Substation 4 is the slack bus.
3.2. Aggregation and Calculation of Network Parameters of the Mangystau System
- A.
- Calculation of the inertia of the turbogenerators
- B.
- Calculation of the system element reactance values
- Generator reactance
3.3. Setting the Pre-Emergency Mode
3.4. Actions and Assumptions for Achieving the Goal
- −
- −
- The sequence for replacing the synchronous generators, as shown in Figure 6—Station 2 (250 MW generation, H = 11.5 s), Station 1 (75 MW generation, H = 1.998 s), and G-3 Station 3 (20 MW generation, H = 2.604 s).
- −
- Simulation and analysis of the rotor angle behavior of the synchronous generators remaining in operation during a three-phase short circuit on the Station 3 220 kV–Substation 4 220 kV lines and its automatic reclosure.
- −
- Transient stability analysis, carried out using PowerWorld software 23.
- −
- The intermittency of power generation from the DFIGs is neglected. In other words, all DFIG technologies are equipped with storage systems.
- −
- The location of DFIG stations is neglected due to the fact that there are no real projects for the implementation of wind power plants of such relatively high power. The replacement of stations based on synchronous machines using DFIG technologies is carried out exactly at the location of the replaced stations.
- −
- The work of automatic excitation control (AEC) and primary frequency control via governors is neglected in the dynamic simulation.
- −
- Our focus is only on the generators’ rotor angle transient stability.
4. Results
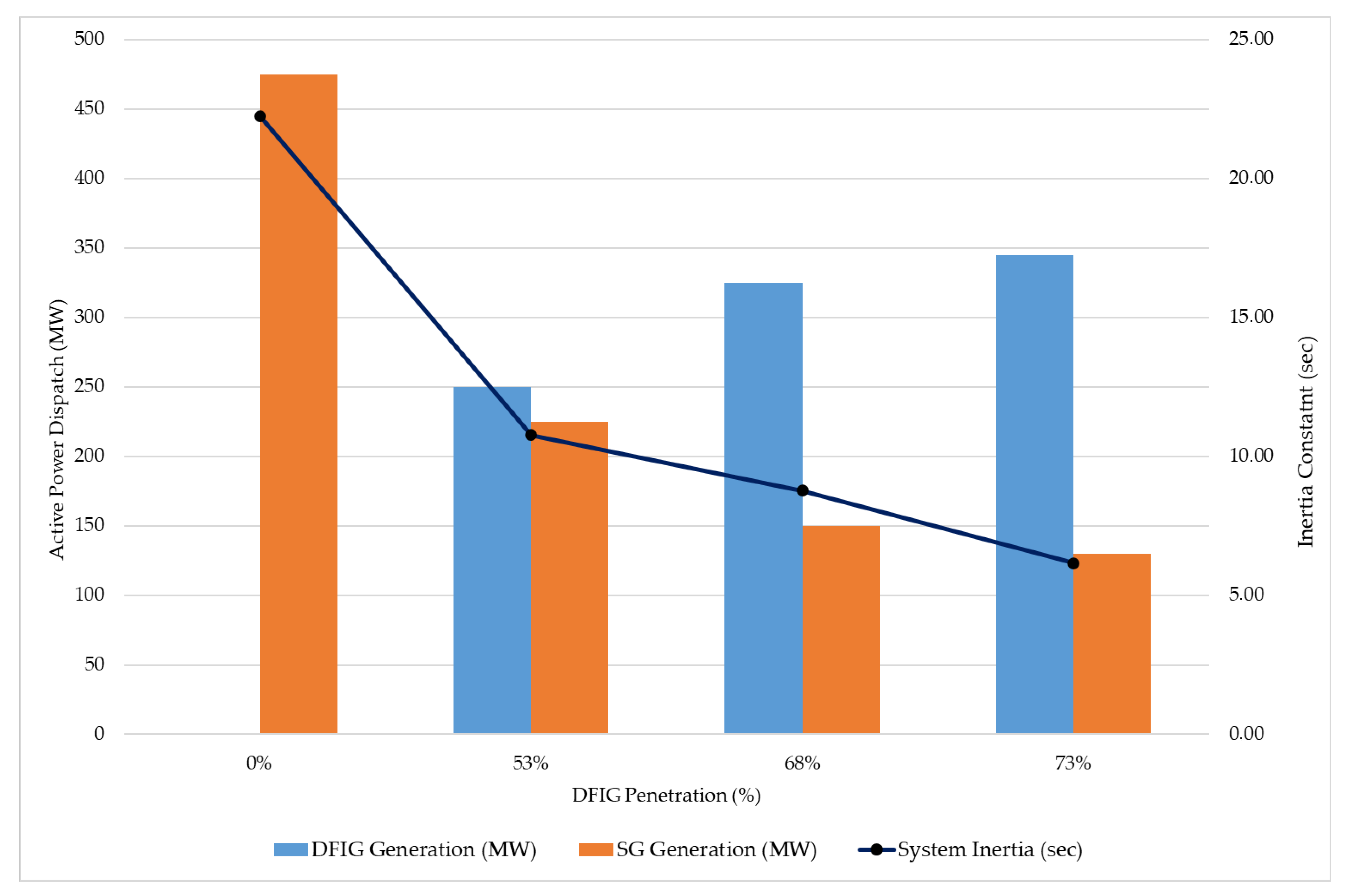
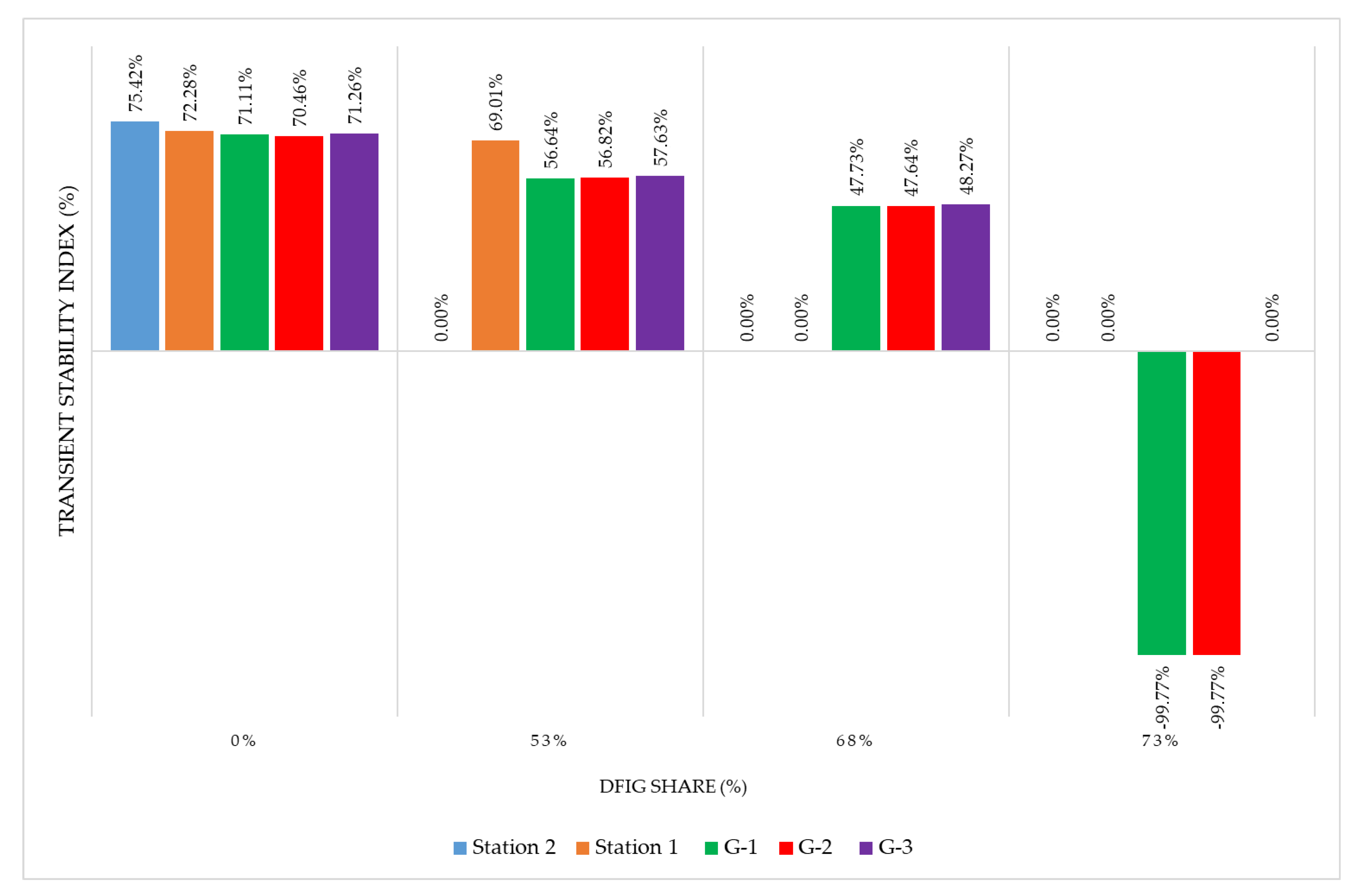
- (1)
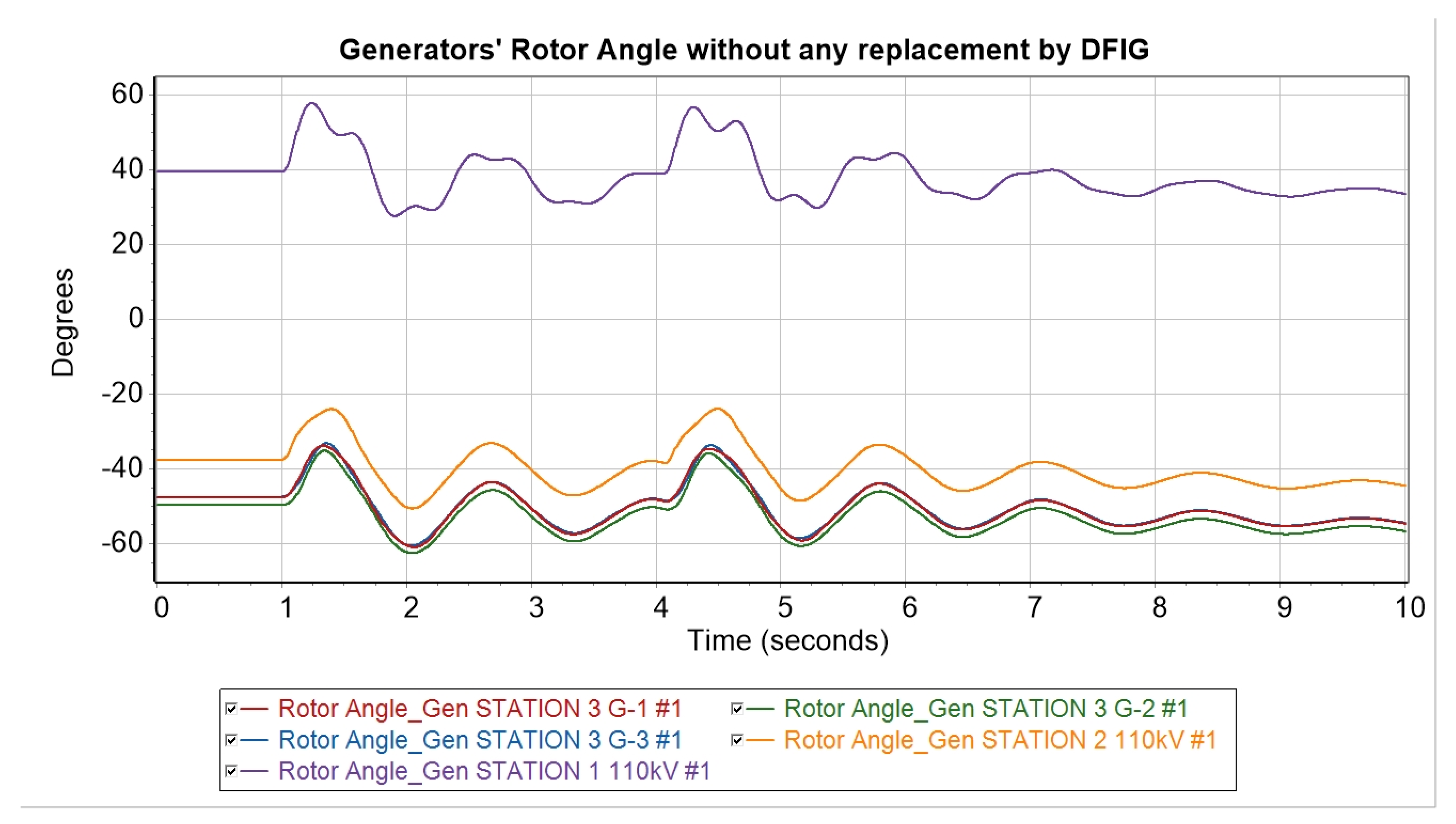
- A total of 0% generation from DFIGs—the base scenario in which the generators of each station are synchronous. Equivalent inertia: 22.26 s.
- (2)
- A total of 53% generation from DFIGs—the replacement of synchronous generators at Station 2. In this scenario, the rotor angle of the equivalent generator of Station 2 becomes zero since DFIGs do not have rotor angle physically. Therefore, those generators replaced by DFIGs are ignored. Equivalent inertia: 10.76 s.
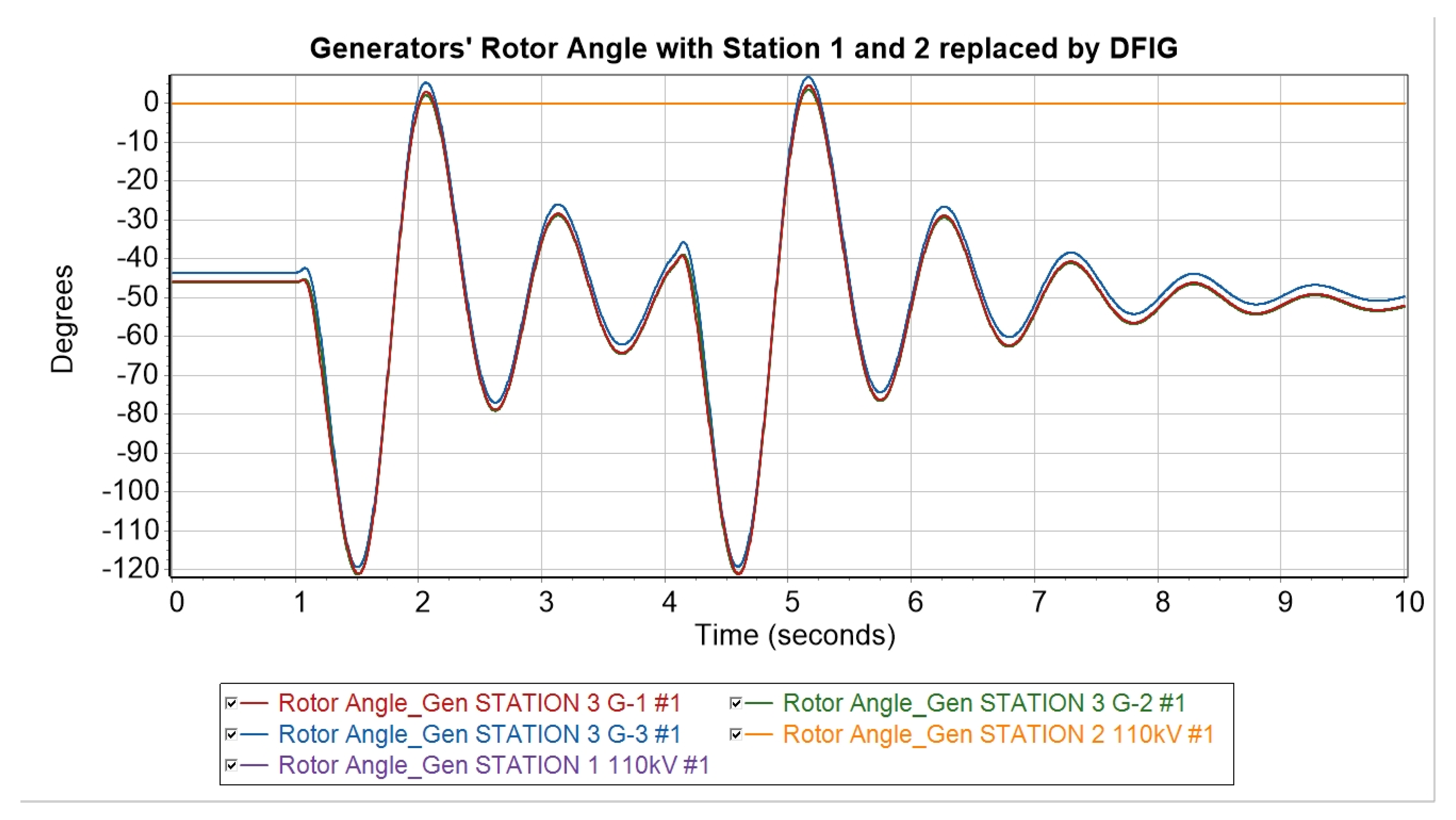
- (3)
- A total of 68% generation from DFIGs—the replacement of synchronous generators at Station 1. The remaining synchronous machines are G-1, G-2, and G-3 at Station 3. Equivalent inertia: 8.76 s.
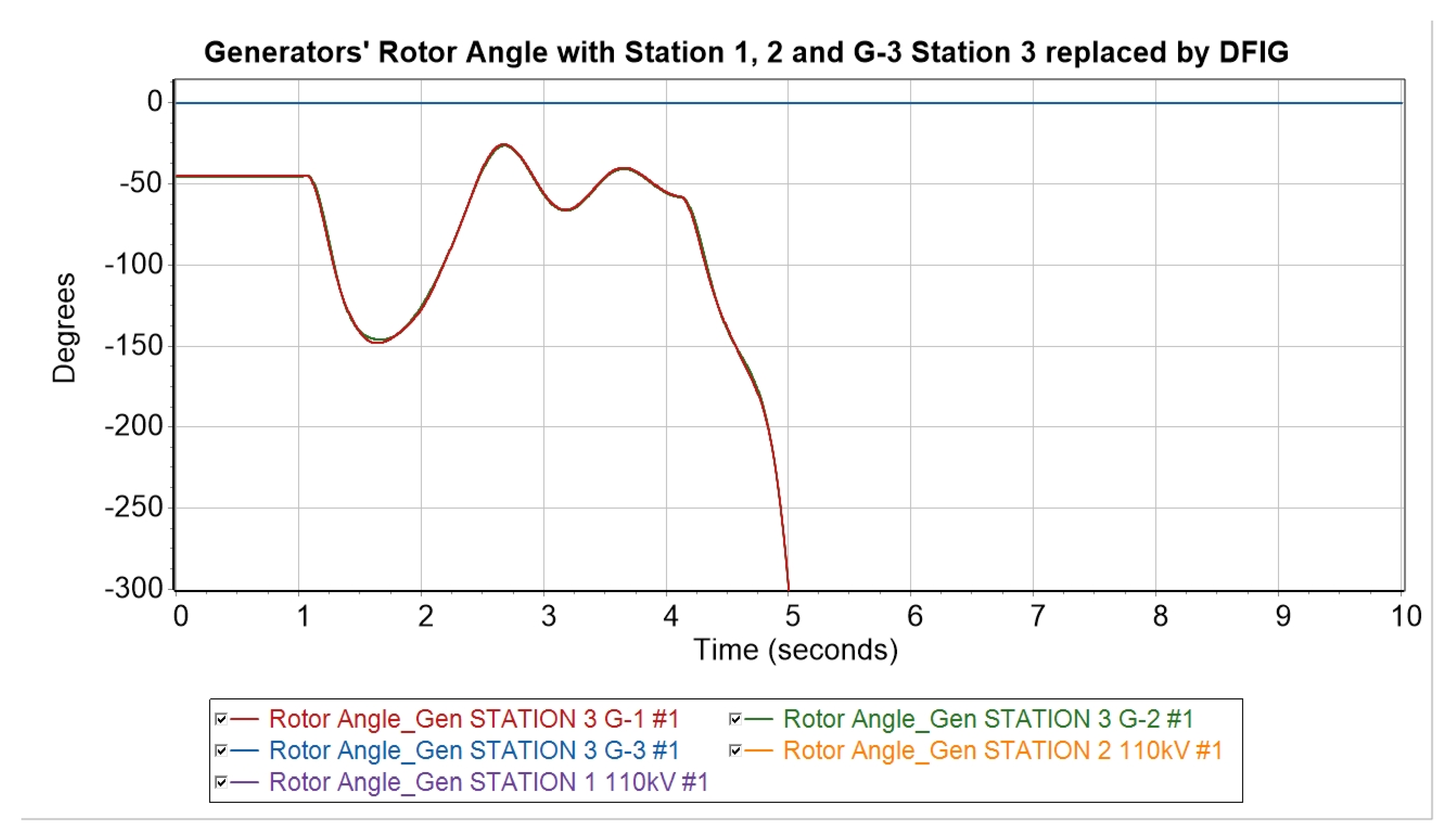
- (4)
- A total of 73% generation from DFIGs—the replacement of one synchronous generator at Station 3 (G-3). In this scenario, the system is supported by only two Station 3 synchronous generators (G-1 and G-2). Equivalent inertia: 6.16 s.
- (5)
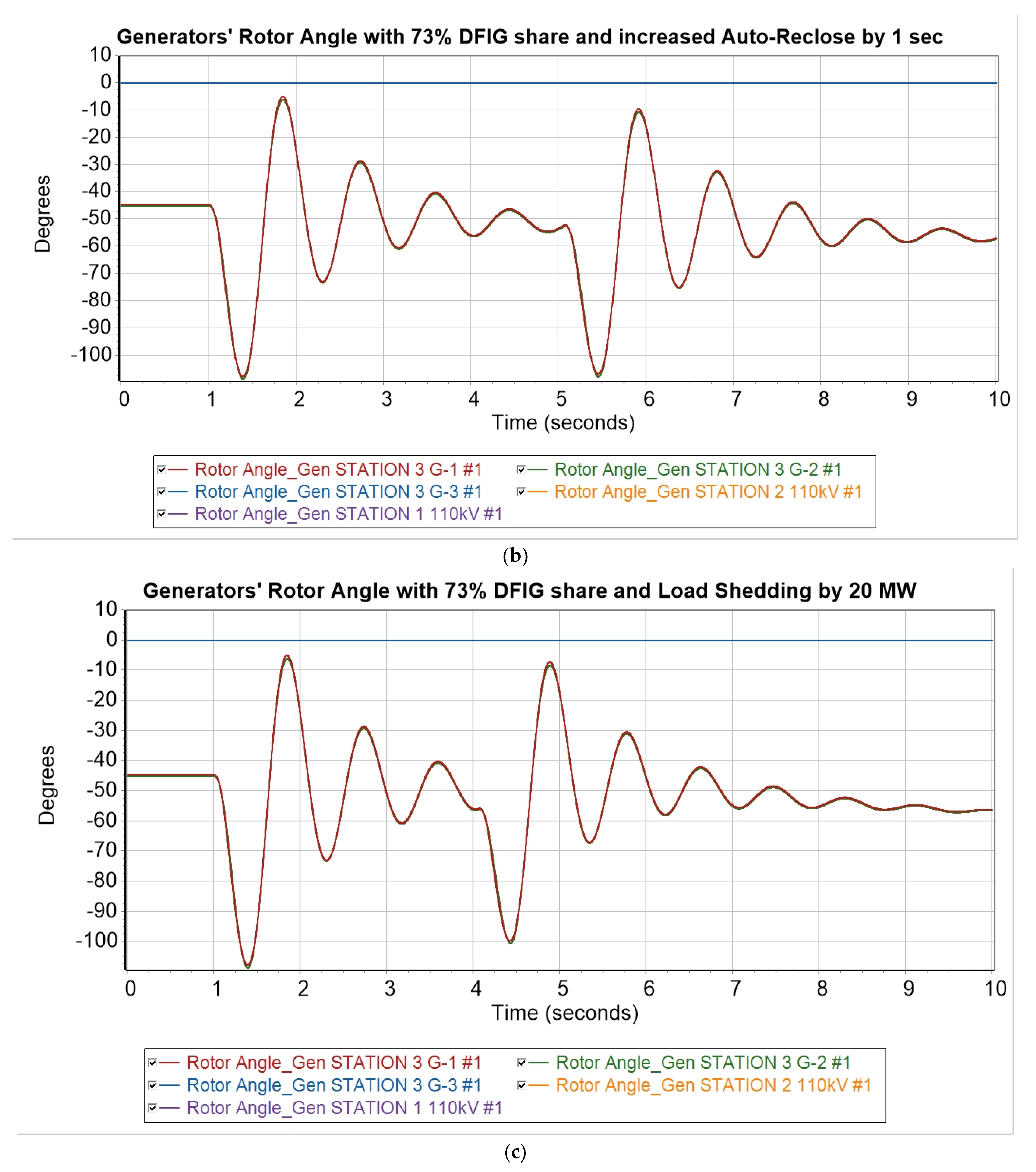
- A total of 73% generation from DFIGs and an increase in the automatic reclosure time by 1 s—a scenario similar to scenario 4.
- (6)
- A total of 73% generation from DFIGs with a disconnection of 20 MW of load on Substation 2—a scenario similar to scenario 4, but with part of the load disconnected via special load-shedding automation (SLSA) as a means of preventing instability.
5. Flexible Automatic Dosage of Exposures Algorithm
- −
- The state of the synchronous generators—switched on/off via SCADA systems. Owing to the commutation state of the generators, it can derive the equivalent amount of inertia in the power system using Equation (15). For instance, with 73% of the synchronous generators replaced by DFIGs, there are only G-1 and G-2 remaining at Station 3. The total equivalent inertia is 6.16 s. However, if G-2 is switched off for repairment, the amount of inertia reduces by around 3 s. Thus, the power system deteriorates in terms of transient stability. In other words, with the control of inertia, we have the dynamic state of the power system with respect to the transient stability.
- −
- The power output of the synchronous generators. With, for example, little wind power (because of weather conditions), the amount of power output from the synchronous generators increases in order to meet the frequency constraints. However, with a high power output, the power system might be much closer to the transient stability limit (Equation (10)). In other words, the power system would breach the stability limit and fall out of synchronism. It is assumed that G-1 and G-2 have a uniform power output.
- −
- Auto-reclose timing (t1, t2, etc.), which is sent to the auto-reclose scheme inside the protection and automation cabinet of the two 220 kV transmission lines between Station 3 and Substation 4.
- −
- Load shedding (LS1, LS2, etc.), which is implemented at load nodes with no generation.
- −
- Generation limitation, which is sent to the surplus Unified Power System of Kazakhstan. This control exposure is executed only if the load shedding has already been operated.
- −
- Network division. This option is necessary if it is obvious that transient stability is not maintained. This network division separates the Mangystau power system from the Unified Power System of Kazakhstan.
6. Conclusions
- 1.
- According to the research papers mentioned in the Introduction section, the transient stability of synchronous generators is dependent on many factors:
- −
- The nature of contingencies—e.g., a one, two, or three-phase short circuit, the presence of an auto-reclose scheme, a stable or unstable short circuit, etc.;
- −
- The location of the short circuit on the line and its distance from a generator.
- −
- The fault elimination time and circuit breakers’ tripping time;
- −
- The voltage control devices of the generators involving those coming from renewable energy sources, and the availability of excitation-boost devices;
- −
- The pre-emergency mode—the amount of power generated from each synchronous generator (Equation (10)), the voltages at each node, and the power flow through the interconnection line;
- −
- The infrastructure of the facility—e.g., the availability of parallel transmission lines and their quantity.
- 2.
- Scenarios 5 and 6, analyzed in the Results section, have proved the notion that increasing the auto-reclose delay time and utilizing special load-shedding automation could be successful strategies to enhance the stability of the Mangystau power system. Both methods prevented the system from falling out of synchronism with a 73% share of DFIG generation (or with the replacement of G-3 at Station 3). In addition, these two strategies are extremely simple and free from investments since they have already been implemented. Nevertheless, the load-shedding strategy is fraught with more consumers being disconnected from the grid, which could deteriorate the quality of business and production in other sectors.
- 3.
- A new Flexible Automatic Dosage of Exposures algorithm has been proposed in this paper. This algorithm offers a promising solution to address the difficulties associated with superseding coal-fired synchronous generation with doubly fed induction generators in the Mangystau power system. By manipulating the auto-reclose timing and load-shedding parameters, FADE presents the capability to ameliorate transient stability, thereby providing the system with heightened flexibility, environmental sustainability, and operational reliability.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2022. Mitigation of Climate Change; IPCC: Geneva, Switzerland, 2022. [Google Scholar]
- Ritchie, H.; Roser, M.; Rosado, P. CO2 and Greenhouse Gas Emissions. 2020. Available online: https://ourworldindata.org/co2-and-greenhouse-gas-emissions (accessed on 12 December 2023).
- Government of Kazakhstan (GOV.KZ). Kazakh Prime-Minister Askar Mamin Took Part in the UN Climate Change Conference (COP26) in Glasgow, Reaffirming the Country’s Commitment to the Global Climate Change Agenda. 2021. Available online: https://www.gov.kz/memleket/entities/mfa-zagreb/press/news/details/278599?lang=en#:~:text=Kazakhstan%20signed%20the%20Paris%20Agreement%20on%20November%204%2C%202016 (accessed on 6 December 2016).
- Ministry of Energy of Republic of Kazakhstan. Development of Renewable Energy Sources. 2023. Available online: https://www.gov.kz/memleket/entities/energo/activities/4910?lang=en (accessed on 6 December 2016).
- Glover, D.; Overbye, T.; Sarma, M. Power System Analysis and Design, 6th ed.; Cengage Learning: Boston, MA, USA, 2015. [Google Scholar]
- Makolo, P.; Zamora, R.; Lie, T. The role of inertia for grid flexibility under high penetration of variable renewables—A review of challenges and solutions. Renew. Sustain. Energy Rev. 2021, 147, 111223. [Google Scholar] [CrossRef]
- Australian Energy Market Operator (AEMO). Black System South Australia. 28 September 2016; AEMO: Melbourne, Australia, 2017. [Google Scholar]
- Australian Energy Market Operator (AEMO). Final Report–Queensland and South Australia System Separation on 25 August 2018; AEMO: Melbourne, Australia, 2019. [Google Scholar]
- Wu, X.; Dai, J.; Tang, Y.; Xue, F. Adaptive under-frequency load shedding scheme forpower systems with high wind power penetrationconsidering operating regions. IET Gener. Trans. Dist. 2022, 16, 4400–4416. [Google Scholar] [CrossRef]
- Miller, N.W. Keeping It Together: Transient Stability in a World of Wind and Solar Generation. IEEE Power Energy Mag. 2015, 13, 31–39. [Google Scholar] [CrossRef]
- Papadopoulos, P.N.; Milanovic, J.V. Probabilistic Framework for Transient Stability Assessment of Power Systems with High Penetration of Renewable Generation. IEEE Trans. Power Syst. 2017, 32, 3078–3088. [Google Scholar] [CrossRef]
- Kawabe, K.; Tanaka, K. Impact of Dynamic Behavior of Photovoltaic Power Generation Systems on Short-Term Voltage Stability. Power Syst. IEEE Trans. 2015, 30, 3416–3424. [Google Scholar] [CrossRef]
- Ovcharenko, N. Avtomatika Elekricheskih Stancyi i Elektroenergeticheskih Sistem [Automation of Electrical Stations and Power Systems]; NC ENAS: Moscow, Russia, 2000; 503p, ISBN 5-93196-020-1. [Google Scholar]
- Naik, P.; Nair, N.; Swain, A. Impact of reduced inertia on transient stability of networks with asynchronous generation. Int. Trans. Electr. Energy Syst. 2015, 26, 175–191. [Google Scholar] [CrossRef]
- Liu, S.; Li, G.; Zhou, M. Power System Transient Stability Analysis with Integration of DFIGs Based on Center of Inertia. CSEE J. Power Energy Syst. 2016, 2, 20–29. [Google Scholar] [CrossRef]
- He, C.; He, X.; Geng, H.; Sun, H.; Xu, S. Transient Stability of Low-Inertia Power Systems with Inverter-Based Generation. IEEE Trans. Energy Convers. 2022, 37, 2903–2912. [Google Scholar] [CrossRef]
- Ulbig, A.; Theodor, S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation. IFAC Proc. Vol. 2014, 47, 7290–7297. [Google Scholar] [CrossRef]
- Collados-Rodriguez, C.; Cheah-Mane, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability Analysis of Systems with High VSC Penetration: Where is the Limit? IEEE Trans. Power Deliv. 2020, 35, 2021–2031. [Google Scholar] [CrossRef]
- Collados-Rodriguez, C.; Cheah-Mane, M.; Prieto-Araujo, E.; Gomis-Bellmunt, O. Stability and operation limits of power systems with high penetration of power electronics. Int. J. Electr. Power Energy Syst. 2022, 138, 107728. [Google Scholar] [CrossRef]
- Vittal, E.; O’Malley, M.; Keane, A. Rotor Angle Stability with High Penetrations of Wind Generation. IEEE Trans. Power Syst. 2012, 27, 353–362. [Google Scholar] [CrossRef]
- Edrah, M.; Lo, K.; Anaya-Lara, O. Impacts of High Penetration of DFIG Wind Turbines on Rotor Angle Stability of Power Systems. IEEE Trans. Sustain. Energy 2015, 6, 759–766. [Google Scholar] [CrossRef]
- Tina, G.; Maione, G.; Licciardello, S. Evaluation of Technical Solutions to Improve Transient Stability in Power Systems with Wind Power Generation. Energies 2022, 15, 7055. [Google Scholar] [CrossRef]
- Wu, X.; Xu, A.; Zhao, J.; Deng, H.; Xu, P. Review on transient stability prediction methods based on real time wide-area phasor measurements. In Proceedings of the 4th International Conference Electric Utility Deregulation Restructuring Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 320–326. [Google Scholar] [CrossRef]
- Min, D.; Kim, S.J.; Seo, S.; Moon, Y.H.; Sun, K.; Chow, J.H.; Hur, K. Computing safety margins of a generation rejection scheme: A framework for online implementation. IEEE Trans. Smart Grid 2018, 9, 2337–2346. [Google Scholar] [CrossRef]
- Suprême, H.; Dessaint, L.A.; Kamwa, I.; Heniche-Oussédik, A. Development of new predictors based on the concept of center of power for transient and dynamic instability detection. IEEE Trans. Smart Grid 2018, 9, 3605–3615. [Google Scholar] [CrossRef]
- Paul, A.; Kamwa, I.; Joos, G. PMU signals responses-based RAS for instability mitigation through on_the _y identi_cation and shedding of the run-away generators. IEEE Trans. Power Syst. 2020, 35, 1707–1717. [Google Scholar] [CrossRef]
- Schmietendorf, K.; Peinke, J.; Friedrich, R.; Kamps, O. Selforganized synchronization and voltage stability in networks of synchronous machines. Eur. Phys. J. Spec. Top. 2014, 2592, 2577–2592. [Google Scholar] [CrossRef]
- Shi, L.; Dai, S.; Ni, Y.; Yao, L.; Bazargan, M. Transient stability of power systems with high penetration of DFIG based wind farms. In Proceedings of the 2009 IEEE Power & Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar]
- JSC “Kazakhstan Electricity Grid Operating Company” (KEGOC). National Power System. 2023. Available online: https://www.kegoc.kz/en/electric-power/natsionalnaya-energosistema/ (accessed on 9 July 2004).
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- PowerWorld Corporation. Machine Model WT3G1. 2023. Available online: https://www.powerworld.com/WebHelp/Content/TransientModels_HTML/Machine%20Model%20WT3G1.htm?tocpath=Transient%20Stability%20Add-On%20(TS)%7CTransient%20Models%7CGenerator%7CMachine%7C_____48 (accessed on 17 March 2023).





| Station Name | Generator | Nominal Capacity (MVA) | Moment of Inertia (kg m2) | Transient Reactance (pu) | Synchronous Reactance (pu) |
|---|---|---|---|---|---|
| Station 1 75 MW | G-1 | 40 | 1350 | 0.231 | 2.458 |
| G-2 | 40 | 1350 | 0.231 | 2.458 | |
| G-3 | 40 | 1350 | 0.231 | 2.458 | |
| Station 2 630 MW | G-1 | 75 | 2400 | 0.291 | 2.043 |
| G-2 | 75 | 2400 | 0.291 | 2.043 | |
| G-3 | 75 | 2400 | 0.291 | 2.043 | |
| G-4 | 125 | 3250 | 0.278 | 1.91 | |
| G-5 | 75 | 2400 | 0.291 | 2.043 | |
| G-6 | 75 | 2400 | 0.291 | 2.043 | |
| G-8 | 78.75 | 2400 | 0.302 | 1.91 | |
| G-9 | 78.75 | 2400 | 0.302 | 1.91 | |
| G-10 | 125 | 3250 | 0.278 | 1.91 | |
| Station 3 625 MW | G-1 | 235 | 6250 | 0.32 | 1.9 |
| G-2 | 241 | 6250 | 0.34 | 2 | |
| G-3 | 259 | 5280 | 0.3 | 2.32 |
| Generator/Station | Transient Reactance per Unit (pu) | Synchronous Reactance per Unit (pu) | Equivalent Inertial Constant (s) at Sbasis = 100 MVA |
|---|---|---|---|
| Station 1 | j0.3267 | j2.307 | 1.998 |
| Station 2 | j0.0544 | j0.27 | 11.5 |
| G-1 Station 3 | j0.136 | j0.807 | 3.083 |
| G-2 Station 3 | j0.141 | j0.829 | 3.081 |
| G-3 Station 3 | j0.116 | j0.897 | 2.604 |
| Unified Power System | j0.13 | j0.913 | 25 |
| “From” Bus Name | “To” Bus Name | Circuit | Nominal Operating Voltage (kV) | Impedance per Unit (Sbase = 100 MVA) |
|---|---|---|---|---|
| Station 1 110 kV | Station 2 110 kV | 1 | 110 | 0.023 + j0.0415 |
| Station 1 110 kV | Station 2 110 kV | 2 | 110 | 0.023 + j0.0415 |
| Station 2 110 kV | Substation 3 | 1 | 110 | 0.007 + j0.026 |
| Station 2 110 kV | Substation 3 | 2 | 110 | 0.007 + j0.026 |
| Substation 3 | Station 3 110 kV | 1 | 110 | 0.007 + j0.027 |
| Substation 3 | Station 3 110 kV | 2 | 110 | 0.007 + j0.027 |
| Station 2 110 kV | Station 3 110 kV | 1 | 110 | j0.0005 |
| Station 2 110 kV | Substation 1 | 1 | 110 | 0.089 + j0.222 |
| Station 2 110 kV | Substation 1 | 2 | 110 | 0.089 + j0.222 |
| Substation 1 | Substation 2 | 1 | 110 | 0.102 + j0.192 |
| Substation 1 | Substation 2 | 2 | 110 | 0.102 + j0.192 |
| Station 3 220 kV | Substation 2 | 1 | 220 | 0.033 + j0.106 |
| Station 3 220 kV | Substation 2 | 2 | 220 | 0.033 + j0.106 |
| Station 3 220 kV | Substation 4 | 1 | 220 | 0.073 + j0.322 |
| Station 3 220 kV | Substation 4 | 2 | 220 | 0.073 + j0.322 |
| “From” Bus Name | “To” Bus Name | Operating Name of Autotransformer (AT) | Reactance per Unit |
|---|---|---|---|
| Station 3 110 kV | Station 3 220 kV | AT-1 | j0.0489 |
| Station 2 110 kV | Station 3 220 kV | AT-2 | j0.049 |
| Substation 2 220 kV | Substation 2 110 kV | AT-1 | j0.0428 |
| Substation 2 220 kV | Substation 2 110 kV | AT-2 | j0.0428 |
| G-1 | Station 3 110 kV | AT-1 | j0.0419 |
| G-2 | Station 3 220 kV | AT-2 | j0.0488 |
| G-3 | Station 3 220 kV | AT-3 | j0.04797 |
| Bus Name | Active Load (MW) | Reactive Load (MVar) |
|---|---|---|
| Station 1 110 kV | 20 | 10 |
| Station 2 110 kV | 100 | 48 |
| Substation 3 110 kV | 100 | 48 |
| Station 3 220 kV | 35 | 40 |
| Substation 1 110 kV | 100 | 62 |
| Substation 2 110 kV | 80 | 39 |
| Substation 4 220 kV | 31 | 19 |
| Total Load | 466 | 266 |
| Generator | Active Power Dispatch (MW) | Voltage (per Unit) |
|---|---|---|
| Station 1 | 75 | 1.05 |
| Station 2 | 250 | 1.09 |
| G-1 Station 3 | 20 | 1.09 |
| G-2 Station 3 | 20 | 1.09 |
| G-3 Station 3 | 20 | 1.09 |
| Unified Power System | 90 | 1 |
| Total Generation | 475 |
| Scenario | Action | Time (s) | Location |
|---|---|---|---|
| Scenario 1–4 | Apply a three-phase short circuit | 1 | Line 1 220 kV at Station 3–Substation 4, 0.5% away from Station 3 |
| Open the circuit breakers | 1.06 | At both sides of the faulted line | |
| Close the circuit breakers via the auto-reclose scheme | 4.06 | ||
| Open the circuit breakers | 4.12 | ||
| Scenario 5 | Close the circuit breakers via the auto-reclose scheme | 5.06 | |
| Open the circuit breakers | 5.12 | ||
| Scenario 6 | Close the circuit breakers via the auto-reclose scheme | 4.06 | |
| Open the circuit breakers | 4.12 | ||
| Reduce the load by 20 MW | 4.2 | Substation 2 Bus 110 kV |
| H (s) | P (MW) | T (s) | LS (MW) | ND |
|---|---|---|---|---|
| 6.16 | 40 | 3.5 | 0 | - |
| 60 | 4.5 | 0 | ||
| 80 | 5.5 | 0 | ||
| 100 | 20 | |||
| 120 | 40 | |||
| 140 | 6 | 40 | ||
| 160 | 80 | |||
| 180 | 120 | |||
| 200 | 200 | |||
| 220 | - | - | + | |
| 240 |
| H (s) | P (MW) | T (s) | LS (MW) | ND |
|---|---|---|---|---|
| 3.16 | 20 | 4.5 | 60 | - |
| 30 | 80 | |||
| 40 | 5.5 | 60 | ||
| 50 | 100 | |||
| 60 | 6.5 | 80 | ||
| 70 | 100 | |||
| 80 | 150 | |||
| 90 | - | - | + |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aisayev, Y.; Tergemes, K.; Zhauyt, A.; Sheryazov, S.; Bakenov, K. The Impact of Replacing Synchronous Generators with Renewable-Energy Technologies on the Transient Stability of the Mangystau Power System: An Introduction to Flexible Automatic Dosage of Exposures. Energies 2024, 17, 2314. https://doi.org/10.3390/en17102314
Aisayev Y, Tergemes K, Zhauyt A, Sheryazov S, Bakenov K. The Impact of Replacing Synchronous Generators with Renewable-Energy Technologies on the Transient Stability of the Mangystau Power System: An Introduction to Flexible Automatic Dosage of Exposures. Energies. 2024; 17(10):2314. https://doi.org/10.3390/en17102314
Chicago/Turabian StyleAisayev, Yerzhan, Kazhybek Tergemes, Algazy Zhauyt, Saken Sheryazov, and Kairat Bakenov. 2024. "The Impact of Replacing Synchronous Generators with Renewable-Energy Technologies on the Transient Stability of the Mangystau Power System: An Introduction to Flexible Automatic Dosage of Exposures" Energies 17, no. 10: 2314. https://doi.org/10.3390/en17102314
APA StyleAisayev, Y., Tergemes, K., Zhauyt, A., Sheryazov, S., & Bakenov, K. (2024). The Impact of Replacing Synchronous Generators with Renewable-Energy Technologies on the Transient Stability of the Mangystau Power System: An Introduction to Flexible Automatic Dosage of Exposures. Energies, 17(10), 2314. https://doi.org/10.3390/en17102314






