Reviewing Control Paradigms and Emerging Trends of Grid-Forming Inverters—A Comparative Study

Abstract

Grid-forming inverters (GFMs) have emerged as crucial components in modern power systems, facilitating the integration of renewable energy sources and enhancing grid stability. The significance of GFMs lies in their ability to autonomously establish grid voltage and frequency, enabling grids to form and improve system flexibility. Discussing control methods for grid-forming inverters is paramount due to their crucial role in shaping grid dynamics and ensuring reliable power delivery. This paper explores the fundamental and advanced control methods employed by GFMs, explaining their operational principles and performance characteristics. Basic control methods typically involve droop control, voltage and frequency regulation, and power-balancing techniques to maintain grid stability under varying operating conditions. Advanced control strategies encompass predictive control, model predictive control (MPC), and adaptive control, which influence advanced algorithms and real-time data for enhanced system responsiveness and efficiency. A detailed analysis and performance comparison of different control methods for GFM is presented, highlighting their strengths, limitations, and suitability for diverse grid environments. Through comprehensive studies, this research interprets the ability of various control strategies to mitigate grid disturbances, optimize power flow, and enhance overall system stability.

1. Introduction

Grid-connected inverters play a pivotal role in renewable energy systems, making them suitable for integration with the electrical grid. These inverters employ sophisticated control algorithms that meet grid specifications. They must adhere to stringent grid codes and standards to ensure compliance with voltage and frequency requirements, as well as power quality criteria. Grid-following inverters are designed to synchronize their output with the voltage and frequency of the grid they are connected to. Employing control algorithms like phase-locked loops (PLLs) or frequency-locked loops, these inverters track grid parameters and adjust their output accordingly. While effective in maintaining synchronization, grid-following inverters may encounter challenges with voltage and frequency regulation during grid disturbances, potentially leading to stability issues and grid instability, particularly in scenarios with high renewable energy penetration or weak grid conditions [1,2,3].

A specialized category of inverters that actively contribute to grid stability by adjusting their reactive power output in response to changes in grid voltage is termed grid-supporting inverters. These inverters utilize control strategies like voltage droop control to provide reactive power support during voltage fluctuations. However, implementing reactive power control adds complexity and cost to the system, and interoperability issues with existing grid infrastructure may arise. Additionally, the effectiveness of grid-supporting inverters may be limited in certain grid conditions or configurations, impacting their suitability for widespread deployment [3]. Despite their grid-stabilizing capabilities, grid-supporting inverters have drawbacks that can hinder their widespread adoption. The control causes increased system complexity and potential compatibility issues with grid standards and their effectiveness may be limited in certain grid conditions [4].

Grid-forming inverters represent a significant advancement in inverter technology, offering autonomous control of grid voltage and frequency. Unlike grid-following inverters, which rely on grid parameters for synchronization, grid-forming inverters establish and maintain grid stability independently. By providing a stable grid reference point, grid-forming inverters enhance system resilience and flexibility, enabling seamless integration of renewable energy sources and enhancing grid reliability. Overall, grid-forming inverters offer enhanced grid stability and resilience, reducing reliance on external grid signals and simplifying system design and operation compared to grid-following and grid-supporting inverters. This is why they are chosen for further study [1,2,3,4].

The development of GFM gained momentum in the late 2000s and early 2010s. Researchers, universities, and companies worldwide have undertaken extensive research and development efforts to design and implement grid-forming inverter technology. This effort has involved control algorithms, power electronics, and system integration innovations. From 2015 to 2018, significant progress was achieved in developing grid-forming technologies, a transformative approach to power system control, allowing inverters to mimic traditional synchronous generators and participate in grid stability and voltage regulation. They use advanced control algorithms to regulate voltage magnitude and frequency, allowing inverters to synchronize with the grid autonomously [5,6,7,8,9].

Researchers explore the feasibility and potential benefits of grid-forming technology, laying the foundation for subsequent advancements. From 2019 to 2021, prototype testing and field trials of GFM were conducted across various renewable energy projects and microgrids. These trials provided valuable insights into real-world performance and identified challenges to address for broader implementation [10,11,12,13]. In 2022, commercialization efforts intensified as GFM started to enter the market. Companies focused on refining product designs, optimizing performance, and ensuring compliance with industry standards, marking a significant milestone in the technology’s evolution. Recent updates and advances in grid-forming inverter technology, from 2022 to 2024, reflect increased adoption in renewable energy projects, microgrids, and remote communities [14,15]. Their capability to stabilize power systems and operate independently of the grid has garnered interest from utilities and energy stakeholders. As of 2023–2024, ongoing research endeavors aim to enhance further grid-forming inverter technology’s efficiency, reliability, and scalability.

The evolution of GFM has been intricately connected with developing and refining control methods. Researchers embarked on a quest to devise control strategies capable of addressing the unique challenges posed by these innovative technologies. The historical trajectory from the inception of GFM to its current state reflects a continuous pursuit of enhanced performance, stability, and adaptability. From voltage and frequency regulation to virtual synchronous generator (VSG) control and droop schemes, these methodologies represent the culmination of years of research and experimentation aimed at unlocking the full potential of GFM [4,16]. Figure 1 illustrates the classification of grid-forming inverter control strategies, and Table 1 thoroughly analyzes various control methods employed in grid-forming inverters. The table concisely compares these control methods’ essential features, advantages, and limitations.

Generally speaking, the control methods listed in Table 1 are in chronological order. The first control method developed in GFM space is the virtual synchronous generator (VSG) control, which emulates the dynamics of synchronous generators by regulating the output voltage and frequency. While it improves the grid stability with inertia emulation, it cannot fully replicate the inertial response of synchronous generators. Frequency and voltage droop control (FVD) was introduced to address this. It can adjust output power and voltage in response to grid frequency in a decentralized fashion. It is very effective in dampening frequency fluctuations and stabilizing the system voltage. However, the decentralized control approach and predetermined operating points are significant drawbacks of this approach. Model predictive control (MPC) and adaptive control algorithms (ACAs), developed more recently, can provide real-time dynamic control capability. This is a robust approach, as real-time control enables such systems to be constantly updated and improved. These systems require correct estimation of the system parameters. Should there be any mismatch between the estimated and actual parameters, these systems tend to lose accuracy. Finally, recent efforts have focused on creating Hierarchical Control Structures (HCSs) that combine the advantages of different control approaches. HCS approaches enable decentralized and adaptive control by utilizing extensive communication networks. Such systems are susceptible to communication problems [17,18] and cybersecurity issues [19,20] that need to be fully addressed.

Overall, GFM is imperative for successfully integrating renewable energy into the existing power grid, facilitating the transition to a more sustainable energy future. GFM offers advantages such as grid support during low or no grid voltage, active frequency and voltage regulation, and inertial response. GFMs can emulate inertia, providing an inertial response by controlling power output in response to frequency deviations. They can smoothly transition between grid-connected and islanded modes, providing a stable power supply [21,22,23,24]. This paper presents a comprehensive exploration, meticulously analyzing the various control mechanisms governing the operation of GFM and scrutinizing their pivotal roles in voltage and frequency regulation. This study delves into the advanced control techniques infused with artificial intelligence, showcasing their transformative potential in strengthening grid performance. This extends beyond mere analysis, as it underscores the profound significance of these control topologies within the dynamic landscape of power system operation.

Table 1. Features of grid-forming inverter control methods.

Control	Description	Limitations	Advantages
Virtual synchronous generator (VSG) [1,25,26,27]	Emulates the dynamics of synchronous generators by regulating the output voltage and frequency. It provides an inertial response during disturbances and stabilizes the grid.	Inertia emulation relies on control algorithms and energy storages, which may not fully replicate the inertial response of synchronous generators. Requires accurate modeling and parameter tuning to mimic synchronous generator behavior effectively. Scalability of VSG can be limited.	Grid stability improvement with inertia emulation. Suitable for standalone/grid-connected operation. It supports power flow in multi-voltage or multi-frequency networks. Fast response time.
Frequency and voltage droop control (FVDC) [25,28,29]	The decentralized control method adjusts output power and voltage in response to grid frequency and voltage deviations, mimicking the behavior of synchronous generators.	Based on predefined droop characteristics, which may not always perfectly match the dynamic requirements. Inherently exhibits overshoot and settling time characteristics during transient conditions. Droop control can interact with other grid control dynamics, leading to potential stability issues or oscillations. Influenced by network impedance, system inertia, and load dynamics.	Droop control operates on a decentralized principle. Dampen frequency fluctuations and stabilize grid voltage, Enables rapid response to grid events and dynamic load conditions. Emulate the inertial response of synchronous generators. Compatible with renewable energy integration
Model predictive control (MPC) [30,31]	The system uses mathematical models to predict system behavior and optimize control actions, offering adaptive and efficient operation under varying grid conditions.	Requires accurate system modeling and real-time measurements. Load variations can lead to model inaccuracies and prediction errors. Limited adaptability to dynamics. Noise, sensor inaccuracies, and communication delays can introduce uncertainty into the MPC control loop.	Enable grid-forming inverters to respond dynamically to grid conditions, load variations, and renewable energy-generation changes. MPC offers flexibility in control design and adaptability to diverse grid configurations.
Adaptive control algorithms (ACAs) [32,33]	The system adapts control parameters based on sensor feedback, ensuring stability and reliability in dynamic grid environments and offering flexibility and robustness.	Relies on accurately estimating system parameters and dynamics to adapt control strategies effectively. Increases the control parameters and system uncertainties. Vulnerable to modeling errors, system identification inaccuracies, and environmental condition variations.	Optimizes control actions in real-time, considering system dynamics, constraints, and objectives. Facilitates rapid response to grid events. Coordinated operation of multiple GFM, energy storage systems, and renewable energy resources.
Hierarchical Control Structures (HCSs)	Integrates multiple controls within a hierarchical framework, coordinating the operation of GFM and other grid assets, offering scalability and flexibility.	Requires coordination and communication among different control levels. Communication delays, network congestion, and bandwidth limitations can affect system responsiveness. Faces scalability challenges in dynamic and evolving grids. Depends on centralized control architectures.	Enables coordinated control. Facilitates optimized resource allocation and energy management across multiple hierarchical levels. Enables decentralized decision-making. Promotes compatibility between different control levels and subsystems within the grid.

Table 1. Features of grid-forming inverter control methods.

Control	Description	Limitations	Advantages
Virtual synchronous generator (VSG) [1,25,26,27]	Emulates the dynamics of synchronous generators by regulating the output voltage and frequency. It provides an inertial response during disturbances and stabilizes the grid.	Inertia emulation relies on control algorithms and energy storages, which may not fully replicate the inertial response of synchronous generators. Requires accurate modeling and parameter tuning to mimic synchronous generator behavior effectively. Scalability of VSG can be limited.	Grid stability improvement with inertia emulation. Suitable for standalone/grid-connected operation. It supports power flow in multi-voltage or multi-frequency networks. Fast response time.
Frequency and voltage droop control (FVDC) [25,28,29]	The decentralized control method adjusts output power and voltage in response to grid frequency and voltage deviations, mimicking the behavior of synchronous generators.	Based on predefined droop characteristics, which may not always perfectly match the dynamic requirements. Inherently exhibits overshoot and settling time characteristics during transient conditions. Droop control can interact with other grid control dynamics, leading to potential stability issues or oscillations. Influenced by network impedance, system inertia, and load dynamics.	Droop control operates on a decentralized principle. Dampen frequency fluctuations and stabilize grid voltage, Enables rapid response to grid events and dynamic load conditions. Emulate the inertial response of synchronous generators. Compatible with renewable energy integration
Model predictive control (MPC) [30,31]	The system uses mathematical models to predict system behavior and optimize control actions, offering adaptive and efficient operation under varying grid conditions.	Requires accurate system modeling and real-time measurements. Load variations can lead to model inaccuracies and prediction errors. Limited adaptability to dynamics. Noise, sensor inaccuracies, and communication delays can introduce uncertainty into the MPC control loop.	Enable grid-forming inverters to respond dynamically to grid conditions, load variations, and renewable energy-generation changes. MPC offers flexibility in control design and adaptability to diverse grid configurations.
Adaptive control algorithms (ACAs) [32,33]	The system adapts control parameters based on sensor feedback, ensuring stability and reliability in dynamic grid environments and offering flexibility and robustness.	Relies on accurately estimating system parameters and dynamics to adapt control strategies effectively. Increases the control parameters and system uncertainties. Vulnerable to modeling errors, system identification inaccuracies, and environmental condition variations.	Optimizes control actions in real-time, considering system dynamics, constraints, and objectives. Facilitates rapid response to grid events. Coordinated operation of multiple GFM, energy storage systems, and renewable energy resources.
Hierarchical Control Structures (HCSs)	Integrates multiple controls within a hierarchical framework, coordinating the operation of GFM and other grid assets, offering scalability and flexibility.	Requires coordination and communication among different control levels. Communication delays, network congestion, and bandwidth limitations can affect system responsiveness. Faces scalability challenges in dynamic and evolving grids. Depends on centralized control architectures.	Enables coordinated control. Facilitates optimized resource allocation and energy management across multiple hierarchical levels. Enables decentralized decision-making. Promotes compatibility between different control levels and subsystems within the grid.

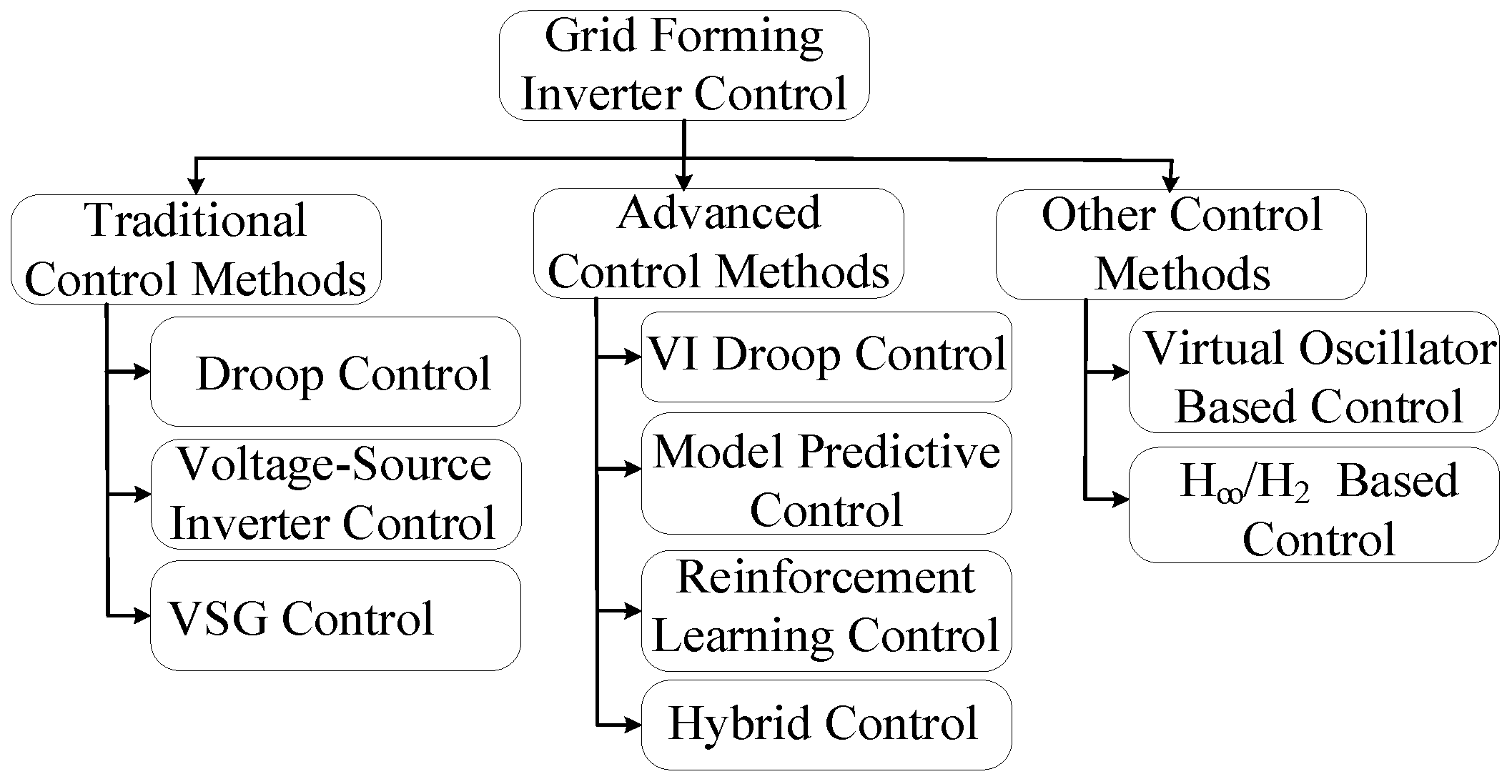
2. Control Strategies for Grid-Forming Inverters

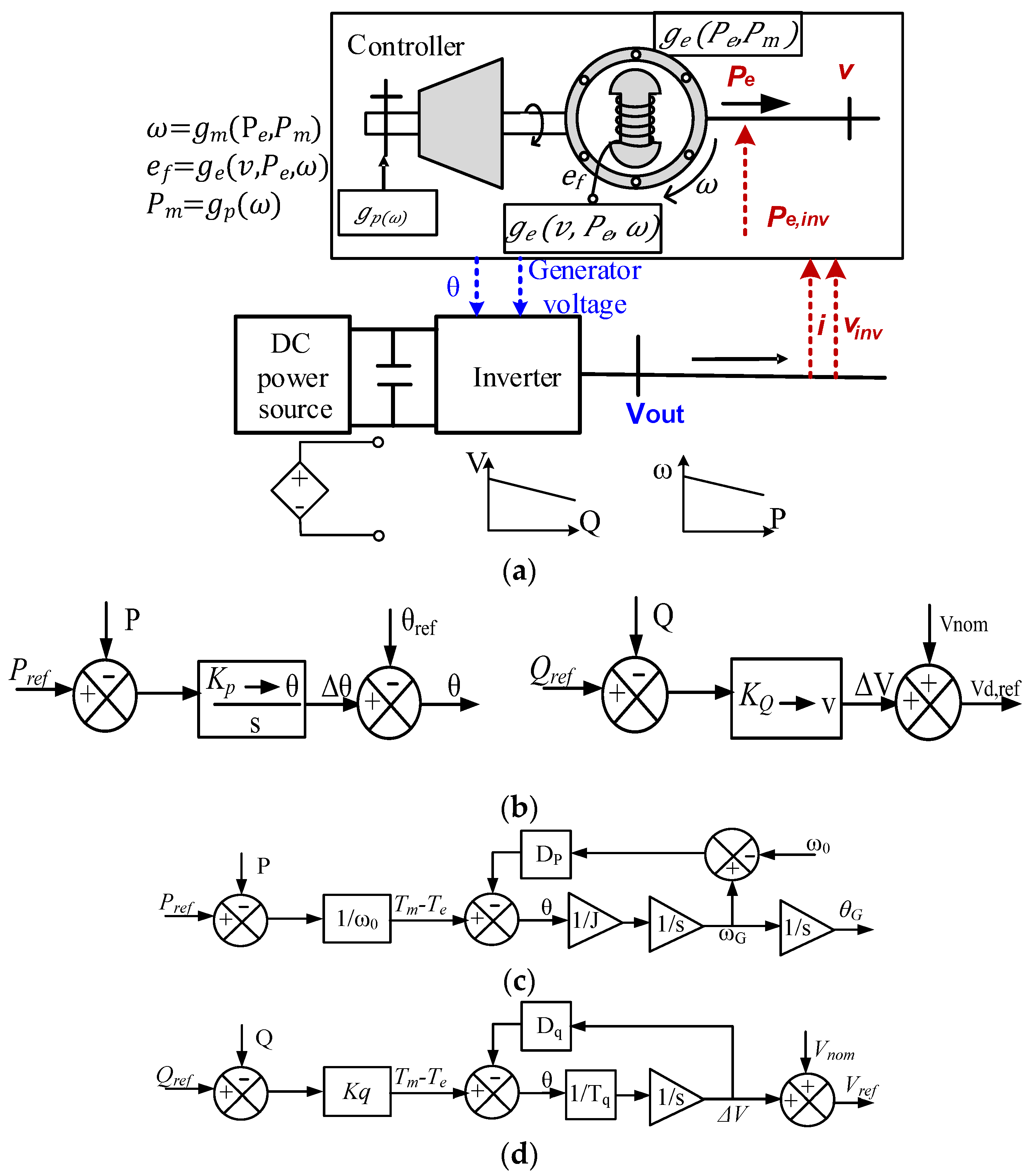
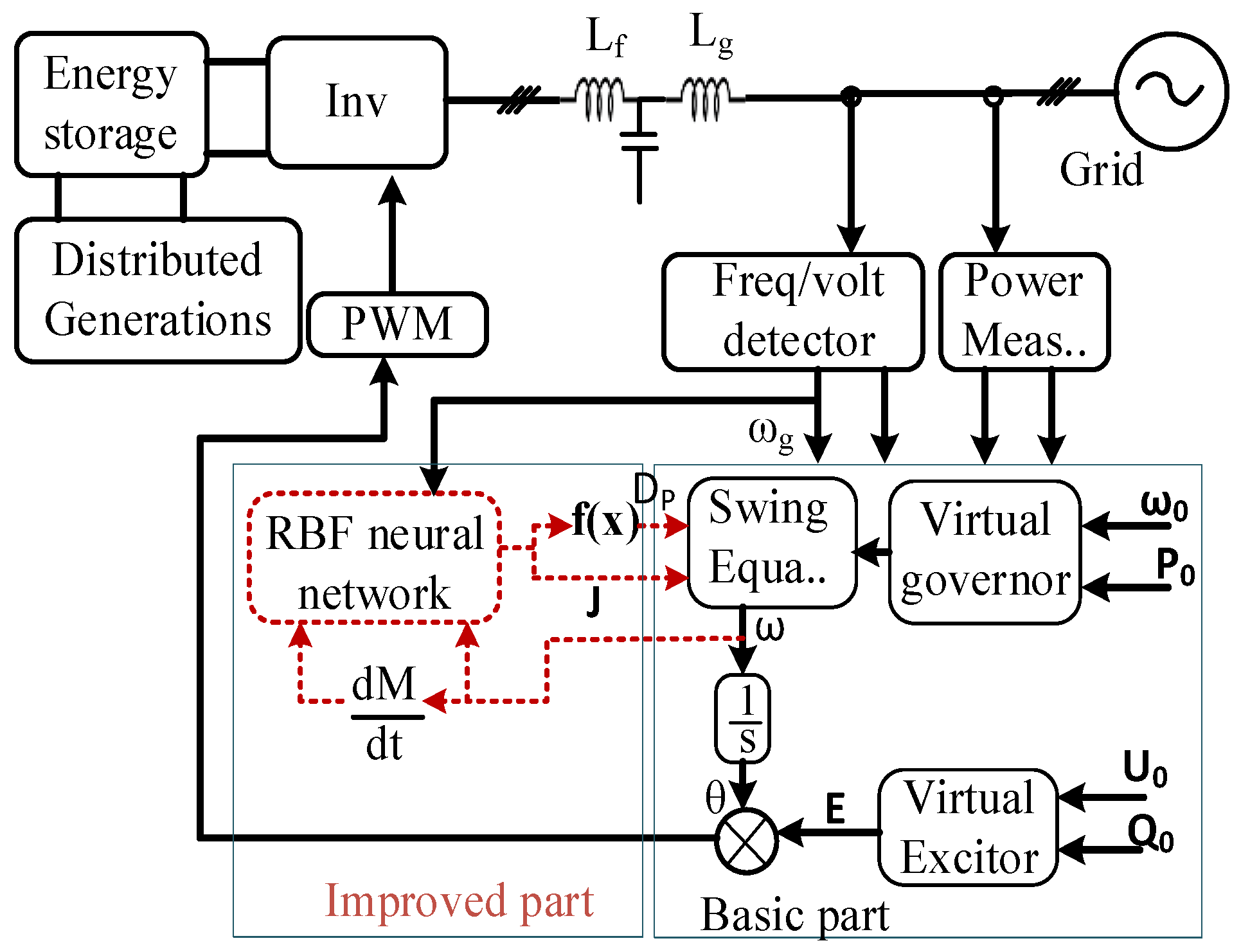
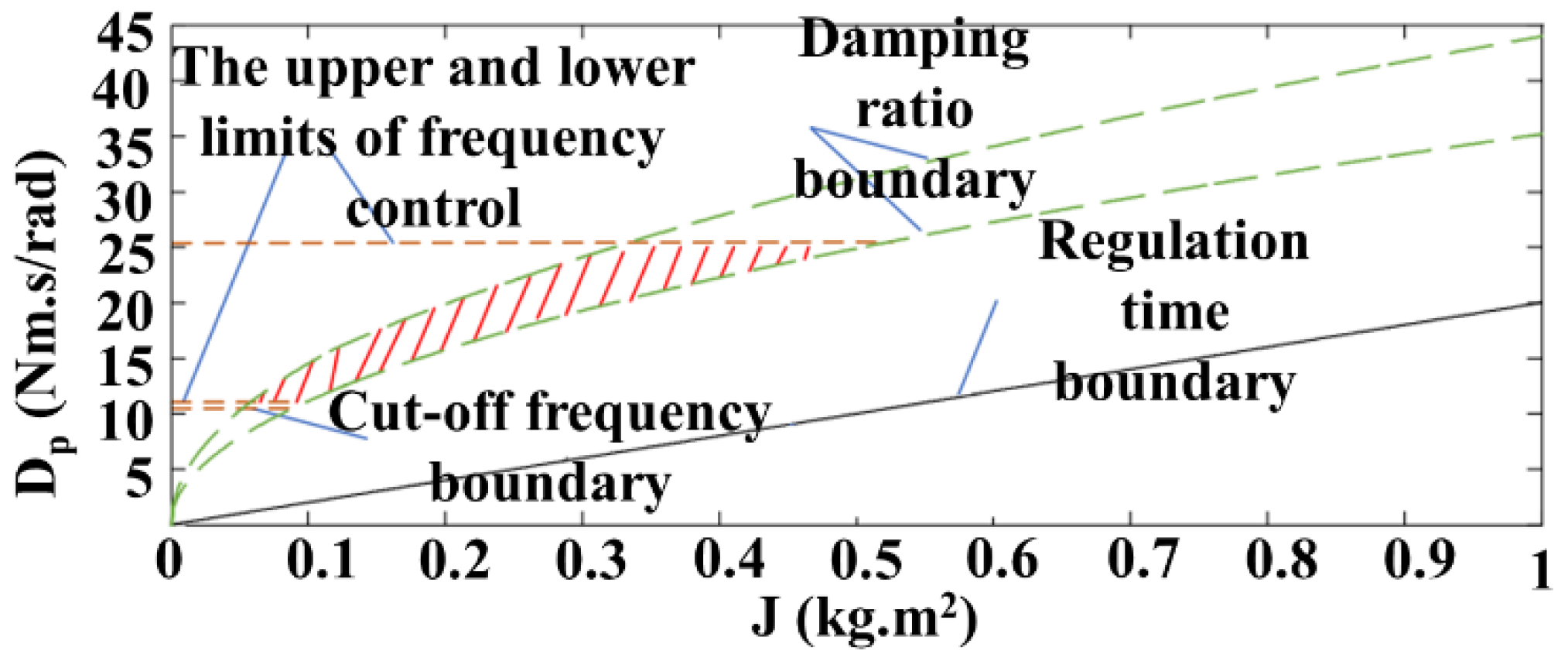
2.1. Virtual Synchronous Generator

The power system requirement is to match the load and generation for fixed-frequency operation. So, what happens if a generation is suddenly withdrawn from the system? The frequency will decline, but what if the system has lower inertia? Then, the inertia still supplies the load, which means that the system has a faster decline in frequency. It causes a higher rate of change in frequency. The swing equation mathematically describes this as a first-order differential Equation (1):

$$\frac{d\mathsf{\Delta }f}{dt}=\frac{f_n}{2{KE}_{sys}}\left(P_m-P_e\right)=\frac{f_n}{2{KE}_{sys}}\mathsf{\Delta }P$$

(1)

Load-damping effects can also be included explicitly in the swing Equation (14):

$$\frac{d\mathsf{\Delta }f}{dt}=\frac{f_n}{2{KE}_{sys}}(\mathsf{\Delta }P-D{P}_{load}\mathsf{\Delta }f)$$

(2)

where $\frac{d\mathsf{\Delta }f}{dt} \mathrm{i}\mathrm{s} \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e} \mathrm{o}\mathrm{f} \mathrm{c}\mathrm{h}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{e} \mathrm{i}\mathrm{n} \mathrm{f}\mathrm{r}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{y}, {KE}_{sys} \mathrm{i}\mathrm{s} \mathrm{s}\mathrm{y}\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{m} \mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{t}\mathrm{i}\mathrm{a},$ P_m is generation, P_e is load, and f_n is frequency.

$${KE}_{sys}=\frac{f_n}{2{\left.\frac{d\mathsf{\Delta }f}{dt}\right|}_{t=0}}\mathsf{\Delta }P$$

(3)

The disturbance and frequency must be instantaneously and accurately measured, and the change rate must be instantaneously measured. Frequency cannot be directly measured in power systems but can be estimated using voltage and current measurements. Methods like zero-crossing and phase-lock loop calculations are suitable for pure sine waves. The inverter-based power system does not have pure sine voltage and current waveforms.

Power electronic inverters can mimic synchronous machines’ inertial response for synthetic connection. For an inverter to provide synthetic inertia equivalent to typical inertia, it needs to act like a voltage source and form its voltage reference, i.e., be grid-forming instead of grid-following. The inverter is typically configured like a grid-forming device and then configured based on the classical synchronous machine model.

$$P_e=\frac{E{V}_g}{X_d^{\prime }}\mathrm{s}\mathrm{i}\mathrm{n} (\delta -\theta )$$

(4)

$$\frac{d\omega }{dt}=\frac{1}{2H}(P_m-P_e)$$

(5)

$$\frac{d\delta }{dt}=\omega$$

(6)

• A frequency disturbance in the system causes the grid voltage phase angle, θ, to change.
• A grid voltage phase angle change causes active power from inverter P_e to change according to (4).
• A change in P_e causes the inverter frequency ω and phase angle δ to change according to (5) and (6).
• A change in inverter phase δ causes active power P_e to change again as per (4).
• Go back to step iii until a new steady state is reached.

That is the grid-forming capability of the inverter, and thus, it works as an active power source to supply energy when power changes occur.

Operation of Inverters as Virtual Synchronous Generators

The load increase causes a reduction in generator speed. The governor controls speed by adjusting the valve position based on the rated MVA. Power reference is determined based on machine speed vs. actual power droop characteristics [16]. The reactive power demand increases, causing generator voltage to decrease from the nominal value. The voltage regulator increases field circuit excitation, causing a terminal voltage increase. Reactive power injection to the grid increases, while reduction leads to machine control loop reduction.

Grid frequency drops due to disturbances reducing grid voltage compared to generator terminal voltage phasors. This results in more real power, P, being fed to the grid due to the difference in machine and grid frequency. The synchronous generator supports the grid during under-frequency events. Grid-voltage sags (Q-control) due to disturbances reduce the voltage magnitude of grid voltage phasors compared to the generator’s voltage magnitude. This causes more Q to be fed to the grid, supporting the grid during voltage-sag disturbance events. The reverse is also true [25,34].

A GFM representing virtual machine is presented in Figure 2. Mechanically, the acceleration of the synchronous generator angle is governed by Equation (7):

$$\mathrm{J}\ddot{\mathsf{\theta }}={\mathrm{T}}_m-{\mathrm{T}}_{\mathrm{e}}-{\mathrm{D}}_{\mathrm{p}}\dot{\mathsf{\theta }}$$

(7)

J represents the moment of inertia of the rotating parts, T_m mechanical torque, T_e electrical torque and D_p is the damping factor due to friction. The electrical torque Te is derived in [35] as:

$${\mathrm{T}}_{\mathrm{e}}=M_{\mathrm{f}}{\mathrm{i}}_{\mathrm{f}}〈\mathrm{i},\widetilde{\mathrm{s}\mathrm{i}\mathrm{n}}\mathsf{\theta }〉$$

(8)

$$J\frac{d{\omega }_G}{dt}+D_p({\omega }_G-{\omega }_o)=\frac{1}{{\omega }_o}(P_m-P_e)=T_m-T_e$$

Inverter’s real and reactive powers are given in (9)–(11).

$$P={\dot{\mathsf{\theta }}M}_{\mathrm{f}}{\mathrm{i}}_{\mathrm{f}}〈\mathrm{i},\widetilde{\mathrm{s}\mathrm{i}\mathrm{n}}\mathsf{\theta }〉$$

(9)

$$Q=-{\dot{\mathsf{\theta }}M}_{\mathrm{f}}{\mathrm{i}}_{\mathrm{f}}〈\mathrm{i},\widetilde{\mathrm{c}\mathrm{o}\mathrm{s}}\mathsf{\theta }〉$$

(10)

$$e_q={\dot{\mathsf{\theta }}M}_{\mathrm{f}}{\mathrm{i}}_{\mathrm{f}}\widetilde{\mathrm{s}\mathrm{i}\mathrm{n}}\left(\mathsf{\theta }-\frac{\pi }{2}\right)={-\dot{\mathsf{\theta }}M}_{\mathrm{f}}{\mathrm{i}}_{\mathrm{f}}\widetilde{\mathrm{c}\mathrm{o}\mathrm{s}}\mathsf{\theta }$$

(11)

Generation of Inverter Angle: T_m is calculated by dividing a set reference value P_ref by the nominal speed. The T_m, generated T_e, and the $D_P\dot{\theta }$ are compared to generate the error. The error is integrated to generate the frequency. This speed $\dot{\theta }$ is the virtual speed generated in the controller. T_e is calculated using Equation (8) which depends on the controller’s virtual angle θ, virtual speed $\dot{\theta }$, phase current i, and signal M_f × i_f [36].

Generation of Inverter Voltage: The reactive power reference Q_ref, negative of the calculated reactive power Q_gap, and voltage drop term E₀-V_m are added to generate the excitation signal M_f × i_f. This excitation signal along with θ, generates a voltage signal.

Virtual Synchronous Generator Mode 1: VSG operates like a grid-following inverter, tracking real power reference. Higher P_ref leads to higher T_m, higher virtual frequency $\dot{\theta }$, which further leads to increasing machine angle $\theta$ concerning grid phase angle θ_G. If δ = θ − θ_G is the difference in phase angle between the machine and the grid, the power flow is governed by the well-known power flow (12).

$$P=\frac{3V_s{V}_{g}sin\delta }{2X}$$

(12)

The higher P means higher T_e, and therefore, the term T_e will subtract with T_m reducing the frequency of $\dot{\theta }$ until the inverter frequency becomes equal to the grid frequency again. However, increasing P_ref has already increased θ earlier, as discussed in the previous paragraph, so that P_ref = P, although the difference in frequencies is again zero. In fact, in a steady state, P_ref always remains equal to P because any difference in power will cause inverter frequency to vary, and inverter angle will vary correspondingly to make the power mismatch zero.

Virtual Synchronous Generator Mode 2: If Q_ref is more than the calculated Q supplied into the grid, the excitation signal M_f i_f is increased. So, an EMF signal of a larger magnitude will be applied to the PWM modulator. Hence, increasing Q_ref will increase E, and since the grid voltage is fixed, more Q will be supplied to the grid as per the (13).

$$\mathit{Q}=\frac{3\mathit{V}\mathit{g}}{2\mathit{X}}\left(\mathit{E}\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }-\mathit{V}\mathit{g}\right)$$

(13)

Since there is an integrator $\frac{1}{\mathit{K}\mathit{s}}$ with M_f i_f, the excitation signal M_f i_f will settle to a constant value when Q = Q_ref with correspondingly higher emf signal E as compared to the Q_ref was lower.

Virtual Synchronous Generator Mode 3: The inverter frequency always converges to the grid frequency. A lower grid frequency means a deviation between θ and θ_G because of the divergence between the inverter and grid frequency.

$$\mathsf{\delta }=\mathsf{\theta }-{\mathsf{\theta }}_{\mathit{G}}=\int (\dot{\mathit{\theta }}-{\dot{\mathit{\theta }}}_{\mathit{G}})\mathbf{d}\mathbf{t}$$

(14)

This results in high δ producing higher current, which results in higher T_e, which decreases inverter frequency close to grid frequency and vice versa. Therefore, T_e of the real power loop ensures the inverter frequency convergence to the grid frequency.

Virtual Synchronous Generator Mode 4: If the grid voltage magnitude deviates from the nominal value, the VSG provides support by exchanging reactive power to the grid. Lower grid voltage magnitude vm means higher ΔQ (positive), which increases M_f i_f, thereby increasing the emf E. Now Q should be equal to a higher value Qref + Q. Therefore, a Q higher than command Qref will be supplied to the grid, and vice versa is expected to increase the grid voltage above the nominal value.

VSC technology provides an inertial response, reducing the impact of sudden load changes on the grid. VSC facilitates renewable integration by offering grid-forming capabilities without external synchronization and plays a significant role in global energy transitions. However, virtual synchronous generator control necessitates intricate algorithms and accurate modeling to replicate synchronous generators’ behavior effectively. This complexity often led to challenges in real-time implementation and posed limitations in scalability and adaptability to varying grid conditions. Furthermore, particularly in large-scale deployment scenarios, this could result in delays or inefficiencies in control execution, potentially compromising grid stability and reliability.

In contrast, droop control emerged as a more practical and decentralized alternative to virtual synchronous generator control. Droop control simplifies control implementation by leveraging straightforward proportional–integral (PI) algorithms that adjust the inverter output power in response to grid voltage or frequency deviations. This simplicity reduces computational overhead and enhances system scalability.

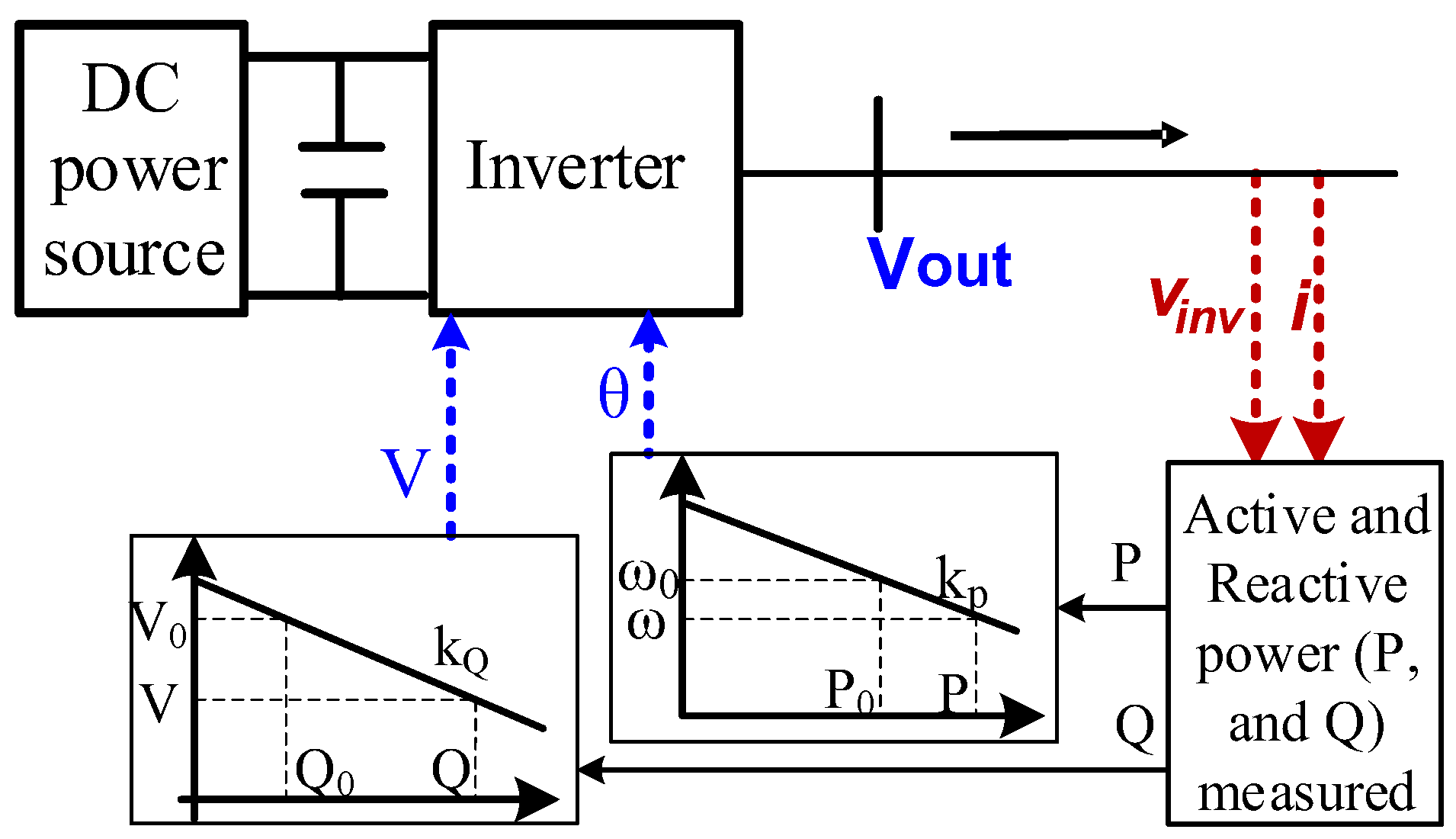
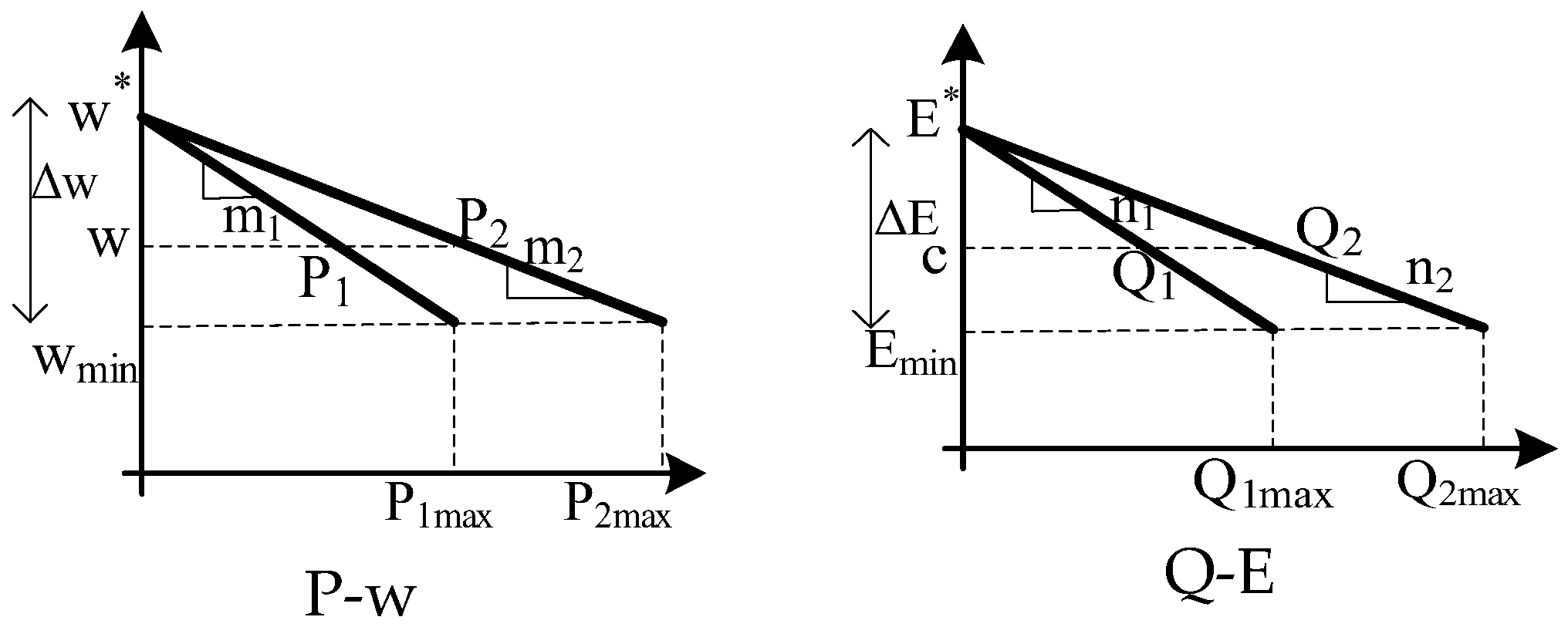
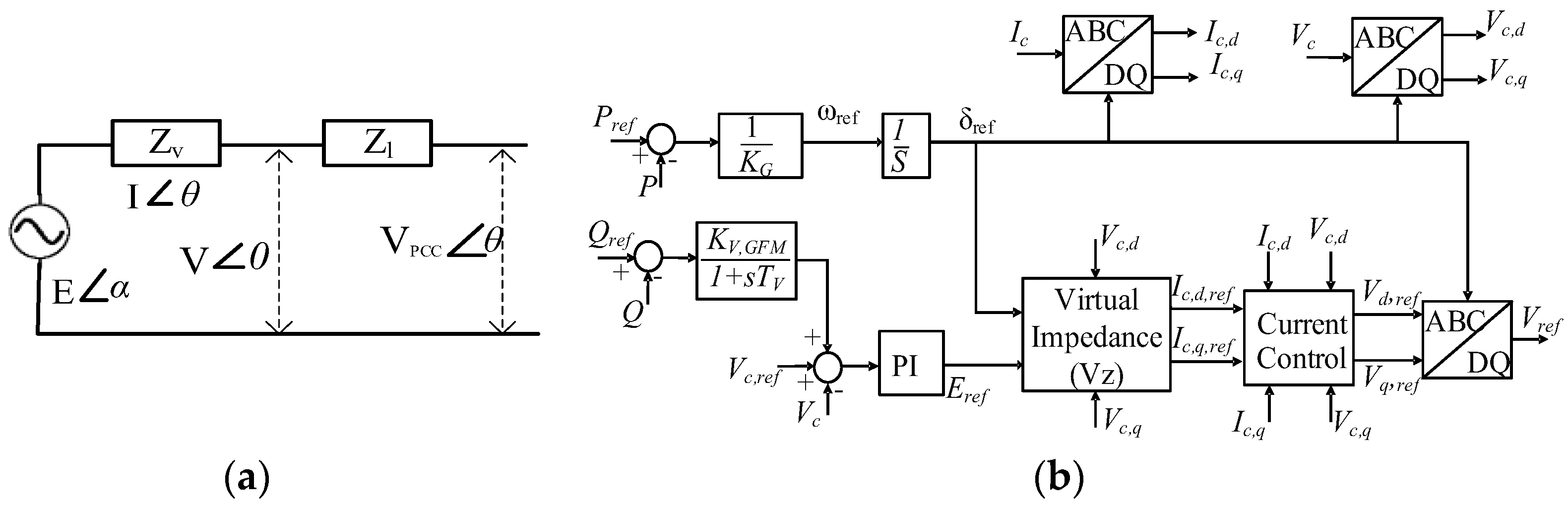
2.2. Droop Control

Droop control is a technique used in GFM to regulate output voltage and frequency. It adjusts the inverter’s output voltage or frequency in response to load or grid conditions changes, mimicking traditional synchronous generators. Figure 3 displays the inverter’s droop control functional diagram [17]. Common droop control involves linear voltage and frequency variations with reactive and active power [13,37].

Active and reactive power in a power system is given in (15)–(16). Vs, Vg, δ, R, and X are source voltage, grid voltage, phase of grid voltage, line resistance, and reactance, respectively [38].

$$\mathit{P}=\frac{\mathit{V}\mathit{s}}{{\mathit{R}}^2+{\mathit{X}}^2}[\mathit{R}\left(\mathit{V}\mathit{s}-\mathit{V}\mathit{g}\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }\right)+\mathit{X}\mathit{V}\mathit{g} \mathit{s}\mathit{i}\mathit{n}\mathit{\delta }]$$

(15)

$$\mathit{Q}=\frac{\mathit{V}\mathit{s}}{{\mathit{R}}^2+{\mathit{X}}^2}[-\mathit{R}\mathit{V}\mathit{g} \mathit{s}\mathit{i}\mathit{n}\mathit{\delta }+\mathit{X}\left(\mathit{V}\mathit{s}-\mathit{V}\mathit{g}\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }\right)]$$

(16)

$$\mathit{V}\mathit{g} \mathit{s}\mathit{i}\mathit{n}\mathit{\delta }=\frac{\mathit{X}\mathit{P}-\mathit{R}\mathit{Q}}{\mathit{V}\mathit{s}};\mathit{V}\mathit{s}-\mathit{V}\mathit{g}\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }=\frac{\mathit{R}\mathit{P}+\mathit{X}\mathit{Q}}{\mathit{V}\mathit{s}}$$

For a long transmission line: X>>R; R can be neglected without significant impact. Hence, $\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }\simeq 1 \mathit{a}\mathit{n}\mathit{d} \mathit{s}\mathit{i}\mathit{n}\mathit{\delta }\simeq \mathit{\delta }$.

$$\mathit{\delta }=\frac{\mathit{X}\mathit{P}}{\mathit{V}\mathit{g}\mathit{V}\mathit{s}}\mathrm{and}\mathit{V}\mathit{s}-\mathit{V}\mathit{g}=\frac{\mathit{X}\mathit{Q}}{\mathit{V}\mathit{s}}$$

(17)

Since P depends on $\mathit{\delta }$ (frequency) $\to$ control of frequency can be achieved by active power P; thus, change in f is controlled by changing P in Equation (18). Similarly, voltage difference depends on Q $\to$ controls of voltage, achieved by changing Q in Equation (19). These (18) and (19) are presented in Figure 3.

$$\mathit{f}-{\mathit{f}}_0=-{\mathit{k}}_{\mathit{p}}\left\{\mathit{P}-{\mathit{P}}_0\right\}$$

(18)

$${\mathit{V}}_{\mathit{s}}-{\mathit{V}}_{\mathit{g}}=-{\mathit{k}}_{\mathit{Q}}\left\{\mathit{Q}-{\mathit{Q}}_0\right\}$$

(19)

where k_P and k_Q are drooping coefficients.

The P-f and Q-V droop control govern the inverter’s internal voltage magnitude and phase angle, as depicted in Figure 3. Q₀ and P₀ are rated, and Q and P are measured values. k_p and k_Q are droop control coefficients. The P-f droop control ensures that several GFM’ phase angles are synchronized. Any disturbance increases the output power of one of the two GFMs operating in parallel under P-f droop control. As a result, the internal voltage’s angular frequency (ω) is decreased by its P-f droop control, reducing the phase angle (θ) and restricting the inverter from raising its output power further. When many GFMs operate simultaneously, the synchronization is ensured by this negative-feedback control technique. Additionally, load sharing amongst GFM is accomplished via the P-f droop control. The Q-V droop control uses a proportional-integral controller to regulate E_droop, ensuring that the amplitude of grid-side voltage has a preset Q-V droop characteristic [39].

But in the cases where we cannot ignore the effect of R, then we have P′ and Q′, which can be written as follows:

$$\left[\begin{array}{c}\mathit{P}\mathit{\prime }\\ \mathit{Q}\mathit{\prime }\end{array}\right]=\left[\begin{array}{cc}\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }& -\mathit{c}\mathit{o}\mathit{s}\mathit{\theta }\\ \mathit{c}\mathit{o}\mathit{s}\mathit{\theta }& \mathit{s}\mathit{i}\mathit{n}\mathit{\theta }\end{array}\right]\left[\begin{array}{c}\mathit{P}\\ \mathit{Q}\end{array}\right]=\left[\begin{array}{cc}\frac{\mathit{X}}{\mathit{Z}}& -\frac{\mathit{R}}{\mathit{Z}}\\ \frac{\mathit{R}}{\mathit{Z}}& \frac{\mathit{X}}{\mathit{Z}}\end{array}\right]\left[\begin{array}{c}\mathit{P}\\ \mathit{Q}\end{array}\right]$$

(20)

$$\mathit{s}\mathit{i}\mathit{n}\mathit{\delta }=\frac{\mathit{Z}\mathit{P}\mathit{\prime }}{\mathit{V}\mathit{s}\mathit{V}\mathit{g}};\mathit{V}\mathit{s}-\mathit{V}\mathit{g}\mathit{c}\mathit{o}\mathit{s}\mathit{\delta }=\frac{\mathit{Z}\mathit{Q}\mathit{\prime }}{\mathit{V}\mathit{s}}$$

Now, the droop in frequency will be as follows:

$$\mathit{f}-{\mathit{f}}_0=-{\mathit{k}}_{\mathit{p}}\left\{\mathit{P}\mathit{\prime }-{\mathit{P}}_0\right\}=-{\mathit{k}}_{\mathit{p}}\left\{\mathit{P}-{\mathit{P}}_0\right\}+{\mathit{k}}_{\mathit{p}}\frac{\mathit{R}}{\mathit{Z}}(\mathit{Q}-{\mathit{Q}}_0)$$

(21)

$${\mathit{V}}_{\mathit{s}}-{\mathit{V}}_{\mathit{g}}=-{\mathit{k}}_{\mathit{Q}}\left\{{\mathit{Q}}^{\mathit{\prime }}-{\mathit{Q}}_0\right\}=-{\mathit{k}}_{\mathit{Q}}\frac{\mathit{R}}{\mathit{Z}}\left\{\mathit{P}-{\mathit{P}}_0\right\}-{\mathit{k}}_{\mathit{Q}}\frac{\mathit{X}}{\mathit{Z}}(\mathit{Q}-{\mathit{Q}}_0)$$

(22)

Figure 4 shows the power influence on frequency and voltage across impedance ratios. The impedances of the two inverters can be unequal, so the power flow is not uniform. Earlier, only P controls frequency; but here P and Q both.

The two parallel connected inverters’ drooping characteristics are shown in Figure 5, with their droop making m1 and m2 [39]. The control technique makes these droops equal. That can be achieved by following steps:

• Sense the inverter’s output current and voltage.
• Calculate P and Q values; m corresponds to k_P, and n corresponds to k_Q
• E* and ω* are rated values; find the voltage and frequency error signal here.
• Generate E sin(ωt), which generates PWM signals for the current and voltage loops.

In this way, V and f are controlled.

Inverter 2 may have different m and n. Increasing m and n values (k_P and k_Q) degrades the voltage regulation, though the power sharing is improved. So, there should be a careful selection of droop coefficients. There are some drawbacks with this droop control of the inverters.

• Slow response and a trade-off between voltage regulation and load power-sharing.
• If harmonics are present in the load, the performance will be degraded.
• If there is a line impedance mismatch, one will be overloaded, and the other will be underloaded, meaning that power sharing will not be equal.
• Conventional droop control does not work with renewable energy, as it constantly changes.

So, to avoid these drawbacks, a modified strategy based on virtual impedance improves unequal power distribution by adjusting droop parameters. In the analysis of virtual impedance control strategies, Figure 6a illustrates the concept of virtual impedance with the inverter impedance, while Figure 6b depicts the implementation of virtual impedance loop-based droop control. The line impedance of each inverter will be different, so we must ensure that the droop coefficient is equal for all, possibly by increasing the virtual impedance.

$${\mathit{V}}_{\mathit{d}\mathit{r}\mathit{o}\mathit{o}\mathit{p}1}=\left[{\mathit{Z}}_{\mathit{l}1}+{\mathit{Z}}_{\mathit{v}1}\right]{\mathit{I}}_{\mathit{l}1}={\mathit{V}}_{\mathit{d}\mathit{r}\mathit{o}\mathit{o}\mathit{p}2}=\left[{\mathit{Z}}_{\mathit{l}2}+{\mathit{Z}}_{\mathit{v}2}\right]{\mathit{I}}_{\mathit{l}2}$$

(23)

For different inverters, ${\mathit{V}}_{\mathit{d}\mathit{r}\mathit{o}\mathit{o}\mathit{p}1}={\mathit{V}}_{\mathit{d}\mathit{r}\mathit{o}\mathit{o}\mathit{p}2}=..{=\mathit{V}}_{\mathit{d}\mathit{r}\mathit{o}\mathit{o}\mathit{p}1\mathit{n}}$.

Z_l1 is the impedance offered by the first inverter, and Z_v1 is the virtual impedance inserted in the network of the first inverter, and so on.

Practically, no impedance for control is implemented. To insert the impedance, 1st inverter is operated in master mode, and the remaining is in slave mode [40].

$${\mathit{Z}}_{\mathit{v}1}=0,{\mathit{Z}}_{\mathit{v}2}={\mathit{Z}}_{\mathit{l}1}-{\mathit{Z}}_{\mathit{l}2};$$

(24)

The output reference current can be calculated as follows (25):

$${\mathit{I}}_{\mathit{c},\mathit{r}\mathit{e}\mathit{f}}=\frac{{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}-{\mathit{V}}_{\mathit{c}}}{{\mathit{r}}_{\mathit{v}\mathit{i}\mathit{r}}+\mathit{j}{\mathit{x}}_{\mathit{v}\mathit{i}\mathit{r}}}$$

(25)

where Vc is the measured voltage at the interface point of the inverter. r_vir + x_vir is the virtual impedance. The system determines the current reference on the d-q coordinate axis using Park’s transformation, using the internal voltage source’s voltage phase angle as a reference phase. This simplifies analysis and control by projecting variables onto the axis. The current reference is used to adjust the output current of the IBR, regulated by a general current control system, to ensure the d-axis and q-axis currents align with reference values. The decoupling control mechanism ensures independence for each axis, allowing for precise control over d- and q-axis currents.

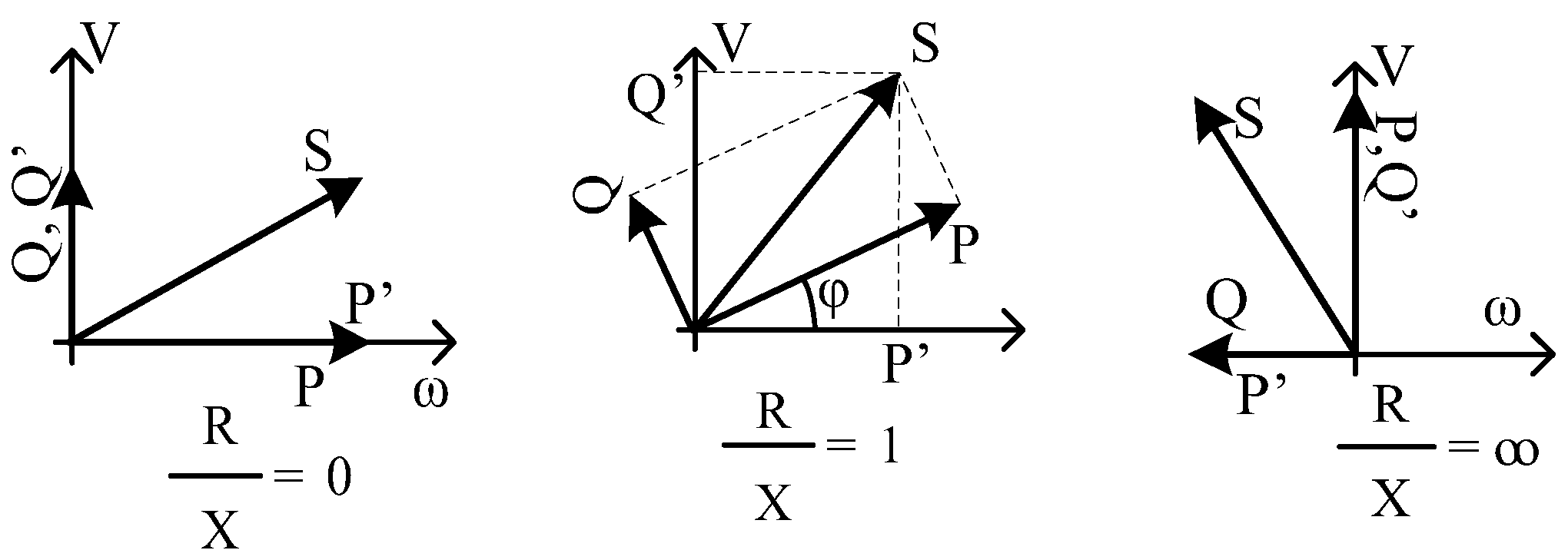
• Influence of Virtual impedance on the output voltage:

The relationship between Eref and Vref as determined by the virtual impedance control method [40]:

$$\mathit{V}\mathit{r}\mathit{e}\mathit{f}=\mathit{E}\mathit{r}\mathit{e}\mathit{f}-\mathit{Z}\mathit{v}\left(\mathit{s}\right)\mathit{i}$$

(26)

where Zv(s) is the transfer function of the virtual impedance of the inverter. Zv represents impedance characteristics, the reference voltage can be transformed into d-q as follows:

$${\mathit{V}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}={\mathit{E}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}-{\mathit{L}}_{\mathit{v}}\mathit{s}{\mathit{i}}_{\mathit{d}}+\mathbf{ꙍ}{\mathit{L}}_{\mathit{v}}{\mathit{i}}_{\mathit{q}}$$

(27)

$${\mathit{V}}_{\mathit{q}\_\mathit{r}\mathit{e}\mathit{f}}={\mathit{E}}_{\mathit{q}\_\mathit{r}\mathit{e}\mathit{f}}-{\mathit{L}}_{\mathit{v}}\mathit{s}{\mathit{i}}_{\mathit{q}}-\mathbf{ꙍ}{\mathit{L}}_{\mathit{v}}{\mathit{i}}_{\mathit{d}}$$

A change in voltage can be approximated [35] as follows:

$${\mathbf{\Delta }\mathit{V}=\mathit{V}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}-{\mathit{E}}_{\mathit{r}\mathit{e}\mathit{f}}={\mathit{i}}_{\mathit{q}}{\mathbf{ꙍ}}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{L}}_{\mathit{v}}$$

(28)

Considering the minute q-axis element of Vref and assuming precise tracking of the command voltage by the IBR output, the approximate calculation of the inverter output power is as follows:

$${\mathit{P}}_{\mathit{d}}=\frac{3}{2}{\mathit{V}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{d}}+\frac{3}{2}{\mathit{V}}_{\mathit{q}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{q}}\approx \frac{3}{2}{\mathit{V}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{d}}$$

(29)

$${\mathit{Q}}_{\mathit{d}}=-\frac{3}{2}{\mathit{V}}_{\mathit{q}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{q}}+\frac{3}{2}{\mathit{V}}_{\mathit{q}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{d}}\approx -\frac{3}{2}{\mathit{V}}_{\mathit{d}\_\mathit{r}\mathit{e}\mathit{f}}{\mathit{i}}_{\mathit{q}}$$

(30)

The amplitude difference can be

$$\mathbf{\Delta }\mathit{V}={\mathit{i}}_{\mathit{q}}{\mathit{ꙍ}}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{L}}_{\mathit{v}}\approx -\frac{2}{3}\frac{{\mathit{Q}}_{\mathit{d}}}{{\mathit{V}}_{{\mathit{d}}_{\mathit{r}\mathit{e}\mathit{f}}}}{\mathit{ꙍ}}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{L}}_{\mathit{v}}\approx -\frac{2}{3}\frac{{\mathit{Q}}_{\mathit{d}}}{{\mathit{V}}_{\mathit{r}\mathit{e}\mathit{f}}}{\mathit{ꙍ}}_{\mathit{r}\mathit{e}\mathit{f}}{\mathit{L}}_{\mathit{v}}$$

(31)

Equation (31) demonstrates that a positive value for ΔV corresponds to a positive output reactive power of the IBR; in contrast, a negative value corresponds to a negative value of ΔV. Since the output reactive power is positive under typical operating conditions, the available value of ΔV is mostly negative; that is, once virtual impedance control is implemented, the real output voltage is lower than the command voltage.

• Influence of virtual impedance on the stability [41]:

In [42,43], the small-signal model of GFM is obtained and considers the differential relationship between the angular frequency and the command voltage.

$$∆\dot{\mathit{\delta }}=∆{\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}$$

$$∆\dot{{\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}}=-\frac{1}{\mathit{\tau }}∆{\mathit{\omega }}_{\mathit{r}\mathit{e}\mathit{f}}-\frac{1}{\mathit{\tau }}{\mathit{k}}_{\mathit{p}\_\mathit{r}\mathit{e}\mathit{f}}∆{\mathit{P}}_{\mathit{d}}$$

(32)

$$∆\dot{{\mathit{V}}_{\mathit{r}\mathit{e}\mathit{f}}}=-\frac{1}{\mathit{\tau }}∆{\mathit{V}}_{\mathit{r}\mathit{e}\mathit{f}}-\frac{1}{\mathit{\tau }}{\mathit{k}}_{\mathit{p}\_\mathit{r}\mathit{e}\mathit{f}}∆{\mathit{Q}}_{\mathit{d}}$$

(33)

For small deviations, the impact of the virtual impedance change on the stability of the GFM system is examined using Equations (32) and (33). When the virtual impedance value is 0, the dominant eigenvalue is a pair of conjugate complex numbers with a damping coefficient of $\mathit{R}\mathit{d}$. As the impedance (L) increases to Lv, the dominant pole shifts from conjugate complex numbers to real numbers. With the increase in the impedance, one of the dominant poles moves towards the virtical axis. This results in a gradual increase in the damping coefficient, reduced overshoot, and improved system stability. The distance between the dominant pole and the virtual axis decreases as the impedance increases, reducing the system’s stability margin.

The transition from both virtual synchronous generator and droop control to virtual oscillator-based control was driven by specific challenges encountered with these strategies. Droop control lacks inherent damping characteristics, leading to oscillations and instability, particularly in systems with high renewable energy penetration. Additionally, Droop control may struggle to maintain precise synchronization with the grid under dynamic operating conditions, potentially impacting power quality and grid stability. These challenges prompted the exploration of alternative control strategies, such as virtual oscillator-based control. Virtual oscillator-based control influences the concept of oscillation synchronization to regulate inverter output, mimicking the behavior of natural oscillators. Synchronizing voltage and frequency oscillations with the grid offers improved stability and resilience compared to VSG and droop control.

2.3. Virtual Oscillator-Based Control

Virtual oscillator control (VOC) is a decentralized control method for GFM applications. It emulates nonlinear oscillator dynamics and is current controlled but lacks regulation of inverter terminal voltage. VOC is a time-domain GFM control technique for inverter terminal characteristics, emulating weakly nonlinear oscillators with sinusoidal oscillations [23,26,44]. The VOC consists of a resonant L-C tank with frequency ω_n and characteristic impedance ε, interacting with an inverter by measured output current.

The current is transformed to the αβ frame, scaled by ki, and rotated by phase R(ϕ). Scaling VOC and inverter output current with gains k_i and k_v. VOC’s time-domain dynamics in Figure 7 are expressed as equations.

$$\mathit{C}\frac{\mathit{d}{\mathit{v}}_{\mathit{c}}}{\mathit{d}\mathit{t}}=-{\mathit{i}}_{\mathit{L}}+{\mathit{i}}_{\mathit{m}}-{\mathit{u}}_1$$

(34)

$$\mathit{L}\frac{\mathit{d}{\mathit{i}}_{\mathit{L}}}{\mathit{d}\mathit{t}}={\mathit{v}}_{\mathit{c}}+{\mathit{v}}_{\mathit{m}}-{\mathbf{\epsilon }\mathit{u}}_2$$

(35)

The oscillator inputs u₁ and u₂ are determined from measured current and setpoints.

$$\left[\begin{array}{c}{\mathit{u}}_1\\ {\mathit{u}}_2\end{array}\right]={\mathit{k}}_{\mathit{i}}\mathit{R}\left(\mathit{\phi }\right)\left[\begin{array}{c}{\mathit{i}}_{\mathit{\alpha }}-{\mathit{i}}_{\mathit{\alpha }}^{\mathit{*}}\\ {\mathit{i}}_{\mathit{\beta }}-{\mathit{i}}_{\mathit{\beta }}^{\mathit{*}}\end{array}\right]$$

(36)

R(ϕ) follows V-Q and f-P steady-state droop law, obtaining voltage command signals, v_αβ, using k_v gain as ${\mathit{v}}_{\mathit{\alpha }\mathit{\beta }}={\mathit{k}}_{\mathit{v}}{\left[{\mathit{v}}_{\mathit{c}}\mathbf{\epsilon }{\mathit{i}}_{\mathit{L}}\right]}^{\mathit{T}}$. The whole virtual oscillator control dynamics can be given as follows:

$$\dot{{\mathit{v}}_{\mathit{\alpha }}}=\frac{\mathit{\xi }}{{\mathit{k}}_{\mathit{v}}^2}\left(2{\mathit{v}}_{\mathit{n}}^2-{\mathit{v}}_{\mathit{v}0}^2\right){\mathit{v}}_{\mathit{\alpha }}-{\mathit{\omega }}_{\mathit{n}}{\mathit{v}}_{\mathit{\beta }}+\frac{{\mathit{k}}_{\mathit{v}}{\mathit{k}}_{\mathit{i}}}{\mathit{C}}\left({\mathit{i}}_{\mathit{\beta }}-{\mathit{i}}_{\mathit{\beta }}^{\mathit{*}}\right)$$

(37)

$$\dot{{\mathit{v}}_{\mathit{\beta }}}=\frac{\mathit{\xi }}{{\mathit{k}}_{\mathit{v}}^2}\left(2{\mathit{v}}_{\mathit{n}}^2-{\mathit{v}}_{\mathit{v}0}^2\right){\mathit{v}}_{\mathit{\beta }}+{\mathit{\omega }}_{\mathit{n}}{\mathit{v}}_{\mathit{\beta }}-\frac{{\mathit{k}}_{\mathit{v}}{\mathit{k}}_{\mathit{i}}}{\mathit{C}}\left({\mathit{i}}_{\mathit{\alpha }}-{\mathit{i}}_{\mathit{\alpha }}^{\mathit{*}}\right)$$

(38)

The oscillator coefficient, ζ, affects the steady-state inverter nominal voltage amplitude, v_n, and convergence speed. The current setpoints, ${\mathit{i}}_{\mathit{\alpha }\mathit{\beta }}^{\mathbf{*}}$ and ${\mathit{v}}_{\mathit{n}\mathit{o}}={\left({\mathit{v}}_{\mathit{\alpha }}^2+{\mathit{v}}_{\mathit{\beta }}^2\right)}^{1/2}$, are obtained from reference active and reactive power and scaled, ${\mathit{v}}_{\mathit{\alpha }\mathit{\beta }}$. VOCs offer several advantages: stability, plug-and-play integration, dynamic response, and frequency regulation.

They enable GFM to provide stable voltage and frequency, even without a grid connection, ensuring overall microgrid stability. VOCs also facilitate dynamic load sharing among inverters, ensuring efficient resource utilization. Additionally, VOCs enable frequency regulation services, ensuring the stability of power systems with high renewable energy penetration.

2.4. Model Predictive Control

Traditional control strategies often rely on fixed parameters that may not be sufficient to handle the dynamic and nonlinear nature of grid operations, especially in systems with high renewable energy integration. MPC aims to overcome this limitation by utilizing mathematical models of the grid and the inverters to predict future system behavior and optimize control actions accordingly. By incorporating system dynamics, constraints, and objectives into its predictive framework, MPC can anticipate grid disturbances, fluctuations in demand, and variations in renewable energy generation, allowing grid-forming inverters to proactively adjust their operating parameters to maintain stability, improve power quality and enhance overall grid performance.

Modern microprocessors greatly solve the computational burden problem, making it feasible to practically apply nonlinear control techniques. Model predictive control has gained more popularity due to its straightforward approach and ability to handle nonlinear systems and constraints. Among different nonlinear controls, finite control set (FCS) model predictive control (MPC) [45] is a straightforward control algorithm to track the desired reference by making use of the predictive model of the system. The state to be controlled is predicted using the predictive model for a one-step-ahead instant and compared against a given reference value.

$${\mathit{v}}_{\mathit{i}}={\mathit{i}}_{\mathit{i}}{\mathit{R}}_{\mathit{i}}+{\mathit{L}}_{\mathit{i}}\frac{\mathit{d}{\mathit{i}}_{\mathit{i}}}{\mathit{d}\mathit{t}}+{\mathit{v}}_{\mathit{c}}$$

(39)

$${\mathit{v}}_{\mathit{c}}={\mathit{i}}_{\mathit{g}}{\mathit{R}}_{\mathit{g}}+{\mathit{L}}_{\mathit{g}}\frac{\mathit{d}{\mathit{i}}_{\mathit{g}}}{\mathit{d}\mathit{t}}+{\mathit{v}}_{\mathit{g}}$$

(40)

$$\frac{\mathit{d}{\mathit{v}}_{\mathit{c}}}{\mathit{d}\mathit{t}}=\frac{1}{{\mathit{C}}_{\mathit{f}}}({\mathit{i}}_{\mathit{i}}-{\mathit{i}}_{\mathit{g}})$$

(41)

Measurements are placed for the inverter output current, ${\mathit{i}}_{\mathit{i}}$; capacitor voltage, ${\mathit{v}}_{\mathit{c}}$; and grid voltage, ${\mathit{v}}_{\mathit{g}}$. Considering that Ri, Rg, Li, Lg, Rd, and C are inverter side resistance, grid side resistance, inverter side inductance, grid side inductance, filter capacitor branch damping resistance, and filter capacitance, respectively, by applying, Euler’s method to (39)–(41), one can obtain the one-step-ahead prediction model given in (42)–(44):

$${\mathit{i}}_{\mathit{i},\mathit{k}+1}=\frac{{\mathit{T}}_{\mathit{s}}}{{\mathit{L}}_{\mathit{i}}}\left({\mathit{v}}_{\mathit{i},\mathit{k}}-{\mathit{v}}_{\mathit{c},\mathit{k}}\right)+\left(1-\frac{{\mathit{R}}_{\mathit{i}}{\mathit{T}}_{\mathit{s}}}{{\mathit{L}}_{\mathit{i}}}\right){\mathit{i}}_{\mathit{i},\mathit{k}}$$

(42)

$${\mathit{i}}_{\mathit{g},\mathit{k}+1}=\frac{{\mathit{T}}_{\mathit{s}}}{{\mathit{L}}_{\mathit{i}}}\left({\mathit{v}}_{\mathit{c},\mathit{k}}-{\mathit{v}}_{\mathit{g},\mathit{k}}\right)+\left(1-\frac{{\mathit{R}}_{\mathit{g}}{\mathit{T}}_{\mathit{s}}}{{\mathit{L}}_{\mathit{g}}}\right){\mathit{i}}_{\mathit{g},\mathit{k}}$$

(43)

$${\mathit{v}}_{\mathit{c},\mathit{k}+1}={\mathit{v}}_{\mathit{c},\mathit{k}}+\left(\frac{{\mathit{T}}_{\mathit{s}}}{{\mathit{C}}_{\mathit{f}}}+{\mathit{R}}_{\mathit{d}}\right)\left({\mathit{i}}_{\mathit{i},\mathit{k}+1}-{\mathit{i}}_{\mathit{g},\mathit{k}+1}\right)$$

(44)

All quantities in the (42)–(44) are expressed in the αβ frame of reference, as shown in (45)–(46).

$${\mathit{i}}_{\mathit{i}}={\mathit{i}}_{\mathit{i}\mathit{\alpha }}+\mathit{j}{\mathit{i}}_{\mathit{i}\mathit{\beta }};{\mathit{i}}_{\mathit{g}}={\mathit{i}}_{\mathit{g}\mathit{\alpha }}+\mathit{j}{\mathit{i}}_{\mathit{g}\mathit{\beta }};$$

(45)

$${\mathit{v}}_{\mathit{i}}={\mathit{v}}_{\mathit{i}\mathit{\alpha }}+\mathit{j}{\mathit{v}}_{\mathit{i}\mathit{\beta }};{\mathit{v}}_{\mathit{c}}={\mathit{v}}_{\mathit{c}\mathit{\alpha }}+\mathit{j}{\mathit{v}}_{\mathit{c}\mathit{\beta }};{\mathit{v}}_{\mathit{g}}={\mathit{v}}_{\mathit{g}\mathit{\alpha }}+\mathit{j}{\mathit{v}}_{\mathit{g}\mathit{\beta }}$$

(46)

where the relationship between the per-phase and alpha–beta quantities is given in (47).

$$\mathit{x}={\mathit{x}}_{\mathit{\alpha }}+\mathit{j}{\mathit{x}}_{\mathit{\beta }}=\frac{2}{3}\left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{ccc}{\mathit{x}}_{\mathit{a}}& {\mathit{x}}_{\mathit{b}}& {\mathit{x}}_{\mathit{c}}\end{array}\right]$$

(47)

Depending on the inverter topology, some algorithms also use filter capacitor voltage as the controlled state [46]. Now, the predicted controlled state, ${\mathit{i}}_{\mathit{g},\mathit{k}+1}$, is compared against the reference value, ${\mathit{i}}_{\mathit{g}}^{\mathit{*}}$, in the objective function (48), which is evaluated for each possible switching.

Also, since there is no other objective other than the grid current tracking, the objective function will only consist of the current-error terms.

$${\mathit{G}}_{\mathit{j}}={\left({\mathit{i}}_{\mathit{g}\mathit{j}\mathit{\alpha },\mathit{k}+1}-\mathit{j}{\mathit{i}}_{\mathit{g}\mathit{\alpha },\mathit{k}+1}^{\mathit{*}}\right)}^2+{\left({\mathit{i}}_{\mathit{g}\mathit{j}\mathit{\beta },\mathit{k}+1}-\mathit{j}{\mathit{i}}_{\mathit{g}\mathit{\beta },\mathit{k}+1}^{\mathit{*}}\right)}^2;\mathit{j}\in \left\{\mathrm{0,1},2,\dots \mathit{N}\right\}$$

(48)

where N is the number of possible active switching.

Since the grid voltages are measured, the reference current, ${\mathit{i}}_{\mathit{g}\mathit{j},\mathit{k}+1}$ in (48), can be obtained from the references of real and reactive powers as in (49).

$$\left[\begin{array}{c}{\mathit{i}}_{\mathit{g}\mathit{\alpha },\mathit{k}}^{\mathit{*}}\\ {\mathit{i}}_{\mathit{g}\mathit{\beta },\mathit{k}}^{\mathit{*}}\end{array}\right]=\frac{1}{\left({\mathit{v}}_{\mathit{g}\mathit{\alpha },\mathit{k}}^2+{\mathit{v}}_{\mathit{g}\mathit{\beta },\mathit{k}}^2\right)}\left[\begin{array}{cc}{\mathit{v}}_{\mathit{g}\mathit{\alpha },\mathit{k}}& {-\mathit{v}}_{\mathit{g}\mathit{\beta },\mathit{k}}\\ {\mathit{v}}_{\mathit{g}\mathit{\beta },\mathit{k}}& {\mathit{v}}_{\mathit{g}\mathit{\alpha },\mathit{k}}\end{array}\right]\left[\begin{array}{c}{\mathit{P}}^{\mathit{*}}\\ {\mathit{Q}}^{\mathit{*}}\end{array}\right]$$

(49)

Then, using four-term Langrage’s extrapolation, ${\mathit{i}}_{\mathit{g}\mathit{\alpha },\mathit{k}+1}^{\mathit{*}}$ is computed as in (50) (see Table 1 of [47]).

$${\mathit{i}}_{\mathit{g},\mathit{k}+1}^{\mathit{*}}=10{\mathit{i}}_{\mathit{g},\mathit{k}}^{\mathit{*}}-20{\mathit{i}}_{\mathit{g},\mathit{k}-1}^{\mathit{*}}+15{\mathit{i}}_{\mathit{g},\mathit{k}-2}^{\mathit{*}}-4{\mathit{i}}_{\mathit{g},\mathit{k}-3}^{\mathit{*}}$$

(50)

MPC can adapt to changing grid conditions and optimize control strategies in real-time, enabling grid-forming inverters to operate more efficiently and effectively in diverse operating environments. However, the FCS-MPC has a limitation: it does not offer a fixed switching frequency [48]. MPC’s effectiveness relies on accurate mathematical models of the grid and the inverters.

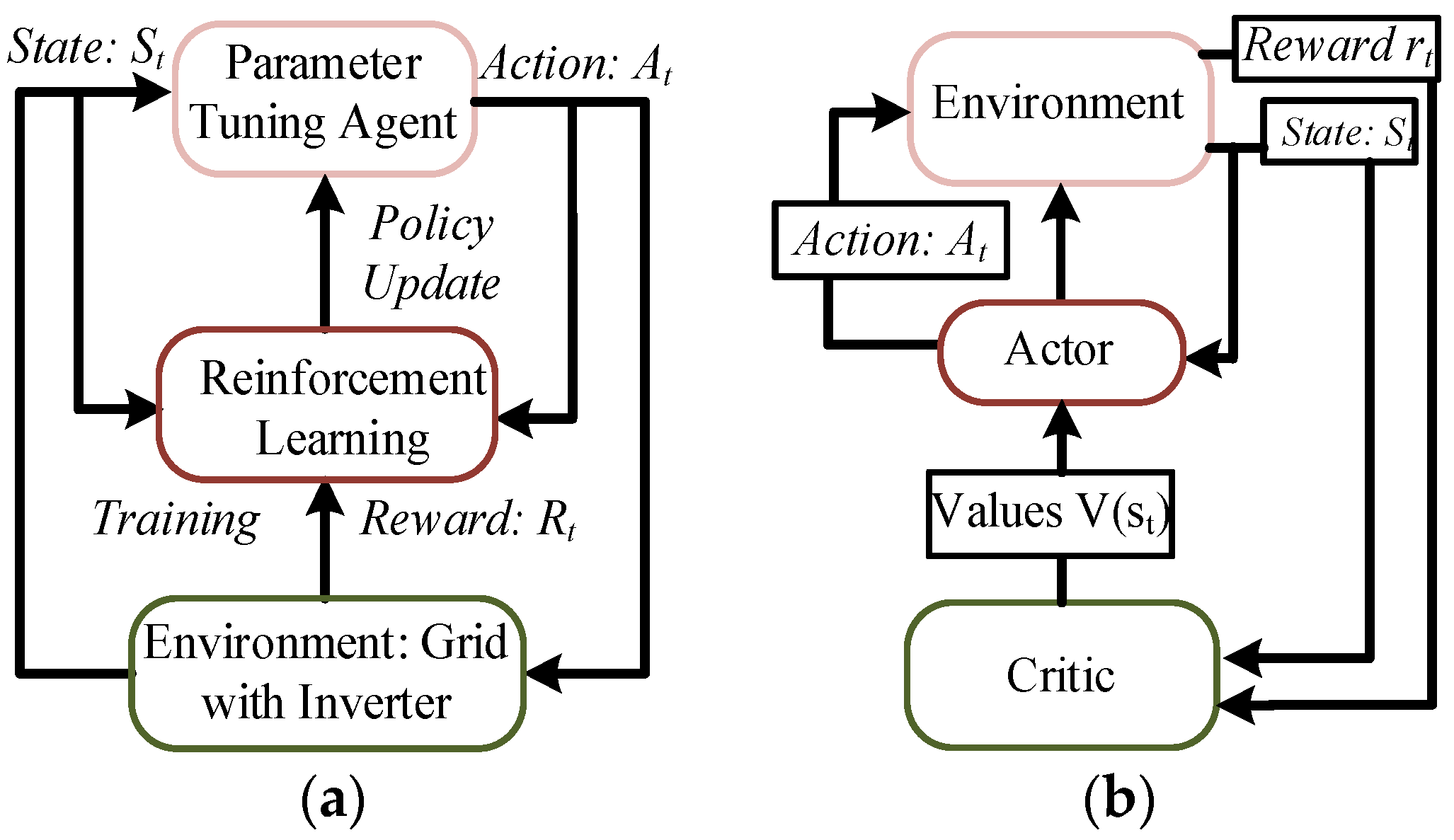
2.5. Reinforcement Learning Based Control

The reinforcement learning technique is a machine-learning paradigm in which an agent learns to make decisions through interaction with its surroundings [49]. Reinforcement-learning techniques are divided into three main categories: value-based methods (Q-learning and deep Q networks), policy-based methods (policy gradients, proximal policy optimization, and actor–critic), and model-based techniques. Q-learning uses a Q-value function to estimate the cumulative reward of actions, while Deep Q Network uses deep neural networks for more complex state spaces. Policy gradients parameterize agents’ policies to maximize rewards [50,51,52].

Figure 8a shows a basic reinforcement learning model with a policy-based algorithm for determining optimal parameters like Dq, Dp, J, and Mf. Policy-based algorithms directly parameterize the policy, mapping states to actions, making them ideal for continuous action spaces or situations with challenging explicit value functions. The model uses a policy-based function to learn neural networks, using them as approximators to represent the policy that maximizes the expected cumulative reward.

The parameters mentioned—Dq, Dp, J, and Mf—are likely components of the system dynamics or control structure [49], as demonstrated below:

• Dq and Dp represent damping coefficients related to the system’s response in the generalized coordinates.
• J represents the moment of inertia of a rotating system.
• Mf represents friction or another factor influencing the motor’s behavior.

Reinforcement learning enhances system stability and efficiency by optimizing parameters, adapting to complex environments, and capturing intricate relationships between system parameters, improving control and decision-making capabilities.

• Actor–Critic Algorithm

In Figure 8b, the actor–critic method is explained; it combines elements of both approaches for more stable learning.

$${\mathit{v}}_{\mathit{o}\mathit{p}\mathit{t}}={\mathit{V}}_{\mathit{r}\mathit{e}\mathit{f}}\left(\mathit{s}\right)-{\mathit{Z}}_{\mathit{o}\mathit{u}\mathit{t}}\left(\mathit{s}\right){\mathit{i}}_{\mathit{s}}\left(\mathit{s}\right)$$

The reinforcement learning model, illustrated in Figure 8, uses a hybrid approach, combining value-based and policy-based reinforcement learning methods to optimize the impedance (Zout) characteristics of a GFM. The model aims to determine optimal output impedance values for an inverter, represented as a complex impedance (R + jX), using machine-learning techniques to modify Z, influencing the inverter’s behavior in response to varying grid conditions. The hybrid approach estimates cumulative rewards for impedance values, guiding optimal system performance. Policy-based actor–critic architectures specify optimal impedance values (Zopt), focusing on policy-making to maximize cumulative reward and provide direct control over inverter behavior [29,53]. The reinforcement learning model uses a Convolutional Neural Network in the actor–critic network to ensure power decoupling in GFM, capturing spatial dependencies and learning optimal impedance values simultaneously.

Brain Emotional Learning-based Controller

The Brain Emotional Learning Controller (BELC) is an intelligent control system miming the human brain’s emotional learning processes, enhancing decision-making and learning. The manipulation of inertial constants, kp, ki, and kg, in virtual synchronous machines is crucial for power system control strategies. These parameters affect the VSM’s response to changes and impact grid stability. Figure 9 illustrates the selection process of optimal values for the kp, ki, and kg, providing the parameter-tuning process in detail. The BELC can optimize these manipulations by leveraging emotional neurons to simulate decision-making states, allowing the controller to adapt and learn from system experiences [54].

The BELC enhances damping in the grid-forming mode in power systems, ensuring stability and preventing oscillations. The controller can dynamically optimize VSMs by adjusting inertial constants, contributing to system stability. The emotional learning aspect allows controllers to adapt to varying conditions and uncertainties, aligning with the trend toward intelligent, adaptive control strategies for real-time performance.

$$\mathit{u}(\mathit{t})=\mathit{S}\mathit{I}(\mathit{t})\left[\mathit{\alpha }{\int }_0^{\mathit{t}}\mathit{S}\mathit{I}\left(\mathit{t}\right)\left[\mathbf{max}\left(0,\mathit{E}\mathit{S}\left(\mathit{t}\right)-\mathit{A}\left(\mathit{t}\right)\right)\right]\mathit{d}\mathit{t}-\mathit{\beta }{\int }_0^{\mathit{t}}\mathit{S}\mathit{I}\left(\mathit{t}\right)\left[\mathbf{A}\left(\mathbf{t}\right)-\mathbf{O}\left(\mathbf{t}\right)-\mathbf{E}\mathbf{S}\left(\mathbf{t}\right)\right]\mathit{d}\mathit{t}\right]$$

(51)

$$\mathit{S}\mathit{I}={\mathit{\lambda }}_1\left({\mathit{P}}_{\mathit{i}\mathit{n}}^{\mathit{*}}-{\mathit{P}}_{\mathit{g}}\right)+{\mathit{\lambda }}_2\int ({\mathit{P}}_{\mathit{i}\mathit{n}}^{\mathit{*}}-{\mathit{P}}_{\mathit{g}})\mathit{d}\mathit{t}$$

(52)

$$\mathit{E}\mathit{S}={\mathit{\delta }}_1\left({\mathit{\omega }}_0-\mathit{\omega }\right)+{\mathit{\delta }}_2\int \left({\mathit{\omega }}_0-\mathit{\omega }\right)\mathit{d}\mathit{t}+{\mathit{\delta }}_3\mathit{u}$$

(53)

$${\mathit{u}}_{\mathit{m}\mathit{i}\mathit{n}}\le \left(\mathit{\alpha }+\mathit{\beta }\right){\left({\mathit{\lambda }}_1+{\mathit{\lambda }}_2\right)}^2\left({\mathit{\delta }}_1+{\mathit{\delta }}_2\right){\mathit{y}}^3\mathit{d}\mathit{t}\le {\mathit{u}}_{\mathit{m}\mathit{a}\mathit{x}}$$

(54)

Figure 10 represents the improved VSG scheme, which uses a neural network to adjust inertia and damping adaptively, with a functional relationship f(x). The control algorithm consists of a P and Q control loop, representing virtual inertia and damping coefficients.

Reference [55] provides the selection of inertia and damping coefficients and emphasizes the importance of tuning these parameters within a reasonable range to ensure system stability. In [56], it is suggested that active and reactive loops can be decoupled, with the influence of the reactive loop ignored. The maximum cut-off frequency is specified to be within 10% of the power frequency, leading to a lower damping coefficient of 11.5.

$${\mathit{D}}_{\mathit{P}}=\frac{∆\mathit{T}}{∆{\mathit{\omega }}_{\mathit{m}\mathit{a}\mathit{x}}}=\frac{∆\mathit{P}}{\mathit{\omega }∆{\mathit{\omega }}_{\mathit{m}\mathit{a}\mathit{x}}}\approx \frac{∆\mathit{P}}{{\mathit{\omega }}_{\mathit{o}}∆{\mathit{\omega }}_{\mathit{m}\mathit{a}\mathit{x}}}$$

(55)

where $∆{\mathit{\omega }}_{\mathit{m}\mathit{a}\mathit{x}}=2\mathit{\pi },$ and the range of D_P is obtained as follows:

$$10.1\le {\mathit{D}}_{\mathit{P}}\le 25.3$$

The shaded area in Figure 11 represents the range of values for the damping coefficient and inertia. The top and lower bounds of the damping coefficient, Dp, are [11.5, 25.3], and the upper and lower bounds of inertia, J, are [0.05, 0.5].

The renewable energy grid connection standard establishes the acceptable value range for these coefficients. The frequency change of 1 Hz results in active power changes in the inverter output, ranging from 40% to 100% of the rated capacity. The inverter has a rated capacity of 50 kVA.

The VSM was improved by employing the radial basis function (RBF) neural network. This enhances the VSM’s stability and adaptability to dynamic power system conditions. The RBF neural network effectively regulates frequency and voltage, ensuring that complex relationships are approximated and stable. This improvement could lead to a more reliable and robust VSM, crucial for overall power system stability and performance.

Numerous operational characteristics of GFM inverter control topologies are compared and presented in

Table 2. Comparison of grid-forming control topologies.

Control Topology	Power Quality	Stability	Fault Ride-Through	Black Start	Scalability	Anti-Islanding	Tracking Accuracy	Response Time	Operating Power Range	Technology Maturity
Droop control	Fair	Poor	Poor	Very Poor	Fair	Fair	Poor	Very Poor	Medium–high	High
V-I droop control	Good	Fair	Fair	Poor	Fair	Good	Fair	Poor	Medium–high	Medium–high
VSG control	Excellent	Good	Good	Fair	Fair	Excellent	Good	Fair	Medium–high	Medium–high
MPC	Good	Good	Good	Fair	Good	Good	Excellent	Good	High	Medium
Reinforcement learning-based [56]	Fair	Good	Fair	Poor	Fair	Fair	Good	Excellent	High	Low

Note: In assessing the characteristics of grid-forming inverter control topologies, a rating of ‘poor’ indicates significant shortcomings in key characteristics, and ‘fair’ suggests acceptable performance but with room for improvement in certain aspects. Control topologies rated as ‘good’ demonstrate a solid performance across various metrics. Finally, a rating of ‘excellent’ signifies superior performance in the evaluated criteria.

. This comparison sheds light on the key attributes and properties of GFM control topologies, providing a comprehensive understanding of its distinctive features. In the comparison table, power quality refers to the reliability and consistency of the electricity supply, encompassing factors like voltage stability, harmonics mitigation, and waveform distortion reduction. Stability ensures the system maintains equilibrium under various conditions and disturbances, providing continuous power delivery. Fault ride-through capability pertains to the system’s resilience in withstanding and recovering from faults without compromising overall operation, thereby minimizing downtime and enhancing grid reliability. Black start capability is the capacity of the power system to initiate and restore operations independently following a complete blackout event, facilitating rapid recovery and restoration of power services. Scalability refers to the system’s flexibility and adaptability to accommodate changes in demand, load patterns, and the integration of renewable energy sources, ensuring efficient and sustainable operation over time. Anti-islanding measures are mechanisms implemented to prevent the formation of isolated power islands, which can pose safety risks and disrupt grid stability during network disturbances. Tracking accuracy encompasses the precision and reliability of control systems in regulating key parameters such as voltage, frequency, and power flow, aligning with desired setpoints or reference signals. Finally, response time refers to the speed at which the control system reacts to changes in operating conditions or command inputs, ensuring timely and effective adjustment to maintain system stability and performance. Understanding these characteristics helps develop control topologies prioritizing reliability, resilience, and efficiency in power system operation.

3. Performance Analysis of Grid-Forming Inverter

In this section, the operational characteristics of GFM, such as autonomous microgrid operation, robust fault right-through capability, fault detection and islanding systems, dynamic behavior, and small signal stability, are discussed. A concise summary of the operational behavior of GFMs is presented in

Table 3. Summary of operational characteristics of grid-forming inverter.

Characteristic	Description
Autonomous microgrid operation	GFMs facilitate autonomous microgrid operation by controlling inverter frequency. They redistribute load among inverters and activate under-frequency load shedding to address overload issues, ensuring system survival during overload events.
Robust fault ride-through capability	GFMs continuously monitor parameters and respond quickly to faults, ensuring resilience during short duration faults. They provide necessary support to the grid, preventing power interruptions and cascading failures. GFMs can withstand faults up to 1.2–2.0 p.u. of their rated value and require current control strategies for future grid integration.
Dynamic behavior and small-signal stability	GFMs contribute to stability by reducing frequency deviations and enhancing frequency response compared to traditional grid-following approaches. Transitioning to GFMs improves frequency stability even with mixed inverter types.
Islanding operational capability	GFMs use voltage, frequency, and current monitoring to detect faults and initiate appropriate actions to maintain grid stability. GFMs automatically transit to islanded mode, supplying power to local loads, and forming small microgrids separate from the main grid, increasing grid resilience.

.

3.1. The Survival of Autonomous Microgrids during Overload Events

The grid is designed to address the overload issue by controlling inverter frequency [57]. When some inverters in the microgrid are overloaded, the GFM can transfer the extra load to other inverters. When almost all inverters in the microgrid are overloaded, this controller can activate the under-frequency load shedding. For example, consider two GFM systems with inverters Inv1 and Inv2. Dispatch the output power of Inv1 to near its maximum at the beginning, and Inv2 is far from its maximum. If it happens, inverters Inv1 and Inv2 increase their currents almost instantaneously to meet this load change. This is just because they behave as voltage sources; they keep their internal voltage constant during the transient. So, their currents come out very rapidly to meet this load change [58]. However, this situation has problems because Inv1 is already close to its maximum before a fault or disturbance. After the disturbance, the GFM output power for Inv1 exceeds its maximum. This causes overloading of Inv1, which further causes issues, maybe collapsing the bus of the inverter or a synchronous generator. So, this overload issue should be solved.

The microgrid can solve this overload issue using two Pmax controllers [59,60]. The key concept to this is that, once Inv1 reaches Pmax, the controller will be activated to reduce the frequency of Inv1 rapidly, and by reducing the frequency, we can change the phase angle between these two inverters, so this can redistribute the power flow between the two inverters. This is just an autonomous load transfer from Inv1 to Inv2, using this Pmax controller [61]. Now, consider three sources: the GFM Inv1, the synchronous generator SG1, and energy storage. Consider this energy storage to be a contingency. This results in overloading the GFM Inv1 and the synchronous machine SG1, and both Inv1 and SG1 are equipped with this Pmax controller. Once this overload happens, the Pmax controllers for both Inv1 and SG1 are activated, and both reduce their frequency. The entire system frequency keeps dropping, and the frequency relay detects this under-frequency event and trips the load, and the system survives.

3.2. Fault Ride-Through Capability

GFM continuously monitors parameters, enabling quick responses and corrective actions to mitigate the impact of faults. The fault ride-through capability of GFMs ensures resilience during faults, allowing them to withstand short-duration faults and provide the necessary support to the grid, preventing power interruptions and cascading failures [62].

GFMs can only withstand a maximum current of 1.2–2.0 p.u. of their rated value. Tripping prevents overcurrent damage, but future IBR networks require them to ride through grid faults and transient instability. Therefore, a current control with transient stability becomes necessary in the future grid. Current limiting strategies can be hardware-based or software-based [63,64]. Hardware like hysteresis compensators and fault current limiters restrain fault currents. However, these are inappropriate for GFM due to their high cost, poor performance, and complex implementation. Software-based approaches offer intellect and can be integrated into controllers [65]. GFMs switch from the usual voltage source to the current source mode, causing overvoltage during asymmetrical faults. However, the current source mode loses inverter voltage source characteristics, requires fast fault detection, and increases the computation burden. Indirect methods modify voltage references without losing source behavior; however, they fail under asymmetrical faults.

Virtual impedances offer overcurrent protection, but the current limitations of inverters may affect GFMs’ stability. Future development of GFMs should focus on maintaining voltage source behavior, limiting faulty phase currents, and ensuring stable synchronization [26]. An adaptive fault ride-through scheme is proposed for GFMs to improve current limiting and synchronization stability in symmetrical and asymmetrical grid faults [66]. This scheme offers effective fault-limiting, healthy phase voltage maintenance, and enhanced negative and zero-sequence current sharing.

3.3. Dynamic Behavior and Small Signal Stability

Inverter-based power integration significantly alters power system dynamics, challenging conventional assumptions of power system networks. Studies show that low-inertia systems are more vulnerable and challenging to ensure small signal stability than 100% inverter-based systems [67,68]. In a study based on simulation results [69], a three-phase unbalanced distribution system connected to a transmission system and grid-following/GFM inverters were penetrated. The system’s frequency stability was affected by changing the inverter penetration level, affecting the system’s overall performance. The study revealed that, in a 100 machine-based system, adding grid-following inverters significantly reduces the frequency. Through a comprehensive analysis, several key insights emerge:

Firstly, in systems where grid-forming inverters are absent, the power infrastructure demonstrates resilience to accommodate up to 70% penetration of grid-following inverters. This threshold underscores the adaptability of existing technologies in managing grid dynamics within defined operational limits. Secondly, the imperative for integrating grid-forming inverters arises as the penetration of inverter-based resources surpasses 70%. This pivotal threshold marks a transition point, emphasizing the necessity of advanced control strategies and technologies to uphold system stability and reliability amidst escalating renewable energy integration. Thirdly, aiming for a comprehensive transition to 100% penetration of IBR necessitates the deployment of at least 12% grid-forming inverters to uphold stability. This underscores the critical role of these inverters in enhancing frequency response and ensuring grid resilience under varying operating conditions. These GFMs inverters enable higher penetration levels of IBR and contribute to superior stability and frequency response characteristics compared to conventional grid-following approaches.

In the system, if part of the IBR is grid-forming and the remaining are grid-following inverters, then it is obtained that the frequency response is still relatively stable because all the machine dynamics disappear. It is discovered that the frequency response for a transition from one steady state to another is even better than that of a traditional synchronous machine-dominated system [70,71,72]. So, GFM can do better than distinguished machines on frequency control. Conclusively, the system needed fewer GFMs than synchronous machines to maintain frequency stability.

3.4. Islanding Operational Capability

GFM-based systems use voltage and frequency monitoring, PLL synchronization, and current monitoring to detect faults. Voltage and frequency deviations from predefined setpoints indicate faults [73]. GFMs can use the rate of change in frequency detection to identify faults like short circuits or sudden load changes. Zero-crossing detection helps to identify distorted waveforms or abnormal zero-crossing patterns. The goal is quickly identifying faults and initiating appropriate actions to maintain grid stability.

Islanding occurs when a distributed energy resource continues to supply power to a portion of the electrical grid, even when the main grid experiences a blackout or loss of connection. When a grid disturbance occurs, the inverter can detect a loss of connection or instability and automatically transition into “islanded” mode, generating AC power to supply local loads, forming a small microgrid separate from the main grid. Islanding of GFM-based systems offers advantages such as increased grid resilience and renewable energy utilization. However, it poses safety concerns, requiring proper anti-islanding protection and sophisticated control algorithms to maintain stable operation.

4. Future Research

Future GFM research might focus on several important issues to improve their effectiveness and power system integration. The following are some possible lines of inquiry based on the information given:

• When transitioning the grid to isolated mode, the grid-forming mode should emulate the behavior of a synchronous generator. This necessitates the precise control of the rate of change in frequency. In the isolated mode of GFM, it assumes sole responsibility for upholding network frequency, either individually or collectively, with all other inverters behaving parallel to GFM inverters. Consequently, it imposes regulations on the rate of change in frequency. Formerly, frequency variation rate control relied on grid steam valve positioning, but now, this responsibility is placed solely on the inverter. It is imperative to explore controlled strategies and refine them deeper to effectively constrain the rate of change in frequency.
• When enhancing resilience through an inverter, the GFM can be effectively employed in conjunction with various energy sources such as batteries, solar PV systems, wind turbines, etc. When grid voltage disturbances necessitate power injection from the inverter, the question arises: where does the inverter source this additional power? Typically, solar PV systems, wind turbines, etc., operate at their maximum power point, leaving no surplus energy available. Thus, additional power must be sourced from battery storage to augment the inverter’s GFM capability. One proposed solution involves operating the inverter at a fixed point relative to the MPP. However, this approach results in underutilizing the GFM capability, consequently diminishing overall efficiency. This underscores the necessity of conducting comprehensive studies to enhance techniques and topologies to optimize the GFM capability, while maintaining high resiliency and efficiency. Such investigations are essential to identify strategies that leverage the full potential of GFM, while minimizing energy wastage, thereby ensuring optimal system performance under varying grid conditions.
• “What methodologies can be employed to integrate Grid Forming Mode capabilities within Vehicle-to-Grid conditions? Given the future widespread adoption of electric vehicles, how can we effectively control their collective connectivity to support GFM operations within the grid?”
• Future research can focus on empirically investigating the interplay between grid-following and grid-forming inverters within a mixed environment. This includes analyzing the impact of varying ratios of grid-following to grid-forming inverters on grid stability, frequency control, and overall system performance. Additionally, research efforts should explore novel control strategies and coordination mechanisms to optimize the operation of grid-forming inverters in such heterogeneous environments, ultimately enhancing grid resilience and reliability.
• Explore sophisticated stability analysis methodologies, such as small-signal stability analysis and transient stability simulations, to mark out stability boundaries and operational limits in power system networks. Furthermore, future research activities should aim to control the findings from stability analysis to inform decision-making processes regarding the deployment and integration of GFM inverters. By identifying critical stability constraints and evaluating the impact of different deployment scenarios, researchers can develop strategies to optimize the utilization of GFM inverters, while ensuring grid stability and reliability.
• How can advanced simulation models be developed to accurately capture the dynamic behavior of loads and transmission lines, thereby providing a realistic representation of grid-forming inverter performance in dynamic operating conditions? Specifically, how can these models effectively account for the time-varying characteristics of loads and the dynamic response of transmission lines to disturbances?
• Investigations are needed to clarify how variations in filter parameters, such as inductive and capacitive reactance, impact the stability of GFM inverter-based systems, particularly in scenarios involving multiple interconnected inverters. Additionally, the impact of coupling reactance on the stability of inverter-based systems deserves thorough analysis. Furthermore, researchers should explore how the relationships between filter parameters and stability margins can be examined to identify optimal design configurations that enhance stability and mitigate potential instability issues.
• Future research should prioritize conducting transient stability studies to carefully evaluate the dynamic behavior of GFM-based systems under various operating conditions. This involves accurately modeling the transient response of grid-forming inverters and analyzing their interactions with synchronous generators, loads, and transmission lines during dynamic scenarios. To achieve this, it is essential to incorporate detailed representations of inverter control algorithms, system dynamics, and grid infrastructure into simulation frameworks to ensure realistic results.

5. Conclusions

This paper provided a comprehensive overview of GFM in modern electric power systems. The control methods for GFM were thoroughly discussed, ranging from basic techniques, such as droop control and voltage/frequency regulation, to more advanced strategies, like model predictive control and adaptive control. Through a detailed analysis and comparison, this paper has shed light on the strengths, limitations, and suitability of different control methods for diverse grid environments. It has been demonstrated that each approach has its advantages and trade-offs, depending on system complexity, operating conditions, and desired performance metrics. Ultimately, the research presented here underscores the importance of selecting appropriate control strategies to mitigate grid disturbances, optimize power flow, and enhance overall system stability. By understanding the characteristics of various control methods, stakeholders in the power industry can make decisions to ensure reliable and flexible power delivery in dynamic grid environments.