An Efficient Shunt Modulated AC Green Plug–Switched Filter Compensation Scheme for Nonlinear Loads
Abstract
:1. Introduction
2. Literature Review
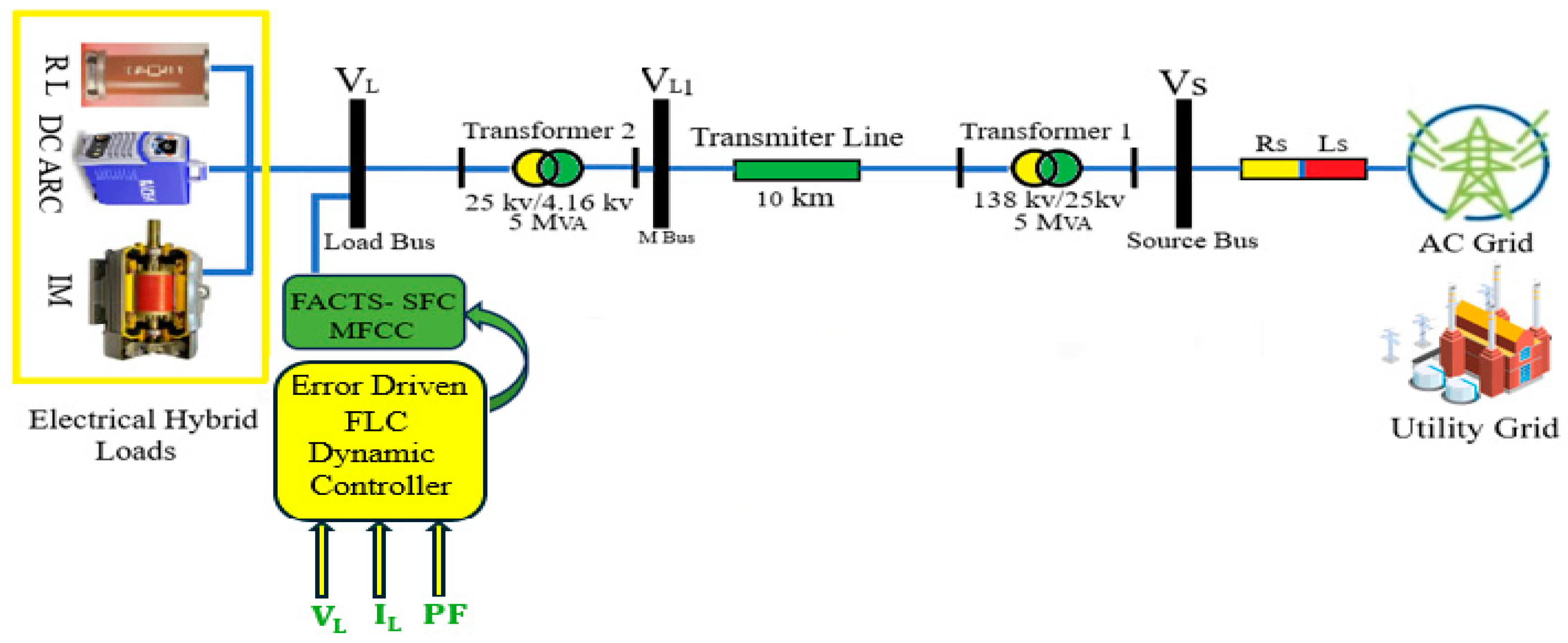
3. System Description
- A three-phase AC grid source;
- A novel modulated filter-capacitor compensator (MFCC-SFC) filter scheme;
- A novel dynamic error-driven tri-loop type-2 FLC;
- Three different electrical hybrid nonlinear loads;
- Transformers for voltage change from 138 kv to 25 kv and then from 25 kv to 4.16 kv.
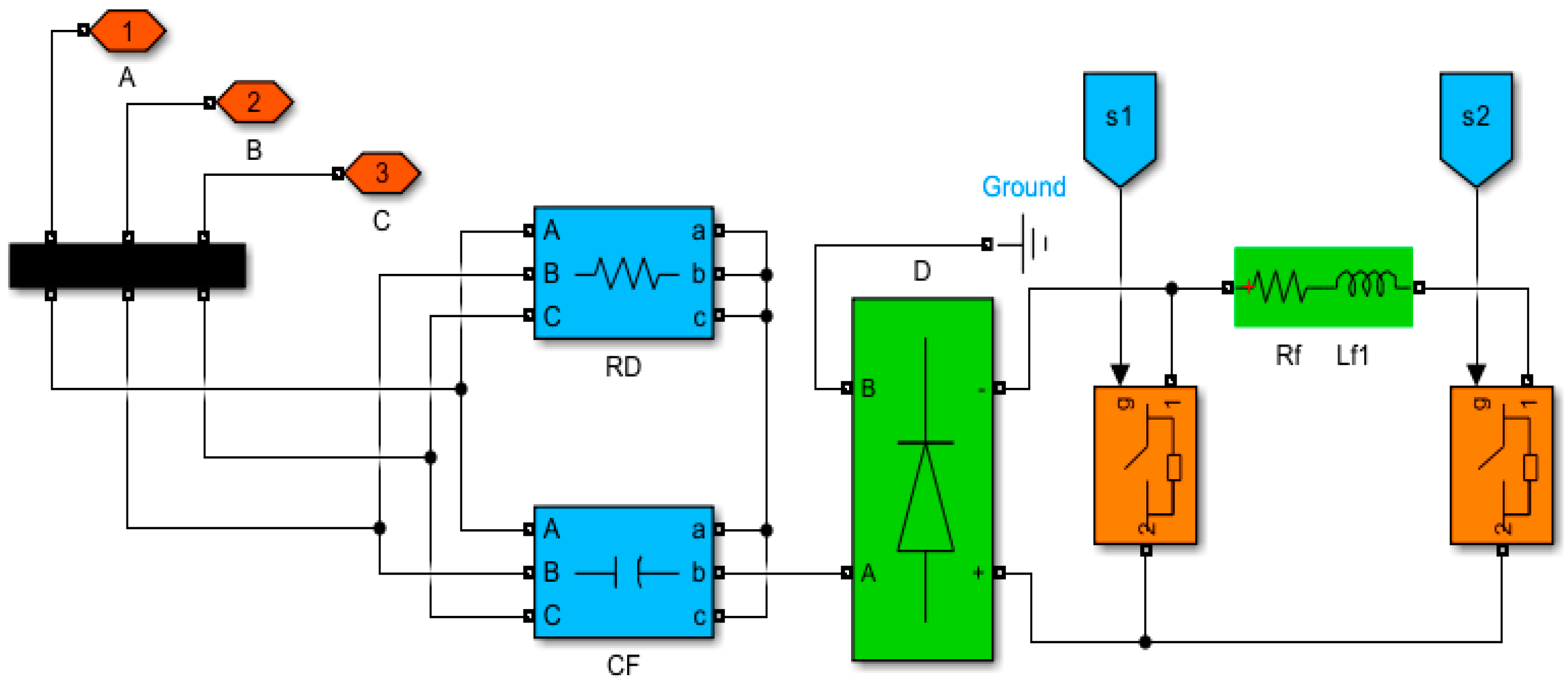
4. FACTS-MFCC-SFC Scheme
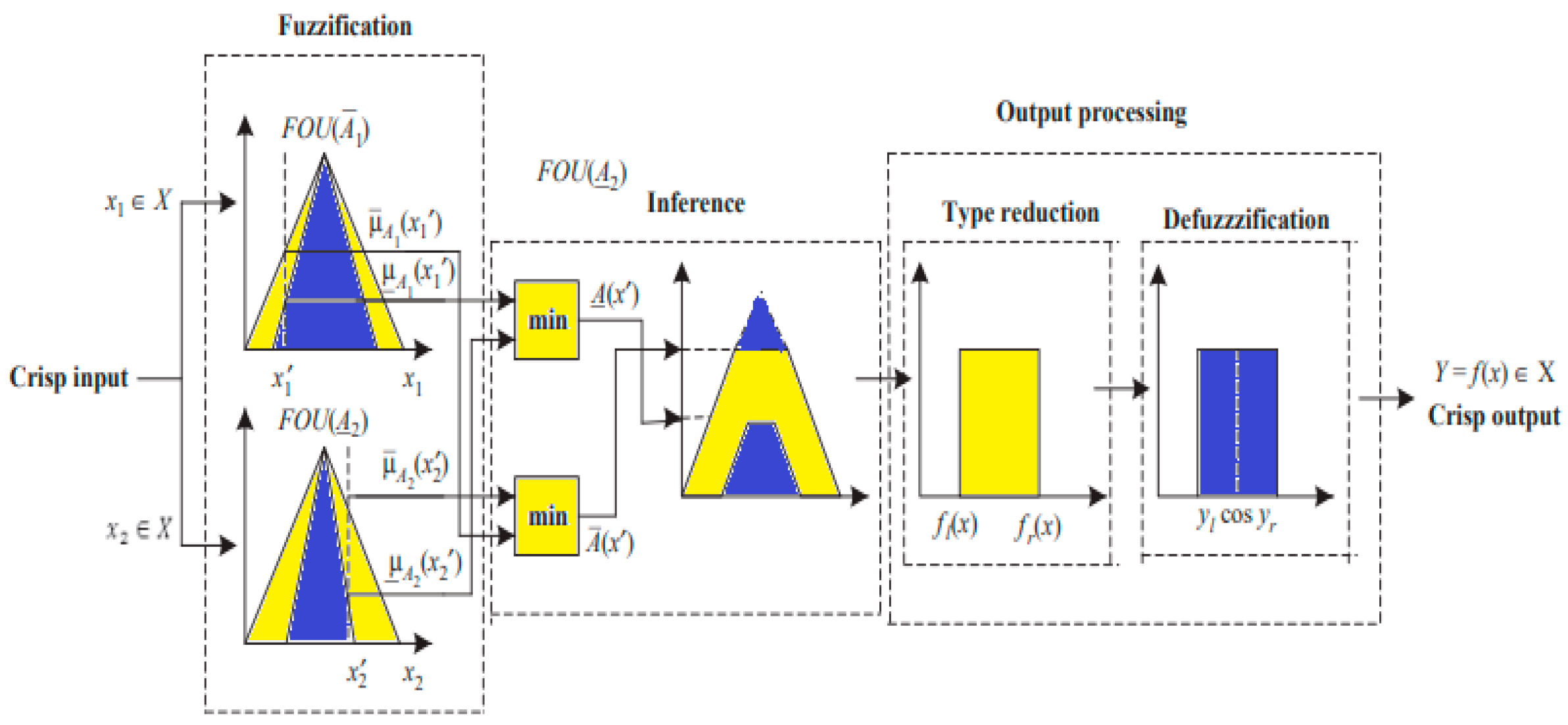
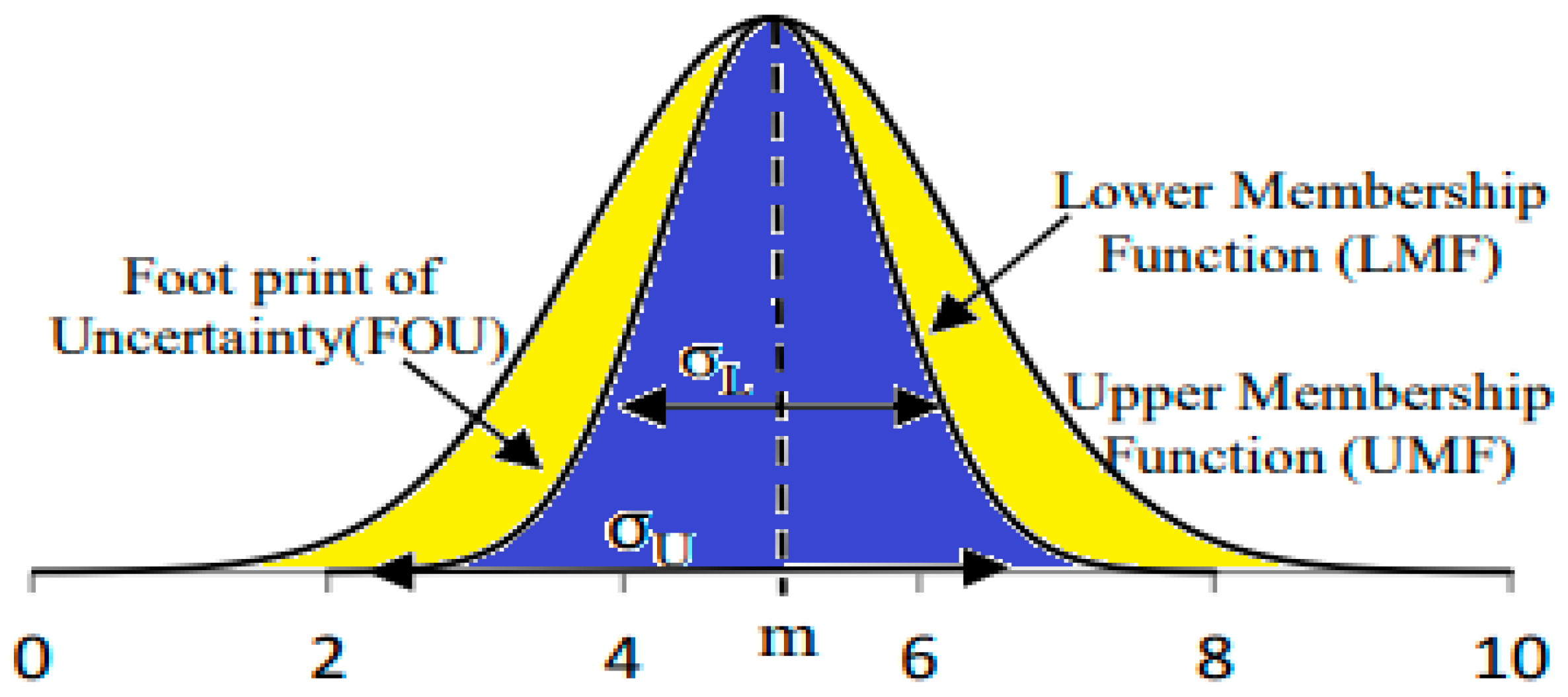
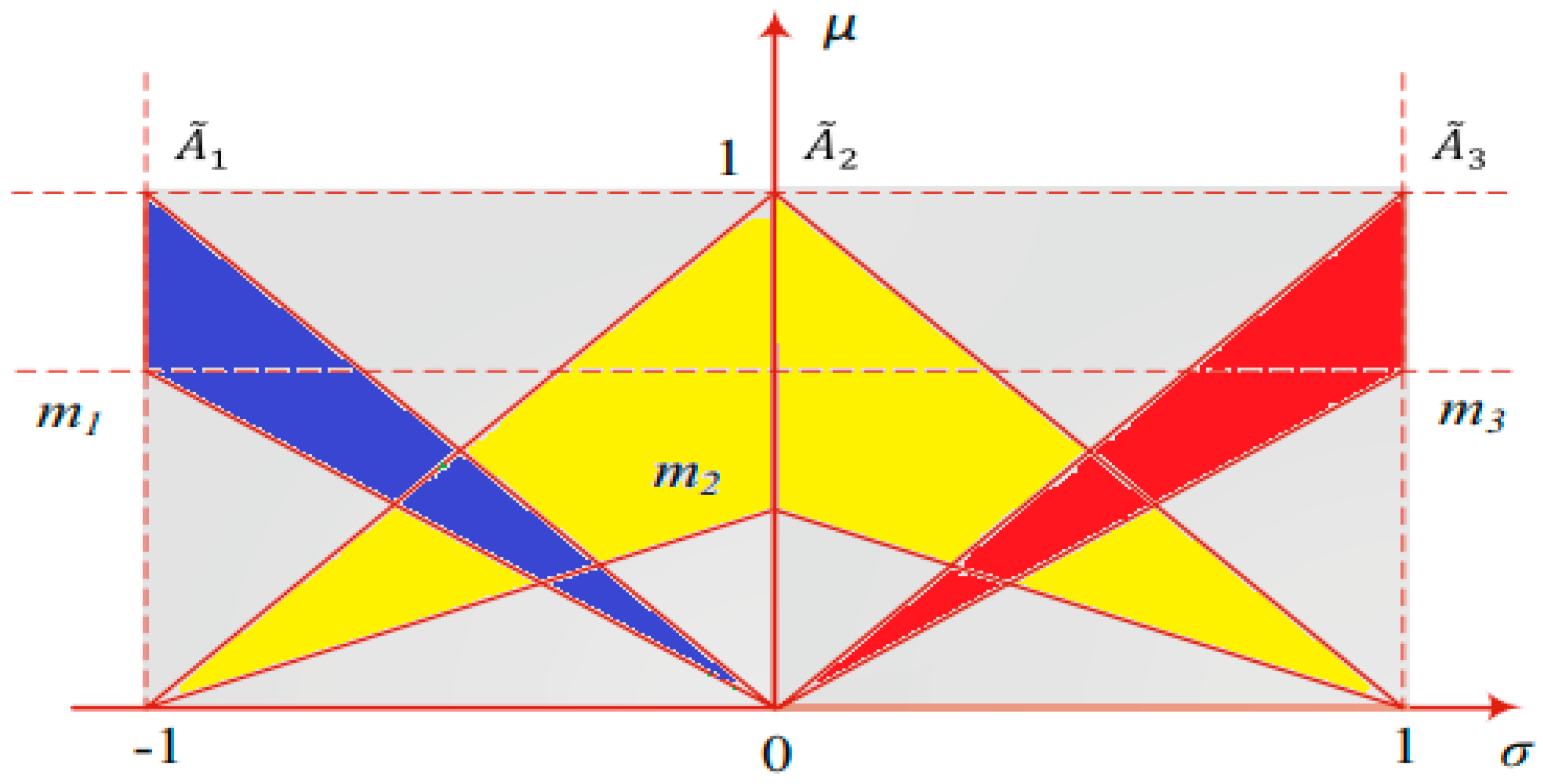
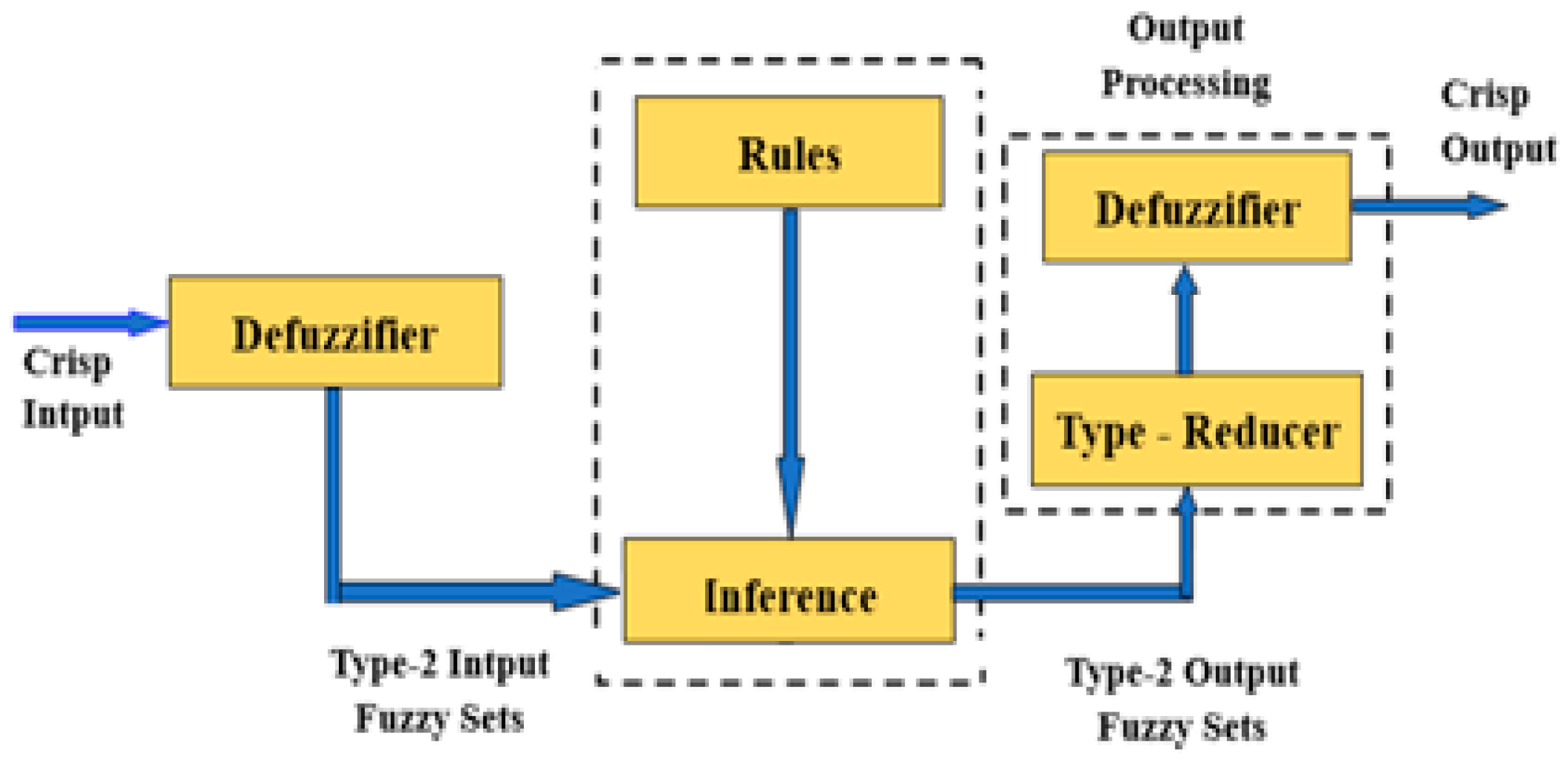
5. Type-2 Fuzzy Logic Controller
6. Simulation Results and Discussion
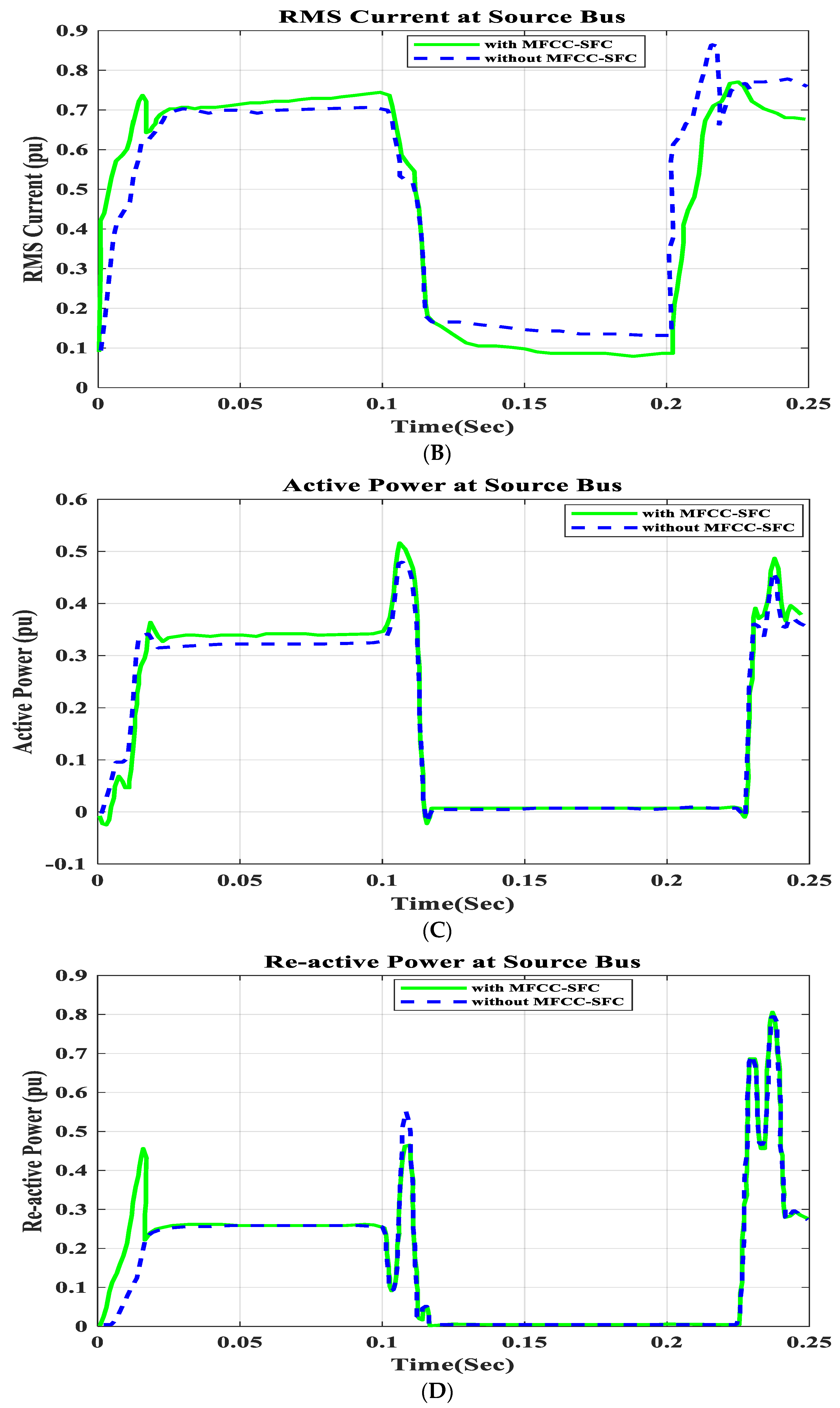
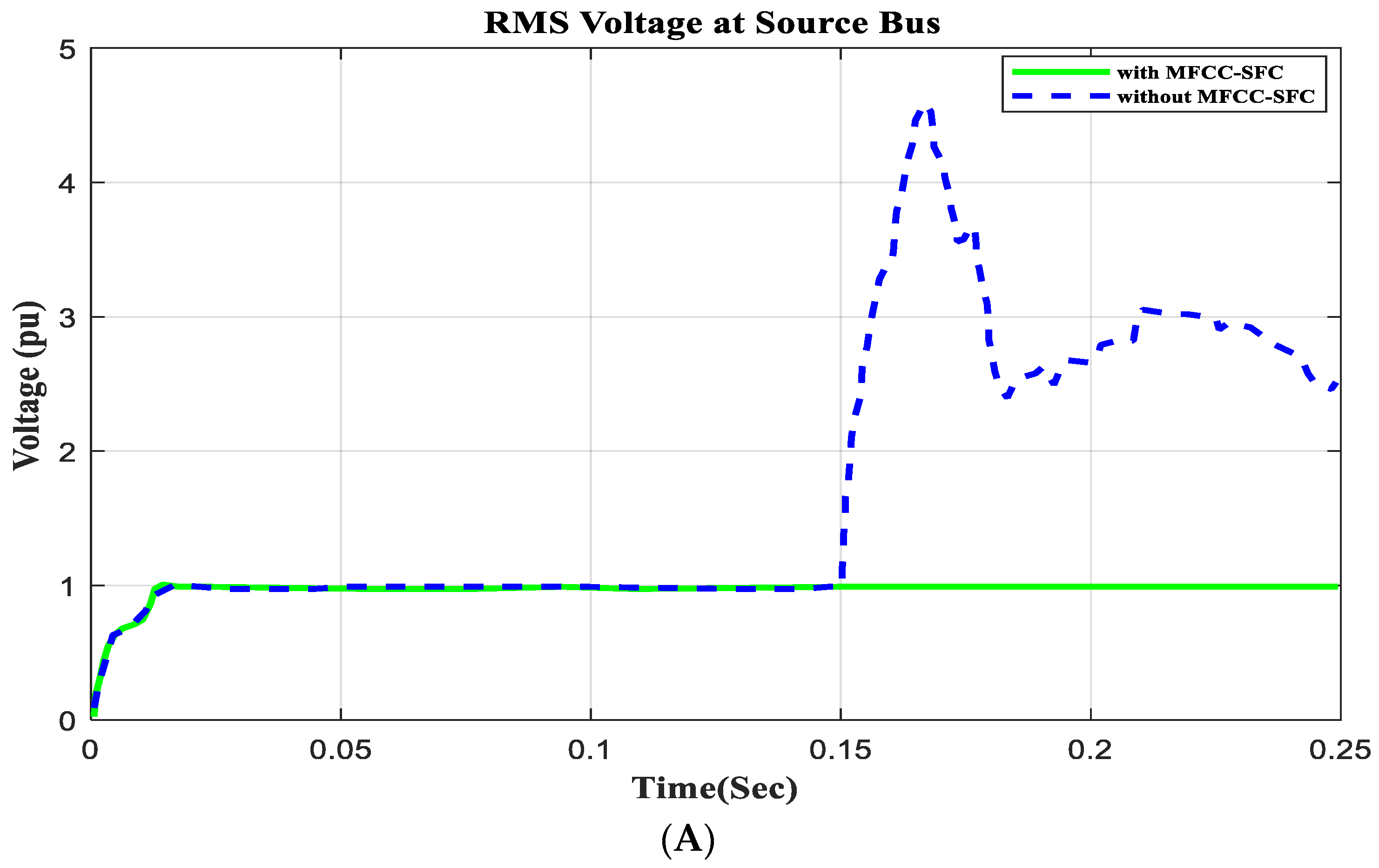
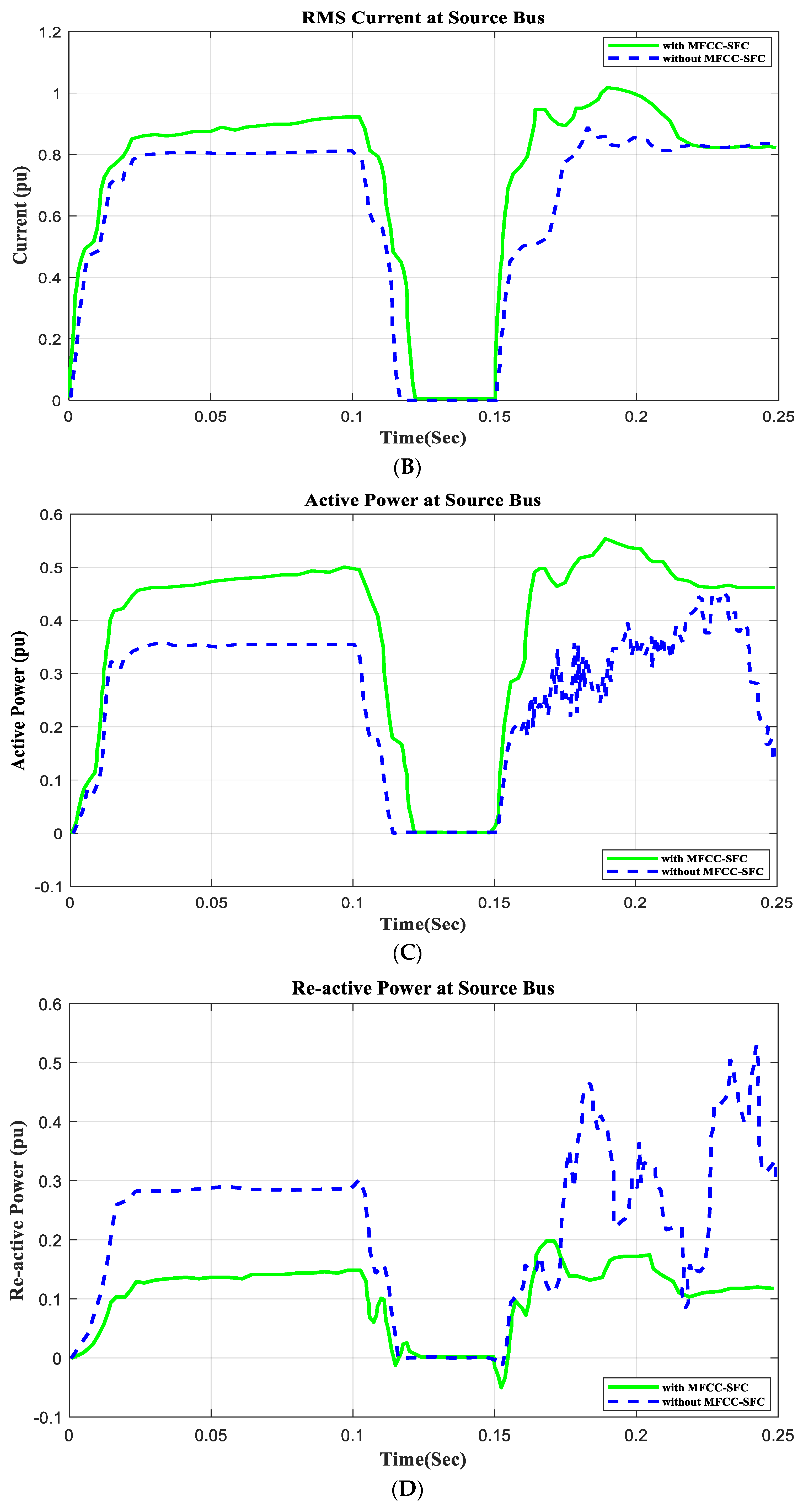
6.1. V, I, P, Q, and PF at Source Bus with Short Circuit Operation
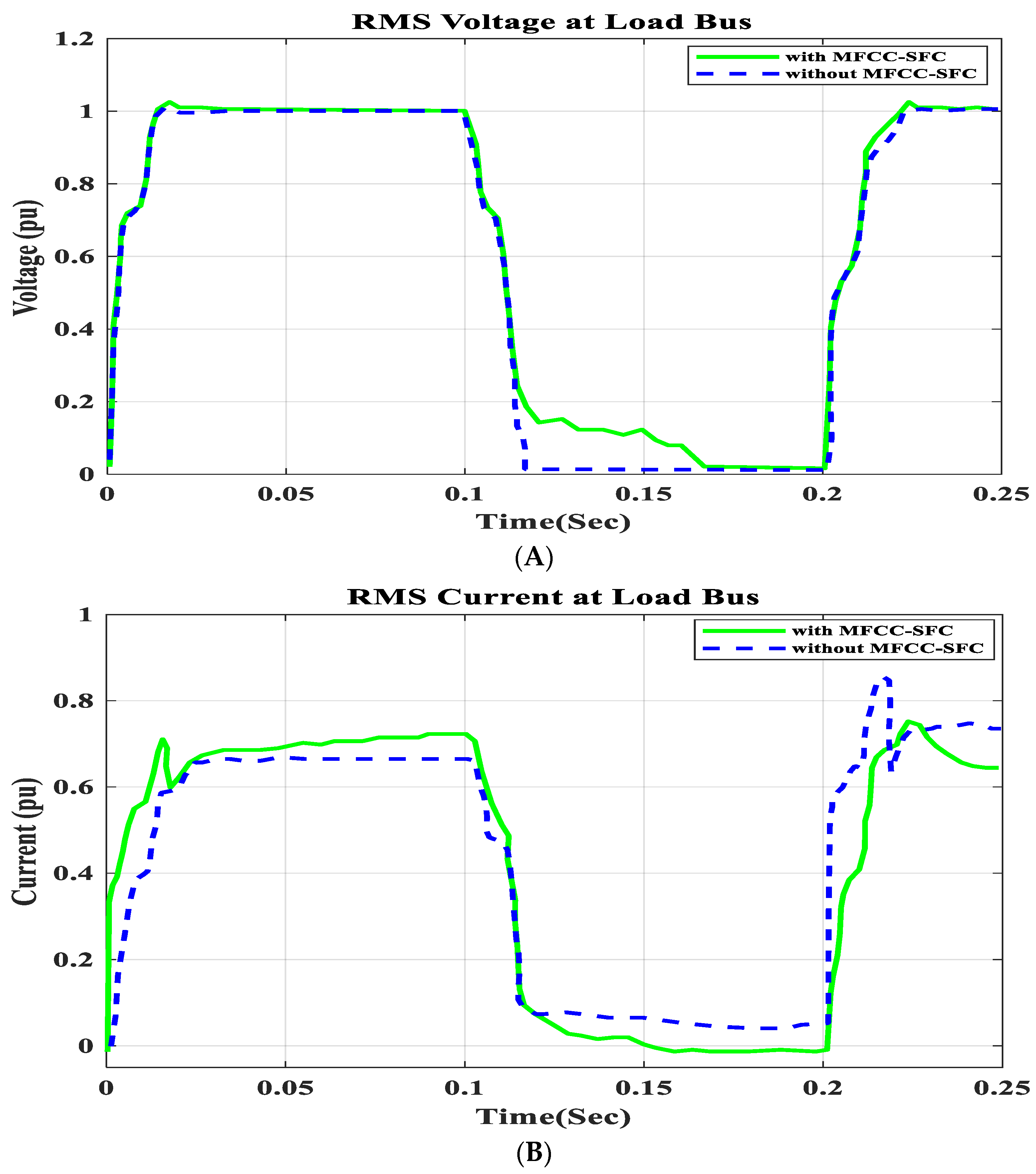
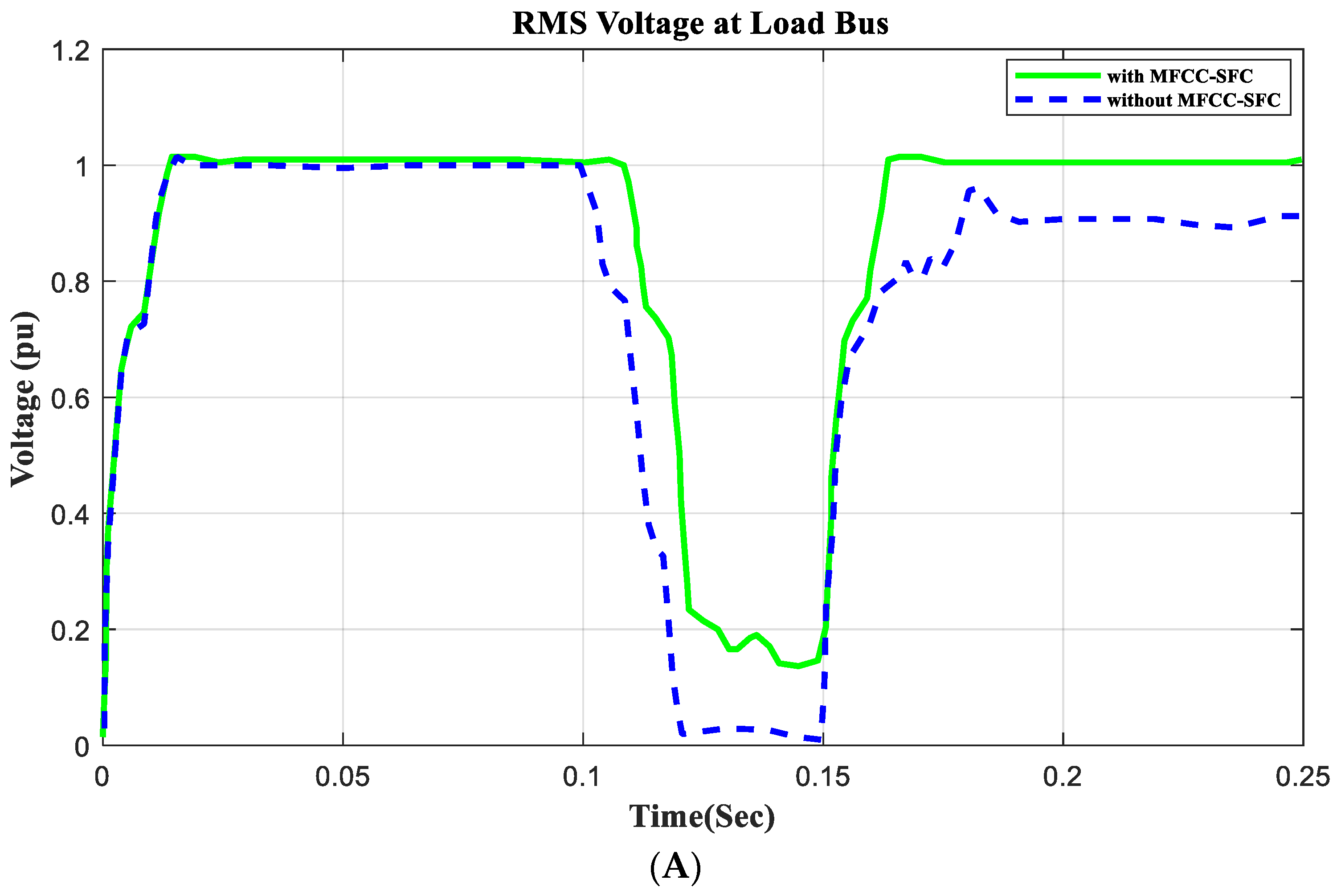
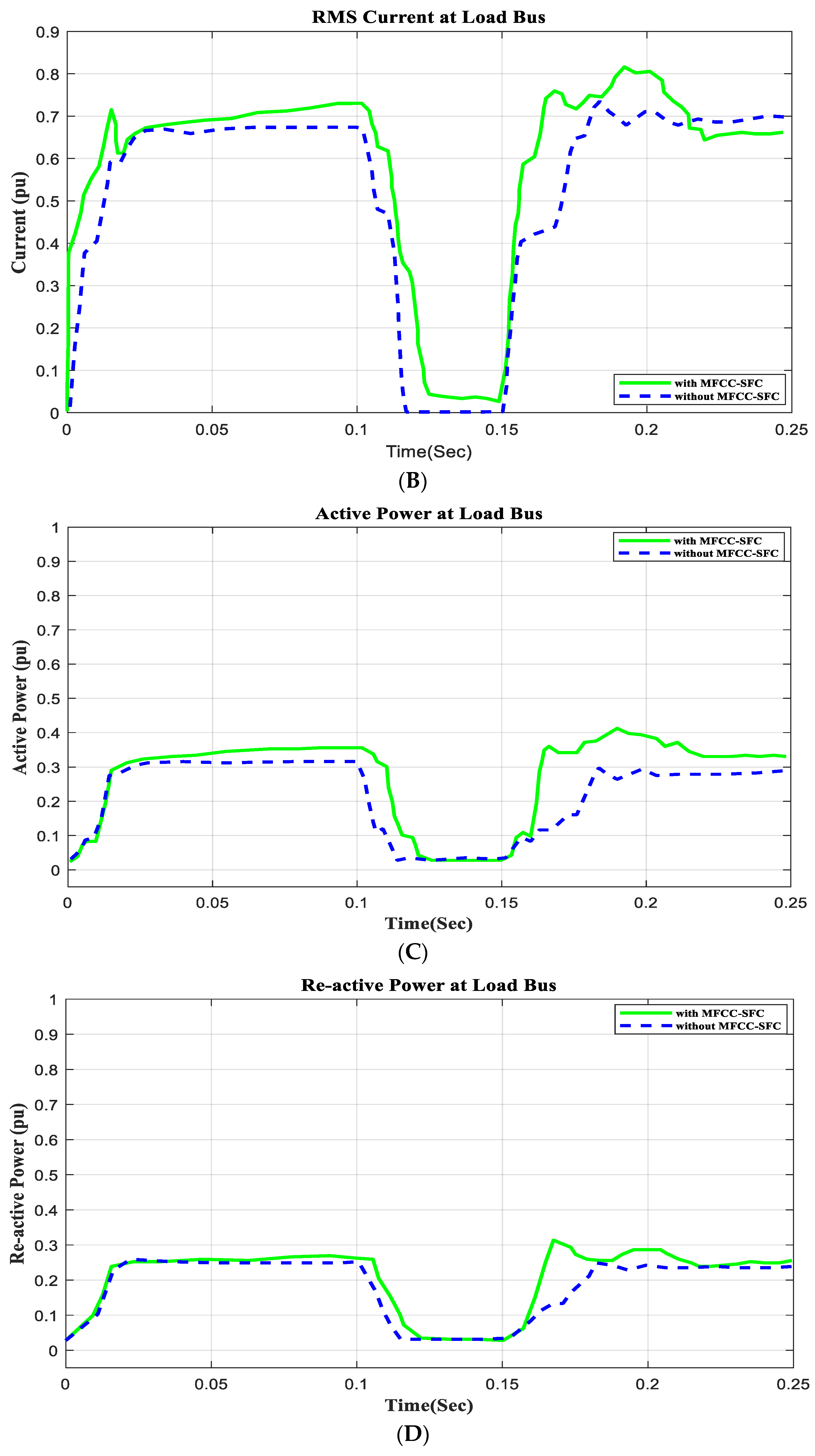
6.2. V, I, P, Q, and PF at Load Bus with Short Circuit Operation
6.3. Application Short Circuit Condition
6.4. V, I, P, Q, and PF at Source Bus with Open Circuit Operation
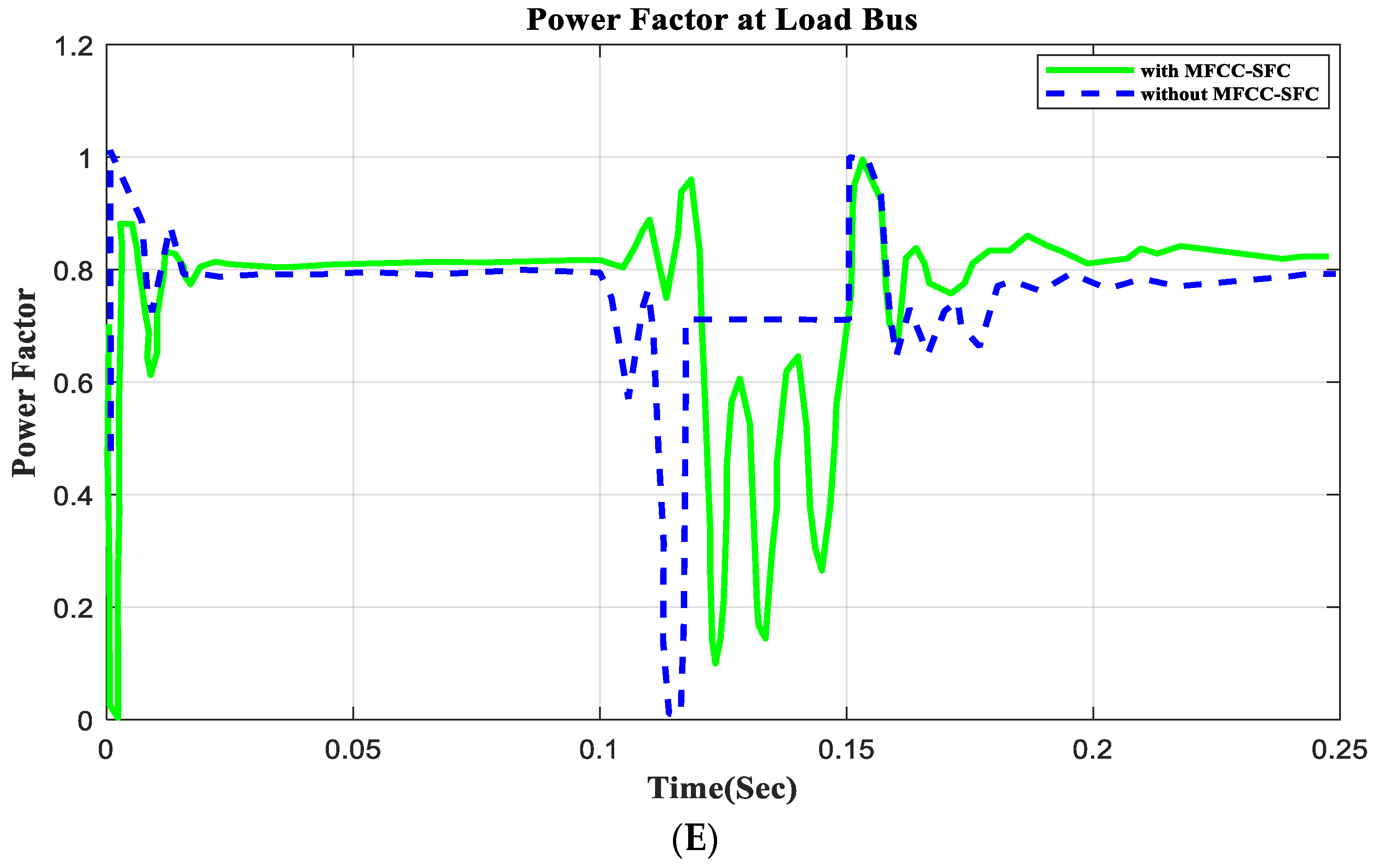
6.5. V, I, P, Q, and PF under at Load Bus with Open Circuit Operation
6.6. Application of Open Circuit Condition
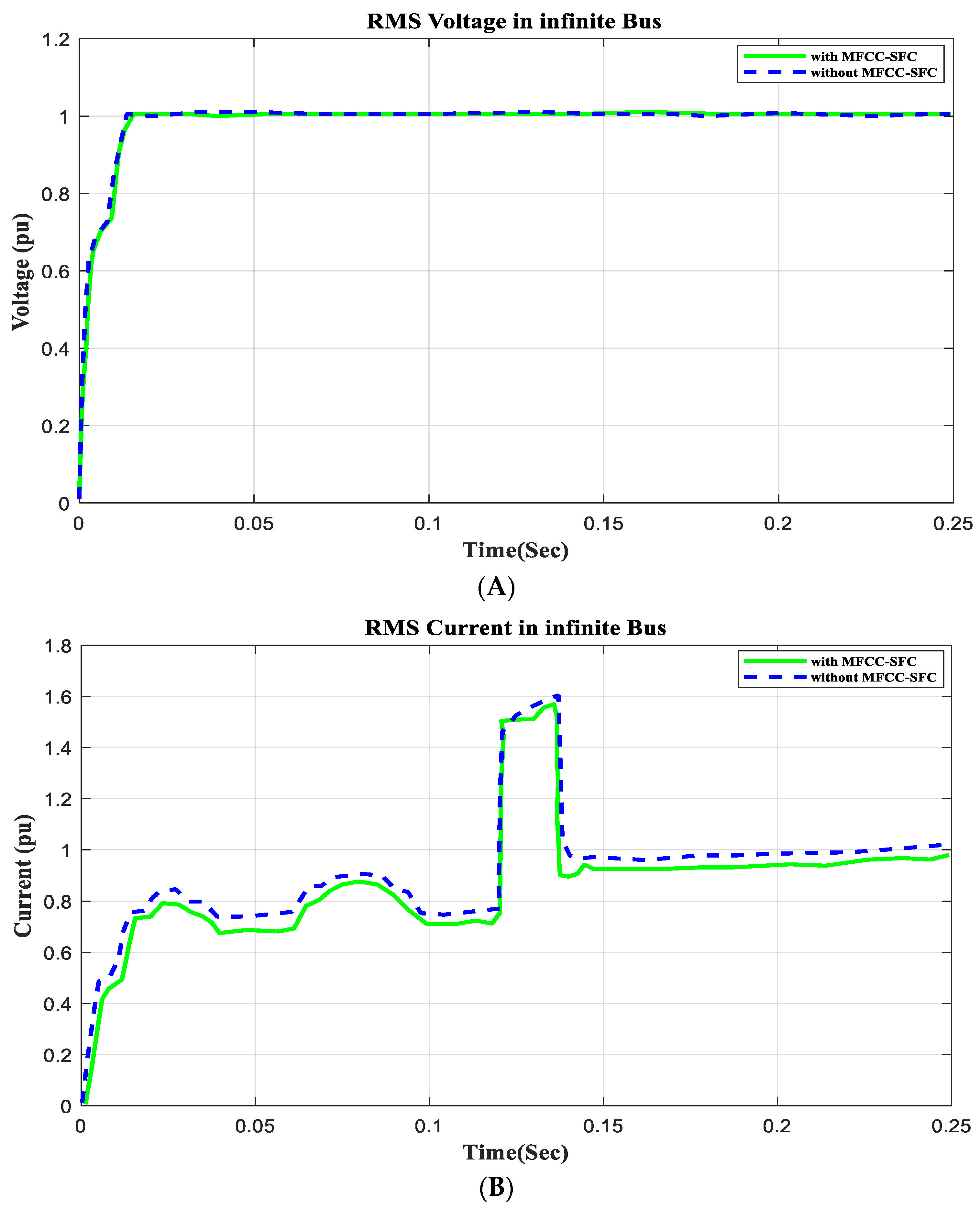
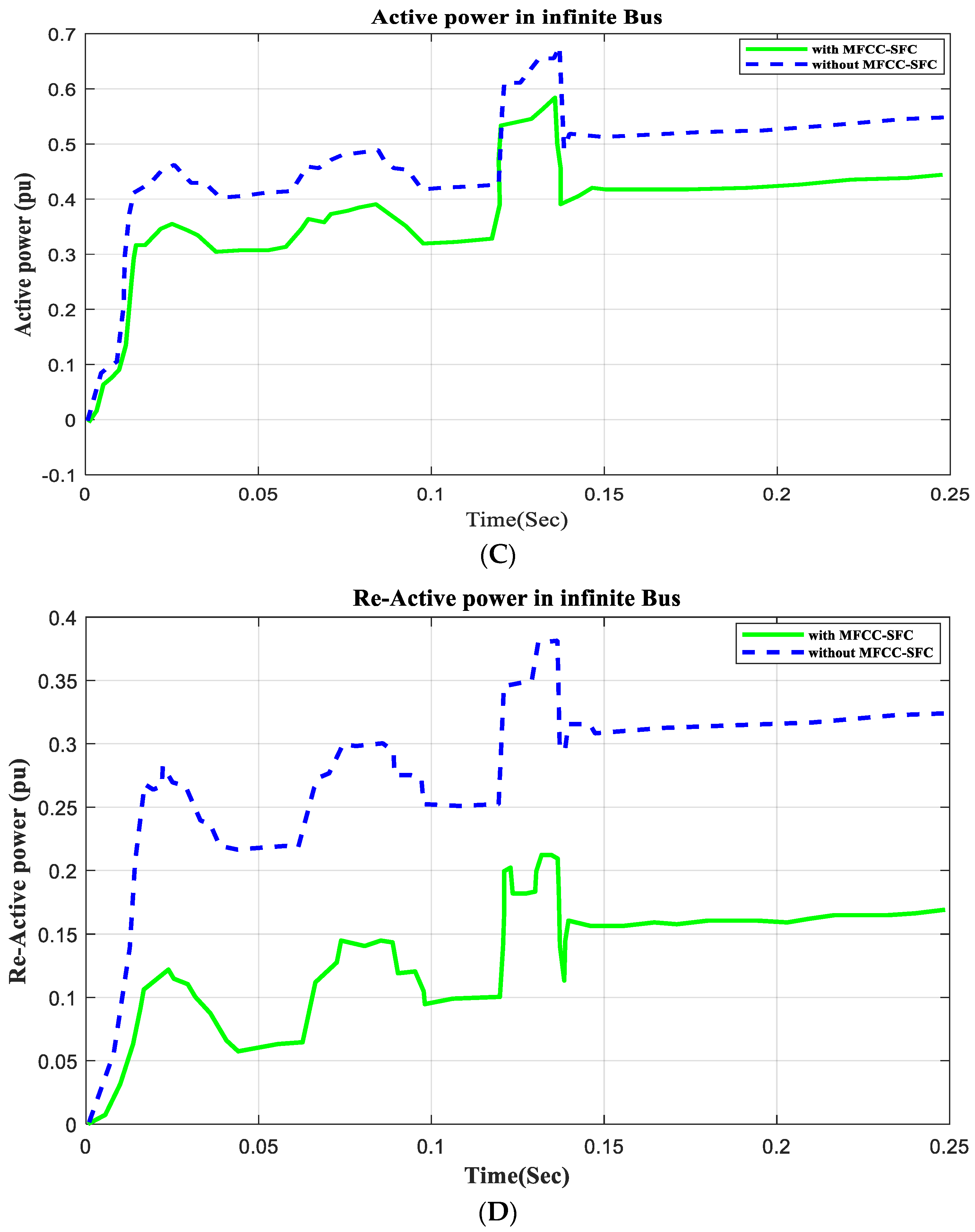
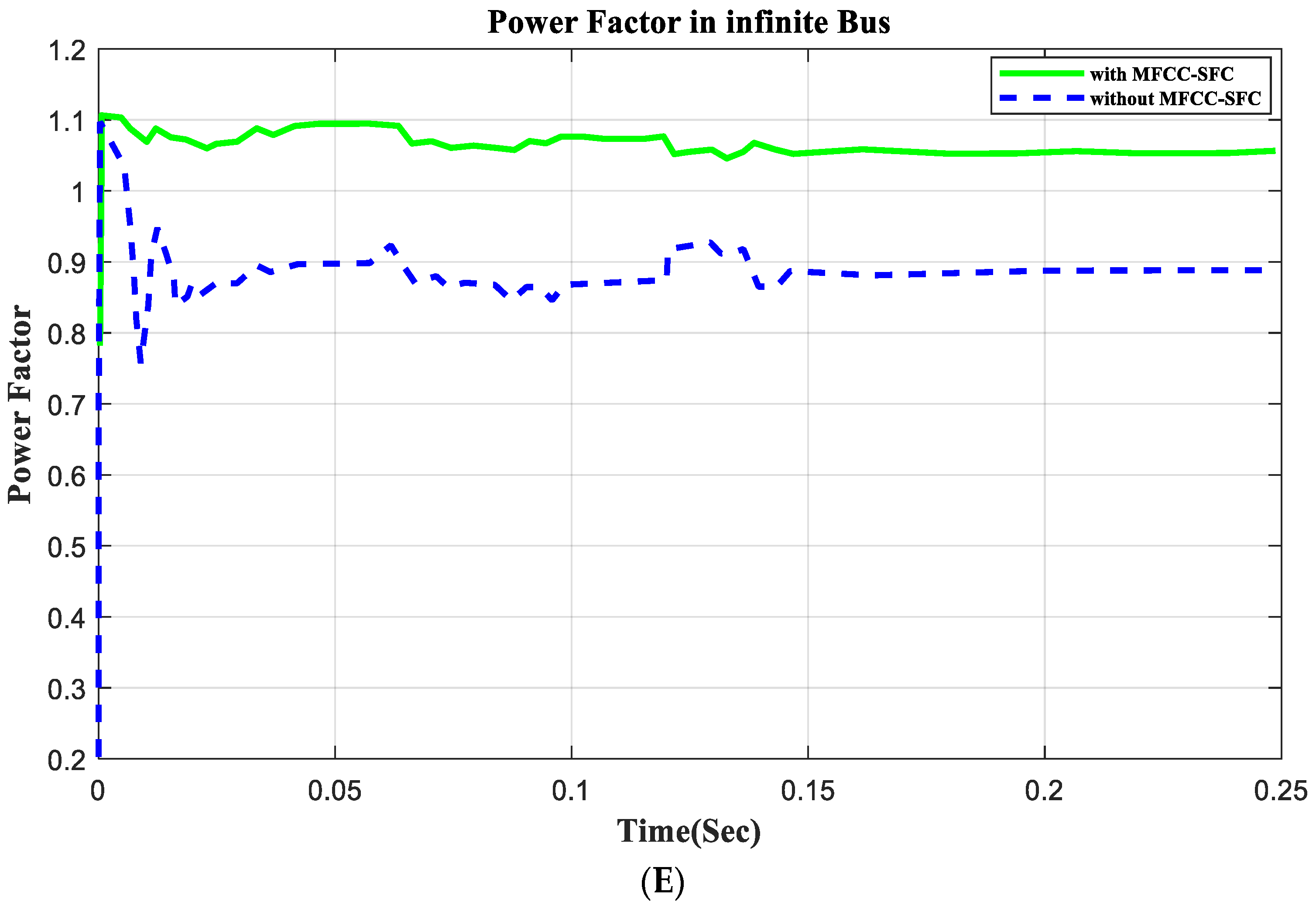
6.7. V, I, P, Q, and PF in Infinite Bus
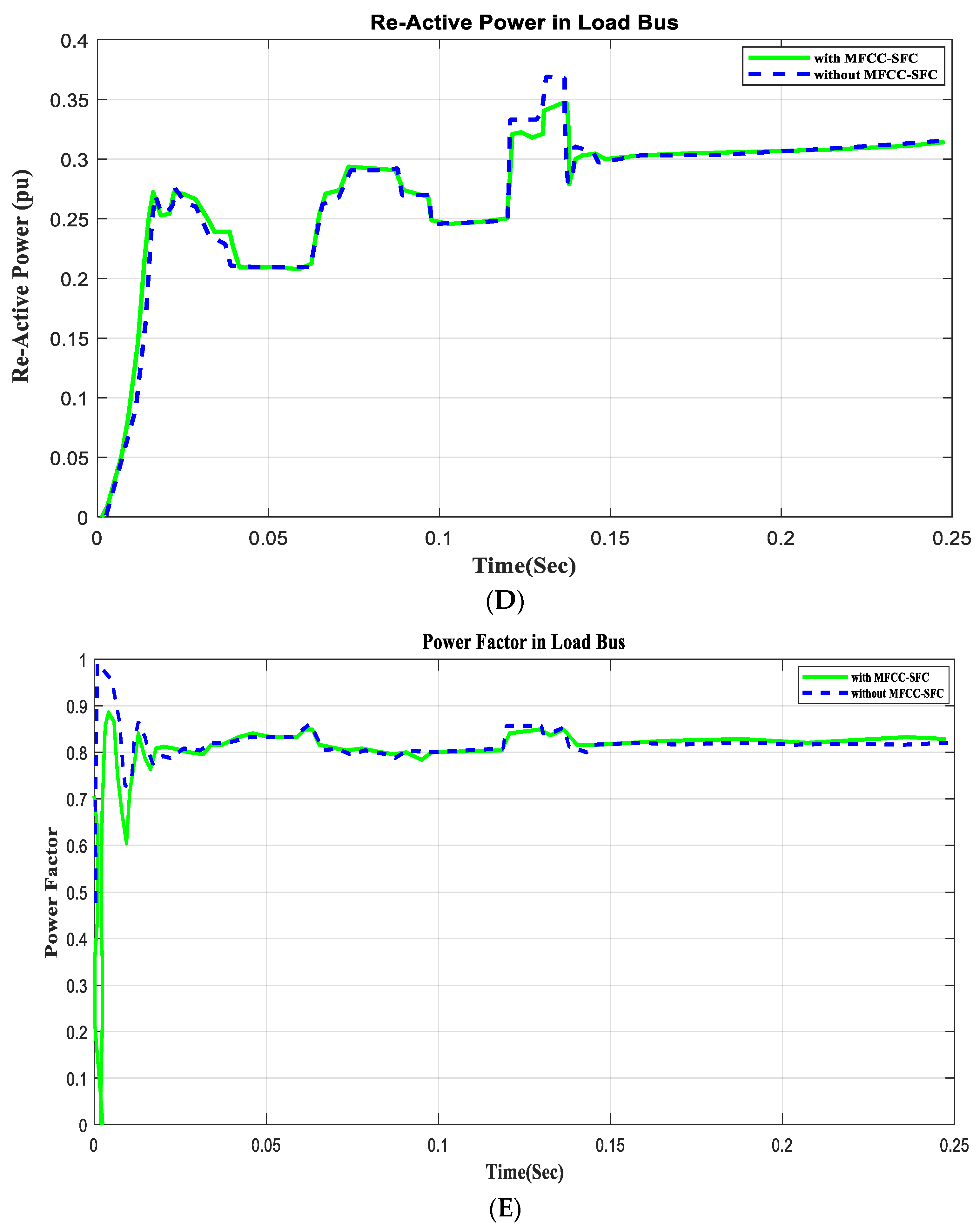
6.8. V, I, P, Q, and PF in Load Bus
7. Open and Close Circuits
8. Hybrid Load Variations
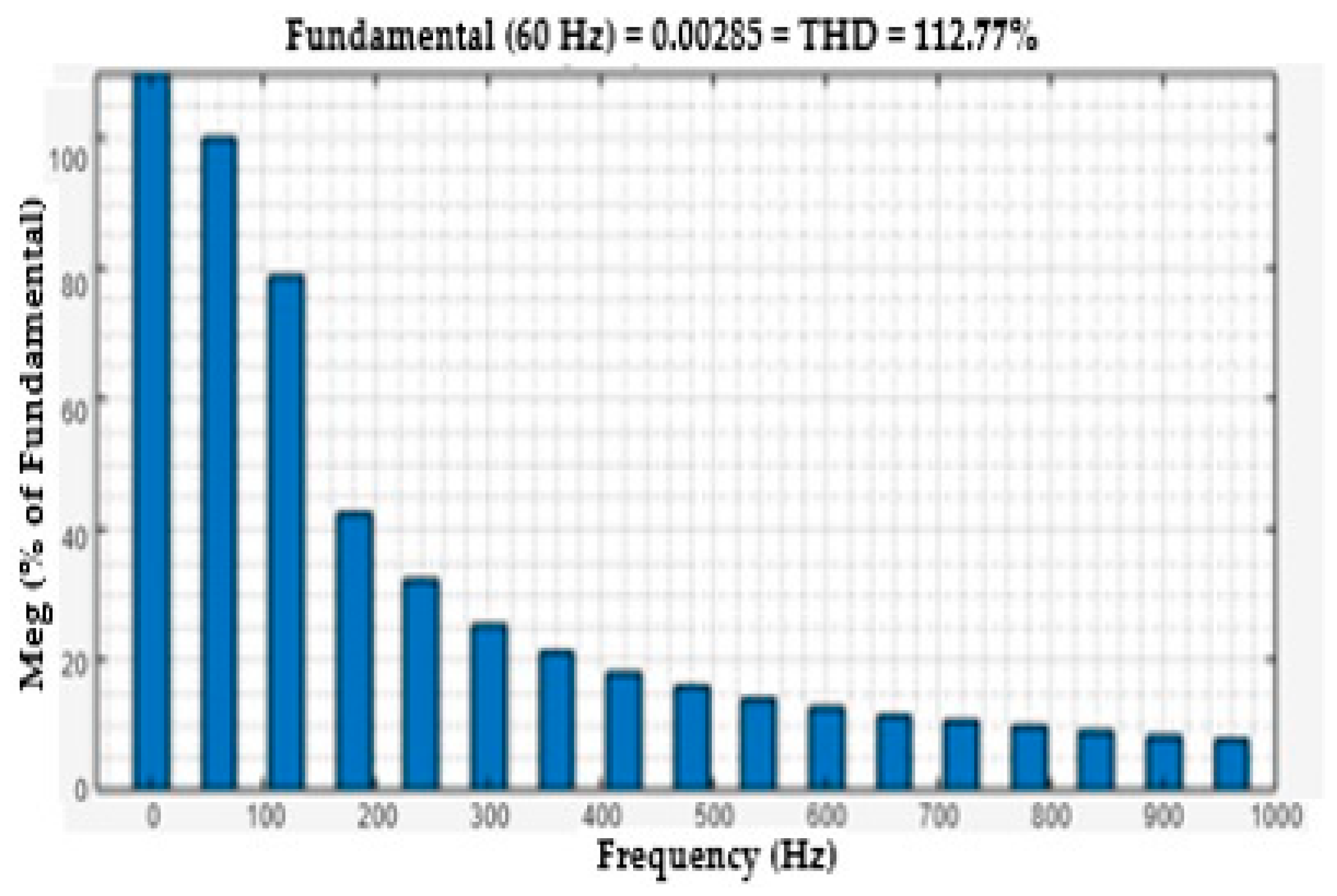
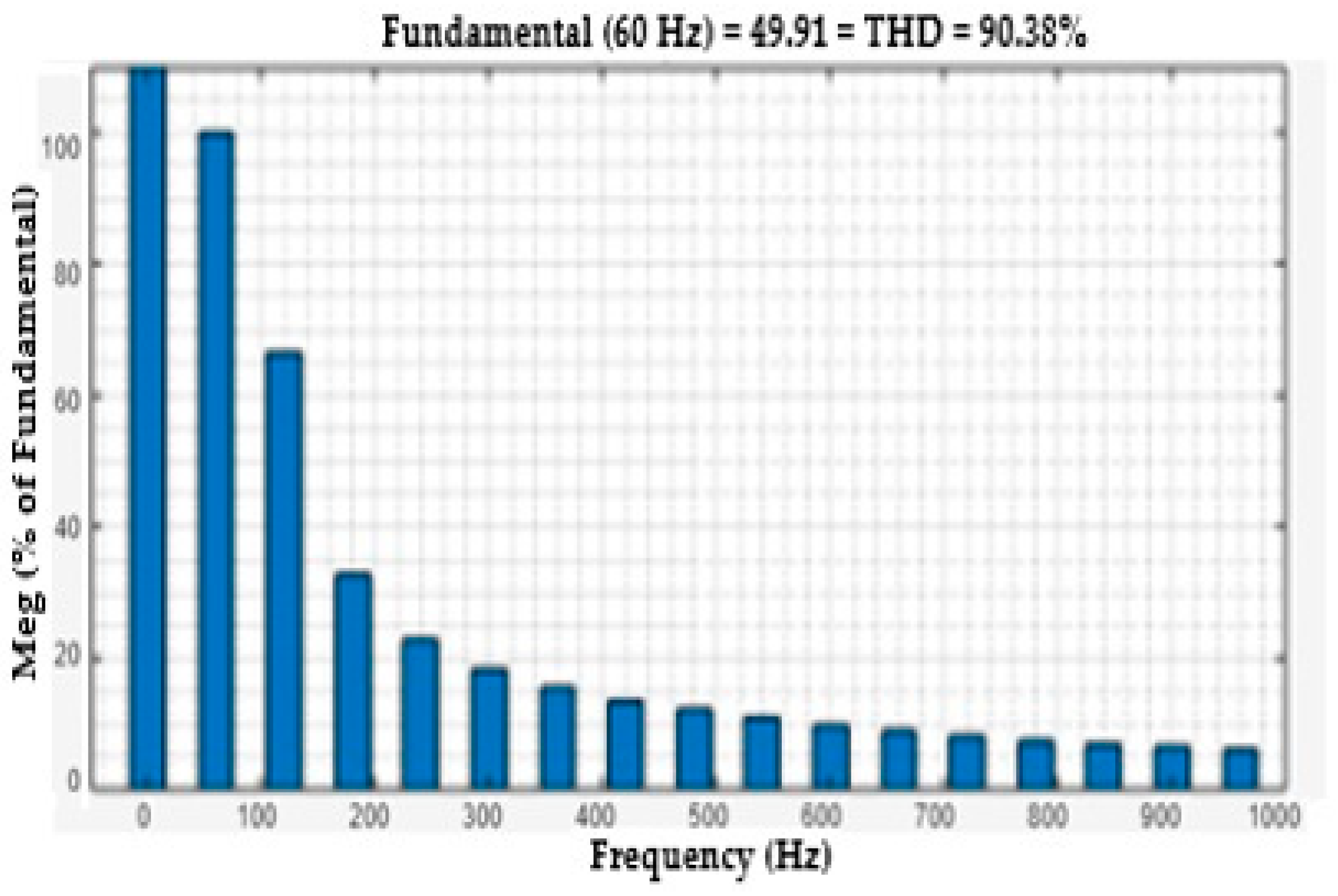
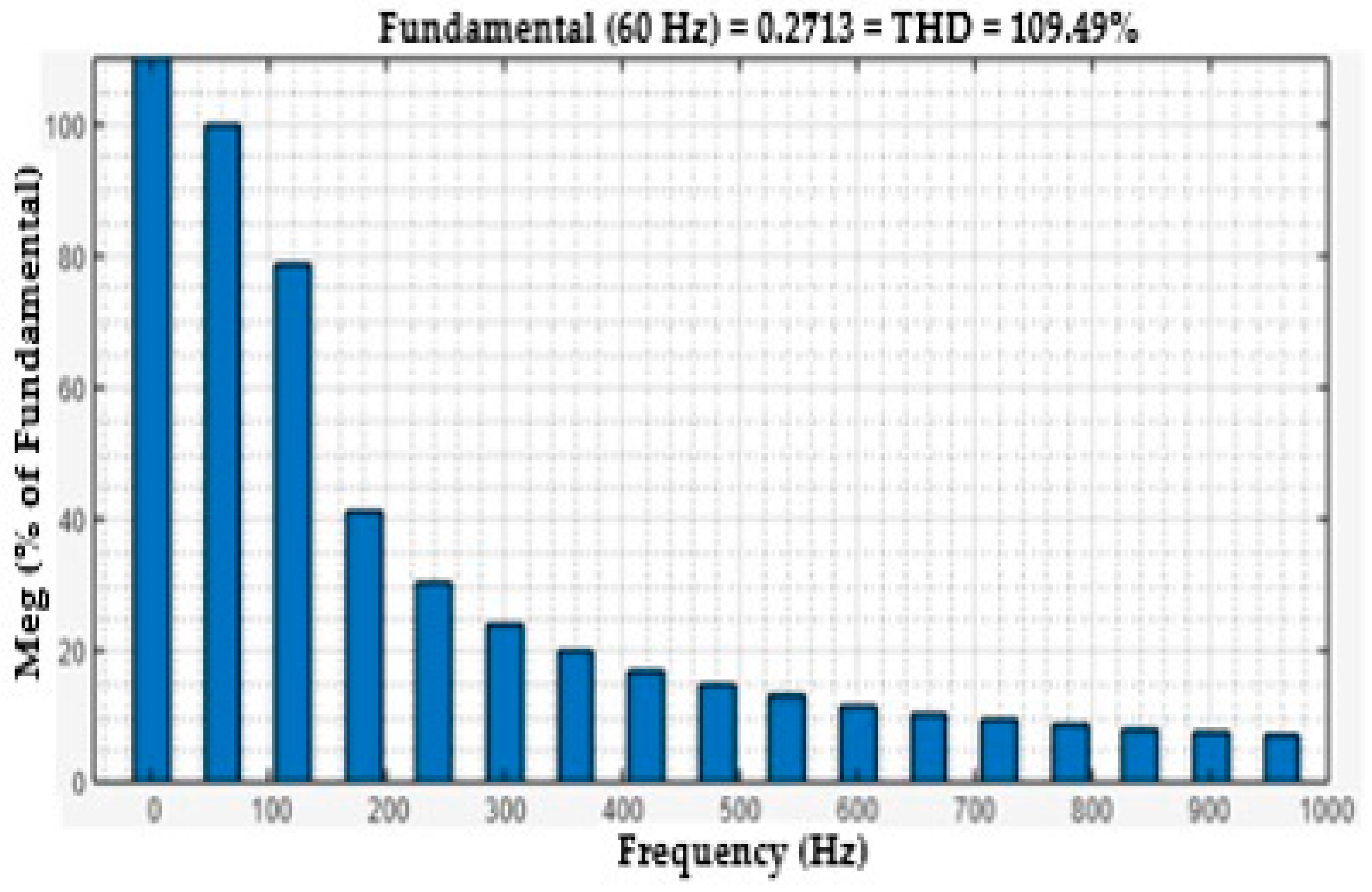
9. Power System Harmonics Analysis
10. Discussion of Digital Simulation Results
11. Conclusions and Extended Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. System Specifications
| Parameters | Value |
| AC Utility Grid Parameters | |
| Nominal Voltage | 138 kv (L-L), 100 MW |
| Ratio X/R | 10 |
| Base Power Vs Bus | 100 MVA |
| Base Power VL Bus | 200 MVA |
| Frequency | 1.750 KHz |
| FACTS-MFCC Parameters | |
| 275 µF | |
| , , | 1 Ω, 0.15 Ω, 3 mH |
| Width Modulation Proportional Integral Derivative (WMPID) Controller Parameters | |
| Ke, Kp, , , , | 0.7, 5, 1.5, 0.5, 0.5, 0.1 |
| Transmission Line | |
| Feeder | 25 kv (L-L),10 km |
| R/km, L/km | 0.4 Ω, 0.45 Ω |
Appendix B. Transformer, Motor and Load Specifications
| Parameters | Value |
| Transformer Parameters | |
| Power Transformer 1 | 138 kv to 25 kv, 5 MW |
| Power Transformer 2 | 25 kv to 4.16 kv, 5 MW |
| Hybrid AC Load Parameters | |
| Induction Motor | 2.5 MVA, 4 poles |
| Rs = 0.02765 pu, Ls = 0.0498 pu | |
| Rr = 0.01807 pu, Lr = 0.0497 pu | |
| Lm = 1.354 pu | |
| Linear Load | P = 2500 KW, Q = 2 MVAr |
| Nonlinear Load | P = 1250 KW, Q = 2 MVAr |
References
- Kazemi-Robati, E.; Hafezi, H.; Sepasian, M.S.; Silva, B. Probabilistic planning of virtually-hybrid harmonic filters inmodern distribution systems. In Proceedings of the 2023 International Conference on Smart Energy Systems and Technologies (SEST), Mugla, Turkey, 9 April 2023. [Google Scholar]
- Biswas, S.D.; Chowdhury, S.; Nandi, C.; Das, B. Power quality improvement with hybrid shunt active power filter. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Kerala, India, 17–20 December 2023. [Google Scholar]
- Sharaf, A.M.; Khaki, B. A novel FACTS hybrid modulated filter/capacitor compensator. In Proceedings of the 2012 International Conference on Smart Grid (SGE), Oshawa, ON, Canada, 27–29 August 2012; pp. 1–6. [Google Scholar]
- Golla, M.; Thangavel, S.; Simon, S.P.; Padhy, N.P.; Pannala, S. An improved hybrid control strategy for UAPF-based microgrid system for active power line conditioner with power flow control. In Proceedings of the 2023 IEEE International Conference on Power Electronics, Smart Grid, and Renewable Energy (PESGRE), Kerala, India, 17–20 December 2023. [Google Scholar]
- Yallamilli, R.S.; Mishra, M.K. Instantaneous symmetrical component theory based parallel grid side converter control strategy for microgrid power management. IEEE Trans. Sustain. Energy 2019, 10, 682–692. [Google Scholar] [CrossRef]
- Şahin, M.E.; Sharaf, A.M. A Robust Decoupled Microgrid Charging Scheme Using a DC Green Plug-Switched Filter Compensator. In Fast Charging and Resilient Transportation Infrastructures in Smart Cities; Springer International Publishing: Cham, Switzerland, 2022; pp. 89–116. [Google Scholar]
- Ayman, F.; Sharaf, A.M. A novel filter compensation scheme for hybrid (photovoltaic–fuel cell)-dc utilization systems. Int. J. Adv. Renew. Energy Res. 2012, 1, 283–291. [Google Scholar]
- Mohammed, A. Performance enhancement of stand-alone photovoltaic systems with household loads. In Proceedings of the 2019 2nd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 1–3 May 2019; pp. 1–6. [Google Scholar]
- Sophia, F.; Irtiza, M.; Hoffman, A.; Sardahi, Y. Fuzzy Logic Control for Flexible Joint Manipulator: An Experimental Implementation. Int. J. Mech. Mechatron. Eng. 2024, 18, 16–20. [Google Scholar]
- Chao, W.; Dai, L.; Huang, J.; Chen, M. Research on Hybrid Active Power Filter and Its Control and Protection System for LCC-HVDC. In Proceedings of the 2023 IEEE 11th Joint International Information Technology and Artificial Intelligence Conference (ITAIC), Chongqing, China, 8–10 December 2023; Volume 11. [Google Scholar]
- Wang, L.; Sun, W.; Xu, H.; Dong, J.; Li, C.; Li, W. A Three-Phase-Module-Parallel Si & SiC Hybrid Inverter with Smaller Filter Size and Low Cost. In Proceedings of the 2022 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Haining, China, 28–31 October 2022. [Google Scholar]
- Catata, E.O.H.; Neto, P.J.D.S.; De Paula, M.V.; Silveira, J.P.C.; Barros, T.A.D.S.; Ruppert Filho, E. In-Loop Adaptive Filters to Improve the Power Quality of Switched Reluctance Generator in WECS. IEEE Access 2021, 10, 2941–2951. [Google Scholar] [CrossRef]
- Singh, V.; Iqbal, S.J.; Gupta, S.; Yadav, A. Performance Evaluation of a Shunt Active Power Filter for Current Harmonic Elimination. In Proceedings of the 2021 IEEE Region 10 Symposium (TENSYMP), Jeju, Republic of Korea, 23–25 August 2021. [Google Scholar]
- Lima, V.L.; Dezuo, T.J.M. Robust Switching Rule Design for Single-Phase Shunt Active Power Filter. In Proceedings of the 2021 Brazilian Power Electronics Conference (COBEP), Joao Pessoa, Brazil, 7–10 November 2021. [Google Scholar]
- Lin, H.; Wu, L.; Guo, X.; Chen, G. Shunt active power filter using SiC-MOSFET with high accuracy compensation. In Proceedings of the 2020 IEEE 9th International Power Electronics and Motion Control Conference (IPEMC2020-ECCE Asia), Nanjing, China, 29 November–2 December 2020. [Google Scholar]
- Daftary, D.; Shah, M.T. Design and analysis of hybrid active power filter for current harmonics mitigation. In Proceedings of the 2019 IEEE 16th India Council International Conference (INDICON), Rajkot, India, 13–15 December 2019. [Google Scholar]
- Nolasco, D.H.; Alves, D.K.; Costa, F.B.; Palmeira, E.S.; Ribeiro, R.L.; Nunes, E.A. Application of Fuzzy Systems in Power Quality: Diagnosis of Total Harmonic Distortions. In Proceedings of the 2018 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar]
- Absar, M.N.; Islam, M.F.; Ahmed, A. Power quality improvement of a proposed grid-connected hybrid system by load flow analysis using static VAR compensator. Heliyon 2023, 9, e17915. [Google Scholar] [CrossRef] [PubMed]
- Sharaf, A.M.; Huang, H.; Chang, L. Power quality and nonlinear load voltage stabilization using error driven switched passive power filter. In Proceedings of the IEEE International Symposium on Industrial Electronics, Athens, Greece, 10–14 July 1995; pp. 616–621. [Google Scholar]
- Sharaf, A.M.; Gandoman, F.H. A Flexible Facts Based Scheme for Smart Grid-PV-Battery Storage Systems. Int. J. Distrib. Energy Resour. 2014, 10, 261–271. [Google Scholar]
- Nejabatkhah, F.; Li, Y.; Tian, H. Power quality control of smart hybrid AC/DC Microgrids: An Overview. IEEE Access 2019, 7, 52295–52318. [Google Scholar] [CrossRef]
- Bloul, A.M.; Sharaf, A.M.; Aly, H.H.; Gu, J. An Energy Efficient Green Plug Filter Compensation Scheme for Hybrid Nonlinear Loads. Int. J. Eng. Innov. Res. 2023, 12, 2277–5668. [Google Scholar]
- Dendouga, A.; Dendouga, A.; Essounbouli, N. Performance Enhancement of Wind Turbine Systems using Type-2 Fuzzy Logic Control: Comparative study. In Proceedings of the 19th International Multi-Conference on Systems, Signals & Devices (SSD’22), Serif, Algeria, 6–10 May 2022. [Google Scholar]
- Al-Bashayreh, Q.A.H.; Kiftaro, A.; Alsheikh, M.; Jaradat, M.A. An Intelligent Controller for an Assisted Electric Wheelchair based on Interval Type-2 Fuzzy Logic. In Proceedings of the IEEE Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2023. [Google Scholar]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An Overview on Thermal Safety Issues of Lithium-ion Batteries for Electric Vehicle Application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Dong, H.; Xi, J. Model Predictive Longitudinal Motion Control for the Unmanned Ground Vehicle with a Trajectory Tracking Model. IEEE Trans. Veh. Technol. 2022, 71, 1397–1410. [Google Scholar] [CrossRef]
- Agrawal, S.; Sharma, D.; Gupta, V.K.; Somani, R.K. Performance Evaluation of 3-Phase 4-Wire SAPF based on Synchronizing EPLL with Fuzzy Logic Controller. In Proceedings of the 2nd IEEE International Conference on Power Electronics, Intelligent Control and Energy Systems, ICPEICES, Delhi, India, 22–24 October 2018. [Google Scholar]
- Zobaa, A.F.; Abdel Aleem, S.H. Power Quality in Future Electrical Power Systems; Energy Engineering; IET Digital Library: London, UK, 2017; pp. 200–230. [Google Scholar]
- Hagras, H. A Hierarchical type-2 Fuzzy Logic Control Architecture for Autonomous Mobile Robots. IEEE Trans. Fuzzy Syst. 2004, 12, 524–539. [Google Scholar] [CrossRef]
- EI-Arini, M.M.; Youssef, M.T.; Hendawy, H.H. Voltage sag analysis and its reduction to improve power system performance. In Proceedings of the IEEE Eleventh International Middle East Power Systems Conference, Clemson, SC, USA, 19–21 December 2006. [Google Scholar]
- Mendel, J.; Hagras, H.; Tan, W.W.; Melek, W.W.; Ying, H. Introduction to Type-2 Fuzzy Logic Control: Theory and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Mendel, J.; John, R. Type-2 Fuzzy Sets Made Simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Hamza, M.F.; Yap, H.J.; Choudhury, I. Advances on the Use of Meta-Heuristic Algorithms to Optimize Type-2 Fuzzy Logic Systems for Prediction, Classification, Clustering and Pattern Recognition. J. Comput. Theor. Nanosci. 2016, 13, 96–109. [Google Scholar] [CrossRef]








| Buses | Source Bus, vs. (pu) | Load Bus, VL (pu) | ||||||
|---|---|---|---|---|---|---|---|---|
| V | I | P | PF | V | I | P | PF | |
| Without MFCC | 1.0 | 0.7 | 0.46 | 0.68 | 1.0 | 0.65 | 0.35 | 0.75 |
| With MFCC | 1.01 | 0.75 | 0.52 | 0.8.2 | 1.05 | 0.7 | 0.4 | 0.79 |
| Improvement | 0.01 | 0.05 | 0.06 | 0.14 | 0.05 | 0.05 | 0.05 | 0.04 |
| % Improvement | 1% | 5% | 6% | 14% | 5% | 5% | 5% | 4% |
| Buses | Source Bus, vs. (pu) | Load Bus, VL (pu) | ||||||
|---|---|---|---|---|---|---|---|---|
| V | I | P | PF | V | I | P | PF | |
| Without MFCC | 1.0 | 0.8 | 0.35 | 0.78 | 0.8 | 0.68 | 0.3 | 0.8 |
| With MFCC | 1.01 | 0.9 | 0.5 | 0.98 | 1.0 | 0.75 | 0.4 | 0.98 |
| Improvement | 0.01 | 0.1 | 0.15 | 0.2 | 0.2 | 0.05 | 0.1 | 0.18 |
| % Improvement | 1% | 10% | 15% | 20% | 20% | 7% | 10% | 18% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bloul, A.M.; Abuhamdah, M.; Sharaf, A.M.; Aly, H.H.; Gu, J. An Efficient Shunt Modulated AC Green Plug–Switched Filter Compensation Scheme for Nonlinear Loads. Energies 2024, 17, 2426. https://doi.org/10.3390/en17102426
Bloul AM, Abuhamdah M, Sharaf AM, Aly HH, Gu J. An Efficient Shunt Modulated AC Green Plug–Switched Filter Compensation Scheme for Nonlinear Loads. Energies. 2024; 17(10):2426. https://doi.org/10.3390/en17102426
Chicago/Turabian StyleBloul, Albe M., Mohamad Abuhamdah, Adel M. Sharaf, Hamed H. Aly, and Jason Gu. 2024. "An Efficient Shunt Modulated AC Green Plug–Switched Filter Compensation Scheme for Nonlinear Loads" Energies 17, no. 10: 2426. https://doi.org/10.3390/en17102426






