Research on Strategies for Air-Source Heat Pump Load Aggregation to Participate in Multi-Scenario Demand Response
Abstract
:1. Introduction
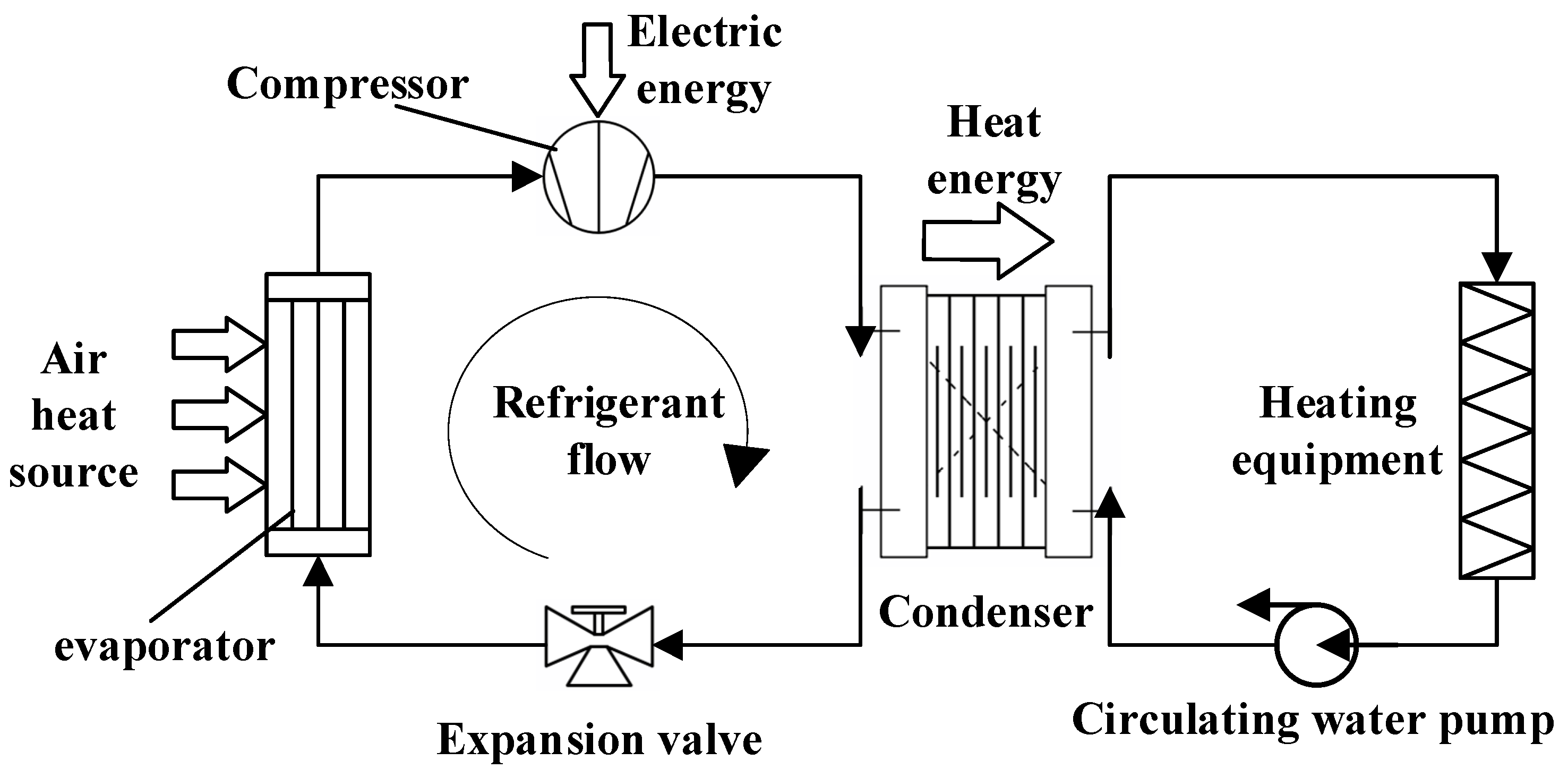
2. Air-Source Heat Pump Load Aggregation Management and Control Architecture
3. Thermodynamic Modeling of Air-Source Heat Pump Loads
3.1. Analysis of Air-Source Heat Pump Load Operation Mechanism
3.2. Air-Source Heat Pump Load Aggregation Model
3.2.1. Heat Pump Unit’s Mainframe Model
3.2.2. Heat Pump Water-Cycle Modeling
3.2.3. Heat Pump End Heat-Exchange Modeling
4. Optimized Operation Control Methods for Air-Source Heat Pump Loads
4.1. MPC-Based Optimal Operation Control Method for Heat Pump Loads
4.1.1. Objective Function
4.1.2. Constraints
4.2. Methodology for Assessing Adjustable Capacity
5. Air-Source Heat Pump Load Aggregation Regulation Model
5.1. Optimization and Synergistic Task Assignment for Multiple Heat Pump Loads
5.1.1. Objective Function
5.1.2. Constraints
5.2. Aggregate Regulated Heat Pump-Load Recovery Modeling
5.3. Solution Method Based on Multi-Objective Atomic Orbit Search Algorithm
6. Calculated Simulation
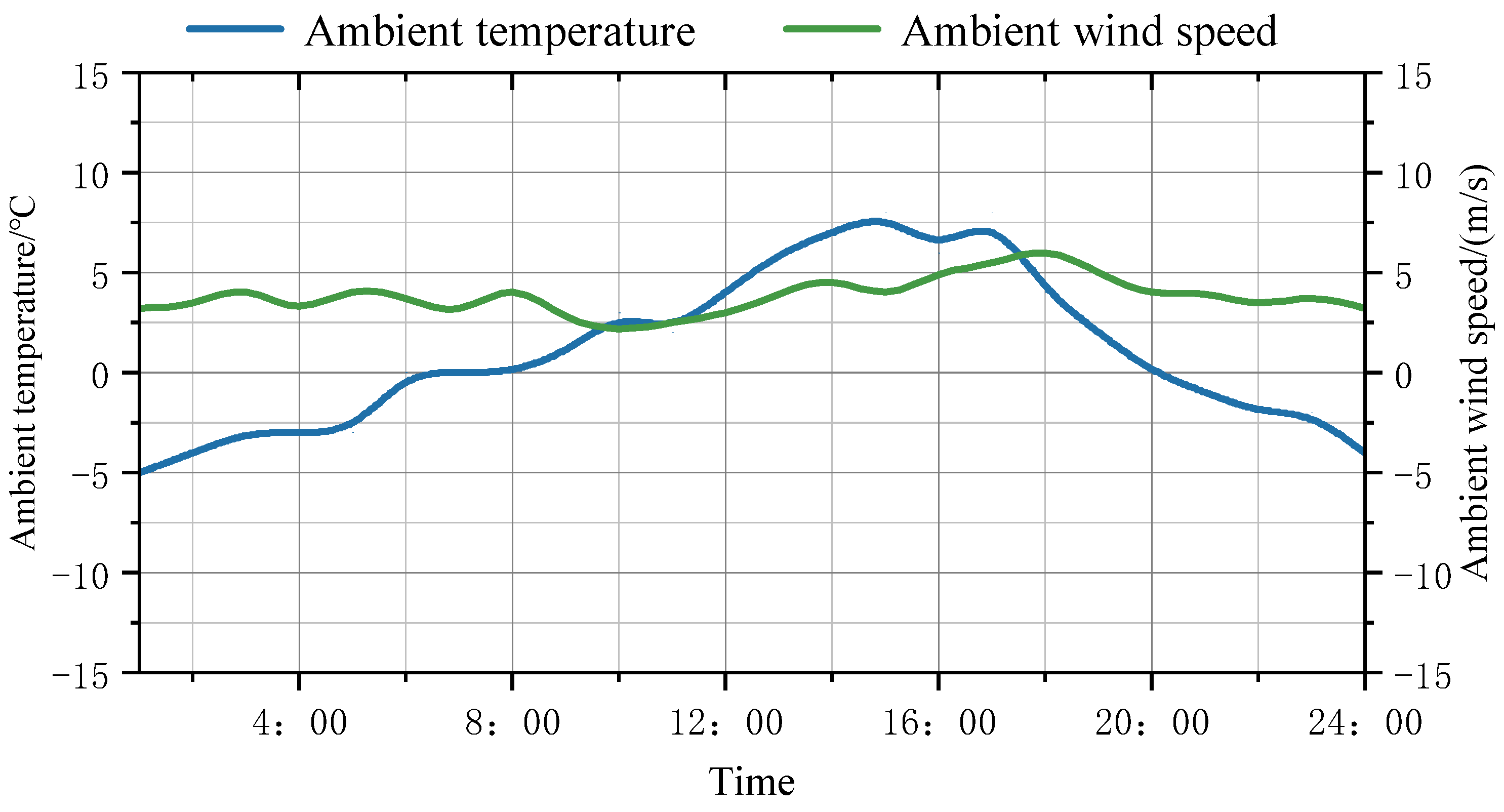
6.1. Basic Data
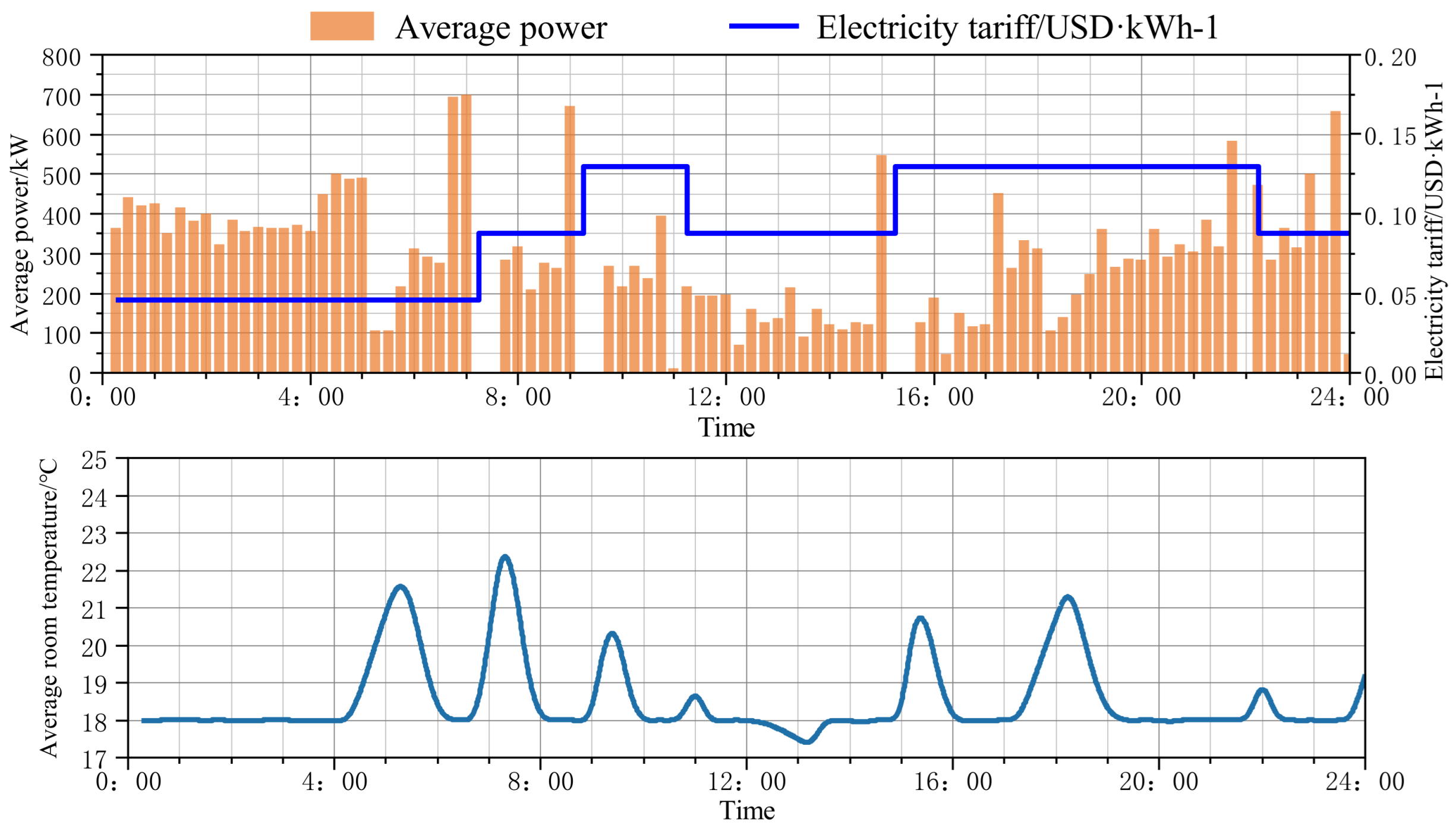
6.2. Analysis of MPC-Based Heat Pump Load Optimization Operation Methods
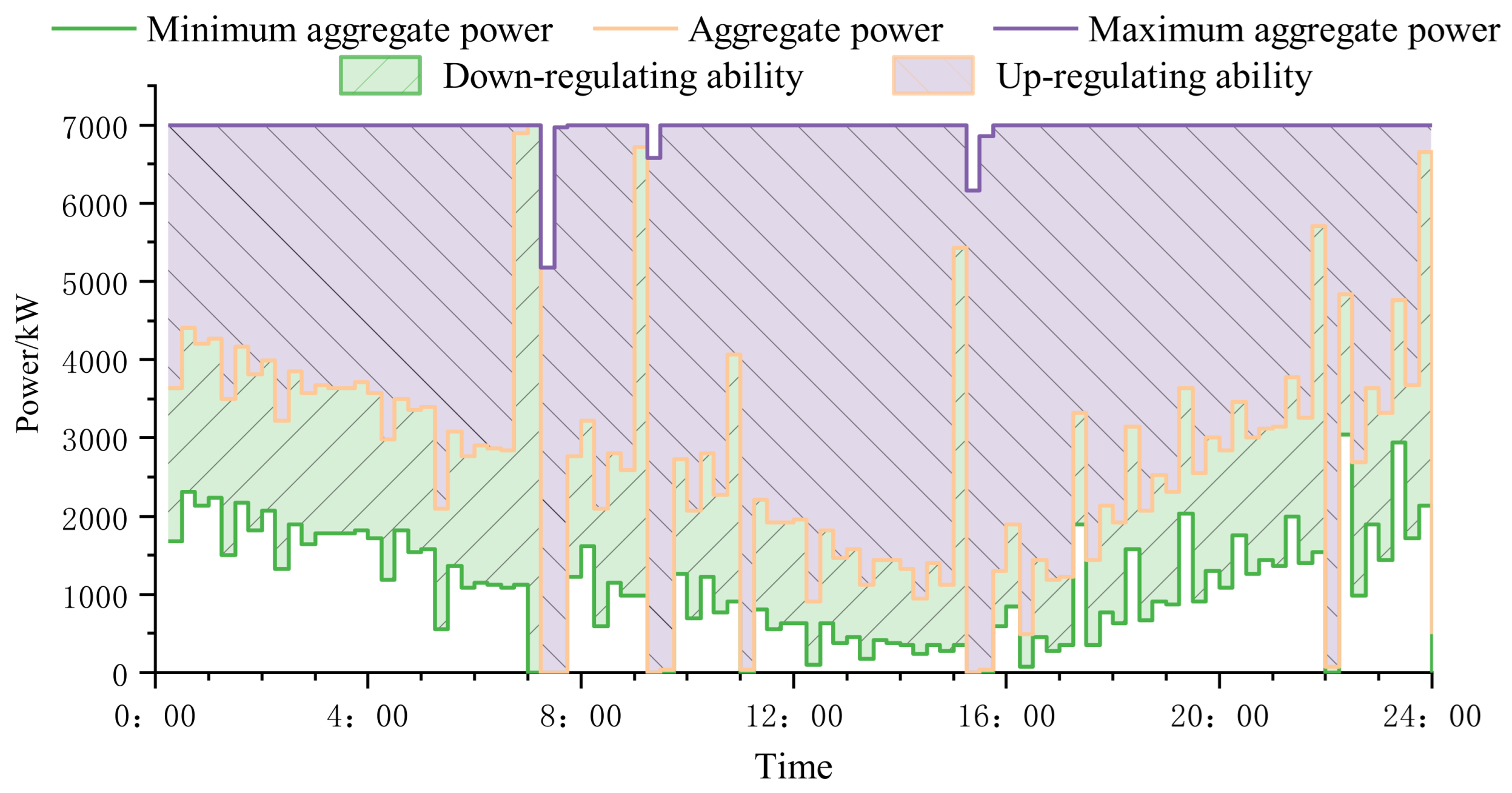
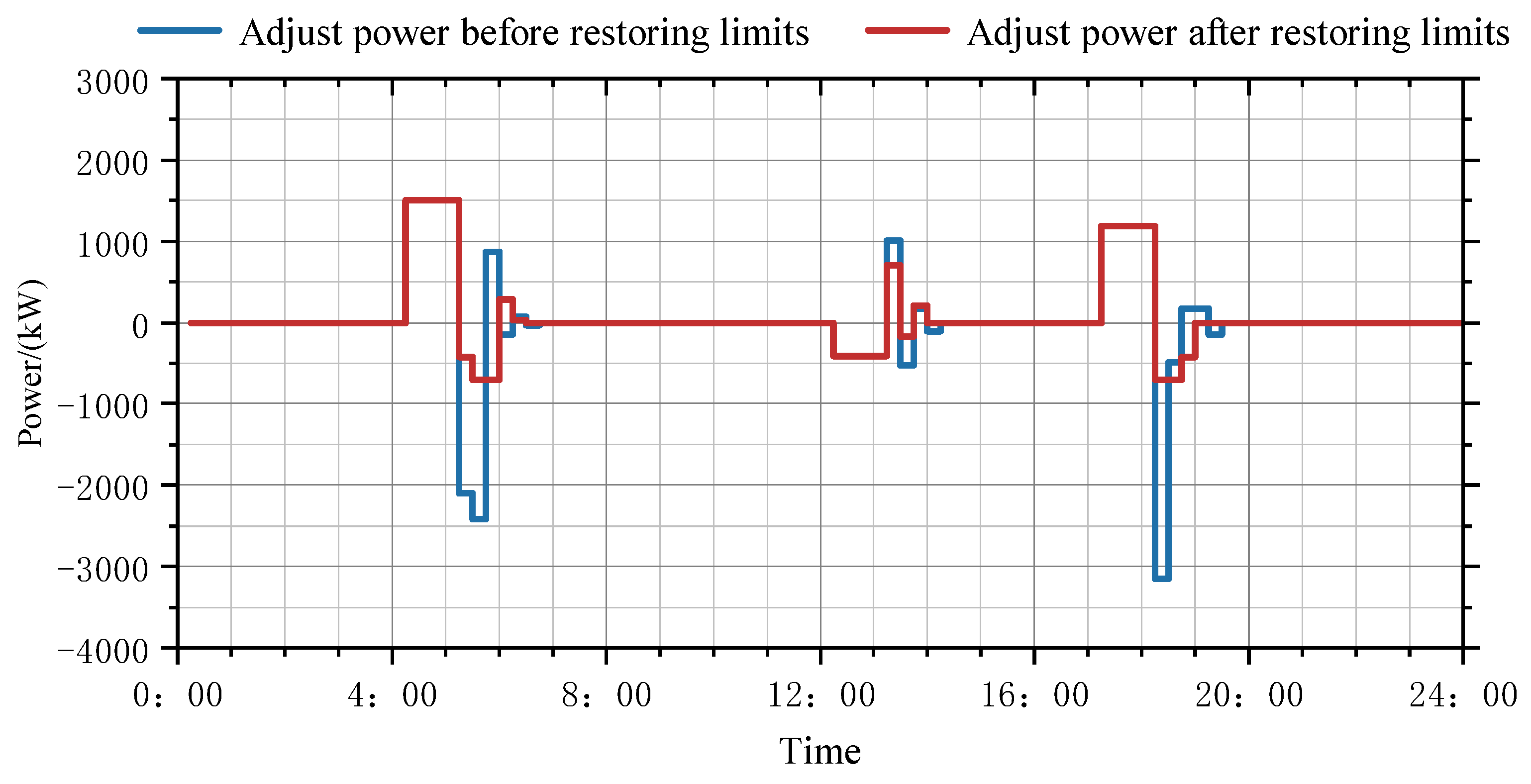
6.3. Heat Pump Load’s Participation in Demand Response and Load Recovery Analysis
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, G.; Lin, J.; Sifuentes, F.; Liu, X.; Abhyankar, N.; Phadke, A. Rapid cost decrease of renewables and storage accelerates the decarbonization of China’s power system. Nat. Commun. 2020, 11, 2486. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Li, F.; Zhang, G.; Yin, C. Analysis of energy storage demand for peak shaving and frequency regulation of power systems with high penetration of renewable energy. Energy 2023, 267, 126586. [Google Scholar] [CrossRef]
- Wang, X.; Xia, L.; Bales, C.; Zhang, X.; Copertaro, B.; Pan, S.; Wu, J. A systematic review of recent air source heat pump (ASHP) systems assisted by solar thermal, photovoltaic and photovoltaic/thermal sources. Renew. Energy 2020, 146, 2472–2487. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Jiang, Y.; Zhou, H.; Ju, P. A review of key technologies for temperature-controlled loads to provide auxiliary services for power systems. Power Syst. Autom. 2022, 46, 191–207. (In Chinese) [Google Scholar] [CrossRef]
- Afram, A.; Janabi-Sharifi, F. Theory and applications of HVAC control systems—A review of model predictive control (MPC). Build. Environ. 2014, 72, 343–355. [Google Scholar] [CrossRef]
- Sturzenegger, D.; Gyalistras, D.; Gwerder, M.; Sagerschnig, C.; Morari, M.; Smith, R. Model Predictive Control of a Swiss office building. Clima 2013, 2013, 3227–3236. [Google Scholar] [CrossRef]
- Masy, G.; Georges, E.; Verhelst, C.; Lemort, V.; André, P. Smart grid energy flexible buildings through the use of heat pumps and building thermal mass as energy storage in the Belgian context. Sci. Technol. Built Environ. 2015, 21, 800–811. [Google Scholar] [CrossRef]
- Li, X.; Malkawi, A. Multi-objective optimization for thermal mass model predictive control in small and medium size commercial buildings under summer weather conditions. Energy 2016, 112, 1194–1206. [Google Scholar] [CrossRef]
- Li, N.; Chu, X.; Zhang, W.; Liu, M. Multiregional air conditioning load aggregation model considering parameter space differences. J. Electr. Power Syst. Autom. 2012, 24, 19–24. (In Chinese) [Google Scholar] [CrossRef]
- Wang, Y.; Tong, Y.; Huang, M.; Yang, L.; Zhao, H. Research on virtual energy storage model of air conditioning load based on demand side response. Power Grid Technol. 2017, 41, 394–401. (In Chinese) [Google Scholar] [CrossRef]
- Wang, D.; Lan, Y.; Jia, H.; Hu, Q.; Yu, J.; Yao, C. Double-layer optimization of central air conditioning cluster demand response based on elastic temperature adjustable margin. Power Syst. Autom. 2018, 42, 118–126. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.; Yao, J.; Yong, T.; Ju, P.; Yang, S.; Shi, X. Research on evaluation method of aggregate power and response potential of residential temperature-controlled loads. Chin. J. Electr. Eng. 2017, 37, 5519–5528. (In Chinese) [Google Scholar] [CrossRef]
- Feng, X.F.; Lin, G.Y.; Xu, Q.S.; Lu, S.X.; Xie, T.K. Double-layer dynamic optimization dispatching decision method for cluster air-conditioning load. Electr. Power Autom. Equip. 2020, 40, 29–36. (In Chinese) [Google Scholar] [CrossRef]
- Wang, X.Y.; Xu, J.; Liao, S.Y.; Ke, D.P. Flexible load regulation margin evaluation method considering virtual energy storage characteristics. Huadian Technol. 2021, 43, 37–45. (In Chinese) [Google Scholar] [CrossRef]
- Lu, N. An evaluation of the HVAC load potential for providing load balancing service. IEEE Trans. Smart Grid 2012, 3, 263–1270. [Google Scholar] [CrossRef]
- Bashash, S.; Fathy, H.K. Modeling and control of aggregate air conditioning loads for robust renewable power management. IEEE Trans. Control Syst. Technol. 2012, 21, 1318–1327. [Google Scholar] [CrossRef]
- Zhou, L.; Li, Y.; Gao, C. Improvement of temperature adjustment method and control strategy for aggregate air conditioning load. Chin. J. Electr. Eng. 2014, 34, 5579–5589. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, T.Y.; Jv, P.; Wang, C. Air conditioning load aggregation power model considering the randomness of user adjustment behavior. Power Syst. Autom. 2020, 44, 105–113. (In Chinese) [Google Scholar] [CrossRef]
- Liu, M.; Tian, Y.; Cheng, D.; Zhang, Y.; Ding, L. Modelling and control of central air-conditioning loads for power system emergency frequency control. IET Gener. Transm. Distrib. 2022, 16, 4054–4067. [Google Scholar] [CrossRef]
- Azizi, M.; Talatahari, S.; Khodadadi, N.; Sareh, P. Multiobjective atomic orbital search (MOAOS) for global and engineering design optimization. IEEE Access 2022, 10, 67727–67746. [Google Scholar] [CrossRef]
- Cheng, D.Y. Research on Source-Load Collaborative Backup Optimal Configuration Based on Air Conditioning Load Modeling. Ph.D. Thesis, Shandong University, Jinan, China, 2019. (In Chinese). [Google Scholar]



| Serial Number | Single Heat Pump Power/kW | Cout,i/J °C−1 | Cre,i/J·°C−1 | Cair,i/J·°C−1 | Kwater,i/W·°C−1 | Kroom-water,i/W·°C−1 | Kair,i/W·°C |
|---|---|---|---|---|---|---|---|
| 1 | 35 | 6.7 × 107 | 6.7 × 108 | 1.5 × 107 | 2.8 × 105 | 6.6 × 104 | 5.2 × 104 |
| 2 | 30 | 5.8 × 107 | 4.5 × 108 | 9.0 × 106 | 1.4 × 105 | 3.3 × 104 | 3.8 × 104 |
| 3 | 35 | 6.3 × 107 | 6.2 × 108 | 1.3 × 107 | 2.9 × 105 | 6.6 × 104 | 5.1 × 104 |
| 4 | 30 | 4.5 × 107 | 5.6 × 108 | 4.2 × 107 | 2.3 × 105 | 4.5 × 104 | 3.3 × 104 |
| 5 | 40 | 6.7 × 107 | 6.7 × 108 | 1.5 × 107 | 2.8 × 105 | 6.6 × 104 | 5.2 × 104 |
| 6 | 35 | 6.5 × 107 | 6.6 × 108 | 1.7 × 107 | 2.8 × 105 | 6.4 × 104 | 5.4 × 104 |
| 7 | 40 | 7.1 × 107 | 7.5 × 108 | 2.1 × 107 | 3.1 × 105 | 7.6 × 104 | 6.4 × 104 |
| 8 | 30 | 5.4 × 107 | 4.3 × 108 | 2.0 × 107 | 1.9 × 105 | 7.6 × 104 | 5.9 × 104 |
| 9 | 45 | 6.9 × 107 | 6.5 × 108 | 1.4 × 107 | 3.4 × 105 | 3.6 × 104 | 5.7 × 104 |
| 10 | 30 | 4.9 × 107 | 5.1 × 108 | 1.5 × 107 | 5.8 × 105 | 4.3 × 104 | 4.1 × 104 |
| Period of Time | Electricity Tariff/ USD·kWh−1 | Period of Time | Electricity Tariff/ USD·kWh−1 |
|---|---|---|---|
| 00:00–07:00 | 0.046 | 11:00–15:00 | 0.088 |
| 07:00–09:00 | 0.088 | 15:00–22:00 | 0.130 |
| 09:00–11:00 | 0.130 | 22:00–24:00 | 0.088 |
| Strategy | Running Cost/USD | Power Consumption/kWh |
|---|---|---|
| 1 | 7115.20 | 82,491 |
| 2 | 6155.21 | 72,647 |
| 3 | 5673.94 | 68,631 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, H.; Xie, X.; Liu, M.; Niu, S.; Su, H. Research on Strategies for Air-Source Heat Pump Load Aggregation to Participate in Multi-Scenario Demand Response. Energies 2024, 17, 2471. https://doi.org/10.3390/en17112471
Liang H, Xie X, Liu M, Niu S, Su H. Research on Strategies for Air-Source Heat Pump Load Aggregation to Participate in Multi-Scenario Demand Response. Energies. 2024; 17(11):2471. https://doi.org/10.3390/en17112471
Chicago/Turabian StyleLiang, Haiping, Xin Xie, Meng Liu, Shengsuo Niu, and Haifeng Su. 2024. "Research on Strategies for Air-Source Heat Pump Load Aggregation to Participate in Multi-Scenario Demand Response" Energies 17, no. 11: 2471. https://doi.org/10.3390/en17112471
APA StyleLiang, H., Xie, X., Liu, M., Niu, S., & Su, H. (2024). Research on Strategies for Air-Source Heat Pump Load Aggregation to Participate in Multi-Scenario Demand Response. Energies, 17(11), 2471. https://doi.org/10.3390/en17112471





