Comparison Study of the Wideband Oscillation Risk of MMC between Grid-Following and Grid-Forming Control
Abstract
1. Introduction
2. Broadband Mathematical Modeling of MMC
2.1. Configuration of MMC
2.2. Harmonic State-Space Modeling Theory
2.3. Broadband Impedance Model of Grid-Forming MMC
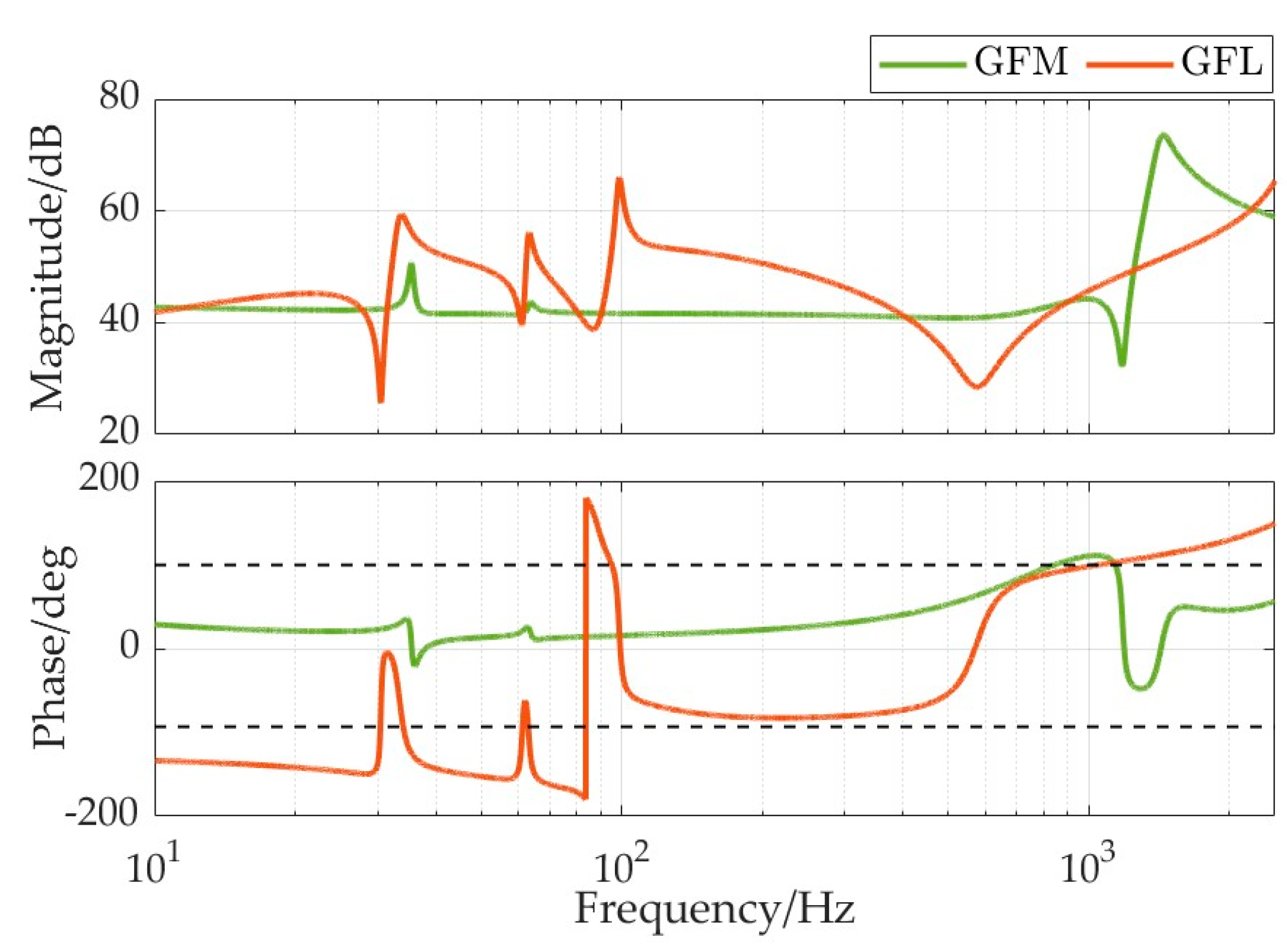
2.4. Verification of the Broadband Impedance Model
3. Analysis of Key Factors Influencing Wideband Impedance Characteristics of MMC
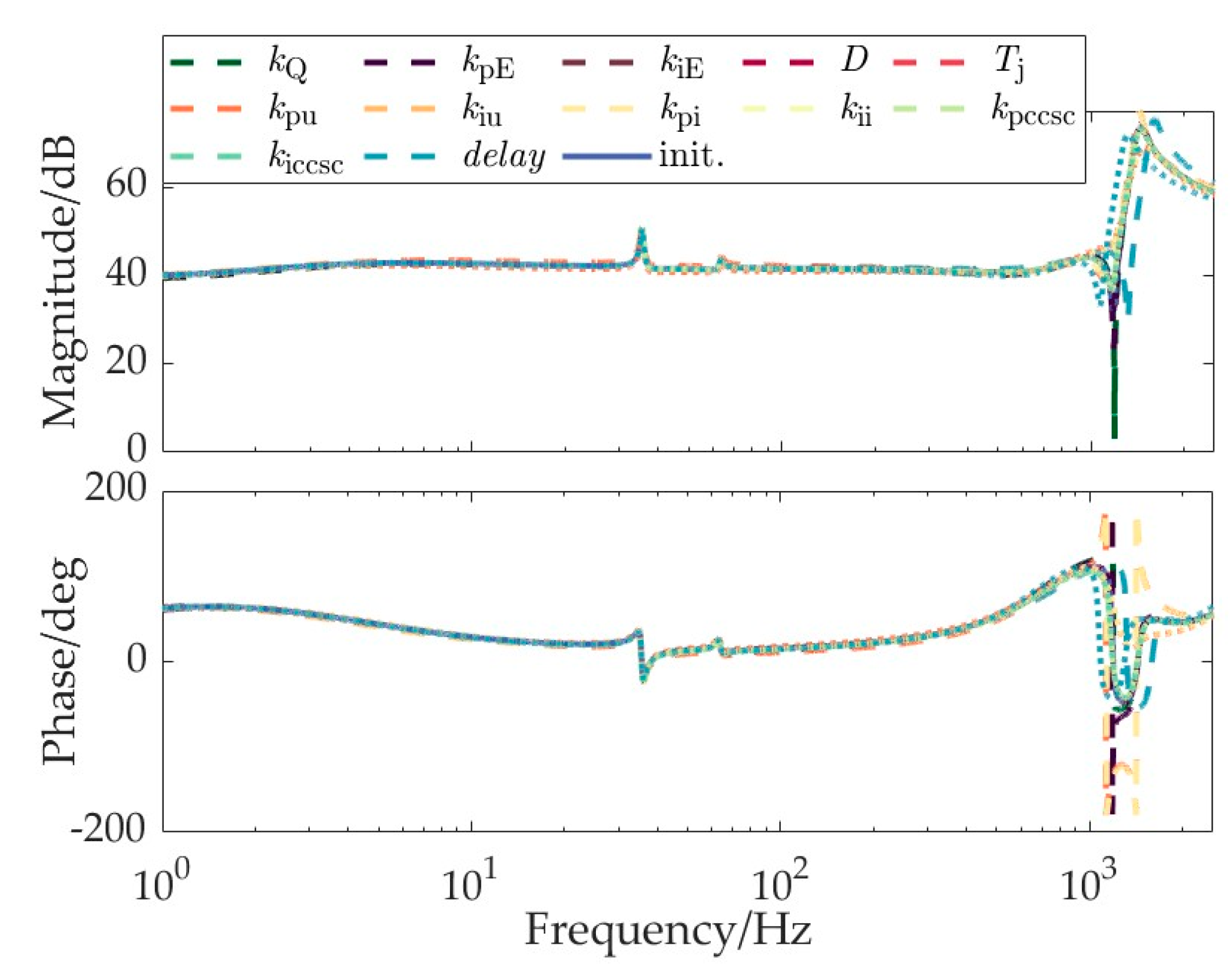
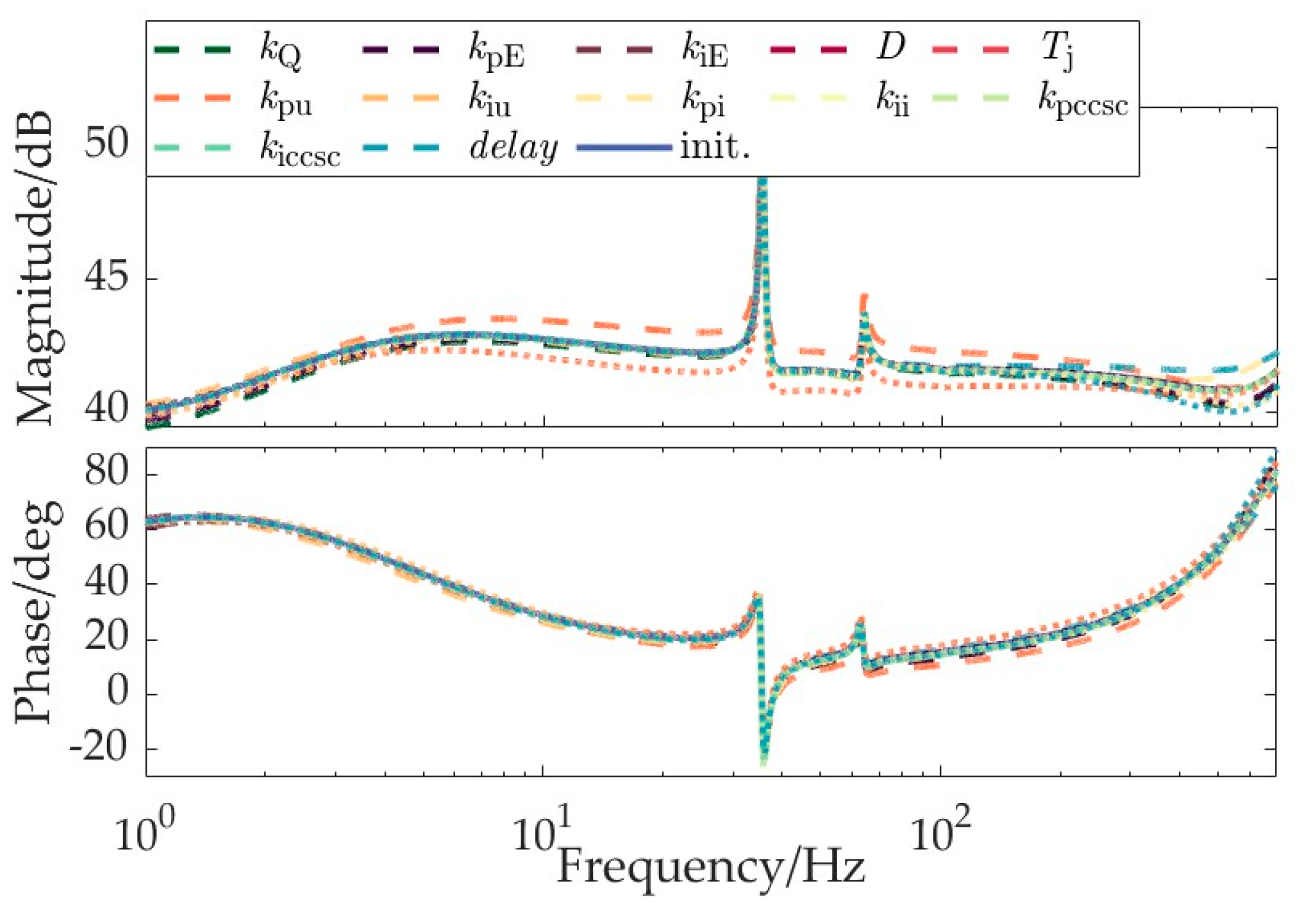
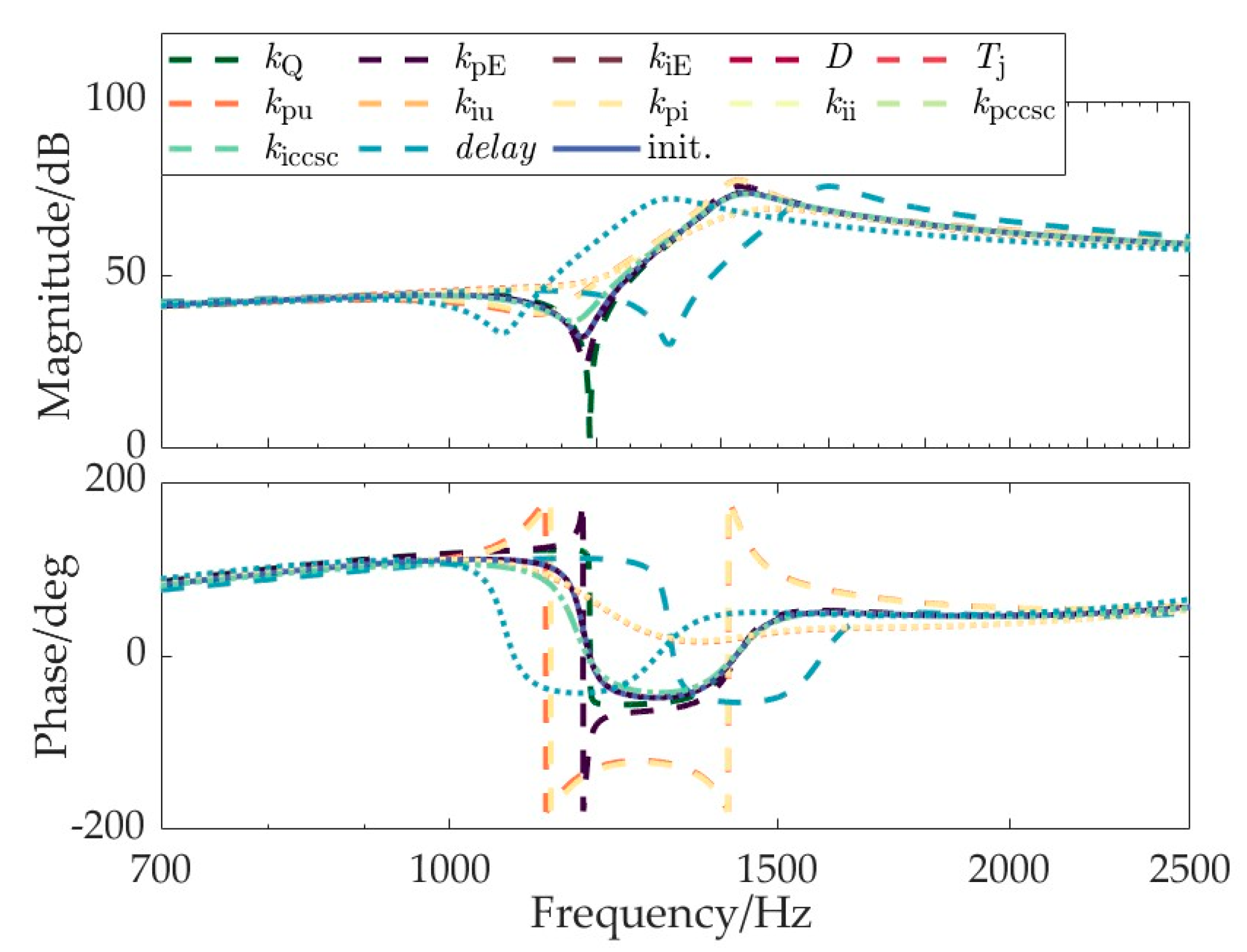
3.1. Analysis of Factors Affecting Wideband Impedance of MMC under Grid-Forming Control
3.2. Comparison of Influencing Factors for MMC under Two Control Modes
- From the perspective of the key influencing factors on impedance characteristics across different frequency bands: The influence of power control/voltage control is significant in the low-frequency range. In the high-frequency range, the effects of control delay and the proportional coefficient of current control are dominant. For grid-following MMC, there exists a mid-frequency band where the impact of PLL is significant. Conversely, for grid-forming MMC, the influence of virtual synchronous control parameters remains insignificant in terms of wideband impedance. Moreover, the virtual excitation control parameters of grid-forming MMC exhibit significant effects across different frequency bands;
- From the perspective of optimizing parameters to suppress oscillations: Under grid-following control, the influencing factors in each frequency band are relatively independent, with fewer factors affecting individual frequency bands, resulting in lower flexibility in parameter optimization. Under grid-forming control, oscillation risks only exist in relatively high-frequency bands, where there are more influencing factors. Therefore, there is more flexibility in parameter optimization.
4. Analysis and Simulation of Wideband Oscillation Risk in Grid-Forming MMC
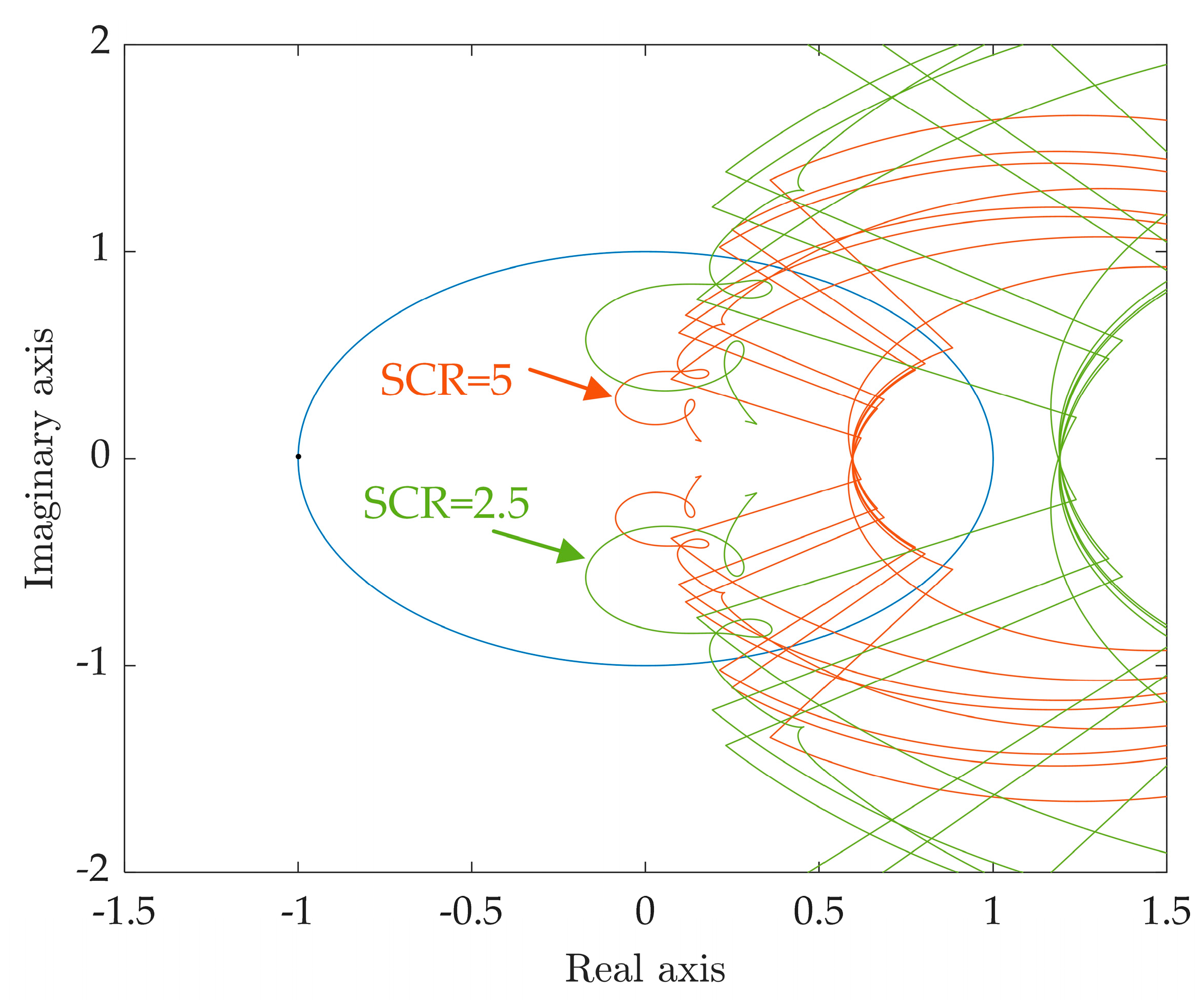
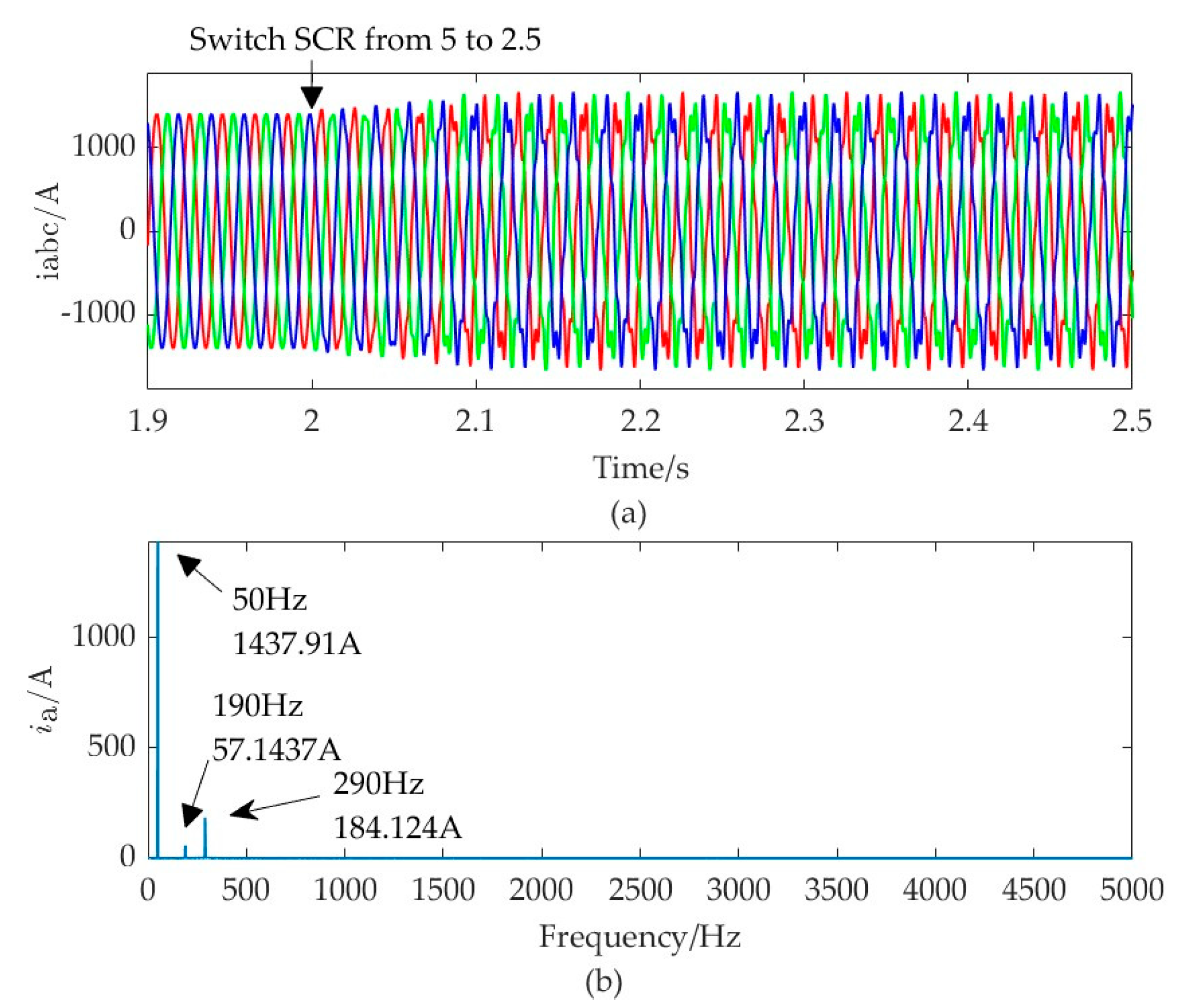
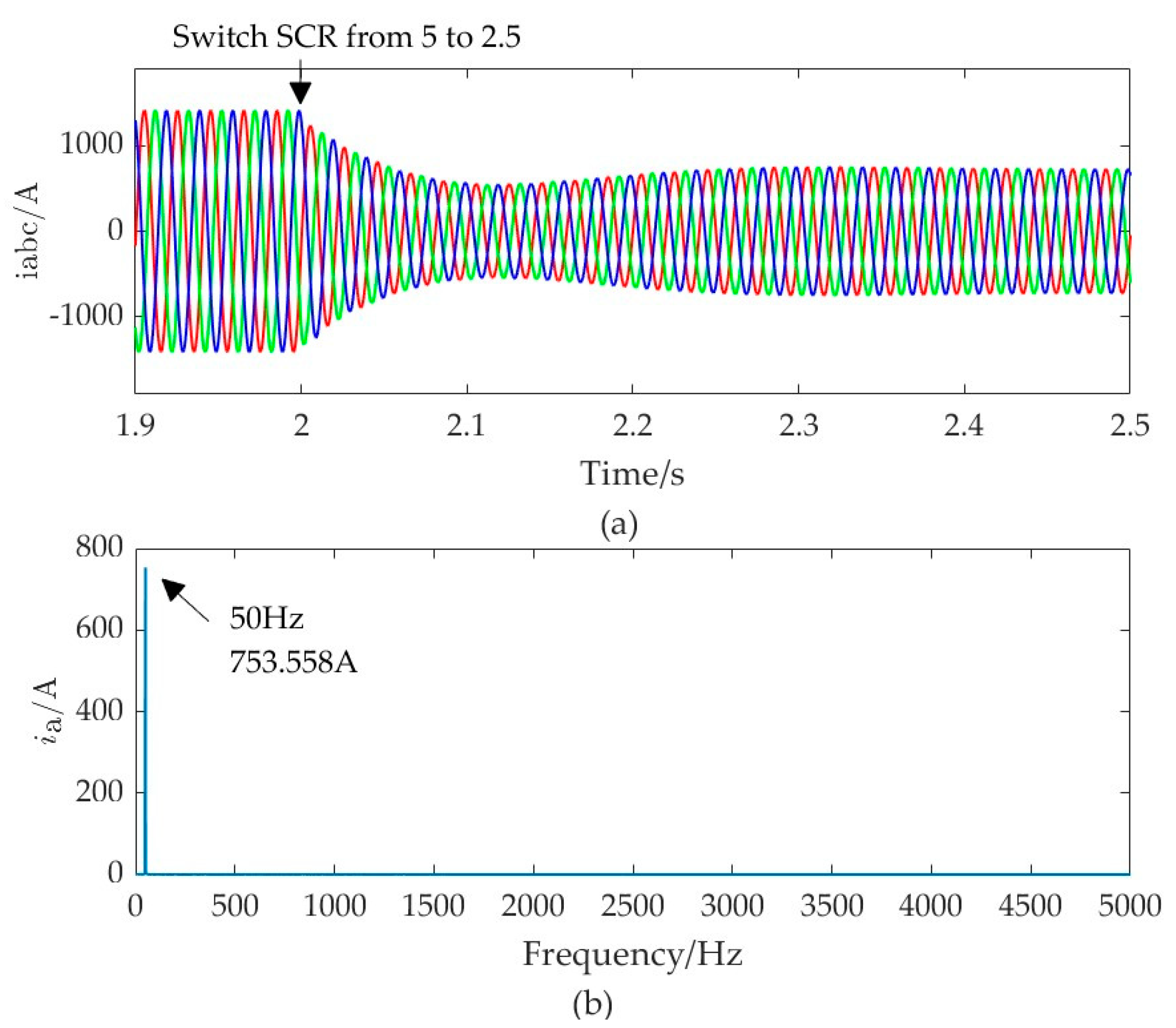
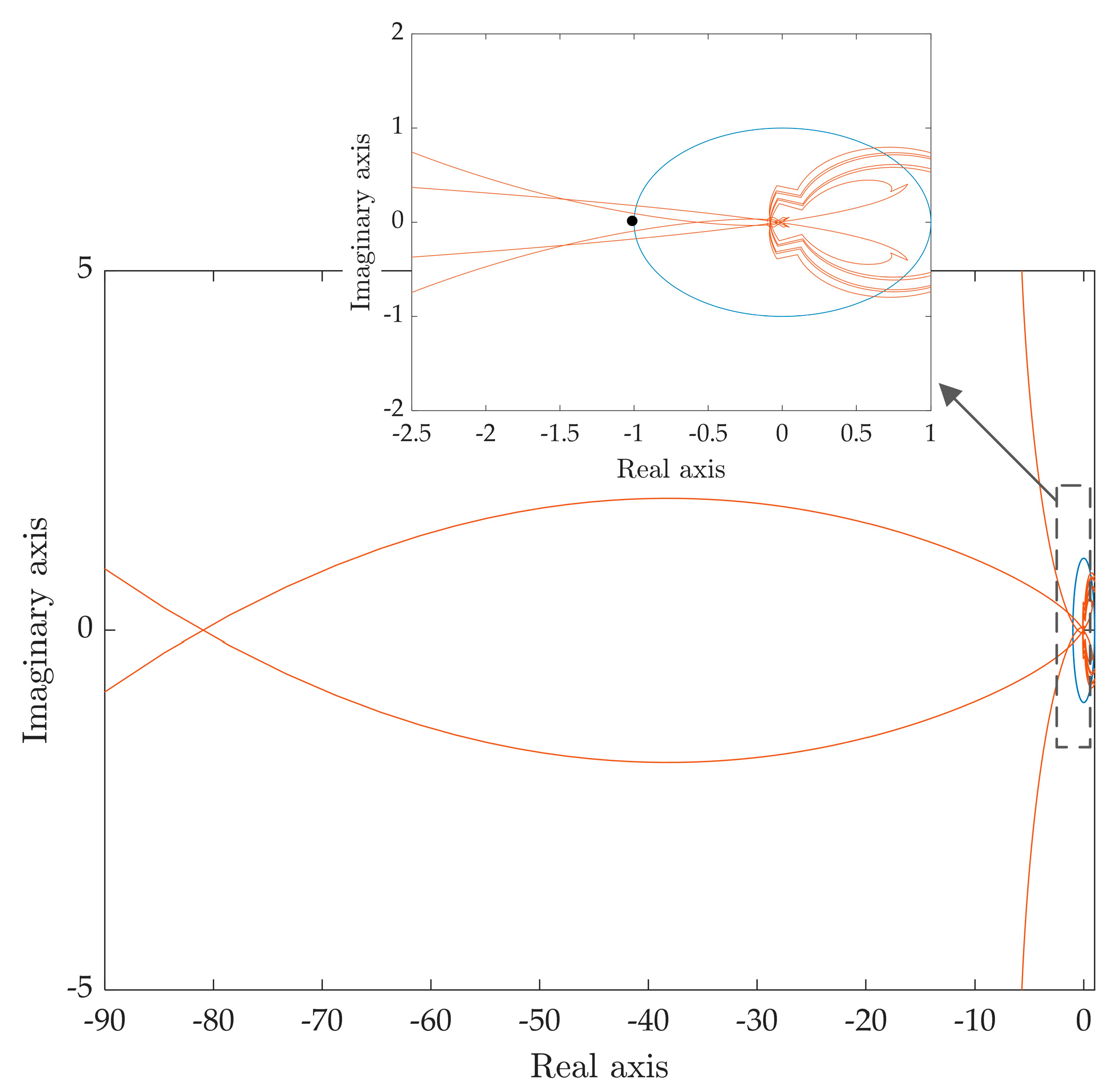
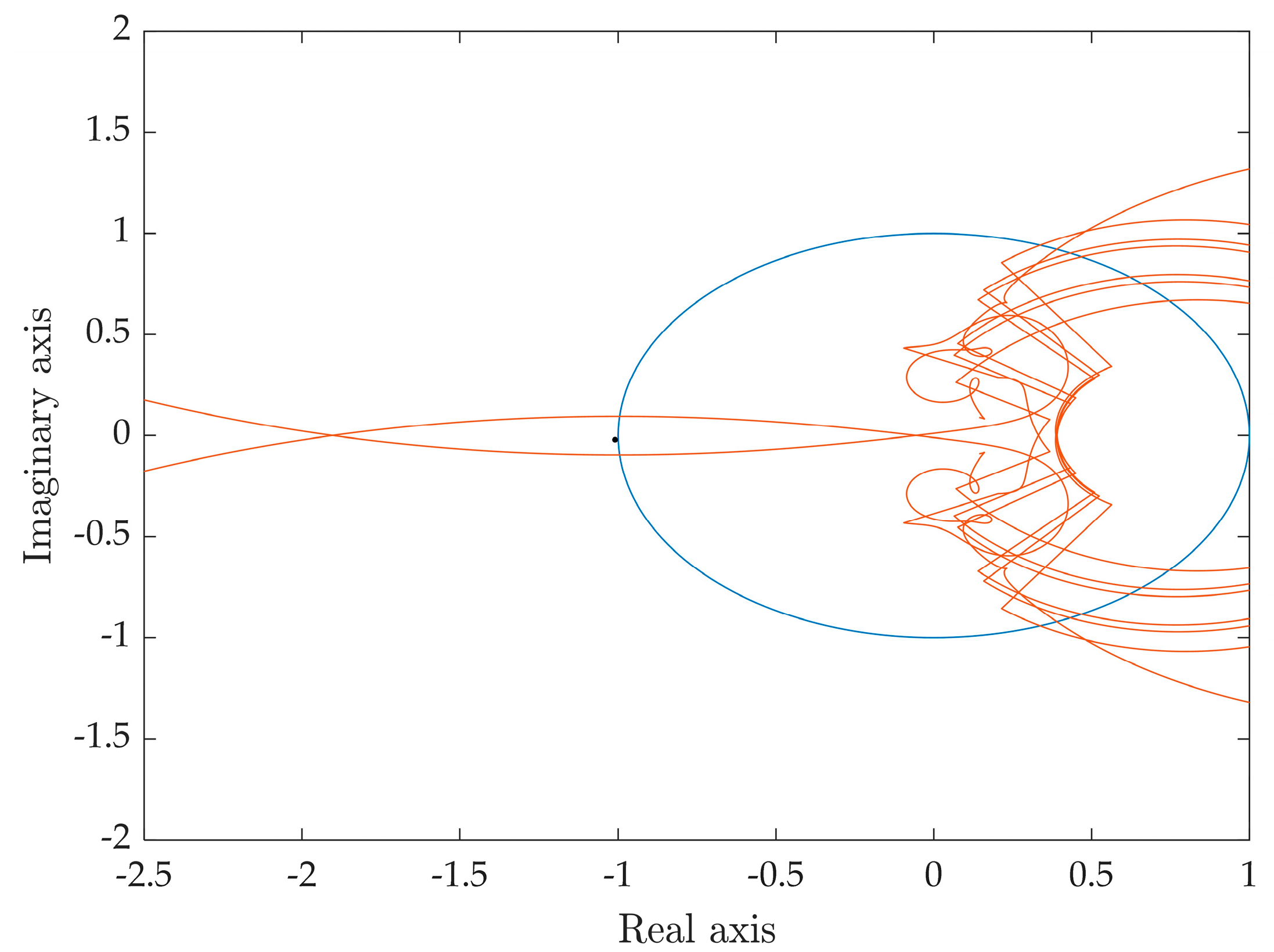
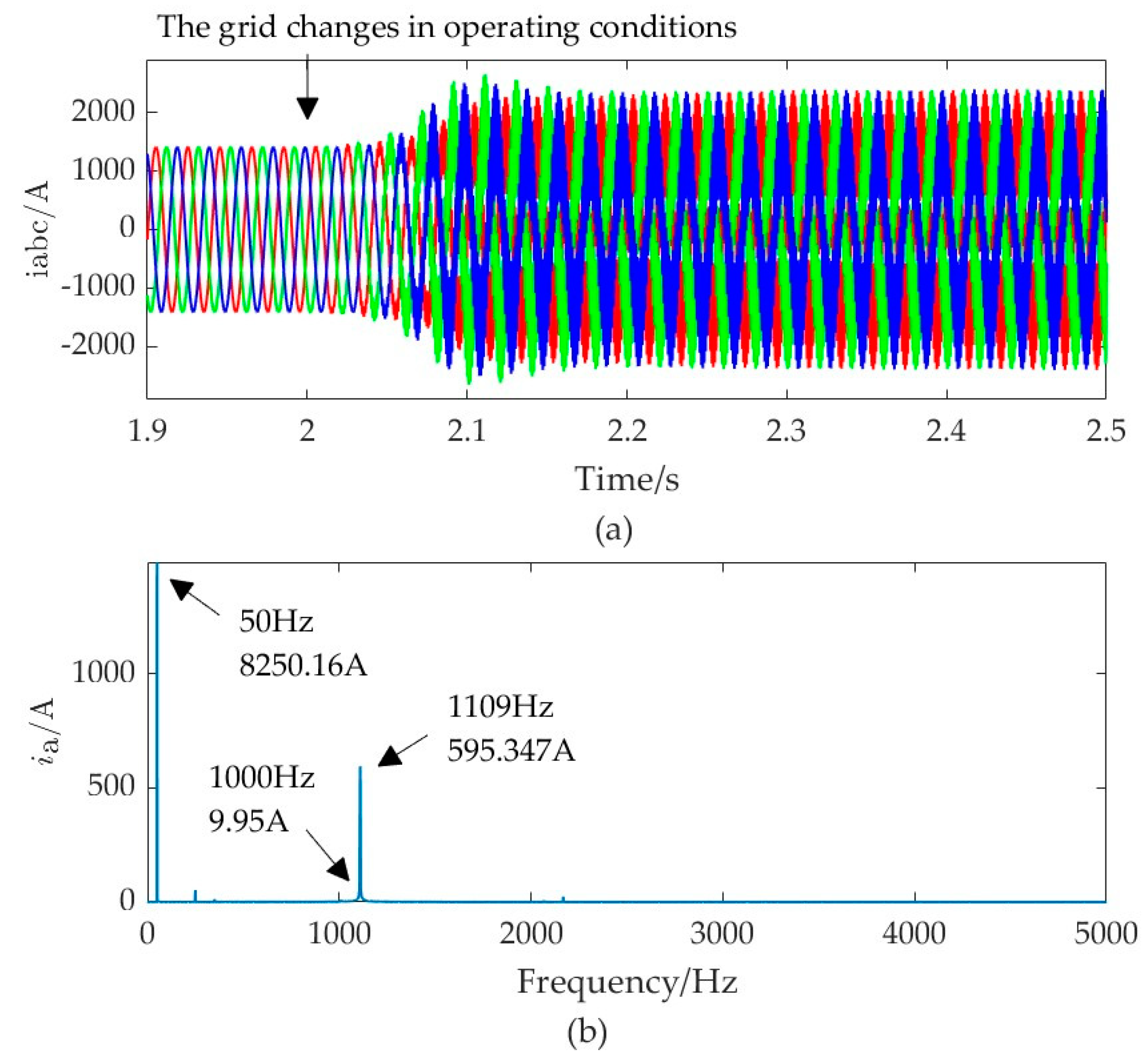
4.1. Oscillation Risk Caused by Grid Strength Variations
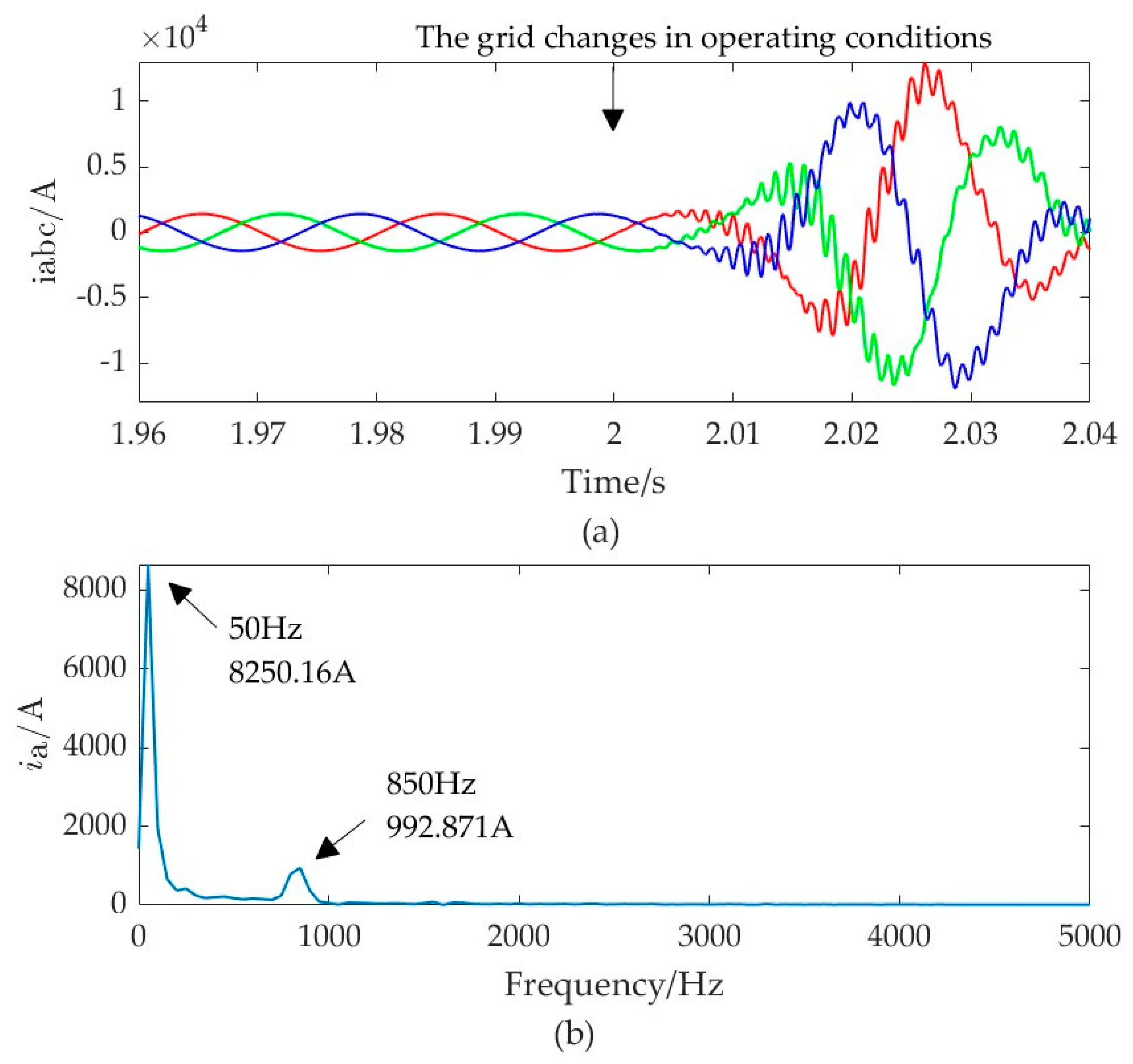
4.2. Oscillation Risk Caused by the Resonance Peak of Grid Impedance in a High-Frequency Range
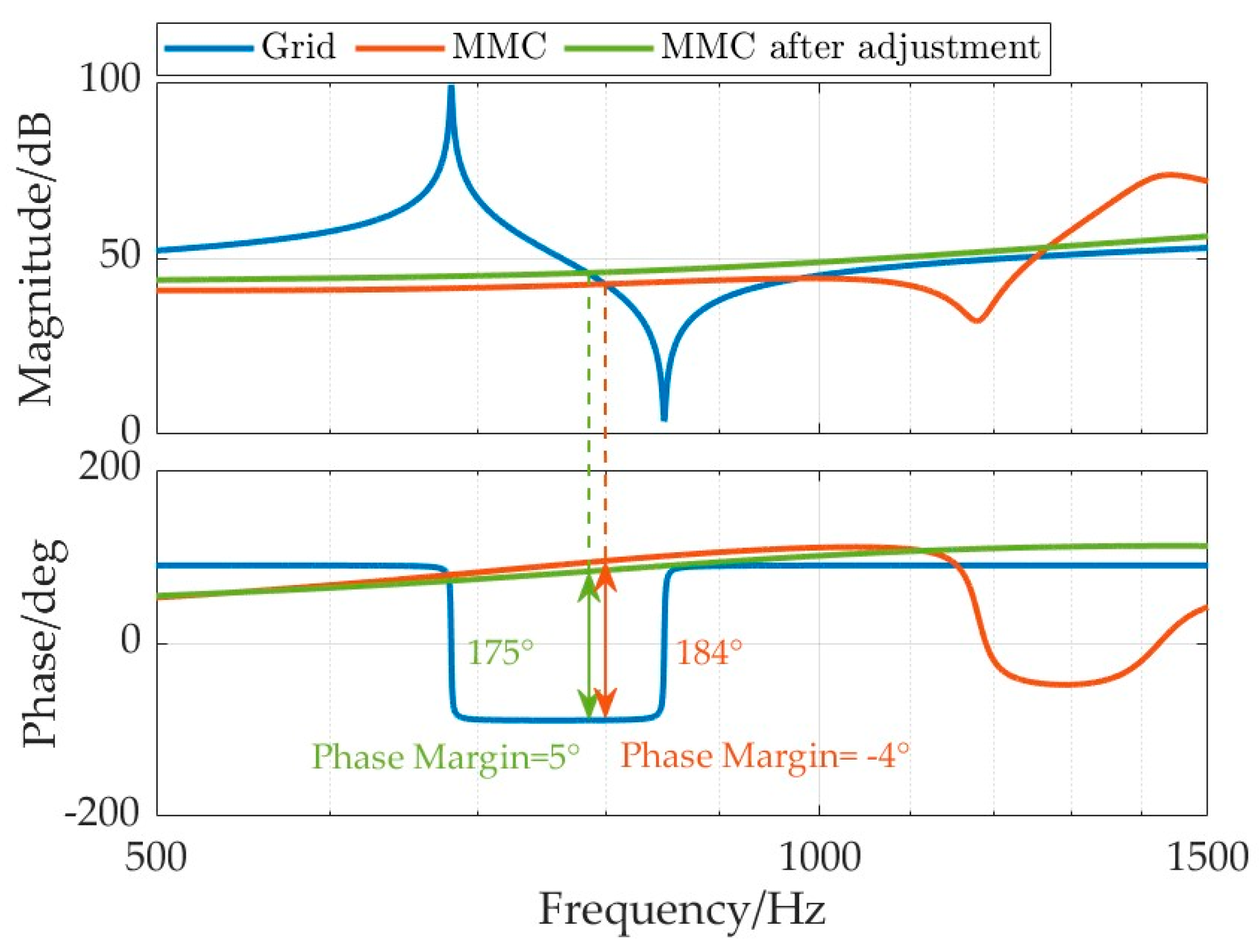
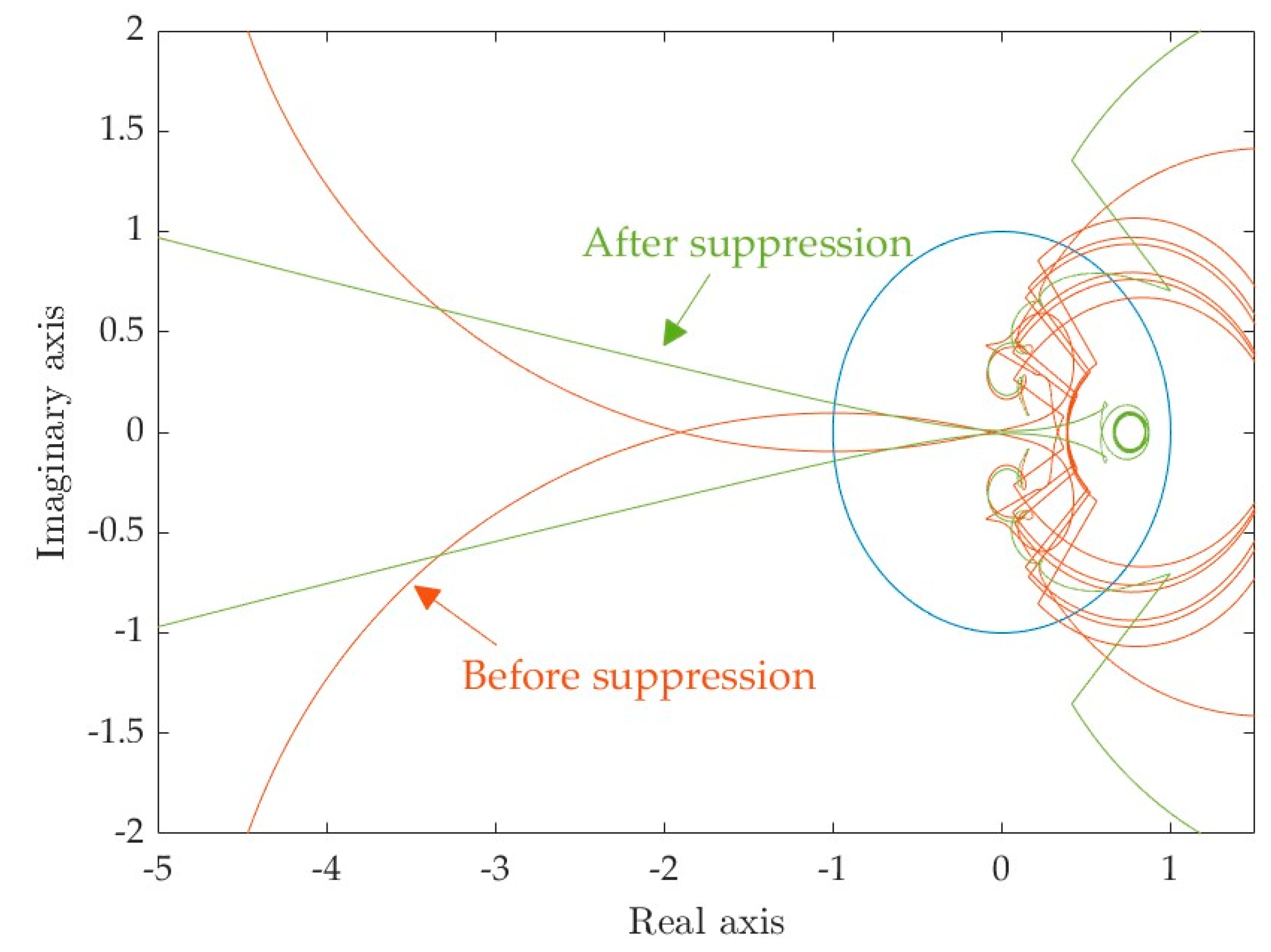
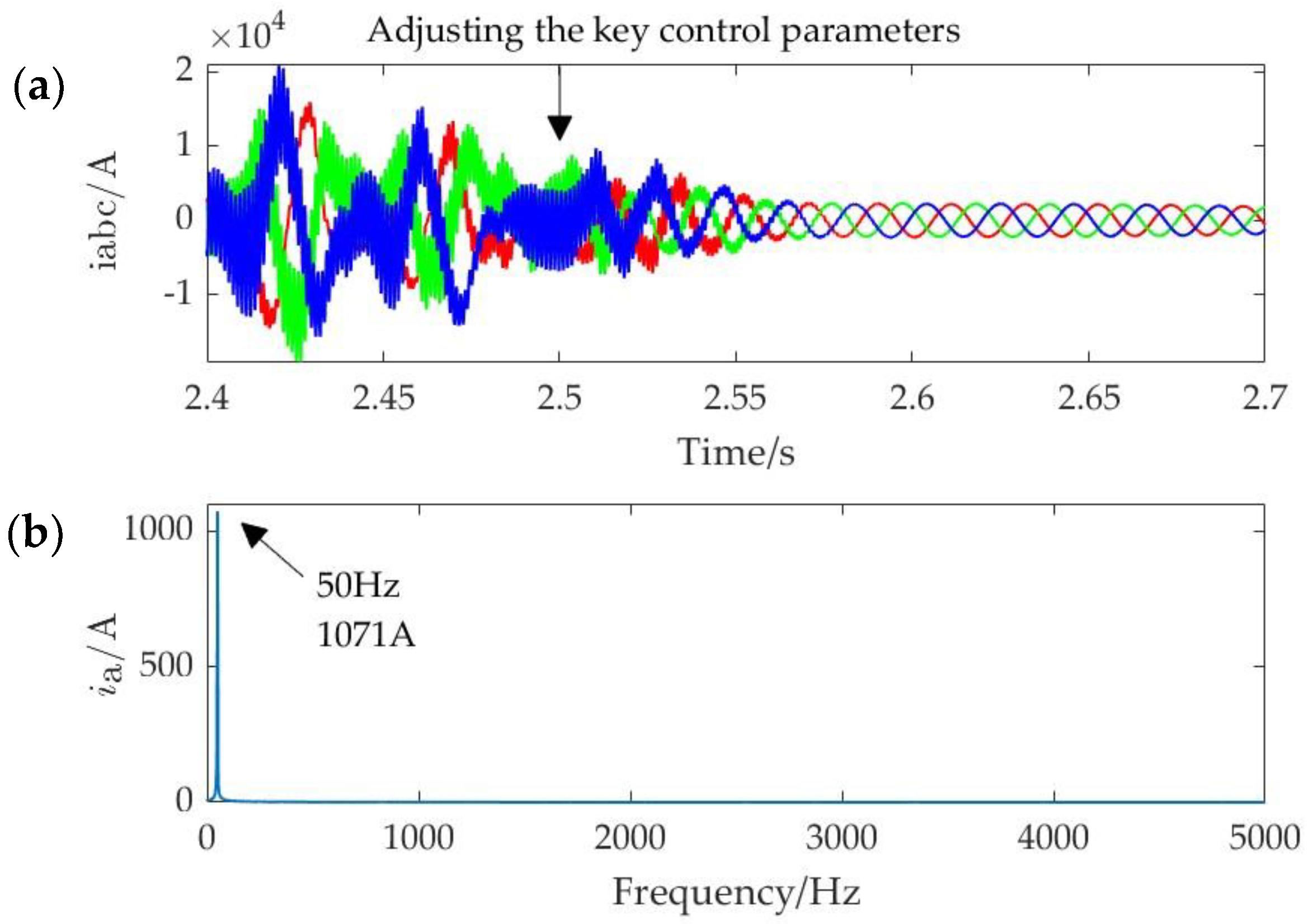
4.3. Wideband Oscillation Suppression Based on Key Control Parameter Adjustment
5. Conclusions
- Compared to grid-following control, grid-forming control can confine the negative damping frequency band of MMC impedance characteristics from the wideband to the high-frequency band;
- Under grid-following control, the influencing factors in each frequency band are relatively independent, with fewer factors affecting individual frequency bands, resulting in lower flexibility in parameter optimization. Under grid-forming control, oscillation risks only exist in relatively high-frequency bands, where there are more influencing factors. Therefore, there is higher flexibility in parameter optimization;
- When the grid strength weakens, grid-following MMC faces instability risks, while grid-forming MMC can maintain stability. In instances where high-frequency resonance peaks exist in the impedance of the grid, both control modes of MMC may face instability risks;
- Adjusting the key control parameters of MMC can effectively suppress wideband oscillations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Symbols | Explanation |
|---|---|
| uv | AC terminal voltage of MMC |
| us | Grid voltage |
| i | AC-side current |
| uCu uCl | Upper and lower pole voltages |
| mu ml | Modulation signals of upper and lower bridge arms |
| Equivalent voltages of the upper and lower bridge arms | |
| idiff | Differential-mode current |
| idc udc | DC-side current and voltage |
| Rarm Larm | Equivalent resistance and inductance of the bridge arms |
| Rg Lg | Equivalent resistance and inductance of the grid |
| Carm | Equivalent capacitance of the bridge arm |
| Tj | Inertia time constant |
| D | Damping coefficient |
| ω | Virtual angular velocity |
| θ | Virtual phase angle |
| Δx, Δu, Δy | State vector, input vector, and output vector |
| AHx, AHz, BH | Coefficient matrices |
| Ubase Ibase | Base values for voltage and current |
| PH | Matrix representing the dynamic of coordinate transformation |
| GHpll | Matrix representing the dynamic of PLL |
| Matrix representing the dynamic of virtual phase angle | |
| Matrix representing the dynamic of output voltage and current | |
| h | Highest harmonic order |
| Modulation signals matrix for the upper and lower bridge arms | |
| Modulation signals matrix outputted by the main control and CCSC | |
| Harmonic transfer matrix | |
| Ypn11 | MMCs sequence admittance matrix |
Appendix B
Appendix C
Appendix D
| Grid | MMC | ||
|---|---|---|---|
| Quantity | Value | Quantity | Value |
| Rated frequency of the system f1 (Hz) | 50 | Rated capacity of MMC Sbase (MVA) | 1500 |
| Rated voltage of the system us (kV) | 437 | Transmission power of MMC Pref (MW) | 750 |
| Equivalent resistance of the system Rg (Ω) | 0 | Rated DC voltage of MMC udc (kV) | 840 |
| Equivalent inductance of the system Lg (mH) | 81 | Number of parallel submodule units in the bridge arm N | 500 |
| Capacitance of each submodule CSM (μF) | 11,000 | ||
| Resistance of single bridge arm Rarm (Ω) | 0.1 | ||
| Inductance of single bridge arm Larm (mH) | 140 | ||
| Quantity | Grid-Following | Grid-Forming |
|---|---|---|
| Inductance of the branch Lg2 (mH) | 156.4 | 156.4 |
| Capacitance of the branch Cg2 (μF) | 0.1125 | 0.2 |
| Resistance of the branch Rg2 (Ω) | 1.5 | 1.5 |
| Resonance frequency fg2 (Hz) | 1200 | 900 |
| Grid-Following | Grid-Forming | ||
|---|---|---|---|
| Quantity | Value | Quantity | Value |
| Proportional coefficient for the power loop kpp | 0.2 | Proportional coefficient for the virtual excitation kpE | 0.2 |
| Integral coefficient for the power loop kip | 50 | Integral coefficient for the virtual excitation kiE | 0.8 |
| Proportional coefficient for the current loop kpi | 0.8 | Droop coefficient for reactive power-voltage kQ | 3 |
| Integral coefficient for the current loop kii | 10 | Inertia time constant Tj (s) | 0.036 |
| Proportional coefficient for CCSC kpccsc | 1 | Damping coefficient D | 84.7 |
| Integral coefficient for CCSC kiccsc | 20 | Proportional coefficient for the voltage control kpu | 2 |
| Proportional coefficient for PLL kppll | 43.17 | Integral coefficient for the voltage control kiu | 50 |
| Integral coefficient for PLL kipll | 932.08 | Proportional coefficient for the current control kpi | 0.8 |
| Control delay delay (μs) | 250 | Integral coefficient for the current control kii | 101 |
| Proportional coefficient for CCSC kpccsc | 1 | ||
| Integral coefficient for CCSC kiccsc | 20 | ||
| Control delay delay (μs) | 250 | ||
References
- Xu, J.; Liu, W.; Liu, S. Current state and development trends of power system converter grid-forming control technology. Power Syst. Technol. 2022, 46, 3586–3594. [Google Scholar]
- Zhang, L.; Harnefors, L.; Nee, H.P. Power-synchronization control of grid-connected voltage-source converters. IEEE Trans. Power Syst. 2009, 25, 809–820. [Google Scholar] [CrossRef]
- Ma, X.; Liu, Y.; Tian, J. Key technologies and challenges of grid-forming control for flexible DC transmission system. Autom. Electr. Power Syst. 2023, 47, 1–11. [Google Scholar]
- Cao, Y.; Wang, W.; Li, Y. A virtual synchronous generator control strategy for VSC-MTDC systems. IEEE Trans. Energy Convers. 2017, 33, 750–761. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodriguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar]
- Yu, J.; Wang, S.; Liu, Z. Accurate small-signal terminal characteristic model and SISO stability analysis approach for parallel grid-forming inverters in islanded microgrids. IEEE Trans. Power Electron. 2023, 38, 6597–6612. [Google Scholar] [CrossRef]
- Ramezani, M.; Li, S.; Musavi, F. Seamless transition of synchronous inverters using synchronizing virtual torque and flux linkage. IEEE Trans. Ind. Electron. 2019, 67, 319–328. [Google Scholar] [CrossRef]
- Zhan, C.; Wu, H.; Wang, X. An overview of stability studies of grid-forming voltage source converters. Proc. CSEE 2023, 43, 2339–2358. [Google Scholar]
- Zhang, H.; Xiang, W.; Lin, W. Grid forming converters in renewable energy sources dominated power grid: Control strategy, stability, application, and challenges. J. Mod. Power Syst. Clean Energy 2021, 9, 1239–1256. [Google Scholar] [CrossRef]
- Rosso, R.; Cassoli, J.; Buticchi, G. Robust stability analysis of LCL filter based synchronverter under different grid conditions. IEEE Trans. Power Electron. 2018, 34, 5842–5853. [Google Scholar] [CrossRef]
- Chen, J.; Ren, Y.; Meng, Q. Sub-synchronous oscillation suppression strategy for grid-forming direct-drive permanent magnet synchronous generator with UDE supplementary damping branch. Trans. China Electrotech. Soc. 2023, 36, 1–16. [Google Scholar]
- Wu, J.; Chen, X.; Zhang, D. Grid-connected stability analysis and improvement strategy for grid-forming energy storage system in new energy access scene. Proc. CSEE 2024, 44, 1–14. [Google Scholar]
- Liu, J. Stability Mechanism and Power Oscillation Analysis of Power System with High-Penetration wind Power and Photovoltaic Generation. Ph.D. Thesis, Zhejiang University, Hangzhou, China, 2022. [Google Scholar]
- Liu, P.; Xie, X.; Li, Y. Mechanism and characteristics of grid-forming control for improving sub/super synchronous oscillation stability of grid-following-based grid-connected converter. Power Syst. Technol. 2024, 48, 1–9. [Google Scholar]
- Hu, Y.; Tian, Z.; Zha, X. Impedance stability analysis and promotion strategy of islanded microgrid dominated by grid-connected and grid-following converters. Autom. Electr. Power Syst. 2022, 46, 121–131. [Google Scholar]
- Liu, Z.; Luo, J.; Liang, N. Analysis of influence of virtual synchronous control on sub-synchronous oscillation damping for grid-connected wind power system. Autom. Electr. Power Syst. 2023, 47, 135–147. [Google Scholar]
- Wu, G. Passivity-Based High-Frequency Oscillation Mitigation Strategies for Three-Phase Grid-Forming Inverters. Master’s Thesis, Huazhong Institute of Scinence and Technology, Wuhan, China, 2022. [Google Scholar]
- Zong, H.; Zhang, C.; Bao, Y. Frequency-domain modeling and synchronization perspective interaction mechanism of GFL-GFM converter system. J. Shanghai Jiaotong Univ. 2023, 37, 1–22. [Google Scholar]
- Wu, W.; Chen, Y.; Zhou, L. Sequence impedance modeling and stability analysis for virtual synchronous generator connected to the weak grid. Proc. CSEE 2019, 39, 1560–1571. [Google Scholar]
- Wu, W.; Zhou, L.; Chen, Y. Sequence-impedance-based stability comparison between vsgs and traditional grid-connected inverters. IEEE Trans. Power Electron. 2019, 34, 46–52. [Google Scholar] [CrossRef]
- Huang, Y.; Ma, X.; Zhang, J. Study on the optimization of damping control strategy for grid-forming VSC-HVDC. Power Syst. Technol. 2023, 47, 21–29. [Google Scholar]
- Zou, C.; Rao, H.; Xu, S. Analysis of resonance between a VSC-HVDC converter and the AC grid. IEEE Trans. Power Electron. 2018, 33, 10157–10168. [Google Scholar] [CrossRef]
- Zhu, S. MMC Models Considering Harmonic Interaction and Their Application to Small-Signal Stability Analysis. Ph.D. Thesis, Wuhan University, Wuhan, China, 2021. [Google Scholar]
- Yang, S.; Liu, K.; Qin, L. A broadband active damping method for high-frequency resonance suppression in mmc-hvdc system. Int. J. Electr. Power Energy Syst. 2023, 146, 108791. [Google Scholar] [CrossRef]
- Pan, R.; Liu, D.; Liu, S. Stability comparison between grid-forming and grid-following based wind farms integrated mmc-hvdc. J. Mod. Power Syst. Clean Energy 2023, 11, 1341–1355. [Google Scholar] [CrossRef]
- Zhu, S.; Qin, L.; Liu, K. Impedance modeling of modular multilevel converter in d-q and modified sequence domains. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 4361–4382. [Google Scholar] [CrossRef]
- Zhu, S.; Liu, K.; Liao, X. Dq frame impedance modeling of modular multilevel converter and its application in high-frequency resonance analysis. IEEE Trans. Power Deliv. 2020, 36, 1517–1530. [Google Scholar] [CrossRef]
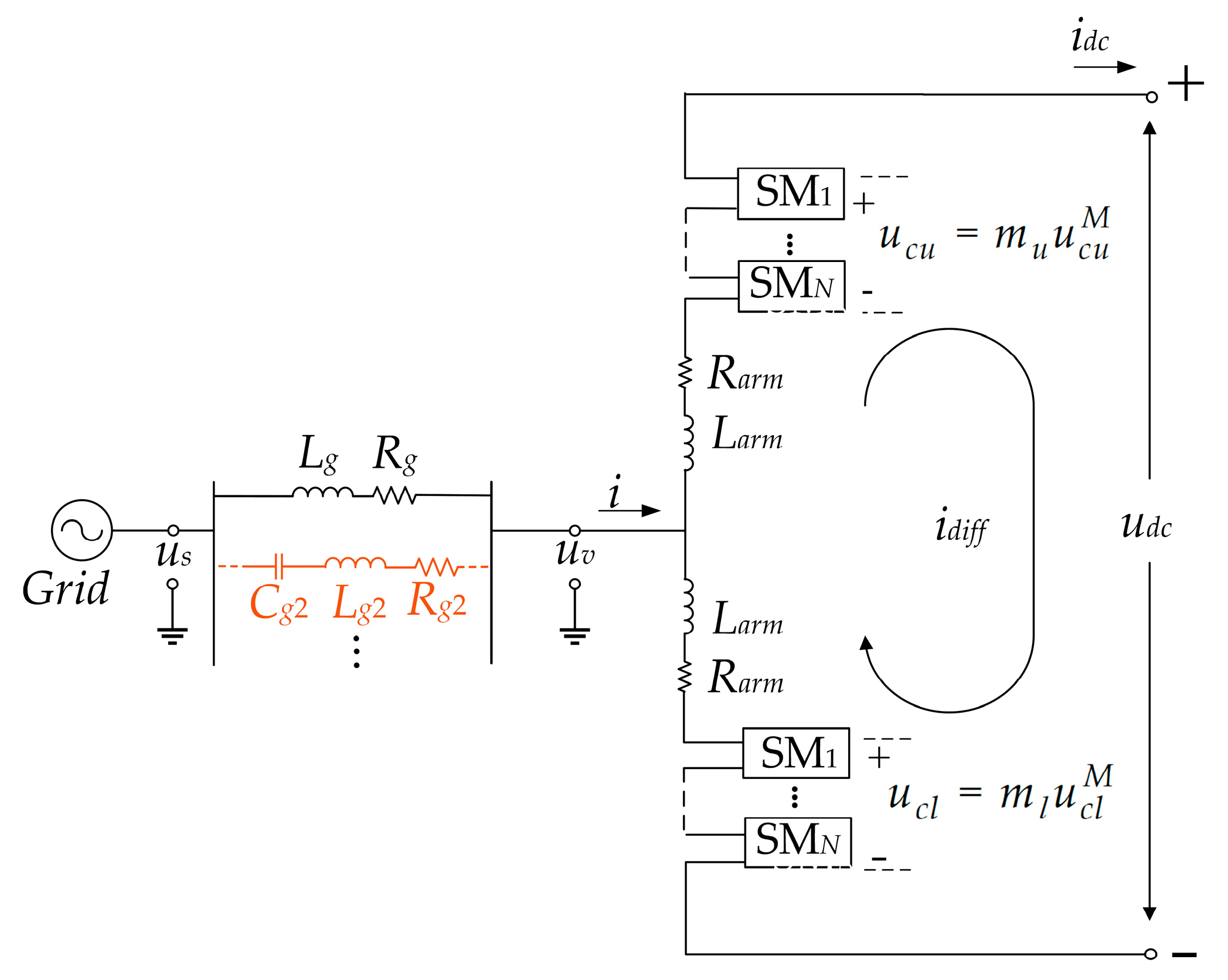
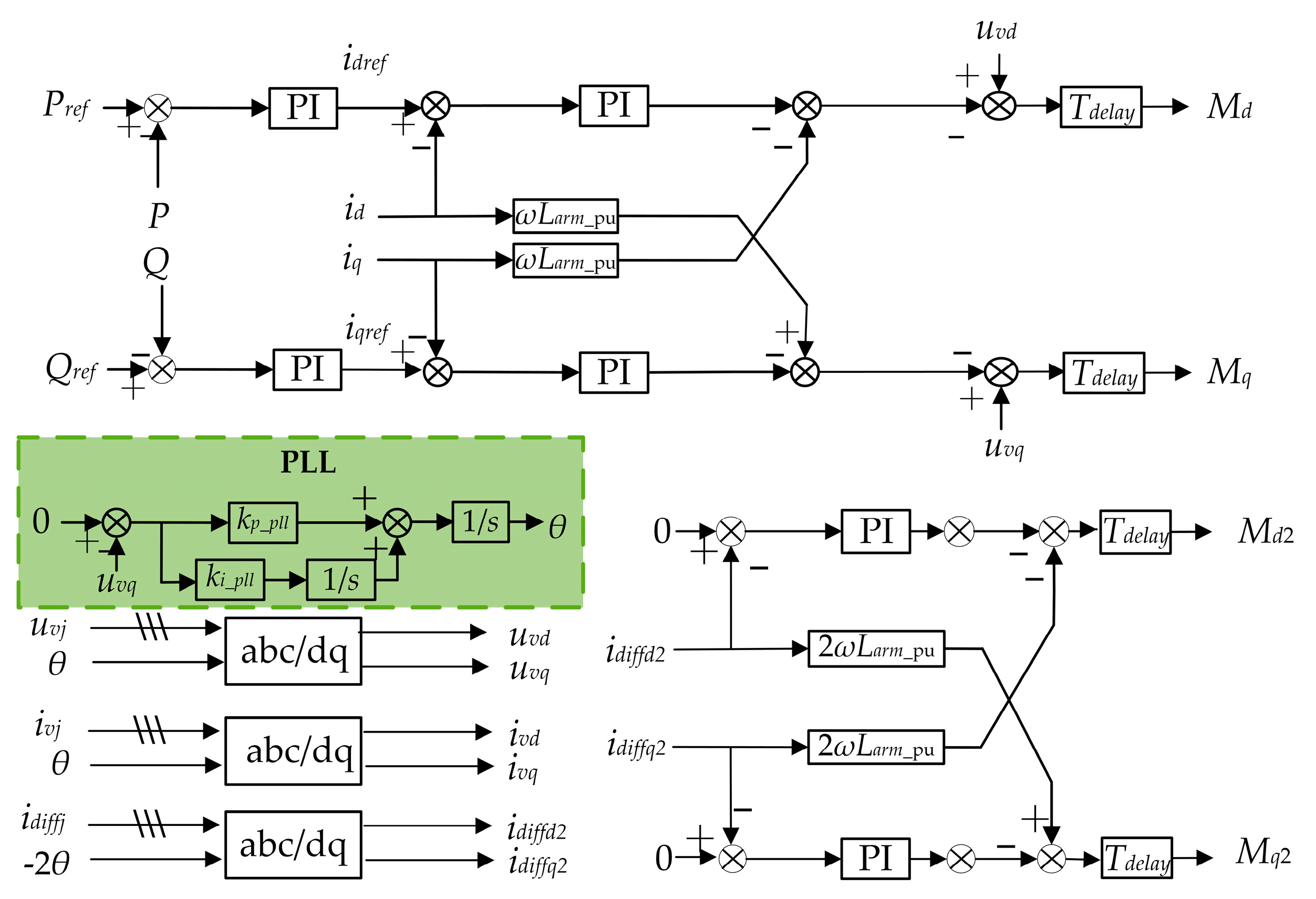
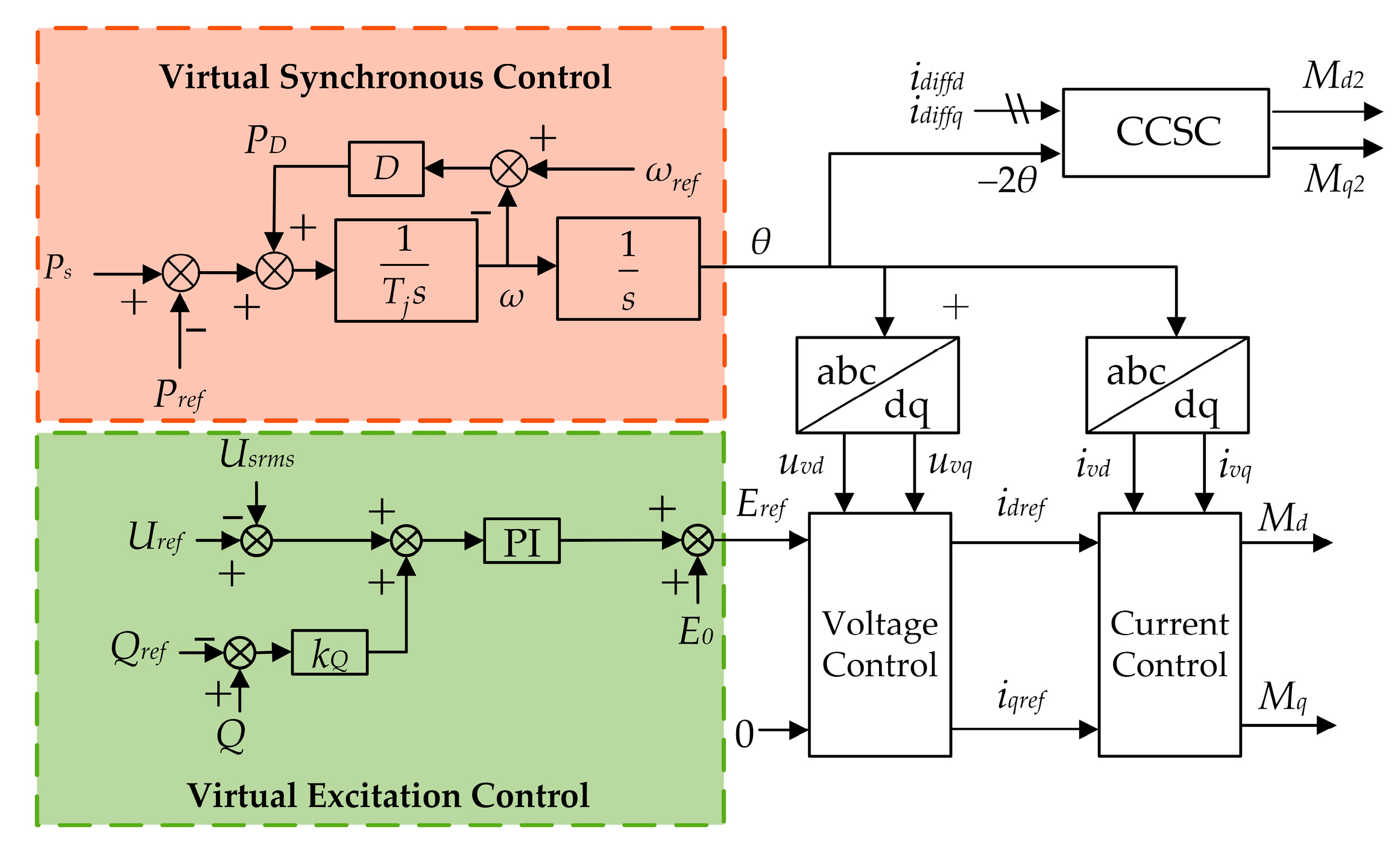

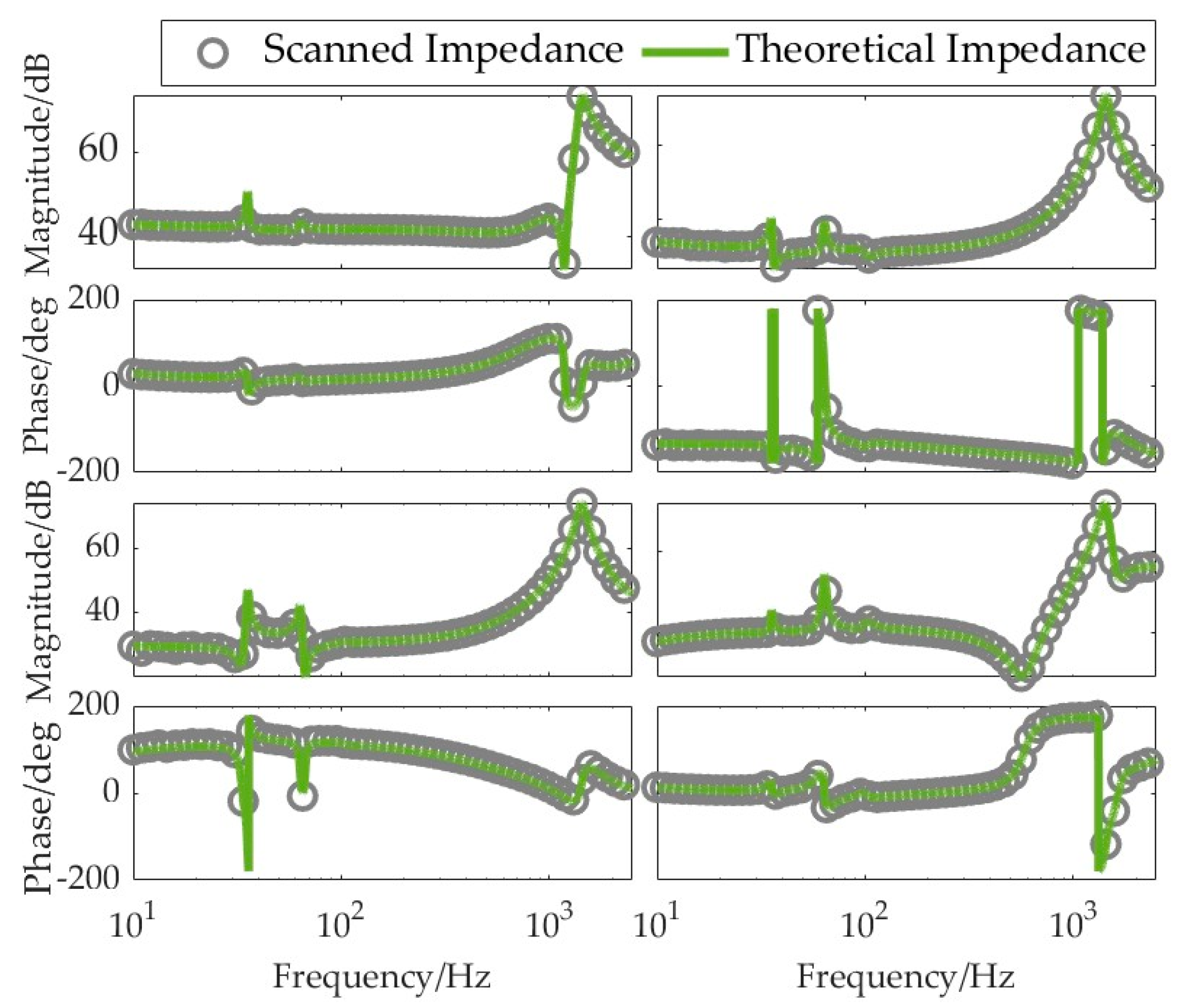

| Research | References | Limitation |
|---|---|---|
| Impedance modeling of grid-forming MMC | [10,11,12,19,20,21,22,23,24,25] | Studies about grid-forming control mostly focus on low-voltage converters. Research on grid-forming MMC are relatively limited. |
| Influencing factors of grid-forming converter impedance characteristics | [13,14,15,16,17,18] | Specific key control parameters affecting impedance characteristics are not clear. |
| Frequency Range | Grid-Following MMC | Frequency Range | Grid-Forming MMC |
|---|---|---|---|
| Below 30 Hz | kpp, kppll | Below 700 Hz | kpu, kpi, kpE, delay |
| 30–100 Hz | kpp, kip, kppll, kpi, kii | ||
| 100–2500 Hz | kpi, delay | 700–2500 Hz | kpu, kpi, delay |
| Proportional Coefficient of the Voltage Control kpu | Proportional Coefficient of the Current Control kpi | |
|---|---|---|
| Initial parameters | 2.000 | 0.800 |
| Adjusted parameters | 1.960 | 0.384 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Xie, J.; Zeng, C.; Yang, S.; Sun, H.; Qin, L. Comparison Study of the Wideband Oscillation Risk of MMC between Grid-Following and Grid-Forming Control. Energies 2024, 17, 2507. https://doi.org/10.3390/en17112507
Cheng Y, Xie J, Zeng C, Yang S, Sun H, Qin L. Comparison Study of the Wideband Oscillation Risk of MMC between Grid-Following and Grid-Forming Control. Energies. 2024; 17(11):2507. https://doi.org/10.3390/en17112507
Chicago/Turabian StyleCheng, Yanjun, Jun Xie, Chuihui Zeng, Shiqi Yang, Haichang Sun, and Liang Qin. 2024. "Comparison Study of the Wideband Oscillation Risk of MMC between Grid-Following and Grid-Forming Control" Energies 17, no. 11: 2507. https://doi.org/10.3390/en17112507
APA StyleCheng, Y., Xie, J., Zeng, C., Yang, S., Sun, H., & Qin, L. (2024). Comparison Study of the Wideband Oscillation Risk of MMC between Grid-Following and Grid-Forming Control. Energies, 17(11), 2507. https://doi.org/10.3390/en17112507








